High-Accuracy Lower-Limb Intent Recognition: A KPCA-ISSA-SVM Approach with sEMG-IMU Sensor Fusion
Abstract
1. Introduction
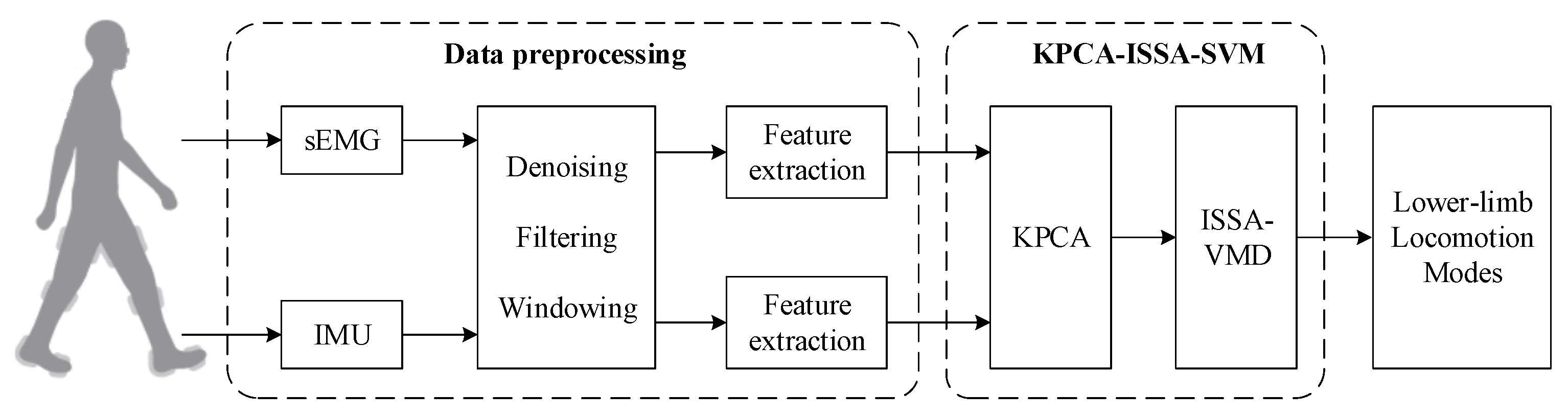
2. Method Overview
3. Data Preprocessing
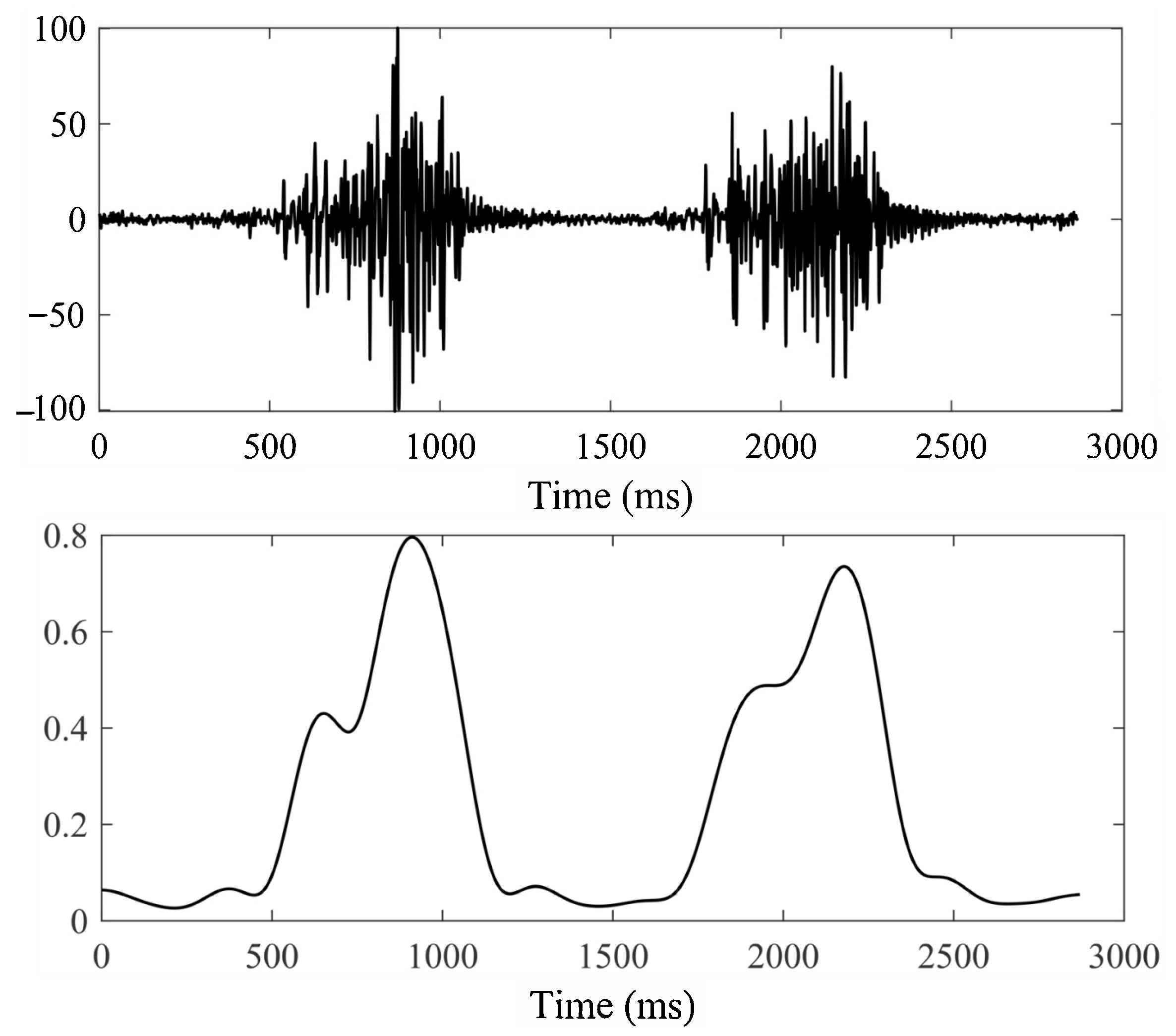
3.1. sEMG Feature Extraction
3.2. Kinematic Feature Extraction
4. KPCA-ISSA-SVM
4.1. Kernel Principal Component Analysis
4.2. Support Vector Machine
4.3. Improved Sparrow Search Algorithm
4.3.1. Population Initialization Based on Chaotic Opposition-Based Learning Strategy
4.3.2. Explorers’ Position-Updating Strategy
4.3.3. Followers’ Position-Updating Strategy
4.3.4. Scouts’ Position-Updating Strategy
5. Experimentation
5.1. Experimental Protocol
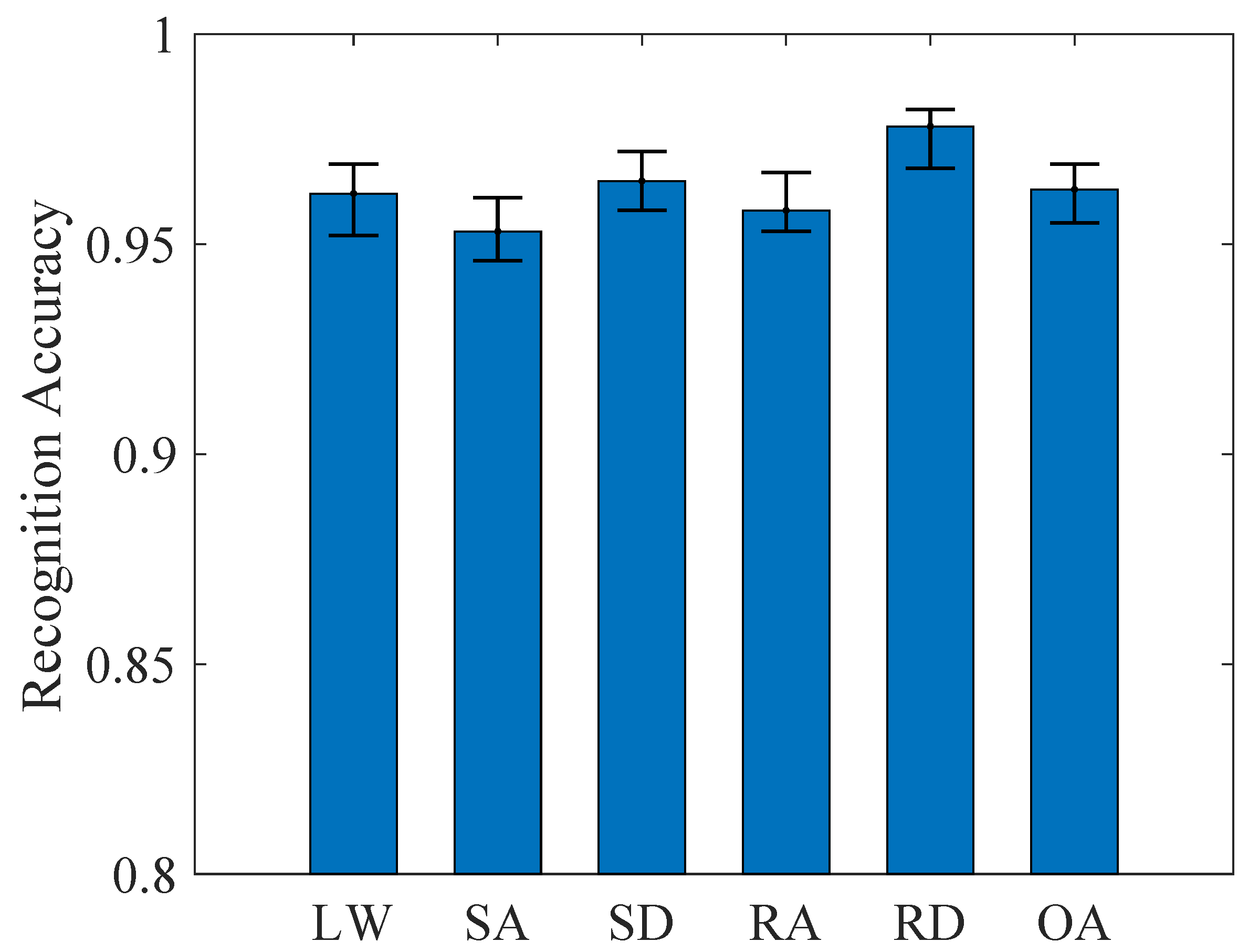
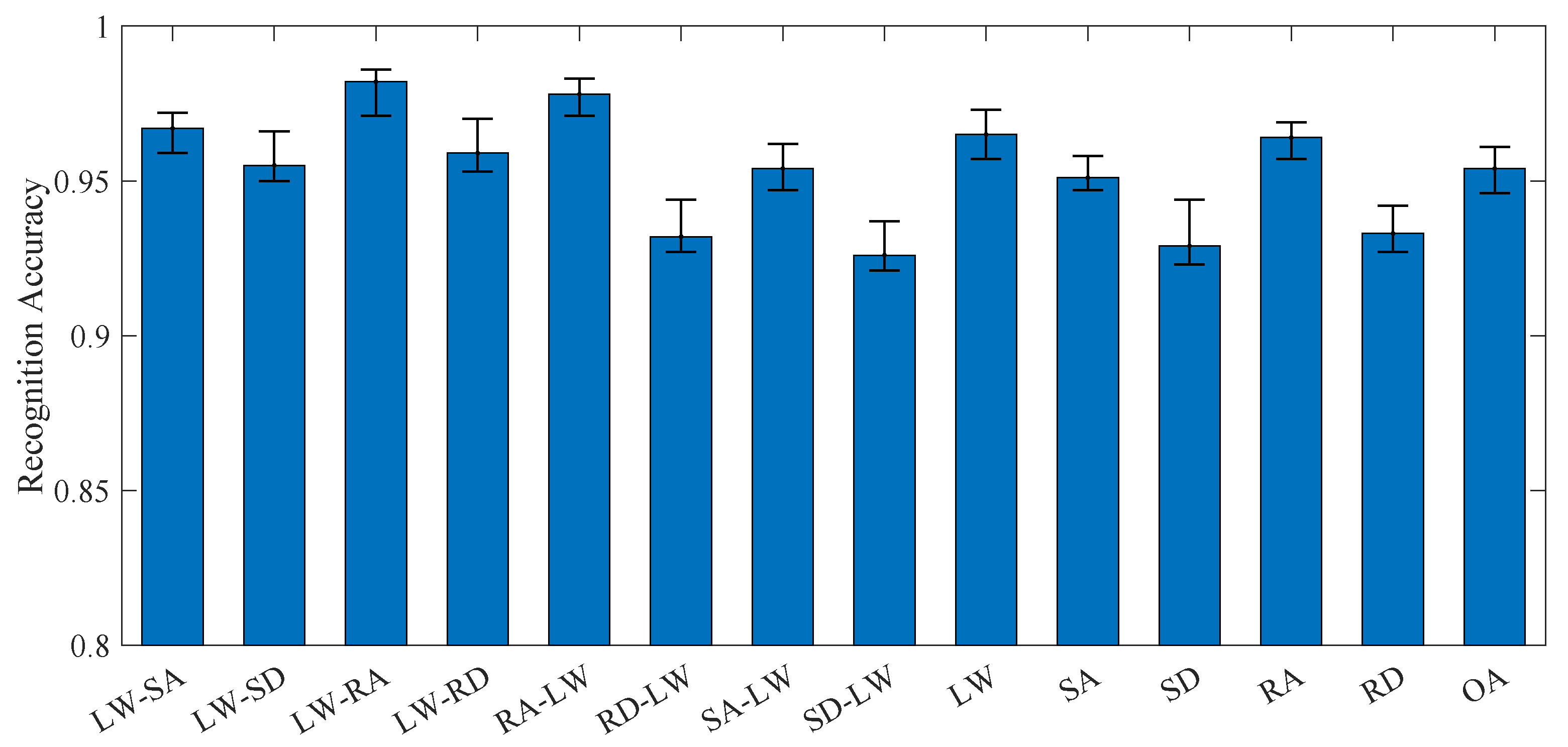
5.2. Offline Experimental Results
5.3. Online Experimental Results
5.4. Comparative Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, L.-L.; Cao, G.-Z.; Liang, H.-J.; Zhang, Y.-P.; Cui, F. Human lower limb motion intention recognition for exoskeletons: A review. IEEE Sens. J. 2023, 23, 30007–30036. [Google Scholar] [CrossRef]
- Shi, M.; Yang, C.; Zhang, D. A novel human-machine collaboration model of an ankle joint rehabilitation robot driven by eeg signals. Math. Probl. Eng. 2021, 2021, 5564235. [Google Scholar] [CrossRef]
- Luptáková, I.D.; Kubovčík, M.; Pospíchal, J. Wearable sensor-based human activity recognition with transformer model. Sensors 2022, 22, 1911. [Google Scholar] [CrossRef]
- Semwal, V.B.; Gupta, A.; Lalwani, P. An optimized hybrid deep learning model using ensemble learning approach for human walking activities recognition. J. Supercomput. 2021, 77, 12256–12279. [Google Scholar] [CrossRef]
- Ding, Z.; Yang, C.; Wang, Z.; Yin, X.; Jiang, F. Online adaptive prediction of human motion intention based on semg. Sensors 2021, 21, 2882. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-Y.; Zhao, X.-G.; Zhang, B.; Ding, Q.-C.; Zhang, D.-H.; Han, J.-D. Review of semg-based motion intent recognition methods in non-ideal conditions. Acta Autom. Sin. 2021, 47, 955–969. [Google Scholar]
- Zhang, L.; Liu, G.; Han, B.; Wang, Z.; Zhang, T. sEMG based human motion intention recognition. J. Robot. 2019, 2019, 3679174. [Google Scholar] [CrossRef]
- Semwal, V.B.; Gaud, N.; Lalwani, P.; Bijalwan, V.; Alok, A.K. Pattern identification of different human joints for different human walking styles using inertial measurement unit (imu) sensor. Artif. Intell. 2022, 55, 1149–1169. [Google Scholar] [CrossRef]
- Gu, C.; Lin, W.; He, X.; Zhang, L.; Zhang, M. Imu-based motion capture system for rehabilitation applications: A systematic review. Biomim. Intell. Robot. 2023, 3, 100097. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Huang, Y.; Wang, D.; Miao, Y. Human motion pattern recognition and feature extraction: An approach using multi-information fusion. Micromachines 2022, 13, 1205. [Google Scholar] [CrossRef] [PubMed]
- Bian, Q.; Castellani, M.; Shepherd, D.; Duan, J.; Ding, Z. Gait intention prediction using a lower-limb musculoskeletal model and long short-term memory neural networks. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 822–830. [Google Scholar] [CrossRef]
- Gao, X.; Yan, L.; Wang, G.; Gerada, C. Hybrid recurrent neural network architecture-based intention recognition for human–robot collaboration. IEEE Trans. Cybern. 2021, 53, 1578–1586. [Google Scholar] [CrossRef]
- Shahini, N.; Bahrami, Z.; Sheykhivand, S.; Marandi, S.; Danishvar, M.; Danishvar, S.; Roosta, Y. Automatically identified eeg signals of movement intention based on cnn network (end-to-end). Electronics 2022, 11, 3297. [Google Scholar] [CrossRef]
- Yu, Z.; Lee, M. Human motion based intent recognition using a deep dynamic neural model. Robot. Auton. Syst. 2015, 71, 134–149. [Google Scholar] [CrossRef]
- Zhu, M.; Guan, X.; Li, Z.; He, L.; Wang, Z.; Cai, K. semg-based lower limb motion prediction using cnn-lstm with improved pca optimization algorithm. J. Bionic Eng. 2023, 20, 612–627. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, H.; Zou, Y. An electromyography signals-based human-robot collaboration system for human motion intention recognition and realization. Robot. Comput.-Integr. Manuf. 2022, 77, 102359. [Google Scholar] [CrossRef]
- Yin, K.; Chen, J.; Xiang, K.; Pang, M.; Tang, B.; Li, J.; Yang, L. Artificial human balance control by calf muscle activation modelling. IEEE Access 2020, 8, 86732–86744. [Google Scholar] [CrossRef]
- Embry, K.R.; Villarreal, D.J.; Macaluso, R.L.; Gregg, R.D. Modeling the kinematics of human locomotion over continuously varying speeds and inclines. IEEE Trans. Neural Syst. Rehabil. 2018, 26, 2342–2350. [Google Scholar] [CrossRef]
- Yin, K.; Li, Y.; Li, X.; Zhao, H. Human motion intention recognition via semg and joint kinematics fusion using mpso-svm for intelligent transportation systems. CHAIN 2025, 2, 198–209. [Google Scholar] [CrossRef]
- Wang, E.; Chen, X.; Li, Y.; Fu, Z.; Huang, J. Lower limb motion intent recognition based on sensor fusion and fuzzy multitask learning. IEEE Trans. Fuzzy Syst. 2024, 32, 2903–2914. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Y.; Ji, S.; Gao, C.; Zhang, S.; Fu, J. A novel gait phase recognition method based on dpf-lstm-cnn using wearable inertial sensors. Sensors 2023, 23, 5905. [Google Scholar] [CrossRef]
- Su, B.-Y.; Wang, J.; Liu, S.-Q.; Sheng, M.; Jiang, J.; Xiang, K. A cnn-based method for intent recognition using inertial measurement units and intelligent lower limb prosthesis. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1032–1042. [Google Scholar] [CrossRef]
- Tao, Y.; Huang, Y.; Zheng, J.; Chen, J.; Zhang, Z.; Guo, Y.; Li, P. Multi-channel semg based human lower limb motion intention recognition method. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 1037–1042. [Google Scholar]
- Tu, P.; Li, J.; Wang, H. Lower limb motion recognition with improved svm based on surface electromyography. Sensors 2024, 24, 3097. [Google Scholar] [CrossRef]
- Yu, X.; He, W.; Li, Y.; Xue, C.; Li, J.; Zou, J.; Yang, C. Bayesian estimation of human impedance and motion intention for human–robot collaboration. IEEE Trans. Cybern. 2019, 51, 1822–1834. [Google Scholar] [CrossRef]
- Su, B.; Wang, J.; Liu, S.; Sheng, M.; Xiang, K. An improved motion intent recognition method for intelligent lower limb prosthesis driven by inertial motion capture data. Acta Autom. Sin. 2020, 46, 1517–1530. [Google Scholar]
- Yin, K.; Xue, Y.; Yu, Y.; Xie, S. Variable impedance control for bipedal robot standing balance based on artificial muscle activation model. J. Robot. 2021, 2021, 8142161. [Google Scholar] [CrossRef]
- Xue, Y.; Yu, Y.; Yin, K.; Du, H.; Li, P.; Dai, K.; Ju, Z. Using adaptive directed acyclic graph for human in-hand motion identification with hybrid surface electromyography and kinect. Symmetry 2022, 14, 2093. [Google Scholar] [CrossRef]
- Pani, A.K. Nonlinear process monitoring using kernel principal component analysis: A review of the basic and modified techniques with industrial applications. Braz. J. Chem. Eng. 2022, 39, 327–344. [Google Scholar] [CrossRef]
- Han, Y.; Song, G.; Liu, F.; Geng, Z.; Ma, B.; Xu, W. Fault monitoring using novel adaptive kernel principal component analysis integrating grey relational analysis. Process Saf. Environ. Prot. 2022, 157, 397–410. [Google Scholar] [CrossRef]
- Guido, R.; Ferrisi, S.; Lofaro, D.; Conforti, D. An overview on the advancements of support vector machine models in healthcare applications: A review. Information 2024, 15, 235. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in sparrow search algorithm: A comprehensive survey. Arch. Comput. Methods Eng. 2023, 30, 427–455. [Google Scholar] [CrossRef] [PubMed]
- Yin, K.; Tang, B.; Li, M.; Zhao, H. A multi-objective optimization approach based on an enhanced particle swarm optimisation algorithm with evolutionary game theory. IEEE Access 2023, 11, 77566–77584. [Google Scholar] [CrossRef]
- Feng, Z.; Huang, J.; Jin, S.; Wang, G.; Chen, Y. Artificial intelligence-based multi-objective optimisation for proton exchange membrane fuel cell: A literature review. J. Power Sources 2022, 520, 230808. [Google Scholar] [CrossRef]
- Ma, J.; Hao, Z.; Sun, W. Enhancing sparrow search algorithm via multi-strategies for continuous optimisation problems. Inf. Process. Manag. 2022, 59, 102854. [Google Scholar] [CrossRef]
- Shimotori, D.; Kato, K.; Yoshimi, T.; Kondo, I. Validation of gait kinematics with ramp and stair ascent and descent revealed by markerless motion capture in simulated living space: Test-retest reliability study. JMIR Rehabil. Assist. Technol. 2025, 12, e66886. [Google Scholar] [CrossRef] [PubMed]
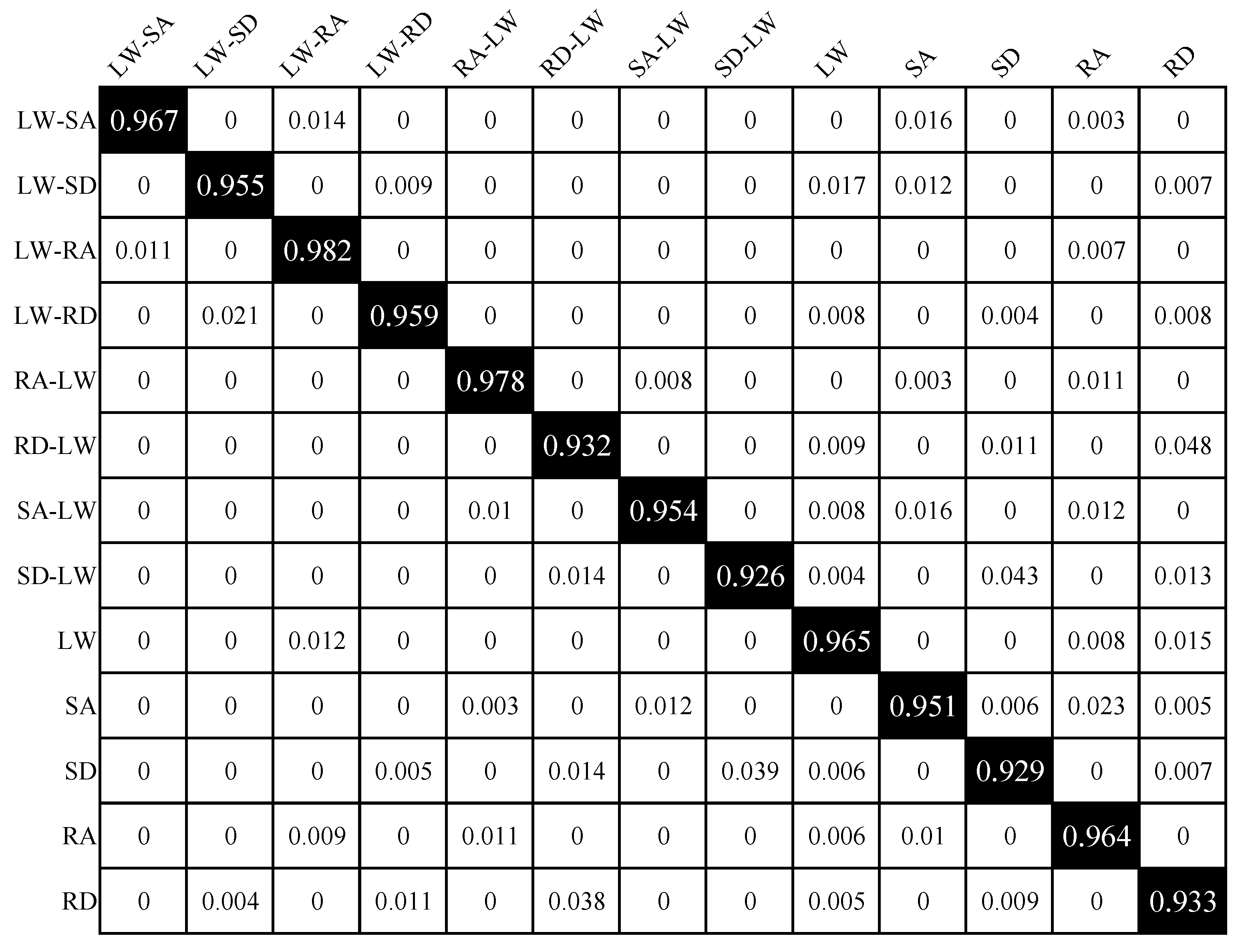
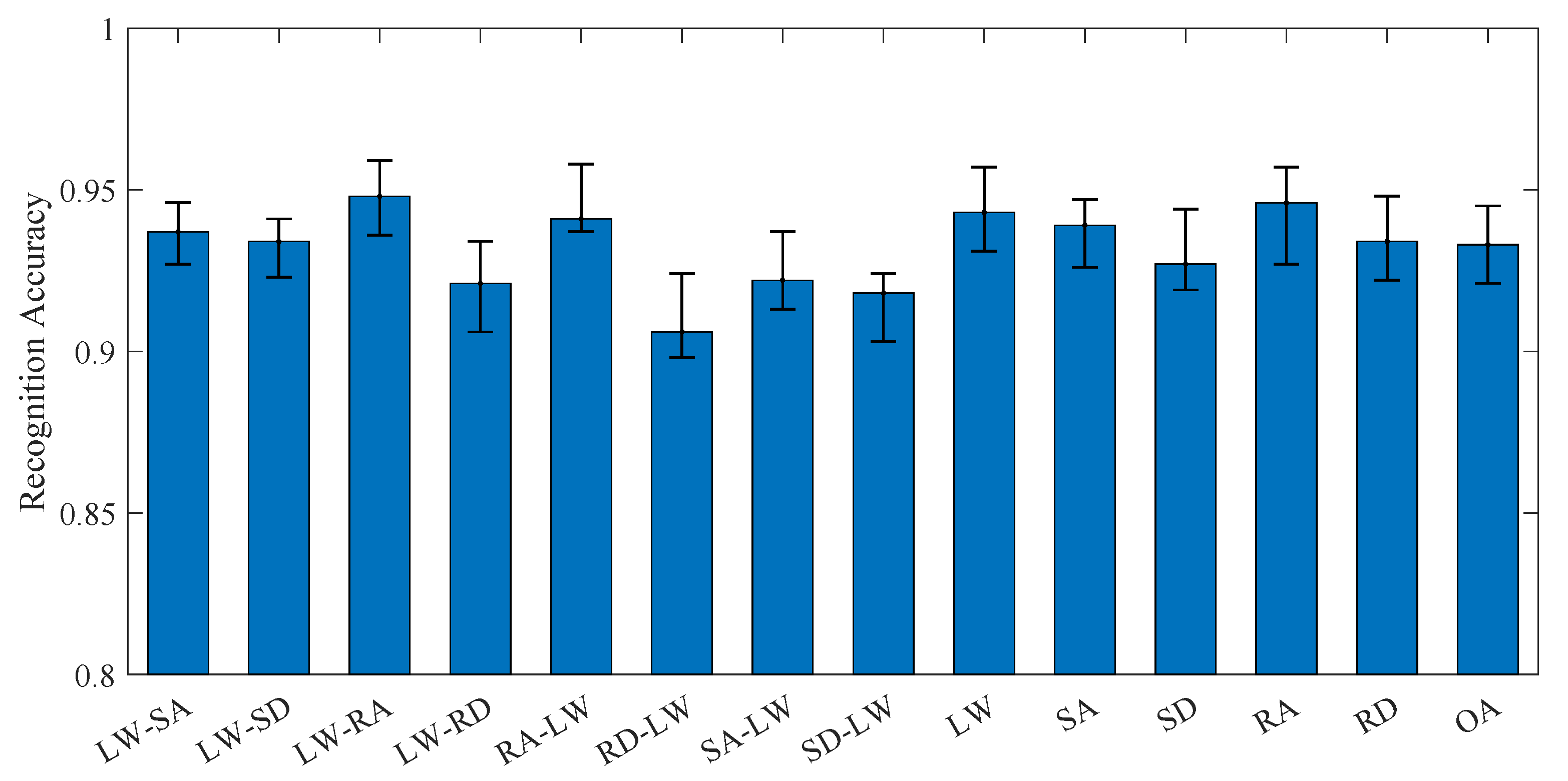
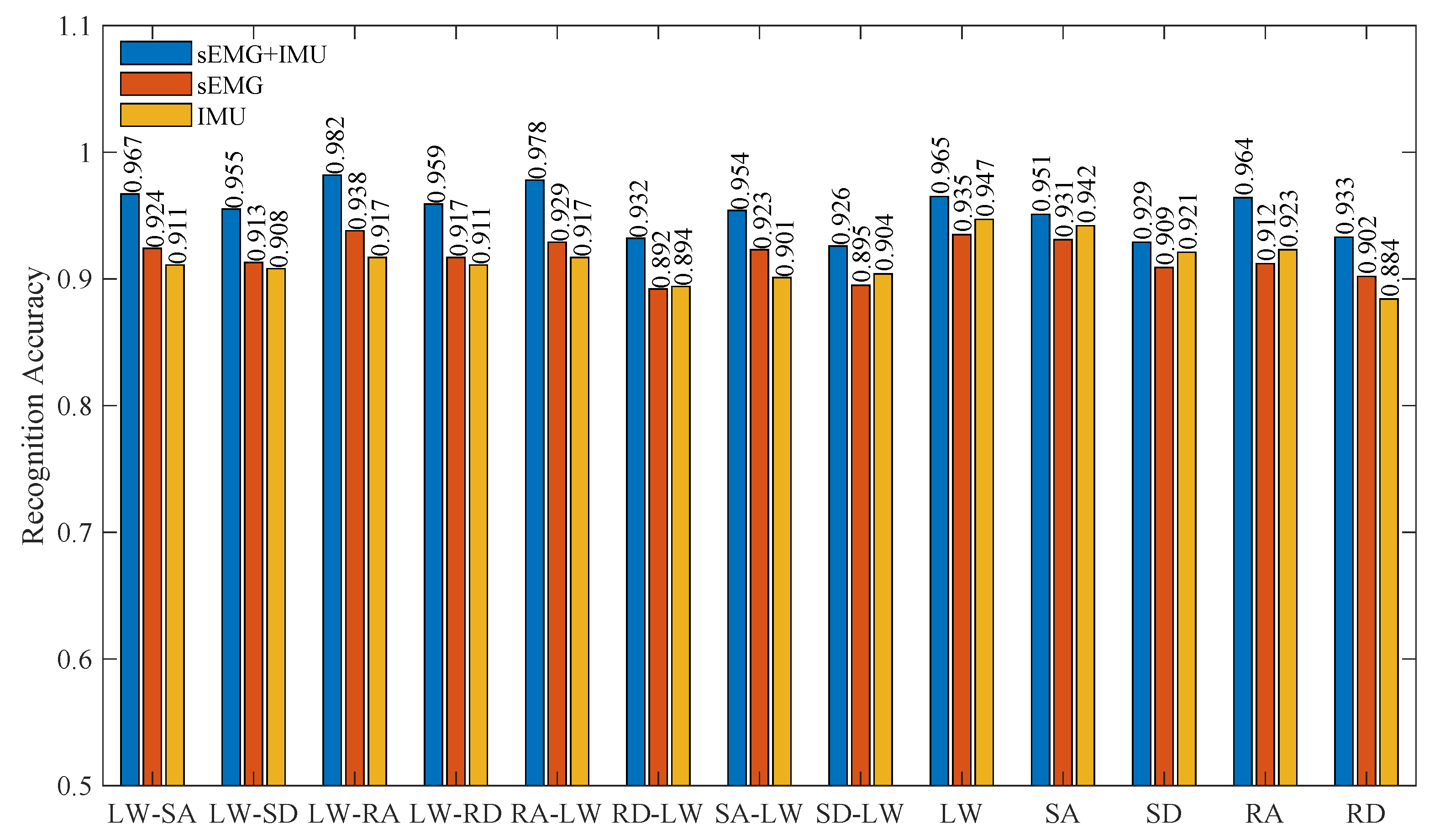
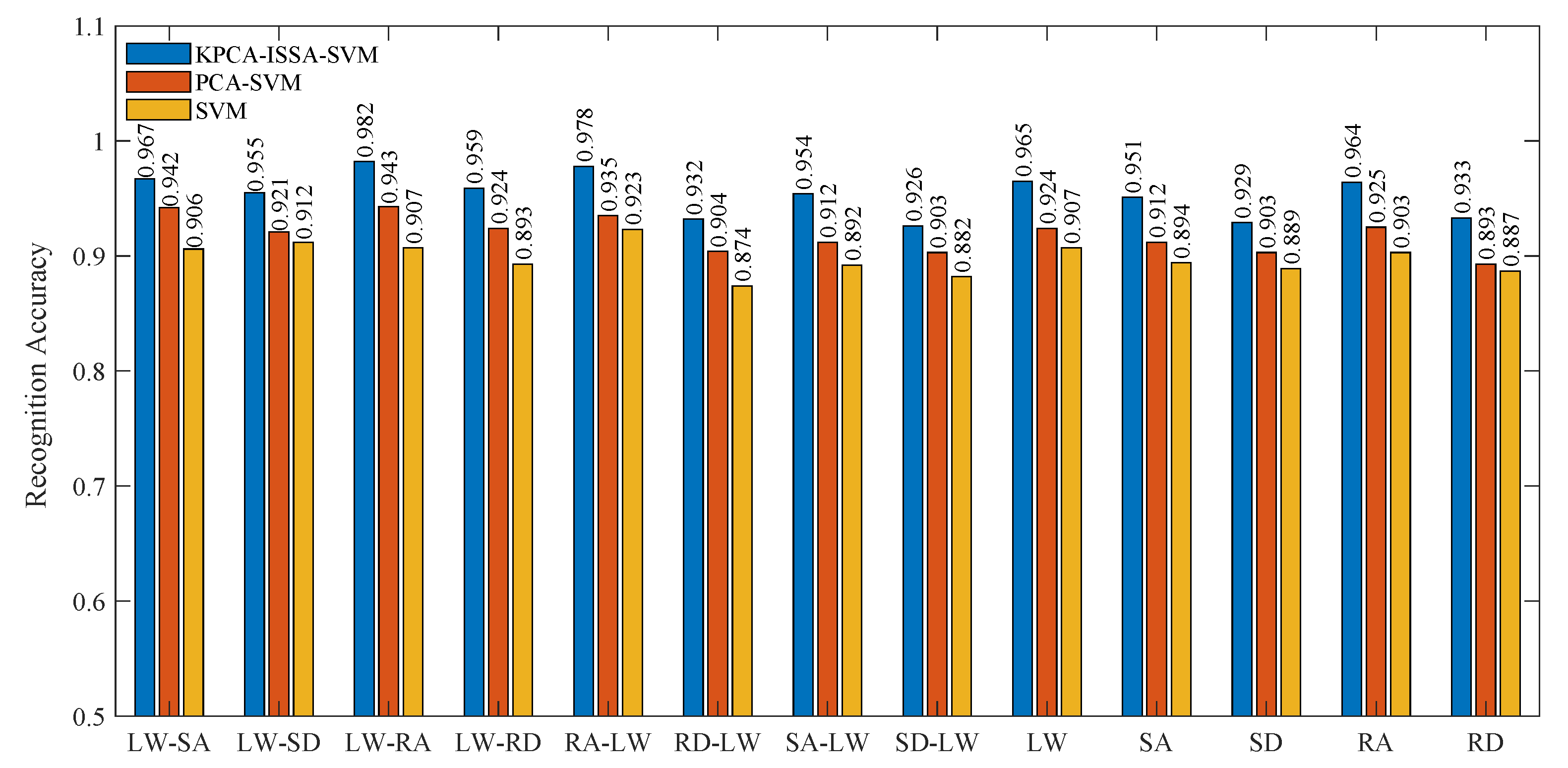
| NO. | Locomotion Mode | Description |
|---|---|---|
| 1 | Level Walking-to-Stair Ascent (LW-SA) | Transition phase from level walking to stair ascent |
| 2 | Level Walking-to-Stair Descent (LW-SD) | Transition phase from level walking to stair descent |
| 3 | Level Walking-to-Ramp Ascent (LW-RA) | Transition phase from level walking to ramp ascent |
| 4 | Level Walking-to-Ramp Descent (LW-RD) | Transition phase from level walking to ramp descent |
| 5 | Ramp Ascent-to-Level Walking (RA-LW) | Transition phase from ramp ascent to level walking |
| 6 | Ramp Descent-to-Level Walking (RD-LW) | Transition phase from ramp descent to level walking |
| 7 | Stair Ascent-to-Level Walking (SA-LW) | Transition phase from stair ascent to level walking |
| 8 | Stair Descent-to-Level Walking (SD-LW) | Transition phase from stair descent to level walking |
| 9 | Level Walking (LW) | Continuous level walking on flat ground |
| 10 | Stair Ascent (SA) | Continuous ascending stairs |
| 11 | Stair Descent (SD) | Continuous descending stairs |
| 12 | Ramp Ascent (RA) | Continuous ascending slope |
| 13 | Ramp Descent (RD) | Continuous descending slope |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, K.; Hao, P.; Zhao, H.; Lou, P.; Chen, Y. High-Accuracy Lower-Limb Intent Recognition: A KPCA-ISSA-SVM Approach with sEMG-IMU Sensor Fusion. Biomimetics 2025, 10, 609. https://doi.org/10.3390/biomimetics10090609
Yin K, Hao P, Zhao H, Lou P, Chen Y. High-Accuracy Lower-Limb Intent Recognition: A KPCA-ISSA-SVM Approach with sEMG-IMU Sensor Fusion. Biomimetics. 2025; 10(9):609. https://doi.org/10.3390/biomimetics10090609
Chicago/Turabian StyleYin, Kaiyang, Pengchao Hao, Huanli Zhao, Pengyu Lou, and Yi Chen. 2025. "High-Accuracy Lower-Limb Intent Recognition: A KPCA-ISSA-SVM Approach with sEMG-IMU Sensor Fusion" Biomimetics 10, no. 9: 609. https://doi.org/10.3390/biomimetics10090609
APA StyleYin, K., Hao, P., Zhao, H., Lou, P., & Chen, Y. (2025). High-Accuracy Lower-Limb Intent Recognition: A KPCA-ISSA-SVM Approach with sEMG-IMU Sensor Fusion. Biomimetics, 10(9), 609. https://doi.org/10.3390/biomimetics10090609





