DRIME: A Distributed Data-Guided RIME Algorithm for Numerical Optimization Problems
Abstract
1. Introduction
- (1)
- A RIME variant has been proposed called DRIME, which combines a distributed data-driven guided learning strategy, a soft-rime search strategy based on weighted mean, and a hard-rime puncture mechanism based on a candidate pool.
- (2)
- The DRIME algorithm overcomes the shortcomings of the basic RIME algorithm, including its lack of information exchange between populations, the deficiency of imbalance between exploitation and exploration, and insufficient global search capability, and it improves the probability of the RIME algorithm to jump out of the local optimum.
- (3)
- The DRIME algorithm outperformed other RIME variants and variants of other algorithms in the CEC2017 test set, the CEC2022 test set, and engineering constraint optimization problems.
2. Overview of the RIME Algorithm
2.1. Initialization Phase of Rime Ice
2.2. Soft-Rime Search Phase
2.3. Hard-Rime Puncture Phase
| Algorithm 1. Pseudocode of basic RIME algorithm |
|
Initialize the rime population R using Equation (1) Obtain the current best agent and best fitness While Update the parameter using Equation (3) For i = 1: N %% Soft-rime search phase If Update ice agent using Equation (2) End If %% Hard-rime puncture phase If Update ice agent using Equation (4) End If End for End While |
3. Proposed DRIME Algorithm
3.1. Distributed Data-Driven Guided Learning Strategy (DGLS)
3.2. Soft-Rime Search Strategy Based on Weighted Mean (SWM)
3.3. Hard-Rime Puncture Mechanism Based on Candidate Pool (HCP)
3.4. The Structure of DRIME and Time Complexity
| Algorithm 2. Pseudocode of DRIME algorithm |
|
Initialize the rime population R using Equation (1) Get the current best agent and best fitness While Update the parameter using Equation (3) Calculate the using Equation (6) Calculate the using Equation (7) Construct the using Equation (12) For i = 1: N If If Update ice agent using Equation (2) // Soft-rime search phase Else Update ice agent using Equation (11) // SWM End If End If If Update ice agent using Equation (14) // HCP End If CCC = CCC + 1 If Update ice agent using Equation (5) // DGLS End If End for End While |
4. Simulation Experiment and Result Analysis Using Test Suites
4.1. Descriptions of Benchmark Functions and Performance Metrics
4.2. Parameter Sensitivity Analysis Using CEC-2017 Test Suite
4.3. Strategy Effectiveness Analysis Using CEC-2017 Test Suite
4.4. Comparison Results with Other RIME Variants Using CEC-2017 Test Suite
4.5. Comparison Results with Other Metaheuristic Variants Using CEC-2022 Test Suite
4.6. Discussion
5. Simulation Experiment and Result Analysis Using Engineering Constrained Optimization Problems
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| No. | Index | RIME | DRIME-D | DRIME-S | DRIME-H | DRIME-DS | DRIME-DH | DRIME-SH | DRIME |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.2219E+05 | 3.5895E+03 | 4.5814E+04 | 2.2281E+04 | 3.5013E+03 | 3.7723E+03 | 3.1607E+04 | 5.1814E+02 |
| Avg | 6.9551E+05 | 3.8625E+04 | 4.1107E+05 | 3.2524E+05 | 2.6761E+04 | 5.7547E+04 | 3.0731E+05 | 3.2371E+03 | |
| Std | 4.6496E+05 | 3.0267E+04 | 3.5935E+05 | 2.9557E+05 | 2.3337E+04 | 4.7798E+04 | 3.6184E+05 | 2.5383E+03 | |
| Rank | 8 | 3 | 7 | 6 | 2 | 4 | 5 | 1 | |
| F2 | Best | 3.1278E+02 | 3.0054E+02 | 3.0299E+02 | 3.0558E+02 | 3.0053E+02 | 3.0176E+02 | 3.1322E+02 | 3.0006E+02 |
| Avg | 3.9436E+02 | 3.0469E+02 | 3.9843E+02 | 3.7192E+02 | 3.0425E+02 | 3.0541E+02 | 4.6467E+02 | 3.0034E+02 | |
| Std | 1.1728E+02 | 3.6627E+00 | 8.4635E+01 | 7.3071E+01 | 3.4653E+00 | 2.6526E+00 | 1.3086E+02 | 2.6805E-01 | |
| Rank | 6 | 3 | 7 | 5 | 2 | 4 | 8 | 1 | |
| F3 | Best | 4.0026E+02 | 4.0433E+02 | 4.0430E+02 | 4.0025E+02 | 4.0434E+02 | 4.0136E+02 | 4.0551E+02 | 4.0448E+02 |
| Avg | 4.1270E+02 | 4.0643E+02 | 4.0667E+02 | 4.0681E+02 | 4.0681E+02 | 4.0623E+02 | 4.0713E+02 | 4.0637E+02 | |
| Std | 1.8963E+01 | 9.6669E-01 | 1.2497E+00 | 1.8525E+00 | 6.8944E-01 | 1.3593E+00 | 7.6417E-01 | 6.6339E-01 | |
| Rank | 8 | 3 | 4 | 6 | 5 | 1 | 7 | 2 | |
| F4 | Best | 5.0536E+02 | 5.0504E+02 | 5.0311E+02 | 5.0324E+02 | 5.0334E+02 | 5.0501E+02 | 5.0384E+02 | 5.0398E+02 |
| Avg | 5.1764E+02 | 5.1232E+02 | 5.1263E+02 | 5.1300E+02 | 5.0775E+02 | 5.1346E+02 | 5.0934E+02 | 5.0746E+02 | |
| Std | 8.1125E+00 | 4.7715E+00 | 5.5847E+00 | 5.3996E+00 | 3.0514E+00 | 4.7521E+00 | 3.9123E+00 | 3.4503E+00 | |
| Rank | 8 | 4 | 5 | 6 | 2 | 7 | 3 | 1 | |
| F5 | Best | 6.0045E+02 | 6.0010E+02 | 6.0014E+02 | 6.0013E+02 | 6.0007E+02 | 6.0010E+02 | 6.0020E+02 | 6.0002E+02 |
| Avg | 6.0104E+02 | 6.0031E+02 | 6.0053E+02 | 6.0087E+02 | 6.0021E+02 | 6.0023E+02 | 6.0077E+02 | 6.0008E+02 | |
| Std | 5.6063E-01 | 2.2793E-01 | 3.4640E-01 | 6.0573E-01 | 1.1904E-01 | 9.4700E-02 | 5.0125E-01 | 5.9760E-02 | |
| Rank | 8 | 4 | 5 | 7 | 2 | 3 | 6 | 1 | |
| F6 | Best | 7.1053E+02 | 7.0746E+02 | 7.1804E+02 | 7.1631E+02 | 7.1565E+02 | 7.1397E+02 | 7.1299E+02 | 7.1247E+02 |
| Avg | 7.2943E+02 | 7.2428E+02 | 7.2762E+02 | 7.2509E+02 | 7.2294E+02 | 7.2509E+02 | 7.2090E+02 | 7.1894E+02 | |
| Std | 7.9386E+00 | 7.2337E+00 | 5.6998E+00 | 5.2170E+00 | 5.5757E+00 | 5.3730E+00 | 4.8690E+00 | 5.8972E+00 | |
| Rank | 8 | 4 | 7 | 5 | 3 | 6 | 2 | 1 | |
| F7 | Best | 8.0846E+02 | 8.0507E+02 | 8.0443E+02 | 8.0405E+02 | 8.0141E+02 | 8.0404E+02 | 8.0220E+02 | 8.0100E+02 |
| Avg | 8.1839E+02 | 8.1435E+02 | 8.1079E+02 | 8.1017E+02 | 8.0724E+02 | 8.1169E+02 | 8.0567E+02 | 8.0552E+02 | |
| Std | 6.7686E+00 | 5.2871E+00 | 4.0586E+00 | 4.2998E+00 | 3.7404E+00 | 5.0377E+00 | 2.1891E+00 | 4.1056E+00 | |
| Rank | 8 | 7 | 5 | 4 | 3 | 6 | 2 | 1 | |
| F8 | Best | 9.0019E+02 | 9.0000E+02 | 9.0009E+02 | 9.0004E+02 | 9.0001E+02 | 9.0003E+02 | 9.0004E+02 | 9.0000E+02 |
| Avg | 9.0174E+02 | 9.0030E+02 | 9.0056E+02 | 9.0180E+02 | 9.0010E+02 | 9.0015E+02 | 9.0033E+02 | 9.0001E+02 | |
| Std | 2.5919E+00 | 4.1355E-01 | 3.2045E-01 | 3.3080E+00 | 1.3445E-01 | 1.2222E-01 | 3.0524E-01 | 2.8392E-02 | |
| Rank | 7 | 4 | 6 | 8 | 2 | 3 | 5 | 1 | |
| F9 | Best | 1.1590E+03 | 1.1331E+03 | 1.1264E+03 | 1.0151E+03 | 1.1404E+03 | 1.1235E+03 | 1.0113E+03 | 1.1443E+03 |
| Avg | 1.6026E+03 | 1.5593E+03 | 1.5354E+03 | 1.5796E+03 | 1.5588E+03 | 1.5580E+03 | 1.5884E+03 | 1.5124E+03 | |
| Std | 2.1943E+02 | 2.0724E+02 | 2.4918E+02 | 2.7331E+02 | 2.5311E+02 | 2.2399E+02 | 2.3342E+02 | 2.4264E+02 | |
| Rank | 8 | 5 | 2 | 6 | 4 | 3 | 7 | 1 | |
| F10 | Best | 1.1056E+03 | 1.1024E+03 | 1.1025E+03 | 1.1047E+03 | 1.1037E+03 | 1.1030E+03 | 1.1091E+03 | 1.1030E+03 |
| Avg | 1.1210E+03 | 1.1102E+03 | 1.1150E+03 | 1.1171E+03 | 1.1101E+03 | 1.1105E+03 | 1.1178E+03 | 1.1076E+03 | |
| Std | 1.2616E+01 | 5.4217E+00 | 7.0316E+00 | 7.2381E+00 | 4.5713E+00 | 5.5135E+00 | 7.1831E+00 | 2.6459E+00 | |
| Rank | 8 | 3 | 5 | 6 | 2 | 4 | 7 | 1 | |
| F11 | Best | 4.9078E+03 | 2.6766E+03 | 9.0094E+03 | 7.5456E+03 | 5.4051E+03 | 2.5449E+03 | 5.1492E+04 | 2.2731E+03 |
| Avg | 1.4452E+06 | 1.7971E+04 | 8.3751E+05 | 1.1895E+06 | 1.9997E+04 | 1.6864E+04 | 8.0360E+05 | 6.0176E+03 | |
| Std | 1.5106E+06 | 1.6292E+04 | 1.4605E+06 | 1.3230E+06 | 2.1421E+04 | 1.1322E+04 | 6.2834E+05 | 2.4674E+03 | |
| Rank | 8 | 3 | 6 | 7 | 4 | 2 | 5 | 1 | |
| F12 | Best | 1.6575E+03 | 1.3300E+03 | 1.4944E+03 | 1.8916E+03 | 1.3600E+03 | 1.3167E+03 | 2.2680E+03 | 1.3216E+03 |
| Avg | 1.0495E+04 | 2.9898E+03 | 1.1172E+04 | 9.4386E+03 | 1.8446E+03 | 1.8498E+03 | 7.9133E+03 | 1.5404E+03 | |
| Std | 8.5958E+03 | 3.1775E+03 | 8.6055E+03 | 4.2887E+03 | 7.9424E+02 | 1.5742E+03 | 3.4327E+03 | 6.2107E+02 | |
| Rank | 7 | 4 | 8 | 6 | 2 | 3 | 5 | 1 | |
| F13 | Best | 1.4227E+03 | 1.4107E+03 | 1.4267E+03 | 1.4429E+03 | 1.4074E+03 | 1.4112E+03 | 1.4312E+03 | 1.4060E+03 |
| Avg | 4.1977E+03 | 1.4315E+03 | 4.1473E+03 | 2.6994E+03 | 1.4259E+03 | 1.4227E+03 | 2.8549E+03 | 1.4197E+03 | |
| Std | 3.4476E+03 | 3.0089E+01 | 3.2898E+03 | 1.6586E+03 | 6.1351E+00 | 6.3962E+00 | 1.4309E+03 | 7.9296E+00 | |
| Rank | 8 | 4 | 7 | 5 | 3 | 2 | 6 | 1 | |
| F14 | Best | 1.5158E+03 | 1.5034E+03 | 1.5234E+03 | 1.5440E+03 | 1.5056E+03 | 1.5036E+03 | 1.5238E+03 | 1.5024E+03 |
| Avg | 5.0169E+03 | 1.7054E+03 | 4.1238E+03 | 3.4168E+03 | 1.5147E+03 | 1.5104E+03 | 2.9819E+03 | 1.5065E+03 | |
| Std | 5.2530E+03 | 1.0091E+03 | 4.1005E+03 | 2.4671E+03 | 5.4618E+00 | 6.5682E+00 | 1.7433E+03 | 3.7066E+00 | |
| Rank | 8 | 4 | 7 | 6 | 3 | 2 | 5 | 1 | |
| F15 | Best | 1.6020E+03 | 1.6014E+03 | 1.6027E+03 | 1.6021E+03 | 1.6038E+03 | 1.6018E+03 | 1.6036E+03 | 1.6034E+03 |
| Avg | 1.6849E+03 | 1.6742E+03 | 1.6769E+03 | 1.6918E+03 | 1.6720E+03 | 1.6836E+03 | 1.7155E+03 | 1.6465E+03 | |
| Std | 9.2352E+01 | 8.6779E+01 | 8.2573E+01 | 9.9287E+01 | 8.1837E+01 | 9.7465E+01 | 1.0655E+02 | 5.5149E+01 | |
| Rank | 6 | 3 | 4 | 7 | 2 | 5 | 8 | 1 | |
| F16 | Best | 1.7176E+03 | 1.7051E+03 | 1.7016E+03 | 1.7218E+03 | 1.7134E+03 | 1.7072E+03 | 1.7223E+03 | 1.7061E+03 |
| Avg | 1.7558E+03 | 1.7502E+03 | 1.7320E+03 | 1.7664E+03 | 1.7411E+03 | 1.7362E+03 | 1.7407E+03 | 1.7348E+03 | |
| Std | 3.9600E+01 | 4.3662E+01 | 1.5943E+01 | 4.5421E+01 | 1.8745E+01 | 2.0316E+01 | 8.2779E+00 | 1.1868E+01 | |
| Rank | 7 | 6 | 1 | 8 | 5 | 3 | 4 | 2 | |
| F17 | Best | 2.8204E+03 | 1.8496E+03 | 4.4786E+03 | 2.3324E+03 | 1.8331E+03 | 1.8191E+03 | 2.0401E+03 | 1.8130E+03 |
| Avg | 2.0451E+04 | 3.8993E+03 | 1.9077E+04 | 1.4101E+04 | 1.9507E+03 | 3.1183E+03 | 6.9415E+03 | 1.8338E+03 | |
| Std | 1.4541E+04 | 4.5940E+03 | 1.0767E+04 | 9.6656E+03 | 1.6053E+02 | 2.2940E+03 | 4.2099E+03 | 1.3569E+01 | |
| Rank | 8 | 4 | 7 | 6 | 2 | 3 | 5 | 1 | |
| F18 | Best | 1.9076E+03 | 1.9038E+03 | 1.9096E+03 | 1.9216E+03 | 1.9029E+03 | 1.9020E+03 | 1.9891E+03 | 1.9019E+03 |
| Avg | 6.1091E+03 | 2.0331E+03 | 5.1171E+03 | 4.4412E+03 | 1.9062E+03 | 1.9053E+03 | 4.2581E+03 | 1.9038E+03 | |
| Std | 6.0540E+03 | 4.8146E+02 | 4.8035E+03 | 2.9502E+03 | 1.6738E+00 | 1.7768E+00 | 1.6743E+03 | 1.1183E+00 | |
| Rank | 8 | 4 | 7 | 6 | 3 | 2 | 5 | 1 | |
| F19 | Best | 2.0105E+03 | 2.0013E+03 | 2.0152E+03 | 2.0091E+03 | 2.0111E+03 | 2.0047E+03 | 2.0215E+03 | 2.0022E+03 |
| Avg | 2.0317E+03 | 2.0291E+03 | 2.0288E+03 | 2.0314E+03 | 2.0299E+03 | 2.0273E+03 | 2.0292E+03 | 2.0252E+03 | |
| Std | 1.0805E+01 | 1.4478E+01 | 1.0101E+01 | 9.5125E+00 | 1.1239E+01 | 1.1701E+01 | 6.0957E+00 | 6.9262E+00 | |
| Rank | 8 | 4 | 3 | 7 | 6 | 2 | 5 | 1 | |
| F20 | Best | 2.2004E+03 | 2.2001E+03 | 2.2011E+03 | 2.2002E+03 | 2.2001E+03 | 2.2002E+03 | 2.2022E+03 | 2.2001E+03 |
| Avg | 2.2733E+03 | 2.2740E+03 | 2.2653E+03 | 2.2692E+03 | 2.2622E+03 | 2.2608E+03 | 2.2784E+03 | 2.2694E+03 | |
| Std | 5.9619E+01 | 5.6190E+01 | 5.5737E+01 | 5.5634E+01 | 5.3994E+01 | 5.6342E+01 | 4.8285E+01 | 5.1784E+01 | |
| Rank | 6 | 7 | 3 | 4 | 2 | 1 | 8 | 5 | |
| F21 | Best | 2.2012E+03 | 2.2156E+03 | 2.2007E+03 | 2.2269E+03 | 2.3018E+03 | 2.2451E+03 | 2.3022E+03 | 2.3002E+03 |
| Avg | 2.2955E+03 | 2.2976E+03 | 2.2957E+03 | 2.3019E+03 | 2.3053E+03 | 2.3028E+03 | 2.3068E+03 | 2.3024E+03 | |
| Std | 3.0607E+01 | 2.2929E+01 | 2.9283E+01 | 2.0295E+01 | 1.8477E+00 | 1.1029E+01 | 2.3031E+00 | 1.4445E+00 | |
| Rank | 1 | 3 | 2 | 4 | 7 | 6 | 8 | 5 | |
| F22 | Best | 2.6095E+03 | 2.6084E+03 | 2.6073E+03 | 2.6079E+03 | 2.6012E+03 | 2.6066E+03 | 2.6004E+03 | 2.6030E+03 |
| Avg | 2.6203E+03 | 2.6167E+03 | 2.6156E+03 | 2.6169E+03 | 2.6107E+03 | 2.6162E+03 | 2.6142E+03 | 2.6109E+03 | |
| Std | 7.0979E+00 | 5.5420E+00 | 6.4120E+00 | 6.5452E+00 | 5.1061E+00 | 5.3966E+00 | 6.7360E+00 | 5.5501E+00 | |
| Rank | 8 | 6 | 4 | 7 | 1 | 5 | 3 | 2 | |
| F23 | Best | 2.5019E+03 | 2.5005E+03 | 2.5015E+03 | 2.5014E+03 | 2.5006E+03 | 2.5008E+03 | 2.5031E+03 | 2.5014E+03 |
| Avg | 2.7064E+03 | 2.6945E+03 | 2.7068E+03 | 2.7042E+03 | 2.7046E+03 | 2.6893E+03 | 2.6986E+03 | 2.7270E+03 | |
| Std | 8.8530E+01 | 9.4538E+01 | 8.5739E+01 | 8.8171E+01 | 8.1301E+01 | 1.0234E+02 | 8.6021E+01 | 4.2795E+01 | |
| Rank | 6 | 2 | 7 | 4 | 5 | 1 | 3 | 8 | |
| F24 | Best | 2.8979E+03 | 2.8980E+03 | 2.8990E+03 | 2.8991E+03 | 2.8980E+03 | 2.8978E+03 | 2.9000E+03 | 2.8982E+03 |
| Avg | 2.9270E+03 | 2.9321E+03 | 2.9377E+03 | 2.9420E+03 | 2.9343E+03 | 2.9275E+03 | 2.9414E+03 | 2.9324E+03 | |
| Std | 2.3831E+01 | 2.2103E+01 | 1.9591E+01 | 1.4616E+01 | 1.9988E+01 | 2.3727E+01 | 1.2905E+01 | 2.0593E+01 | |
| Rank | 1 | 3 | 6 | 8 | 5 | 2 | 7 | 4 | |
| F25 | Best | 2.8235E+03 | 2.8080E+03 | 2.6127E+03 | 2.8115E+03 | 2.8026E+03 | 2.8071E+03 | 2.8136E+03 | 2.9001E+03 |
| Avg | 2.9097E+03 | 2.9013E+03 | 2.8994E+03 | 2.9110E+03 | 2.8949E+03 | 2.8984E+03 | 2.9043E+03 | 2.9004E+03 | |
| Std | 3.1105E+01 | 2.1785E+01 | 6.1009E+01 | 3.8008E+01 | 2.4935E+01 | 2.7270E+01 | 2.2530E+01 | 8.9534E-01 | |
| Rank | 7 | 5 | 3 | 8 | 1 | 2 | 6 | 4 | |
| F26 | Best | 3.0905E+03 | 3.0895E+03 | 3.0901E+03 | 3.0886E+03 | 3.0905E+03 | 3.0876E+03 | 3.0902E+03 | 3.0900E+03 |
| Avg | 3.0985E+03 | 3.0980E+03 | 3.0964E+03 | 3.0991E+03 | 3.0957E+03 | 3.0955E+03 | 3.0960E+03 | 3.0952E+03 | |
| Std | 9.4378E+00 | 1.4099E+01 | 2.5506E+00 | 1.0789E+01 | 2.2082E+00 | 3.3985E+00 | 2.4771E+00 | 3.0830E+00 | |
| Rank | 7 | 6 | 5 | 8 | 3 | 2 | 4 | 1 | |
| F27 | Best | 3.1015E+03 | 3.1004E+03 | 3.1023E+03 | 3.1024E+03 | 3.1008E+03 | 3.1010E+03 | 3.1016E+03 | 3.1003E+03 |
| Avg | 3.2572E+03 | 3.2333E+03 | 3.2063E+03 | 3.2536E+03 | 3.2402E+03 | 3.2613E+03 | 3.2907E+03 | 3.2472E+03 | |
| Std | 1.1253E+02 | 1.2342E+02 | 1.0036E+02 | 1.1942E+02 | 1.3029E+02 | 1.2310E+02 | 1.3368E+02 | 1.4411E+02 | |
| Rank | 6 | 2 | 1 | 5 | 3 | 7 | 8 | 4 | |
| F28 | Best | 3.1525E+03 | 3.1427E+03 | 3.1457E+03 | 3.1473E+03 | 3.1556E+03 | 3.1360E+03 | 3.1557E+03 | 3.1510E+03 |
| Avg | 3.1995E+03 | 3.1815E+03 | 3.1848E+03 | 3.1870E+03 | 3.1844E+03 | 3.1749E+03 | 3.1883E+03 | 3.1781E+03 | |
| Std | 4.9256E+01 | 2.5236E+01 | 2.6601E+01 | 2.9648E+01 | 1.4725E+01 | 1.7328E+01 | 1.5833E+01 | 1.5368E+01 | |
| Rank | 8 | 3 | 5 | 6 | 4 | 1 | 7 | 2 | |
| F29 | Best | 8.0433E+03 | 3.9963E+03 | 1.0205E+04 | 5.0418E+03 | 4.1305E+03 | 4.0197E+03 | 2.5672E+04 | 3.6850E+03 |
| Avg | 3.2685E+05 | 3.2953E+05 | 1.7603E+05 | 2.5267E+05 | 1.1084E+05 | 3.0453E+05 | 1.5266E+05 | 3.7257E+04 | |
| Std | 5.4279E+05 | 4.9300E+05 | 3.4969E+05 | 3.9368E+05 | 3.9324E+05 | 5.4020E+05 | 3.0872E+05 | 1.7219E+05 | |
| Rank | 7 | 8 | 4 | 5 | 2 | 6 | 3 | 1 |
| No. | Index | RIME | DRIME-D | DRIME-S | DRIME-H | DRIME-DS | DRIME-DH | DRIME-SH | DRIME |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.3991E+07 | 7.6444E+05 | 4.0734E+06 | 5.3393E+06 | 9.5526E+05 | 1.6346E+06 | 4.1556E+06 | 1.0336E+05 |
| Avg | 3.0638E+07 | 5.2785E+06 | 1.3978E+07 | 1.9984E+07 | 4.3864E+06 | 4.2573E+06 | 1.8225E+07 | 5.4087E+05 | |
| Std | 1.1145E+07 | 3.4771E+06 | 7.2505E+06 | 8.9374E+06 | 3.5656E+06 | 2.2210E+06 | 1.2113E+07 | 4.4719E+05 | |
| Rank | 8 | 4 | 5 | 7 | 3 | 2 | 6 | 1 | |
| F2 | Best | 1.1749E+04 | 1.2062E+03 | 1.3494E+04 | 9.7901E+03 | 1.1740E+03 | 1.7719E+03 | 2.1753E+04 | 5.5212E+02 |
| Avg | 3.1796E+04 | 3.2963E+03 | 2.5759E+04 | 2.5010E+04 | 3.2855E+03 | 4.1048E+03 | 3.1233E+04 | 1.4789E+03 | |
| Std | 9.2105E+03 | 1.2282E+03 | 6.3144E+03 | 9.0928E+03 | 1.3508E+03 | 1.6924E+03 | 5.6478E+03 | 6.3419E+02 | |
| Rank | 8 | 3 | 6 | 5 | 2 | 4 | 7 | 1 | |
| F3 | Best | 4.8063E+02 | 4.8709E+02 | 4.7930E+02 | 4.8668E+02 | 5.1229E+02 | 4.7412E+02 | 5.1719E+02 | 4.9689E+02 |
| Avg | 5.1810E+02 | 5.1983E+02 | 5.2057E+02 | 5.2457E+02 | 5.2447E+02 | 5.1989E+02 | 5.2889E+02 | 5.2169E+02 | |
| Std | 2.1827E+01 | 2.0361E+01 | 2.1018E+01 | 2.2904E+01 | 5.8185E+00 | 2.2392E+01 | 6.0839E+00 | 7.5835E+00 | |
| Rank | 1 | 2 | 4 | 7 | 6 | 3 | 8 | 5 | |
| F4 | Best | 5.5683E+02 | 5.4282E+02 | 5.2882E+02 | 5.4254E+02 | 5.2675E+02 | 5.3871E+02 | 5.3481E+02 | 5.3063E+02 |
| Avg | 5.9960E+02 | 5.6360E+02 | 5.5669E+02 | 5.7714E+02 | 5.4463E+02 | 5.5995E+02 | 5.6565E+02 | 5.4376E+02 | |
| Std | 2.2829E+01 | 1.3738E+01 | 1.4349E+01 | 1.9243E+01 | 1.0900E+01 | 1.5000E+01 | 1.9216E+01 | 1.2058E+01 | |
| Rank | 8 | 5 | 3 | 7 | 2 | 4 | 6 | 1 | |
| F5 | Best | 6.0381E+02 | 6.0096E+02 | 6.0155E+02 | 6.0181E+02 | 6.0089E+02 | 6.0086E+02 | 6.0262E+02 | 6.0037E+02 |
| Avg | 6.0871E+02 | 6.0202E+02 | 6.0259E+02 | 6.0645E+02 | 6.0298E+02 | 6.0203E+02 | 6.0725E+02 | 6.0146E+02 | |
| Std | 3.8322E+00 | 9.2152E-01 | 7.3774E-01 | 3.0662E+00 | 1.3695E+00 | 9.0190E-01 | 2.6206E+00 | 7.5368E-01 | |
| Rank | 8 | 2 | 4 | 6 | 5 | 3 | 7 | 1 | |
| F6 | Best | 8.1869E+02 | 7.9040E+02 | 7.9111E+02 | 8.1801E+02 | 7.7101E+02 | 7.8234E+02 | 7.9331E+02 | 7.6244E+02 |
| Avg | 8.8809E+02 | 8.2999E+02 | 8.3024E+02 | 8.6215E+02 | 8.2357E+02 | 8.2540E+02 | 8.3519E+02 | 8.0749E+02 | |
| Std | 3.5951E+01 | 2.0906E+01 | 1.8906E+01 | 2.3889E+01 | 2.4613E+01 | 2.5534E+01 | 2.3051E+01 | 3.0163E+01 | |
| Rank | 8 | 4 | 5 | 7 | 2 | 3 | 6 | 1 | |
| F7 | Best | 8.5403E+02 | 8.3943E+02 | 8.3334E+02 | 8.3354E+02 | 8.2495E+02 | 8.4177E+02 | 8.2817E+02 | 8.1895E+02 |
| Avg | 8.9334E+02 | 8.6051E+02 | 8.5511E+02 | 8.6763E+02 | 8.3809E+02 | 8.6398E+02 | 8.4979E+02 | 8.3161E+02 | |
| Std | 2.5469E+01 | 1.5079E+01 | 1.3987E+01 | 1.6239E+01 | 8.6010E+00 | 1.6606E+01 | 1.2685E+01 | 7.4953E+00 | |
| Rank | 8 | 5 | 4 | 7 | 2 | 6 | 3 | 1 | |
| F8 | Best | 9.9061E+02 | 9.0361E+02 | 9.1102E+02 | 9.1313E+02 | 9.0439E+02 | 9.0161E+02 | 9.4313E+02 | 9.0167E+02 |
| Avg | 1.7869E+03 | 9.2965E+02 | 9.5319E+02 | 1.2616E+03 | 9.3744E+02 | 9.2366E+02 | 1.0759E+03 | 9.1526E+02 | |
| Std | 1.1099E+03 | 2.2604E+01 | 3.3780E+01 | 3.5714E+02 | 3.3849E+01 | 2.5653E+01 | 9.7015E+01 | 1.0496E+01 | |
| Rank | 8 | 3 | 5 | 7 | 4 | 2 | 6 | 1 | |
| F9 | Best | 3.9506E+03 | 3.6228E+03 | 3.8761E+03 | 3.4490E+03 | 4.0650E+03 | 3.3254E+03 | 3.5049E+03 | 3.0332E+03 |
| Avg | 4.9603E+03 | 4.6841E+03 | 4.7693E+03 | 4.7902E+03 | 5.0863E+03 | 4.7270E+03 | 4.7269E+03 | 4.4306E+03 | |
| Std | 6.1288E+02 | 5.8455E+02 | 5.6356E+02 | 7.0290E+02 | 6.8405E+02 | 7.0641E+02 | 7.0798E+02 | 6.4303E+02 | |
| Rank | 7 | 2 | 5 | 6 | 8 | 4 | 3 | 1 | |
| F10 | Best | 1.2250E+03 | 1.1796E+03 | 1.2223E+03 | 1.2000E+03 | 1.1741E+03 | 1.1529E+03 | 1.2365E+03 | 1.1616E+03 |
| Avg | 1.3521E+03 | 1.2236E+03 | 1.2802E+03 | 1.2946E+03 | 1.2258E+03 | 1.2210E+03 | 1.2868E+03 | 1.2087E+03 | |
| Std | 7.4446E+01 | 2.4881E+01 | 2.7870E+01 | 4.4833E+01 | 2.7521E+01 | 3.1192E+01 | 2.5433E+01 | 2.3476E+01 | |
| Rank | 8 | 3 | 5 | 7 | 4 | 2 | 6 | 1 | |
| F11 | Best | 3.2897E+06 | 3.0954E+05 | 1.3256E+06 | 3.2750E+06 | 8.0092E+05 | 1.1176E+05 | 3.5717E+06 | 4.1685E+05 |
| Avg | 1.9070E+07 | 3.4831E+06 | 8.9218E+06 | 1.9189E+07 | 3.6736E+06 | 1.9187E+06 | 1.2077E+07 | 1.4532E+06 | |
| Std | 1.7785E+07 | 4.0717E+06 | 5.5327E+06 | 1.3479E+07 | 2.6011E+06 | 2.1763E+06 | 4.6337E+06 | 6.1274E+05 | |
| Rank | 7 | 3 | 5 | 8 | 4 | 2 | 6 | 1 | |
| F12 | Best | 5.3195E+04 | 1.4138E+04 | 1.9179E+04 | 2.7354E+04 | 1.5613E+04 | 6.5060E+03 | 2.5756E+04 | 6.6651E+03 |
| Avg | 2.2965E+05 | 3.8035E+04 | 7.6089E+04 | 1.3986E+05 | 2.7183E+04 | 2.3169E+04 | 5.2734E+04 | 1.7523E+04 | |
| Std | 1.6260E+05 | 1.7286E+04 | 5.0305E+04 | 7.6957E+04 | 7.0779E+03 | 1.2652E+04 | 3.4545E+04 | 6.3923E+03 | |
| Rank | 8 | 4 | 6 | 7 | 3 | 2 | 5 | 1 | |
| F13 | Best | 6.2942E+03 | 1.5174E+03 | 4.3398E+03 | 4.5272E+03 | 1.5259E+03 | 1.5007E+03 | 3.5765E+03 | 1.4710E+03 |
| Avg | 5.5110E+04 | 1.6120E+03 | 4.5846E+04 | 5.4210E+04 | 1.5618E+03 | 1.5525E+03 | 4.8513E+04 | 1.5007E+03 | |
| Std | 4.3914E+04 | 1.7311E+02 | 4.0661E+04 | 4.6535E+04 | 1.6792E+01 | 2.5674E+01 | 4.4461E+04 | 1.6259E+01 | |
| Rank | 8 | 4 | 5 | 7 | 3 | 2 | 6 | 1 | |
| F14 | Best | 1.0383E+04 | 2.5935E+03 | 5.0735E+03 | 1.6286E+04 | 2.5322E+03 | 2.7334E+03 | 5.9796E+03 | 1.7322E+03 |
| Avg | 6.5643E+04 | 1.0960E+04 | 1.6113E+04 | 3.8189E+04 | 4.3868E+03 | 5.6913E+03 | 1.1580E+04 | 2.2916E+03 | |
| Std | 4.3771E+04 | 7.9631E+03 | 1.0006E+04 | 1.9599E+04 | 1.3352E+03 | 3.3484E+03 | 5.3028E+03 | 4.1223E+02 | |
| Rank | 8 | 4 | 6 | 7 | 2 | 3 | 5 | 1 | |
| F15 | Best | 1.8874E+03 | 1.9167E+03 | 1.9740E+03 | 2.1321E+03 | 1.8599E+03 | 1.6787E+03 | 2.2235E+03 | 1.9480E+03 |
| Avg | 2.6901E+03 | 2.5520E+03 | 2.4287E+03 | 2.5247E+03 | 2.5029E+03 | 2.4538E+03 | 2.6101E+03 | 2.4857E+03 | |
| Std | 3.7575E+02 | 3.1657E+02 | 2.6057E+02 | 2.2668E+02 | 3.0347E+02 | 3.6459E+02 | 2.0323E+02 | 3.0596E+02 | |
| Rank | 8 | 6 | 1 | 5 | 4 | 2 | 7 | 3 | |
| F16 | Best | 1.8151E+03 | 1.7559E+03 | 1.7657E+03 | 1.8078E+03 | 1.7636E+03 | 1.7601E+03 | 1.7823E+03 | 1.7644E+03 |
| Avg | 2.0959E+03 | 1.9748E+03 | 1.9149E+03 | 2.0537E+03 | 1.9031E+03 | 1.9672E+03 | 1.9900E+03 | 1.8781E+03 | |
| Std | 1.7482E+02 | 1.5003E+02 | 1.1000E+02 | 1.6341E+02 | 1.2890E+02 | 1.5119E+02 | 1.5989E+02 | 8.9640E+01 | |
| Rank | 8 | 5 | 3 | 7 | 2 | 4 | 6 | 1 | |
| F17 | Best | 7.9874E+04 | 3.1765E+03 | 5.4288E+04 | 3.8096E+04 | 5.8222E+03 | 3.3922E+03 | 5.1729E+04 | 2.0838E+03 |
| Avg | 1.2517E+06 | 1.6802E+04 | 7.8089E+05 | 1.0291E+06 | 1.2426E+04 | 1.0819E+04 | 3.3835E+05 | 4.0202E+03 | |
| Std | 1.0054E+06 | 7.9836E+03 | 8.7478E+05 | 1.2380E+06 | 4.5231E+03 | 5.1421E+03 | 2.4257E+05 | 2.0100E+03 | |
| Rank | 8 | 4 | 6 | 7 | 3 | 2 | 5 | 1 | |
| F18 | Best | 1.3328E+04 | 2.2430E+03 | 3.8006E+03 | 8.2813E+03 | 2.4028E+03 | 2.0852E+03 | 6.3614E+03 | 2.0235E+03 |
| Avg | 3.4982E+05 | 1.0441E+04 | 3.7439E+04 | 1.5445E+05 | 5.6001E+03 | 9.0015E+03 | 7.8918E+04 | 3.3183E+03 | |
| Std | 3.4980E+05 | 1.0367E+04 | 3.3873E+04 | 2.3581E+05 | 2.0195E+03 | 8.8017E+03 | 9.2874E+04 | 1.4974E+03 | |
| Rank | 8 | 4 | 5 | 7 | 2 | 3 | 6 | 1 | |
| F19 | Best | 2.1877E+03 | 2.0812E+03 | 2.1060E+03 | 2.1681E+03 | 2.2184E+03 | 2.1308E+03 | 2.2235E+03 | 2.1136E+03 |
| Avg | 2.4353E+03 | 2.3402E+03 | 2.3653E+03 | 2.3843E+03 | 2.2715E+03 | 2.3453E+03 | 2.2858E+03 | 2.2479E+03 | |
| Std | 1.3278E+02 | 1.7278E+02 | 1.6179E+02 | 1.2088E+02 | 6.7670E+01 | 1.5257E+02 | 6.2661E+01 | 5.0813E+01 | |
| Rank | 8 | 4 | 6 | 7 | 2 | 5 | 3 | 1 | |
| F20 | Best | 2.3659E+03 | 2.3399E+03 | 2.3355E+03 | 2.3421E+03 | 2.3271E+03 | 2.3436E+03 | 2.3267E+03 | 2.3195E+03 |
| Avg | 2.3986E+03 | 2.3706E+03 | 2.3530E+03 | 2.3713E+03 | 2.3520E+03 | 2.3658E+03 | 2.3528E+03 | 2.3386E+03 | |
| Std | 1.7502E+01 | 1.5365E+01 | 1.1063E+01 | 1.6503E+01 | 1.8467E+01 | 1.3308E+01 | 1.5381E+01 | 1.9274E+01 | |
| Rank | 8 | 6 | 4 | 7 | 2 | 5 | 3 | 1 | |
| F21 | Best | 2.3205E+03 | 2.3121E+03 | 2.3160E+03 | 2.3175E+03 | 2.3106E+03 | 2.3134E+03 | 2.3143E+03 | 2.3025E+03 |
| Avg | 3.4742E+03 | 2.8099E+03 | 2.3236E+03 | 3.0801E+03 | 2.3166E+03 | 2.6857E+03 | 2.3261E+03 | 2.3085E+03 | |
| Std | 1.8013E+03 | 1.2801E+03 | 4.6785E+00 | 1.5543E+03 | 4.4453E+00 | 1.1447E+03 | 7.4730E+00 | 3.2937E+00 | |
| Rank | 8 | 6 | 3 | 7 | 2 | 5 | 4 | 1 | |
| F22 | Best | 2.7124E+03 | 2.6897E+03 | 2.6849E+03 | 2.6892E+03 | 2.6816E+03 | 2.6884E+03 | 2.6954E+03 | 2.6729E+03 |
| Avg | 2.7568E+03 | 2.7301E+03 | 2.7120E+03 | 2.7378E+03 | 2.7065E+03 | 2.7217E+03 | 2.7202E+03 | 2.6954E+03 | |
| Std | 2.4505E+01 | 2.2625E+01 | 1.7172E+01 | 2.4331E+01 | 1.7052E+01 | 1.9403E+01 | 1.3168E+01 | 9.5088E+00 | |
| Rank | 8 | 6 | 3 | 7 | 2 | 5 | 4 | 1 | |
| F23 | Best | 2.8690E+03 | 2.8480E+03 | 2.8519E+03 | 2.8605E+03 | 2.8376E+03 | 2.8560E+03 | 2.8493E+03 | 2.8353E+03 |
| Avg | 2.9117E+03 | 2.8914E+03 | 2.8801E+03 | 2.8969E+03 | 2.8671E+03 | 2.8909E+03 | 2.8683E+03 | 2.8578E+03 | |
| Std | 2.2493E+01 | 2.5171E+01 | 1.5765E+01 | 1.9783E+01 | 1.9307E+01 | 1.9629E+01 | 1.3424E+01 | 1.3832E+01 | |
| Rank | 8 | 6 | 4 | 7 | 2 | 5 | 3 | 1 | |
| F24 | Best | 2.8943E+03 | 2.8889E+03 | 2.8890E+03 | 2.8907E+03 | 2.8988E+03 | 2.8901E+03 | 2.9298E+03 | 2.9025E+03 |
| Avg | 2.9232E+03 | 2.9169E+03 | 2.9184E+03 | 2.9223E+03 | 2.9351E+03 | 2.9111E+03 | 2.9485E+03 | 2.9293E+03 | |
| Std | 2.7158E+01 | 1.7576E+01 | 1.6170E+01 | 1.9699E+01 | 1.4970E+01 | 2.0488E+01 | 9.5033E+00 | 9.6698E+00 | |
| Rank | 5 | 2 | 3 | 4 | 7 | 1 | 8 | 6 | |
| F25 | Best | 4.2530E+03 | 4.0580E+03 | 2.8843E+03 | 3.1042E+03 | 3.9276E+03 | 4.0402E+03 | 2.9118E+03 | 2.8244E+03 |
| Avg | 4.7937E+03 | 4.3811E+03 | 4.2585E+03 | 4.5321E+03 | 4.3544E+03 | 4.4033E+03 | 4.6958E+03 | 4.1381E+03 | |
| Std | 2.5309E+02 | 1.9582E+02 | 3.2276E+02 | 4.0317E+02 | 3.4911E+02 | 2.1379E+02 | 7.0553E+02 | 3.8884E+02 | |
| Rank | 8 | 4 | 2 | 6 | 3 | 5 | 7 | 1 | |
| F26 | Best | 3.2126E+03 | 3.2132E+03 | 3.2115E+03 | 3.2169E+03 | 3.2312E+03 | 3.2080E+03 | 3.2274E+03 | 3.2275E+03 |
| Avg | 3.2350E+03 | 3.2371E+03 | 3.2274E+03 | 3.2346E+03 | 3.2449E+03 | 3.2303E+03 | 3.2499E+03 | 3.2394E+03 | |
| Std | 1.3741E+01 | 1.4185E+01 | 8.5678E+00 | 1.0896E+01 | 8.9307E+00 | 1.3456E+01 | 1.0848E+01 | 7.6155E+00 | |
| Rank | 4 | 5 | 1 | 3 | 7 | 2 | 8 | 6 | |
| F27 | Best | 3.2268E+03 | 3.2257E+03 | 3.2418E+03 | 3.2620E+03 | 3.2302E+03 | 3.2226E+03 | 3.2839E+03 | 3.2372E+03 |
| Avg | 3.3045E+03 | 3.2867E+03 | 3.3026E+03 | 3.3160E+03 | 3.2989E+03 | 3.2790E+03 | 3.3128E+03 | 3.2901E+03 | |
| Std | 4.6372E+01 | 3.6571E+01 | 2.1287E+01 | 4.1564E+01 | 1.9186E+01 | 2.5438E+01 | 1.6709E+01 | 1.3314E+01 | |
| Rank | 6 | 2 | 5 | 8 | 4 | 1 | 7 | 3 | |
| F28 | Best | 3.5081E+03 | 3.4715E+03 | 3.4554E+03 | 3.5361E+03 | 3.4819E+03 | 3.4627E+03 | 3.5292E+03 | 3.4884E+03 |
| Avg | 3.8439E+03 | 3.7374E+03 | 3.6655E+03 | 3.8386E+03 | 3.6428E+03 | 3.7199E+03 | 3.7652E+03 | 3.5727E+03 | |
| Std | 1.8650E+02 | 1.4860E+02 | 1.5881E+02 | 1.7895E+02 | 1.3438E+02 | 1.7171E+02 | 1.4886E+02 | 7.9040E+01 | |
| Rank | 8 | 5 | 3 | 7 | 2 | 4 | 6 | 1 | |
| F29 | Best | 2.3332E+05 | 2.4081E+04 | 2.2046E+05 | 2.5097E+05 | 2.3033E+04 | 1.6590E+04 | 3.0036E+05 | 1.4092E+04 |
| Avg | 2.4397E+06 | 1.5570E+05 | 8.7634E+05 | 2.1945E+06 | 7.2225E+04 | 7.0292E+04 | 3.0593E+06 | 2.3200E+04 | |
| Std | 2.0619E+06 | 1.5443E+05 | 5.8123E+05 | 1.3247E+06 | 5.2229E+04 | 9.5801E+04 | 1.3977E+06 | 9.4801E+03 | |
| Rank | 7 | 4 | 5 | 6 | 3 | 2 | 8 | 1 |
| No. | Index | RIME | DRIME-D | DRIME-S | DRIME-H | DRIME-DS | DRIME-DH | DRIME-SH | DRIME |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 6.8842E+07 | 1.1229E+07 | 2.6951E+07 | 4.8922E+07 | 1.7144E+07 | 1.3659E+07 | 5.9938E+07 | 4.0061E+06 |
| Avg | 1.6944E+08 | 4.9376E+07 | 7.9082E+07 | 1.3133E+08 | 6.3718E+07 | 3.9428E+07 | 1.6596E+08 | 2.0985E+07 | |
| Std | 7.6863E+07 | 2.6791E+07 | 3.5014E+07 | 5.6907E+07 | 4.3985E+07 | 2.0648E+07 | 8.4964E+07 | 1.2195E+07 | |
| Rank | 8 | 3 | 5 | 6 | 4 | 2 | 7 | 1 | |
| F2 | Best | 5.6999E+04 | 1.4024E+04 | 5.7187E+04 | 5.1857E+04 | 1.0705E+04 | 9.0775E+03 | 7.0485E+04 | 6.4166E+03 |
| Avg | 1.0342E+05 | 2.1710E+04 | 8.2396E+04 | 9.0327E+04 | 1.8606E+04 | 2.0696E+04 | 9.2906E+04 | 1.1025E+04 | |
| Std | 2.6705E+04 | 6.1452E+03 | 1.3124E+04 | 1.8187E+04 | 4.7448E+03 | 4.5363E+03 | 9.8947E+03 | 2.7665E+03 | |
| Rank | 8 | 4 | 5 | 6 | 2 | 3 | 7 | 1 | |
| F3 | Best | 5.0124E+02 | 5.4367E+02 | 5.9847E+02 | 5.8217E+02 | 6.2434E+02 | 5.5332E+02 | 6.7983E+02 | 6.1259E+02 |
| Avg | 6.7392E+02 | 6.5097E+02 | 6.5763E+02 | 6.6400E+02 | 6.9777E+02 | 6.5509E+02 | 7.2854E+02 | 6.6641E+02 | |
| Std | 7.0428E+01 | 5.9318E+01 | 4.5162E+01 | 4.0517E+01 | 3.3749E+01 | 4.2226E+01 | 3.0955E+01 | 2.3270E+01 | |
| Rank | 6 | 1 | 3 | 4 | 7 | 2 | 8 | 5 | |
| F4 | Best | 6.1377E+02 | 5.8455E+02 | 5.8051E+02 | 6.1549E+02 | 5.6834E+02 | 5.8311E+02 | 6.1142E+02 | 5.6453E+02 |
| Avg | 7.0896E+02 | 6.3644E+02 | 6.2185E+02 | 6.5131E+02 | 6.0555E+02 | 6.2273E+02 | 6.3998E+02 | 5.9621E+02 | |
| Std | 4.7270E+01 | 2.9374E+01 | 2.7384E+01 | 2.5404E+01 | 2.2218E+01 | 2.2991E+01 | 1.6078E+01 | 1.6224E+01 | |
| Rank | 8 | 5 | 3 | 7 | 2 | 4 | 6 | 1 | |
| F5 | Best | 6.0966E+02 | 6.0340E+02 | 6.0303E+02 | 6.0649E+02 | 6.0417E+02 | 6.0243E+02 | 6.0664E+02 | 6.0127E+02 |
| Avg | 6.1745E+02 | 6.0641E+02 | 6.0603E+02 | 6.1379E+02 | 6.0910E+02 | 6.0664E+02 | 6.1462E+02 | 6.0404E+02 | |
| Std | 4.9970E+00 | 2.6165E+00 | 2.0779E+00 | 3.7287E+00 | 2.7240E+00 | 3.4057E+00 | 3.9966E+00 | 1.3802E+00 | |
| Rank | 8 | 3 | 2 | 6 | 5 | 4 | 7 | 1 | |
| F6 | Best | 9.7473E+02 | 9.0287E+02 | 8.9254E+02 | 9.6701E+02 | 8.7195E+02 | 8.9040E+02 | 8.9257E+02 | 8.3515E+02 |
| Avg | 1.1025E+03 | 9.6137E+02 | 9.6839E+02 | 1.0447E+03 | 9.5689E+02 | 9.4862E+02 | 9.8966E+02 | 9.2051E+02 | |
| Std | 5.8103E+01 | 3.6185E+01 | 3.5425E+01 | 4.8305E+01 | 4.4980E+01 | 3.3563E+01 | 4.3218E+01 | 4.2875E+01 | |
| Rank | 8 | 4 | 5 | 7 | 3 | 2 | 6 | 1 | |
| F7 | Best | 9.7874E+02 | 8.8096E+02 | 8.8617E+02 | 9.1852E+02 | 8.6805E+02 | 8.6989E+02 | 8.9683E+02 | 8.6561E+02 |
| Avg | 1.0211E+03 | 9.3426E+02 | 9.2826E+02 | 9.7468E+02 | 9.0749E+02 | 9.2144E+02 | 9.4691E+02 | 8.9997E+02 | |
| Std | 2.8451E+01 | 2.7876E+01 | 2.3561E+01 | 3.1959E+01 | 2.4293E+01 | 3.3034E+01 | 2.3190E+01 | 2.5593E+01 | |
| Rank | 8 | 5 | 4 | 7 | 2 | 3 | 6 | 1 | |
| F8 | Best | 2.3410E+03 | 9.9473E+02 | 1.1502E+03 | 1.5894E+03 | 1.2954E+03 | 1.0378E+03 | 1.7011E+03 | 1.0340E+03 |
| Avg | 4.7837E+03 | 1.2545E+03 | 1.6265E+03 | 3.2937E+03 | 1.6685E+03 | 1.3178E+03 | 2.7659E+03 | 1.2891E+03 | |
| Std | 2.0008E+03 | 1.8262E+02 | 3.7879E+02 | 1.2221E+03 | 2.7017E+02 | 2.1971E+02 | 5.4356E+02 | 2.0886E+02 | |
| Rank | 8 | 1 | 4 | 7 | 5 | 3 | 6 | 2 | |
| F9 | Best | 6.9718E+03 | 6.0779E+03 | 6.3990E+03 | 7.0923E+03 | 5.2324E+03 | 6.1550E+03 | 6.2358E+03 | 6.0615E+03 |
| Avg | 8.4727E+03 | 8.0093E+03 | 8.1804E+03 | 8.3135E+03 | 7.9582E+03 | 7.6611E+03 | 8.1973E+03 | 7.5995E+03 | |
| Std | 7.1243E+02 | 6.8480E+02 | 8.1634E+02 | 9.2031E+02 | 1.0785E+03 | 9.9074E+02 | 9.6119E+02 | 9.6850E+02 | |
| Rank | 8 | 4 | 5 | 7 | 3 | 2 | 6 | 1 | |
| F10 | Best | 1.5596E+03 | 1.2771E+03 | 1.3439E+03 | 1.4571E+03 | 1.3068E+03 | 1.2982E+03 | 1.4769E+03 | 1.2720E+03 |
| Avg | 1.7438E+03 | 1.3643E+03 | 1.5450E+03 | 1.6190E+03 | 1.3997E+03 | 1.3586E+03 | 1.7139E+03 | 1.3273E+03 | |
| Std | 1.3661E+02 | 4.2645E+01 | 8.5326E+01 | 1.2086E+02 | 4.9182E+01 | 3.2250E+01 | 9.6210E+01 | 4.0439E+01 | |
| Rank | 8 | 3 | 5 | 6 | 4 | 2 | 7 | 1 | |
| F11 | Best | 2.5340E+07 | 4.2343E+06 | 9.2450E+06 | 1.3893E+07 | 1.8414E+07 | 3.9642E+06 | 5.0953E+07 | 3.9022E+06 |
| Avg | 1.6119E+08 | 2.6636E+07 | 6.4051E+07 | 1.1900E+08 | 4.8430E+07 | 2.1478E+07 | 1.1918E+08 | 1.7893E+07 | |
| Std | 9.4393E+07 | 2.0104E+07 | 3.1884E+07 | 7.0784E+07 | 2.3545E+07 | 1.5136E+07 | 3.3639E+07 | 9.2710E+06 | |
| Rank | 8 | 3 | 5 | 6 | 4 | 2 | 7 | 1 | |
| F12 | Best | 1.7622E+05 | 3.9324E+04 | 8.3632E+04 | 1.5958E+05 | 2.4203E+04 | 1.3478E+04 | 1.2649E+05 | 1.5808E+04 |
| Avg | 8.6703E+05 | 7.8250E+04 | 3.9502E+05 | 7.0257E+05 | 4.3286E+04 | 3.0531E+04 | 3.6808E+05 | 2.0819E+04 | |
| Std | 5.4712E+05 | 2.5628E+04 | 2.7333E+05 | 4.6678E+05 | 1.4136E+04 | 9.8550E+03 | 2.8331E+05 | 3.6439E+03 | |
| Rank | 8 | 4 | 6 | 7 | 3 | 2 | 5 | 1 | |
| F13 | Best | 1.4859E+04 | 1.7043E+03 | 5.9307E+04 | 1.0732E+05 | 1.8393E+03 | 1.7197E+03 | 9.1187E+04 | 1.5816E+03 |
| Avg | 3.4422E+05 | 2.4598E+03 | 3.2347E+05 | 3.1018E+05 | 2.0704E+03 | 2.2215E+03 | 2.8552E+05 | 1.6520E+03 | |
| Std | 2.3876E+05 | 1.0667E+03 | 1.8652E+05 | 1.1861E+05 | 2.1865E+02 | 7.7410E+02 | 1.2982E+05 | 4.2203E+01 | |
| Rank | 8 | 4 | 7 | 6 | 2 | 3 | 5 | 1 | |
| F14 | Best | 5.9325E+04 | 5.4444E+03 | 1.4716E+04 | 3.1202E+04 | 6.0818E+03 | 4.8916E+03 | 1.9496E+04 | 3.7229E+03 |
| Avg | 1.6172E+05 | 1.7407E+04 | 5.7953E+04 | 1.2734E+05 | 1.3251E+04 | 1.2218E+04 | 7.2578E+04 | 6.9619E+03 | |
| Std | 7.5990E+04 | 6.4615E+03 | 3.5581E+04 | 7.9048E+04 | 4.8655E+03 | 6.2291E+03 | 6.5924E+04 | 1.6229E+03 | |
| Rank | 8 | 4 | 5 | 7 | 3 | 2 | 6 | 1 | |
| F15 | Best | 2.8888E+03 | 2.3568E+03 | 2.1413E+03 | 2.8750E+03 | 2.3318E+03 | 2.4614E+03 | 2.3269E+03 | 2.1112E+03 |
| Avg | 3.5722E+03 | 3.3121E+03 | 2.8044E+03 | 3.3146E+03 | 2.7016E+03 | 3.0659E+03 | 2.7828E+03 | 2.5272E+03 | |
| Std | 4.5475E+02 | 4.0429E+02 | 4.0448E+02 | 2.9803E+02 | 2.0846E+02 | 3.6727E+02 | 3.1264E+02 | 2.6810E+02 | |
| Rank | 8 | 6 | 4 | 7 | 2 | 5 | 3 | 1 | |
| F16 | Best | 2.4104E+03 | 2.1830E+03 | 2.2797E+03 | 2.3834E+03 | 2.2480E+03 | 2.1528E+03 | 2.3025E+03 | 2.2575E+03 |
| Avg | 3.1609E+03 | 2.7990E+03 | 2.8522E+03 | 2.9706E+03 | 2.7490E+03 | 2.7837E+03 | 2.8759E+03 | 2.7246E+03 | |
| Std | 3.3127E+02 | 2.7240E+02 | 3.0014E+02 | 3.1538E+02 | 2.6557E+02 | 2.8475E+02 | 2.4462E+02 | 2.2001E+02 | |
| Rank | 8 | 4 | 5 | 7 | 2 | 3 | 6 | 1 | |
| F17 | Best | 2.0622E+05 | 1.8308E+04 | 2.2999E+05 | 4.2525E+05 | 1.4246E+04 | 1.2619E+04 | 6.4348E+05 | 3.6396E+03 |
| Avg | 3.1300E+06 | 3.9390E+04 | 2.2081E+06 | 3.5798E+06 | 2.4992E+04 | 3.1249E+04 | 2.0300E+06 | 8.3535E+03 | |
| Std | 2.4282E+06 | 1.6947E+04 | 1.4597E+06 | 2.4560E+06 | 6.2697E+03 | 1.3418E+04 | 6.2573E+05 | 4.5065E+03 | |
| Rank | 7 | 4 | 6 | 8 | 2 | 3 | 5 | 1 | |
| F18 | Best | 7.6775E+04 | 4.7780E+03 | 1.3249E+04 | 4.7473E+04 | 1.3799E+04 | 3.5611E+03 | 5.2486E+04 | 1.0285E+04 |
| Avg | 1.2091E+06 | 2.5676E+04 | 6.4263E+04 | 7.9577E+05 | 2.3370E+04 | 1.5497E+04 | 1.4870E+05 | 1.6155E+04 | |
| Std | 1.0279E+06 | 1.4872E+04 | 3.2194E+04 | 8.2275E+05 | 6.2811E+03 | 6.9362E+03 | 5.6727E+04 | 2.9681E+03 | |
| Rank | 8 | 4 | 5 | 7 | 3 | 1 | 6 | 2 | |
| F19 | Best | 2.4917E+03 | 2.4222E+03 | 2.2993E+03 | 2.5340E+03 | 2.2420E+03 | 2.6339E+03 | 2.3514E+03 | 2.2472E+03 |
| Avg | 3.0445E+03 | 2.8730E+03 | 2.8522E+03 | 2.9920E+03 | 2.7611E+03 | 2.9723E+03 | 2.8210E+03 | 2.6364E+03 | |
| Std | 3.1228E+02 | 2.6321E+02 | 2.7514E+02 | 2.2737E+02 | 2.6063E+02 | 2.0337E+02 | 3.1726E+02 | 2.3806E+02 | |
| Rank | 8 | 5 | 4 | 7 | 2 | 6 | 3 | 1 | |
| F20 | Best | 2.4708E+03 | 2.3773E+03 | 2.3695E+03 | 2.4228E+03 | 2.3555E+03 | 2.3822E+03 | 2.3876E+03 | 2.3532E+03 |
| Avg | 2.5238E+03 | 2.4354E+03 | 2.4197E+03 | 2.4626E+03 | 2.4005E+03 | 2.4259E+03 | 2.4298E+03 | 2.3836E+03 | |
| Std | 3.2690E+01 | 2.9704E+01 | 2.4794E+01 | 2.0295E+01 | 2.9132E+01 | 2.2537E+01 | 2.1438E+01 | 2.0439E+01 | |
| Rank | 8 | 6 | 3 | 7 | 2 | 4 | 5 | 1 | |
| F21 | Best | 7.9296E+03 | 7.5058E+03 | 7.8433E+03 | 7.4386E+03 | 2.3687E+03 | 6.3818E+03 | 2.3789E+03 | 2.3353E+03 |
| Avg | 1.0109E+04 | 9.7136E+03 | 9.7054E+03 | 9.7030E+03 | 8.2635E+03 | 9.0114E+03 | 9.5690E+03 | 8.2025E+03 | |
| Std | 9.8119E+02 | 1.0575E+03 | 1.0090E+03 | 1.0186E+03 | 3.3855E+03 | 8.9966E+02 | 2.6488E+03 | 3.2379E+03 | |
| Rank | 8 | 7 | 6 | 5 | 2 | 3 | 4 | 1 | |
| F22 | Best | 2.8446E+03 | 2.8331E+03 | 2.8244E+03 | 2.8472E+03 | 2.8197E+03 | 2.8466E+03 | 2.8300E+03 | 2.7913E+03 |
| Avg | 2.9741E+03 | 2.9050E+03 | 2.8696E+03 | 2.9342E+03 | 2.8692E+03 | 2.8980E+03 | 2.8907E+03 | 2.8347E+03 | |
| Std | 6.2520E+01 | 4.4425E+01 | 3.1244E+01 | 5.2863E+01 | 3.5649E+01 | 2.4428E+01 | 2.5956E+01 | 2.3233E+01 | |
| Rank | 8 | 6 | 3 | 7 | 2 | 5 | 4 | 1 | |
| F23 | Best | 3.0060E+03 | 3.0147E+03 | 2.9837E+03 | 3.0093E+03 | 2.9583E+03 | 2.9927E+03 | 2.9820E+03 | 2.9502E+03 |
| Avg | 3.0981E+03 | 3.0803E+03 | 3.0278E+03 | 3.0650E+03 | 3.0132E+03 | 3.0556E+03 | 3.0365E+03 | 2.9809E+03 | |
| Std | 4.4117E+01 | 4.0485E+01 | 2.2892E+01 | 3.9217E+01 | 2.9039E+01 | 3.4204E+01 | 3.0245E+01 | 1.7682E+01 | |
| Rank | 8 | 7 | 3 | 6 | 2 | 5 | 4 | 1 | |
| F24 | Best | 3.0794E+03 | 3.0407E+03 | 3.0779E+03 | 3.0908E+03 | 3.1513E+03 | 3.0719E+03 | 3.1712E+03 | 3.1392E+03 |
| Avg | 3.1591E+03 | 3.1248E+03 | 3.1759E+03 | 3.1736E+03 | 3.2116E+03 | 3.1234E+03 | 3.2597E+03 | 3.1865E+03 | |
| Std | 4.3522E+01 | 3.2373E+01 | 4.4457E+01 | 5.2837E+01 | 3.4061E+01 | 3.8251E+01 | 4.3347E+01 | 2.8716E+01 | |
| Rank | 3 | 2 | 5 | 4 | 7 | 1 | 8 | 6 | |
| F25 | Best | 5.4970E+03 | 4.9030E+03 | 4.7098E+03 | 5.1428E+03 | 4.7188E+03 | 4.4625E+03 | 5.7398E+03 | 4.8458E+03 |
| Avg | 6.2197E+03 | 5.2969E+03 | 5.2194E+03 | 5.7559E+03 | 5.4517E+03 | 5.2209E+03 | 6.5919E+03 | 5.2630E+03 | |
| Std | 4.3409E+02 | 3.0327E+02 | 2.8945E+02 | 3.3792E+02 | 3.4429E+02 | 2.7085E+02 | 6.4049E+02 | 1.9879E+02 | |
| Rank | 7 | 4 | 1 | 6 | 5 | 2 | 8 | 3 | |
| F26 | Best | 3.3828E+03 | 3.3615E+03 | 3.3679E+03 | 3.3911E+03 | 3.4594E+03 | 3.3698E+03 | 3.4829E+03 | 3.3985E+03 |
| Avg | 3.4677E+03 | 3.4733E+03 | 3.4409E+03 | 3.4955E+03 | 3.5382E+03 | 3.4642E+03 | 3.5947E+03 | 3.4901E+03 | |
| Std | 5.0072E+01 | 6.2015E+01 | 3.9575E+01 | 8.0240E+01 | 4.2303E+01 | 5.5016E+01 | 6.5057E+01 | 4.4434E+01 | |
| Rank | 3 | 4 | 1 | 6 | 7 | 2 | 8 | 5 | |
| F27 | Best | 3.3303E+03 | 3.3782E+03 | 3.4057E+03 | 3.3569E+03 | 3.4844E+03 | 3.3644E+03 | 3.5166E+03 | 3.4371E+03 |
| Avg | 3.4680E+03 | 3.4689E+03 | 3.4976E+03 | 3.4896E+03 | 3.6221E+03 | 3.4715E+03 | 3.6518E+03 | 3.5491E+03 | |
| Std | 7.4788E+01 | 5.7980E+01 | 6.7463E+01 | 7.7676E+01 | 6.9326E+01 | 5.1127E+01 | 6.9556E+01 | 5.0592E+01 | |
| Rank | 1 | 2 | 5 | 4 | 7 | 3 | 8 | 6 | |
| F28 | Best | 3.9736E+03 | 3.6380E+03 | 3.8659E+03 | 3.9180E+03 | 3.8510E+03 | 3.8954E+03 | 4.1923E+03 | 3.8499E+03 |
| Avg | 4.6282E+03 | 4.2313E+03 | 4.2389E+03 | 4.5937E+03 | 4.3210E+03 | 4.3048E+03 | 4.5727E+03 | 4.1930E+03 | |
| Std | 3.5122E+02 | 3.2531E+02 | 2.5734E+02 | 3.6678E+02 | 2.5488E+02 | 2.7314E+02 | 2.0024E+02 | 1.5125E+02 | |
| Rank | 8 | 2 | 3 | 7 | 5 | 4 | 6 | 1 | |
| F29 | Best | 3.5875E+07 | 1.4594E+07 | 1.7073E+07 | 3.4513E+07 | 3.1068E+07 | 8.0112E+06 | 7.3721E+07 | 1.1161E+07 |
| Avg | 5.8634E+07 | 2.4029E+07 | 3.4440E+07 | 6.2055E+07 | 4.9682E+07 | 1.3578E+07 | 1.0282E+08 | 2.1554E+07 | |
| Std | 1.7764E+07 | 7.5368E+06 | 9.6168E+06 | 1.7402E+07 | 1.2143E+07 | 3.5107E+06 | 1.6889E+07 | 6.1361E+06 | |
| Rank | 6 | 3 | 4 | 7 | 5 | 1 | 8 | 2 |
| No. | Index | RIME | DRIME-D | DRIME-S | DRIME-H | DRIME-DS | DRIME-DH | DRIME-SH | DRIME |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Best | 8.9770E+08 | 4.1054E+08 | 4.8701E+08 | 7.3966E+08 | 4.3739E+08 | 4.8051E+08 | 1.0262E+09 | 1.8597E+08 |
| Avg | 1.5648E+09 | 7.2491E+08 | 7.8224E+08 | 1.2931E+09 | 1.0680E+09 | 7.3183E+08 | 1.7410E+09 | 4.5502E+08 | |
| Std | 3.8504E+08 | 1.7556E+08 | 1.9183E+08 | 3.2408E+08 | 4.3808E+08 | 2.4677E+08 | 5.6854E+08 | 2.1106E+08 | |
| Rank | 7 | 2 | 4 | 6 | 5 | 3 | 8 | 1 | |
| F2 | Best | 3.0629E+05 | 8.1425E+04 | 2.0672E+05 | 2.3581E+05 | 6.5277E+04 | 1.0826E+05 | 2.1051E+05 | 5.4624E+04 |
| Avg | 3.7345E+05 | 1.3799E+05 | 2.6222E+05 | 3.3492E+05 | 8.7971E+04 | 1.4853E+05 | 2.5284E+05 | 7.0773E+04 | |
| Std | 4.2162E+04 | 2.4849E+04 | 2.6697E+04 | 4.8400E+04 | 1.1204E+04 | 2.4280E+04 | 1.7051E+04 | 9.0094E+03 | |
| Rank | 8 | 3 | 6 | 7 | 2 | 4 | 5 | 1 | |
| F3 | Best | 9.2913E+02 | 9.1827E+02 | 9.8009E+02 | 9.3543E+02 | 1.0122E+03 | 8.9736E+02 | 1.0644E+03 | 9.2033E+02 |
| Avg | 1.1140E+03 | 1.0294E+03 | 1.0647E+03 | 1.1251E+03 | 1.1100E+03 | 1.0331E+03 | 1.2355E+03 | 1.0414E+03 | |
| Std | 8.4048E+01 | 6.3630E+01 | 6.4550E+01 | 1.0056E+02 | 6.2417E+01 | 7.4486E+01 | 8.4769E+01 | 6.8193E+01 | |
| Rank | 6 | 1 | 4 | 7 | 5 | 2 | 8 | 3 | |
| F4 | Best | 9.8405E+02 | 8.0246E+02 | 7.8648E+02 | 8.8861E+02 | 7.8909E+02 | 7.9250E+02 | 9.1442E+02 | 7.6337E+02 |
| Avg | 1.1105E+03 | 8.9929E+02 | 8.8522E+02 | 1.0171E+03 | 8.8904E+02 | 8.9459E+02 | 9.8371E+02 | 8.3476E+02 | |
| Std | 7.8946E+01 | 4.9735E+01 | 4.4703E+01 | 7.5043E+01 | 5.4520E+01 | 5.4467E+01 | 3.8567E+01 | 5.5361E+01 | |
| Rank | 8 | 5 | 2 | 7 | 3 | 4 | 6 | 1 | |
| F5 | Best | 6.2116E+02 | 6.0916E+02 | 6.1195E+02 | 6.2030E+02 | 6.1376E+02 | 6.1071E+02 | 6.2441E+02 | 6.0875E+02 |
| Avg | 6.3233E+02 | 6.1635E+02 | 6.1594E+02 | 6.2817E+02 | 6.2152E+02 | 6.1568E+02 | 6.3208E+02 | 6.1504E+02 | |
| Std | 5.3855E+00 | 3.6484E+00 | 3.0324E+00 | 3.8997E+00 | 3.9459E+00 | 2.9474E+00 | 3.8124E+00 | 2.8775E+00 | |
| Rank | 8 | 4 | 3 | 6 | 5 | 2 | 7 | 1 | |
| F6 | Best | 1.7638E+03 | 1.3104E+03 | 1.3360E+03 | 1.5797E+03 | 1.2303E+03 | 1.2509E+03 | 1.4285E+03 | 1.2401E+03 |
| Avg | 1.8845E+03 | 1.4485E+03 | 1.4985E+03 | 1.7524E+03 | 1.4676E+03 | 1.3865E+03 | 1.6200E+03 | 1.3717E+03 | |
| Std | 8.2051E+01 | 7.7140E+01 | 6.6815E+01 | 9.5638E+01 | 1.0628E+02 | 6.0128E+01 | 8.5829E+01 | 8.2306E+01 | |
| Rank | 8 | 3 | 5 | 7 | 4 | 2 | 6 | 1 | |
| F7 | Best | 1.2700E+03 | 1.1258E+03 | 1.1292E+03 | 1.2210E+03 | 1.1042E+03 | 1.1296E+03 | 1.2288E+03 | 1.0340E+03 |
| Avg | 1.4183E+03 | 1.2119E+03 | 1.1946E+03 | 1.3285E+03 | 1.2038E+03 | 1.2081E+03 | 1.2967E+03 | 1.1217E+03 | |
| Std | 8.4831E+01 | 4.8780E+01 | 4.6168E+01 | 6.2342E+01 | 4.8860E+01 | 4.9272E+01 | 3.8791E+01 | 4.1154E+01 | |
| Rank | 8 | 5 | 2 | 7 | 3 | 4 | 6 | 1 | |
| F8 | Best | 1.0631E+04 | 2.6509E+03 | 4.4201E+03 | 9.0533E+03 | 4.7367E+03 | 3.1090E+03 | 1.3128E+04 | 4.3350E+03 |
| Avg | 2.2456E+04 | 5.0535E+03 | 7.7561E+03 | 1.8042E+04 | 9.5806E+03 | 4.4571E+03 | 1.6651E+04 | 6.6472E+03 | |
| Std | 7.8428E+03 | 1.4373E+03 | 2.0313E+03 | 5.2229E+03 | 2.3857E+03 | 1.0624E+03 | 2.1085E+03 | 1.1423E+03 | |
| Rank | 8 | 2 | 4 | 7 | 5 | 1 | 6 | 3 | |
| F9 | Best | 1.7015E+04 | 1.5835E+04 | 1.4934E+04 | 1.6093E+04 | 1.5225E+04 | 1.5052E+04 | 1.6698E+04 | 1.4964E+04 |
| Avg | 1.9568E+04 | 1.9267E+04 | 1.8290E+04 | 1.8666E+04 | 2.1158E+04 | 1.8749E+04 | 1.9809E+04 | 1.8742E+04 | |
| Std | 1.2078E+03 | 1.6163E+03 | 1.4406E+03 | 1.6826E+03 | 3.3141E+03 | 1.6845E+03 | 2.1039E+03 | 2.5902E+03 | |
| Rank | 6 | 5 | 1 | 2 | 8 | 4 | 7 | 3 | |
| F10 | Best | 6.4350E+03 | 2.6082E+03 | 6.5749E+03 | 6.5748E+03 | 3.3022E+03 | 2.6927E+03 | 1.1361E+04 | 2.6623E+03 |
| Avg | 1.0324E+04 | 3.5106E+03 | 1.0568E+04 | 9.9497E+03 | 3.9388E+03 | 3.2575E+03 | 1.8125E+04 | 3.1655E+03 | |
| Std | 2.3534E+03 | 3.6694E+02 | 2.4258E+03 | 1.9364E+03 | 4.0055E+02 | 3.4538E+02 | 3.1061E+03 | 2.9751E+02 | |
| Rank | 6 | 3 | 7 | 5 | 4 | 2 | 8 | 1 | |
| F11 | Best | 2.9446E+08 | 1.4715E+08 | 2.9286E+08 | 2.8080E+08 | 4.3340E+08 | 1.5534E+08 | 4.8213E+08 | 3.3608E+08 |
| Avg | 7.9315E+08 | 4.3223E+08 | 5.5190E+08 | 7.6233E+08 | 5.6918E+08 | 3.6312E+08 | 6.7380E+08 | 4.3000E+08 | |
| Std | 3.0286E+08 | 1.8430E+08 | 1.4377E+08 | 3.0241E+08 | 1.1797E+08 | 1.5322E+08 | 9.7163E+07 | 4.9462E+07 | |
| Rank | 8 | 3 | 4 | 7 | 5 | 1 | 6 | 2 | |
| F12 | Best | 1.3984E+06 | 6.0985E+04 | 4.8624E+05 | 6.9845E+05 | 3.4275E+04 | 4.1750E+04 | 3.2828E+05 | 1.8665E+04 |
| Avg | 4.2650E+06 | 1.2603E+05 | 1.2447E+06 | 2.7896E+06 | 6.0901E+04 | 8.3238E+04 | 1.6683E+06 | 2.3730E+04 | |
| Std | 4.1321E+06 | 4.3398E+04 | 6.1621E+05 | 1.5377E+06 | 5.3372E+04 | 3.0701E+04 | 1.0668E+06 | 3.1901E+03 | |
| Rank | 8 | 4 | 5 | 7 | 2 | 3 | 6 | 1 | |
| F13 | Best | 1.4184E+06 | 1.1947E+04 | 1.2974E+06 | 1.5213E+06 | 5.3429E+03 | 9.1460E+03 | 2.8930E+06 | 2.0737E+03 |
| Avg | 5.1483E+06 | 3.0093E+04 | 3.5269E+06 | 4.4013E+06 | 1.8792E+04 | 2.3127E+04 | 4.2129E+06 | 3.6614E+03 | |
| Std | 2.4045E+06 | 1.6807E+04 | 1.3065E+06 | 2.3299E+06 | 8.8927E+03 | 1.1042E+04 | 7.1744E+05 | 2.4276E+03 | |
| Rank | 8 | 4 | 5 | 7 | 2 | 3 | 6 | 1 | |
| F14 | Best | 1.4018E+05 | 1.7003E+04 | 5.7279E+04 | 1.5196E+05 | 1.6092E+04 | 8.7381E+03 | 4.4947E+04 | 1.0036E+04 |
| Avg | 7.0962E+05 | 2.8459E+05 | 2.0193E+05 | 4.8666E+05 | 2.1733E+04 | 1.6700E+04 | 2.4432E+05 | 1.2583E+04 | |
| Std | 4.6458E+05 | 1.3528E+06 | 1.2768E+05 | 2.9531E+05 | 3.0188E+03 | 5.2715E+03 | 1.9855E+05 | 1.3319E+03 | |
| Rank | 8 | 6 | 4 | 7 | 3 | 2 | 5 | 1 | |
| F15 | Best | 4.7109E+03 | 4.3822E+03 | 3.8354E+03 | 3.9894E+03 | 4.3096E+03 | 4.4412E+03 | 4.5370E+03 | 3.3743E+03 |
| Avg | 6.1292E+03 | 5.9358E+03 | 5.4679E+03 | 6.0565E+03 | 5.2928E+03 | 5.6363E+03 | 5.8111E+03 | 5.1112E+03 | |
| Std | 8.1024E+02 | 7.5826E+02 | 7.7912E+02 | 7.7983E+02 | 5.0896E+02 | 6.5913E+02 | 5.6480E+02 | 6.0194E+02 | |
| Rank | 8 | 6 | 3 | 7 | 2 | 4 | 5 | 1 | |
| F16 | Best | 4.4819E+03 | 3.7651E+03 | 3.8030E+03 | 3.9451E+03 | 3.4557E+03 | 3.6036E+03 | 3.6302E+03 | 2.8039E+03 |
| Avg | 5.2664E+03 | 4.7229E+03 | 4.4207E+03 | 4.9875E+03 | 4.2084E+03 | 4.5575E+03 | 4.4310E+03 | 4.0253E+03 | |
| Std | 4.1898E+02 | 4.3555E+02 | 3.7812E+02 | 5.2234E+02 | 4.0321E+02 | 5.0020E+02 | 3.8993E+02 | 4.0261E+02 | |
| Rank | 8 | 6 | 3 | 7 | 2 | 5 | 4 | 1 | |
| F17 | Best | 2.7467E+06 | 5.2545E+04 | 1.3980E+06 | 1.2959E+06 | 5.1301E+04 | 5.1064E+04 | 1.9984E+06 | 1.7350E+04 |
| Avg | 8.1556E+06 | 1.0268E+05 | 3.3888E+06 | 5.9812E+06 | 7.0415E+04 | 7.7756E+04 | 3.1128E+06 | 3.6221E+04 | |
| Std | 3.4667E+06 | 3.0172E+04 | 1.1656E+06 | 2.9122E+06 | 1.2779E+04 | 1.9685E+04 | 5.6074E+05 | 1.3042E+04 | |
| Rank | 8 | 4 | 6 | 7 | 2 | 3 | 5 | 1 | |
| F18 | Best | 2.3432E+06 | 6.9368E+04 | 1.7372E+05 | 1.7845E+06 | 1.6439E+05 | 1.7922E+04 | 5.7161E+05 | 4.1133E+04 |
| Avg | 1.2306E+07 | 3.3961E+05 | 5.2294E+05 | 5.9457E+06 | 3.7152E+05 | 5.4707E+04 | 1.1542E+06 | 1.3806E+05 | |
| Std | 6.4231E+06 | 3.2416E+05 | 3.0877E+05 | 2.8307E+06 | 1.8326E+05 | 2.5200E+04 | 3.6885E+05 | 6.3792E+04 | |
| Rank | 8 | 3 | 5 | 7 | 4 | 1 | 6 | 2 | |
| F19 | Best | 4.5594E+03 | 4.1911E+03 | 3.8849E+03 | 4.5130E+03 | 3.9301E+03 | 3.2561E+03 | 3.9140E+03 | 3.1375E+03 |
| Avg | 5.3192E+03 | 4.9463E+03 | 4.7914E+03 | 5.2042E+03 | 4.6470E+03 | 4.8143E+03 | 4.6079E+03 | 4.3069E+03 | |
| Std | 4.7803E+02 | 4.1678E+02 | 4.5632E+02 | 3.1962E+02 | 3.7665E+02 | 5.8348E+02 | 4.8795E+02 | 5.0682E+02 | |
| Rank | 8 | 6 | 4 | 7 | 3 | 5 | 2 | 1 | |
| F20 | Best | 2.8427E+03 | 2.6144E+03 | 2.6298E+03 | 2.7293E+03 | 2.5850E+03 | 2.6583E+03 | 2.6604E+03 | 2.5424E+03 |
| Avg | 2.9663E+03 | 2.7378E+03 | 2.6996E+03 | 2.8651E+03 | 2.6886E+03 | 2.7335E+03 | 2.7546E+03 | 2.5954E+03 | |
| Std | 6.5904E+01 | 5.9858E+01 | 3.9706E+01 | 7.1787E+01 | 7.0904E+01 | 4.3024E+01 | 4.8331E+01 | 3.5985E+01 | |
| Rank | 8 | 5 | 3 | 7 | 2 | 4 | 6 | 1 | |
| F21 | Best | 1.8244E+04 | 1.8028E+04 | 1.6001E+04 | 1.8001E+04 | 1.8655E+04 | 1.8219E+04 | 1.8058E+04 | 1.7569E+04 |
| Avg | 2.2003E+04 | 2.1049E+04 | 2.1065E+04 | 2.1703E+04 | 2.1771E+04 | 2.1160E+04 | 2.1374E+04 | 2.0584E+04 | |
| Std | 1.3610E+03 | 1.6228E+03 | 2.2546E+03 | 1.4929E+03 | 1.8793E+03 | 1.3331E+03 | 2.1951E+03 | 2.2566E+03 | |
| Rank | 8 | 2 | 3 | 6 | 7 | 4 | 5 | 1 | |
| F22 | Best | 3.2334E+03 | 3.2459E+03 | 3.1214E+03 | 3.1846E+03 | 3.1427E+03 | 3.2093E+03 | 3.2161E+03 | 3.0879E+03 |
| Avg | 3.4149E+03 | 3.3503E+03 | 3.1926E+03 | 3.3459E+03 | 3.2412E+03 | 3.3170E+03 | 3.2921E+03 | 3.1578E+03 | |
| Std | 8.2638E+01 | 7.3948E+01 | 4.1678E+01 | 6.3792E+01 | 4.9117E+01 | 6.2955E+01 | 6.4551E+01 | 4.3185E+01 | |
| Rank | 8 | 7 | 2 | 6 | 3 | 5 | 4 | 1 | |
| F23 | Best | 3.7678E+03 | 3.6694E+03 | 3.5793E+03 | 3.7846E+03 | 3.5807E+03 | 3.7354E+03 | 3.6546E+03 | 3.5022E+03 |
| Avg | 3.9611E+03 | 3.8840E+03 | 3.7046E+03 | 3.9113E+03 | 3.7046E+03 | 3.8745E+03 | 3.7854E+03 | 3.5991E+03 | |
| Std | 1.0294E+02 | 9.0606E+01 | 5.1293E+01 | 7.3307E+01 | 4.8487E+01 | 8.6730E+01 | 8.1218E+01 | 4.3531E+01 | |
| Rank | 8 | 6 | 2 | 7 | 3 | 5 | 4 | 1 | |
| F24 | Best | 3.6044E+03 | 3.5604E+03 | 3.6819E+03 | 3.6252E+03 | 3.7473E+03 | 3.6216E+03 | 3.8089E+03 | 3.6855E+03 |
| Avg | 3.8823E+03 | 3.7318E+03 | 3.7984E+03 | 3.8561E+03 | 3.8697E+03 | 3.7324E+03 | 3.9671E+03 | 3.7750E+03 | |
| Std | 1.3329E+02 | 8.5337E+01 | 5.9844E+01 | 1.2452E+02 | 6.8911E+01 | 8.4161E+01 | 8.7047E+01 | 6.6123E+01 | |
| Rank | 7 | 1 | 4 | 5 | 6 | 2 | 8 | 3 | |
| F25 | Best | 1.1328E+04 | 9.2692E+03 | 9.2462E+03 | 1.0567E+04 | 1.0566E+04 | 9.3506E+03 | 1.4335E+04 | 1.0327E+04 |
| Avg | 1.3047E+04 | 1.0950E+04 | 1.0357E+04 | 1.2314E+04 | 1.2984E+04 | 1.1099E+04 | 1.6992E+04 | 1.2120E+04 | |
| Std | 8.9873E+02 | 8.2882E+02 | 5.0322E+02 | 1.0641E+03 | 1.1268E+03 | 7.1887E+02 | 1.3756E+03 | 1.1013E+03 | |
| Rank | 7 | 2 | 1 | 5 | 6 | 3 | 8 | 4 | |
| F26 | Best | 3.6059E+03 | 3.6400E+03 | 3.5696E+03 | 3.6594E+03 | 3.8460E+03 | 3.5864E+03 | 3.9704E+03 | 3.7547E+03 |
| Avg | 3.7678E+03 | 3.7358E+03 | 3.6976E+03 | 3.8352E+03 | 3.9538E+03 | 3.7357E+03 | 4.1126E+03 | 3.8663E+03 | |
| Std | 1.0508E+02 | 7.0069E+01 | 7.6044E+01 | 9.4861E+01 | 5.4366E+01 | 9.4377E+01 | 7.7166E+01 | 5.7117E+01 | |
| Rank | 4 | 3 | 1 | 5 | 7 | 2 | 8 | 6 | |
| F27 | Best | 3.9053E+03 | 3.7708E+03 | 3.9151E+03 | 3.9002E+03 | 4.0500E+03 | 3.7643E+03 | 4.0666E+03 | 3.8831E+03 |
| Avg | 4.4116E+03 | 4.0032E+03 | 4.0487E+03 | 4.2211E+03 | 4.3197E+03 | 3.9862E+03 | 4.2964E+03 | 4.0196E+03 | |
| Std | 3.7284E+02 | 1.7655E+02 | 1.0137E+02 | 2.0927E+02 | 1.3792E+02 | 1.4358E+02 | 1.1794E+02 | 8.2876E+01 | |
| Rank | 8 | 2 | 4 | 5 | 7 | 1 | 6 | 3 | |
| F28 | Best | 7.2055E+03 | 5.8822E+03 | 6.2691E+03 | 6.8154E+03 | 6.4996E+03 | 5.5875E+03 | 7.1913E+03 | 6.1746E+03 |
| Avg | 8.1762E+03 | 7.2406E+03 | 6.9686E+03 | 7.9736E+03 | 7.2518E+03 | 6.8874E+03 | 8.1596E+03 | 6.9884E+03 | |
| Std | 5.2046E+02 | 5.8976E+02 | 4.2836E+02 | 6.1890E+02 | 4.3790E+02 | 5.1168E+02 | 4.6525E+02 | 4.4857E+02 | |
| Rank | 8 | 4 | 2 | 6 | 5 | 1 | 7 | 3 | |
| F29 | Best | 3.7308E+07 | 8.0644E+06 | 1.6563E+07 | 3.7415E+07 | 2.4745E+07 | 3.3686E+06 | 5.2336E+07 | 9.3543E+06 |
| Avg | 9.8516E+07 | 2.7585E+07 | 3.4680E+07 | 1.1485E+08 | 6.9989E+07 | 9.9647E+06 | 9.3678E+07 | 2.9735E+07 | |
| Std | 4.8600E+07 | 1.7460E+07 | 1.3125E+07 | 4.6390E+07 | 2.7973E+07 | 4.2379E+06 | 2.0876E+07 | 1.0504E+07 | |
| Rank | 7 | 2 | 4 | 8 | 5 | 1 | 6 | 3 |
| No. | Index | DRIME | ACGRIME | TERIME | IRIME | DNMRIME | GLSRIME | HERIME |
|---|---|---|---|---|---|---|---|---|
| F1 | Best | 5.1814E+02 | 3.3067E+05 | 7.5237E+06 | 2.2307E+07 | 2.7128E+05 | 9.6798E+04 | 5.4938E+05 |
| Mean | 3.2371E+03 | 1.2818E+07 | 5.1310E+07 | 7.6251E+07 | 3.0813E+06 | 6.8640E+05 | 2.3975E+06 | |
| Std | 2.5383E+03 | 1.6586E+07 | 3.3615E+07 | 4.3877E+07 | 2.7421E+06 | 4.5168E+05 | 1.6278E+06 | |
| Rank | 1 | 5 | 6 | 7 | 4 | 2 | 3 | |
| F2 | Best | 3.0006E+02 | 4.6380E+02 | 1.1004E+03 | 1.3107E+03 | 3.8840E+02 | 3.0677E+02 | 5.3700E+02 |
| Mean | 3.0034E+02 | 3.1631E+03 | 3.5008E+03 | 6.9038E+03 | 9.1730E+02 | 3.7202E+02 | 9.4899E+02 | |
| Std | 2.6805E-01 | 1.4854E+03 | 1.7516E+03 | 3.1164E+03 | 4.2869E+02 | 5.9531E+01 | 3.6599E+02 | |
| Rank | 1 | 5 | 6 | 7 | 3 | 2 | 4 | |
| F3 | Best | 4.0448E+02 | 4.0571E+02 | 4.0802E+02 | 4.0858E+02 | 4.0092E+02 | 4.0014E+02 | 4.0326E+02 |
| Mean | 4.0637E+02 | 4.1359E+02 | 4.1607E+02 | 4.1414E+02 | 4.1460E+02 | 4.1251E+02 | 4.0687E+02 | |
| Std | 6.6339E-01 | 1.2472E+01 | 1.4985E+01 | 1.1695E+01 | 2.1446E+01 | 1.8262E+01 | 1.6816E+00 | |
| Rank | 1 | 4 | 7 | 5 | 6 | 3 | 2 | |
| F4 | Best | 5.0398E+02 | 5.0606E+02 | 5.1330E+02 | 5.2060E+02 | 5.0738E+02 | 5.0579E+02 | 5.0682E+02 |
| Mean | 5.0746E+02 | 5.2031E+02 | 5.3550E+02 | 5.3680E+02 | 5.2536E+02 | 5.1786E+02 | 5.1739E+02 | |
| Std | 3.4503E+00 | 6.9714E+00 | 1.0886E+01 | 8.9340E+00 | 1.0592E+01 | 6.0282E+00 | 8.6039E+00 | |
| Rank | 1 | 4 | 6 | 7 | 5 | 3 | 2 | |
| F5 | Best | 6.0002E+02 | 6.0054E+02 | 6.0513E+02 | 6.0374E+02 | 6.0061E+02 | 6.0032E+02 | 6.0067E+02 |
| Mean | 6.0008E+02 | 6.0229E+02 | 6.1061E+02 | 6.0704E+02 | 6.0291E+02 | 6.0110E+02 | 6.0153E+02 | |
| Std | 5.9760E-02 | 1.4271E+00 | 5.1388E+00 | 2.5475E+00 | 1.6607E+00 | 6.1004E-01 | 5.5189E-01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 2 | 3 | |
| F6 | Best | 7.1247E+02 | 7.1905E+02 | 7.4747E+02 | 7.3911E+02 | 7.2770E+02 | 7.1499E+02 | 7.2436E+02 |
| Mean | 7.1894E+02 | 7.3829E+02 | 7.7161E+02 | 7.6619E+02 | 7.4097E+02 | 7.3200E+02 | 7.3729E+02 | |
| Std | 5.8972E+00 | 1.1978E+01 | 1.4910E+01 | 1.1363E+01 | 9.0340E+00 | 8.7371E+00 | 8.9954E+00 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 2 | 3 | |
| F7 | Best | 8.0100E+02 | 8.0734E+02 | 8.2000E+02 | 8.1798E+02 | 8.0808E+02 | 8.0877E+02 | 8.0452E+02 |
| Mean | 8.0552E+02 | 8.1733E+02 | 8.3943E+02 | 8.3427E+02 | 8.2176E+02 | 8.1940E+02 | 8.1646E+02 | |
| Std | 4.1056E+00 | 5.6577E+00 | 1.2212E+01 | 1.0795E+01 | 7.2783E+00 | 7.5120E+00 | 7.0936E+00 | |
| Rank | 1 | 3 | 7 | 6 | 5 | 4 | 2 | |
| F8 | Best | 9.0000E+02 | 9.0385E+02 | 9.3837E+02 | 9.1130E+02 | 9.0070E+02 | 9.0013E+02 | 9.0043E+02 |
| Mean | 9.0001E+02 | 9.2141E+02 | 1.0574E+03 | 9.5783E+02 | 9.1436E+02 | 9.0192E+02 | 9.0348E+02 | |
| Std | 2.8392E-02 | 1.6873E+01 | 1.3403E+02 | 3.6822E+01 | 3.4698E+01 | 2.3450E+00 | 3.8248E+00 | |
| Rank | 1 | 5 | 7 | 6 | 4 | 2 | 3 | |
| F9 | Best | 1.1443E+03 | 1.2823E+03 | 1.6184E+03 | 1.5535E+03 | 1.1926E+03 | 1.1509E+03 | 1.1851E+03 |
| Mean | 1.5124E+03 | 1.6859E+03 | 2.1115E+03 | 2.0620E+03 | 1.8057E+03 | 1.5815E+03 | 1.7087E+03 | |
| Std | 2.4264E+02 | 1.9338E+02 | 2.8942E+02 | 2.8209E+02 | 3.5364E+02 | 2.1274E+02 | 2.3124E+02 | |
| Rank | 1 | 3 | 7 | 6 | 5 | 2 | 4 | |
| F10 | Best | 1.1030E+03 | 1.1134E+03 | 1.1195E+03 | 1.1190E+03 | 1.1084E+03 | 1.1033E+03 | 1.1076E+03 |
| Mean | 1.1076E+03 | 1.1363E+03 | 1.1672E+03 | 1.1983E+03 | 1.1363E+03 | 1.1190E+03 | 1.1283E+03 | |
| Std | 2.6459E+00 | 1.8658E+01 | 5.0604E+01 | 7.3858E+01 | 3.8084E+01 | 8.2126E+00 | 1.6923E+01 | |
| Rank | 1 | 4 | 6 | 7 | 5 | 2 | 3 | |
| F11 | Best | 2.2731E+03 | 7.0765E+03 | 4.3035E+05 | 5.2080E+05 | 1.4891E+05 | 1.0822E+04 | 3.3161E+04 |
| Mean | 6.0176E+03 | 1.0415E+06 | 4.6612E+06 | 5.2371E+06 | 2.1520E+06 | 1.5505E+06 | 5.5664E+05 | |
| Std | 2.4674E+03 | 1.4556E+06 | 4.6815E+06 | 3.3826E+06 | 2.4412E+06 | 1.7284E+06 | 6.0174E+05 | |
| Rank | 1 | 3 | 6 | 7 | 5 | 4 | 2 | |
| F12 | Best | 1.3216E+03 | 1.4699E+03 | 2.1123E+03 | 4.0927E+03 | 2.1731E+03 | 1.5516E+03 | 1.7123E+03 |
| Mean | 1.5404E+03 | 8.8473E+03 | 3.4039E+04 | 2.2892E+04 | 1.0694E+04 | 1.0359E+04 | 4.7785E+03 | |
| Std | 6.2107E+02 | 9.1047E+03 | 2.9406E+04 | 2.3484E+04 | 8.4689E+03 | 8.3378E+03 | 3.7273E+03 | |
| Rank | 1 | 3 | 7 | 6 | 5 | 4 | 2 | |
| F13 | Best | 1.4060E+03 | 1.4349E+03 | 1.4437E+03 | 1.4472E+03 | 1.4287E+03 | 1.4355E+03 | 1.4359E+03 |
| Mean | 1.4197E+03 | 1.9845E+03 | 2.0474E+03 | 2.0490E+03 | 2.5083E+03 | 3.2916E+03 | 1.4588E+03 | |
| Std | 7.9296E+00 | 7.3686E+02 | 7.3150E+02 | 7.0483E+02 | 1.0336E+03 | 2.4803E+03 | 1.4634E+01 | |
| Rank | 1 | 3 | 4 | 5 | 6 | 7 | 2 | |
| F14 | Best | 1.5024E+03 | 1.5377E+03 | 1.6628E+03 | 1.6407E+03 | 1.5753E+03 | 1.5236E+03 | 1.5454E+03 |
| Mean | 1.5065E+03 | 2.1469E+03 | 5.9798E+03 | 3.4177E+03 | 3.5726E+03 | 4.3072E+03 | 1.6534E+03 | |
| Std | 3.7066E+00 | 9.8283E+02 | 6.2037E+03 | 1.6218E+03 | 2.2672E+03 | 3.4889E+03 | 1.0082E+02 | |
| Rank | 1 | 3 | 7 | 4 | 5 | 6 | 2 | |
| F15 | Best | 1.6034E+03 | 1.6029E+03 | 1.6220E+03 | 1.6188E+03 | 1.6246E+03 | 1.6031E+03 | 1.6062E+03 |
| Mean | 1.6465E+03 | 1.6700E+03 | 1.7257E+03 | 1.6947E+03 | 1.7920E+03 | 1.6747E+03 | 1.6664E+03 | |
| Std | 5.5149E+01 | 7.0261E+01 | 1.1038E+02 | 7.0183E+01 | 1.0105E+02 | 8.6550E+01 | 8.1616E+01 | |
| Rank | 1 | 3 | 6 | 5 | 7 | 4 | 2 | |
| F16 | Best | 1.7061E+03 | 1.7147E+03 | 1.7331E+03 | 1.7335E+03 | 1.7255E+03 | 1.7106E+03 | 1.7286E+03 |
| Mean | 1.7348E+03 | 1.7448E+03 | 1.7694E+03 | 1.7732E+03 | 1.7489E+03 | 1.7484E+03 | 1.7504E+03 | |
| Std | 1.1868E+01 | 1.4806E+01 | 2.7793E+01 | 2.3828E+01 | 1.5326E+01 | 3.2241E+01 | 1.8149E+01 | |
| Rank | 1 | 2 | 6 | 7 | 4 | 3 | 5 | |
| F17 | Best | 1.8130E+03 | 2.2192E+03 | 9.9290E+03 | 7.4769E+03 | 4.1502E+03 | 3.2168E+03 | 2.2587E+03 |
| Mean | 1.8338E+03 | 2.4056E+04 | 5.4859E+04 | 7.9348E+04 | 2.0018E+04 | 1.9780E+04 | 7.4998E+03 | |
| Std | 1.3569E+01 | 1.4407E+04 | 5.9321E+04 | 1.1262E+05 | 1.4007E+04 | 1.3298E+04 | 4.5430E+03 | |
| Rank | 1 | 5 | 6 | 7 | 4 | 3 | 2 | |
| F18 | Best | 1.9019E+03 | 1.9144E+03 | 1.9528E+03 | 1.9435E+03 | 1.9302E+03 | 1.9150E+03 | 1.9165E+03 |
| Mean | 1.9038E+03 | 4.2748E+03 | 8.6585E+03 | 3.6782E+03 | 7.8346E+03 | 5.3413E+03 | 1.9525E+03 | |
| Std | 1.1183E+00 | 4.6648E+03 | 7.3340E+03 | 1.9018E+03 | 6.2439E+03 | 4.4800E+03 | 3.2453E+01 | |
| Rank | 1 | 4 | 7 | 3 | 6 | 5 | 2 | |
| F19 | Best | 2.0022E+03 | 2.0204E+03 | 2.0404E+03 | 2.0356E+03 | 2.0173E+03 | 2.0085E+03 | 2.0222E+03 |
| Mean | 2.0252E+03 | 2.0323E+03 | 2.0725E+03 | 2.0650E+03 | 2.0416E+03 | 2.0314E+03 | 2.0476E+03 | |
| Std | 6.9262E+00 | 9.3229E+00 | 1.9951E+01 | 1.6765E+01 | 1.6514E+01 | 1.1030E+01 | 1.2731E+01 | |
| Rank | 1 | 3 | 7 | 6 | 4 | 2 | 5 | |
| F20 | Best | 2.2001E+03 | 2.2033E+03 | 2.2039E+03 | 2.2065E+03 | 2.1038E+03 | 2.2002E+03 | 2.2037E+03 |
| Mean | 2.2694E+03 | 2.2622E+03 | 2.2238E+03 | 2.2529E+03 | 2.2401E+03 | 2.2687E+03 | 2.2923E+03 | |
| Std | 5.1784E+01 | 5.5331E+01 | 4.1994E+01 | 5.8145E+01 | 6.0624E+01 | 5.9400E+01 | 4.8337E+01 | |
| Rank | 6 | 4 | 1 | 3 | 2 | 5 | 7 | |
| F21 | Best | 2.3002E+03 | 2.2293E+03 | 2.2327E+03 | 2.2451E+03 | 2.2472E+03 | 2.2235E+03 | 2.2403E+03 |
| Mean | 2.3024E+03 | 2.3011E+03 | 2.3046E+03 | 2.3134E+03 | 2.3070E+03 | 2.2972E+03 | 2.3068E+03 | |
| Std | 1.4445E+00 | 2.5145E+01 | 3.2063E+01 | 2.1801E+01 | 1.4687E+01 | 2.7946E+01 | 1.2747E+01 | |
| Rank | 3 | 2 | 4 | 7 | 6 | 1 | 5 | |
| F22 | Best | 2.6030E+03 | 2.6119E+03 | 2.6192E+03 | 2.6194E+03 | 2.6099E+03 | 2.6109E+03 | 2.6103E+03 |
| Mean | 2.6109E+03 | 2.6231E+03 | 2.6404E+03 | 2.6328E+03 | 2.6254E+03 | 2.6196E+03 | 2.6197E+03 | |
| Std | 5.5501E+00 | 6.3402E+00 | 1.1698E+01 | 7.7455E+00 | 9.4443E+00 | 7.1074E+00 | 5.8055E+00 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 2 | 3 | |
| F23 | Best | 2.5014E+03 | 2.5171E+03 | 2.5165E+03 | 2.5342E+03 | 2.5022E+03 | 2.5015E+03 | 2.5089E+03 |
| Mean | 2.7270E+03 | 2.6939E+03 | 2.6898E+03 | 2.7162E+03 | 2.6942E+03 | 2.7059E+03 | 2.7293E+03 | |
| Std | 4.2795E+01 | 9.1954E+01 | 1.1356E+02 | 9.1291E+01 | 1.0202E+02 | 8.9147E+01 | 5.9068E+01 | |
| Rank | 6 | 2 | 1 | 5 | 3 | 4 | 7 | |
| F24 | Best | 2.8982E+03 | 2.9022E+03 | 2.9063E+03 | 2.9049E+03 | 2.8982E+03 | 2.8981E+03 | 2.8993E+03 |
| Mean | 2.9324E+03 | 2.9391E+03 | 2.9518E+03 | 2.9411E+03 | 2.9318E+03 | 2.9267E+03 | 2.9363E+03 | |
| Std | 2.0593E+01 | 1.7716E+01 | 2.2104E+01 | 1.9462E+01 | 2.7527E+01 | 2.4221E+01 | 1.9785E+01 | |
| Rank | 3 | 5 | 7 | 6 | 2 | 1 | 4 | |
| F25 | Best | 2.9001E+03 | 2.9371E+03 | 2.9285E+03 | 2.9359E+03 | 2.6256E+03 | 2.8208E+03 | 2.8336E+03 |
| Mean | 2.9004E+03 | 3.0041E+03 | 2.9698E+03 | 2.9847E+03 | 2.9281E+03 | 2.9073E+03 | 2.9505E+03 | |
| Std | 8.9534E-01 | 4.1346E+01 | 3.3066E+01 | 2.6742E+01 | 1.0171E+02 | 3.1717E+01 | 4.3012E+01 | |
| Rank | 1 | 7 | 5 | 6 | 3 | 2 | 4 | |
| F26 | Best | 3.0900E+03 | 3.0917E+03 | 3.0952E+03 | 3.0921E+03 | 3.0899E+03 | 3.0891E+03 | 3.0897E+03 |
| Mean | 3.0952E+03 | 3.0961E+03 | 3.1007E+03 | 3.0957E+03 | 3.1051E+03 | 3.0981E+03 | 3.0957E+03 | |
| Std | 3.0830E+00 | 2.3771E+00 | 3.6364E+00 | 1.9684E+00 | 2.6113E+01 | 9.3359E+00 | 3.2619E+00 | |
| Rank | 1 | 4 | 6 | 2 | 7 | 5 | 3 | |
| F27 | Best | 3.1003E+03 | 3.1455E+03 | 3.1470E+03 | 3.1701E+03 | 3.1712E+03 | 3.1049E+03 | 3.1688E+03 |
| Mean | 3.2472E+03 | 3.2721E+03 | 3.2289E+03 | 3.2611E+03 | 3.2780E+03 | 3.2578E+03 | 3.2876E+03 | |
| Std | 1.4411E+02 | 9.8123E+01 | 6.8487E+01 | 8.7826E+01 | 4.4606E+01 | 1.0908E+02 | 1.0322E+02 | |
| Rank | 2 | 5 | 1 | 4 | 6 | 3 | 7 | |
| F28 | Best | 3.1510E+03 | 3.1634E+03 | 3.1641E+03 | 3.1673E+03 | 3.1624E+03 | 3.1458E+03 | 3.1435E+03 |
| Mean | 3.1781E+03 | 3.1998E+03 | 3.2352E+03 | 3.2320E+03 | 3.2272E+03 | 3.2015E+03 | 3.1998E+03 | |
| Std | 1.5368E+01 | 3.3335E+01 | 4.8027E+01 | 4.3537E+01 | 4.5461E+01 | 4.2963E+01 | 3.3793E+01 | |
| Rank | 1 | 3 | 7 | 6 | 5 | 4 | 2 | |
| F29 | Best | 3.6850E+03 | 1.5305E+04 | 6.2882E+03 | 1.7845E+04 | 4.0761E+03 | 1.0473E+04 | 6.2787E+03 |
| Mean | 3.7257E+04 | 7.7955E+05 | 8.4200E+05 | 4.5259E+05 | 4.3102E+05 | 3.9316E+05 | 1.7435E+05 | |
| Std | 1.7219E+05 | 7.8556E+05 | 7.0777E+05 | 3.6341E+05 | 6.9757E+05 | 5.8292E+05 | 3.9112E+05 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 3 | 2 |
| No. | Index | DRIME | ACGRIME | TERIME | IRIME | DNMRIME | GLSRIME | HERIME |
|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.0336E+05 | 4.8841E+08 | 1.2960E+09 | 8.4963E+08 | 4.8641E+07 | 1.4735E+07 | 6.2973E+07 |
| Mean | 5.4087E+05 | 1.3448E+09 | 3.3320E+09 | 1.6033E+09 | 1.6532E+08 | 4.6103E+07 | 1.4147E+08 | |
| Std | 4.4719E+05 | 6.2776E+08 | 1.0997E+09 | 4.5194E+08 | 7.1437E+07 | 2.4082E+07 | 5.7468E+07 | |
| Rank | 1 | 5 | 7 | 6 | 4 | 2 | 3 | |
| F2 | Best | 5.5212E+02 | 3.2891E+04 | 4.0986E+04 | 5.1987E+04 | 2.1997E+04 | 1.4403E+04 | 2.2396E+04 |
| Mean | 1.4789E+03 | 4.4268E+04 | 7.2898E+04 | 1.0542E+05 | 3.5318E+04 | 3.3418E+04 | 4.0920E+04 | |
| Std | 6.3419E+02 | 6.4916E+03 | 1.6017E+04 | 3.4314E+04 | 6.7233E+03 | 9.1794E+03 | 9.8096E+03 | |
| Rank | 1 | 5 | 6 | 7 | 3 | 2 | 4 | |
| F3 | Best | 4.9689E+02 | 5.4655E+02 | 6.0906E+02 | 5.5146E+02 | 5.0778E+02 | 4.8078E+02 | 5.0223E+02 |
| Mean | 5.2169E+02 | 6.6563E+02 | 7.4032E+02 | 6.7119E+02 | 5.5675E+02 | 5.2737E+02 | 5.6426E+02 | |
| Std | 7.5835E+00 | 7.3116E+01 | 1.0862E+02 | 6.1113E+01 | 2.9843E+01 | 2.9919E+01 | 4.1480E+01 | |
| Rank | 1 | 5 | 7 | 6 | 3 | 2 | 4 | |
| F4 | Best | 5.3063E+02 | 5.9279E+02 | 6.6056E+02 | 6.3627E+02 | 6.0834E+02 | 5.6999E+02 | 5.7764E+02 |
| Mean | 5.4376E+02 | 6.3550E+02 | 7.1749E+02 | 6.8435E+02 | 6.4332E+02 | 6.0107E+02 | 6.1189E+02 | |
| Std | 1.2058E+01 | 2.2472E+01 | 2.9071E+01 | 2.5816E+01 | 2.6525E+01 | 2.2103E+01 | 2.7785E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 2 | 3 | |
| F5 | Best | 6.0037E+02 | 6.0442E+02 | 6.1688E+02 | 6.1467E+02 | 6.0675E+02 | 6.0309E+02 | 6.0510E+02 |
| Mean | 6.0146E+02 | 6.1319E+02 | 6.3002E+02 | 6.2156E+02 | 6.1966E+02 | 6.0965E+02 | 6.0887E+02 | |
| Std | 7.5368E-01 | 5.1186E+00 | 7.4612E+00 | 4.1436E+00 | 6.6782E+00 | 4.5907E+00 | 3.1014E+00 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 3 | 2 | |
| F6 | Best | 7.6244E+02 | 8.3319E+02 | 1.0073E+03 | 9.4120E+02 | 8.7771E+02 | 8.4552E+02 | 8.3710E+02 |
| Mean | 8.0749E+02 | 8.9098E+02 | 1.1095E+03 | 9.9628E+02 | 9.3706E+02 | 9.0891E+02 | 9.0316E+02 | |
| Std | 3.0163E+01 | 2.8834E+01 | 6.6344E+01 | 3.4708E+01 | 3.0782E+01 | 2.8721E+01 | 2.8076E+01 | |
| Rank | 1 | 2 | 7 | 6 | 5 | 4 | 3 | |
| F7 | Best | 8.1895E+02 | 8.9347E+02 | 9.6151E+02 | 9.2753E+02 | 8.9590E+02 | 8.6156E+02 | 8.6186E+02 |
| Mean | 8.3161E+02 | 9.2489E+02 | 1.0258E+03 | 9.7279E+02 | 9.4118E+02 | 9.1644E+02 | 8.9859E+02 | |
| Std | 7.4953E+00 | 1.7143E+01 | 3.3795E+01 | 2.5930E+01 | 2.2525E+01 | 2.9832E+01 | 2.0905E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 3 | 2 | |
| F8 | Best | 9.0167E+02 | 1.5021E+03 | 2.3938E+03 | 2.0870E+03 | 2.0969E+03 | 1.0240E+03 | 9.7810E+02 |
| Mean | 9.1526E+02 | 2.3034E+03 | 5.2723E+03 | 3.3540E+03 | 4.2497E+03 | 2.1969E+03 | 1.2764E+03 | |
| Std | 1.0496E+01 | 5.1485E+02 | 2.1518E+03 | 8.3031E+02 | 1.8090E+03 | 1.4347E+03 | 1.9355E+02 | |
| Rank | 1 | 4 | 7 | 5 | 6 | 3 | 2 | |
| F9 | Best | 3.0332E+03 | 4.3911E+03 | 4.9054E+03 | 5.0989E+03 | 4.2081E+03 | 3.3031E+03 | 4.1513E+03 |
| Mean | 4.4306E+03 | 5.3795E+03 | 6.7718E+03 | 6.7347E+03 | 5.6576E+03 | 4.9137E+03 | 5.4832E+03 | |
| Std | 6.4303E+02 | 5.3014E+02 | 6.9386E+02 | 6.2874E+02 | 5.9367E+02 | 7.8958E+02 | 6.4670E+02 | |
| Rank | 1 | 3 | 7 | 6 | 5 | 2 | 4 | |
| F10 | Best | 1.1616E+03 | 1.3201E+03 | 1.3841E+03 | 1.5170E+03 | 1.2287E+03 | 1.2068E+03 | 1.2766E+03 |
| Mean | 1.2087E+03 | 1.5285E+03 | 1.5537E+03 | 1.8199E+03 | 1.3511E+03 | 1.3553E+03 | 1.3577E+03 | |
| Std | 2.3476E+01 | 1.5127E+02 | 1.7449E+02 | 2.5976E+02 | 5.9422E+01 | 6.8214E+01 | 5.0528E+01 | |
| Rank | 1 | 5 | 6 | 7 | 2 | 3 | 4 | |
| F11 | Best | 4.1685E+05 | 4.7962E+06 | 4.4022E+07 | 1.3099E+07 | 4.0568E+06 | 2.8368E+06 | 2.4011E+06 |
| Mean | 1.4532E+06 | 3.2360E+07 | 1.3008E+08 | 6.0499E+07 | 2.9955E+07 | 2.9073E+07 | 1.9569E+07 | |
| Std | 6.1274E+05 | 2.6793E+07 | 5.9344E+07 | 3.5924E+07 | 1.9657E+07 | 3.9080E+07 | 1.7633E+07 | |
| Rank | 1 | 5 | 7 | 6 | 4 | 3 | 2 | |
| F12 | Best | 6.6651E+03 | 3.0771E+04 | 2.0116E+06 | 7.7864E+05 | 1.9981E+05 | 8.8731E+04 | 1.5059E+05 |
| Mean | 1.7523E+04 | 3.1011E+05 | 2.7515E+07 | 6.0575E+06 | 8.3208E+05 | 3.3007E+05 | 4.8519E+05 | |
| Std | 6.3923E+03 | 6.1089E+05 | 2.2988E+07 | 6.7088E+06 | 8.1931E+05 | 1.7692E+05 | 3.7970E+05 | |
| Rank | 1 | 2 | 7 | 6 | 5 | 3 | 4 | |
| F13 | Best | 1.4710E+03 | 1.3800E+04 | 3.2359E+04 | 1.0429E+04 | 6.8502E+03 | 5.5607E+03 | 3.2881E+03 |
| Mean | 1.5007E+03 | 1.6460E+05 | 2.0947E+05 | 1.5245E+05 | 1.0551E+05 | 5.8419E+04 | 9.4105E+03 | |
| Std | 1.6259E+01 | 2.4078E+05 | 2.0618E+05 | 1.1400E+05 | 7.9645E+04 | 3.6039E+04 | 6.8349E+03 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 3 | 2 | |
| F14 | Best | 1.7322E+03 | 6.1418E+03 | 2.0093E+05 | 5.0626E+04 | 1.5981E+04 | 2.4272E+04 | 1.1373E+04 |
| Mean | 2.2916E+03 | 1.9363E+04 | 2.7200E+06 | 1.5671E+05 | 1.1890E+05 | 6.6010E+04 | 5.3294E+04 | |
| Std | 4.1223E+02 | 1.0715E+04 | 3.7554E+06 | 1.0075E+05 | 9.5072E+04 | 3.4445E+04 | 3.2617E+04 | |
| Rank | 1 | 2 | 7 | 6 | 5 | 4 | 3 | |
| F15 | Best | 1.9480E+03 | 2.0443E+03 | 2.5661E+03 | 2.3203E+03 | 2.2850E+03 | 1.8566E+03 | 2.1492E+03 |
| Mean | 2.4857E+03 | 2.6595E+03 | 3.0565E+03 | 2.9367E+03 | 2.7732E+03 | 2.6203E+03 | 2.6483E+03 | |
| Std | 3.0596E+02 | 3.0151E+02 | 3.1510E+02 | 2.7176E+02 | 2.9717E+02 | 2.8277E+02 | 2.9941E+02 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 2 | 3 | |
| F16 | Best | 1.7644E+03 | 1.8114E+03 | 1.8990E+03 | 1.8465E+03 | 1.8406E+03 | 1.8533E+03 | 1.8289E+03 |
| Mean | 1.8781E+03 | 2.0837E+03 | 2.2319E+03 | 2.2215E+03 | 2.1648E+03 | 2.1095E+03 | 2.0881E+03 | |
| Std | 8.9640E+01 | 1.6642E+02 | 1.9376E+02 | 1.9749E+02 | 1.7615E+02 | 1.6759E+02 | 1.7869E+02 | |
| Rank | 1 | 2 | 7 | 6 | 5 | 4 | 3 | |
| F17 | Best | 2.0838E+03 | 1.5737E+05 | 3.2312E+05 | 3.2971E+05 | 1.8164E+05 | 9.8760E+04 | 4.6539E+04 |
| Mean | 4.0202E+03 | 1.3578E+06 | 3.7876E+06 | 3.3920E+06 | 1.5970E+06 | 1.1443E+06 | 2.2500E+05 | |
| Std | 2.0100E+03 | 1.6140E+06 | 3.1266E+06 | 3.6537E+06 | 4.4564E+06 | 1.2295E+06 | 1.3385E+05 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 3 | 2 | |
| F18 | Best | 2.0235E+03 | 6.3676E+03 | 2.8112E+05 | 7.0371E+04 | 6.2003E+04 | 1.2922E+04 | 6.4667E+03 |
| Mean | 3.3183E+03 | 1.4031E+05 | 2.4671E+06 | 5.6837E+05 | 7.1626E+05 | 3.8888E+05 | 1.0203E+05 | |
| Std | 1.4974E+03 | 2.5767E+05 | 1.8858E+06 | 5.0652E+05 | 5.3642E+05 | 3.7354E+05 | 9.7780E+04 | |
| Rank | 1 | 3 | 7 | 5 | 6 | 4 | 2 | |
| F19 | Best | 2.1136E+03 | 2.2249E+03 | 2.1895E+03 | 2.2448E+03 | 2.2011E+03 | 2.1544E+03 | 2.1143E+03 |
| Mean | 2.2479E+03 | 2.4231E+03 | 2.4515E+03 | 2.4874E+03 | 2.4735E+03 | 2.4410E+03 | 2.4599E+03 | |
| Std | 5.0813E+01 | 1.5198E+02 | 1.5118E+02 | 1.4624E+02 | 1.4685E+02 | 1.5792E+02 | 1.4567E+02 | |
| Rank | 1 | 2 | 4 | 7 | 6 | 3 | 5 | |
| F20 | Best | 2.3195E+03 | 2.3806E+03 | 2.4632E+03 | 2.4264E+03 | 2.3757E+03 | 2.3652E+03 | 2.3710E+03 |
| Mean | 2.3386E+03 | 2.4195E+03 | 2.5173E+03 | 2.4670E+03 | 2.4220E+03 | 2.4047E+03 | 2.4031E+03 | |
| Std | 1.9274E+01 | 2.0210E+01 | 2.8866E+01 | 1.8847E+01 | 2.4847E+01 | 1.9789E+01 | 1.8972E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 3 | 2 | |
| F21 | Best | 2.3025E+03 | 2.4430E+03 | 2.6129E+03 | 2.5170E+03 | 2.3326E+03 | 2.3217E+03 | 2.3515E+03 |
| Mean | 2.3085E+03 | 2.5653E+03 | 5.1810E+03 | 4.4405E+03 | 2.3712E+03 | 3.7244E+03 | 2.6902E+03 | |
| Std | 3.2937E+00 | 8.1662E+01 | 2.8219E+03 | 2.6040E+03 | 2.2478E+01 | 1.8850E+03 | 1.1834E+03 | |
| Rank | 1 | 3 | 7 | 6 | 2 | 5 | 4 | |
| F22 | Best | 2.6729E+03 | 2.7334E+03 | 2.8174E+03 | 2.7859E+03 | 2.7297E+03 | 2.7223E+03 | 2.7126E+03 |
| Mean | 2.6954E+03 | 2.7740E+03 | 2.8806E+03 | 2.8255E+03 | 2.7818E+03 | 2.7741E+03 | 2.7627E+03 | |
| Std | 9.5088E+00 | 1.9033E+01 | 3.4206E+01 | 1.8417E+01 | 2.9431E+01 | 2.6143E+01 | 2.4350E+01 | |
| Rank | 1 | 3 | 7 | 6 | 5 | 4 | 2 | |
| F23 | Best | 2.8353E+03 | 2.9043E+03 | 3.0279E+03 | 2.9300E+03 | 2.9014E+03 | 2.8745E+03 | 2.8876E+03 |
| Mean | 2.8578E+03 | 2.9482E+03 | 3.0758E+03 | 3.0064E+03 | 2.9474E+03 | 2.9135E+03 | 2.9354E+03 | |
| Std | 1.3832E+01 | 2.5985E+01 | 3.1344E+01 | 3.1738E+01 | 2.8896E+01 | 1.9960E+01 | 2.1181E+01 | |
| Rank | 1 | 5 | 7 | 6 | 4 | 2 | 3 | |
| F24 | Best | 2.9025E+03 | 2.9808E+03 | 2.9784E+03 | 2.9686E+03 | 2.9158E+03 | 2.9039E+03 | 2.9013E+03 |
| Mean | 2.9293E+03 | 3.0490E+03 | 3.1056E+03 | 3.0390E+03 | 2.9718E+03 | 2.9425E+03 | 2.9409E+03 | |
| Std | 9.6698E+00 | 3.8988E+01 | 7.1104E+01 | 4.4591E+01 | 2.5050E+01 | 3.0919E+01 | 2.3965E+01 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 3 | 2 | |
| F25 | Best | 2.8244E+03 | 3.7719E+03 | 4.3158E+03 | 3.9297E+03 | 3.0812E+03 | 4.4363E+03 | 3.5239E+03 |
| Mean | 4.1381E+03 | 4.8631E+03 | 6.0762E+03 | 5.6024E+03 | 4.5786E+03 | 4.8746E+03 | 4.7859E+03 | |
| Std | 3.8884E+02 | 6.0370E+02 | 4.8961E+02 | 4.0049E+02 | 1.0200E+03 | 3.6468E+02 | 3.2753E+02 | |
| Rank | 1 | 4 | 7 | 6 | 2 | 5 | 3 | |
| F26 | Best | 3.2275E+03 | 3.2163E+03 | 3.2382E+03 | 3.2143E+03 | 3.2000E+03 | 3.2106E+03 | 3.2136E+03 |
| Mean | 3.2394E+03 | 3.2508E+03 | 3.2814E+03 | 3.2477E+03 | 3.2000E+03 | 3.2383E+03 | 3.2436E+03 | |
| Std | 7.6155E+00 | 2.2702E+01 | 1.9138E+01 | 1.4444E+01 | 7.6087E-05 | 1.3731E+01 | 1.5140E+01 | |
| Rank | 3 | 6 | 7 | 5 | 1 | 2 | 4 | |
| F27 | Best | 3.2372E+03 | 3.3275E+03 | 3.3612E+03 | 3.3230E+03 | 3.2960E+03 | 3.2615E+03 | 3.2601E+03 |
| Mean | 3.2901E+03 | 3.4473E+03 | 3.4709E+03 | 3.4557E+03 | 3.3201E+03 | 3.3143E+03 | 3.3309E+03 | |
| Std | 1.3314E+01 | 6.6006E+01 | 7.3040E+01 | 7.9150E+01 | 2.5143E+01 | 4.9278E+01 | 3.2898E+01 | |
| Rank | 1 | 5 | 7 | 6 | 3 | 2 | 4 | |
| F28 | Best | 3.4884E+03 | 3.5795E+03 | 3.5442E+03 | 3.6876E+03 | 3.5085E+03 | 3.5564E+03 | 3.5498E+03 |
| Mean | 3.5727E+03 | 3.8971E+03 | 4.0219E+03 | 3.9822E+03 | 3.8964E+03 | 3.9120E+03 | 3.8454E+03 | |
| Std | 7.9040E+01 | 1.9970E+02 | 2.1906E+02 | 1.6226E+02 | 1.7720E+02 | 1.7851E+02 | 1.7905E+02 | |
| Rank | 1 | 4 | 7 | 6 | 3 | 5 | 2 | |
| F29 | Best | 1.4092E+04 | 3.1747E+05 | 5.8935E+05 | 2.9409E+05 | 2.0665E+05 | 5.0334E+05 | 3.7614E+05 |
| Mean | 2.3200E+04 | 2.9804E+06 | 3.7727E+06 | 1.8312E+06 | 4.3743E+06 | 2.2049E+06 | 1.3340E+06 | |
| Std | 9.4801E+03 | 2.6411E+06 | 3.3171E+06 | 1.2379E+06 | 2.4402E+06 | 1.7938E+06 | 9.3962E+05 | |
| Rank | 1 | 5 | 6 | 3 | 7 | 4 | 2 |
| No. | Index | DRIME | ACGRIME | TERIME | IRIME | DNMRIME | GLSRIME | HERIME |
|---|---|---|---|---|---|---|---|---|
| F1 | Best | 4.0061E+06 | 4.3160E+09 | 7.4463E+09 | 5.0200E+09 | 4.8836E+08 | 1.1144E+08 | 4.7760E+08 |
| Mean | 2.0985E+07 | 9.6500E+09 | 1.4032E+10 | 7.4145E+09 | 9.3538E+08 | 2.1448E+08 | 8.9173E+08 | |
| Std | 1.2195E+07 | 2.8044E+09 | 4.4315E+09 | 1.6001E+09 | 2.5324E+08 | 7.7010E+07 | 2.5048E+08 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 2 | 3 | |
| F2 | Best | 6.4166E+03 | 9.6258E+04 | 1.1077E+05 | 1.6648E+05 | 6.6120E+04 | 8.1551E+04 | 9.4597E+04 |
| Mean | 1.1025E+04 | 1.2230E+05 | 1.9550E+05 | 2.3373E+05 | 1.0506E+05 | 1.0801E+05 | 1.2541E+05 | |
| Std | 2.7665E+03 | 1.5333E+04 | 3.5815E+04 | 3.9088E+04 | 1.8836E+04 | 1.9201E+04 | 1.5473E+04 | |
| Rank | 1 | 4 | 6 | 7 | 2 | 3 | 5 | |
| F3 | Best | 6.1259E+02 | 9.5752E+02 | 1.1993E+03 | 9.4378E+02 | 6.5411E+02 | 5.9392E+02 | 6.6341E+02 |
| Mean | 6.6641E+02 | 1.4279E+03 | 1.6360E+03 | 1.2605E+03 | 8.2876E+02 | 7.0132E+02 | 7.6319E+02 | |
| Std | 2.3270E+01 | 2.7922E+02 | 2.6796E+02 | 1.6559E+02 | 8.2911E+01 | 6.7552E+01 | 6.4043E+01 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 2 | 3 | |
| F4 | Best | 5.6453E+02 | 7.3863E+02 | 8.7670E+02 | 7.6958E+02 | 7.5898E+02 | 6.5922E+02 | 6.7235E+02 |
| Mean | 5.9621E+02 | 8.2722E+02 | 9.5194E+02 | 8.6983E+02 | 8.5904E+02 | 7.1999E+02 | 7.3665E+02 | |
| Std | 1.6224E+01 | 4.7839E+01 | 4.7833E+01 | 4.1180E+01 | 5.0941E+01 | 4.1845E+01 | 3.7656E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 2 | 3 | |
| F5 | Best | 6.0127E+02 | 6.1454E+02 | 6.3323E+02 | 6.2104E+02 | 6.2001E+02 | 6.0974E+02 | 6.0965E+02 |
| Mean | 6.0404E+02 | 6.2463E+02 | 6.4524E+02 | 6.3015E+02 | 6.3694E+02 | 6.1936E+02 | 6.1665E+02 | |
| Std | 1.3802E+00 | 5.7147E+00 | 7.1778E+00 | 4.8244E+00 | 9.1159E+00 | 4.7932E+00 | 3.4328E+00 | |
| Rank | 1 | 4 | 7 | 5 | 6 | 3 | 2 | |
| F6 | Best | 8.3515E+02 | 1.0492E+03 | 1.3950E+03 | 1.1734E+03 | 1.1204E+03 | 1.0488E+03 | 9.8411E+02 |
| Mean | 9.2051E+02 | 1.1531E+03 | 1.6014E+03 | 1.2702E+03 | 1.2355E+03 | 1.1590E+03 | 1.1112E+03 | |
| Std | 4.2875E+01 | 6.0461E+01 | 1.0043E+02 | 4.5683E+01 | 6.1200E+01 | 6.6925E+01 | 5.5200E+01 | |
| Rank | 1 | 3 | 7 | 6 | 5 | 4 | 2 | |
| F7 | Best | 8.6561E+02 | 1.0636E+03 | 1.1452E+03 | 1.0909E+03 | 1.0540E+03 | 9.2434E+02 | 9.7990E+02 |
| Mean | 8.9997E+02 | 1.1281E+03 | 1.2406E+03 | 1.1541E+03 | 1.1265E+03 | 1.0352E+03 | 1.0330E+03 | |
| Std | 2.5593E+01 | 3.8945E+01 | 4.5361E+01 | 3.8378E+01 | 4.1006E+01 | 4.4583E+01 | 2.8093E+01 | |
| Rank | 1 | 5 | 7 | 6 | 4 | 3 | 2 | |
| F8 | Best | 1.0340E+03 | 5.4360E+03 | 8.0719E+03 | 8.1368E+03 | 3.4808E+03 | 2.9768E+03 | 2.1596E+03 |
| Mean | 1.2891E+03 | 9.7377E+03 | 1.5865E+04 | 1.1704E+04 | 1.4169E+04 | 7.0123E+03 | 3.3747E+03 | |
| Std | 2.0886E+02 | 3.1598E+03 | 4.9580E+03 | 2.8518E+03 | 6.4904E+03 | 3.6817E+03 | 1.0067E+03 | |
| Rank | 1 | 4 | 7 | 5 | 6 | 3 | 2 | |
| F9 | Best | 6.0615E+03 | 7.8792E+03 | 1.0238E+04 | 9.9878E+03 | 7.3709E+03 | 6.6421E+03 | 7.9677E+03 |
| Mean | 7.5995E+03 | 9.6049E+03 | 1.1354E+04 | 1.1399E+04 | 9.5865E+03 | 8.5313E+03 | 9.5969E+03 | |
| Std | 9.6850E+02 | 7.1470E+02 | 6.8686E+02 | 8.0164E+02 | 1.2410E+03 | 9.6025E+02 | 1.0518E+03 | |
| Rank | 1 | 5 | 6 | 7 | 3 | 2 | 4 | |
| F10 | Best | 1.2720E+03 | 1.9162E+03 | 1.7759E+03 | 3.0395E+03 | 1.6190E+03 | 1.4811E+03 | 1.5161E+03 |
| Mean | 1.3273E+03 | 2.8564E+03 | 2.9761E+03 | 4.4648E+03 | 1.9868E+03 | 1.7601E+03 | 1.8652E+03 | |
| Std | 4.0439E+01 | 5.7464E+02 | 6.5546E+02 | 1.0974E+03 | 1.7930E+02 | 1.3505E+02 | 1.7615E+02 | |
| Rank | 1 | 5 | 6 | 7 | 4 | 2 | 3 | |
| F11 | Best | 3.9022E+06 | 1.3678E+08 | 6.1262E+08 | 3.3268E+08 | 6.0217E+07 | 1.7972E+07 | 6.1562E+07 |
| Mean | 1.7893E+07 | 3.9805E+08 | 1.3215E+09 | 5.1778E+08 | 2.9731E+08 | 1.6899E+08 | 2.1223E+08 | |
| Std | 9.2710E+06 | 2.0055E+08 | 5.5261E+08 | 1.4919E+08 | 1.8002E+08 | 9.0723E+07 | 1.3960E+08 | |
| Rank | 1 | 5 | 7 | 6 | 4 | 2 | 3 | |
| F12 | Best | 1.5808E+04 | 2.2377E+05 | 2.0397E+07 | 1.6026E+07 | 1.2121E+06 | 4.9978E+05 | 4.2918E+05 |
| Mean | 2.0819E+04 | 8.8138E+06 | 1.1565E+08 | 3.8972E+07 | 6.6019E+06 | 1.4702E+06 | 2.6279E+06 | |
| Std | 3.6439E+03 | 1.8336E+07 | 7.4485E+07 | 1.9922E+07 | 5.6882E+06 | 7.0791E+05 | 2.2628E+06 | |
| Rank | 1 | 5 | 7 | 6 | 4 | 2 | 3 | |
| F13 | Best | 1.5816E+03 | 1.6835E+05 | 3.2142E+05 | 1.1499E+05 | 9.7100E+04 | 7.5670E+04 | 2.1875E+04 |
| Mean | 1.6520E+03 | 1.2608E+06 | 1.7423E+06 | 7.7348E+05 | 6.3666E+05 | 3.9081E+05 | 1.1939E+05 | |
| Std | 4.2203E+01 | 9.7651E+05 | 1.0786E+06 | 4.8758E+05 | 4.3643E+05 | 2.6936E+05 | 5.5707E+04 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 3 | 2 | |
| F14 | Best | 3.7229E+03 | 1.6900E+04 | 3.4446E+06 | 3.0362E+05 | 1.0442E+05 | 3.7243E+04 | 6.1344E+04 |
| Mean | 6.9619E+03 | 1.3479E+05 | 2.1192E+07 | 2.5133E+06 | 9.1928E+05 | 2.4854E+05 | 2.7178E+05 | |
| Std | 1.6229E+03 | 2.6137E+05 | 1.6330E+07 | 1.8905E+06 | 1.0788E+06 | 1.6771E+05 | 2.1330E+05 | |
| Rank | 1 | 2 | 7 | 6 | 5 | 3 | 4 | |
| F15 | Best | 2.1112E+03 | 2.7311E+03 | 3.6773E+03 | 2.6840E+03 | 2.7565E+03 | 2.8784E+03 | 2.4884E+03 |
| Mean | 2.5272E+03 | 3.3281E+03 | 4.5629E+03 | 3.9563E+03 | 3.6803E+03 | 3.5003E+03 | 3.3935E+03 | |
| Std | 2.6810E+02 | 3.6666E+02 | 4.0005E+02 | 3.9452E+02 | 3.6800E+02 | 3.3075E+02 | 4.5568E+02 | |
| Rank | 1 | 2 | 7 | 6 | 5 | 4 | 3 | |
| F16 | Best | 2.2575E+03 | 2.5518E+03 | 2.4124E+03 | 2.6005E+03 | 2.7540E+03 | 2.5052E+03 | 2.4218E+03 |
| Mean | 2.7246E+03 | 3.0939E+03 | 3.5473E+03 | 3.3702E+03 | 3.2013E+03 | 3.1138E+03 | 3.0158E+03 | |
| Std | 2.2001E+02 | 2.8413E+02 | 4.1792E+02 | 3.0022E+02 | 2.3169E+02 | 3.2528E+02 | 2.9847E+02 | |
| Rank | 1 | 3 | 7 | 6 | 5 | 4 | 2 | |
| F17 | Best | 3.6396E+03 | 8.1870E+05 | 1.2530E+06 | 8.0491E+05 | 7.0788E+05 | 7.4940E+05 | 2.8211E+05 |
| Mean | 8.3535E+03 | 4.1321E+06 | 1.0436E+07 | 5.7925E+06 | 3.8129E+06 | 3.8833E+06 | 1.4088E+06 | |
| Std | 4.5065E+03 | 3.2992E+06 | 7.6470E+06 | 4.7025E+06 | 2.0800E+06 | 2.6030E+06 | 1.0344E+06 | |
| Rank | 1 | 5 | 7 | 6 | 3 | 4 | 2 | |
| F18 | Best | 1.0285E+04 | 5.7372E+04 | 1.6781E+06 | 2.0122E+05 | 1.0604E+05 | 1.2285E+05 | 8.5345E+04 |
| Mean | 1.6155E+04 | 7.1641E+05 | 1.2194E+07 | 1.5156E+06 | 1.0430E+06 | 1.6525E+06 | 4.4752E+05 | |
| Std | 2.9681E+03 | 8.7414E+05 | 9.7777E+06 | 8.8988E+05 | 1.2848E+06 | 1.4633E+06 | 3.2383E+05 | |
| Rank | 1 | 3 | 7 | 5 | 4 | 6 | 2 | |
| F19 | Best | 2.2472E+03 | 2.3842E+03 | 2.7148E+03 | 2.5950E+03 | 2.5504E+03 | 2.6511E+03 | 2.3827E+03 |
| Mean | 2.6364E+03 | 3.0737E+03 | 3.4159E+03 | 3.2706E+03 | 3.1597E+03 | 3.0874E+03 | 3.0737E+03 | |
| Std | 2.3806E+02 | 2.6561E+02 | 2.9494E+02 | 2.8950E+02 | 2.6206E+02 | 2.4262E+02 | 3.3943E+02 | |
| Rank | 1 | 2 | 7 | 6 | 5 | 4 | 3 | |
| F20 | Best | 2.3532E+03 | 2.4795E+03 | 2.6692E+03 | 2.5989E+03 | 2.4901E+03 | 2.4426E+03 | 2.4735E+03 |
| Mean | 2.3836E+03 | 2.5607E+03 | 2.7396E+03 | 2.6726E+03 | 2.5666E+03 | 2.5339E+03 | 2.5362E+03 | |
| Std | 2.0439E+01 | 4.0378E+01 | 4.0096E+01 | 3.6702E+01 | 4.0530E+01 | 6.1555E+01 | 3.8940E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 2 | 3 | |
| F21 | Best | 2.3353E+03 | 4.1046E+03 | 1.1452E+04 | 1.2159E+04 | 2.5727E+03 | 7.5733E+03 | 8.8890E+03 |
| Mean | 8.2025E+03 | 1.1186E+04 | 1.3390E+04 | 1.3182E+04 | 1.1167E+04 | 1.0037E+04 | 1.1463E+04 | |
| Std | 3.2379E+03 | 2.0236E+03 | 9.2853E+02 | 6.0341E+02 | 3.3163E+03 | 1.0058E+03 | 1.0215E+03 | |
| Rank | 1 | 4 | 7 | 6 | 3 | 2 | 5 | |
| F22 | Best | 2.7913E+03 | 2.9374E+03 | 3.1276E+03 | 3.0226E+03 | 2.9164E+03 | 2.8762E+03 | 2.9014E+03 |
| Mean | 2.8347E+03 | 3.0275E+03 | 3.2210E+03 | 3.1192E+03 | 3.0473E+03 | 2.9780E+03 | 2.9947E+03 | |
| Std | 2.3233E+01 | 4.2403E+01 | 5.8147E+01 | 4.3726E+01 | 5.6929E+01 | 4.8666E+01 | 4.3853E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 2 | 3 | |
| F23 | Best | 2.9502E+03 | 3.0795E+03 | 3.3218E+03 | 3.2209E+03 | 3.0803E+03 | 3.0266E+03 | 3.0659E+03 |
| Mean | 2.9809E+03 | 3.1871E+03 | 3.4722E+03 | 3.2751E+03 | 3.1984E+03 | 3.1350E+03 | 3.1438E+03 | |
| Std | 1.7682E+01 | 4.3817E+01 | 6.5021E+01 | 2.9485E+01 | 7.6943E+01 | 4.7174E+01 | 4.2948E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 2 | 3 | |
| F24 | Best | 3.1392E+03 | 3.3488E+03 | 3.4123E+03 | 3.3512E+03 | 3.1686E+03 | 3.0908E+03 | 3.1687E+03 |
| Mean | 3.1865E+03 | 4.0210E+03 | 4.0792E+03 | 3.7676E+03 | 3.3245E+03 | 3.1796E+03 | 3.2615E+03 | |
| Std | 2.8716E+01 | 3.0357E+02 | 3.8422E+02 | 2.2412E+02 | 8.5180E+01 | 5.4280E+01 | 6.4202E+01 | |
| Rank | 2 | 6 | 7 | 5 | 4 | 1 | 3 | |
| F25 | Best | 4.8458E+03 | 5.2553E+03 | 8.0799E+03 | 4.9044E+03 | 3.5944E+03 | 5.5947E+03 | 5.6521E+03 |
| Mean | 5.2630E+03 | 6.4561E+03 | 8.9675E+03 | 7.4811E+03 | 5.0324E+03 | 6.3443E+03 | 6.4500E+03 | |
| Std | 1.9879E+02 | 9.6001E+02 | 5.2806E+02 | 7.2226E+02 | 1.6906E+03 | 5.4285E+02 | 3.9498E+02 | |
| Rank | 2 | 5 | 7 | 6 | 1 | 3 | 4 | |
| F26 | Best | 3.3985E+03 | 3.4150E+03 | 3.5303E+03 | 3.4280E+03 | 3.2000E+03 | 3.3848E+03 | 3.3742E+03 |
| Mean | 3.4901E+03 | 3.6151E+03 | 3.7244E+03 | 3.5845E+03 | 3.3695E+03 | 3.5157E+03 | 3.5173E+03 | |
| Std | 4.4434E+01 | 9.1322E+01 | 8.9351E+01 | 9.9326E+01 | 1.9144E+02 | 8.3029E+01 | 6.8193E+01 | |
| Rank | 2 | 6 | 7 | 5 | 1 | 3 | 4 | |
| F27 | Best | 3.4371E+03 | 3.9395E+03 | 4.0177E+03 | 3.6898E+03 | 3.3000E+03 | 3.3475E+03 | 3.4815E+03 |
| Mean | 3.5491E+03 | 4.6911E+03 | 4.6910E+03 | 4.3581E+03 | 3.7339E+03 | 3.5405E+03 | 3.6529E+03 | |
| Std | 5.0592E+01 | 3.5288E+02 | 6.3082E+02 | 4.9196E+02 | 1.9468E+02 | 1.1703E+02 | 1.2466E+02 | |
| Rank | 2 | 7 | 6 | 5 | 4 | 1 | 3 | |
| F28 | Best | 3.8499E+03 | 3.9833E+03 | 4.2297E+03 | 4.1955E+03 | 4.1836E+03 | 4.0593E+03 | 4.1059E+03 |
| Mean | 4.1930E+03 | 4.8126E+03 | 4.9729E+03 | 4.8320E+03 | 5.0491E+03 | 4.7147E+03 | 4.6534E+03 | |
| Std | 1.5125E+02 | 4.2405E+02 | 3.8542E+02 | 3.4029E+02 | 4.2764E+02 | 2.9177E+02 | 2.8700E+02 | |
| Rank | 1 | 4 | 6 | 5 | 7 | 3 | 2 | |
| F29 | Best | 1.1161E+07 | 3.9769E+07 | 2.4891E+07 | 1.8713E+07 | 3.2753E+07 | 2.7108E+07 | 2.3689E+07 |
| Mean | 2.1554E+07 | 8.3325E+07 | 5.5545E+07 | 4.2073E+07 | 9.9016E+07 | 6.1804E+07 | 4.6483E+07 | |
| Std | 6.1361E+06 | 2.4541E+07 | 2.8287E+07 | 1.4859E+07 | 3.4262E+07 | 2.2536E+07 | 1.5251E+07 | |
| Rank | 1 | 6 | 4 | 2 | 7 | 5 | 3 |
| No. | Index | DRIME | ACGRIME | TERIME | IRIME | DNMRIME | GLSRIME | HERIME |
|---|---|---|---|---|---|---|---|---|
| F1 | Best | 1.8597E+08 | 3.9328E+10 | 6.4886E+10 | 2.9514E+10 | 5.0905E+09 | 1.3819E+09 | 3.9484E+09 |
| Mean | 4.5502E+08 | 5.0241E+10 | 8.1611E+10 | 3.9491E+10 | 8.0830E+09 | 2.6819E+09 | 6.1836E+09 | |
| Std | 2.1106E+08 | 6.6045E+09 | 1.2335E+10 | 6.5991E+09 | 1.8400E+09 | 6.5276E+08 | 1.2475E+09 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 2 | 3 | |
| F2 | Best | 5.4624E+04 | 2.4434E+05 | 3.9951E+05 | 3.8923E+05 | 2.2300E+05 | 2.6540E+05 | 3.2376E+05 |
| Mean | 7.0773E+04 | 2.8223E+05 | 5.2072E+05 | 5.7180E+05 | 2.6333E+05 | 3.9684E+05 | 3.7742E+05 | |
| Std | 9.0094E+03 | 1.5469E+04 | 7.1239E+04 | 1.0355E+05 | 1.6610E+04 | 5.5156E+04 | 3.2786E+04 | |
| Rank | 1 | 3 | 6 | 7 | 2 | 5 | 4 | |
| F3 | Best | 9.2033E+02 | 3.3326E+03 | 4.2514E+03 | 3.2770E+03 | 1.3181E+03 | 1.0685E+03 | 1.2032E+03 |
| Mean | 1.0414E+03 | 5.5311E+03 | 7.3815E+03 | 4.8939E+03 | 1.8251E+03 | 1.2902E+03 | 1.5948E+03 | |
| Std | 6.8193E+01 | 1.2841E+03 | 2.0117E+03 | 1.0735E+03 | 2.7954E+02 | 1.5098E+02 | 2.4419E+02 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 2 | 3 | |
| F4 | Best | 7.6337E+02 | 1.2541E+03 | 1.5347E+03 | 1.3782E+03 | 1.1830E+03 | 1.1217E+03 | 1.0682E+03 |
| Mean | 8.3476E+02 | 1.4486E+03 | 1.6720E+03 | 1.5119E+03 | 1.4967E+03 | 1.2467E+03 | 1.1685E+03 | |
| Std | 5.5361E+01 | 9.4593E+01 | 8.3029E+01 | 6.9030E+01 | 1.3937E+02 | 6.9196E+01 | 4.9622E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 3 | 2 | |
| F5 | Best | 6.0875E+02 | 6.3135E+02 | 6.4871E+02 | 6.4413E+02 | 6.4487E+02 | 6.3577E+02 | 6.2449E+02 |
| Mean | 6.1504E+02 | 6.4396E+02 | 6.6914E+02 | 6.5521E+02 | 6.6088E+02 | 6.5070E+02 | 6.3294E+02 | |
| Std | 2.8775E+00 | 5.4798E+00 | 8.3877E+00 | 4.5340E+00 | 9.0183E+00 | 1.0144E+01 | 5.3088E+00 | |
| Rank | 1 | 3 | 7 | 5 | 6 | 4 | 2 | |
| F6 | Best | 1.2401E+03 | 1.8517E+03 | 3.1998E+03 | 2.1830E+03 | 1.8387E+03 | 1.8575E+03 | 1.7025E+03 |
| Mean | 1.3717E+03 | 2.1400E+03 | 3.6928E+03 | 2.3523E+03 | 2.0790E+03 | 2.0783E+03 | 1.9046E+03 | |
| Std | 8.2306E+01 | 1.2327E+02 | 2.9908E+02 | 9.8547E+01 | 1.4747E+02 | 1.0387E+02 | 8.0924E+01 | |
| Rank | 1 | 5 | 7 | 6 | 4 | 3 | 2 | |
| F7 | Best | 1.0340E+03 | 1.5629E+03 | 1.8626E+03 | 1.6912E+03 | 1.5117E+03 | 1.3382E+03 | 1.3299E+03 |
| Mean | 1.1217E+03 | 1.6586E+03 | 2.0173E+03 | 1.8296E+03 | 1.7272E+03 | 1.5378E+03 | 1.4510E+03 | |
| Std | 4.1154E+01 | 4.6134E+01 | 9.1561E+01 | 8.6443E+01 | 1.2716E+02 | 1.0532E+02 | 6.5784E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 3 | 2 | |
| F8 | Best | 4.3350E+03 | 2.2956E+04 | 4.2520E+04 | 3.0321E+04 | 3.5883E+04 | 2.4220E+04 | 9.1247E+03 |
| Mean | 6.6472E+03 | 3.7888E+04 | 6.2629E+04 | 4.5665E+04 | 5.0205E+04 | 3.8782E+04 | 1.5460E+04 | |
| Std | 1.1423E+03 | 6.0589E+03 | 1.4153E+04 | 7.0134E+03 | 6.9621E+03 | 9.6107E+03 | 3.3082E+03 | |
| Rank | 1 | 3 | 7 | 5 | 6 | 4 | 2 | |
| F9 | Best | 1.4964E+04 | 1.8336E+04 | 2.3400E+04 | 2.3718E+04 | 1.8916E+04 | 1.7115E+04 | 2.0189E+04 |
| Mean | 1.8742E+04 | 2.1915E+04 | 2.6207E+04 | 2.7134E+04 | 2.1932E+04 | 1.9877E+04 | 2.2493E+04 | |
| Std | 2.5902E+03 | 1.6053E+03 | 1.5107E+03 | 1.5093E+03 | 2.3557E+03 | 1.4441E+03 | 1.3086E+03 | |
| Rank | 1 | 3 | 6 | 7 | 4 | 2 | 5 | |
| F10 | Best | 2.6623E+03 | 2.9090E+04 | 3.4028E+04 | 8.7468E+04 | 1.4369E+04 | 9.2486E+03 | 1.2090E+04 |
| Mean | 3.1655E+03 | 4.8985E+04 | 5.7630E+04 | 1.2768E+05 | 2.5968E+04 | 1.6822E+04 | 2.2318E+04 | |
| Std | 2.9751E+02 | 1.1152E+04 | 1.5455E+04 | 2.5904E+04 | 5.9185E+03 | 3.9107E+03 | 5.2959E+03 | |
| Rank | 1 | 5 | 6 | 7 | 4 | 2 | 3 | |
| F11 | Best | 3.3608E+08 | 1.8996E+09 | 6.0531E+09 | 2.7739E+09 | 7.5838E+08 | 3.4544E+08 | 3.7702E+08 |
| Mean | 4.3000E+08 | 4.8801E+09 | 1.1714E+10 | 4.4593E+09 | 1.4476E+09 | 1.2164E+09 | 1.1711E+09 | |
| Std | 4.9462E+07 | 1.6328E+09 | 3.2462E+09 | 1.0683E+09 | 4.5234E+08 | 6.6048E+08 | 4.5570E+08 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 3 | 2 | |
| F12 | Best | 1.8665E+04 | 1.0586E+07 | 2.6106E+08 | 8.4496E+07 | 5.9183E+06 | 2.6084E+06 | 3.8870E+06 |
| Mean | 2.3730E+04 | 1.0022E+08 | 5.6490E+08 | 1.4527E+08 | 1.6880E+07 | 6.4402E+06 | 1.1457E+07 | |
| Std | 3.1901E+03 | 8.0293E+07 | 2.6528E+08 | 4.6143E+07 | 6.7492E+06 | 2.3102E+06 | 5.1872E+06 | |
| Rank | 1 | 5 | 7 | 6 | 4 | 2 | 3 | |
| F13 | Best | 2.0737E+03 | 3.9317E+06 | 3.8999E+06 | 2.3711E+06 | 1.4175E+06 | 1.3645E+06 | 9.2361E+05 |
| Mean | 3.6614E+03 | 6.6797E+06 | 1.4047E+07 | 7.5816E+06 | 3.9435E+06 | 5.9876E+06 | 2.3067E+06 | |
| Std | 2.4276E+03 | 2.0600E+06 | 6.4837E+06 | 2.6250E+06 | 1.4042E+06 | 3.5157E+06 | 8.9681E+05 | |
| Rank | 1 | 5 | 7 | 6 | 3 | 4 | 2 | |
| F14 | Best | 1.0036E+04 | 4.2785E+04 | 2.5759E+07 | 5.2135E+06 | 8.2252E+05 | 3.9109E+05 | 2.8735E+05 |
| Mean | 1.2583E+04 | 1.3612E+06 | 8.4521E+07 | 2.2520E+07 | 2.8842E+06 | 1.6707E+06 | 2.0102E+06 | |
| Std | 1.3319E+03 | 2.2465E+06 | 5.8730E+07 | 1.0246E+07 | 1.4897E+06 | 2.5877E+06 | 4.2532E+06 | |
| Rank | 1 | 2 | 7 | 6 | 5 | 3 | 4 | |
| F15 | Best | 3.3743E+03 | 5.5161E+03 | 7.8063E+03 | 7.3628E+03 | 5.2052E+03 | 5.2825E+03 | 5.2019E+03 |
| Mean | 5.1112E+03 | 6.4767E+03 | 9.6269E+03 | 8.2317E+03 | 6.7504E+03 | 6.8295E+03 | 6.4934E+03 | |
| Std | 6.0194E+02 | 6.7387E+02 | 8.5225E+02 | 4.6052E+02 | 7.5944E+02 | 7.6965E+02 | 6.6698E+02 | |
| Rank | 1 | 2 | 7 | 6 | 4 | 5 | 3 | |
| F16 | Best | 2.8039E+03 | 4.0408E+03 | 5.8967E+03 | 4.8243E+03 | 4.3033E+03 | 4.3542E+03 | 4.3623E+03 |
| Mean | 4.0253E+03 | 5.4390E+03 | 6.7896E+03 | 6.0732E+03 | 5.3867E+03 | 5.4130E+03 | 5.4031E+03 | |
| Std | 4.0261E+02 | 6.4325E+02 | 5.2678E+02 | 5.7452E+02 | 5.6059E+02 | 5.3053E+02 | 6.1661E+02 | |
| Rank | 1 | 5 | 7 | 6 | 2 | 4 | 3 | |
| F17 | Best | 1.7350E+04 | 2.0880E+06 | 5.6762E+06 | 2.2980E+06 | 1.2931E+06 | 1.0417E+06 | 1.3971E+06 |
| Mean | 3.6221E+04 | 6.5180E+06 | 2.4884E+07 | 9.0866E+06 | 4.2033E+06 | 8.5962E+06 | 3.7657E+06 | |
| Std | 1.3042E+04 | 3.0273E+06 | 1.2162E+07 | 4.4881E+06 | 1.7955E+06 | 6.1433E+06 | 1.4362E+06 | |
| Rank | 1 | 4 | 7 | 6 | 3 | 5 | 2 | |
| F18 | Best | 4.1133E+04 | 8.7197E+05 | 2.4860E+07 | 1.1794E+07 | 1.3664E+06 | 4.5249E+06 | 1.7425E+06 |
| Mean | 1.3806E+05 | 8.1380E+06 | 9.0344E+07 | 3.6250E+07 | 1.3147E+07 | 1.8419E+07 | 7.1568E+06 | |
| Std | 6.3792E+04 | 6.4734E+06 | 6.1796E+07 | 1.3974E+07 | 1.0640E+07 | 1.0468E+07 | 4.5118E+06 | |
| Rank | 1 | 3 | 7 | 6 | 4 | 5 | 2 | |
| F19 | Best | 3.1375E+03 | 4.1496E+03 | 5.0702E+03 | 4.9590E+03 | 4.6511E+03 | 3.9881E+03 | 3.8986E+03 |
| Mean | 4.3069E+03 | 5.1494E+03 | 6.5159E+03 | 6.2055E+03 | 5.5565E+03 | 5.2381E+03 | 5.2328E+03 | |
| Std | 5.0682E+02 | 5.1948E+02 | 5.0371E+02 | 5.4310E+02 | 6.2758E+02 | 5.4873E+02 | 4.9672E+02 | |
| Rank | 1 | 2 | 7 | 6 | 5 | 4 | 3 | |
| F20 | Best | 2.5424E+03 | 2.9650E+03 | 3.2625E+03 | 3.1773E+03 | 2.9197E+03 | 2.8910E+03 | 2.8675E+03 |
| Mean | 2.5954E+03 | 3.0930E+03 | 3.5492E+03 | 3.3496E+03 | 3.1273E+03 | 3.1137E+03 | 2.9999E+03 | |
| Std | 3.5985E+01 | 7.8918E+01 | 1.3029E+02 | 7.4472E+01 | 1.0236E+02 | 1.1516E+02 | 6.4532E+01 | |
| Rank | 1 | 3 | 7 | 6 | 5 | 4 | 2 | |
| F21 | Best | 1.7569E+04 | 1.3940E+04 | 2.6139E+04 | 2.6893E+04 | 3.5630E+03 | 1.9394E+04 | 2.1437E+04 |
| Mean | 2.0584E+04 | 2.4752E+04 | 2.8916E+04 | 2.9650E+04 | 2.3792E+04 | 2.2116E+04 | 2.5250E+04 | |
| Std | 2.2566E+03 | 2.3637E+03 | 1.4059E+03 | 1.2664E+03 | 5.5420E+03 | 1.3158E+03 | 1.8875E+03 | |
| Rank | 1 | 4 | 6 | 7 | 3 | 2 | 5 | |
| F22 | Best | 3.0879E+03 | 3.4415E+03 | 3.8255E+03 | 3.6354E+03 | 3.4704E+03 | 3.3584E+03 | 3.3638E+03 |
| Mean | 3.1578E+03 | 3.5512E+03 | 4.0575E+03 | 3.7764E+03 | 3.6559E+03 | 3.5266E+03 | 3.5104E+03 | |
| Std | 4.3185E+01 | 5.4284E+01 | 1.1057E+02 | 7.7362E+01 | 9.4871E+01 | 9.5931E+01 | 7.2241E+01 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 3 | 2 | |
| F23 | Best | 3.5022E+03 | 3.9897E+03 | 4.5437E+03 | 4.1909E+03 | 3.9805E+03 | 3.9065E+03 | 3.9146E+03 |
| Mean | 3.5991E+03 | 4.1538E+03 | 4.7647E+03 | 4.3827E+03 | 5.0629E+03 | 4.0611E+03 | 4.0821E+03 | |
| Std | 4.3531E+01 | 8.5632E+01 | 1.3936E+02 | 8.2386E+01 | 1.1831E+03 | 9.1414E+01 | 7.4456E+01 | |
| Rank | 1 | 4 | 6 | 5 | 7 | 2 | 3 | |
| F24 | Best | 3.6855E+03 | 5.5811E+03 | 7.1098E+03 | 6.0777E+03 | 4.1517E+03 | 3.8757E+03 | 3.9996E+03 |
| Mean | 3.7750E+03 | 6.9432E+03 | 1.0489E+04 | 6.7266E+03 | 4.5363E+03 | 4.1478E+03 | 4.3253E+03 | |
| Std | 6.6123E+01 | 5.8063E+02 | 1.7705E+03 | 4.3405E+02 | 2.5074E+02 | 2.2139E+02 | 2.0282E+02 | |
| Rank | 1 | 6 | 7 | 5 | 4 | 2 | 3 | |
| F25 | Best | 1.0327E+04 | 1.5205E+04 | 1.7354E+04 | 1.5855E+04 | 6.9212E+03 | 1.2156E+04 | 1.2600E+04 |
| Mean | 1.2120E+04 | 2.0587E+04 | 2.0276E+04 | 1.7151E+04 | 1.6894E+04 | 1.4350E+04 | 1.4023E+04 | |
| Std | 1.1013E+03 | 3.1495E+03 | 1.4051E+03 | 7.3193E+02 | 3.8529E+03 | 1.0778E+03 | 7.8640E+02 | |
| Rank | 1 | 7 | 6 | 5 | 4 | 3 | 2 | |
| F26 | Best | 3.7547E+03 | 3.7500E+03 | 4.1491E+03 | 3.7030E+03 | 3.2000E+03 | 3.7114E+03 | 3.6303E+03 |
| Mean | 3.8663E+03 | 3.9459E+03 | 4.4170E+03 | 3.9933E+03 | 3.7067E+03 | 3.8971E+03 | 3.8426E+03 | |
| Std | 5.7117E+01 | 1.1816E+02 | 1.7142E+02 | 9.5782E+01 | 3.6265E+02 | 1.3734E+02 | 9.3087E+01 | |
| Rank | 3 | 5 | 7 | 6 | 1 | 4 | 2 | |
| F27 | Best | 3.8831E+03 | 7.3664E+03 | 9.7387E+03 | 6.6589E+03 | 4.4132E+03 | 3.9053E+03 | 4.4837E+03 |
| Mean | 4.0196E+03 | 9.4479E+03 | 1.3978E+04 | 8.3477E+03 | 4.8711E+03 | 4.8804E+03 | 5.3844E+03 | |
| Std | 8.2876E+01 | 9.5457E+02 | 2.2875E+03 | 7.7473E+02 | 3.0214E+02 | 6.1081E+02 | 7.3620E+02 | |
| Rank | 1 | 6 | 7 | 5 | 2 | 3 | 4 | |
| F28 | Best | 6.1746E+03 | 7.2910E+03 | 8.1055E+03 | 8.0273E+03 | 7.8375E+03 | 7.5730E+03 | 6.8076E+03 |
| Mean | 6.9884E+03 | 8.8324E+03 | 9.1358E+03 | 9.0762E+03 | 8.8764E+03 | 8.5958E+03 | 8.1343E+03 | |
| Std | 4.4857E+02 | 5.3314E+02 | 6.0512E+02 | 7.3307E+02 | 5.6548E+02 | 6.4556E+02 | 6.6291E+02 | |
| Rank | 1 | 4 | 7 | 6 | 5 | 3 | 2 | |
| F29 | Best | 9.3543E+06 | 5.3418E+07 | 1.1807E+08 | 8.7870E+07 | 6.7614E+07 | 5.5284E+07 | 3.3540E+07 |
| Mean | 2.9735E+07 | 2.1424E+08 | 2.4597E+08 | 1.7817E+08 | 1.7591E+08 | 1.9984E+08 | 1.0431E+08 | |
| Std | 1.0504E+07 | 7.7033E+07 | 8.4721E+07 | 5.5652E+07 | 6.9471E+07 | 9.0530E+07 | 5.2053E+07 | |
| Rank | 1 | 6 | 7 | 4 | 3 | 5 | 2 |
| No. | Index | DRIME | EOSMA | GLS-MPA | ISGTOA | EMTLBO | LSHADE-SPACMA | APSM-jSO |
|---|---|---|---|---|---|---|---|---|
| F1 | Best | 3.0002E+02 | 1.2467E+03 | 3.9630E+02 | 7.3559E+02 | 1.2638E+03 | 3.1911E+02 | 3.1975E+02 |
| Mean | 3.0020E+02 | 2.9857E+03 | 1.2092E+03 | 1.9775E+03 | 3.9370E+03 | 4.4028E+02 | 3.7410E+02 | |
| Std | 1.4672E-01 | 1.1523E+03 | 6.0770E+02 | 8.2658E+02 | 1.4037E+03 | 2.2402E+02 | 4.3890E+01 | |
| Rank | 1 | 6 | 4 | 5 | 7 | 3 | 2 | |
| F2 | Best | 4.0000E+02 | 4.0577E+02 | 4.0079E+02 | 4.0025E+02 | 4.0175E+02 | 4.0558E+02 | 4.0073E+02 |
| Mean | 4.0057E+02 | 4.1951E+02 | 4.1741E+02 | 4.0942E+02 | 4.2635E+02 | 4.0775E+02 | 4.0761E+02 | |
| Std | 1.8908E+00 | 1.3433E+01 | 2.2760E+01 | 1.1371E+01 | 1.9773E+01 | 1.6658E+00 | 3.0934E+00 | |
| Rank | 1 | 6 | 5 | 4 | 7 | 3 | 2 | |
| F3 | Best | 6.0001E+02 | 6.0197E+02 | 6.0122E+02 | 6.0008E+02 | 6.0725E+02 | 6.0146E+02 | 6.0148E+02 |
| Mean | 6.0008E+02 | 6.0396E+02 | 6.0664E+02 | 6.0023E+02 | 6.1248E+02 | 6.0241E+02 | 6.0256E+02 | |
| Std | 4.5623E-02 | 1.4518E+00 | 3.7382E+00 | 1.4080E-01 | 2.6019E+00 | 4.9018E-01 | 6.4149E-01 | |
| Rank | 1 | 5 | 6 | 2 | 7 | 3 | 4 | |
| F4 | Best | 8.0100E+02 | 8.0817E+02 | 8.0709E+02 | 8.0617E+02 | 8.2802E+02 | 8.2406E+02 | 8.2296E+02 |
| Mean | 8.0631E+02 | 8.2974E+02 | 8.1867E+02 | 8.2653E+02 | 8.4735E+02 | 8.3729E+02 | 8.4367E+02 | |
| Std | 3.2727E+00 | 7.8692E+00 | 6.8865E+00 | 9.2396E+00 | 7.3932E+00 | 5.7350E+00 | 7.1487E+00 | |
| Rank | 1 | 4 | 2 | 3 | 7 | 5 | 6 | |
| F5 | Best | 9.0000E+02 | 9.0149E+02 | 9.0101E+02 | 9.0000E+02 | 9.0860E+02 | 9.0125E+02 | 9.0137E+02 |
| Mean | 9.0004E+02 | 9.0830E+02 | 9.3457E+02 | 9.0008E+02 | 9.2118E+02 | 9.0330E+02 | 9.0342E+02 | |
| Std | 1.1728E-01 | 4.3773E+00 | 2.1704E+01 | 1.4355E-01 | 8.8962E+00 | 1.3681E+00 | 1.7665E+00 | |
| Rank | 1 | 5 | 7 | 2 | 6 | 3 | 4 | |
| F6 | Best | 1.8067E+03 | 6.7346E+03 | 1.8910E+03 | 2.9768E+03 | 1.8892E+03 | 2.0447E+03 | 2.2923E+03 |
| Mean | 1.8499E+03 | 7.1976E+04 | 3.6534E+03 | 6.4743E+03 | 3.6396E+03 | 3.0700E+03 | 3.9545E+03 | |
| Std | 4.7378E+01 | 8.6235E+04 | 1.8236E+03 | 3.0557E+03 | 1.8423E+03 | 9.8815E+02 | 1.2744E+03 | |
| Rank | 1 | 7 | 4 | 6 | 3 | 2 | 5 | |
| F7 | Best | 2.0018E+03 | 2.0202E+03 | 2.0054E+03 | 2.0093E+03 | 2.0368E+03 | 2.0332E+03 | 2.0374E+03 |
| Mean | 2.0173E+03 | 2.0388E+03 | 2.0270E+03 | 2.0355E+03 | 2.0617E+03 | 2.0425E+03 | 2.0514E+03 | |
| Std | 8.4174E+00 | 7.7721E+00 | 1.0293E+01 | 8.3766E+00 | 9.3100E+00 | 4.5166E+00 | 7.5242E+00 | |
| Rank | 1 | 4 | 2 | 3 | 7 | 5 | 6 | |
| F8 | Best | 2.2051E+03 | 2.2247E+03 | 2.2089E+03 | 2.2131E+03 | 2.2251E+03 | 2.2244E+03 | 2.2252E+03 |
| Mean | 2.2222E+03 | 2.2309E+03 | 2.2231E+03 | 2.2290E+03 | 2.2320E+03 | 2.2287E+03 | 2.2309E+03 | |
| Std | 4.5423E+00 | 2.5177E+00 | 2.9881E+00 | 3.6336E+00 | 3.3632E+00 | 1.7950E+00 | 2.7025E+00 | |
| Rank | 1 | 5 | 2 | 4 | 7 | 3 | 6 | |
| F9 | Best | 2.5293E+03 | 2.5315E+03 | 2.5293E+03 | 2.5293E+03 | 2.5312E+03 | 2.5293E+03 | 2.5295E+03 |
| Mean | 2.5294E+03 | 2.5423E+03 | 2.5309E+03 | 2.5293E+03 | 2.5360E+03 | 2.5294E+03 | 2.5299E+03 | |
| Std | 9.4325E-02 | 5.9188E+00 | 2.9474E+00 | 2.2059E-02 | 3.1567E+00 | 3.4485E-02 | 3.4836E-01 | |
| Rank | 3 | 7 | 5 | 1 | 6 | 2 | 4 | |
| F10 | Best | 2.5002E+03 | 2.5004E+03 | 2.5003E+03 | 2.5004E+03 | 2.5006E+03 | 2.5004E+03 | 2.5004E+03 |
| Mean | 2.5040E+03 | 2.5006E+03 | 2.5007E+03 | 2.5132E+03 | 2.5010E+03 | 2.5006E+03 | 2.5156E+03 | |
| Std | 2.0065E+01 | 1.2838E-01 | 1.9641E-01 | 3.8620E+01 | 8.2727E-01 | 1.0298E-01 | 4.5473E+01 | |
| Rank | 5 | 2 | 3 | 6 | 4 | 1 | 7 | |
| F11 | Best | 2.6251E+03 | 2.7581E+03 | 2.7292E+03 | 2.6081E+03 | 2.7603E+03 | 2.7310E+03 | 2.7752E+03 |
| Mean | 2.9024E+03 | 3.0631E+03 | 2.8483E+03 | 2.7669E+03 | 2.8703E+03 | 2.7778E+03 | 3.0244E+03 | |
| Std | 5.2819E+01 | 2.0215E+02 | 1.8146E+02 | 1.3738E+02 | 1.7731E+02 | 6.8433E+01 | 5.9996E+01 | |
| Rank | 5 | 7 | 3 | 1 | 4 | 2 | 6 | |
| F12 | Best | 2.8627E+03 | 2.8656E+03 | 2.8614E+03 | 2.8587E+03 | 2.8640E+03 | 2.8630E+03 | 2.8642E+03 |
| Mean | 2.8654E+03 | 2.8670E+03 | 2.8642E+03 | 2.8633E+03 | 2.8661E+03 | 2.8646E+03 | 2.8652E+03 | |
| Std | 1.0279E+00 | 1.2031E+00 | 1.4228E+00 | 1.4756E+00 | 1.2038E+00 | 6.2745E-01 | 4.7693E-01 | |
| Rank | 5 | 7 | 2 | 1 | 6 | 3 | 4 |
| No. | Index | DRIME | EOSMA | GLS-MPA | ISGTOA | EMTLBO | LSHADE-SPACMA | APSM-jSO |
|---|---|---|---|---|---|---|---|---|
| F1 | Best | 3.0497E+02 | 8.7616E+03 | 4.0382E+03 | 7.3815E+03 | 1.1842E+04 | 4.1624E+02 | 8.4551E+02 |
| Mean | 3.3503E+02 | 1.5822E+04 | 1.0588E+04 | 1.4211E+04 | 2.2919E+04 | 2.0665E+03 | 2.6063E+03 | |
| Std | 2.8664E+01 | 4.3551E+03 | 3.2946E+03 | 4.3340E+03 | 7.9294E+03 | 4.6981E+03 | 1.5004E+03 | |
| Rank | 1 | 6 | 4 | 5 | 7 | 2 | 3 | |
| F2 | Best | 4.4950E+02 | 4.7153E+02 | 4.7263E+02 | 4.3177E+02 | 4.7459E+02 | 4.4515E+02 | 4.4991E+02 |
| Mean | 4.5783E+02 | 5.0605E+02 | 5.2247E+02 | 4.6044E+02 | 5.2255E+02 | 4.4842E+02 | 4.5173E+02 | |
| Std | 8.4541E+00 | 2.6998E+01 | 3.8051E+01 | 1.4800E+01 | 4.3122E+01 | 1.4802E+00 | 1.9822E+00 | |
| Rank | 3 | 5 | 6 | 4 | 7 | 1 | 2 | |
| F3 | Best | 6.0008E+02 | 6.0474E+02 | 6.0967E+02 | 6.0034E+02 | 6.1328E+02 | 6.0148E+02 | 6.0242E+02 |
| Mean | 6.0043E+02 | 6.0972E+02 | 6.1928E+02 | 6.0135E+02 | 6.2089E+02 | 6.0202E+02 | 6.0367E+02 | |
| Std | 4.6460E-01 | 3.4019E+00 | 5.2551E+00 | 7.1706E-01 | 4.4356E+00 | 3.0820E-01 | 8.8521E-01 | |
| Rank | 1 | 5 | 6 | 2 | 7 | 3 | 4 | |
| F4 | Best | 8.0722E+02 | 8.6308E+02 | 8.3813E+02 | 8.3881E+02 | 9.1778E+02 | 8.8861E+02 | 8.9409E+02 |
| Mean | 8.2054E+02 | 8.9232E+02 | 8.7323E+02 | 8.9698E+02 | 9.3338E+02 | 9.0833E+02 | 9.1923E+02 | |
| Std | 1.1572E+01 | 1.1936E+01 | 1.7386E+01 | 2.5461E+01 | 8.9492E+00 | 8.0436E+00 | 1.0812E+01 | |
| Rank | 1 | 3 | 2 | 4 | 7 | 5 | 6 | |
| F5 | Best | 9.0001E+02 | 9.3501E+02 | 1.0361E+03 | 9.0039E+02 | 9.6077E+02 | 9.0198E+02 | 9.0326E+02 |
| Mean | 9.0052E+02 | 1.0330E+03 | 1.4148E+03 | 9.0802E+02 | 1.0551E+03 | 9.0478E+02 | 9.0985E+02 | |
| Std | 7.9534E-01 | 7.0684E+01 | 2.5375E+02 | 1.3174E+01 | 7.1880E+01 | 1.1807E+00 | 5.9775E+00 | |
| Rank | 1 | 5 | 7 | 3 | 6 | 2 | 4 | |
| F6 | Best | 1.9620E+03 | 7.3205E+04 | 2.4298E+03 | 2.2454E+03 | 5.4226E+03 | 9.5935E+03 | 4.1953E+04 |
| Mean | 2.8321E+03 | 6.3594E+05 | 1.8336E+05 | 6.3993E+03 | 7.7360E+04 | 3.4160E+04 | 1.2375E+05 | |
| Std | 6.8932E+02 | 4.6314E+05 | 3.5938E+05 | 4.6565E+03 | 8.8667E+04 | 1.1985E+04 | 4.8172E+04 | |
| Rank | 1 | 7 | 6 | 2 | 4 | 3 | 5 | |
| F7 | Best | 2.0272E+03 | 2.0610E+03 | 2.0449E+03 | 2.0578E+03 | 2.0969E+03 | 2.0919E+03 | 2.0943E+03 |
| Mean | 2.0447E+03 | 2.0965E+03 | 2.0729E+03 | 2.0856E+03 | 2.1561E+03 | 2.1213E+03 | 2.1344E+03 | |
| Std | 1.1041E+01 | 1.8864E+01 | 1.9881E+01 | 1.6962E+01 | 2.4403E+01 | 1.2468E+01 | 2.2518E+01 | |
| Rank | 1 | 4 | 2 | 3 | 7 | 5 | 6 | |
| F8 | Best | 2.2244E+03 | 2.2310E+03 | 2.2232E+03 | 2.2322E+03 | 2.2330E+03 | 2.2366E+03 | 2.2356E+03 |
| Mean | 2.2266E+03 | 2.2404E+03 | 2.2310E+03 | 2.2406E+03 | 2.2839E+03 | 2.2426E+03 | 2.2444E+03 | |
| Std | 1.2058E+00 | 5.5594E+00 | 3.8483E+00 | 5.0694E+00 | 6.6817E+01 | 3.2525E+00 | 4.4134E+00 | |
| Rank | 1 | 3 | 2 | 4 | 7 | 5 | 6 | |
| F9 | Best | 2.4818E+03 | 2.4908E+03 | 2.4833E+03 | 2.4809E+03 | 2.4903E+03 | 2.4808E+03 | 2.4813E+03 |
| Mean | 2.4834E+03 | 2.4981E+03 | 2.4996E+03 | 2.4814E+03 | 2.5008E+03 | 2.4809E+03 | 2.4819E+03 | |
| Std | 1.0742E+00 | 4.8031E+00 | 1.2125E+01 | 4.4272E-01 | 7.1851E+00 | 1.9691E-02 | 4.2590E-01 | |
| Rank | 4 | 5 | 6 | 2 | 7 | 1 | 3 | |
| F10 | Best | 2.5003E+03 | 2.5007E+03 | 2.5006E+03 | 2.5005E+03 | 2.5007E+03 | 2.5005E+03 | 2.5007E+03 |
| Mean | 2.5086E+03 | 2.5080E+03 | 2.5015E+03 | 2.8497E+03 | 2.5421E+03 | 2.5008E+03 | 2.5094E+03 | |
| Std | 3.1016E+01 | 3.7933E+01 | 1.5041E+00 | 1.0366E+03 | 1.2269E+02 | 1.4472E-01 | 4.4999E+01 | |
| Rank | 4 | 3 | 2 | 7 | 6 | 1 | 5 | |
| F11 | Best | 2.9533E+03 | 3.7787E+03 | 3.5594E+03 | 2.9155E+03 | 3.7200E+03 | 3.0197E+03 | 3.2743E+03 |
| Mean | 3.0020E+03 | 4.1439E+03 | 4.2950E+03 | 2.9270E+03 | 4.1415E+03 | 3.0695E+03 | 3.5196E+03 | |
| Std | 4.0613E+01 | 2.0977E+02 | 4.0318E+02 | 1.0313E+01 | 2.0632E+02 | 2.6716E+01 | 1.3406E+02 | |
| Rank | 2 | 6 | 7 | 1 | 5 | 3 | 4 | |
| F12 | Best | 2.9405E+03 | 2.9691E+03 | 2.9492E+03 | 2.9380E+03 | 2.9561E+03 | 2.9365E+03 | 2.9465E+03 |
| Mean | 2.9538E+03 | 3.0008E+03 | 2.9743E+03 | 2.9511E+03 | 2.9759E+03 | 2.9459E+03 | 2.9591E+03 | |
| Std | 7.2714E+00 | 1.6865E+01 | 1.6759E+01 | 1.1757E+01 | 1.7107E+01 | 5.1191E+00 | 7.3760E+00 | |
| Rank | 3 | 7 | 5 | 2 | 6 | 1 | 4 |
Appendix B
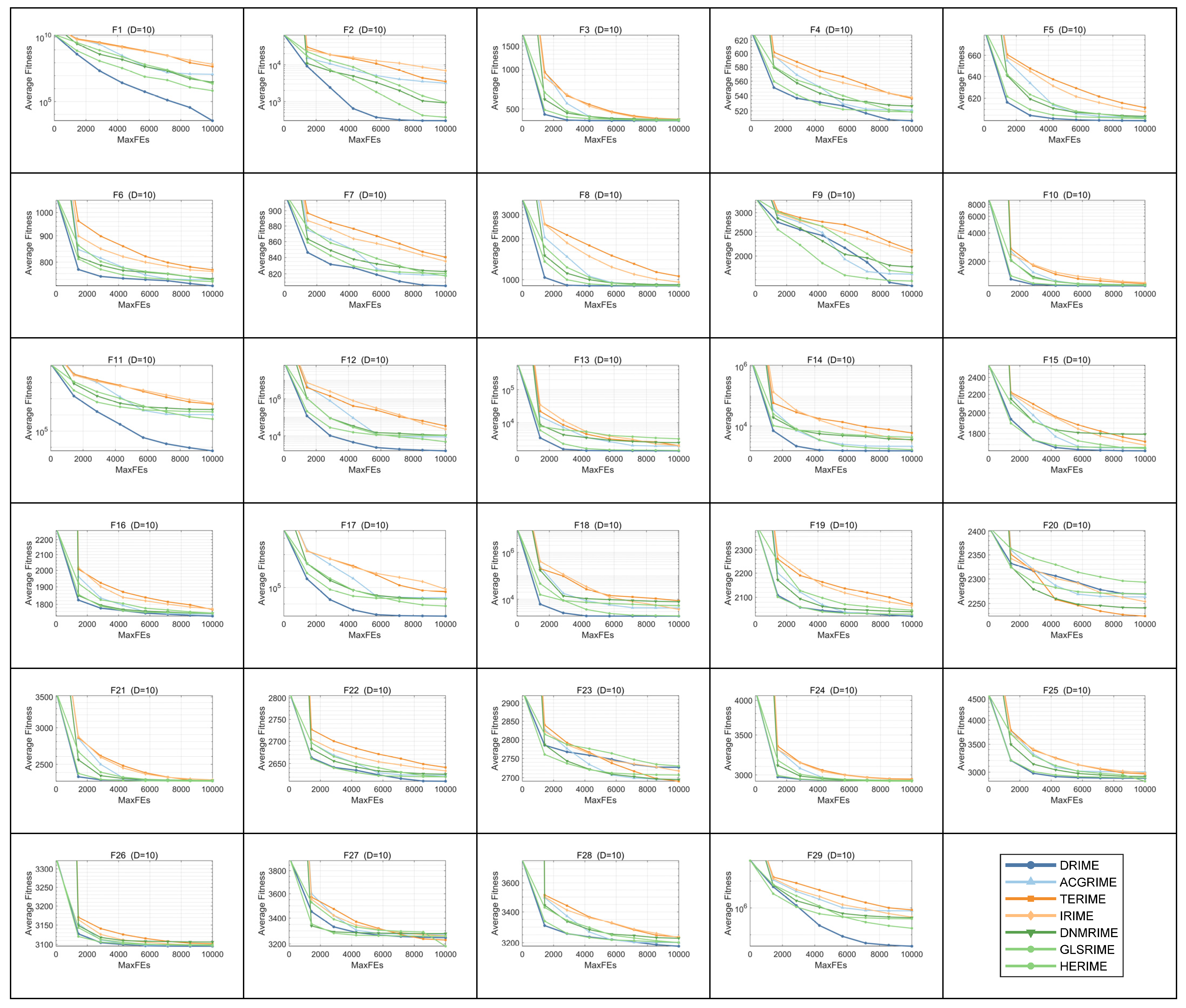
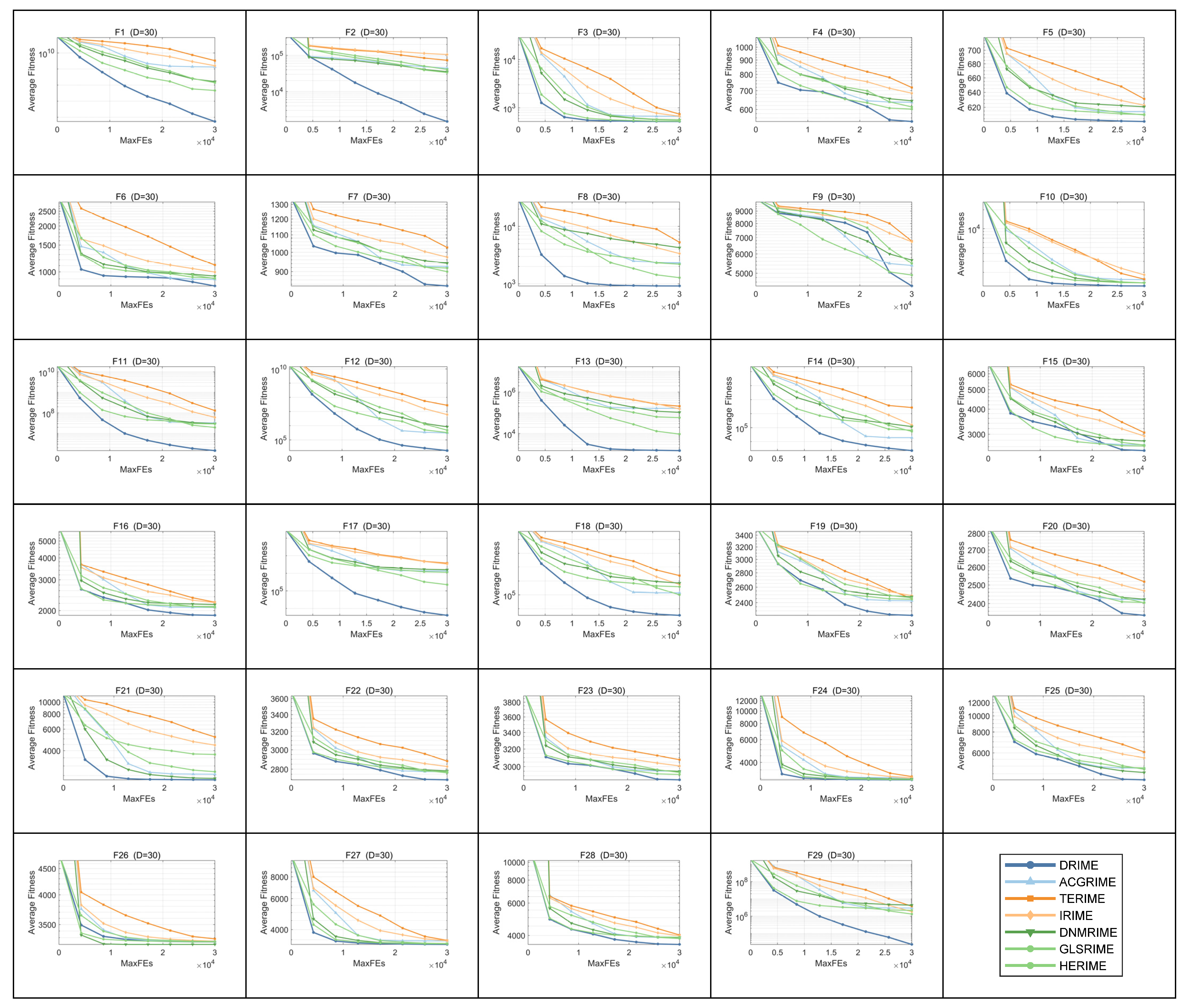
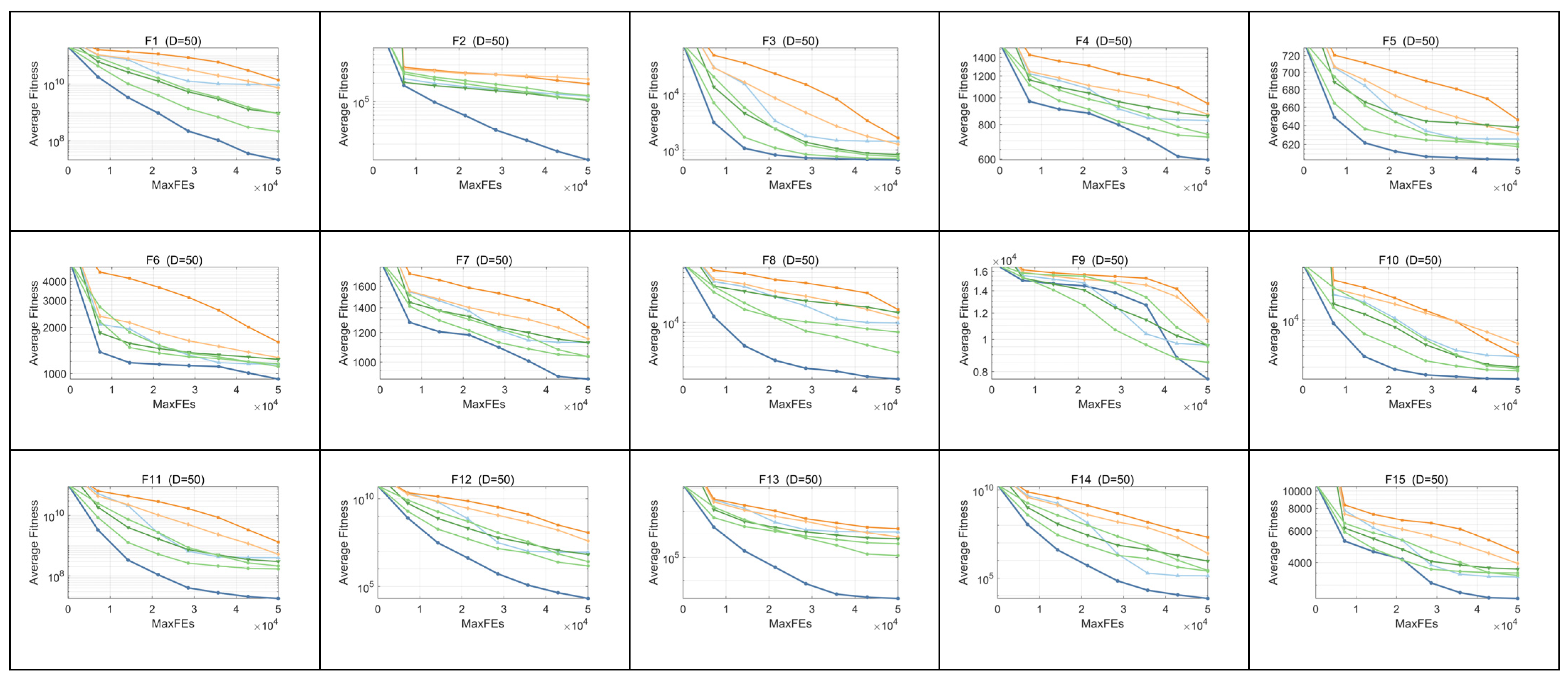
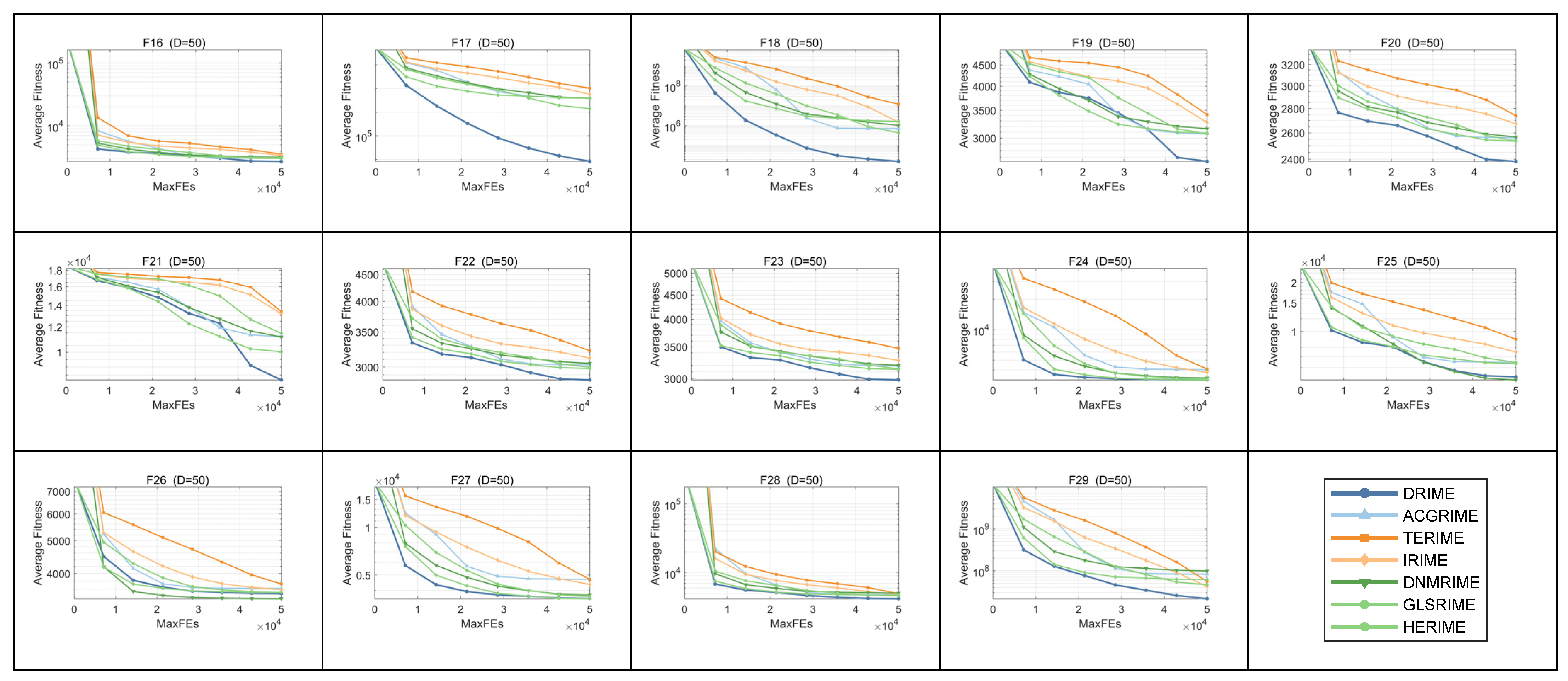
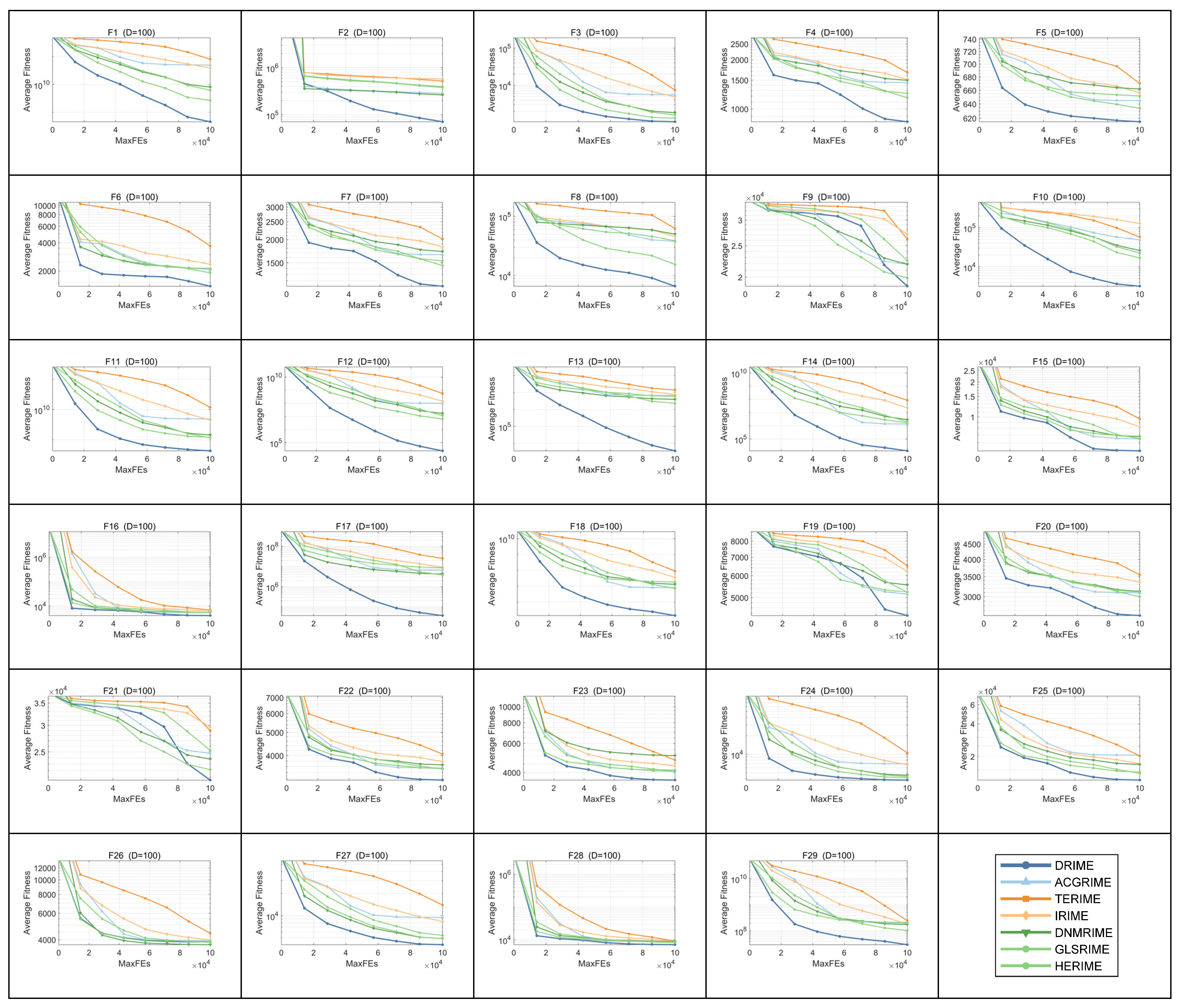
References
- Ezugwu, A.E.; Adeleke, O.J.; Akinyelu, A.A.; Viriri, S. A Conceptual Comparison of Several Metaheuristic Algorithms on Continuous Optimisation Problems. Neural Comput. Appl. 2020, 32, 6207–6251. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Y.; Cao, L.; Xiong, M. Comprehensive Adaptive Enterprise Optimization Algorithm and Its Engineering Applications. Biomimetics 2025, 10, 302. [Google Scholar] [CrossRef] [PubMed]
- Tang, A.; Zhou, H.; Han, T.; Xie, L. A Modified Manta Ray Foraging Optimization for Global Optimization Problems. IEEE Access 2021, 9, 128702–128721. [Google Scholar] [CrossRef]
- Mraihi, T.; Driss, O.B.; EL-Haouzi, H.B. Distributed Permutation Flow Shop Scheduling Problem with Worker Flexibility: Review, Trends and Model Proposition. Expert Syst. Appl. 2024, 238, 121947. [Google Scholar] [CrossRef]
- El Amrani, A.M.; Fri, M.; Benmoussa, O.; Rouky, N. The Integration of Urban Freight in Public Transportation: A Systematic Literature Review. Sustainability 2024, 16, 5286. [Google Scholar] [CrossRef]
- Tang, A.D.; Han, T.; Zhou, H.; Xie, L. An Improved Equilibrium Optimizer with Application in Unmanned Aerial Vehicle Path Planning. Sensors 2021, 21, 1814. [Google Scholar] [CrossRef]
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.-R.; Han, B.; Tang, A. Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic Algorithm for Global Optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [CrossRef]
- Devadas, V. Linear Programming Model for Optimum Resource Allocation in Rural Systems. Energy Sources 1997, 19, 613–621. [Google Scholar] [CrossRef]
- Kira, D.; Kusy, M.; Rakita, I. A Stochastic Linear Programming Approach to Hierarchical Production Planning. J. Oper. Res. Soc. 1997, 48, 207–211. [Google Scholar] [CrossRef]
- Di Puglia Pugliese, L.; Guerriero, F. Dynamic Programming Approaches to Solve the Shortest Path Problem with Forbidden Paths. Optim. Methods Softw. 2013, 28, 221–255. [Google Scholar] [CrossRef]
- Tang, A.D.; Tang, S.Q.; Han, T.; Zhou, H.; Xie, L. A Modified Slime Mould Algorithm for Global Optimization. Comput. Intell. Neurosci. 2021, 2021, 2298215. [Google Scholar] [CrossRef] [PubMed]
- Droste, S.; Jansen, T.; Wegener, I. Upper and Lower Bounds for Randomized Search Heuristics in Black-Box Optimization. Theory Comput. Syst. 2006, 39, 525–544. [Google Scholar] [CrossRef]
- Zhou, H.; Cheng, H.Y.; Wei, Z.L.; Zhao, X.; Tang, A.D.; Xie, L. A Hybrid Butterfly Optimization Algorithm for Numerical Optimization Problems. Comput. Intell. Neurosci. 2021, 2021, 7981670. [Google Scholar] [CrossRef] [PubMed]
- Abd Elaziz, M.; Elsheikh, A.H.; Oliva, D.; Abualigah, L.; Lu, S.; Ewees, A.A. Advanced Metaheuristic Techniques for Mechanical Design Problems: Review. Arch. Comput. Methods Eng. 2022, 29, 695–716. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Abualigah, L. An Improved Moth-Flame Optimization Algorithm with Adaptation Mechanism to Solve Numerical and Mechanical Engineering Problems. Entropy 2021, 23, 1637. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Han, T.; Zhou, H.; Tang, S.; Zhao, H. A Novel Adaptive L-SHADE Algorithm and Its Application in UAV Swarm Resource Configuration Problem. Inf. Sci. 2022, 606, 350–367. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, H.; Han, T.; Zhou, H.; Li, C. A Grey Wolf Optimizer Using Gaussian Estimation of Distribution and Its Application in the Multi-UAV Multi-Target Urban Tracking Problem. Appl. Soft Comput. J. 2019, 78, 240–260. [Google Scholar] [CrossRef]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Review of Metaheuristic Optimization Algorithms for Power Systems Problems. Sustainability 2023, 15, 9434. [Google Scholar] [CrossRef]
- Hmida, J.B.; Morshed, M.J.; Lee, J.; Chambers, T. Hybrid Imperialist Competitive and Greywolf Algorithm to Solve Multiobjective Optimal Power Flow Withwind and Solar Units. Energies 2018, 11, 2891. [Google Scholar] [CrossRef]
- Hu, G.; Zhao, F.; Houssein, E.H. Competitive Dual-Students Using Bi-Level Contrastive Learning for Semi-Supervised Medical Image Segmentation. Eng. Appl. Artif. Intell. 2025, 144, 110082. [Google Scholar] [CrossRef]
- Liu, Q.X.; Li, N.; Jia, H.M.; Qi, Q.; Abualigah, L. A Chimp-Inspired Remora Optimization Algorithm for Multilevel Thresholding Image Segmentation Using Cross Entropy. Artif. Intell. Rev. 2023, 56, 159–216. [Google Scholar] [CrossRef]
- Jin, B.; Gonçalves, N.; Cruz, L.; Medvedev, I.; Yu, Y.; Wang, J. Simulated Multimodal Deep Facial Diagnosis. Expert Syst. Appl. 2024, 252, 123881. [Google Scholar] [CrossRef]
- Huang, L.; Guo, S.S.; Zhang, W.; Tang, H.T.; Wang, G.S.; Cui, J.Y. A Hybrid Optimization Algorithm for Large-Scale Flexible Job-Shop Scheduling Problems. Eng. Optim. 2025, 1–34. [Google Scholar] [CrossRef]
- Feng, H.; Cao, K.; Huang, G.; Liu, H. ABWOA: Adaptive Boundary Whale Optimization Algorithm for Large-Scale Digital Twin Network Construction. J. Cloud Comput. Syst. Appl. 2024, 13, 110. [Google Scholar] [CrossRef]
- Alrammah, H.; Gu, Y.; Yun, D.Q.; Zhang, N. Tri-Objective Optimization for Large-Scale Workflow Scheduling and Execution in Clouds. J. Netw. Syst. Manag. 2024, 32, 89. [Google Scholar] [CrossRef]
- Yu, L.; Ren, C.; Meng, Z. A Surrogate-Assisted Differential Evolution with Fitness-Independent Parameter Adaptation for High-Dimensional Expensive Optimization. Inf. Sci. 2024, 662, 120246. [Google Scholar] [CrossRef]
- Ren, C.L.; Xu, Q.T.; Meng, Z.Y.; Pan, J.S. Surrogate-Assisted Fully-Informed Particle Swarm Optimization for High-Dimensional Expensive Optimization. Appl. Soft Comput. 2024, 167, 112464. [Google Scholar] [CrossRef]
- Liu, S.L.; Wang, H.D.; Peng, W.; Yao, W. Surrogate-Assisted Evolutionary Algorithms for Expensive Combinatorial Optimization: A Survey. Complex Intell. Syst. 2024, 10, 5933–5949. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Opara, K.R.; Arabas, J. Differential Evolution: A Survey of Theoretical Analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Beyer, H.-G.; Beyer, H.-G.; Schwefel, H.-P.; Schwefel, H.-P. Evolution Strategies—A Comprehensive Introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Ahvanooey, M.T.; Li, Q.; Wu, M.; Wang, S. A Survey of Genetic Programming and Its Applications. KSII Trans. Internet Inf. Syst. 2019, 13, 1765–1794. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Q.K. Alpha Evolution: An Efficient Evolutionary Algorithm with Evolution Path Adaptation and Matrix Generation. Eng. Appl. Artif. Intell. 2024, 137, 109202. [Google Scholar] [CrossRef]
- Huang, W.; Xu, J. Particle Swarm Optimization. In Springer Tracts in Civil Engineering; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Dorigo, M.; Di Caro, G. Ant Colony Optimization: A New Meta-Heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation, CEC 1999, Washington, DC, USA, 6–9 July 1999. [Google Scholar]
- Jia, H.M.; Zhou, X.L.; Zhang, J.R.; Mirjalili, S. Superb Fairy-Wren Optimization Algorithm: A Novel Metaheuristic Algorithm for Solving Feature Selection Problems. Clust. Comput. J. Networks Softw. Tools Appl. 2025, 28, 246. [Google Scholar] [CrossRef]
- Alkharsan, A.; Ata, O. HawkFish Optimization Algorithm: A Gender-Bending Approach for Solving Complex Optimization Problems. Electronics 2025, 14, 611. [Google Scholar] [CrossRef]
- Xiao, Y.N.; Cui, H.; Abu Khurma, R.; Castillo, P.A. Artificial Lemming Algorithm: A Novel Bionic Meta-Heuristic Technique for Solving Real-World Engineering Optimization Problems. Artif. Intell. Rev. 2025, 58, 84. [Google Scholar] [CrossRef]
- Hu, G.; Cheng, M.; Houssein, E.H.; Hussien, A.G.; Abualigah, L. SDO: A Novel Sled Dog-Inspired Optimizer for Solving Engineering Problems. Adv. Eng. Informatics 2024, 62, 102783. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Liu, G.W.; Jiang, F. Chinese Pangolin Optimizer: A Novel Bio-Inspired Metaheuristic for Solving Optimization Problems. J. Supercomput. 2025, 81, 517. [Google Scholar] [CrossRef]
- Tian, A.Q.; Liu, F.F.; Lv, H.X. Snow Geese Algorithm: A Novel Migration-Inspired Meta-Heuristic Algorithm for Constrained Engineering Optimization Problems. Appl. Math. Model. 2024, 126, 327–347. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z.; Li, H.; Yildiz, A.R.; Mirjalili, S. Starfish Optimization Algorithm (SFOA): A Bio-Inspired Metaheuristic Algorithm for Global Optimization Compared with 100 Optimizers. Neural Comput. Appl. 2025, 37, 3641–3683. [Google Scholar] [CrossRef]
- Abu Falahah, I.; Al-Baik, O.; Alomari, S.; Bektemyssova, G.; Gochhait, S.; Leonova, I.; Malik, O.P.; Werner, F.; Dehghani, M. Frilled Lizard Optimization: A Novel Bio-Inspired Optimizer for Solving Engineering Applications. Comput. Mater. Contin. 2024, 79, 3631–3678. [Google Scholar] [CrossRef]
- Wang, W.C.; Tian, W.C.; Xu, D.M.; Zang, H.F. Arctic Puffin Optimization: A Bio-Inspired Metaheuristic Algorithm for Solving Engineering Design Optimization. Adv. Eng. Softw. 2024, 195, 103694. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Mirjalili, S. Eel and Grouper Optimizer: A Nature-Inspired Optimization Algorithm. Clust. Comput. J. Networks Softw. Tools Appl. 2024, 27, 12745–12786. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Saha, A.K.; Pal, J.; Abualigah, L.; Mirjalili, S. Greater Cane Rat Algorithm (GCRA): A Nature-Inspired Metaheuristic for Optimization Problems. Heliyon 2024, 10, e31629. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.F.; Liu, D.; Chen, J.D.; He, L. Secretary Bird Optimization Algorithm: A New Metaheuristic for Solving Global Optimization Problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Sang-To, T.; Hoang-Le, M.; Wahab, M.A.; Cuong-Le, T. An Efficient Planet Optimization Algorithm for Solving Engineering Problems. Sci. Rep. 2022, 12, 8362. [Google Scholar] [CrossRef]
- Qi, A.L.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H.L. FATA: An Efficient Optimization Method Based on Geophysics. Neurocomputing 2024, 607, 128289. [Google Scholar] [CrossRef]
- Cymerys, K.; Oszust, M. Attraction–Repulsion Optimization Algorithm for Global Optimization Problems. Swarm Evol. Comput. 2024, 84, 101459. [Google Scholar] [CrossRef]
- Sowmya, R.; Premkumar, M.; Jangir, P. Newton-Raphson-Based Optimizer: A New Population-Based Metaheuristic Algorithm for Continuous Optimization Problems. Eng. Appl. Artif. Intell. 2024, 128, 107532. [Google Scholar] [CrossRef]
- Deng, L.; Liu, S. Snow Ablation Optimizer: A Novel Metaheuristic Technique for Numerical Optimization and Engineering Design. Expert Syst. Appl. 2023, 225, 120069. [Google Scholar] [CrossRef]
- Hashim, F.A.; Mostafa, R.R.; Hussien, A.G.; Mirjalili, S.; Sallam, K.M. Fick’s Law Algorithm: A Physical Law-Based Algorithm for Numerical Optimization. Knowl.-Based Syst. 2023, 260, 110146. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems. CAD Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Nemati, M.; Zandi, Y.; Sabouri, J. Application of a Novel Metaheuristic Algorithm Inspired by Connected Banking System in Truss Size and Layout Optimum Design Problems and Optimization Problems. Sci. Rep. 2024, 14, 27345. [Google Scholar] [CrossRef]
- Jia, H.; Wen, Q.; Wang, Y.; Mirjalili, S. Catch Fish Optimization Algorithm: A New Human Behavior Algorithm for Solving Clustering Problems. Cluster Comput. 2024, 27, 13295–13332. [Google Scholar] [CrossRef]
- Abdulhameed, S.; Rashid, T.A. Child Drawing Development Optimization Algorithm Based on Child’s Cognitive Development. Arab. J. Sci. Eng. 2022, 47, 1337–1351. [Google Scholar] [CrossRef]
- Faridmehr, I.; Nehdi, M.L.; Davoudkhani, I.F.; Poolad, A. Mountaineering Team-Based Optimization: A Novel Human-Based Metaheuristic Algorithm. Mathematics 2023, 11, 1273. [Google Scholar] [CrossRef]
- Trojovský, P. A New Human-Based Metaheuristic Algorithm for Solving Optimization Problems Based on Preschool Education. Sci. Rep. 2023, 13, 21472. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G. Human Evolutionary Optimization Algorithm. Expert Syst. Appl. 2024, 241, 122638. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Luan, T.M.; Khatir, S.; Tran, M.T.; De Baets, B.; Cuong-Le, T. Exponential-Trigonometric Optimization Algorithm for Solving Complicated Engineering Problems. Comput. Methods Appl. Mech. Eng. 2024, 432, 117411. [Google Scholar] [CrossRef]
- Cheng, J.; De Waele, W. Weighted Average Algorithm: A Novel Meta-Heuristic Optimization Algorithm Based on the Weighted Average Position Concept. Knowl.-Based Syst. 2024, 305, 112564. [Google Scholar] [CrossRef]
- Beltran, L.A.; Navarro, M.A.; Oliva, D.; Campos-Peña, D.; Ramos-Frutos, J.; Zapotecas-Martínez, S. Quasi-Random Fractal Search (QRFS): A Dynamic Metaheuristic with Sigmoid Population Decrement for Global Optimization. Expert Syst. Appl. 2024, 254, 124400. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Exponential Distribution Optimizer (EDO): A Novel Math-Inspired Algorithm for Global Optimization and Engineering Problems. Artif. Intell. Rev. 2023, 56, 9329–9400. [Google Scholar] [CrossRef]
- Zhao, S.J.; Zhang, T.R.; Cai, L.; Yang, R.H. Triangulation Topology Aggregation Optimizer: A Novel Mathematics-Based Meta-Heuristic Algorithm for Continuous Optimization and Engineering Applications. Expert Syst. Appl. 2024, 238, 121744. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A Physics-Based Optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Li, W.K.; Yang, X.; Yin, Y.C.; Wang, Q. A Novel Hybrid Improved RIME Algorithm for Global Optimization Problems. Biomimetics 2025, 10, 14. [Google Scholar] [CrossRef]
- Zhou, T.T.; Shang, C. Parameter Identification of Photovoltaic Models by an Enhanced RIME Algorithm. Int. J. Energy Res. 2024, 2024, 9777345. [Google Scholar] [CrossRef]
- Xie, C.K.; Li, S.B.; Qin, X.Q.; Fu, S.W.; Zhang, X.X. Multiple Elite Strategy Enhanced RIME Algorithm for 3D UAV Path Planning. Sci. Rep. 2024, 14, 21734. [Google Scholar] [CrossRef]
- Wang, L.; Xu, J.L.; Jia, L.Y.; Wang, T.; Xu, Y.J.; Liu, X.C. Multi-Strategy RIME Optimization Algorithm for Feature Selection of Network Intrusion Detection. Comput. Secur. 2025, 153, 104393. [Google Scholar] [CrossRef]
- Zhong, R.; Zhang, C.; Yu, J. Hierarchical RIME Algorithm with Multiple Search Preferences for Extreme Learning Machine Training. Alexandria Eng. J. 2025, 110, 77–98. [Google Scholar] [CrossRef]
- Sun, M.J.; Chen, Y.; Heidari, A.A.; Liu, L.; Chen, H.L.; He, Q.X. Double Enhanced Solution Quality Boosted RIME Algorithm with Crisscross Operations for Breast Cancer Image Segmentation. J. Bionic Eng. 2024, 21, 3151–3178. [Google Scholar] [CrossRef]
- Wu, H.Y.; Chen, Y.; Cai, Z.N.; Heidari, A.A.; Chen, H.L.; Liang, G.X. Dual-Weight Decay Mechanism and Nelder-Mead Simplex Boosted RIME Algorithm for Optimal Power Flow. J. Big Data 2024, 11, 172. [Google Scholar] [CrossRef]
- Gu, T.; Zhang, Y.J.; Wang, L.M.; Zhang, Y.F.; Deveci, M.; Wen, X. A Comprehensive Analysis of Multi-Strategic RIME Algorithm for UAV Path Planning in Varied Terrains. J. Ind. Inf. Integr. 2025, 43, 100742. [Google Scholar] [CrossRef]
- Aljaidi, M.; Mashru, N.; Patel, P.; Adalja, D.; Jangir, P.; Arpita; Pandya, S.B.; Khishe, M. MORIME: A Multi-Objective RIME Optimization Framework for Efficient Truss Design. Results Eng. 2025, 25, 103933. [Google Scholar] [CrossRef]
- Pandya, S.B.; Kalita, K.; Jangir, P.; Cep, R.; Migdady, H.; Chohan, J.S.; Abualigah, L.; Mallik, S. Multi-Objective RIME Algorithm-Based Techno Economic Analysis for Security Constraints Load Dispatch and Power Flow Including Uncertainties Model of Hybrid Power Systems. Energy Rep. 2024, 11, 4423–4451. [Google Scholar] [CrossRef]
- Yu, S.D.; Chen, H.L.; Heidari, A.A.; Liang, G.X.; Chen, Y.; Chen, Z.Q.; Jin, X.X. Multi-Strategy Ensemble Binary RIME Optimization for Feature Selection. Neurocomputing 2025, 639, 130284. [Google Scholar] [CrossRef]
- Jin, B.; Cruz, L.; Goncalves, N. Pseudo RGB-D Face Recognition. IEEE Sens. J. 2022, 22, 21780–21794. [Google Scholar] [CrossRef]
- Jia, H.; Lu, C. Guided Learning Strategy: A Novel Update Mechanism for Metaheuristic Algorithms Design and Improvement. Knowl.-Based Syst. 2024, 286, 111402. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Batis, M.; Chen, Y.; Wang, M.J.; Liu, L.; Heidari, A.A.; Chen, H.L. ACGRIME: Adaptive Chaotic Gaussian RIME Optimizer for Global Optimization and Feature Selection. Clust. Comput. J. Networks Softw. TOOLS Appl. 2025, 28, 61. [Google Scholar] [CrossRef]
- Chen, S.-S.; Jiang, Y.-T.; Chen, W.; Li, X.-Y. TERIME: An Improved RIME Algorithm with Enhanced Exploration and Exploitation for Robust Parameter Extraction of Photovoltaic Models. J. Bionic Eng. 2025, 22, 1535–1556. [Google Scholar] [CrossRef]
- Huang, J.; Chen, Y.; Heidari, A.A.; Liu, L.; Chen, H.; Liang, G. IRIME: Mitigating Exploitation-Exploration Imbalance in RIME Optimization for Feature Selection. iScience 2024, 27, 110561. [Google Scholar] [CrossRef]
- Zheng, Y.P.; Kuang, F.J.; Heidari, A.A.; Yuan, L.P.; Zhang, S.Y.; Chen, H.L. RIME Optimization with Dynamic Multi-Dimensional Random Mechanism and Nelder-Mead Simplex for Photovoltaic Parameter Estimation. Sci. Rep. 2025, 15, 20951. [Google Scholar] [CrossRef]
- Yin, S.; Luo, Q.; Zhou, Y. EOSMA: An Equilibrium Optimizer Slime Mould Algorithm for Engineering Design Problems. Arab. J. Sci. Eng. 2022, 47, 10115–10146. [Google Scholar] [CrossRef]
- Zhang, Y.; Chi, A. Group Teaching Optimization Algorithm with Information Sharing for Numerical Optimization and Engineering Optimization. J. Intell. Manuf. 2023, 34, 1547–1571. [Google Scholar] [CrossRef]
- Jiang, Z.; Zou, F.; Chen, D.; Cao, S.; Liu, H.; Guo, W. An Ensemble Multi-Swarm Teaching–Learning-Based Optimization Algorithm for Function Optimization and Image Segmentation. Appl. Soft Comput. 2022, 130, 109653. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Fattouh, A.M.; Jambi, K.M. LSHADE with Semi-Parameter Adaptation Hybrid with CMA-ES for Solving CEC 2017 Benchmark Problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation, CEC 2017—Proceedings, Donostia, Spain, 5–8 June 2017. [Google Scholar]
- Li, Y.; Han, T.; Zhou, H.; Wei, Y.; Wang, Y.; Tan, M.; Huang, C. APSM-JSO: A Novel JSO Variant with an Adaptive Parameter Selection Mechanism and a New External Archive Updating Mechanism. Swarm Evol. Comput. 2023, 78, 101283. [Google Scholar] [CrossRef]
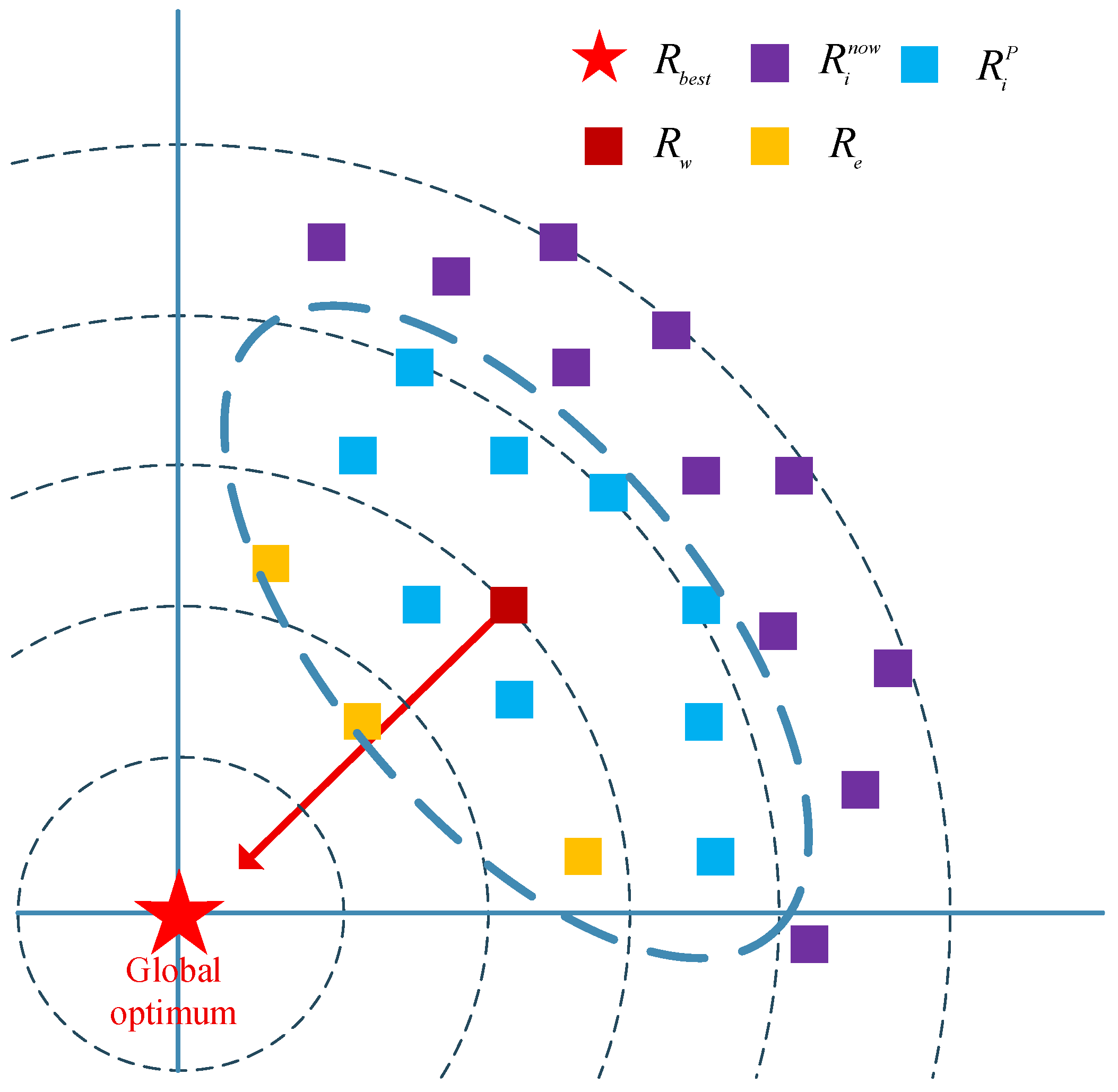
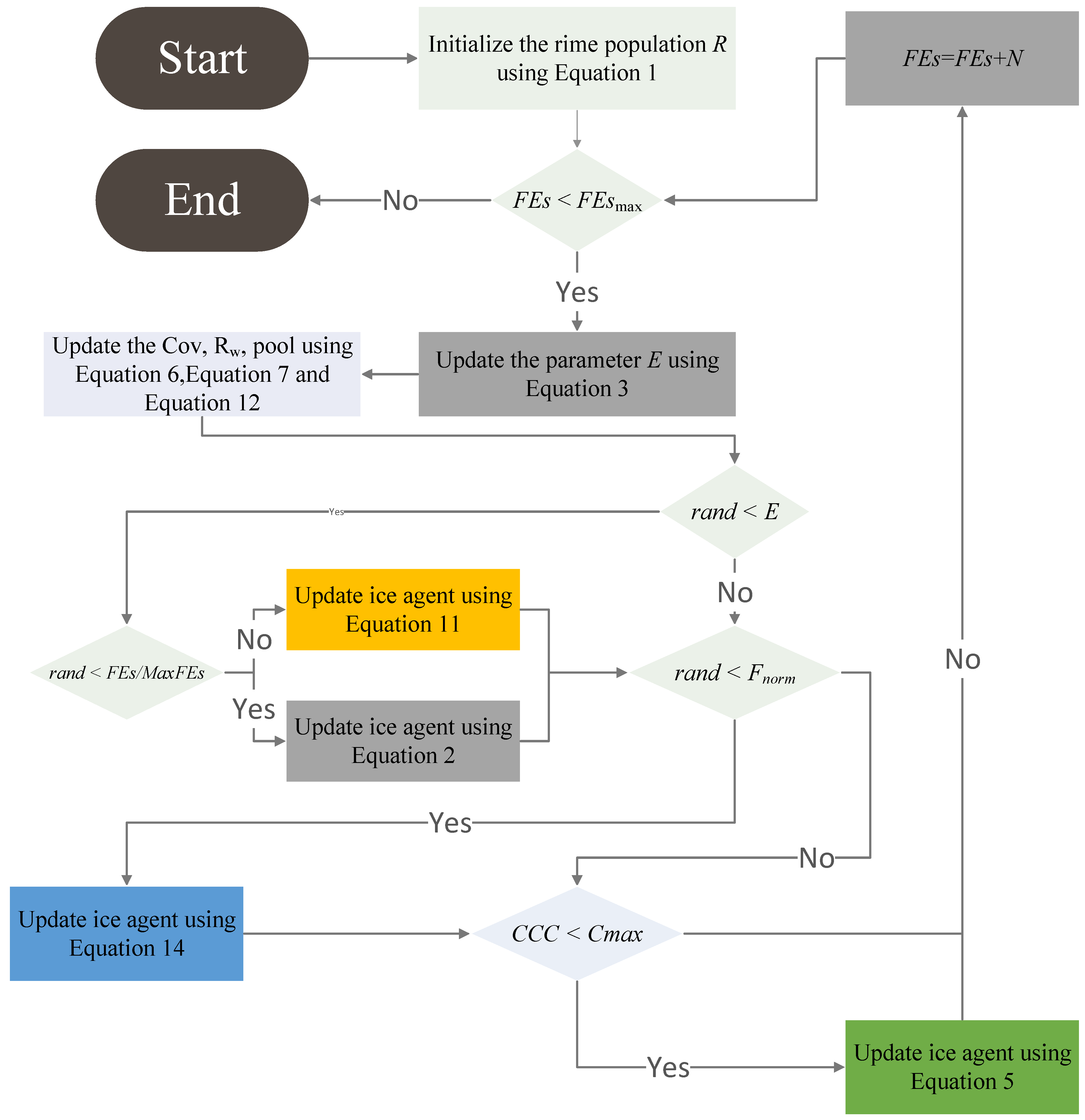
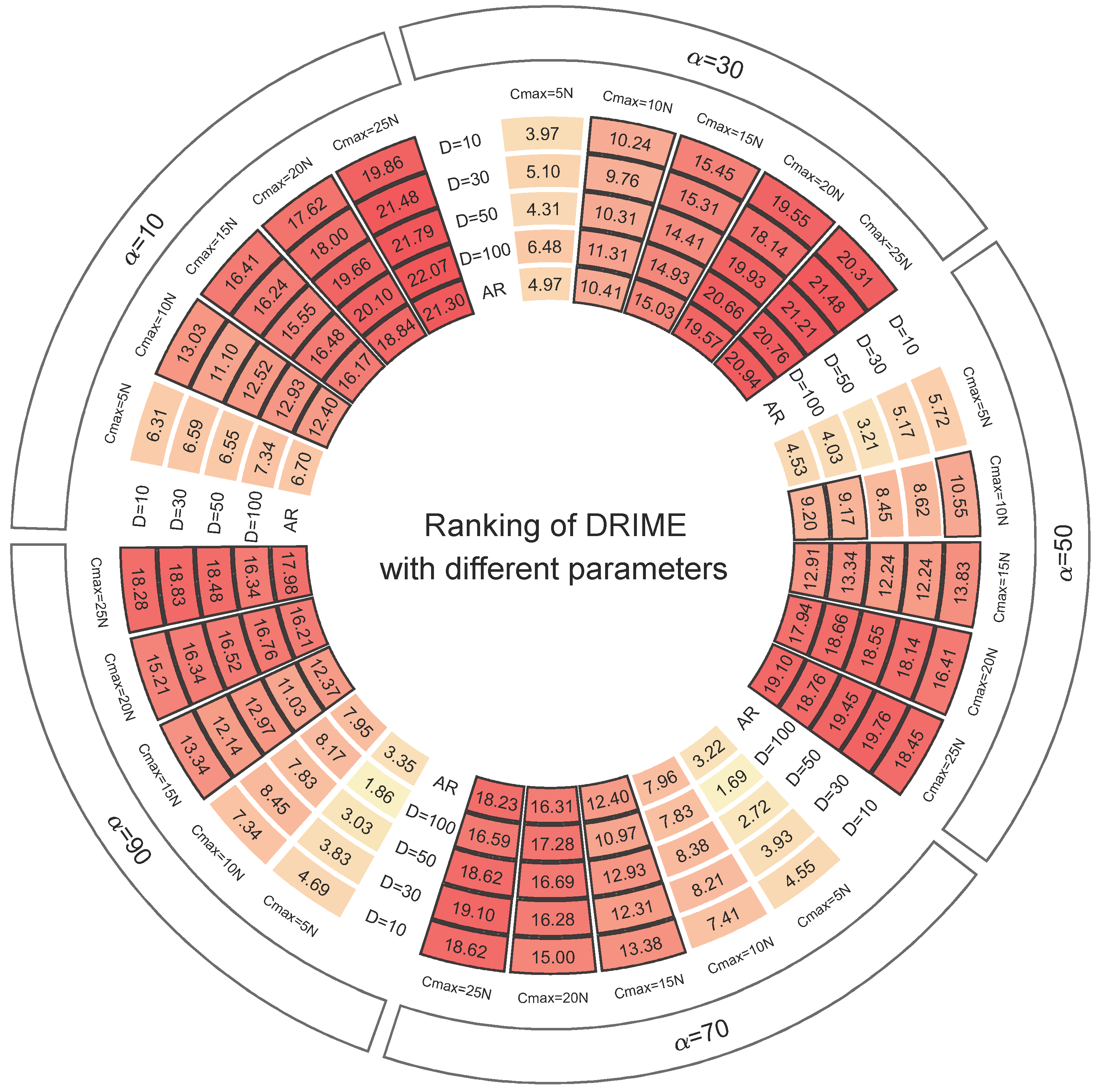
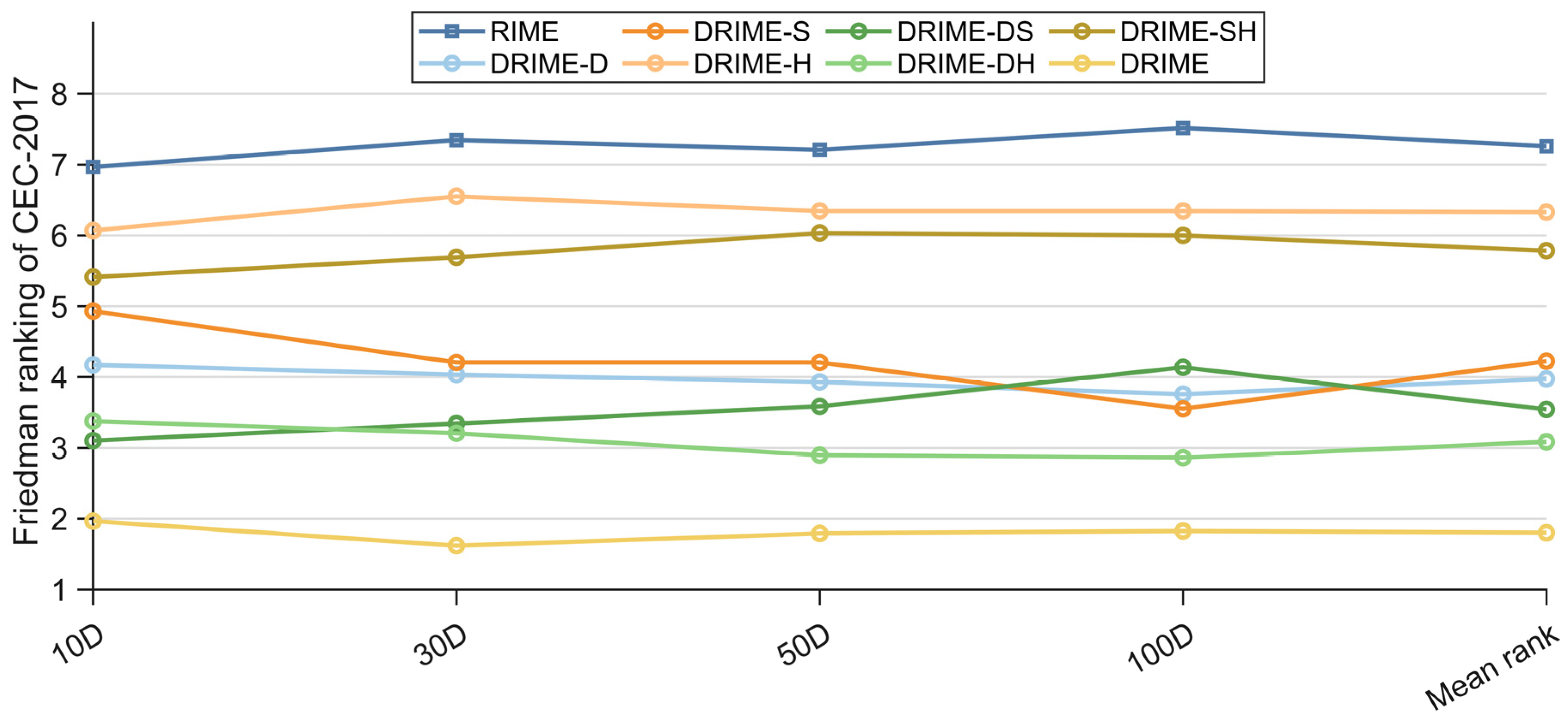
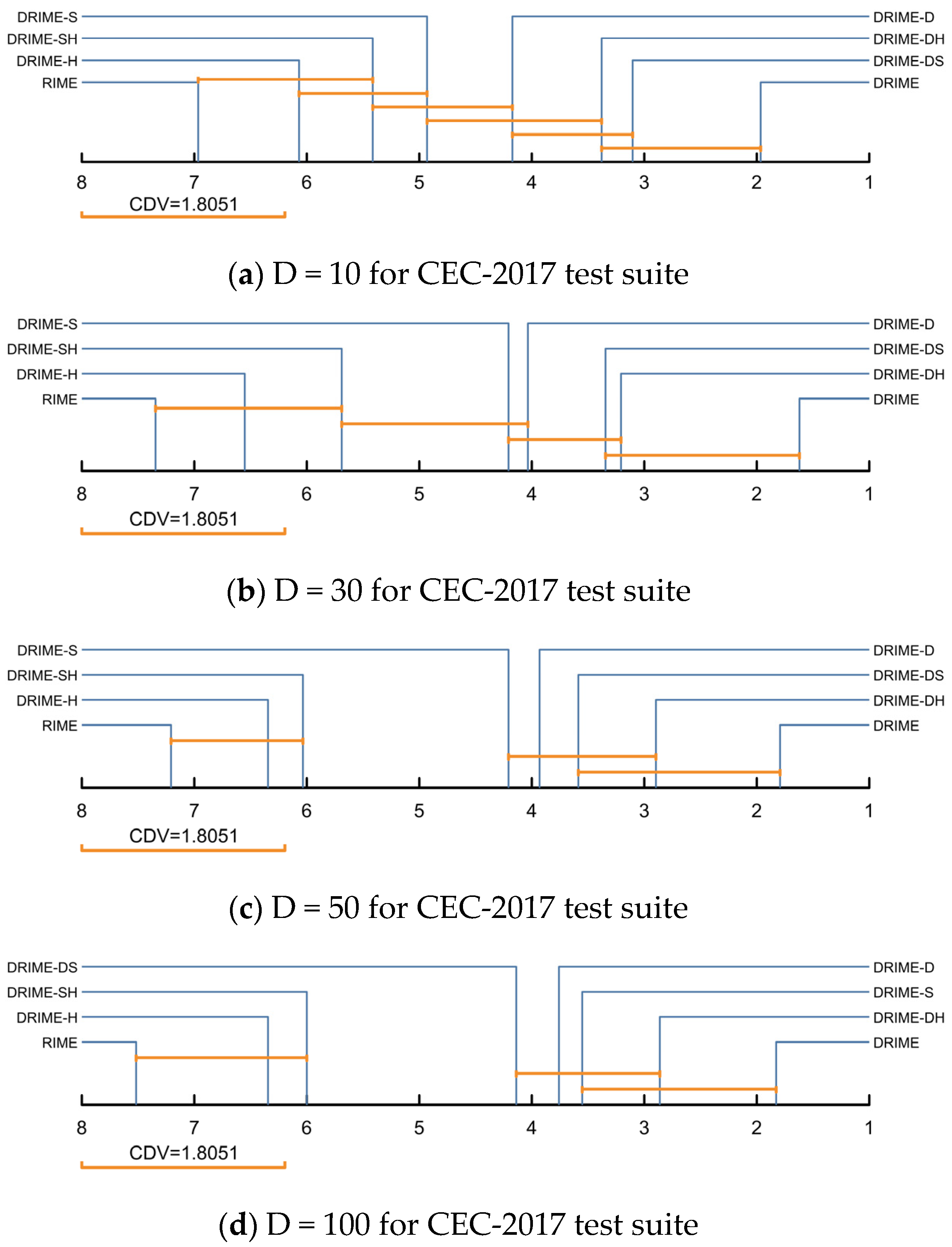
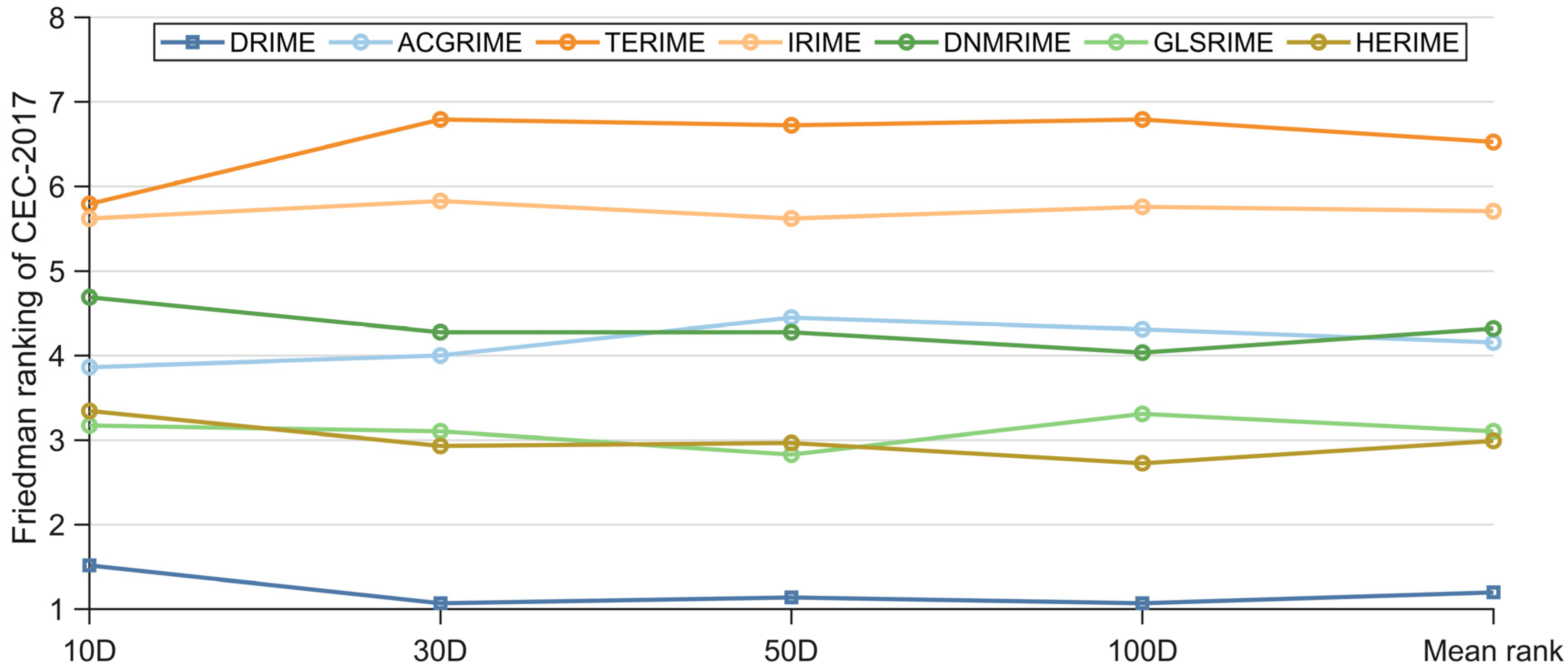
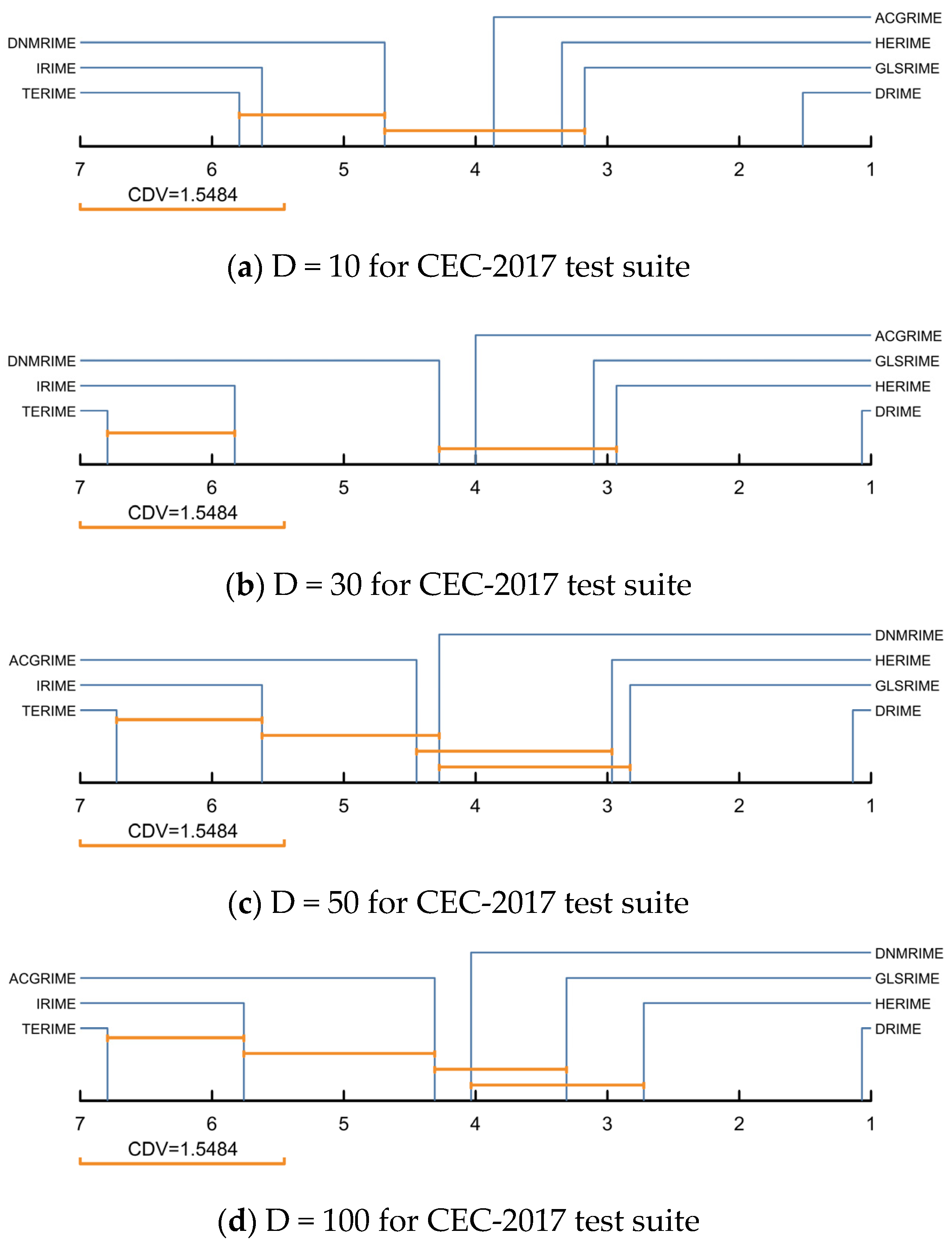
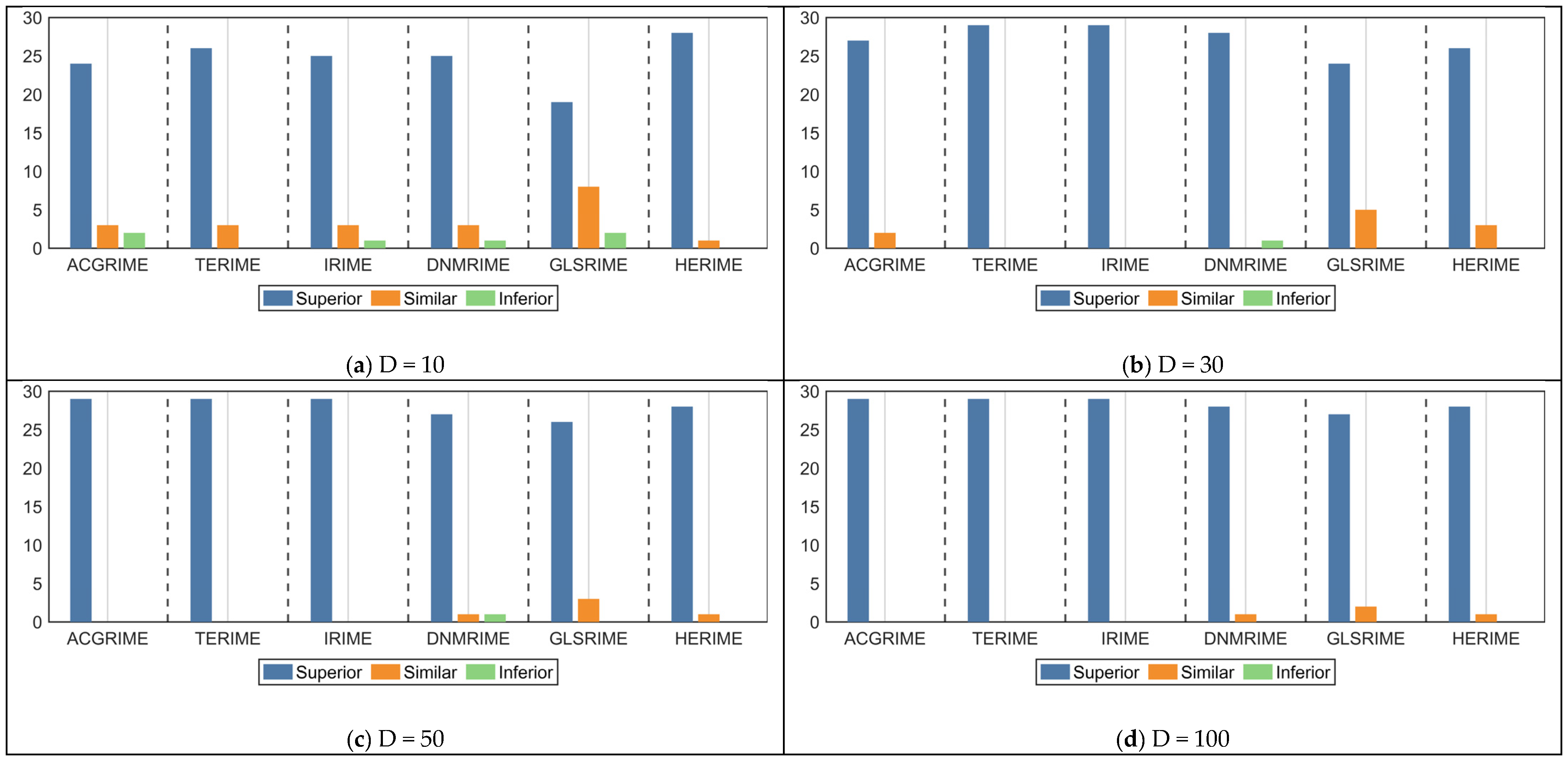
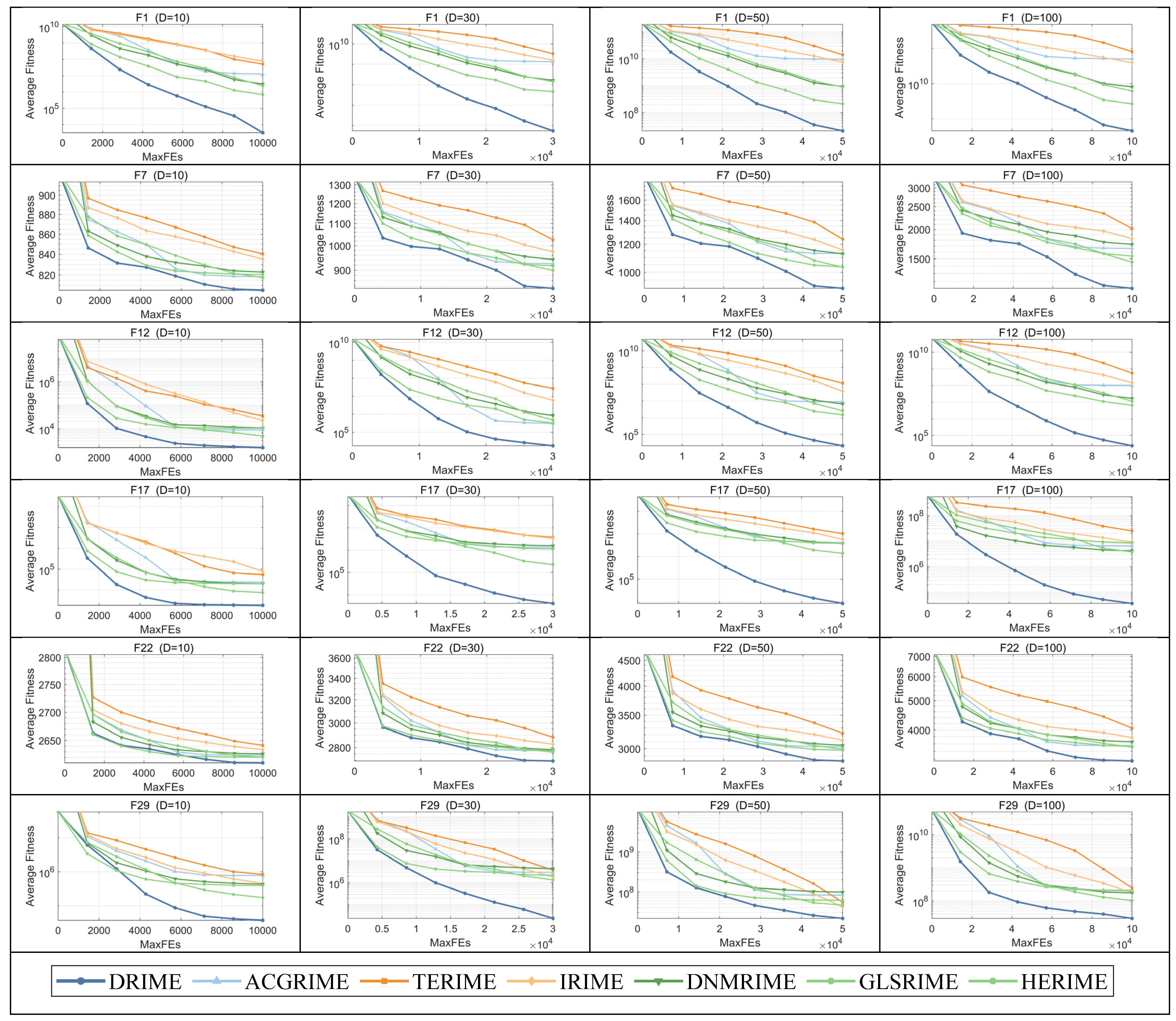
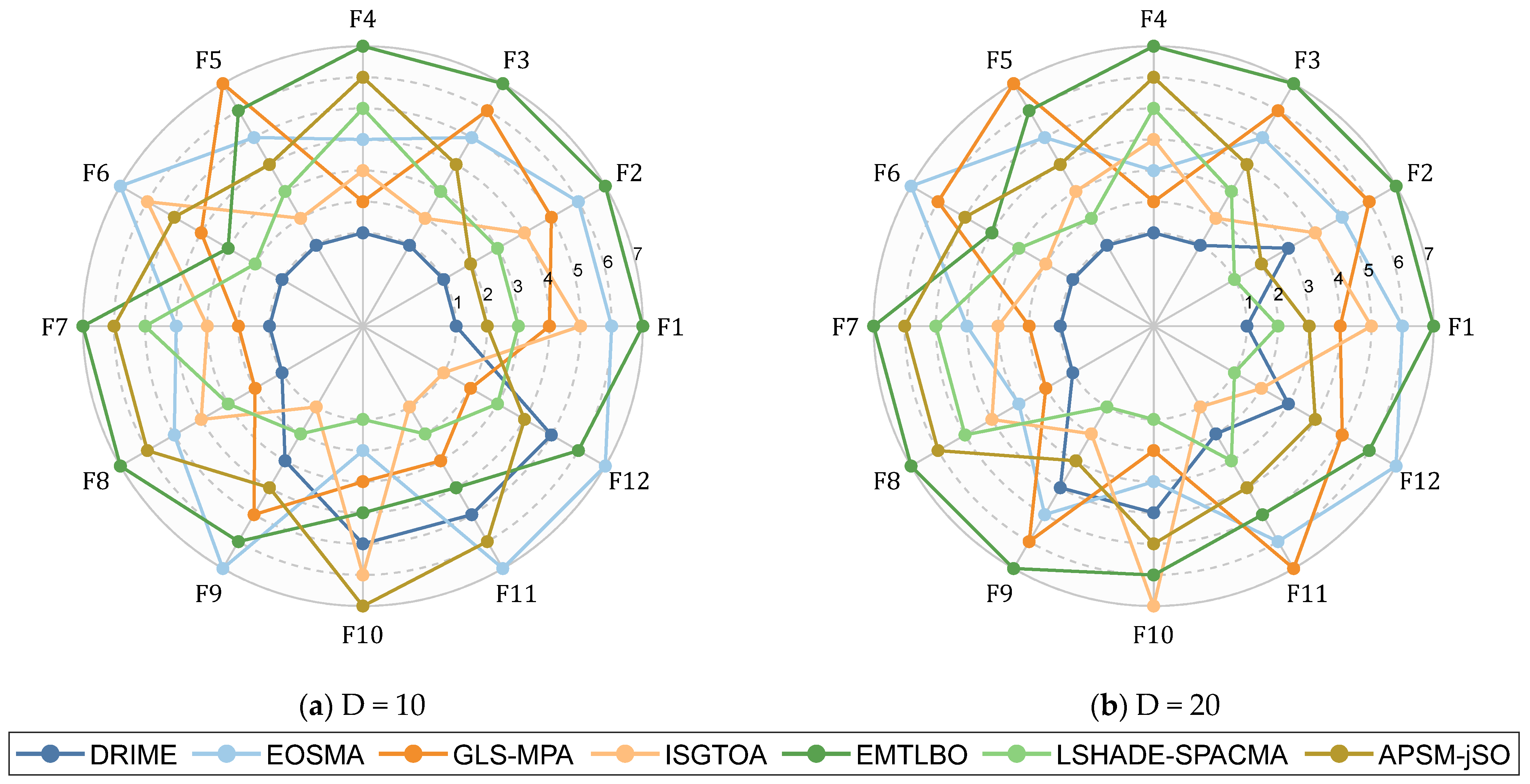
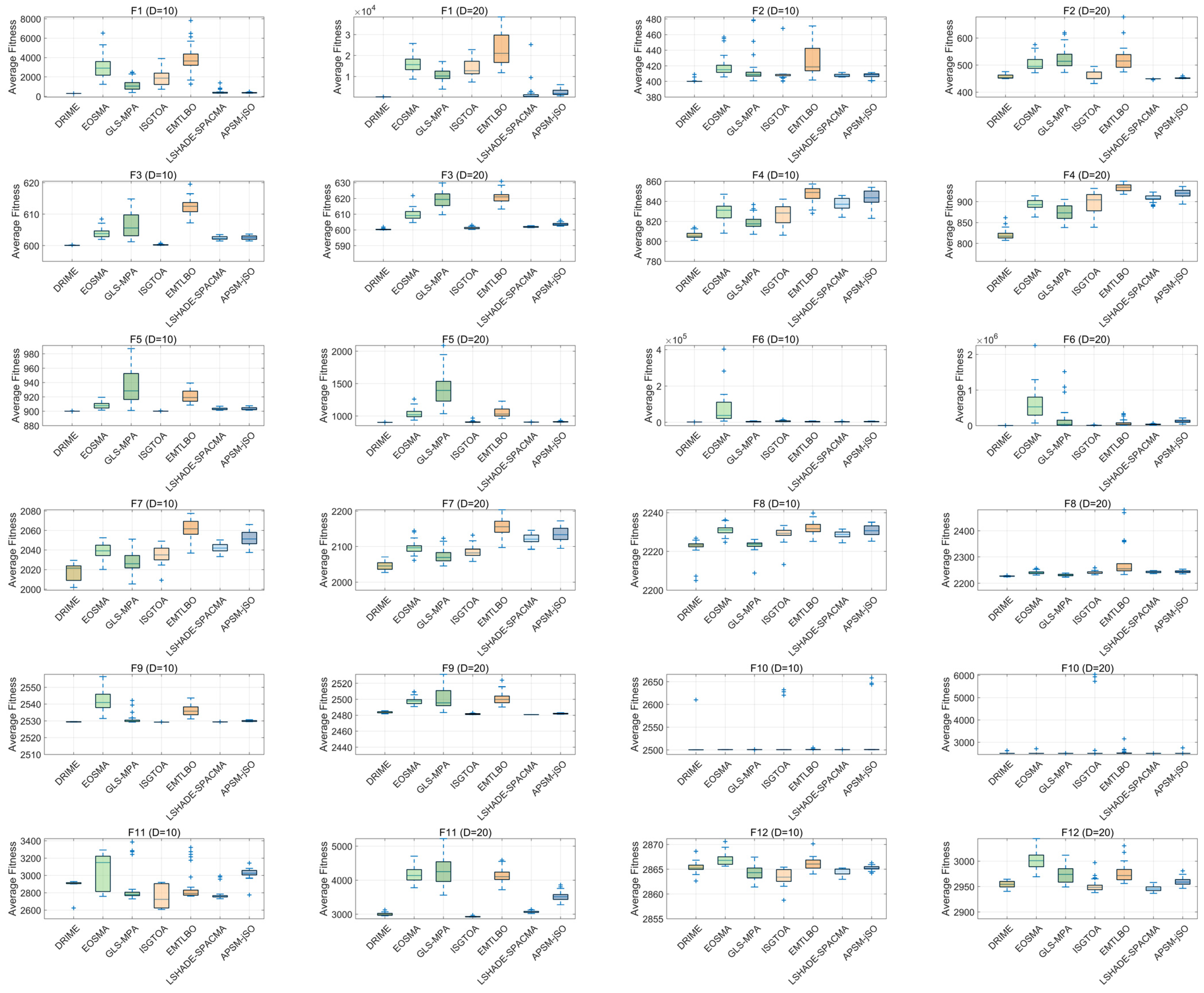
| Hardware | |
| CPU | AMD R9 7945HX (2.5 GHz) |
| RAM | 32 GB |
| Operating system | 64-bit Windows 11 |
| Software | |
| Programming language | MATLAB R2023a |
| Common Setting | |
| Dimension of test suites | |
| Algorithm setting | |
| DRIME | |
| RIME | |
| ACGRIME | |
| TERIME | |
| IRIME | |
| DNMRIME | |
| GLSRIME | |
| HERIME | |
| EOSMA | |
| GLS-MPA | |
| ISGTOA | |
| EMTLBO | |
| LSHADE-SPACMA | |
| APSM-jSO | |
| Type | No. | Functions Name | Min |
|---|---|---|---|
| Unimodal functions | F1 | Shifted and Rotated Bent Cigar Function | 100 |
| F2 | Shifted and Rotated Zakharov Function | 300 | |
| Multimodal functions | F3 | Shifted and Rotated Rosenbrock’s Function | 400 |
| F4 | Shifted and Rotated Rastrigin’s Function | 500 | |
| F5 | Shifted and Rotated Expanded Scaffer’s F6 Function | 600 | |
| F6 | Shifted and Rotated Lunacek Bi_Rastrigin Function | 700 | |
| F7 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| F8 | Shifted and Rotated Levy Function | 900 | |
| F9 | Shifted and Rotated Schwefel’s Function | 1000 | |
| Hybrid functions | F10 | Hybrid Function 1 (N = 3) | 1100 |
| F11 | Hybrid Function 2 (N = 3) | 1200 | |
| F12 | Hybrid Function 3 (N = 3) | 1300 | |
| F13 | Hybrid Function 4 (N = 4) | 1400 | |
| F14 | Hybrid Function 5 (N = 4) | 1500 | |
| F15 | Hybrid Function 6 (N = 4) | 1600 | |
| F16 | Hybrid Function 6 (N = 5) | 1700 | |
| F17 | Hybrid Function 6 (N = 5) | 1800 | |
| F18 | Hybrid Function 6 (N = 5) | 1900 | |
| F19 | Hybrid Function 6 (N = 6) | 2000 | |
| Composition functions | F20 | Composition Function 1 (N = 3) | 2100 |
| F21 | Composition Function 2 (N = 3) | 2200 | |
| F22 | Composition Function 3 (N = 4) | 2300 | |
| F23 | Composition Function 4 (N = 4) | 2400 | |
| F24 | Composition Function 5 (N = 5) | 2500 | |
| F25 | Composition Function 6 (N = 5) | 2600 | |
| F26 | Composition Function 7 (N = 6) | 2700 | |
| F27 | Composition Function 8 (N = 6) | 2800 | |
| F28 | Composition Function 9 (N = 3) | 2900 | |
| F29 | Composition Function 10 (N = 3) | 3000 |
| Type | No. | Functions Name | Min |
|---|---|---|---|
| Unimodal functions | F1 | Shifted and Full Rotated Zakharov Function | 300 |
| Basic functions | F2 | Shifted and Full Rotated Rosenbrock’s Function | 400 |
| F3 | Shifted and Full Rotated Expanded Schaffer’s f6 Function | 600 | |
| F4 | Shifted and Full Rotated Non-Continuous Rastrigin’s Function | 800 | |
| F5 | Shifted and Full Rotated Levy Function | 900 | |
| Hybrid functions | F6 | Hybrid Function 1 (N = 3) | 1800 |
| F7 | Hybrid Function 2 (N = 6) | 2000 | |
| F8 | Hybrid Function 3 (N = 5) | 2200 | |
| Composition functions | F9 | Composition Function 1 (N = 5) | 2300 |
| F10 | Composition Function 2 (N = 4) | 2400 | |
| F11 | Composition Function 3 (N = 5) | 2600 | |
| F12 | Composition Function 4 (N = 6) | 2700 |
| Test Suite | Dimension | RIME | DRIME-D | DRIME-S | DRIME-H | DRIME-DS | DRIME-DH | DRIME-SH | DRIME | p-Value |
|---|---|---|---|---|---|---|---|---|---|---|
| CEC-2017 | 10 | 6.966 | 4.172 | 4.931 | 6.069 | 3.103 | 3.379 | 5.414 | 1.966 | 2.62E-17 |
| 30 | 7.345 | 4.034 | 4.207 | 6.552 | 3.345 | 3.207 | 5.690 | 1.621 | 2.46E-23 | |
| 50 | 7.207 | 3.931 | 4.207 | 6.345 | 3.586 | 2.897 | 6.034 | 1.793 | 3.07E-22 | |
| 100 | 7.517 | 3.759 | 3.552 | 6.345 | 4.138 | 2.862 | 6.000 | 1.828 | 3.47E-24 | |
| Mean rank | 7.259 | 3.974 | 4.224 | 6.328 | 3.543 | 3.086 | 5.784 | 1.802 | N/A | |
| Overall rank | 8 | 4 | 5 | 7 | 3 | 2 | 6 | 1 | N/A | |
| vs. RIME (+/=/−) | CEC-2017 Test Suite | |||
|---|---|---|---|---|
| D = 10 | D = 30 | D = 50D | D = 100 | |
| DRIME-D | 17/10/2 | 23/6/0 | 23/6/0 | 26/3/0 |
| DRIME-S | 8/20/1 | 24/5/0 | 22/7/0 | 27/2/0 |
| DRIME-H | 4/25/0 | 17/12/0 | 14/15/0 | 17/11/1 |
| DRIME-DS | 19/9/1 | 24/2/3 | 23/2/4 | 22/5/2 |
| DRIME-DH | 18/10/1 | 26/3/0 | 25/4/0 | 28/1/0 |
| DRIME-SH | 9/19/1 | 16/8/5 | 14/9/6 | 15/9/5 |
| DRIME | 19/8/2 | 25/3/1 | 25/2/2 | 27/1/1 |
| Algorithm | CEC-2017 Test Suite | |||||
|---|---|---|---|---|---|---|
| D = 10 | D = 30 | D = 50 | D = 100 | Mean Rank | Overall Rank | |
| DRIME | 1.517 | 1.069 | 1.138 | 1.069 | 1.198 | 1 |
| ACGRIME | 3.862 | 4.000 | 4.448 | 4.310 | 4.155 | 4 |
| TERIME | 5.793 | 6.793 | 6.724 | 6.793 | 6.526 | 9 |
| IRIME | 5.621 | 5.828 | 5.621 | 5.759 | 5.707 | 5 |
| DNMRIME | 4.690 | 4.276 | 4.276 | 4.034 | 4.319 | 7 |
| GLSRIME | 3.172 | 3.103 | 2.828 | 3.310 | 3.103 | 2 |
| HERIME | 3.345 | 2.931 | 2.966 | 2.724 | 2.991 | 3 |
| p-value | 3.98E-16 | 1.04E-26 | 1.14E-25 | 1.27E-26 | N/A | N/A |
| DRIME vs. +/=/− | CEC-2017 Test Suite | ||||
|---|---|---|---|---|---|
| 10D | 30D | 50D | 100D | Total | |
| ACGRIME | 24/3/2 | 27/2/0 | 29/0/0 | 29/0/0 | 109/5/2 |
| TERIME | 26/3/0 | 29/0/0 | 29/0/0 | 29/0/0 | 113/3/0 |
| IRIME | 25/3/1 | 29/0/0 | 29/0/0 | 29/0/0 | 112/3/1 |
| DNMRIME | 25/3/1 | 28/0/1 | 27/1/1 | 28/1/0 | 108/5/3 |
| GLSRIME | 19/8/2 | 24/5/0 | 26/3/0 | 27/2/0 | 96/18/2 |
| HERIME | 28/1/0 | 26/3/0 | 28/1/0 | 28/1/0 | 110/6/0 |
| Algorithm | CEC-2022 Test Suite | |||||
|---|---|---|---|---|---|---|
| D = 10 | D = 20 | Mean Rank | Overall Rank | |||
| Rank | +/=/− | Rank | +/=/− | |||
| DRIME | 2.167 | N/A | 1.917 | N/A | 2.042 | 1 |
| EOSMA | 5.417 | 11/0/1 | 4.917 | 11/0/1 | 5.167 | 6 |
| GLS-MPA | 3.750 | 8/1/3 | 4.583 | 11/0/1 | 4.167 | 4 |
| ISGTOA | 3.167 | 9/0/3 | 3.250 | 8/1/3 | 3.208 | 3 |
| EMTLBO | 5.917 | 10/0/2 | 6.333 | 12/0/0 | 6.125 | 7 |
| LSHADE-SPACMA | 2.917 | 8/1/3 | 2.667 | 8/0/4 | 2.792 | 2 |
| APSM-jSO | 4.667 | 11/1/0 | 4.333 | 10/0/2 | 4.500 | 5 |
| p-value | 5.21E-05 | N/A | 5.39E-06 | N/A | N/A | N/A |
| Problem | Name | D | g | h |
|---|---|---|---|---|
| 1RC01 | Tension/compression spring design problem | 3 | 3 | 0 |
| 3RC03 | Three-bar truss design problem | 2 | 3 | 0 |
| 8RC06 | Cantilever beam design problem | 5 | 1 | 0 |
| 10RC08 | Step-cone pulley problem | 5 | 8 | 3 |
| 11RC09 | Planetary gear train design | 9 | 10 | 1 |
| 12RC10 | Robot gripper problem | 7 | 7 | 0 |
| 2RC02 | Pressure vessel design problem | 4 | 4 | 0 |
| 4RC04 | Welded beam design problem | 4 | 5 | 0 |
| 6RC05 | Gear train design problem | 4 | 1 | 1 |
| 9RC07 | Multiple disk clutch brake design problem | 5 | 7 | 0 |
| No. | Index | DRIME | RIME | GLSRIME | HERIME | ACGRIME | IRIME | LSHADE-SPACMA | APSM-jSO | EOSMA | ISGTOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| RC01 | Best | 1.2740E-02 | 1.2771E-02 | 1.2771E-02 | 1.2760E-02 | 1.2736E-02 | 1.2994E-02 | 1.2668E-02 | 1.2668E-02 | 1.2893E-02 | 1.2980E-02 |
| Mean | 1.3521E-02 | 1.7133E-02 | 1.7142E-02 | 1.4146E-02 | 1.4331E-02 | 1.4721E-02 | 1.2767E-02 | 1.2767E-02 | 1.3632E-02 | 1.5631E-02 | |
| Std | 9.4567E-04 | 2.5215E-03 | 2.3678E-03 | 1.5973E-03 | 1.5278E-03 | 2.1996E-03 | 1.0472E-04 | 1.0472E-04 | 6.2080E-04 | 2.8563E-03 | |
| Rank | 3 | 9 | 10 | 5 | 6 | 7 | 1 | 1 | 4 | 8 | |
| RC02 | Best | 2.6389E+02 | 2.6390E+02 | 2.6390E+02 | 2.6389E+02 | 2.6389E+02 | 2.6390E+02 | 2.6389E+02 | 2.6389E+02 | 2.6389E+02 | 2.6391E+02 |
| Mean | 2.6389E+02 | 2.6426E+02 | 2.6426E+02 | 2.6426E+02 | 2.6425E+02 | 2.6434E+02 | 2.6396E+02 | 2.6396E+02 | 2.6394E+02 | 2.6461E+02 | |
| Std | 1.4260E-05 | 4.6889E-01 | 4.6889E-01 | 9.5125E-01 | 4.5378E-01 | 4.7651E-01 | 9.7391E-02 | 9.7391E-02 | 4.7128E-02 | 6.6927E-01 | |
| Rank | 1 | 6 | 6 | 8 | 5 | 9 | 3 | 3 | 2 | 10 | |
| RC03 | Best | 1.3400E+00 | 1.3469E+00 | 1.3480E+00 | 1.3470E+00 | 1.3415E+00 | 1.3879E+00 | 1.3452E+00 | 1.3452E+00 | 1.3424E+00 | 1.5199E+00 |
| Mean | 1.3416E+00 | 1.3764E+00 | 1.3893E+00 | 1.4647E+00 | 1.3666E+00 | 1.6497E+00 | 1.4192E+00 | 1.4192E+00 | 1.3464E+00 | 2.0056E+00 | |
| Std | 1.3214E-03 | 3.4472E-02 | 3.3474E-02 | 9.8274E-02 | 2.7026E-02 | 1.5146E-01 | 7.1154E-02 | 7.1154E-02 | 2.8608E-03 | 3.2327E-01 | |
| Rank | 1 | 4 | 5 | 8 | 3 | 9 | 6 | 6 | 2 | 10 | |
| RC04 | Best | 1.6117E+01 | 1.6404E+01 | 1.6400E+01 | 1.6544E+01 | 1.6329E+01 | 1.6528E+01 | 1.6169E+01 | 1.6169E+01 | 1.6560E+01 | 1.7112E+01 |
| Mean | 1.6491E+01 | 1.7062E+01 | 1.7124E+01 | 1.7488E+01 | 1.8099E+01 | 2.1606E+01 | 1.6940E+01 | 1.6940E+01 | 1.7117E+01 | 2.1567E+01 | |
| Std | 2.8586E-01 | 3.7382E-01 | 4.7502E-01 | 5.9431E-01 | 6.8694E+00 | 9.2808E+00 | 4.1347E-01 | 4.1347E-01 | 5.3814E-01 | 4.4724E+00 | |
| Rank | 1 | 4 | 6 | 7 | 8 | 10 | 2 | 2 | 5 | 9 | |
| RC05 | Best | 2.3545E-01 | 2.3646E-01 | 2.3526E-01 | 2.4000E-01 | 2.3646E-01 | 2.3767E-01 | 2.4426E-01 | 2.4426E-01 | 2.3526E-01 | 2.5000E-01 |
| Mean | 2.4011E-01 | 2.4658E-01 | 2.4536E-01 | 2.6548E-01 | 2.6923E-01 | 2.5826E-01 | 2.5786E-01 | 2.5786E-01 | 2.4953E-01 | 4.5522E-01 | |
| Std | 3.7260E-03 | 8.4660E-03 | 9.1866E-03 | 2.2825E-02 | 8.8221E-02 | 2.0693E-02 | 1.2772E-02 | 1.2772E-02 | 1.1543E-02 | 3.1791E-01 | |
| Rank | 1 | 3 | 2 | 8 | 9 | 7 | 5 | 5 | 4 | 10 | |
| RC06 | Best | 3.1759E-16 | 1.0594E-16 | 1.3354E-16 | 1.0385E-16 | 8.8979E-17 | 1.2920E-16 | 7.3320E-17 | 7.3320E-17 | 3.7858E+00 | 1.2100E-16 |
| Mean | 3.8084E+00 | 3.7333E+00 | 4.0742E+00 | 2.9825E+00 | 3.8061E-01 | 1.2416E-01 | 1.6401E-16 | 1.6401E-16 | 5.0977E+00 | 5.3276E+00 | |
| Std | 1.0772E+00 | 2.2000E+00 | 1.9343E+00 | 2.7949E+00 | 1.4487E+00 | 6.8006E-01 | 1.6328E-16 | 1.6328E-16 | 6.6783E-01 | 3.0407E+00 | |
| Rank | 7 | 6 | 8 | 5 | 4 | 3 | 1 | 1 | 9 | 10 | |
| RC07 | Best | 6.0316E+03 | 6.0607E+03 | 6.0970E+03 | 6.1805E+03 | 6.0737E+03 | 6.6278E+03 | 5.8727E+03 | 5.8727E+03 | 6.1816E+03 | 6.8880E+03 |
| Mean | 6.4443E+03 | 7.1760E+03 | 7.2177E+03 | 7.9064E+03 | 6.7900E+03 | 9.7875E+03 | 6.7791E+03 | 6.7791E+03 | 6.7849E+03 | 1.2288E+04 | |
| Std | 2.6059E+02 | 5.9588E+02 | 5.1348E+02 | 1.0857E+03 | 5.8148E+02 | 2.7116E+03 | 7.8089E+02 | 7.8089E+02 | 3.7280E+02 | 3.6257E+03 | |
| Rank | 1 | 6 | 7 | 8 | 5 | 9 | 2 | 2 | 4 | 10 | |
| RC08 | Best | 1.6984E+00 | 1.7206E+00 | 1.7360E+00 | 1.7496E+00 | 1.7008E+00 | 1.7614E+00 | 1.7011E+00 | 1.7011E+00 | 1.7254E+00 | 1.8214E+00 |
| Mean | 1.7199E+00 | 2.1473E+00 | 2.1167E+00 | 1.9213E+00 | 1.9516E+00 | 2.0730E+00 | 1.8130E+00 | 1.8130E+00 | 1.8242E+00 | 2.0852E+00 | |
| Std | 4.2266E-02 | 3.9882E-01 | 3.9066E-01 | 2.3583E-01 | 2.4368E-01 | 1.8136E-01 | 9.7650E-02 | 9.7650E-02 | 1.0342E-01 | 2.1107E-01 | |
| Rank | 1 | 10 | 9 | 5 | 6 | 7 | 2 | 2 | 4 | 8 | |
| RC09 | Best | 2.7009E-12 | 2.7009E-12 | 2.7009E-12 | 2.3078E-11 | 2.3078E-11 | 2.3078E-11 | 2.3078E-11 | 2.3078E-11 | 2.7009E-12 | 2.3078E-11 |
| Mean | 9.9098E-10 | 2.8632E-09 | 3.5502E-09 | 4.8868E-09 | 1.0367E-08 | 1.3215E-08 | 2.7130E-09 | 2.7130E-09 | 1.2784E-09 | 9.7270E-09 | |
| Std | 1.4477E-09 | 2.9893E-09 | 6.9102E-09 | 9.5729E-09 | 1.3411E-08 | 3.1990E-08 | 3.2437E-09 | 3.2437E-09 | 2.4179E-09 | 1.1082E-08 | |
| Rank | 1 | 5 | 6 | 7 | 9 | 10 | 3 | 3 | 2 | 8 | |
| RC10 | Best | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 |
| Mean | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | 3.9247E+08 | |
| Std | 1.8187E-07 | 1.8187E-07 | 1.8187E-07 | 1.8187E-07 | 1.8187E-07 | 1.8187E-07 | 1.8187E-07 | 1.8187E-07 | 3.7527E-01 | 1.8187E-07 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 | 1 | |
| Friedman Rank | 2.200 | 5.850 | 6.450 | 6.600 | 6.000 | 7.600 | 3.450 | 3.450 | 4.600 | 8.800 | |
| +/=/− | N/A | 8/1/1 | 9/1/0 | 8/2/0 | 8/1/1 | 8/1/1 | 6/2/2 | 6/2/2 | 8/2/0 | 9/1/0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Shao, Y.; Fu, B.; Kou, L. DRIME: A Distributed Data-Guided RIME Algorithm for Numerical Optimization Problems. Biomimetics 2025, 10, 589. https://doi.org/10.3390/biomimetics10090589
Yang J, Shao Y, Fu B, Kou L. DRIME: A Distributed Data-Guided RIME Algorithm for Numerical Optimization Problems. Biomimetics. 2025; 10(9):589. https://doi.org/10.3390/biomimetics10090589
Chicago/Turabian StyleYang, Jinghao, Yuanyuan Shao, Bin Fu, and Lei Kou. 2025. "DRIME: A Distributed Data-Guided RIME Algorithm for Numerical Optimization Problems" Biomimetics 10, no. 9: 589. https://doi.org/10.3390/biomimetics10090589
APA StyleYang, J., Shao, Y., Fu, B., & Kou, L. (2025). DRIME: A Distributed Data-Guided RIME Algorithm for Numerical Optimization Problems. Biomimetics, 10(9), 589. https://doi.org/10.3390/biomimetics10090589







