Three Strategies Enhance the Bionic Coati Optimization Algorithm for Global Optimization and Feature Selection Problems
Abstract
1. Introduction
- An adaptive search strategy is proposed, which integrates individual learning capabilities and the learnability of disparities, effectively enhancing the algorithm’s global exploration capabilities.
- A balancing factor is introduced, incorporating phase-based and dynamically adjustable characteristics, to achieve a well-balanced interplay between the exploration and exploitation phases.
- A centroid guidance strategy is devised, which combines the concept of centroid guidance with the utilization of fractional-order historical memory, thereby improving the algorithm’s exploitation capabilities.
- By integrating the aforementioned three strategies, the bionic ABCCOA algorithm is formulated. Experimental results on 27 FS problems demonstrate its superiority in terms of classification accuracy, stability, and runtime. This confirms that bionic ABCCOA is a promising bionic FS method.
2. Mathematical Model of Coati Optimization Algorithm
2.1. Population Initialization Phase
2.2. Global Exploration Phase
2.3. Local Exploitation Phase
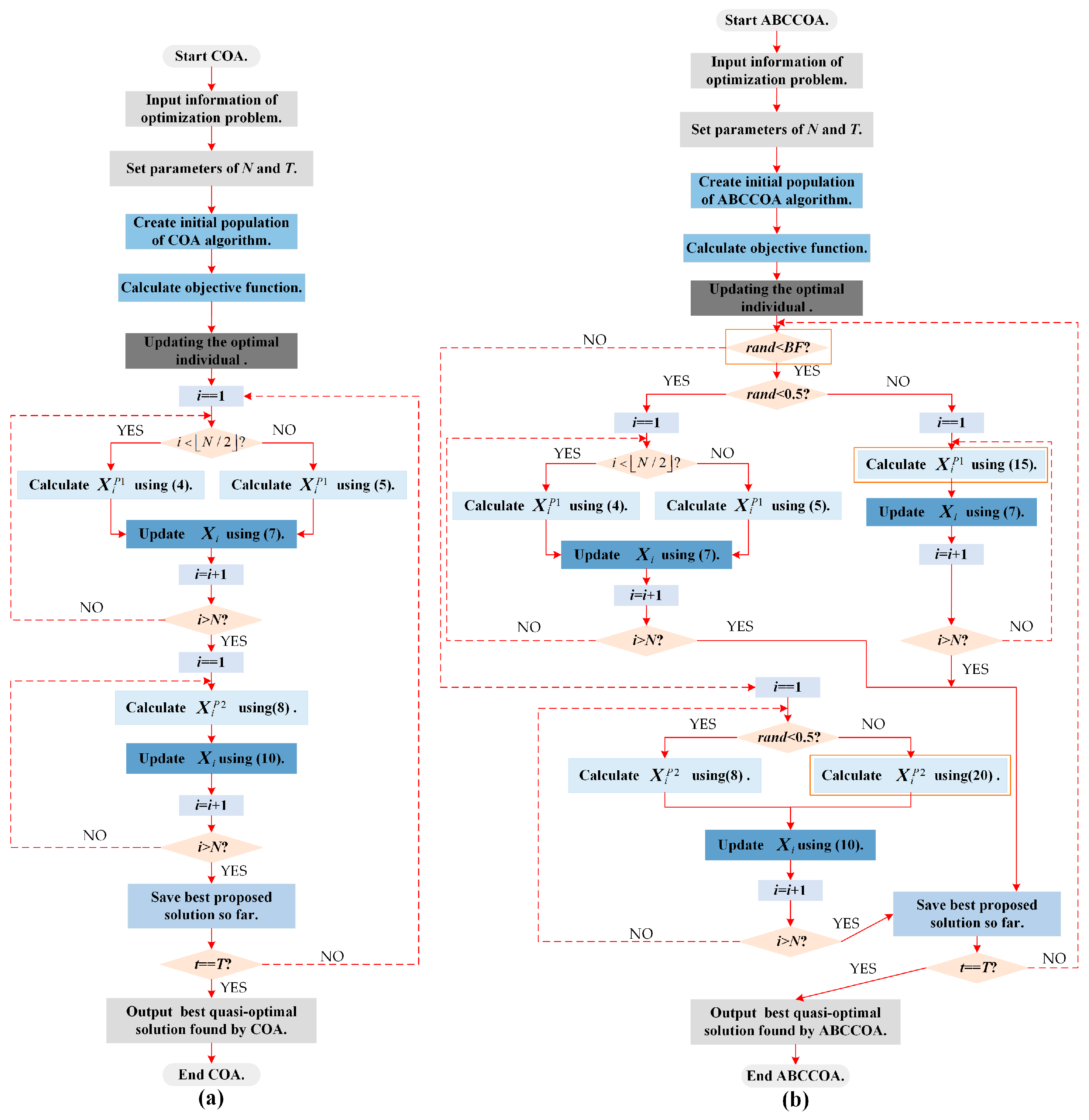
2.4. Execution Framework of COA Algorithm
| Algorithm 1: Pseudo code of COA algorithm |
| Input: Population size (N), Dimension (D), Upper bound (ub) and lower bound (lb), Maximum of iterations (T). |
| Output: Global best solution (Xbest). |
| 1. Initialize population based on Equation (1) and calculate the individual fitness function values of the population. 2. for t = 1:T 3. Calculate positions of iguanas using the globally best individual. 4. Phase 1: The attack behavior of coatis (Global Exploration Phase) 5. for 6. for j = 1:D 7. Calculate the jth dimensional new state of the ith individual based on Equation (4). 8. end for 9. end for 10. for 11. for j = 1:D 12. Calculate the jth dimensional new state of the ith individual based on Equation (5). 13. end for 14. end for 15. Use Equation (7) to preserve the new state of individual . 16. Phase 2: The escape behavior of coatis (Local Exploitation Phase) 17. for i = 1:N 18. for j = 1:D 19. Calculate the jth dimensional new state of the ith individual based on Equation (8). 20. end for 21. end for 22. Use Equation (10) to preserve the new state of individual . 23. Save the global best solution Xbest. 24. end for 25. Output the global best solution Xbest obtained by solving the optimization problem using the COA algorithm. |
3. The Proposal of ABCCOA Algorithm
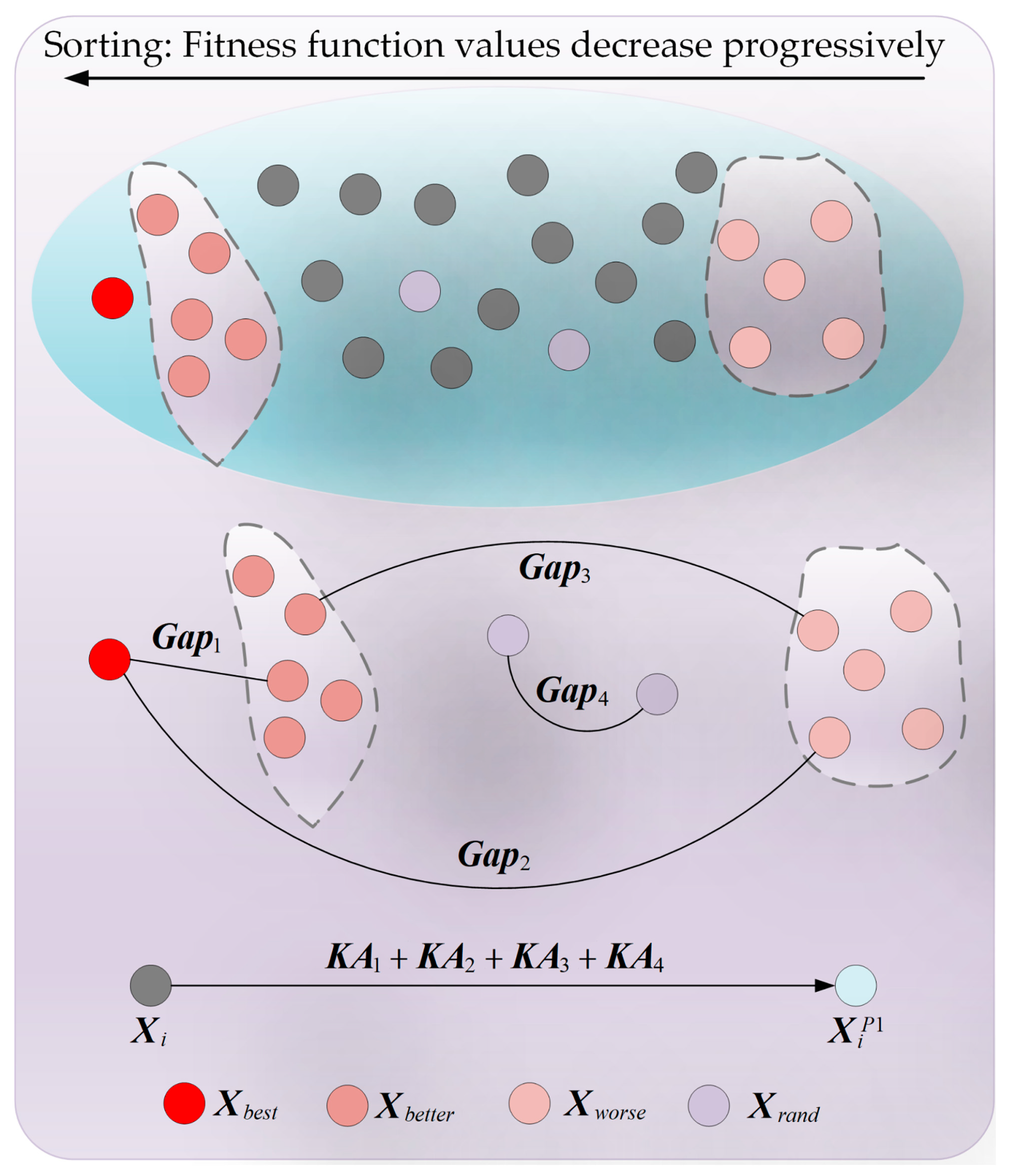
3.1. Adaptive Search Strategy
3.2. Balancing Factor
3.3. Centroid Guidance Strategy
3.4. Execution Framework of ABCCOA Algorithm
| Algorithm 2: Pseudo code of ABCCOA algorithm |
| Input: Population size (), Dimension (), Upper bound () and lower bound (), Maximum of iterations (). |
| Output: Global best solution (). |
| 1. Initialize population based on Equation (1) and calculate the individual fitness function values of the population. 2. for 3. Calculate positions of iguanas using the globally best individual. 4. Calculate Balancing Factor based on Equation (18). 5. if 6. Phase 1: The attack behavior of coatis (Global Exploration Phase) 7. if 8. for 9. for 10. Calculate the dimensional new state of the individual based on Equation (4). 11. end for 12. end for 13. for 14. for 15. Calculate the dimensional new state of the individual based on Equation (5). 16. end for 17. end for 18. else 19. for 20. Calculate the new state of the individual based on Equation (15). 21. end for 22. end if 23. Use Equation (7) to preserve the new state of individual . 24. else 25. Phase 2: The escape behavior of coatis (Local Exploitation Phase) 26. if 27. for 28. for 29. Calculate the dimensional new state of the individual based on Equation (8). 30. end for 31. end for 32. else 33. for 34. Calculate the new state of the individual based on Equation (20). 35. end for 36. end if 37. end if 38. Use Equation (10) to preserve the new state of individual . 39. Save the global best solution . 40. end for 41. Output the global best solution obtained by solving the optimization problem using the COA algorithm. |
4. Experimental Results and Discussion on CEC2020 and Real Problems
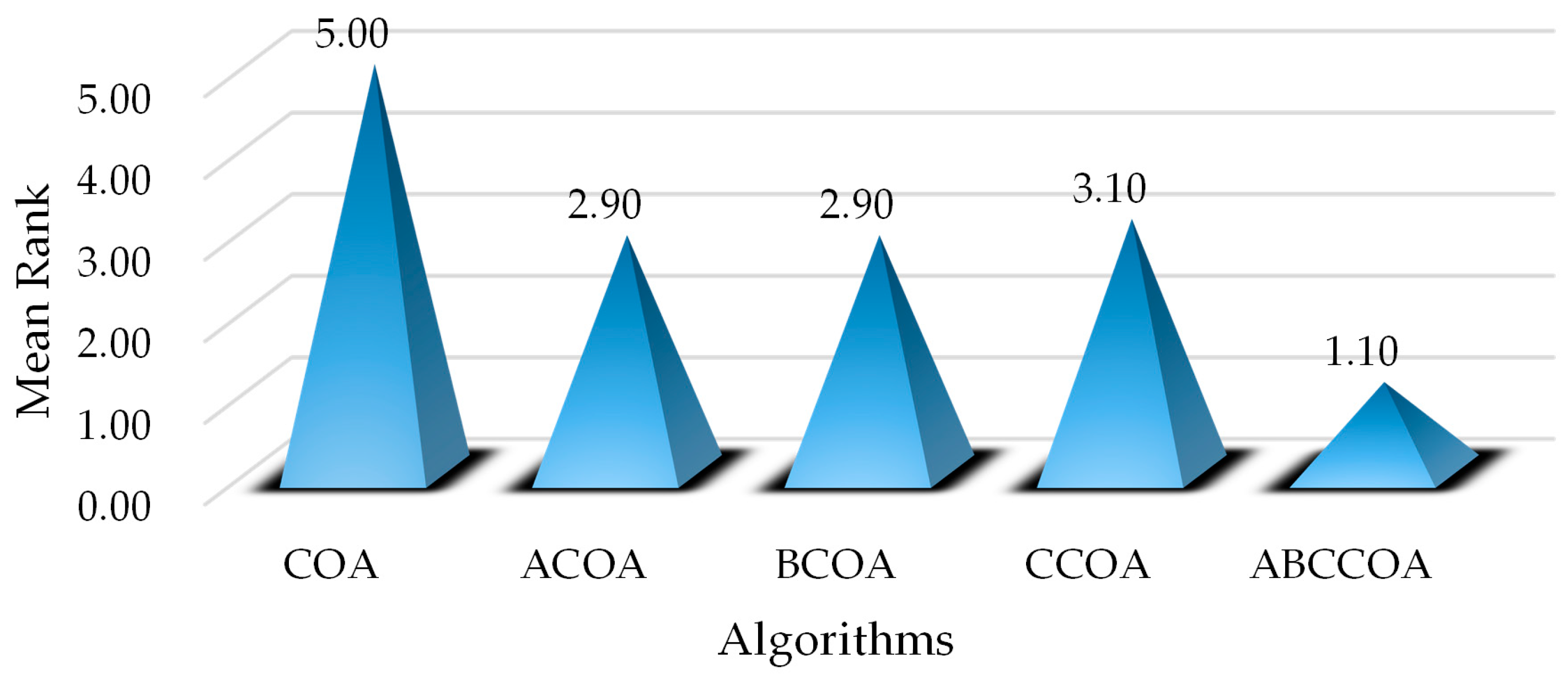
4.1. Strategies and Parameter Analysis
4.2. Population Diversity Analysis
4.3. Exploration/Exploitation Balance Analysis
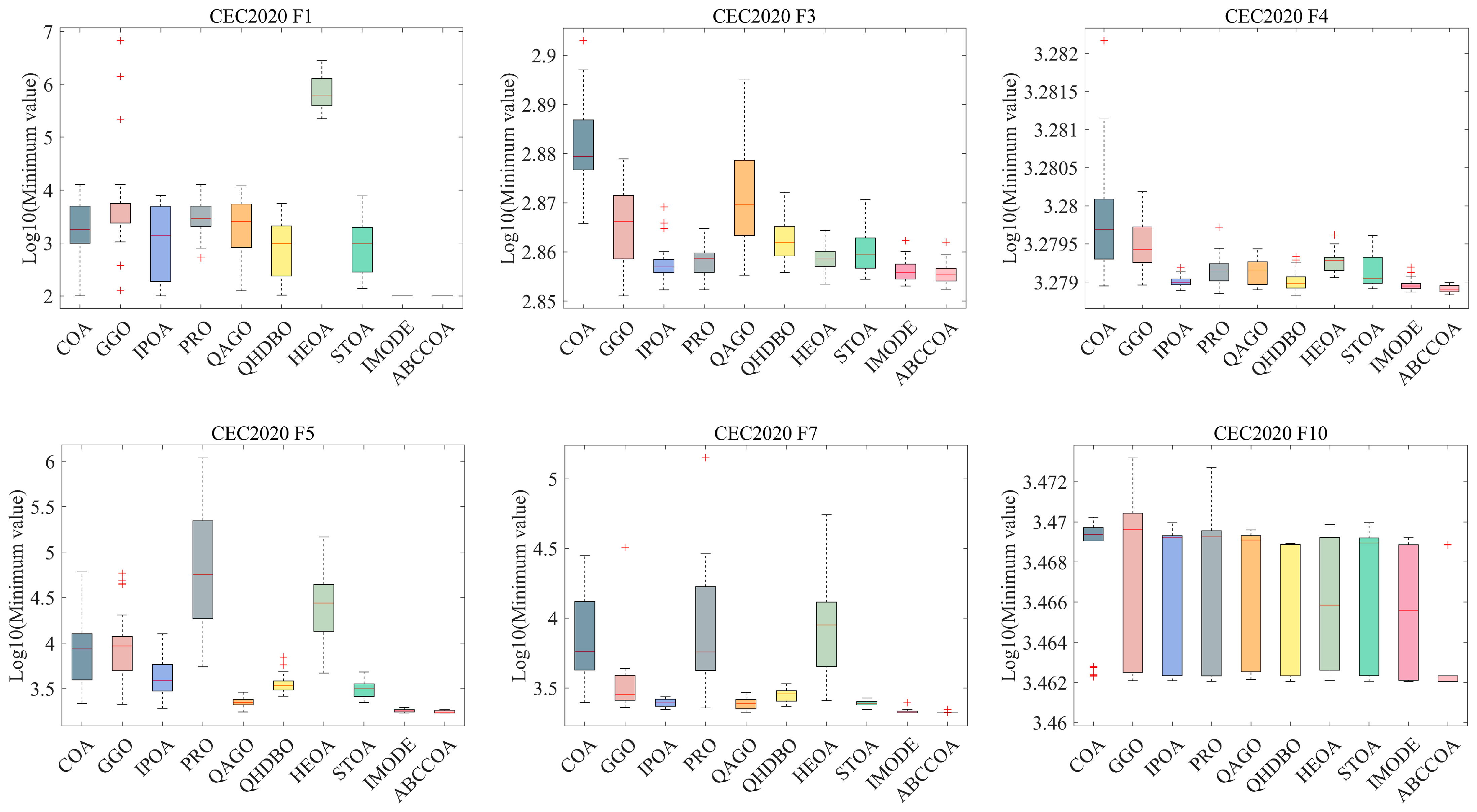
4.4. Fitness Function Values Analysis on CEC2020
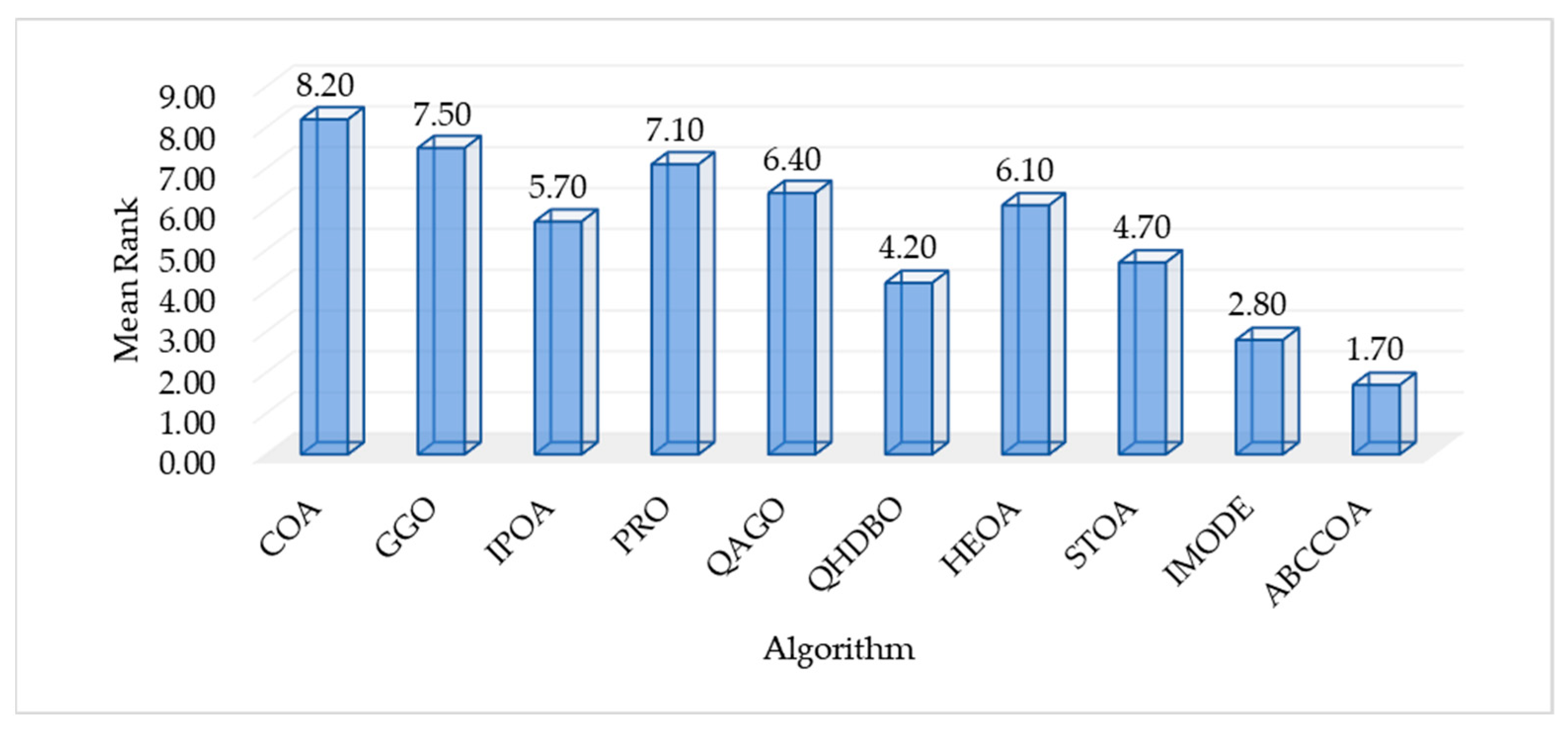
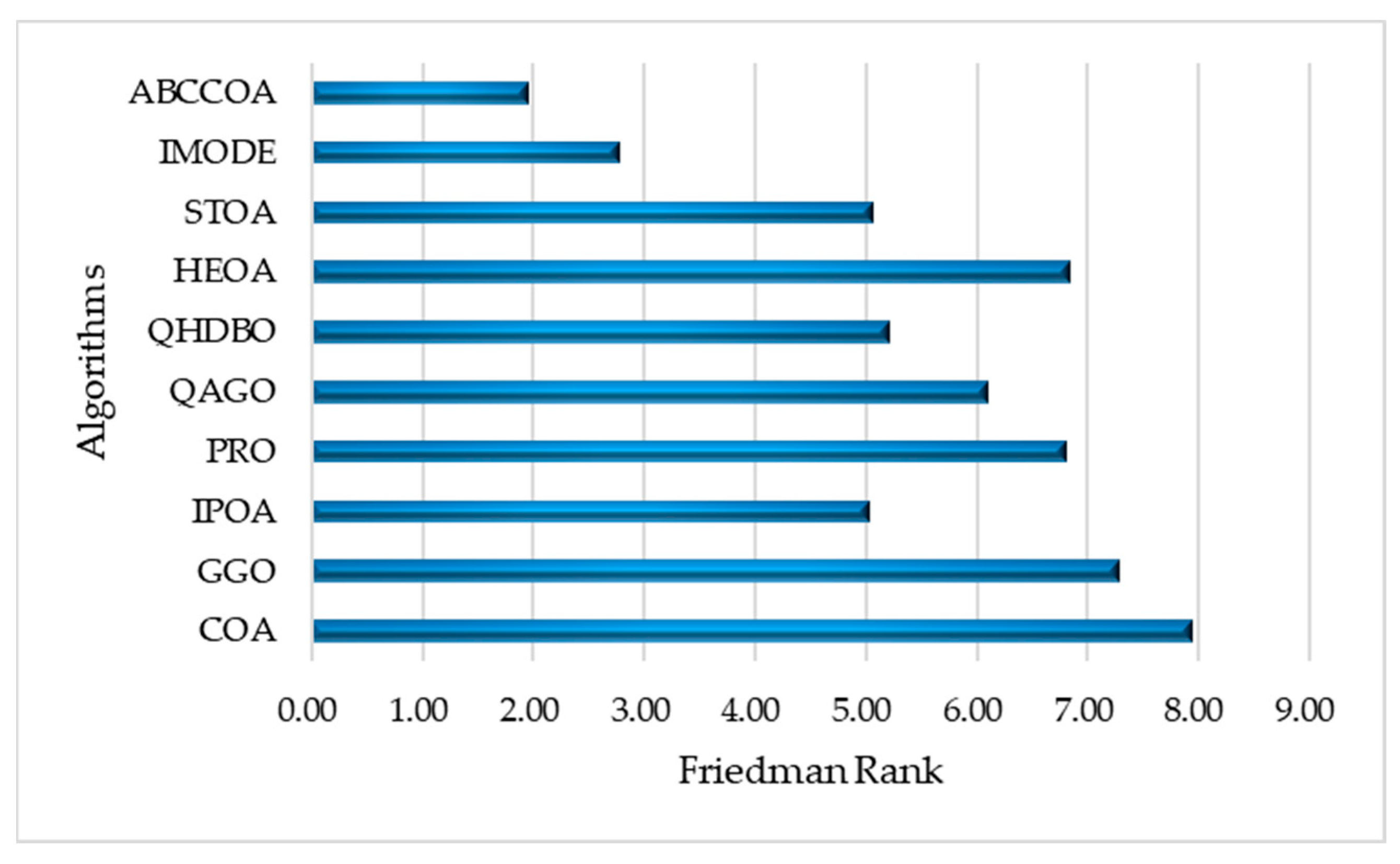
4.5. Nonparametric Test Analysis on CEC2020
4.6. Convergence Analysis on CEC2020
4.7. Fitness Function Values Analysis on Real Problems
5. Experimental Results and Discussion on FS Problems
5.1. FS Problems Model
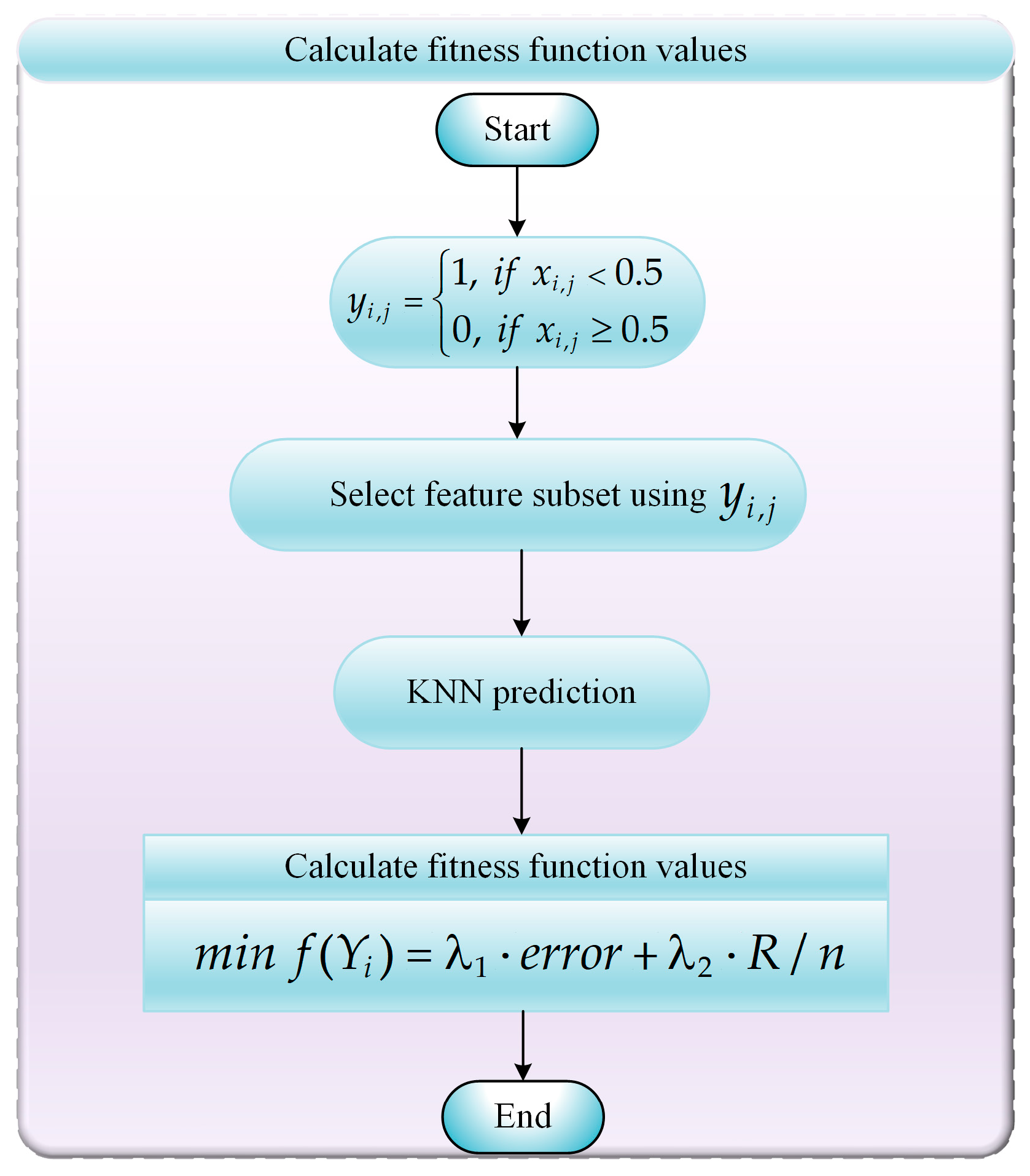
- Step 1: Using Equation (23), we convert real-valued individual in the ABCCOA algorithm into a binary individual .
- Step 2: The binary individual is utilized to select a feature subset combination from the original dataset. Here, indicates that the jth feature in the original dataset is selected in the ith feature subset combination, whereas indicates that the jth feature is not selected.
- Step 3: The classification accuracy of the selected feature subset combinations is computed using a K-Nearest Neighbors (KNN) classifier, where K is set to 5.
- Step 4: The objective function value for the feature subset combination is computed using Equation (22) with the information output by the KNN classifier.
5.2. Fitness Function Values Analysis of FS Problems
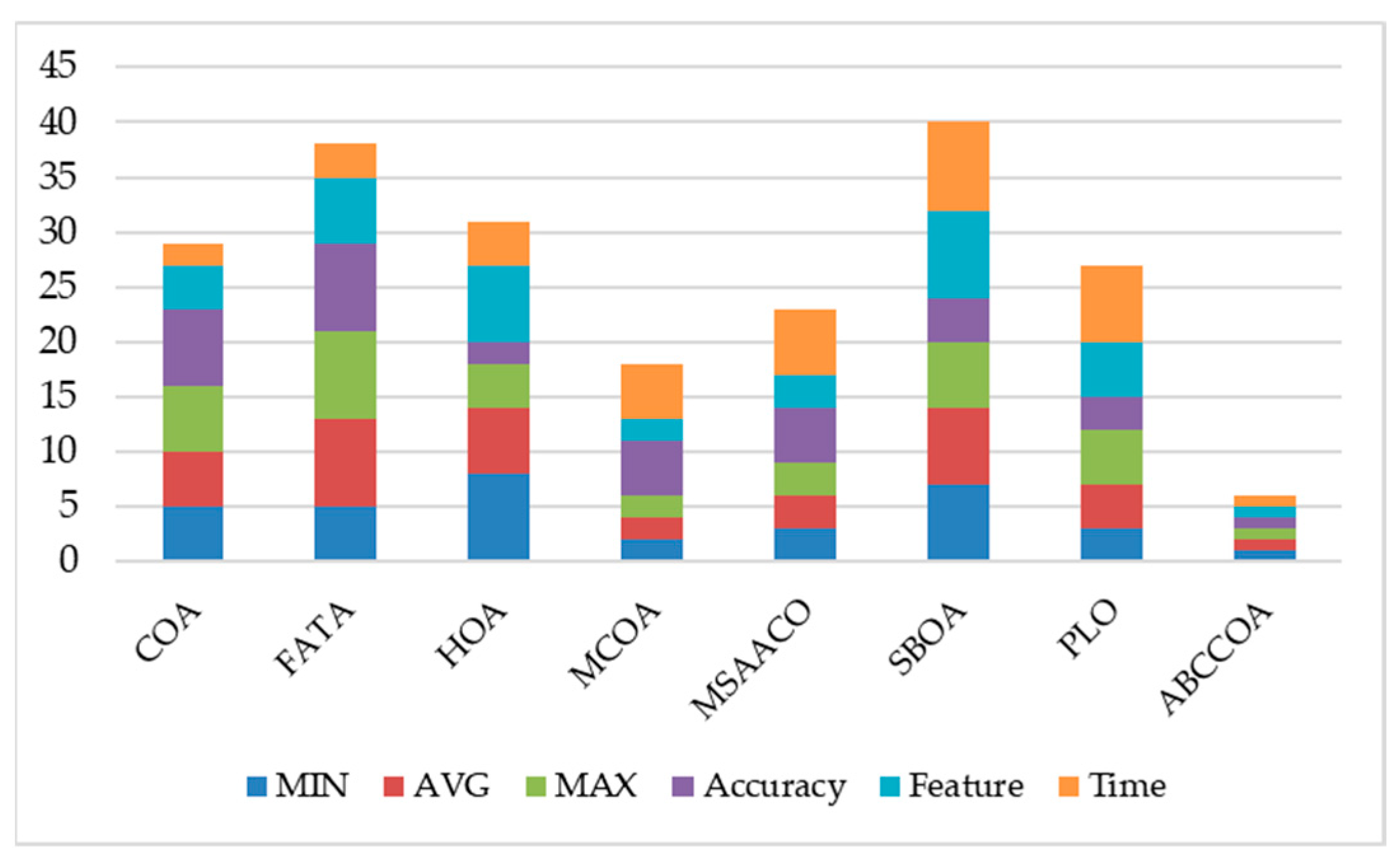
5.3. Classification Accuracy and Feature Subset Size Analysis of FS Problems
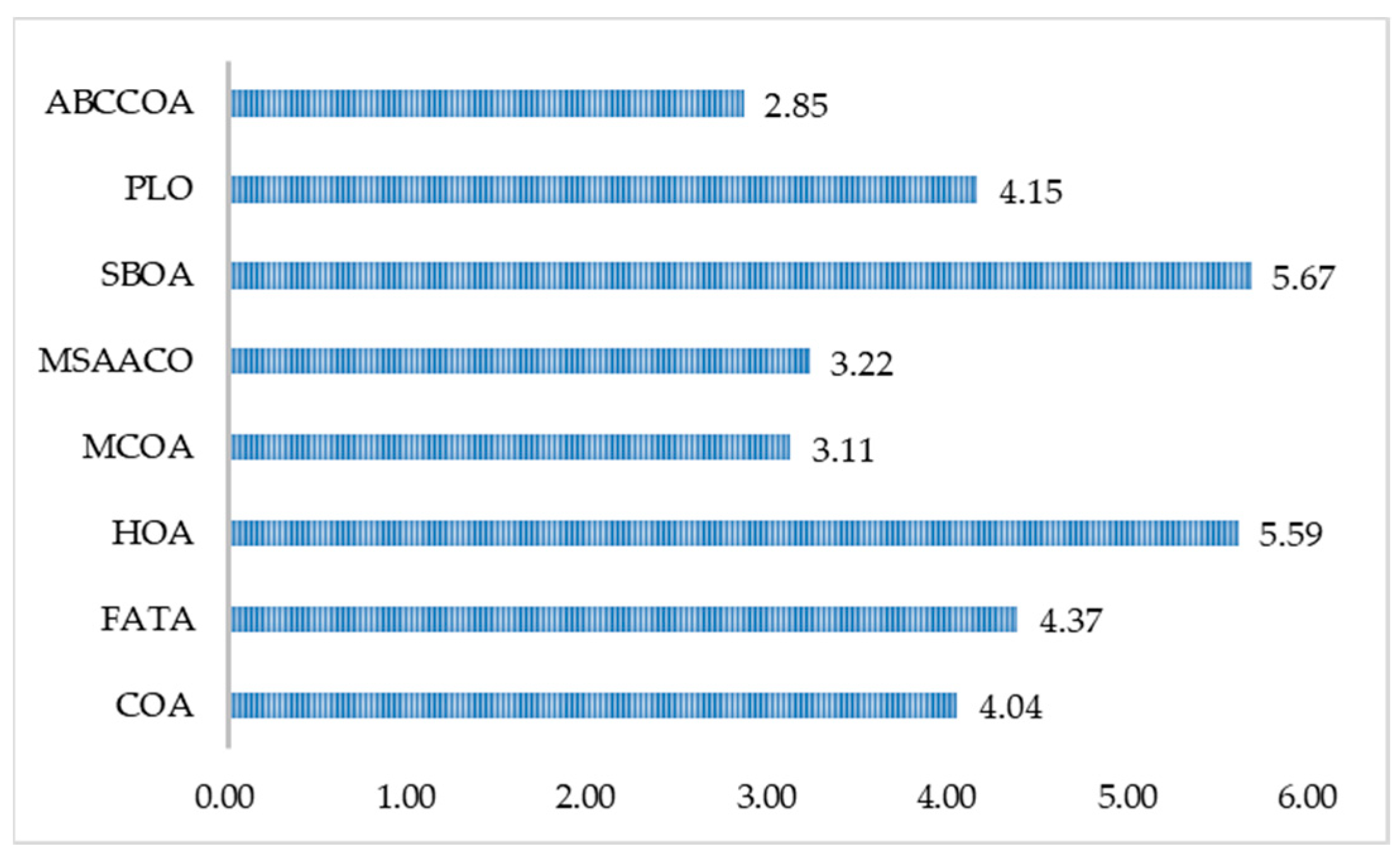
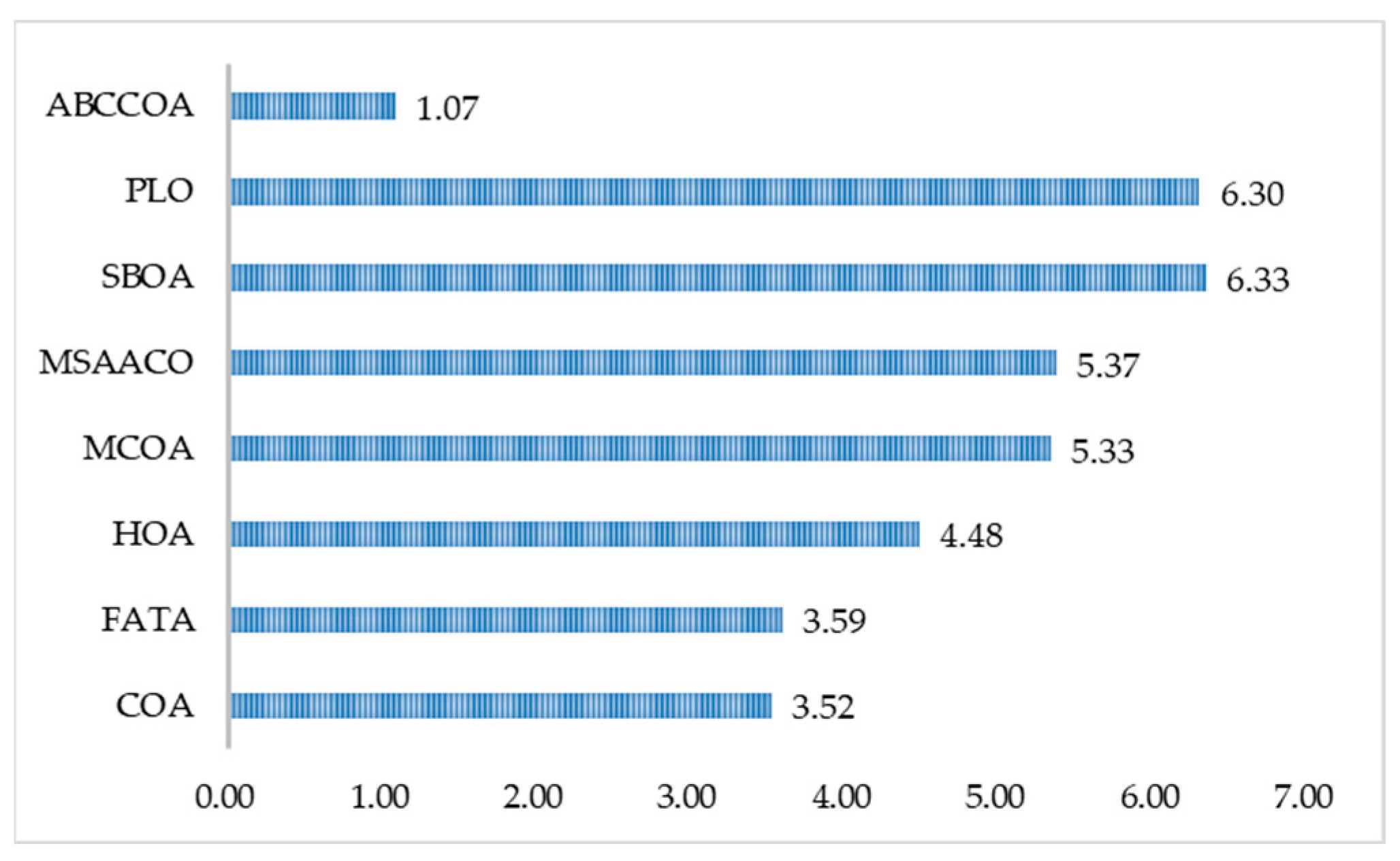
5.4. Runtime Analysis of FS Problems
5.5. Comprehensive Analysis of FS Problems
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Problems | Metrics | COA | GGO | IPOA | PRO | QAGO | QHDBO | HEOA | STOA | IMODE | ABCCOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC2020_F1 | Mean | 3.1909 × 103 | 2.8022 × 105 | 2.3920 × 103 | 4.0006 × 103 | 3.7112 × 103 | 1.4334 × 103 | 9.2230 × 105 | 1.7426 × 103 | 1.0000 × 102 | 1.0000 × 102 |
| Std | 3.3719 × 103 | 1.2304 × 106 | 2.4564 × 103 | 3.0737 × 103 | 3.5303 × 103 | 1.5126 × 103 | 6.8025 × 105 | 2.1007 × 103 | 0.0000 × 100 | 1.0556 × 10−14 | |
| CEC2020_F2 | Mean | 1.9082 × 103 | 1.8364 × 103 | 1.4853 × 103 | 1.4333 × 103 | 1.9506 × 103 | 1.6920 × 103 | 1.2850 × 103 | 1.8119 × 103 | 1.3453 × 103 | 1.2784 × 103 |
| Std | 3.3197 × 102 | 3.3372 × 102 | 2.1359 × 102 | 1.8320 × 102 | 2.6218 × 102 | 1.6673 × 102 | 1.0412 × 102 | 2.6013 × 102 | 2.1524 × 102 | 1.1347 × 102 | |
| CEC2020_F3 | Mean | 7.6108 × 102 | 7.3357 × 102 | 7.2055 × 102 | 7.2118 × 102 | 7.4366 × 102 | 7.2806 × 102 | 7.2263 × 102 | 7.2482 × 102 | 7.1801 × 102 | 7.1718 × 102 |
| Std | 1.5046 × 101 | 1.2631 × 101 | 6.1067 × 100 | 4.3600 × 100 | 1.8048 × 101 | 6.4219 × 100 | 4.5734 × 100 | 6.8581 × 100 | 3.8629 × 100 | 3.5531 × 100 | |
| CEC2020_F4 | Mean | 1.9045 × 103 | 1.9033 × 103 | 1.9011 × 103 | 1.9017 × 103 | 1.9017 × 103 | 1.9011 × 103 | 1.9022 × 103 | 1.9016 × 103 | 1.9009 × 103 | 1.9007 × 103 |
| Std | 2.9976 × 100 | 1.5294 × 100 | 3.1868 × 10−1 | 8.0634 × 10−1 | 6.9471 × 10−1 | 5.5801 × 10−1 | 5.4287 × 10−1 | 8.4758 × 10−1 | 3.4417 × 10−1 | 2.1239 × 10−1 | |
| CEC2020_F5 | Mean | 1.0452 × 104 | 1.3219 × 104 | 4.7648 × 103 | 1.9134 × 105 | 2.2577 × 103 | 3.6506 × 103 | 3.8663 × 104 | 3.1948 × 103 | 1.8119 × 103 | 1.7500 × 103 |
| Std | 1.0876 × 104 | 1.5027 × 104 | 2.6024 × 103 | 2.7411 × 105 | 2.5618 × 102 | 9.3224 × 102 | 3.6543 × 104 | 6.6865 × 102 | 6.4939 × 101 | 5.4569 × 101 | |
| CEC2020_F6 | Mean | 1.7598 × 103 | 1.8005 × 103 | 1.6973 × 103 | 1.7170 × 103 | 1.7293 × 103 | 1.6193 × 103 | 1.6773 × 103 | 1.6311 × 103 | 1.6249 × 103 | 1.6113 × 103 |
| Std | 1.0650 × 102 | 1.1254 × 102 | 6.9794 × 101 | 7.4794 × 101 | 1.0833 × 102 | 3.1798 × 101 | 7.9426 × 101 | 4.9920 × 101 | 4.7920 × 101 | 2.9837 × 101 | |
| CEC2020_F7 | Mean | 9.1304 × 103 | 5.0144 × 103 | 2.4814 × 103 | 1.4209 × 104 | 2.4609 × 103 | 2.8087 × 103 | 1.1044 × 104 | 2.4544 × 103 | 2.1410 × 103 | 2.1062 × 103 |
| Std | 7.1463 × 103 | 7.4174 × 103 | 1.7018 × 102 | 2.5252 × 104 | 2.3036 × 102 | 2.8361 × 102 | 1.0598 × 104 | 1.1367 × 102 | 8.0007 × 101 | 2.1880 × 101 | |
| CEC2020_F8 | Mean | 2.3080 × 103 | 2.3057 × 103 | 2.3100 × 103 | 2.3100 × 103 | 2.3072 × 103 | 2.3077 × 103 | 2.3030 × 103 | 2.3068 × 103 | 2.3069 × 103 | 2.3100 × 103 |
| Std | 1.0866 × 101 | 1.8825 × 101 | 1.0581 × 10−12 | 2.3739 × 10−3 | 1.5463 × 101 | 1.2572 × 101 | 2.3518 × 101 | 1.7244 × 101 | 1.7146 × 101 | 4.5475 × 10−13 | |
| CEC2020_F9 | Mean | 2.7744 × 103 | 2.7070 × 103 | 2.7354 × 103 | 2.7440 × 103 | 2.7310 × 103 | 2.6821 × 103 | 2.7374 × 103 | 2.7055 × 103 | 2.7344 × 103 | 2.6550 × 103 |
| Std | 1.9217 × 101 | 1.0097 × 102 | 4.4992 × 101 | 4.7359 × 101 | 7.9166 × 101 | 9.2976 × 101 | 5.8952 × 101 | 7.8665 × 101 | 4.4548 × 101 | 1.1648 × 102 | |
| CEC2020_F10 | Mean | 2.9306 × 103 | 2.9390 × 103 | 2.9337 × 103 | 2.9304 × 103 | 2.9309 × 103 | 2.9197 × 103 | 2.9220 × 103 | 2.9315 × 103 | 2.9212 × 103 | 2.9026 × 103 |
| Std | 4.7628 × 101 | 2.6650 × 101 | 2.1468 × 101 | 2.4738 × 101 | 2.1773 × 101 | 2.2733 × 101 | 2.0299 × 101 | 2.1700 × 101 | 2.3416 × 101 | 1.3847 × 101 | |
| Mean Rank | 8.20 | 7.50 | 5.70 | 7.10 | 6.40 | 4.20 | 6.10 | 4.70 | 2.80 | 1.70 | |
| Final Rank | 10 | 9 | 5 | 8 | 7 | 3 | 6 | 4 | 2 | 1 |
| Problems | COA | GGO | IPOA | PRO | QAGO | QHDBO | HEOA | STOA | IMODE |
|---|---|---|---|---|---|---|---|---|---|
| CEC2020_F1 | − | − | − | − | − | − | − | − | = |
| CEC2020_F2 | − | − | − | − | − | − | = | − | − |
| CEC2020_F3 | − | − | − | − | − | − | − | − | − |
| CEC2020_F4 | − | − | − | − | − | − | − | − | − |
| CEC2020_F5 | − | − | − | − | − | − | − | − | − |
| CEC2020_F6 | − | − | − | − | − | − | − | − | = |
| CEC2020_F7 | − | − | − | − | − | − | − | − | − |
| CEC2020_F8 | + | + | − | − | + | + | + | + | = |
| CEC2020_F9 | − | − | − | − | − | = | − | = | − |
| CEC2020_F10 | − | − | − | − | − | − | − | − | − |
| +/−/= | 1/9/0 | 1/9/0 | 0/10/0 | 0/10/0 | 1/9/0 | 1/8/1 | 1/8/1 | 1/8/1 | 0/7/3 |
| Problems | Metrics | COA | GGO | IPOA | PRO | QAGO | QHDBO | HEOA | STOA | IMODE | ABCCOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| RP1 | Mean | 5.261 × 102 | 5.347 × 102 | 5.257 × 102 | 5.599 × 102 | 5.262 × 102 | 5.247 × 102 | 5.249 × 102 | 5.360 × 102 | 5.246 × 102 | 5.245 × 102 |
| Std | 1.981 × 100 | 8.537 × 100 | 1.596 × 100 | 1.022 × 101 | 2.812 × 100 | 1.118 × 100 | 1.179 × 100 | 6.981 × 100 | 6.270 × 10−02 | 1.919 × 10−2 | |
| RP2 | Mean | −3.067 × 104 | −3.067 × 104 | −3.067 × 104 | −3.005 × 104 | −3.067 × 104 | −3.067 × 104 | −3.067 × 104 | −3.067 × 104 | −3.067 × 104 | −3.067 × 104 |
| Std | 7.768 × 10−7 | 3.223 × 10−4 | 3.374 × 10−11 | 2.249 × 102 | 1.100 × 10−11 | 1.110 × 10−11 | 1.110 × 10−11 | 3.598 × 10−2 | 1.042 × 10−6 | 1.392 × 10−6 | |
| RP3 | Mean | 1.280 × 10−2 | 1.274 × 10−2 | 1.267 × 10−2 | 2.226 × 10−2 | 1.268 × 10−2 | 1.267 × 10−2 | 1.267 × 10−2 | 1.314 × 10−2 | 1.267 × 10−2 | 1.267 × 10−2 |
| Std | 1.402 × 10−4 | 1.021 × 10−4 | 5.570 × 10−6 | 8.296 × 10−3 | 2.380 × 10−5 | 5.254 × 10−6 | 5.682 × 10−8 | 4.130 × 10−4 | 1.170 × 10−7 | 4.378 × 10−13 | |
| RP4 | Mean | 2.691 × 100 | 2.916 × 100 | 2.664 × 100 | 3.429 × 100 | 2.660 × 100 | 2.673 × 100 | 2.668 × 100 | 2.735 × 100 | 2.660 × 100 | 2.659 × 100 |
| Std | 5.083 × 10−2 | 3.480 × 10−1 | 1.415 × 10−2 | 4.178 × 10−1 | 7.474 × 10−3 | 5.196 × 10−2 | 1.761 × 10−2 | 9.737 × 10−2 | 7.470 × 10−3 | 1.712 × 10−6 | |
| RP5 | Mean | 1.670 × 100 | 1.685 × 100 | 1.670 × 100 | 1.974 × 100 | 1.670 × 100 | 1.670 × 100 | 1.670 × 100 | 1.737 × 100 | 1.670 × 100 | 1.670 × 100 |
| Std | 2.497 × 10−4 | 6.173 × 10−2 | 1.187 × 10−8 | 1.204 × 10−1 | 5.800 × 10−10 | 2.258 × 10−16 | 2.182 × 10−16 | 4.694 × 10−2 | 1.950 × 10−7 | 1.934 × 10−16 | |
| Mean Rank | 5.80 | 6.60 | 3.20 | 10.00 | 3.40 | 3.00 | 2.40 | 7.20 | 1.60 | 1.00 | |
| Final Rank | 7 | 8 | 5 | 10 | 6 | 4 | 3 | 9 | 2 | 1 |
| Datasets | Metrics | COA | FATA | HOA | MCOA | MSAACO | SBOA | PLO | ABCCOA |
|---|---|---|---|---|---|---|---|---|---|
| Aggregation | MIN | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.106 | 0.106 | 0.100 |
| AVG | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.106 | 0.106 | 0.100 | |
| MAX | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.106 | 0.106 | 0.100 | |
| Banana | MIN | 0.211 | 0.196 | 0.192 | 0.199 | 0.212 | 0.195 | 0.197 | 0.188 |
| AVG | 0.211 | 0.196 | 0.192 | 0.199 | 0.212 | 0.195 | 0.197 | 0.188 | |
| MAX | 0.211 | 0.196 | 0.192 | 0.199 | 0.212 | 0.195 | 0.197 | 0.188 | |
| Iris | MIN | 0.025 | 0.080 | 0.025 | 0.050 | 0.050 | 0.075 | 0.115 | 0.025 |
| AVG | 0.025 | 0.088 | 0.025 | 0.050 | 0.051 | 0.075 | 0.115 | 0.025 | |
| MAX | 0.025 | 0.110 | 0.025 | 0.050 | 0.055 | 0.075 | 0.115 | 0.025 | |
| Bupa | MIN | 0.285 | 0.285 | 0.333 | 0.333 | 0.307 | 0.350 | 0.311 | 0.285 |
| AVG | 0.296 | 0.292 | 0.334 | 0.333 | 0.313 | 0.350 | 0.311 | 0.285 | |
| MAX | 0.344 | 0.311 | 0.337 | 0.333 | 0.337 | 0.350 | 0.311 | 0.285 | |
| Glass | MIN | 0.312 | 0.290 | 0.269 | 0.259 | 0.259 | 0.312 | 0.248 | 0.226 |
| AVG | 0.314 | 0.308 | 0.269 | 0.265 | 0.260 | 0.323 | 0.255 | 0.250 | |
| MAX | 0.333 | 0.356 | 0.269 | 0.280 | 0.270 | 0.344 | 0.312 | 0.270 | |
| Breastcancer | MIN | 0.059 | 0.059 | 0.053 | 0.053 | 0.055 | 0.053 | 0.053 | 0.048 |
| AVG | 0.060 | 0.060 | 0.063 | 0.053 | 0.055 | 0.053 | 0.053 | 0.050 | |
| MAX | 0.066 | 0.066 | 0.068 | 0.053 | 0.055 | 0.053 | 0.055 | 0.059 | |
| Lipid | MIN | 0.245 | 0.247 | 0.253 | 0.229 | 0.245 | 0.237 | 0.258 | 0.222 |
| AVG | 0.247 | 0.263 | 0.253 | 0.240 | 0.249 | 0.252 | 0.262 | 0.222 | |
| MAX | 0.251 | 0.268 | 0.257 | 0.261 | 0.265 | 0.263 | 0.268 | 0.222 | |
| HeartEW | MIN | 0.090 | 0.140 | 0.190 | 0.147 | 0.138 | 0.113 | 0.122 | 0.105 |
| AVG | 0.110 | 0.165 | 0.248 | 0.164 | 0.142 | 0.123 | 0.129 | 0.107 | |
| MAX | 0.147 | 0.190 | 0.281 | 0.188 | 0.147 | 0.154 | 0.156 | 0.122 | |
| Zoo | MIN | 0.089 | 0.070 | 0.038 | 0.070 | 0.076 | 0.038 | 0.044 | 0.031 |
| AVG | 0.121 | 0.095 | 0.041 | 0.073 | 0.114 | 0.071 | 0.065 | 0.035 | |
| MAX | 0.134 | 0.109 | 0.050 | 0.076 | 0.134 | 0.083 | 0.115 | 0.044 | |
| Vote | MIN | 0.029 | 0.029 | 0.031 | 0.035 | 0.046 | 0.048 | 0.050 | 0.027 |
| AVG | 0.042 | 0.049 | 0.035 | 0.045 | 0.050 | 0.061 | 0.054 | 0.027 | |
| MAX | 0.048 | 0.060 | 0.050 | 0.070 | 0.058 | 0.098 | 0.062 | 0.027 | |
| Congress | MIN | 0.017 | 0.039 | 0.037 | 0.027 | 0.060 | 0.048 | 0.042 | 0.017 |
| AVG | 0.017 | 0.052 | 0.038 | 0.027 | 0.065 | 0.048 | 0.048 | 0.025 | |
| MAX | 0.017 | 0.062 | 0.042 | 0.027 | 0.068 | 0.048 | 0.056 | 0.035 | |
| Lymphography | MIN | 0.064 | 0.110 | 0.059 | 0.084 | 0.107 | 0.090 | 0.084 | 0.059 |
| AVG | 0.086 | 0.132 | 0.076 | 0.090 | 0.139 | 0.113 | 0.103 | 0.067 | |
| MAX | 0.110 | 0.163 | 0.107 | 0.095 | 0.172 | 0.132 | 0.126 | 0.084 | |
| Vehicle | MIN | 0.257 | 0.262 | 0.241 | 0.267 | 0.257 | 0.236 | 0.247 | 0.236 |
| AVG | 0.275 | 0.285 | 0.266 | 0.279 | 0.273 | 0.251 | 0.257 | 0.251 | |
| MAX | 0.288 | 0.300 | 0.289 | 0.294 | 0.295 | 0.263 | 0.267 | 0.263 | |
| WDBC | MIN | 0.061 | 0.037 | 0.069 | 0.066 | 0.046 | 0.068 | 0.056 | 0.037 |
| AVG | 0.066 | 0.053 | 0.086 | 0.067 | 0.049 | 0.089 | 0.070 | 0.046 | |
| MAX | 0.075 | 0.064 | 0.102 | 0.070 | 0.058 | 0.103 | 0.081 | 0.055 | |
| BreastEW | MIN | 0.039 | 0.036 | 0.037 | 0.035 | 0.039 | 0.041 | 0.039 | 0.021 |
| AVG | 0.058 | 0.045 | 0.043 | 0.039 | 0.047 | 0.050 | 0.054 | 0.038 | |
| MAX | 0.067 | 0.051 | 0.055 | 0.056 | 0.057 | 0.061 | 0.064 | 0.059 | |
| SonarEW | MIN | 0.054 | 0.125 | 0.057 | 0.049 | 0.034 | 0.035 | 0.044 | 0.015 |
| AVG | 0.073 | 0.152 | 0.074 | 0.077 | 0.053 | 0.050 | 0.073 | 0.038 | |
| MAX | 0.093 | 0.189 | 0.089 | 0.091 | 0.081 | 0.062 | 0.099 | 0.050 | |
| Libras | MIN | 0.153 | 0.138 | 0.238 | 0.204 | 0.178 | 0.271 | 0.164 | 0.092 |
| AVG | 0.170 | 0.158 | 0.245 | 0.228 | 0.200 | 0.296 | 0.192 | 0.129 | |
| MAX | 0.194 | 0.178 | 0.259 | 0.262 | 0.218 | 0.328 | 0.224 | 0.144 | |
| Hillvalley | MIN | 0.341 | 0.313 | 0.376 | 0.261 | 0.318 | 0.294 | 0.374 | 0.266 |
| AVG | 0.360 | 0.323 | 0.391 | 0.281 | 0.331 | 0.310 | 0.396 | 0.298 | |
| MAX | 0.374 | 0.337 | 0.404 | 0.304 | 0.345 | 0.322 | 0.416 | 0.323 | |
| Musk | MIN | 0.063 | 0.109 | 0.076 | 0.020 | 0.018 | 0.088 | 0.070 | 0.064 |
| AVG | 0.093 | 0.133 | 0.098 | 0.033 | 0.028 | 0.109 | 0.090 | 0.080 | |
| MAX | 0.112 | 0.145 | 0.112 | 0.040 | 0.045 | 0.127 | 0.109 | 0.088 | |
| Clean | MIN | 0.067 | 0.073 | 0.084 | 0.075 | 0.020 | 0.047 | 0.075 | 0.017 |
| AVG | 0.089 | 0.091 | 0.094 | 0.103 | 0.044 | 0.078 | 0.083 | 0.027 | |
| MAX | 0.126 | 0.105 | 0.100 | 0.128 | 0.066 | 0.102 | 0.094 | 0.034 | |
| Semeion | MIN | 0.114 | 0.106 | 0.131 | 0.070 | 0.119 | 0.089 | 0.080 | 0.063 |
| AVG | 0.123 | 0.115 | 0.139 | 0.082 | 0.128 | 0.097 | 0.088 | 0.080 | |
| MAX | 0.133 | 0.123 | 0.145 | 0.096 | 0.135 | 0.110 | 0.093 | 0.106 | |
| Madelon | MIN | 0.244 | 0.230 | 0.237 | 0.158 | 0.107 | 0.190 | 0.183 | 0.091 |
| AVG | 0.268 | 0.262 | 0.251 | 0.201 | 0.121 | 0.209 | 0.204 | 0.109 | |
| MAX | 0.287 | 0.281 | 0.259 | 0.259 | 0.136 | 0.225 | 0.243 | 0.125 | |
| Isolet | MIN | 0.161 | 0.151 | 0.178 | 0.164 | 0.065 | 0.136 | 0.134 | 0.060 |
| AVG | 0.172 | 0.162 | 0.184 | 0.176 | 0.086 | 0.147 | 0.153 | 0.075 | |
| MAX | 0.184 | 0.177 | 0.189 | 0.184 | 0.110 | 0.157 | 0.178 | 0.097 | |
| Lung | MIN | 0.072 | 0.051 | 0.051 | 0.115 | 0.087 | 0.047 | 0.038 | 0.021 |
| AVG | 0.093 | 0.072 | 0.081 | 0.122 | 0.095 | 0.082 | 0.071 | 0.042 | |
| MAX | 0.124 | 0.093 | 0.098 | 0.135 | 0.113 | 0.120 | 0.113 | 0.063 | |
| MLL | MIN | 0.081 | 0.071 | 0.082 | 0.072 | 0.101 | 0.123 | 0.053 | 0.041 |
| AVG | 0.090 | 0.100 | 0.101 | 0.096 | 0.125 | 0.147 | 0.074 | 0.061 | |
| MAX | 0.101 | 0.117 | 0.125 | 0.123 | 0.145 | 0.160 | 0.092 | 0.082 | |
| Ovarian | MIN | 0.110 | 0.061 | 0.101 | 0.071 | 0.062 | 0.041 | 0.051 | 0.012 |
| AVG | 0.123 | 0.093 | 0.118 | 0.095 | 0.083 | 0.072 | 0.079 | 0.020 | |
| MAX | 0.180 | 0.118 | 0.123 | 0.114 | 0.098 | 0.081 | 0.100 | 0.034 | |
| CNS | MIN | 0.118 | 0.084 | 0.071 | 0.088 | 0.080 | 0.117 | 0.101 | 0.061 |
| AVG | 0.133 | 0.108 | 0.099 | 0.115 | 0.109 | 0.136 | 0.119 | 0.086 | |
| MAX | 0.153 | 0.126 | 0.119 | 0.142 | 0.137 | 0.150 | 0.125 | 0.091 | |
| Mean Rank | MIN | 4.70 | 4.70 | 5.04 | 4.44 | 4.63 | 5.00 | 4.63 | 1.19 |
| AVG | 4.85 | 5.26 | 5.04 | 4.44 | 4.67 | 5.15 | 4.70 | 1.15 | |
| MAX | 5.07 | 5.11 | 4.44 | 4.33 | 4.37 | 5.07 | 4.85 | 1.63 | |
| Final Rank | MIN | 5 | 5 | 8 | 2 | 3 | 7 | 3 | 1 |
| AVG | 5 | 8 | 6 | 2 | 3 | 7 | 4 | 1 | |
| MAX | 6 | 8 | 4 | 2 | 3 | 6 | 5 | 1 |
| Datasets | COA | FATA | HOA | MCOA | MSAACO | SBOA | PLO | ABCCOA |
|---|---|---|---|---|---|---|---|---|
| Aggregation | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 99.36 | 99.36 | 100.00 |
| Banana | 87.64 | 89.34 | 89.81 | 88.96 | 87.55 | 89.43 | 89.25 | 90.19 |
| Iris | 100.00 | 96.33 | 100.00 | 100.00 | 99.67 | 100.00 | 90.00 | 100.00 |
| Bupa | 73.04 | 72.90 | 66.81 | 66.67 | 69.28 | 66.67 | 71.01 | 73.04 |
| Glass | 69.05 | 69.52 | 73.81 | 75.00 | 76.19 | 68.57 | 75.00 | 76.19 |
| Breastcancer | 97.12 | 96.76 | 96.40 | 97.84 | 96.40 | 97.84 | 97.55 | 97.12 |
| Lipid | 74.31 | 73.62 | 74.31 | 75.52 | 75.00 | 74.66 | 72.84 | 77.59 |
| HeartEW | 90.56 | 85.37 | 74.63 | 85.19 | 87.41 | 90.37 | 88.89 | 92.41 |
| Zoo | 90.50 | 93.50 | 100.00 | 95.00 | 91.00 | 95.50 | 97.00 | 100.00 |
| Vote | 96.67 | 97.36 | 99.08 | 96.55 | 96.78 | 96.67 | 96.32 | 97.70 |
| Congress | 98.85 | 96.78 | 97.13 | 97.70 | 94.02 | 95.40 | 98.05 | 98.85 |
| Lymphography | 94.14 | 88.97 | 95.52 | 93.10 | 87.93 | 91.38 | 91.72 | 95.86 |
| Vehicle | 73.49 | 71.95 | 74.32 | 72.49 | 73.49 | 76.45 | 75.56 | 75.98 |
| WDBC | 94.07 | 96.55 | 92.48 | 93.63 | 95.75 | 92.21 | 93.54 | 96.64 |
| BreastEW | 96.37 | 98.23 | 99.29 | 98.05 | 96.99 | 97.96 | 96.99 | 99.20 |
| SonarEW | 95.61 | 85.37 | 98.29 | 93.90 | 96.10 | 98.54 | 95.12 | 98.05 |
| Libras | 83.75 | 84.72 | 79.31 | 76.53 | 79.58 | 71.39 | 82.64 | 87.78 |
| Hillvalley | 61.82 | 65.37 | 62.73 | 70.50 | 65.37 | 70.33 | 60.50 | 67.85 |
| Musk | 92.11 | 87.79 | 93.47 | 98.32 | 99.16 | 92.74 | 94.95 | 98.32 |
| Clean | 91.05 | 93.47 | 96.42 | 91.05 | 97.68 | 95.79 | 95.47 | 99.26 |
| Semeion | 91.42 | 91.60 | 91.70 | 94.56 | 90.53 | 94.34 | 95.31 | 94.65 |
| Madelon | 74.29 | 74.52 | 79.37 | 80.38 | 88.85 | 82.25 | 82.54 | 89.29 |
| Isolet | 84.34 | 85.02 | 86.98 | 83.22 | 92.99 | 89.16 | 88.26 | 93.99 |
| Lung | 89.80 | 92.12 | 91.20 | 86.80 | 89.50 | 91.09 | 92.21 | 95.38 |
| MLL | 90.01 | 89.11 | 88.93 | 89.38 | 86.23 | 83.70 | 91.80 | 93.25 |
| Ovarian | 86.38 | 89.71 | 86.98 | 89.56 | 90.81 | 92.01 | 91.23 | 97.79 |
| CNS | 85.38 | 88.13 | 89.12 | 87.30 | 88.03 | 84.98 | 86.89 | 90.50 |
| Mean Rank | 5.07 | 5.11 | 4.26 | 4.70 | 4.70 | 4.63 | 4.59 | 1.44 |
| Final Rank | 7 | 8 | 2 | 5 | 5 | 4 | 3 | 1 |
| Datasets | COA | FATA | HOA | MCOA | MSAACO | SBOA | PLO | ABCCOA |
|---|---|---|---|---|---|---|---|---|
| Aggregation | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| Banana | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| Iris | 1.00 | 2.20 | 1.00 | 2.00 | 1.90 | 3.00 | 1.00 | 1.00 |
| Bupa | 3.20 | 2.90 | 2.10 | 2.00 | 2.20 | 3.00 | 3.00 | 3.00 |
| Glass | 3.20 | 3.00 | 3.00 | 3.60 | 4.10 | 3.60 | 2.70 | 3.20 |
| Breastcancer | 3.10 | 2.80 | 2.80 | 3.00 | 2.00 | 3.00 | 2.80 | 2.20 |
| Lipid | 1.60 | 2.60 | 2.20 | 2.00 | 2.40 | 2.40 | 1.80 | 2.00 |
| HeartEW | 3.20 | 4.30 | 2.60 | 4.00 | 3.70 | 4.70 | 3.80 | 5.00 |
| Zoo | 5.60 | 5.90 | 6.50 | 4.50 | 5.30 | 4.80 | 6.00 | 5.60 |
| Vote | 1.90 | 4.10 | 4.30 | 2.30 | 3.30 | 5.00 | 3.30 | 1.00 |
| Congress | 1.00 | 3.70 | 2.00 | 1.00 | 1.80 | 1.00 | 4.90 | 2.30 |
| Lymphography | 5.90 | 5.80 | 6.50 | 5.00 | 5.40 | 6.30 | 5.10 | 5.40 |
| Vehicle | 6.50 | 5.90 | 6.30 | 5.70 | 6.20 | 7.10 | 6.60 | 6.30 |
| WDBC | 3.80 | 6.60 | 5.40 | 2.80 | 3.10 | 5.60 | 3.70 | 4.70 |
| BreastEW | 7.60 | 8.60 | 11.10 | 6.40 | 6.10 | 9.40 | 8.00 | 9.20 |
| SonarEW | 19.90 | 12.30 | 34.90 | 13.30 | 10.80 | 21.90 | 17.60 | 12.20 |
| Libras | 21.70 | 18.30 | 52.60 | 14.90 | 14.80 | 34.80 | 32.10 | 16.90 |
| Hillvalley | 16.60 | 11.00 | 55.30 | 15.20 | 19.20 | 43.40 | 40.80 | 8.80 |
| Musk | 36.20 | 38.70 | 64.80 | 29.70 | 34.40 | 72.30 | 73.10 | 108.00 |
| Clean | 13.40 | 54.10 | 103.20 | 38.00 | 38.60 | 67.80 | 70.00 | 34.50 |
| Semeion | 116.60 | 100.20 | 163.80 | 83.50 | 109.70 | 118.00 | 116.80 | 80.80 |
| Madelon | 183.60 | 161.50 | 326.10 | 123.40 | 104.20 | 247.30 | 234.60 | 61.80 |
| Isolet | 194.10 | 167.20 | 412.10 | 152.20 | 138.70 | 302.20 | 289.80 | 131.70 |
| Lung | 138.2 | 98.3 | 187.6 | 387.8 | 30.9 | 210.6 | 56.8 | 19.43 |
| MLL | 73.4 | 198.2 | 137.8 | 102.5 | 88.4 | 49.8 | 56.3 | 30.8 |
| Ovarian | 98.2 | 70.38 | 89.8 | 83.2 | 76.4 | 87.6 | 33.5 | 17.8 |
| CNS | 93.2 | 74.8 | 101.5 | 81.2 | 94.2 | 78.2 | 59.3 | 26.5 |
| Mean Rnak | 4.04 | 4.37 | 5.59 | 3.11 | 3.22 | 5.67 | 4.15 | 2.85 |
| Final Rank | 4 | 6 | 7 | 2 | 3 | 8 | 5 | 1 |
| Datasets | COA | FATA | HOA | MCOA | MSAACO | SBOA | PLO | ABCCOA |
|---|---|---|---|---|---|---|---|---|
| Aggregation | 9.62 | 6.01 | 7.01 | 8.45 | 9.78 | 8.20 | 10.02 | 5.66 |
| Banana | 11.09 | 8.84 | 9.92 | 15.21 | 18.29 | 22.26 | 21.92 | 8.12 |
| Iris | 5.49 | 6.97 | 6.48 | 8.74 | 8.75 | 9.22 | 8.97 | 4.95 |
| Bupa | 6.19 | 7.95 | 8.70 | 9.36 | 8.61 | 9.40 | 9.81 | 5.78 |
| Glass | 5.97 | 8.61 | 10.26 | 9.12 | 9.11 | 9.43 | 9.53 | 5.74 |
| Breastcancer | 6.57 | 9.23 | 7.36 | 10.30 | 9.47 | 10.30 | 10.63 | 6.94 |
| Lipid | 6.88 | 9.49 | 10.68 | 9.79 | 9.02 | 10.19 | 10.12 | 6.28 |
| HeartEW | 8.58 | 9.45 | 7.06 | 9.83 | 9.88 | 9.75 | 9.72 | 6.46 |
| Zoo | 8.65 | 9.26 | 9.82 | 9.63 | 9.49 | 9.48 | 9.33 | 6.41 |
| Vote | 8.10 | 9.47 | 8.60 | 10.14 | 10.07 | 10.20 | 9.88 | 6.28 |
| Congress | 7.46 | 9.55 | 9.78 | 9.81 | 9.98 | 9.94 | 10.06 | 6.03 |
| Lymphography | 8.24 | 9.19 | 9.94 | 9.35 | 9.63 | 9.87 | 9.46 | 6.48 |
| Vehicle | 10.62 | 10.96 | 8.23 | 11.52 | 11.90 | 11.79 | 11.81 | 7.81 |
| WDBC | 9.46 | 9.68 | 7.40 | 10.34 | 13.04 | 10.01 | 10.86 | 6.39 |
| BreastEW | 10.15 | 9.43 | 9.40 | 10.99 | 10.85 | 11.01 | 10.93 | 7.06 |
| SonarEW | 8.78 | 8.43 | 9.28 | 9.41 | 9.01 | 9.76 | 9.53 | 6.59 |
| Libras | 9.71 | 8.72 | 9.49 | 10.00 | 10.17 | 8.99 | 11.50 | 6.93 |
| Hillvalley | 9.87 | 9.27 | 9.69 | 10.59 | 10.81 | 11.50 | 12.19 | 6.42 |
| Musk | 11.68 | 10.34 | 10.33 | 10.90 | 11.20 | 12.20 | 12.96 | 6.55 |
| Clean | 10.19 | 9.72 | 9.87 | 11.11 | 10.17 | 11.94 | 12.01 | 6.59 |
| Semeion | 25.24 | 21.99 | 22.09 | 25.53 | 24.20 | 27.37 | 27.87 | 18.77 |
| Madelon | 42.40 | 57.20 | 63.49 | 42.30 | 43.07 | 66.32 | 64.94 | 38.34 |
| Isolet | 26.61 | 34.41 | 33.64 | 31.50 | 31.37 | 44.53 | 41.53 | 26.89 |
| Lung | 159.01 | 116.91 | 119.00 | 105.60 | 101.40 | 90.30 | 89.50 | 79.29 |
| MLL | 198.02 | 210.98 | 198.23 | 141.45 | 138.12 | 158.10 | 110.98 | 90.18 |
| Ovarian | 181.24 | 178.91 | 198.22 | 138.91 | 145.98 | 156.32 | 129.98 | 101.30 |
| CNS | 78.27 | 86.44 | 87.68 | 93.21 | 101.20 | 93.03 | 87.88 | 69.00 |
| Mean Rnak | 3.52 | 3.59 | 4.48 | 5.33 | 5.37 | 6.33 | 6.30 | 1.07 |
| Final Rank | 2 | 3 | 4 | 5 | 6 | 8 | 7 | 1 |
References
- Wu, Q.; Gu, J. Design and research of robot visual servo system based on artificial intelligence. Agro Food Ind. Hi-Tech 2017, 28, 125–128. [Google Scholar]
- Chen, J.; Zhang, M.; Xu, B.; Sun, J.; Mujumdar, A.S. Artificial intelligence assisted technologies for controlling the drying of fruits and vegetables using physical fields: A review. Trends Food Sci. Technol. 2020, 105, 251–260. [Google Scholar] [CrossRef]
- Khulal, U.; Zhao, J.; Hu, W.; Chen, Q. Nondestructive quantifying total volatile basic nitrogen (TVB-N) content in chicken using hyperspectral imaging (HSI) technique combined with different data dimension reduction algorithms. Food Chem. 2016, 197, 1191–1199. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Geng, W.; Hassan, M.M.; Zuo, M.; Wei, W.; Wu, X.; Chen, Q. Rapid detection of chloramphenicol in food using SERS flexible sensor coupled artificial intelligent tools. Food Control 2021, 128, 108186. [Google Scholar] [CrossRef]
- El-Mesery, H.S.; Qenawy, M.; Ali, M.; Hu, Z.; Adelusi, O.A.; Njobeh, P.B. Artificial intelligence as a tool for predicting the quality attributes of garlic (Allium sativum L.) slices during continuous infrared-assisted hot air drying. J. Food Sci. 2024, 89, 7693–7712. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Lei, X.; Zeng, J.; Qi, Y.; Yuan, Q.; Huang, W.; Lyu, X. Research progress in mechanized and intelligentized pollination technologies for fruit and vegetable crops. Int. J. Agric. Biol. Eng. 2024, 17, 11–21. [Google Scholar] [CrossRef]
- Chen, Q.; Hu, W.; Su, J.; Li, H.; Ouyang, Q.; Zhao, J. Nondestructively sensing of total viable count (TVC) in chicken using an artificial olfaction system based colorimetric sensor array. J. Food Eng. 2016, 168, 259–266. [Google Scholar] [CrossRef]
- Li, H.; Kutsanedzie, F.; Zhao, J.; Chen, Q. Quantifying total viable count in pork meat using combined hyperspectral imaging and artificial olfaction techniques. Food Anal. Methods 2016, 9, 3015–3024. [Google Scholar] [CrossRef]
- Li, H.; Zhang, B.; Hu, W.; Liu, Y.; Dong, C.; Chen, Q. Monitoring black tea fermentation using a colorimetric sensor array-based artificial olfaction system. J. Food Process. Preserv. 2018, 42, e13348. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, C.; Gerrits, M.C.; Acquah, S.J.; Zhang, H.; Wu, H.; Fu, H. Parametrization of aerodynamic and canopy resistances for modeling evapotranspiration of greenhouse cucumber. Agric. For. Meteorol. 2018, 262, 370–378. [Google Scholar] [CrossRef]
- Wang, X.; Cai, H.; Zheng, Z.; Yu, L.; Wang, Z.; Li, L. Modelling root water uptake under deficit irrigation and rewetting in Northwest China. Agron. J. 2020, 112, 158–174. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Ma, T.; Li, W. Estimation of summer maize biomass based on a crop growth model. Emir. J. Food Agric. (EJFA) 2021, 33, 742–750. [Google Scholar] [CrossRef]
- Wang, L.; Lin, M.; Han, Z.; Han, L.; He, L.; Sun, W. Simulating the effects of drought stress timing and the amount irrigation on cotton yield using the CSM-CROPGRO-cotton model. Agronomy 2023, 14, 14. [Google Scholar] [CrossRef]
- Ni, J.; Xue, Y.; Zhou, Y.; Miao, M. Rapid identification of greenhouse tomato senescent leaves based on the sucrose-spectral quantitative prediction model. Biosyst. Eng. 2024, 238, 200–211. [Google Scholar] [CrossRef]
- Chauhdary, J.N.; Li, H.; Pan, X.; Zaman, M.; Anjum, S.A.; Yang, F.; Azamat, U. Modeling effects of climate change on crop phenology and yield of wheat–maize cropping system and exploring sustainable solutions. J. Sci. Food Agric. 2025, 105, 3679–3700. [Google Scholar] [CrossRef]
- Xiao-wei, H.; Zhi-Hua, L.; Xiao-bo, Z.; Ji-yong, S.; Han-ping, M.; Jie-wen, Z.; Holmes, M. Detection of meat-borne trimethylamine based on nanoporous colorimetric sensor arrays. Food Chem. 2016, 197, 930–936. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Y.; Xu, L.; Zhao, Z. Sensor for monitoring rice grain sieve losses in combine harvesters. Biosyst. Eng. 2016, 147, 51–66. [Google Scholar] [CrossRef]
- Zhou, C.; Yu, X.; Qin, X.; Ma, H.; Yagoub, A.E.A.; Hu, J. Hydrolysis of rapeseed meal protein under simulated duodenum digestion: Kinetic modeling and antioxidant activity. LWT-Food Sci. Technol. 2016, 68, 523–531. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Zhu, X.; Yuan, S. Droplet characterisation of a complete fluidic sprinkler with different nozzle dimensions. Biosyst. Eng. 2016, 148, 90–100. [Google Scholar] [CrossRef]
- Yuexia, C.; Long, C.; Ruochen, W.; Xing, X.; Yujie, S.; Yanling, L. Modeling and test on height adjustment system of electrically-controlled air suspension for agricultural vehicles. Int. J. Agric. Biol. Eng. 2016, 9, 40–47. [Google Scholar]
- Darko, R.O.; Shouqi, Y.; Haofang, Y.; Junping, L.; Abbey, A. Calibration and validation of Aqua Crop for deficit and full irrigation of tomato. Int. J. Agric. Biol. Eng. 2016, 9, 104–110. [Google Scholar]
- Wu, X.; Wu, B.; Sun, J.; Yang, N. Classification of apple varieties using near infrared reflectance spectroscopy and fuzzy discriminant c-means clustering model. J. Food Process Eng. 2017, 40, e12355. [Google Scholar] [CrossRef]
- Lu, X.; Sun, J.; Mao, H.; Wu, X.; Gao, H. Quantitative determination of rice starch based on hyperspectral imaging technology. Int. J. Food Prop. 2017, 20, S1037–S1044. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, C.; Oue, H.; Peng, G.J.; Darko, R.O. Determination of crop and soil evaporation coefficients for estimating evapotranspiration in a paddy field. Int. J. Agric. Biol. Eng. 2017, 10, 130–139. [Google Scholar]
- Gao, J.; Qi, H. Soil throwing experiments for reverse rotary tillage at various depths, travel speeds, and rotational speeds. Trans. ASABE 2017, 60, 1113–1121. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, J.; Li, J.; Wu, X.; Dai, C. Quantitative analysis of cadmium content in tomato leaves based on hyperspectral image and feature selection. Appl. Eng. Agric. 2018, 34, 789–798. [Google Scholar] [CrossRef]
- Liu, C.; Yu, H.; Liu, Y.; Zhang, L.; Li, D.; Zhang, J.; Sui, Y. Prediction of Anthocyanin Content in Purple-Leaf Lettuce Based on Spectral Features and Optimized Extreme Learning Machine Algorithm. Agronomy 2024, 14, 2915. [Google Scholar] [CrossRef]
- Duan, N.; Gong, W.; Wu, S.; Wang, Z. Selection and application of ssDNA aptamers against clenbuterol hydrochloride based on ssDNA library immobilized SELEX. J. Agric. Food Chem. 2017, 65, 1771–1777. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, F.; Wu, S.; Guo, Z.; Huang, X.; Hu, X.; Zou, X. Noise-free microbial colony counting method based on hyperspectral features of agar plates. Food Chem. 2019, 274, 925–932. [Google Scholar] [CrossRef]
- Yao, K.; Sun, J.; Zhou, X.; Nirere, A.; Tian, Y.; Wu, X. Nondestructive detection for egg freshness grade based on hyperspectral imaging technology. J. Food Process Eng. 2020, 43, e13422. [Google Scholar] [CrossRef]
- Jiang, H.; He, Y.; Chen, Q. Determination of acid value during edible oil storage using a portable NIR spectroscopy system combined with variable selection algorithms based on an MPA-based strategy. J. Sci. Food Agric. 2021, 101, 3328–3335. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Sun, J.; Yao, K.; Wu, X.; Shen, J.; Cao, Y.; Zhou, X. Nondestructive detection of total soluble solids in grapes using VMD-RC and hyperspectral imaging. J. Food Sci. 2022, 87, 326–338. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Sun, Z.; Zuo, M.; Zou, X.; Wang, T.; Li, J. Quantitative detection of restructured steak adulteration based on hyperspectral technology combined with a wavelength selection algorithm cascade strategy. Food Sci. Technol. Res. 2021, 27, 859–869. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Z.; Zou, C.; Jiang, S.; El-Seedi, H.R.; Zou, X. General model of multi-quality detection for apple from different origins by Vis/NIR transmittance spectroscopy. J. Food Meas. Charact. 2022, 16, 2582–2595. [Google Scholar] [CrossRef]
- Wang, C.; Luo, X.; Guo, Z.; Wang, A.; Zhou, R.; Cai, J. Influence of the peel on online detecting soluble solids content of pomelo using Vis-NIR spectroscopy coupled with chemometric analysis. Food Control 2025, 167, 110777. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Pan, W.; Chen, Q.; Ouyang, Q.; Zhao, J. Dual-color upconversion nanoparticles (UCNPs)-based fluorescent immunoassay probes for sensitive sensing foodborne pathogens. Food Anal. Methods 2017, 10, 2036–2045. [Google Scholar] [CrossRef]
- Mao, H.; Hang, T.; Zhang, X.; Lu, N. Both multi-segment light intensity and extended photoperiod lighting strategies, with the same daily light integral, promoted Lactuca sativa L. growth and photosynthesis. Agronomy 2019, 9, 857. [Google Scholar] [CrossRef]
- Wang, P.; Li, H.; Hassan, M.M.; Guo, Z.; Zhang, Z.Z.; Chen, Q. Fabricating an acetylcholinesterase modulated UCNPs-Cu2+ fluorescence biosensor for ultrasensitive detection of organophosphorus pesticides-diazinon in food. J. Agric. Food Chem. 2019, 67, 4071–4079. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, M.; Pan, Q.; Jin, X.; Wang, G.; Zhao, Y.; Hu, Y. Identification of tea plant cultivars based on canopy images using deep learning methods. Sci. Hortic. 2025, 339, 113908. [Google Scholar] [CrossRef]
- Chen, X.; Hou, T.; Liu, S.; Guo, Y.; Hu, J.; Xu, G.; Liu, W. Design of a Micro-Plant Factory Using a Validated CFD Model. Agriculture 2024, 14, 2227. [Google Scholar] [CrossRef]
- Niu, Z.; Huang, T.; Xu, C.; Sun, X.; Taha, M.F.; He, Y.; Qiu, Z. A Novel Approach to Optimize Key Limitations of Azure Kinect DK for Efficient and Precise Leaf Area Measurement. Agriculture 2025, 15, 173. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, H.; Mu, M.; Dong, Y. A dynamic collaborative adversarial domain adaptation network for unsupervised rotating machinery fault diagnosis. Reliab. Eng. Syst. Saf. 2024, 255, 110662. [Google Scholar] [CrossRef]
- Yan, J.; Cheng, Y.; Zhang, F.; Zhou, N.; Wang, H.; Jin, B.; Wang, M.; Zhang, W. Multi-Modal Imitation Learning for Arc Detection in Complex Railway Environments. IEEE Trans. Instrum. Meas. 2025, 74, 3556896. [Google Scholar] [CrossRef]
- Han, D.; Qi, H.; Wang, S.; Hou, D.; Wang, C. Adaptive stepsize forward–backward pursuit and acoustic emission-based health state assessment of high-speed train bearings. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]
- Yang, N.; Qian, Y.; EL-Mesery, H.S.; Zhang, R.; Wang, A.; Tang, J. Rapid detection of rice disease using microscopy image identification based on the synergistic judgment of texture and shape features and decision tree–confusion matrix method. J. Sci. Food Agric. 2019, 99, 6589–6600. [Google Scholar] [CrossRef]
- Shi, J.; Hu, X.; Zou, X.; Zhao, J.; Zhang, W.; Holmes, M.; Zhang, X. A rapid and nondestructive method to determine the distribution map of protein, carbohydrate and sialic acid on Edible bird’s nest by hyper-spectral imaging and chemometrics. Food Chem. 2017, 229, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Sun, J.; Yao, K.; Dai, C. Generalized and hetero two-dimensional correlation analysis of hyperspectral imaging combined with three-dimensional convolutional neural network for evaluating lipid oxidation in pork. Food Control 2023, 153, 109940. [Google Scholar] [CrossRef]
- Tchabo, W.; Ma, Y.; Kwaw, E.; Zhang, H.; Xiao, L.; Apaliya, M.T. Statistical interpretation of chromatic indicators in correlation to phytochemical profile of a sulfur dioxide-free mulberry (Morus nigra) wine submitted to non-thermal maturation processes. Food Chem. 2018, 239, 470–477. [Google Scholar] [CrossRef]
- Sun, L.; Feng, S.; Chen, C.; Liu, X.; Cai, J. Identification of eggshell crack for hen egg and duck egg using correlation analysis based on acoustic resonance method. J. Food Process Eng. 2020, 43, e13430. [Google Scholar] [CrossRef]
- Khan, I.A.; Luo, J.; Shi, H.; Zou, Y.; Khan, A.; Zhu, Z.; Huang, M. Mitigation of heterocyclic amines by phenolic compounds in allspice and perilla frutescens seed extract: The correlation between antioxidant capacities and mitigating activities. Food Chem. 2022, 368, 130845. [Google Scholar] [CrossRef]
- Li, Y.; Ruan, S.; Zhou, A.; Xie, P.; Azam, S.R.; Ma, H. Ultrasonic modification on fermentation characteristics of Bacillus varieties: Impact on protease activity, peptide content and its correlation coefficient. LWT 2022, 154, 112852. [Google Scholar] [CrossRef]
- Sun, J.; Jiang, S.; Mao, H.; Wu, X.; Li, Q. Classification of black beans using visible and near infrared hyperspectral imaging. Int. J. Food Prop. 2016, 19, 1687–1695. [Google Scholar] [CrossRef]
- Liu, J.; Abbas, I.; Noor, R.S. Development of deep learning-based variable rate agrochemical spraying system for targeted weeds control in strawberry crop. Agronomy 2021, 11, 1480. [Google Scholar] [CrossRef]
- Zareef, M.; Chen, Q.; Hassan, M.M.; Arslan, M.; Hashim, M.M.; Ahmad, W.; Agyekum, A.A. An overview on the applications of typical non-linear algorithms coupled with NIR spectroscopy in food analysis. Food Eng. Rev. 2020, 12, 173–190. [Google Scholar] [CrossRef]
- Ma, L.; Yang, X.; Xue, S.; Zhou, R.; Wang, C.; Guo, Z.; Cai, J. “Raman plus X” dual-modal spectroscopy technology for food analysis: A review. Compr. Rev. Food Sci. Food Saf. 2025, 24, e70102. [Google Scholar] [CrossRef]
- Askr, H.; Abdel-Salam, M.; Hassanien, A.E. Copula entropy-based golden jackal optimization algorithm for high-dimensional feature selection problems. Expert Syst. Appl. 2024, 238, 121582. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; Hu, G.; Çelik, E.; Gharehchopogh, F.S.; El-Hasnony, I.M. Chaotic RIME optimization algorithm with adaptive mutualism for feature selection problems. Comput. Biol. Med. 2024, 179, 108803. [Google Scholar] [CrossRef]
- Tijjani, S.; Ab Wahab, M.N.; Noor, M.H.M. An enhanced particle swarm optimization with position update for optimal feature selection. Expert. Syst. Appl. 2024, 247, 123337. [Google Scholar] [CrossRef]
- Fang, Y.; Yao, Y.; Lin, X.; Wang, J.; Zhai, H. A feature selection based on genetic algorithm for intrusion detection of industrial control systems. Comput. Secur. 2024, 139, 103675. [Google Scholar] [CrossRef]
- Ye, Z.; Luo, J.; Zhou, W.; Wang, M.; He, Q. An ensemble framework with improved hybrid breeding optimization-based feature selection for intrusion detection. Future Gener. Comput. Syst. 2024, 151, 124–136. [Google Scholar] [CrossRef]
- Wang, Y.; Ran, S.; Wang, G.G. Role-oriented binary grey wolf optimizer using foraging-following and Lévy flight for feature selection. Appl. Math. Model. 2024, 126, 310–326. [Google Scholar] [CrossRef]
- Houssein, E.H.; Oliva, D.; Celik, E.; Emam, M.M.; Ghoniem, R.M. Boosted sooty tern optimization algorithm for global optimization and feature selection. Expert Syst. Appl. 2023, 213, 119015. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, H.; Zhan, Z.H.; Li, J.; Zhang, H. Growth Optimizer: A powerful metaheuristic algorithm for solving continuous and discrete global optimization problems. Knowl.-Based Syst. 2023, 261, 110206. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Khodadadi, N.; Mirjalili, S.; Abdelhamid, A.A.; Eid, M.M.; Ibrahim, A. Greylag goose optimization: Nature-inspired optimization algorithm. Expert Syst. Appl. 2024, 238, 122147. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G. Human evolutionary optimization algorithm. Expert Syst. Appl. 2024, 241, 122638. [Google Scholar] [CrossRef]
- SeyedGarmroudi, S.; Kayakutlu, G.; Kayalica, M.O.; Çolak, Ü. Improved Pelican optimization algorithm for solving load dispatch problems. Energy 2024, 289, 129811. [Google Scholar] [CrossRef]
- Taheri, A.; RahimiZadeh, K.; Beheshti, A.; Baumbach, J.; Rao, R.V.; Mirjalili, S.; Gandomi, A.H. Partial reinforcement optimizer: An evolutionary optimization algorithm. Expert Syst. Appl. 2024, 238, 122070. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Q.; Bu, X.; Zhang, H. Quadruple parameter adaptation growth optimizer with integrated distribution, confrontation, and balance features for optimization. Expert Syst. Appl. 2024, 235, 121218. [Google Scholar] [CrossRef]
- Zhu, F.; Li, G.; Tang, H.; Li, Y.; Lv, X.; Wang, X. Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion for solving engineering problems. Expert Syst. Appl. 2024, 236, 121219. [Google Scholar] [CrossRef]
- Dhiman, G.; Kaur, A. STOA: A bio-inspired based optimization algorithm for industrial engineering problems. Eng. Appl. Artif. Intell. 2019, 82, 148–174. [Google Scholar] [CrossRef]
- Sallam, K.M.; Elsayed, S.M.; Chakrabortty, R.K.; Ryan, M.J. Improved multi-operator differential evolution algorithm for solving unconstrained problems. In Proceedings of the 2020 IEEE congress on evolutionary computation (CEC), Glasgow, UK, 19–24 July 2020; IEEE: Piscataway, NJ, USA; pp. 1–8. [Google Scholar]
- Tian, Z.; Gai, M. Football team training algorithm: A novel sport-inspired meta-heuristic optimization algorithm for global optimization. Expert Syst. Appl. 2024, 245, 123088. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl.-Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Jia, H.; Zhou, X.; Zhang, J.; Abualigah, L.; Yildiz, A.R.; Hussien, A.G. Modified crayfish optimization algorithm for solving multiple engineering application problems. Artif. Intell. Rev. 2024, 57, 127. [Google Scholar] [CrossRef]
- Cui, J.; Wu, L.; Huang, X.; Xu, D.; Liu, C.; Xiao, W. Multi-strategy adaptable ant colony optimization algorithm and its application in robot path planning. Knowl.-Based Syst. 2024, 288, 111459. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. Polar lights optimizer: Algorithm and applications in image segmentation and feature selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]






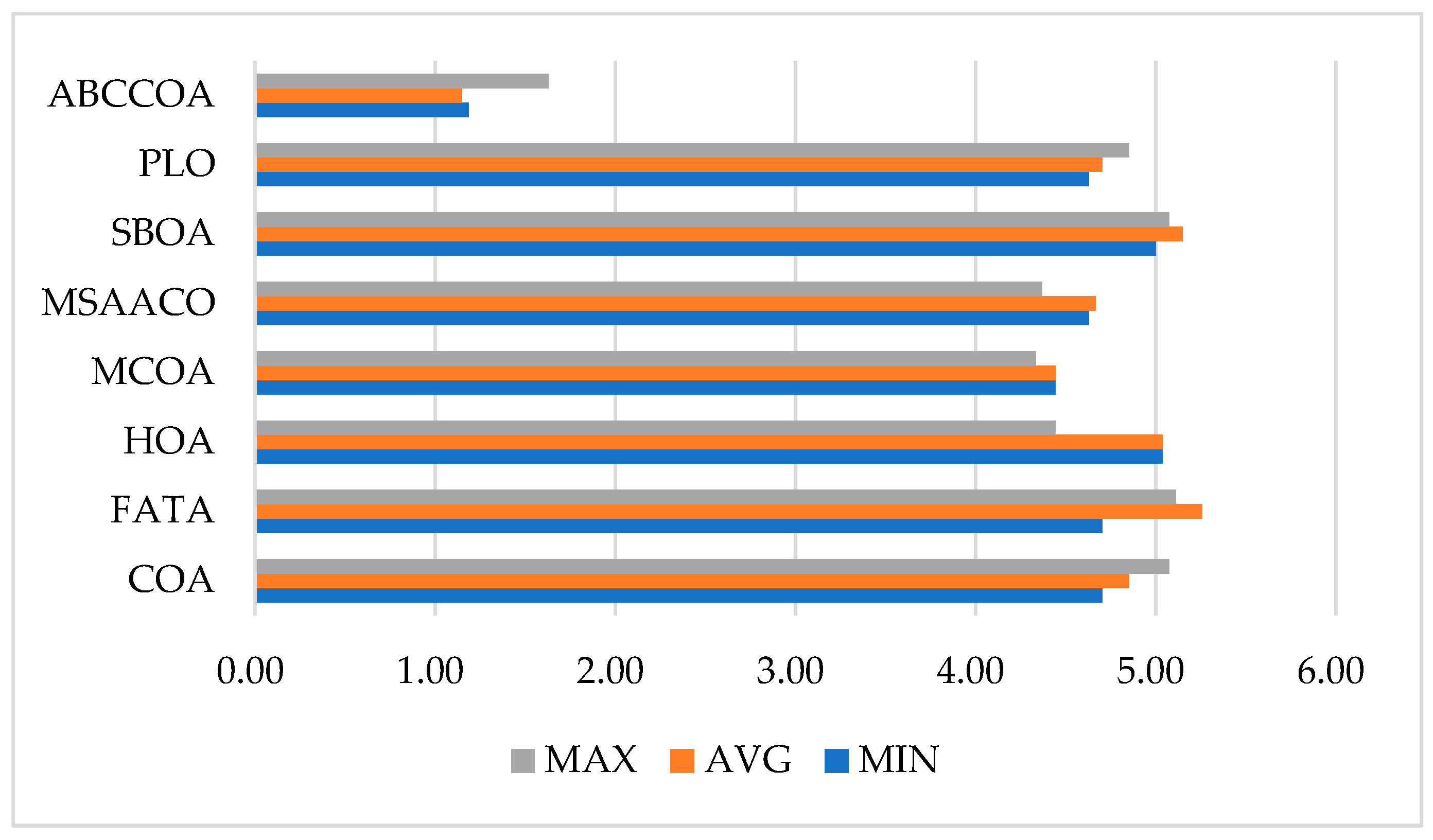

| Functions | Type | Name | Values |
|---|---|---|---|
| CEC2020_F1 | Unimodal | Shifted and Rotated Bent Cigar Function | 100 |
| CEC2020_F2 | Multi-modal | Shifted and Rotated Schwefel’s Function | 1100 |
| CEC2020_F3 | Shifted and Rotated unacek bi-Rastrigin Function | 700 | |
| CEC2020_F4 | Expanded Rosenbrock’s plus Griewangk’s Function | 1900 | |
| CEC2020_F5 | Hybrid | Hybrid Function 1 (N = 3) | 1700 |
| CEC2020_F6 | Hybrid Function 2 (N = 4) | 1600 | |
| CEC2020_F7 | Hybrid Function 3 (N = 5) | 2100 | |
| CEC2020_F8 | Composition | Composition Function 1 (N = 3) | 2200 |
| CEC2020_F9 | Composition Function 2 (N = 4) | 2400 | |
| CEC2020_F10 | Composition Function 3 (N = 5) | 2500 |
| Algorithms | Time | Parameters Setting |
|---|---|---|
| COA [63] | 2023 | No Parameters |
| GGO [65] | 2024 | |
| HEOA [66] | 2024 | |
| IPOA [67] | 2024 | |
| PRO [68] | 2024 | |
| QAGO [69] | 2024 | |
| QHDBO [70] | 2024 | |
| STOA [71] | 2019 | |
| IMODE [72] | 2020 |
| Type | Name | Feature Number | Classification Number | Instance Size |
|---|---|---|---|---|
| Low | Aggregation | 2 | 7 | 788 |
| Banana | 2 | 2 | 5300 | |
| Iris | 4 | 3 | 150 | |
| Bupa | 6 | 2 | 345 | |
| Glass | 9 | 7 | 214 | |
| Breastcancer | 9 | 2 | 699 | |
| Lipid | 10 | 2 | 583 | |
| HeartEW | 13 | 2 | 270 | |
| Medium | Zoo | 16 | 7 | 101 |
| Vote | 16 | 2 | 435 | |
| Congress | 16 | 2 | 435 | |
| Lymphography | 18 | 4 | 148 | |
| Vehicle | 18 | 4 | 846 | |
| WDBC | 30 | 2 | 569 | |
| BreastEW | 30 | 2 | 569 | |
| SonarEW | 60 | 2 | 208 | |
| High | Libras | 90 | 15 | 360 |
| Hillvalley | 100 | 2 | 606 | |
| Musk | 166 | 2 | 476 | |
| Clean | 167 | 2 | 476 | |
| Semeion | 256 | 10 | 1593 | |
| Madelon | 500 | 2 | 2600 | |
| Isolet | 617 | 26 | 1559 | |
| Lung | 12,533 | 5 | 203 | |
| MLL | 12,582 | 3 | 72 | |
| Ovarian | 15154 | 2 | 253 | |
| CNS | 7129 | 2 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Q.; Yuan, S.; Fang, Y. Three Strategies Enhance the Bionic Coati Optimization Algorithm for Global Optimization and Feature Selection Problems. Biomimetics 2025, 10, 380. https://doi.org/10.3390/biomimetics10060380
Cao Q, Yuan S, Fang Y. Three Strategies Enhance the Bionic Coati Optimization Algorithm for Global Optimization and Feature Selection Problems. Biomimetics. 2025; 10(6):380. https://doi.org/10.3390/biomimetics10060380
Chicago/Turabian StyleCao, Qingzheng, Shuqi Yuan, and Yi Fang. 2025. "Three Strategies Enhance the Bionic Coati Optimization Algorithm for Global Optimization and Feature Selection Problems" Biomimetics 10, no. 6: 380. https://doi.org/10.3390/biomimetics10060380
APA StyleCao, Q., Yuan, S., & Fang, Y. (2025). Three Strategies Enhance the Bionic Coati Optimization Algorithm for Global Optimization and Feature Selection Problems. Biomimetics, 10(6), 380. https://doi.org/10.3390/biomimetics10060380







