Biomimetic Visual Information Spatiotemporal Encoding Method for In Vitro Biological Neural Networks
Abstract
1. Introduction
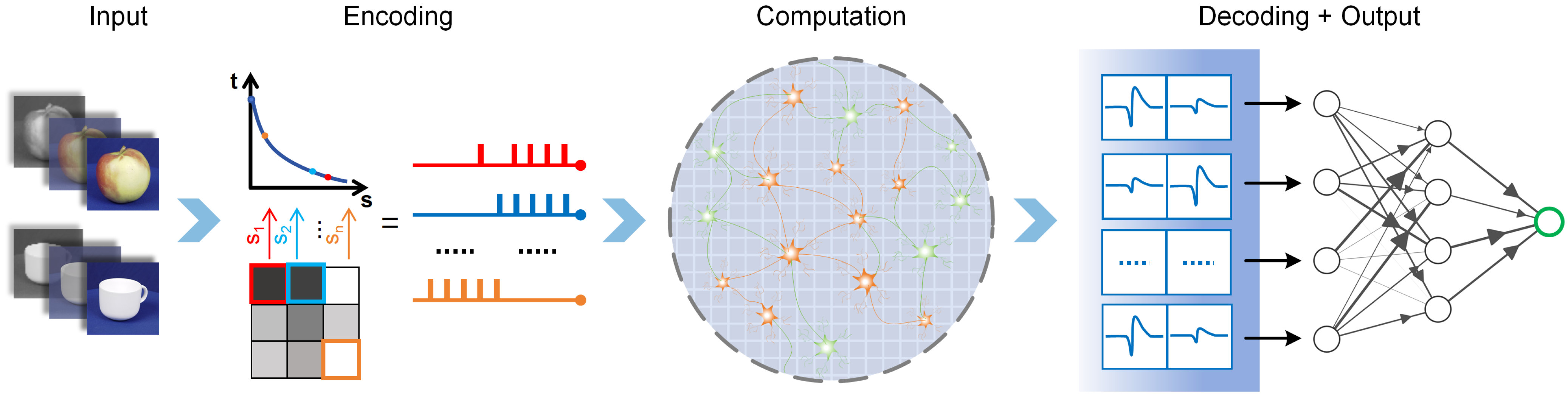
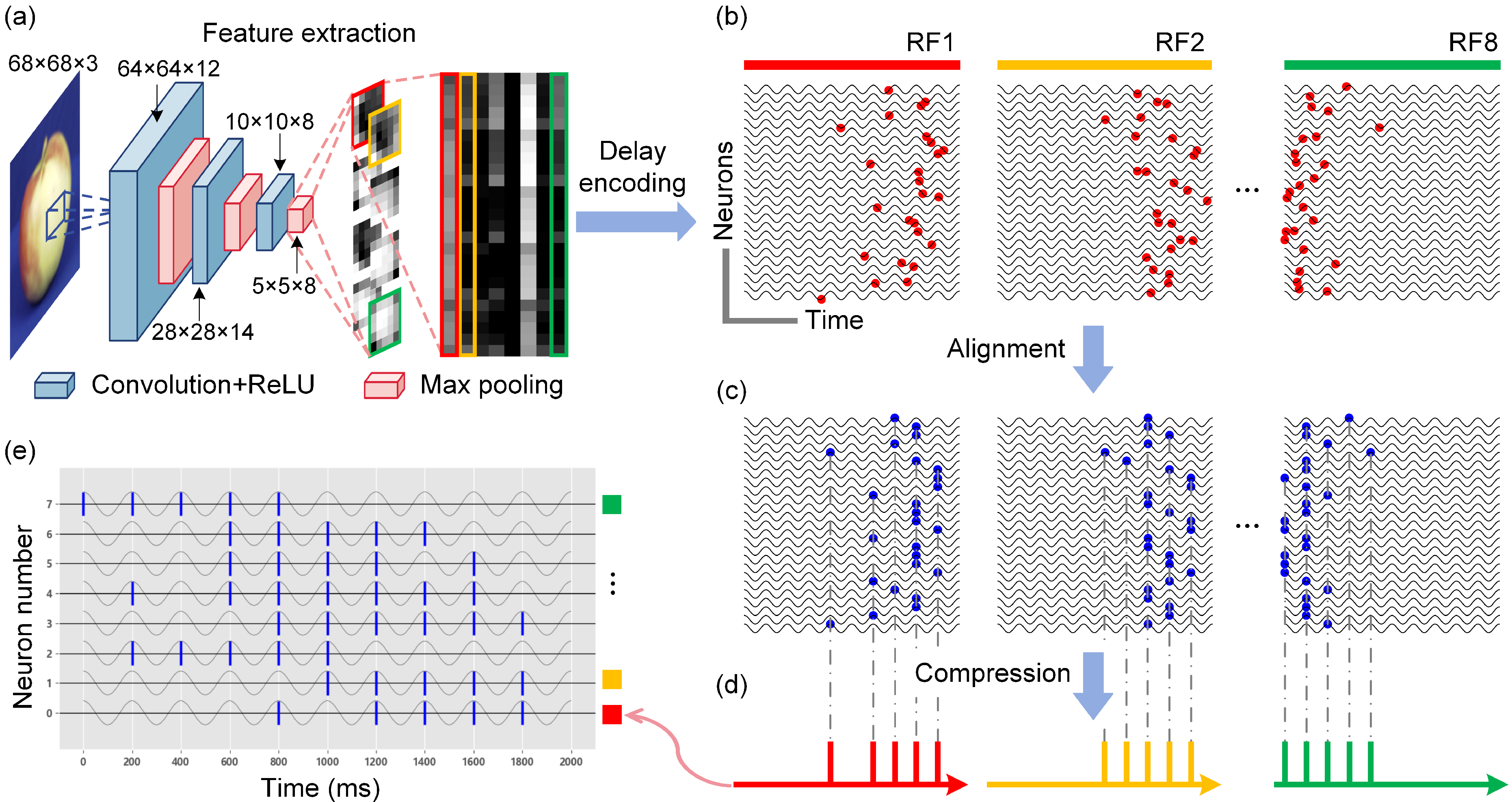
- We propose a biomimetic visual information spatiotemporal encoding method for in vitro BNNs, enabling them to perceive complex visual information effectively. The proposed encoding method first utilizes a convolutional neural network (CNN) to extract features from high-dimensional colored images and then uses a delayed phase encoding scheme to transform the highly compressed features into spatiotemporal pulse sequences that can be accepted by BNNs.
- We propose an unsupervised training process for in vitro BNNs to fulfil image recognition tasks using the proposed encoding scheme and a logistic regression decoding strategy. The images are encoded into pulse sequences and input to the in vitro BNN via an electrical stimulus. The evoked neural network’s activity is decoded into the classes of the images. The in vitro BNN is trained by repetitive stimuli to improve the recognition performance.
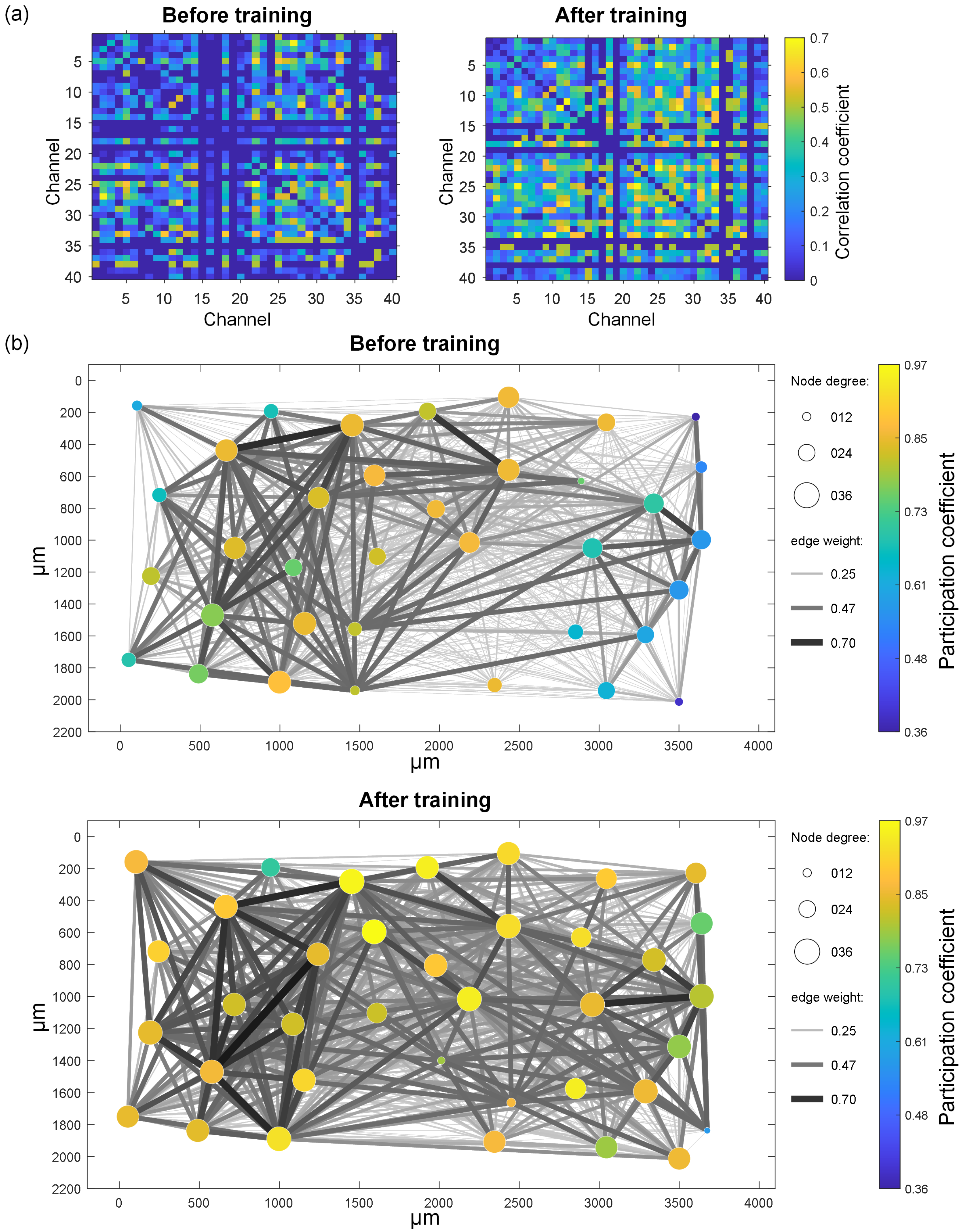
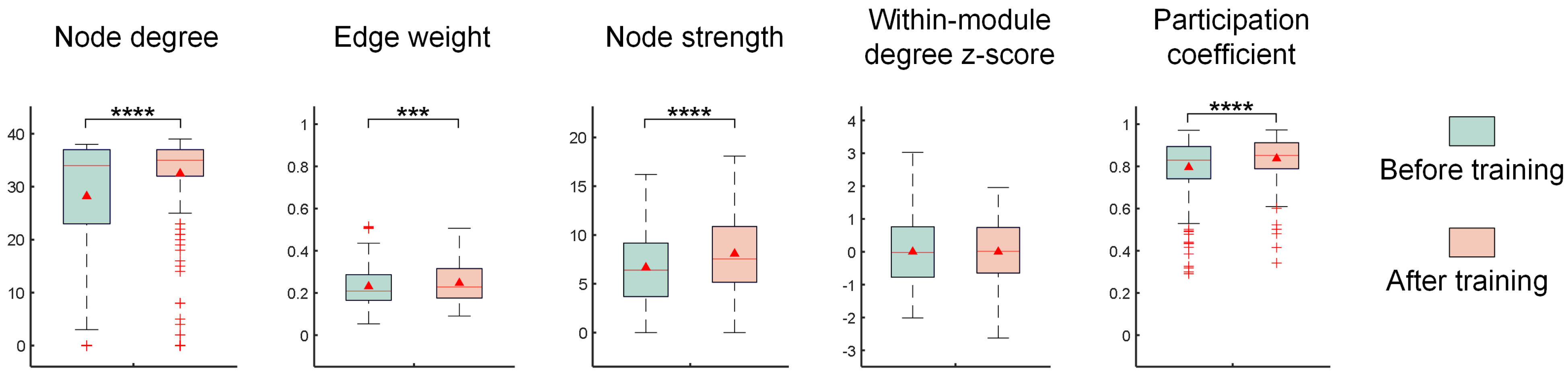
- Experimental results show that the image recognition performance of in vitro BNNs is enhanced by this unsupervised training process. A functional connectivity analysis on in vitro BNNs reveals that the trained BNNs show significant improvements in the node degree, node strength, edge weight, and inter-module participation coefficient. These changes indicate the reshaping of the network’s functional structure and enhanced capabilities for cross-module information exchange. These functional connectivity changes may be the main factors that enable the in vitro BNNs to achieve improved performance.
2. Materials and Methods
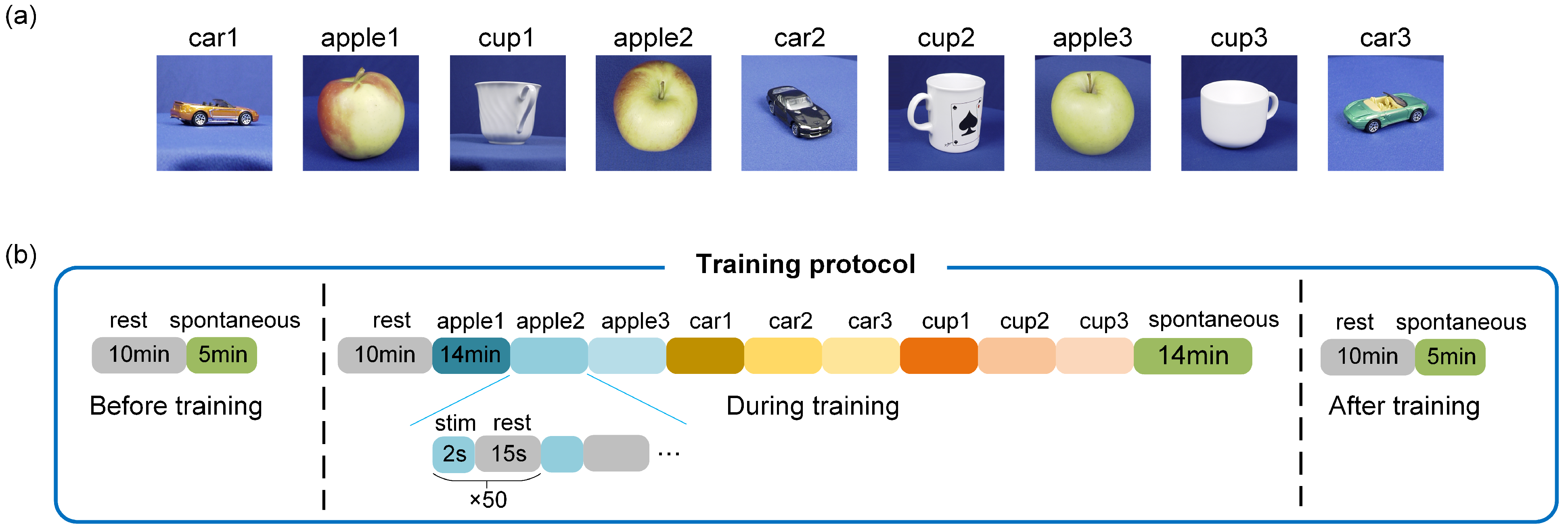
2.1. In Vitro Biological Neural Network Culture and Signal Acquisition
2.2. Visual Information Encoding and Decoding Methods
2.2.1. Improved Delayed Phase Encoding
2.2.2. Logistic Regression Decoding
2.3. Network Functional Connectivity Analysis
3. Experiment and Results
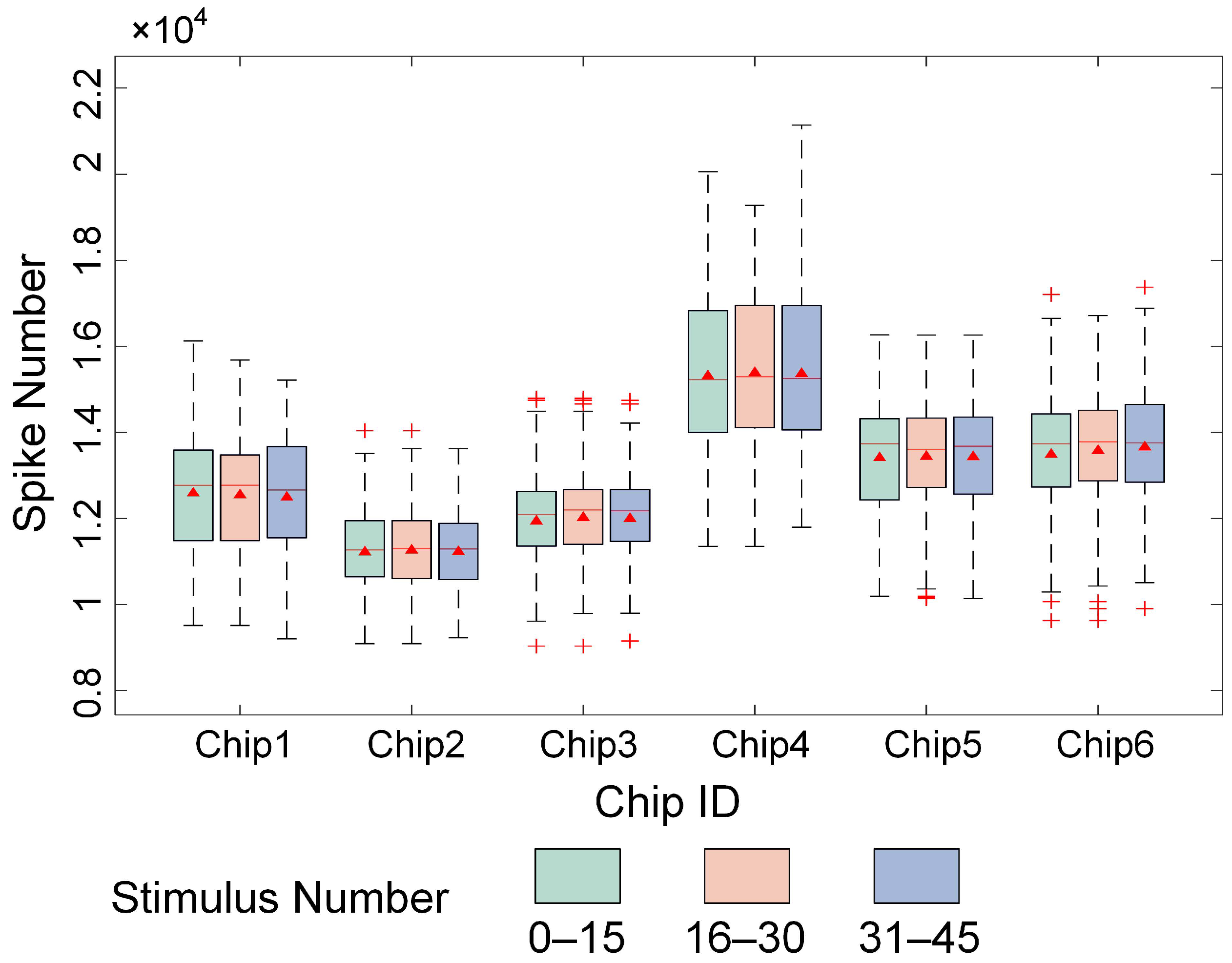
3.1. High-Density Recording of Spontaneous and Evoked Activity in In Vitro Biological Neural Networks
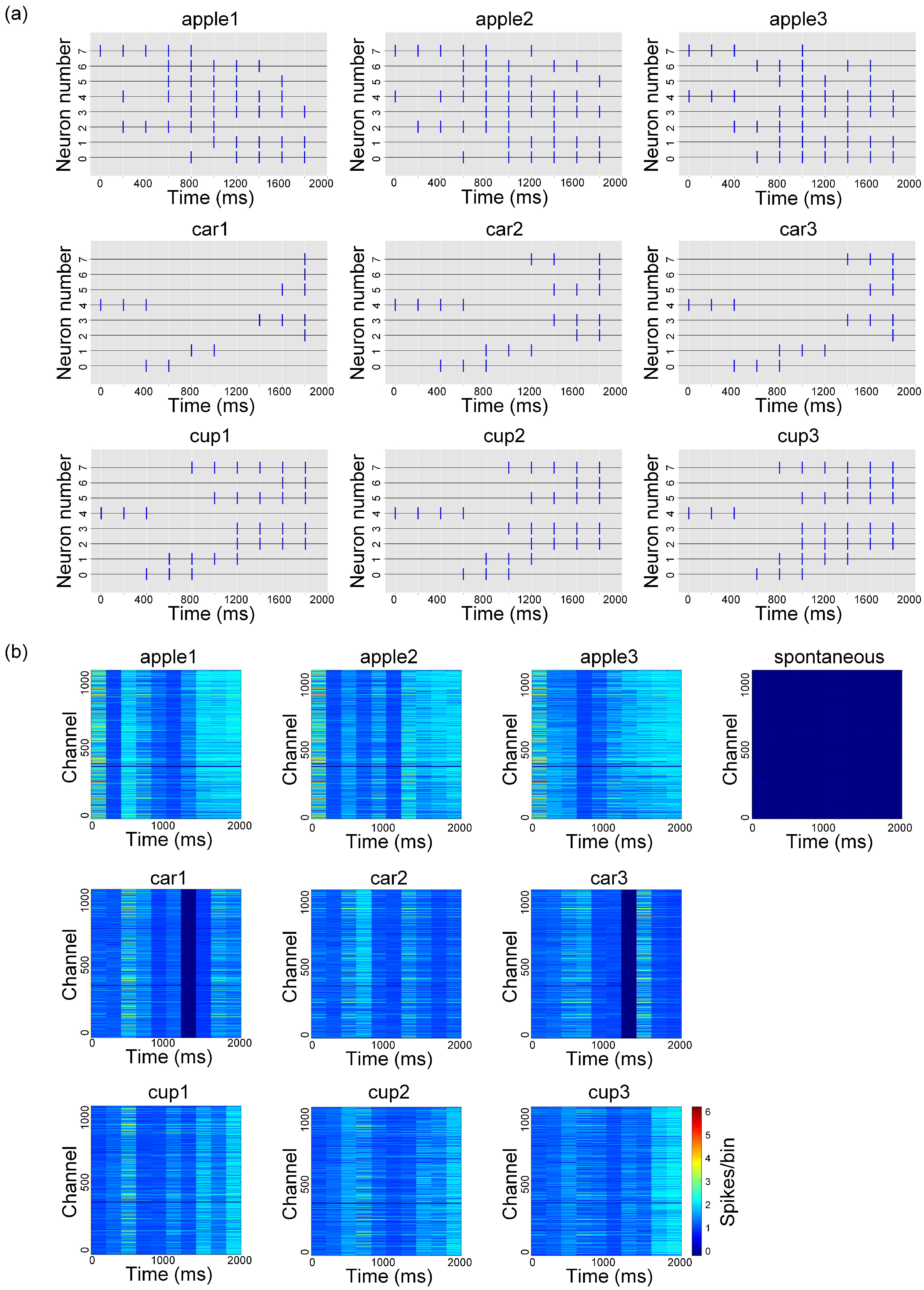
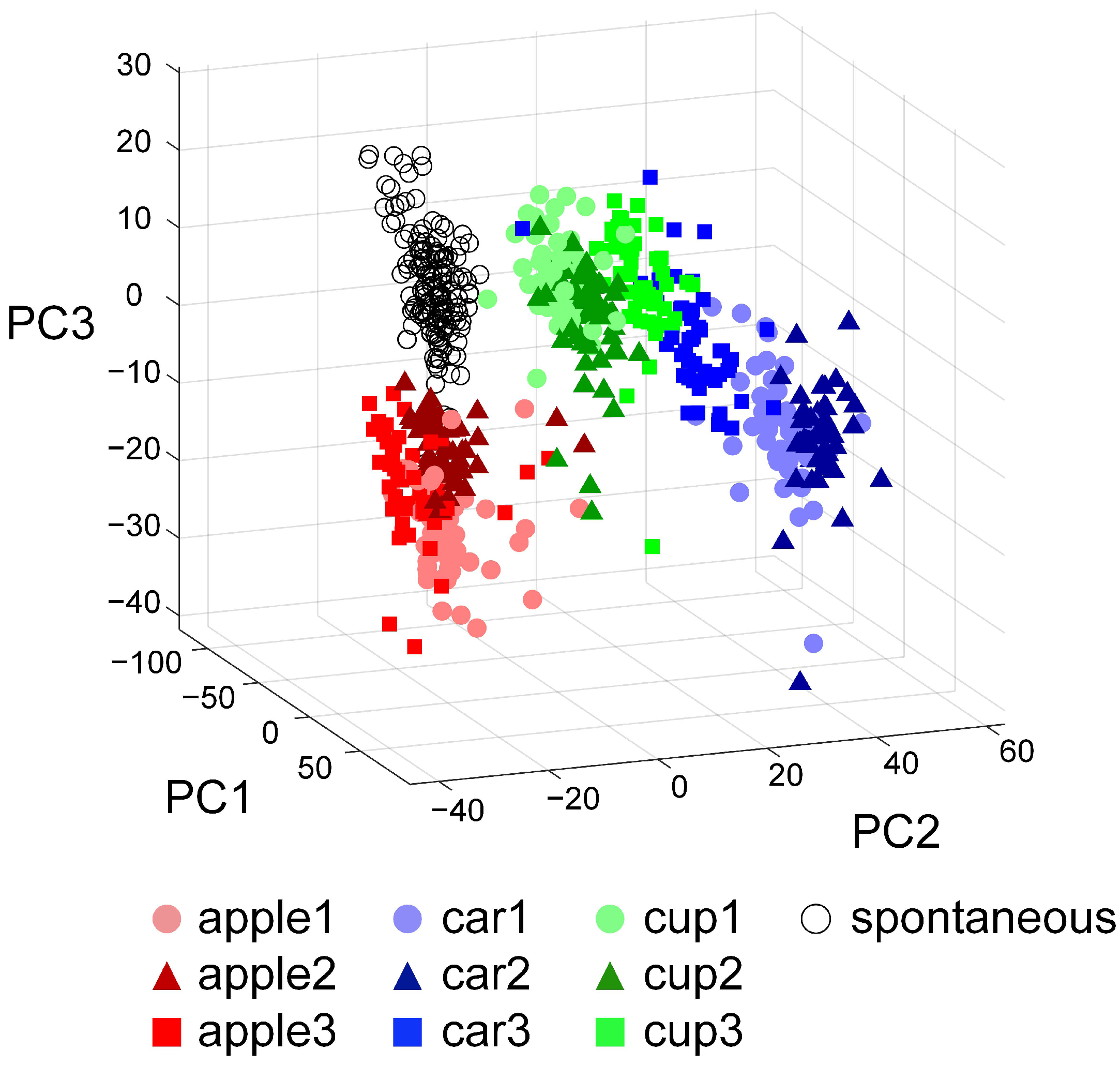
3.2. Experimental Validation of the Visual Information Encoding Method for In Vitro Biological Neural Networks
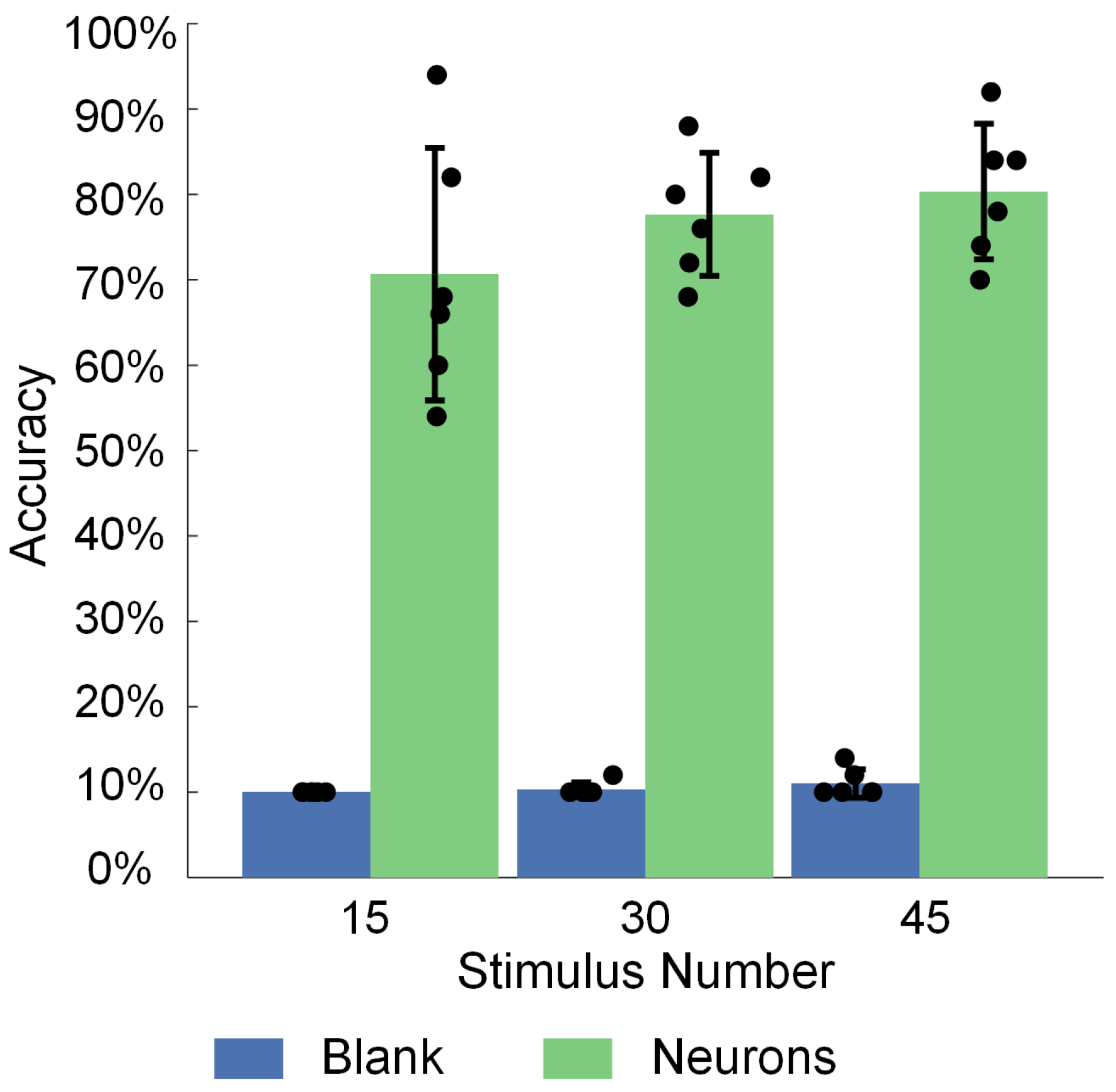
3.3. Spatiotemporal Combined Stimulus Pattern Recognition and Learning Behavior in Biological Neural Networks
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BNN | Biological neural network |
| HD-MEA | High-density microelectrode array |
| CNN | Convolutional neural network |
| ReLU | Rectified linear unit |
| RF | Receptive field |
| SMO | Sub-threshold membrane oscillation |
| PCA | Principal component analysis |
| STTC | Spike time tiling coefficient |
| ANN | Artificial neural network |
| LSTM | Long short-term memory |
References
- Marković, D.; Mizrahi, A.; Querlioz, D.; Grollier, J. Physics for neuromorphic computing. Nat. Rev. Phys. 2020, 2, 499–510. [Google Scholar] [CrossRef]
- Goswami, S.; Pramanick, R.; Patra, A.; Rath, S.P.; Foltin, M.; Ariando, A.; Thompson, D.; Venkatesan, T.; Goswami, S.; Williams, R.S. Decision trees within a molecular memristor. Nature 2021, 597, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Parisi, G.I.; Kemker, R.; Part, J.L.; Kanan, C.; Wermter, S. Continual lifelong learning with neural networks: A review. Neural Netw. 2019, 113, 54–71. [Google Scholar] [CrossRef] [PubMed]
- Isomura, T.; Kotani, K.; Jimbo, Y.; Friston, K.J. Experimental validation of the free-energy principle with in vitro neural networks. Nat. Commun. 2023, 14, 4547. [Google Scholar] [CrossRef]
- Isomura, T.; Kotani, K.; Jimbo, Y. Cultured cortical neurons can perform blind source separation according to the free-energy principle. PLoS Comput. Biol. 2015, 11, e1004643. [Google Scholar] [CrossRef]
- Sumi, T.; Yamamoto, H.; Katori, Y.; Ito, K.; Moriya, S.; Konno, T.; Sato, S.; Hirano-Iwata, A. Biological neurons act as generalization filters in reservoir computing. Proc. Natl. Acad. Sci. USA 2023, 120, e2217008120. [Google Scholar] [CrossRef]
- Warwick, K. Implications and consequences of robots with biological brains. Ethics. Inf. Technol. 2010, 12, 223–234. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, T.; Wei, Z.; Chen, X.; Shimoda, S.; Fukuda, T.; Huang, Q.; Shi, Q. A real-time neuro-robot system for robot state control. In Proceedings of the 2022 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Guiyang, China, 17–22 July 2022; pp. 124–129. [Google Scholar]
- Duru, J.; Maurer, B.; Doran, C.G.; Jelitto, R.; Küchler, J.; Ihle, S.J.; Ruff, T.; John, R.; Genocchi, B.; Vörös, J. Investigation of the input-output relationship of engineered neural networks using high-density microelectrode arrays. Biosens. Bioelectron. 2023, 239, 115591. [Google Scholar] [CrossRef]
- Borra, F.; Cocco, S.; Monasson, R. Task learning through stimulation-induced plasticity in neural networks. PRX Life 2024, 2, 043014. [Google Scholar] [CrossRef]
- Bisio, M.; Pimashkin, A.; Buccelli, S.; Tessadori, J.; Semprini, M.; Levi, T.; Colombi, I.; Gladkov, A.; Mukhina, I.; Averna, A.; et al. Closed-Loop Systems and In Vitro Neuronal Cultures: Overview and Applications. In In Vitro Neuronal Networks: From Culturing Methods to Neuro-Technological Applications; Chiappalone, M., Pasquale, V., Frega, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 22, pp. 351–387. [Google Scholar]
- Yang, L.; Zhang, C.; Wang, R.; Zhang, Y.; Tan, W.; Liu, L. Bio-syncretic robots composed of living-electromechanical systems. Robot 2023, 45, 89–109. [Google Scholar]
- Mishra, A.K.; Kim, J.; Baghdadi, H.; Johnson, B.R.; Hodge, K.T.; Shepherd, R.F. Sensorimotor control of robots mediated by electrophysiological measurements of fungal mycelia. Sci. Robot. 2024, 9, eadk8019. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Liang, Q.; Wei, Z.; Chen, X.; Shi, Q.; Yu, Z.; Sun, T. An overview of in vitro biological neural networks for robot intelligence. Cyborg. Bionic. Syst. 2023, 4, 0001. [Google Scholar] [CrossRef] [PubMed]
- Novellino, A.; D’ Angelo, P.; Cozzi, L.; Chiappalone, M.; Sanguineti, V.; Martinoia, S. Connecting neurons to a mobile robot: An in vitro bidirectional neural interface. Comput. Intell. Neurosci. 2007, 2007, 012725. [Google Scholar] [CrossRef]
- Tessadori, J.; Bisio, M.; Martinoia, S.; Chiappalone, M. Modular neuronal assemblies embodied in a closed-loop environment: Toward future integration of brains and machines. Front. Neural Circuits 2012, 6, 99. [Google Scholar] [CrossRef] [PubMed]
- Aaser, P.; Knudsen, M.; Ramstad, O.H.; van de Wijdeven, R.; Nichele, S.; Sandvig, I.; Tufte, G.; Stefan Bauer, U.; Halaas, Ø.; Hendseth, S.; et al. Towards making a cyborg: A closed-loop reservoir-neuro system. In Proceedings of the ECAL 2017, the Fourteenth European Conference on Artificial Life, Lyon, France, 4–8 September 2017; pp. 430–437. [Google Scholar]
- Warwick, K.; Xydas, D.; Nasuto, S.J.; Becerra, V.M.; Hammond, M.W.; Downes, J.; Marshall, S.; Whalley, B.J. Controlling a mobile robot with a biological brain. Def. Sci. J. 2010, 60, 5–14. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, X.; Shimoda, S.; Huang, Q.; Shi, Q.; Fukuda, T.; Sun, T. A modular biological neural network-based neuro-robotic system via local chemical stimulation and calcium imaging. IEEE Robot. Autom. Lett. 2023, 8, 5839–5846. [Google Scholar] [CrossRef]
- Yada, Y.; Yasuda, S.; Takahashi, H. Physical reservoir computing with force learning in a living neuronal culture. Appl. Phys. Lett. 2021, 119, 173701. [Google Scholar] [CrossRef]
- Li, Y.; Sun, R.; Wang, Y.; Li, H.; Zheng, X. A novel robot system integrating biological and mechanical intelligence based on dissociated neural network-controlled closed-loop environment. PLoS ONE 2016, 11, e0165600. [Google Scholar] [CrossRef] [PubMed]
- Kagan, B.J.; Kitchen, A.C.; Tran, N.T.; Habibollahi, F.; Khajehnejad, M.; Parker, B.J.; Bhat, A.; Rollo, B.; Razi, A.; Friston, K.J. In vitro neurons learn and exhibit sentience when embodied in a simulated game-world. Neuron 2022, 110, 3952–3969. [Google Scholar] [CrossRef]
- Cai, H.; Ao, Z.; Tian, C.; Wu, Z.; Liu, H.; Tchieu, J.; Gu, M.; Mackie, K.; Guo, F. Brain organoid reservoir computing for artificial intelligence. Nat. Electron. 2023, 6, 1032–1039. [Google Scholar] [CrossRef]
- Ades, C.; Abd, M.A.; Hutchinson, D.T.; Tognoli, E.; Du, E.; Wei, J.; Engeberg, E.D. Biohybrid Robotic Hand to Investigate Tactile Encoding and Sensorimotor Integration. Biomimetics 2024, 9, 78. [Google Scholar] [CrossRef] [PubMed]
- Tang, F.; Zhang, J.; Zhang, C.; Liu, L. Brain-Inspired Architecture for Spiking Neural Networks. Biomimetics 2024, 9, 646. [Google Scholar] [CrossRef] [PubMed]
- Ao, T.; Cao, X.; Fu, L.; Yi, Z. Research Advances on Robot Intelligent Control Based on Spiking Neural Network. Inf. Control 2024, 53, 453–470. [Google Scholar]
- Amos, G.; Ihle, S.J.; Clément, B.F.; Duru, J.; Girardin, S.; Maurer, B.; Delipinar, T.; Vörös, J.; Ruff, T. Engineering an in vitro retinothalamic nerve model. Front. Neurosci. 2024, 18, 1396966. [Google Scholar] [CrossRef]
- Chiappalone, M.; Massobrio, P.; Martinoia, S. Network plasticity in cortical assemblies. Eur. J. Neurosci. 2008, 28, 221–237. [Google Scholar] [CrossRef]
- Serre, T. Deep learning: The good, the bad, and the ugly. Annu. Rev. Vis. Sci. 2019, 5, 399–426. [Google Scholar] [CrossRef]
- Gollisch, T.; Meister, M. Eye smarter than scientists believed: Neural computations in circuits of the retina. Neuron 2010, 65, 150–164. [Google Scholar] [CrossRef] [PubMed]
- Habibollahi, F.; Kagan, B.J.; Burkitt, A.N.; French, C. Critical dynamics arise during structured information presentation within embodied in vitro neuronal networks. Nat. Commun. 2023, 14, 5287. [Google Scholar] [CrossRef]
- Pimashkin, A.; Gladkov, A.; Agrba, E.; Mukhina, I.; Kazantsev, V. Selectivity of stimulus induced responses in cultured hippocampal networks on microelectrode arrays. Cogn. Neurodyn. 2016, 10, 287–299. [Google Scholar] [CrossRef]
- Hu, J.; Tang, H.; Tan, K.C.; Li, H.; Shi, L. A spike-timing-based integrated model for pattern recognition. Neural Comput. 2013, 25, 450–472. [Google Scholar] [CrossRef]
- Chen, W.; Li, X.; Feng, X.; Pu, J.; Luo, M. Long-term characterization of functional structure of cultured hippocampal neuronal networks. Chin. Sci. Bull. 2010, 55, 2531–2538. [Google Scholar]
- Sit, T.P.; Feord, R.C.; Dunn, A.W.; Chabros, J.; Oluigbo, D.; Smith, H.H.; Burn, L.; Chang, E.; Boschi, A.; Yuan, Y.; et al. MEA-NAP: A flexible network analysis pipeline for neuronal 2D and 3D organoid multielectrode recordings. Cell Rep. Methods 2024, 4, 100901. [Google Scholar] [CrossRef] [PubMed]
- Cutts, C.S.; Eglen, S.J. Detecting pairwise correlations in spike trains: An objective comparison of methods and application to the study of retinal waves. J. Neurosci. 2014, 34, 14288–14303. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S. Consensus clustering in complex networks. Sci. Rep. 2012, 2, 336. [Google Scholar] [CrossRef]
- Sporns, O.; Betzel, R.F. Modular brain networks. Annu. Rev. Psychol. 2016, 67, 613–640. [Google Scholar] [CrossRef]
- Shao, W.W.; Shao, Q.; Xu, H.H.; Qiao, G.J.; Wang, R.X.; Ma, Z.Y.; Meng, W.W.; Yang, Z.B.; Zang, Y.L.; Li, X.H. Repetitive training enhances the pattern recognition capability of cultured neural networks. PLoS Comput. Biol. 2025, 21, e1013043. [Google Scholar] [CrossRef]
- Ruaro, M.E.; Bonifazi, P.; Torre, V. Toward the neurocomputer: Image processing and pattern recognition with neuronal cultures. IEEE Trans. Biomed. Eng. 2005, 52, 371–383. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Xu, S.; Deng, Y.; Luo, J.; He, E.; Liu, Y.; Zhang, K.; Yang, Y.; Xu, S.; Sha, L.; Song, Y.; et al. High-throughput PEDOT: PSS/PtNPs-modified microelectrode array for simultaneous recording and stimulation of hippocampal neuronal networks in gradual learning process. ACS Appl. Mater. Interfaces 2022, 14, 15736–15746. [Google Scholar] [CrossRef]
- Yang, Y.; Deng, Y.; Xu, S.; Liu, Y.; Liang, W.; Zhang, K.; Lv, S.; Sha, L.; Yin, H.; Wu, Y.; et al. PPy/SWCNTs-modified microelectrode Array for learning and memory model construction through electrical stimulation and detection of in vitro hippocampal neuronal network. ACS Appl. Bio Mater. 2023, 6, 3414–3422. [Google Scholar] [CrossRef]
- Poli, D.; Massobrio, P. High-frequency electrical stimulation promotes reshaping of the functional connections and synaptic plasticity in in vitro cortical networks. Phys. Biol. 2018, 15, 06LT01. [Google Scholar] [CrossRef] [PubMed]
- Gladkov, A.; Kolpakov, V.; Pigareva, Y.; Kazantsev, V.; Mukhina, I.; Pimashkin, A. Functional connectivity of neural network in dissociated hippocampal culture grown on microelectrode array. Mod. Technol. Med. 2017, 9, 61–66. [Google Scholar] [CrossRef][Green Version]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Madhavan, R.; Chao, Z.C.; Potter, S.M. Plasticity of recurring spatiotemporal activity patterns in cortical networks. Phys. Biol. 2007, 4, 181. [Google Scholar] [CrossRef] [PubMed]
- Shao, Q.; Meng, W.w.; LI, X.H.; Shao, W.w. Plasticity of Cultured Neural Networks In Vitro. Prog. Biochem. Biophys. 2024, 51, 1000–1009. [Google Scholar]
- Bigi, W.; Baecchi, C.; Del Bimbo, A. Automatic Interest Recognition from Posture and Behaviour. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; MM ’20. pp. 2472–2480. [Google Scholar]
- Buckchash, H.; Raman, B. DuTriNet: Dual-Stream Triplet Siamese Network for Self-Supervised Action Recognition by Modeling Temporal Correlations. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020; pp. 488–495. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lv, B.; Tang, F.; Wang, Y.; Liu, B.; Liu, L. Biomimetic Visual Information Spatiotemporal Encoding Method for In Vitro Biological Neural Networks. Biomimetics 2025, 10, 359. https://doi.org/10.3390/biomimetics10060359
Wang X, Lv B, Tang F, Wang Y, Liu B, Liu L. Biomimetic Visual Information Spatiotemporal Encoding Method for In Vitro Biological Neural Networks. Biomimetics. 2025; 10(6):359. https://doi.org/10.3390/biomimetics10060359
Chicago/Turabian StyleWang, Xingchen, Bo Lv, Fengzhen Tang, Yukai Wang, Bin Liu, and Lianqing Liu. 2025. "Biomimetic Visual Information Spatiotemporal Encoding Method for In Vitro Biological Neural Networks" Biomimetics 10, no. 6: 359. https://doi.org/10.3390/biomimetics10060359
APA StyleWang, X., Lv, B., Tang, F., Wang, Y., Liu, B., & Liu, L. (2025). Biomimetic Visual Information Spatiotemporal Encoding Method for In Vitro Biological Neural Networks. Biomimetics, 10(6), 359. https://doi.org/10.3390/biomimetics10060359




