The Conceptual Design of a Variable Camber Wing
Abstract
1. Introduction
2. Research Methodology
2.1. Aerodynamic Theory of VCWs
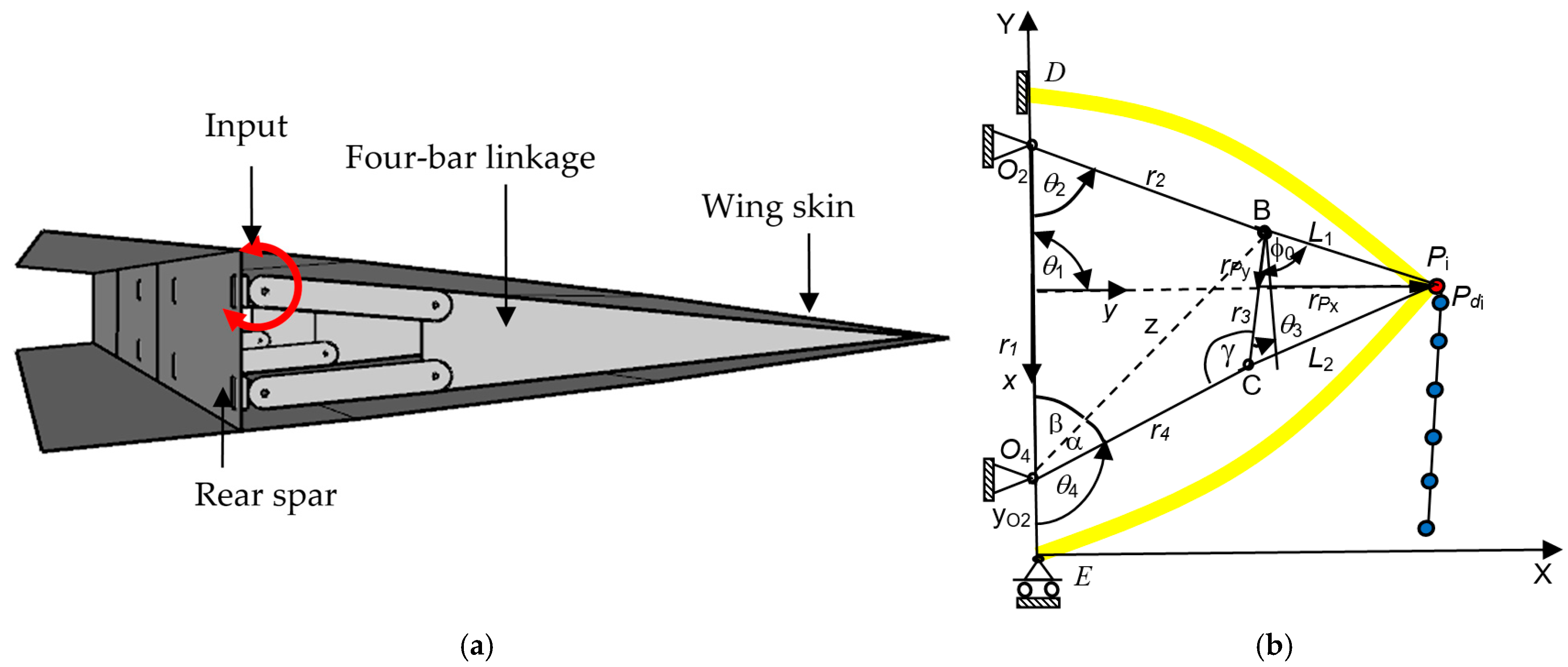
2.2. Four-Bar Linkage Synthesis for VCWs
2.3. VCW Mechanism Synthesis
2.4. Optimization Technique
| Algorithm 1. ATLBO-DA Algorithm |
| Input: maximum number of generations (nit), population size (nP) Output: xbest, fbest Initialization: Step 0.1 Generate np initial students {xi} and perform function evaluations {fi}. Step 0.2 Initiate four 1 × 2 matrices, TRR_Success, TRR_Fail, LRR_Success and LRR_Fail, all of which elements are set to be ones. Main procedure Step 1 While (the termination conditions are not met) do {Teacher Phase} Step 2 Calculate the mean position of solutions {xi} written as Mavg. Step 3 Calculate the probabilities of selecting the intervals for TRR: . Step 4 For i = 1 to nP Step 4.1 Perform roulette wheel selection with PTRRj. Step 4.1.1 If j = 1 is selected, TRR = 0.4 + 0.1 rand is sampled. Step 4.1.2 Else, if j = 2 is selected, TRR = 0.5 + 0.1 rand is sampled. Step 4.2 Generate Pr = rand and select a teacher. Step 4.2.1 If Pr ≤ TRR, set the best solution as a teacher Mbest. Step 4.2.2 Else, if Pr > TRR, randomly select a solution in AD and set it as a teacher Mbest. Step 4.3 Create xinew using following formular and perform function evaluation. xnew = xold + Difference_Mean where Difference_Meani = ri (Mi, best − TfMi,avg), and Tf = round(1 + ri). Step 4.3.1 If xinew is better than xi, add 1 point to the j-th element of TRR_Success. Step 4.3.2 Else, add 1 point to the j-th element of TRR_Fail. Step 5 Replace {xi} by nP best solutions from {xi}∪{xinew}. {Learning Phase} Step 6 Calculate the probabilities of selecting the intervals for LRR similar to that for TRR in step 3. Step 7 For i = 1 to nP Step 7.1 Perform roulette wheel selection with PLRRj. Step 7.1.1 If j = 1 is selected, LRR = 0.4 + 0.1 rand is sampled. Step 7.1.2 Else, if j = 2 is selected, TRR = 0.5 + 0.1 rand is sampled. Step 7.2 Generate Pr = rand. Step 7.2.1 If Pr ≤ LRR, create xinew using two-student learning and perform function evaluation. Step 7.2.2 Else, create xinew using three-student learning and perform function evaluation. Step 7.3 Update LRR_Success and LRR_Fail. Step 7.3.1 If xinew is better than xi, add 1 point to the j-th element of LRR_Success. Step 7.3.2 Else, add 1 point to the j-th element of LRR_Fail. Step 8 Replace {xi} by nP best solutions from {xi}∪{xinew}. Calculate the objective function value of xinew. Step 9 Update the diversity archive with the non-dominated solutions obtained from {xi}old∪{xi}new. Step 10 End While |
2.5. Structural Strength
2.5.1. Response Surface
2.5.2. Finite Element Analysis
3. Results and Discussion
3.1. The Desired Aerodynamic Performance of the Wing
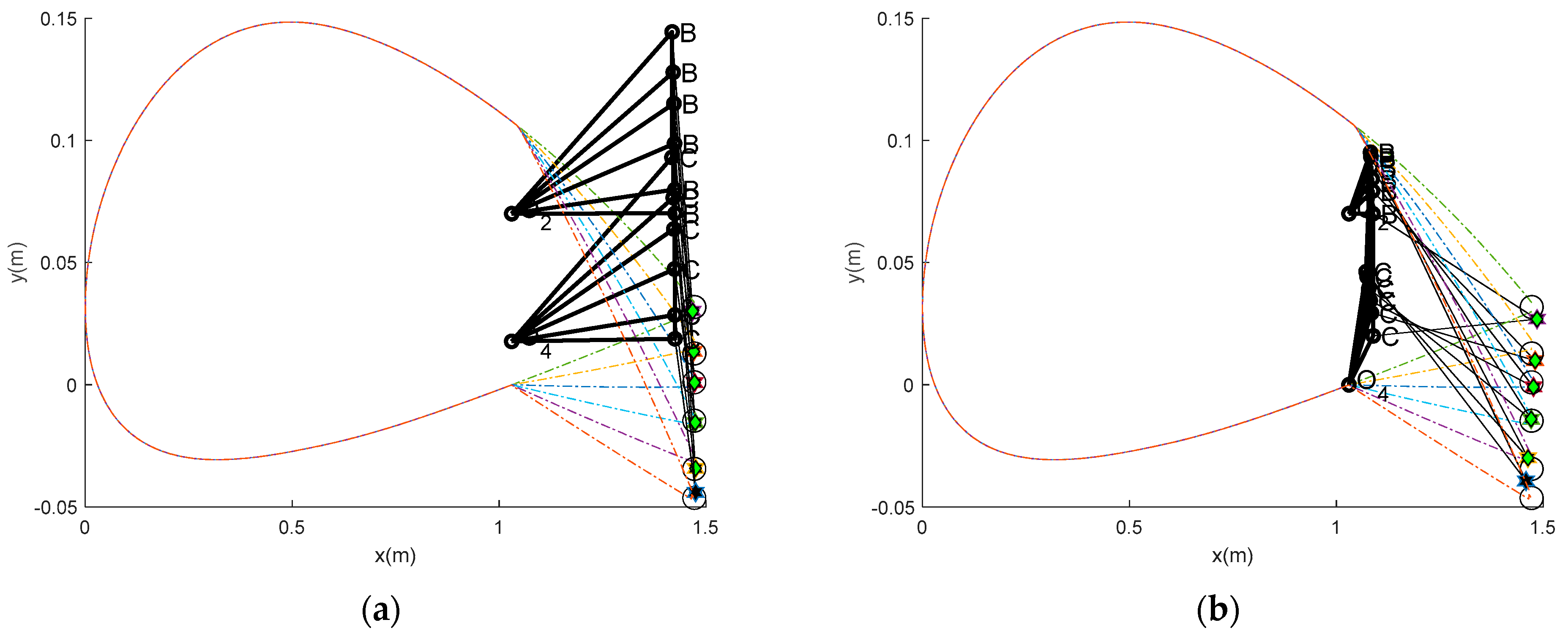
3.2. Mechanism Synthesis
3.3. Actual Aerodynamic Performance and Structural Testing
3.3.1. Material Properties
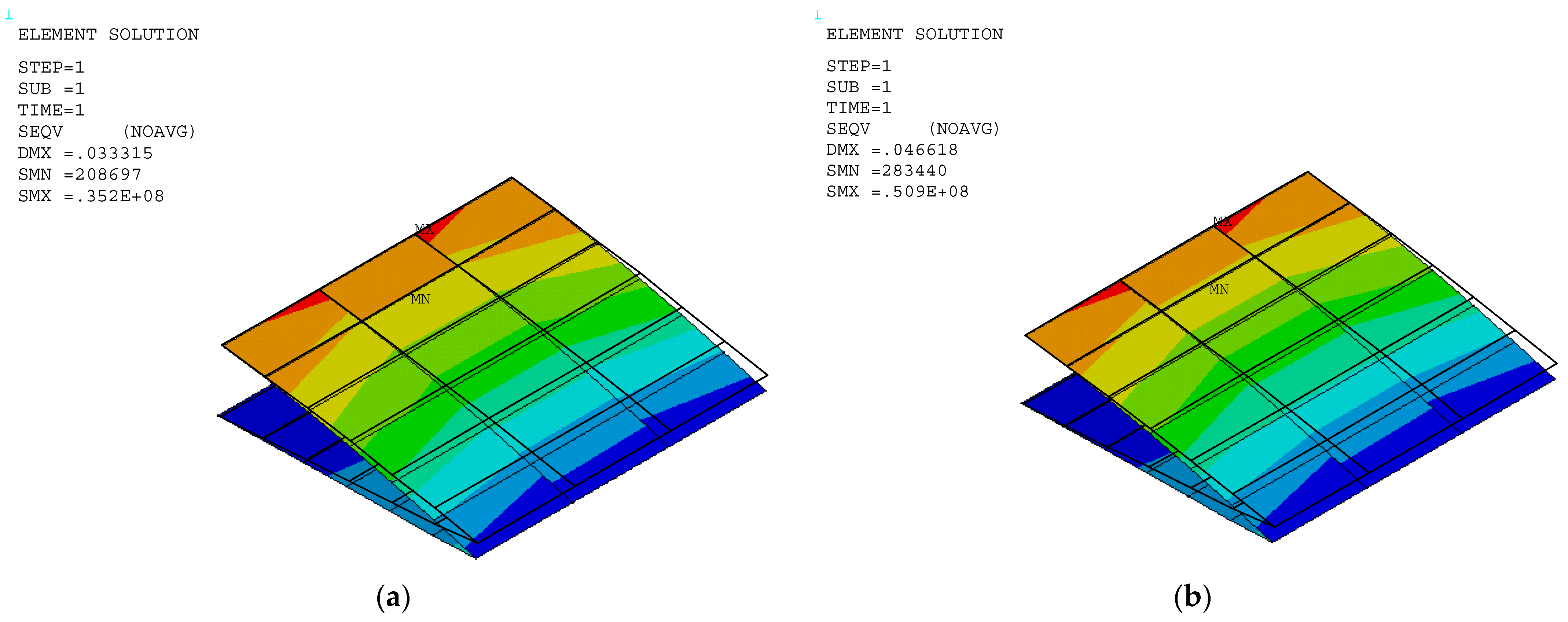
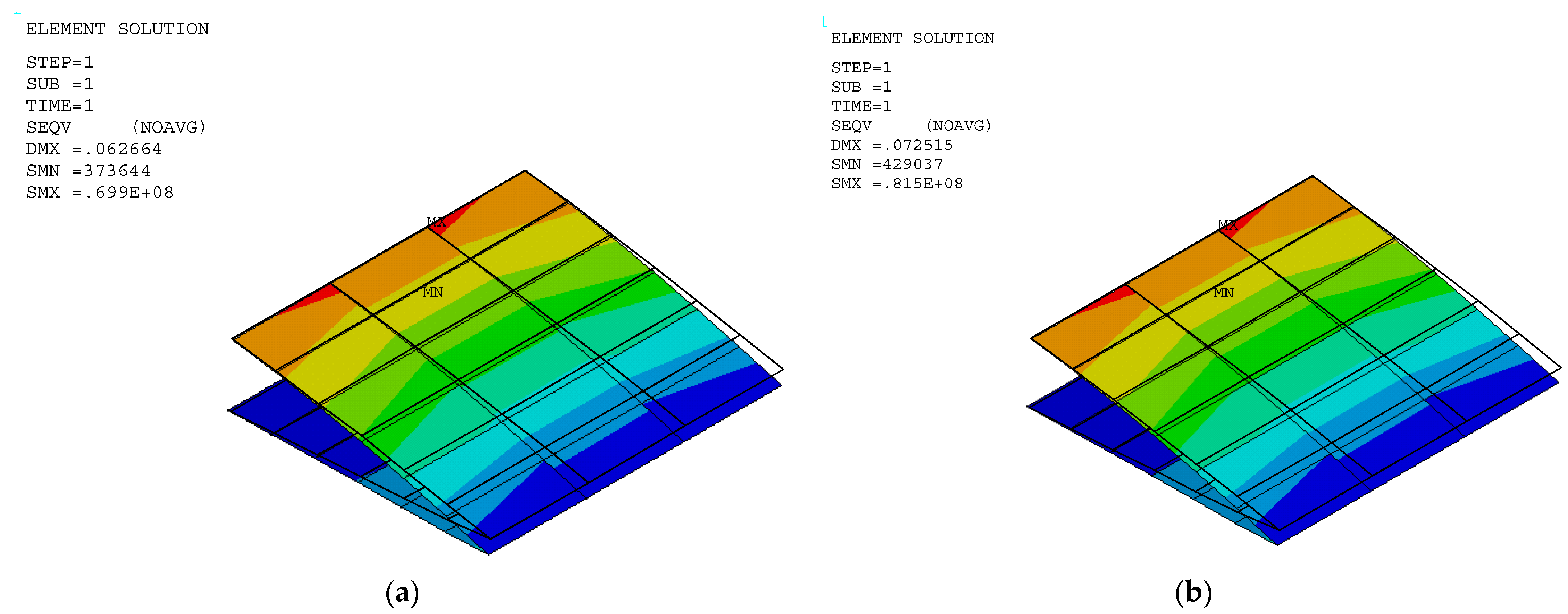
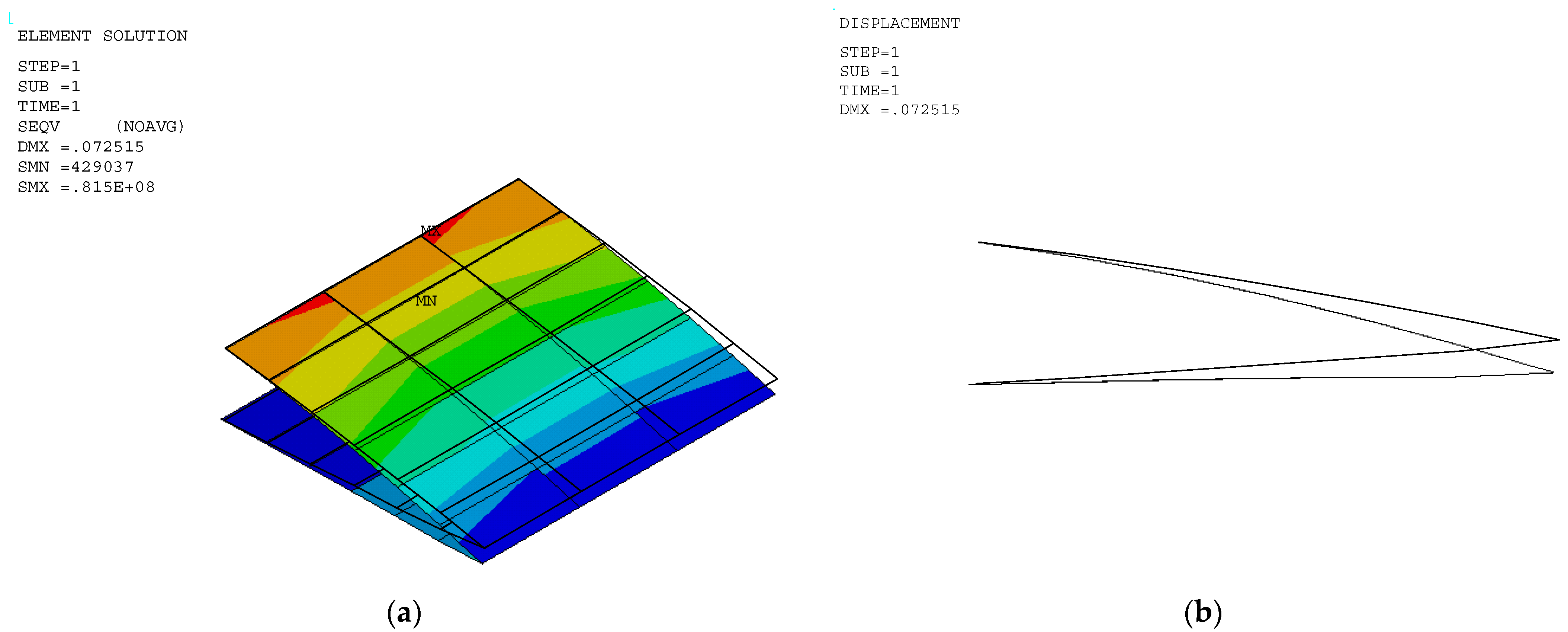
3.3.2. Stress of VCW Trailing Edge
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Majid, T.; Jo, B.W. Status and Challenges on design and implementation of camber morphing mechanisms. Int. J. Aerosp. Eng. 2021, 2021, 6399937. [Google Scholar] [CrossRef]
- La, S.; Joe, W.Y.; Akbar, M.; Alsaidi, B. Surveys on skin design for morphing wing aircraft: Status and challenges. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0315. [Google Scholar]
- Communier, D.; Botez, R.M.; Wong, T. Design and validation of a new morphing camber system by testing in the price—Païdoussis subsonic wind tunnel. Aerospace 2020, 7, 23. [Google Scholar] [CrossRef]
- Zhao, A.; Zou, H.; Jin, H.; Wen, D. Structural design and verification of an innovative whole adaptive variable camber wing. Aerosp. Sci. Technol. 2019, 89, 11–18. [Google Scholar] [CrossRef]
- Chanzy, Q.; Keane, A. Analysis and experimental validation of morphing UAV wings. Aeronaut. J. 2018, 122, 390–408b. [Google Scholar] [CrossRef]
- Meguid, S.; Su, Y.; Wang, Y. Complete morphing wing design using flexible-rib system. Int. J. Mech. Matter. Des. 2017, 13, 159–171. [Google Scholar] [CrossRef]
- Yokozeki, T.; Sugiura, A.; Hirano, Y. Development of variable camber morphing airfoil using corrugated structure. J. Aircr. 2014, 51, 1023–1029. [Google Scholar] [CrossRef]
- Takahashi, H.; Yokozeki, T.; Hirano, Y. Development of variable camber wing with morphing leading and trailing sections using corrugated structures. J. Intell. Mater. Syst. Struct. 2016, 27, 2827–2836. [Google Scholar] [CrossRef]
- Maki, M. Experimental study of a morphing wing configuration with multi-slotted variable-camber mechanism. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Washington, DC, USA, 13–17 June 2016; p. 3849. [Google Scholar]
- Kuya, Y.; Ito, R.; Maki, M.; Sawada, K. Numerical study of flow field around a multislotted high-lift wing. J. Aircr. 2020, 58, 383–389. [Google Scholar] [CrossRef]
- Rivero, A.E.; Weaver, P.M.; Cooper, J.E.; Woods, B.K. Parametric structural modelling of fish bone active camber morphing aerofoils. J. Intell. Mater. Syst. Struct. 2018, 29, 2008–2026. [Google Scholar] [CrossRef]
- Bombardieri, R.; Cavallaro, R.; Sanchez, R.; Gauger, N.R. Aerostructural wing shape optimization assisted by algorithmic differentiation. Struct. Multidiscip. Optim. 2021, 64, 739–760. [Google Scholar] [CrossRef]
- Najmi, J.; Khan, H.A.; Javaid, S.S.; Hameed, A.; Siddiqui, F. Aeroelastic tailoring for aerospace applications. Heliyon 2024, 10, e24151. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Yun, G.J. Variable camber morphing wing mechanism using deployable scissor structure: Design, analysis and manufacturing. Adv. Aircr. Spacecr. Sci. 2022, 9, 103–117. [Google Scholar]
- Zhou, J.; Sun, X.; Sun, Q.; Xue, J.; Song, K.; Li, Y.; Dong, L. Design and validation of the trailing edge of a variable camber wing based on a two-dimensional airfoil. Biomimetics 2024, 9, 312. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Ge, W.; Zhou, J.; Zhang, Y.; Zhao, D.; Wang, Z.; Dong, D. Design and experiment of concentrated flexibility-based variable camber morphing wing. Chin. J. Aeronaut. 2022, 35, 455–469. [Google Scholar] [CrossRef]
- Sun, X.; Xue, J.; Zhou, J.; Wang, Z.; Wang, W.; Zhang, M. Design and validation of a variable camber wing structure. Chin. J. Aeronaut. 2024, 37, 1–11. [Google Scholar] [CrossRef]
- Bureerat, S.; Sleesongsom, S. Constraint handling technique for four-bar linkage path generation using self-adaptive teaching–learning-based optimization with a diversity archive. Eng. Optim. 2021, 53, 513–530. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A Review of Morphing Aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 283–876. [Google Scholar] [CrossRef]
- Dharmdas, A.; Patil, A.Y.; Baig, A.; Hosmani, O.Z.; Mathad, S.N.; Patil, M.B.; Kumar, R.; Kotturshettar, B.B.; Fattah, I.M.R. An Experimental and Simulation Study of the Active Camber Morphing Concept on Airfoils Using Bio-Inspired Structures. Biomimetics 2023, 8, 251. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, Z.; Zhang, H.; Song, C.; Yang, C. Wind Tunnel Tests of 3D-Printed Variable Camber Morphing Wing. Aerospace 2022, 9, 699. [Google Scholar] [CrossRef]
- Joo, J.J.; Marks, C.R.; Zientarski, L.; Culler, A.J. Variable camber compliant wing-design. In Proceedings of the 23rd AIAA/AHS Adaptive Structures Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 1050. [Google Scholar]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Wansaseub, K.; Sleesongsom, S.; Panagant, N.; Pholdee, N.; Bureerat, S. Surrogate-Assisted Reliability Optimisation of an Aircraft Wing with Static and Dynamic Aeroelastic Constraints. Int. J. Aeronaut. Space Sci. 2020, 21, 723–732. [Google Scholar] [CrossRef]
- Hicks, R.M.; Cliff, S.E. An Evaluation of Three Two-Dimensional Computational Fluid Dynamics Codes Including Low Reynolds Numbers and Transonic Mach Numbers; NASA T-M-102840; NASA: Washington, DC, USA, 1991.
- Lafountain, C.; Cohen, K.; Abdallah, S. Use of XFOIL in design of camber-controlled morphing UAVs. Comput. Appl. Eng. Educ. 2012, 20, 673–680. [Google Scholar] [CrossRef]
- Phukaokaew, W.; Sleesongsom, S.; Panagant, N.; Bureerat, S. Synthesis of four-bar linkage motion generation using optimization algorithms. Adv. Comput. Des. 2019, 4, 197–210. [Google Scholar]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 2nd ed.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Sleesongsom, S.; Bureerat, S. Aircraft morphing wing design by using partial topology optimization. Struct. Multidiscip. Optim. 2013, 48, 1109–1128. [Google Scholar] [CrossRef]
- Gandhi, F.; Anusonti-Inthra, P. Skin design studies for variable camber morphing airfoils. Smart Mater. Struct. 2008, 17, 015025. [Google Scholar] [CrossRef]
- XFOIL 6.9 User Primer. The Last Update 30 November 2001. Available online: http://web.mit.edu/drela/Public/web/xfoil/xfoil_doc.txt (accessed on 20 February 2025).



| Target Point | Position (m) | Angle (δi, °) | CL | CD | CL/CD |
|---|---|---|---|---|---|
| 1 | (0.4416, 0.0318) | 0 | 0.6034 | 0.0065 | 92.83 |
| 2 | (0.4416, −0.0337) | 2 | 0.7460 | 0.0069 | 108.12 |
| 3 | (0.4413, −0.0626) | 4 | 0.8752 | 0.0076 | 115.16 |
| 4 | (0.4414, −0.0783) | 6 | 1.0026 | 0.0093 | 107.81 |
| 5 | (0.4415, −0.0980) | 8 | 1.1008 | 0.0111 | 99.18 |
| 6 | (0.4414, −0.1099) | 10 | 1.1787 | 0.0138 | 85.41 |
| Parameter | Best | Worst |
|---|---|---|
| r1 | 0.0700 | 0.0522 |
| r2 | 0.0579 | 0.3947 |
| r3 | 0.0500 | 0.0514 |
| r4 | 0.0621 | 0.3947 |
| rPx | 0.0500 | 0.1141 |
| rPy | 0.3957 | 0.0500 |
| 0 | 10.8650 | |
| 9.2592 | 8.4342 | |
| 14.1952 | 6.5619 | |
| 19.1367 | 4.1709 | |
| 23.6499 | 1.4421 | |
| 25.7118 | 0.0209 | |
| min | 0.000631 | 0.00005546 |
| mean | 0.000631 | |
| max | 0.000633 | |
| std | 5.67396 × 10−7 | |
| Successful run | 16 | |
| Target Point | Desired Angle (δi°) | Actual Angle (δaci°) | Displacement (Δy, m) | CL (% Difference) | CD (% Difference) | CL/CD (% Difference) |
|---|---|---|---|---|---|---|
| 1 | 0 | 0.7220 | 0.005 | 0.6720 (11.3689) | 0.0066 (1.5385) | 101.3575 (9.1861) |
| 2 | 2 | 2.7971 | 0.022 | 0.7967 (6.7962) | 0.0072 (4.3478) | 110.9610 (2.6276) |
| 3 | 4 | 4.0892 | 0.033 | 0.8810 (0.6627) | 0.0077 (1.3158) | 114.7135 (0.3877) |
| 4 | 6 | 5.7725 | 0.046 | 0.9887 (1.3864) | 0.0092 (1.0753) | 107.8190 (0.0083) |
| 5 | 8 | 7.8541 | 0.062 | 1.0945 (0.5723) | 0.0109 (1.8018) | 100.3208 (1.1502) |
| 6 | 10 | 9.1764 | 0.07 | 1.1487 (2.5452) | 0.0125 (9.4203) | 91.8225 (7.5079) |
| Property | Value | Unit |
|---|---|---|
| Young’s modulus (E) | 70 × 109 | Pa |
| Yield stress (σy) | 100 × 106 | Pa |
| Poisson’s ratio (ν) | 0.3 | - |
| Density (ρ) | 2700 | kg/m3 |
| Degree | Maximum Stress (MPa) | Actual Maximum Displacement (m) | Desired Displacement (m) |
|---|---|---|---|
| 0 | 5.3 | 0.005 | 0.005 |
| 2 | 22.5 | 0.023 | 0.022 |
| 4 | 35.2 | 0.033 | 0.033 |
| 6 | 50.9 | 0.047 | 0.046 |
| 8 | 69.9 | 0.063 | 0.062 |
| 10 | 81.5 | 0.073 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortez, S.T.P.; Winyangkul, S.; Sleesongsom, S. The Conceptual Design of a Variable Camber Wing. Biomimetics 2025, 10, 353. https://doi.org/10.3390/biomimetics10060353
Cortez STP, Winyangkul S, Sleesongsom S. The Conceptual Design of a Variable Camber Wing. Biomimetics. 2025; 10(6):353. https://doi.org/10.3390/biomimetics10060353
Chicago/Turabian StyleCortez, Spencer Troy P., Seksan Winyangkul, and Suwin Sleesongsom. 2025. "The Conceptual Design of a Variable Camber Wing" Biomimetics 10, no. 6: 353. https://doi.org/10.3390/biomimetics10060353
APA StyleCortez, S. T. P., Winyangkul, S., & Sleesongsom, S. (2025). The Conceptual Design of a Variable Camber Wing. Biomimetics, 10(6), 353. https://doi.org/10.3390/biomimetics10060353










