Development of a Passive Back-Support Exoskeleton Mimicking Human Spine Motion for Multi-Posture Assistance in Occupational Tasks
Abstract
1. Introduction
2. Motion Analysis of Human Spine
2.1. Anatomical Mechanism
2.2. Modeling of Spine Bending
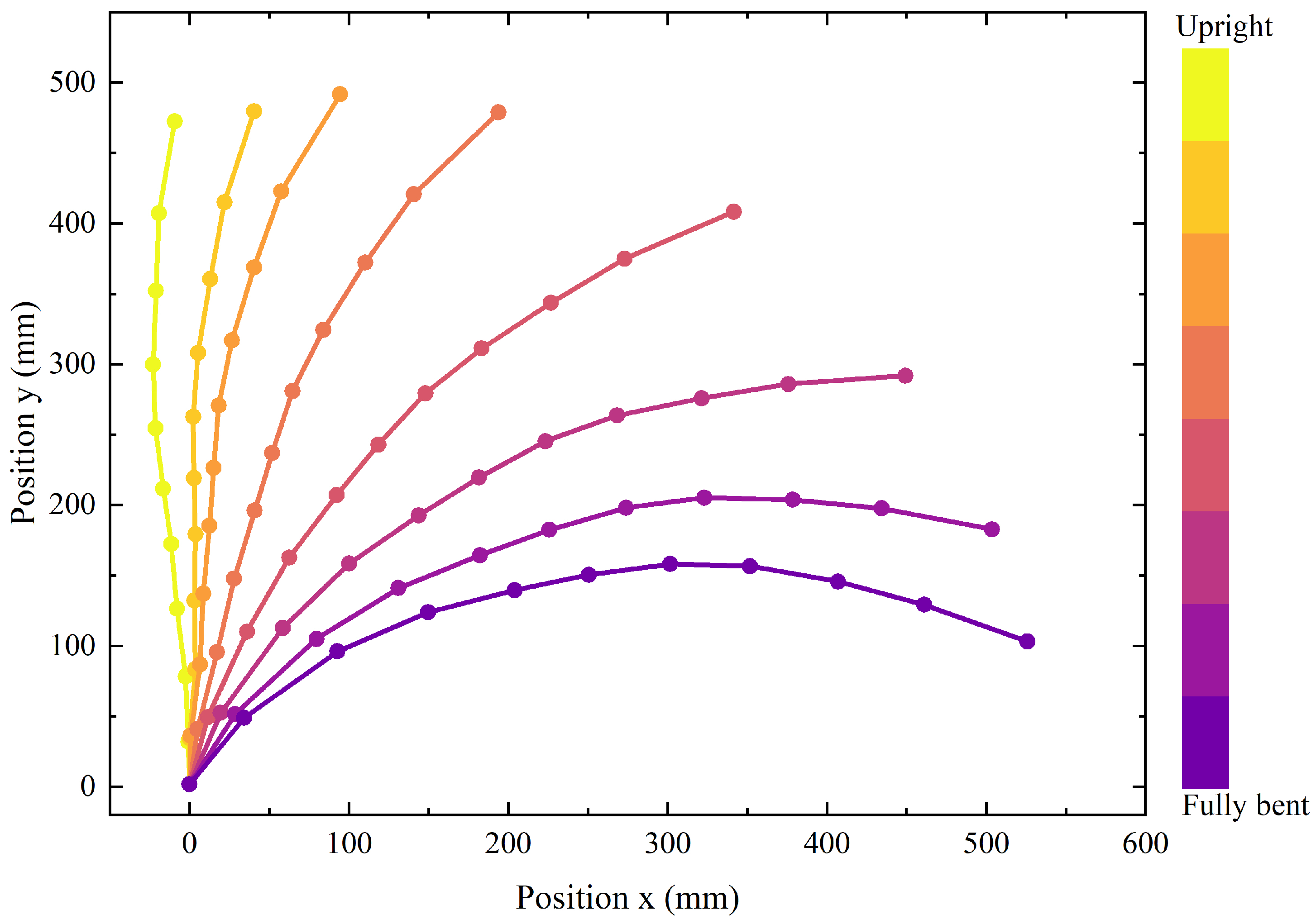
2.2.1. Kinematic Data Collection
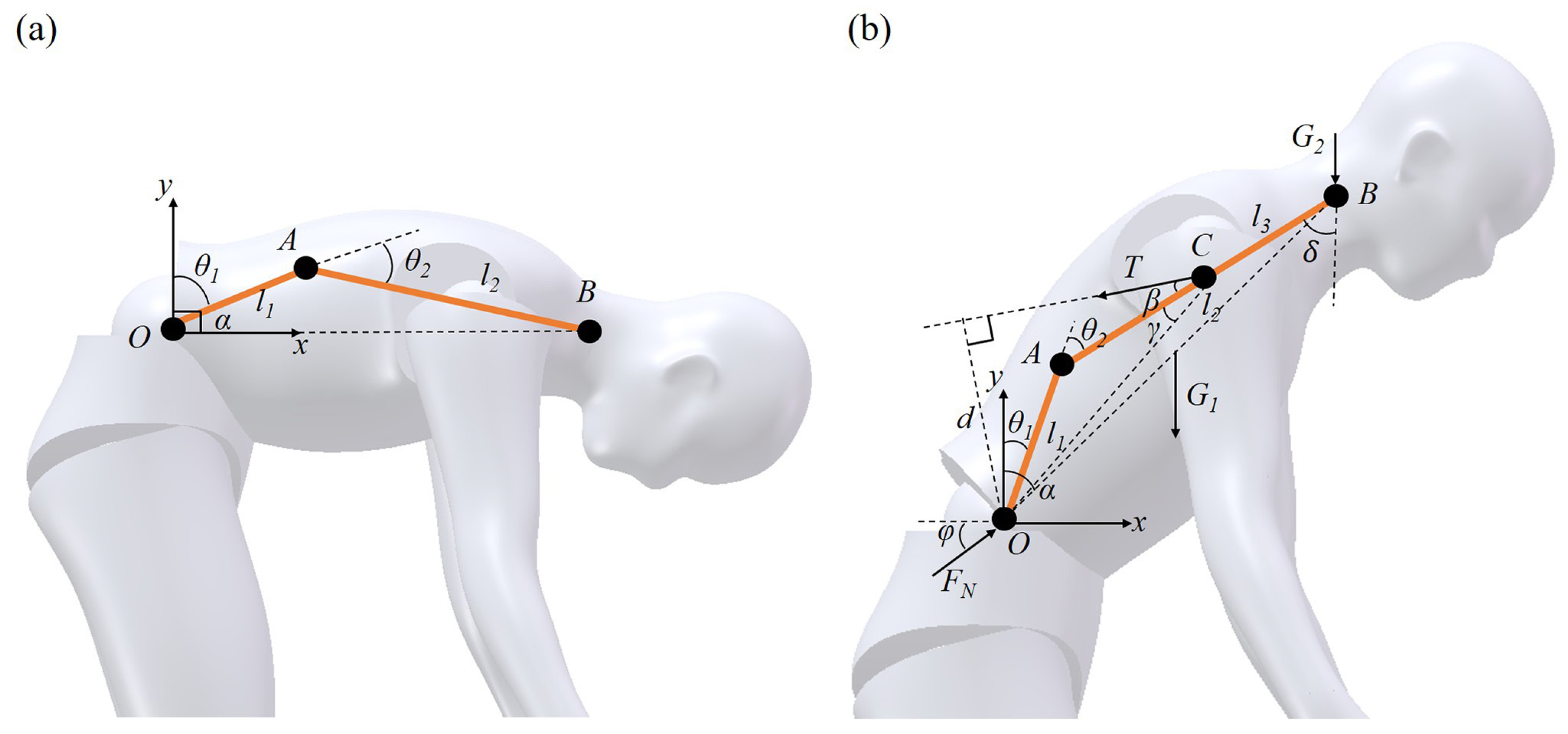
2.2.2. Biomechanical Analysis
3. Design of Back-Support Exoskeleton
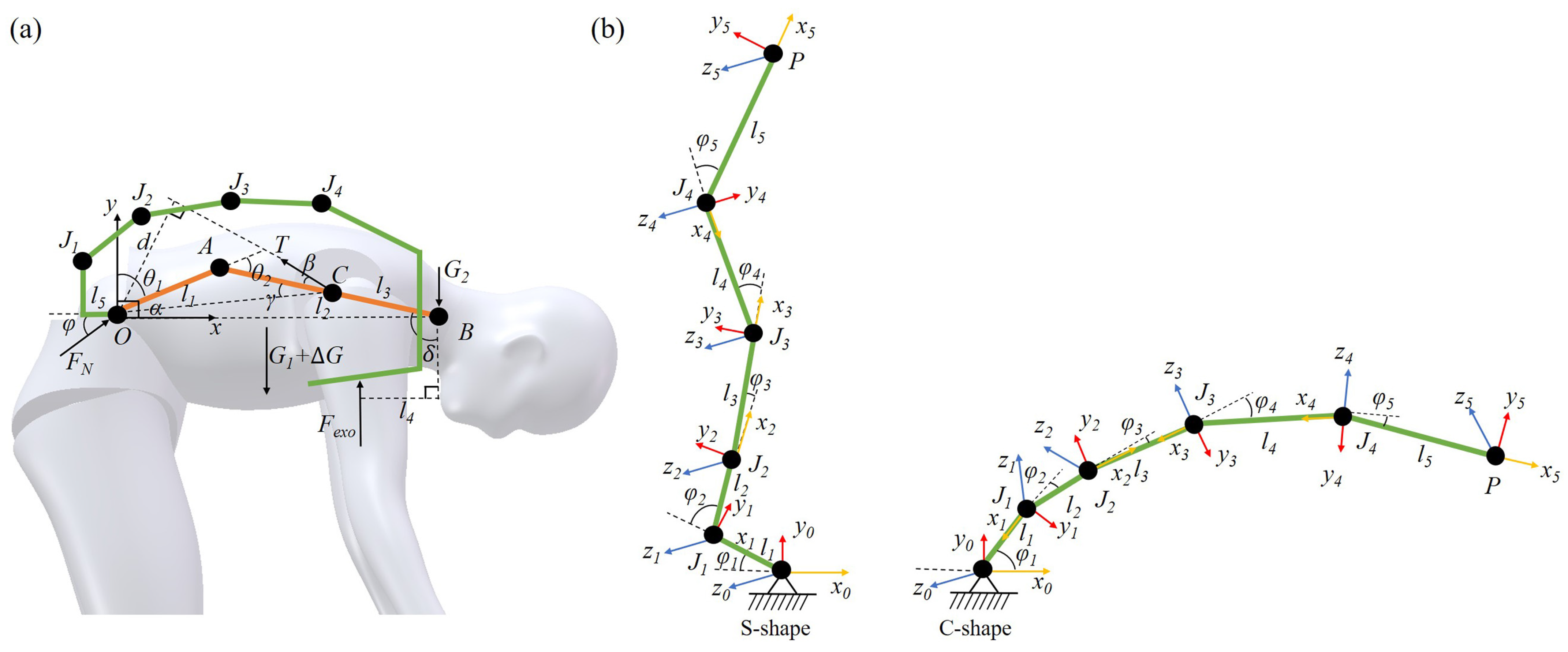
3.1. Exoskeleton Modeling
3.2. Structural Description
4. Experiments and Results
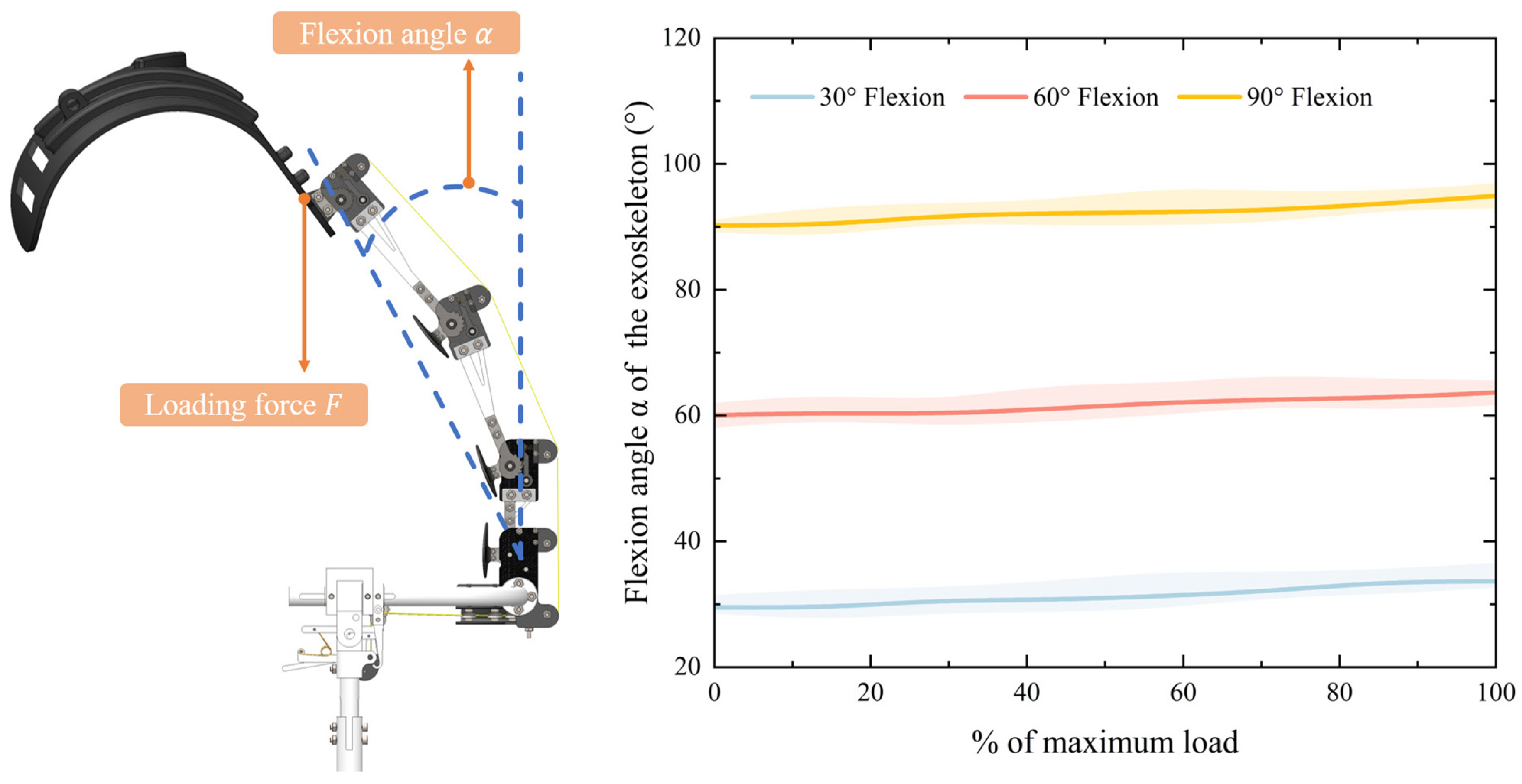
4.1. Experimental Conditions
4.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kok, J.D.; De Vroonhof, P.; Snijders, J.; Roullis, G.; Clarke, M.; Peereboom, K.; Isusi, I. Work-Related MSDs: Prevalence, Costs and Demographics in the EU (European Risk Observatory Executive Summary); Publications Office of the European Union: Luxembourg, 2019; pp. 1–18. [Google Scholar]
- Benos, L.; Tsaopoulos, D.; Bochtis, D. A review on ergonomics in agriculture. Part I: Manual operations. Appl. Sci. 2020, 10, 1905. [Google Scholar] [CrossRef]
- Fulmer, S.; Punnett, L.; Tucker Slingerland, D.; Earle-Richardson, G. Ergonomic exposures in apple harvesting: Preliminary observations. Am. J. Ind. Med. 2002, 42, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Barros-Gomes, S.; Orme, N.; Nhola, L.F.; Scott, C.; Helfinstine, K.; Pislaru, S.V.; Kane, G.C.; Singh, M.; Pellikka, P.A. Characteristics and consequences of work-related musculoskeletal pain among cardiac sonographers compared with peer employees: A multisite cross-sectional study. J. Am. Soc. Echocardiogr. 2019, 32, 1138–1146. [Google Scholar] [CrossRef] [PubMed]
- Claes, F.; Berger, J.; Stassijns, G. Arm and neck pain in ultrasonographers. Hum. Factors 2015, 57, 238–245. [Google Scholar] [CrossRef]
- Umer, W.; Antwi-Afari, M.F.; Li, H.; Szeto, G.P.; Wong, A.Y. The prevalence of musculoskeletal symptoms in the construction industry: A systematic review and meta-analysis. Int. Arch. Occup. Environ. Health 2018, 91, 125–144. [Google Scholar] [CrossRef]
- Skals, S.; Bláfoss, R.; Andersen, M.S.; de Zee, M.; Andersen, L.L. Manual material handling in the supermarket sector. Part 1: Joint angles and muscle activity of trapezius descendens and erector spinae longissimus. Appl. Ergon. 2021, 92, 103340. [Google Scholar] [CrossRef]
- Govaerts, R.; Tassignon, B.; Ghillebert, J.; Serrien, B.; De Bock, S.; Ampe, T.; El Makrini, I.; Vanderborght, B.; Meeusen, R.; De Pauw, K. Prevalence and incidence of work-related musculoskeletal disorders in secondary industries of 21st century Europe: A systematic review and meta-analysis. BMC Musculoskelet. Disord. 2021, 22, 751. [Google Scholar] [CrossRef]
- Katz, J.N. Lumbar disc disorders and low-back pain: Socioeconomic factors and consequences. J. Bone Jt. Surg. 2006, 88, 21–24. [Google Scholar] [CrossRef]
- Ali, A.; Fontanari, V.; Schmoelz, W.; Agrawal, S.K. Systematic review of back-support exoskeletons and soft robotic suits. Front. Bioeng. Biotechnol. 2021, 9, 765257. [Google Scholar] [CrossRef]
- De Bock, S.; Ghillebert, J.; Govaerts, R.; Tassignon, B.; Rodriguez-Guerrero, C.; Crea, S.; Veneman, J.; Geeroms, J.; Meeusen, R.; De Pauw, K. Benchmarking occupational exoskeletons: An evidence mapping systematic review. Appl. Ergon. 2022, 98, 103582. [Google Scholar] [CrossRef]
- Okunola, A.; Akanmu, A.; Jebelli, H.; Afolabi, A. Assessment of active back-support exoskeleton on carpentry framing tasks: Muscle activity, range of motion, discomfort, and exertion. Int. J. Ind. Ergon. 2025, 107, 103716. [Google Scholar] [CrossRef]
- Ji, X.; Wang, D.; Li, P.; Zheng, L.; Sun, J.; Wu, X. SIAT-WEXv2: A Wearable Exoskeleton for Reducing Lumbar Load during Lifting Tasks. Complexity 2020, 2020, 8849427. [Google Scholar] [CrossRef]
- Poliero, T.; Lazzaroni, M.; Toxiri, S.; Di Natali, C.; Caldwell, D.G.; Ortiz, J. Applicability of an active back-support exoskeleton to carrying activities. Front. Robot. AI 2020, 7, 579963. [Google Scholar] [CrossRef] [PubMed]
- Ratke, E.J.; McMaster, H.; Vellucci, C.L.; Larson, D.J.; Holmes, M.W.; Beaudette, S.M. Ability of a passive back support exoskeleton to mitigate fatigue related adaptations in a complex repetitive lifting task. J. Biomech. 2025, 181, 112553. [Google Scholar] [CrossRef] [PubMed]
- Koopman, A.S.; Kingma, I.; de Looze, M.P.; van Dieën, J.H. Effects of a passive back exoskeleton on the mechanical loading of the low-back during symmetric lifting. J. Biomech. 2020, 102, 109486. [Google Scholar] [CrossRef] [PubMed]
- Lamers, E.P.; Yang, A.J.; Zelik, K.E. Feasibility of a biomechanically-assistive garment to reduce low back loading during leaning and lifting. IEEE Trans. Biomed. Eng. 2017, 65, 1674–1680. [Google Scholar] [CrossRef]
- van Sluijs, R.M.; Wehrli, M.; Brunner, A.; Lambercy, O. Evaluation of the physiological benefits of a passive back-support exoskeleton during lifting and working in forward leaning postures. J. Biomech. 2023, 149, 111489. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.L.; Lin, W.C. Enhancing understanding: Back muscle strength and individual flexibility impact on the flexion-relaxation phenomenon in the lumbar erector spinae. J. Electromyogr. Kinesiol. 2024, 79, 102949. [Google Scholar] [CrossRef]
- Cael, C. Functional Anatomy: Musculoskeletal Anatomy, Kinesiology, and Palpation for Manual Therapists with Navigate Advantage Access; Jones & Bartlett Learning: Burlington, MA, USA, 2022. [Google Scholar]
- Barson, A. The vertebral level of termination of the spinal cord during normal and abnormal development. J. Anat. 1970, 106, 489. [Google Scholar]
- Schlösser, T.P.; Semple, T.; Carr, S.B.; Padley, S.; Loebinger, M.R.; Hogg, C.; Castelein, R.M. Scoliosis convexity and organ anatomy are related. Eur. Spine J. 2017, 26, 1595–1599. [Google Scholar] [CrossRef]
- Panjabi, M.M.; White III, A.A. Basic biomechanics of the spine. Neurosurgery 1980, 7, 76–93. [Google Scholar] [CrossRef] [PubMed]
- Anatomy, U. Erector Spine 3D Model. Available online: https://sketchfab.com/3d-models/erector-spinae-muscles-e5f0faac281444e8ae11d4d1d4af0d03 (accessed on 10 May 2025).
- Esola, M.A.; McClure, P.W.; Fitzgerald, G.K.; Siegler, S. Analysis of lumbar spine and hip motion during forward bending in subjects with and without a history of low back pain. Spine 1996, 21, 71–78. [Google Scholar] [CrossRef]
- GB/T 17245-2004; Inertial Parameters of Adult Human Body. Standards Press of China: Beijing, China, 2004. Available online: https://std.samr.gov.cn/gb/search/gbDetailed?id=71F772D7CCA3D3A7E05397BE0A0AB82A (accessed on 10 May 2025).
- Chang, S.E.; Pesek, T.; Pote, T.R.; Hull, J.; Geissinger, J.; Simon, A.A.; Alemi, M.M.; Asbeck, A.T. Design and preliminary evaluation of a flexible exoskeleton to assist with lifting. Wearable Technol. 2020, 1, e10. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhang, H. Assessment and Evaluation in Rehabilitation; People’s Medical Publishing House: Beijing, China, 2012. [Google Scholar]
- Liu, Y.; Liu, Y.; Song, Q. The design of bionic back shelf for weight bearing exoskeleton. In Proceedings of the 2021 11th International Conference on Biomedical Engineering and Technology, Tokyo, Japan, 17–20 March 2021; pp. 173–180. [Google Scholar]
- Vacheron, J.; Poumarat, G.; Chandezon, R.; Vanneuville, G. Changes of contour of the spine caused by load carrying. Surg. Radiol. Anat. 1999, 21, 109–113. [Google Scholar] [CrossRef] [PubMed]
- van Sluijs, R.; Scholtysik, T.; Brunner, A.; Kuoni, L.; Bee, D.; Kos, M.; Bartenbach, V.; Lambercy, O. Design and evaluation of the OmniSuit: A passive occupational exoskeleton for back and shoulder support. Appl. Ergon. 2024, 120, 104332. [Google Scholar] [CrossRef]
- So, B.C.L.; Hua, C.; Chen, T.; Gao, Q.; Man, S.S. Biomechanical assessment of a passive back-support exoskeleton during repetitive lifting and carrying: Muscle activity, kinematics, and physical capacity. J. Saf. Res. 2022, 83, 210–222. [Google Scholar] [CrossRef]







| (°) | (rad) | (rad) | T (N) | (N) |
|---|---|---|---|---|
| 30° | 0.2239 | 0.4478 | 456.8564 | 531.2132 |
| 60° | 0.6261 | 0.6261 | 665.7924 | 695.3729 |
| 90° | 1.1762 | 0.5881 | 797.2055 | 809.2684 |
| Linkage Number | Length (mm) | Original Angle | Angle Range |
|---|---|---|---|
| 112 | 26 | 0 | |
| 70 | 80 | [−18.8, 51.4] | |
| 120 | 6 | [−4.2, 25.8] | |
| 130 | 30 | [−6.9, 29.1] | |
| 150 | 45 | [−10, 20] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Chen, Z.; Zhang, Y.; Zhang, Q.; Wang, X.; Tian, M. Development of a Passive Back-Support Exoskeleton Mimicking Human Spine Motion for Multi-Posture Assistance in Occupational Tasks. Biomimetics 2025, 10, 349. https://doi.org/10.3390/biomimetics10060349
Wu J, Chen Z, Zhang Y, Zhang Q, Wang X, Tian M. Development of a Passive Back-Support Exoskeleton Mimicking Human Spine Motion for Multi-Posture Assistance in Occupational Tasks. Biomimetics. 2025; 10(6):349. https://doi.org/10.3390/biomimetics10060349
Chicago/Turabian StyleWu, Jiyuan, Zhiquan Chen, Yinglong Zhang, Qi Zhang, Xingsong Wang, and Mengqian Tian. 2025. "Development of a Passive Back-Support Exoskeleton Mimicking Human Spine Motion for Multi-Posture Assistance in Occupational Tasks" Biomimetics 10, no. 6: 349. https://doi.org/10.3390/biomimetics10060349
APA StyleWu, J., Chen, Z., Zhang, Y., Zhang, Q., Wang, X., & Tian, M. (2025). Development of a Passive Back-Support Exoskeleton Mimicking Human Spine Motion for Multi-Posture Assistance in Occupational Tasks. Biomimetics, 10(6), 349. https://doi.org/10.3390/biomimetics10060349








