The Drosophila Connectome as a Computational Reservoir for Time-Series Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Connectome Extraction
- The unique IDs of the pre-synaptic and post-synaptic neurons;
- The Cleft score: a measure of how well-defined the synaptic cleft is;
- The Connection score: a measure of the size of the synapse;
- The probability of the synaptic neurotransmitter being Gamma-Aminobutyric Acid, Acetylcholine, Glutamate, Octopamine, Serotonin, or Dopamine.
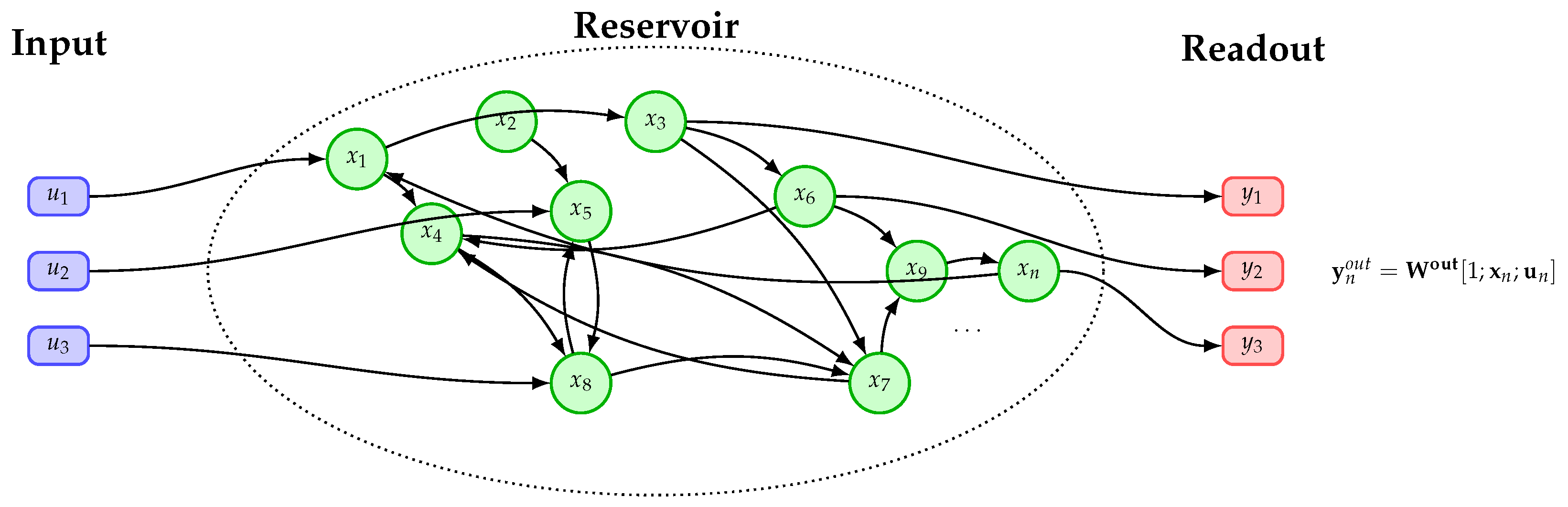
2.2. Echo-State Network
2.3. Time-Series Generation
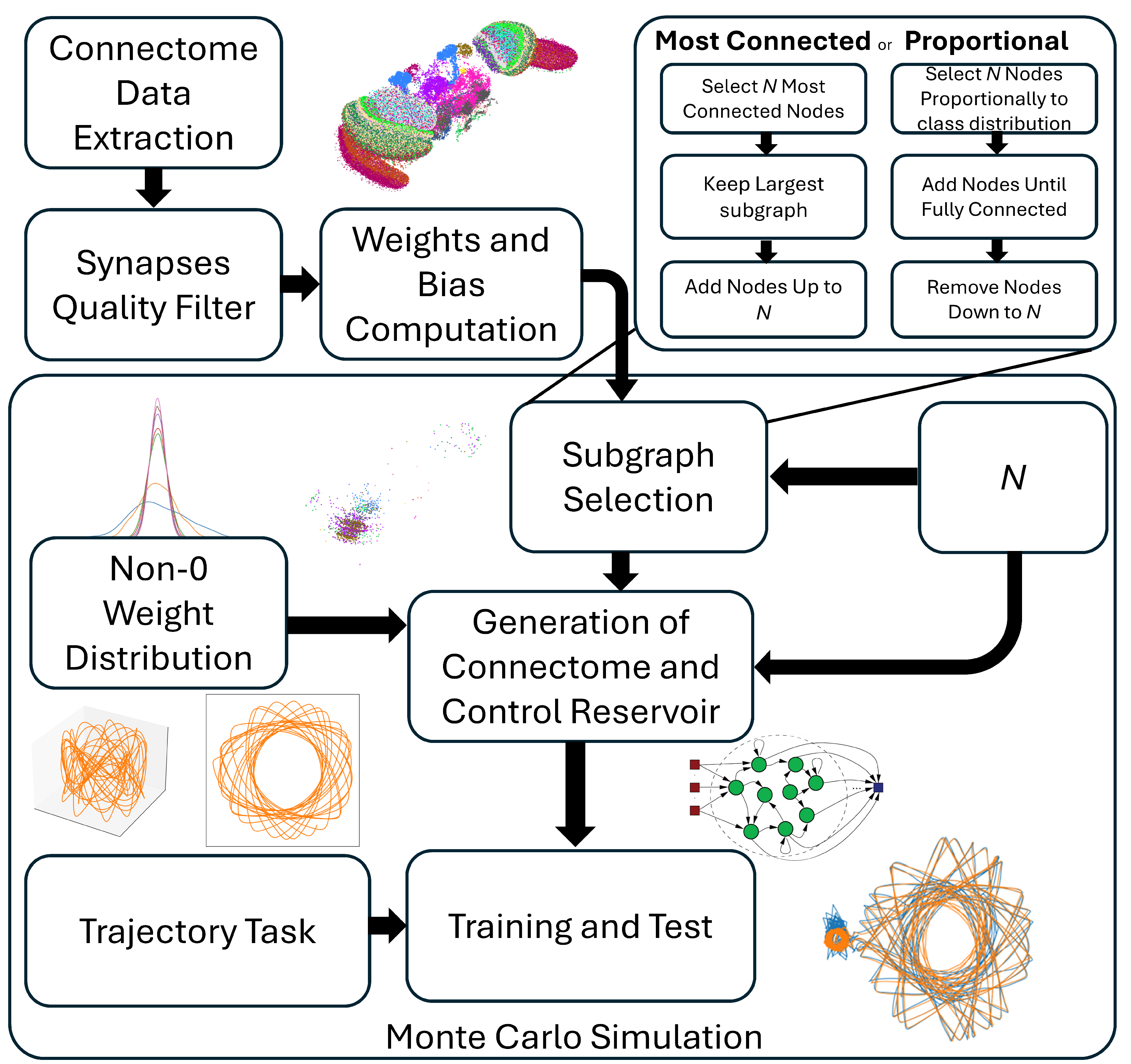
2.4. Experimental Protocol
3. Results
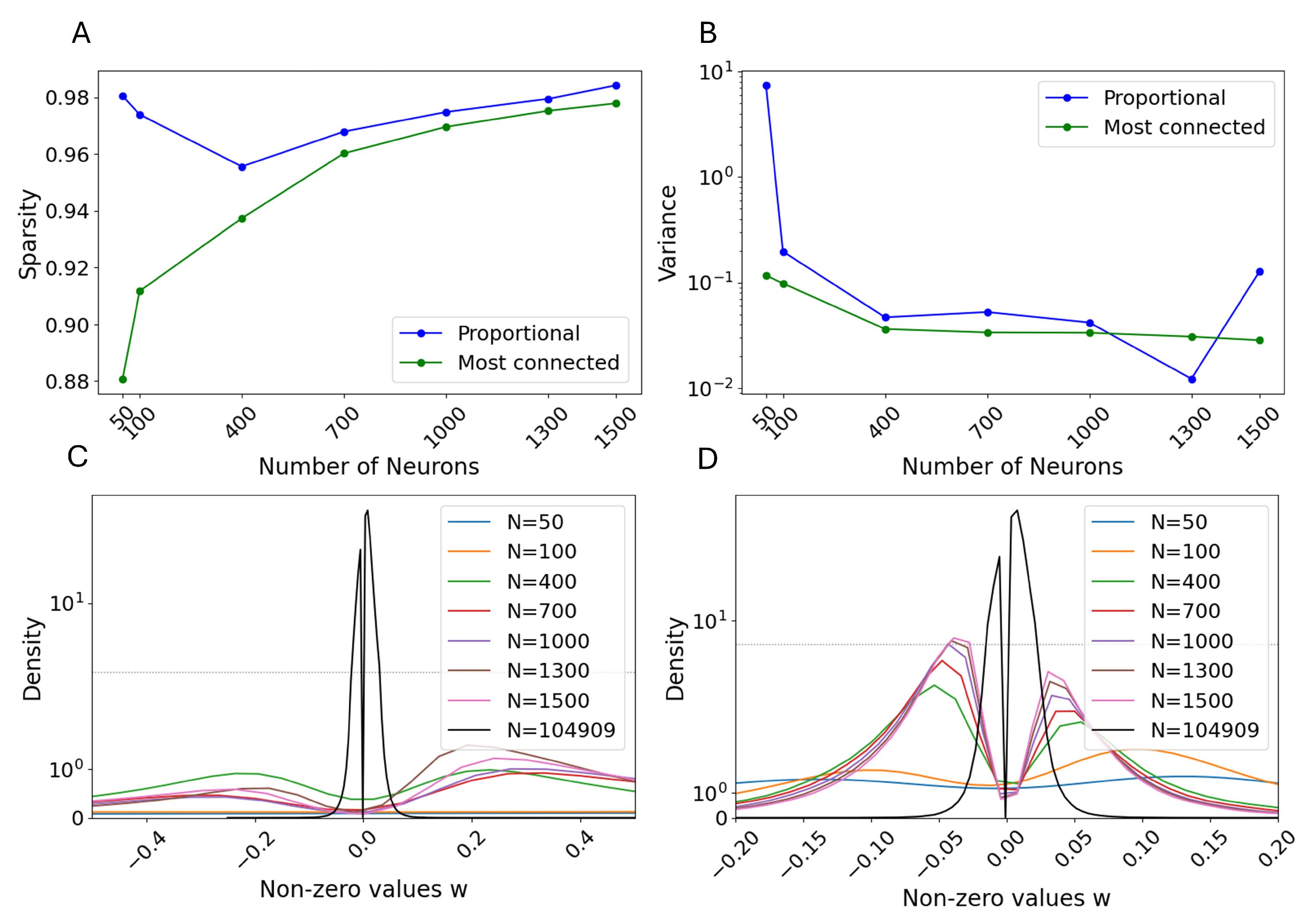
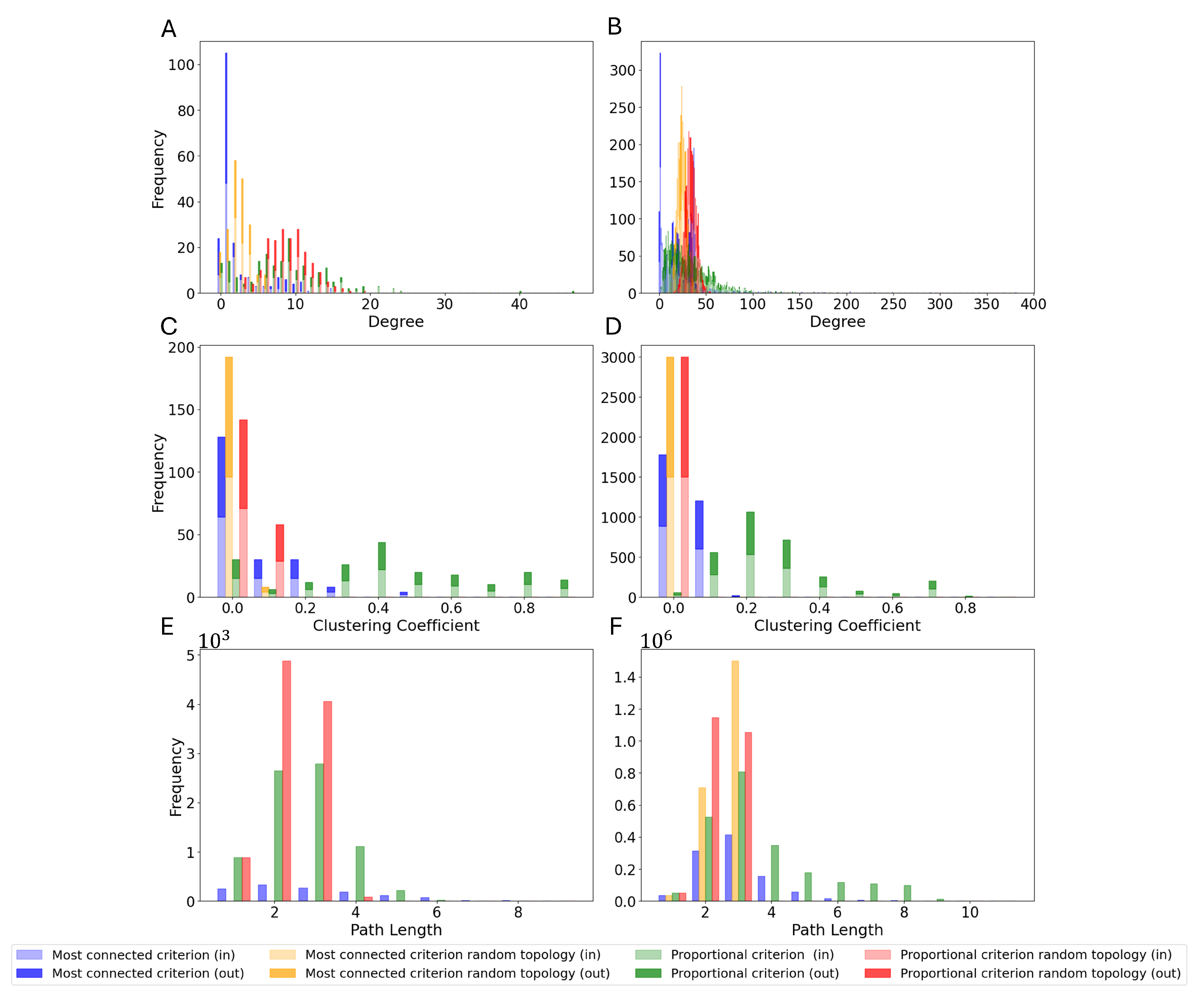
3.1. Selection Criteria
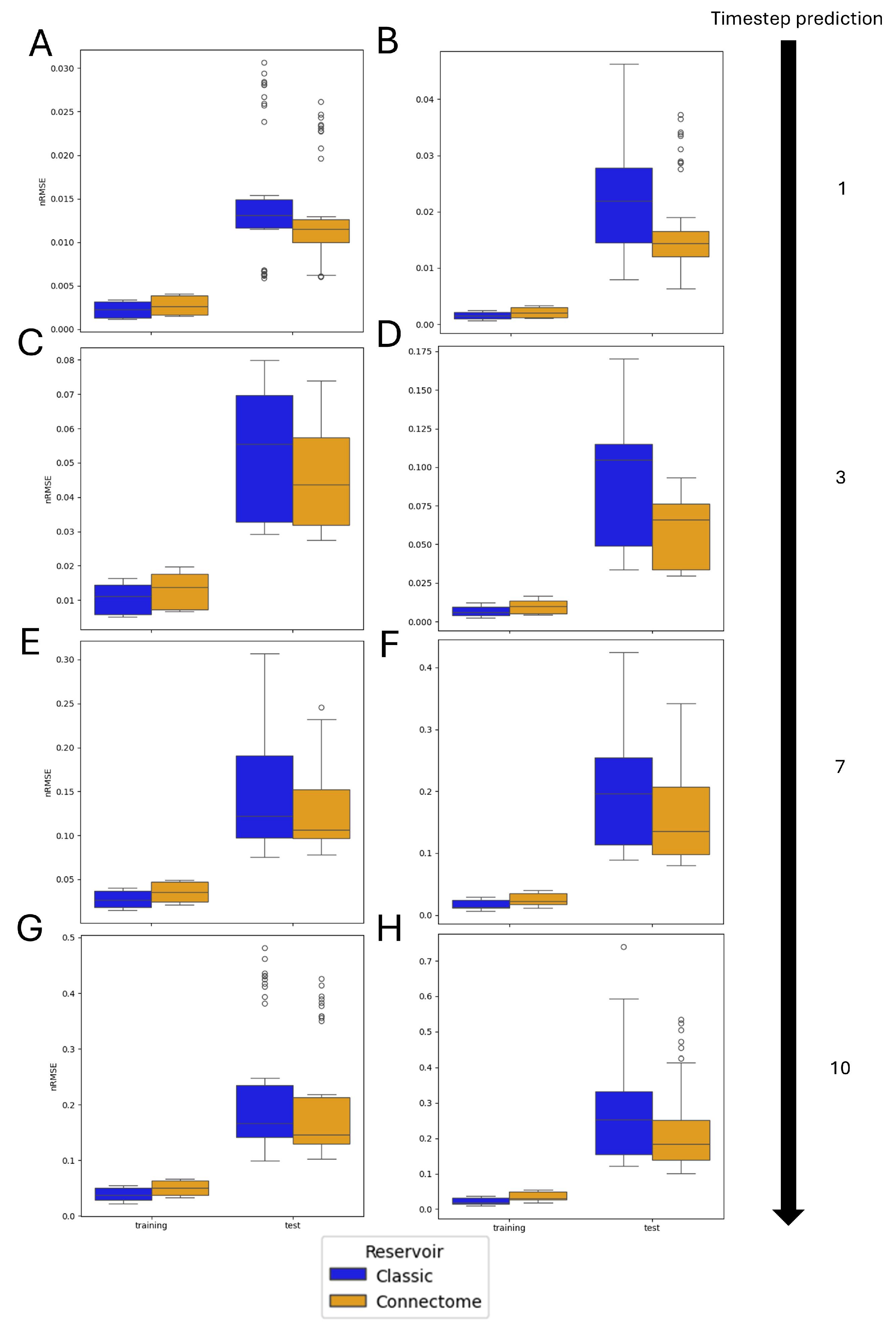
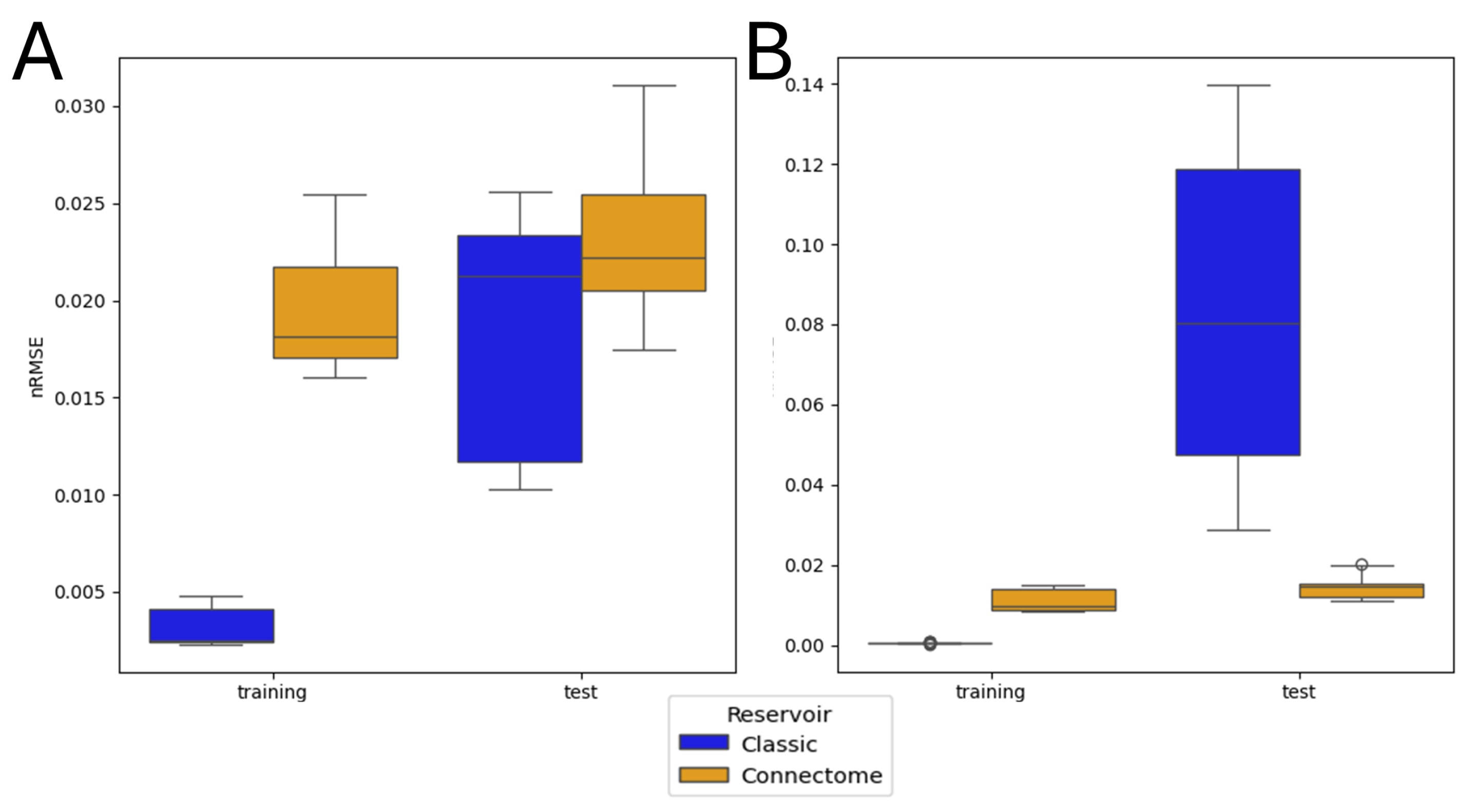
3.2. Single Simulation
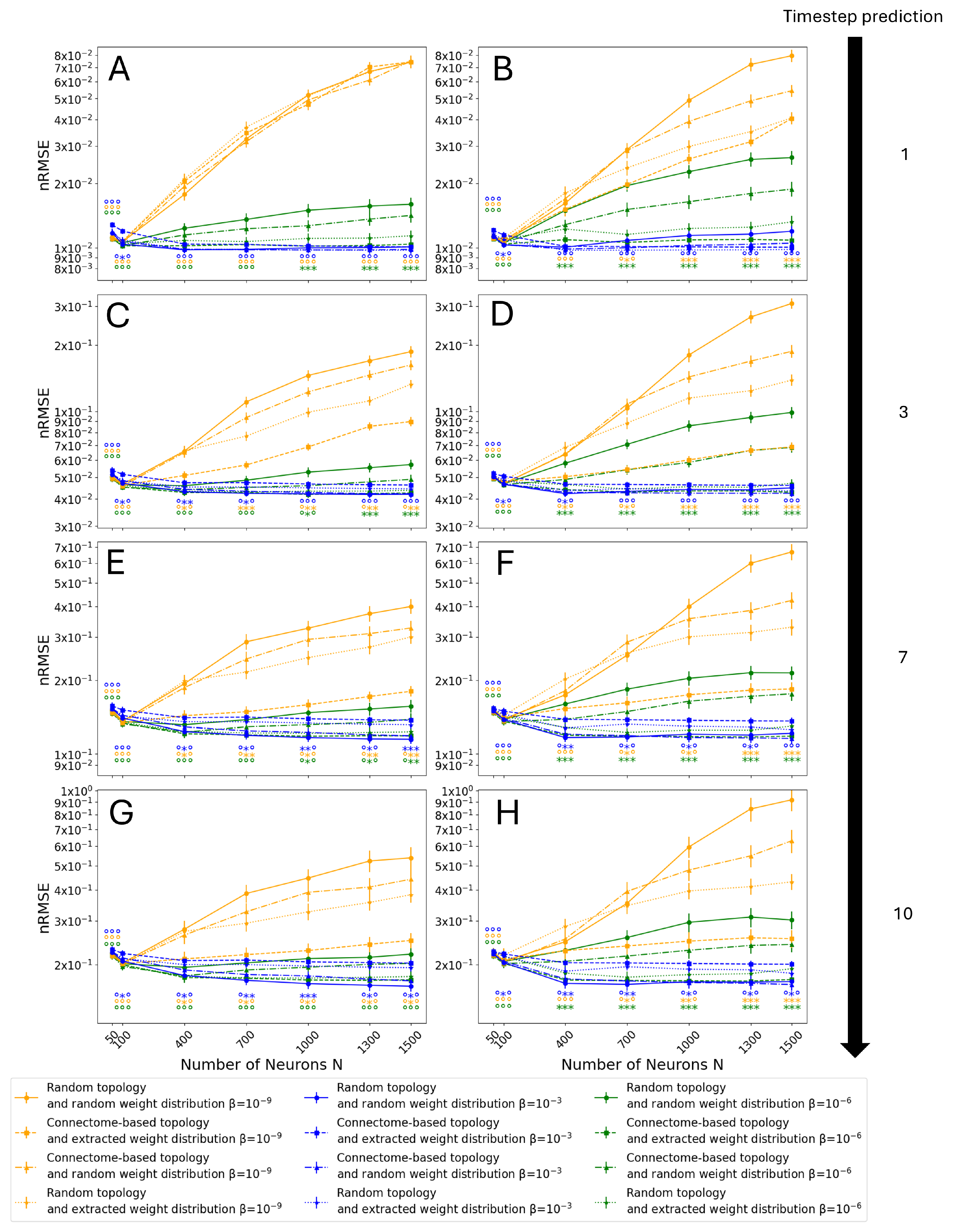
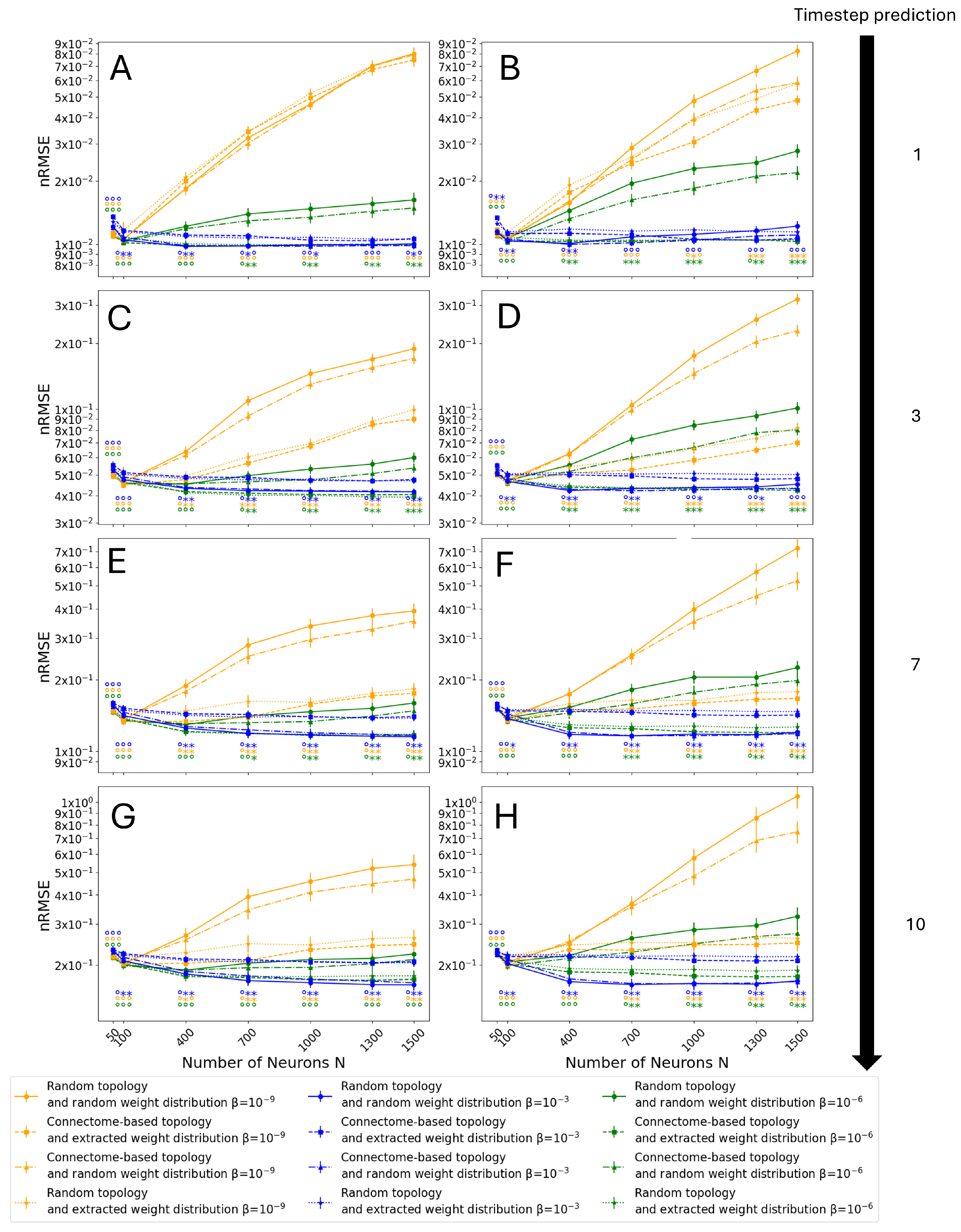
3.3. Monte Carlo Simulations
- Random topology and random weight distribution, which is the standard way to create ESNs, and represents the control group;
- Connectome-based topology and extracted weight distribution, utilizing all the data extracted from the Drosophila connectome;
- Connectome-based topology and random weight distribution to solely isolate the contribution of the topology of the connectome;
- Random topology and extracted weight distribution to solely isolate the contribution of the weight distribution of the connectome.
3.4. Entire Connectome Simulations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Narayanan, D.; Shoeybi, M.; Casper, J.; LeGresley, P.; Patwary, M.; Korthikanti, V.; Vainbrand, D.; Kashinkunti, P.; Bernauer, J.; Catanzaro, B.; et al. Efficient large-scale language model training on gpu clusters using megatron-lm. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MO, USA, 14–19 November 2021; pp. 1–15. [Google Scholar]
- Kaplan, J.; McCandlish, S.; Henighan, T.; Brown, T.B.; Chess, B.; Child, R.; Gray, S.; Radford, A.; Wu, J.; Amodei, D. Scaling laws for neural language models. arXiv 2020, arXiv:2001.08361. [Google Scholar]
- Henighan, T.; Kaplan, J.; Katz, M.; Chen, M.; Hesse, C.; Jackson, J.; Jun, H.; Brown, T.B.; Dhariwal, P.; Gray, S.; et al. Scaling laws for autoregressive generative modeling. arXiv 2020, arXiv:2010.14701. [Google Scholar]
- Lin, T.; Wang, Y.; Liu, X.; Qiu, X. A survey of transformers. AI Open 2022, 3, 111–132. [Google Scholar] [CrossRef]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in vision: A survey. ACM Comput. Surv. (CSUR) 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Shakya, A.K.; Pillai, G.; Chakrabarty, S. Reinforcement learning algorithms: A brief survey. Expert Syst. Appl. 2023, 231, 120495. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Nian, R.; Liu, J.; Huang, B. A review on reinforcement learning: Introduction and applications in industrial process control. Comput. Chem. Eng. 2020, 139, 106886. [Google Scholar] [CrossRef]
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks; GMD Forschungszentrum Informationstechnik: Sankt Augustin, Germany, 2001. [Google Scholar] [CrossRef]
- Maass, W.; Natschläger, T.; Markram, H. Real-Time Computing Without Stable States: A New Framework for Neural Computation Based on Perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef]
- Lukoševičius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Schrauwen, B.; Verstraeten, D.; Van Campenhout, J. An overview of reservoir computing: Theory, applications and implementations. In Proceedings of the 15th European Symposium on Artificial Neural Networks, Bruges, Belgium, 25–27 April 2007; pp. 471–482. [Google Scholar]
- Cressie, N.; Sainsbury-Dale, M.; Zammit-Mangion, A. Basis-function models in spatial statistics. Annu. Rev. Stat. Its Appl. 2022, 9, 373–400. [Google Scholar] [CrossRef]
- Abdi, G.; Mazur, T.; Szaciłowski, K. An organized view of reservoir computing: A perspective on theory and technology development. Jpn. J. Appl. Phys. 2024, 63, 050803. [Google Scholar] [CrossRef]
- Cucchi, M.; Abreu, S.; Ciccone, G.; Brunner, D.; Kleemann, H. Hands-on reservoir computing: A tutorial for practical implementation. Neuromorphic Comput. Eng. 2022, 2, 032002. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Scardapane, S.; Løkse, S.; Jenssen, R. Reservoir computing approaches for representation and classification of multivariate time series. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2169–2179. [Google Scholar] [CrossRef]
- Yan, M.; Huang, C.; Bienstman, P.; Tino, P.; Lin, W.; Sun, J. Emerging opportunities and challenges for the future of reservoir computing. Nat. Commun. 2024, 15, 2056. [Google Scholar] [CrossRef]
- Shahi, S.; Fenton, F.H.; Cherry, E.M. Prediction of chaotic time series using recurrent neural networks and reservoir computing techniques: A comparative study. Mach. Learn. Appl. 2022, 8, 100300. [Google Scholar] [CrossRef]
- Viehweg, J.; Worthmann, K.; Mäder, P. Parameterizing echo state networks for multi-step time series prediction. Neurocomputing 2023, 522, 214–228. [Google Scholar] [CrossRef]
- Hauser, H.; Fuechslin, R.M.; Nakajima, K. Morphological computation: The body as a computational resource. In Opinions and Outlooks on Morphological Computation; Self-published; University of Bristol: Bristol, UK, 2014; pp. 226–244. [Google Scholar]
- Nakajima, K.; Hauser, H.; Li, T.; Pfeifer, R. Information processing via physical soft body. Sci. Rep. 2015, 5, 10487. [Google Scholar] [CrossRef]
- Hülser, T.; Köster, F.; Jaurigue, L.; Lüdge, K. Role of delay-times in delay-based photonic reservoir computing. Opt. Mater. Express 2022, 12, 1214–1231. [Google Scholar] [CrossRef]
- Zhong, Y.; Tang, J.; Li, X.; Liang, X.; Liu, Z.; Li, Y.; Xi, Y.; Yao, P.; Hao, Z.; Gao, B.; et al. A memristor-based analogue reservoir computing system for real-time and power-efficient signal processing. Nat. Electron. 2022, 5, 672–681. [Google Scholar] [CrossRef]
- Chen, Z.; Renda, F.; Le Gall, A.; Mocellin, L.; Bernabei, M.; Dangel, T.; Ciuti, G.; Cianchetti, M.; Stefanini, C. Data-driven methods applied to soft robot modeling and control: A review. IEEE Trans. Autom. Sci. Eng. 2024, 22, 2241–2256. [Google Scholar] [CrossRef]
- Margin, D.A.; Ivanciu, I.A.; Dobrota, V. Deep reservoir computing using echo state networks and liquid state machine. In Proceedings of the 2022 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Sofia, Bulgaria, 6–9 June 2022; pp. 208–213. [Google Scholar]
- Soures, N.; Merkel, C.; Kudithipudi, D.; Thiem, C.; McDonald, N. Reservoir computing in embedded systems: Three variants of the reservoir algorithm. IEEE Consum. Electron. Mag. 2017, 6, 67–73. [Google Scholar] [CrossRef]
- Lukoševičius, M. A practical guide to applying echo state networks. In Neural Networks: Tricks of the Trade, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 659–686. [Google Scholar]
- Rodan, A.; Tino, P. Minimum complexity echo state network. IEEE Trans. Neural Netw. 2010, 22, 131–144. [Google Scholar] [CrossRef]
- Gallicchio, C.; Micheli, A. Deep echo state network (deepesn): A brief survey. arXiv 2017, arXiv:1712.04323. [Google Scholar]
- Liang, X.; Tang, J.; Zhong, Y.; Gao, B.; Qian, H.; Wu, H. Physical Reservoir Computing with Emerging Electronics. Nat. Electron. 2024, 7, 193–206. [Google Scholar] [CrossRef]
- Ismail, M.; Mahata, C.; Kang, M.; Kim, S. SnO2-Based Memory Device with Filamentary Switching Mechanism for Advanced Data Storage and Computing. Nanomaterials 2023, 13, 2603. [Google Scholar] [CrossRef]
- Wan, X.; Yuan, Q.; Sun, L.; Chen, K.; Khim, D.; Luo, Z. Reservoir Computing Enabled by Polymer Electrolyte-Gated MoS2 Transistors for Time-Series Processing. Polymers 2025, 17, 1178. [Google Scholar] [CrossRef]
- Prudnikov, N.; Malakhov, S.; Kulagin, V.; Emelyanov, A.; Chvalun, S.; Demin, V.; Erokhin, V. Multi-Terminal Nonwoven Stochastic Memristive Devices Based on Polyamide-6 and Polyaniline for Neuromorphic Computing. Biomimetics 2023, 8, 189. [Google Scholar] [CrossRef]
- Moroz, L.L. On the independent origins of complex brains and neurons. Brain Behav. Evol. 2009, 74, 177–190. [Google Scholar] [CrossRef]
- Marder, E.; Goaillard, J.M. Variability, compensation and homeostasis in neuron and network function. Nat. Rev. Neurosci. 2006, 7, 563–574. [Google Scholar] [CrossRef] [PubMed]
- Schöfmann, C.M.; Fasli, M.; Barros, M. Biologically Plausible Neural Networks for Reservoir Computing Solutions. Authorea Prepr. 2024. [Google Scholar]
- Armendarez, N.X.; Mohamed, A.S.; Dhungel, A.; Hossain, M.R.; Hasan, M.S.; Najem, J.S. Brain-inspired reservoir computing using memristors with tunable dynamics and short-term plasticity. ACS Appl. Mater. Interfaces 2024, 16, 6176–6188. [Google Scholar] [CrossRef]
- Sumi, T.; Yamamoto, H.; Katori, Y.; Ito, K.; Moriya, S.; Konno, T.; Sato, S.; Hirano-Iwata, A. Biological neurons act as generalization filters in reservoir computing. Proc. Natl. Acad. Sci. USA 2023, 120, e2217008120. [Google Scholar] [CrossRef]
- Liu, X.; Parhi, K.K. Reservoir computing using DNA oscillators. ACS Synth. Biol. 2022, 11, 780–787. [Google Scholar] [CrossRef] [PubMed]
- Damicelli, F.; Hilgetag, C.C.; Goulas, A. Brain connectivity meets reservoir computing. PLoS Comput. Biol. 2022, 18, e1010639. [Google Scholar] [CrossRef]
- Morra, J.; Daley, M. Using connectome features to constrain echo state networks. In Proceedings of the 2023 International Joint Conference on Neural Networks (IJCNN), Gold Coast, Australia, 18–23 June 2023; pp. 1–8. [Google Scholar]
- Kawai, Y.; Park, J.; Asada, M. A small-world topology enhances the echo state property and signal propagation in reservoir computing. Neural Netw. 2019, 112, 15–23. [Google Scholar] [CrossRef]
- Suárez, L.E.; Richards, B.A.; Lajoie, G.; Misic, B. Learning function from structure in neuromorphic networks. Nat. Mach. Intell. 2021, 3, 771–786. [Google Scholar] [CrossRef]
- Schlegel, P.; Yin, Y.; Bates, A.S.; Dorkenwald, S.; Eichler, K.; Brooks, P.; Han, D.S.; Gkantia, M.; Dos Santos, M.; Munnelly, E.J.; et al. Whole-brain annotation and multi-connectome cell typing of Drosophila. Nature 2024, 634, 139–152. [Google Scholar] [CrossRef]
- White, J.G.; Southgate, E.; Thomson, J.N.; Brenner, S. The structure of the nervous system of the nematode Caenorhabditis elegans. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1986, 314, 1–340. [Google Scholar]
- Bardozzo, F.; Terlizzi, A.; Simoncini, C.; Lió, P.; Tagliaferri, R. Elegans-AI: How the connectome of a living organism could model artificial neural networks. Neurocomputing 2024, 584, 127598. [Google Scholar] [CrossRef]
- Morra, J.; Daley, M. Imposing Connectome-Derived topology on an echo state network. In Proceedings of the 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18–23 July 2022; pp. 1–6. [Google Scholar]
- Wie, B. Space Vehicle Dynamics and Control; AIAA: Reston, VA, USA, 1998. [Google Scholar]
- Perraudin, N.; Srivastava, A.; Lucchi, A.; Kacprzak, T.; Hofmann, T.; Réfrégier, A. Cosmological N-body simulations: A challenge for scalable generative models. Comput. Astrophys. Cosmol. 2019, 6, 1–17. [Google Scholar] [CrossRef]
- Nudell, B.M.; Grinnell, A.D. Regulation of synaptic position, size, and strength in anuran skeletal muscle. J. Neurosci. 1983, 3, 161–176. [Google Scholar] [CrossRef]
- Holler, S.; Köstinger, G.; Martin, K.A.; Schuhknecht, G.F.; Stratford, K.J. Structure and function of a neocortical synapse. Nature 2021, 591, 111–116. [Google Scholar] [CrossRef] [PubMed]
- McDonald, G.C. Ridge regression. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 93–100. [Google Scholar] [CrossRef]
- Biscani, F.; Izzo, D. Revisiting high-order Taylor methods for astrodynamics and celestial mechanics. Mon. Not. R. Astron. Soc. 2021, 504, 2614–2628. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Djouadi, A.; Snorrason, O.; Garber, F.D. The quality of training sample estimates of the bhattacharyya coefficient. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 92–97. [Google Scholar] [CrossRef]
- Nishimura, R.; Fukushima, M. Comparing Connectivity-To-Reservoir Conversion Methods for Connectome-Based Reservoir Computing. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; pp. 1–8. [Google Scholar]
- Matsumoto, I.; Nobukawa, S.; Kurikawa, T.; Wagatsuma, N.; Sakemi, Y.; Kanamaru, T.; Sviridova, N.; Aihara, K. Optimal excitatory and inhibitory balance for high learning performance in spiking neural networks with long-tailed synaptic weight distributions. In Proceedings of the 2023 International Joint Conference on Neural Networks (IJCNN), Gold Coast, Australia, 18–23 June 2023; pp. 1–8. [Google Scholar]
- Blass, A.; Harary, F. Properties of almost all graphs and complexes. J. Graph Theory 1979, 3, 225–240. [Google Scholar] [CrossRef]
- Scheffer, L.K.; Xu, C.S.; Januszewski, M.; Lu, Z.; Takemura, S.-y.; Hayworth, K.J.; Huang, G.B.; Shinomiya, K.; Maitlin-Shepard, J.; Berg, S.; et al. A Connectome and Analysis of the Adult Drosophila Central Brain. eLife 2020, 9, e57443. [Google Scholar] [CrossRef]
- Loeffler, A.; Zhu, R.; Hochstetter, J.; Li, M.; Fu, K.; Diaz-Alvarez, A.; Nakayama, T.; Shine, J.M.; Kuncic, Z. Topological properties of neuromorphic nanowire networks. Front. Neurosci. 2020, 14, 184. [Google Scholar] [CrossRef] [PubMed]
- Diaz-Alvarez, A.; Higuchi, R.; Sanz-Leon, P.; Marcus, I.; Shingaya, Y.; Stieg, A.Z.; Gimzewski, J.K.; Kuncic, Z.; Nakayama, T. Emergent dynamics of neuromorphic nanowire networks. Sci. Rep. 2019, 9, 14920. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, L.; Caffo, B.S.; Gracias, D.H.; Huang, Q.; Morales Pantoja, I.E.; Tang, B.; Zack, D.J.; Berlinicke, C.A.; Boyd, J.L.; Harris, T.D.; et al. Organoid intelligence (OI): The new frontier in biocomputing and intelligence-in-a-dish. Front. Sci. 2023, 1, 1017235. [Google Scholar] [CrossRef]

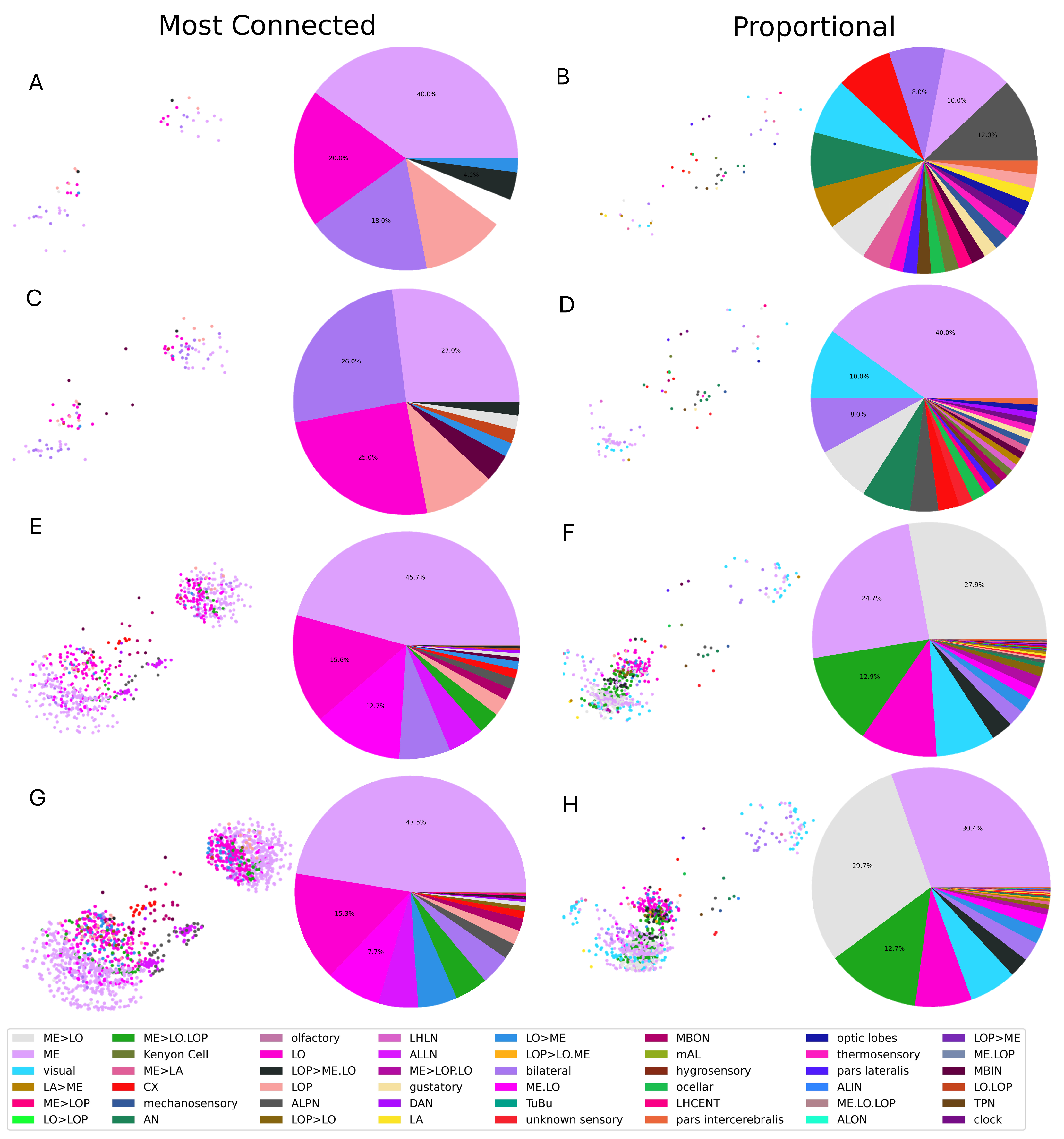


| Neuron Class | Full Name | Function | Neuron Class | Full Name | Function |
|---|---|---|---|---|---|
| CX | Central Complex | Motor control, navigation | Kenyon Cell | Kenyon Cell | Learning and memory |
| ALPN | Antennal Lobe Projection Neuron | Olfactory signal relay | LO | Lamina Output Neuron | Early visual processing |
| bilateral | Bilateral Neuron | Cross-hemisphere connections | ME | Medulla Neuron | Visual processing |
| ME>LOP | Medulla to Lobula Plate | Motion detection | ME>LO | Medulla to Lobula | Higher-order vision |
| LO>LOP | Lobula to Lobula Plate | Object motion detection | ME>LA | Medulla to Lamina | Visual contrast enhancement |
| LA>ME | Lamina to Medulla | Photoreceptor signal relay | ME>LO.LOP | Medulla to Lobula and Lobula Plate | Motion and feature integration |
| ALLN | Allatotropinergic Neuron | Hormonal regulation | olfactory | Olfactory Neuron | Detects airborne stimuli |
| DAN | Dopaminergic Neuron | Learning, reward, motivation | MBON | Mushroom Body Output Neuron | Readout of learned behaviors |
| ME>LOP.LO | Medulla to Lobula Plate and Lobula | Visual integration | LOP>ME.LO | Lobula Plate to Medulla and Lobula | Motion-sensitive feedback |
| LOP | Lobula Plate Neuron | Optic flow detection | LOP>LO.ME | Lobula Plate to Lobula and Medulla | Visual-motor integration |
| LOP>LO | Lobula Plate to Lobula | Motion-sensitive projection | LA | Lamina Neuron | First visual synaptic layer |
| AN | Antennal Neuron | Mechanosensory and olfactory processing | visual | Visual Neuron | General vision processing |
| TuBu | Tubercle Bulb Neuron | Connects brain to vision | LHCENT | Lateral Horn Centroid | Odor valence processing |
| ALIN | Antennal Lobe Interneuron | Olfactory modulation | mAL | Mushroom Body-associated Antennal Lobe Neuron | Olfactory-learning link |
| LHLN | Lateral Horn Local Neuron | Innate odor-driven behavior | ME.LO | Medulla and Lobula Neuron | General vision processing |
| mechanosensory | Mechanosensory Neuron | Touch, vibration detection | ME.LO.LOP | Medulla, Lobula, and Lobula Plate Neuron | Multi-layer vision processing |
| LO>ME | Lobula to Medulla | Visual feedback | hygrosensory | Hygrosensory Neuron | Detects humidity |
| pars lateralis | Pars Lateralis Neuron | Hormonal/circadian regulation | unknown sensory | Unknown Sensory Neuron | Uncharacterized sensory function |
| LO.LOP | Lobula and Lobula Plate Neuron | Motion and space awareness | ocellar | Ocellar Neuron | Light intensity detection |
| optic lobes | Optic Lobe Neuron | General vision processing | pars intercerebralis | Pars Intercerebralis Neuron | Hormonal regulation |
| ME.LOP | Medulla and Lobula Plate Neuron | Motion and edge detection | gustatory | Gustatory Neuron | Taste processing |
| ALON | Antennal Lobe Olfactory Neuron | Olfactory cue processing | MBIN | Mushroom Body Input Neuron | Learning circuit modulation |
| thermosensory | Thermosensory Neuron | Temperature sensing | clock | Clock Neuron | Circadian rhythm control |
| LOP>ME | Lobula Plate to Medulla | Motion-sensitive feedback | TPN | Transmedullary Projection Neuron | Optic lobes to brain |
| Type | Neuron Classes |
|---|---|
| Input | olfactory, visual, mechanosensory, hygrosensory, thermosensory, gustatory, ocellar, unknown sensory |
| Intermediate | CX, ALPN, LO, bilateral, ME, ME>LOP, ME>LO, LO>LOP, ME>LA, LA>ME, ME>LO.LOP, ALLN, LOP>ME.LO, LOP>LO.ME, LA, AN, ALIN, mAL, LHLN, ME.LO, ME.LO.LOP, LO>ME, optic lobes, ME.LOP, TPN |
| Output | MBON, DAN, LHCENT, clock, pars intercerebralis, pars lateralis, Kenyon Cell, ALON, LOP>ME, LOP>LO.ME, LOP>LO, LOP, TuBu |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costi, L.; Hadjiivanov, A.; Dold, D.; Hale, Z.F.; Izzo, D. The Drosophila Connectome as a Computational Reservoir for Time-Series Prediction. Biomimetics 2025, 10, 341. https://doi.org/10.3390/biomimetics10050341
Costi L, Hadjiivanov A, Dold D, Hale ZF, Izzo D. The Drosophila Connectome as a Computational Reservoir for Time-Series Prediction. Biomimetics. 2025; 10(5):341. https://doi.org/10.3390/biomimetics10050341
Chicago/Turabian StyleCosti, Leone, Alexander Hadjiivanov, Dominik Dold, Zachary F. Hale, and Dario Izzo. 2025. "The Drosophila Connectome as a Computational Reservoir for Time-Series Prediction" Biomimetics 10, no. 5: 341. https://doi.org/10.3390/biomimetics10050341
APA StyleCosti, L., Hadjiivanov, A., Dold, D., Hale, Z. F., & Izzo, D. (2025). The Drosophila Connectome as a Computational Reservoir for Time-Series Prediction. Biomimetics, 10(5), 341. https://doi.org/10.3390/biomimetics10050341








