Routing and Scheduling in Time-Sensitive Networking by Evolutionary Algorithms
Abstract
1. Introduction
- (1)
- We proposed an innovative approach for route selection in TSN using a genetic algorithm for each flow. A fitness function that incorporates multiple factors including flow combinability, route length, and network load is formulated to identify routes that enhance efficient implementation of scheduling. To reduce the search space of the GA, we developed a method to eliminate infeasible routes by leveraging flow combinability analysis.
- (2)
- An efficient method for finding a feasible scheduling solution for TSN based on differential evolution algorithm was developed. We proposed a straightforward and effective encoding scheme designed to substantially reduce the search space of the algorithm. Furthermore, we employ the differential evolution algorithm to tackle the feasible scheduling problem in TSN utilizing the number of constraints that must be satisfied by a feasible schedule as our objective function.
2. Related Work
2.1. Routing
2.2. Joint Routing and Scheduling
2.3. Scheduling
3. Routing Based on Flow Combinability
3.1. Flow Grouping Method Utilizing the Greatest Common Divisor
| Algorithm 1. Flow Grouping Based on Greatest Common Divisor |
| Input: flow set Output: flow grouping 1 Sort the flows in descending order based on their periods, denoted as 2 3 while there exist ungrouped flows within do 4 for do 5 if has not been grouped then 6 break 7 end if 8 end for 9 10 for do 11 if has not been grouped and then 12 13 end if 14 end for 15 16 end while 17 return |
3.2. Route Selection Based on Genetic Algorithm
3.2.1. Individual Coding
3.2.2. Fitness Function
3.2.3. Feasible Path for Flow
| Algorithm 2 Optional Path Set Construction |
| Input: A simple path set of , flow , a link set of Output: Optional path for flow 1 , 2 for do 3 4 for do 5 6 7 if in then 8 9 end if 10 end for 11 12 end for 13 for do 14 if then 15 16 end if 17 end for 18 return |
| Algorithm 3 Feasible Path Set Construction |
| Input: , Output: Feasible path for each flow within the -th group 1 2 if k = 1 then 3 for do 4 5 6 end for 7 return 8 end if 9 for do 10 11 for do 12 13 14 if then 15 16 for do 17 if not in then 18 19 end if 20 end for 21 end if 22 end for 23 24 25 end for 26 return |
3.2.4. Route Selection Algorithm
| Algorithm 4 Route selection based on genetic algorithm |
| Input: the simple path for all flows (), flows set (), flows grouping () Output: Route for each flow 1 2 for do 3 4 Initialize population size, crossover probability, mutation probability 5 Initialize the population and calculate the optimal individual 6 for do 7 Implement selection, crossover and mutation operations 8 Update the optimal individual 9 end for 10 Update based on the optimal individual 11 end for 12 return |
4. Scheduling for TSN Based on Differential Evolution Algorithm
4.1. Scheduling Problem and Modeling
4.2. Gene Coding
| Algorithm 5 Computing the transmission time of each frame at every node along its path |
| Input: The transmission time of the first frame Output: The transmission time of each frame at every node along its path 1 2 for do 3 .append() 4 5 while do 6 Y.append() 7 8 end while 9 end for 10 return |
4.3. The Fitness Function and Its Calculation
| Algorithm 6 Deriving Link Information |
| Input: and its path Output: Link information 1 , 2 for do 3 4 for do 5 6 7 end for 8 end for 9 return |
| Algorithm 7 Finding Shared Link |
| Input: Link information Output: The set of shared link 1 for do 2 3 4 5 6 while do 7 8 9 if and then 10 11 end if 12 j = j + 1 13 end while 14 if then 15 16 end if 17 end for 18 return |
| Algorithm 8 Computing the fitness of individual |
| Input: Individual Output: The fitness of individual 1 2 Computing the transmission time of each frame by Algorithm 5 and store it in 3 for do 4 if then else end if 5 , 6 while do 7 if then end if 8 9 end while 10 if then end if 11 if then 12 13 end if 14 end for 15 for in do 16 for in do 17 for in do 18 if then 19 20 21 for do 22 for do 23 if then 24 25 end if 26 end for 27 end for 28 end if 29 end for 30 end for 31 end for 32 return |
4.4. Optimization Objective of Differential Evolution Algorithm
4.5. Differential Evolution Algorithm for TSN Scheduling
4.5.1. Scheduling Coding
4.5.2. Operators of Differential Evolution Algorithm
5. Simulation Experiment
5.1. TSN with Each Flow Has a Unique Shortest Path and All Flows Can Be Combined
5.1.1. Experiment 1
5.1.2. Experiment 2
5.1.3. Experiment 3
5.2. TSN with Each Flow Has a Unique Shortest Path but Not All Flows Can Be Combined
5.3. TSN with Some Flows Have Multiple Shortest Paths and Not All Flows Can Be Combined
5.4. Runtime
5.5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TSN | Time-Sensitive Networking |
| QoS | Quality of Service |
| SMT | Satisfiability Modulo Theories |
| ILP | Integer Linear Program |
| GA | Genetic Algorithm |
| DE | Differential Evolution |
| RTRS | Real-Time Routing Scheduler |
| WCED | Worst-Case End-to-End Delay |
| JRS | Joint Routing and Scheduling |
| DoC | Degree of Conflict |
| EPIC | Efficient Probing Instructed by Conflicts |
| MGA | Mixed Initial Population Genetic Algorithm |
| GCD | Greatest Common Divisor |
| SOW | Sum of Weights |
| LCM | Least Common Multiple |
| SP | Shortest Path |
| DA | Doc Aware |
Appendix A
Appendix A.1. Proof of Theorem 1
Appendix A.2. Proof of Theorem 2
Appendix A.3. Proof of Theorem 3
Appendix A.4. Proof of Theorem 4
Appendix A.5. Proof of Theorem 5
Appendix A.6. Proof of Theorem 6
References
- Akram, B.O.; Noordin, N.K.; Hashim, F.; Rasid, M.A.F.; Salman, M.I.; Abdulghani, A.M. Enhancing reliability of time-triggered traffic in joint scheduling and routing optimization within time-sensitive networks. IEEE Access 2024, 12, 78379–78396. [Google Scholar] [CrossRef]
- Messenger, J.L. Time-sensitive networking: An introduction. IEEE Commun. Stand. Mag. 2018, 2, 29–33. [Google Scholar] [CrossRef]
- Chen, Z.; Lu, Y.; Wang, H.; Qin, J.; Wang, M.; Pan, W. Dynamic stream partitioning for time-triggered traffic in Time-Sensitive Networking. Comput. Netw. 2024, 248, 110492. [Google Scholar] [CrossRef]
- Zhou, Y.; Samii, S.; Eles, P.; Peng, Z. Time-triggered scheduling for time-sensitive networking with preemption. In Proceedings of the 2022 27th Asia and South Pacific Design Automation Conference (ASP-DAC), Taipei, China, 17–20 January 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Xue, C.; Zhang, T.; Zhou, Y.; Nixon, M.; Loveless, A.; Han, S. Real-time scheduling for time-sensitive networking: A systematic review and experimental study. arXiv 2023, arXiv:2305.16772. [Google Scholar] [CrossRef]
- Stüber, T.; Osswald, L.; Lindner, S.; Menth, M. A survey of scheduling algorithms for the time-aware shaper in time-sensitive networking (TSN). IEEE Access 2023, 11, 61192–61233. [Google Scholar] [CrossRef]
- Alnajim, A.; Salehi, S.; Shen, C.-C. Incremental path-selection and scheduling for time-sensitive networks. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Big Island, HI, USA, 9–13 December 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Chang, S.-H.; Chen, H.; Cheng, B.-C. Time-predictable routing algorithm for Time-Sensitive Networking: Schedulable guarantee of Time-Triggered streams. Comput. Commun. 2021, 172, 183–195. [Google Scholar] [CrossRef]
- Ojewale, M.A.; Yomsi, P.M. Routing heuristics for load-balanced transmission in TSN-based networks. ACM Sigbed Rev. 2020, 16, 20–25. [Google Scholar] [CrossRef]
- Huang, K.; Wu, J.; Jiang, X.; Xiong, D.; Huang, K.; Yao, H.; Xu, W.; Peng, Y.; Liu, Z. A period-aware routing method for IEEE 802.1 Qbv TSN networks. Electronics 2020, 10, 58. [Google Scholar] [CrossRef]
- Gavrilut, V.; Zhao, L.; Raagaard, M.L.; Pop, P. AVB-aware routing and scheduling of time-triggered traffic for TSN. IEEE Access 2018, 6, 75229–75243. [Google Scholar] [CrossRef]
- Huang, J.-Y.; Hsu, M.-H.; Shen, C.-A. A novel routing algorithm for the acceleration of flow scheduling in time-sensitive networks. Sensors 2020, 20, 6400. [Google Scholar] [CrossRef]
- Li, Y.; Yin, Z.; Ma, Y.; Xu, F.; Yu, H.; Han, G.; Bi, Y. Heuristic routing algorithms for time-sensitive networks in smart factories. Sensors 2022, 22, 4153. [Google Scholar] [CrossRef] [PubMed]
- Pahlevan, M.; Tabassam, N.; Obermaisser, R. Heuristic list scheduler for time triggered traffic in time sensitive networks. ACM Sigbed Rev. 2019, 16, 15–20. [Google Scholar] [CrossRef]
- Huang, K.; Wan, X.; Wang, K.; Jiang, X.; Chen, J.; Deng, Q.; Xu, W.; Peng, Y.; Liu, Z. Reliability-aware multipath routing of time-triggered traffic in time-sensitive networks. Electronics 2021, 10, 125. [Google Scholar] [CrossRef]
- Nayak, N.G.; Dürr, F.; Rothermel, K. Routing algorithms for IEEE802. 1Qbv networks. ACM Sigbed Rev. 2018, 15, 13–18. [Google Scholar] [CrossRef]
- Li, J.; Wei, M.; Huo, C.; Kim, K. A Time-Sensitive Networking Traffic Scheduling Method Based on Q-Learning Routing Optimization. In Proceedings of the 2024 18th International Conference on Ubiquitous Information Management and Communication (IMCOM), Kuala Lumpur, Malaysia, 3–5 January 2024; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar] [CrossRef]
- Min, J.; Kim, Y.; Kim, M.; Paek, J.; Govindan, R. Reinforcement learning based routing for time-aware shaper scheduling in time-sensitive networks. Comput. Netw. 2023, 235, 109983. [Google Scholar] [CrossRef]
- Schweissguth, E.; Timmermann, D.; Parzyjegla, H.; Danielis, P.; Muhl, G. ILP-based routing and scheduling of multicast realtime traffic in time-sensitive networks. In Proceedings of the 2020 IEEE 26th International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA), Gangnueng, Republic of Korea, 19–21 August 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Nie, H.; Li, S.; Liu, Y. An enhanced routing and scheduling mechanism for time-triggered traffic with large period differences in time-sensitive networking. Appl. Sci. 2022, 12, 4448. [Google Scholar] [CrossRef]
- Pang, Z.; Huang, X.; Li, Z.; Zhang, S.; Xu, Y.; Wan, H.; Zhao, X. Flow scheduling for conflict-free network updates in time-sensitive software-defined networks. IEEE Trans. Ind. Inform. 2020, 17, 1668–1678. [Google Scholar] [CrossRef]
- Yu, Q.; Gu, M. Adaptive group routing and scheduling in multicast time-sensitive networks. IEEE Access 2020, 8, 37855–37865. [Google Scholar] [CrossRef]
- Vlk, M.; Hanzálek, Z.; Tang, S. Constraint programming approaches to joint routing and scheduling in time-sensitive networks. Comput. Ind. Eng. 2021, 157, 107317. [Google Scholar] [CrossRef]
- Wang, X.; Yao, H.; Mai, T.; Xiong, Z.; Wang, F.; Liu, Y. Joint routing and scheduling with cyclic queuing and forwarding for time-sensitive networks. IEEE Trans. Veh. Technol. 2022, 72, 3793–3804. [Google Scholar] [CrossRef]
- Yu, H.; Taleb, T.; Zhang, J. Deep reinforcement learning-based deterministic routing and scheduling for mixed-criticality flows. IEEE Trans. Ind. Inform. 2022, 19, 8806–8816. [Google Scholar] [CrossRef]
- Reusch, N.; Craciunas, S.S.; Pop, P. Dependability-aware routing and scheduling for Time-Sensitive Networking. IET Cyber-Phys. Syst. Theory Appl. 2022, 7, 124–146. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, Y.; Xue, Y.; Chen, J.; Du, A.; Wang, X. Joint scheduling and routing for end-to-end deterministic transmission in TSN. Peer–Peer Netw. Appl. 2025, 18, 87. [Google Scholar] [CrossRef]
- Pahlevan, M.; Obermaisser, R. Genetic algorithm for scheduling time-triggered traffic in time-sensitive networks. In Proceedings of the 2018 IEEE 23rd International Conference on Emerging Technologies and Factory Automation (ETFA), Torino, Italy, 4–7 September 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Dürr, F.; Nayak, N.G. No-wait packet scheduling for IEEE time-sensitive networks (TSN). In Proceedings of the 24th International Conference on Real-Time Networks and Systems, Brest, France, 19–21 October 2016. [Google Scholar] [CrossRef]
- Craciunas, S.S.; Oliver, R.S.; Chmelík, M.; Steiner, W. Scheduling real-time communication in IEEE 802.1 Qbv time sensitive networks. In Proceedings of the 24th International Conference on Real-Time Networks and Systems, Brest, France, 19–21 October 2016. [Google Scholar] [CrossRef]
- Pop, P.; Raagaard, M.L.; Craciunas, S.S.; Steiner, W. Design optimisation of cyber-physical distributed systems using IEEE time-sensitive networks. IET Cyber-Phys. Syst. Theory Appl. 2016, 1, 86–94. [Google Scholar] [CrossRef]
- Atallah, A.A.; Hamad, G.B.; Mohamed, O.A. Routing and scheduling of time-triggered traffic in time-sensitive networks. IEEE Trans. Ind. Inform. 2019, 16, 4525–4534. [Google Scholar] [CrossRef]
- Berisa, A.; Zhao, L.; Craciunas, S.S.; Ashjaei, M.; Mubeen, S.; Daneshtalab, M.; Sjödin, M. AVB-aware routing and scheduling for critical traffic in time-sensitive networks with preemption. In Proceedings of the 30th International Conference on Real-Time Networks and Systems, Paris, France, 6–7 June 2022. [Google Scholar] [CrossRef]
- Vlk, M.; Brejchová, K.; Hanzálek, Z.; Tang, S. Large-scale periodic scheduling in time-sensitive networks. Comput. Oper. Res. 2022, 137, 105512. [Google Scholar] [CrossRef]
- Yao, M.; Liu, J.; Du, J.; Yan, D.; Zhang, Y.; Liu, W.; So, A.M.-C. A unified flow scheduling method for time sensitive networks. Comput. Netw. 2023, 233, 109847. [Google Scholar] [CrossRef]
- Gong, W.; Wang, Y.; Cai, Z.; Wang, L. Finding multiple roots of nonlinear equation systems via a repulsion-based adaptive differential evolution. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 1499–1513. [Google Scholar] [CrossRef]
- Hellmanns, D.; Haug, L.; Hildebrand, M.; Dürr, F.; Kehrer, S.; Hummen, R. How to optimize joint routing and scheduling models for TSN using integer linear programming. In Proceedings of the 29th International Conference on Real-Time Networks and Systems, Nantes, France, 7–9 April 2021. [Google Scholar] [CrossRef]


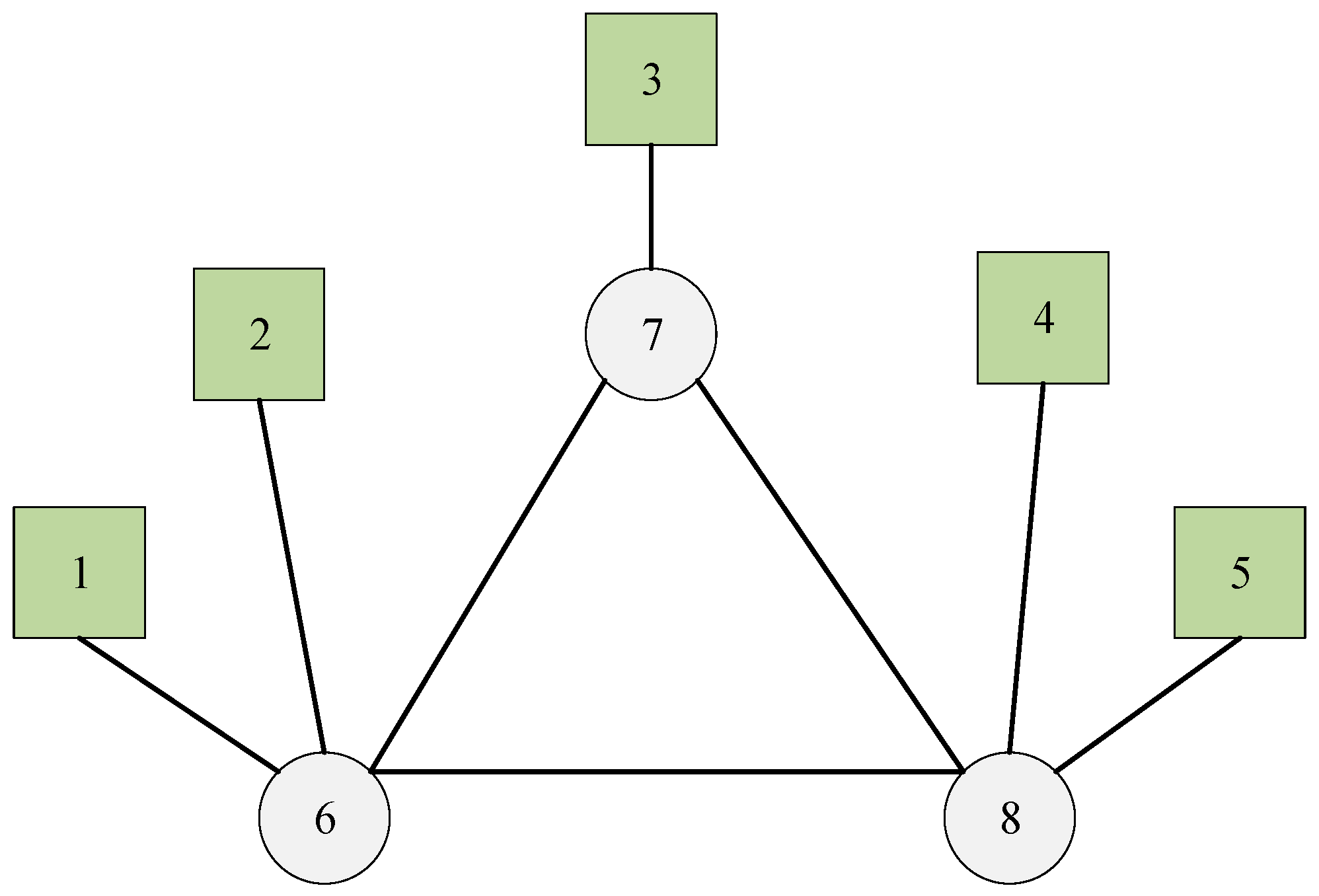
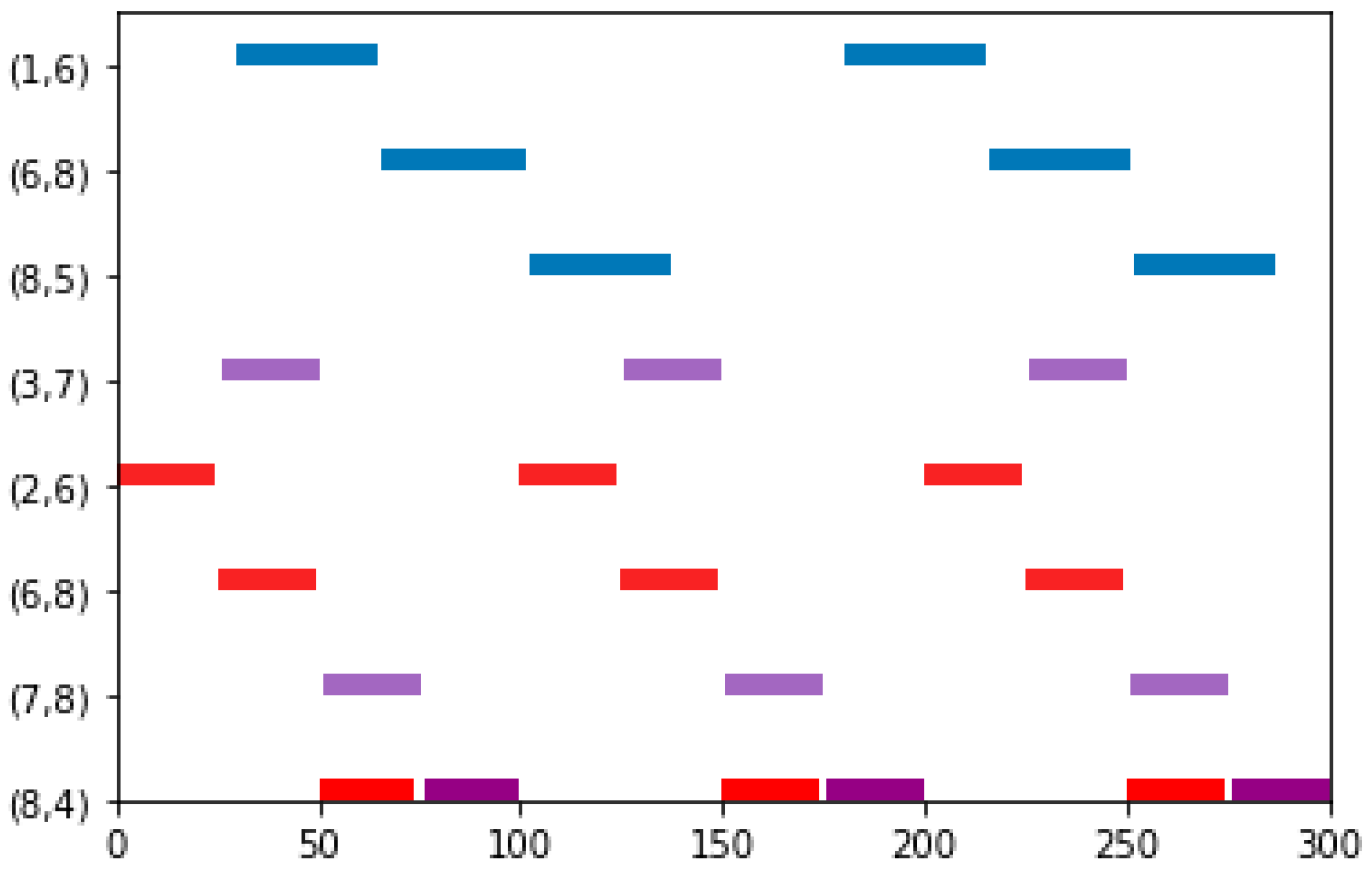
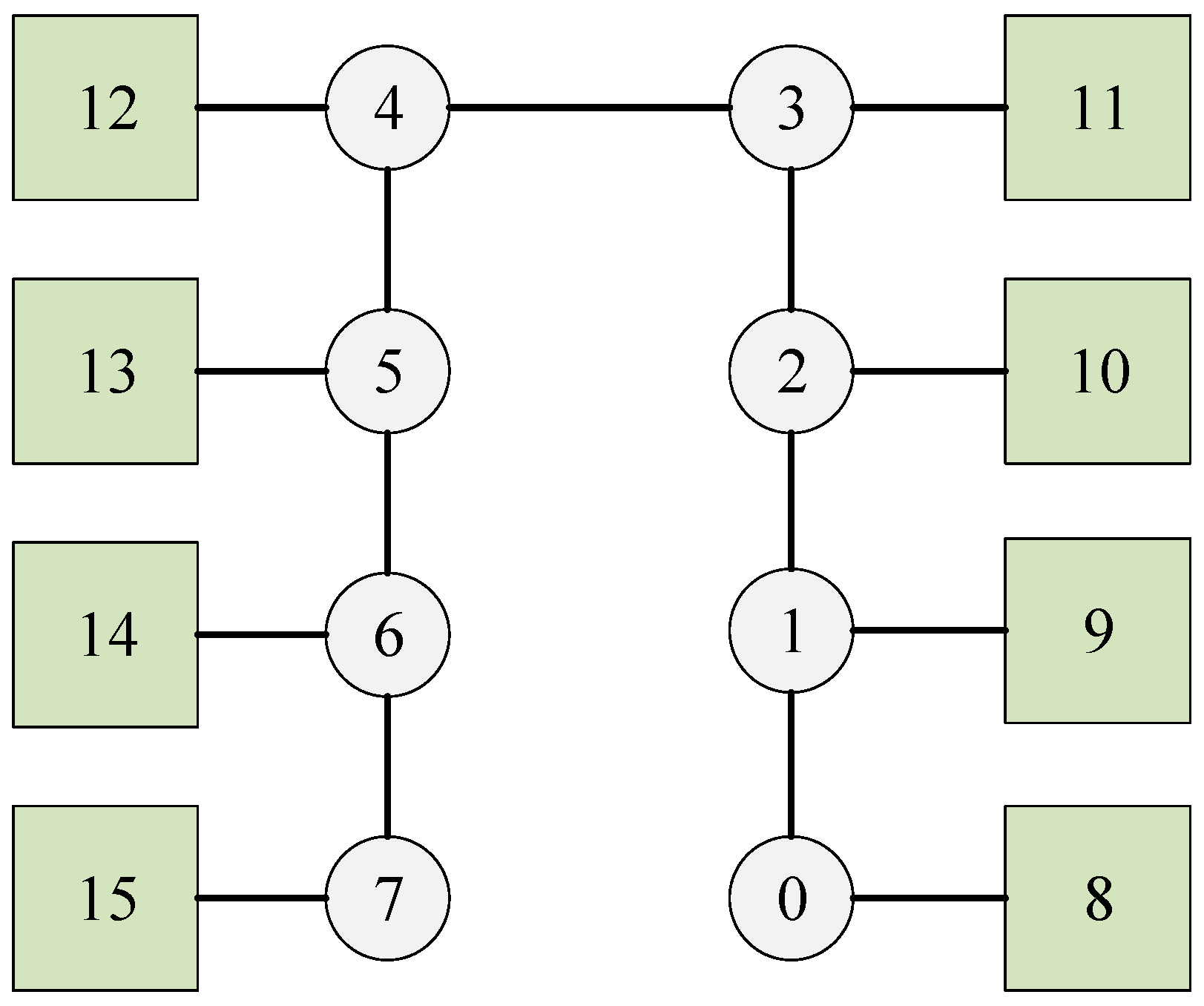
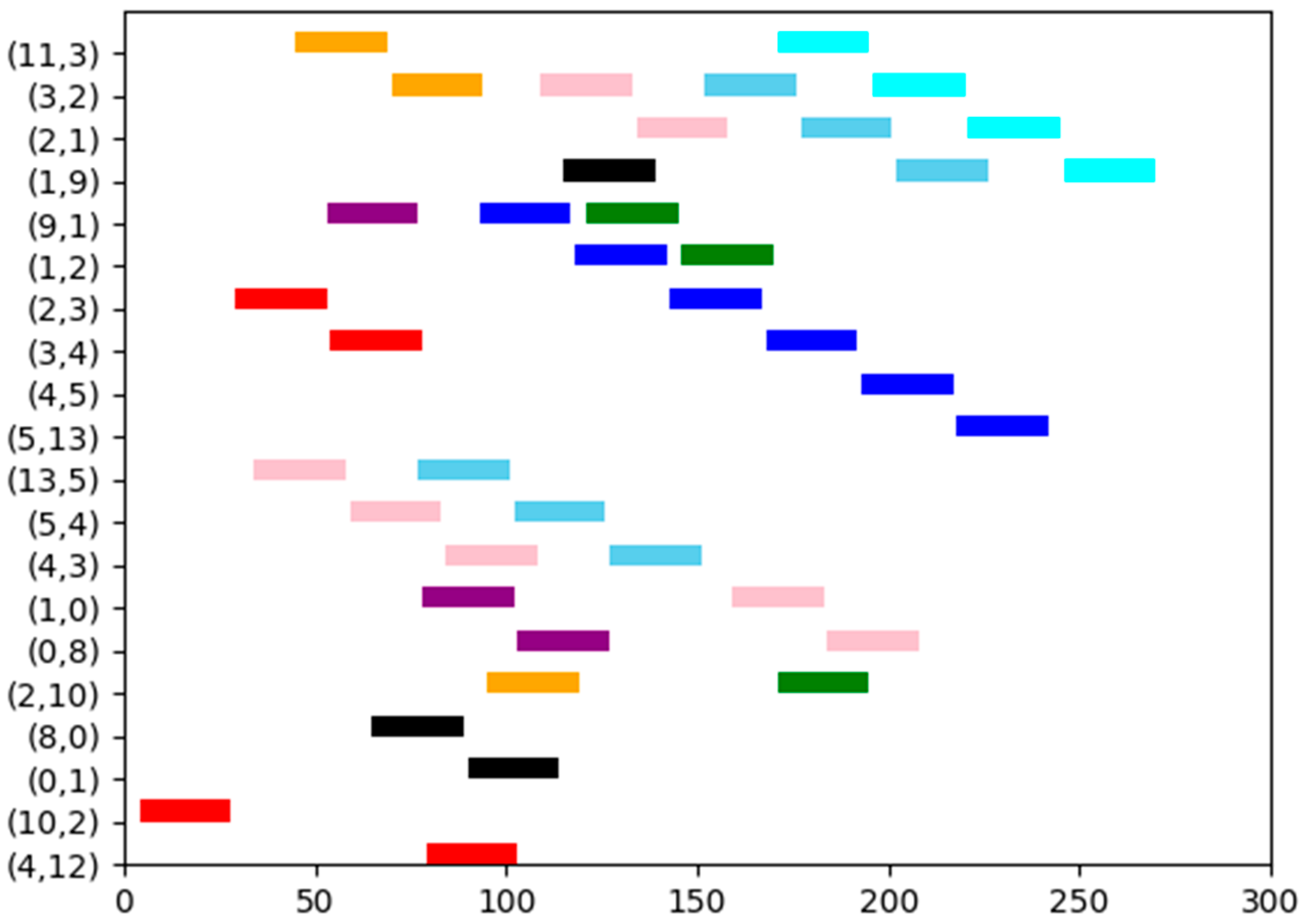

| Talker | Listener | Size | Deadline | Period | The Shortest Path | |
|---|---|---|---|---|---|---|
| Flow0 | 1 | 5 | 35 | 150 | 150 | 1-6-8-5 |
| Flow1 | 2 | 4 | 24 | 100 | 100 | 2-6-8-4 |
| Flow2 | 3 | 4 | 24 | 100 | 100 | 3-7-8-4 |
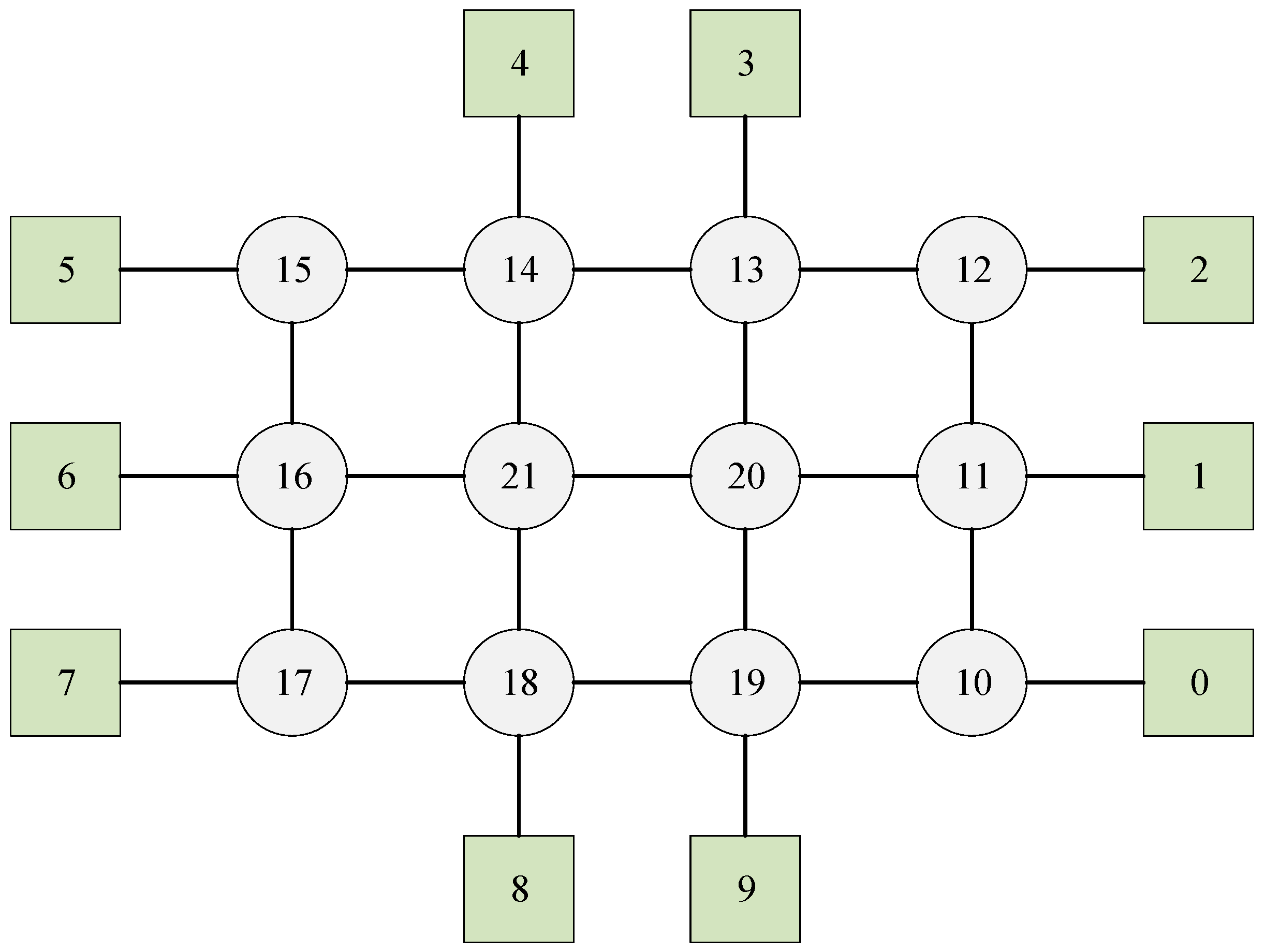
| Talker | Listener | Size | Deadline | Period | The Shortest Path | |
|---|---|---|---|---|---|---|
| Flow0 | 11 | 9 | 24 | 300 | 300 | 11-3-2-1-9 |
| Flow1 | 9 | 13 | 24 | 300 | 300 | 9-1-2-3-4-5-13 |
| Flow2 | 13 | 9 | 24 | 300 | 300 | 13-5-4-3-2-1-9 |
| Flow3 | 9 | 8 | 24 | 300 | 300 | 9-1-0-8 |
| Flow4 | 13 | 8 | 24 | 300 | 300 | 13-5-4-3-2-1-0-8 |
| Flow5 | 11 | 10 | 24 | 300 | 300 | 11-3-2-10 |
| Flow6 | 8 | 9 | 24 | 300 | 300 | 8-0-1-9 |
| Flow7 | 9 | 10 | 24 | 300 | 300 | 9-1-2-10 |
| Flow8 | 10 | 12 | 24 | 300 | 300 | 10-2-3-4-12 |
| Talker | Listener | Size | Deadline | Period | The Shortest Path | |
|---|---|---|---|---|---|---|
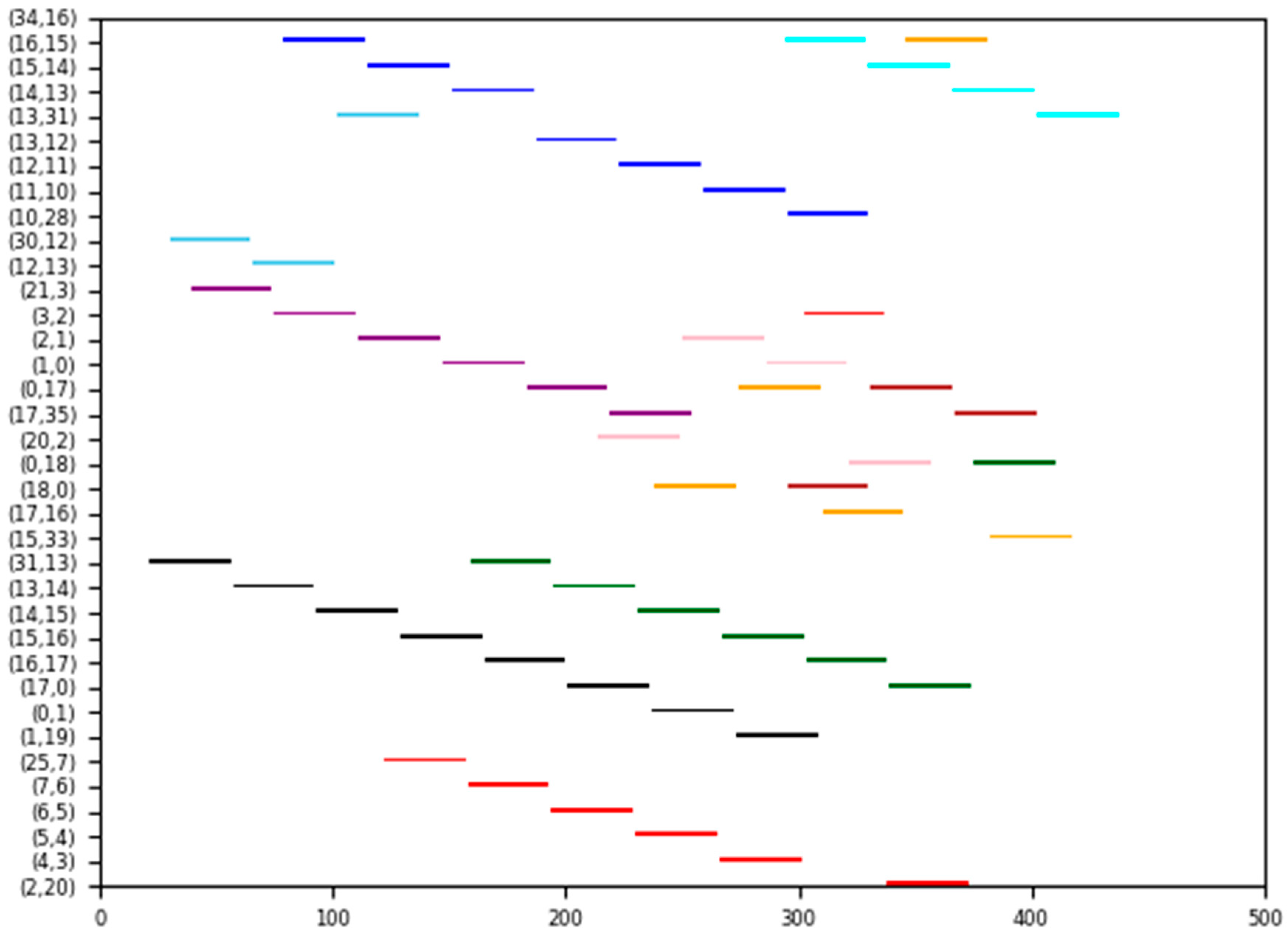
| Flow0 | 34 | 31 | 35 | 500 | 500 | 34-16-15-14-13-31 |
| Flow1 | 34 | 28 | 35 | 500 | 500 | 34-16-15-14-13-12-11-10-28 |
| Flow2 | 30 | 31 | 35 | 500 | 500 | 30-12-13-31 |
| Flow3 | 21 | 35 | 35 | 500 | 500 | 21-3-2-1-0-17-35 |
| Flow4 | 20 | 18 | 35 | 500 | 500 | 20-2-1-0-18 |
| Flow5 | 18 | 33 | 35 | 500 | 500 | 18-0-17-16-15-33 |
| Flow6 | 31 | 19 | 35 | 500 | 500 | 31-13-14-15-16-17-0-1-19 |
| Flow7 | 18 | 35 | 35 | 500 | 500 | 18-0-17-35 |
| Flow8 | 25 | 20 | 35 | 500 | 500 | 25-7-6-5-4-3-2-20 |
| Flow9 | 31 | 18 | 35 | 500 | 500 | 31-13-14-15-16-17-0-18 |
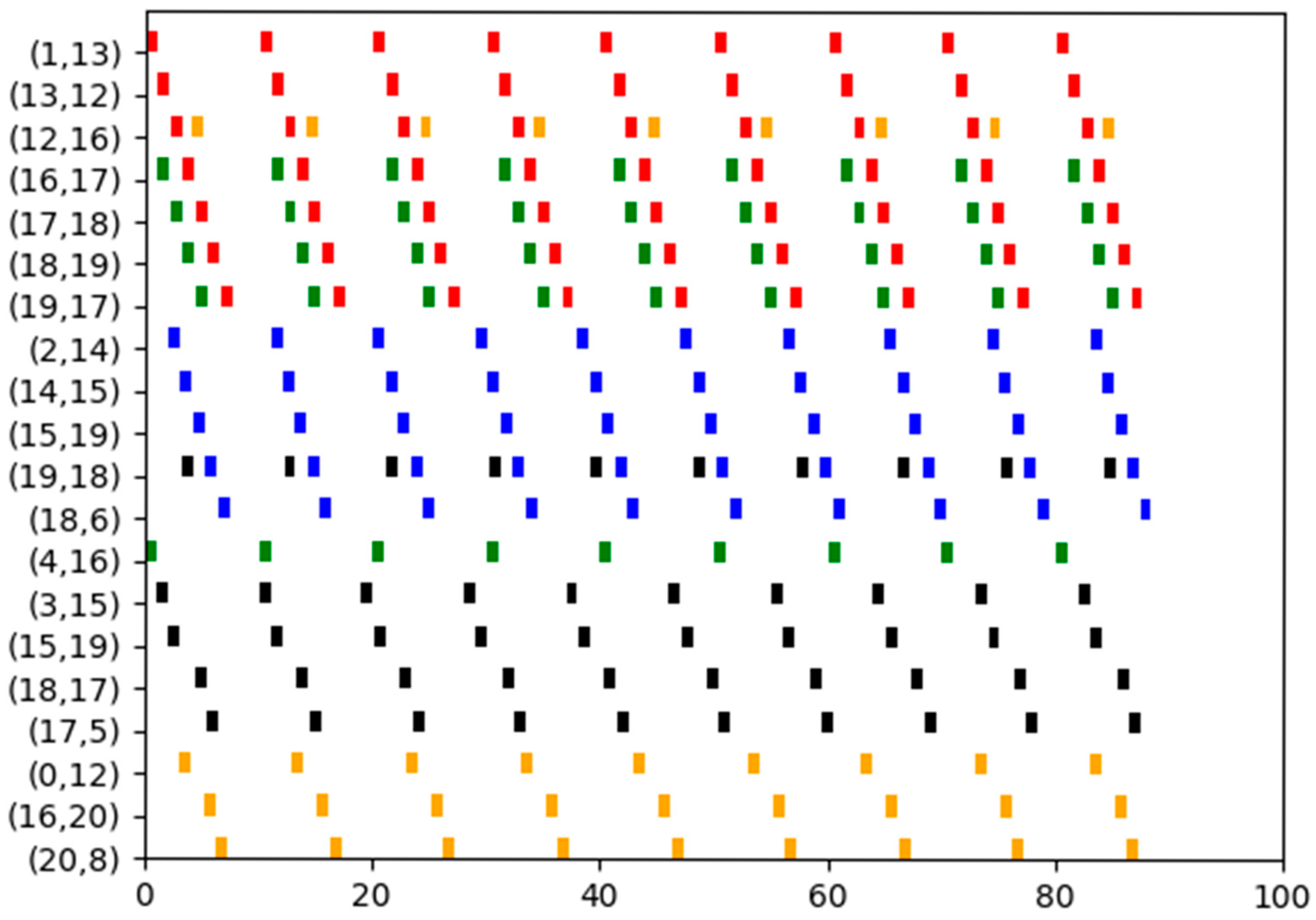
| Talker | Listener | Size | Deadline | Period | The Shortest Path | |
|---|---|---|---|---|---|---|
| Flow0 | 1 | 7 | 1 | 8 | 10 | 1-13-14-15-19-7 |
| Flow1 | 2 | 6 | 1 | 9 | 9 | 2-14-15-19-18-6 |
| Flow2 | 4 | 7 | 1 | 8 | 10 | 4-16-17-18-19-7 |
| Flow3 | 3 | 5 | 1 | 9 | 9 | 3-15-19-18-17-5 |
| Flow4 | 0 | 8 | 1 | 8 | 10 | 0-12-16-20-8 |
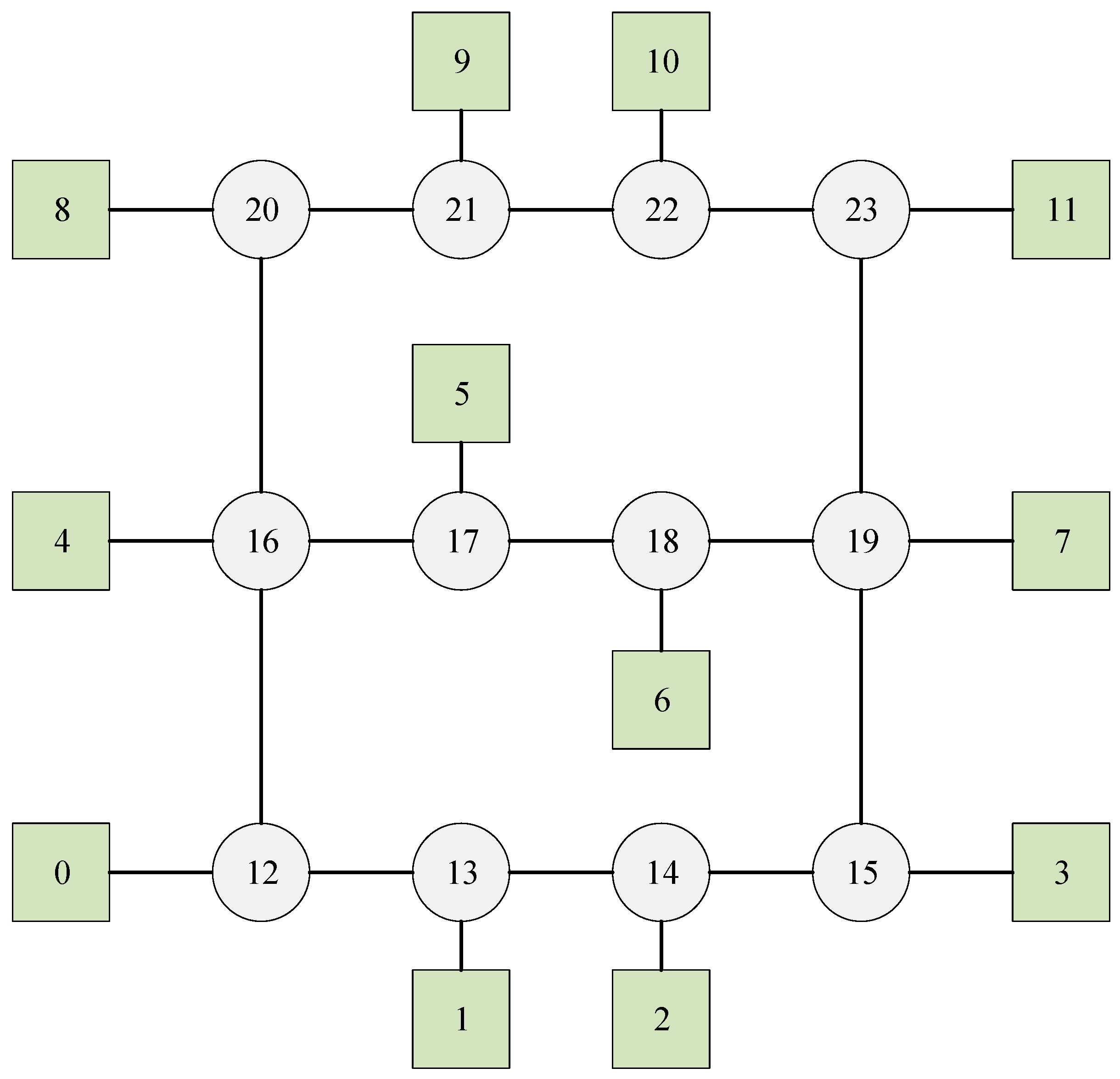
| Talker | Listener | Size | Deadline | Period | The Shortest Path | |
|---|---|---|---|---|---|---|
| Flow0 | 0 | 4 | 1 | 10 | 10 | 0-10-11-20-21-14-4 |
| 0-10-11-12-13-14-4 | ||||||
| 0-10-19-20-21-14-4 | ||||||
| 0-10-19-20-13-14-4 | ||||||
| 0-10-19-18-21-14-4 | ||||||
| 0-10-11-20-13-14-4 | ||||||
| Flow1 | 1 | 6 | 1 | 9 | 9 | 1-11-12-13-14-15-16-6 |
| Flow2 | 9 | 3 | 1 | 9 | 9 | 9-19-20-13-3 |
| Flow3 | 8 | 5 | 1 | 9 | 9 | 8-18-21-16-15-5 |
| 8-18-21-14-15-5 | ||||||
| 8-18-17-16-15-5 | ||||||
| Flow4 | 2 | 5 | 1 | 9 | 9 | 2-12-13-14-15-5 |
| Flow5 | 0 | 7 | 1 | 10 | 10 | 0-10-19-18-17-7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liao, W.; Xia, X.; Wang, Z.; Duan, Y. Routing and Scheduling in Time-Sensitive Networking by Evolutionary Algorithms. Biomimetics 2025, 10, 333. https://doi.org/10.3390/biomimetics10050333
Wang Z, Liao W, Xia X, Wang Z, Duan Y. Routing and Scheduling in Time-Sensitive Networking by Evolutionary Algorithms. Biomimetics. 2025; 10(5):333. https://doi.org/10.3390/biomimetics10050333
Chicago/Turabian StyleWang, Zengkai, Weizhi Liao, Xiaoyun Xia, Zijia Wang, and Yaolong Duan. 2025. "Routing and Scheduling in Time-Sensitive Networking by Evolutionary Algorithms" Biomimetics 10, no. 5: 333. https://doi.org/10.3390/biomimetics10050333
APA StyleWang, Z., Liao, W., Xia, X., Wang, Z., & Duan, Y. (2025). Routing and Scheduling in Time-Sensitive Networking by Evolutionary Algorithms. Biomimetics, 10(5), 333. https://doi.org/10.3390/biomimetics10050333







