Comprehensive Adaptive Enterprise Optimization Algorithm and Its Engineering Applications
Abstract
1. Introduction
2. Research Status of Optimization Algorithms
3. Enterprise Optimization Algorithm
3.1. Personnel Initialization
3.2. Enterprise Business
3.2.1. Optimal Rules for Enterprise Business Development
3.2.2. Enterprise Business (Task)
3.2.3. Enterprise Structure (Structure)
3.2.4. Enterprise Technology (Technology)
3.2.5. Enterprise People (People)
3.2.6. Conversion Mechanism
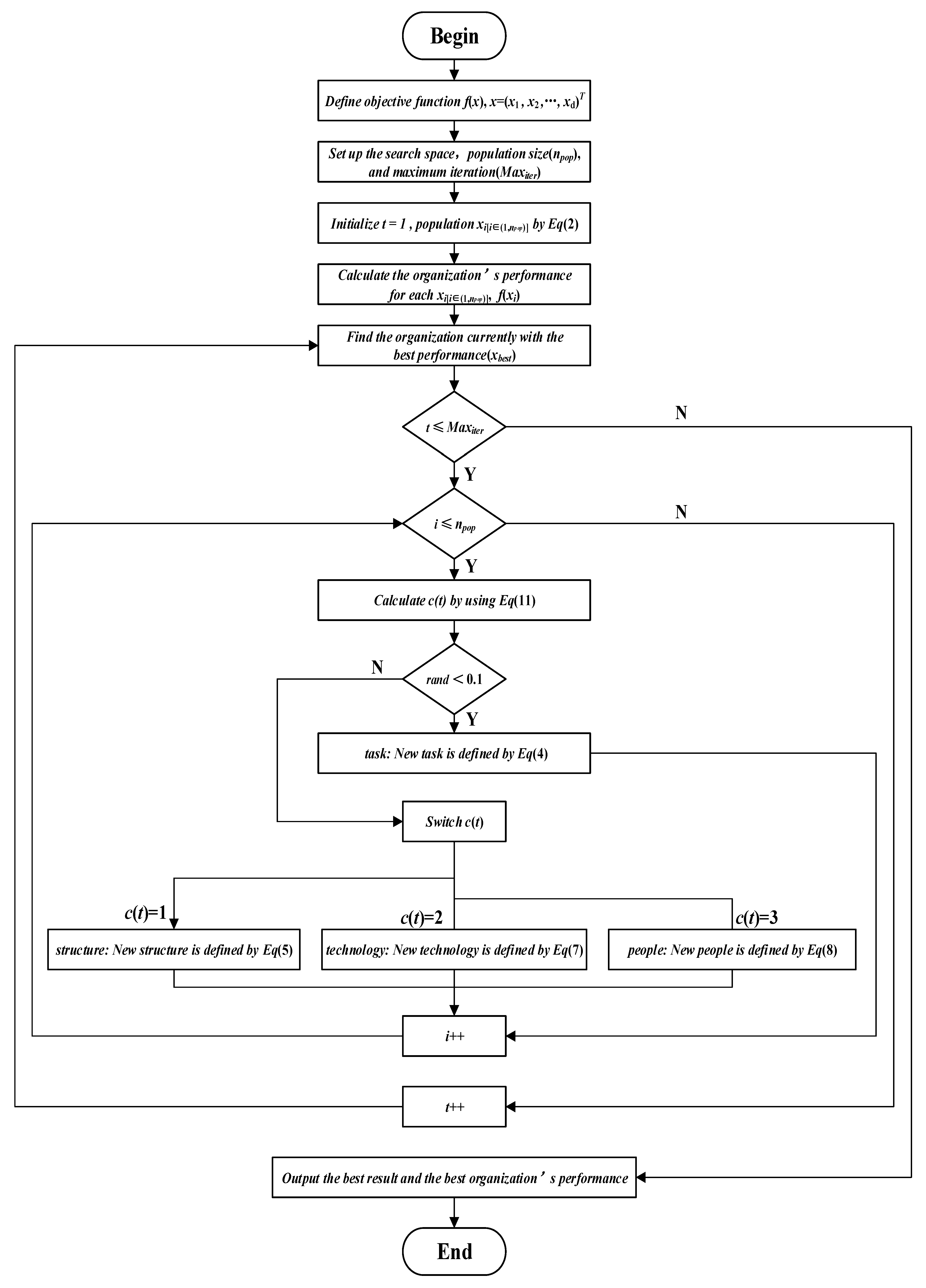
3.2.7. Optimization Algorithm Process
4. Comprehensive Adaptive Enterprise Optimization Algorithm
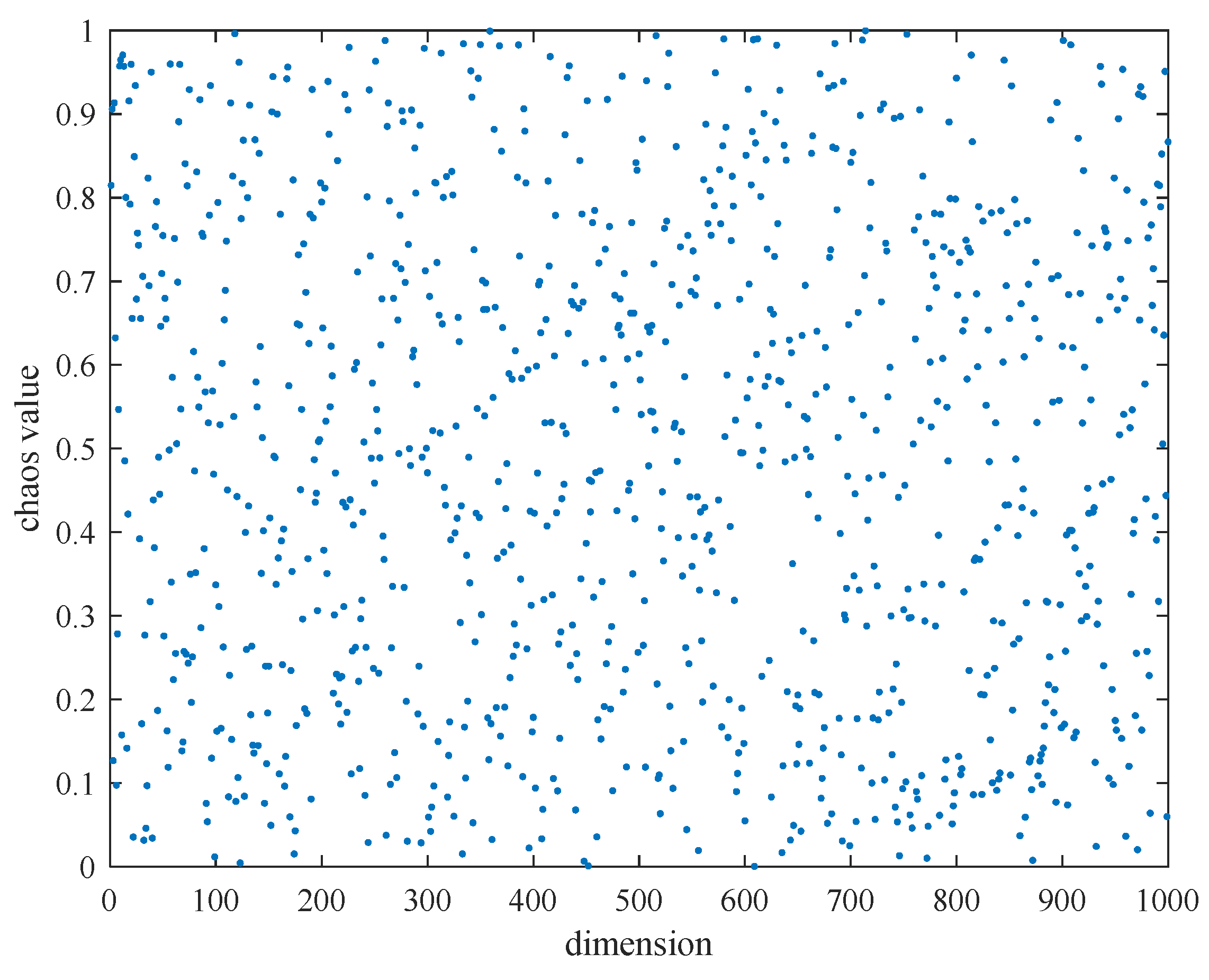
4.1. Tent Chaotic Map Based on Random Variables
4.2. Lens Imaging Reverse Learning Strategy
4.3. Adaptive Inertia Weight Strategy
4.4. Implementation Steps of the CAED
| Algorithm 1: Comprehensive Adaptive Enterprise Development Optimizer | |
| Step 1: Initialization objective function f(x), x = (x1, x2, …, xd)T, population size (npop), and maximum iteration (Maxiter) search space, up and lp limits for initialization Initialize time: t = 1 Initialize population xi(i = 1, 2, …, npop) by using Equation (13) * The fitness value based on the objective function(organization’s performance) Find the organization currently with the best fitness value(xbest) Repeat | |
| Step 2: | Calculate the c(t) and ω according by Equations (11) and (19), go to Step 3 |
| Step 3: | If rand < 0.1 |
| New task is defined by Equation (4) | |
| Adaptive weighting according to Equation (18) and updating individual positions * | |
| Else | |
| Switch c(t) | |
| Case c(t) = 1 | |
| New structure is defined by Equation (5) | |
| Adaptive weighting according to Equation (18) and updating individual positions * | |
| Case c(t) = 2 | |
| New technology is defined by Equation (7) | |
| Adaptive weighting according to Equation (18) and updating individual positions * | |
| Case c(t) = 3 | |
| New people is defined by Equation (8) | |
| Adaptive weighting according to Equation (18) and updating individual positions * | |
| End of switch | |
| End of if | |
| Update the organization currently with the best fitness value(xbest) | |
| Update the time: t ++ | |
| If t < 0.7Maxiter, go to Step 3 | |
| Else If t > 0.7Maxiter and t < Maxiter: go to Step 4 | |
| Else: go to Step 5 | |
| Step 4 | According to the lens imaging reverse learning strategy, the individual position is updated by Equation (27) * |
| Step 5 | Output the optimal solution |
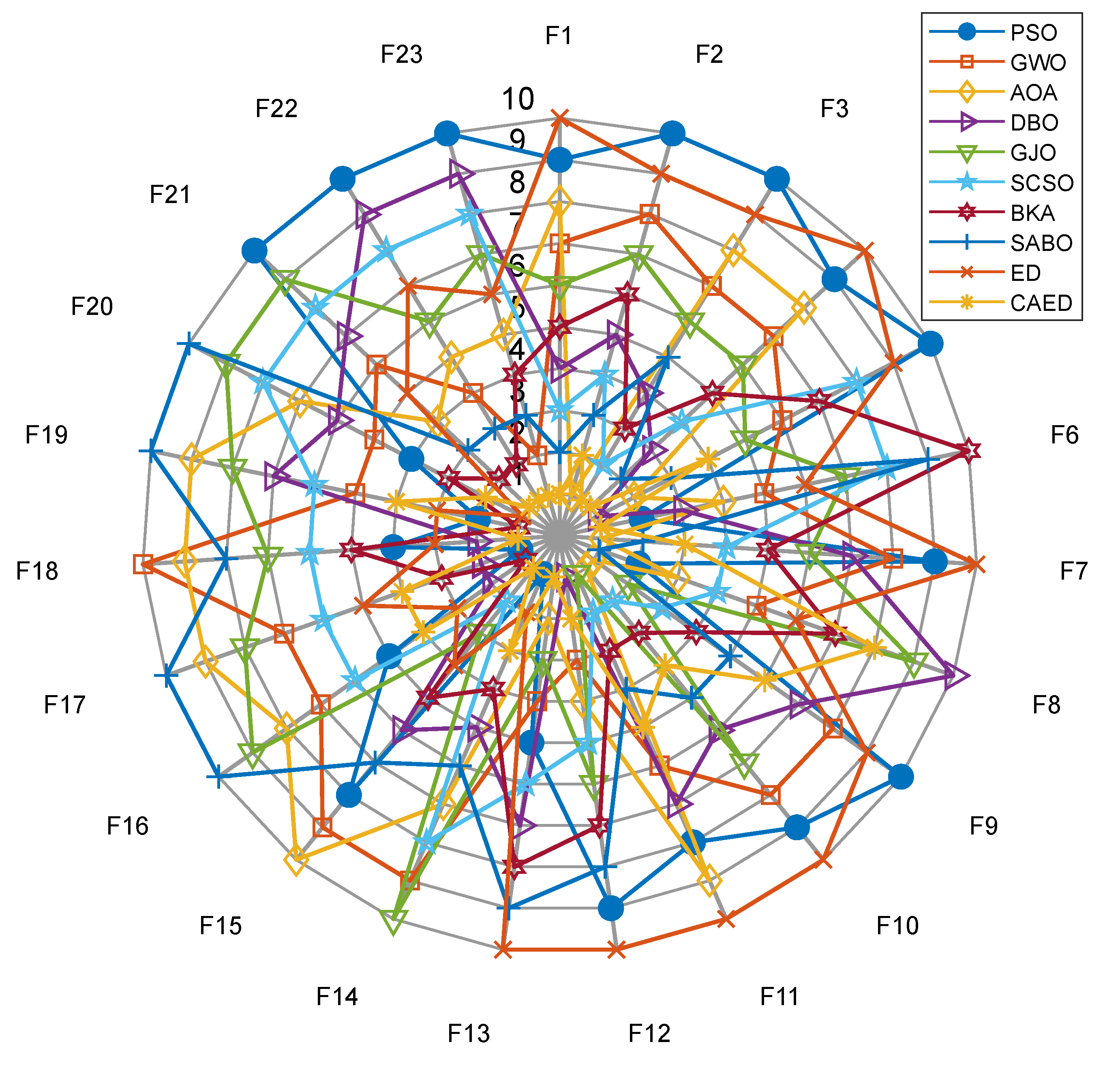
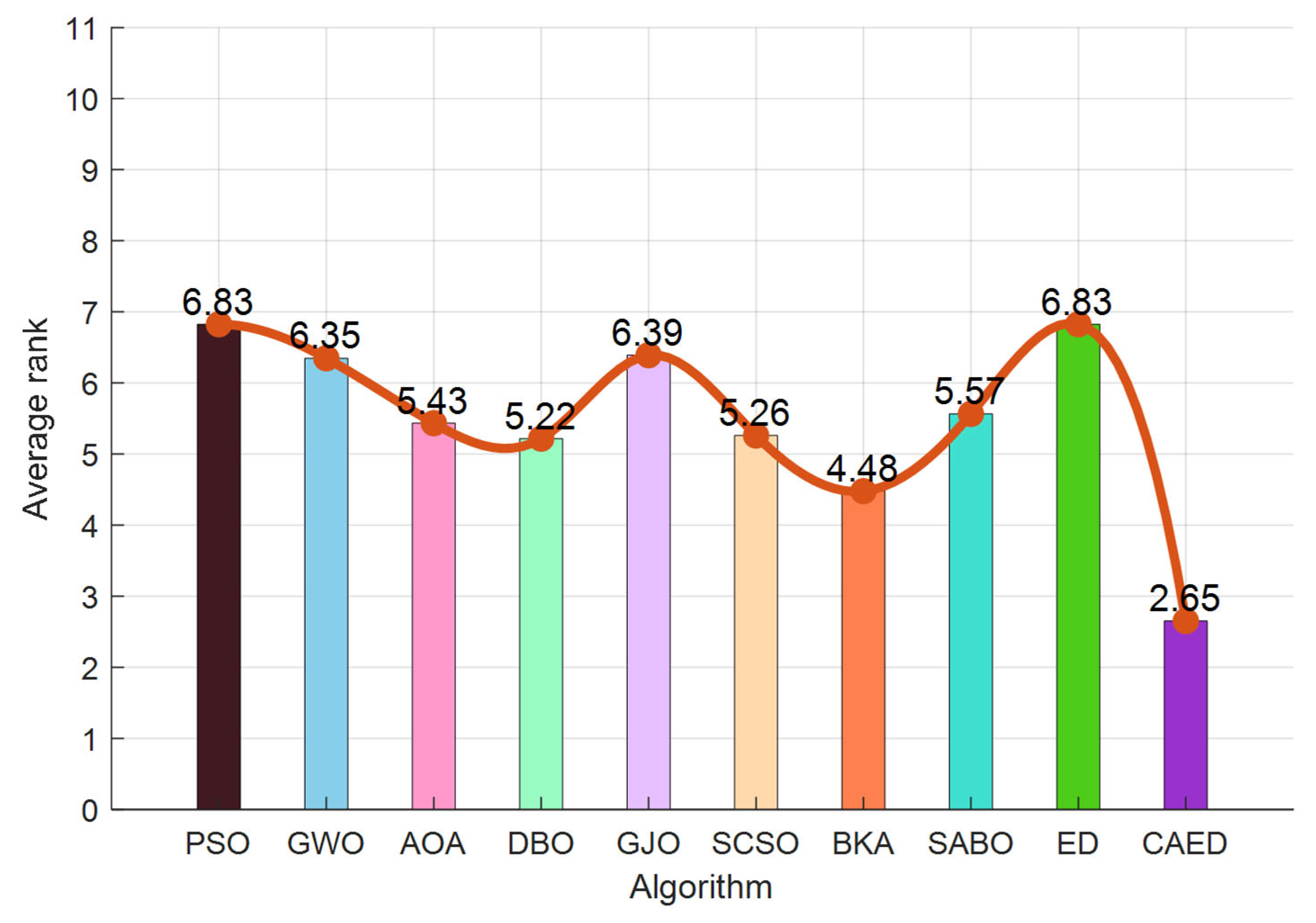
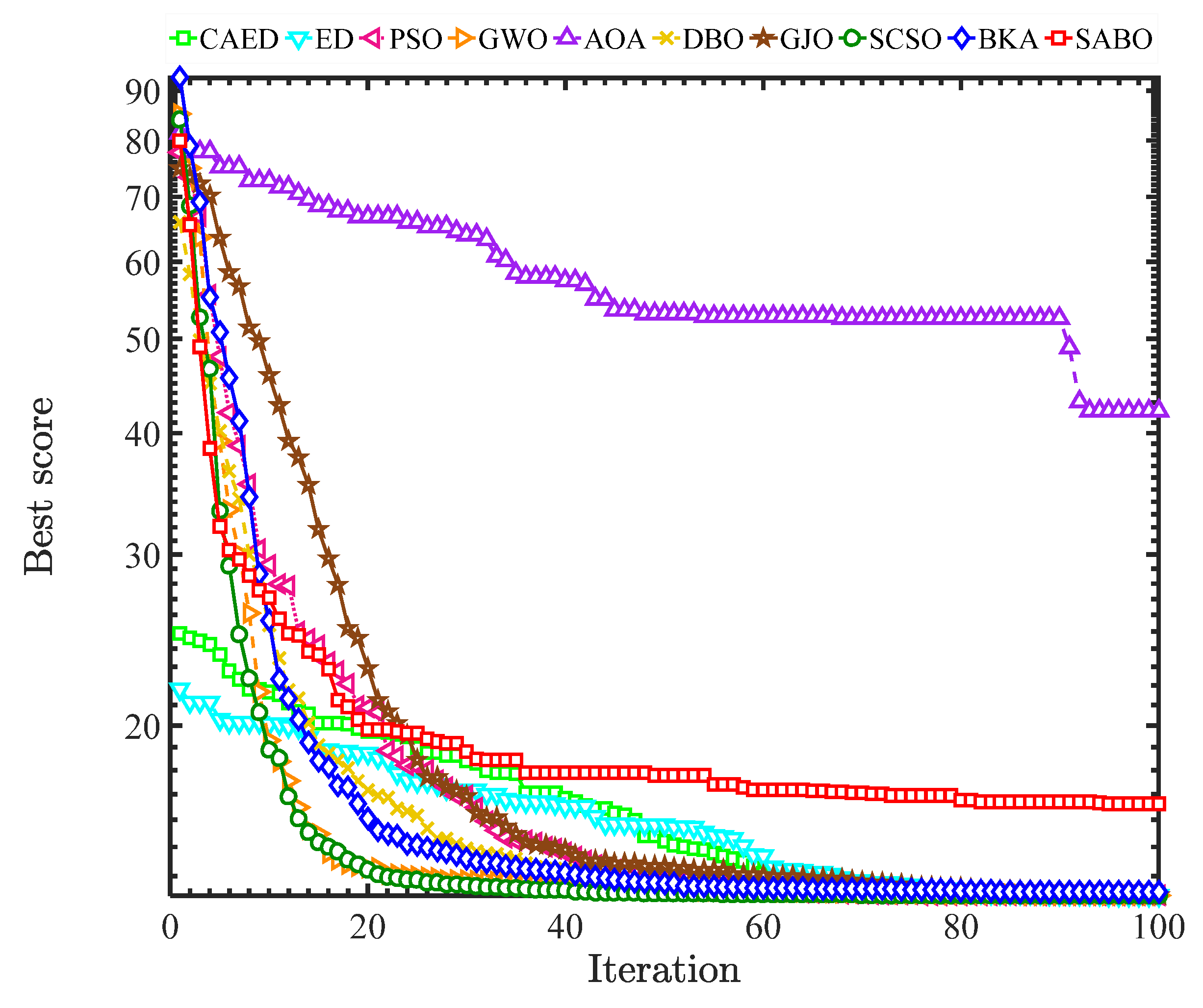
5. Algorithm Performance Testing and Comparative Analysis
5.1. Experimental Design and Test Functions
5.2. Experimental Results and Algorithm Analysis and Comparison
5.3. Analysis of Algorithm Time Complexity
5.4. Application of the CAED in Engineering
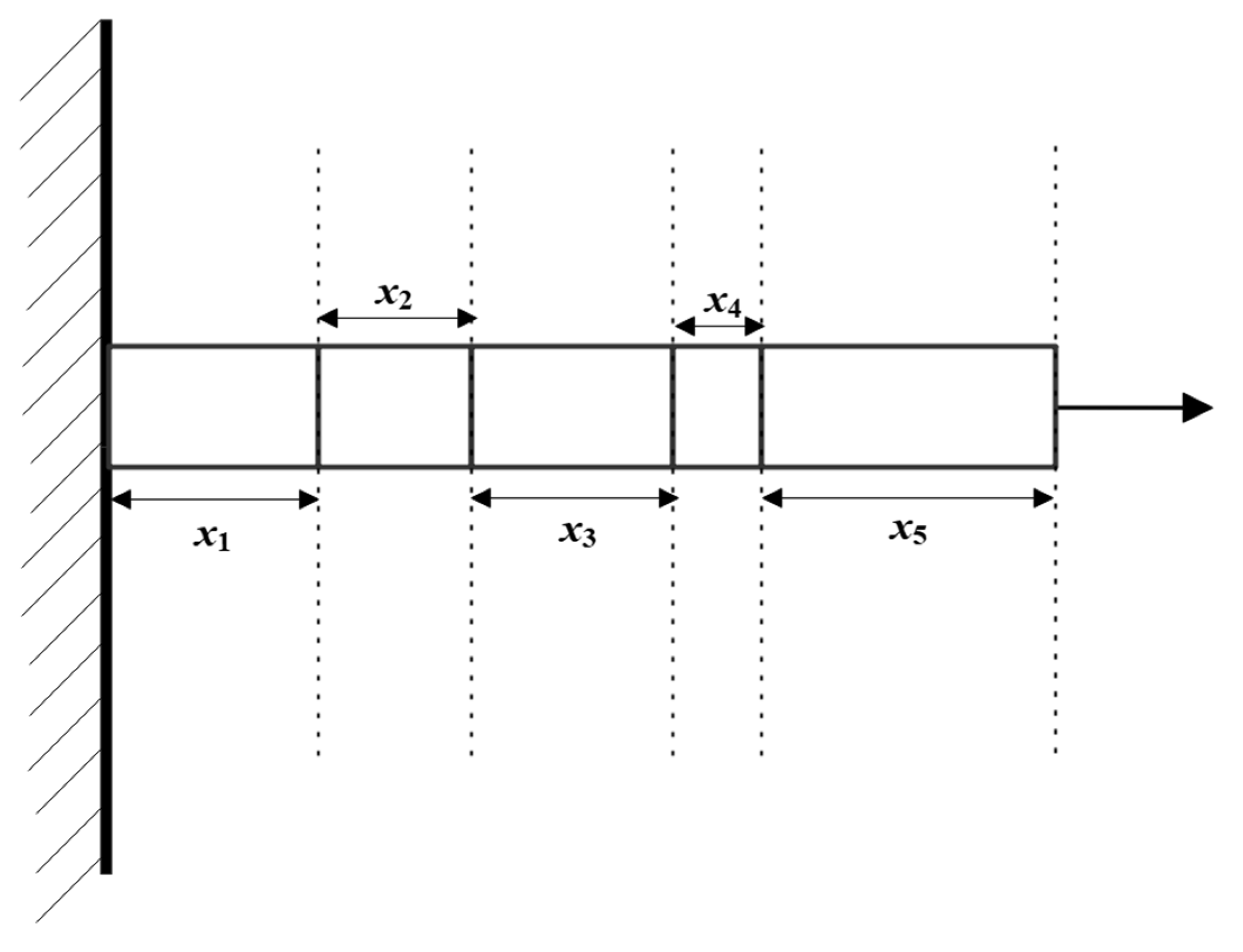
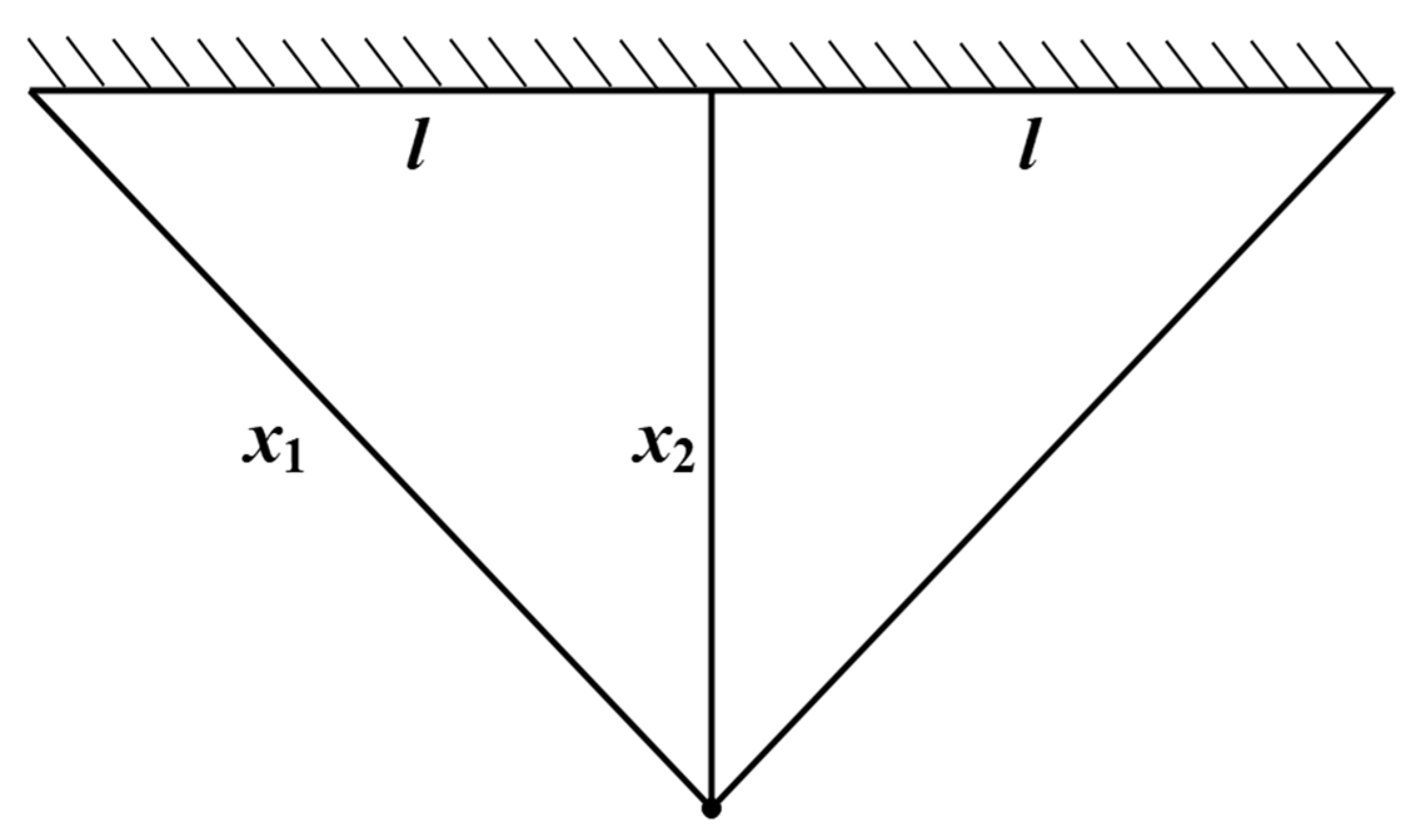
5.4.1. Optimization of Cantilever Beam Design
- Objective function:
- Constraint conditions:
- Boundary constraints:
5.4.2. Optimization of Three-Bar Truss Design
- Objective function:
- Constraint conditions:
- Boundary constraints:
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, S.; Zhou, C.; Yan, S.; Xue, J. Human memory optimization algorithm: A memory-inspired optimizer for global optimization problems. Expert Syst. Appl. 2024, 237, 121597. [Google Scholar] [CrossRef]
- Aggarwal, S.; Tripathi, S. MODE/CMA-ES: Integrated multi-operator differential evolution technique with CMA-ES. Appl. Soft Comput. 2025, 176, 113177. [Google Scholar] [CrossRef]
- Sakovich, N.; Aksenov, D.; Pleshakova, E.; Gataullin, S. MAMGD: Gradient-based optimization method using exponential decay. Technologies 2024, 12, 154. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Tan, X. Chaos and elite reverse learning–Enhanced sparrow search algorithm for IIoT sensing communication optimization. Alex. Eng. J. 2025, 125, 663–676. [Google Scholar] [CrossRef]
- Yang, X.; Zeng, G.; Cao, Z.; Huang, X.; Zhao, J. Parameters estimation of complex solar photovoltaic models using bi-parameter coordinated updating L-SHADE with parameter decomposition method. Case Stud. Therm. Eng. 2024, 61, 104917. [Google Scholar] [CrossRef]
- Bodalal, R.; Shuaeib, F. Marine predators algorithm for sizing optimization of truss structures with continuous variables. Computation 2023, 11, 91. [Google Scholar] [CrossRef]
- Li, W.; Tang, J.; Wang, L. Many-objective evolutionary algorithm with multi-strategy selection mechanism and adaptive reproduction operation. J. Supercomput. 2024, 80, 24435–24482. [Google Scholar] [CrossRef]
- Hu, G.; Song, K.; Abdel-salam, M. Sub-population evolutionary particle swarm optimization with dynamic fitness-distance balance and elite reverse learning for engineering design problems. Adv. Eng. Softw. 2025, 202, 103866. [Google Scholar] [CrossRef]
- Hwang, J.; Kale, G.; Patel, P.P.; Vishwakarma, R.; Aliasgari, M.; Hedayatipour, A.; Rezaei, A.; Sayadi, H. Machine learning in chaos-based encryption: Theory, implementations, and applications. IEEE Access 2023, 11, 125749–125767. [Google Scholar] [CrossRef]
- Chen, C.; Cao, L.; Chen, Y.; Chen, B.; Yue, Y. A comprehensive survey of convergence analysis of beetle antennae search algorithm and its applications. Artif. Intell. Rev. 2024, 57, 141. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Zhang, Y. Novel WSN Coverage Optimization Strategy Via Monarch Butterfly Algorithm and Particle Swarm Optimization. Wirel. Pers. Commun. 2024, 135, 2255–2280. [Google Scholar] [CrossRef]
- Truong, D.N.; Chou, J.S. Metaheuristic algorithm inspired by enterprise development for global optimization and structural engineering problems with frequency constraints. Eng. Struct. 2024, 318, 118679. [Google Scholar] [CrossRef]
- Cai, X.; Wang, W.; Wang, Y. Multi-strategy enterprise development optimizer for numerical optimization and constrained problems. Sci. Rep. 2025, 15, 10538. [Google Scholar] [CrossRef] [PubMed]
- Jawad, Z.N.; Balázs, V. Machine learning-driven optimization of enterprise resource planning (ERP) systems: A comprehensive review. Beni-Suef Univ. J. Basic Appl. Sci. 2024, 13, 4–20. [Google Scholar] [CrossRef]
- Simuni, G. Auto ML for Optimizing Enterprise AI Pipelines: Challenges and Opportunities. Int. IT J. Res. 2024, 2, 174–184. [Google Scholar]
- Akl, D.T.; Saafan, M.M.; Haikal, A.Y.; El-Gendy, E.M. IHHO: An improved Harris Hawks optimization algorithm for solving engineering problems. Neural Comput. Appl. 2024, 36, 12185–12298. [Google Scholar] [CrossRef]
- Hu, G.; Huang, F.; Chen, K.; Wei, G. MNEARO: A meta swarm intelligence optimization algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2024, 419, 116664. [Google Scholar] [CrossRef]
- Özçelik, Y.B.; Altan, A. Overcoming nonlinear dynamics in diabetic retinopathy classification: A robust AI-based model with chaotic swarm intelligence optimization and recurrent long short-term memory. Fractal Fract. 2023, 7, 598. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Ibrahim, A.M. An efficient hybrid swarm intelligence optimization algorithm for solving nonlinear systems and clustering problems. Soft Comput. 2023, 27, 8867–8895. [Google Scholar] [CrossRef]
- Tang, J.; Duan, H.; Lao, S. Swarm intelligence algorithms for multiple unmanned aerial vehicles collaboration: A comprehensive review. Artif. Intell. Rev. 2023, 56, 4295–4327. [Google Scholar] [CrossRef]
- Shitharth, S.; Yonbawi, S.; Manoharan, H.; Alahmari, S.; Yafoz, A.; Mujlid, H. Physical stint virtual representation of biomedical signals with wireless sensors using swarm intelligence optimization algorithm. IEEE Sens. J. 2023, 23, 3870–3877. [Google Scholar] [CrossRef]
- Chao, W.; Zhang, S.; Tianhang, M.A.; Yuetong, X.; Chen, M.Z.; Lei, W. Swarm intelligence: A survey of model classification and applications. Chin. J. Aeronaut. 2025, 38, 102982. [Google Scholar]
- Heng, H.; Ghazali, M.H.M.; Rahiman, W. Exploring the application of ant colony optimization in path planning for Unmanned Surface Vehicles. Ocean Eng. 2024, 311, 118738. [Google Scholar] [CrossRef]
- Nayak, J.; Swapnarekha, H.; Naik, B.; Dhiman, G.; Vimal, S. 25 years of particle swarm optimization: Flourishing voyage of two decades. Arch. Comput. Methods Eng. 2023, 30, 1663–1725. [Google Scholar] [CrossRef]
- Maaroof, B.B.; Rashid, T.A.; Abdulla, J.M.; Hassan, B.A.; Alsadoon, A.; Mohammadi, M.; Khishe, M.; Mirjalili, S. Current studies and applications of shuffled frog leaping algorithm: A review. Arch. Comput. Methods Eng. 2022, 29, 3459–3474. [Google Scholar] [CrossRef]
- Yang, Y.; Li, G.; Luo, T.; Al-Bahrani, M.; Al-Ammar, E.A.; Sillanpaa, M.; Ali, S.; Leng, X. The innovative optimization techniques for forecasting the energy consumption of buildings using the shuffled frog leaping algorithm and different neural networks. Energy 2023, 268, 126548. [Google Scholar] [CrossRef]
- Hu, B.; Zheng, X.; Lai, W. EPKO: Enhanced pied kingfisher optimizer for numerical optimization and engineering problems. Expert Syst. Appl. 2025, 278, 127416. [Google Scholar] [CrossRef]
- Reka, R.; Manikandan, A.; Venkataramanan, C.; Madanachitran, R. An energy efficient clustering with enhanced chicken swarm optimization algorithm with adaptive position routing protocol in mobile adhoc network. Telecommun. Syst. 2023, 84, 183–202. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Guo, Y.; Han, M.; Wan, B.; Liang, S. A multi-objective chicken swarm optimization algorithm based on dual external archive with various elites. Appl. Soft Comput. 2023, 133, 109920. [Google Scholar] [CrossRef]
- Zhang, S. Innovative application of particle swarm algorithm in the improvement of digital enterprise management efficiency. Syst. Soft Comput. 2024, 6, 200151. [Google Scholar] [CrossRef]
- Yin, L.; Tian, J.; Chen, X. Consistent African vulture optimization algorithm for electrical energy exchange in commercial buildings. Energy 2025, 318, 134741. [Google Scholar] [CrossRef]
- Truong, D.N.; Chou, J.S. Multiobjective enterprise development algorithm for optimizing structural design by weight and displacement. Appl. Math. Model. 2025, 137, 115676. [Google Scholar] [CrossRef]
- Akraam, M.; Rashid, T.; Zafar, S. An image encryption scheme proposed by modifying chaotic tent map using fuzzy numbers. Multimed. Tools Appl. 2023, 82, 16861–16879. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Fu, S.; Chen, J.; He, L. Enhanced Aquila optimizer based on tent chaotic mapping and new rules. Sci. Rep. 2024, 14, 3013. [Google Scholar] [CrossRef]
- Zhang, Q.; Hongshun, L.; Jian, G.; Yifan, W.; Luyao, L.; Hongzheng, L.; Haoxi, C. Improved GWO-MCSVM algorithm based on nonlinear convergence factor and tent chaotic mapping and its application in transformer condition assessment. Electr. Power Syst. Res. 2023, 224, 109754. [Google Scholar] [CrossRef]
- Ai, C.; He, S.; Fan, X. Parameter estimation of fractional-order chaotic power system based on lens imaging learning strategy state transition algorithm. IEEE Access 2023, 11, 13724–13737. [Google Scholar] [CrossRef]
- Li, W.; Luo, H.; Wang, L. Multifactorial brain storm optimization algorithm based on direct search transfer mechanism and concave lens imaging learning strategy. J. Supercomput. 2023, 79, 6168–6202. [Google Scholar] [CrossRef]
- Yuan, P.; Zhang, T.; Yao, L.; Lu, Y.; Zhuang, W. A hybrid golden jackal optimization and golden sine algorithm with dynamic lens-imaging learning for global optimization problems. Appl. Sci. 2022, 12, 9709. [Google Scholar] [CrossRef]
- Liao, Y.J.; Tarng, W.; Wang, T.L. The effects of an augmented reality lens imaging learning system on students’ science achievement, learning motivation, and inquiry skills in physics inquiry activities. Educ. Inf. Technol. 2024, 30, 5059–5104. [Google Scholar] [CrossRef]
- Jena, J.J.; Satapathy, S.C. A new adaptive tuned Social Group Optimization (SGO) algorithm with sigmoid-adaptive inertia weight for solving engineering design problems. Multimed. Tools Appl. 2024, 83, 3021–3055. [Google Scholar] [CrossRef]
- John, N.; Janamala, V.; Rodrigues, J. An adaptive inertia weight teaching–learning-based optimization for optimal energy balance in microgrid considering islanded conditions. Energy Syst. 2024, 15, 141–166. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An overview of variants and advancements of PSO algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Liu, Y.; As’arry, A.; Hassan, M.K.; Hairuddin, A.A.; Mohamad, H. Review of the grey wolf optimization algorithm: Variants and applications. Neural Comput. Appl. 2024, 36, 2713–2735. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Lou, T.; Yue, Z.; Chen, Z.; Qi, R.; Li, G. A hybrid multi-strategy SCSO algorithm for robot path planning. Evol. Syst. 2025, 16, 54. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Subtraction-average-based optimizer: A new swarm-inspired metaheuristic algorithm for solving optimization problems. Biomimetics 2023, 8, 149. [Google Scholar] [CrossRef]

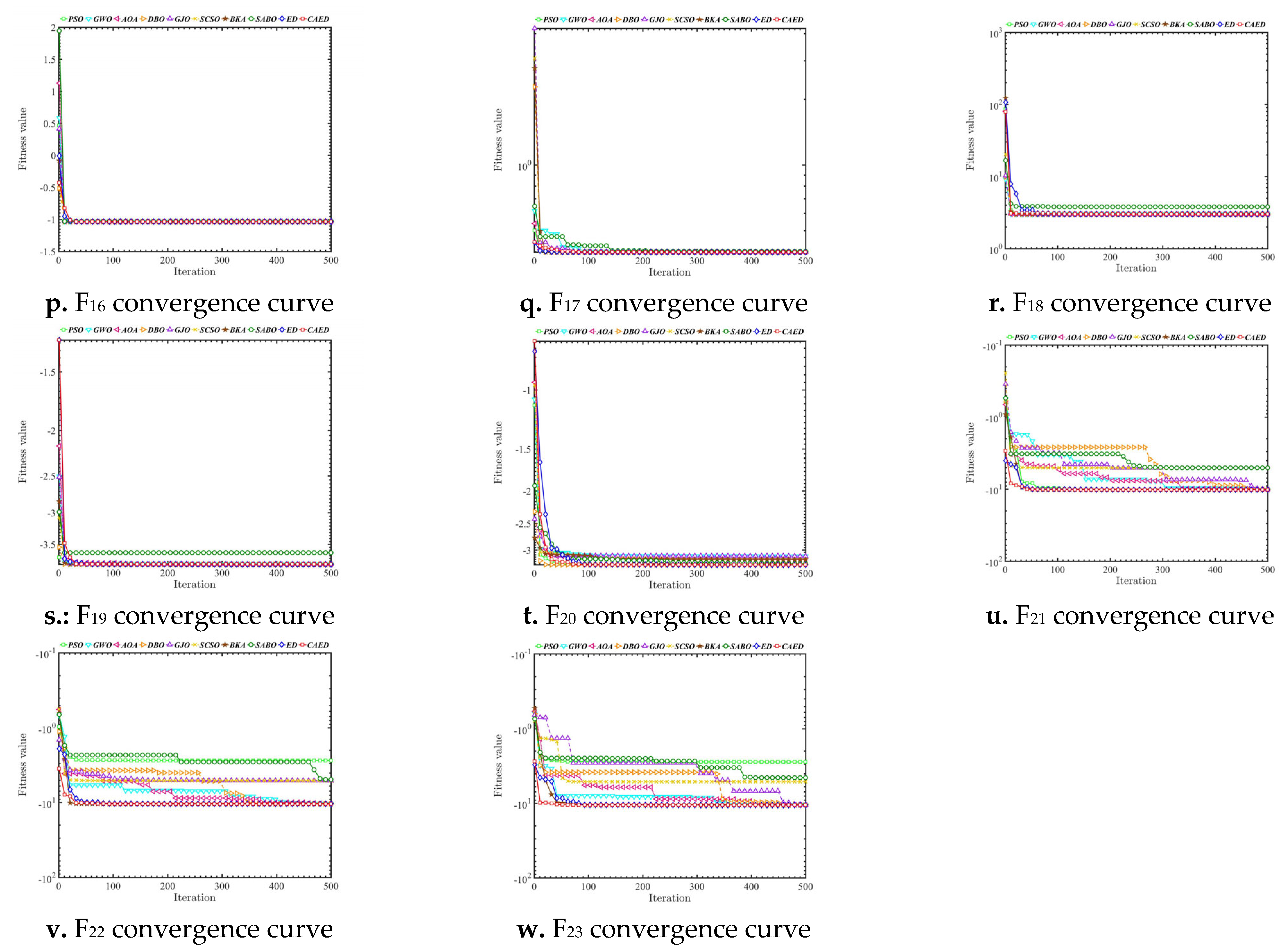
| Test Function | n | S | Fmin |
|---|---|---|---|
| 50 | [−100,100]n | 0 | |
| 50 | [−10,10]n | 0 | |
| 50 | [−100,100]n | 0 | |
| 50 | [−100,100]n | 0 | |
| 50 | [−30,30]n | 0 | |
| 50 | [−100,100]n | 0 | |
| 50 | [−1.28,1.28]n | 0 | |
| 50 | [−500,500]n | −12,569.5 | |
| 50 | [−5.12,5.12]n | 0 | |
| 50 | [−32,32]n | 0 | |
| 50 | [−600,600]n | 0 | |
| 50 | [−50,50]n | 0 | |
| 50 | [−50,50]n | 0 | |
| 2 | [−65.536, 65.536]n | 0 | |
| 4 | [−5,5]n | 0.000307 | |
| 2 | [−5,5]n | −1.01362 | |
| 2 | [−5,10] × [0,15] | 0.398 | |
| 2 | [−2,2]n | 3 | |
| 4 | [0,1]n | −3.86 | |
| 6 | [0,1]n | −3.32 | |
| 4 | [0,10]n | −10 | |
| 4 | [0,10]n | −10 | |
| 4 | [0,10]n | −10 |
| F1 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
|---|---|---|---|---|---|---|---|---|---|---|
| min | 5.00 × 10−4 | 5.18 × 10−29 | 2.32 × 10−158 | 1.53 × 10−194 | 1.21 × 10−57 | 1.33 × 10−124 | 2.29 × 10−107 | 1.64 × 10−201 | 4.60 × 10−3 | 0.00 |
| std | 2.07 × 10−2 | 1.54 × 10−27 | 8.09 × 10−38 | 3.73 × 10−116 | 2.84 × 10−54 | 3.57 × 10−108 | 2.27 × 10−77 | 0.00 | 2.96 × 10−1 | 0.00 |
| avg | 8.89 × 10−3 | 1.22 × 10−27 | 1.48 × 10−38 | 6.82 × 10−117 | 1.96 × 10−54 | 6.52 × 10−109 | 4.15 × 10−78 | 8.01 × 10−195 | 2.56 × 10−1 | 0.00 |
| median | 3.72 × 10−3 | 5.66 × 10−28 | 3.48 × 10−86 | 7.51 × 10−140 | 7.10 × 10−55 | 2.36 × 10−119 | 3.04 × 10−98 | 1.07 × 10−197 | 1.07 × 10−1 | 0.00 |
| worse | 1.16 × 10−1 | 5.74 × 10−27 | 4.43 × 10−37 | 2.05 × 10−115 | 1.12 × 10−53 | 1.95 × 10−107 | 1.24 × 10−76 | 2.37 × 10−193 | 10.6 | 0.00 |
| time | 2.94 × 10−2 | 5.46 × 10−2 | 3.51 × 10−2 | 4.77 × 10−2 | 7.36 × 10−2 | 6.82 × 10−1 | 4.31 × 10−2 | 6.80 × 10−2 | 6.70 × 10−2 | 8.97 × 10−2 |
| conv | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 |
| F2 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 2.16 × 10−3 | 1.16 × 10−17 | 0 | 5.80 × 10−82 | 1.00 × 10−33 | 1.54 × 10−65 | 7.48 × 10−54 | 7.23 × 10−113 | 5.57 × 10−2 | 0.00 |
| std | 40.9 | 6.40 × 10−17 | 0 | 1.63 × 10−53 | 3.81 × 10−32 | 9.08 × 10−60 | 1.15 × 10−44 | 1.39 × 10−110 | 4.03 × 10−1 | 0.00 |
| avg | 20.3 | 8.16 × 10−17 | 0 | 2.98 × 10−54 | 2.20 × 10−32 | 1.87 × 10−60 | 2.09 × 10−45 | 6.74 × 10−111 | 3.10 × 10−1 | 0.00 |
| median | 2.04 × 10−2 | 6.16 × 10−17 | 0 | 6.59 × 10−68 | 8.68 × 10−33 | 9.08 × 10−63 | 5.97 × 10−50 | 1.41 × 10−111 | 1.97 × 10−1 | 0.00 |
| worse | 10.3 | 3.31 × 10−16 | 0 | 8.94 × 10−53 | 2.04 × 10−31 | 4.99 × 10−59 | 6.27 × 10−44 | 5.39 × 10−110 | 22.6 | 0.00 |
| time | 3.08 × 10−2 | 5.62 × 10−2 | 3.76 × 10−2 | 5.13 × 10−2 | 7.46 × 10−2 | 6.82 × 10−1 | 5.48 × 10−2 | 6.87 × 10−2 | 7.06 × 10−2 | 9.13 × 10−2 |
| conv | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 |
| F3 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 4.96 × 102 | 9.60 × 10−9 | 8.20 × 10−141 | 7.93 × 10−143 | 3.67 × 10−24 | 6.02 × 10−115 | 4.20 × 10−102 | 1.23 × 10−87 | 1.53 × 103 | 0.00 |
| std | 2.18 × 103 | 3.80 × 10−5 | 7.86 × 10−3 | 5.50 × 10−53 | 3.44 × 10−14 | 5.37 × 10−98 | 2.09 × 10−80 | 7.80 × 10−45 | 1.24 × 103 | 0.00 |
| avg | 2.51 × 103 | 1.52 × 10−5 | 3.80 × 10−3 | 1.00 × 10−53 | 6.65 × 10−15 | 1.60 × 10−98 | 3.81 × 10−81 | 1.48 × 10−45 | 3.37 × 103 | 0.00 |
| median | 1.60 × 103 | 3.19 × 10−6 | 4.24 × 10−36 | 1.88 × 10−116 | 4.65 × 10−20 | 4.71 × 10−103 | 1.20 × 10−96 | 8.67 × 10−62 | 3.25 × 103 | 0.00 |
| worse | 9.13 × 103 | 1.97 × 10−4 | 2.57 × 10−2 | 3.01 × 10−52 | 1.89 × 10−13 | 2.23 × 10−97 | 1.14 × 10−79 | 4.28 × 10−44 | 6.37 × 103 | 0.00 |
| time | 1.04 × 10−1 | 1.29 × 10−1 | 1.10 × 10−1 | 1.25 × 10−1 | 1.56 × 10−1 | 7.55 × 10−1 | 2.01 × 10−1 | 1.42 × 10−1 | 1.39 × 10−1 | 2.34 × 10−1 |
| conv | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 |
| F4 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 4.21 × 10 | 1.60 × 10−7 | 1.88 × 10−66 | 8.79 × 10−84 | 9.56 × 10−19 | 6.62 × 10−56 | 9.49 × 10−53 | 8.11 × 10−79 | 9.62 × 10 | 0.00 |
| std | 15.8 | 2.77 × 10−6 | 2.10 × 10−2 | 1.20 × 10−53 | 5.60 × 10−15 | 3.16 × 10−48 | 1.18 × 10−42 | 6.38 × 10−77 | 38.9 | 0.00 |
| avg | 68.4 | 1.57 × 10−6 | 2.35 × 10−2 | 2.19 × 10−54 | 1.72 × 10−15 | 5.85 × 10−49 | 2.18 × 10−43 | 3.75 × 10−77 | 22.6 | 0.00 |
| median | 64.8 | 5.28 × 10−7 | 3.70 × 10−2 | 1.26 × 10−66 | 6.97 × 10−17 | 1.27 × 10−52 | 7.73 × 10−50 | 1.43 × 10−77 | 22.6 | 0.00 |
| worse | 99.6 | 1.35 × 10−5 | 4.90 × 10−2 | 6.58 × 10−53 | 2.82 × 10−14 | 1.73 × 10−47 | 6.47 × 10−42 | 2.63 × 10−76 | 29.1 | 0.00 |
| time | 3.02 × 10−2 | 5.37 × 10−2 | 3.52 × 10−2 | 4.89 × 10−2 | 7.29 × 10−2 | 6.79 × 10−1 | 5.16 × 10−2 | 6.85 × 10−2 | 6.94 × 10−2 | 8.77 × 10−2 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 |
| F5 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 29.4 | 25.2 | 27.0 | 25.2 | 26.5 | 26.0 | 26.0 | 27.9 | 93.9 | 25.9 |
| std | 1.64 × 104 | 8.67 × 10−1 | 3.72 × 10−1 | 2.55 × 10−1 | 6.32 × 10−1 | 8.77 × 10−1 | 9.87 × 10−1 | 3.26 × 10−1 | 2.50 × 102 | 4.02 × 10−1 |
| avg | 3.22 × 103 | 26.9 | 28.4 | 25.8 | 27.8 | 27.8 | 27.7 | 28.5 | 3.22 × 102 | 26.6 |
| median | 87.8 | 27.0 | 28.5 | 25.7 | 28.0 | 28.0 | 27.9 | 28.6 | 2.50 × 102 | 26.7 |
| worse | 9.01 × 104 | 28.7 | 28.9 | 26.5 | 28.8 | 28.8 | 28.9 | 28.9 | 1.43 × 103 | 27.3 |
| time | 3.88 × 10−2 | 6.31 × 10−2 | 4.49 × 10−2 | 5.68 × 10−2 | 8.44 × 10−2 | 6.92 × 10−1 | 6.87 × 10−2 | 7.69 × 10−2 | 7.71 × 10−2 | 1.03 × 10−1 |
| convergence | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 |
| F6 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 3.71 × 10−4 | 2.58 × 10−3 | 2.62 × 10 | 3.26 × 10−6 | 17.5 | 4.98 × 10−1 | 9.75 × 10−1 | 14.1 | 4.54 × 10−3 | 2.60 × 10−4 |
| std | 1.15 × 10−2 | 3.44 × 10−1 | 2.40 × 10−1 | 4.48 × 10−2 | 4.73 × 10−1 | 5.88 × 10−1 | 1.39 × 10 | 6.37 × 10−1 | 2.25 × 10−1 | 5.51 × 10−3 |
| avg | 1.01 × 10−2 | 8.13 × 10−1 | 32.4 | 9.38 × 10−3 | 2.59 × 10 | 19.0 | 19.4 | 26.5 | 2.21 × 10−1 | 4.29 × 10−3 |
| median | 5.72 × 10−3 | 7.58 × 10−1 | 32.8 | 1.67 × 10−4 | 2.51 × 10 | 19.9 | 14.0 | 25.3 | 1.67 × 10−1 | 2.23 × 10−3 |
| worse | 5.61 × 10−2 | 1.27 × 10 | 36.9 | 2.46 × 10−1 | 3.73 × 10 | 27.9 | 67.7 | 39.3 | 7.66 × 10−1 | 2.84 × 10−2 |
| time | 3.00 × 10−2 | 5.34 × 10−2 | 3.56 × 10−2 | 4.75 × 10−2 | 7.32 × 10−2 | 6.88 × 10−1 | 5.06 × 10−2 | 6.82 × 10−2 | 6.99 × 10−2 | 8.27 × 10−2 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F7 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 2.21 × 10−2 | 1.04 × 10−3 | 1.43 × 10−6 | 3.15 × 10−5 | 7.11 × 10−5 | 5.13 × 10−6 | 6.53 × 10−6 | 1.12 × 10−5 | 6.22 × 10−2 | 2.01 × 10−6 |
| std | 1.49 × 10−2 | 7.05 × 10−4 | 7.42 × 10−5 | 1.02 × 10−3 | 1.40 × 10−3 | 1.74 × 10−4 | 2.31 × 10−4 | 1.18 × 10−4 | 4.50 × 10−2 | 1.54 × 10−4 |
| avg | 5.05 × 10−2 | 2.05 × 10−3 | 8.34 × 10−5 | 1.14 × 10−3 | 6.64 × 10−4 | 1.26 × 10−4 | 2.60 × 10−4 | 1.52 × 10−4 | 1.25 × 10−1 | 1.00 × 10−4 |
| median | 5.14 × 10−2 | 1.89 × 10−3 | 7.73 × 10−5 | 1.02 × 10−3 | 3.81 × 10−4 | 9.24 × 10−5 | 1.86 × 10−4 | 1.19 × 10−4 | 1.12 × 10−1 | 5.26 × 10−5 |
| worse | 8.32 × 10−2 | 3.85 × 10−3 | 2.97 × 10−4 | 4.15 × 10−3 | 7.90 × 10−3 | 9.41 × 10−4 | 7.57 × 10−4 | 4.06 × 10−4 | 2.59 × 10−1 | 8.11 × 10−4 |
| time | 8.17 × 10−2 | 1.06 × 10−1 | 8.93 × 10−2 | 1.00 × 10−1 | 1.31 × 10−1 | 7.35 × 10−1 | 1.53 × 10−1 | 1.19 × 10−1 | 1.19 × 10−1 | 1.85 × 10−1 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F8 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | −1.01 × 104 | −7.61 × 103 | −6.02 × 103 | −1.22 × 104 | −6.43 × 103 | −8.59 × 103 | −1.15 × 104 | −4.08 × 103 | −1.24 × 104 | −1.18 × 104 |
| std | 6.40 × 102 | 9.57 × 102 | 4.15 × 102 | 1.61 × 103 | 1.16 × 103 | 7.83 × 102 | 1.54 × 103 | 3.13 × 102 | 1.32 × 103 | 8.87 × 102 |
| avg | −8.31 × 103 | −5.95 × 103 | −5.30 × 103 | −8.51 × 103 | −4.26 × 103 | −6.85 × 103 | −8.45 × 103 | −3.06 × 103 | −1.03 × 104 | −9.40 × 103 |
| median | −8.34 × 103 | −6.05 × 103 | −5.32 × 103 | −8.40 × 103 | −4.06 × 103 | −6.84 × 103 | −8.31 × 103 | −3.03 × 103 | −1.06 × 104 | −9.25 × 103 |
| worse | −7.28 × 103 | −3.15 × 103 | −4.53 × 103 | −5.95 × 103 | −2.76 × 103 | −5.42 × 103 | −4.40 × 103 | −2.50 × 103 | −7.77 × 103 | −7.80 × 103 |
| time | 4.06 × 10−2 | 6.64 × 10−2 | 4.89 × 10−2 | 6.28 × 10−2 | 8.63 × 10−2 | 6.95 × 10−1 | 7.57 × 10−2 | 7.94 × 10−2 | 8.29 × 10−2 | 1.06 × 10−1 |
| convergence | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 |
| F9 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 18.9 | 5.68 × 10−14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 58.0 | 0 |
| std | 16.7 | 51.1 | 0.00 | 9.08 × 10−1 | 0.00 | 0.00 | 0.00 | 0.00 | 82.2 | 0 |
| avg | 51.0 | 37.4 | 0.00 | 1.66 × 10−1 | 0.00 | 0.00 | 0.00 | 0.00 | 72.1 | 0 |
| median | 47.8 | 15.6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 72.7 | 0 |
| worse | 94.6 | 23.4 | 0.00 | 49.7 | 0.00 | 0.00 | 0.00 | 0.00 | 86.0 | 0 |
| time | 3.95 × 10−2 | 5.83 × 10−2 | 3.83 × 10−2 | 5.64 × 10−2 | 7.65 × 10−2 | 6.83 × 10−1 | 5.83 × 10−2 | 6.98 × 10−2 | 7.96 × 10−2 | 9.06 × 10−2 |
| convergence | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 |
| F10 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 9.29 × 10−3 | 7.55 × 10−14 | 8.88 × 10−16 | 8.88 × 10−16 | 4.44 × 10−15 | 8.88 × 10−16 | 8.88 × 10−16 | 4.44 × 10−15 | 1.80 × 10 | 8.88 × 10−16 |
| std | 7.31 × 10−1 | 1.64 × 10−14 | 0.00 | 9.01 × 10−16 | 1.53 × 10−15 | 0.00 | 0.00 | 0.00 | 9.97 × 10−1 | 0.00 |
| avg | 8.62 × 10−1 | 1.03 × 10−13 | 8.88 × 10−16 | 1.13 × 10−15 | 7.16 × 10−15 | 8.88 × 10−16 | 8.88 × 10−16 | 4.44 × 10−15 | 35.2 | 8.88 × 10−16 |
| median | 11.6 | 1.00 × 10−13 | 8.88 × 10−16 | 8.88 × 10−16 | 7.99 × 10−15 | 8.88 × 10−16 | 8.88 × 10−16 | 4.44 × 10−15 | 33.3 | 8.88 × 10−16 |
| worse | 21.3 | 1.36 × 10−13 | 8.88 × 10−16 | 4.44 × 10−15 | 7.99 × 10−15 | 8.88 × 10−16 | 8.88 × 10−16 | 4.44 × 10−15 | 57.3 | 8.88 × 10−16 |
| time | 3.88 × 10−2 | 5.79 × 10−2 | 3.97 × 10−2 | 5.35 × 10−2 | 7.69 × 10−2 | 6.85 × 10−1 | 5.74 × 10−2 | 7.06 × 10−2 | 7.97 × 10−2 | 9.54 × 10−2 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 |
| F11 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 8.32 × 10−4 | 0.00 | 2.29 × 10−2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.41 × 10−2 | 0.00 |
| std | 2.68 × 10−2 | 1.59 × 10−2 | 1.43 × 10−1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.31 × 10−1 | 0.00 |
| avg | 3.15 × 10−2 | 5.66 × 10−3 | 1.98 × 10−1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 2.37 × 10−1 | 0.00 |
| median | 2.37 × 10−2 | 0.00 | 1.74 × 10−1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 2.17 × 10−1 | 0.00 |
| worse | 1.11 × 10−1 | 7.61 × 10−2 | 6.26 × 10−1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.38 × 10−1 | 0.00 |
| time | 4.51 × 10−2 | 6.44 × 10−2 | 4.72 × 10−2 | 5.99 × 10−2 | 8.48 × 10−2 | 6.88 × 10−1 | 7.33 × 10−2 | 7.68 × 10−2 | 8.47 × 10−2 | 1.07 × 10−1 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F12 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 1.07 × 10−5 | 1.33 × 10−2 | 4.20 × 10−1 | 8.57 × 10−8 | 6.91 × 10−2 | 3.70 × 10−2 | 2.55 × 10−2 | 8.75 × 10−2 | 1.49 × 10−1 | 2.49 × 10−5 |
| std | 1.85 × 10−1 | 2.44 × 10−2 | 4.87 × 10−2 | 1.62 × 10−3 | 1.24 × 10−1 | 4.30 × 10−2 | 1.89 × 10−1 | 9.00 × 10−2 | 17.6 | 2.50 × 10−4 |
| avg | 1.53 × 10−1 | 4.75 × 10−2 | 5.25 × 10−1 | 4.31 × 10−4 | 2.29 × 10−1 | 9.36 × 10−2 | 1.15 × 10−1 | 2.32 × 10−1 | 25.6 | 2.15 × 10−4 |
| median | 1.04 × 10−1 | 4.05 × 10−2 | 5.35 × 10−1 | 3.95 × 10−6 | 2.11 × 10−1 | 9.14 × 10−2 | 4.44 × 10−2 | 2.27 × 10−1 | 19.5 | 1.12 × 10−4 |
| worse | 7.28 × 10−1 | 1.01 × 10−1 | 6.11 × 10−1 | 6.86 × 10−3 | 7.56 × 10−1 | 2.24 × 10−1 | 7.27 × 10−1 | 4.05 × 10−1 | 58.4 | 1.09 × 10−3 |
| time | 1.63 × 10−1 | 1.87 × 10−1 | 1.70 × 10−1 | 1.85 × 10−1 | 2.37 × 10−1 | 8.16 × 10−1 | 3.20 × 10−1 | 2.00 × 10−1 | 1.94 × 10−1 | 3.39 × 10−1 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F13 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 3.30 × 10−4 | 1.02 × 10−1 | 25.7 | 1.06 × 10−5 | 12.3 | 16.2 | 5.38 × 10−1 | 14.4 | 48.3 | 4.32 × 10−5 |
| std | 1.61 × 10−1 | 3.35 × 10−1 | 9.29 × 10−2 | 3.97 × 10−1 | 1.90 × 10−1 | 3.12 × 10−1 | 4.84 × 10−1 | 6.18 × 10−1 | 13.4 | 3.41 × 10−4 |
| avg | 1.25 × 10−1 | 6.23 × 10−1 | 28.3 | 4.31 × 10−1 | 16.7 | 24.3 | 17.3 | 24.1 | 22.6 | 3.39 × 10−4 |
| median | 6.61 × 10−2 | 6.31 × 10−1 | 28.4 | 3.71 × 10−1 | 16.7 | 25.0 | 17.3 | 28.5 | 20.2 | 2.32 × 10−4 |
| worse | 6.95 × 10−1 | 13.1 | 30.0 | 16.4 | 20.9 | 28.0 | 29.9 | 30.5 | 63.2 | 1.45 × 10−3 |
| time | 1.66 × 10−1 | 1.87 × 10−1 | 1.65 × 10−1 | 1.87 × 10−1 | 2.34 × 10−1 | 8.10 × 10−1 | 3.19 × 10−1 | 2.01 × 10−1 | 1.94 × 10−1 | 3.36 × 10−1 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F14 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 9.98 × 10−1 | 9.98 × 10−1 | 1.99 × 10 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 9.98 × 10−1 | 10.0 | 9.98 × 10−1 | 9.98 × 10−1 |
| std | 5.83 × 10−17 | 32.2 | 36.5 | 9.23 × 10−1 | 41.8 | 30.9 | 5.03 × 10−1 | 15.4 | 0.00 | 8.25 × 10−17 |
| avg | 9.98 × 10−1 | 30.6 | 10.1 | 13.9 | 40.7 | 33.6 | 11.3 | 29.4 | 9.98 × 10−1 | 9.98 × 10−1 |
| median | 9.98 × 10−1 | 24.9 | 12.7 | 9.98 × 10−1 | 29.8 | 29.8 | 9.98 × 10−1 | 29.8 | 9.98 × 10−1 | 9.98 × 10−1 |
| worse | 9.98 × 10−1 | 12.7 | 12.7 | 49.5 | 12.7 | 10.8 | 29.8 | 61.8 | 9.98 × 10−1 | 9.98 × 10−1 |
| time | 2.48 × 10−1 | 2.45 × 10−1 | 2.47 × 10−1 | 2.74 × 10−1 | 2.73 × 10−1 | 2.92 × 10−1 | 5.02 × 10−1 | 2.66 × 10−1 | 2.88 × 10−1 | 5.24 × 10−1 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F15 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 3.11 × 10−4 | 3.09 × 10−4 | 3.50 × 10−4 | 3.07 × 10−4 | 3.08 × 10−4 | 3.07 × 10−4 | 3.07 × 10−4 | 3.18 × 10−4 | 4.40 × 10−4 | 3.07 × 10−4 |
| std | 7.42 × 10−3 | 8.54 × 10−3 | 2.90 × 10−2 | 4.20 × 10−4 | 6.07 × 10−3 | 3.19 × 10−4 | 5.06 × 10−3 | 2.10 × 10−3 | 2.39 × 10−4 | 7.71 × 10−9 |
| avg | 4.08 × 10−3 | 5.14 × 10−3 | 2.05 × 10−2 | 9.91 × 10−4 | 2.47 × 10−3 | 4.40 × 10−4 | 1.78 × 10−3 | 9.26 × 10−4 | 1.08 × 10−3 | 3.07 × 10−4 |
| median | 7.30 × 10−4 | 4.30 × 10−4 | 1.01 × 10−2 | 1.22 × 10−3 | 4.71 × 10−4 | 3.08 × 10−4 | 3.07 × 10−4 | 4.80 × 10−4 | 1.22 × 10−3 | 3.07 × 10−4 |
| worse | 2.04 × 10−2 | 2.04 × 10−2 | 1.01 × 10−1 | 1.66 × 10−3 | 2.04 × 10−2 | 1.60 × 10−3 | 2.04 × 10−2 | 1.20 × 10−2 | 1.23 × 10−3 | 3.08 × 10−4 |
| time | 1.73 × 10−2 | 2.08 × 10−2 | 2.01 × 10−2 | 4.61 × 10−2 | 4.22 × 10−2 | 1.05 × 10−1 | 4.29 × 10−2 | 3.84 × 10−2 | 6.69 × 10−2 | 8.48 × 10−2 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F16 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 |
| std | 6.52 × 10−16 | 1.59 × 10−8 | 1.42 × 10−7 | 5.68 × 10−16 | 1.87 × 10−7 | 1.15 × 10−9 | 5.76 × 10−16 | 1.40 × 10−2 | 6.52 × 10−16 | 6.32 × 10−16 |
| avg | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.2 | −10.3 | −10.3 |
| median | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 |
| worse | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −10.3 | −9.86−1 | −10.3 | −10.3 |
| time | 1.75 × 10−2 | 1.88 × 10−2 | 1.85 × 10−2 | 4.35 × 10−2 | 3.81 × 10−2 | 6.12 × 10−2 | 3.83 × 10−2 | 3.64 × 10−2 | 6.54 × 10−2 | 8.52 × 10−2 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F17 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 3.98 × 10−1 | 3.98 × 10−1 | 3.99 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| std | 0.00 | 3.47 × 10−4 | 9.23 × 10−3 | 0.00 | 2.00 × 10−3 | 3.86 × 10−8 | 1.95 × 10−15 | 1.27 × 10−1 | 0.00 | 0.00 |
| avg | 3.98 × 10−1 | 3.98 × 10−1 | 4.09 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 4.48 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| median | 3.98 × 10−1 | 3.98 × 10−1 | 4.06 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 4.01 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| worse | 3.98 × 10−1 | 4.00 × 10−1 | 4.34 × 10−1 | 3.98 × 10−1 | 4.09 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 1.00 | 3.98 × 10−1 | 3.98 × 10−1 |
| time | 1.29 × 10−2 | 1.45 × 10−2 | 1.53 × 10−2 | 4.15 × 10−2 | 3.47 × 10−2 | 5.72 × 10−2 | 3.44 × 10−2 | 3.17 × 10−2 | 6.36 × 10−2 | 7.69 × 10−2 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F18 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 |
| std | 14.8 | 41.0−5 | 11.0 | 49.3 | 1.99 × 10−6 | 1.38 × 10−5 | 2.31 × 10−15 | 16.0 | 1.06 × 10−15 | 1.59 × 10−15 |
| avg | 57.0 | 3.00 | 84.0 | 39.0 | 3.00 | 3.00 | 3.00 | 39.7 | 3.00 | 3.00 |
| median | 300 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 32.6 | 3.00 | 3.00 |
| worse | 84.0 | 3.00 | 30.0 | 30.0 | 3.00 | 3.00 | 3.00 | 87.7 | 3.00 | 3.00 |
| time | 1.25 × 10−2 | 1.39 × 10−2 | 1.36 × 10−2 | 3.90 × 10−2 | 3.37 × 10−2 | 5.62 × 10−2 | 3.37 × 10−2 | 3.15 × 10−2 | 6.33 × 10−2 | 7.62 × 10−2 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F19 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | −38.6 | −38.6 | −38.6 | −38.6 | −38.6 | −38.6 | −38.6 | −38.6 | −38.6 | −38.6 |
| std | 2.60 × 10−15 | 2.15 × 10−3 | 3.80 × 10−3 | 3.21 × 10−3 | 3.92 × 10−3 | 3.20 × 10−3 | 2.40 × 10−15 | 2.41 × 10−1 | 2.71 × 10−15 | 2.71 × 10−15 |
| avg | −38.6 | −38.6 | −38.5 | −38.6 | −38.6 | −38.6 | −38.6 | −35.6 | −38.6 | −38.6 |
| median | −38.6 | −38.6 | −38.5 | −38.6 | −38.6 | −38.6 | −38.6 | −36.1 | −38.6 | −38.6 |
| worse | −38.6 | −38.5 | −38.4 | −3.85 | −38.5 | −38.5 | −38.6 | −29.8 | −38.6 | −38.6 |
| time | 1.99 × 10−2 | 2.26 × 10−2 | 2.22 × 10−2 | 4.88 × 10−2 | 4.33 × 10−2 | 8.59 × 10−2 | 4.90 × 10−2 | 4.06 × 10−2 | 7.21 × 10−2 | 9.41 × 10−2 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F20 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | −33.2 | −33.2 | −31.5 | −33.2 | −33.2 | −33.2 | −332 | −33.2 | −33.2 | −33.2 |
| std | 6.54 × 10−2 | 1.00 × 10−1 | 8.73 × 10−2 | 1.05 × 10−1 | 9.09 × 10−2 | 1.18 × 10−1 | 6.03 × 10−2 | 1.60 × 10−1 | 1.36 × 10−15 | 1.42 × 10−15 |
| avg | −32.8 | −32.3 | −30.4 | −32.4 | −31.7 | −32.4 | −32.9 | −32.2 | −33.2 | −33.2 |
| median | −33.2 | −32.6 | −30.5 | −33.2 | −31.3 | −33.2 | −33.2 | −33.1 | −33.2 | −33.2 |
| worse | −31.4 | −30.2 | −28.4 | −28.5 | −30.2 | −28.4 | −31.2 | −25.9 | −33.2 | −33.2 |
| time | 2.30 × 10−2 | 2.72 × 10−2 | 2.46 × 10−2 | 5.01 × 10−2 | 5.01 × 10−2 | 1.53 × 10−1 | 5.11 × 10−2 | 4.43 × 10−2 | 7.41 × 10−2 | 9.30 × 10−2 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F21 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | −10.2 | −10.2 | −56.1 | −10.2 | −10.2 | −10.2 | −10.2 | −50.5 | −10.1 | −10.2 |
| std | 35.9 | 23.7 | 7.32 × 10−1 | 26.9 | 29.1 | 22.1 | 2.39 × 10−6 | 5.69 × 10−1 | 22.3 | 5.96 × 10−15 |
| avg | −69.3 | −88.9 | −35.3 | −75.4 | −78.7 | −53.8 | −10.2 | −47.9 | −77.4 | −10.2 |
| median | −10.2 | −10.2 | −34.8 | −76.2 | −10.1 | −50.6 | −10.2 | −50.5 | −88.8 | −10.2 |
| worse | −26.3 | −26.3 | −22.4 | −26.3 | −26.3 | −8.82 × 10−1 | −10.2 | −28.8 | −50.6 | −10.2 |
| time | 2.64 × 10−2 | 2.84 × 10−2 | 2.77 × 10−2 | 5.39 × 10−2 | 4.98 × 10−2 | 1.13 × 10−1 | 5.94 × 10−2 | 4.79 × 10−2 | 7.76 × 10−2 | 1.01 × 10−1 |
| convergence | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F22 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | −10.4 | −10.4 | −10.1 | −10.4 | −10.4 | −10.4 | −10.4 | −50.9 | −10.4 | −10.4 |
| std | 297 | 1.08 × 10−3 | 192 | 268 | 134 | 265 | 6.17 × 10−5 | 4.66 × 10−1 | 2.39 | 9.33 × 10−16 |
| avg | −86.8 | −10.4 | −44.4 | −85.6 | −10.0 | −69.9 | −10.4 | −48.0 | −79.0 | −10.4 |
| median | −10.4 | −10.4 | −42.7 | −10.4 | −10.4 | −50.9 | −10.4 | −50.5 | −93.6 | −10.4 |
| worse | −27.7 | −10.4 | −12.5 | −27.7 | −50.9 | −37.2 | −10.4 | −31.9 | −50.9 | −10.4 |
| time | 3.06 × 10−2 | 3.30 × 10−2 | 3.22 × 10−2 | 5.77 × 10−2 | 5.42 × 10−2 | 1.17 × 10−1 | 6.78 × 10−2 | 5.03 × 10−2 | 8.02 × 10−2 | 1.11 × 10−1 |
| convergence | 1.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| F23 | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO | ED | CAED |
| min | −10.5 | −10.5 | −63.7 | −10.5 | −10.5 | −10.5 | −10.5 | −97.5 | −10.5 | −10.5 |
| std | 356 | 9.79 × 10−1 | 12.3 | 27.4 | 21.8 | 26.1 | 16.4 | 11.0 | 22.3 | 1.14−15 |
| avg | −82.6 | −10.4 | −37.4 | −89.4 | −98.2 | −66.7 | −10.1 | −48.5 | −90.0 | −10.5 |
| median | −10.5 | −10.5 | −37.9 | −10.5 | −10.5 | −51.3 | −10.5 | −48.7 | −10.2 | −10.5 |
| worse | −24.2 | −51.7 | −17.6 | −28.1 | −24.2 | −28.1 | −33.3 | −28.0 | −51.3 | −10.5 |
| time | 3.65 × 10−2 | 3.94 × 10−2 | 3.87 × 10−2 | 6.44 × 10−2 | 6.10 × 10−2 | 1.24 × 10−1 | 7.64 × 10−2 | 5.72 × 10−2 | 8.81 × 10−2 | 1.23 × 10−1 |
| convergence | 1.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Cantilever Beam | CAED | ED | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO |
|---|---|---|---|---|---|---|---|---|---|---|
| worst | 13.3605 | 13.3621 | 13.3616 | 13.3619 | 22.8580 | 13.3622 | 13.3695 | 13.3604 | 13.3606 | 14.7054 |
| best | 13.3925 | 13.4365 | 13.3737 | 13.3661 | 90.0301 | 13.3892 | 13.4033 | 13.3812 | 14.7070 | 18.8989 |
| std | 0.0098 | 0.0248 | 0.0045 | 0.0013 | 19.7027 | 0.0077 | 0.0119 | 0.0065 | 0.4254 | 1.4752 |
| mean | 13.3712 | 13.3830 | 13.3670 | 13.3636 | 42.1413 | 13.3707 | 13.3817 | 13.3647 | 13.4963 | 16.6254 |
| median | 13.3696 | 13.3717 | 13.3672 | 13.3635 | 36.4074 | 13.3686 | 13.3775 | 13.3616 | 13.3609 | 16.3014 |
| Cantilever Beam | CAED | ED | PSO | GWO | AOA | DBO | GJO | SCSO | BKA | SABO |
|---|---|---|---|---|---|---|---|---|---|---|
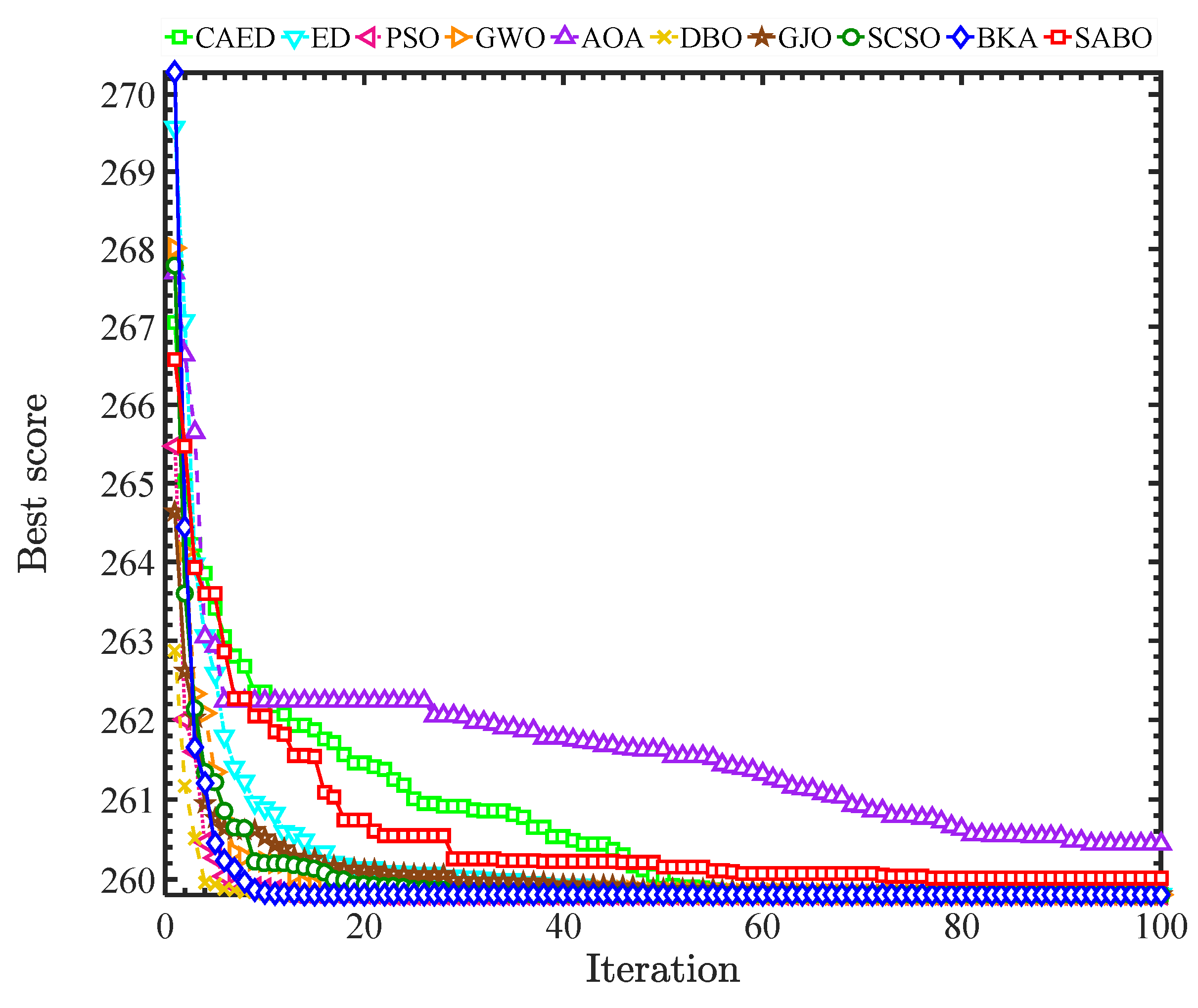
| worst | 259.8050467 | 259.8050467 | 259.8050467 | 259.8050675 | 259.8500987 | 259.8050467 | 259.8050759 | 259.8050484 | 259.8050467 | 259.8243953 |
| best | 259.805047 | 259.8050477 | 259.8050467 | 259.8062248 | 262.649983 | 259.8050467 | 259.8120313 | 259.8052105 | 259.8050467 | 260.3863756 |
| std | 1.1171 × 10−7 | 3.21343 × 10−7 | 1.15786 × 10−11 | 0.000340549 | 0.809067725 | 6.71779 × 10−13 | 0.00247157 | 4.89464 × 10−5 | 4.96273 × 10−13 | 0.17902373 |
| mean | 259.8050467 | 259.8050469 | 259.8050467 | 259.8053782 | 260.4395624 | 259.8050467 | 259.8076083 | 259.8050817 | 259.8050467 | 260.0190289 |
| median | 259.8050467 | 259.8050469 | 259.8050467 | 259.8053139 | 260.2590527 | 259.8050467 | 259.8069449 | 259.8050596 | 259.8050467 | 259.9452844 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zheng, Y.; Cao, L.; Xiong, M. Comprehensive Adaptive Enterprise Optimization Algorithm and Its Engineering Applications. Biomimetics 2025, 10, 302. https://doi.org/10.3390/biomimetics10050302
Wang S, Zheng Y, Cao L, Xiong M. Comprehensive Adaptive Enterprise Optimization Algorithm and Its Engineering Applications. Biomimetics. 2025; 10(5):302. https://doi.org/10.3390/biomimetics10050302
Chicago/Turabian StyleWang, Shuxin, Yejun Zheng, Li Cao, and Mengji Xiong. 2025. "Comprehensive Adaptive Enterprise Optimization Algorithm and Its Engineering Applications" Biomimetics 10, no. 5: 302. https://doi.org/10.3390/biomimetics10050302
APA StyleWang, S., Zheng, Y., Cao, L., & Xiong, M. (2025). Comprehensive Adaptive Enterprise Optimization Algorithm and Its Engineering Applications. Biomimetics, 10(5), 302. https://doi.org/10.3390/biomimetics10050302






