Modular Snake-like Robot Designed for On-Site Reconfiguration in Space Exploration
Abstract
1. Introduction
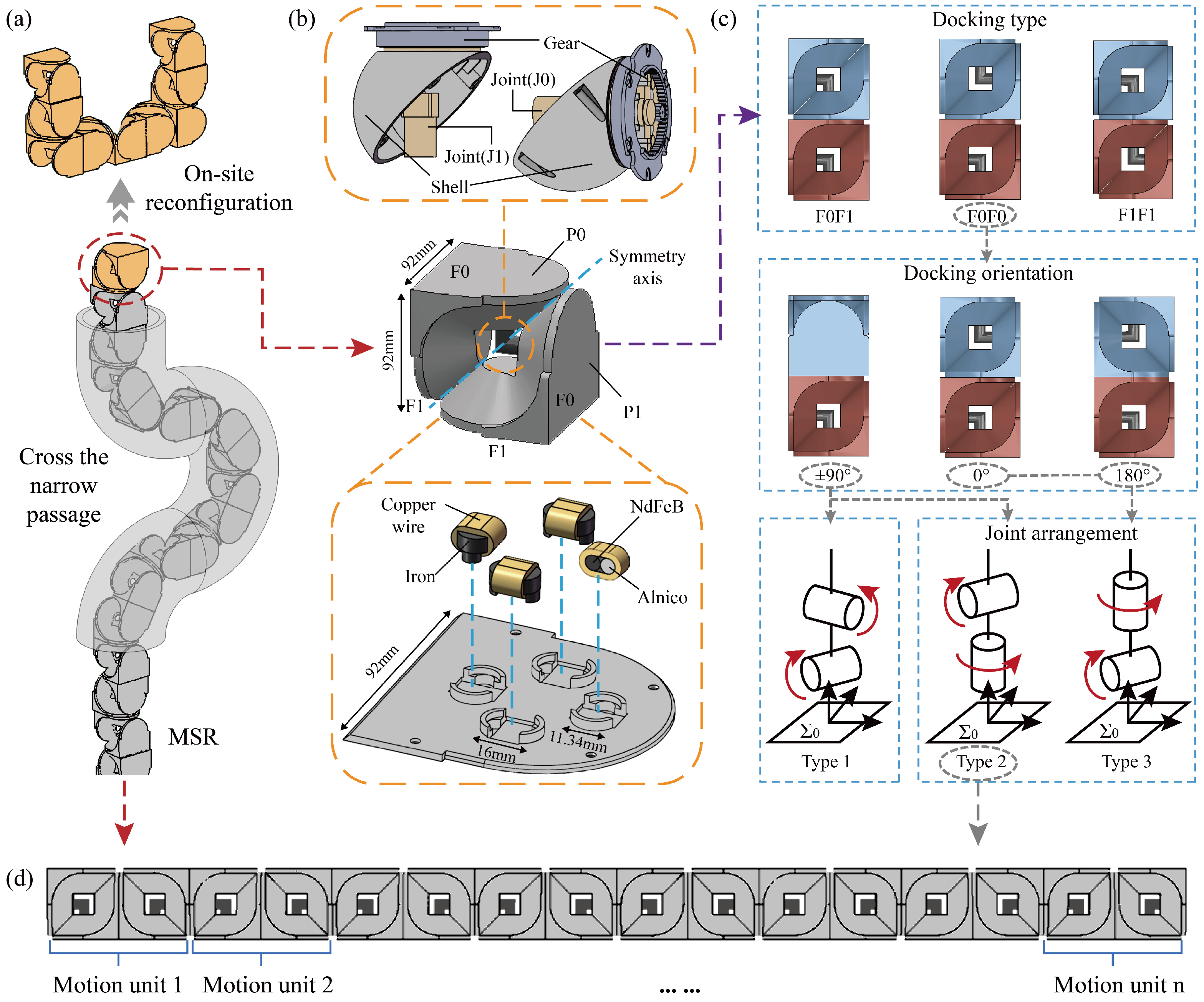
2. Structure and Feasibility Analysis of MSR
2.1. Subot
2.2. Functional Compatibility
2.3. Structural Constrains
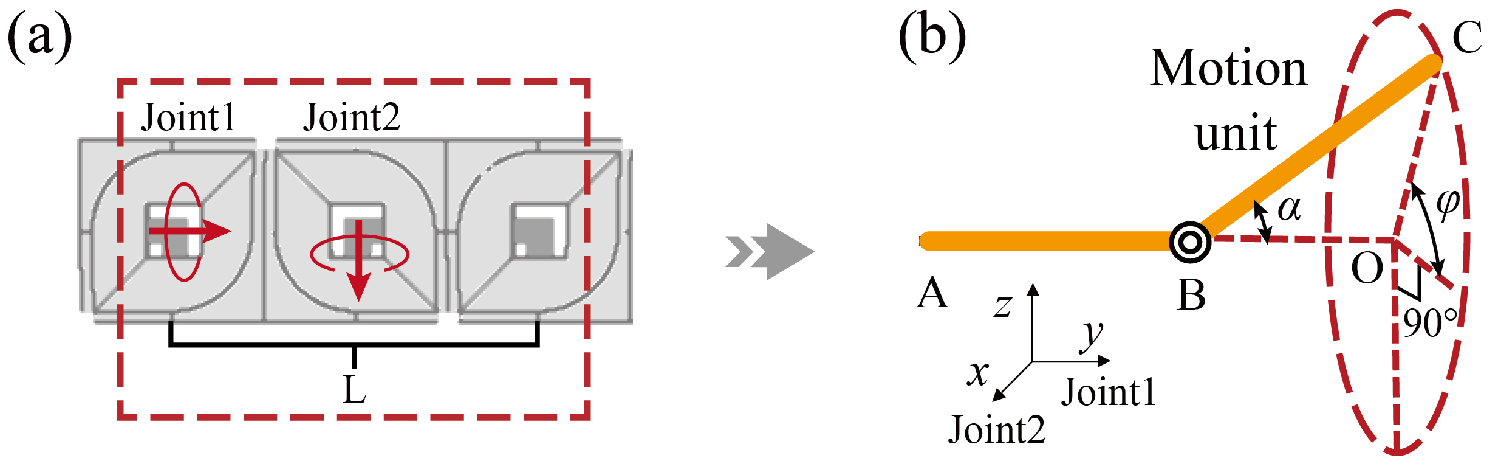
3. Joints Coordination Motion Schemes
3.1. Generation of Propulsion Speed
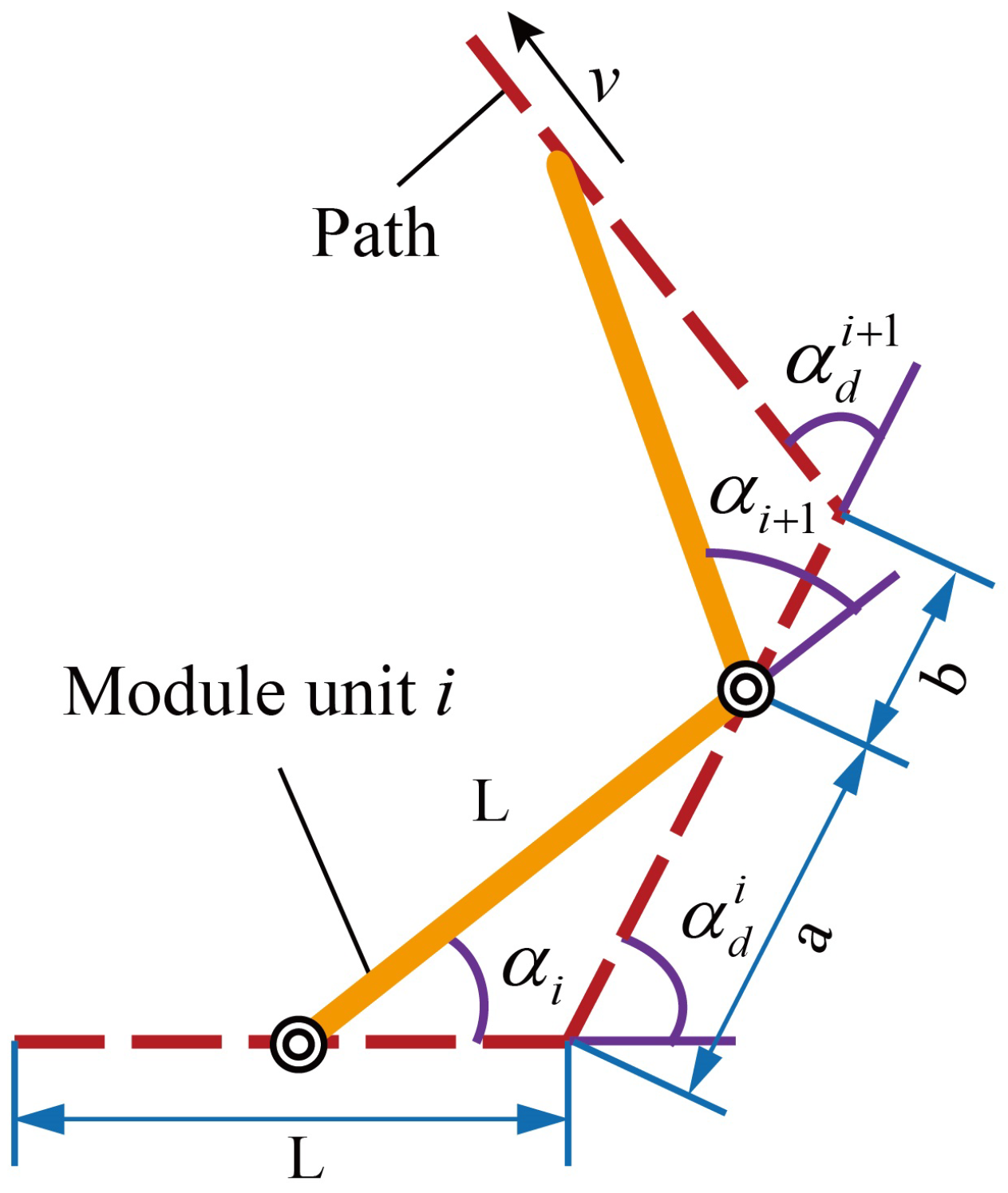
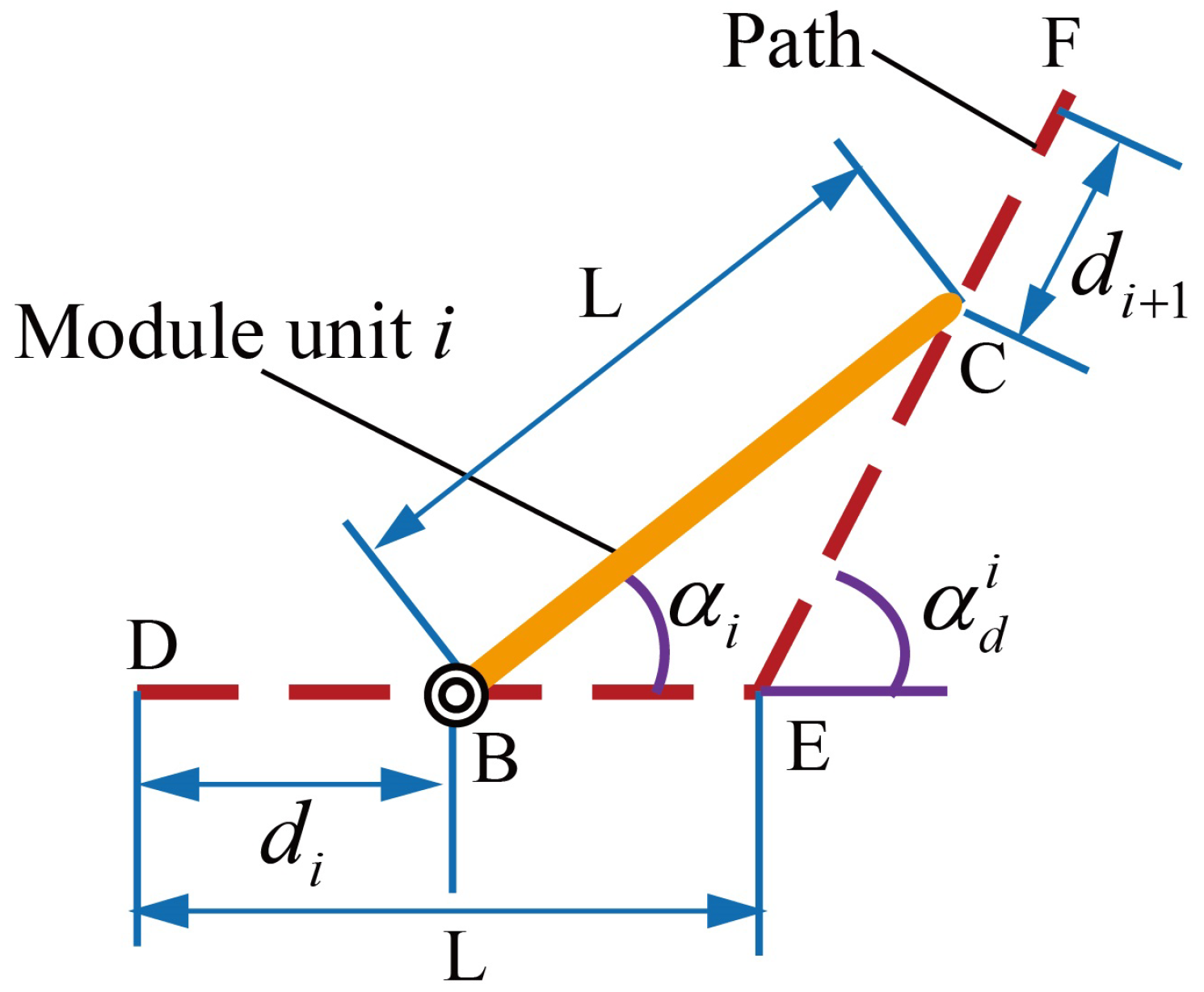
3.2. Kinematic Analysis
4. Path Planning
4.1. State-Action Design
4.2. Reward Design
- (1)
- Distance is the intuitive metric for judging success. Using it as part of the reward system encourages the agent to move to the target. Euclidean distance is utilized as the reward value as follows:where is a scaling factor to control the magnitude of the reward.
- (2)
- Collision is strictly prohibited in path planning. To ensure the agent avoids obstacles, collision is incorporated as part of the reward function, as follows:where is a large penalty value designed to emphasize the importance of avoiding collisions.
- (3)
- In path planning, it is necessary to take joint deflection angle constraints into account to ensure the feasibility of movement. Under normal situations, the motion units are fully decoupled due to the utilization of the transitional modules and the dynamic motion unit method. Hence, the maximum joint deflection angle corresponds to the path point deflection angle, which can be constrained during action generation. However, for the 2D or special environments, it is required to utilize Equation (2) to calculate the maximum joint deflection angle and use it as a reward to train the agent. Moreover, in all situations, the path point deflection angle is incorporated into the reward function to improve the smoothness of the path.where is a scaling factor used to control the magnitude of the reward.
- (4)
- Adding the step number into the reward function can reduce the length of the planned path. On the one hand, it can reduce energy consumption and improve the efficiency, on the other hand, it helps prevent potential detours.where is a scaling factor used to control the magnitude of the reward.
4.3. PPO Algorithm
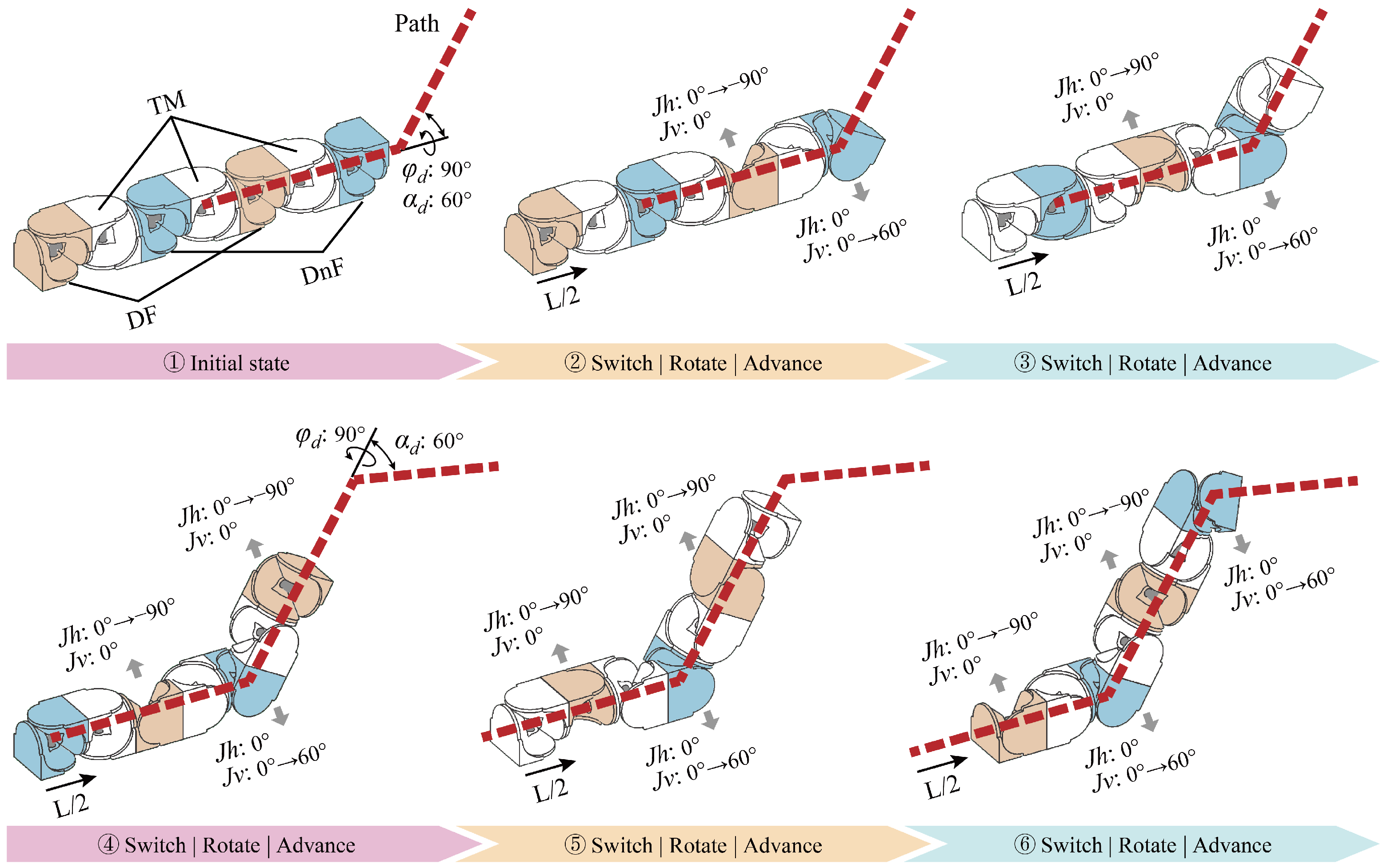
5. Simulation Experiments
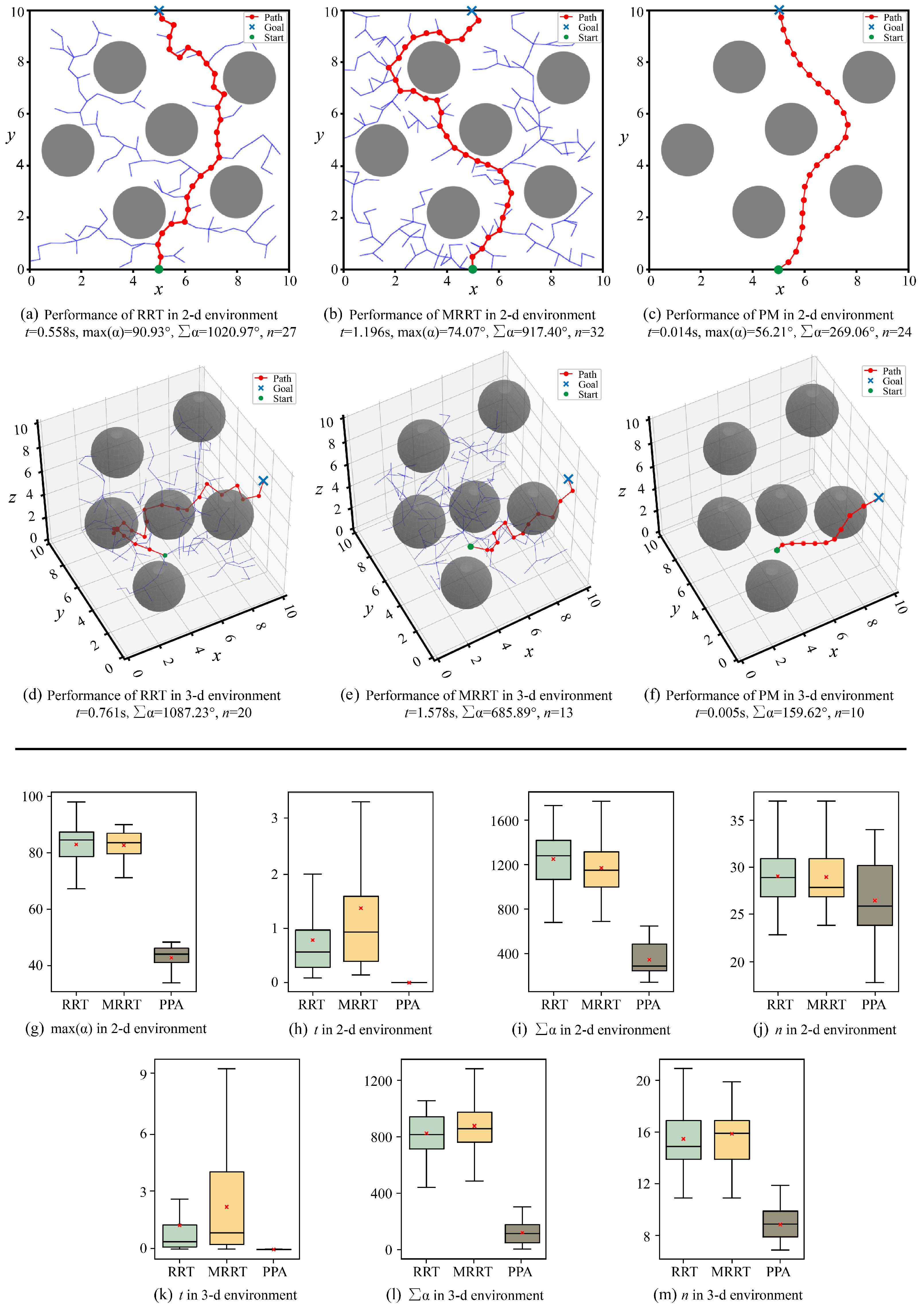
5.1. Simulation Comparisons
5.2. Simulations of Potential Applications
6. Conclusions and Prospect
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yue, C.F.; Lin, T.; Zhang, X.; Chen, X.Q.; Cao, X.B. Hierarchical path planning for multi-arm spacecraft with general translational and rotational locomotion mode. Sci. China Technol. Sci. 2023, 66, 1180–1191. [Google Scholar] [CrossRef]
- Kim, U.Y.; Jung, D.; Jeong, H.; Park, J.; Jung, H.M.; Cheong, J.; Choi, H.R.; Do, H.; Park, C. Integrated linkage-driven dexterous anthropomorphic robotic hand. Nat. Commun. 2021, 12, 7177. [Google Scholar] [CrossRef]
- Niu, L.Z.; Ding, L.; Zhang, S.J.; Yang, H.G.; Gao, H.B.; Deng, Z.Q.; Liu, G.J.; Hossain, M. SoSpider: A bio-inspired multimodal untethered soft hexapod robot for planetary lava tube exploration. Sci. China Technol. Sci. 2023, 66, 3090–3106. [Google Scholar] [CrossRef]
- Chen, T.G.; Newdick, S.; Di, J.L.; Bosio, C.; Ongole, N.; Lapôtre, M.; Pavone, M.; Cutkosky, M.R. Locomotion as manipulation with ReachBot. Sci. Robot. 2024, 9, eadi9762. [Google Scholar] [CrossRef]
- Sui, X.; Lai, M.Z.; Qi, J.; Yang, Z.Y.; Zhao, N.; Zhao, J.; Cai, H.G.; Zhu, Y.H. A Fluid-Driven Loop-Type Modular Soft Robot with Integrated Locomotion and Manipulation Capability. Biomimetics 2023, 8, 390. [Google Scholar] [CrossRef]
- Luo, H.B.; Lam, T.L. Auto-Optimizing Connection Planning Method for Chain-Type Modular Self-Reconfiguration Robots. IEEE Trans. Robot. 2023, 39, 1353–1372. [Google Scholar] [CrossRef]
- Saintyves, B.; Spenko, M.; Jaeger, H.M. A self-organizing robotic aggregate using solid and liquid-like collective states. Sci. Robot. 2024, 9, adh4130. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, G.L.; Zheng, T.J.; Shen, W.; Fang, Z.; Zhang, C. Tension reduction method for a modular cable-driven robotic arm with co-shared cables. Intell. Serv. Robot. 2022, 15, 27–38. [Google Scholar] [CrossRef]
- Belke, C.H.; Holdcroft, K.; Sigrist, A.; Paik, J. Morphological flexibility in robotic systems through physical polygon meshing. Nat. Mach. Intell. 2023, 5, 669–675. [Google Scholar] [CrossRef]
- Gregg, C.E.; Catanoso, D.; Formoso, O.I.B.; Kostitsyna, I.; Ochalek, M.E.; Olatunde, T.J.; Park, I.W.; Sebastianelli, F.M.; Taylor, E.M.; Trinh, G.T.; et al. Ultralight, strong, and self-reprogrammable mechanical metamaterials. Sci. Robot. 2024, 9, eadi2746. [Google Scholar] [CrossRef] [PubMed]
- Nisser, M.; Cheng, L.; Makaram, Y.; Suzuki, R.; Mueller, S. ElectroVoxel: Electromagnetically actuated pivoting for scalable modular self-reconfigurable robots. In Proceedings of the International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 4254–4260. [Google Scholar]
- Zhao, N.; Gao, L.; Yang, Z.; Qi, J.; Han, K.; Sui, X.; Zhao, J.; Zhu, Y. Meta-Module Mutual Assistance: A Bioinspired Design for Self-Assembly of Modular Space Robot. Adv. Intell. Syst. 2023, 5, 2200450. [Google Scholar] [CrossRef]
- Li, C.Y.; Hu, C.H.; Angeles, J.; Qin, Z.B.; Xie, H.X.; Wang, X.F.; Xiao, H. Dynamics of a modular manipulator with multiple actuation modes for space applications. Mech. Mach. Theory 2023, 189, 105408. [Google Scholar] [CrossRef]
- Zhang, E.; Sai, H.; Li, Y.; Sun, X.; Zhang, T.; Xu, Z. Modular robotic manipulator and ground assembly system for on-orbit assembly of space telescopes. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 2283–2293. [Google Scholar] [CrossRef]
- Yang, Z.; Lai, M.; Qi, J.; Zhao, N.; Sui, X.; Zhao, J.; Zhu, Y. Reorientation and obstacle avoidance control of free-floating modular robots using sinusoidal oscillator. Chin. J. Aeronaut. 2024, 6, 262–275. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, S.; Zhou, N.; Qi, J.; Zhao, N.; Fan, J.; Zhao, J.; Zhu, Y. Efficient Locomotion for Space Robots Inspired by the Flying Snake. Aerospace 2024, 11, 1025. [Google Scholar] [CrossRef]
- Cortez, R.; Sandoval-Chileño, M.A.; Lozada-Castillo, N.; Luviano-Juárez, A. Snake Robot with Motion Based on Shape Memory Alloy Spring-Shaped Actuators. Biomimetics 2024, 9, 180. [Google Scholar] [CrossRef]
- Wang, W.; Wang, K.; Zhang, H.X. Crawling gait realization of the mini-modular climbing caterpillar robot. Prog. Nat. Sci. 2009, 19, 1821–1829. [Google Scholar] [CrossRef]
- Mishra, A.K.; Mondini, A.; Del Dottore, E.; Sadeghi, A.; Tramacere, F.; Mazzolai, B. Modular Continuum Manipulator: Analysis and Characterization of Its Basic Module. Biomimetics 2018, 3, 3. [Google Scholar] [CrossRef]
- Vaquero, T.; Daddi, G.; Thakker, R. EELS: Autonomous snake-like robot with task and motion planning capabilities for ice world exploration. Sci. Robot. 2024, 88, eadh8332. [Google Scholar] [CrossRef]
- Peng, Y.; Nabae, H.; Funabora, Y.; Suzumori, K. Controlling a peristaltic robot inspired by inchworms. Biomim. Intell. Robot. 2024, 1, 100146. [Google Scholar] [CrossRef]
- Bai, X.; Peng, Y.; Li, D.; Liu, Z.; Mao, Z. Novel soft robotic finger model driven by electrohydrodynamic (EHD) pump. J. Zhejiang-Univ.-Sci. 2024, 25, 596–604. [Google Scholar] [CrossRef]
- Palmer, D.; Cobos-Guzman, S.; Axinte, D. Real-time method for tip following navigation of continuum snake arm robots. Robot. Auton. Syst. 2014, 62, 1478–1485. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, J.M.; Xiao, X.; Ou, J.; Qin, F.T. A snake-inspired path planning algorithm based on reinforcement learning and self-motion for hyper-redundant manipulators. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221110022. [Google Scholar] [CrossRef]
- Bloss, R. Snake-like robots “reach” into many types of applications. Ind. Robot. Int. J. 2012, 39, 436–440. [Google Scholar] [CrossRef]
- Qin, G.D.; Cheng, Y.; Pan, H.T.; Zhao, W.L.; Shi, S.S.; Ji, A.H.; Wu, H.P. Systematic design of snake arm maintainer in nuclear industry. Fusion Eng. Des. 2022, 176, 113049. [Google Scholar] [CrossRef]
- Jia, L.F.; Huang, Y.P.; Chen, T.; Guo, Y.; Yin, Y.; Chen, J. MDA plus RRT: A general approach for resolving the problem of angle constraint for hyper-redundant manipulator. Expert Syst. Appl. 2022, 193, 116379. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X.L.; Jin, H.Z.; Bie, D.Y.; Zhu, Y.H. Automatic Locomotion Generation for a UBot Modular Robot—Towards Both High-speed and Multiple Patterns. Int. J. Adv. Robot. Syst. 2015, 12, 32. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Bie, D.Y.; Iqbal, S.; Wang, X.L.; Gao, Y.S.; Zhao, J. A Simplified Approach to Realize Cellular Automata for UBot Modular Self-Reconfigurable Robots. J. Intell. Robot. Syst. 2015, 79, 37–54. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, S.; Han, K.; Qi, J.; Zhao, N.; Sui, X.; Fan, J.; Zhao, J.; Zhu, Y. Design of a multi-environmentally adaptable modular self-reconfigurable robot. IEEE Robot. Autom. Lett. 2024, 9, 8627–8634. [Google Scholar] [CrossRef]
- Zhao, N.; Gao, Y.S.; Qi, J.; Yang, Z.Y.; Zhao, S.K.; Sui, X.; Han, K.; Zhao, J.; Zhu, Y.H. An efficient self-reconfiguration method to deploy space modular robots. Sci. China Technol. Sci. 2024, 67, 3962–3964. [Google Scholar] [CrossRef]
- Xie, H.B.; Wang, C.; Li, S.S.; Hu, L.; Yang, H. A geometric approach for follow-the-leader motion of serpentine manipulator. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419874638. [Google Scholar] [CrossRef]
- Zawidzki, M.; Szklarski, J. Transformations of Arm-Z modular manipulator with Particle Swarm Optimization. Adv. Eng. Softw. 2018, 126, 147–160. [Google Scholar] [CrossRef]
- Ji, H.C.; Xie, H.B.; Wang, C.; Yang, H. E-RRT*: Path Planning for Hyper-Redundant Manipulators. IEEE Robot. Autom. Lett. 2023, 8, 8128–8135. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Hua, X.T.; Wang, G.L.; Xu, J.; Chen, K. Reinforcement learning-based collision-free path planner for redundant robot in narrow duct. J. Intell. Manuf. 2021, 32, 471–482. [Google Scholar] [CrossRef]
- You, C.X.; Lu, J.B.; Filev, D.; Tsiotras, P. Advanced planning for autonomous vehicles using reinforcement learning and deep inverse reinforcement learning. Robot. Auton. Syst. 2019, 114, 1–18. [Google Scholar] [CrossRef]
- Luo, H.; Zhou, N.; Zhang, H.; Han, K.; Zhao, N.; Yang, Z.; Qi, J.; Zhao, S.; Zhao, J.; Zhu, Y. A Microgravity Simulation Experimental Platform for Small Space Robots in Orbit. arXiv 2025, arXiv:2504.18842. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, N.; Zhao, S.; Zheng, T.; Qi, J.; Yang, Z.; Sui, X.; Han, K.; Luo, H.; Zhou, N.; Zhao, J.; et al. Modular Snake-like Robot Designed for On-Site Reconfiguration in Space Exploration. Biomimetics 2025, 10, 293. https://doi.org/10.3390/biomimetics10050293
Zhao N, Zhao S, Zheng T, Qi J, Yang Z, Sui X, Han K, Luo H, Zhou N, Zhao J, et al. Modular Snake-like Robot Designed for On-Site Reconfiguration in Space Exploration. Biomimetics. 2025; 10(5):293. https://doi.org/10.3390/biomimetics10050293
Chicago/Turabian StyleZhao, Ning, Sikai Zhao, Tianjiao Zheng, Jian Qi, Zhiyuan Yang, Xin Sui, Kai Han, Hang Luo, Nanlin Zhou, Jie Zhao, and et al. 2025. "Modular Snake-like Robot Designed for On-Site Reconfiguration in Space Exploration" Biomimetics 10, no. 5: 293. https://doi.org/10.3390/biomimetics10050293
APA StyleZhao, N., Zhao, S., Zheng, T., Qi, J., Yang, Z., Sui, X., Han, K., Luo, H., Zhou, N., Zhao, J., & Zhu, Y. (2025). Modular Snake-like Robot Designed for On-Site Reconfiguration in Space Exploration. Biomimetics, 10(5), 293. https://doi.org/10.3390/biomimetics10050293






