An Improved Whale Optimization Algorithm for the Clean Production Transformation of Automotive Body Painting
Abstract
1. Introduction
- (1)
- An improved whale optimization algorithm (NEDWOA) is proposed, incorporating a nonlinear convergence factor, elite opposition-based learning, and adaptive dynamic parameters. The NEDWOA demonstrates significant improvements in global search capability, convergence speed, and robustness.
- (2)
- The clean production problem in automotive body painting is defined as a multi-objective optimization issue involving material flow, energy flow, and environmental emissions in the painting process. From the perspective of “low-carbon consumption + emission-reducing production”, a multi-level, multi-objective decision-making model for automotive painting is established, considering both process and operational layers, with objectives including material cost, painting energy consumption, carbon emissions, and painting time.
- (3)
- The NEDWOA is applied to optimize the automotive painting model, proposing a production method for automotive body painting based on the NEDWOA. Taking the new energy vehicles from the TJ Automotive Manufacturing Plant in China as an example, compared to other algorithms, the proposed algorithm achieves superior optimization results, improving painting production efficiency by 42.1%, achieving a waste gas purification rate of over 98%, enhancing average energy-saving effects by more than 18.2%, and reducing manufacturing costs by 17.9%.
2. Improved Whale Optimization Algorithm
- (1)
- Nonlinear convergence factor: replaces the linear-decreasing convergence factor with a nonlinear version to flexibly balance exploration and exploitation.
- (2)
- Elite opposition-based learning: generates reverse solutions from high-quality elite individuals to increase population diversity.
- (3)
- Dynamic parameter self-adaptation: adjusts parameters in real time based on search states to enhance adaptability.
2.1. Improved Strategy
- (1)
- Nonlinear Convergence Factor
- (2)
- Elite Opposition-Based Learning
- (3)
- Dynamic Parameter Self-Adaptation
2.2. NEDWOA
| Algorithm 1: Pseudo-code of the NEDWOA |
| Input: number of search agents: N, Dim, and Max_Iter Output: optimal fitness value Initialize position of every individual whale Calculate the fitness value for all search agents The search agent with the best fitness was selected as the lead whale While lter < Max_Iter Calculating the nonlinear convergence factor a by the Equation (1) Calculating the dynamic parameter self-adaptation σ2(t) by the Equation (3) Calculating the spiral coefficient b by the Equation (4) Calculating the random search probability p by the Equation (5) Calculating the coefficient vector A by the Equation (7) Calculating the coefficient vector D by the Equation (8) Assign random numbers between [−1, 1] to l and between [0, 1] to rrand, respectively, If (p < 0.5) If (|A| < 1) Update the position of the current search agent by the Equation (6) else if (|A| ≥ 1) Select a random search agent Xrand Update the position of the current search agent by the Equation (12) End if else if (p ≥ 0.5) Update the position of the current search by the Equation (11) End if End for Update the current position of whale populations using elite opposition-based learning by the Equation (2) Update a, σ, l, b, and p Check if the agent is out of the search boundary and correct it Calculate the fitness value for all search agents Sort populations in ascending order according to fitness The search agents are sorted in ascending order according to the fitness value Update X* if there is a better solution Iter = Iter + 1 End while Return X* and optimal fitness value |
2.3. Experimental Results and Discussion
- (1)
- Benchmark functions
- (2)
- Effect of each proposed component
3. Analysis of “Low Carbon Consumption + Emission Reduction Production” Spraying Model
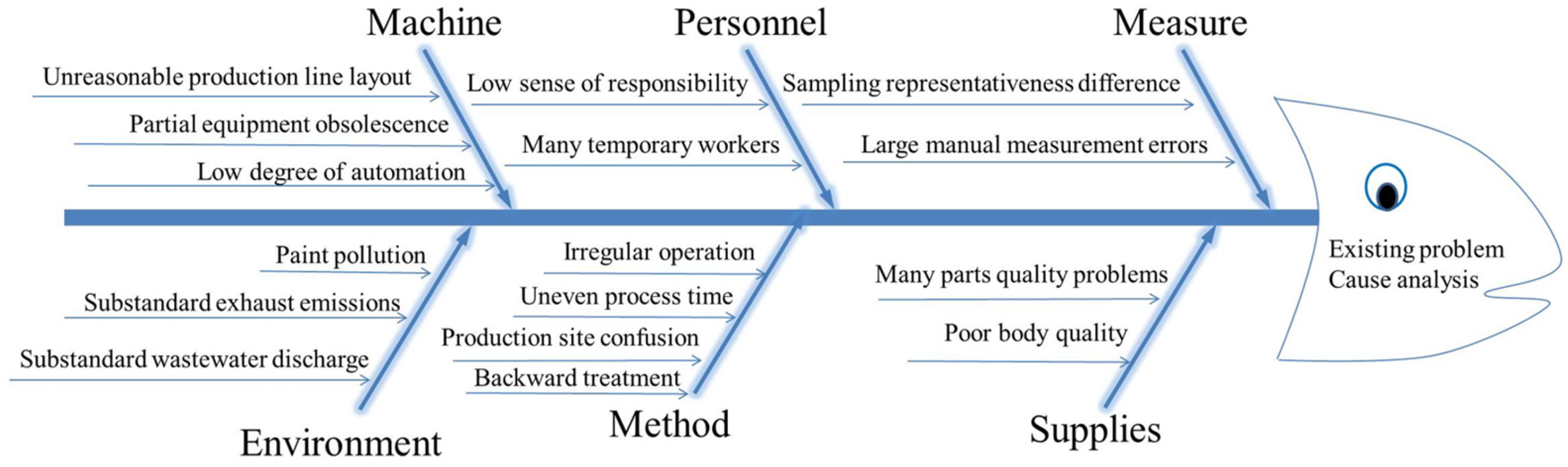
3.1. Analysis of Automobile Spraying Process Problems
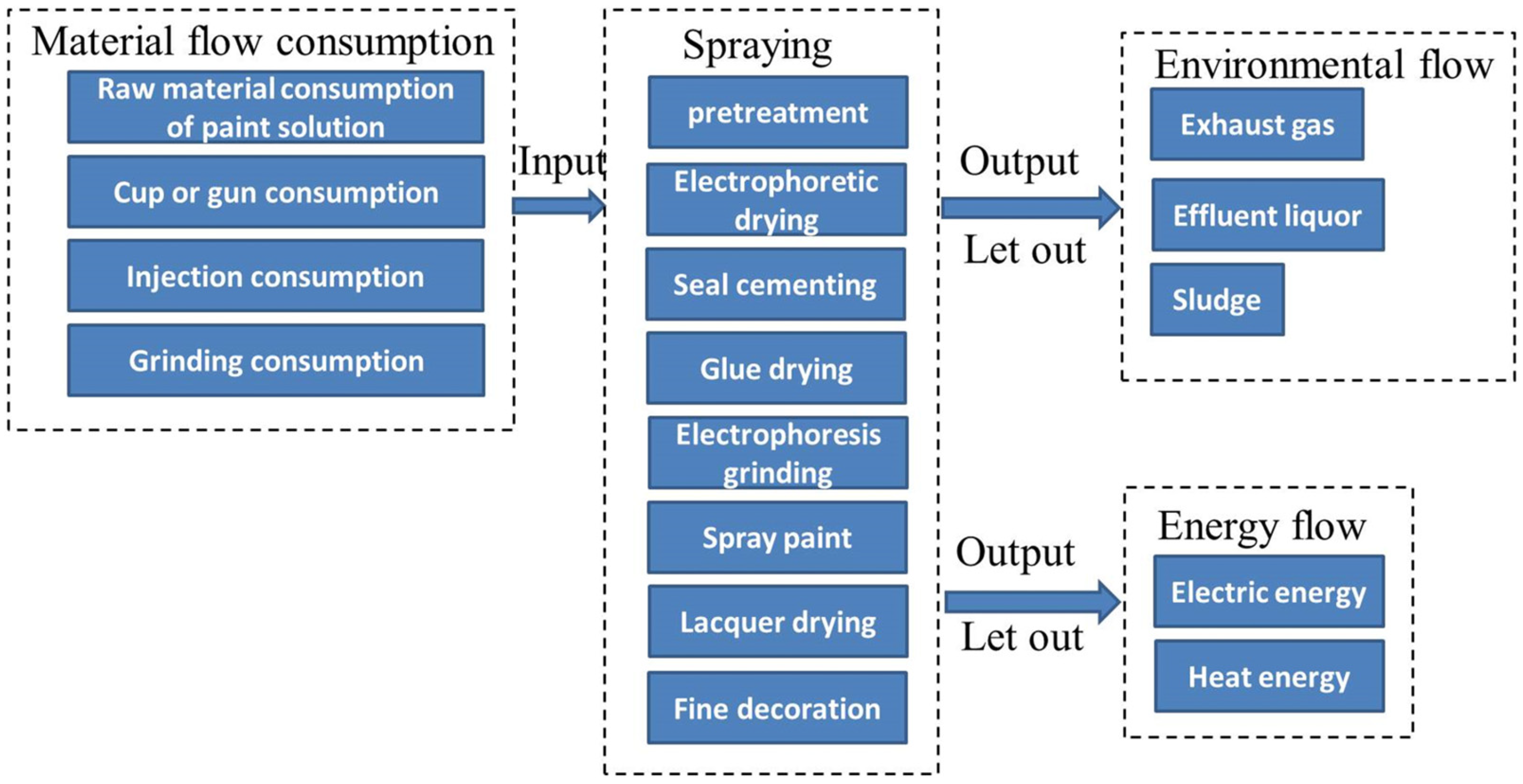
3.2. Energy Consumption Model
3.2.1. Energy Consumption in the Painting Stage
3.2.2. Other Energy Consumption
3.3. Carbon Emissions Model
4. Multi-Layer and Multi-Objective Optimization Model and Method for Spraying Process
4.1. Objective Function
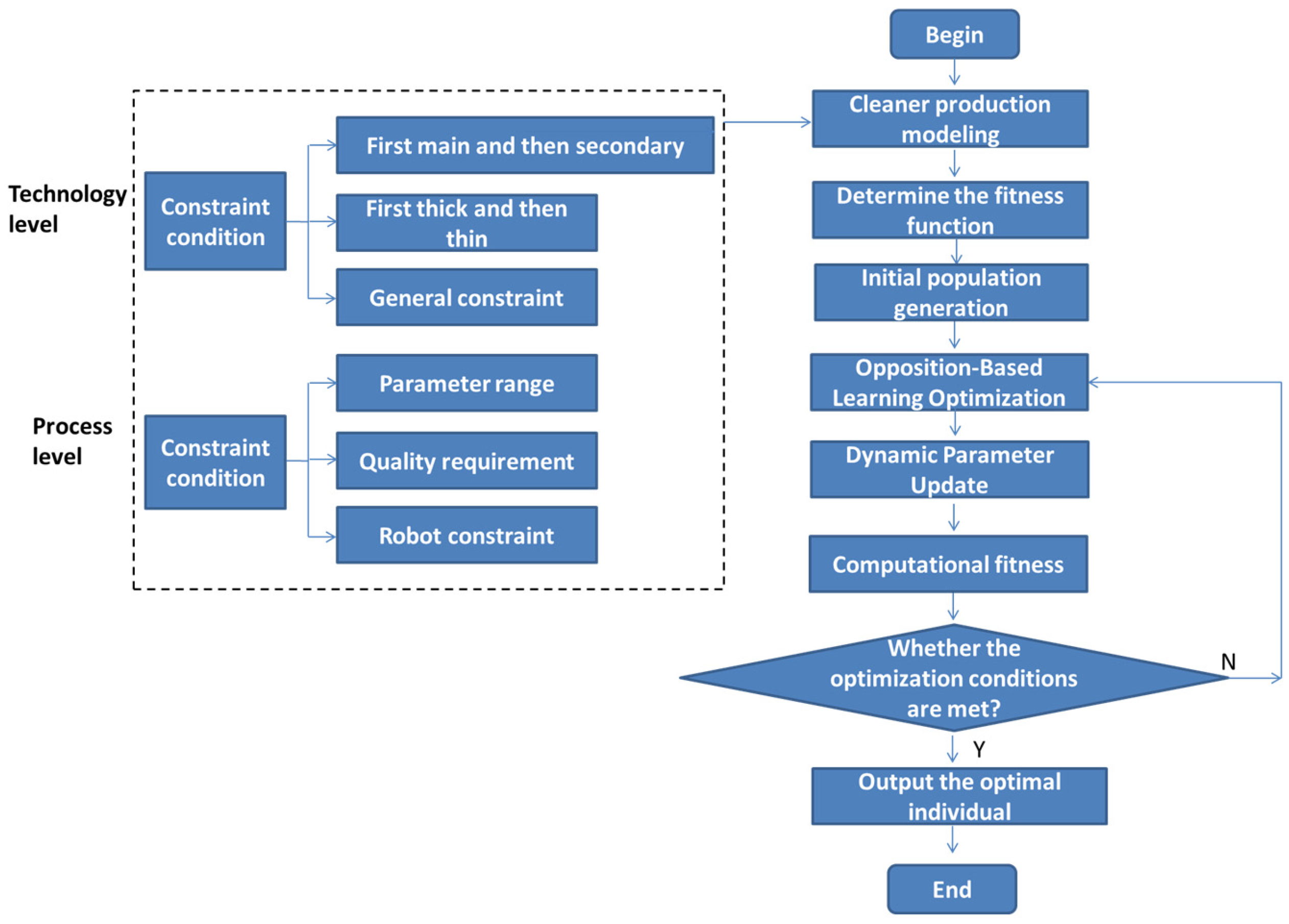
4.2. Constraint Condition
4.3. Optimization Method Based on the NEDWOA
Determination of Fitness Function
5. Case Study
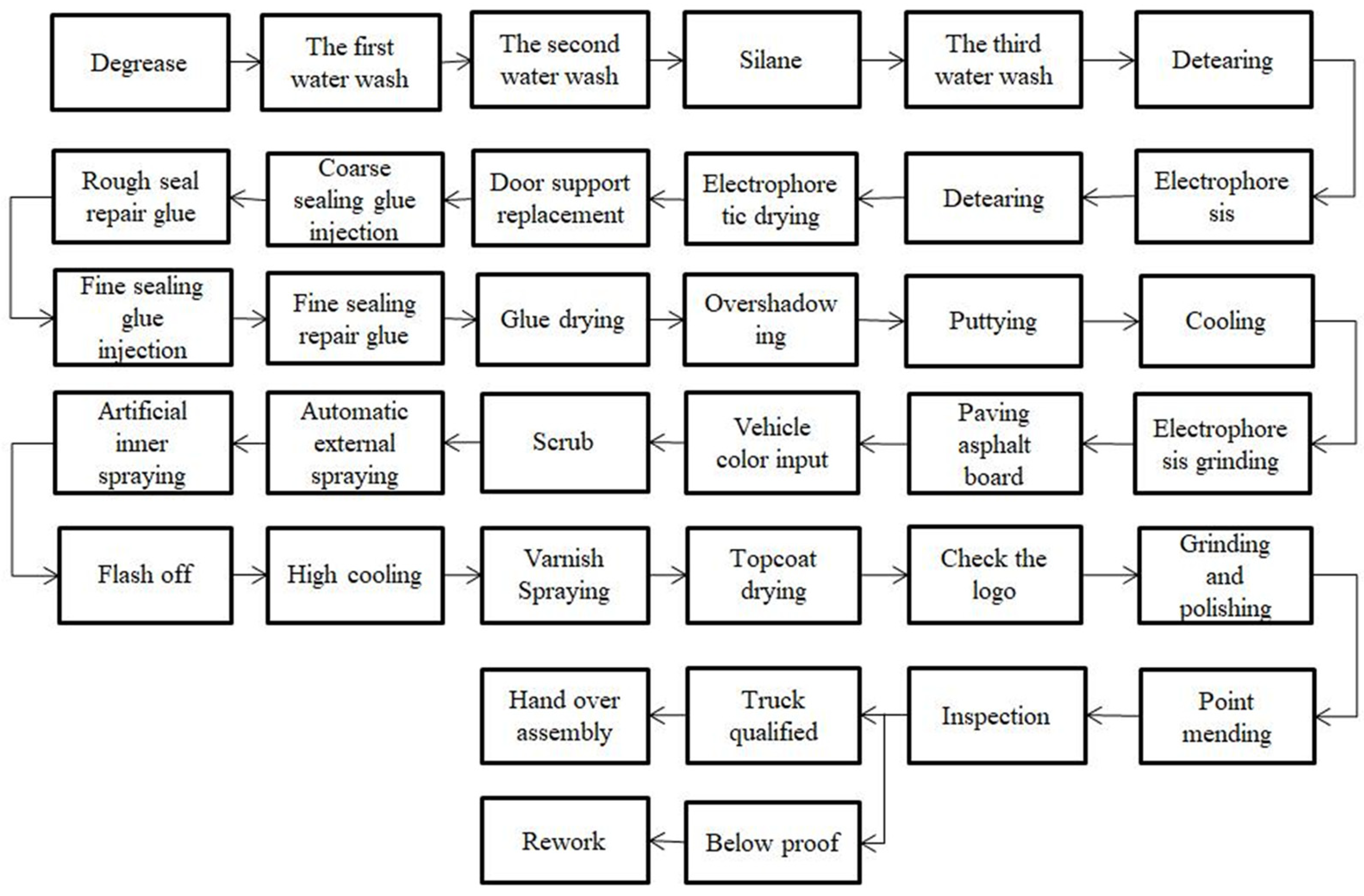
5.1. Spraying Process Parameter Setting and Calculation
5.2. Spraying Optimization Based on EDOWOA
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Shi, G.; Lowell, Z. “Production-living-ecology” transition adaptation and willingness to consume clean energy: Evidence from Jiangsu Province, China. J. Clean. Prod. 2025, 493, 144950. [Google Scholar] [CrossRef]
- Xu, Y.; Peng, J.; Tian, J.; Fu, S.; Hu, C.; Fu, S.; Feng, Y. The impact and mechanism analysis of Clean Development Mechanism on the synergistic effects of pollution mitigation and carbon reduction. Environ. Res. 2024, 260, 119659. [Google Scholar] [CrossRef] [PubMed]
- Giannetti, B.F.; Agostinho, F.; Cabello Eras, J.J. Cleaner production for achieving the sustainable development goals. J. Clean. Prod. 2020, 271, 209–315. [Google Scholar] [CrossRef]
- Ma, S.; Ding, W.; Liu, Y.; Zhang, Y.; Ren, S.; Kong, X.; Leng, J. Industry 4.0 and cleaner production: A comprehensive review of sustainable and intelligent manufacturing for energy-intensive manufacturing industries. J. Clean. Prod. 2024, 467, 142879. [Google Scholar] [CrossRef]
- Yu, H.; Zhao, Y.; Yang, N.; Pan, Z.; Yu, H. Construction of cleaner production management system in China: Mode innovation of cleaner production. Environ. Sci. Pollut. Res. Int. 2022, 29, 17626–17644. [Google Scholar] [CrossRef]
- Lv, L.; Deng, Z.; Liu, T.; Wan, L. Multilayer and Multi-objective Optimization Model and Applications of Grinding Process Plan for Cleaner Production. China Mech. Eng. 2022, 33, 589–599. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, Y.; Lv, J.; Ren, S.; Yang, H.; Chao, W. Data-driven cleaner production strategy for energy-intensive manufacturing industries: Case studies from Southern and Northern China. Adv. Eng. Inform. 2022, 53, 101684. [Google Scholar] [CrossRef]
- Wang, M.; Hu, Y.; Wang, S. The complementary model of green consumption and low-carbon production under the dual-carbon goal. Syst. Eng.-Theory Pract. 2024, 5, 1–26. [Google Scholar]
- Sharma, R.; Gupta, H. Harmonizing sustainability in industry 5.0 era: Transformative strategies for cleaner production and sustainable competitive advantage. J. Clean. Prod. 2024, 445, 141118. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, F.; Yu, H.; Yang, N.; Zhao, Y.; Yang, J.; Yu, H. Performance evaluation of the practical application of cleaner production management system: A case study of steel enterprise. J. Clean. Prod. 2022, 379, 134468. [Google Scholar] [CrossRef]
- Gary, J.; Zhao, P.; Bao, Z. Dual-Credit Policy of New Energy Automobiles in China: Corporate Innovation Capability. Sustainability 2024, 16, 7504. [Google Scholar] [CrossRef]
- Qin, S.; Xiong, Y. Innovation strategies of Chinese new energy vehicle enterprises under the influence of non-financial policies: Effects, mechanisms and implications. Energy Policy 2022, 164, 112946. [Google Scholar] [CrossRef]
- Julio, L.R.; Tatiana, R.C. A framework for environmental and energy analysis of the automobile painting process. Procedia CIRP 2014, 15, 171–175. [Google Scholar] [CrossRef]
- Jia, L. VOCs Pollution Status and Emission Reduction Countermeasures Automobile Painting Industry As an Example. Leather Manuf. Environ. Technol. 2023, 4, 112–113, 123. [Google Scholar] [CrossRef]
- Yadav, A.; Sachdeva, A.; Garg, R.K.; Qureshi, K.M.; Mewada, B.G.; Qureshi, M.R.N.M.; Mansour, M. Achieving Net-Zero in the Manufacturing Supply Chain through Carbon Capture and LCA: A Comprehensive Framework with BWM-Fuzzy DEMATEL. Sustainability 2024, 16, 6972. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, R.; Zhan, L.; Xu, Z. Research on pollution characteristics of volatile organic compounds based on the remanufacturing process of automobile gearbox. J. Clean. Prod. 2022, 384, 135548. [Google Scholar] [CrossRef]
- Wang, H. Research on Process Planning and Operation Zoning of Automotive Painting Robots. Electroplat. Finish. 2022, 41, 1170–1175. [Google Scholar] [CrossRef]
- Liu, S. Robot spraying copying technology and optimization of car spraying process. J. Intern. Combust. Engine Accessories 2024, 19, 62–64. [Google Scholar] [CrossRef]
- Yang, Q.; Meng, X.; Zhao, H.; Cao, C.; Liu, Y.; Huisingh, D. Sustainable operations-oriented painting process optimisation in automobile maintenance service. J. Clean. Prod. 2021, 324, 129191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Jangir, P.; Kumar, A.; Jangir, N.; Totlani, R. A novel hybrid PSO–WOA algorithm for global numerical functions optimization. In Advances in Computer and Computational Sciences; Advances in Intelligent Systems and Computing; Springer: Singapore, 2017; Volume 554, pp. 53–60. [Google Scholar]
- Lai, X.-D.; Yuan, Y.-F.; Xu, J.-Z.; Wang, M.-W. LiDAR waveform decomposition based on modified differential evolution algorithm. J. Infrared Millim. Waves 2021, 40, 381–390. [Google Scholar]
- Zhang, J.; Li, H.; Parizi, M.K. HWMWOA: A Hybrid WMA–WOA Algorithm with Adaptive Cauchy Mutation for Global Optimization and Data Classification. Int. J. Inf. Technol. Decis. Mak. 2023, 22, 1195–1252. [Google Scholar] [CrossRef]
- Fan, Q.; Chen, Z.; Zhang, W.; Fang, X. ESSAWOA: Enhanced whale optimization algorithm integrated with salp swarm algorithm for global optimization. Eng. Comput. 2020, 38, 797–814. [Google Scholar] [CrossRef]
- Aljaidi, M.; Ramesh, J.V.N.; Kiran, A.; Jangir, P.; Arpita; Pandya, S.B.; Mbasso, W.F.; Abualigah, L.; Alkoradees, A.F.; Khishe, M. MaOSSA: A new high-efficiency many-objective salp swarm algorithm with information feedback mechanism for industrial engineering problems. Results Eng. 2025, 25, 104372. [Google Scholar] [CrossRef]
- Kalananda, A.; Reddy, V.K.; Komanapalli; Narayana, V.L. A combinatorial social group whale optimization algorithm for numerical and engineering optimization problems. Appl. Soft Comput. 2021, 99, 106903. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Ibrahim, A.M. Solving nonlinear systems and unconstrained optimization problems by hybridizing whale optimization algorithm and flower pollination algorithm. Math. Comput. Simul. 2021, 190, 1342–1369. [Google Scholar] [CrossRef]
- Bozorgi, S.M.; Yazdani, S. IWOA: An improved whale optimization algorithm for optimization problems. J. Comput. Des. Eng. 2019, 6, 243–259. [Google Scholar]
- Wang, H.; Wu, F.; Zhang, L. Application of variational mode decomposition optimized with improved whale optimization algorithm in bearing failure diagnosis. Alex. Eng. J. 2021, 60, 4689–4699. [Google Scholar] [CrossRef]
- Mohammed, H.Q.; Hany, M.; Hasanien, S.A. Enhanced whale optimization algorithm for maximum power point tracking of variable-speed wind generators. Appl. Soft Comput. J. 2020, 86, 105937. [Google Scholar]
- Long, W.; Wu, T.; Jiao, J.; Tang, M.; Xu, M. Refraction-learning-based whale optimization algorithm for high-dimensional problems and parameter estimation of PV model. Eng. Appl. Artif. Intell. 2020, 89, 103457. [Google Scholar] [CrossRef]
- Cao, D.; Xu, Y.; Yang, Z.; Dong, H.; Li, X. An enhanced whale optimization algorithm with improved dynamic opposite learning and adaptive inertia weight strategy. Complex Intell. Syst. 2022, 9, 767–795. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X.; Chen, Y.; Liu, Z. A Modified Whale Optimization Algorithm for Large-scale Global Optimization Problems. Expert Syst. Appl. 2018, 114, 563–577. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, L. Whale Optimization Algorithm Based on Lamarckian Learning for Global Optimization Problems. IEEE Access 2019, 7, 36642–36666. [Google Scholar] [CrossRef]
- Wang, T.Y.; He, X.H.; He, C.L. A hybrid whale optimization algorithm based on adaptive strategy. J. Xihua Norm. Univ. (Nat. Sci. Ed.) 2021, 41, 92–99. [Google Scholar]
- Kushwah, R.; Kaushik, M.; Chugh, K. A modified whale optimization algorithm to overcome delayed convergence in artificial neural networks. Soft Comput. 2021, 25, 10275–10286. [Google Scholar] [CrossRef]
- Liang, Z.; Shu, T.; Ding, Z. A Novel Improved Whale Optimization Algorithm for Global Optimization and Engineering Applications. Mathematics 2024, 12, 636. [Google Scholar] [CrossRef]
- Jiang, R.; Yang, M.; Wang, S.; Chao, T. An improved whale optimization algorithm with armed force program and strategic adjustment. Appl. Math. Model. 2020, 81, 603–623. [Google Scholar] [CrossRef]
- Yuan, X.; Miao, Z.; Liu, Z.; Yan, Z.; Zhou, F. Multi-Strategy Ensemble Whale Optimization Algorithm and Its Application to Analog Circuits Intelligent Fault Diagnosis. Appl. Sci. 2020, 10, 3667. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, S. Hybrid whale optimization algorithm with gathering strategies for high-dimensional problems. Expert Syst. Appl. 2021, 179, 115032. [Google Scholar] [CrossRef]
- Li, M.; Xu, G.; Lai, Q.; Chen, J. A chaotic strategy-based quadratic Opposition-Based Learning adaptive variable-speed whale optimization algorithm. Math. Comput. Simul. 2022, 193, 71–99. [Google Scholar] [CrossRef]
- Li, N.; Xu, W.; Zeng, Q. A Hybrid WOA-CNN-BiLSTM Framework with Enhanced Accuracy for Low-Voltage Shunt Capacitor Remaining Life Prediction in Power Systems. Energy 2025, 326, 136183. [Google Scholar] [CrossRef]
- Thakur, D.; Dangi, S.; Lalwani, P. A novel hybrid deep learning approach with GWO–WOA optimization technique for human activity recognition. Biomed. Signal Process. Control 2025, 99, 106870. [Google Scholar] [CrossRef]
- Trivedi, L.N.; Pradeep, J.; Narottam, J.; Arvind, K.; Dilip, L. Novel adaptive whale optimization algorithm for global optimization. Indian J. Sci. Technol. 2016, 9, 1–6. [Google Scholar] [CrossRef]
- Lin, B.; Teng, Y. Synergistic disparities of pollution reduction and carbon mitigation in the industrial chain: Evidence from China’s industrial sector. Environ. Res. 2024, 248, 118226. [Google Scholar] [CrossRef]
- Li, X.; Xu, Z.; Jiang, X.; Wang, T.; Li, Q.; Li, J.; Xia, X.; Chen, X. Numerical Simulations of Paint Droplet Hydrodynamics and Distributions in an Airless Spray Coating Process. Surf. Technol. 2024, 53, 158–166. [Google Scholar] [CrossRef]
- Ciauarellal, M. An Approximate JKR Solution for a General Contact, Including Rough Contacts. J. Mech. Phys. Solids 2018, 114, 209–218. [Google Scholar] [CrossRef]
- Hærvig, J.; Kleinhans, U.; Wieland, C.; Spliethoff, H.; Jensen, A.; Sørensen, K.; Condra, T. On the Adhesive JKR Contact and Rolling Models for Reduced Particle Stiffness Discrete Element Simulations. Powder Technol. 2017, 319, 472–482. [Google Scholar] [CrossRef]
- Zhong, Y.; Du, H.; Zhang, Y.; Peng, H. Thermocapillary migration of heterogeneous droplets with unidirectional temperature gradient. Chin. J. Process Eng. 2018, 18, 697–703. [Google Scholar] [CrossRef]
- Narita, H.; Kawamura, H.; Norihisa, T.; Chen, L.-Y.; Fujimoto, H.; Hasebe, T. Development of Prediction System of Environmental Burden for Machine Tool Operation (2nd Report, Proposal of Evaluation indicator for EcoEfficiency). Opt. Lett. 2006, 71, 1392–1399. [Google Scholar]
- Han, H.; Hang, D.; Peng, L.; Zhu, W. Spraying trajectory planning and structure design of full profiling automatie electrostatie painting machine. J. Mach. Des. 2014, 31, 75–80. [Google Scholar] [CrossRef]

| Improvement Form | Specific Algorithm | Improve Features |
|---|---|---|
| Integrate with other algorithms | PSO-WOA [21] | PSO is used for the development phase and WOA is used for the exploration phase. |
| MDE-WOA [22] | It effectively improves the problem of local optimization and reduces the complexity. | |
| WOA-PS [23] | Combining with the pattern search algorithm for power system planning. | |
| ESSAWOA [24] | The nonlinear parameter SSA is used in the development stage to accelerate the convergence speed of the development stage. | |
| WOA-Salp [25] | Combining with the Salp group algorithm to improved search optimization capabilities. | |
| HS-WOA [26] | The global search ability and convergence performance of the algorithm are enhanced by combining multiple strategies. | |
| WOA-FPA [27] | Combining with Flower Pollination Algorithm to solve complex nonlinear systems and unconstrained optimization problems. | |
| Strategic innovation | IWPA [28] | The exploration ability of whale optimization algorithm is improved. |
| IWOA [29] | Perform bearing fault diagnosis. | |
| EWOA [30] | An enhancement of the meta-heuristic whale optimization algorithm using for maximum power point tracking of variable speed wind turbine. | |
| RLWOA [31] | Refraction learning-based whale optimization algorithm. Performance tests were performed on 1,001,000, and 10,000 dimensions of the benchmark function. | |
| Improved whale optimization algorithm based on inertial weight [32] | Inertia weight is introduced to improve the convergence performance. | |
| MWOA [33] | Population initialization optimization, position update mechanism improvement, convergence factor optimization. | |
| WOALam [34] | WOA based on Lamarckian learning can balance global and local search capabilities well. | |
| Multi-strategy integration | HWOA [35] | The adaptive strategy is introduced to update the whale population position by using the local search mechanism of bat algorithm, and then improve the global optimization and local optimization of the balance algorithm by using the adaptive strategy. |
| MWOA [36] | A modified whale optimization algorithm to overcome delayed convergence in artificial neural networks. | |
| AWOA [37] | The adaptive parameter adjustment strategy is introduced, which has better competitive performance compared with the standard WOA. | |
| WAROA [38] | Military combat strategy is introduced to enhance the population collaborative search ability and global optimization performance. | |
| MSWOA [39] | The initial population data of chaotic initialization strategy are introduced, the Levy flight strategy is introduced to balance local search and global search, and the improved position correction mechanism is used to further improve the exploration level. | |
| HWOAG [40] | The information collection mechanism is introduced to enhance the knowledge accumulation ability of the algorithm. | |
| CQAWOA [41] | The chaotic mapping initialization strategy and the quadratic adversarial learning strategy are introduced to construct a negative feedback adjustment network in the algorithm | |
| WOA-CNN-BiLSTM [42] | An improved bidirectional long short-term memory network method combining convolutional neural networks and whale optimization algorithm was proposed. | |
| GWO–WOA [43] | A novel hybrid deep learning optimization technique for human activity recognition. |
| Name | Equation | Dimension | Search Space |
|---|---|---|---|
| Sphere | 30 | [−100, 100] | |
| Schwefel 2.22 | 30 | [−10, 10] | |
| Schwefel 1.12 | 30 | [−100, 100] | |
| Schwefel 2.21 | 30 | [−100, 100] | |
| Rosenbrock | 30 | [−30, 30] | |
| Step | 30 | [−100, 100] | |
| Quartic | 30 | [−1.28, 1.28] | |
| Schwefel 2.26 | 30 | [−500, 500] | |
| Rastrigin | 30 | [−5.12, 5.12] | |
| Ackley | 30 | [−32, 32] | |
| Alpine | 30 | [−10, 10] | |
| Penalized 1.1 | 30 | [−50, 50] | |
| Penalized 1.2 | 30 | [−50, 50] | |
| Michalewicz | 2 | [−65.536, 65.536] | |
| Kowalik | 4 | [−5, 5] | |
| Six-Hump Camel-Back | 2 | [−5, 5] | |
| Branin | 2 | [−5, 5] | |
| Goldstein-Price | 2 | [−2, 2] | |
| Hartmann-3D | 3 | [0, 1] | |
| Hartmann-6D | 6 | [0, 1] | |
| Shekel 5 | 4 | [0, 10] | |
| Shekel 7 | 4 | [0, 10] | |
| Shekel 10 | 4 | [0, 10] |
| Functions | Evaluation Indexes | WOAa | WOAo | WOAσ |
|---|---|---|---|---|
| F1 | Avg | 4.52 × 10−89 | 6.90 × 10−62 | 2.74 × 10−114 |
| Std | 2.73 × 10−88 | 3.26 × 10−64 | 3.66 × 10−117 | |
| F2 | Avg | 6.38 × 10−50 | 7.39 × 10−34 | 4.42 × 10−76 |
| Std | 5.71 × 10−49 | 3.82 × 10−33 | 2.55 × 10−78 | |
| F3 | Avg | 2.74 × 10−7 | 7.16 × 10−9 | 3.41 × 10−13 |
| Std | 2.89 × 10−6 | 2.07 × 10−8 | 3.78 × 10−14 | |
| F4 | Avg | 5.58 × 10−38 | 7.19 × 10−33 | 3.52 × 10−60 |
| Std | 6.59 × 10−39 | 2.44 × 10−34 | 4.58 × 10−59 | |
| F5 | Avg | 3.06 × 100 | 2.76 × 101 | 3.74 × 10−1 |
| Std | 3.02 × 10−1 | 4.73 × 10−1 | 1.62 × 10−1 | |
| F6 | Avg | 6.25 × 10−4 | 5.51 × 10−5 | 4.66 × 10−6 |
| Std | 3.27 × 10−5 | 1.90 × 10−6 | 5.42 × 10−7 | |
| F7 | Avg | 2.78 × 10−3 | 1.13 × 10−4 | 3.51 × 10−5 |
| Std | 8.52 × 10−4 | 2.71 × 10−5 | 2.46 × 10−5 | |
| F8 | Avg | −1.22 × 104 | −1.22 × 104 | −1.24 × 104 |
| Std | 1.41 × 102 | 6.97 × 102 | 3.22 × 101 | |
| F9 | Avg | 2.54 × 10−35 | 1.89 × 10−35 | 7.22 × 10−61 |
| Std | 4.37 × 10−35 | 1.04 × 10−34 | 7.25 × 10−63 | |
| F10 | Avg | 3.25 × 10−15 | 2.31 × 10−15 | 4.72 × 10−17 |
| Std | 1.77 × 10−15 | 1.77 × 10−15 | 5.66 × 10−18 | |
| F11 | Avg | 3.47 × 10−9 | 3.47 × 10−9 | 8.56 × 10−39 |
| Std | 2.64 × 10−11 | 2.64 × 10−11 | 4.77 × 10−38 | |
| F12 | Avg | 2.90 × 10−3 | 2.90 × 10−3 | 6.35 × 10−4 |
| Std | 1.33 × 10−2 | 1.33 × 10−2 | 5.21 × 10−5 | |
| F13 | Avg | 7.61 × 10−4 | 7.61 × 10−4 | 5.26 × 10−11 |
| Std | 2.56 × 10−4 | 2.56 × 10−4 | 3.42 × 10−10 | |
| F14 | Avg | 2.44 × 100 | 2.44 × 100 | 1.89 × 100 |
| Std | 2.50 × 100 | 2.50 × 100 | 1.24 × 10−1 | |
| F15 | Avg | 5.42 × 10−4 | 5.42 × 10−4 | 3.98 × 10−4 |
| Std | 4.33 × 10−4 | 4.33 × 10−4 | 5.26 × 10−6 | |
| F16 | Avg | −1.03 × 100 | −1.03 × 100 | −1.03 × 100 |
| Std | 5.55 × 10−6 | 5.55 × 10−6 | 3.56 × 10−7 | |
| F17 | Avg | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 |
| Std | 6.54 × 10−4 | 6.54 × 10−4 | 6.42 × 10−5 | |
| F18 | Avg | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 |
| Std | 6.71 × 10−4 | 6.71 × 10−4 | 2.53 × 10−4 | |
| F19 | Avg | −3.86 × 100 | −3.86 × 100 | −3.86 × 100 |
| Std | 8.16 × 10−5 | 8.16 × 10−5 | 3.74 × 10−6 | |
| F20 | Avg | −3.25 × 100 | −3.25 × 100 | −3.29 × 100 |
| Std | 9.03 × 10−2 | 9.03 × 10−2 | 7.69 × 10−2 | |
| F21 | Avg | −1.01 × 101 | −1.01 × 101 | −1.02 × 101 |
| Std | 5.48 × 10−1 | 5.48 × 10−1 | 8.76 × 10−2 | |
| F22 | Avg | −1.04 × 101 | −1.04 × 101 | −1.04 × 101 |
| Std | 5.44 × 10−3 | 5.44 × 10−3 | 1.68 × 10−3 | |
| F23 | Avg | −1.04 × 101 | −1.04 × 101 | −1.04 × 101 |
| Std | 5.11 × 10−4 | 5.11 × 10−4 | 5.86 × 10−6 |
| Functions | Evaluation Indexes | WOA | WOA-RBF | WOA-VMD | MSWOA | NEDWOA |
|---|---|---|---|---|---|---|
| F1 | Avg | 7.91 × 10−74 | 8.32 × 10−93 | 0.00 × 100 | 3.58 × 10−89 | 0.00 × 100 |
| Std | 4.32 × 10−74 | 1.23 × 10−64 | 0.00 × 100 | 2.40 × 10−84 | 0.00 × 100 | |
| F2 | Avg | 1.86 × 10−49 | 7.59 × 10−72 | 5.23 × 10−52 | 5.27 × 10−197 | 0.00 × 100 |
| Std | 2.39 × 10−48 | 2.56 × 10−93 | 3.43 × 10−51 | 3.21 × 10−198 | 0.00 × 100 | |
| F3 | Avg | 4.31 × 10−6 | 5.43 × 101 | 0.00 × 100 | 4.39 × 10−41 | 0.00 × 100 |
| Std | 2.93 × 10−5 | 4.67 × 102 | 0.00 × 100 | 2.41 × 10−40 | 0.00 × 100 | |
| F4 | Avg | 7.25 × 10−14 | 2.07 × 10−4 | 3.16 × 10−187 | 1.51 × 10−27 | 1.35 × 10−93 |
| Std | 3.97 × 10−12 | 1.40 × 10−4 | 2.78 × 10−187 | 6.84 × 10−27 | 2.57 × 10−95 | |
| F5 | Avg | 2.79 × 101 | 2.06 × 10−2 | 1.86 × 10−1 | 2.62 × 101 | 2.94 × 10−1 |
| Std | 7.63 × 10−1 | 2.23 × 10−2 | 3.75 × 10−1 | 3.49 × 100 | 3.39 × 10−1 | |
| F6 | Avg | 7.79 × 10−3 | 2.34 × 10−2 | 6.63 × 10−1 | 1.53 × 10−4 | 5.21 × 10−9 |
| Std | 5.32 × 10−2 | 2.51 × 10−1 | 4.27 × 10−1 | 1.89 × 10−3 | 1.46 × 10−8 | |
| F7 | Avg | 5.51 × 10−3 | 7.25 × 10−4 | 4.76 × 10−4 | 3.28 × 10−6 | 7.45 × 10−5 |
| Std | 1.15 × 10−2 | 3.85 × 10−4 | 7.46 × 10−4 | 3.21 × 10−5 | 6.96 × 10−5 | |
| F8 | Avg | −8.98 × 103 | −10,745.9 | −12,569.52 | −12,621.32 | −12,568.81 |
| Std | 1.91 × 103 | 1.76 × 103 | 3.36 × 10−2 | 2.57 × 10−2 | 1.21 × 10−2 | |
| F9 | Avg | 1.06 × 10−21 | 7.28 × 10−5 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 |
| Std | 2.39 × 10−21 | 7.35 × 10−5 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| F10 | Avg | 5.39 × 10−15 | 6.39 × 10−3 | 4.47 × 10−16 | 4.56 × 10−16 | 5.76 × 10−18 |
| Std | 2.93 × 10−6 | 3.71 × 10−3 | 5.58 × 10−15 | 2.32 × 10−14 | 6.56 × 10−21 | |
| F11 | Avg | 1.26 × 10−2 | 1.38 × 100 | 3.96 × 10−200 | 9.37 × 10−75 | 1.26 × 10−45 |
| Std | 3.97 × 10−1 | 5.21 × 100 | 0.00 × 100 | 3.96 × 10−74 | 2.87 × 10−46 | |
| F12 | Avg | 3.05 × 10−3 | 6.41 × 10−6 | 7.27 × 10−3 | 9.32 × 10−4 | 6.85 × 10−5 |
| Std | 7.60 × 10−2 | 6.39 × 10−6 | 6.47 × 10−3 | 2.89 × 10−3 | 3.43 × 10−5 | |
| F13 | Avg | 8.97 × 100 | 7.57 × 10−5 | 9.81 × 10−3 | 1.41 × 10−2 | 7.15 × 10−12 |
| Std | 6.69 × 100 | 6.56 × 10−5 | 1.51 × 10−2 | 1.74 × 10−2 | 1.78 × 10−11 | |
| F14 | Avg | 3.76 × 100 | −1.5037 | −1.0246 | −1.5496 | 1.24 × 100 |
| Std | 2.59 × 100 | 2.45 × 10−1 | 6.32 × 10−2 | 2.81 × 10−1 | 1.38 × 10−1 | |
| F15 | Avg | 1.81 × 10−3 | 8.79 × 10−4 | 4.51 × 10−3 | 5.13 × 10−4 | 3.79 × 10−4 |
| Std | 2.39 × 10−3 | 5.91 × 10−4 | 7.49 × 10−3 | 2.19 × 10−4 | 3.94 × 10−4 | |
| F16 | Avg | −0.99997 | −1.0316 | −1.0316 | −1.0316 | −1.0316 |
| Std | 2.93 × 10−5 | 3.46 × 10−6 | 1.61 × 10−5 | 2.78 × 10−5 | 1.19 × 10−7 | |
| F17 | Avg | 0.42718 | 0.3980 | 0.3991 | 0.3980 | 0.39996 |
| Std | 3.97 × 10−1 | 8.31 × 10−6 | 2.71 × 10−4 | 3.52 × 10−5 | 2.78 × 10−5 | |
| F18 | Avg | 3.001 | 3.0022 | 4.3658 | 1.15 × 101 | 3.00007 |
| Std | 7.62 × 10−1 | 2.23 × 10−4 | 7.5019 × 100 | 1.30 × 101 | 1.78 × 10−4 | |
| F19 | Avg | −3.8349 | −3.8467 | −3.7589 | −3.84 | −3.8563 |
| Std | 5.92 × 10−2 | 5.37 × 10−2 | 1.89 × 10−1 | 4.79 × 10−2 | 3.66 × 10−7 | |
| F20 | Avg | −3.1533 | −3.2054 | −2.9182 | −3.1220 | −3.2723 |
| Std | 1.18 × 10−1 | 9.35 × 10−2 | 0.2876 | 0.1336 | 6.49 × 10−2 | |
| F21 | Avg | −8.2895 | −10.1443 | −10.0391 | −10.0279 | −10.1526 |
| Std | 2.73 × 100 | 7.54 × 10−3 | 1.30 × 10−1 | 2.16 × 10−1 | 2.23 × 10−3 | |
| F22 | Avg | −8.7296 | −10.2382 | −10.2612 | −10.2975 | −10.4023 |
| Std | 3.42 × 100 | 1.05 × 100 | 2.04 × 10−1 | 1.18 × 10−1 | 9.11 × 10−3 | |
| F23 | Avg | −7.1025 | −10.3469 | −10.3186 | −10.3227 | −10.3732 |
| Std | 2.37 × 100 | 7.56 × 10−2 | 1.22 × 10−1 | 8.53 × 10−2 | 5.13 × 10−2 | |
| p/h | 1.97 × 10−7/+ | 4.16 × 10−6/+ | 5.16 × 10−6/+ | 1.47 × 10−5/+ | ||
| Total rank | 5 | 4 | 3 | 2 | 1 | |
| Parameter | Taking Values | Parameter | Taking Values |
|---|---|---|---|
| spraying distance | 250 mm | static voltage U | 60 kV |
| cup speed n | priming paint (32 kr/min) | average film thickness δ | priming paint (20 μm) |
| inter coatings (32 kr/min) | inter coatings (40 μm) | ||
| final coating (40 kr/min) | varnish (40 μm) | ||
| metallic paint (16 μm) | |||
| paint flux Q | 300 cc/min | forming air flow rate | 300 NL/min |
| travel speed v | 400 mm/s | plane tilt angle α | 0° |
| Metric | MSWOA | WOA-RBF | WOA-VMD | NEDWOA |
|---|---|---|---|---|
| Energy Consumption (kWh) | 352 | 367 | 358 | 346 |
| Carbon Emissions (kg CO2) | 251 | 263 | 259 | 245 |
| Processing Time (h) | 4.9 | 5.8 | 6.1 | 4.2 |
| Total consumption | 180.57 | 188.88 | 185.06 | 176.79 |
| Serial Number | Improvement Goals | Original Production Data | Current Production Data | Analysis Results |
|---|---|---|---|---|
| 1 | Production efficiency improvement | 675/month | 959/month | 42.1% |
| 2 | Increased value-added ratio of production | 44.6% | 46.2% | 1.6% |
| 3 | Production personnel reduction rate | 16 patients | 12 patients | 25% |
| 4 | Production cost reduction | 719 yuan/piece | 590 yuan/piece | 17.9% |
| 5 | Improvement of production quality | defective index 15% | defective index 7% | 8% |
| 6 | Exhaust gas purification rate | 32% | 98% | 66% |
| 7 | Energy consumption | 423 kwh | 346 kwh | 18.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Li, X.; Yang, T.; Wu, H.; Zhang, L. An Improved Whale Optimization Algorithm for the Clean Production Transformation of Automotive Body Painting. Biomimetics 2025, 10, 273. https://doi.org/10.3390/biomimetics10050273
Yang Q, Li X, Yang T, Wu H, Zhang L. An Improved Whale Optimization Algorithm for the Clean Production Transformation of Automotive Body Painting. Biomimetics. 2025; 10(5):273. https://doi.org/10.3390/biomimetics10050273
Chicago/Turabian StyleYang, Qin, Xinning Li, Teng Yang, Hu Wu, and Liwen Zhang. 2025. "An Improved Whale Optimization Algorithm for the Clean Production Transformation of Automotive Body Painting" Biomimetics 10, no. 5: 273. https://doi.org/10.3390/biomimetics10050273
APA StyleYang, Q., Li, X., Yang, T., Wu, H., & Zhang, L. (2025). An Improved Whale Optimization Algorithm for the Clean Production Transformation of Automotive Body Painting. Biomimetics, 10(5), 273. https://doi.org/10.3390/biomimetics10050273







