Snake Optimization Algorithm Augmented by Adaptive t-Distribution Mixed Mutation and Its Application in Energy Storage System Capacity Optimization
Abstract
1. Introduction
1.1. Problem Statement and Motivation
1.2. Contribution
- Introduces the Tent chaotic map and quasi-reverse learning strategy to initialize the population, improve the spatial distribution structure of the population’s individual initialization stage, and improve the convergence speed of the algorithm.
- The exploration and development stages are dynamically chosen based on the algorithm’s fitness throughout the optimization process, which effectively cuts down on needless time spent and quickens the rate of convergence.
- Swaps out the original algorithm’s population renewal technique with the adaptive t-distribution mixed mutation foraging approach. In the development stage, the novel renewal method guarantees population variety; in the exploration stage, it increases the individual richness of the algorithm and boosts optimization capability.
- Verifies the DTHSO algorithm’s engineering viability through simulation tests on issues in two engineering domains and a comparison with alternative optimization methods on 23 CEC2005 test functions.
2. Related Works
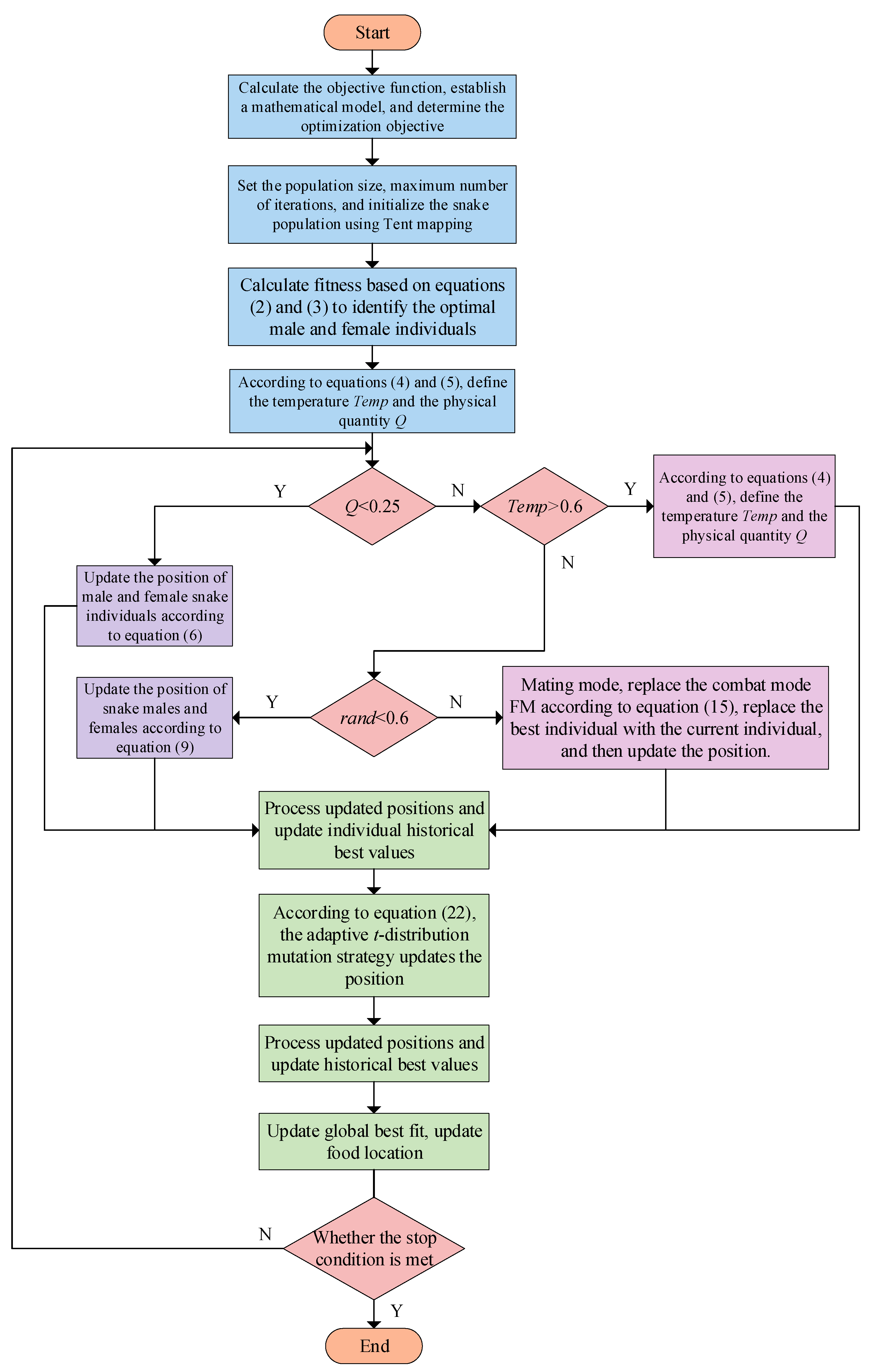
3. Snake Optimization Algorithm (SO)
3.1. Initialize Population
3.2. Division of Male and Female Populations
3.3. Evaluation of Temperature and Food Intake
3.4. Exploration Stage
3.5. Development Phase
- (1)
- Combat mode.
- (2)
- Mating mode.
4. Snake Optimization Algorithm with Adaptive t-Distribution Mixed Mutation
4.1. Chaotic Map Based on Tent and Quasi-Reverse Learning Strategy
4.2. Adaptive t-Distribution Mutation SO Algorithm Strategy (DTHSO)
4.3. Heterogeneous Attraction Strategy
4.4. Analysis of Algorithm Time Complexity
4.5. The Algorithm Process of DTHSO Algorithm
5. Algorithm Comparison and Result Analysis
5.1. Comparison of Test Function Results
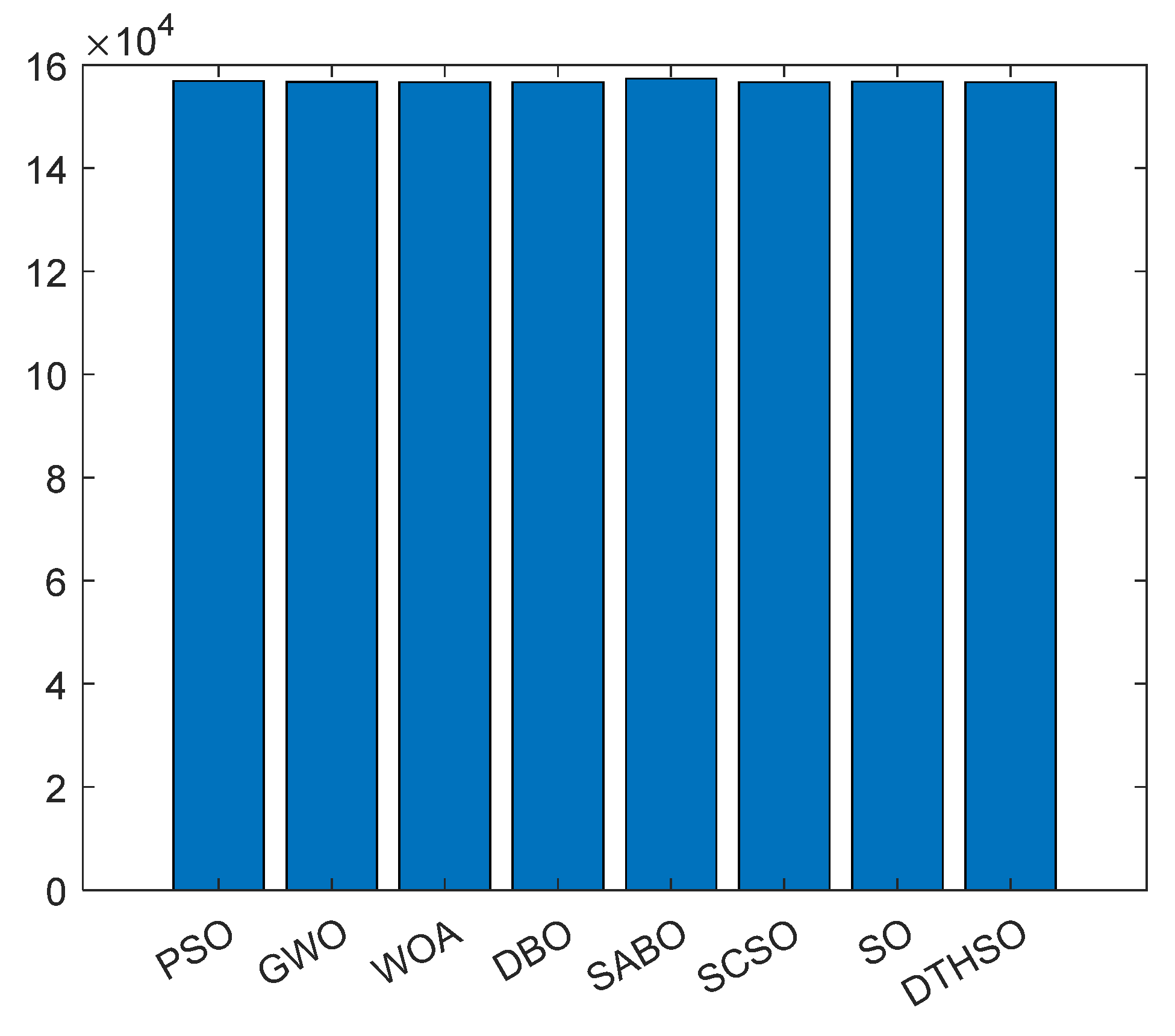
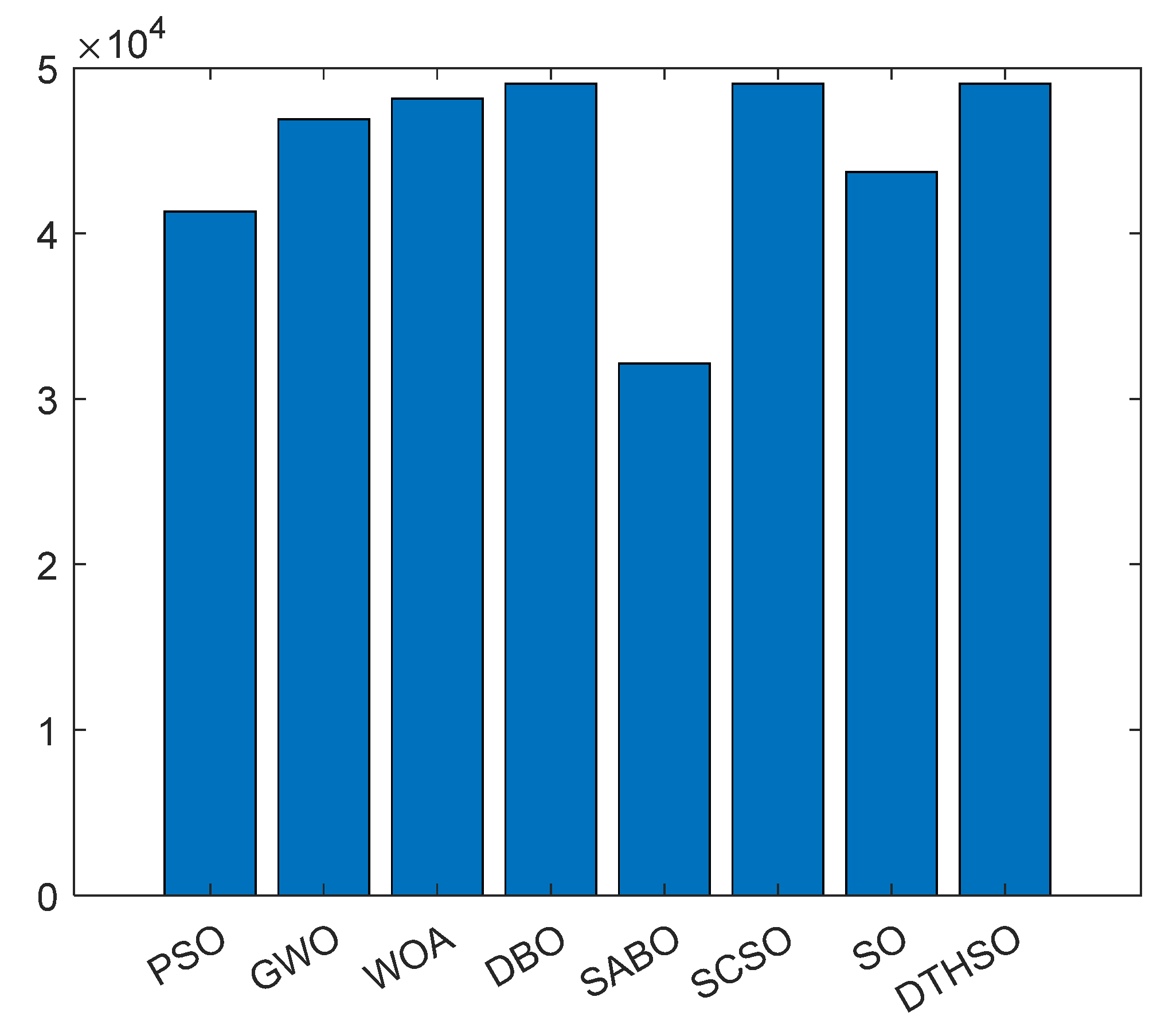
5.2. Comparison of Energy Storage Optimization Scheduling
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, J.; Duan, H.; Lao, S. Swarm intelligence algorithms for multiple unmanned aerial vehicles collaboration: A comprehensive review. Artif. Intell. Rev. 2023, 56, 4295–4327. [Google Scholar] [CrossRef]
- Attiya, I.; Abd Elaziz, M.; Abualigah, L.; Nguyen, T.; Abd, A. An improved hybrid swarm intelligence for scheduling iot application tasks in the cloud. IEEE Trans. Ind. Inform. 2022, 18, 6264–6272. [Google Scholar] [CrossRef]
- Nasir, M.H.; Khan, S.A.; Khan, M.M.; Fatima, M. Swarm intelligence inspired intrusion detection systems—A systematic literature review. Comput. Netw. 2022, 205, 108708. [Google Scholar] [CrossRef]
- Sakovich, N.; Aksenov, D.; Pleshakova, E.; Gataullin, S. MAMGD: Gradient-Based Optimization Method Using Exponential Decay. Technologies 2024, 12, 154. [Google Scholar] [CrossRef]
- Wang, S.; Cao, L.; Chen, Y.; Chen, C.; Yue, Y.; Zhu, W. Gorilla optimization algorithm combining sine cosine and cauchy variations and its engineering applications. Sci. Rep. 2024, 14, 7578. [Google Scholar] [CrossRef]
- Jiang, S.; Yue, Y.; Chen, C.; Chen, Y.; Cao, Y. A Multi-Objective Optimization Problem Solving Method Based on Improved Golden Jackal Optimization Algorithm and Its Application. Biomimetics 2024, 9, 270. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Cao, L.; Chen, Y.; Yue, Y. A comprehensive survey of convergence analysis of beetle antennae search algorithm and its applications. Artif. Intell. Rev. 2024, 57, 141. [Google Scholar] [CrossRef]
- Hu, G.; Huang, F.; Chen, K.; Wei, G. MNEARO: A meta swarm intelligence optimization algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2024, 419, 116664. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Li, B.; Ding, H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]
- Prity, F.S.; Uddin, K.M.A.; Nath, N. Exploring swarm intelligence optimization techniques for task scheduling in cloud computing: Algorithms, performance analysis, and future prospects. Iran J. Comput. Sci. 2024, 7, 337–358. [Google Scholar] [CrossRef]
- Bacanin, N.; Zivkovic, M.; Stoean, C.; Antonijevic, M.; Janicijevic, S.; Sarac, M.; Janicijevic, I. Application of natural language processing and machine learning boosted with swarm intelligence for spam email filtering. Mathematics 2022, 10, 4173. [Google Scholar] [CrossRef]
- Klein, L.; Zelinka, I.; Seidl, D. Optimizing parameters in swarm intelligence using reinforcement learning: An application of Proximal Policy Optimization to the iSOMA algorithm. Swarm Evol. Comput. 2024, 85, 101487. [Google Scholar] [CrossRef]
- Chen, B.; Cao, L.; Chen, C.; Chen, Y.; Yue, Y. A comprehensive survey on the chicken swarm optimization algorithm and its applications: State-of-the-art and research challenges. Artif. Intell. Rev. 2024, 57, 170. [Google Scholar] [CrossRef]
- Maleki, A. Optimization based on modified swarm intelligence techniques for a stand-alone hybrid photovoltaic/diesel/battery system. Sustain. Energy Technol. Assess. 2022, 51, 101856. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, H.; Zhou, J. A dual cluster head hierarchical routing protocol for wireless sensor networks based on hybrid swarm intelligence optimization. IEEE Internet Things J. 2024, 11, 16710–16721. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, X.; Zhang, M.; Lei, X.; Lu, H.; Shi, Y. Solving multimodal optimization problems by a knowledge-driven brain storm optimization algorithm. Appl. Soft Comput. 2024, 150, 111105. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Yao, L.; Yuan, P.; Tsai, C.Y.; Zhang, T.; Lu, Y.; Ding, S. ESO: An enhanced snake optimizer for real-world engineering problems. Expert Syst. Appl. 2023, 230, 120594. [Google Scholar] [CrossRef]
- Hu, G.; Yang, R.; Abbas, M.; Wei, G. BEESO: Multi-strategy boosted snake-inspired optimizer for engineering applications. J. Bionic Eng. 2023, 20, 1791–1827. [Google Scholar] [CrossRef]
- Khurma, R.A.; Albashish, D.; Braik, M.; Alzaqebah, A.; Qasem, A.; Adwan, O. An augmented Snake Optimizer for diseases and COVID-19 diagnosis. Biomed. Signal Process. Control 2023, 84, 104718. [Google Scholar] [CrossRef]
- Al-Shourbaji, I.; Kachare, P.H.; Alshathri, S.; Duraibi, S.; Elnaim, B.; Elaziz, M.A. An efficient parallel reptile search algorithm and snake optimizer approach for feature selection. Mathematics 2022, 10, 2351. [Google Scholar] [CrossRef]
- Belabbes, F.; Cotfas, D.T.; Cotfas, P.A.; Medles, M. Using the snake optimization metaheuristic algorithms to extract the photovoltaic cells parameters. Energy Convers. Manag. 2023, 292, 117373. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Q.; Huang, T. Resilient penalty function method for distributed constrained optimization under byzantine attack. Inf. Sci. 2022, 596, 362–379. [Google Scholar] [CrossRef]
- Li, W.; Sun, B.; Sun, Y.; Huang, Y.; Cheung, Y.; Gu, F. DC-SHADE-IF: An infeasible–feasible regions constrained optimization approach with diversity controller. Expert Syst. Appl. 2023, 224, 119999. [Google Scholar] [CrossRef]
- Hussien, A.G.; Heidari, A.A.; Ye, X.; Liang, G.; Chen, H.; Pan, Z. Boosting whale optimization with evolution strategy and Gaussian random walks: An image segmentation method. Eng. Comput. 2023, 39, 1935–1979. [Google Scholar] [CrossRef]
- Pereira, J.L.J.; Oliver, G.A.; Francisco, M.B.; Cunha, S.; Gomes, G.F. A review of multi-objective optimization: Methods and algorithms in mechanical engineering problems. Arch. Comput. Methods Eng. 2022, 29, 2285–2308. [Google Scholar] [CrossRef]
- Xiao, N.; Liu, X.; Yuan, Y. A class of smooth exact penalty function methods for optimization problems with orthogonality constraints. Optim. Methods Softw. 2022, 37, 1205–1241. [Google Scholar] [CrossRef]
- Kumari, S.; Khurana, P.; Singla, S.; Kumar, A. Solution of constrained problems using particle swarm optimiziation. Int. J. Syst. Assur. Eng. Manag. 2022, 13, 1688–1695. [Google Scholar] [CrossRef]
- Liao, W.; Xia, X.; Jia, X.; Shen, S.; Zhuang, H.; Zhang, X. A Spider Monkey Optimization Algorithm Combining Opposition-Based Learning and Orthogonal Experimental Design. Comput. Mater. Contin. 2023, 76, 3297–3323. [Google Scholar] [CrossRef]
- Wei, W.; Wang, J.; Tao, M. Constrained differential evolution with multiobjective sorting mutation operators for constrained optimization. Appl. Soft Comput. 2015, 33, 207–222. [Google Scholar] [CrossRef]
- Gao, S.; de Silva, C.W. Estimation distribution algorithms on constrained optimization problems. Appl. Math. Comput. 2018, 339, 323–345. [Google Scholar] [CrossRef]
- Rahimi, I.; Gandomi, A.H.; Chen, F.; Mezura, E. A review on constraint handling techniques for population-based algorithms: From single-objective to multi-objective optimization. Arch. Comput. Methods Eng. 2023, 30, 2181–2209. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Wang, G.G. Improved differential evolution using two-stage mutation strategy for multimodal multi-objective optimization. Swarm Evol. Comput. 2023, 78, 101232. [Google Scholar] [CrossRef]
- Masood, A.; Hameed, M.M.; Srivastava, A.; Pham, Q.B.; Ahmad, K.; Razali, F.M.; Baowidan, S.A. Improving PM2.5 prediction in New Delhi using a hybrid extreme learning machine coupled with snake optimization algorithm. Sci. Rep. 2023, 13, 21057. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Jiao, S.; Li, Y.; Zhang, Q. Capacity optimization of a hybrid energy storage system considering wind-Solar reliability evaluation based on a novel multi-strategy snake optimization algorithm. Expert Syst. Appl. 2023, 231, 120602. [Google Scholar] [CrossRef]
- Wang, L.; Fan, G.; Wang, Q.; Li, H.; Huo, J.; Wei, S.; Niu, Q. Snake optimizer LSTM-based UWB positioning method for unmanned crane. PLoS ONE 2023, 18, e0293618. [Google Scholar] [CrossRef]
- Li, H.; Xu, G.; Chen, B.; Huang, S.; Xia, Y.; Chai, S. Dual-mutation mechanism-driven snake optimizer for scheduling multiple budget constrained workflows in the cloud. Appl. Soft Comput. 2023, 149, 110966. [Google Scholar] [CrossRef]
- Janjanam, L.; Saha, S.K.; Kar, R. Optimal design of Hammerstein cubic spline filter for nonlinear system modeling based on snake optimizer. IEEE Trans. Ind. Electron. 2022, 70, 8457–8467. [Google Scholar] [CrossRef]
- Cheng, R.; Qiao, Z.; Li, J.; Huang, J. Traffic signal timing optimization model based on video surveillance data and snake optimization algorithm. Sensors 2023, 23, 5157. [Google Scholar] [CrossRef]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2322–2335. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, P.; Miao, Z.; Zhao, H.; Mou, J.; Zhou, W. Energy performance prediction of pump as turbine (PAT) based on PIWOA-BP neural network. Renew. Energy 2024, 222, 119873. [Google Scholar] [CrossRef]
- Yang, X.; Liu, J.; Liu, Y.; Xu, P.; Yu, L.; Zhu, L.; Chen, H.; Deng, W. A novel adaptive sparrow search algorithm based on chaotic mapping and t-distribution mutation. Appl. Sci. 2021, 11, 11192. [Google Scholar] [CrossRef]
- Ilboudo, W.E.L.; Kobayashi, T.; Matsubara, T. Adaterm: Adaptive t-distribution estimated robust moments for noise-robust stochastic gradient optimization. Neurocomputing 2023, 557, 126692. [Google Scholar] [CrossRef]
- Yin, S.; Luo, Q.; Du, Y.; Zhou, Y. DTSMA: Dominant swarm with adaptive t-distribution mutation-based slime mould algorithm. Math. Biosci. Eng. 2022, 19, 2240–2285. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Q.; Ma, L.; Zhang, Z. Sparrow search algorithm with adaptive t distribution for multi-objective low-carbon multimodal transportation planning problem with fuzzy demand and fuzzy time. Expert Syst. Appl. 2024, 238, 122042. [Google Scholar] [CrossRef]
- Corbett, B.; Loi, R.; Zhou, W.; Liu, D.; Ma, Z. Transfer print techniques for heterogeneous integration of photonic components. Prog. Quantum Electron. 2017, 52, 1–17. [Google Scholar] [CrossRef]
- Zamfirache, I.A.; Precup, R.E.; Roman, R.C.; Petriu., E.M. Policy iteration reinforcement learning-based control using a grey wolf optimizer algorithm. Inf. Sci. 2022, 585, 162–175. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Amiriebrahimabadi, M.; Mansouri, N. A comprehensive survey of feature selection techniques based on whale optimization algorithm. Multimed. Tools Appl. 2024, 83, 47775–47846. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Subtraction-average-based optimizer: A new swarm-inspired metaheuristic algorithm for solving optimization problems. Biomimetics 2023, 8, 149. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Rao, H.; Wen, C.; Jia, H.; Liu, Q.; Abualigah, L. Modified sand cat swarm optimization algorithm for solving constrained engineering optimization problems. Mathematics 2022, 10, 4350. [Google Scholar] [CrossRef]
- Wang, Y.; Song, F.; Ma, Y.; Zhang, Y.; Yang, J.; Liu, Y.; Zhang, F.; Zhu, J. Research on capacity planning and optimization of regional integrated energy system based on hybrid energy storage system. Appl. Therm. Eng. 2020, 180, 115834. [Google Scholar] [CrossRef]
- Pang, M.; Shi, Y.; Wang, W.; Pang, S. Optimal sizing and control of hybrid energy storage system for wind power using hybrid parallel PSO-GA algorithm. Energy Explor. Exploit. 2019, 37, 558–578. [Google Scholar] [CrossRef]
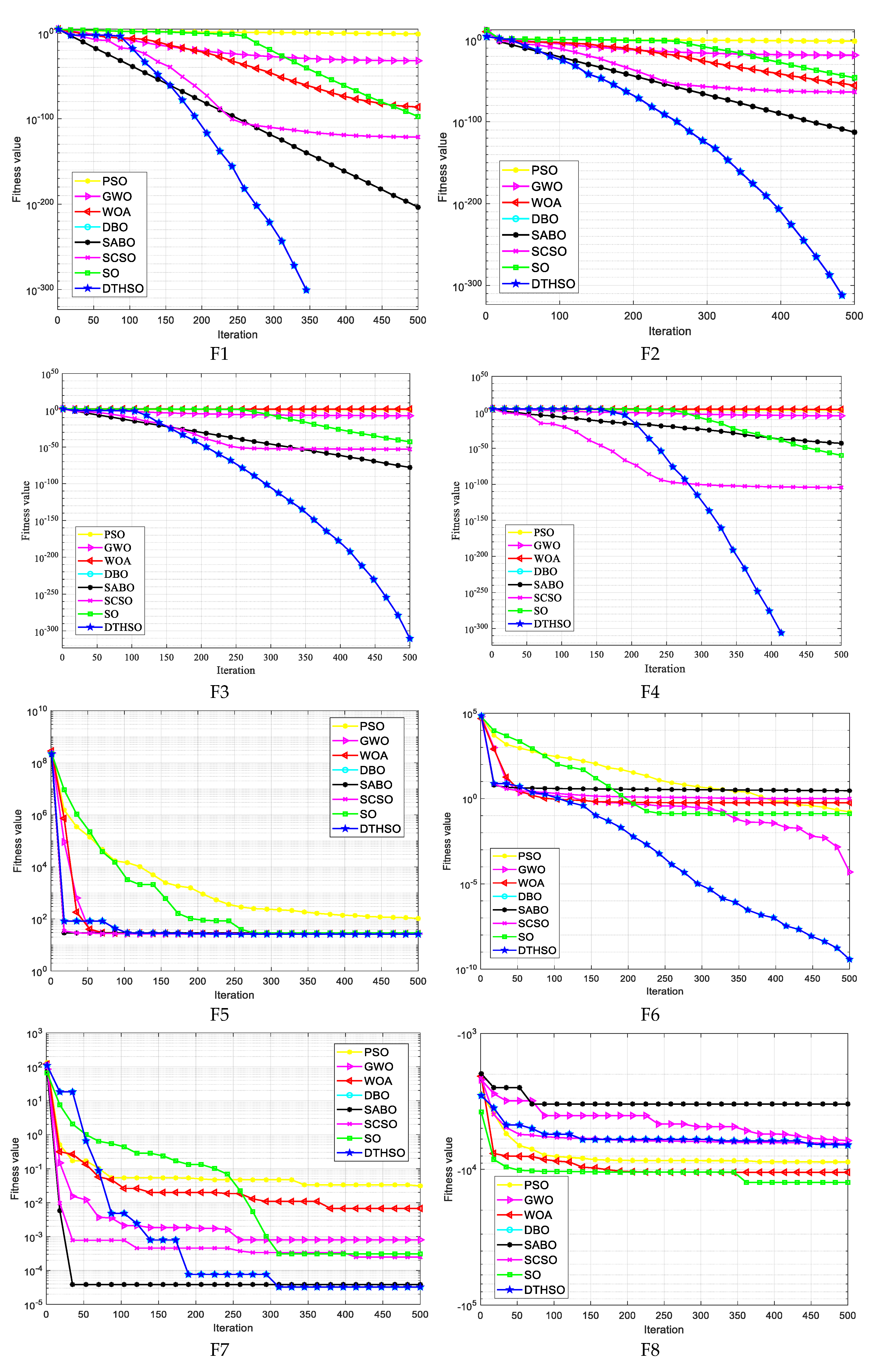
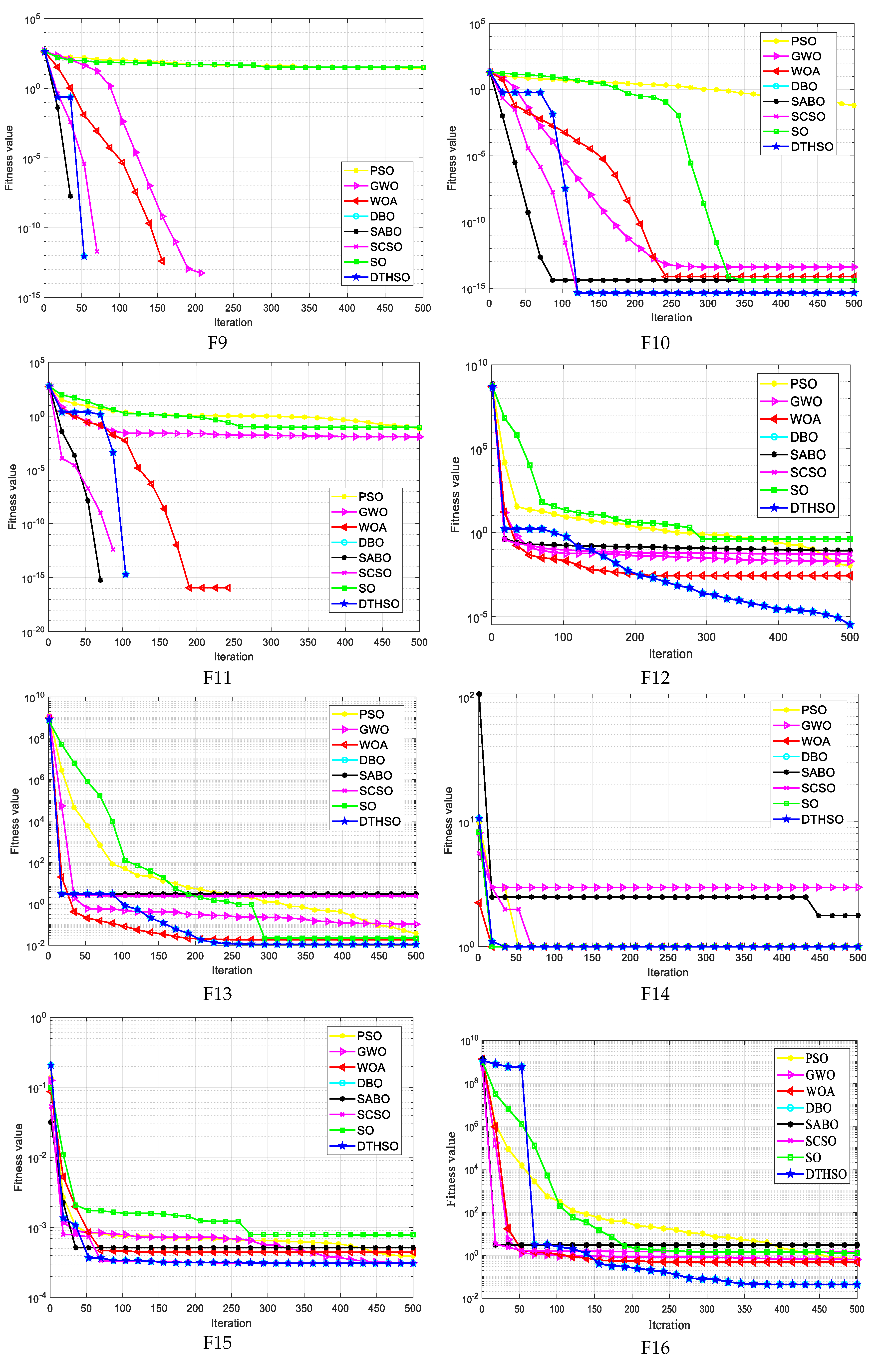
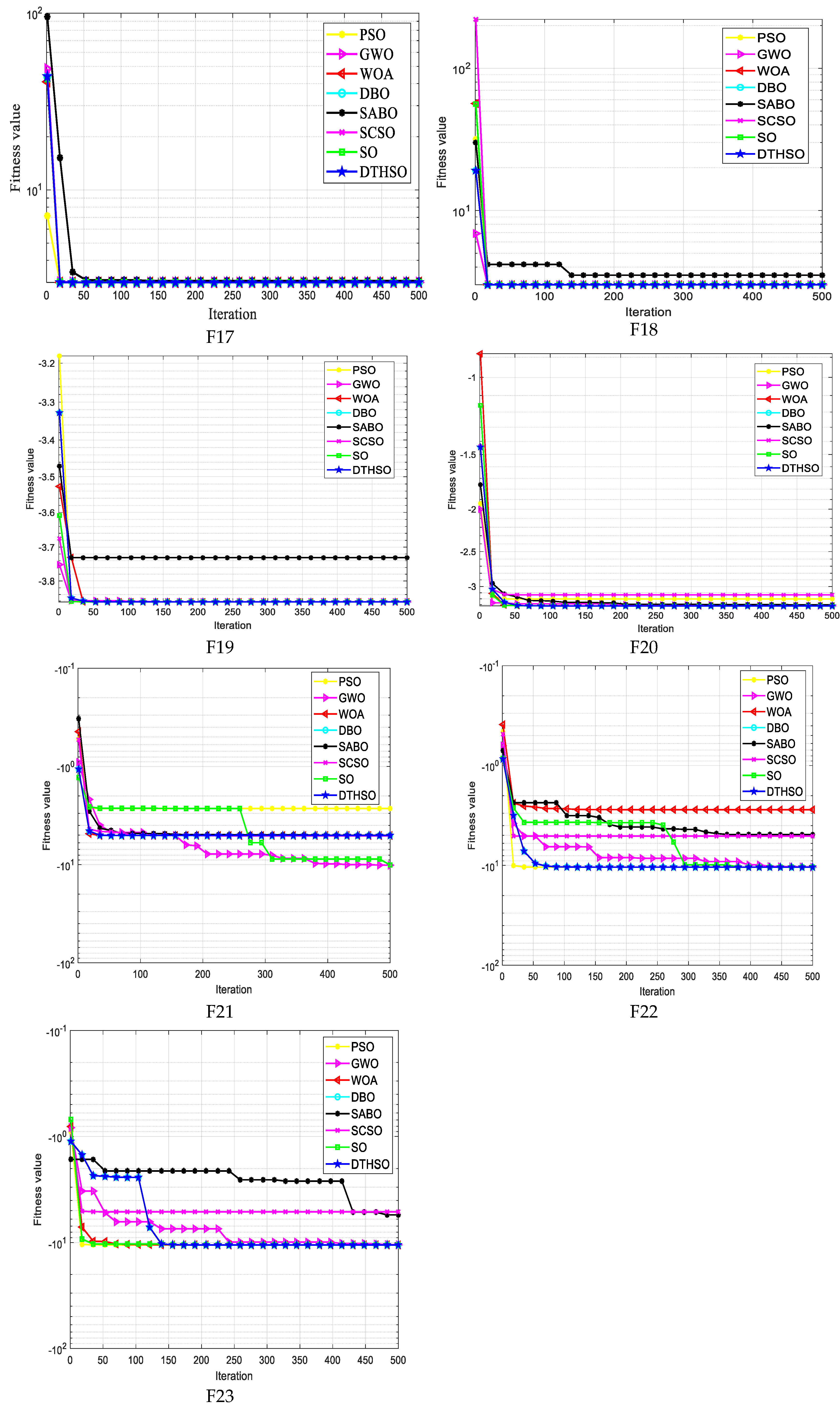






| Function | Equation | Dimension | Bounds | Optimum |
|---|---|---|---|---|
| F1 | 30 | [−100, 100] | 0 | |
| F2 | 30 | [−10, 100] | 0 | |
| F3 | 30 | [−100, 100] | 0 | |
| F4 | 30 | [−100, 100] | 0 | |
| F5 | 30 | [−10, 100] | 0 | |
| F6 | 30 | [−100, 100] | 0 | |
| F7 | 30 | [−1.28, 1.28] | 0 | |
| F8 | 30 | [−10, 100] | 0 | |
| F9 | 30 | [−100, 100] | 0 | |
| F10 | 30 | [−5.12, 5.12] | 0 | |
| F11 | 30 | [−32, 32] | 0 | |
| F12 | 30 | [−600, 600] | 0 | |
| F13 | 30 | [−50, 50] | 0 | |
| F14 | 2 | [−65, 65] | 0 | |
| F15 | 4 | [−5, 5] | 0.0003 | |
| F16 | 2 | [−5, 5] | −1.0316 | |
| F17 | 2 | [−5, 10] | 0.3978 | |
| F18 | 2 | [−2, 2] | 3 | |
| F19 | 3 | [1, 3] | −3.86 | |
| F20 | 6 | [0, 1] | −3.32 | |
| F21 | 4 | [0, 10] | −10.1532 | |
| F22 | 4 | [0, 10] | −10.4028 | |
| F23 | 4 | [0, 10] | −10.5363 |
| Function | Algorithm | Mean | Std | Best | Worst |
|---|---|---|---|---|---|
| F1 | PSO | 7.23×10−10 | 1.29×10−9 | 5.28×10−12 | 5.18 × 10−9 |
| GWO | 1.25 × 10−56 | 5.57 × 10−56 | 3.41 × 10−60 | 3.07 × 10−55 | |
| WOA | 6.99 × 10−74 | 3.83 × 10−73 | 7.73 × 10−91 | 2.1 × 10−72 | |
| DBO | 1.2 × 10−102 | 6.76 × 10−102 | 3 × 10−154 | 3.7 × 10−101 | |
| SABO | 1.6 × 10−199 | 0 | 5.8 × 10−205 | 3.2 × 10−198 | |
| SCSO | 2.1 × 10−131 | 7.61 × 10−131 | 7.6 × 10−146 | 4.1 × 10−130 | |
| SO | 3.96 × 10−161 | 1.6 × 10−160 | 2.47 × 10−174 | 8.08 × 10−160 | |
| DTHSO | 0 | 0 | 0 | 0 | |
| F2 | PSO | 1.45 × 10−6 | 8.83 × 10−7 | 2.94 × 10−7 | 4 × 10−6 |
| GWO | 7.94 × 10−33 | 1.55 × 10−32 | 2.9 × 10−35 | 7.8 × 10−32 | |
| WOA | 4.86 × 10−51 | 2.66 × 10−50 | 3.93 × 10−60 | 1.46 × 10−49 | |
| DBO | 2.7 × 10−55 | 9.45 × 10−55 | 2.4 × 10−85 | 4.53 × 10−54 | |
| SABO | 1.5 × 10−109 | 1.9 × 10−109 | 4 × 10−112 | 7.2 × 10−109 | |
| SCSO | 5.12 × 10−69 | 2.4 × 10−68 | 4.34 × 10−76 | 1.31 × 10−67 | |
| SO | 2.307 × 10−87 | 5.077 × 10−87 | 5.735 × 10−91 | 2.574 × 10−86 | |
| DTHSO | 0 | 0 | 0 | 0 | |
| F3 | PSO | 0.002794 | 0.003631 | 9.86 × 10−5 | 0.01412 |
| GWO | 1.59 × 10−24 | 4.89 × 10−24 | 5.58 × 10−31 | 2.12 × 10−23 | |
| WOA | 255.6735 | 476.0306 | 0.380031 | 2629.944 | |
| DBO | 3.84 × 10−89 | 2.11 × 10−88 | 8.9 × 10−161 | 1.15 × 10−87 | |
| SABO | 6.56 × 10−74 | 3.59 × 10−73 | 1.7 × 10−122 | 1.97 × 10−72 | |
| SCSO | 5.9 × 10−111 | 3.3 × 10−110 | 1 × 10−126 | 1.8 × 10−109 | |
| SO | 1.96 × 10−131 | 9.46 × 10−131 | 4.85 × 10−144 | 5.19 × 10−130 | |
| DTHSO | −2.5 × 10−27 | 4.19 × 10−26 | 0 | −7.4 × 10−26 | |
| F4 | PSO | 0.001705 | 0.001292 | 0.000198 | 0.00573 |
| GWO | 3.47 × 10−18 | 6.38 × 10−18 | 1.98 × 10−20 | 3.11 × 10−17 | |
| WOA | 5.260061 | 13.52821 | 0.000802 | 64.69591 | |
| DBO | 9.37 × 10−44 | 5.13 × 10−43 | 4.59 × 10−79 | 2.81 × 10−42 | |
| SABO | 7.44 × 10−85 | 1.47 × 10−84 | 7.91 × 10−88 | 6.65 × 10−84 | |
| SCSO | 1.77 × 10−57 | 9.08 × 10−57 | 2.16 × 10−64 | 4.98 × 10−56 | |
| SO | 4.259 × 10−72 | 2.307 × 10−71 | 3.529 × 10−77 | 1.264 × 10−70 | |
| DTHSO | 0 | 0 | 0 | 0 | |
| F5 | PSO | 8.409876 | 11.91073 | 3.796652 | 69.3338 |
| GWO | 6.497992 | 0.501592 | 6.090313 | 8.062182 | |
| WOA | 11.54476 | 25.59158 | 6.131159 | 147.0338 | |
| DBO | 5.467078 | 0.723774 | 4.935106 | 8.073513 | |
| SABO | 7.414 | 0.442234 | 6.832093 | 8.704741 | |
| SCSO | 6.973817 | 0.616379 | 6.154244 | 8.072619 | |
| SO | 2.1036632 | 0.4884498 | 1.2576818 | 3.1305641 | |
| DTHSO | 5.002573 | 0.336522 | 4.322848 | 6.107432 | |
| F6 | PSO | 6.35 × 10−10 | 1.34 × 10−9 | 9.24 × 10−12 | 6.14 × 10−9 |
| GWO | 3.62 × 10−6 | 1.24 × 10−6 | 1.55 × 10−6 | 6.49 × 10−6 | |
| WOA | 0.002019 | 0.004102 | 0.000199 | 0.019776 | |
| DBO | 2.31 × 10−23 | 8.34 × 10−23 | 6.63 × 10−30 | 4.52 × 10−22 | |
| SABO | 0.044301 | 0.089992 | 0.000408 | 0.283947 | |
| SCSO | 0.050203 | 0.138549 | 2.38 × 10−7 | 0.505572 | |
| SO | 1.002 × 10−14 | 3.614 × 10−14 | 5.11 × 10−22 | 1.777 × 10−13 | |
| DTHSO | 1.4 × 10−12 | 2.22 × 10−12 | 7.53 × 10-16 | 1.02 × 10−11 | |
| F7 | PSO | 0.002595 | 0.001898 | 0.000397 | 0.008926 |
| GWO | 0.000609 | 0.000427 | 9.96 × 10-5 | 0.001877 | |
| WOA | 0.002982 | 0.003414 | 0.000123 | 0.015604 | |
| DBO | 0.000979 | 0.000631 | 7.1 × 10−5 | 0.002622 | |
| SABO | 0.000177 | 0.000154 | 1.19 × 10−5 | 0.000602 | |
| SCSO | 0.000137 | 0.000285 | 1.23 × 10−6 | 0.001529 | |
| SO | 0.0002989 | 0.0002446 | 3.4 × 10−5 | 0.0009868 | |
| DTHSO | 0.000143 | 9.87 × 10-05 | 5.39 × 10−6 | 0.000431 | |
| F8 | PSO | −3096.79 | 288.6078 | −3854.25 | −2432.97 |
| GWO | −2743.88 | 281.8803 | −3298.59 | −2220.43 | |
| WOA | −3399.65 | 564.8312 | −4189.78 | −2451.76 | |
| DBO | −3483.12 | 461.9972 | −4188.44 | −2522.59 | |
| SABO | −1752.48 | 169.5616 | −2290.32 | −1493.77 | |
| SCSO | −2578.91 | 308.291 | −3143.56 | −2040.75 | |
| SO | −3399.49 | 410.44483 | −4189.829 | −2161.412 | |
| DTHSO | −3588.87 | 292.6576 | −4071.39 | −3003.93 | |
| F9 | PSO | 6.311851 | 2.836308 | 1.989918 | 13.92943 |
| GWO | 0.716722 | 1.688813 | 0.00 | 6.30707 | |
| WOA | 2.190373 | 9.516246 | 0.00 | 50.33645 | |
| DBO | 1.094453 | 4.183475 | 0.00 | 17.90923 | |
| SABO | 0 | 0 | 0 | 0 | |
| SCSO | 0 | 0 | 0 | 0 | |
| SO | 0 | 0 | 0 | 0 | |
| DTHSO | 0 | 0 | 0 | 0 | |
| F10 | PSO | 8.19 × 10−6 | 6.06 × 10−6 | 1.2 × 10−6 | 2.26 × 10−5 |
| GWO | 6.84 × 10−15 | 1.45 × 10−15 | 4 × 10−15 | 7.55 × 10−15 | |
| WOA | 3.76 × 10−15 | 2.79 × 10−15 | 4.44 × 10−16 | 7.55 × 10−15 | |
| DBO | 4.44 × 10−16 | 0 | 4.44 × 10−16 | 4.44 × 10−16 | |
| SABO | 4 × 10−15 | 0 | 4 × 10−15 | 4 × 10−15 | |
| SCSO | 4.44 × 10−16 | 0 | 4.44 × 10−16 | 4.44 × 10−16 | |
| SO | 4.441 × 10−16 | 0 | 4.441 × 10−16 | 4.441 × 10−16 | |
| DTHSO | 4.44 × 10−16 | 0 | 4.44 × 10−16 | 4.44 × 10−16 | |
| F11 | PSO | 0.09904 | 0.04232 | 0.019701 | 0.211569 |
| GWO | 0.018567 | 0.01878 | 0 | 0.057892 | |
| WOA | 0.056709 | 0.119564 | 0 | 0.436088 | |
| DBO | 0.014353 | 0.033802 | 0 | 0.137842 | |
| SABO | 0.005436 | 0.029776 | 0 | 0.163089 | |
| SCSO | 0 | 0 | 0 | 0 | |
| SO | 0 | 0 | 0 | 0 | |
| DTHSO | 0 | 0 | 0 | 0 | |
| F12 | PSO | 1.53 × 10−10 | 7.41 × 10−10 | 3.1 × 10−13 | 4.07 × 10−9 |
| GWO | 0.008348 | 0.012343 | 2.31 × 10−7 | 0.041028 | |
| WOA | 0.008671 | 0.010178 | 0.000297 | 0.031783 | |
| DBO | 1.17 × 10−24 | 4.3 × 10−24 | 2.59 × 10−30 | 2.11 × 10−23 | |
| SABO | 0.043332 | 0.035159 | 0.001848 | 0.137659 | |
| SCSO | 0.026321 | 0.031426 | 1.84 × 10−7 | 0.160187 | |
| SO | 1.236 × 10−15 | 6.554 × 10−15 | 2.017 × 10−20 | 3.593 × 10−14 | |
| DTHSO | 8.28 × 10−13 | 1.34 × 10−12 | 8.69 × 10−15 | 6.75 × 10−12 | |
| F13 | PSO | 2.55 × 10−9 | 1.32 × 10−8 | 7.47 × 10−13 | 7.26 × 10−8 |
| GWO | 0.013255 | 0.034356 | 1.41 × 10−6 | 0.100487 | |
| WOA | 0.055794 | 0.080734 | 0.000845 | 0.3936 | |
| DBO | 0.025435 | 0.048919 | 1.25 × 10−28 | 0.196254 | |
| SABO | 0.169119 | 0.118543 | 0.002289 | 0.426229 | |
| SCSO | 0.144537 | 0.139871 | 1.11 × 10−6 | 0.431344 | |
| SO | 0.0116692 | 0.026104 | 2.409 × 10−20 | 0.0988826 | |
| DTHSO | 0.023507 | 0.09711 | 8.78 × 10−12 | 0.496478 | |
| F14 | PSO | 1.130146 | 0.565887 | 0.998004 | 3.96825 |
| GWO | 4.591674 | 4.023538 | 0.998004 | 12.67051 | |
| WOA | 4.295642 | 4.112566 | 0.998004 | 10.76318 | |
| DBO | 2.276595 | 2.557553 | 0.998004 | 10.76318 | |
| SABO | 3.896304 | 3.329865 | 1.031531 | 12.67081 | |
| SCSO | 3.871835 | 3.954056 | 0.998004 | 12.67051 | |
| SO | 2.5357039 | 3.0117596 | 0.9980038 | 10.763181 | |
| DTHSO | 1.262551 | 0.685995 | 0.998004 | 2.982105 | |
| F15 | PSO | 0.003209 | 0.006853 | 0.000307 | 0.020363 |
| GWO | 0.008244 | 0.013001 | 0.000309 | 0.05662 | |
| WOA | 0.000553 | 0.000255 | 0.000308 | 0.001377 | |
| DBO | 0.000771 | 0.000346 | 0.000307 | 0.001333 | |
| SABO | 0.000905 | 0.001796 | 0.000316 | 0.010149 | |
| SCSO | 0.000547 | 0.000399 | 0.000308 | 0.001595 | |
| SO | 0.0053913 | 0.0087844 | 0.0003075 | 0.0225533 | |
| DTHSO | 0.000311 | 3.94 × 10−6 | 0.000307 | 0.000323 | |
| F16 | PSO | −1.03163 | 6.05 × 10−16 | −1.03163 | −1.03163 |
| GWO | −1.03163 | 1.76 × 10−8 | −1.03163 | −1.03163 | |
| WOA | −1.03163 | 1.17 × 10−9 | −1.03163 | −1.03163 | |
| DBO | −1.03163 | 6.32 × 10−16 | −1.03163 | −1.03163 | |
| SABO | −1.02525 | 0.012055 | −1.03163 | −0.98597 | |
| SCSO | −1.03163 | 7.84 × 10−10 | −1.03163 | −1.03163 | |
| SO | −1.031628 | 5.904 × 10−16 | −1.031628 | −1.031628 | |
| DTHSO | −1.03163 | 5.3 × 10−16 | −1.03163 | −1.03163 | |
| F17 | PSO | 0.397887 | 0 | 0.397887 | 0.397887 |
| GWO | 0.397895 | 2.7 × 10−5 | 0.397887 | 0.398037 | |
| WOA | 0.397894 | 1.54 × 10−5 | 0.397887 | 0.397961 | |
| DBO | 0.397887 | 0 | 0.397887 | 0.397887 | |
| SABO | 0.429105 | 0.053091 | 0.397924 | 0.588487 | |
| SCSO | 0.397887 | 4.69E-08 | 0.397887 | 0.397888 | |
| SO | 0.3978874 | 0 | 0.3978874 | 0.3978874 | |
| DTHSO | 0.397887 | 0 | 0.397887 | 0.397887 | |
| F18 | PSO | 3 | 1.68 × 10−15 | 3 | 3 |
| GWO | 3.000034 | 5.53 × 10−5 | 3 | 3.000225 | |
| WOA | 3.000045 | 7.69 × 10−5 | 3 | 3.000341 | |
| DBO | 3 | 2.86 × 10−15 | 3 | 3 | |
| SABO | 4.58353 | 4.544002 | 3.000243 | 26.43964 | |
| SCSO | 3.000009 | 1.08 × 10−5 | 3 | 3.000038 | |
| SO | 11.1 | 24.715415 | 3 | 84 | |
| DTHSO | 3 | 9.55 × 10−16 | 3 | 3 | |
| F19 | PSO | −3.83701 | 0.141133 | −3.86278 | −3.08976 |
| GWO | −3.86184 | 0.002065 | −3.86278 | −3.8549 | |
| WOA | −3.85786 | 0.007432 | −3.8627 | −3.8231 | |
| DBO | −3.86199 | 0.002405 | −3.86278 | −3.8549 | |
| SABO | −3.63445 | 0.21976 | −3.85595 | −2.97954 | |
| SCSO | −3.86065 | 0.003528 | −3.86278 | −3.8549 | |
| SO | −3.862257 | 0.0019996 | −3.862782 | −3.854901 | |
| DTHSO | −3.86278 | 2.56 × 10−15 | −3.86278 | −3.86278 | |
| F20 | PSO | −3.29029 | 0.053475 | −3.322 | −3.2031 |
| GWO | −3.26275 | 0.071901 | −3.32199 | −3.11526 | |
| WOA | −3.1885 | 0.141879 | −3.32168 | −2.63803 | |
| DBO | −3.23231 | 0.110709 | −3.322 | −2.91606 | |
| SABO | −3.24041 | 0.124298 | −3.32092 | −2.91461 | |
| SCSO | −3.17712 | 0.220596 | −3.32199 | −2.26724 | |
| SO | −3.253135 | 0.0733724 | −3.321995 | −3.132697 | |
| DTHSO | −3.24273 | 0.057005 | −3.322 | −3.2031 | |
| F21 | PSO | −5.52228 | 3.451826 | −10.1532 | −2.63047 |
| GWO | −8.97841 | 2.44141 | −10.1528 | −2.68255 | |
| WOA | −7.52317 | 2.926188 | −10.1525 | −2.62409 | |
| DBO | −7.3624 | 2.689533 | −10.1532 | −2.63047 | |
| SABO | −4.88783 | 0.574508 | −6.62134 | −3.409 | |
| SCSO | −5.68644 | 2.207265 | −10.1532 | −0.88199 | |
| SO | −9.593368 | 2.142856 | −10.1532 | −0.880982 | |
| DTHSO | −5.31576 | 1.387429 | −10.1532 | −2.63047 | |
| F22 | PSO | −6.17398 | 3.390893 | −10.4029 | −2.75193 |
| GWO | −10.4012 | 0.000611 | −10.4025 | −10.4 | |
| WOA | −7.49996 | 3.452079 | −10.402 | −1.8352 | |
| DBO | −8.02273 | 3.057761 | −10.4029 | −1.83759 | |
| SABO | −4.83898 | 0.550266 | −5.08625 | −2.66295 | |
| SCSO | −6.78202 | 2.637799 | −10.4029 | −2.7659 | |
| SO | −8.748751 | 3.0586222 | −10.40294 | −2.765897 | |
| DTHSO | −5.98244 | 2.30892 | −10.4029 | −2.7659 | |
| F23 | PSO | −6.22872 | 3.903871 | −10.5364 | −1.67655 |
| GWO | −10.5344 | 0.001083 | −10.5363 | −10.5314 | |
| WOA | −6.8525 | 3.314703 | −10.5348 | −1.85892 | |
| DBO | −8.8277 | 2.69506 | −10.5364 | −2.42173 | |
| SABO | −4.85353 | 1.101254 | −9.5443 | −2.1511 | |
| SCSO | −6.29194 | 2.805714 | −10.5364 | −0.94888 | |
| SO | −8.697027 | 3.4025103 | −10.53641 | −1.85948 | |
| DTHSO | −7.46185 | 3.206559 | −10.5364 | −2.42173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Y.; Cao, L.; Chen, C.; Chen, Y.; Chen, B. Snake Optimization Algorithm Augmented by Adaptive t-Distribution Mixed Mutation and Its Application in Energy Storage System Capacity Optimization. Biomimetics 2025, 10, 244. https://doi.org/10.3390/biomimetics10040244
Yue Y, Cao L, Chen C, Chen Y, Chen B. Snake Optimization Algorithm Augmented by Adaptive t-Distribution Mixed Mutation and Its Application in Energy Storage System Capacity Optimization. Biomimetics. 2025; 10(4):244. https://doi.org/10.3390/biomimetics10040244
Chicago/Turabian StyleYue, Yinggao, Li Cao, Changzu Chen, Yaodan Chen, and Binhe Chen. 2025. "Snake Optimization Algorithm Augmented by Adaptive t-Distribution Mixed Mutation and Its Application in Energy Storage System Capacity Optimization" Biomimetics 10, no. 4: 244. https://doi.org/10.3390/biomimetics10040244
APA StyleYue, Y., Cao, L., Chen, C., Chen, Y., & Chen, B. (2025). Snake Optimization Algorithm Augmented by Adaptive t-Distribution Mixed Mutation and Its Application in Energy Storage System Capacity Optimization. Biomimetics, 10(4), 244. https://doi.org/10.3390/biomimetics10040244







