An Efficient Multi-Objective White Shark Algorithm
Abstract
1. Introduction
- (1)
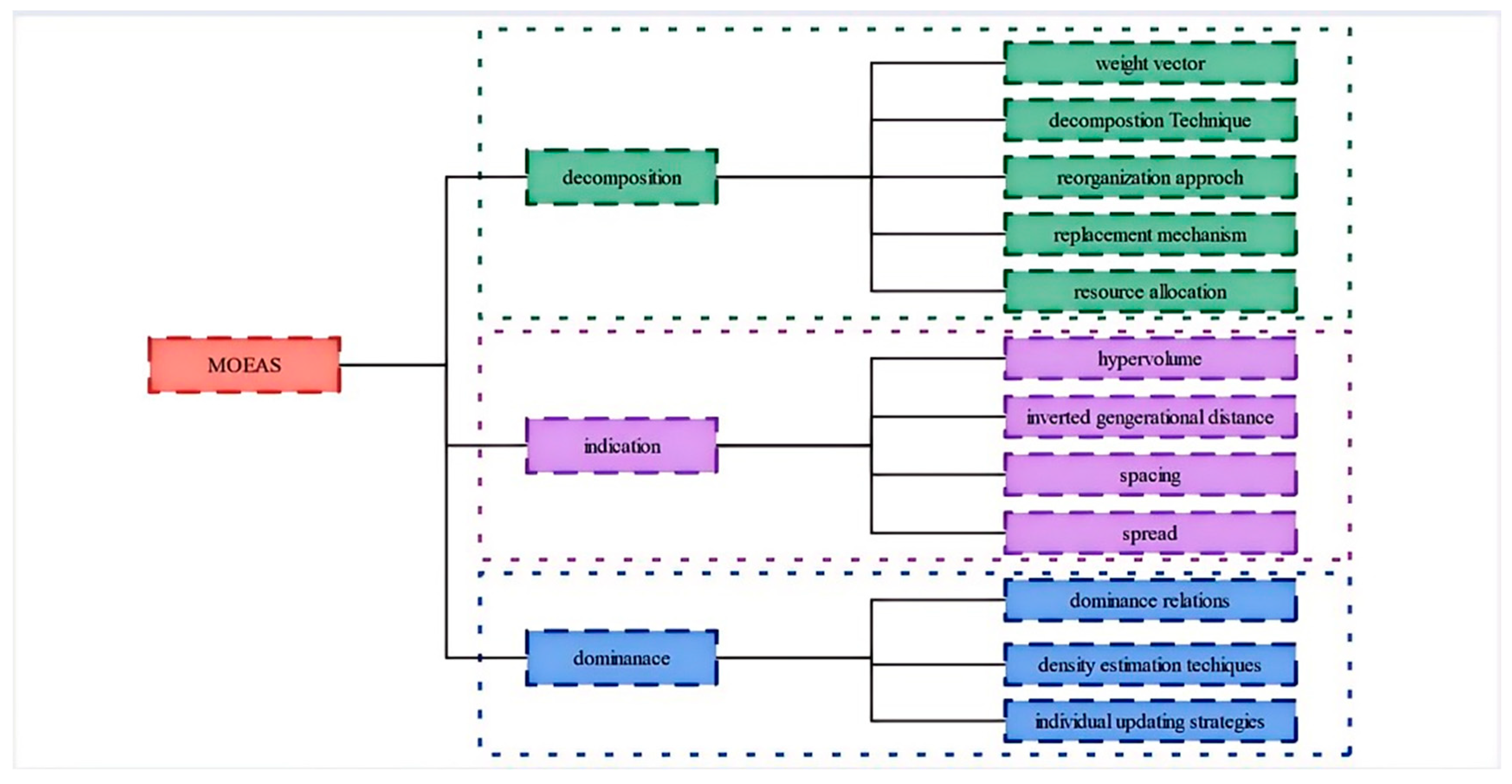
- Decomposition-based MOEAs
- (2)
- Indicator-based MOEAs
- (3)
- Domination-based MOEAs
- Introduces a MONSWSO solution framework based on NSGA-II. The WSO boasts impressive exploration and development capabilities. By integrating the WSO with an elite non-dominated sorting (NDS) mechanism and a Pareto archive, the MONSWSO was developed. This novel method exhibits enhanced robustness and more efficient search capabilities.
- By incorporating a chaotic reverse initialization learning strategy, we generate a more diverse initialization population. Additionally, an adaptive evolution design is introduced to enhance local exploitation capabilities. Furthermore, a hybrid escape energy vortex fish aggregation strategy is utilized to promote the exploration of potential regions.
- Through a series of case studies with varying characteristics, including 23 MO benchmark functions and 4 MO engineering optimization problems, the performance of MONSWSO is rigorously verified through the analysis of five key measures. A practical MO optimization example, such as the optimal setup of an underpass tunnel above a pit, is presented to demonstrate the reliability of MONSWSO’s ability to tackle real-world problems.
2. Related Concepts
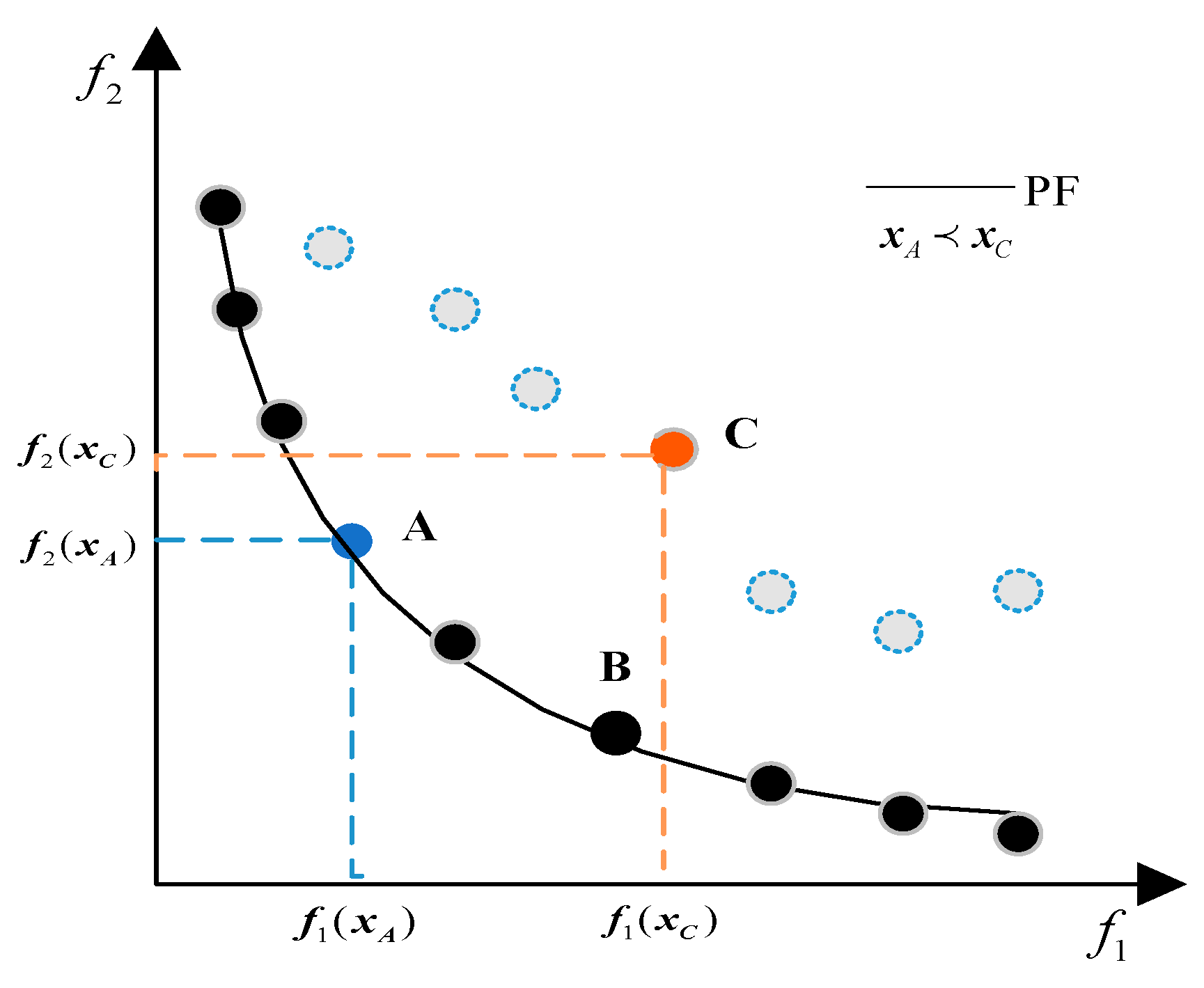
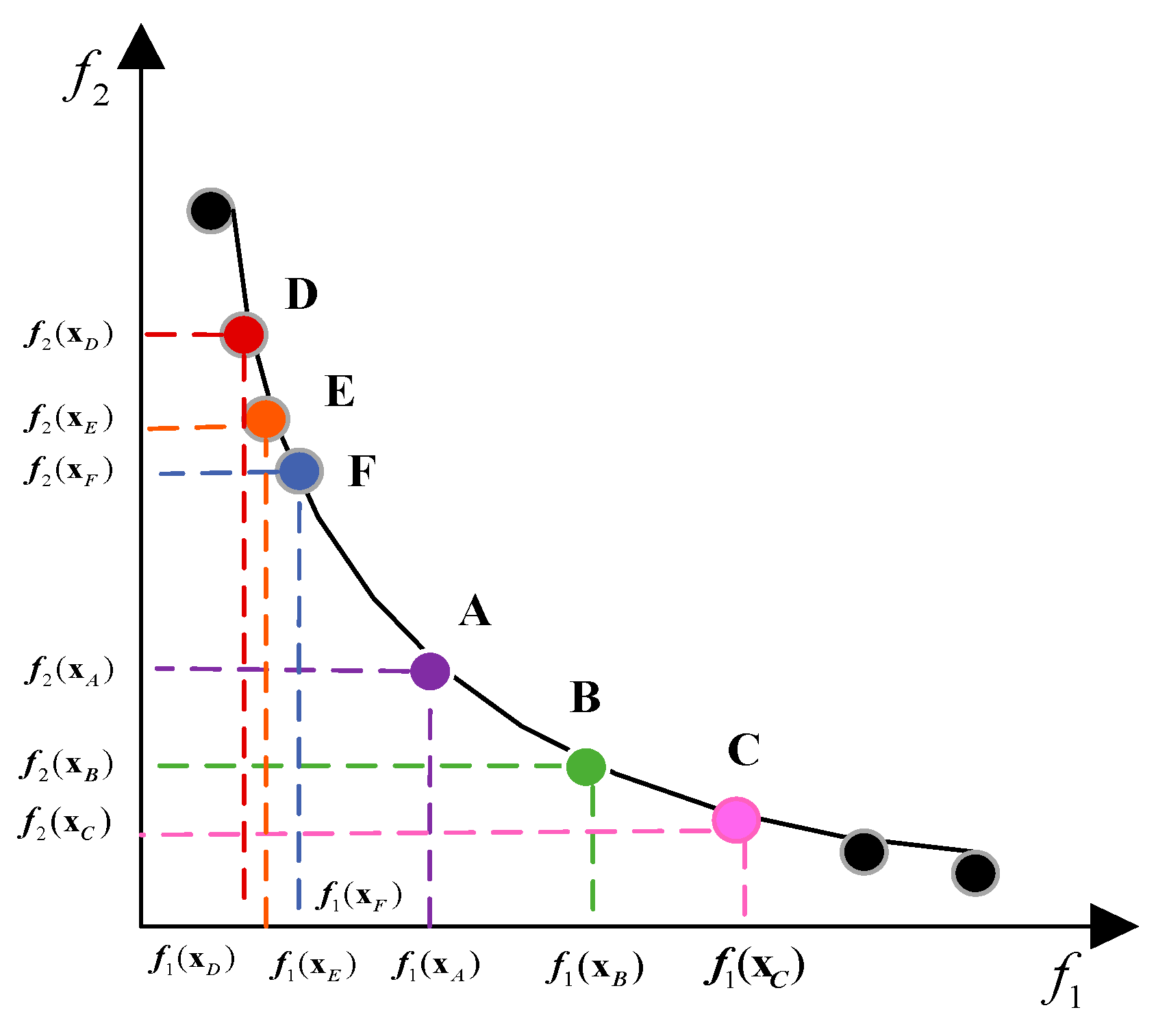
2.1. MO Optimization
2.2. NDS and CD
2.3. Elite Retention Strategies
3. Multi-Objective White Shark Algorithm
3.1. WSO
3.1.1. Move Towards the Quarry
3.1.2. Surrounding the Best Prey
3.1.3. Moving Closer to the Best Sharks
3.1.4. Cluster Behavior
3.2. MONSWSO
3.2.1. Improved WSO
- (1)
- Chaotic reverse initialization
- (2)
- Adaptive evolution and vortex effects
3.2.2. Multi-Objective WSO Algorithm
- The most optimal individual of the population in generation is selected by NDS of and randomly selecting one of the individuals in the first tier as .
- The principle of initial population selection is to merge the chaotic initialized population and the inverse population, select individuals from the elite non-dominated ordering of the resulting individuals to form the initial population , and record the optimal individuals.
| Algorithm 1: The iterative process of MONSWSO |
| Input: , , , |
| Output: |
| 1: Select , according to Equations (11)–(13) |
| 2: While do 3: Update |
| 4: Update , , , |
| 5: For |
| 6: Use Equations (3)–(6) to renew solutions |
| 7: End for |
| 8: For |
| 9: If 10: Update individuals according to Equation (16) 11: Else 12: Update individuals according to Equations (17) and (18) 13: End if 14: End for |
| 15: Combine and |
| 16: Sort the combined group with the elitist NDS and find excellent individuals |
| 17: |
| 18: End while |
| 19: Obtain the optimal population |
4. Numerical Simulations
4.1. Experimental Setting
4.2. Multi-Target Testing Experiments
4.2.1. The Two-Objective Test Problem
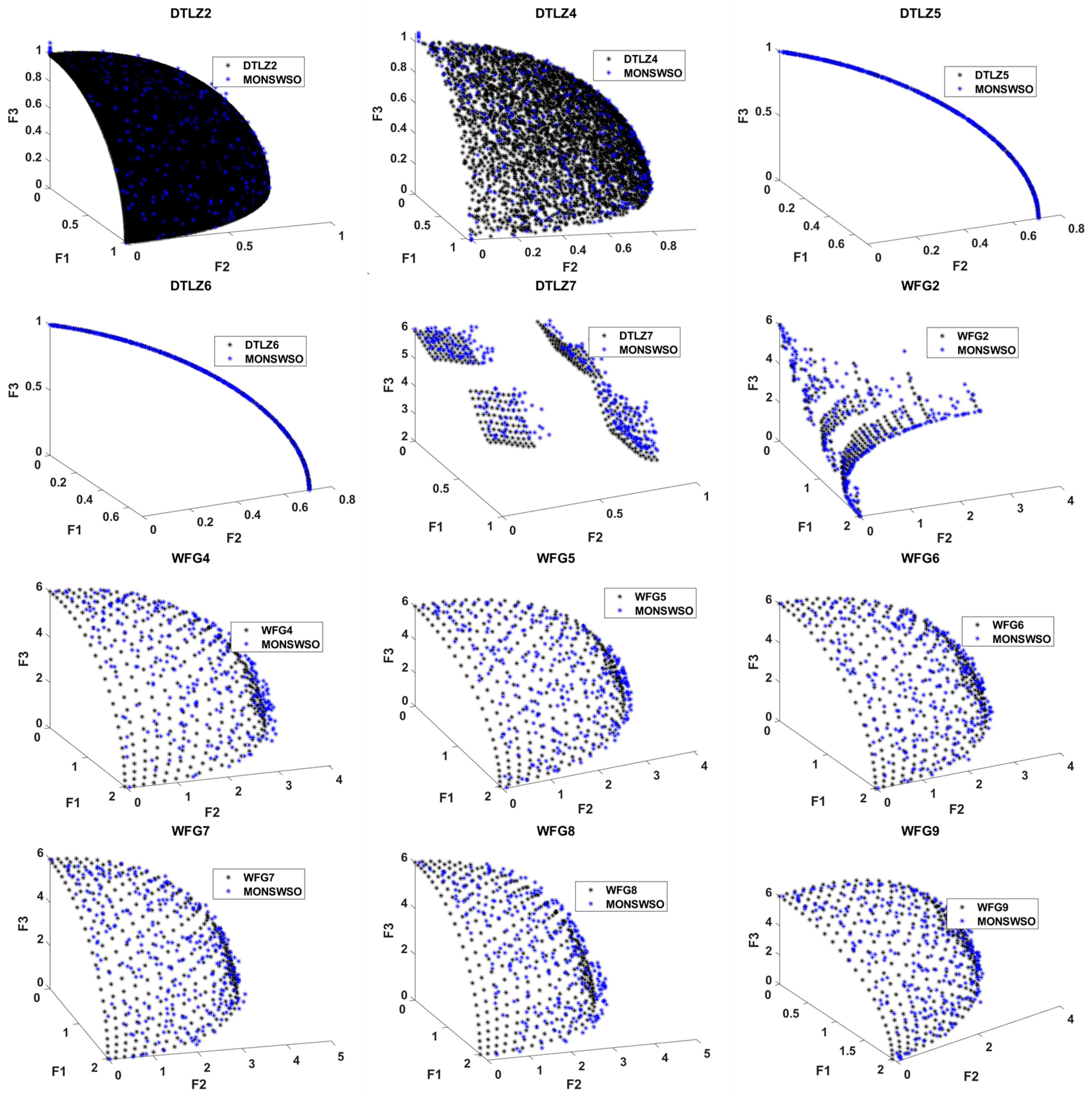
4.2.2. Three-Objective Test Problems
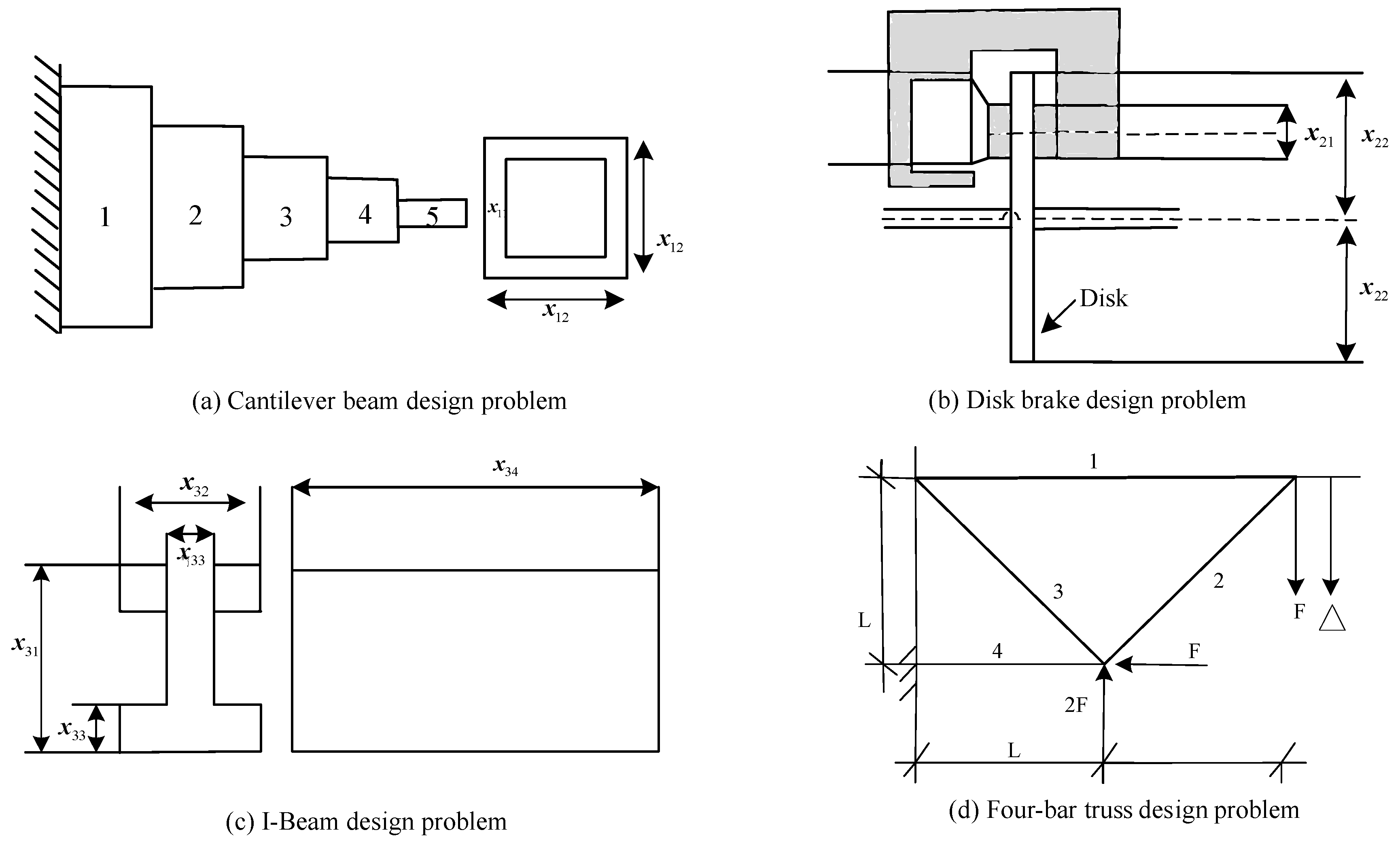
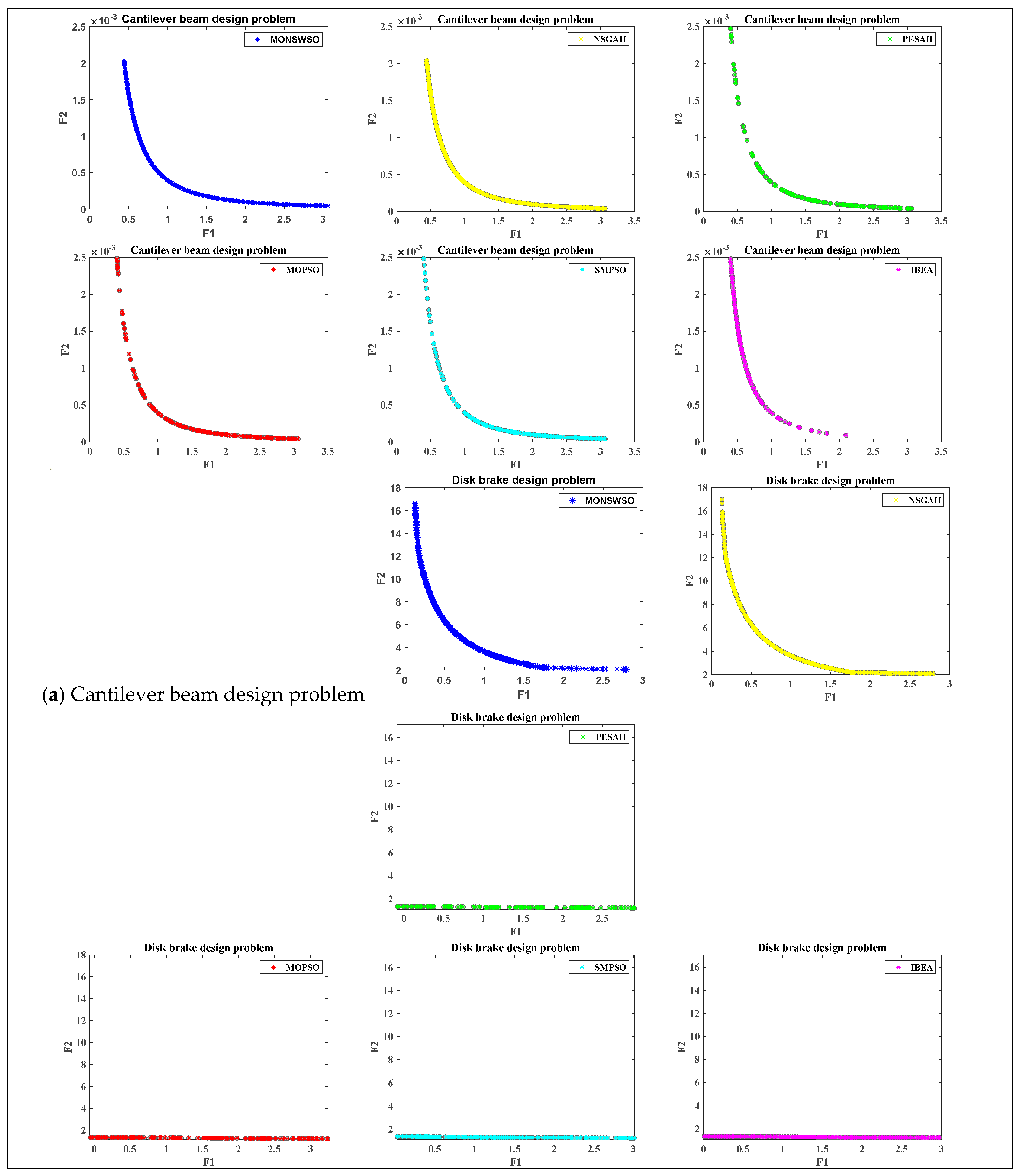
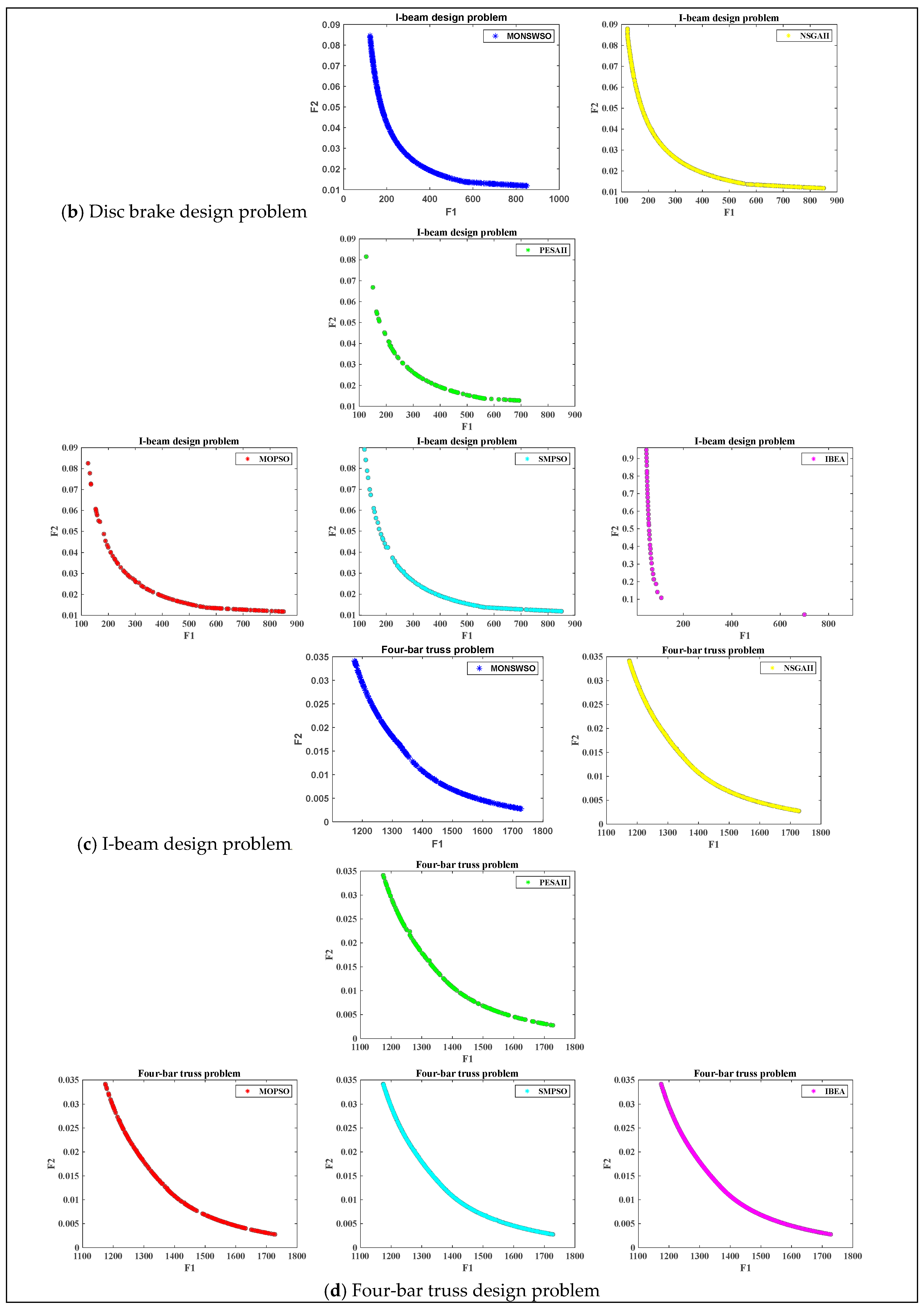
4.3. MO Engineering Design Issues
4.4. Optimization Design for Foundation Pit Above Metro Tunnel
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Abbreviation | Meaning |
|---|---|
| MO | multi-objective |
| WSO | White Shark Optimization algorithm |
| NDS | non-dominated sorting |
| CD | crowding distance |
| IGD | inverse generation distance |
| Spacing | spatial homogeneity |
| Spread | spatial distribution |
| HV | hypervolume |
| PF | pareto front |
| MONSWSO | multi-objective White Shark Optimization algorithm |
| WCs | weight vectors |
| POS | Pareto optimal solutions |
References
- Gao, W.; Liu, L.; Wang, Z. A Review of Decomposition-Based Evolutionary Multi-Objective Optimization Algorithms. J. Softw. 2022, 34, 4743–4771. [Google Scholar]
- Zhang, Q.F.; Hui, L. MOEA/D: A multi-objective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2008, 11, 712–731. [Google Scholar] [CrossRef]
- Tan, Y.Y.; Jiao, Y.C.; Li, H.; Wang, X.-K. MOEA/D+ uniform design: A new version of MOEA/D for optimization problems with many objectives. Comput. Oper. Res. 2013, 40, 1648–1660. [Google Scholar] [CrossRef]
- Ma, X.L.; Qi, Y.T.; Li, L.L.; Liu, F.; Jiao, L.; Wu, J. MOEA/D with uniform decomposition measurement for many-objective problems. Soft Comput. 2014, 18, 2541–2564. [Google Scholar] [CrossRef]
- Harada, K.; Hiwa, S.; Hiroyasu, T. Adaptive weight vector assignment method for MOEA/D. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–9. [Google Scholar]
- Li, Z.X.; He, L.; Chu, Y.J. An improved decomposition multi-objective optimization algorithm with weight vector adaptation strategy. In Proceedings of the 2017 13th International Conference on Semantics, Knowledge and Grids (SKG), Beijing, China, 13–14 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 19–24. [Google Scholar]
- Qi, Y.T.; Ma, X.L.; Liu, F.; Jiao, L.; Sun, J.; Wu, J. MOEA/D with adaptive weight adjustment. Evol. Comput. 2014, 22, 231–264. [Google Scholar] [CrossRef]
- Sato, H. Analysis of inverted PBI and comparison with other scalarizing functions in decomposition based MOEAs. J. Heuristics 2015, 21, 819–849. [Google Scholar] [CrossRef]
- Jiang, S.Y.; Yang, S.X.; Wang, Y.; Liu, X. Scalarizing functions in decomposition based multi-objective evolutionary algorithms. IEEE Trans. Evol. Comput. 2017, 22, 296–313. [Google Scholar] [CrossRef]
- Liu, H.L.; Gu, F.Q.; Zhan, Q.F. Decomposition of a multi-objective optimization problem into a number of simple multi-objective subproblems. IEEE Trans. Evol. Comput. 2014, 18, 450–455. [Google Scholar] [CrossRef]
- Wang, Z.K.; Zhang, Q.F.; Li, H. Balancing convergence and diversity by using two different reproduction operators in MOEA/D: Some preliminary work. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2849–2854. [Google Scholar]
- Ke, L.J.; Zhang, Q.F.; Battiti, R. MOEA/D-ACO: A multi-objective evolutionary algorithm using decomposition and antcolony. IEEE Trans. Cybern. 2013, 43, 1845–1859. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans. Evol. Comput. 2014, 19, 694–716. [Google Scholar] [CrossRef]
- Cai, X.Y.; Li, Y.X.; Fan, Z.; Zhang, Q. An external archive guided multi-objective evolutionary algorithm based on decomposition for combinatorial optimization. IEEE Trans. Evol. Comput. 2014, 19, 508–523. [Google Scholar]
- Bader, J.; Zitzler, E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.N.; Yen, G.G.; Yi, Z. IGD indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Trans. Evol. Comput. 2018, 23, 173–187. [Google Scholar] [CrossRef]
- Yang, S.X.; Li, M.Q.; Liu, X.C.; Zheng, J. A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 17, 721–736. [Google Scholar] [CrossRef]
- Yu, W.; Xie, C.; Bi, Y. A High-Dimensional Multi-Objective Particle Swarm Optimization Algorithm Based on Adaptive Fuzzy Dominance. Acta Autom. Sin. 2018, 44, 2278–2289. [Google Scholar]
- Yuan, Y.; Xu, H.; Wang, B.; Yao, X. A new dominance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2016, 20, 16–37. [Google Scholar] [CrossRef]
- Elarbi, M.; Bechikh, S.; Gupta, A.; Ben Said, L.; Ong, Y.-S. A new decomposition based NSGA-II for many-objective optimization. IEEE Trans. Syst. Man Cybern. 2017, 48, 1191–1210. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, X.Y.; Cheng, R.; He, C.; Jin, Y. Guiding evolutionary multi-objective optimization with generic front modeling. IEEE Trans. Cybern. 2018, 50, 1106–1119. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; TIK Report; ETH Zurich, Computer Engineering and Networks Laboratory: Zurich, Switzerland, 2001. [Google Scholar]
- Chalabi, N.E.; Attia, A.; Bouziane, A.; Hassaballah, M. An improved marine predator algorithm based on epsilon dominance and pareto archive for multi-objective optimization. Eng. Appl. Artif. Intell. 2023, 119, 105718–105743. [Google Scholar] [CrossRef]
- Adra, S.F.; Fleming, P.J. Diversity management in evolutionary many-objective optimization. IEEE Trans. Evol. Comput. 2011, 15, 183–195. [Google Scholar] [CrossRef]
- Li, M.Q.; Yang, S.X.; Liu, X.H. Shift-based density estimation for pareto based algorithms in many-objective optimization. IEEE Trans. Evol. Comput. 2014, 18, 348–365. [Google Scholar] [CrossRef]
- Hancer, E.; Xue, B.; Zhang, M.; Karaboga, D.; Akay, B. A multi-objective artificial bee colony approach to feature selection using fuzzy mutual information. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2420–2427. [Google Scholar]
- Abdullahi, M.; Ngadi, M.A.; Dishing, S.I.; Abdulhamid, S.M.; Ahmad, B.I. An efficient symbiotic organisms search algorithm with chaotic optimization strategy for multi-objective task scheduling problems in cloud computing environment. J. Netw. Comput. Appl. 2019, 133, 60–74. [Google Scholar] [CrossRef]
- Houssein, E.H.; Mahdy, M.A.; Shebl, D.; Manzoor, A.; Sarkar, R.; Mohamed, W.M. An efficient slime mould algorithm for solving multi-objective optimization problems. Expert Syst. Appl. 2022, 187, 115870. [Google Scholar] [CrossRef]
- Khishe, M.; Orouji, N.; Mosavi, M.R. Multi-objective chimp optimizer: An innovative algorithm for multi-objective problems. Expert Syst. Appl. 2023, 211, 118734. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Atwan, J.; Al-Betar, M.A.; Awadallah, M.A. White shark optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl. Based Syst. 2022, 243, 108457. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Haupt, R.; Haupt, S. Practical Genetic Algorithm; John Wiley and Sons: New York, NY, USA, 2004; pp. 38–39. [Google Scholar]
- Tizhoosh, H. Opposition-based learn: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; IEEE Computer Society: Washington, DC, USA, 2005; Volume 1, pp. 695–701. [Google Scholar]
- Feng, Z.K.; Duan, J.F.; Niu, W.J.; Jiang, Z.-Q.; Liu, Y. Enhanced sine cosine algorithm using opposition learning, adaptive evolution and neighborhood search strategies for multivariable parameter optimization problems. Appl. Soft Comput. 2022, 119, 108562. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Wang, X.; Zou, X. Modeling the fear effect in predator prey interactions with adaptive avoidance of predators. Bull. Math. Biol. 2017, 79, 1–35. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, S.; Zhao, K.; Wang, Y. A salp swarm algorithm based on harris eagle foraging strategy. Math. Comput. Simul. 2023, 203, 858–877. [Google Scholar] [CrossRef]
- Chegini, S.N.; Bagheri, A.; Najafi, F. PSOSCALF: A new hybrid pso based on sine cosine algorithm and levy flight for solving optimization problems. Appl. Soft Comput. 2018, 73, 697–726. [Google Scholar] [CrossRef]
- Sierra, M.R.; Coello Coello, C.A. Improving PSO-based multi-objective optimization using crowding, mutation and ε-dominance. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2005; pp. 505–519. [Google Scholar]
- Schott, J.R. Fault Tolerant Design Using Single and Multi-Criteria Genetic Algorithm Optimization. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Knowles, J.; Corne, D. The pareto archived evolution strategy: A new baseline algorithm for pareto multi-objective optimisation. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 1, pp. 98–105. [Google Scholar]
- Coello, C.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Saremi, S. Multi-objective ant lion optimizer: A multi-objective optimization algorithm for solving engineering problems. Appl. Intell. 2017, 46, 79–95. [Google Scholar] [CrossRef]
- Emary, E.; Yamany, W.; Hassanien, A.E.; Snasel, V. Multi-objective gray-wolf optimization for attribute reduction. Procedia Comput. Sci. 2015, 65, 623–632. [Google Scholar] [CrossRef]
- Nebro, A.J.; Durillo, J.J.; Garcia-Nieto, J.; Coello, C.C.; Luna, F.; Alba, E. SMPSO: A new PSO-based metaheuristic for multi-objective optimization. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making (MCDM), Nashville, TN, USA, 30 March–2 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 66–73. [Google Scholar]
- Zitzler, E.; Künzli, S. Indicator-based selection in multi-objective search. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2004; pp. 832–842. [Google Scholar]
- Gurugubelli, S.; Kallepalli, D. Weight and deflection optimization of cantilever beam using a modified non-dominated sorting genetic algorithm. IOSR J. Eng. 2014, 4, 19–23. [Google Scholar] [CrossRef]
- Gong, W.Y.; Cai, Z.H.; Zhu, L. An efficient multi-objective differential evolution algorithm for engineering design. Struct. Multidiscip. Optim. 2009, 38, 137–157. [Google Scholar] [CrossRef]
- Khazaee, A.; Naimi, H.M. Two multi-objective genetic algorithms for finding optimum design of an I-beam. Engineering 2011, 3, 1054–1061. [Google Scholar] [CrossRef][Green Version]
- Coello, C.C.; Pulido, G.T. Multi-objective structural optimization using a microgenetic algorithm. Struct. Multidiscip. Optim. 2005, 30, 388–403. [Google Scholar] [CrossRef]
- Cheng, F.Y.; Li, X.S. Generalized center method for multi-objective engineering optimization. Eng. Optim. 1999, 31, 641–661. [Google Scholar] [CrossRef]
- Bu, K.; Zhao, Y.; Zheng, X. Optimization Design of Metro Tunnel Excavation Above Foundation Pit Engineering Based on NSGA-II Genetic Algorithm. J. Railw. Sci. Eng. 2021, 18, 459–467. [Google Scholar]


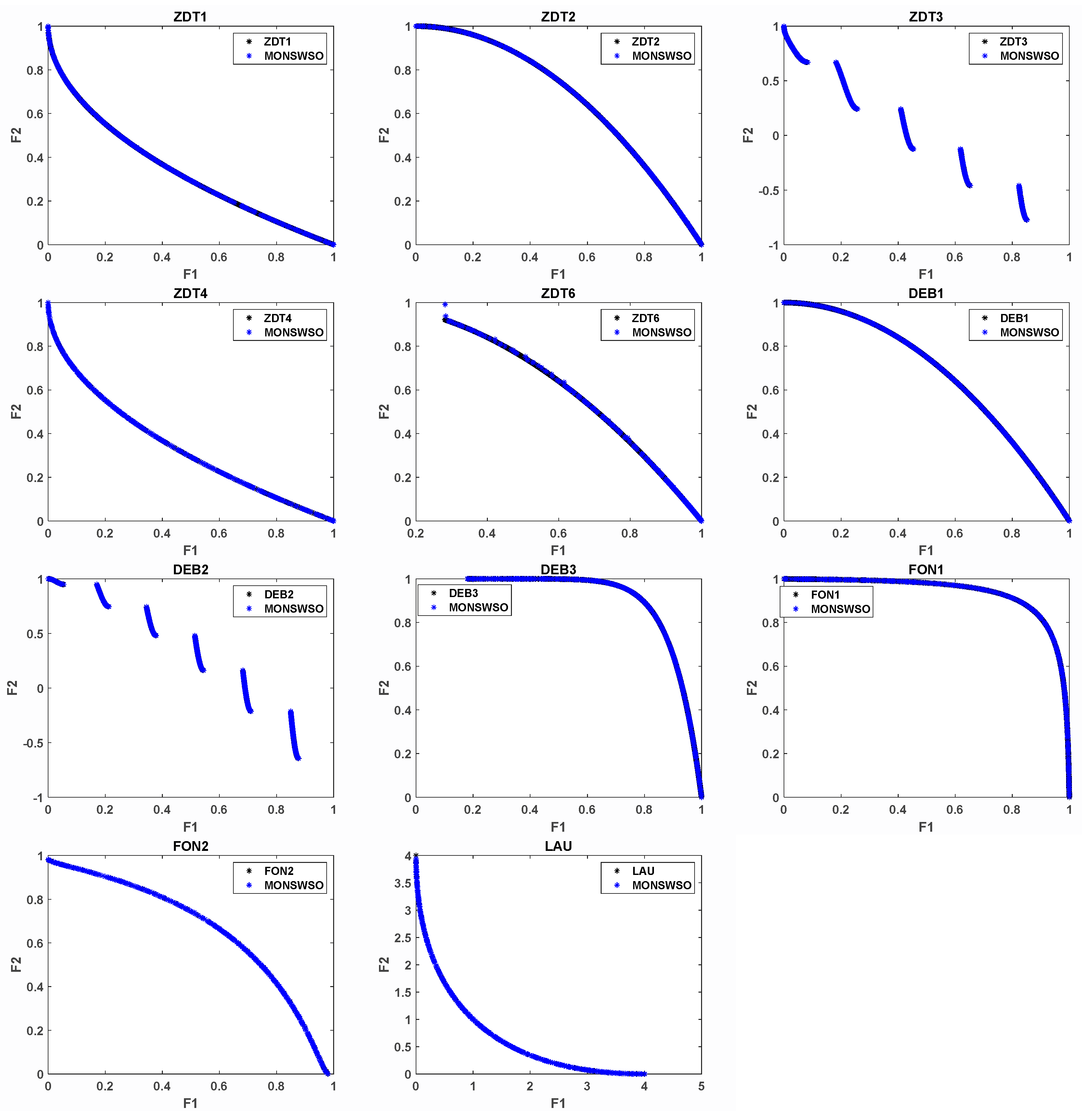

| Function | ZDT1-ZDT4 | ZDT6 | DEB1-DEB3 | FON1-FON2 | LAU | DTLZ2, DTLZ4-7 | WFG2, WFG4-9 |
|---|---|---|---|---|---|---|---|
| Targets | 2 | −2 | 2 | 2 | 2 | 3 | 3 |
| Dimensions | 30 | 10 | 2 | 2 | 2 | 12 | 12 |
| Variable range | [0,1] | [0,1] | [0,1] | [−4,4] | [−50,50] | [0,1] | [0,2:2:24] |
| Function | Four-Bar Truss | Cantilever Beam | Disk Brake | I Beam |
|---|---|---|---|---|
| Targets | 2 | −2 | 2 | 2 |
| Dimensions (constrain) | 4 (0) | 2 (2) | 4 (5) | 4 (1) |
| Algorithms | MONSWSO | NSGAII | PESAII | MOPSO | MOALO | MOGWO | |
|---|---|---|---|---|---|---|---|
| Indicators | M (Sd) | M (Sd) | M (Sd) | M (Sd) | M (Sd) | M (Sd) | |
| ZDT1 | IGD | 0.00132 (0.00006) | 0.00223 (0.00024) − | 0.0049 (0.00064) − | 0.30310 (0.0049) − | 0.23260 (0.03573) − | 0.00595 (0.00542) − |
| Spacing | 0.00224 (0.00010) | 0.00321 (0.01786) − | 0.00439 (0.00074) − | 0.00582 (0.00062) − | 0.00232 (0.00278) − | 0.00517 (0.00438) − | |
| Spread | 0.35420 (0.01856) | 0.47234 (0.04477) − | 0.98300 (0.04530) − | 0.85800 (0.04300) − | 1.09400 (0.03887) − | 1.26600 (0.12940) − | |
| HV | 0.7229 (0.00004) | 0.7229 (0.00002) + | 0.36316 (0.17000) = | 0.71922 (0.00122) − | 0.51140 (0.02140) − | 0.70600 (0.00651) − | |
| ZDT2 | IGD | 0.00201 (0.00052) | 0.01990 (0.09580) − | 0.00592 (0.00099) − | 0.47000 (0.50800) − | 0.58610 (0.01956) − | 0.00616 (0.00496) − |
| Spacing | 0.00233 (0.00034) | 0.00582 (0.01260) − | 0.00445 (0.00096) − | 0.00582 (0.00367) − | 0.00319 (0.00017) − | 0.00618 (0.00456) − | |
| Spread | 0.35250 (0.02730) | 0.42000 (0.11200) − | 0.92000 (0.05020) − | 0.86500 (0.11000) − | 1.00200 (0.00225) − | 1.16200 (0.17660) − | |
| HV | 0.44750 (0.00001) | 0.44721 (0.00003) − | 0.43879 (0.00239) − | 0.01394 (0.03050) − | 0.09167 (0.00129) − | 0.41970 (0.00781) − | |
| ZDT3 | IGD | 0.00164 (0.00005) | 0.00217 (0.00007) − | 0.00390 (0.00119) − | 0.32400 (0.11100) − | 0.05629 (0.03323) − | 0.00436 (0.00480) − |
| Spacing | 0.00225 (0.00014) | 0.00327 (0.00026) − | 0.00457 (0.00090) − | 0.00680 (0.00165) − | 0.00749 (0.00806) − | 0.00759 (0.0032) − | |
| Spread | 0.35960 (0.02214) | 0.40700 (0.02940) − | 0.92700 (0.04870) − | 0.85000 (0.02960) − | 1.31400 (0.16610) − | 1.11600 (0.06785) − | |
| HV | 0.60070 (0.00004) | 0.59064 (0.00003) − | 0.60941 (0.02800) + | 0.28254 (0.07930) − | 0.66060 (0.05070) + | 0.60810 (0.03257) + | |
| ZDT4 | IGD | 0.00150 (0.00007) | 0.00302 (0.00055) − | 0.00361 (0.00205) − | 11.50000 (5.44000) − | 0.14828 (0.06440) − | 0.14489 (0.00465) − |
| Spacing | 0.00217 (0.00012) | 0.00342 (0.00028) − | 0.00480 (0.00105) − | 0.00801 (0.00858) = | 0.00549 (0.00394) − | 0.00363 (0.00527) − | |
| Spread | 0.36740 (0.02234) | 0.38800 (0.04290) = | 0.90800 (0.10400) − | 0.98100 (0.01690) − | 1.08300 (0.05164) − | 1.22140 (0.05273) − | |
| HV | 0.73150 (0.00006) | 0.71276 (0.00026) − | 0.71550 (0.00202) − | NaN (NaN) − | 0.55400 (0.04146) − | 0.70630 (0.00533) − | |
| ZDT6 | IGD | 0.00135 (0.00049) | 0.00193 (0.00008) − | 0.00274 (0.00040) − | 0.00265 (0.02600) − | 0.01759 (0.01080) − | 0.00445 (0.04722) − |
| Spacing | 0.00337 (0.00537) | 0.00283 (0.00019) + | 0.04880 (0.00064) = | 0.01890 (0.01720) − | 0.00752 (0.01445) − | 0.01107 (0.01149) − | |
| Spread | 0.29960 (0.11480) | 0.38400 (0.02780) = | 1.09000 (0.31100) − | 1.01000 (0.20600) − | 1.58100 (0.11970) − | 1.05300 (0.07541) − | |
| HV | 0.40980 (0.00071) | 0.39070 (0.00004) − | 0.38751 (0.00059) − | 0.38212 (0.01423) − | 0.34680 (0.01225) − | 0.36670 (0.00838) − | |
| DEB1 | IGD | 0.00186 (0.00054) | 0.00162 (0.00005) − | 0.00277 (0.00022) − | 0.00477 (0.00030) − | 0.02599 (0.00581) − | 0.00584 (0.00307) − |
| Spacing | 0.00227 (0.00028) | 0.00251 (0.00009) − | 0.00373 (0.00026) − | 0.00601 (0.00062) − | 0.00509 (0.00386) − | 0.00622 (0.00433) − | |
| Spread | 0.34620 (0.03558) | 0.42300 (0.03140) − | 0.82300 (0.04650) − | 0.91800 (0.04620) − | 1.22200 (0.10150) − | 1.16000 (0.06317) − | |
| HV | 0.44750 (0.00012) | 0.44236 (0.00005) − | 0.44350 (0.00110) − | 0.44608 (0.00025) − | 0.39830 (0.00383) − | 0.42210 (0.00494) − | |
| DEB2 | IGD | 0.00164 (0.00011) | 0.13600 (0.00002) − | 0.15600 (0.00003) − | 0.15600 (0.00044) − | 0.02847 (0.01877) − | 0.00542 (0.00452) − |
| Spacing | 0.00211 (0.00005) | 0.00269 (0.00014) − | 0.00412 (0.00031) − | 0.00447 (0.00030) − | 0.00454 (0.01530) − | 0.00766 (0.00989) − | |
| Spread | 0.37490 (0.01518) | 0.60800 (0.03400) − | 0.90200 (0.02830) − | 1.15000 (0.03610) − | 1.33100 (0.29300) − | 1.16700 (0.12040) − | |
| HV | 0.47640 (0.00002) | 0.45039 (0.00001) − | 0.44994 (0.00007) − | 0.45020 (0.00048) − | 0.44570 (0.01793) − | 0.45660 (0.00541) − | |
| DEB3 | IGD | 0.00159 (0.00016) | 0.00524 (0.00094) − | 0.00763 (0.00092) − | 0.00928 (0.00653) − | 0.03210 (0.02386) − | 0.00710 (0.02386) − |
| Spacing | 0.00197 (0.00013) | 0.00664 (0.00054) − | 0.00867 (0.00071) − | 0.00848 (0.00073) − | 0.00446 (0.00506) − | 0.00616 (0.00506) − | |
| Spread | 0.34710 (0.02220) | 0.42400 (0.05370) − | 0.83400 (0.07320) − | 0.74900 (0.05960) − | 1.35800 (0.17400) − | 1.01800 (0.17400) − | |
| HV | 0.24310 (0.00010) | 0.23158 (0.00011) − | 0.22980 (0.00075) − | 0.22943 (0.00237) − | 0.20430 (0.00631) − | 0.21700 (0.00626) − | |
| FON1 | IGD | 0.00203 (0.00019) | 0.00284 (0.00006) − | 0.00335 (0.00024) − | 0.00293 (0.00018) − | 0.05434 (0.01743) − | 0.07805 (0.00944) − |
| Spacing | 0.00242 (0.00038) | 0.00284 (0.00010) − | 0.00375 (0.00024) − | 0.00328 (0.00018) − | 0.00145 (0.00454) + | 0.01701 (0.00235) − | |
| Spread | 0.36340 (0.02442) | 0.41600 (0.02910) − | 0.89600 (0.03140) − | 0.75500 (0.02730) − | 1.07200 (0.12220) + | 1.04600 (0.12670) − | |
| HV | 0.22590 (0.00001) | 0.22585 (0.00003) − | 0.22409 (0.00056) − | 0.22544 (0.00019) − | 0.18950 (0.00964) − | 0.21190 (0.00371) − | |
| FON2 | IGD | 0.00216 (0.00023) | 0.00201 (0.00015) + | 0.00482 (0.00115) − | 0.00356 (0.00057) − | 0.04959 (0.01091) − | 0.01508 (0.00407) − |
| Spacing | 0.00232 (0.00003) | 0.00239 (0.00008) − | 0.00407 (0.00038) − | 0.00354 (0.00035) − | 0.00294 (0.00379) − | 0.00412 (0.00159) − | |
| Spread | 0.35780 (0.02195) | 0.41000 (0.02840) − | 0.92500 (0.02970) − | 0.81000 (0.03920) − | 1.03500 (0.11720) − | 0.86640 (0.01767) − | |
| HV | 0.43130 (0.00006) | 0.42085 (0.00007) − | 0.42570 (0.00163) − | 0.42965 (0.00062) − | 0.38510 (0.00695) − | 0.41080 (0.00252) − | |
| LAU | IGD | 0.00688 (0.00065) | 0.00674 (0.00076) + | 0.01560 (0.00161) − | 0.01190 (0.00163) − | 0.14070 (0.03893) − | 0.02493 (0.02529) − |
| Spacing | 0.00832 (0.00040) | 0.01030 (0.00048) − | 0.01690 (0.00258) − | 0.01470 (0.00065) − | 0.04747 (0.01946) − | 0.03520 (0.01049) − | |
| Spread | 0.34570 (0.02212) | 0.48300 (0.03310) − | 1.01000 (0.05430) − | 0.82600 (0.02760) − | 1.37100 (0.10770) − | 1.15600 (0.13540) − | |
| HV | 0.88100 (0.00002) | 0.76107 (0.00001) − | 0.85937 (0.00037) − | 0.81007 (0.00013) − | 0.84080 (0.00355) − | 0.85330 (0.00262) − | |
| +/−/= | IGD | 2/9/0 | 0/11/0 | 0/11/0 | 1/10/0 | 0/11/0 | |
| Spacing | 1/10/0 | 0/10/0 | 0/10/0 | 1/10/0 | 0/11/0 | ||
| Spread | 0/9/2 | 0/11/0 | 0/11/0 | 0/11/0 | 0/11/0 | ||
| HV | 1/10/0 | 1/9/1 | 0/11/0 | 1/10/0 | 1/10/0 |
| Algorithms | MONSWSO | NSGAII | PESAII | MOPSO | MOALO | MOGWO | |
|---|---|---|---|---|---|---|---|
| Indicators | M (Sd) | M (Sd) | M (Sd) | M (Sd) | M (Sd) | M (Sd) | |
| DTLZ2 | IGD | 0.03697 (0.00042) | 0.03910 (0.00094) = | 0.03930 (0.00062) = | 0.04840 (0.00346) − | 0.11950 (0.01543) − | 0.09500 (0.02922) − |
| Spacing | 0.03002 (0.00228) | 0.03210 (0.00108) − | 0.03290 (0.00112) − | 0.03130 (0.00175) − | 0.06412 (0.00824) − | 0.03458 (0.00169) − | |
| Spread | 0.34650 (0.00312) | 0.50135 (0.01760) = | 0.55242 (0.03930) = | 0.38481 (0.02241) = | 1.36412 (0.00824) − | 0.55458 (0.00169) − | |
| HV | 0.54650 (0.00310) | 0.56335 (0.00265) + | 0.56312 (0.00195) + | 0.54534 (0.00926) − | 0.40042 (0.02112) − | 0.43421 (0.03326) − | |
| DTLZ4 | IGD | 0.03851 (0.00067) | 0.03920 (0.00069) = | 0.03959 (0.00069) − | 0.14384 (0.10000) − | 0.36850 (0.01417) − | 0.09210 (0.02972) − |
| Spacing | 0.02868 (0.00148) | 0.03260 (0.00127) = | 0.03332 (0.00085) − | 0.02575 (0.01460) + | 0.03810 (0.01984) − | 0.03430 (0.00246) − | |
| Spread | 0.39160 (0.02081) | 0.51175 (0.02330) − | 0.53451 (0.03280) − | 0.55518 (0.13900) − | 1.47900 (0.08540) − | 0.81820 (0.02073) − | |
| HV | 0.56371 (0.00168) | 0.56511 (0.00151) + | 0.56752 (0.00192) + | 0.48967 (0.04455) = | 0.29450 (0.06226) − | 0.17904 (0.01743) − | |
| DTLZ5 | IGD | 0.00181 (0.00011) | 0.00189 (0.00007) = | 0.00412 (0.00042) − | 0.00411 (0.00040) − | 0.03650 (0.02382) − | 0.01494 (0.01102) − |
| Spacing | 0.00277 (0.00008) | 0.00302 (0.00022) = | 0.00568 (0.00081) − | 0.00543 (0.00054) − | 0.02064 (0.01341) − | 0.00711 (0.00188) − | |
| Spread | 0.38140 (0.01083) | 0.43658 (0.04740) − | 0.92704 (0.04120) − | 0.95067 (0.06150) − | 1.38600 (0.12390) − | 1.17800 (0.08354) − | |
| HV | 0.20142 (0.00003) | 0.20157 (0.000001) + | 0.19886 (0.00135) = | 0.19771 (0.00165) = | 0.13895 (0.01752) − | 0.1669 (0.02245) − | |
| DTLZ6 | IGD | 0.00165 (0.00014) | 0.00188 (0.00005) − | 0.00462 (0.00027) − | 1.77190 (0.87200) − | 0.05422 (0.04962) − | 0.00373 (0.00136) − |
| Spacing | 0.00283 (0.00011) | 0.00357 (0.00016) − | 0.00531 (0.00052) − | 0.06821 (0.02460) − | 0.08127 (0.05243) − | 0.00391 (0.00148) − | |
| Spread | 0.40600 (0.02047) | 0.61763 (0.03520) − | 1.16700 (0.04690) − | 0.59714 (0.07260) − | 1.46300 (0.20750) − | 0.86790 (0.07747) − | |
| HV | 0.20173 (0.00006) | 0.20162 (0.00003) − | 0.19909 (0.00074) − | NAN (NAN) − | 0.16622 (0.01276) − | 0.1921 (0.00822) − | |
| DTLZ7 | IGD | 0.03978 (0.00311) | 0.04108 (0.00230) = | 0.04209 (0.00223) = | 0.72841 (0.39800) − | 0.57880 (0.02365) − | 0.04730 (0.06067) = |
| Spacing | 0.03029 (0.00217) | 0.03808 (0.00345) − | 0.03496 (0.00205) − | 0.01827 (0.01090) + | 0.01196 (0.00506) + | 0.03877 (0.00791) − | |
| Spread | 0.44560 (0.01032) | 0.48693 (0.02530) − | 0.58002 (0.04870) − | 0.57881 (0.16200) − | 1.09600 (0.04316) − | 0.70110 (0.06978) − | |
| HV | 0.21452 (0.00195) | 0.28210 (0.00058) + | 0.28087 (0.00129) + | 0.12391 (0.07210) − | 0.16390 (0.02612) − | 0.10900 (0.03344) − | |
| WFG2 | IGD | 0.11830 (0.00380) | 0.12433 (0.00621) − | 0.12430 (0.00710) − | 0.17405 (0.01980) − | 0.28800 (0.02969) − | 0.15840 (0.01953) − |
| Spacing | 0.14530 (0.01960) | 0.12909 (0.04000) + | 0.10783 (0.00670) + | 0.09866 (0.04640) + | 0.14490 (0.01973) + | 0.11460 (0.02953) + | |
| Spread | 0.36950 (0.01541) | 0.47087 (0.02160) − | 0.52292 (0.04230) − | 0.44214 (0.02980) − | 1.08400 (0.09980) − | 0.47540 (0.03116) − | |
| HV | 0.93256 (0.00191) | 0.93443 (0.00081) + | 0.93132 (0.00182) − | 0.86914 (0.01842) − | 0.82560 (0.02620) − | 0.8645 (0.00572) − | |
| WFG4 | IGD | 0.21010 (0.00484) | 0.16118 (0.00246) + | 0.16457 (0.00337) + | 0.22022 (0.00712) − | 0.61810 (0.10020) − | 0.38840 (0.23370) − |
| Spacing | 0.12400 (0.00762) | 0.12022 (0.00626) + | 0.11795 (0.00625) + | 0.12415 (0.00837) = | 0.17380 (0.02253) − | 0.13520 (0.03277) + | |
| Spread | 0.39918 (0.00729) | 0.42288 (0.02560) − | 0.42300 (0.02340) − | 0.40542 (0.03290) − | 1.49400 (0.03258) − | 0.52890 (0.03700) − | |
| HV | 0.5175 (0.00176) | 0.55013 (0.00212) − | 0.54642 (0.00310) − | 0.49404 (0.00439) − | 0.37492 (0.02349) − | 0.3317 (0.02252) − | |
| WFG5 | IGD | 0.19690 (0.00326) | 0.18070 (0.00334) + | 0.18195 (0.00323) + | 0.20280 (0.01350) − | 0.39650 (0.05902) − | 0.49797 (0.15670) − |
| Spacing | 0.10710 (0.00505) | 0.11930 (0.00541) − | 0.12474 (0.00949) − | 0.11514 (0.00817) − | 0.19550 (0.01606) − | 0.12720 (0.02631) − | |
| Spread | 0.36950 (0.01541) | 0.47087 (0.02160) − | 0.52292 (0.04230) − | 0.44214 (0.02980) − | 1.08400 (0.09980) − | 0.47540 (0.03116) − | |
| HV | 0.50263 (0.00253) | 0.51788 (0.00317) + | 0.49825 (0.00531) − | 0.46605 (0.00881) − | 0.41842 (0.02600) − | 0.27884 (0.01552) − | |
| WFG6 | IGD | 0.16722 (0.00433) | 0.20847 (0.00874) − | 0.19431 (0.01260) − | 0.23406 (0.02620) − | 0.60000 (0.07342) − | 0.47700 (0.07941) − |
| Spacing | 0.11364 (0.00617) | 0.12953 (0.00768) − | 0.12812 (0.00712) = | 0.17190 (0.00677) − | 0.20220 (0.02319) − | 0.15830 (0.02722) − | |
| Spread | 0.38990 (0.01927) | 0.49648 (0.02690) − | 0.52410 (0.01850) − | 0.40585 (0.02080) = | 1.58300 (0.03202) − | 0.62880 (0.04042) − | |
| HV | 0.54564 (0.00222) | 0.49859 (0.00952) − | 0.50025 (0.01250) − | 0.46985 (0.00964) − | 0.33832 (0.0263) − | 0.26622 (0.01669) − | |
| WFG7 | IGD | 0.16956 (0.00359) | 0.16431 (0.00348) + | 0.16579 (0.00223) + | 0.24305 (0.01340) − | 0.57120 (0.05648) − | 0.61830 (0.08866) − |
| Spacing | 0.11299 (0.00376) | 0.12813 (0.00938) = | 0.12793 (0.00662) = | 0.11785 (0.00805) = | 0.19230 (0.01449) − | 0.10970 (0.03292) + | |
| Spread | 0.39097 (0.01326) | 0.53448 (0.02520) − | 0.54623 (0.03090) − | 0.41414 (0.02160) = | 1.46500 (0.02506) − | 0.61280 (0.04507) − | |
| HV | 0.54378 (0.00242) | 0.56474 (0.00128) + | 0.54612 (0.00403) + | 0.47741 (0.00639) − | 0.35372 (0.00930) − | 0.26422 (0.01316) − | |
| WFG8 | IGD | 0.27467 (0.00301) | 0.27150 (0.00373) + | 0.25909 (0.00557) + | 0.39959 (0.01510) − | 0.75280 (0.07509) − | 0.66374 (0.15700) − |
| Spacing | 0.11605 (0.00352) | 0.13303 (0.00665) − | 0.13346 (0.00661) − | 0.12294 (0.00562) = | 0.17890 (0.02275) − | 0.14190 (0.02361) = | |
| Spread | 0.40327 (0.01505) | 0.54412 (0.02860) − | 0.55864 (0.03350) − | 0.40969 (0.02190) = | 1.55200 (0.03676) − | 0.58990 (0.03998) − | |
| HV | 0.53927 (0.00220) | 0.56474 (0.00128) + | 0.54612 (0.00403) + | 0.47741 (0.00639) − | 0.30262 (0.00840) − | 0.19697 (0.02371) − | |
| WFG9 | IGD | 0.15622 (0.00445) | 0.16649 (0.00399) − | 0.16057 (0.00172) − | 0.18701 (0.01120) − | 0.46700 (0.06412) − | 0.54952 (0.25570) − |
| Spacing | 0.10778 (0.00371) | 0.11692 (0.00481) − | 0.11654 (0.00549) − | 0.11812 (0.00448) − | 0.18730 (0.01528) − | 0.12890 (0.02646) − | |
| Spread | 0.38916 (0.01534) | 0.46482 (0.02810) − | 0.44877 (0.03030) − | 0.40412 (0.02940) = | 1.37900 (0.27080) − | 0.59610 (0.03859) − | |
| HV | 0.46776 (0.00393) | 0.53804 (0.00174) + | 0.52620 (0.00255) + | 0.50723 (0.00739) + | 0.42399 (0.03350) − | 0.26681 (0.02237) − | |
| +/−/= | IGD | 4/4/4 | 4/6/2 | 0/12/0 | 0/12/0 | 0/11/1 | |
| Spacing | 2/7/3 | 2/8/2 | 3/5/4 | 2/10/0 | 3/7/2 | ||
| Spread | 0/11/1 | 0/11/1 | 0/7/5 | 0/12/0 | 0/12/0 | ||
| HV | 10/2/0 | 7/4/1 | 1/9/2 | 0/12/0 | 0/12/0 |
| Algorithm | Spacing | |||||||
|---|---|---|---|---|---|---|---|---|
| Problem a | Problem b | Problem c | Problem d | |||||
| M | Sd | M | Sd | M | Sd | M | Sd | |
| MONSWSO | 0.00427 | 0.00032 | 0.01752 | 0.00051 | 1.11920 | 0.01200 | 0.87604 | 0.04870 |
| NSGAII | 0.00560 | 0.00012 | 0.02985 | 0.01010 | 4.26730 | 0.40300 | 0.88125 | 0.05470 |
| PESAII | 0.01014 | 0.00096 | NaN | NaN | 5.42750 | 0.86800 | 1.19350 | 0.09310 |
| MOPSO | 0.00926 | 0.00082 | NaN | NaN | 5.89620 | 1.81000 | 1.16510 | 0.09820 |
| SMPSO | 0.00669 | 0.00065 | NaN | NaN | 6.00830 | 0.73800 | 0.86004 | 0.04320 |
| IBEA | 0.04012 | 0.01533 | NaN | NaN | NaN | NaN | 1.07990 | 0.03230 |
| Algorithm | Problem Design Objectives | Problem Design Parameters | |||||
|---|---|---|---|---|---|---|---|
| MONSWSO | 12.31259 | 282.03516 | 10 | 0.5 | 20 | 0.6 | 41 |
| 13.27690 | 237.44859 | 5 | 0.6 | 19.5 | 0.6 | 41 | |
| NSGAII | 12.95089 | 251.52024 | 6 | 0.6 | 20.5 | 0.6 | 41 |
| 12.45820 | 275.49024 | 8 | 0.6 | 20.5 | 0.6 | 41 | |
| PESAII | 11.93554 | 315.12135 | 10 | 0.7 | 20 | 0.6 | 41 |
| 11.95881 | 313.31412 | 10 | 0.7 | 20.5 | 0.6 | 41 | |
| MOPSO | 11.89600 | 320.23870 | 9 | 0.8 | 20.5 | 0.6 | 41 |
| 11.40560 | 363.94390 | 10 | 1 | 20 | 0.6 | 41 | |
| SMPSO | 11.52850 | 351.95890 | 9 | 1 | 20 | 0.6 | 41 |
| 12.96330 | 276.69480 | 7 | 0.7 | 20 | 0.6 | 39 | |
| IBEA | 12.62490 | 253.66840 | 9 | 0.4 | 20 | 0.6 | 41 |
| 12.56850 | 284.28370 | 6 | 0.8 | 20.5 | 0.6 | 41 | |
| MOALO | 11.80487 | 332.80187 | 8 | 0.9 | 20 | 0.6 | 41 |
| 12.54890 | 267.25680 | 8 | 0.5 | 20 | 0.6 | 41 | |
| MOGWO | 12.55031 | 260.80876 | 9 | 0.4 | 21 | 0.6 | 41 |
| 12.45241 | 294.43582 | 6 | 0.8 | 20.5 | 0.6 | 41 | |
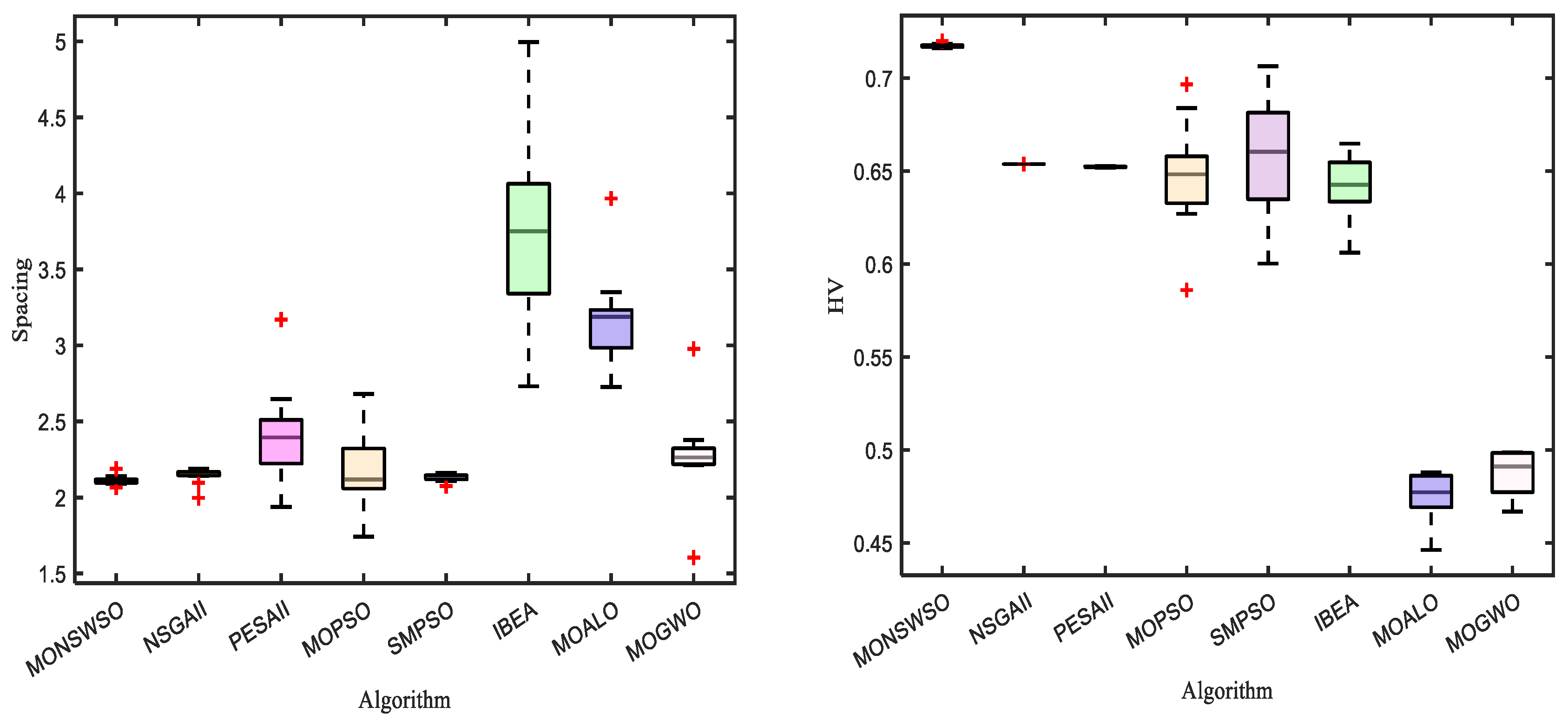
| Algorithm | Spacing | HV | ||||||
|---|---|---|---|---|---|---|---|---|
| M | Sd | Best | Mid | M | Sd | Best | Mid | |
| MONSWSO | 2.11610 | 0.03834 | 2.06270 | 2.10952 | 0.71729 | 0.00112 | 0.71993 | 0.71040 |
| NSGAII | 2.14021 | 0.10221 | 2.08900 | 2.13762 | 0.65374 | 0.00001 | 0.65411 | 0.65374 |
| PESAII | 2.31313 | 0.38521 | 2.11154 | 2.30851 | 0.65224 | 0.00029 | 0.65350 | 0.65219 |
| MOPSO | 2.16012 | 0.36815 | 2.07235 | 2.17433 | 0.65263 | 0.05120 | 0.69272 | 0.65277 |
| SMPSO | 2.11922 | 0.04162 | 2.07525 | 2.12742 | 0.65383 | 0.04160 | 0.70644 | 0.65364 |
| IBEA | 3.79824 | 0.55214 | 3.24743 | 3.55814 | 0.64373 | 0.02110 | 0.65385 | 0.64373 |
| MOALO | 3.18780 | 0.50137 | 2.73218 | 3.32476 | 0.47226 | 0.00601 | 0.48693 | 0.47108 |
| MOGWO | 2.26113 | 0.41588 | 2.19739 | 2.23096 | 0.48691 | 0.00082 | 0.48868 | 0.48729 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Qiang, Y.; Dai, F.; Wang, J.; Li, S. An Efficient Multi-Objective White Shark Algorithm. Biomimetics 2025, 10, 112. https://doi.org/10.3390/biomimetics10020112
Guo W, Qiang Y, Dai F, Wang J, Li S. An Efficient Multi-Objective White Shark Algorithm. Biomimetics. 2025; 10(2):112. https://doi.org/10.3390/biomimetics10020112
Chicago/Turabian StyleGuo, Wenyan, Yufan Qiang, Fang Dai, Junfeng Wang, and Shenglong Li. 2025. "An Efficient Multi-Objective White Shark Algorithm" Biomimetics 10, no. 2: 112. https://doi.org/10.3390/biomimetics10020112
APA StyleGuo, W., Qiang, Y., Dai, F., Wang, J., & Li, S. (2025). An Efficient Multi-Objective White Shark Algorithm. Biomimetics, 10(2), 112. https://doi.org/10.3390/biomimetics10020112




