MECOA: A Multi-Strategy Enhanced Coati Optimization Algorithm for Global Optimization and Photovoltaic Models Parameter Estimation
Abstract
1. Introduction
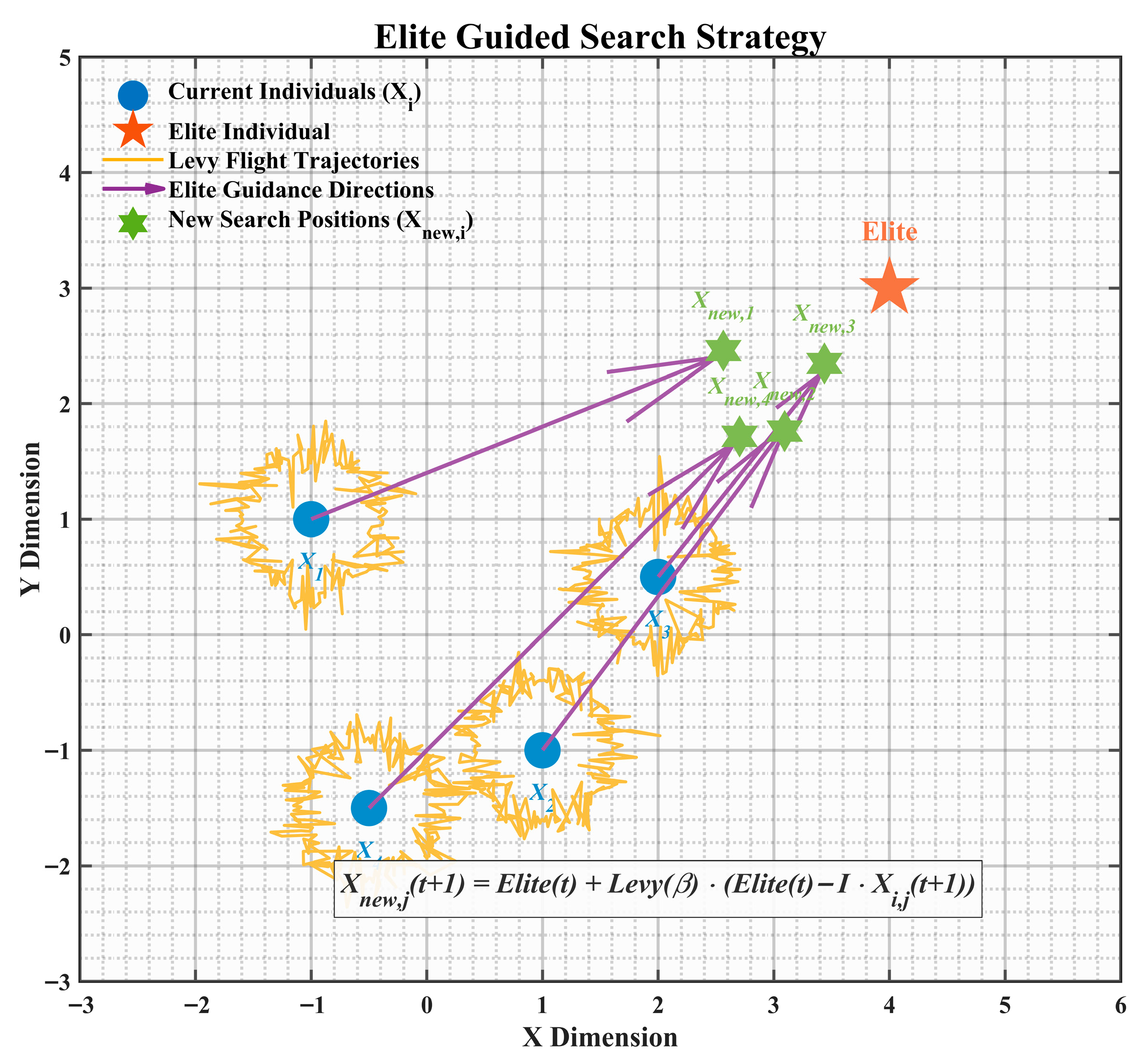
- Elite-guided search strategy: An elite pool composed of the top three individuals replaces the single global best solution. By integrating the heavy-tailed property of Lévy flights, MECOA achieves a balance between large-step jumps and fine-grained local searches, thereby enhancing global exploration while maintaining population diversity.
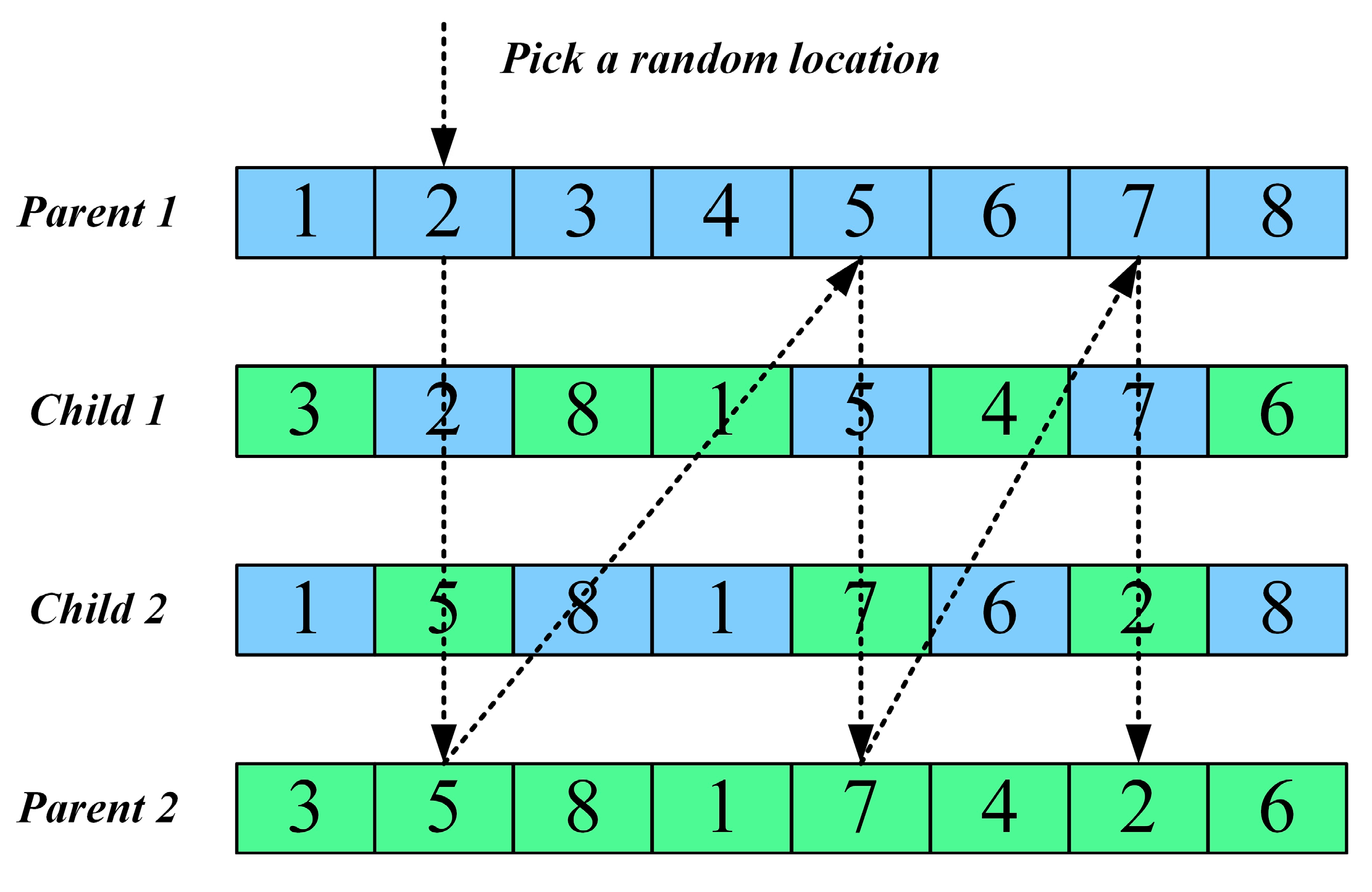
- Horizontal crossover strategy: Inspired by biological gene recombination, this strategy performs random pairing and linear combination among individuals to promote the dissemination and sharing of superior information, improving cooperative search efficiency across the population.
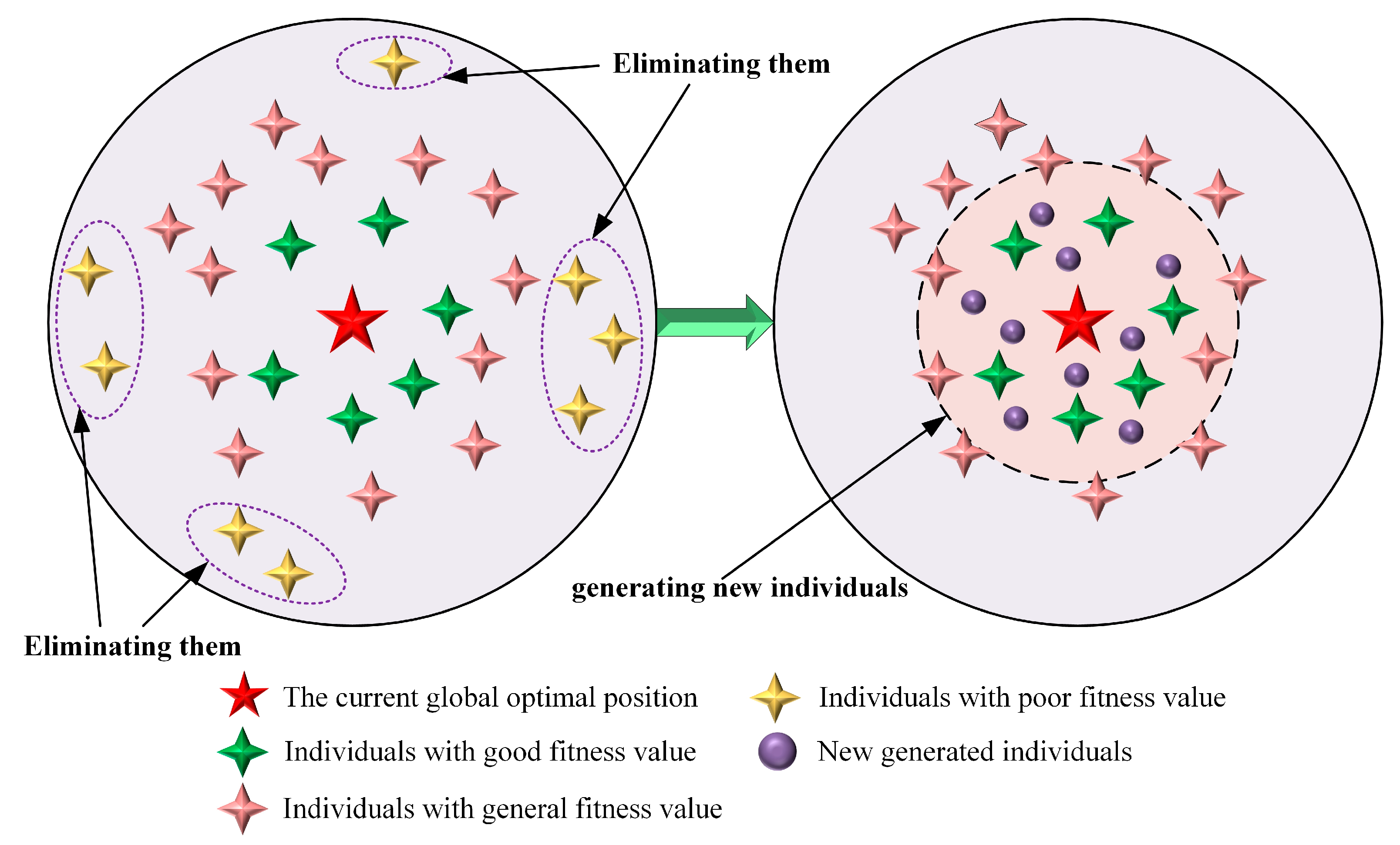
- Precise elimination mechanism: At each iteration, 20% of the low-fitness individuals are discarded, and new individuals are generated around the neighborhood of the current global best solution. This not only improves population quality but also avoids ineffective searches.
- Comprehensive benchmark validation: MECOA is compared against seven mainstream metaheuristic algorithms, including GWO, WOA, and PSO, on the CEC2017 (30/50/100-dimensional) and CEC2022 (20-dimensional) benchmark suites. The evaluation focuses on population diversity, exploration–exploitation balance, convergence speed, and accuracy, validating the superior optimization performance of MECOA.
- Application to PV model parameter identification: MECOA is applied to both the SDM and DDM PV models. Using experimental data from the Photowatt-PWP201 PV module and the RTC France solar cell, the algorithm’s effectiveness is validated through root mean square error (RMSE), integrated absolute error (IAE), and curve-fitting comparisons, demonstrating its practical value for solving complex real-world problems.
2. Coati Optimization Algorithm (COA)
2.1. Initialize Population
2.2. Exploration
2.3. Exploitation
| Algorithm 1: the pseudo-code of the COA |
| 1: Begin 2: Initialize: the relevant parameters iterations 3: Calculate the fitness of the objective function. 4: do 5: Exploration: 6: do 7: coati using Equation (2). 8: End for 9: do 10: coati using Equations (3) and (4). 11: End for 12: Exploitation: 13: do 14: coati using Equations (5) and (6). 15: End for 16: 17: End for 18: return best solution 19: end |
3. Proposed MECOA
3.1. Elite-Guided Search Strategy
3.2. Horizontal Crossover Strategy
3.3. Precision Elimination Mechanism
| Algorithm 2: the pseudo-code of the MECOA |
| 1: Begin 2: Initialize: the relevant parameters iterations 3: Calculate the fitness of the objective function. 4: do 5: Exploration: 6: do 7: coati using Equations (8)–(10). 8: End for 9: do 10: coati using Equations (3) and (4). 11: End for 12: Exploitation: 13: do 14: coati using Equations (5) and (6). 15: End for 16: coati using Equation (11). 17: Eliminate and generate new individuals by Equations (12) and (13) 18: 19: End for 20: return best solution 21: end |
3.4. Computational Time Complexity
4. Experimental Results and Detailed Analyses
4.1. Competitor Algorithms and Parameters Setting
4.2. Qualitative Analysis of MECOA
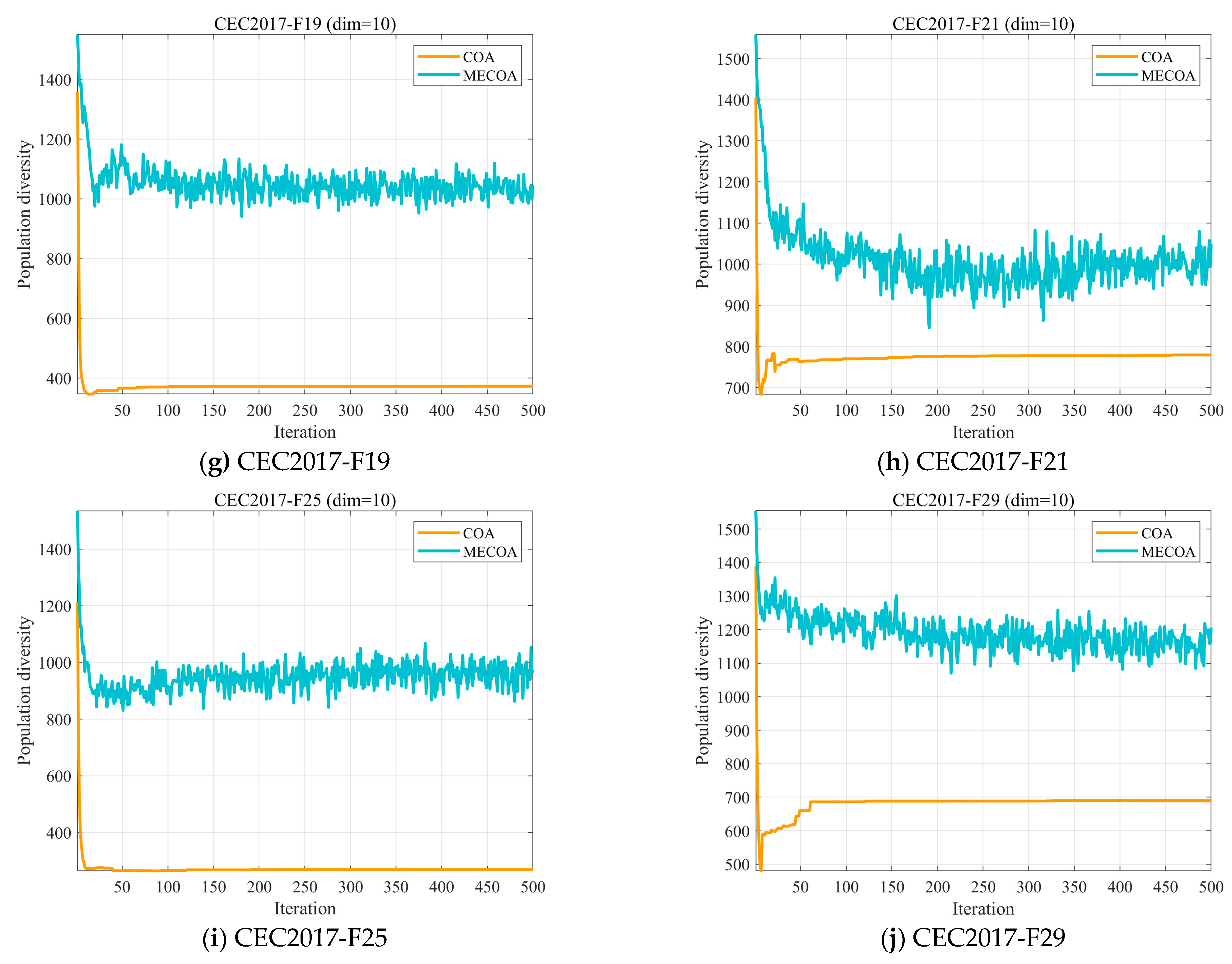
4.2.1. Analysis of the Population Diversity
4.2.2. Analysis of the Exploration and Exploitation
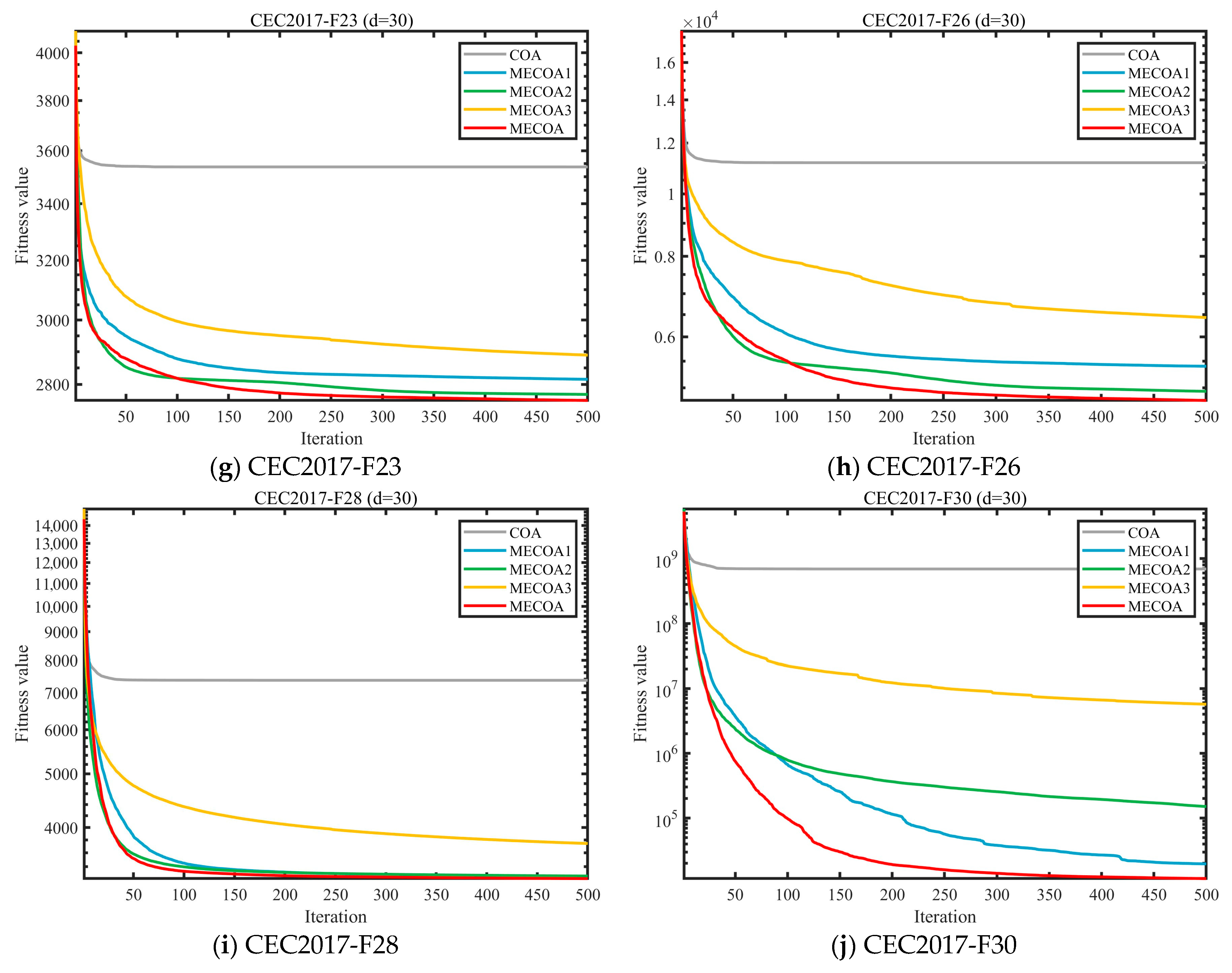
4.2.3. Ablation Experiments
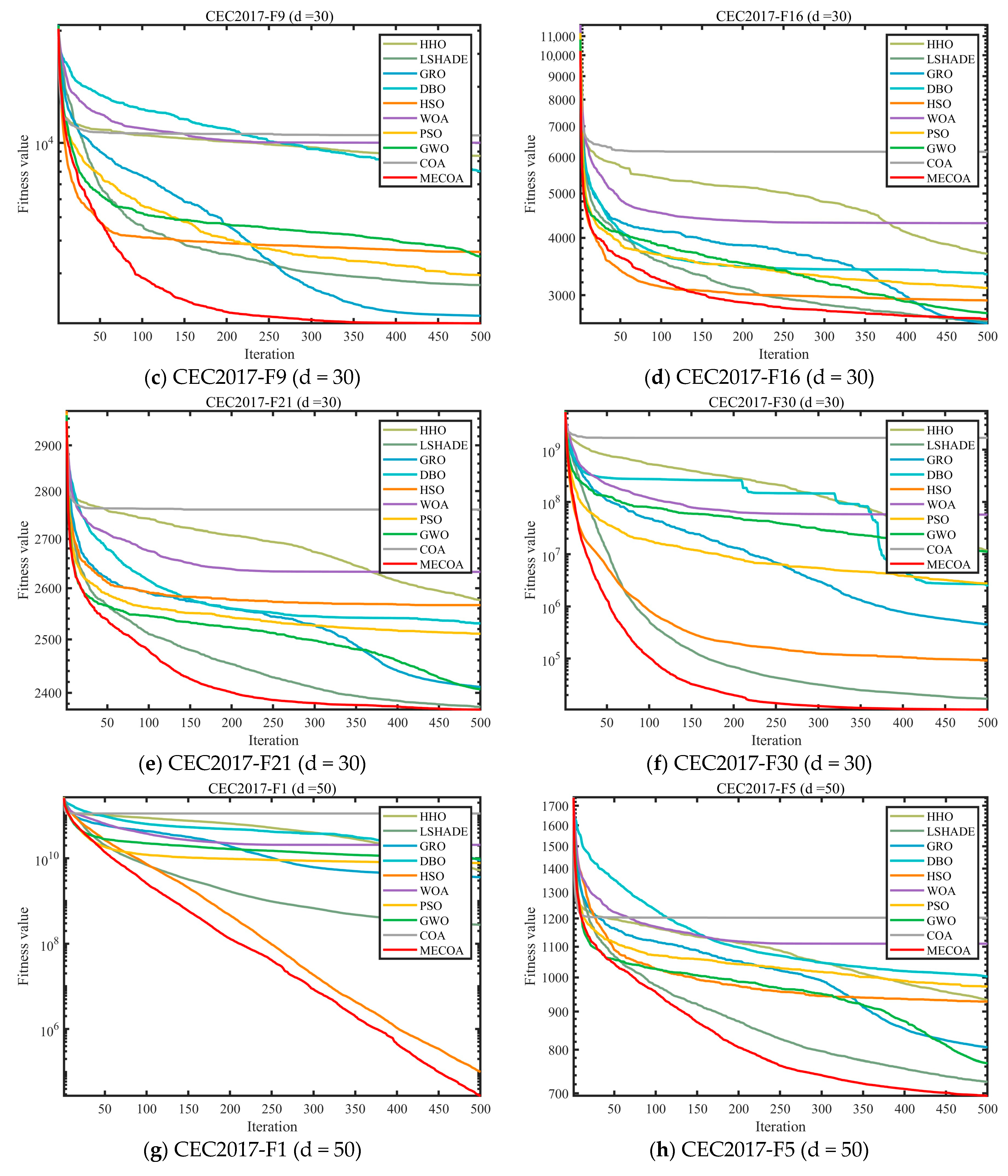
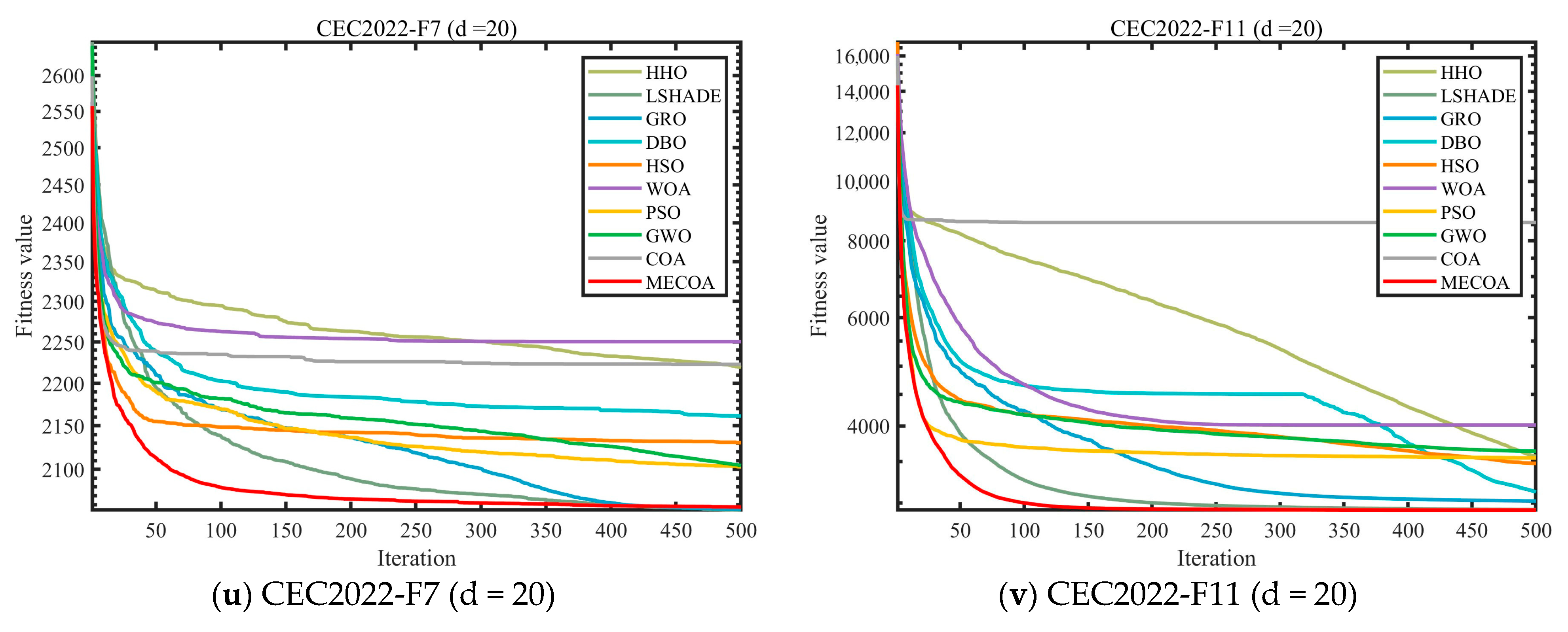
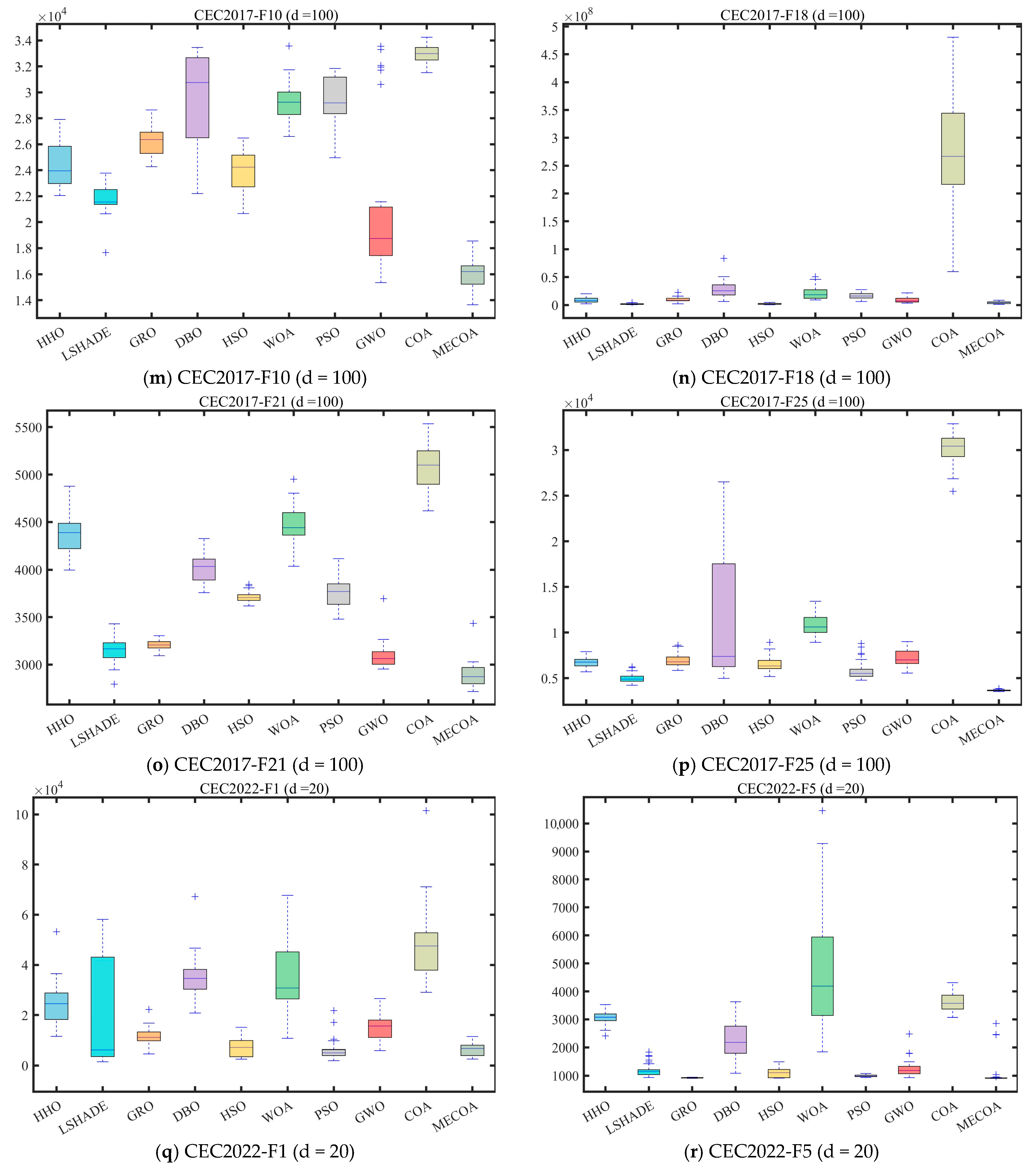
4.3. Compare Using CEC 2017 and CEC2022 Test Functions
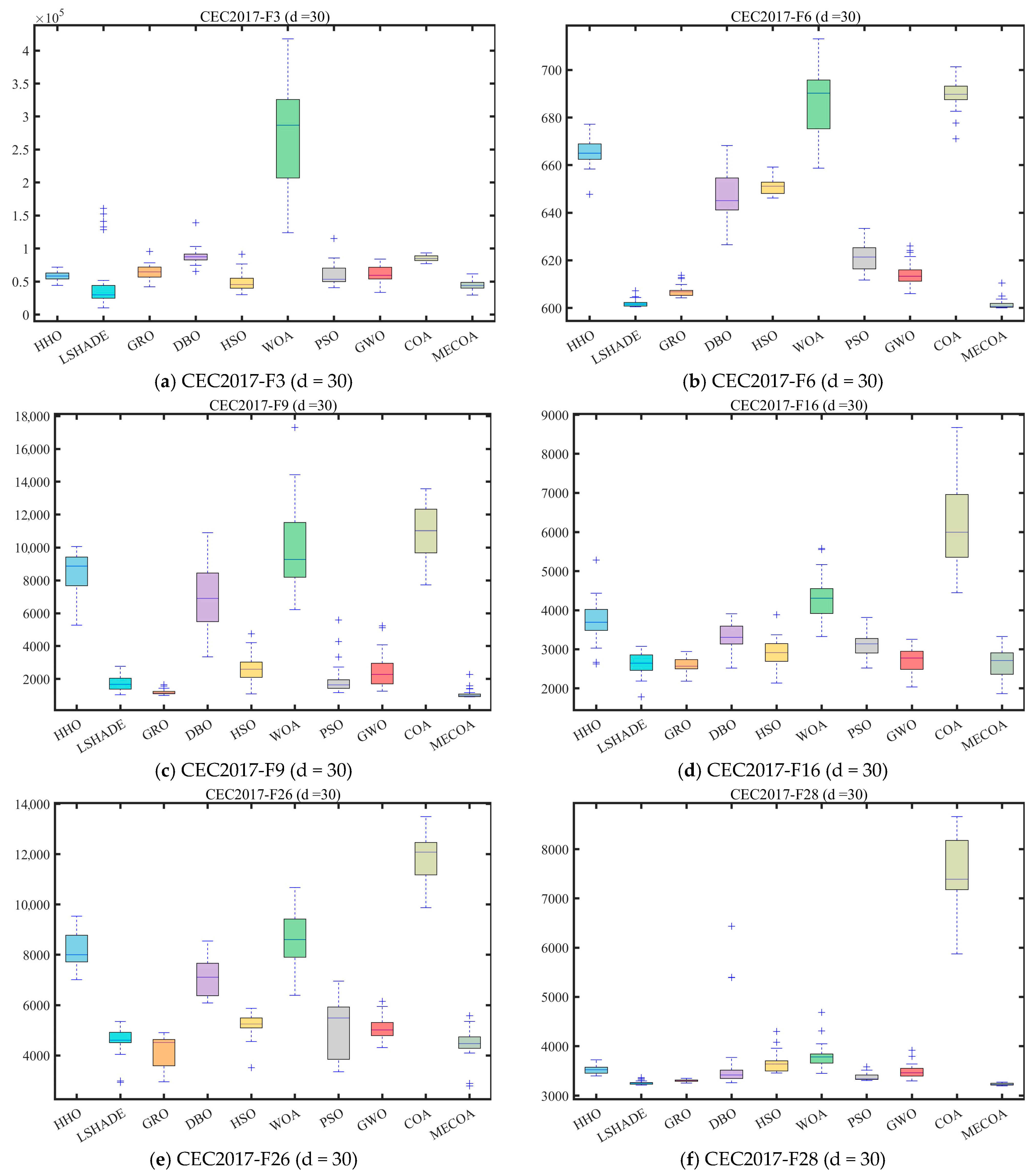
4.4. Statistical Analysis
4.4.1. Wilcoxon Rank Sum Test
4.4.2. Friedman Mean Rank Test
5. MECOA for Photovoltaic Models Parameter Estimation
5.1. Photovoltaic Model
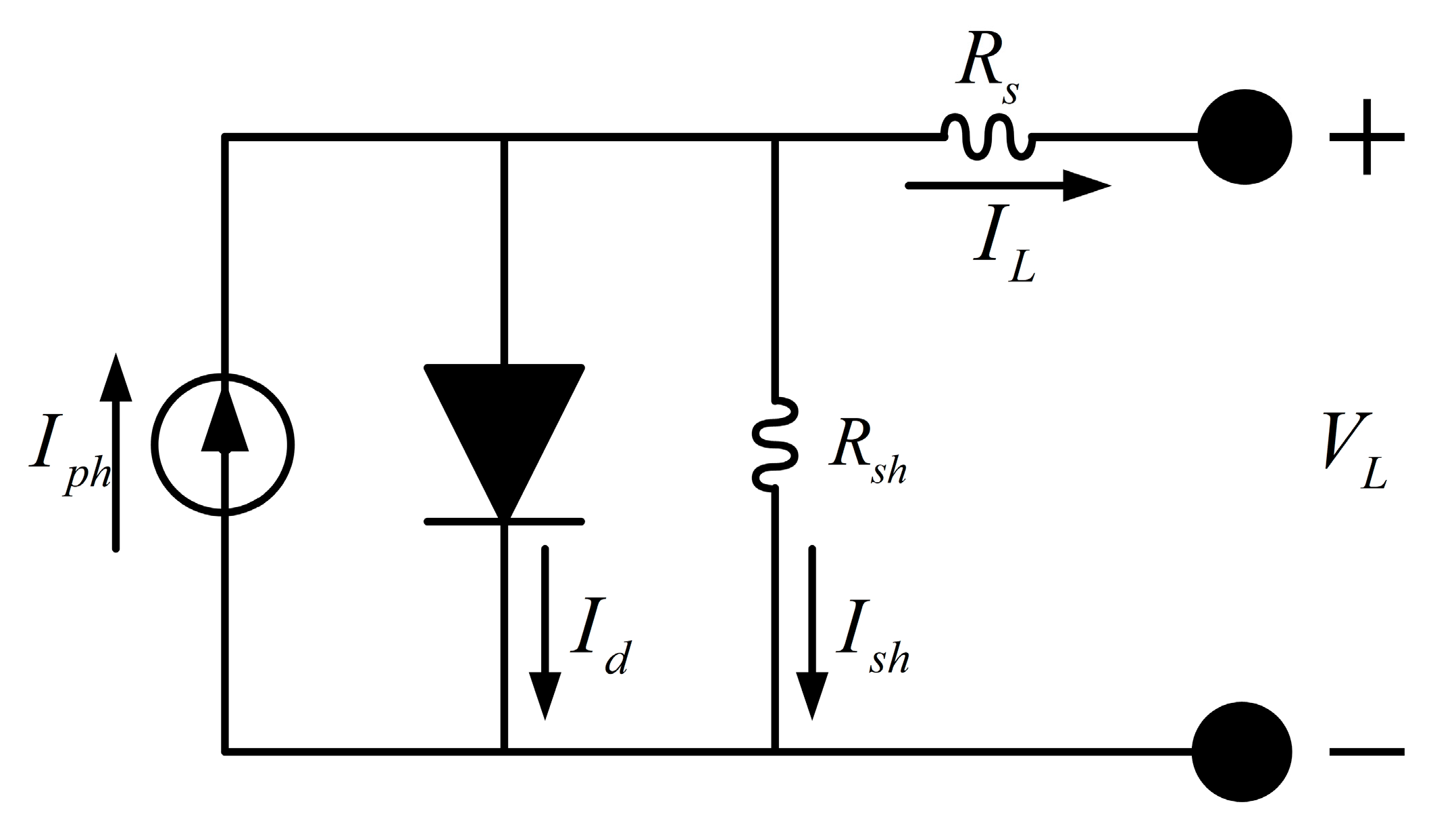
5.1.1. Single Diode Model (SDM)
5.1.2. Double Diode Model (DDM)
5.2. Problem Formulation
5.3. Experimental Results and Analysis
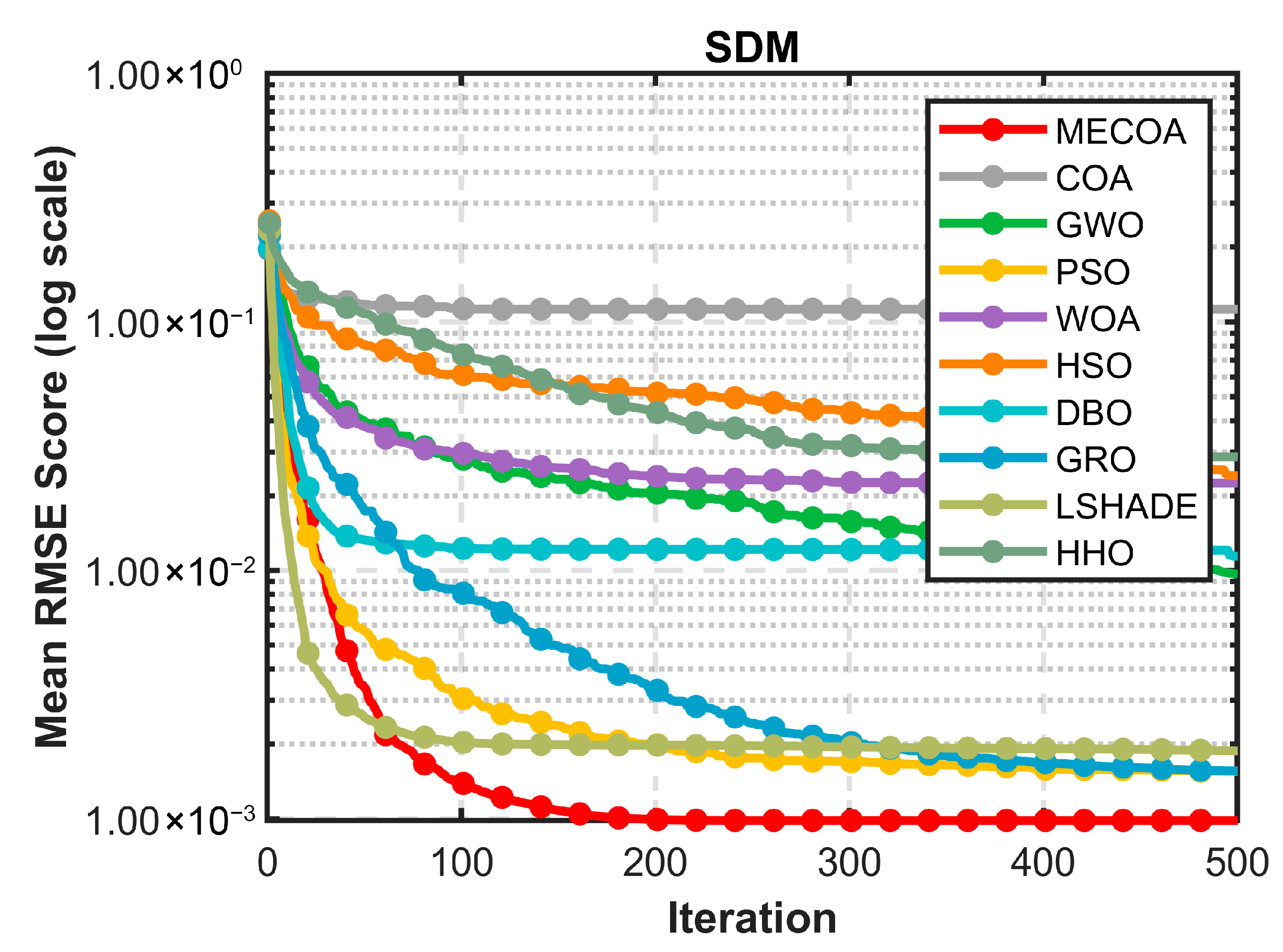
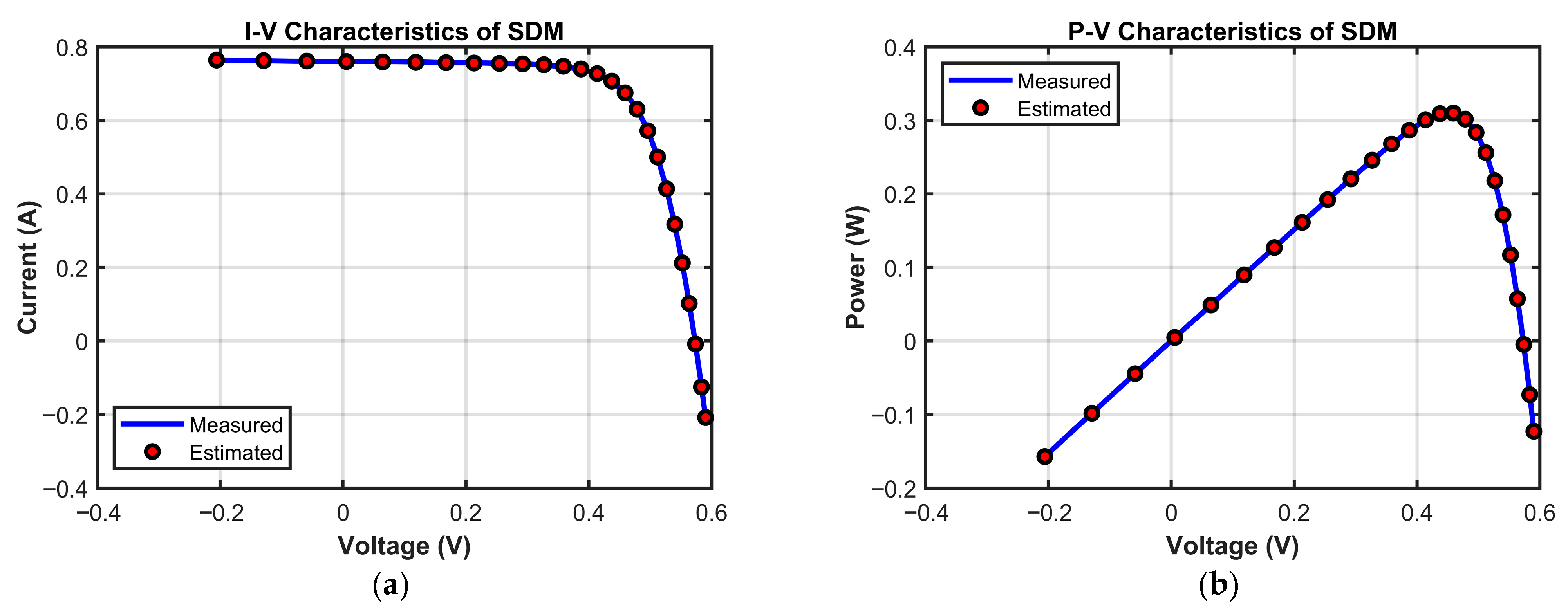
5.3.1. Results of SDM
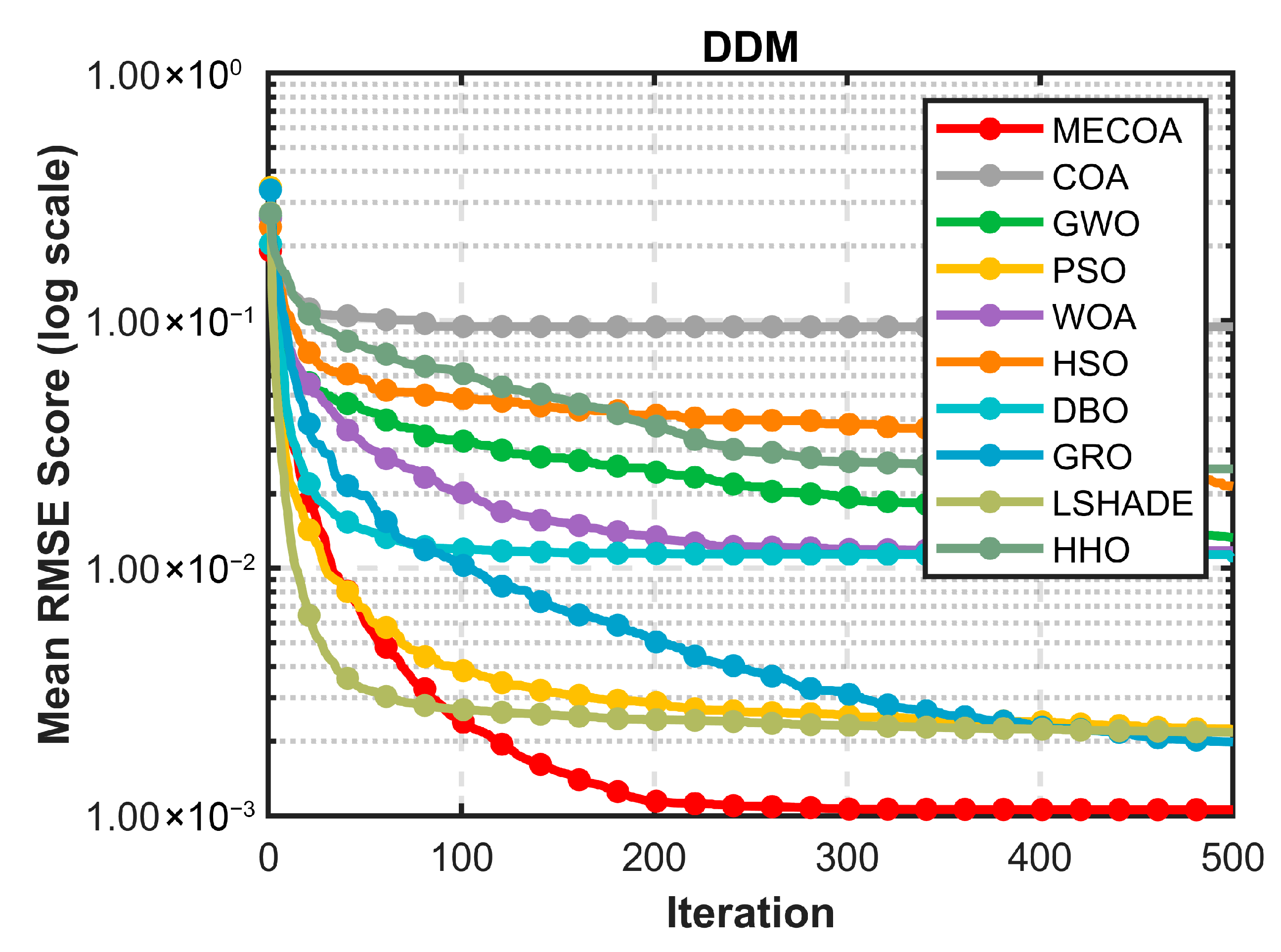
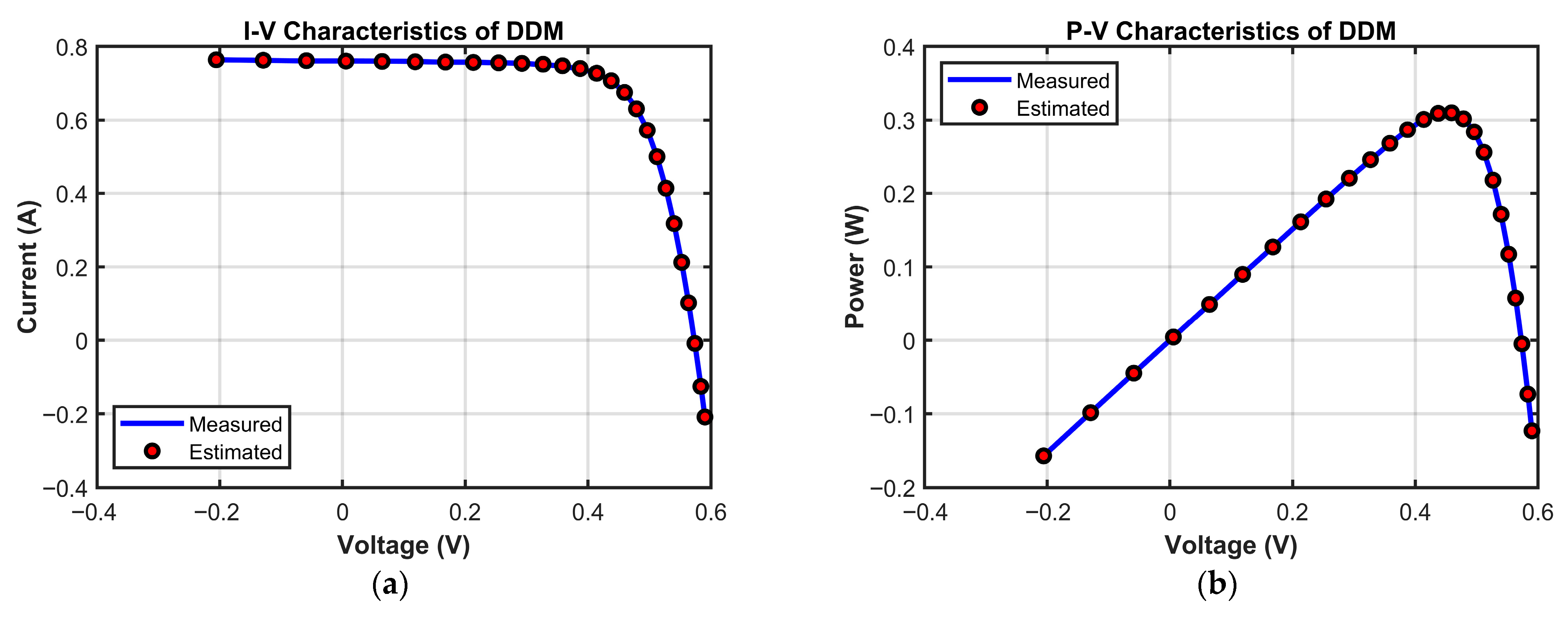
5.3.2. Results of DDM
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| ID | HHO | LSHADE | GRO | DBO | HSO | WOA | PSO | GWO | COA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.0199 × 10−11 | 3.3384 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.3221 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F2 | 3.0199 × 10−11 | 5.4617 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.6955 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F3 | 1.3594 × 10−7 | 2.0523 × 10−3 | 5.5329 × 10−8 | 3.0199 × 10−11 | 4.9178 × 10−1 | 3.0199 × 10−11 | 8.8829 × 10−6 | 5.5999 × 10−7 | 3.0199 × 10−11 |
| F4 | 3.0199 × 10−11 | 8.2357 × 10−2 | 7.3803 × 10−10 | 8.9934 × 10−11 | 4.5043 × 10−11 | 3.0199 × 10−11 | 2.2273 × 10−9 | 3.6897 × 10−11 | 3.0199 × 10−11 |
| F5 | 3.0199 × 10−11 | 1.4945 × 10−1 | 4.6856 × 10−8 | 3.3384 × 10−11 | 1.3289 × 10−10 | 3.0199 × 10−11 | 3.3384 × 10−11 | 8.8829 × 10−6 | 3.0199 × 10−11 |
| F6 | 3.0199 × 10−11 | 1.0315 × 10−2 | 8.1014 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.4941 × 10−11 | 3.0199 × 10−11 |
| F7 | 3.0199 × 10−11 | 6.9125 × 10−4 | 2.3885 × 10−4 | 1.6132 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.6897 × 10−11 | 2.5721 × 10−7 | 3.0199 × 10−11 |
| F8 | 4.9752 × 10−11 | 6.6273 × 10−1 | 5.1857 × 10−7 | 3.6897 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.9590 × 10−5 | 3.0199 × 10−11 |
| F9 | 3.0199 × 10−11 | 1.0105 × 10−8 | 8.1465 × 10−5 | 3.0199 × 10−11 | 3.1589 × 10−10 | 3.0199 × 10−11 | 3.1967 × 10−9 | 2.3715 × 10−10 | 3.0199 × 10−11 |
| F10 | 1.8368 × 10−2 | 1.5581 × 10−8 | 1.1143 × 10−3 | 7.9782 × 10−2 | 2.4386 × 10−9 | 9.8231 × 10−1 | 3.4783 × 10−1 | 2.1540 × 10−6 | 2.0338 × 10−9 |
| F11 | 3.0199 × 10−11 | 1.8608 × 10−6 | 8.1014 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.3384 × 10−11 | 3.0199 × 10−11 |
| F12 | 3.0199 × 10−11 | 5.2650 × 10−5 | 2.0023 × 10−6 | 3.3384 × 10−11 | 5.2640 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 6.0658 × 10−11 | 3.0199 × 10−11 |
| F13 | 3.0199 × 10−11 | 5.7929 × 10−1 | 4.1127 × 10−7 | 6.7220 × 10−10 | 4.1191 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.0937 × 10−10 | 3.0199 × 10−11 |
| F14 | 8.1014 × 10−10 | 8.9934 × 10−11 | 5.5699 × 10−3 | 9.7917 × 10−5 | 1.3853 × 10−6 | 7.3891 × 10−11 | 1.9883 × 10−2 | 1.8682 × 10−5 | 6.6955 × 10−11 |
| F15 | 4.0772 × 10−11 | 1.0315 × 10−2 | 1.7479 × 10−5 | 2.0283 × 10−7 | 2.9205 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 9.9186 × 10−11 | 3.0199 × 10−11 |
| F16 | 3.4971 × 10−9 | 8.3026 × 10−1 | 5.7929 × 10−1 | 5.0922 × 10−8 | 1.3272 × 10−2 | 3.3384 × 10−11 | 2.5974 × 10−5 | 4.5530 × 10−1 | 3.0199 × 10−11 |
| F17 | 9.9186 × 10−11 | 8.8830 × 10−1 | 4.2259 × 10−3 | 4.1997 × 10−10 | 2.6099 × 10−10 | 7.3891 × 10−11 | 3.5638 × 10−4 | 5.4933 × 10−1 | 3.0199 × 10−11 |
| F18 | 8.8411 × 10−7 | 6.6955 × 10−11 | 5.2978 × 10−1 | 1.9112 × 10−2 | 5.5999 × 10−7 | 3.6459 × 10−8 | 1.0035 × 10−3 | 1.4412 × 10−2 | 1.7769 × 10−10 |
| F19 | 3.0199 × 10−11 | 8.3146 × 10−3 | 6.0971 × 10−3 | 4.5726 × 10−9 | 7.4827 × 10−2 | 3.0199 × 10−11 | 3.6897 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F20 | 3.1589 × 10−10 | 3.3285 × 10−1 | 5.4933 × 10−1 | 4.8011 × 10−7 | 9.0688 × 10−3 | 2.4386 × 10−9 | 2.5101 × 10−2 | 1.9579 × 10−1 | 6.0658 × 10−11 |
| F21 | 3.0199 × 10−11 | 1.0869 × 10−1 | 3.5201 × 10−7 | 7.3891 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.8608 × 10−6 | 3.0199 × 10−11 |
| F22 | 3.0199 × 10−11 | 1.7769 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F23 | 3.0199 × 10−11 | 6.2040 × 10−1 | 3.0059 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.8682 × 10−5 | 3.0199 × 10−11 |
| F24 | 3.0199 × 10−11 | 5.0120 × 10−2 | 6.9125 × 10−4 | 3.0199 × 10−11 | 3.3384 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.8790 × 10−6 | 3.0199 × 10−11 |
| F25 | 3.0199 × 10−11 | 7.7272 × 10−2 | 2.2273 × 10−9 | 2.6099 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.4742 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F26 | 3.0199 × 10−11 | 1.4128 × 10−1 | 4.8252 × 10−1 | 3.0199 × 10−11 | 3.2555 × 10−7 | 3.0199 × 10−11 | 1.0315 × 10−2 | 2.7726 × 10−5 | 3.0199 × 10−11 |
| F27 | 3.0199 × 10−11 | 3.1119 × 10−1 | 2.6099 × 10−10 | 6.1210 × 10−10 | 5.4941 × 10−11 | 3.0199 × 10−11 | 2.6015 × 10−8 | 1.8731 × 10−7 | 3.0199 × 10−11 |
| F28 | 3.0199 × 10−11 | 9.0307 × 10−4 | 9.9186 × 10−11 | 3.6897 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F29 | 3.0199 × 10−11 | 2.4581 × 10−1 | 5.5923 × 10−1 | 3.4971 × 10−9 | 1.2057 × 10−10 | 3.0199 × 10−11 | 9.8329 × 10−8 | 3.0317 × 10−2 | 3.0199 × 10−11 |
| F30 | 3.0199 × 10−11 | 5.2650 × 10−5 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.4971 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| ID | HHO | LSHADE | GRO | DBO | HSO | WOA | PSO | GWO | COA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 3 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 | 5.18568 × 10−7 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F2 | 3 × 10−11 | 3.3593 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 | 4.1825 × 10−9 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F3 | 0.04841 | 0.38709978 | 0.01031467 | 2.67842 × 10−6 | 1.8731 × 10−7 | 0.000104066 | 0.830255284 | 0.03916707 | 0.111986872 |
| F4 | 3 × 10−11 | 3.8307 × 10−5 | 3.0199 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F5 | 4.5 × 10−11 | 3.8307 × 10−5 | 8.352 × 10−8 | 1.77691 × 10−10 | 1.46431 × 10−10 | 3.01986 × 10−11 | 3.68973 × 10−11 | 1.7294 × 10−7 | 3.01986 × 10−11 |
| F6 | 3 × 10−11 | 3.3242 × 10−6 | 8.891 × 10−10 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 4.97517 × 10−11 | 2.8716 × 10−10 | 3.01986 × 10−11 |
| F7 | 5 × 10−11 | 1.1077 × 10−6 | 0.00761706 | 1.84999 × 10−8 | 2.43863 × 10−9 | 7.38908 × 10−11 | 9.26029 × 10−9 | 9.2113 × 10−5 | 3.01986 × 10−11 |
| F8 | 3.8 × 10−10 | 0.37903631 | 3.5923 × 10−5 | 2.87158 × 10−10 | 8.15274 × 10−11 | 3.01986 × 10−11 | 1.46431 × 10−10 | 0.00422592 | 3.01986 × 10−11 |
| F9 | 3 × 10−11 | 1.0937 × 10−10 | 4.1825 × 10−9 | 3.01986 × 10−11 | 4.97517 × 10−11 | 3.01986 × 10−11 | 8.15274 × 10−11 | 4.0772 × 10−11 | 3.01986 × 10−11 |
| F10 | 1 × 10−5 | 1.85 × 10−8 | 5.9706 × 10−5 | 0.012732115 | 9.26029 × 10−9 | 0.464272911 | 0.153667235 | 2.0283 × 10−7 | 2.22727 × 10−9 |
| F11 | 5.5 × 10−11 | 6.5261 × 10−7 | 4.5043 × 10−11 | 4.97517 × 10−11 | 9.91863 × 10−11 | 3.01986 × 10−11 | 8.15274 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F12 | 3 × 10−11 | 7.6588 × 10−5 | 3.0199 × 10−11 | 3.01986 × 10−11 | 1 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F13 | 3 × 10−11 | 2.5721 × 10−7 | 3.3384 × 10−11 | 3.01986 × 10−11 | 1.10234 × 10−8 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F14 | 8.1 × 10−10 | 1.4643 × 10−10 | 0.12967022 | 6.04595 × 10−7 | 5.46175 × 10−9 | 6.06576 × 10−11 | 0.00728836 | 0.00076973 | 3.01986 × 10−11 |
| F15 | 3 × 10−11 | 0.92344213 | 3.9648 × 10−8 | 3.01986 × 10−11 | 0.000952074 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F16 | 1.1 × 10−8 | 0.42038633 | 0.83025528 | 5.53286 × 10−8 | 0.347827783 | 3.01986 × 10−11 | 4.80107 × 10−7 | 0.45529691 | 3.01986 × 10−11 |
| F17 | 5.1 × 10−6 | 0.05942792 | 0.17612755 | 2.0338 × 10−9 | 0.000283887 | 1.46431 × 10−10 | 4.80107 × 10−7 | 0.28377805 | 3.01986 × 10−11 |
| F18 | 6 × 10−7 | 3.8249 × 10−9 | 0.52014461 | 9.79171 × 10−5 | 4.11271 × 10−7 | 3.01986 × 10−11 | 0.00022539 | 0.01563812 | 3.01986 × 10−11 |
| F19 | 3 × 10−11 | 0.44641944 | 0.00055611 | 2.37147 × 10−10 | 0.010314672 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F20 | 0.01221 | 0.36322231 | 0.00289133 | 0.002499392 | 0.016954881 | 4.11776 × 10−6 | 0.003033948 | 0.2580515 | 4.07716 × 10−11 |
| F21 | 3 × 10−11 | 3.3242 × 10−6 | 1.1023 × 10−8 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.33839 × 10−11 | 1.2023 × 10−8 | 3.01986 × 10−11 |
| F22 | 0.15798 | 0.00556994 | 0.03643886 | 0.145319127 | 0.004032978 | 0.304176818 | 0.864993706 | 0.02068075 | 8.10136 × 10−10 |
| F23 | 3 × 10−11 | 9.8329 × 10−8 | 8.1014 × 10−10 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 2.2273 × 10−9 | 3.01986 × 10−11 |
| F24 | 3 × 10−11 | 0.01628481 | 0.00090307 | 3.01986 × 10−11 | 4.97517 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 0.00015846 | 3.01986 × 10−11 |
| F25 | 3 × 10−11 | 2.7726 × 10−5 | 3.0199 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F26 | 3.3 × 10−11 | 8.6634 × 10−5 | 5.8587 × 10−6 | 4.50432 × 10−11 | 3.82016 × 10−10 | 3.01986 × 10−11 | 0.025101283 | 8.4848 × 10−9 | 3.01986 × 10−11 |
| F27 | 3 × 10−11 | 0.02708632 | 6.0658 × 10−11 | 3.01986 × 10−11 | 8.89099 × 10−10 | 3.01986 × 10−11 | 5.26501 × 10−5 | 2.0338 × 10−9 | 3.01986 × 10−11 |
| F28 | 3 × 10−11 | 5.5329 × 10−8 | 3.0199 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.33839 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| F29 | 3 × 10−11 | 0.01501413 | 0.03778202 | 5.07231 × 10−10 | 2.66947 × 10−9 | 3.01986 × 10−11 | 2.1544 × 10−10 | 2.4327 × 10−5 | 3.01986 × 10−11 |
| F30 | 3 × 10−11 | 3.1589 × 10−10 | 3.0199 × 10−11 | 3.01986 × 10−11 | 4.19968 × 10−10 | 3.01986 × 10−11 | 3.01986 × 10−11 | 3.0199 × 10−11 | 3.01986 × 10−11 |
| ID | HHO | LSHADE | GRO | DBO | HSO | WOA | PSO | GWO | COA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.3384 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F2 | 3.0199 × 10−11 | 1.2118 × 10−12 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.3384 × 10−11 | 5.4941 × 10−11 | 3.0199 × 10−11 |
| F3 | 2.7829 × 10−7 | 6.0971 × 10−3 | 4.5043 × 10−11 | 3.0199 × 10−11 | 1.4423 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 8.4848 × 10−9 |
| F4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F5 | 4.9752 × 10−11 | 2.9205 × 10−2 | 3.5923 × 10−5 | 1.6947 × 10−9 | 6.0658 × 10−11 | 3.0199 × 10−11 | 1.6132 × 10−10 | 5.1060 × 10−1 | 3.0199 × 10−11 |
| F6 | 3.0199 × 10−11 | 9.7052 × 10−1 | 2.4994 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.8202 × 10−10 | 1.5638 × 10−2 | 3.0199 × 10−11 |
| F7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.6099 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.3384 × 10−11 | 2.3897 × 10−8 | 3.0199 × 10−11 |
| F8 | 3.0199 × 10−11 | 1.3250 × 10−4 | 3.5923 × 10−5 | 3.1589 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.0772 × 10−11 | 1.5969 × 10−3 | 3.0199 × 10−11 |
| F9 | 1.4110 × 10−9 | 5.4933 × 10−1 | 7.5059 × 10−1 | 1.7769 × 10−10 | 2.3768 × 10−7 | 1.7769 × 10−10 | 1.4733 × 10−7 | 7.6973 × 10−4 | 3.6897 × 10−11 |
| F10 | 3.0199 × 10−11 | 3.3384 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.5201 × 10−7 | 3.0199 × 10−11 |
| F11 | 8.9934 × 10−11 | 4.2067 × 10−2 | 4.4440 × 10−7 | 3.0199 × 10−11 | 1.5292 × 10−5 | 3.0199 × 10−11 | 2.9047 × 10−1 | 1.1882 × 10−1 | 3.0199 × 10−11 |
| F12 | 3.0199 × 10−11 | 4.0772 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.9426 × 10−5 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F13 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F14 | 4.5043 × 10−11 | 9.5207 × 10−4 | 5.4617 × 10−9 | 8.1527 × 10−11 | 2.0283 × 10−7 | 4.0772 × 10−11 | 1.6132 × 10−10 | 1.4294 × 10−8 | 3.0199 × 10−11 |
| F15 | 3.0199 × 10−11 | 1.8567 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.4941 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F16 | 2.7726 × 10−5 | 7.1719 × 10−1 | 3.5547 × 10−1 | 1.3703 × 10−3 | 8.8830 × 10−1 | 3.0199 × 10−11 | 7.6588 × 10−5 | 3.7108 × 10−1 | 3.0199 × 10−11 |
| F17 | 3.3520 × 10−8 | 6.3088 × 10−1 | 2.2658 × 10−3 | 9.9186 × 10−11 | 1.0547 × 10−1 | 3.0199 × 10−11 | 2.0338 × 10−9 | 3.7782 × 10−2 | 3.0199 × 10−11 |
| F18 | 6.2828 × 10−6 | 1.4733 × 10−7 | 3.3520 × 10−8 | 5.4941 × 10−11 | 1.6062 × 10−6 | 3.0199 × 10−11 | 5.4941 × 10−11 | 2.0023 × 10−6 | 3.0199 × 10−11 |
| F19 | 3.0199 × 10−11 | 2.4386 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.8608 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F20 | 8.7663 × 10−1 | 1.1711 × 10−2 | 5.9706 × 10−5 | 9.5139 × 10−6 | 1.1937 × 10−6 | 9.2603 × 10−9 | 1.5964 × 10−7 | 4.8413 × 10−2 | 3.3384 × 10−11 |
| F21 | 3.0199 × 10−11 | 7.0881 × 10−8 | 5.5727 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.8500 × 10−8 | 3.0199 × 10−11 |
| F22 | 3.5137 × 10−2 | 2.2360 × 10−2 | 2.7086 × 10−2 | 8.0727 × 10−1 | 1.8368 × 10−2 | 8.7663 × 10−1 | 2.9047 × 10−1 | 1.3703 × 10−3 | 1.2870 × 10−9 |
| F23 | 3.0199 × 10−11 | 3.3384 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F24 | 3.0199 × 10−11 | 4.5043 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F25 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F26 | 3.0199 × 10−11 | 1.4294 × 10−8 | 3.8202 × 10−10 | 3.0199 × 10−11 | 4.6159 × 10−10 | 3.0199 × 10−11 | 2.9215 × 10−9 | 8.4848 × 10−9 | 3.0199 × 10−11 |
| F27 | 3.0199 × 10−11 | 4.1997 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.6099 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F28 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F29 | 3.0199 × 10−11 | 3.1589 × 10−10 | 4.9752 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F30 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.3384 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| ID | HHO | LSHADE | GRO | DBO | HSO | WOA | PSO | GWO | COA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 2.5020 × 104 | 2.0844 × 104 | 1.1523 × 104 | 3.4854 × 104 | 6.9839 × 103 | 3.5309 × 104 | 6.1707 × 103 | 1.4939 × 104 | 4.8494 × 104 |
| F2 | 7.9622 × 103 | 2.0796 × 104 | 3.3754 × 103 | 9.4736 × 103 | 3.5306 × 103 | 1.4132 × 104 | 4.1031 × 103 | 4.5072 × 103 | 1.4396 × 104 |
| F3 | 5.6473 × 102 | 4.5225 × 102 | 4.6239 × 102 | 5.1391 × 102 | 5.6096 × 102 | 6.4079 × 102 | 4.8639 × 102 | 4.9492 × 102 | 3.1412 × 103 |
| F4 | 6.2359 × 101 | 1.6089 × 101 | 1.1233 × 101 | 5.4477 × 101 | 6.8850 × 101 | 8.1424 × 101 | 3.8022 × 101 | 4.2415 × 101 | 8.0479 × 102 |
| F5 | 6.6414 × 102 | 6.0102 × 102 | 6.0171 × 102 | 6.3396 × 102 | 6.3699 × 102 | 6.6710 × 102 | 6.1091 × 102 | 6.0795 × 102 | 6.8067 × 102 |
| F6 | 7.1620 × 100 | 1.4216 × 100 | 5.7498 × 10−1 | 9.8236 × 100 | 5.5161 × 100 | 1.5568 × 101 | 4.3013 × 100 | 4.3004 × 100 | 9.1194 × 100 |
| F7 | 8.8456 × 102 | 8.4077 × 102 | 8.4551 × 102 | 9.0809 × 102 | 9.1655 × 102 | 9.3691 × 102 | 9.0685 × 102 | 8.6097 × 102 | 9.7816 × 102 |
| F8 | 1.3611 × 101 | 1.2088 × 101 | 1.0662 × 101 | 2.9836 × 101 | 1.1827 × 101 | 4.2020 × 101 | 2.1665 × 101 | 2.8044 × 101 | 1.7881 × 101 |
| F9 | 3.0452 × 103 | 1.2054 × 103 | 9.2297 × 102 | 2.2795 × 103 | 1.1005 × 103 | 4.6551 × 103 | 9.9209 × 102 | 1.2627 × 103 | 3.5843 × 103 |
| F10 | 2.6241 × 102 | 2.3868 × 102 | 1.1269 × 101 | 6.5896 × 102 | 1.7129 × 102 | 2.0886 × 103 | 3.8085 × 101 | 3.1269 × 102 | 3.2798 × 102 |
| F11 | 1.9306 × 105 | 5.7172 × 103 | 8.8106 × 104 | 1.1521 × 106 | 4.5929 × 103 | 7.0905 × 106 | 2.0186 × 106 | 2.8656 × 106 | 2.5864 × 109 |
| F12 | 1.4743 × 105 | 4.9782 × 103 | 1.4887 × 105 | 2.0816 × 106 | 3.7156 × 103 | 1.1621 × 107 | 1.3833 × 106 | 7.2868 × 106 | 8.8284 × 108 |
References
- Restrepo-Cuestas, B.J.; Montano, J. Bishop model parameter estimation in photovoltaic cells using metaheuristic optimization techniques. Sol. Energy 2024, 270, 112410. [Google Scholar] [CrossRef]
- Ayang, A.; Wamkeue, R.; Ouhrouche, M.; Djongyang, N.; Essiane Salomé, N.; Pombe, J.K.; Ekemb, G. Maximum likelihood parameters estimation of single-diode model of Photovoltaic generator. Renew. Energy 2019, 130, 111–121. [Google Scholar] [CrossRef]
- Choulli, I.; Elyaqouti, M.; hanafi Arjdal, E.; Ben hmamou, D.; Saadaoui, D.; Lidaighbi, S.; Elhammoudy, A.; Abazine, I.; El aidi idrissi, Y. DIWJAYA: JAYA driven by individual weights for enhanced photovoltaic model parameter estimation. Energy Convers. Manag. 2024, 305, 118258. [Google Scholar] [CrossRef]
- Chaib, L.; Tadj, M.; Choucha, A.; Khemili, F.Z.; El-Fergany, A. Improved crayfish optimization algorithm for parameters estimation of photovoltaic models. Energy Convers. Manag. 2024, 313, 118627. [Google Scholar] [CrossRef]
- Ćalasan, M.; Vujošević, S.; Micev, M.; Abdel Aleem, S.H.E.; Hasanien, H.M. Accurate modeling and parameters estimation of photovoltaic models: Analytical and artificial intelligence solutions. Results Eng. 2024, 24, 103433. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ.; Kiran, M.S. A tree seed algorithm with multi-strategy for parameter estimation of solar photovoltaic models. Appl. Soft Comput. 2024, 167, 112220. [Google Scholar] [CrossRef]
- Wang, D.; Sun, X.; Kang, H.; Shen, Y.; Chen, Q. Heterogeneous differential evolution algorithm for parameter estimation of solar photovoltaic models. Energy Rep. 2022, 8, 4724–4746. [Google Scholar] [CrossRef]
- Weng, X.; Heidari, A.A.; Liang, G.; Chen, H.; Ma, X.; Mafarja, M.; Turabieh, H. Laplacian Nelder-Mead spherical evolution for parameter estimation of photovoltaic models. Energy Convers. Manag. 2021, 243, 114223. [Google Scholar] [CrossRef]
- Liang, J.; Qiao, K.; Yu, K.; Ge, S.; Qu, B.; Xu, R.; Li, K. Parameters estimation of solar photovoltaic models via a self-adaptive ensemble-based differential evolution. Sol. Energy 2020, 207, 336–346. [Google Scholar] [CrossRef]
- Wang, H.; Yu, X.; Lu, Y. A reinforcement learning-based ranking teaching-learning-based optimization algorithm for parameters estimation of photovoltaic models. Swarm Evol. Comput. 2025, 93, 101844. [Google Scholar] [CrossRef]
- Yang, X.; Zeng, G.; Cao, Z.; Huang, X.; Zhao, J. Parameters estimation of complex solar photovoltaic models using bi-parameter coordinated updating L-SHADE with parameter decomposition method. Case Stud. Therm. Eng. 2024, 61, 104917. [Google Scholar] [CrossRef]
- Abido, M.A.; Khalid, M.S. Seven-parameter PV model estimation using Differential Evolution. Electr. Eng. 2018, 100, 971–981. [Google Scholar] [CrossRef]
- Garip, Z. Parameters estimation of three-diode photovoltaic model using fractional-order Harris Hawks optimization algorithm. Optik 2022, 272, 170391. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Elgendy, M.A.; Abdeen, A.M. Parameters estimation of single- and multiple-diode photovoltaic model using whale optimisation algorithm. IET Renew. Power Gener. 2018, 12, 1755–1761. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Zhang, H.; Heidari, A.A.; Wang, M.; Zhang, L.; Chen, H.; Li, C. Orthogonal Nelder-Mead moth flame method for parameters identification of photovoltaic modules. Energy Convers. Manag. 2020, 211, 112764. [Google Scholar] [CrossRef]
- Oliva, D.; Abd El Aziz, M.; Ella Hassanien, A. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar] [CrossRef]
- Wu, Z.; Yu, D.; Kang, X. Parameter identification of photovoltaic cell model based on improved ant lion optimizer. Energy Convers. Manag. 2017, 151, 107–115. [Google Scholar] [CrossRef]
- Su, P.; Ji, J.; Cai, J.; Gao, Y.; Han, K. Dynamic simulation and experimental study of a variable speed photovoltaic DC refrigerator. Renew. Energy 2020, 152, 155–164. [Google Scholar] [CrossRef]
- Di Piazza, M.C.; Luna, M.; Vitale, G. Dynamic PV Model Parameter Identification by Least-Squares Regression. IEEE J. Photovolt. 2013, 3, 799–806. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Yan, X.; Hu, C.; Bai, D.; Wang, L. Parameter estimation of photovoltaic models with memetic adaptive differential evolution. Sol. Energy 2019, 190, 465–474. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Chakrabortty, R.K.; Ryan, M. Parameter estimation of photovoltaic models using an improved marine predators algorithm. Energy Convers. Manag. 2021, 227, 113491. [Google Scholar] [CrossRef]
- Jiao, S.; Chong, G.; Huang, C.; Hu, H.; Wang, M.; Heidari, A.A.; Chen, H.; Zhao, X. Orthogonally adapted Harris Hawk Optimization for parameter estimation of photovoltaic models. Energy 2020, 203, 117804. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, K.; Zhang, T.; Wang, Y.; Peng, C.; Gao, S. A population diversity-controlled differential evolution for parameter estimation of solar photovoltaic models. Sustain. Energy Technol. Assess. 2021, 51, 101938. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Ramakrishnan, C.; Kumar, C.; Sowmya, R.; Deb, S.; Kumar, N.M. An enhanced Gradient-based Optimizer for parameter estimation of various solar photovoltaic models. Energy Rep. 2022, 8, 15249–15285. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2022, 259, 110011. [Google Scholar] [CrossRef]
- Qi, Z.; Yingjie, D.; Shan, Y.; Xu, L.; Dongcheng, H.; Guoqi, X. An improved Coati Optimization Algorithm with multiple strategies for engineering design optimization problems. Sci. Rep. 2024, 14, 20435. [Google Scholar] [CrossRef]
- Wu, X.; Ding, Y.; Wang, L.; Zhang, H. A Multi-Strategy Adaptive Coati Optimization Algorithm for Constrained Optimization Engineering Design Problems. Biomimetics 2025, 5, 323. [Google Scholar] [CrossRef]
- Ma, H.; Liao, Y.; Wang, D.; Yin, Z.; Wei, C.; Chen, Q.; Xu, W. Heterogeneous multi-UAVs cooperative task allocation based on the improved coati optimization algorithm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2025, 239, 1843–1857. [Google Scholar] [CrossRef]
- Luo, X.; Yuan, Y.; Fu, Y.; Huang, H.; Wei, J. A multi-strategy improved Coati optimization algorithm for solving global optimization problems. Clust. Comput. 2025, 28, 264. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mostafa, R.R.; Hussien, A.G.; Helmy, F. An efficient adaptive-mutated Coati optimization algorithm for feature selection and global optimization. Alex. Eng. J. 2023, 85, 29–48. [Google Scholar] [CrossRef]
- Houssein, E.H.; Samee, N.A.; Mahmoud, N.F.; Hussain, K. Dynamic Coati Optimization Algorithm for Biomedical Classification Tasks. Comput. Biol. Med. 2023, 164, 107237. [Google Scholar] [CrossRef] [PubMed]
- Balavignesh, S.; Kumar, C.; Sripriya, R.; Senjyu, T. An enhanced coati optimization algorithm for optimizing energy management in smart grids for home appliances. Energy Rep. 2024, 11, 3695–3720. [Google Scholar] [CrossRef]
- Yildizdan, G.; Bas, E. A new binary coati optimization algorithm for binary optimization problems. Neural Comput. Appl. 2023, 36, 2797–2834. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition and Special Session on Constrained Single Objective Real-Parameter Optimization; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Luo, W.; Lin, X.; Li, C.; Yang, S.; Shi, Y. Benchmark functions for CEC 2022 competition on seeking multiple optima in dynamic environments. arXiv 2022, arXiv:2201.00523. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; IEEE: New York, NY, USA, 2014; pp. 1658–1665. [Google Scholar]
- Zolf, K. Gold rush optimizer: A new population-based metaheuristic algorithm. Oper. Res. Decis. 2023, 33, 113–150. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Proceedings of ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Akbari, E.; Rahimnejad, A.; Gadsden, S.A. Holistic swarm optimization: A novel metaphor-less algorithm guided by whole population information for addressing exploration-exploitation dilemma. Comput. Methods Appl. Mech. Eng. 2025, 445, 118208. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Ou, Y.; Qin, F.; Zhou, K.-Q.; Yin, P.-F.; Mo, L.-P.; Mohd Zain, A.J.S. An improved grey wolf optimizer with multi-strategies coverage in wireless sensor networks. Symmetry 2024, 16, 286. [Google Scholar] [CrossRef]
- Wang, W.-c.; Tian, W.-c.; Xu, D.-m.; Zang, H.-f. Arctic puffin optimization: A bio-inspired metaheuristic algorithm for solving engineering design optimization. Adv. Eng. Softw. 2024, 195, 103694. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Mohammed, B.O.; Aghdasi, H.S.; Salehpour, P. Dhole optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Clust. Comput. 2025, 28, 430. [Google Scholar] [CrossRef]
- Lyu, L.; Yang, F. MMPA: A modified marine predator algorithm for 3D UAV path planning in complex environments with multiple threats. Expert Syst. Appl. 2024, 257, 124955. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, C.; Soleimanian Gharehchopogh, F.; Mirjalili, S. An improved whale optimization algorithm based on multi-population evolution for global optimization and engineering design problems. Expert Syst. Appl. 2023, 215, 119269. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, R.; Li, S. A Novel Improved Dung Beetle Optimization Algorithm for Collaborative 3D Path Planning of UAVs. Biomimetics 2025, 7, 420. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, S.; Zhou, M.; Wang, Y.; Lei, Z.; Zhang, T.; Wang, J. Scale-free network-based differential evolution to solve function optimization and parameter estimation of photovoltaic models. Swarm Evol. Comput. 2022, 74, 101142. [Google Scholar] [CrossRef]
- Wang, S.; Yu, Y.; Hu, W. Static and dynamic solar photovoltaic models’ parameters estimation using hybrid Rao optimization algorithm. J. Clean. Prod. 2021, 315, 128080. [Google Scholar] [CrossRef]
- El-Dabah, M.A.; El-Sehiemy, R.A.; Becherif, M.; Ebrahim, M.A. Parameter estimation of triple diode photovoltaic model using an artificial ecosystem-based optimizer. Int. Trans. Electr. Energy Syst. 2021, 31, e13043. [Google Scholar] [CrossRef]
- Beşkirli, A.; Dağ, İ. An efficient tree seed inspired algorithm for parameter estimation of Photovoltaic models. Energy Rep. 2021, 8 (Suppl. S1), 291–298. [Google Scholar] [CrossRef]
- Liu, Y.; Chong, G.; Heidari, A.A.; Chen, H.; Liang, G.; Ye, X.; Cai, Z.; Wang, M. Horizontal and vertical crossover of Harris hawk optimizer with Nelder-Mead simplex for parameter estimation of photovoltaic models. Energy Convers. Manag. 2020, 223, 113211. [Google Scholar] [CrossRef]












| Algorithms | Parameter Name | Parameter Value | Reference |
|---|---|---|---|
| HHO | [−1, 1], [0, 2] | [37] | |
| LSHADE | 0.11, 2.6, 18, 6 | [38] | |
| GRO | [0, 1], [0, 1], [0, 1], [0, 1] | [39] | |
| GWO | [0, 2] | [40] | |
| WOA | [0, 1], [−1, 1], [0, 2], 1 | [41] | |
| PSO | 1.5, 1.5, 0.8 | [42] | |
| HSO | 3 | [43] | |
| DBO | 0.2 | [44] | |
| COA | , [0, 1] | [26] | |
| MECOA | , [0, 1], [1, 0], 3 | / |
| ID | Metric | HHO | LSHADE | GRO | DBO | HSO | WOA | PSO | GWO | COA | MECOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 4.1107 × 108 | 3.6721 × 105 | 1.0753 × 108 | 2.4805 × 108 | 6.1181 × 103 | 5.8582 × 109 | 1.3247 × 109 | 3.0686 × 109 | 5.6810 × 1010 | 3.1733 × 103 |
| std | 3.1478 × 108 | 5.3059 × 105 | 5.6316 × 107 | 1.7051 × 108 | 6.0959 × 103 | 1.7355 × 109 | 8.1821 × 108 | 1.6721 × 109 | 8.7827 × 109 | 3.9694 × 103 | |
| F2 | mean | 1.5996 × 1033 | 1.2758 × 1022 | 1.8072 × 1026 | 3.0597 × 1036 | 3.0055 × 1016 | 5.1973 × 1038 | 3.1859 × 1032 | 7.0161 × 1032 | 2.9637 × 1049 | 8.1099 × 1015 |
| std | 4.5164 × 1033 | 6.4351 × 1022 | 4.8210 × 1026 | 1.6441 × 1037 | 1.1000 × 1017 | 2.8455 × 1039 | 1.6787 × 1033 | 2.6766 × 1033 | 1.5159 × 1050 | 4.2137 × 1016 | |
| F3 | mean | 5.7432 × 104 | 4.8043 × 104 | 6.3291 × 104 | 8.8863 × 104 | 4.8713 × 104 | 2.7515 × 105 | 6.0481 × 104 | 6.0888 × 104 | 8.5224 × 104 | 4.4375 × 104 |
| std | 7.0112 × 103 | 4.4631 × 104 | 1.2228 × 104 | 1.2038 × 104 | 1.4406 × 104 | 7.6068 × 104 | 1.7215 × 104 | 1.1901 × 104 | 4.5502 × 103 | 7.6606 × 103 | |
| F4 | mean | 7.0781 × 102 | 5.1237 × 102 | 5.6064 × 102 | 6.6220 × 102 | 7.0943 × 102 | 1.2366 × 103 | 6.2482 × 102 | 6.4340 × 102 | 1.5185 × 104 | 5.0212 × 102 |
| std | 7.1959 × 101 | 2.5528 × 101 | 2.5295 × 101 | 1.2569 × 102 | 1.2090 × 102 | 3.6325 × 102 | 1.5635 × 102 | 7.9575 × 101 | 2.3636 × 103 | 2.6193 × 101 | |
| F5 | mean | 7.6289 × 102 | 5.8202 × 102 | 6.2409 × 102 | 7.5349 × 102 | 6.9545 × 102 | 8.5705 × 102 | 7.1783 × 102 | 6.1740 × 102 | 9.2241 × 102 | 5.8091 × 102 |
| std | 3.7876 × 101 | 1.4737 × 101 | 1.7906 × 101 | 4.3719 × 101 | 3.0541 × 101 | 4.6659 × 101 | 2.5496 × 101 | 3.3636 × 101 | 3.1621 × 101 | 2.9537 × 101 | |
| F6 | mean | 6.6541 × 102 | 6.0198 × 102 | 6.0712 × 102 | 6.4622 × 102 | 6.5100 × 102 | 6.8721 × 102 | 6.2130 × 102 | 6.1415 × 102 | 6.8979 × 102 | 6.0150 × 102 |
| std | 6.1745 × 100 | 1.5816 × 100 | 2.4867 × 100 | 1.0706 × 101 | 3.1641 × 100 | 1.3323 × 101 | 5.7538 × 100 | 4.9727 × 100 | 6.3279 × 100 | 2.1166 × 100 | |
| F7 | mean | 1.3274 × 103 | 8.5957 × 102 | 8.5449 × 102 | 1.0492 × 103 | 1.0777 × 103 | 1.3225 × 103 | 1.0022 × 103 | 9.1280 × 102 | 1.4279 × 103 | 8.2662 × 102 |
| std | 5.4312 × 101 | 3.4578 × 101 | 2.4253 × 101 | 9.4247 × 101 | 1.0181 × 102 | 8.7207 × 101 | 2.4789 × 101 | 5.5275 × 101 | 4.3708 × 101 | 5.0906 × 101 | |
| F8 | mean | 9.8393 × 102 | 8.7463 × 102 | 9.0497 × 102 | 1.0196 × 103 | 1.0423 × 103 | 1.0763 × 103 | 1.0134 × 103 | 9.0426 × 102 | 1.1488 × 103 | 8.7379 × 102 |
| std | 2.5492 × 101 | 1.9124 × 101 | 1.5160 × 101 | 4.3889 × 101 | 2.3301 × 101 | 5.3430 × 101 | 2.9905 × 101 | 2.9971 × 101 | 2.7291 × 101 | 2.5496 × 101 | |
| F9 | mean | 8.5035 × 103 | 1.7322 × 103 | 1.1860 × 103 | 7.0417 × 103 | 2.6027 × 103 | 1.0028 × 104 | 1.9539 × 103 | 2.4580 × 103 | 1.0977 × 104 | 1.0803 × 103 |
| std | 1.2485 × 103 | 4.6382 × 102 | 1.5450 × 102 | 1.9211 × 103 | 8.5930 × 102 | 2.6304 × 103 | 9.4225 × 102 | 1.0005 × 103 | 1.5040 × 103 | 2.7911 × 102 | |
| F10 | mean | 6.2931 × 103 | 4.6901 × 103 | 5.7395 × 103 | 6.4320 × 103 | 4.0828 × 103 | 7.4366 × 103 | 7.3047 × 103 | 4.9311 × 103 | 8.8917 × 103 | 7.1188 × 103 |
| std | 9.3116 × 102 | 4.4642 × 102 | 5.1852 × 102 | 1.1906 × 103 | 7.0217 × 102 | 8.1064 × 102 | 5.2445 × 102 | 1.2447 × 103 | 3.6575 × 102 | 1.5274 × 103 | |
| F11 | mean | 1.6280 × 103 | 1.3580 × 103 | 1.3250 × 103 | 1.9608 × 103 | 1.7492 × 103 | 8.7987 × 103 | 1.4762 × 103 | 2.1669 × 103 | 9.0969 × 103 | 1.1903 × 103 |
| std | 1.6298 × 102 | 4.5126 × 102 | 5.5865 × 101 | 8.8919 × 102 | 1.5741 × 102 | 2.6420 × 103 | 6.3213 × 101 | 8.4988 × 102 | 2.3266 × 103 | 4.9143 × 101 | |
| F12 | mean | 9.8478 × 107 | 3.6417 × 105 | 3.6494 × 106 | 5.9405 × 107 | 5.0189 × 105 | 4.8470 × 108 | 7.4939 × 107 | 1.2045 × 108 | 1.4601 × 1010 | 1.1907 × 106 |
| std | 1.0465 × 108 | 2.9713 × 105 | 2.6326 × 106 | 8.4824 × 107 | 5.4005 × 105 | 3.1206 × 108 | 9.6553 × 107 | 1.1781 × 108 | 3.5273 × 109 | 1.0900 × 106 | |
| F13 | mean | 1.2179 × 106 | 1.7146 × 104 | 1.2029 × 105 | 1.6934 × 107 | 2.0771 × 104 | 1.1126 × 107 | 3.9640 × 107 | 2.0814 × 107 | 9.6377 × 109 | 2.2917 × 104 |
| std | 1.2649 × 106 | 1.5973 × 104 | 1.8402 × 105 | 3.0722 × 107 | 1.4337 × 104 | 8.7464 × 106 | 1.9272 × 108 | 4.6872 × 107 | 4.6873 × 109 | 2.3310 × 104 | |
| F14 | mean | 1.3457 × 106 | 3.1133 × 103 | 3.6069 × 104 | 3.2044 × 105 | 2.1205 × 104 | 2.3679 × 106 | 1.3998 × 105 | 8.8152 × 105 | 6.4887 × 106 | 7.1816 × 104 |
| std | 1.5358 × 106 | 8.0776 × 103 | 3.4594 × 104 | 4.6497 × 105 | 3.6500 × 104 | 2.0160 × 106 | 1.2514 × 105 | 9.3720 × 105 | 8.6577 × 106 | 5.2037 × 104 | |
| F15 | mean | 1.2239 × 105 | 3.5224 × 103 | 2.1646 × 104 | 5.8622 × 104 | 9.8225 × 103 | 4.5198 × 106 | 1.7119 × 105 | 1.0203 × 106 | 5.4757 × 108 | 8.8567 × 103 |
| std | 7.2936 × 104 | 5.2390 × 103 | 1.6629 × 104 | 5.9533 × 104 | 4.9667 × 103 | 7.3459 × 106 | 1.1123 × 105 | 1.7367 × 106 | 3.0962 × 108 | 8.9965 × 103 | |
| F16 | mean | 3.6895 × 103 | 2.6327 × 103 | 2.6062 × 103 | 3.3303 × 103 | 2.9236 × 103 | 4.3068 × 103 | 3.1115 × 103 | 2.7426 × 103 | 6.1611 × 103 | 2.6631 × 103 |
| std | 5.3181 × 102 | 2.9160 × 102 | 1.8335 × 102 | 3.3558 × 102 | 3.4835 × 102 | 5.9082 × 102 | 2.6156 × 102 | 2.8738 × 102 | 1.1732 × 103 | 3.8557 × 102 | |
| F17 | mean | 2.8578 × 103 | 2.0643 × 103 | 1.9369 × 103 | 2.7256 × 103 | 2.6632 × 103 | 2.7775 × 103 | 2.2630 × 103 | 2.0469 × 103 | 5.6839 × 103 | 2.0522 × 103 |
| std | 3.3469 × 102 | 1.7207 × 102 | 1.1749 × 102 | 3.0752 × 102 | 2.9788 × 102 | 3.5264 × 102 | 2.3018 × 102 | 1.6810 × 102 | 3.6799 × 103 | 1.4891 × 102 | |
| F18 | mean | 3.7140 × 106 | 4.7849 × 104 | 6.8449 × 105 | 3.7074 × 106 | 1.6843 × 105 | 1.4817 × 107 | 1.7988 × 106 | 1.6290 × 106 | 6.4413 × 107 | 9.4170 × 105 |
| std | 3.4751 × 106 | 3.6808 × 104 | 6.0971 × 105 | 5.0565 × 106 | 1.6412 × 105 | 1.5112 × 107 | 1.6360 × 106 | 1.6282 × 106 | 6.0122 × 107 | 1.1129 × 106 | |
| F19 | mean | 1.9945 × 106 | 4.3361 × 103 | 2.1302 × 104 | 1.8693 × 106 | 1.8342 × 104 | 1.5633 × 107 | 2.8549 × 106 | 1.0543 × 107 | 7.4352 × 108 | 8.2078 × 103 |
| std | 1.1150 × 106 | 9.8783 × 103 | 5.4099 × 104 | 3.2498 × 106 | 4.2381 × 104 | 1.6490 × 107 | 1.3437 × 107 | 3.2088 × 107 | 3.9554 × 108 | 8.8601 × 103 | |
| F20 | mean | 2.8709 × 103 | 2.4195 × 103 | 2.3463 × 103 | 2.7540 × 103 | 2.5176 × 103 | 2.8771 × 103 | 2.5065 × 103 | 2.4336 × 103 | 3.0711 × 103 | 2.3812 × 103 |
| std | 1.5088 × 102 | 1.2340 × 102 | 8.8549 × 101 | 2.4627 × 102 | 1.9814 × 102 | 2.1093 × 102 | 1.8572 × 102 | 1.1878 × 102 | 1.8456 × 102 | 1.9558 × 102 | |
| F21 | mean | 2.5767 × 103 | 2.3743 × 103 | 2.4107 × 103 | 2.5310 × 103 | 2.5665 × 103 | 2.6327 × 103 | 2.5109 × 103 | 2.4066 × 103 | 2.7608 × 103 | 2.3693 × 103 |
| std | 4.6694 × 101 | 1.7178 × 101 | 1.9159 × 101 | 6.4870 × 101 | 1.8542 × 101 | 6.6968 × 101 | 2.7872 × 101 | 2.4863 × 101 | 4.4661 × 101 | 2.5988 × 101 | |
| F22 | mean | 7.0763 × 103 | 3.6065 × 103 | 2.3513 × 103 | 4.6010 × 103 | 4.9918 × 103 | 8.0611 × 103 | 6.3454 × 103 | 5.0260 × 103 | 9.7076 × 103 | 2.3013 × 103 |
| std | 1.7546 × 103 | 1.8614 × 103 | 1.4691 × 101 | 2.4308 × 103 | 1.3508 × 103 | 1.5788 × 103 | 3.2120 × 103 | 2.0110 × 103 | 8.6244 × 102 | 2.2045 × 100 | |
| F23 | mean | 3.2605 × 103 | 2.7347 × 103 | 2.7566 × 103 | 3.0130 × 103 | 2.9075 × 103 | 3.1371 × 103 | 2.9434 × 103 | 2.7733 × 103 | 3.7039 × 103 | 2.7342 × 103 |
| std | 1.7473 × 102 | 2.1152 × 101 | 2.2106 × 101 | 8.6895 × 101 | 1.8873 × 101 | 1.0520 × 102 | 7.9112 × 101 | 4.6973 × 101 | 1.7782 × 102 | 2.5887 × 101 | |
| F24 | mean | 3.4816 × 103 | 2.9104 × 103 | 2.9185 × 103 | 3.1930 × 103 | 3.0421 × 103 | 3.2774 × 103 | 3.1047 × 103 | 2.9624 × 103 | 3.7462 × 103 | 2.8996 × 103 |
| std | 1.4435 × 102 | 2.8065 × 101 | 1.8105 × 101 | 8.5674 × 101 | 1.3871 × 101 | 1.0372 × 102 | 6.5260 × 101 | 6.3363 × 101 | 1.5763 × 102 | 3.5803 × 101 | |
| F25 | mean | 3.0103 × 103 | 2.8950 × 103 | 2.9372 × 103 | 3.0284 × 103 | 3.1767 × 103 | 3.2322 × 103 | 2.9603 × 103 | 3.0333 × 103 | 5.1718 × 103 | 2.8946 × 103 |
| std | 3.3228 × 101 | 1.1559 × 101 | 1.6611 × 101 | 2.0940 × 102 | 1.0891 × 102 | 8.2588 × 101 | 3.4337 × 101 | 8.3133 × 101 | 4.8777 × 102 | 1.5208 × 101 | |
| F26 | mean | 8.1758 × 103 | 4.6024 × 103 | 4.2376 × 103 | 7.1389 × 103 | 5.2199 × 103 | 8.5751 × 103 | 5.1071 × 103 | 5.0694 × 103 | 1.1853 × 104 | 4.4716 × 103 |
| std | 6.4388 × 102 | 5.5303 × 102 | 6.0748 × 102 | 7.4041 × 102 | 4.2030 × 102 | 1.0148 × 103 | 1.0494 × 103 | 4.5537 × 102 | 8.8811 × 102 | 5.8138 × 102 | |
| F27 | mean | 3.6346 × 103 | 3.2360 × 103 | 3.2765 × 103 | 3.3379 × 103 | 3.3371 × 103 | 3.4997 × 103 | 3.2736 × 103 | 3.2725 × 103 | 4.5804 × 103 | 3.2328 × 103 |
| std | 1.7477 × 102 | 1.3427 × 101 | 1.8409 × 101 | 6.9835 × 101 | 6.1672 × 101 | 1.4416 × 102 | 3.3530 × 101 | 3.2320 × 101 | 4.4454 × 102 | 1.1764 × 101 | |
| F28 | mean | 3.5307 × 103 | 3.2606 × 103 | 3.3044 × 103 | 3.6554 × 103 | 3.6565 × 103 | 3.7937 × 103 | 3.3754 × 103 | 3.4921 × 103 | 7.5300 × 103 | 3.2315 × 103 |
| std | 8.6854 × 101 | 3.6030 × 101 | 2.2459 × 101 | 7.3159 × 102 | 1.8736 × 102 | 2.4560 × 102 | 7.0268 × 101 | 1.2826 × 102 | 7.0124 × 102 | 2.2304 × 101 | |
| F29 | mean | 5.0347 × 103 | 3.7407 × 103 | 3.7759 × 103 | 4.4793 × 103 | 4.4948 × 103 | 5.4635 × 103 | 4.1717 × 103 | 3.9361 × 103 | 9.2036 × 103 | 3.8064 × 103 |
| std | 5.0884 × 102 | 1.4172 × 102 | 1.4230 × 102 | 4.0144 × 102 | 2.5717 × 102 | 5.5975 × 102 | 1.9013 × 102 | 2.1531 × 102 | 3.4490 × 103 | 2.1361 × 102 | |
| F30 | mean | 1.1691 × 107 | 1.7023 × 104 | 4.5057 × 105 | 2.4176 × 106 | 9.2302 × 104 | 5.7094 × 107 | 2.7594 × 106 | 1.1271 × 107 | 1.6934 × 109 | 1.0534 × 104 |
| std | 1.3088 × 107 | 7.2449 × 103 | 4.3308 × 105 | 4.8580 × 106 | 1.4973 × 105 | 4.5369 × 107 | 1.7944 × 106 | 1.2721 × 107 | 1.1804 × 109 | 3.7981 × 103 |
| ID | Metric | HHO | LSHADE | GRO | DBO | HSO | WOA | PSO | GWO | COA | MECOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 5.2137 × 109 | 2.7695 × 108 | 3.5930 × 109 | 8.9757 × 109 | 1.0068 × 105 | 2.0660 × 1010 | 7.7516 × 109 | 9.7982 × 109 | 1.1208 × 1011 | 2.7669 × 104 |
| std | 1.5003 × 109 | 3.9925 × 108 | 1.5202 × 109 | 1.5012 × 1010 | 8.3188 × 104 | 5.6817 × 109 | 4.6202 × 109 | 4.6267 × 109 | 9.6488 × 109 | 1.7790 × 104 | |
| F2 | mean | 4.3132 × 1065 | 1.0000 × 1030 | 5.4116 × 1053 | 2.4859 × 1067 | 4.9430 × 1047 | 1.2559 × 1077 | 8.0987 × 1054 | 2.7349 × 1062 | 1.3161 × 1083 | 3.7071 × 1039 |
| std | 1.4622 × 1066 | 1.4314 × 1014 | 2.0785 × 1054 | 1.3600 × 1068 | 2.0930 × 1048 | 4.6640 × 1077 | 3.8897 × 1055 | 1.4980 × 1063 | 4.1915 × 1083 | 1.8199 × 1040 | |
| F3 | mean | 1.7078 × 105 | 1.7506 × 105 | 1.6484 × 105 | 2.6913 × 105 | 1.3648 × 105 | 2.6093 × 105 | 1.8969 × 105 | 1.6823 × 105 | 1.9843 × 105 | 1.8536 × 105 |
| std | 1.8550 × 104 | 8.8643 × 104 | 2.2778 × 104 | 8.1583 × 104 | 2.4171 × 104 | 8.8211 × 104 | 3.9654 × 104 | 2.6071 × 104 | 2.8870 × 104 | 3.2360 × 104 | |
| F4 | mean | 1.9888 × 103 | 6.6469 × 102 | 1.0098 × 103 | 1.4629 × 103 | 1.2863 × 103 | 5.0318 × 103 | 1.2268 × 103 | 1.6721 × 103 | 3.6483 × 104 | 5.9120 × 102 |
| std | 4.5606 × 102 | 6.1843 × 101 | 1.1026 × 102 | 1.2690 × 103 | 2.1753 × 102 | 1.4348 × 103 | 5.7083 × 102 | 6.6605 × 102 | 6.9315 × 103 | 5.6339 × 101 | |
| F5 | mean | 9.3303 × 102 | 7.2541 × 102 | 8.0597 × 102 | 1.0027 × 103 | 9.2838 × 102 | 1.1100 × 103 | 9.7267 × 102 | 7.6811 × 102 | 1.2028 × 103 | 6.9446 × 102 |
| std | 2.0267 × 101 | 3.0875 × 101 | 3.6893 × 101 | 1.1241 × 102 | 4.1957 × 101 | 8.0249 × 101 | 4.4943 × 101 | 6.1258 × 101 | 3.1830 × 101 | 7.1812 × 101 | |
| F6 | mean | 6.8195 × 102 | 6.1235 × 102 | 6.2084 × 102 | 6.6567 × 102 | 6.6729 × 102 | 6.9895 × 102 | 6.3895 × 102 | 6.2555 × 102 | 7.0123 × 102 | 6.0562 × 102 |
| std | 3.9053 × 100 | 5.6072 × 100 | 3.6217 × 100 | 1.1998 × 101 | 3.9612 × 100 | 1.0233 × 101 | 1.0817 × 101 | 6.0654 × 100 | 4.6698 × 100 | 5.8574 × 100 | |
| F7 | mean | 1.9164 × 103 | 1.2341 × 103 | 1.1008 × 103 | 1.4311 × 103 | 1.6413 × 103 | 1.8950 × 103 | 1.3490 × 103 | 1.1801 × 103 | 2.0383 × 103 | 1.0801 × 103 |
| std | 7.8876 × 101 | 1.0093 × 102 | 3.9732 × 101 | 1.4170 × 102 | 2.3089 × 102 | 9.6685 × 101 | 4.6078 × 101 | 1.1114 × 102 | 7.2422 × 101 | 2.1445 × 102 | |
| F8 | mean | 1.2221 × 103 | 1.0364 × 103 | 1.0905 × 103 | 1.2907 × 103 | 1.2771 × 103 | 1.4048 × 103 | 1.2588 × 103 | 1.0727 × 103 | 1.4986 × 103 | 1.0314 × 103 |
| std | 3.1994 × 101 | 3.9365 × 101 | 2.7816 × 101 | 1.1376 × 102 | 4.1288 × 101 | 1.0383 × 102 | 3.8484 × 101 | 4.5336 × 101 | 2.3463 × 101 | 7.6378 × 101 | |
| F9 | mean | 3.1401 × 104 | 6.8519 × 103 | 5.0537 × 103 | 2.7782 × 104 | 7.9430 × 103 | 3.9481 × 104 | 1.0073 × 104 | 1.1896 × 104 | 3.8158 × 104 | 1.9810 × 103 |
| std | 2.6585 × 103 | 2.1216 × 103 | 1.5785 × 103 | 7.1389 × 103 | 1.9584 × 103 | 1.0466 × 104 | 5.5805 × 103 | 4.5395 × 103 | 2.6625 × 103 | 1.1159 × 103 | |
| F10 | mean | 1.0285 × 104 | 8.6921 × 103 | 1.0920 × 104 | 1.1398 × 104 | 8.2248 × 103 | 1.3315 × 104 | 1.3075 × 104 | 8.4839 × 103 | 1.5359 × 104 | 1.2942 × 104 |
| std | 8.4606 × 102 | 4.5260 × 102 | 6.9223 × 102 | 2.1790 × 103 | 1.0465 × 103 | 8.4120 × 102 | 9.0843 × 102 | 1.9989 × 103 | 4.5876 × 102 | 2.2758 × 103 | |
| F11 | mean | 3.0738 × 103 | 2.2073 × 103 | 3.3910 × 103 | 4.6514 × 103 | 2.5835 × 103 | 8.7510 × 103 | 2.6476 × 103 | 8.1711 × 103 | 2.6956 × 104 | 1.4335 × 103 |
| std | 9.1130 × 102 | 2.2823 × 103 | 9.4345 × 102 | 1.9803 × 103 | 3.3100 × 102 | 2.7011 × 103 | 4.0402 × 102 | 3.3043 × 103 | 1.8200 × 103 | 2.2445 × 102 | |
| F12 | mean | 9.4715 × 108 | 1.4584 × 107 | 1.3611 × 108 | 7.8021 × 108 | 6.7708 × 106 | 4.1470 × 109 | 2.8227 × 109 | 2.1783 × 109 | 8.6643 × 1010 | 6.4281 × 106 |
| std | 5.1821 × 108 | 1.0570 × 107 | 6.5411 × 107 | 5.9931 × 108 | 5.5294 × 106 | 2.0643 × 109 | 2.7947 × 109 | 3.0386 × 109 | 1.5839 × 1010 | 4.4134 × 106 | |
| F13 | mean | 3.0242 × 107 | 2.2900 × 104 | 8.4599 × 105 | 1.1186 × 108 | 2.7526 × 104 | 4.9172 × 108 | 5.1265 × 108 | 2.6768 × 108 | 5.0561 × 1010 | 7.7910 × 103 |
| std | 2.9034 × 107 | 1.2378 × 104 | 1.1201 × 106 | 1.7038 × 108 | 1.7274 × 104 | 3.1696 × 108 | 8.8354 × 108 | 2.4616 × 108 | 1.5226 × 1010 | 6.9980 × 103 | |
| F14 | mean | 6.0940 × 106 | 3.6508 × 104 | 3.7364 × 105 | 2.9611 × 106 | 7.6855 × 104 | 6.7368 × 106 | 9.4919 × 105 | 1.8728 × 106 | 8.7118 × 107 | 6.2743 × 105 |
| std | 5.1373 × 106 | 4.0535 × 104 | 2.7082 × 105 | 2.8786 × 106 | 6.9697 × 104 | 3.5199 × 106 | 7.1701 × 105 | 2.3118 × 106 | 6.6283 × 107 | 6.2620 × 105 | |
| F15 | mean | 1.7014 × 106 | 8.1910 × 103 | 7.9025 × 104 | 5.4275 × 107 | 1.4101 × 104 | 6.9414 × 107 | 7.9300 × 106 | 4.0723 × 107 | 9.0674 × 109 | 8.4934 × 103 |
| std | 1.9635 × 106 | 5.5806 × 103 | 1.2354 × 105 | 1.5780 × 108 | 5.6589 × 103 | 1.1872 × 108 | 6.0419 × 106 | 7.9230 × 107 | 3.4838 × 109 | 5.7570 × 103 | |
| F16 | mean | 4.9801 × 103 | 3.5798 × 103 | 3.4695 × 103 | 4.8166 × 103 | 3.6405 × 103 | 6.5143 × 103 | 4.4875 × 103 | 3.3981 × 103 | 1.0206 × 104 | 3.5586 × 103 |
| std | 7.9662 × 102 | 4.0721 × 102 | 3.5515 × 102 | 7.3828 × 102 | 4.5550 × 102 | 9.4506 × 102 | 5.1954 × 102 | 4.6782 × 102 | 1.2064 × 103 | 5.8769 × 102 | |
| F17 | mean | 3.7664 × 103 | 3.2546 × 103 | 2.9898 × 103 | 4.2541 × 103 | 3.5523 × 103 | 4.5371 × 103 | 3.8485 × 103 | 3.3370 × 103 | 1.3011 × 104 | 3.1295 × 103 |
| std | 3.7792 × 102 | 2.2740 × 102 | 2.3366 × 102 | 4.9645 × 102 | 2.6609 × 102 | 5.1555 × 102 | 3.7298 × 102 | 5.7612 × 102 | 8.9962 × 103 | 4.6873 × 102 | |
| F18 | mean | 1.1617 × 107 | 7.5696 × 105 | 4.1222 × 106 | 1.4782 × 107 | 1.1165 × 106 | 6.5029 × 107 | 7.9975 × 106 | 1.0520 × 107 | 1.7106 × 108 | 3.4760 × 106 |
| std | 6.8261 × 106 | 1.9250 × 106 | 2.7732 × 106 | 1.5731 × 107 | 1.0862 × 106 | 3.9097 × 107 | 6.7805 × 106 | 1.3932 × 107 | 9.0701 × 107 | 2.1292 × 106 | |
| F19 | mean | 1.7317 × 106 | 1.4982 × 104 | 9.2581 × 104 | 9.9115 × 106 | 2.5985 × 104 | 2.3461 × 107 | 7.1907 × 106 | 8.2127 × 106 | 3.7551 × 109 | 1.3988 × 104 |
| std | 1.1422 × 106 | 9.1014 × 103 | 2.1545 × 105 | 1.0752 × 107 | 2.1385 × 104 | 2.8891 × 107 | 5.3672 × 106 | 1.2276 × 107 | 1.7262 × 109 | 1.2031 × 104 | |
| F20 | mean | 3.5942 × 103 | 3.4239 × 103 | 3.0063 × 103 | 3.6532 × 103 | 3.0673 × 103 | 3.9386 × 103 | 3.6336 × 103 | 3.2335 × 103 | 4.2819 × 103 | 3.3079 × 103 |
| std | 3.7340 × 102 | 2.2836 × 102 | 2.2848 × 102 | 3.6243 × 102 | 2.9160 × 102 | 4.1794 × 102 | 2.5685 × 102 | 4.6445 × 102 | 1.8370 × 102 | 4.2664 × 102 | |
| F21 | mean | 2.9464 × 103 | 2.5170 × 103 | 2.5715 × 103 | 2.9119 × 103 | 2.8687 × 103 | 3.1022 × 103 | 2.7787 × 103 | 2.5804 × 103 | 3.2759 × 103 | 2.4549 × 103 |
| std | 8.7288 × 101 | 4.0302 × 101 | 3.5224 × 101 | 7.4281 × 101 | 3.3916 × 101 | 1.2843 × 102 | 4.3494 × 101 | 8.2233 × 101 | 9.7682 × 101 | 7.0230 × 101 | |
| F22 | mean | 1.2502 × 104 | 1.0455 × 104 | 9.4722 × 103 | 1.1949 × 104 | 9.8028 × 103 | 1.4869 × 104 | 1.3357 × 104 | 1.0407 × 104 | 1.6906 × 104 | 1.1443 × 104 |
| std | 8.9190 × 102 | 8.6257 × 102 | 4.2045 × 103 | 1.9901 × 103 | 1.1162 × 103 | 1.0439 × 103 | 3.8655 × 103 | 2.1141 × 103 | 5.4705 × 102 | 5.8185 × 103 | |
| F23 | mean | 4.0450 × 103 | 3.0010 × 103 | 3.0366 × 103 | 3.5214 × 103 | 3.2832 × 103 | 3.8144 × 103 | 3.4247 × 103 | 3.0619 × 103 | 4.5956 × 103 | 2.9074 × 103 |
| std | 2.5014 × 102 | 5.4636 × 101 | 3.1744 × 101 | 1.3704 × 102 | 3.0180 × 101 | 1.8678 × 102 | 1.3420 × 102 | 9.3251 × 101 | 1.7703 × 102 | 5.9313 × 101 | |
| F24 | mean | 4.3283 × 103 | 3.1554 × 103 | 3.2006 × 103 | 3.7239 × 103 | 3.3444 × 103 | 3.9398 × 103 | 3.5933 × 103 | 3.2485 × 103 | 4.8470 × 103 | 3.1116 × 103 |
| std | 2.5913 × 102 | 4.9311 × 101 | 3.1883 × 101 | 1.5509 × 102 | 1.7953 × 101 | 1.5273 × 102 | 1.8624 × 102 | 1.4830 × 102 | 2.2433 × 102 | 1.0775 × 102 | |
| F25 | mean | 3.7779 × 103 | 3.1591 × 103 | 3.5461 × 103 | 3.5848 × 103 | 3.6828 × 103 | 5.4046 × 103 | 3.4402 × 103 | 3.7204 × 103 | 1.5812 × 104 | 3.1017 × 103 |
| std | 1.8774 × 102 | 5.2419 × 101 | 1.3576 × 102 | 1.1904 × 103 | 2.3048 × 102 | 7.3704 × 102 | 3.1726 × 102 | 2.8291 × 102 | 1.3992 × 103 | 3.3099 × 101 | |
| F26 | mean | 1.2114 × 104 | 6.6845 × 103 | 6.7625 × 103 | 1.1570 × 104 | 8.2150 × 103 | 1.4694 × 104 | 7.3765 × 103 | 7.2725 × 103 | 1.7639 × 104 | 5.9019 × 103 |
| std | 1.3101 × 103 | 7.5030 × 102 | 8.2691 × 102 | 1.8257 × 103 | 7.2507 × 102 | 1.6923 × 103 | 2.2415 × 103 | 6.6936 × 102 | 6.4504 × 102 | 8.5417 × 102 | |
| F27 | mean | 5.0551 × 103 | 3.5206 × 103 | 3.7872 × 103 | 4.1305 × 103 | 3.7101 × 103 | 4.9531 × 103 | 3.6234 × 103 | 3.6636 × 103 | 7.0554 × 103 | 3.4593 × 103 |
| std | 5.2887 × 102 | 1.0735 × 102 | 9.6665 × 101 | 2.6467 × 102 | 1.4073 × 102 | 7.2703 × 102 | 1.6235 × 102 | 9.0939 × 101 | 8.0479 × 102 | 8.4314 × 101 | |
| F28 | mean | 4.9085 × 103 | 3.5189 × 103 | 4.0101 × 103 | 6.3259 × 103 | 5.2162 × 103 | 6.2591 × 103 | 4.1551 × 103 | 4.6298 × 103 | 1.3825 × 104 | 3.3766 × 103 |
| std | 4.1988 × 102 | 1.5575 × 102 | 2.2614 × 102 | 2.3474 × 103 | 1.3029 × 103 | 6.2880 × 102 | 7.3827 × 102 | 4.6716 × 102 | 1.4379 × 103 | 3.9247 × 101 | |
| F29 | mean | 7.3728 × 103 | 4.6400 × 103 | 4.6102 × 103 | 6.1678 × 103 | 5.4541 × 103 | 9.2553 × 103 | 5.6736 × 103 | 4.9276 × 103 | 1.4366 × 105 | 4.4187 × 103 |
| std | 7.4823 × 102 | 3.2113 × 102 | 3.2281 × 102 | 1.0027 × 103 | 4.2731 × 102 | 1.8806 × 103 | 4.7353 × 102 | 4.0527 × 102 | 1.1491 × 105 | 3.9739 × 102 | |
| F30 | mean | 1.4551 × 108 | 3.2684 × 106 | 2.4910 × 107 | 4.7270 × 107 | 7.0330 × 106 | 3.5475 × 108 | 1.0102 × 108 | 1.5965 × 108 | 8.5971 × 109 | 1.0628 × 106 |
| std | 4.5237 × 107 | 1.9997 × 106 | 1.2072 × 107 | 4.7052 × 107 | 4.6356 × 106 | 2.0793 × 108 | 4.4565 × 107 | 4.6354 × 107 | 2.5061 × 109 | 2.5886 × 105 |
| ID | Metric | HHO | LSHADE | GRO | DBO | HSO | WOA | PSO | GWO | COA | MECOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 5.0850 × 1010 | 1.6435 × 1010 | 5.2779 × 1010 | 9.8544 × 1010 | 3.5068 × 109 | 1.1043 × 1011 | 3.2798 × 1010 | 5.8304 × 1010 | 2.7212 × 1011 | 2.1586 × 108 |
| std | 8.3834 × 109 | 5.1586 × 109 | 9.4344 × 109 | 7.3152 × 1010 | 3.0089 × 109 | 1.3204 × 1010 | 7.9350 × 109 | 9.2761 × 109 | 1.1305 × 1010 | 1.7219 × 108 | |
| F2 | mean | 7.5868 × 10152 | 1.0000 × 1030 | 1.7586 × 10133 | 1.1859 × 10153 | 4.4402 × 10199 | 1.2524 × 10177 | 2.1655 × 10137 | 1.2343 × 10142 | 7.1299 × 10179 | 1.3295 × 10115 |
| std | 6.5535 × 104 | 1.4314 × 1014 | 9.2327 × 10133 | 6.5535 × 104 | 6.5535 × 104 | 6.5535 × 104 | 1.1861 × 10138 | 6.7605 × 10142 | 6.5535 × 104 | 7.1622 × 10115 | |
| F3 | mean | 3.9241 × 105 | 4.1216 × 105 | 4.4569 × 105 | 6.8364 × 105 | 3.5691 × 105 | 9.5747 × 105 | 6.0785 × 105 | 5.3827 × 105 | 3.5450 × 105 | 3.2751 × 105 |
| std | 1.3400 × 105 | 1.2945 × 105 | 6.4595 × 104 | 2.9336 × 105 | 3.5848 × 104 | 1.3350 × 105 | 1.3339 × 105 | 7.7076 × 104 | 1.5784 × 104 | 1.0279 × 104 | |
| F4 | mean | 9.5936 × 103 | 2.2773 × 103 | 6.0054 × 103 | 1.7031 × 104 | 3.0228 × 103 | 2.1781 × 104 | 4.2501 × 103 | 6.0432 × 103 | 1.0593 × 105 | 1.0000 × 103 |
| std | 1.9007 × 103 | 5.6810 × 102 | 1.2622 × 103 | 1.5737 × 104 | 7.6859 × 102 | 4.6744 × 103 | 1.7074 × 103 | 1.6353 × 103 | 1.4308 × 104 | 1.0910 × 102 | |
| F5 | mean | 1.6852 × 103 | 1.3141 × 103 | 1.4139 × 103 | 1.7061 × 103 | 1.7023 × 103 | 1.9697 × 103 | 1.6838 × 103 | 1.2670 × 103 | 2.1216 × 103 | 1.2014 × 103 |
| std | 5.8267 × 101 | 9.7818 × 101 | 7.0318 × 101 | 2.0979 × 102 | 6.8363 × 101 | 1.4146 × 102 | 1.0963 × 102 | 1.5839 × 102 | 4.7867 × 101 | 2.2003 × 102 | |
| F6 | mean | 6.9102 × 102 | 6.3442 × 102 | 6.4859 × 102 | 6.8224 × 102 | 6.9190 × 102 | 7.0926 × 102 | 6.7049 × 102 | 6.4511 × 102 | 7.1182 × 102 | 6.3515 × 102 |
| std | 3.8493 × 100 | 8.8115 × 100 | 4.7306 × 100 | 1.3744 × 101 | 4.8096 × 100 | 1.0108 × 101 | 1.2135 × 101 | 4.6405 × 100 | 2.7306 × 100 | 1.5950 × 101 | |
| F7 | mean | 3.8058 × 103 | 2.8700 × 103 | 2.2995 × 103 | 2.9231 × 103 | 4.8637 × 103 | 3.8031 × 103 | 2.4200 × 103 | 2.1653 × 103 | 4.0342 × 103 | 1.7935 × 103 |
| std | 9.2442 × 101 | 3.3361 × 102 | 1.4627 × 102 | 3.0800 × 102 | 6.2268 × 102 | 1.2695 × 102 | 1.1043 × 102 | 1.2776 × 102 | 7.6417 × 101 | 2.5404 × 102 | |
| F8 | mean | 2.1301 × 103 | 1.6467 × 103 | 1.6879 × 103 | 2.1358 × 103 | 2.0328 × 103 | 2.3892 × 103 | 2.0349 × 103 | 1.5546 × 103 | 2.6098 × 103 | 1.4382 × 103 |
| std | 5.3542 × 101 | 8.4025 × 101 | 4.9459 × 101 | 2.4099 × 102 | 5.6925 × 101 | 9.9540 × 101 | 9.9295 × 101 | 6.8111 × 101 | 4.4347 × 101 | 2.2488 × 102 | |
| F9 | mean | 6.7254 × 104 | 3.3841 × 104 | 3.0647 × 104 | 7.5889 × 104 | 6.3396 × 104 | 8.2395 × 104 | 6.4347 × 104 | 4.8549 × 104 | 8.0031 × 104 | 3.4714 × 104 |
| std | 4.8152 × 103 | 6.9663 × 103 | 6.6986 × 103 | 8.7823 × 103 | 1.4237 × 104 | 1.7482 × 104 | 1.5664 × 104 | 1.0875 × 104 | 3.3729 × 103 | 1.6728 × 104 | |
| F10 | mean | 2.4278 × 104 | 2.1718 × 104 | 2.6228 × 104 | 2.9455 × 104 | 2.3863 × 104 | 2.9245 × 104 | 2.9317 × 104 | 2.0957 × 104 | 3.2937 × 104 | 1.5984 × 104 |
| std | 1.5748 × 103 | 1.0770 × 103 | 1.1263 × 103 | 3.7516 × 103 | 1.5601 × 103 | 1.4456 × 103 | 1.9591 × 103 | 5.9230 × 103 | 6.8388 × 102 | 1.1235 × 103 | |
| F11 | mean | 1.5197 × 105 | 6.7825 × 104 | 1.0781 × 105 | 2.2728 × 105 | 5.5497 × 104 | 2.9342 × 105 | 8.9120 × 104 | 8.6754 × 104 | 2.5362 × 105 | 7.7407 × 104 |
| std | 3.4501 × 104 | 4.7233 × 104 | 1.5991 × 104 | 6.8762 × 104 | 1.2860 × 104 | 1.0518 × 105 | 2.9977 × 104 | 1.7924 × 104 | 5.3151 × 104 | 2.1368 × 104 | |
| F12 | mean | 1.1392 × 1010 | 6.5499 × 108 | 5.0465 × 109 | 8.2037 × 109 | 1.5984 × 108 | 3.0914 × 1010 | 1.1910 × 1010 | 1.1477 × 1010 | 2.0737 × 1011 | 7.7277 × 107 |
| std | 4.5191 × 109 | 3.5281 × 108 | 1.9784 × 109 | 2.3030 × 109 | 9.9900 × 107 | 8.2367 × 109 | 7.8319 × 109 | 5.7806 × 109 | 2.0105 × 1010 | 2.7771 × 107 | |
| F13 | mean | 2.6950 × 108 | 2.1303 × 105 | 5.6758 × 107 | 3.3783 × 108 | 7.0344 × 104 | 2.6985 × 109 | 1.8565 × 109 | 1.9527 × 109 | 4.9729 × 1010 | 8.2504 × 103 |
| std | 1.7504 × 108 | 2.0690 × 105 | 2.7850 × 107 | 1.8676 × 108 | 2.7637 × 104 | 1.1945 × 109 | 2.0145 × 109 | 1.7043 × 109 | 5.2413 × 109 | 5.9638 × 103 | |
| F14 | mean | 1.0251 × 107 | 1.5248 × 106 | 6.4785 × 106 | 1.7086 × 107 | 9.7551 × 105 | 1.9106 × 107 | 1.1533 × 107 | 9.0002 × 106 | 1.1245 × 108 | 2.4411 × 106 |
| std | 3.8292 × 106 | 1.2058 × 106 | 2.4473 × 106 | 1.0985 × 107 | 4.9479 × 105 | 9.9207 × 106 | 5.2883 × 106 | 5.1168 × 106 | 4.7743 × 107 | 1.3030 × 106 | |
| F15 | mean | 1.9120 × 107 | 1.9242 × 104 | 1.9285 × 106 | 8.2431 × 107 | 3.2171 × 104 | 4.8168 × 108 | 3.3454 × 108 | 3.8948 × 108 | 2.5908 × 1010 | 4.6131 × 103 |
| std | 2.5675 × 107 | 8.1373 × 103 | 1.5703 × 106 | 1.3948 × 108 | 1.3672 × 104 | 1.7711 × 108 | 4.3513 × 108 | 5.0807 × 108 | 4.9609 × 109 | 4.2903 × 103 | |
| F16 | mean | 1.0009 × 104 | 7.4696 × 103 | 7.7847 × 103 | 9.4878 × 103 | 7.3437 × 103 | 1.7118 × 104 | 9.9028 × 103 | 6.8399 × 103 | 2.5178 × 104 | 7.6405 × 103 |
| std | 1.1714 × 103 | 7.7777 × 102 | 5.8825 × 102 | 1.6834 × 103 | 7.8964 × 102 | 2.1157 × 103 | 8.3863 × 102 | 1.1068 × 103 | 3.2079 × 103 | 1.9559 × 103 | |
| F17 | mean | 8.6345 × 103 | 5.9419 × 103 | 5.3155 × 103 | 9.5544 × 103 | 5.6776 × 103 | 4.0400 × 104 | 8.6387 × 103 | 5.5572 × 103 | 1.2528 × 107 | 6.0978 × 103 |
| std | 1.7134 × 103 | 6.8084 × 102 | 3.5960 × 102 | 1.3831 × 103 | 5.0662 × 102 | 9.6818 × 104 | 1.1636 × 103 | 5.8648 × 102 | 1.1007 × 107 | 1.0947 × 103 | |
| F18 | mean | 8.8262 × 106 | 1.6907 × 106 | 9.7042 × 106 | 2.8512 × 107 | 1.9747 × 106 | 2.1340 × 107 | 1.6448 × 107 | 9.4214 × 106 | 2.7664 × 108 | 4.2531 × 106 |
| std | 4.1571 × 106 | 9.2075 × 105 | 4.0797 × 106 | 1.5911 × 107 | 1.2130 × 106 | 1.1216 × 107 | 5.7230 × 106 | 5.0643 × 106 | 1.1413 × 108 | 1.8128 × 106 | |
| F19 | mean | 4.7876 × 107 | 1.0794 × 105 | 3.8311 × 106 | 9.8608 × 107 | 2.2061 × 104 | 4.6681 × 108 | 3.9595 × 108 | 2.8434 × 108 | 2.5921 × 1010 | 5.7330 × 103 |
| std | 2.6442 × 107 | 2.2108 × 105 | 3.0234 × 106 | 1.0617 × 108 | 2.7757 × 104 | 3.3125 × 108 | 2.2797 × 108 | 2.6011 × 108 | 4.6169 × 109 | 5.3334 × 103 | |
| F20 | mean | 6.1488 × 103 | 6.3870 × 103 | 5.5538 × 103 | 6.8840 × 103 | 5.1464 × 103 | 7.3068 × 103 | 6.9648 × 103 | 5.9266 × 103 | 8.0265 × 103 | 6.0346 × 103 |
| std | 5.0949 × 102 | 5.1708 × 102 | 3.2772 × 102 | 7.6237 × 102 | 6.2550 × 102 | 6.7620 × 102 | 5.7093 × 102 | 1.1543 × 103 | 3.7455 × 102 | 5.9908 × 102 | |
| F21 | mean | 4.3740 × 103 | 3.1534 × 103 | 3.2081 × 103 | 4.0195 × 103 | 3.7161 × 103 | 4.4563 × 103 | 3.7606 × 103 | 3.0936 × 103 | 5.0783 × 103 | 2.8916 × 103 |
| std | 1.9695 × 102 | 1.4327 × 102 | 5.9296 × 101 | 1.6355 × 102 | 5.3238 × 101 | 2.0372 × 102 | 1.3810 × 102 | 1.4037 × 102 | 2.2658 × 102 | 1.3913 × 102 | |
| F22 | mean | 2.7461 × 104 | 2.4349 × 104 | 2.8362 × 104 | 2.8673 × 104 | 2.5556 × 104 | 3.2070 × 104 | 3.2653 × 104 | 2.3191 × 104 | 3.5177 × 104 | 2.8804 × 104 |
| std | 1.6569 × 103 | 1.0176 × 103 | 3.0779 × 103 | 4.5582 × 103 | 1.6409 × 103 | 1.6899 × 103 | 1.5858 × 103 | 5.6784 × 103 | 7.9538 × 102 | 7.2798 × 103 | |
| F23 | mean | 5.7779 × 103 | 3.6422 × 103 | 3.8781 × 103 | 4.7517 × 103 | 4.0017 × 103 | 5.3556 × 103 | 4.9548 × 103 | 3.7084 × 103 | 6.7788 × 103 | 3.2544 × 103 |
| std | 4.1293 × 102 | 1.0523 × 102 | 6.9131 × 101 | 2.9642 × 102 | 5.9166 × 101 | 3.2347 × 102 | 2.5340 × 102 | 8.9972 × 101 | 3.2194 × 102 | 7.6494 × 101 | |
| F24 | mean | 8.2297 × 103 | 4.3505 × 103 | 4.6047 × 103 | 5.9477 × 103 | 4.6149 × 103 | 6.7944 × 103 | 5.8639 × 103 | 4.4785 × 103 | 1.0369 × 104 | 3.8012 × 103 |
| std | 6.8145 × 102 | 1.5558 × 102 | 1.1001 × 102 | 4.3238 × 102 | 8.8937 × 101 | 3.5570 × 102 | 3.8534 × 102 | 1.9610 × 102 | 7.9820 × 102 | 1.1188 × 102 | |
| F25 | mean | 6.7515 × 103 | 5.0019 × 103 | 6.9760 × 103 | 1.1317 × 104 | 6.5505 × 103 | 1.0791 × 104 | 5.8914 × 103 | 7.1036 × 103 | 3.0020 × 104 | 3.6694 × 103 |
| std | 5.6997 × 102 | 5.1719 × 102 | 7.7302 × 102 | 6.6673 × 103 | 8.3952 × 102 | 1.0933 × 103 | 1.0490 × 103 | 8.3000 × 102 | 1.7025 × 103 | 7.0659 × 101 | |
| F26 | mean | 3.1234 × 104 | 1.6951 × 104 | 1.9962 × 104 | 2.5740 × 104 | 1.9476 × 104 | 3.8184 × 104 | 2.0254 × 104 | 1.7589 × 104 | 5.3547 × 104 | 1.2418 × 104 |
| std | 2.2384 × 103 | 1.5965 × 103 | 1.8900 × 103 | 3.7105 × 103 | 1.2179 × 103 | 3.8575 × 103 | 3.4570 × 103 | 1.6380 × 103 | 2.0847 × 103 | 2.3066 × 103 | |
| F27 | mean | 7.3081 × 103 | 3.9532 × 103 | 4.5824 × 103 | 4.8279 × 103 | 4.2539 × 103 | 6.2389 × 103 | 3.9877 × 103 | 4.3722 × 103 | 1.5259 × 104 | 3.5992 × 103 |
| std | 1.1185 × 103 | 1.8808 × 102 | 2.4352 × 102 | 5.6574 × 102 | 2.0874 × 102 | 1.2036 × 103 | 2.9870 × 102 | 1.7565 × 102 | 1.7319 × 103 | 8.8412 × 101 | |
| F28 | mean | 9.3433 × 103 | 6.8646 × 103 | 9.0259 × 103 | 1.9828 × 104 | 1.5706 × 104 | 1.4888 × 104 | 6.8571 × 103 | 9.5755 × 103 | 3.0889 × 104 | 3.7730 × 103 |
| std | 1.0648 × 103 | 1.2605 × 103 | 9.8975 × 102 | 6.7889 × 103 | 5.2411 × 103 | 1.2098 × 103 | 1.9675 × 103 | 1.3731 × 103 | 1.0995 × 103 | 7.9945 × 101 | |
| F29 | mean | 1.2958 × 104 | 8.4151 × 103 | 8.7955 × 103 | 1.1632 × 104 | 9.3537 × 103 | 2.1642 × 104 | 1.0937 × 104 | 9.3243 × 103 | 7.1789 × 105 | 6.5334 × 103 |
| std | 1.5056 × 103 | 6.4508 × 102 | 5.4654 × 102 | 1.7337 × 103 | 5.5826 × 102 | 4.2213 × 103 | 9.2909 × 102 | 8.5982 × 102 | 3.9245 × 105 | 7.7130 × 102 | |
| F30 | mean | 7.5026 × 108 | 5.1994 × 106 | 4.6741 × 107 | 2.8336 × 108 | 1.0240 × 106 | 2.6442 × 109 | 1.4417 × 109 | 1.2662 × 109 | 4.3489 × 1010 | 6.6470 × 104 |
| std | 3.7454 × 108 | 8.0547 × 106 | 2.2900 × 107 | 2.0682 × 108 | 7.7077 × 105 | 8.3361 × 108 | 1.3296 × 109 | 1.0593 × 109 | 5.7026 × 109 | 4.2205 × 104 |
| ID | Metric | HHO | LSHADE | GRO | DBO | HSO | WOA | PSO | GWO | COA | MECOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 2.5020 × 104 | 2.0844 × 104 | 1.1523 × 104 | 3.4854 × 104 | 6.9839 × 103 | 3.5309 × 104 | 6.1707 × 103 | 1.4939 × 104 | 4.8494 × 104 | 6.3581 × 103 |
| std | 7.9622 × 103 | 2.0796 × 104 | 3.3754 × 103 | 9.4736 × 103 | 3.5306 × 103 | 1.4132 × 104 | 4.1031 × 103 | 4.5072 × 103 | 1.4396 × 104 | 2.6046 × 103 | |
| F2 | mean | 5.6473 × 102 | 4.5225 × 102 | 4.6239 × 102 | 5.1391 × 102 | 5.6096 × 102 | 6.4079 × 102 | 4.8639 × 102 | 4.9492 × 102 | 3.1412 × 103 | 4.5168 × 102 |
| std | 6.2359 × 101 | 1.6089 × 101 | 1.1233 × 101 | 5.4477 × 101 | 6.8850 × 101 | 8.1424 × 101 | 3.8022 × 101 | 4.2415 × 101 | 8.0479 × 102 | 2.0567 × 101 | |
| F3 | mean | 6.6414 × 102 | 6.0102 × 102 | 6.0171 × 102 | 6.3396 × 102 | 6.3699 × 102 | 6.6710 × 102 | 6.1091 × 102 | 6.0795 × 102 | 6.8067 × 102 | 6.0019 × 102 |
| std | 7.1620 × 100 | 1.4216 × 100 | 5.7498 × 10−1 | 9.8236 × 100 | 5.5161 × 100 | 1.5568 × 101 | 4.3013 × 100 | 4.3004 × 100 | 9.1194 × 100 | 3.2379 × 10−1 | |
| F4 | mean | 8.8456 × 102 | 8.4077 × 102 | 8.4551 × 102 | 9.0809 × 102 | 9.1655 × 102 | 9.3691 × 102 | 9.0685 × 102 | 8.6097 × 102 | 9.7816 × 102 | 8.4865 × 102 |
| std | 1.3611 × 101 | 1.2088 × 101 | 1.0662 × 101 | 2.9836 × 101 | 1.1827 × 101 | 4.2020 × 101 | 2.1665 × 101 | 2.8044 × 101 | 1.7881 × 101 | 3.0290 × 101 | |
| F5 | mean | 3.0452 × 103 | 1.2054 × 103 | 9.2297 × 102 | 2.2795 × 103 | 1.1005 × 103 | 4.6551 × 103 | 9.9209 × 102 | 1.2627 × 103 | 3.5843 × 103 | 1.1355 × 103 |
| std | 2.6241 × 102 | 2.3868 × 102 | 1.1269 × 101 | 6.5896 × 102 | 1.7129 × 102 | 2.0886 × 103 | 3.8085 × 101 | 3.1269 × 102 | 3.2798 × 102 | 5.7056 × 102 | |
| F6 | mean | 1.9306 × 105 | 5.7172 × 103 | 8.8106 × 104 | 1.1521 × 106 | 4.5929 × 103 | 7.0905 × 106 | 2.0186 × 106 | 2.8656 × 106 | 2.5864 × 109 | 6.6726 × 103 |
| std | 1.4743 × 105 | 4.9782 × 103 | 1.4887 × 105 | 2.0816 × 106 | 3.7156 × 103 | 1.1621 × 107 | 1.3833 × 106 | 7.2868 × 106 | 8.8284 × 108 | 5.6779 × 103 | |
| F7 | mean | 2.2192 × 103 | 2.0541 × 103 | 2.0550 × 103 | 2.1615 × 103 | 2.1305 × 103 | 2.2503 × 103 | 2.1028 × 103 | 2.1043 × 103 | 2.2229 × 103 | 2.0574 × 103 |
| std | 6.7863 × 101 | 1.5759 × 101 | 9.2004 × 100 | 7.2788 × 101 | 3.1905 × 101 | 8.8439 × 101 | 4.3621 × 101 | 4.0593 × 101 | 3.8353 × 101 | 2.2978 × 101 | |
| F8 | mean | 2.3253 × 103 | 2.2400 × 103 | 2.2300 × 103 | 2.3217 × 103 | 2.4858 × 103 | 2.3009 × 103 | 2.2830 × 103 | 2.2578 × 103 | 2.4597 × 103 | 2.2262 × 103 |
| std | 1.1230 × 102 | 3.7019 × 101 | 2.3831 × 100 | 7.0321 × 101 | 1.2476 × 102 | 6.4976 × 101 | 7.3121 × 101 | 4.8767 × 101 | 1.3446 × 102 | 5.2111 × 100 | |
| F9 | mean | 2.5549 × 103 | 2.4808 × 103 | 2.4837 × 103 | 2.5079 × 103 | 2.7196 × 103 | 2.6059 × 103 | 2.5079 × 103 | 2.5350 × 103 | 3.4909 × 103 | 2.4808 × 103 |
| std | 5.0915 × 101 | 7.1710 × 10−2 | 1.7872 × 100 | 2.7544 × 101 | 1.0935 × 102 | 6.1629 × 101 | 3.6250 × 101 | 2.9324 × 101 | 3.1304 × 102 | 1.0706 × 10−3 | |
| F10 | mean | 4.2017 × 103 | 2.5044 × 103 | 2.5756 × 103 | 3.1158 × 103 | 3.8643 × 103 | 5.0736 × 103 | 3.9381 × 103 | 3.4296 × 103 | 6.1242 × 103 | 2.5096 × 103 |
| std | 7.5501 × 102 | 7.3701 × 101 | 1.7652 × 102 | 1.0763 × 103 | 5.5343 × 102 | 1.3868 × 103 | 1.0598 × 103 | 6.5754 × 102 | 1.5881 × 103 | 3.3854 × 101 | |
| F11 | mean | 3.5679 × 103 | 2.9253 × 103 | 3.0197 × 103 | 3.1244 × 103 | 3.4762 × 103 | 4.0140 × 103 | 3.5482 × 103 | 3.6394 × 103 | 8.5693 × 103 | 2.9200 × 103 |
| std | 8.7589 × 102 | 1.2019 × 102 | 1.2078 × 102 | 1.8337 × 102 | 2.0040 × 102 | 5.4091 × 102 | 3.9256 × 102 | 4.1996 × 102 | 5.1443 × 102 | 4.0684 × 101 | |
| F12 | mean | 3.2846 × 103 | 2.9665 × 103 | 2.9666 × 103 | 3.0417 × 103 | 3.0027 × 103 | 3.1615 × 103 | 2.9858 × 103 | 2.9784 × 103 | 3.5887 × 103 | 2.9582 × 103 |
| std | 1.8799 × 102 | 1.8551 × 101 | 1.0933 × 101 | 7.5363 × 101 | 2.9013 × 101 | 1.4165 × 102 | 3.4969 × 101 | 2.6680 × 101 | 2.7026 × 102 | 1.2357 × 101 |
| Statistical Results | HHO | LSHADE | GRO | DBO | HSO | WOA | PSO | GWO | COA |
|---|---|---|---|---|---|---|---|---|---|
| CEC2017 d = 30 (+/=/−) | (30/0/0) | (16/0/14) | (25/0/5) | (29/0/1) | (27/0/3) | (29/0/1) | (29/0/1) | (27/0/3) | (30/0/0) |
| CEC2017 d = 50 (+/=/−) | (30/0/0) | (23/0/7) | (26/0/4) | (29/0/1) | (27/1/2) | (28/0/2) | (27/0/3) | (27/0/3) | (29/0/1) |
| CEC2017 d = 100 (+/=/−) | (29/0/1) | (26/0/4) | (28/0/2) | (29/0/1) | (28/0/2) | (29/0/1) | (28/0/2) | (27/0/3) | (30/0/0) |
| CEC2022 d = 20 (+/=/−) | (12/0/0) | (8/0/4) | (9/0/3) | (12/0/0) | (10/0/2) | (12/0/0) | (11/0/1) | (12/0/0) | (12/0/0) |
| Suites | CEC2017 | CEC2022 | ||||||
|---|---|---|---|---|---|---|---|---|
| Dimensions | 30 | 50 | 100 | 20 | ||||
| Algorithms | ||||||||
| HHO | 7.47 | 8 | 6.90 | 8 | 6.50 | 7 | 5.75 | 7 |
| LSHADE | 2.03 | 2 | 2.43 | 2 | 2.63 | 2 | 8.83 | 9 |
| GRO | 3.13 | 3 | 3.47 | 3 | 4.30 | 4 | 5.50 | 6 |
| DBO | 6.20 | 7 | 6.60 | 7 | 6.87 | 8 | 2.50 | 2 |
| HSO | 4.97 | 4 | 4.00 | 4 | 4.07 | 3 | 5.08 | 4 |
| WOA | 8.83 | 9 | 8.87 | 9 | 8.77 | 9 | 5.42 | 5 |
| PSO | 5.53 | 6 | 5.97 | 6 | 6.10 | 6 | 8.50 | 8 |
| GWO | 5.03 | 5 | 4.77 | 5 | 4.30 | 4 | 2.92 | 3 |
| COA | 9.93 | 10 | 9.93 | 10 | 9.63 | 10 | 8.92 | 10 |
| MECOA | 1.87 | 1 | 2.07 | 1 | 1.83 | 1 | 1.58 | 1 |
| Parameters | Single Diode PV Models | Double Diode Models | ||
|---|---|---|---|---|
| Lower Bound | Upper Bound | Lower Bound | Upper Bound | |
| 0 | 1 | 0 | 2 | |
| 0 | 1 | 0 | 50 | |
| 0 | 0.5 | 0 | 2 | |
| 0 | 100 | 0 | 2000 | |
| 1 | 2 | 1 | 50 | |
| 0 | 1 | 0 | 50 | |
| 0 | 1 | 0 | 50 | |
| 1 | 2 | 1 | 50 | |
| 1 | 2 | 1 | 50 | |
| Algorithm | |||||||
|---|---|---|---|---|---|---|---|
| MECOA | 0.760776 | 3.23 × 10−7 | 0.036377 | 53.71853 | 1.481184 | 9.8602 × 10−4 | / |
| COA | 0.736804 | 6.45 × 10−7 | 0.026129 | 48.3867 | 1.560194 | 2.0133 × 10−2 | + |
| GWO | 0.761306 | 3.36 × 10−7 | 0.036002 | 47.50041 | 1.485585 | 1.1562 × 10−3 | + |
| PSO | 0.760938 | 2.92 × 10−7 | 0.0368 | 50.47772 | 1.471148 | 1.0081 × 10−3 | + |
| WOA | 0.760176 | 6.47 × 10−7 | 0.033886 | 75.6056 | 1.554826 | 2.0407 × 10−3 | + |
| HSO | 0.763224 | 0.000001 | 0.029551 | 51.0347 | 1.602817 | 8.1496 × 10−3 | + |
| DBO | 0.760811 | 3.03 × 10−7 | 0.036638 | 51.80582 | 1.4747 | 9.9402 × 10−4 | + |
| GRO | 0.761088 | 3.33 × 10−7 | 0.036353 | 56.44247 | 1.484082 | 1.0534 × 10−3 | + |
| LSHADE | 0.760763 | 3.32 × 10−7 | 0.036262 | 54.51104 | 1.484096 | 9.8756 × 10−4 | + |
| HHO | 0.760011 | 5.56 × 10−7 | 0.03354 | 88.23509 | 1.537796 | 1.9496 × 10−3 | + |
| Algorithm | ||||||
|---|---|---|---|---|---|---|
| 1 | −0.2057 | 0.764 | 0.764088 | 8.77 × 10−5 | −0.15717 | 1.8 × 10−5 |
| 2 | −0.1291 | 0.762 | 0.762663 | 0.000663 | −0.09846 | 8.56 × 10−5 |
| 3 | −0.0588 | 0.7605 | 0.761355 | 0.000855 | −0.04477 | 5.03 × 10−5 |
| 4 | 0.0057 | 0.7605 | 0.760154 | 0.000346 | 0.004333 | 1.97 × 10−6 |
| 5 | 0.0646 | 0.76 | 0.759055 | 0.000945 | 0.049035 | 6.1 × 10−5 |
| 6 | 0.1185 | 0.759 | 0.758042 | 0.000958 | 0.089828 | 0.000113 |
| 7 | 0.1678 | 0.757 | 0.757092 | 9.17 × 10−5 | 0.12704 | 1.54 × 10−5 |
| 8 | 0.2132 | 0.757 | 0.756141 | 0.000859 | 0.161209 | 0.000183 |
| 9 | 0.2545 | 0.7555 | 0.755087 | 0.000413 | 0.19217 | 0.000105 |
| 10 | 0.2924 | 0.754 | 0.753664 | 0.000336 | 0.220371 | 9.83 × 10−5 |
| 11 | 0.3269 | 0.7505 | 0.751391 | 0.000891 | 0.24563 | 0.000291 |
| 12 | 0.3585 | 0.7465 | 0.747354 | 0.000854 | 0.267926 | 0.000306 |
| 13 | 0.3873 | 0.7385 | 0.740117 | 0.001617 | 0.286647 | 0.000626 |
| 14 | 0.4137 | 0.728 | 0.727382 | 0.000618 | 0.300918 | 0.000256 |
| 15 | 0.4373 | 0.7065 | 0.706973 | 0.000473 | 0.309159 | 0.000207 |
| 16 | 0.459 | 0.6755 | 0.67528 | 0.00022 | 0.309954 | 0.000101 |
| 17 | 0.4784 | 0.632 | 0.630758 | 0.001242 | 0.301755 | 0.000594 |
| 18 | 0.496 | 0.573 | 0.571928 | 0.001072 | 0.283676 | 0.000532 |
| 19 | 0.5119 | 0.499 | 0.499607 | 0.000607 | 0.255749 | 0.000311 |
| 20 | 0.5265 | 0.413 | 0.413649 | 0.000649 | 0.217786 | 0.000342 |
| 21 | 0.5398 | 0.3165 | 0.31751 | 0.00101 | 0.171392 | 0.000545 |
| 22 | 0.5521 | 0.212 | 0.212155 | 0.000155 | 0.117131 | 8.55 × 10−5 |
| 23 | 0.5633 | 0.1035 | 0.102251 | 0.001249 | 0.057598 | 0.000703 |
| 24 | 0.5736 | −0.01 | −0.00872 | 0.001282 | −0.005 | 0.000736 |
| 25 | 0.5833 | −0.123 | −0.12551 | 0.002507 | −0.07321 | 0.001463 |
| 26 | 0.59 | −0.21 | −0.20847 | 0.001528 | −0.123 | 0.000901 |
| Sum of IAE | N/A | N/A | N/A | 0.021526866 | N/A | 0.008730779 |
| Algorithm | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| MECOA | 0.760781 | 0.036737 | 55.46508 | 7.42 × 10−7 | 2 | 2.26768 × 10−7 | 1.451308 | 9.8249 × 10−4 | / |
| COA | 0.760854 | 0.034999 | 22.04328 | 2.57 × 10−7 | 1.46486 | 1.19441 × 10−7 | 1.746827 | 6.0117 × 10−3 | + |
| GWO | 0.758741 | 0.036344 | 83.81247 | 2.85 × 10−7 | 1.473204 | 2.29143 × 10−7 | 1.817755 | 1.4900 × 10−3 | + |
| PSO | 0.760893 | 0.035505 | 57.09248 | 0 | 1.978735 | 3.96844 × 10−7 | 1.502243 | 1.0704 × 10−3 | + |
| WOA | 0.760363 | 0.034279 | 86.84143 | 5.01 × 10−7 | 2 | 5.63352 × 10−7 | 1.543155 | 2.3850 × 10−3 | + |
| HSO | 0.763077 | 0.032916 | 58.03336 | 9.61 × 10−7 | 1.608205 | 9.13978 × 10−7 | 2 | 6.3207 × 10−3 | + |
| DBO | 0.760747 | 0.036135 | 55.52361 | 3.36 × 10−7 | 1.485573 | 4.70286 × 10−8 | 1.976181 | 9.9314 × 10−4 | + |
| GRO | 0.760182 | 0.036359 | 73.42288 | 1.73 × 10−7 | 1.436726 | 7.27111 × 10−7 | 1.809215 | 1.1164 × 10−3 | + |
| LSHADE | 0.760625 | 0.035299 | 64.71443 | 2.79 × 10−7 | 1.780844 | 3.28378 × 10−7 | 1.490441 | 1.1489 × 10−3 | + |
| HHO | 0.759459 | 0.038787 | 68.62729 | 1.59 × 10−7 | 1.424276 | 8.08597 × 10−8 | 1.562643 | 1.8914 × 10−3 | + |
| Algorithm | ||||||
|---|---|---|---|---|---|---|
| 1 | −0.2057 | 0.764 | 0.763984622 | 1.53782 × 10−5 | −0.157151637 | 3.1633 × 10−6 |
| 2 | −0.1291 | 0.762 | 0.7626048 | 0.0006048 | −0.09845228 | 7.80796 × 10−5 |
| 3 | −0.0588 | 0.7605 | 0.761337939 | 0.000837939 | −0.044766671 | 4.92708 × 10−5 |
| 4 | 0.0057 | 0.7605 | 0.76017361 | 0.00032639 | 0.00433299 | 1.86042 × 10−6 |
| 5 | 0.0646 | 0.76 | 0.759107134 | 0.000892866 | 0.049038321 | 5.76791 × 10−5 |
| 6 | 0.1185 | 0.759 | 0.75812057 | 0.00087943 | 0.089837288 | 0.000104212 |
| 7 | 0.1678 | 0.757 | 0.757187549 | 0.000187549 | 0.127056071 | 3.14707 × 10−5 |
| 8 | 0.2132 | 0.757 | 0.756242458 | 0.000757542 | 0.161230892 | 0.000161508 |
| 9 | 0.2545 | 0.7555 | 0.755176245 | 0.000323755 | 0.192192354 | 8.23956 × 10−5 |
| 10 | 0.2924 | 0.754 | 0.753721605 | 0.000278395 | 0.220388197 | 8.14028 × 10−5 |
| 11 | 0.3269 | 0.7505 | 0.751398897 | 0.000898897 | 0.2456323 | 0.00029385 |
| 12 | 0.3585 | 0.7465 | 0.747301852 | 0.000801852 | 0.267907714 | 0.000287464 |
| 13 | 0.3873 | 0.7385 | 0.740011687 | 0.001511687 | 0.286606526 | 0.000585476 |
| 14 | 0.4137 | 0.728 | 0.727248374 | 0.000751626 | 0.300862652 | 0.000310948 |
| 15 | 0.4373 | 0.7065 | 0.706851707 | 0.000351707 | 0.309106251 | 0.000153801 |
| 16 | 0.459 | 0.6755 | 0.675211521 | 0.000288479 | 0.309922088 | 0.000132412 |
| 17 | 0.4784 | 0.632 | 0.630761056 | 0.001238944 | 0.301756089 | 0.000592711 |
| 18 | 0.496 | 0.573 | 0.571994359 | 0.001005641 | 0.283709202 | 0.000498798 |
| 19 | 0.5119 | 0.499 | 0.499705332 | 0.000705332 | 0.25579916 | 0.00036106 |
| 20 | 0.5265 | 0.413 | 0.41373286 | 0.00073286 | 0.217830351 | 0.000385851 |
| 21 | 0.5398 | 0.3165 | 0.317545722 | 0.001045722 | 0.171411181 | 0.000564481 |
| 22 | 0.5521 | 0.212 | 0.212123062 | 0.000123062 | 0.117113142 | 6.79424 × 10−5 |
| 23 | 0.5633 | 0.1035 | 0.10216384 | 0.00133616 | 0.057548891 | 0.000752659 |
| 24 | 0.5736 | −0.01 | −0.008791274 | 0.001208726 | −0.005042674 | 0.000693326 |
| 25 | 0.5833 | −0.123 | −0.125543202 | 0.002543202 | −0.07322935 | 0.00148345 |
| 26 | 0.59 | −0.21 | −0.208372508 | 0.001627492 | −0.12293978 | 0.00096022 |
| Sum of IAE | N/A | N/A | N/A | 0.021275434 | N/A | 0.00877549 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Luo, M. MECOA: A Multi-Strategy Enhanced Coati Optimization Algorithm for Global Optimization and Photovoltaic Models Parameter Estimation. Biomimetics 2025, 10, 839. https://doi.org/10.3390/biomimetics10120839
Chen H, Luo M. MECOA: A Multi-Strategy Enhanced Coati Optimization Algorithm for Global Optimization and Photovoltaic Models Parameter Estimation. Biomimetics. 2025; 10(12):839. https://doi.org/10.3390/biomimetics10120839
Chicago/Turabian StyleChen, Hang, and Maomao Luo. 2025. "MECOA: A Multi-Strategy Enhanced Coati Optimization Algorithm for Global Optimization and Photovoltaic Models Parameter Estimation" Biomimetics 10, no. 12: 839. https://doi.org/10.3390/biomimetics10120839
APA StyleChen, H., & Luo, M. (2025). MECOA: A Multi-Strategy Enhanced Coati Optimization Algorithm for Global Optimization and Photovoltaic Models Parameter Estimation. Biomimetics, 10(12), 839. https://doi.org/10.3390/biomimetics10120839







