NDFNGO: Enhanced Northern Goshawk Optimization Algorithm for Image Segmentation
Abstract
1. Introduction
- By leveraging the diversity and adaptability of the differential strategy, a nonlinear differential learning strategy is proposed to enhance the global search capability of the NGO algorithm.
- Leveraging the dynamic behaviors inherent in exponential, cosine, and arctangent functions, a decay factor is incorporated to fine-tune the equilibrium between the NGO algorithm’s global search breadth and local refinement depth.
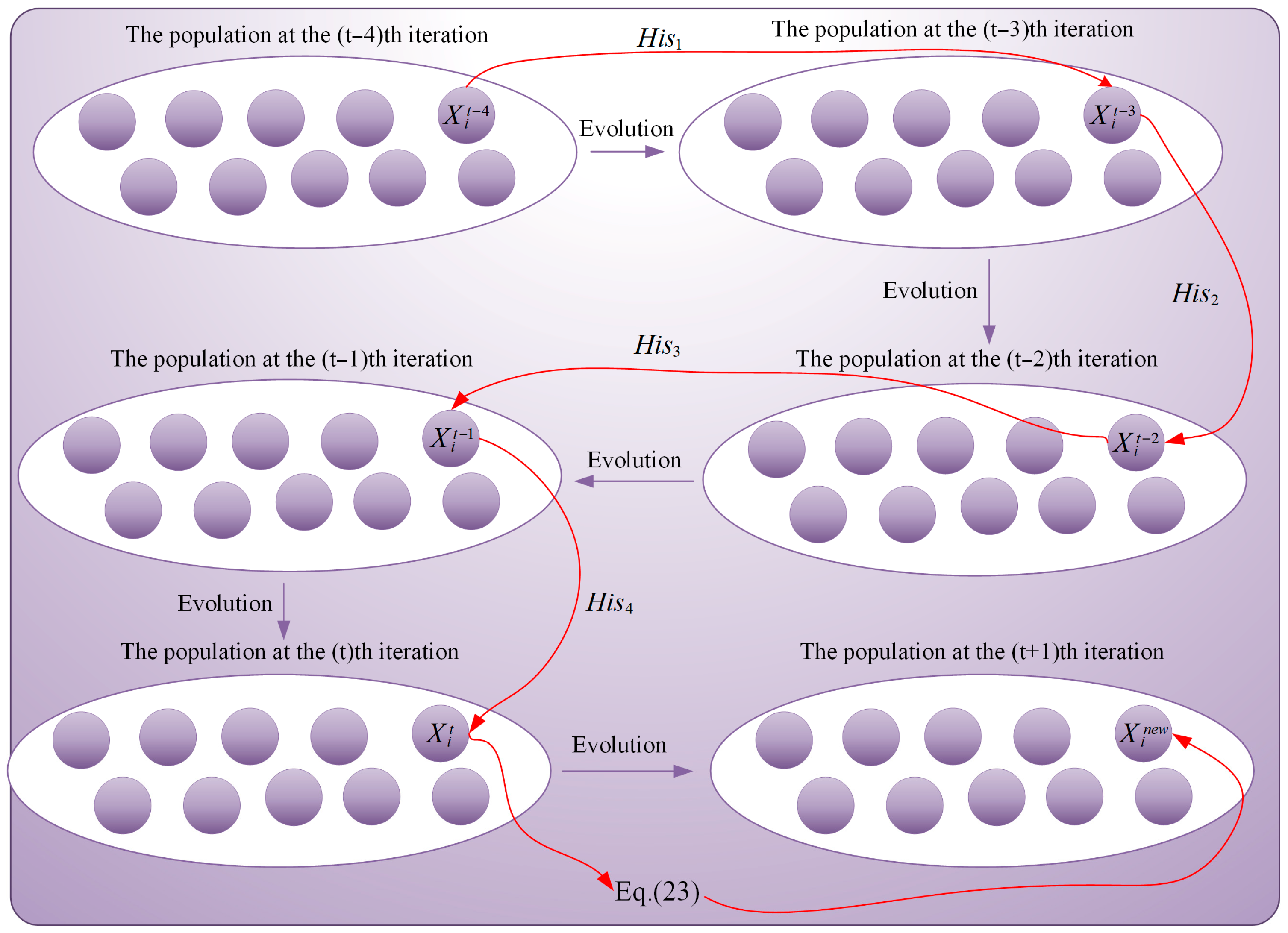
- By incorporating historical individual information, a Fractional-order adaptive learning strategy is proposed to strengthen the algorithm’s local exploitation ability.
- By integrating the aforementioned three improvement strategies into the NGO algorithm, the NDFNGO algorithm is proposed.
- The utilization of the NDFNGO algorithm for segmenting mural imagery successfully substantiated the viability of this technique, confirming its considerable potential for this specialized field.
2. Mathematical Model of Northern Goshawk Optimization
2.1. Population Initialization Phase
2.2. Global Exploration Phase
2.3. Local Exploitation Phase
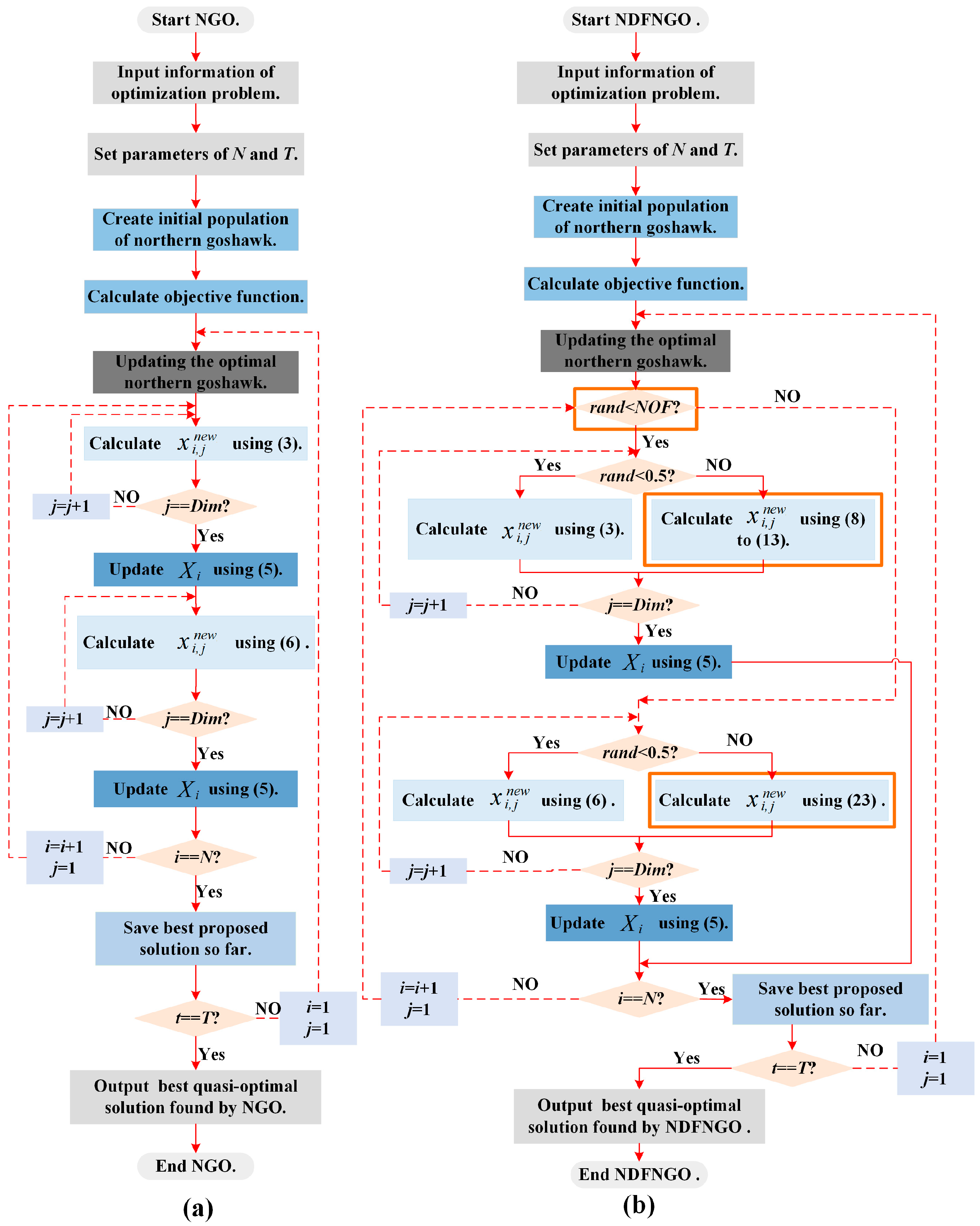
2.4. Implementation Framework of NGO
3. Mathematical Model of NDFNGO Algorithm
3.1. Nonlinear Differential Learning Strategy
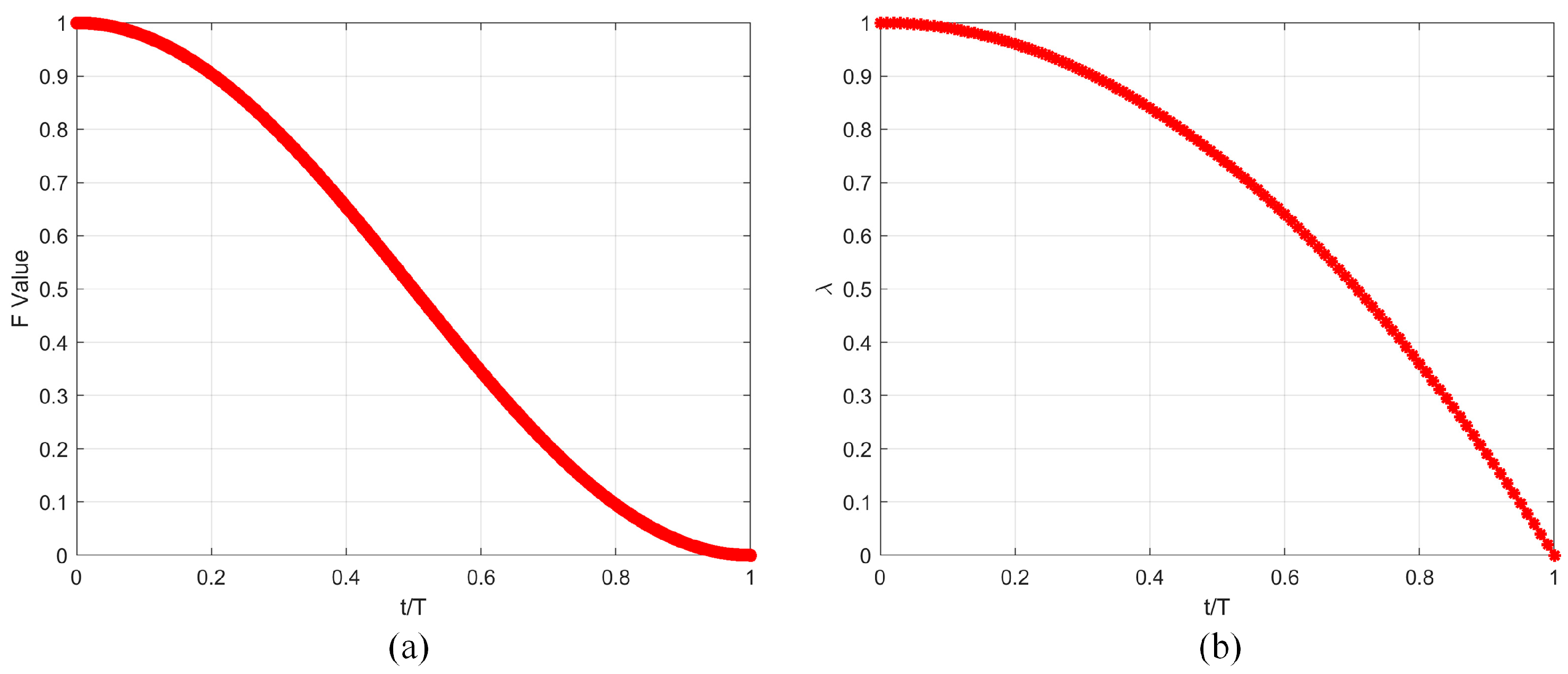
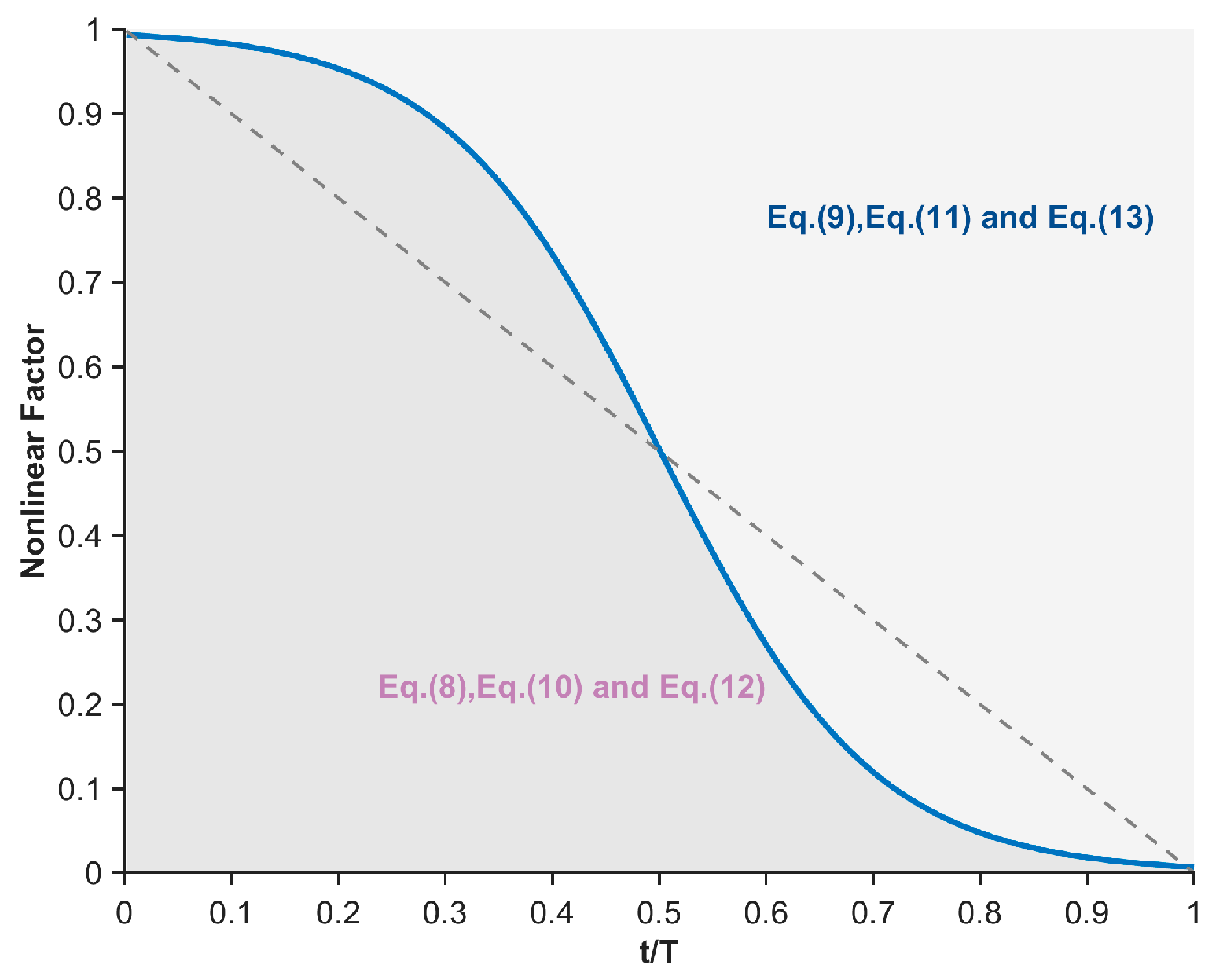
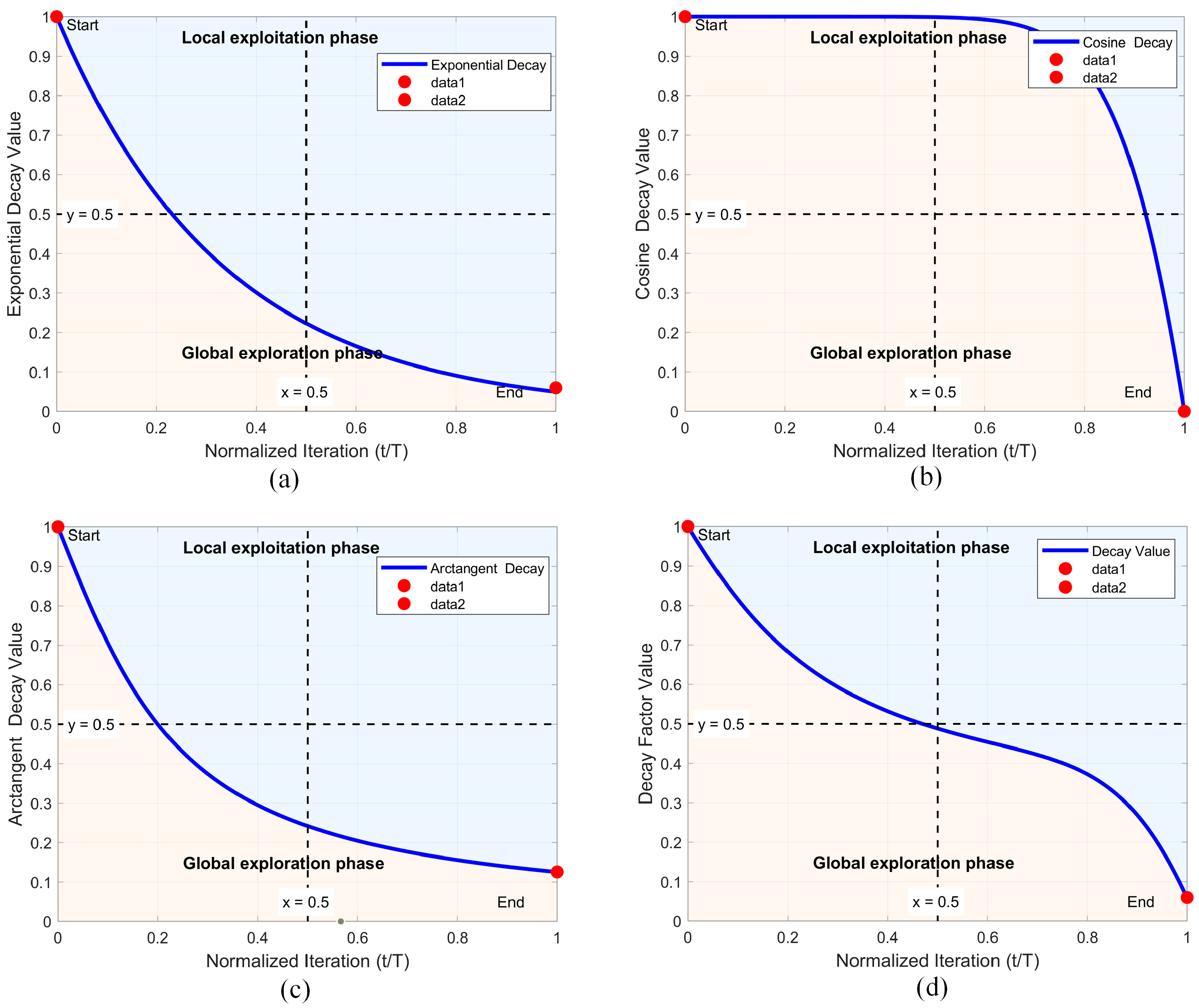
3.2. Decay Factor
3.3. Fractional-Order Adaptive Learning Strategy
3.4. Implementation Framework of NDFNGO
3.5. Time Complexity Analysis
4. Experimental Validation and Discussion on Real-World Applications
5. Experimental Results and Discussion on Image Segmentation
| Algorithms | Year | Parameter Settings |
|---|---|---|
| OPBNGO [48] | 2025 | |
| NGO [37] | 2021 | |
| ANBPO [43] | 2025 | |
| DENGO [49] | 2024 | |
| IMODE [50] | 2020 |
5.1. Model of Mural Image Segmentation
5.2. Decay Factor Parameter Settings
5.3. Comparative Analysis of Linear Factors
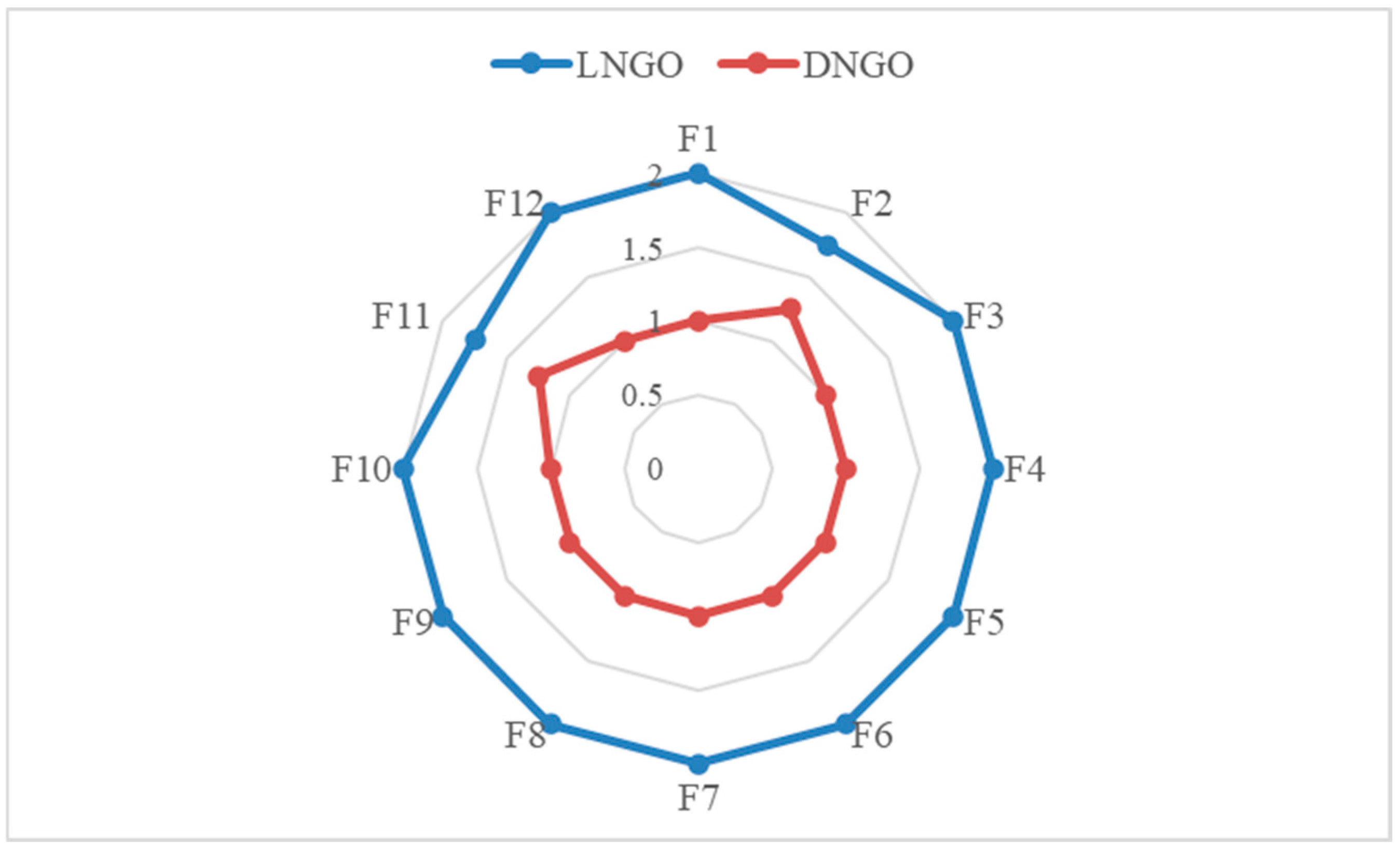
5.4. Population Diversity Analysis
5.5. Exploration/Exploitation Balance Analysis
5.6. Run Parameter Settings
5.7. Ablation on Strategies Effectiveness
5.8. Fitness Function Values Analysis
5.9. PSNR Metrics Analysis
5.10. SSIM Metrics Analysis
5.11. FSIM Metrics Analysis
5.12. Comprehensive Metric Analysis
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H. Intelligent restoration of ancient murals based on discrete differential algorithm. J. Comput. Methods Sci. Eng. 2021, 21, 803–814. [Google Scholar] [CrossRef]
- Jiao, L.J.; Wang, W.J.; Li, B.J.; Zhao, Q.S. Wutai Mountain mural inpainting based on improved block matching algorithm. J. Comput. Aid Des. Comput. Graph. 2019, 31, 119–125. [Google Scholar] [CrossRef]
- Yu, T.; Lin, C.; Zhang, S.; Ding, X.; Wu, J.; Zhang, J. End-to-end partial convolutions neural networks for Dunhuang grottoes wall-painting restoration. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar]
- Han, P.H.; Chen, Y.S.; Liu, I.S.; Jang, Y.P.; Tsai, L.; Chang, A.; Hung, Y.P. A compelling virtual tour of the dunhuang cave with an immersive head-mounted display. IEEE Comput. Graph. Appl. 2020, 40, 40–55. [Google Scholar] [CrossRef]
- Abualigah, L.; Almotairi, K.H.; Elaziz, M.A. Multilevel thresholding image segmentation using meta-heuristic optimization algorithms: Comparative analysis, open challenges and new trends. Appl. Intell. 2023, 53, 11654–11704. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl. Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Rocca, P.; Oliveri, G.; Massa, A. Differential evolution as applied to electromagnetics. IEEE Antennas Propag. Mag. 2011, 53, 38–49. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Khodadadi, N.; Barshandeh, S.; Trojovský, P.; Gharehchopogh, F.S.; El-kenawy, E.S.M.; Mirjalili, S. Puma optimizer (PO): A novel metaheuristic optimization algorithm and its application in machine learning. Clust. Comput. 2024, 27, 5235–5283. [Google Scholar] [CrossRef]
- Ghiaskar, A.; Amiri, A.; Mirjalili, S. Polar fox optimization algorithm: A novel meta-heuristic algorithm. Neural Comput. Appl. 2024, 36, 20983–21022. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z.; Fan, H.; Zhang, J.; Mirjalili, S.; Cao, Q. Electric eel foraging optimization: A new bio-inspired optimizer for engineering applications. Expert Syst. Appl. 2024, 238, 122200. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Awadallah, M.A.; Braik, M.S.; Makhadmeh, S.; Doush, I.A. Elk herd optimizer: A novel nature-inspired metaheuristic algorithm. Artif. Intell. Rev. 2024, 57, 48. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl. Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T. Water evaporation optimization: A novel physically inspired optimization algorithm. Comput. Struct. 2016, 167, 69–85. [Google Scholar] [CrossRef]
- Zhang, H.; San, H.; Sun, H.; Ding, L.; Wu, X. A novel optimization method: Wave search algorithm. J. Supercomput. 2024, 80, 16824–16859. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Abd Elazeem, A.M. Convex combination search algorithm: A novel metaheuristic optimization algorithm for solving global optimization and engineering design problems. J. Eng. Res. 2024, 13, 2320–2339. [Google Scholar] [CrossRef]
- Khouni, S.E.; Menacer, T. Nizar optimization algorithm: A novel metaheuristic algorithm for global optimization and engineering applications: SE Khouni, T. Menacer. J. Supercomput. 2024, 80, 3229–3281. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Moosavi, S.H.S.; Bardsiri, V.K. Poor and rich optimization algorithm: A new human-based and multi populations algorithm. Eng. Appl. Artif. Intell. 2019, 86, 165–181. [Google Scholar] [CrossRef]
- Shabani, A.; Asgarian, B.; Salido, M.; Gharebaghi, S.A. Search and rescue optimization algorithm: A new optimization method for solving constrained engineering optimization problems. Expert Syst. Appl. 2020, 161, 113698. [Google Scholar] [CrossRef]
- Matoušová, I.; Trojovský, P.; Dehghani, M.; Trojovská, E.; Kostra, J. Mother optimization algorithm: A new human-based metaheuristic approach for solving engineering optimization. Sci. Rep. 2023, 13, 10312. [Google Scholar] [CrossRef]
- Ni, L.; Ping, Y.; Yao, N.; Jiao, J.; Wang, G. Literature research optimizer: A new human-based metaheuristic algorithm for optimization problems. Arab. J. Sci. Eng. 2024, 49, 12817–12865. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G.; Ma, L.; Zhu, T.; Wu, X.; Heidari, A.A.; Chen, H. Parrot optimizer: Algorithm and applications to medical problems. Comput. Biol. Med. 2024, 172, 108064. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Wu, Z.; Chen, H. Artemisinin optimization based on malaria therapy: Algorithm and applications to medical image segmentation. Displays 2024, 84, 102740. [Google Scholar] [CrossRef]
- Das, A.; Namtirtha, A.; Dutta, A. Lévy–Cauchy arithmetic optimization algorithm combined with rough K-means for image segmentation. Appl. Soft Comput. 2023, 140, 110268. [Google Scholar] [CrossRef]
- Qiao, L.; Liu, K.; Xue, Y.; Tang, W.; Salehnia, T. A multi-level thresholding image segmentation method using hybrid Arithmetic Optimization and Harris Hawks Optimizer algorithms. Expert Syst. Appl. 2024, 241, 122316. [Google Scholar] [CrossRef]
- Chen, D.; Ge, Y.; Wan, Y.; Deng, Y.; Chen, Y.; Zou, F. Poplar optimization algorithm: A new meta-heuristic optimization technique for numerical optimization and image segmentation. Expert Syst. Appl. 2022, 200, 117118. [Google Scholar] [CrossRef]
- Houssein, E.H.; Abdalkarim, N.; Hussain, K.; Mohamed, E. Accurate multilevel thresholding image segmentation via oppositional Snake Optimization algorithm: Real cases with liver disease. Comput. Biol. Med. 2024, 169, 107922. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yu, F.; Wang, D.; Liu, T.; Hu, R. Multi-threshold segmentation of breast cancer images based on improved dandelion optimization algorithm. J. Supercomput. 2024, 80, 3849–3874. [Google Scholar] [CrossRef]
- Wang, J.; Bei, J.; Song, H.; Zhang, H.; Zhang, P. A whale optimization algorithm with combined mutation and removing similarity for global optimization and multilevel thresholding image segmentation. Appl. Soft Comput. 2023, 137, 110130. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern goshawk optimization: A new swarm-based algorithm for solving optimization problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Liang, Y.; Hu, X.; Hu, G.; Dou, W. An enhanced northern goshawk optimization algorithm and its application in practical optimization problems. Mathematics 2022, 10, 4383. [Google Scholar] [CrossRef]
- Yang, F.; Jiang, H.; Lyu, L. Multi-strategy fusion improved Northern Goshawk optimizer is used for engineering problems and UAV path planning. Sci. Rep. 2024, 14, 23300. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Lin, S.; Zhang, Z.; Deng, Q. Differential evolution based on two-stage mutation strategy and multi-stage parameter control. Appl. Soft Comput. 2025, 180, 113387. [Google Scholar] [CrossRef]
- Li, M.; Wang, J.; Deng, S.; Zhao, Y.; Li, Y. Enhanced black widow optimization algorithm incorporating food sufficiency strategy and differential mutation strategy for feature selection of high-dimensional data. Expert Syst. Appl. 2025, 290, 128506. [Google Scholar] [CrossRef]
- Liu, X.; Li, G.; Yang, H.; Zhang, N.; Wang, L.; Shao, P. Agricultural UAV trajectory planning by incorporating multi-mechanism improved grey wolf optimization algorithm. Expert Syst. Appl. 2023, 233, 120946. [Google Scholar] [CrossRef]
- Wang, J.; Fan, J.; Zhang, X.; Qian, B. Adaptive Nonlinear Bernstein-Guided Parrot Optimizer for Mural Image Segmentation. Biomimetics 2025, 10, 482. [Google Scholar] [CrossRef] [PubMed]
- Pahnehkolaei, S.M.A.; Alfi, A.; Machado, J.T. Analytical stability analysis of the fractional-order particle swarm optimization algorithm. Chaos Solitons Fractals 2022, 155, 111658. [Google Scholar] [CrossRef]
- Kumar, A.; Wu, G.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N.; Das, S. A test-suite of non-convex constrained optimization problems from the real-world and some baseline results. Swarm Evol. Comput. 2020, 56, 100693. [Google Scholar] [CrossRef]
- Houssein, E.H.; Helmy, B.E.D.; Oliva, D.; Elngar, A.A.; Shaban, H. A novel black widow optimization algorithm for multilevel thresholding image segmentation. Expert Syst. Appl. 2021, 167, 114159. [Google Scholar] [CrossRef]
- Abd El Aziz, M.; Ewees, A.A.; Hassanien, A.E. Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- Wang, J.; Bao, Z.; Dong, H. An Improved Northern Goshawk Optimization Algorithm for Mural Image Segmentation. Biomimetics 2025, 10, 373. [Google Scholar] [CrossRef] [PubMed]
- Xie, R.; Li, S.; Wu, F. An Improved northern goshawk optimization algorithm for feature selection. J. Bionic Eng. 2024, 21, 2034–2072. [Google Scholar] [CrossRef]
- Sallam, K.M.; Elsayed, S.M.; Chakrabortty, R.K.; Ryan, M.J. Improved multi-operator differential evolution algorithm for solving unconstrained problems. In Proceedings of the 2020 IEEE congress on evolutionary computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]







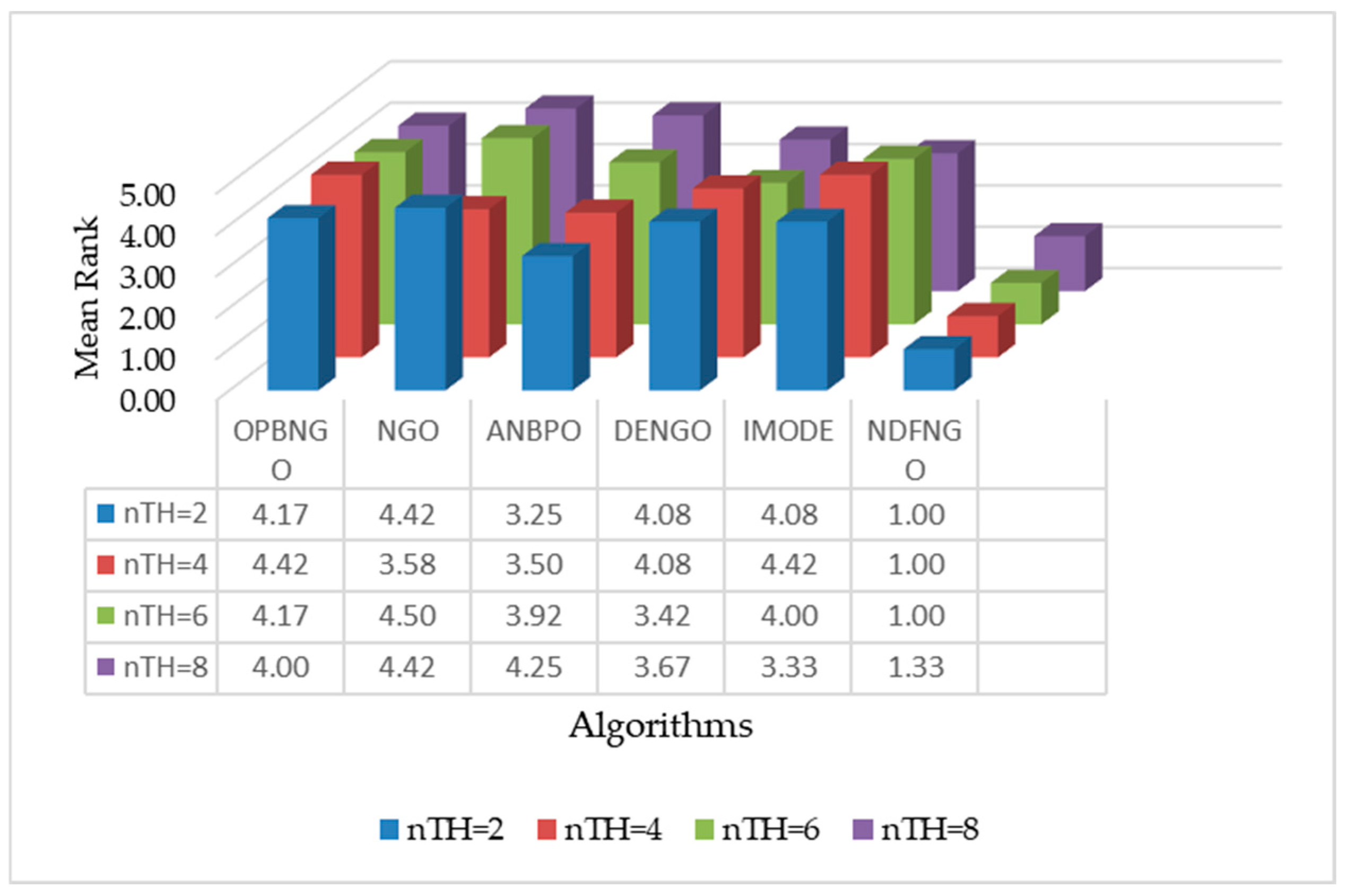


| Problems | Metrics | OPBNGO | NGO | ANBPO | DENGO | IMODE | NDFNGO |
|---|---|---|---|---|---|---|---|
| TCSDcase | Mean | 0.0131 | 0.0129 | 0.0127 | 0.0157 | 0.0142 | 0.0127 |
| Std | 9.4069 × 10−04 | 3.4657 × 10−04 | 8.3209 × 10−06 | 2.1191 × 10−03 | 1.3389 × 10−03 | 4.9656 × 10−08 | |
| WBD | Mean | 1.6821 | 1.6702 | 1.6702 | 1.9266 | 1.8660 | 1.6702 |
| Std | 3.7290 × 10−02 | 2.4247 × 10−05 | 1.8647 × 10−08 | 9.6425 × 10−02 | 9.6793 × 10−02 | 1.9340 × 10−16 | |
| TenBTD | Mean | 528.8000 | 527.3900 | 524.7400 | 558.5300 | 738.2100 | 524.4800 |
| Std | 2.9888 × 10+00 | 2.9417 × 10+00 | 3.9746 × 10−01 | 8.3592 × 10+00 | 6.8925 × 10+01 | 4.0911 × 10−02 | |
| TBTDP | Mean | 263.9000 | 263.9000 | 263.9000 | 266.4200 | 264.4100 | 263.9000 |
| Std | 2.5972 × 10−04 | 4.7756 × 10−04 | 3.1531 × 10−12 | 2.9474 × 10+00 | 6.7010 × 10−01 | 0.0000 × 10+00 |
| Image | nTH | OPBNGO | NGO | ANBPO | DENGO | IMODE | NDFNGO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | ||
| F1 | 2 | 1.868 × 10+03 | 1.436 × 10−01 | 1.812 × 10+03 | 9.825 × 10−01 | 1.750 × 10+03 | 7.935 × 10−01 | 1.741 × 10+03 | 2.075 × 10−01 | 1.857 × 10+03 | 1.280 × 10−01 | 1.921 × 10+03 | 6.792 × 10−03 |
| 4 | 1.970 × 10+03 | 8.097 × 10−01 | 1.996 × 10+03 | 7.163 × 10−01 | 1.918 × 10+03 | 1.802 × 10−01 | 1.903 × 10+03 | 5.640 × 10−01 | 1.969 × 10+03 | 5.685 × 10−01 | 2.084 × 10+03 | 2.144 × 10−03 | |
| 6 | 2.027 × 10+03 | 5.658 × 10−01 | 2.028 × 10+03 | 9.724 × 10−01 | 2.047 × 10+03 | 3.306 × 10−02 | 2.052 × 10+03 | 1.694 × 10−01 | 2.066 × 10+03 | 1.668 × 10−01 | 2.197 × 10+03 | 4.662 × 10−03 | |
| 8 | 2.125 × 10+03 | 5.934 × 10−02 | 2.147 × 10+03 | 1.576 × 10−01 | 2.107 × 10+03 | 5.240 × 10−01 | 2.174 × 10+03 | 9.556 × 10−01 | 2.169 × 10+03 | 3.412 × 10−02 | 2.170 × 10+03 | 1.220 × 10−03 | |
| F2 | 2 | 1.862 × 10+03 | 5.750 × 10−01 | 1.876 × 10+03 | 8.802 × 10−01 | 1.862 × 10+03 | 7.863 × 10−01 | 1.714 × 10+03 | 2.514 × 10−02 | 1.756 × 10+03 | 6.524 × 10−01 | 1.943 × 10+03 | 8.818 × 10−03 |
| 4 | 1.995 × 10+03 | 8.161 × 10−01 | 1.972 × 10+03 | 9.189 × 10−01 | 1.987 × 10+03 | 2.256 × 10−01 | 1.982 × 10+03 | 5.538 × 10−01 | 1.991 × 10+03 | 9.564 × 10−01 | 2.024 × 10+03 | 7.479 × 10−03 | |
| 6 | 2.009 × 10+03 | 3.430 × 10−01 | 2.004 × 10+03 | 1.678 × 10−01 | 2.049 × 10+03 | 7.734 × 10−01 | 2.038 × 10+03 | 3.866 × 10−01 | 2.016 × 10+03 | 4.290 × 10−01 | 2.148 × 10+03 | 6.244 × 10−03 | |
| 8 | 2.186 × 10+03 | 6.211 × 10−01 | 2.178 × 10+03 | 9.082 × 10−02 | 2.195 × 10+03 | 3.377 × 10−01 | 2.155 × 10+03 | 4.249 × 10−01 | 2.192 × 10+03 | 9.347 × 10−01 | 2.213 × 10+03 | 9.620 × 10−03 | |
| F3 | 2 | 1.851 × 10+03 | 6.881 × 10−01 | 1.849 × 10+03 | 8.050 × 10−01 | 1.829 × 10+03 | 5.729 × 10−01 | 1.836 × 10+03 | 6.558 × 10−01 | 1.898 × 10+03 | 5.898 × 10−01 | 1.961 × 10+03 | 5.569 × 10−03 |
| 4 | 1.949 × 10+03 | 4.491 × 10−01 | 1.984 × 10+03 | 9.164 × 10−01 | 1.988 × 10+03 | 1.916 × 10−01 | 1.955 × 10+03 | 3.579 × 10−01 | 1.938 × 10+03 | 1.699 × 10−01 | 2.058 × 10+03 | 2.752 × 10−02 | |
| 6 | 2.030 × 10+03 | 8.881 × 10−01 | 2.012 × 10+03 | 6.892 × 10−01 | 2.024 × 10+03 | 9.621 × 10−01 | 2.074 × 10+03 | 4.924 × 10−01 | 2.047 × 10+03 | 8.865 × 10−01 | 2.180 × 10+03 | 1.355 × 10−01 | |
| 8 | 2.151 × 10+03 | 7.879 × 10−01 | 2.135 × 10+03 | 5.473 × 10−01 | 2.152 × 10+03 | 2.532 × 10−01 | 2.175 × 10+03 | 1.880 × 10−01 | 2.108 × 10+03 | 6.841 × 10−01 | 2.217 × 10+03 | 1.978 × 10−01 | |
| F4 | 2 | 1.949 × 10+03 | 5.573 × 10−01 | 1.951 × 10+03 | 8.416 × 10−01 | 2.092 × 10+03 | 8.822 × 10−01 | 2.011 × 10+03 | 4.750 × 10−01 | 1.975 × 10+03 | 8.280 × 10−01 | 2.163 × 10+03 | 9.956 × 10−03 |
| 4 | 2.130 × 10+03 | 1.195 × 10−01 | 2.113 × 10+03 | 2.342 × 10−01 | 2.144 × 10+03 | 3.572 × 10−02 | 2.169 × 10+03 | 3.553 × 10−01 | 2.133 × 10+03 | 1.365 × 10−02 | 2.235 × 10+03 | 4.224 × 10−03 | |
| 6 | 2.294 × 10+03 | 7.226 × 10−01 | 2.224 × 10+03 | 3.939 × 10−01 | 2.240 × 10+03 | 7.516 × 10−02 | 2.263 × 10+03 | 5.199 × 10−01 | 2.269 × 10+03 | 4.632 × 10−01 | 2.290 × 10+03 | 1.482 × 10−03 | |
| 8 | 2.396 × 10+03 | 5.077 × 10−01 | 2.383 × 10+03 | 4.632 × 10−01 | 2.324 × 10+03 | 6.963 × 10−01 | 2.385 × 10+03 | 1.656 × 10−01 | 2.351 × 10+03 | 7.580 × 10−01 | 2.428 × 10+03 | 5.469 × 10−04 | |
| F5 | 2 | 1.939 × 10+03 | 8.780 × 10−01 | 1.932 × 10+03 | 9.665 × 10−01 | 1.943 × 10+03 | 7.130 × 10−01 | 2.046 × 10+03 | 2.864 × 10−02 | 2.072 × 10+03 | 9.764 × 10−01 | 2.178 × 10+03 | 3.565 × 10−04 |
| 4 | 2.104 × 10+03 | 6.893 × 10−03 | 2.158 × 10+03 | 6.308 × 10−01 | 2.191 × 10+03 | 3.083 × 10−01 | 2.181 × 10+03 | 8.016 × 10−01 | 2.147 × 10+03 | 3.722 × 10−01 | 2.209 × 10+03 | 7.847 × 10−03 | |
| 6 | 2.273 × 10+03 | 3.353 × 10−01 | 2.233 × 10+03 | 5.279 × 10−01 | 2.269 × 10+03 | 4.237 × 10−01 | 2.235 × 10+03 | 9.597 × 10−01 | 2.229 × 10+03 | 7.703 × 10−01 | 2.345 × 10+03 | 9.597 × 10−03 | |
| 8 | 2.307 × 10+03 | 6.411 × 10−01 | 2.370 × 10+03 | 2.398 × 10−01 | 2.354 × 10+03 | 4.410 × 10−01 | 2.304 × 10+03 | 9.145 × 10−01 | 2.315 × 10+03 | 2.322 × 10−01 | 2.426 × 10+03 | 9.472 × 10−03 | |
| F6 | 2 | 2.161 × 10+03 | 3.758 × 10−01 | 2.204 × 10+03 | 2.140 × 10−01 | 2.101 × 10+03 | 7.289 × 10−01 | 2.261 × 10+03 | 3.895 × 10−01 | 2.272 × 10+03 | 2.227 × 10−01 | 2.380 × 10+03 | 5.454 × 10−03 |
| 4 | 2.315 × 10+03 | 2.029 × 10−01 | 2.307 × 10+03 | 3.005 × 10−02 | 2.371 × 10+03 | 5.266 × 10−01 | 2.315 × 10+03 | 6.845 × 10−01 | 2.389 × 10+03 | 7.657 × 10−01 | 2.445 × 10+03 | 1.819 × 10−03 | |
| 6 | 2.418 × 10+03 | 9.388 × 10−01 | 2.483 × 10+03 | 8.073 × 10−01 | 2.469 × 10+03 | 4.836 × 10−01 | 2.472 × 10+03 | 4.621 × 10−01 | 2.474 × 10+03 | 9.264 × 10−01 | 2.513 × 10+03 | 6.420 × 10−03 | |
| 8 | 2.529 × 10+03 | 6.009 × 10−02 | 2.509 × 10+03 | 6.941 × 10−01 | 2.511 × 10+03 | 3.436 × 10−02 | 2.545 × 10+03 | 5.293 × 10−01 | 2.521 × 10+03 | 2.472 × 10−01 | 2.568 × 10+03 | 1.745 × 10−03 | |
| F7 | 2 | 1.877 × 10+03 | 7.012 × 10−01 | 1.851 × 10+03 | 2.791 × 10−01 | 1.804 × 10+03 | 7.594 × 10−01 | 1.748 × 10+03 | 5.869 × 10−01 | 1.768 × 10+03 | 7.637 × 10−01 | 1.992 × 10+03 | 9.866 × 10−03 |
| 4 | 1.987 × 10+03 | 8.641 × 10−01 | 1.996 × 10+03 | 3.896 × 10−01 | 1.908 × 10+03 | 5.693 × 10−01 | 1.961 × 10+03 | 1.467 × 10−01 | 1.973 × 10+03 | 1.008 × 10−01 | 2.045 × 10+03 | 4.586 × 10−03 | |
| 6 | 2.091 × 10+03 | 5.088 × 10−01 | 2.023 × 10+03 | 6.092 × 10−01 | 2.037 × 10+03 | 5.751 × 10−01 | 2.059 × 10+03 | 5.536 × 10−02 | 2.048 × 10+03 | 5.382 × 10−01 | 2.143 × 10+03 | 2.119 × 10−03 | |
| 8 | 2.102 × 10+03 | 9.334 × 10−01 | 2.173 × 10+03 | 2.125 × 10−01 | 2.113 × 10+03 | 9.127 × 10−01 | 2.135 × 10+03 | 6.418 × 10−01 | 2.162 × 10+03 | 1.259 × 10−01 | 2.248 × 10+03 | 4.798 × 10−01 | |
| F8 | 2 | 2.107 × 10+03 | 6.872 × 10−01 | 2.205 × 10+03 | 2.521 × 10−01 | 2.252 × 10+03 | 7.299 × 10−01 | 2.221 × 10+03 | 3.558 × 10−01 | 2.142 × 10+03 | 2.216 × 10−01 | 2.336 × 10+03 | 7.602 × 10−01 |
| 4 | 2.392 × 10+03 | 8.887 × 10−01 | 2.349 × 10+03 | 1.340 × 10−01 | 2.311 × 10+03 | 7.907 × 10−02 | 2.328 × 10+03 | 5.869 × 10−01 | 2.375 × 10+03 | 5.027 × 10−01 | 2.405 × 10+03 | 5.920 × 10−03 | |
| 6 | 2.401 × 10+03 | 2.753 × 10−01 | 2.410 × 10+03 | 2.295 × 10−01 | 2.465 × 10+03 | 4.047 × 10−01 | 2.427 × 10+03 | 6.835 × 10−02 | 2.439 × 10+03 | 6.842 × 10−01 | 2.535 × 10+03 | 2.325 × 10−03 | |
| 8 | 2.540 × 10+03 | 5.411 × 10−01 | 2.520 × 10+03 | 1.969 × 10−01 | 2.521 × 10+03 | 7.684 × 10−01 | 2.536 × 10+03 | 1.122 × 10−01 | 2.542 × 10+03 | 9.398 × 10−02 | 2.583 × 10+03 | 9.629 × 10−04 | |
| F9 | 2 | 1.798 × 10+03 | 8.340 × 10−01 | 1.716 × 10+03 | 4.649 × 10−01 | 1.890 × 10+03 | 9.573 × 10−01 | 1.874 × 10+03 | 8.512 × 10−01 | 1.798 × 10+03 | 4.318 × 10−01 | 1.970 × 10+03 | 7.397 × 10−03 |
| 4 | 1.988 × 10+03 | 2.022 × 10−01 | 1.979 × 10+03 | 3.818 × 10−01 | 1.904 × 10+03 | 2.686 × 10−01 | 1.991 × 10+03 | 9.710 × 10−01 | 1.930 × 10+03 | 9.093 × 10−01 | 2.082 × 10+03 | 2.088 × 10−03 | |
| 6 | 2.092 × 10+03 | 2.431 × 10−01 | 2.084 × 10+03 | 8.573 × 10−01 | 2.074 × 10+03 | 9.516 × 10−01 | 2.063 × 10+03 | 8.121 × 10−01 | 2.017 × 10+03 | 6.737 × 10−01 | 2.110 × 10+03 | 5.475 × 10−03 | |
| 8 | 2.120 × 10+03 | 4.479 × 10−02 | 2.124 × 10+03 | 8.606 × 10−02 | 2.193 × 10+03 | 1.661 × 10−01 | 2.190 × 10+03 | 3.003 × 10−01 | 2.117 × 10+03 | 2.418 × 10−01 | 2.263 × 10+03 | 6.940 × 10−03 | |
| F10 | 2 | 1.787 × 10+03 | 1.176 × 10−01 | 1.745 × 10+03 | 7.112 × 10−01 | 1.800 × 10+03 | 9.043 × 10−01 | 1.880 × 10+03 | 6.732 × 10−01 | 1.873 × 10+03 | 7.050 × 10−01 | 1.979 × 10+03 | 2.886 × 10−03 |
| 4 | 1.965 × 10+03 | 8.431 × 10−01 | 1.970 × 10+03 | 5.963 × 10−01 | 1.991 × 10+03 | 3.374 × 10−01 | 1.993 × 10+03 | 8.791 × 10−01 | 1.970 × 10+03 | 7.548 × 10−01 | 2.074 × 10+03 | 4.712 × 10−04 | |
| 6 | 2.043 × 10+03 | 9.635 × 10−01 | 2.005 × 10+03 | 7.618 × 10−01 | 2.049 × 10+03 | 6.476 × 10−03 | 2.025 × 10+03 | 2.741 × 10−01 | 2.056 × 10+03 | 7.356 × 10−01 | 2.144 × 10+03 | 2.077 × 10−03 | |
| 8 | 2.176 × 10+03 | 7.049 × 10−01 | 2.133 × 10+03 | 7.790 × 10−01 | 2.167 × 10+03 | 4.048 × 10−02 | 2.166 × 10+03 | 5.768 × 10−01 | 2.113 × 10+03 | 3.084 × 10−01 | 2.247 × 10+03 | 8.322 × 10−03 | |
| F11 | 2 | 2.035 × 10+03 | 3.069 × 10−01 | 1.968 × 10+03 | 4.495 × 10−01 | 2.003 × 10+03 | 1.254 × 10−01 | 2.074 × 10+03 | 7.945 × 10−01 | 1.990 × 10+03 | 1.179 × 10−01 | 2.199 × 10+03 | 9.718 × 10−03 |
| 4 | 2.187 × 10+03 | 6.189 × 10−01 | 2.136 × 10+03 | 4.831 × 10−01 | 2.132 × 10+03 | 1.130 × 10−01 | 2.176 × 10+03 | 8.028 × 10−01 | 2.146 × 10+03 | 8.088 × 10−01 | 2.211 × 10+03 | 3.010 × 10−03 | |
| 6 | 2.215 × 10+03 | 7.368 × 10−01 | 2.246 × 10+03 | 5.242 × 10−01 | 2.237 × 10+03 | 7.779 × 10−01 | 2.213 × 10+03 | 3.877 × 10−01 | 2.273 × 10+03 | 3.829 × 10−01 | 2.335 × 10+03 | 2.053 × 10−03 | |
| 8 | 2.349 × 10+03 | 9.694 × 10−01 | 2.341 × 10+03 | 1.088 × 10−01 | 2.358 × 10+03 | 3.607 × 10−01 | 2.355 × 10+03 | 4.397 × 10−01 | 2.348 × 10+03 | 4.817 × 10−01 | 2.478 × 10+03 | 2.227 × 10−03 | |
| F12 | 2 | 2.093 × 10+03 | 1.576 × 10−01 | 2.010 × 10+03 | 4.318 × 10−01 | 1.906 × 10+03 | 7.553 × 10−01 | 1.912 × 10+03 | 7.941 × 10−01 | 1.932 × 10+03 | 2.295 × 10−01 | 2.135 × 10+03 | 2.729 × 10−03 |
| 4 | 2.103 × 10+03 | 9.795 × 10−01 | 2.144 × 10+03 | 3.142 × 10−01 | 2.107 × 10+03 | 9.070 × 10−01 | 2.131 × 10+03 | 2.514 × 10−02 | 2.140 × 10+03 | 8.637 × 10−01 | 2.273 × 10+03 | 3.783 × 10−04 | |
| 6 | 2.217 × 10+03 | 4.049 × 10−01 | 2.223 × 10+03 | 7.166 × 10−01 | 2.294 × 10+03 | 9.043 × 10−01 | 2.266 × 10+03 | 9.975 × 10−01 | 2.204 × 10+03 | 6.749 × 10−01 | 2.348 × 10+03 | 3.577 × 10−03 | |
| 8 | 2.302 × 10+03 | 3.994 × 10−01 | 2.355 × 10+03 | 9.461 × 10−01 | 2.350 × 10+03 | 8.854 × 10−01 | 2.356 × 10+03 | 7.773 × 10−02 | 2.358 × 10+03 | 4.363 × 10−01 | 2.410 × 10+03 | 8.887 × 10−03 | |
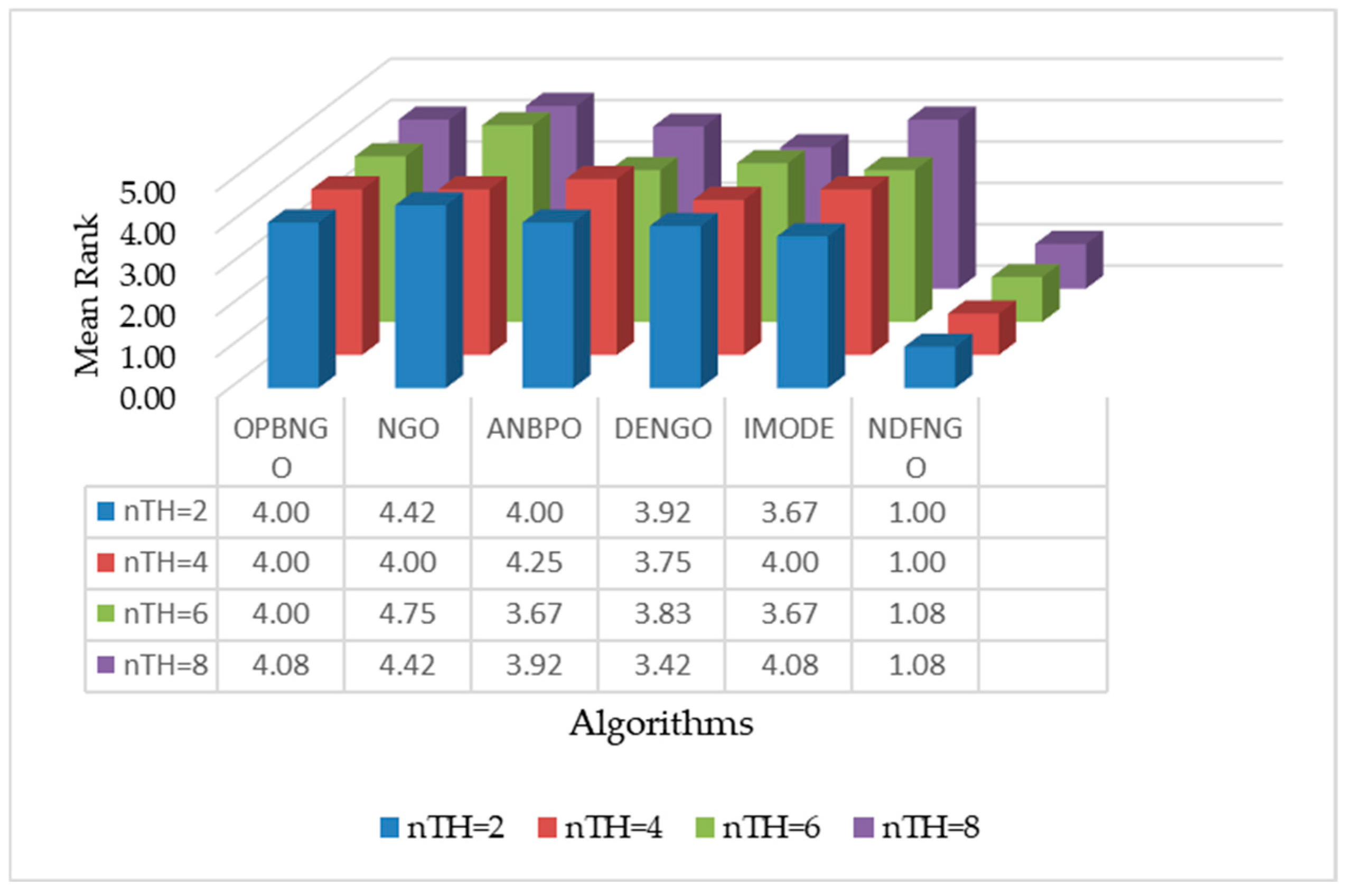
| Mean Rank | 3.98 | 4.38 | 4.00 | 3.75 | 3.88 | 1.02 | |||||||
| Final Rank | 4 | 6 | 5 | 2 | 3 | 1 | |||||||
| Image | nTH | OPBNGO vs. NDFNGO | NGO vs. NDFNGO | ANBPO vs. NDFNGO | DENGO vs. NDFNGO | IMODE vs. NDFNGO |
|---|---|---|---|---|---|---|
| F1 | 2 | 6.768 × 10−10/− | 5.970 × 10−10/− | 7.815 × 10−10/− | 1.821 × 10−10/− | 8.752 × 10−10/− |
| 4 | 1.009 × 10−04/− | 5.269 × 10−10/− | 9.154 × 10−10/− | 9.663 × 10−10/− | 2.014 × 10−10/− | |
| 6 | 4.964 × 10−05/− | 6.541 × 10−06/− | 9.043 × 10−06/− | 3.130 × 10−06/− | 7.145 × 10−10/− | |
| 8 | 5.496 × 10−05/− | 8.184 × 10−06/− | 4.362 × 10−10/− | 2.339 × 10−10/+ | 6.732 × 10−10/− | |
| F2 | 2 | 5.800 × 10−05/− | 4.235 × 10−06/− | 2.855 × 10−10/− | 4.548 × 10−10/− | 5.287 × 10−10/− |
| 4 | 6.651 × 10−10/− | 8.678 × 10−06/− | 7.210 × 10−05/− | 1.211 × 10−05/− | 8.546 × 10−10/− | |
| 6 | 4.902 × 10−10/− | 7.429 × 10−06/− | 6.244 × 10−05/− | 5.811 × 10−05/− | 3.985 × 10−07/− | |
| 8 | 7.795 × 10−10/− | 4.103 × 10−06/− | 6.097 × 10−05/− | 9.278 × 10−05/− | 3.547 × 10−07/− | |
| F3 | 2 | 6.890 × 10−04/− | 5.746 × 10−05/− | 4.020 × 10−05/− | 1.340 × 10−04/− | 5.096 × 10−07/− |
| 4 | 5.425 × 10−04/− | 3.041 × 10−05/− | 3.204 × 10−05/− | 8.372 × 10−04/− | 6.602 × 10−07/− | |
| 6 | 9.998 × 10−04/− | 1.318 × 10−05/− | 2.000 × 10−05/− | 5.841 × 10−04/− | 3.815 × 10−07/− | |
| 8 | 8.336 × 10−04/− | 4.741 × 10−05/− | 2.463 × 10−05/− | 6.398 × 10−04/− | 7.777 × 10−07/− | |
| F4 | 2 | 9.327 × 10−04/− | 7.407 × 10−05/− | 4.719 × 10−05/− | 4.397 × 10−04/− | 6.950 × 10−07/− |
| 4 | 1.576 × 10−04/− | 1.543 × 10−05/− | 4.274 × 10−10/− | 8.568 × 10−05/− | 5.593 × 10−07/− | |
| 6 | 8.087 × 10−04/+ | 9.178 × 10−05/− | 9.226 × 10−10/− | 3.189 × 10−05/− | 3.066 × 10−07/− | |
| 8 | 1.939 × 10−04/− | 5.563 × 10−05/− | 8.574 × 10−10/− | 6.928 × 10−05/− | 7.088 × 10−07/− | |
| F5 | 2 | 5.961 × 10−04/− | 4.737 × 10−05/− | 6.143 × 10−10/− | 6.619 × 10−05/− | 1.677 × 10−07/− |
| 4 | 2.461 × 10−04/− | 5.283 × 10−05/− | 6.545 × 10−10/− | 2.468 × 10−05/− | 5.735 × 10−10/− | |
| 6 | 6.708 × 10−04/− | 9.241 × 10−05/− | 1.306 × 10−10/− | 5.330 × 10−05/− | 2.343 × 10−10/− | |
| 8 | 4.392 × 10−04/− | 5.346 × 10−10/− | 9.048 × 10−10/− | 4.552 × 10−05/− | 7.910 × 10−10/− | |
| F6 | 2 | 4.226 × 10−10/− | 8.761 × 10−10/− | 7.729 × 10−10/− | 1.479 × 10−10/− | 5.520 × 10−10/− |
| 4 | 8.601 × 10−07/− | 5.520 × 10−10/− | 3.985 × 10−10/− | 6.545 × 10−10/− | 5.664 × 10−10/− | |
| 6 | 6.797 × 10−10/− | 6.848 × 10−10/− | 5.301 × 10−10/− | 5.554 × 10−06/− | 9.956 × 10−10/− | |
| 8 | 5.673 × 10−10/− | 8.398 × 10−10/− | 6.438 × 10−10/− | 6.184 × 10−06/− | 8.317 × 10−10/− | |
| F7 | 2 | 5.487 × 10−10/− | 9.152 × 10−10/− | 2.375 × 10−07/− | 6.693 × 10−05/− | 8.524 × 10−10/− |
| 4 | 9.462 × 10−08/− | 5.946 × 10−10/− | 2.533 × 10−07/− | 1.262 × 10−05/− | 8.839 × 10−06/− | |
| 6 | 3.607 × 10−07/− | 6.821 × 10−10/− | 9.543 × 10−07/− | 2.492 × 10−05/− | 1.915 × 10−05/− | |
| 8 | 9.173 × 10−06/− | 3.377 × 10−10/− | 2.815 × 10−07/− | 9.841 × 10−05/− | 9.577 × 10−06/− | |
| F8 | 2 | 4.857 × 10−06/− | 4.467 × 10−10/− | 2.923 × 10−07/− | 9.620 × 10−05/− | 1.119 × 10−05/− |
| 4 | 5.545 × 10−06/− | 5.971 × 10−10/− | 4.307 × 10−07/− | 6.637 × 10−06/− | 8.165 × 10−05/− | |
| 6 | 3.727 × 10−06/− | 3.718 × 10−10/− | 3.143 × 10−07/− | 9.411 × 10−05/− | 5.706 × 10−05/− | |
| 8 | 5.594 × 10−06/− | 9.423 × 10−10/− | 4.912 × 10−07/− | 4.912 × 10−05/− | 6.574 × 10−05/− | |
| F9 | 2 | 4.342 × 10−06/− | 2.374 × 10−10/− | 9.563 × 10−07/− | 7.432 × 10−06/− | 7.277 × 10−05/− |
| 4 | 8.214 × 10−06/− | 6.600 × 10−10/− | 6.054 × 10−07/− | 1.705 × 10−05/− | 6.248 × 10−05/− | |
| 6 | 1.521 × 10−06/− | 7.999 × 10−10/− | 4.454 × 10−10/− | 2.383 × 10−06/− | 8.007 × 10−05/− | |
| 8 | 5.334 × 10−06/− | 2.365 × 10−10/− | 2.270 × 10−10/− | 9.035 × 10−05/− | 2.421 × 10−05/− | |
| F10 | 2 | 5.834 × 10−06/− | 4.431 × 10−10/− | 7.957 × 10−10/− | 1.602 × 10−05/− | 1.460 × 10−05/− |
| 4 | 1.972 × 10−06/− | 2.486 × 10−10/− | 8.996 × 10−10/− | 4.881 × 10−04/− | 5.905 × 10−10/− | |
| 6 | 9.924 × 10−10/− | 7.601 × 10−10/− | 8.215 × 10−10/− | 1.301 × 10−04/− | 6.759 × 10−10/− | |
| 8 | 4.997 × 10−05/− | 9.604 × 10−10/− | 4.964 × 10−06/− | 8.388 × 10−04/− | 5.952 × 10−05/− | |
| F11 | 2 | 7.541 × 10−05/− | 1.503 × 10−10/− | 5.368 × 10−07/− | 7.290 × 10−04/− | 9.979 × 10−05/− |
| 4 | 4.837 × 10−05/− | 1.839 × 10−10/− | 7.881 × 10−07/− | 1.769 × 10−04/− | 7.884 × 10−05/− | |
| 6 | 3.215 × 10−05/− | 6.485 × 10−10/− | 5.249 × 10−07/− | 1.602 × 10−04/− | 2.874 × 10−05/− | |
| 8 | 9.189 × 10−05/− | 7.684 × 10−10/− | 9.614 × 10−07/− | 1.202 × 10−04/− | 9.669 × 10−05/− | |
| F12 | 2 | 3.791 × 10−05/− | 4.255 × 10−10/− | 3.207 × 10−07/− | 1.316 × 10−04/− | 4.115 × 10−05/− |
| 4 | 4.003 × 10−05/− | 4.406 × 10−10/− | 9.963 × 10−10/− | 3.056 × 10−04/− | 8.660 × 10−05/− | |
| 6 | 9.109 × 10−10/− | 5.117 × 10−10/− | 1.869 × 10−10/− | 4.933 × 10−04/− | 6.586 × 10−05/− | |
| 8 | 4.418 × 10−10/− | 2.650 × 10−10/− | 6.791 × 10−10/− | 2.754 × 10−10/− | 6.336 × 10−10/− | |
| +/−/= | 1/47/0 | 0/48/0 | 0/48/0 | 1/47/0 | 0/48/0 |
| Image | nTH | OPBNGO | NGO | ANBPO | DENGO | IMODE | NDFNGO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | ||
| F1 | 2 | 18.740 | 3.977 × 10−03 | 18.584 | 7.881 × 10−03 | 18.260 | 2.908 × 10−03 | 18.395 | 4.023 × 10−03 | 18.863 | 5.322 × 10−03 | 19.930 | 9.388 × 10−03 |
| 4 | 23.087 | 1.199 × 10−03 | 23.874 | 5.939 × 10−03 | 23.669 | 5.717 × 10−03 | 23.896 | 3.082 × 10−03 | 23.573 | 2.457 × 10−03 | 24.483 | 1.262 × 10−03 | |
| 6 | 25.571 | 9.486 × 10−03 | 25.388 | 3.049 × 10−03 | 25.347 | 5.440 × 10−03 | 25.632 | 5.732 × 10−03 | 25.319 | 2.779 × 10−03 | 26.897 | 4.736 × 10−03 | |
| 8 | 26.711 | 9.164 × 10−03 | 26.033 | 3.990 × 10−03 | 26.963 | 3.884 × 10−03 | 26.127 | 6.187 × 10−03 | 26.978 | 5.777 × 10−03 | 26.903 | 9.847 × 10−03 | |
| F2 | 2 | 18.028 | 1.689 × 10−03 | 18.026 | 5.161 × 10−03 | 18.385 | 9.102 × 10−03 | 18.360 | 7.021 × 10−03 | 18.702 | 4.119 × 10−03 | 19.803 | 3.654 × 10−03 |
| 4 | 23.752 | 8.943 × 10−03 | 23.633 | 7.519 × 10−03 | 23.485 | 8.122 × 10−03 | 23.848 | 2.559 × 10−03 | 23.731 | 3.547 × 10−03 | 24.577 | 2.434 × 10−03 | |
| 6 | 25.704 | 4.504 × 10−03 | 25.673 | 8.605 × 10−03 | 25.095 | 9.918 × 10−03 | 25.404 | 1.644 × 10−03 | 25.196 | 8.970 × 10−03 | 26.753 | 2.334 × 10−03 | |
| 8 | 27.036 | 5.091 × 10−03 | 27.659 | 9.706 × 10−03 | 27.757 | 3.058 × 10−03 | 27.119 | 6.987 × 10−03 | 27.540 | 2.464 × 10−03 | 28.444 | 7.874 × 10−03 | |
| F3 | 2 | 18.367 | 2.394 × 10−03 | 18.745 | 1.004 × 10−03 | 18.724 | 6.973 × 10−03 | 18.104 | 4.351 × 10−03 | 18.275 | 3.271 × 10−03 | 19.510 | 4.487 × 10−03 |
| 4 | 23.964 | 4.988 × 10−03 | 23.297 | 6.722 × 10−03 | 23.952 | 9.500 × 10−03 | 23.192 | 7.664 × 10−03 | 23.986 | 5.542 × 10−03 | 24.519 | 6.265 × 10−03 | |
| 6 | 25.806 | 8.541 × 10−03 | 25.925 | 5.226 × 10−03 | 25.385 | 9.534 × 10−03 | 25.997 | 9.863 × 10−03 | 25.751 | 4.506 × 10−03 | 26.922 | 8.833 × 10−03 | |
| 8 | 27.111 | 8.135 × 10−03 | 27.197 | 8.807 × 10−03 | 27.256 | 6.910 × 10−03 | 27.742 | 1.761 × 10−03 | 27.871 | 3.920 × 10−03 | 28.137 | 8.118 × 10−03 | |
| F4 | 2 | 19.544 | 1.408 × 10−03 | 19.389 | 1.122 × 10−03 | 19.295 | 1.050 × 10−03 | 19.836 | 5.128 × 10−03 | 19.168 | 1.118 × 10−03 | 21.361 | 6.479 × 10−03 |
| 4 | 24.332 | 2.093 × 10−03 | 24.637 | 6.099 × 10−03 | 24.611 | 2.687 × 10−03 | 24.550 | 9.764 × 10−03 | 24.467 | 9.418 × 10−03 | 26.913 | 2.608 × 10−03 | |
| 6 | 26.665 | 3.485 × 10−03 | 26.133 | 8.306 × 10−03 | 26.031 | 1.766 × 10−03 | 26.781 | 5.883 × 10−03 | 26.637 | 5.868 × 10−03 | 28.095 | 2.407 × 10−03 | |
| 8 | 27.287 | 8.737 × 10−03 | 27.659 | 4.683 × 10−03 | 27.037 | 8.229 × 10−03 | 27.210 | 2.982 × 10−03 | 27.634 | 7.117 × 10−03 | 29.470 | 7.463 × 10−03 | |
| F5 | 2 | 19.131 | 5.772 × 10−03 | 19.620 | 6.167 × 10−03 | 19.272 | 4.066 × 10−03 | 19.669 | 9.460 × 10−03 | 19.775 | 1.141 × 10−03 | 20.477 | 1.123 × 10−03 |
| 4 | 24.819 | 9.830 × 10−03 | 24.433 | 8.877 × 10−03 | 24.787 | 2.436 × 10−03 | 24.229 | 2.065 × 10−03 | 24.021 | 5.482 × 10−03 | 25.328 | 2.462 × 10−03 | |
| 6 | 26.064 | 8.485 × 10−03 | 26.983 | 7.877 × 10−03 | 26.523 | 6.567 × 10−03 | 26.407 | 5.778 × 10−03 | 26.831 | 4.257 × 10−03 | 28.899 | 7.470 × 10−03 | |
| 8 | 27.612 | 5.820 × 10−03 | 27.283 | 7.196 × 10−03 | 27.823 | 3.544 × 10−03 | 27.409 | 9.456 × 10−03 | 27.996 | 2.001 × 10−03 | 29.174 | 8.352 × 10−03 | |
| F6 | 2 | 16.247 | 1.419 × 10−03 | 16.010 | 8.873 × 10−03 | 16.775 | 4.131 × 10−03 | 16.159 | 6.590 × 10−03 | 16.521 | 4.508 × 10−03 | 17.314 | 7.155 × 10−03 |
| 4 | 23.527 | 9.483 × 10−03 | 23.735 | 5.313 × 10−03 | 23.059 | 2.197 × 10−03 | 23.355 | 6.979 × 10−03 | 23.177 | 9.638 × 10−03 | 24.701 | 2.858 × 10−03 | |
| 6 | 25.236 | 7.530 × 10−03 | 25.398 | 7.872 × 10−03 | 25.172 | 2.275 × 10−03 | 25.136 | 5.614 × 10−03 | 25.582 | 6.636 × 10−03 | 26.209 | 8.357 × 10−03 | |
| 8 | 27.870 | 1.563 × 10−03 | 27.941 | 5.529 × 10−03 | 27.486 | 9.678 × 10−03 | 27.133 | 7.038 × 10−03 | 27.540 | 7.210 × 10−03 | 28.067 | 1.177 × 10−03 | |
| F7 | 2 | 16.283 | 3.659 × 10−03 | 16.331 | 7.071 × 10−03 | 16.604 | 8.342 × 10−03 | 16.724 | 1.438 × 10−03 | 16.105 | 1.803 × 10−03 | 17.490 | 7.132 × 10−03 |
| 4 | 25.974 | 6.356 × 10−03 | 25.938 | 8.980 × 10−03 | 25.583 | 7.020 × 10−03 | 25.918 | 4.344 × 10−03 | 25.782 | 2.150 × 10−03 | 26.634 | 8.617 × 10−03 | |
| 6 | 26.431 | 8.506 × 10−03 | 26.535 | 4.678 × 10−03 | 26.557 | 5.776 × 10−03 | 26.063 | 8.619 × 10−03 | 26.350 | 1.963 × 10−03 | 27.595 | 4.362 × 10−03 | |
| 8 | 27.606 | 9.900 × 10−03 | 27.979 | 9.828 × 10−03 | 27.739 | 8.358 × 10−03 | 27.100 | 1.276 × 10−03 | 27.222 | 9.397 × 10−03 | 28.600 | 5.510 × 10−03 | |
| F8 | 2 | 19.117 | 9.172 × 10−03 | 19.158 | 9.442 × 10−03 | 19.750 | 8.952 × 10−03 | 19.632 | 1.987 × 10−03 | 19.508 | 5.709 × 10−03 | 20.693 | 3.080 × 10−03 |
| 4 | 23.029 | 6.384 × 10−03 | 23.340 | 7.239 × 10−03 | 23.522 | 1.259 × 10−03 | 23.024 | 7.986 × 10−03 | 23.169 | 6.014 × 10−03 | 24.588 | 9.057 × 10−03 | |
| 6 | 25.009 | 5.526 × 10−03 | 25.620 | 9.646 × 10−03 | 25.446 | 6.696 × 10−03 | 25.856 | 4.924 × 10−03 | 25.962 | 9.393 × 10−03 | 26.196 | 1.679 × 10−03 | |
| 8 | 27.804 | 9.456 × 10−03 | 27.458 | 5.785 × 10−03 | 27.033 | 9.006 × 10−03 | 27.270 | 4.701 × 10−03 | 27.208 | 6.189 × 10−03 | 28.786 | 4.989 × 10−03 | |
| F9 | 2 | 18.588 | 2.863 × 10−03 | 18.831 | 1.265 × 10−03 | 18.596 | 1.495 × 10−03 | 18.042 | 9.795 × 10−03 | 18.420 | 8.571 × 10−03 | 19.955 | 3.574 × 10−03 |
| 4 | 23.845 | 2.057 × 10−03 | 23.020 | 5.619 × 10−03 | 23.033 | 2.687 × 10−03 | 23.043 | 2.759 × 10−03 | 23.318 | 6.995 × 10−03 | 24.136 | 1.885 × 10−03 | |
| 6 | 25.074 | 2.949 × 10−03 | 25.371 | 2.587 × 10−03 | 25.953 | 9.613 × 10−03 | 25.240 | 5.578 × 10−03 | 25.723 | 7.670 × 10−03 | 26.263 | 7.776 × 10−03 | |
| 8 | 26.616 | 4.596 × 10−03 | 26.240 | 9.472 × 10−03 | 26.714 | 2.008 × 10−03 | 26.713 | 4.985 × 10−03 | 26.082 | 4.613 × 10−03 | 27.131 | 1.313 × 10−03 | |
| F10 | 2 | 18.629 | 9.938 × 10−03 | 18.499 | 6.434 × 10−03 | 18.959 | 1.260 × 10−03 | 18.678 | 9.045 × 10−03 | 18.255 | 5.914 × 10−03 | 19.629 | 1.118 × 10−03 |
| 4 | 23.667 | 4.888 × 10−03 | 23.436 | 2.346 × 10−03 | 23.557 | 7.938 × 10−03 | 23.745 | 5.932 × 10−03 | 23.948 | 6.893 × 10−03 | 24.124 | 9.246 × 10−03 | |
| 6 | 25.100 | 5.099 × 10−03 | 25.134 | 9.112 × 10−03 | 25.167 | 3.160 × 10−03 | 25.714 | 5.315 × 10−03 | 25.808 | 1.290 × 10−03 | 26.482 | 5.727 × 10−03 | |
| 8 | 27.046 | 2.120 × 10−03 | 27.635 | 8.370 × 10−03 | 27.773 | 5.928 × 10−03 | 27.577 | 6.364 × 10−03 | 27.239 | 4.581 × 10−03 | 28.069 | 3.847 × 10−03 | |
| F11 | 2 | 19.382 | 6.028 × 10−03 | 19.303 | 8.501 × 10−03 | 19.146 | 5.598 × 10−03 | 19.124 | 6.840 × 10−03 | 19.681 | 7.951 × 10−03 | 21.043 | 9.335 × 10−03 |
| 4 | 24.645 | 6.346 × 10−03 | 24.005 | 3.209 × 10−03 | 24.306 | 3.539 × 10−03 | 24.395 | 7.568 × 10−03 | 24.885 | 4.317 × 10−03 | 26.187 | 8.201 × 10−03 | |
| 6 | 26.622 | 9.302 × 10−03 | 26.265 | 7.334 × 10−03 | 26.864 | 5.853 × 10−03 | 26.319 | 5.527 × 10−03 | 26.150 | 8.444 × 10−03 | 28.217 | 9.467 × 10−03 | |
| 8 | 27.820 | 9.381 × 10−03 | 27.817 | 3.474 × 10−03 | 27.869 | 7.291 × 10−03 | 27.384 | 8.049 × 10−03 | 27.203 | 7.090 × 10−03 | 29.103 | 2.735 × 10−03 | |
| F12 | 2 | 19.735 | 2.889 × 10−03 | 19.582 | 9.411 × 10−03 | 19.586 | 9.191 × 10−03 | 19.648 | 3.422 × 10−03 | 19.214 | 8.185 × 10−03 | 20.117 | 1.723 × 10−03 |
| 4 | 24.797 | 6.820 × 10−03 | 24.862 | 2.122 × 10−03 | 24.836 | 7.953 × 10−03 | 24.139 | 5.769 × 10−03 | 24.164 | 9.248 × 10−03 | 25.030 | 2.209 × 10−03 | |
| 6 | 26.931 | 8.722 × 10−03 | 26.570 | 1.063 × 10−03 | 26.743 | 8.913 × 10−03 | 26.779 | 9.137 × 10−03 | 26.958 | 3.927 × 10−03 | 28.702 | 1.666 × 10−03 | |
| 8 | 27.383 | 9.086 × 10−03 | 27.695 | 1.478 × 10−03 | 27.965 | 5.328 × 10−03 | 27.658 | 5.517 × 10−03 | 27.886 | 3.828 × 10−03 | 29.366 | 5.208 × 10−03 | |
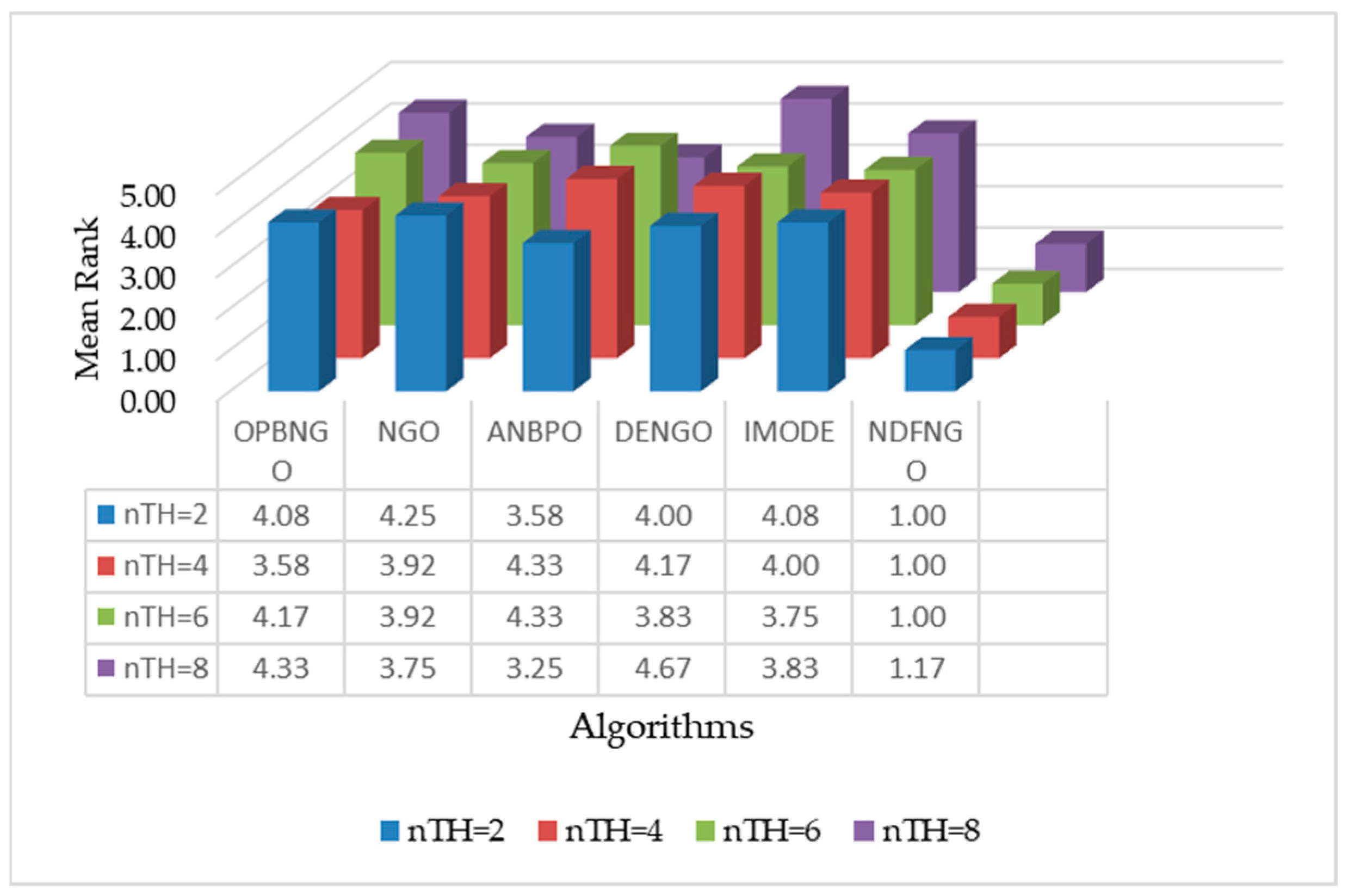
| Mean Rank | 4.04 | 3.96 | 3.88 | 4.17 | 3.92 | 1.04 | |||||||
| Final Rank | 5 | 4 | 2 | 6 | 3 | 1 | |||||||
| Image | nTH | OPBNGO vs. NDFNGO | NGO vs. NDFNGO | ANBPO vs. NDFNGO | DENGO vs. NDFNGO | IMODE vs. NDFNGO |
|---|---|---|---|---|---|---|
| F1 | 2 | 6.227 × 10−10/− | 4.000 × 10−10/− | 6.943 × 10−10/− | 5.476 × 10−10/− | 8.475 × 10−10/− |
| 4 | 3.658 × 10−04/− | 6.248 × 10−10/− | 4.594 × 10−10/− | 5.851 × 10−10/− | 7.372 × 10−10/− | |
| 6 | 2.456 × 10−05/− | 1.920 × 10−06/− | 5.586 × 10−06/− | 8.045 × 10−06/− | 7.409 × 10−10/− | |
| 8 | 4.391 × 10−05/− | 7.782 × 10−06/− | 4.876 × 10−10/+ | 3.774 × 10−10/− | 7.896 × 10−10/+ | |
| F2 | 2 | 5.189 × 10−05/− | 4.759 × 10−06/− | 3.046 × 10−10/− | 4.542 × 10−10/− | 6.647 × 10−10/− |
| 4 | 5.581 × 10−10/− | 8.226 × 10−06/− | 7.871 × 10−05/− | 3.760 × 10−05/− | 1.841 × 10−10/− | |
| 6 | 5.856 × 10−10/− | 2.737 × 10−06/− | 3.821 × 10−05/− | 9.252 × 10−05/− | 2.408 × 10−07/− | |
| 8 | 7.094 × 10−10/− | 3.090 × 10−06/− | 3.871 × 10−06/− | 1.540 × 10−05/− | 1.894 × 10−07/− | |
| F3 | 2 | 2.467 × 10−04/− | 5.733 × 10−05/− | 1.908 × 10−05/− | 2.592 × 10−04/− | 2.541 × 10−07/− |
| 4 | 1.826 × 10−04/− | 3.938 × 10−06/− | 9.751 × 10−05/− | 9.865 × 10−04/− | 2.248 × 10−07/− | |
| 6 | 5.581 × 10−04/− | 5.362 × 10−06/− | 6.444 × 10−05/− | 3.415 × 10−04/− | 5.575 × 10−07/− | |
| 8 | 4.070 × 10−04/− | 6.968 × 10−06/− | 1.327 × 10−05/− | 3.736 × 10−04/− | 1.299 × 10−07/− | |
| F4 | 2 | 7.626 × 10−04/− | 5.237 × 10−05/− | 7.128 × 10−05/− | 1.766 × 10−04/− | 6.819 × 10−08/− |
| 4 | 7.894 × 10−04/− | 7.419 × 10−05/− | 6.099 × 10−10/− | 6.034 × 10−05/− | 2.088 × 10−07/− | |
| 6 | 4.223 × 10−04/− | 1.137 × 10−05/− | 6.156 × 10−10/− | 3.999 × 10−05/− | 6.844 × 10−07/− | |
| 8 | 1.474 × 10−04/− | 7.145 × 10−05/− | 1.678 × 10−10/− | 5.138 × 10−05/− | 7.982 × 10−07/− | |
| F5 | 2 | 1.553 × 10−04/− | 7.577 × 10−05/− | 2.573 × 10−10/− | 6.225 × 10−05/− | 6.983 × 10−07/− |
| 4 | 5.668 × 10−04/− | 2.273 × 10−05/− | 6.796 × 10−10/− | 1.123 × 10−05/− | 3.283 × 10−10/− | |
| 6 | 1.653 × 10−04/− | 6.702 × 10−06/− | 4.466 × 10−10/− | 4.830 × 10−05/− | 6.802 × 10−10/− | |
| 8 | 6.424 × 10−04/− | 1.767 × 10−10/− | 3.524 × 10−10/− | 9.358 × 10−05/− | 7.495 × 10−10/− | |
| F6 | 2 | 9.336 × 10−10/− | 9.203 × 10−10/− | 1.562 × 10−10/− | 4.535 × 10−10/− | 5.522 × 10−10/− |
| 4 | 5.943 × 10−07/− | 6.846 × 10−10/− | 5.807 × 10−10/− | 2.984 × 10−10/− | 9.666 × 10−10/− | |
| 6 | 3.179 × 10−10/− | 6.919 × 10−10/− | 8.190 × 10−10/− | 1.348 × 10−05/− | 5.541 × 10−10/− | |
| 8 | 1.382 × 10−10/− | 2.420 × 10−10/− | 4.224 × 10−10/− | 4.361 × 10−05/− | 8.723 × 10−10/− | |
| F7 | 2 | 2.929 × 10−10/− | 3.919 × 10−10/− | 8.356 × 10−07/− | 9.864 × 10−05/− | 7.028 × 10−10/− |
| 4 | 1.925 × 10−06/− | 1.485 × 10−10/− | 1.557 × 10−07/− | 6.423 × 10−05/− | 8.036 × 10−05/− | |
| 6 | 4.635 × 10−06/− | 1.825 × 10−10/− | 3.525 × 10−07/− | 1.717 × 10−06/− | 8.616 × 10−05/− | |
| 8 | 9.335 × 10−06/− | 6.200 × 10−10/− | 1.425 × 10−07/− | 2.432 × 10−05/− | 6.377 × 10−05/− | |
| F8 | 2 | 1.656 × 10−06/− | 4.604 × 10−10/− | 5.185 × 10−07/− | 7.578 × 10−05/− | 5.151 × 10−06/− |
| 4 | 7.429 × 10−06/− | 3.027 × 10−10/− | 6.672 × 10−07/− | 1.661 × 10−05/− | 2.657 × 10−05/− | |
| 6 | 7.212 × 10−06/− | 2.392 × 10−10/− | 3.096 × 10−08/− | 2.404 × 10−05/− | 2.838 × 10−05/− | |
| 8 | 9.308 × 10−07/− | 2.737 × 10−10/− | 9.867 × 10−07/− | 9.853 × 10−05/− | 4.557 × 10−05/− | |
| F9 | 2 | 9.409 × 10−06/− | 4.030 × 10−10/− | 7.760 × 10−07/− | 3.073 × 10−05/− | 8.876 × 10−05/− |
| 4 | 6.255 × 10−06/− | 1.784 × 10−10/− | 7.556 × 10−07/− | 9.685 × 10−05/− | 2.780 × 10−05/− | |
| 6 | 2.068 × 10−06/− | 6.312 × 10−10/− | 8.135 × 10−10/− | 6.635 × 10−05/− | 1.755 × 10−07/− | |
| 8 | 5.262 × 10−07/− | 5.725 × 10−10/− | 2.495 × 10−10/− | 5.699 × 10−06/− | 2.281 × 10−05/− | |
| F10 | 2 | 7.615 × 10−06/− | 8.218 × 10−10/− | 4.479 × 10−10/− | 1.536 × 10−05/− | 8.488 × 10−05/− |
| 4 | 6.595 × 10−06/− | 9.858 × 10−10/− | 5.051 × 10−10/− | 2.972 × 10−04/− | 9.692 × 10−10/− | |
| 6 | 7.716 × 10−10/− | 4.751 × 10−10/− | 1.431 × 10−10/− | 7.720 × 10−05/− | 9.101 × 10−10/− | |
| 8 | 3.894 × 10−05/− | 2.338 × 10−10/− | 9.194 × 10−06/− | 2.955 × 10−04/− | 7.476 × 10−06/− | |
| F11 | 2 | 2.082 × 10−05/− | 9.971 × 10−10/− | 3.335 × 10−07/− | 6.329 × 10−04/− | 5.873 × 10−07/− |
| 4 | 4.252 × 10−05/− | 6.360 × 10−10/− | 5.328 × 10−07/− | 1.425 × 10−04/− | 9.252 × 10−05/− | |
| 6 | 2.781 × 10−05/− | 3.622 × 10−10/− | 8.685 × 10−07/− | 7.460 × 10−04/− | 4.629 × 10−05/− | |
| 8 | 7.160 × 10−05/− | 6.261 × 10−10/− | 8.480 × 10−07/− | 6.523 × 10−04/− | 1.894 × 10−05/− | |
| F12 | 2 | 4.590 × 10−05/− | 6.689 × 10−10/− | 7.575 × 10−07/− | 7.057 × 10−04/− | 4.799 × 10−05/− |
| 4 | 5.076 × 10−05/− | 6.145 × 10−10/− | 3.669 × 10−10/− | 8.402 × 10−05/− | 9.364 × 10−05/− | |
| 6 | 3.667 × 10−10/− | 7.226 × 10−10/− | 4.580 × 10−10/− | 6.273 × 10−04/− | 6.569 × 10−05/− | |
| 8 | 9.728 × 10−10/− | 7.556 × 10−10/− | 1.639 × 10−10/− | 4.486 × 10−10/− | 6.860 × 10−10/− | |
| +/−/= | 0/48/0 | 0/48/0 | 1/47/0 | 0/48/0 | 1/47/0 |
| Image | nTH | OPBNGO | NGO | ANBPO | DENGO | IMODE | NDFNGO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | ||
| F1 | 2 | 0.751 | 7.950 × 10−03 | 0.753 | 3.433 × 10−03 | 0.753 | 1.852 × 10−04 | 0.751 | 1.177 × 10−05 | 0.751 | 3.810 × 10−04 | 0.779 | 1.134 × 10−07 |
| 4 | 0.782 | 8.698 × 10−03 | 0.785 | 2.504 × 10−03 | 0.787 | 6.821 × 10−03 | 0.788 | 3.810 × 10−05 | 0.785 | 7.682 × 10−04 | 0.809 | 1.190 × 10−07 | |
| 6 | 0.823 | 8.404 × 10−03 | 0.824 | 5.478 × 10−05 | 0.823 | 1.746 × 10−03 | 0.825 | 1.839 × 10−05 | 0.828 | 3.382 × 10−05 | 0.847 | 1.095 × 10−07 | |
| 8 | 0.878 | 9.760 × 10−03 | 0.870 | 5.690 × 10−03 | 0.874 | 3.316 × 10−03 | 0.878 | 9.171 × 10−05 | 0.875 | 5.075 × 10−04 | 0.871 | 1.369 × 10−07 | |
| F2 | 2 | 0.789 | 9.689 × 10−03 | 0.783 | 6.396 × 10−03 | 0.785 | 4.980 × 10−03 | 0.788 | 7.292 × 10−05 | 0.783 | 3.794 × 10−04 | 0.808 | 1.584 × 10−07 |
| 4 | 0.802 | 3.070 × 10−03 | 0.806 | 1.814 × 10−03 | 0.803 | 3.032 × 10−03 | 0.803 | 2.409 × 10−05 | 0.803 | 9.935 × 10−04 | 0.831 | 1.826 × 10−07 | |
| 6 | 0.821 | 2.020 × 10−04 | 0.820 | 2.174 × 10−03 | 0.827 | 4.261 × 10−03 | 0.828 | 8.858 × 10−05 | 0.823 | 2.638 × 10−04 | 0.859 | 1.777 × 10−07 | |
| 8 | 0.874 | 9.518 × 10−05 | 0.878 | 3.864 × 10−03 | 0.876 | 8.013 × 10−03 | 0.877 | 4.246 × 10−05 | 0.879 | 3.790 × 10−04 | 0.892 | 1.619 × 10−07 | |
| F3 | 2 | 0.717 | 8.156 × 10−03 | 0.710 | 1.822 × 10−03 | 0.720 | 6.206 × 10−03 | 0.716 | 1.542 × 10−05 | 0.719 | 4.582 × 10−04 | 0.735 | 1.209 × 10−07 |
| 4 | 0.756 | 8.259 × 10−03 | 0.760 | 7.637 × 10−04 | 0.758 | 9.219 × 10−03 | 0.758 | 4.393 × 10−05 | 0.753 | 5.439 × 10−04 | 0.798 | 1.265 × 10−07 | |
| 6 | 0.803 | 8.630 × 10−03 | 0.803 | 3.231 × 10−03 | 0.810 | 7.398 × 10−04 | 0.808 | 5.386 × 10−05 | 0.808 | 3.395 × 10−04 | 0.836 | 1.154 × 10−07 | |
| 8 | 0.850 | 6.639 × 10−03 | 0.854 | 6.409 × 10−03 | 0.851 | 3.098 × 10−03 | 0.852 | 3.514 × 10−05 | 0.857 | 6.837 × 10−04 | 0.874 | 1.347 × 10−07 | |
| F4 | 2 | 0.732 | 2.788 × 10−03 | 0.737 | 1.524 × 10−03 | 0.736 | 6.008 × 10−03 | 0.734 | 7.786 × 10−05 | 0.739 | 1.627 × 10−04 | 0.755 | 1.140 × 10−07 |
| 4 | 0.785 | 1.853 × 10−03 | 0.787 | 8.678 × 10−03 | 0.789 | 2.051 × 10−03 | 0.782 | 5.020 × 10−07 | 0.781 | 7.109 × 10−04 | 0.802 | 1.471 × 10−07 | |
| 6 | 0.813 | 7.219 × 10−03 | 0.813 | 3.403 × 10−03 | 0.815 | 4.427 × 10−03 | 0.813 | 9.583 × 10−05 | 0.814 | 3.660 × 10−04 | 0.818 | 1.201 × 10−07 | |
| 8 | 0.857 | 7.910 × 10−03 | 0.854 | 8.079 × 10−03 | 0.851 | 2.724 × 10−03 | 0.856 | 5.531 × 10−05 | 0.858 | 6.247 × 10−04 | 0.887 | 1.155 × 10−07 | |
| F5 | 2 | 0.712 | 8.281 × 10−03 | 0.714 | 1.883 × 10−03 | 0.714 | 7.176 × 10−03 | 0.711 | 8.966 × 10−05 | 0.712 | 4.687 × 10−04 | 0.744 | 1.135 × 10−07 |
| 4 | 0.788 | 5.926 × 10−03 | 0.784 | 8.870 × 10−03 | 0.784 | 9.485 × 10−03 | 0.781 | 3.162 × 10−05 | 0.790 | 8.728 × 10−04 | 0.827 | 1.341 × 10−07 | |
| 6 | 0.817 | 3.165 × 10−03 | 0.815 | 3.926 × 10−03 | 0.819 | 3.331 × 10−03 | 0.816 | 3.877 × 10−06 | 0.814 | 9.229 × 10−04 | 0.853 | 1.898 × 10−07 | |
| 8 | 0.861 | 5.966 × 10−03 | 0.866 | 7.462 × 10−03 | 0.865 | 2.377 × 10−03 | 0.869 | 7.304 × 10−07 | 0.863 | 3.790 × 10−04 | 0.887 | 1.566 × 10−07 | |
| F6 | 2 | 0.697 | 9.118 × 10−03 | 0.690 | 5.181 × 10−03 | 0.693 | 6.915 × 10−03 | 0.694 | 7.982 × 10−05 | 0.691 | 4.393 × 10−04 | 0.721 | 1.122 × 10−07 |
| 4 | 0.758 | 5.045 × 10−03 | 0.756 | 2.334 × 10−03 | 0.756 | 8.194 × 10−03 | 0.754 | 4.318 × 10−06 | 0.760 | 9.140 × 10−05 | 0.770 | 1.694 × 10−07 | |
| 6 | 0.807 | 2.424 × 10−03 | 0.804 | 2.267 × 10−03 | 0.801 | 2.105 × 10−05 | 0.806 | 6.401 × 10−05 | 0.802 | 2.095 × 10−04 | 0.815 | 1.408 × 10−07 | |
| 8 | 0.854 | 9.479 × 10−03 | 0.856 | 6.547 × 10−03 | 0.860 | 4.310 × 10−03 | 0.857 | 3.483 × 10−05 | 0.857 | 6.980 × 10−04 | 0.862 | 1.300 × 10−07 | |
| F7 | 2 | 0.789 | 7.739 × 10−03 | 0.786 | 1.682 × 10−03 | 0.785 | 8.538 × 10−03 | 0.783 | 2.795 × 10−05 | 0.784 | 9.661 × 10−04 | 0.815 | 1.509 × 10−07 |
| 4 | 0.829 | 6.510 × 10−03 | 0.826 | 4.740 × 10−03 | 0.827 | 1.070 × 10−03 | 0.827 | 2.520 × 10−05 | 0.824 | 7.427 × 10−05 | 0.851 | 1.728 × 10−07 | |
| 6 | 0.853 | 2.337 × 10−03 | 0.860 | 4.041 × 10−03 | 0.852 | 7.489 × 10−03 | 0.856 | 1.460 × 10−05 | 0.856 | 3.945 × 10−04 | 0.881 | 1.136 × 10−07 | |
| 8 | 0.882 | 6.631 × 10−03 | 0.881 | 1.075 × 10−03 | 0.881 | 1.683 × 10−03 | 0.889 | 3.170 × 10−05 | 0.889 | 4.541 × 10−04 | 0.893 | 1.890 × 10−07 | |
| F8 | 2 | 0.796 | 8.905 × 10−03 | 0.794 | 8.621 × 10−03 | 0.797 | 8.167 × 10−03 | 0.798 | 5.150 × 10−05 | 0.794 | 4.166 × 10−04 | 0.815 | 1.618 × 10−07 |
| 4 | 0.821 | 9.278 × 10−05 | 0.828 | 5.151 × 10−03 | 0.830 | 1.295 × 10−03 | 0.827 | 3.646 × 10−05 | 0.820 | 9.612 × 10−04 | 0.840 | 1.253 × 10−07 | |
| 6 | 0.873 | 5.037 × 10−03 | 0.873 | 2.974 × 10−03 | 0.874 | 5.220 × 10−03 | 0.877 | 1.608 × 10−05 | 0.874 | 9.612 × 10−04 | 0.888 | 1.700 × 10−07 | |
| 8 | 0.898 | 4.809 × 10−03 | 0.893 | 3.357 × 10−03 | 0.891 | 9.209 × 10−03 | 0.899 | 7.477 × 10−05 | 0.893 | 3.253 × 10−04 | 0.908 | 1.086 × 10−07 | |
| F9 | 2 | 0.759 | 3.649 × 10−03 | 0.751 | 5.363 × 10−03 | 0.754 | 4.675 × 10−04 | 0.752 | 7.712 × 10−05 | 0.755 | 2.252 × 10−04 | 0.779 | 1.812 × 10−07 |
| 4 | 0.789 | 8.595 × 10−03 | 0.787 | 6.759 × 10−03 | 0.782 | 5.755 × 10−03 | 0.783 | 3.065 × 10−05 | 0.785 | 9.055 × 10−04 | 0.807 | 1.236 × 10−07 | |
| 6 | 0.826 | 4.735 × 10−03 | 0.824 | 7.296 × 10−03 | 0.824 | 9.369 × 10−03 | 0.821 | 6.452 × 10−05 | 0.826 | 4.373 × 10−04 | 0.844 | 1.804 × 10−07 | |
| 8 | 0.877 | 9.196 × 10−03 | 0.877 | 1.309 × 10−03 | 0.874 | 1.729 × 10−03 | 0.870 | 7.095 × 10−05 | 0.877 | 3.389 × 10−04 | 0.885 | 1.819 × 10−07 | |
| F10 | 2 | 0.781 | 2.626 × 10−03 | 0.782 | 4.398 × 10−03 | 0.789 | 9.497 × 10−03 | 0.787 | 8.817 × 10−05 | 0.784 | 4.307 × 10−04 | 0.796 | 1.318 × 10−07 |
| 4 | 0.805 | 7.190 × 10−03 | 0.808 | 9.170 × 10−03 | 0.806 | 4.185 × 10−03 | 0.809 | 5.003 × 10−05 | 0.807 | 1.972 × 10−04 | 0.836 | 1.385 × 10−07 | |
| 6 | 0.823 | 9.777 × 10−05 | 0.822 | 3.359 × 10−04 | 0.826 | 7.430 × 10−03 | 0.826 | 3.118 × 10−05 | 0.828 | 2.671 × 10−04 | 0.855 | 1.856 × 10−07 | |
| 8 | 0.876 | 9.270 × 10−03 | 0.871 | 1.661 × 10−03 | 0.877 | 7.127 × 10−03 | 0.871 | 2.833 × 10−05 | 0.870 | 7.263 × 10−04 | 0.891 | 1.196 × 10−07 | |
| F11 | 2 | 0.732 | 7.939 × 10−03 | 0.737 | 9.805 × 10−03 | 0.737 | 7.115 × 10−03 | 0.740 | 7.370 × 10−06 | 0.740 | 3.371 × 10−04 | 0.750 | 1.475 × 10−07 |
| 4 | 0.784 | 2.711 × 10−03 | 0.787 | 1.025 × 10−03 | 0.788 | 2.296 × 10−03 | 0.786 | 3.455 × 10−06 | 0.784 | 3.919 × 10−04 | 0.808 | 1.499 × 10−07 | |
| 6 | 0.818 | 9.556 × 10−03 | 0.815 | 9.880 × 10−03 | 0.811 | 7.018 × 10−03 | 0.815 | 8.838 × 10−05 | 0.810 | 6.729 × 10−04 | 0.843 | 1.112 × 10−07 | |
| 8 | 0.859 | 9.476 × 10−03 | 0.851 | 6.214 × 10−03 | 0.852 | 8.763 × 10−03 | 0.853 | 3.603 × 10−05 | 0.855 | 9.111 × 10−04 | 0.881 | 1.588 × 10−07 | |
| F12 | 2 | 0.713 | 7.254 × 10−03 | 0.714 | 1.814 × 10−03 | 0.714 | 2.438 × 10−03 | 0.714 | 4.095 × 10−05 | 0.711 | 1.410 × 10−04 | 0.744 | 1.327 × 10−07 |
| 4 | 0.780 | 7.708 × 10−03 | 0.784 | 4.959 × 10−03 | 0.785 | 7.831 × 10−03 | 0.786 | 9.982 × 10−05 | 0.787 | 6.447 × 10−04 | 0.825 | 1.682 × 10−07 | |
| 6 | 0.816 | 2.283 × 10−03 | 0.820 | 7.529 × 10−03 | 0.816 | 3.676 × 10−03 | 0.816 | 7.475 × 10−05 | 0.814 | 6.491 × 10−05 | 0.851 | 1.082 × 10−07 | |
| 8 | 0.863 | 5.930 × 10−03 | 0.868 | 4.612 × 10−03 | 0.870 | 6.284 × 10−03 | 0.861 | 5.028 × 10−05 | 0.869 | 2.436 × 10−04 | 0.885 | 1.578 × 10−07 | |
| Mean Rank | 4.19 | 4.23 | 3.73 | 3.81 | 3.96 | 1.08 | |||||||
| Final Rank | 5 | 6 | 2 | 3 | 4 | 1 | |||||||
| Image | nTH | OPBNGO vs. NDFNGO | NGO vs. NDFNGO | ANBPO vs. NDFNGO | DENGO vs. NDFNGO | IMODE vs. NDFNGO |
|---|---|---|---|---|---|---|
| F1 | 2 | 2.041 × 10−10/− | 3.783 × 10−10/− | 3.421 × 10−10/− | 1.126 × 10−10/− | 3.111 × 10−10/− |
| 4 | 1.795 × 10−05/− | 4.787 × 10−10/− | 8.773 × 10−10/− | 8.997 × 10−10/− | 8.592 × 10−10/− | |
| 6 | 6.442 × 10−06/− | 8.114 × 10−06/− | 3.994 × 10−06/− | 1.977 × 10−06/− | 3.842 × 10−10/− | |
| 8 | 1.329 × 10−05/+ | 2.006 × 10−06/− | 6.310 × 10−10/+ | 8.049 × 10−10/+ | 6.564 × 10−10/+ | |
| F2 | 2 | 8.423 × 10−05/− | 4.032 × 10−06/− | 1.925 × 10−10/− | 1.928 × 10−10/− | 4.564 × 10−10/− |
| 4 | 8.094 × 10−10/− | 7.453 × 10−06/− | 3.232 × 10−05/− | 5.324 × 10−05/− | 5.939 × 10−10/− | |
| 6 | 2.416 × 10−10/− | 1.364 × 10−06/− | 6.159 × 10−05/− | 8.026 × 10−05/− | 4.885 × 10−07/− | |
| 8 | 8.867 × 10−10/− | 9.917 × 10−06/− | 2.134 × 10−05/− | 8.664 × 10−05/− | 6.742 × 10−07/− | |
| F3 | 2 | 9.290 × 10−04/− | 5.327 × 10−05/− | 3.302 × 10−05/− | 1.763 × 10−04/− | 7.537 × 10−07/− |
| 4 | 1.521 × 10−04/− | 6.430 × 10−06/− | 2.926 × 10−05/− | 3.881 × 10−04/− | 3.075 × 10−08/− | |
| 6 | 6.167 × 10−04/− | 4.471 × 10−05/− | 8.733 × 10−05/− | 1.990 × 10−04/− | 6.773 × 10−07/− | |
| 8 | 2.756 × 10−04/− | 6.044 × 10−05/− | 1.046 × 10−05/− | 3.762 × 10−04/− | 8.068 × 10−07/− | |
| F4 | 2 | 8.068 × 10−04/− | 6.697 × 10−05/− | 3.516 × 10−05/− | 1.960 × 10−04/− | 6.905 × 10−07/− |
| 4 | 2.259 × 10−04/− | 2.660 × 10−05/− | 5.586 × 10−10/− | 2.136 × 10−05/− | 5.636 × 10−07/− | |
| 6 | 4.610 × 10−04/− | 1.231 × 10−05/− | 7.804 × 10−10/− | 2.705 × 10−05/− | 4.319 × 10−07/− | |
| 8 | 5.570 × 10−04/− | 6.757 × 10−06/− | 2.075 × 10−10/− | 1.322 × 10−05/− | 6.860 × 10−07/− | |
| F5 | 2 | 3.556 × 10−04/− | 7.473 × 10−06/− | 4.609 × 10−10/− | 8.529 × 10−05/− | 3.573 × 10−07/− |
| 4 | 5.580 × 10−04/− | 8.848 × 10−05/− | 9.811 × 10−10/− | 8.799 × 10−05/− | 1.482 × 10−10/− | |
| 6 | 6.295 × 10−04/− | 2.208 × 10−05/− | 4.158 × 10−10/− | 8.066 × 10−06/− | 2.098 × 10−10/− | |
| 8 | 3.709 × 10−04/− | 3.900 × 10−10/− | 6.114 × 10−10/− | 2.783 × 10−05/− | 2.230 × 10−10/− | |
| F6 | 2 | 5.399 × 10−10/− | 2.946 × 10−10/− | 9.850 × 10−10/− | 4.750 × 10−10/− | 3.629 × 10−10/− |
| 4 | 7.928 × 10−07/− | 8.631 × 10−10/− | 7.297 × 10−10/− | 7.315 × 10−10/− | 1.398 × 10−10/− | |
| 6 | 1.092 × 10−10/− | 4.448 × 10−10/− | 8.100 × 10−10/− | 7.545 × 10−06/− | 6.895 × 10−10/− | |
| 8 | 7.968 × 10−10/− | 3.103 × 10−10/− | 5.139 × 10−10/− | 9.493 × 10−06/− | 7.622 × 10−10/− | |
| F7 | 2 | 1.219 × 10−10/− | 4.164 × 10−10/− | 8.134 × 10−07/− | 6.562 × 10−05/− | 9.404 × 10−10/− |
| 4 | 3.528 × 10−06/− | 1.236 × 10−10/− | 9.807 × 10−07/− | 7.534 × 10−06/− | 2.574 × 10−05/− | |
| 6 | 5.792 × 10−06/− | 2.924 × 10−10/− | 9.120 × 10−07/− | 5.866 × 10−05/− | 1.482 × 10−05/− | |
| 8 | 6.946 × 10−06/− | 4.305 × 10−10/− | 8.149 × 10−07/− | 4.446 × 10−05/− | 9.107 × 10−05/− | |
| F8 | 2 | 5.899 × 10−06/− | 8.632 × 10−10/− | 5.722 × 10−07/− | 8.540 × 10−07/− | 4.260 × 10−05/− |
| 4 | 1.708 × 10−06/− | 1.496 × 10−10/− | 4.497 × 10−07/− | 3.133 × 10−05/− | 6.143 × 10−05/− | |
| 6 | 7.575 × 10−06/− | 3.622 × 10−10/− | 2.188 × 10−07/− | 1.890 × 10−05/− | 8.983 × 10−05/− | |
| 8 | 7.488 × 10−06/− | 8.792 × 10−10/− | 5.277 × 10−07/− | 6.054 × 10−05/− | 1.746 × 10−05/− | |
| F9 | 2 | 7.898 × 10−07/− | 2.841 × 10−10/− | 9.842 × 10−07/− | 2.053 × 10−05/− | 9.565 × 10−05/− |
| 4 | 8.630 × 10−06/− | 3.841 × 10−10/− | 7.581 × 10−07/− | 6.704 × 10−06/− | 9.730 × 10−05/− | |
| 6 | 1.503 × 10−06/− | 8.899 × 10−10/− | 9.126 × 10−10/− | 9.144 × 10−05/− | 8.932 × 10−05/− | |
| 8 | 5.314 × 10−06/− | 3.261 × 10−10/− | 4.263 × 10−10/− | 3.656 × 10−05/− | 5.404 × 10−05/− | |
| F10 | 2 | 2.977 × 10−06/− | 2.311 × 10−10/− | 7.012 × 10−10/− | 5.589 × 10−05/− | 4.991 × 10−06/− |
| 4 | 3.092 × 10−06/− | 8.917 × 10−10/− | 3.015 × 10−10/− | 4.973 × 10−04/− | 2.561 × 10−10/− | |
| 6 | 1.114 × 10−10/− | 1.029 × 10−10/− | 6.344 × 10−10/− | 8.190 × 10−04/− | 1.569 × 10−10/− | |
| 8 | 3.339 × 10−05/− | 1.500 × 10−10/− | 9.551 × 10−06/− | 5.952 × 10−04/− | 3.903 × 10−06/− | |
| F11 | 2 | 6.204 × 10−05/− | 1.136 × 10−10/− | 3.759 × 10−08/− | 1.532 × 10−04/− | 8.193 × 10−05/− |
| 4 | 4.641 × 10−05/− | 5.562 × 10−10/− | 4.955 × 10−07/− | 2.750 × 10−04/− | 5.610 × 10−05/− | |
| 6 | 9.019 × 10−05/− | 8.999 × 10−10/− | 9.728 × 10−07/− | 3.927 × 10−04/− | 6.577 × 10−05/− | |
| 8 | 5.499 × 10−05/− | 3.666 × 10−10/− | 3.954 × 10−07/− | 6.627 × 10−04/− | 8.314 × 10−05/− | |
| F12 | 2 | 6.267 × 10−05/− | 3.528 × 10−10/− | 2.395 × 10−07/− | 4.585 × 10−04/− | 9.120 × 10−05/− |
| 4 | 9.563 × 10−05/− | 6.784 × 10−10/− | 3.732 × 10−10/− | 6.673 × 10−04/− | 8.262 × 10−05/− | |
| 6 | 2.683 × 10−10/− | 5.494 × 10−10/− | 6.314 × 10−10/− | 2.260 × 10−04/− | 5.989 × 10−05/− | |
| 8 | 8.553 × 10−10/− | 9.174 × 10−10/− | 9.590 × 10−10/− | 5.271 × 10−10/− | 4.052 × 10−10/− | |
| +/−/= | 1/47/0 | 0/48/0 | 1/47/0 | 1/47/0 | 1/47/0 |
| Image | nTH | OPBNGO | NGO | ANBPO | DENGO | IMODE | NDFNGO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | ||
| F1 | 2 | 0.792 | 3.582 × 10−10 | 0.795 | 1.598 × 10−10 | 0.791 | 4.480 × 10−10 | 0.799 | 6.564 × 10−10 | 0.796 | 7.750 × 10−10 | 0.802 | 3.955 × 10−10 |
| 4 | 0.821 | 6.922 × 10−10 | 0.826 | 1.719 × 10−10 | 0.824 | 4.620 × 10−10 | 0.829 | 3.483 × 10−10 | 0.821 | 4.482 × 10−10 | 0.835 | 4.623 × 10−10 | |
| 6 | 0.852 | 7.270 × 10−10 | 0.852 | 6.247 × 10−10 | 0.854 | 2.721 × 10−10 | 0.856 | 8.876 × 10−10 | 0.851 | 1.358 × 10−10 | 0.865 | 7.398 × 10−10 | |
| 8 | 0.875 | 3.212 × 10−10 | 0.870 | 9.669 × 10−10 | 0.872 | 5.288 × 10−10 | 0.873 | 5.569 × 10−10 | 0.872 | 6.637 × 10−10 | 0.874 | 9.897 × 10−10 | |
| F2 | 2 | 0.797 | 9.263 × 10−10 | 0.796 | 7.064 × 10−10 | 0.791 | 6.567 × 10−10 | 0.797 | 2.134 × 10−10 | 0.791 | 3.836 × 10−10 | 0.802 | 8.251 × 10−10 |
| 4 | 0.828 | 4.873 × 10−10 | 0.821 | 9.297 × 10−10 | 0.823 | 2.879 × 10−10 | 0.830 | 2.077 × 10−10 | 0.826 | 2.129 × 10−10 | 0.846 | 1.863 × 10−10 | |
| 6 | 0.854 | 5.704 × 10−10 | 0.851 | 6.564 × 10−10 | 0.859 | 5.436 × 10−10 | 0.855 | 8.569 × 10−10 | 0.858 | 5.795 × 10−10 | 0.872 | 2.039 × 10−10 | |
| 8 | 0.879 | 6.078 × 10−10 | 0.870 | 1.138 × 10−10 | 0.871 | 1.341 × 10−10 | 0.872 | 2.286 × 10−10 | 0.878 | 4.164 × 10−10 | 0.895 | 1.508 × 10−10 | |
| F3 | 2 | 0.802 | 2.232 × 10−10 | 0.805 | 5.087 × 10−10 | 0.809 | 6.191 × 10−10 | 0.803 | 1.405 × 10−10 | 0.805 | 8.023 × 10−10 | 0.811 | 3.932 × 10−10 |
| 4 | 0.831 | 1.410 × 10−10 | 0.836 | 3.233 × 10−10 | 0.831 | 6.418 × 10−10 | 0.831 | 4.264 × 10−10 | 0.837 | 7.238 × 10−10 | 0.854 | 8.247 × 10−10 | |
| 6 | 0.868 | 8.651 × 10−10 | 0.864 | 1.650 × 10−10 | 0.868 | 2.254 × 10−10 | 0.866 | 3.181 × 10−10 | 0.869 | 7.594 × 10−10 | 0.881 | 9.435 × 10−10 | |
| 8 | 0.879 | 5.077 × 10−10 | 0.877 | 1.274 × 10−10 | 0.878 | 3.715 × 10−10 | 0.879 | 2.945 × 10−10 | 0.877 | 1.768 × 10−10 | 0.896 | 7.914 × 10−10 | |
| F4 | 2 | 0.776 | 6.847 × 10−10 | 0.777 | 4.165 × 10−10 | 0.772 | 4.514 × 10−10 | 0.779 | 2.233 × 10−10 | 0.779 | 2.201 × 10−10 | 0.805 | 8.353 × 10−10 |
| 4 | 0.805 | 5.118 × 10−10 | 0.806 | 9.995 × 10−10 | 0.804 | 3.952 × 10−10 | 0.803 | 5.371 × 10−10 | 0.801 | 9.500 × 10−10 | 0.827 | 4.223 × 10−10 | |
| 6 | 0.835 | 3.416 × 10−10 | 0.831 | 8.656 × 10−10 | 0.833 | 8.759 × 10−10 | 0.839 | 3.093 × 10−10 | 0.835 | 3.818 × 10−10 | 0.839 | 7.106 × 10−10 | |
| 8 | 0.857 | 8.863 × 10−10 | 0.859 | 3.273 × 10−10 | 0.852 | 4.462 × 10−10 | 0.858 | 8.388 × 10−10 | 0.850 | 6.001 × 10−10 | 0.891 | 3.975 × 10−10 | |
| F5 | 2 | 0.789 | 8.044 × 10−10 | 0.784 | 7.802 × 10−10 | 0.782 | 8.811 × 10−10 | 0.788 | 3.348 × 10−10 | 0.783 | 8.307 × 10−10 | 0.794 | 4.254 × 10−10 |
| 4 | 0.811 | 8.884 × 10−10 | 0.816 | 5.267 × 10−10 | 0.816 | 1.740 × 10−10 | 0.820 | 3.156 × 10−10 | 0.817 | 7.513 × 10−10 | 0.837 | 5.407 × 10−10 | |
| 6 | 0.838 | 3.824 × 10−10 | 0.835 | 6.882 × 10−10 | 0.836 | 6.696 × 10−10 | 0.832 | 1.820 × 10−10 | 0.838 | 7.729 × 10−10 | 0.874 | 9.272 × 10−10 | |
| 8 | 0.855 | 4.741 × 10−10 | 0.854 | 6.363 × 10−10 | 0.851 | 6.961 × 10−10 | 0.850 | 5.972 × 10−10 | 0.857 | 8.366 × 10−10 | 0.893 | 5.496 × 10−10 | |
| F6 | 2 | 0.757 | 7.677 × 10−10 | 0.754 | 2.670 × 10−10 | 0.751 | 4.163 × 10−10 | 0.755 | 4.338 × 10−10 | 0.757 | 8.012 × 10−10 | 0.774 | 3.754 × 10−10 |
| 4 | 0.791 | 5.936 × 10−10 | 0.790 | 8.439 × 10−10 | 0.796 | 7.908 × 10−10 | 0.795 | 6.918 × 10−10 | 0.793 | 6.394 × 10−10 | 0.817 | 4.901 × 10−10 | |
| 6 | 0.828 | 7.456 × 10−10 | 0.824 | 6.782 × 10−10 | 0.829 | 6.518 × 10−10 | 0.825 | 4.108 × 10−10 | 0.826 | 3.021 × 10−10 | 0.849 | 3.374 × 10−10 | |
| 8 | 0.856 | 3.085 × 10−10 | 0.858 | 8.229 × 10−10 | 0.851 | 2.160 × 10−10 | 0.852 | 3.895 × 10−10 | 0.859 | 4.278 × 10−10 | 0.883 | 9.902 × 10−10 | |
| F7 | 2 | 0.811 | 4.258 × 10−10 | 0.815 | 6.702 × 10−10 | 0.817 | 2.310 × 10−10 | 0.810 | 2.784 × 10−10 | 0.811 | 2.825 × 10−10 | 0.824 | 8.284 × 10−10 |
| 4 | 0.833 | 6.192 × 10−10 | 0.838 | 1.671 × 10−10 | 0.833 | 2.683 × 10−10 | 0.838 | 1.776 × 10−10 | 0.831 | 1.085 × 10−10 | 0.843 | 3.191 × 10−10 | |
| 6 | 0.867 | 8.981 × 10−10 | 0.864 | 3.647 × 10−10 | 0.862 | 1.183 × 10−10 | 0.865 | 7.560 × 10−10 | 0.862 | 9.990 × 10−10 | 0.872 | 5.234 × 10−10 | |
| 8 | 0.878 | 4.767 × 10−10 | 0.875 | 7.128 × 10−10 | 0.871 | 7.024 × 10−10 | 0.871 | 5.229 × 10−10 | 0.876 | 3.522 × 10−10 | 0.893 | 4.809 × 10−10 | |
| F8 | 2 | 0.823 | 7.040 × 10−10 | 0.821 | 7.878 × 10−10 | 0.826 | 7.774 × 10−10 | 0.830 | 1.233 × 10−10 | 0.829 | 3.618 × 10−10 | 0.835 | 4.188 × 10−10 |
| 4 | 0.849 | 7.075 × 10−10 | 0.840 | 5.639 × 10−10 | 0.846 | 9.738 × 10−10 | 0.849 | 1.285 × 10−10 | 0.846 | 7.590 × 10−10 | 0.872 | 2.083 × 10−10 | |
| 6 | 0.863 | 5.392 × 10−10 | 0.865 | 6.742 × 10−10 | 0.866 | 4.634 × 10−10 | 0.868 | 9.521 × 10−10 | 0.865 | 4.466 × 10−10 | 0.890 | 2.810 × 10−10 | |
| 8 | 0.894 | 9.863 × 10−10 | 0.893 | 8.140 × 10−10 | 0.892 | 3.654 × 10−10 | 0.895 | 6.293 × 10−10 | 0.894 | 4.030 × 10−10 | 0.901 | 8.793 × 10−10 | |
| F9 | 2 | 0.797 | 7.451 × 10−10 | 0.791 | 1.304 × 10−10 | 0.796 | 6.096 × 10−10 | 0.790 | 6.537 × 10−10 | 0.798 | 1.483 × 10−10 | 0.800 | 5.032 × 10−10 |
| 4 | 0.822 | 3.101 × 10−10 | 0.823 | 4.205 × 10−10 | 0.821 | 9.435 × 10−10 | 0.826 | 7.138 × 10−10 | 0.823 | 5.072 × 10−10 | 0.830 | 2.175 × 10−10 | |
| 6 | 0.860 | 7.104 × 10−10 | 0.856 | 3.600 × 10−10 | 0.851 | 5.728 × 10−10 | 0.853 | 2.036 × 10−10 | 0.856 | 4.437 × 10−10 | 0.867 | 3.616 × 10−10 | |
| 8 | 0.872 | 3.185 × 10−10 | 0.871 | 2.127 × 10−10 | 0.878 | 6.274 × 10−10 | 0.878 | 7.036 × 10−10 | 0.870 | 9.024 × 10−10 | 0.885 | 3.868 × 10−10 | |
| F10 | 2 | 0.793 | 9.752 × 10−10 | 0.799 | 7.360 × 10−10 | 0.791 | 3.284 × 10−10 | 0.794 | 6.518 × 10−10 | 0.796 | 8.249 × 10−10 | 0.806 | 3.353 × 10−10 |
| 4 | 0.828 | 9.910 × 10−10 | 0.828 | 6.575 × 10−10 | 0.828 | 4.683 × 10−10 | 0.823 | 1.406 × 10−10 | 0.829 | 1.447 × 10−10 | 0.847 | 5.214 × 10−10 | |
| 6 | 0.858 | 3.673 × 10−10 | 0.851 | 7.350 × 10−10 | 0.856 | 8.231 × 10−10 | 0.859 | 9.042 × 10−10 | 0.858 | 7.503 × 10−10 | 0.876 | 4.186 × 10−10 | |
| 8 | 0.876 | 2.215 × 10−10 | 0.876 | 9.176 × 10−10 | 0.878 | 2.549 × 10−10 | 0.874 | 1.084 × 10−10 | 0.870 | 7.610 × 10−10 | 0.899 | 1.798 × 10−10 | |
| F11 | 2 | 0.772 | 7.059 × 10−10 | 0.776 | 3.635 × 10−10 | 0.770 | 1.661 × 10−10 | 0.770 | 3.284 × 10−10 | 0.779 | 7.955 × 10−10 | 0.803 | 7.497 × 10−10 |
| 4 | 0.803 | 6.243 × 10−10 | 0.802 | 4.297 × 10−10 | 0.807 | 8.089 × 10−10 | 0.809 | 4.525 × 10−10 | 0.802 | 8.113 × 10−10 | 0.828 | 7.702 × 10−10 | |
| 6 | 0.833 | 3.865 × 10−10 | 0.835 | 8.834 × 10−10 | 0.833 | 6.711 × 10−10 | 0.834 | 6.055 × 10−10 | 0.836 | 1.791 × 10−10 | 0.854 | 6.002 × 10−10 | |
| 8 | 0.852 | 8.366 × 10−10 | 0.860 | 7.668 × 10−10 | 0.857 | 5.390 × 10−10 | 0.859 | 7.654 × 10−10 | 0.852 | 2.106 × 10−10 | 0.893 | 1.863 × 10−10 | |
| F12 | 2 | 0.782 | 6.817 × 10−10 | 0.788 | 1.326 × 10−10 | 0.787 | 2.074 × 10−10 | 0.786 | 4.141 × 10−10 | 0.788 | 3.203 × 10−10 | 0.790 | 4.985 × 10−10 |
| 4 | 0.816 | 3.454 × 10−10 | 0.813 | 1.127 × 10−10 | 0.814 | 4.790 × 10−10 | 0.814 | 8.003 × 10−10 | 0.817 | 4.417 × 10−10 | 0.838 | 2.051 × 10−10 | |
| 6 | 0.840 | 7.493 × 10−10 | 0.831 | 7.496 × 10−10 | 0.838 | 1.059 × 10−10 | 0.839 | 6.530 × 10−10 | 0.838 | 6.719 × 10−10 | 0.872 | 6.110 × 10−10 | |
| 8 | 0.853 | 6.507 × 10−10 | 0.855 | 7.537 × 10−10 | 0.850 | 8.037 × 10−10 | 0.853 | 7.085 × 10−10 | 0.855 | 7.287 × 10−10 | 0.893 | 8.096 × 10−10 | |
| Mean Rank | 3.85 | 4.31 | 4.42 | 3.60 | 3.77 | 1.04 | |||||||
| Final Rank | 4 | 5 | 6 | 2 | 3 | 1 | |||||||
| Image | nTH | OPBNGO vs. NDFNGO | NGO vs. NDFNGO | ANBPO vs. NDFNGO | DENGO vs. NDFNGO | IMODE vs. NDFNGO |
|---|---|---|---|---|---|---|
| F1 | 2 | 2.175 × 10−10/− | 8.927 × 10−10/− | 1.273 × 10−10/− | 3.529 × 10−10/− | 4.455 × 10−10/− |
| 4 | 1.018 × 10−05/− | 8.487 × 10−10/− | 7.275 × 10−10/− | 3.486 × 10−10/− | 4.896 × 10−10/− | |
| 6 | 9.423 × 10−05/− | 1.820 × 10−06/− | 9.258 × 10−07/− | 7.982 × 10−06/− | 2.860 × 10−10/− | |
| 8 | 3.526 × 10−05/+ | 6.802 × 10−06/− | 4.131 × 10−10/− | 9.953 × 10−10/− | 5.324 × 10−10/− | |
| F2 | 2 | 5.041 × 10−05/− | 4.583 × 10−06/− | 4.635 × 10−10/− | 5.420 × 10−10/− | 2.590 × 10−10/− |
| 4 | 5.400 × 10−10/− | 1.829 × 10−06/− | 7.475 × 10−05/− | 4.405 × 10−05/− | 7.943 × 10−10/− | |
| 6 | 7.524 × 10−10/− | 4.937 × 10−06/− | 5.517 × 10−05/− | 5.918 × 10−05/− | 5.963 × 10−07/− | |
| 8 | 9.069 × 10−10/− | 6.514 × 10−06/− | 6.711 × 10−05/− | 7.567 × 10−05/− | 5.719 × 10−09/− | |
| F3 | 2 | 3.339 × 10−04/− | 9.394 × 10−05/− | 6.789 × 10−05/− | 6.186 × 10−04/− | 4.781 × 10−07/− |
| 4 | 1.948 × 10−04/− | 6.902 × 10−05/− | 7.173 × 10−05/− | 9.650 × 10−04/− | 6.114 × 10−07/− | |
| 6 | 7.223 × 10−04/− | 7.070 × 10−05/− | 3.729 × 10−05/− | 3.315 × 10−04/− | 8.324 × 10−07/− | |
| 8 | 3.075 × 10−04/− | 1.168 × 10−05/− | 5.206 × 10−05/− | 9.456 × 10−04/− | 6.981 × 10−07/− | |
| F4 | 2 | 7.867 × 10−04/− | 9.564 × 10−05/− | 9.800 × 10−05/− | 8.744 × 10−04/− | 6.152 × 10−07/− |
| 4 | 1.307 × 10−04/− | 7.171 × 10−05/− | 6.716 × 10−10/− | 2.882 × 10−05/− | 5.918 × 10−07/− | |
| 6 | 3.866 × 10−04/− | 6.966 × 10−05/− | 7.032 × 10−10/− | 6.640 × 10−05/+ | 4.244 × 10−07/− | |
| 8 | 1.098 × 10−04/− | 7.070 × 10−05/− | 4.138 × 10−10/− | 7.727 × 10−06/− | 4.353 × 10−07/− | |
| F5 | 2 | 7.694 × 10−04/− | 4.673 × 10−05/− | 5.971 × 10−10/− | 8.480 × 10−05/− | 9.401 × 10−07/− |
| 4 | 6.441 × 10−04/− | 5.025 × 10−05/− | 3.385 × 10−10/− | 8.101 × 10−05/− | 2.966 × 10−10/− | |
| 6 | 6.809 × 10−04/− | 4.661 × 10−06/− | 4.377 × 10−10/− | 4.610 × 10−05/− | 9.371 × 10−10/− | |
| 8 | 9.701 × 10−04/− | 9.107 × 10−10/− | 8.452 × 10−10/− | 9.079 × 10−05/− | 2.303 × 10−10/− | |
| F6 | 2 | 8.654 × 10−10/− | 8.417 × 10−10/− | 2.435 × 10−10/− | 9.868 × 10−10/− | 6.733 × 10−10/− |
| 4 | 1.664 × 10−07/− | 5.362 × 10−10/− | 5.826 × 10−10/− | 8.087 × 10−10/− | 1.276 × 10−10/− | |
| 6 | 5.839 × 10−10/− | 5.119 × 10−10/− | 8.437 × 10−10/− | 8.766 × 10−05/− | 2.175 × 10−10/− | |
| 8 | 3.519 × 10−10/− | 6.324 × 10−10/− | 5.102 × 10−10/− | 9.024 × 10−05/− | 7.821 × 10−10/− | |
| F7 | 2 | 5.858 × 10−10/− | 6.881 × 10−10/− | 7.920 × 10−07/− | 2.640 × 10−05/− | 9.232 × 10−10/− |
| 4 | 1.807 × 10−06/− | 1.235 × 10−10/− | 1.238 × 10−07/− | 6.248 × 10−07/− | 1.694 × 10−05/− | |
| 6 | 7.590 × 10−06/− | 7.815 × 10−10/− | 1.757 × 10−07/− | 2.171 × 10−05/− | 7.424 × 10−05/− | |
| 8 | 6.771 × 10−06/− | 6.998 × 10−10/− | 1.041 × 10−07/− | 3.212 × 10−05/− | 6.192 × 10−05/− | |
| F8 | 2 | 8.609 × 10−06/− | 3.800 × 10−10/− | 1.336 × 10−07/− | 2.178 × 10−05/− | 2.731 × 10−06/− |
| 4 | 2.217 × 10−06/− | 9.929 × 10−10/− | 4.068 × 10−07/− | 4.589 × 10−05/− | 8.182 × 10−05/− | |
| 6 | 7.326 × 10−06/− | 7.891 × 10−10/− | 5.728 × 10−07/− | 4.750 × 10−05/− | 4.922 × 10−05/− | |
| 8 | 9.340 × 10−06/− | 1.097 × 10−10/− | 5.184 × 10−07/− | 6.623 × 10−05/− | 4.823 × 10−06/− | |
| F9 | 2 | 3.666 × 10−06/− | 1.018 × 10−10/− | 4.891 × 10−07/− | 5.444 × 10−05/− | 2.355 × 10−05/− |
| 4 | 3.986 × 10−06/− | 6.142 × 10−10/− | 3.678 × 10−07/− | 1.586 × 10−06/− | 8.363 × 10−05/− | |
| 6 | 1.011 × 10−06/− | 9.665 × 10−10/− | 1.301 × 10−10/− | 3.634 × 10−05/− | 1.470 × 10−05/− | |
| 8 | 9.897 × 10−06/− | 5.538 × 10−10/− | 3.913 × 10−10/− | 2.533 × 10−07/− | 2.549 × 10−06/− | |
| F10 | 2 | 3.851 × 10−06/− | 1.356 × 10−10/− | 8.580 × 10−10/− | 1.547 × 10−05/− | 5.992 × 10−05/− |
| 4 | 8.248 × 10−06/− | 9.784 × 10−10/− | 1.620 × 10−10/− | 1.301 × 10−05/− | 1.999 × 10−10/− | |
| 6 | 3.320 × 10−10/− | 7.513 × 10−10/− | 9.400 × 10−10/− | 7.776 × 10−04/− | 3.307 × 10−10/− | |
| 8 | 7.760 × 10−05/− | 7.664 × 10−10/− | 5.908 × 10−06/− | 8.632 × 10−05/− | 7.357 × 10−05/− | |
| F11 | 2 | 4.532 × 10−05/− | 9.017 × 10−10/− | 1.392 × 10−07/− | 8.588 × 10−04/− | 9.569 × 10−05/− |
| 4 | 9.433 × 10−05/− | 5.705 × 10−10/− | 3.826 × 10−07/− | 5.816 × 10−04/− | 7.437 × 10−05/− | |
| 6 | 1.424 × 10−05/− | 9.376 × 10−10/− | 1.052 × 10−07/− | 4.073 × 10−04/− | 5.866 × 10−05/− | |
| 8 | 6.280 × 10−05/− | 4.052 × 10−10/− | 4.565 × 10−07/− | 5.309 × 10−04/− | 1.233 × 10−05/− | |
| F12 | 2 | 1.796 × 10−05/− | 9.273 × 10−10/− | 8.507 × 10−07/− | 5.327 × 10−04/− | 7.199 × 10−05/− |
| 4 | 4.385 × 10−06/− | 5.758 × 10−10/− | 4.057 × 10−10/− | 7.322 × 10−05/− | 2.359 × 10−05/− | |
| 6 | 3.647 × 10−10/− | 7.719 × 10−10/− | 9.230 × 10−10/− | 4.751 × 10−04/− | 5.726 × 10−05/− | |
| 8 | 4.274 × 10−10/− | 2.956 × 10−10/− | 1.371 × 10−10/− | 9.697 × 10−10/− | 7.947 × 10−10/− | |
| +/−/= | 1/47/0 | 0/48/0 | 0/48/0 | 1/47/0 | 1/47/0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Bao, Z.; Shao, Y.; Liang, N. NDFNGO: Enhanced Northern Goshawk Optimization Algorithm for Image Segmentation. Biomimetics 2025, 10, 837. https://doi.org/10.3390/biomimetics10120837
Zhao X, Bao Z, Shao Y, Liang N. NDFNGO: Enhanced Northern Goshawk Optimization Algorithm for Image Segmentation. Biomimetics. 2025; 10(12):837. https://doi.org/10.3390/biomimetics10120837
Chicago/Turabian StyleZhao, Xiajie, Zuowen Bao, Yu Shao, and Na Liang. 2025. "NDFNGO: Enhanced Northern Goshawk Optimization Algorithm for Image Segmentation" Biomimetics 10, no. 12: 837. https://doi.org/10.3390/biomimetics10120837
APA StyleZhao, X., Bao, Z., Shao, Y., & Liang, N. (2025). NDFNGO: Enhanced Northern Goshawk Optimization Algorithm for Image Segmentation. Biomimetics, 10(12), 837. https://doi.org/10.3390/biomimetics10120837






