Parametric FEM-Based Analysis on Adaptive Vein Morphology of Dragonfly Wings Toward Material Efficiency
Abstract
1. Introduction
2. Background
- the gradual reduction in vein radius;
- the changing cross-section;
- the thickness variation.
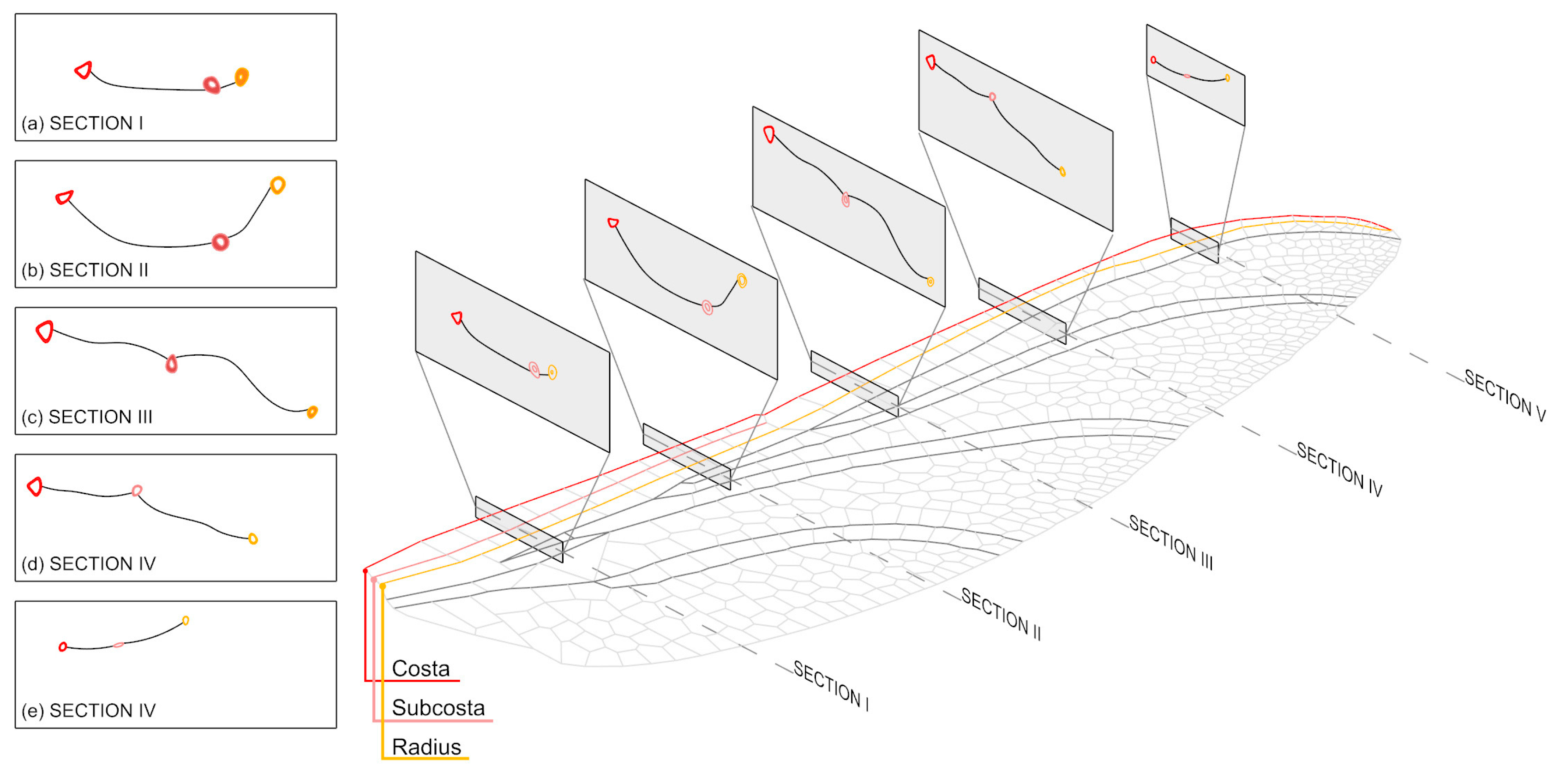
2.1. The Generation Logic of the Main Longitudinal Vein as a Skeleton Framework
2.2. The Changing Cross-Section on the Main Longitudinal Vein
2.3. The Thickness Variation on the Main Longitudinal Vein
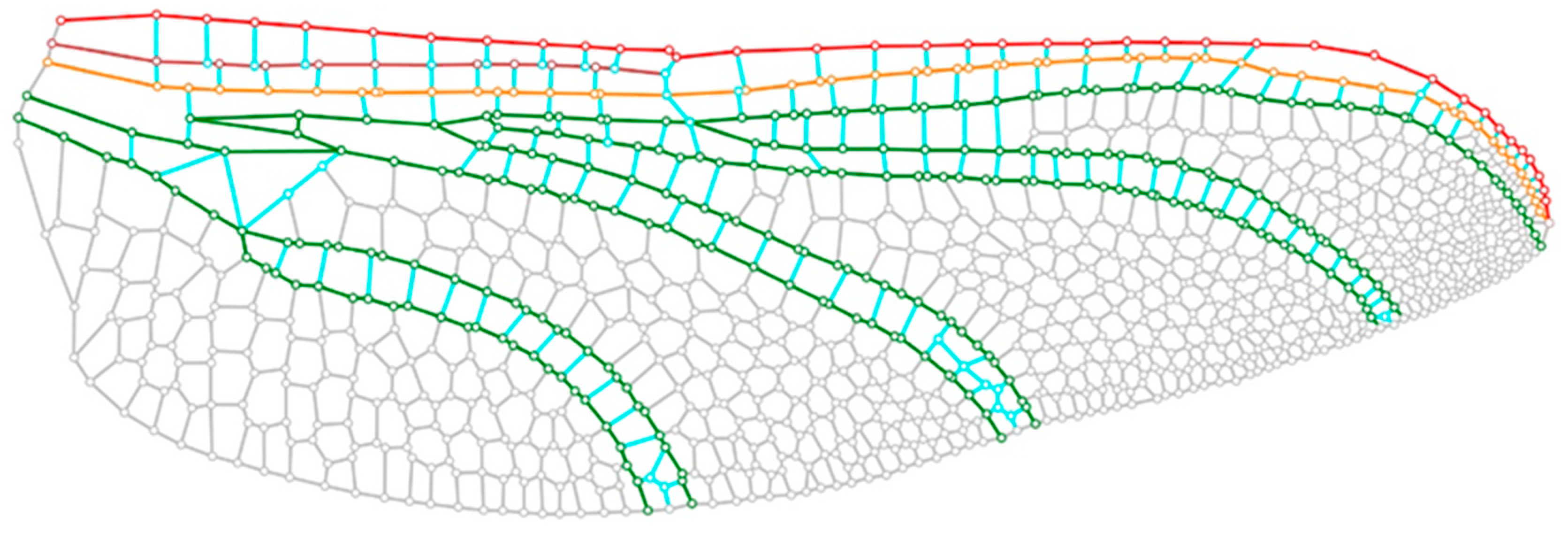
3. Method
3.1. Modelling for FEA and Simulation
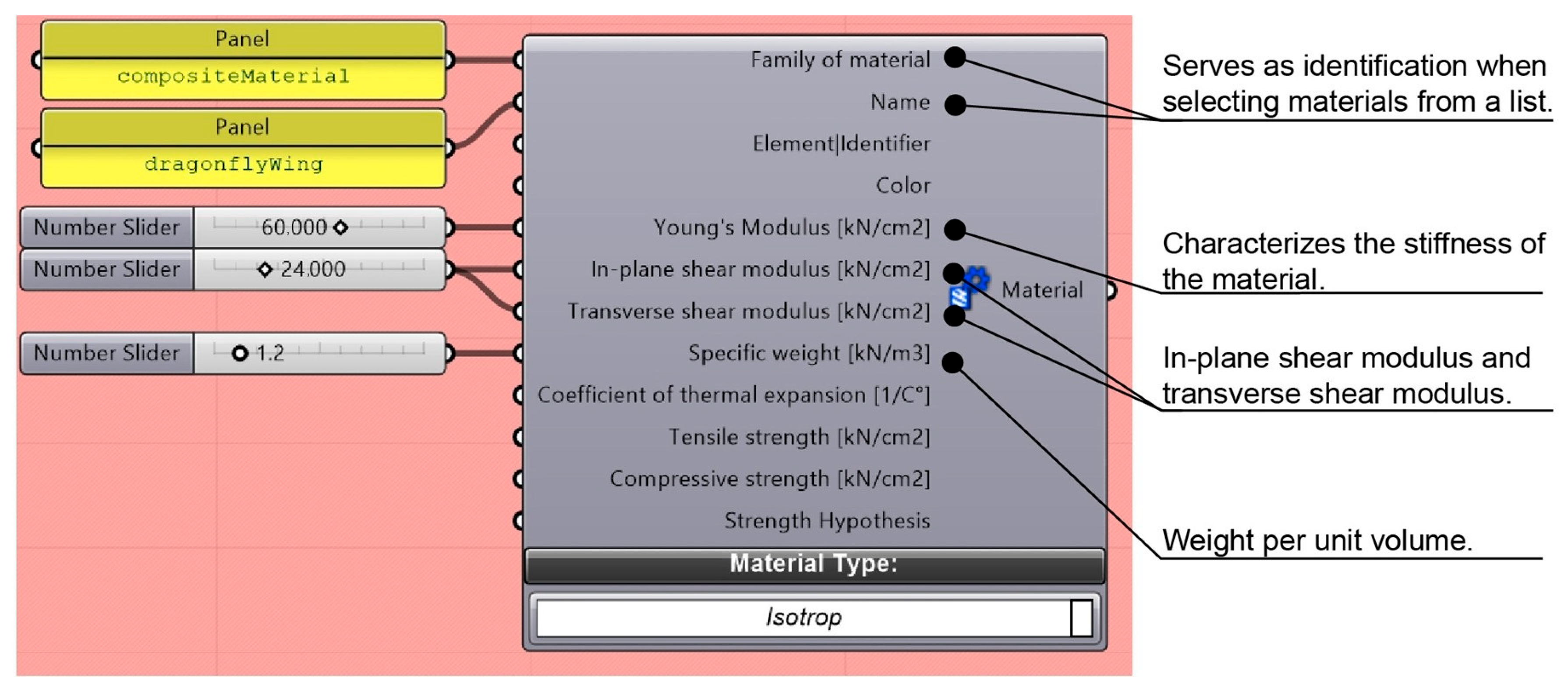
3.2. Material Property Parameter Setting
3.3. Other Settings
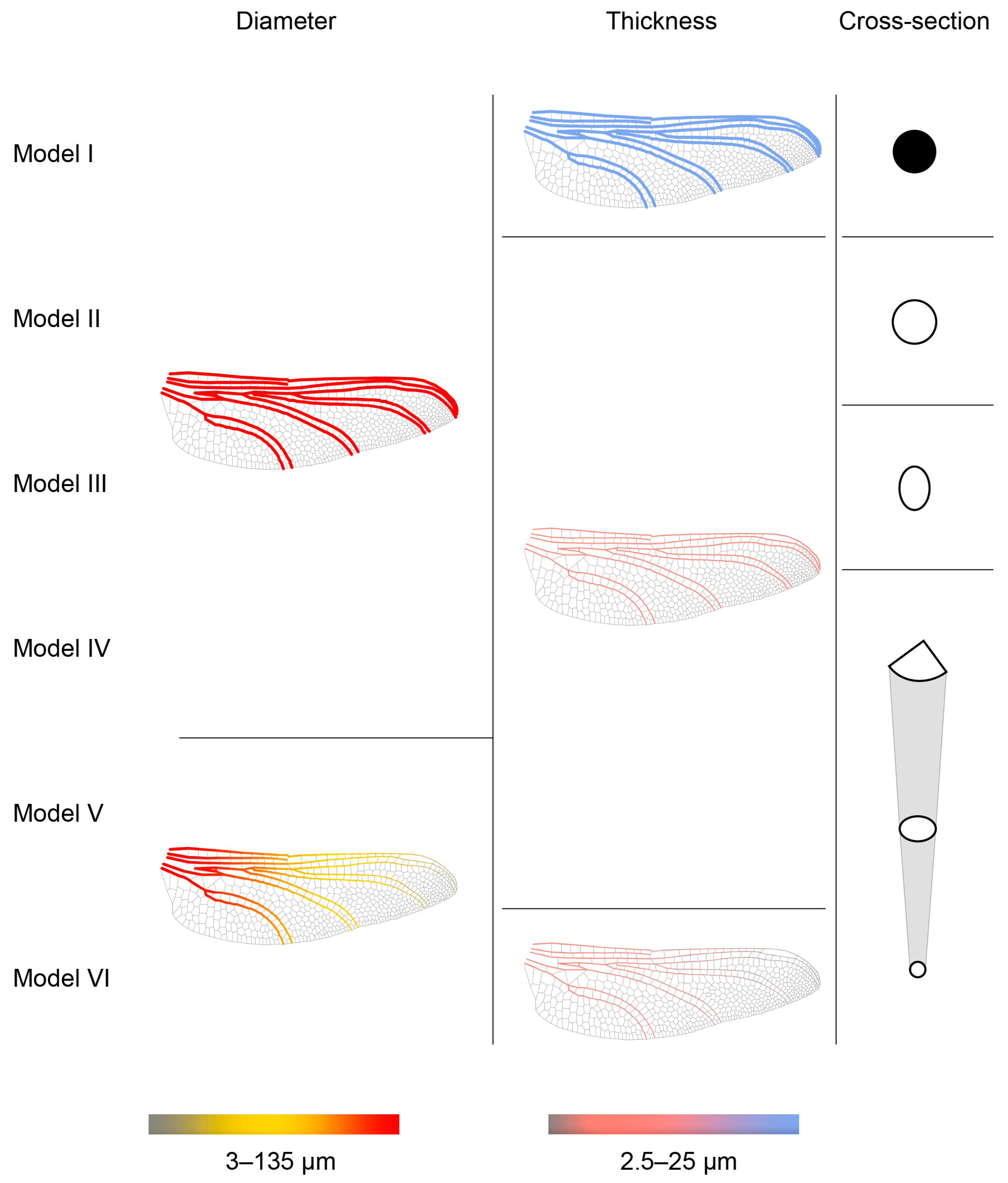
3.4. Parametric Modelling with Morphological Characteristics
3.4.1. Geometry Features on Model I
3.4.2. Geometry Features of Model II–IV
3.4.3. Geometry Features of Model V–VI
4. Results
4.1. Simulation Results
4.1.1. Result Comparison Between Model I and II
4.1.2. Result Comparison Between Model II–IV
4.1.3. Result Comparison Between Model IV–VI
4.2. Outcomes and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FE | Finite element |
| FEA | Finite element analysis |
| FEM | Finite element method |
| CAD | Computer-aided design |
References
- Gosciniak, M.; Januszkiewicz, K. Architecture inspired by Nature. Human body in Santiago Calatrava’s works. Sophisticated approach to architectural design. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 82041. [Google Scholar] [CrossRef]
- Naik, R.R.; Singamaneni, S. Introduction: Bioinspired and biomimetic materials. Chem. Rev. 2017, 117, 12581–12583. [Google Scholar] [CrossRef]
- Chen, T.; Wei, X.; Chen, Z.; Morin, D.; Alvarez, S.V.; Yoon, Y.; Huang, Y. Designing energy-efficient separation membranes: Knowledge from nature for a sustainable future. Adv. Membr. 2022, 2, 100031. [Google Scholar] [CrossRef]
- Farzaneh, H.H.; Lindemann, U. A Practical Guide to Bio-Inspired Design; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Resh, V.H.; Cardé, R.T. Encyclopedia of Insects; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Sun, J.; Bhushan, B. The structure and mechanical properties of dragonfly wings and their role on flyability. Comptes Rendus Mec. 2012, 340, 3–17. [Google Scholar] [CrossRef]
- Sivasankaran, P.N.; Ward, T.A. Spatial network analysis to construct simplified wing structural models for Biomimetic Micro Air Vehicles. Aerosp. Sci. Technol. 2016, 49, 259–268. [Google Scholar] [CrossRef]
- Wang, X.-S.; Li, Y.; Shi, Y.-F. Effects of sandwich microstructures on mechanical behaviors of dragonfly wing vein. Compos. Sci. Technol. 2008, 68, 186–192. [Google Scholar] [CrossRef]
- Ren, L.; Liang, Y. Biological couplings: Function, characteristics and implementation mode. Sci. China Technol. Sci. 2010, 53, 379–387. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, L.; Liu, H.; Yin, C. Measuring wing kinematics, flight trajectory and body attitude during forward flight and turning maneuvers in dragonflies. J. Exp. Biol. 2003, 206, 745–757. [Google Scholar] [CrossRef]
- Chirende, B.; Li, J.; Wen, L.; Simalenga, T.E. Effects of bionic non-smooth surface on reducing soil resistance to disc ploughing. Sci. China Technol. Sci. 2010, 53, 2960–2965. [Google Scholar] [CrossRef]
- Rajabi, H.; Shafiei, A.; Darvizeh, A.; Dirks, J.-H.; Appel, E.; Gorb, S.N. Effect of microstructure on the mechanical and damping behaviour of dragonfly wing veins. R. Soc. Open Sci. 2016, 3, 160006. [Google Scholar] [CrossRef]
- Jongerius, S.; Lentink, D. Structural analysis of a dragonfly wing. Exp. Mech. 2010, 50, 1323–1334. [Google Scholar] [CrossRef]
- Kumar, D.; Mohite, P.M.; Kamle, S. Dragonfly inspired nanocomposite flapping wing for micro air vehicles. J. Bionic Eng. 2019, 16, 894–903. [Google Scholar] [CrossRef]
- Kesel, A.B.; Philippi, U.; Nachtigall, W. Biomechanical aspects of the insect wing: An analysis using the finite element method. Comput. Biol. Med. 1998, 28, 423–437. [Google Scholar] [CrossRef]
- Rajabi, H.; Ghoroubi, N.; Malaki, M.; Darvizeh, A.; Gorb, S. Basal complex and basal venation of Odonata wings: Structural diversity and potential role in the wing deformation. PLoS ONE 2016, 11, e0160610. [Google Scholar] [CrossRef]
- Salami, E.; Ganesan, P.; Ward, T.A.; Viyapuri, R.; Romli, F. Design and mechanical analysis of a 3D-printed biodegradable biomimetic micro air vehicle wing. IOP Conf. Ser. Mater. Sci. Eng. 2016, 152, 12014. [Google Scholar] [CrossRef]
- Ren, L.; Li, X. Functional characteristics of dragonfly wings and its bionic investigation progress. Sci. China Technol. Sci. 2013, 56, 884–897. [Google Scholar] [CrossRef]
- Mykytyuk, P.; Brych, V.; Manzhula, V.; Borysiak, O.; Sachenko, A.; Banasik, A.; Kempa, W.M.; Mykytyuk, Y.; Czupryna-Nowak, A.; Lebid, I. Efficient management of material resources in Low-Carbon construction. Energies 2024, 17, 575. [Google Scholar] [CrossRef]
- Daleyev, D.; Reisinger, J.; Rasoulzadeh, S.; Senk, V.; Embacher, P.; Kovacic, I. Potential of structural multi-objective optimization of reinforced concrete slabs in the context of sustainable development. In Proceedings of the Creative Construction e-Conference, Keszthely, Hungary, 20–23 June 2023; pp. 480–485. [Google Scholar]
- Hájek, P.; Fiala, C. Environmental assessment of floor structures from fibre concrete-study. In Proceedings of the Fibre Concrete, Prague, Czech Republic, 12–13 September 2007. [Google Scholar]
- Knippers, J.; Nickel, K.G.; Speck, T. Biomimetic Research for Architecture and Building Construction; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Newman, D.J. The Functional Wing Morphology of Some Odonata; University of Exeter: Devon, UK, 1982. [Google Scholar]
- Newman, D.; Wootton, R. An approach to the mechanics of pleating in dragonfly wings. J. Exp. Biol. 1986, 125, 361–372. [Google Scholar] [CrossRef]
- Darvizeh, M.; Darvizeh, A.; Rajabi, H.; Rezaei, A. Free vibration analysis of dragonfly wings using finite element method. Int. J. Multiphysics 2009, 3, 101–110. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. I. The quasi-steady analysis. Philos. Trans. R. Soc. Lond. Biol. Sci. 1984, 305, 1–15. [Google Scholar]
- Ellington, C.P. The aerodynamics of hovering insect flight. II. Morphological parameters. Philos. Trans. R. Soc. Lond. Biol. Sci. 1984, 305, 17–40. [Google Scholar]
- Chew, P. Insect Wings. Available online: https://www.brisbaneinsects.com/brisbane_insects/InsectWings.htm (accessed on 13 April 2014).
- Comstock, J.H.; Needham, J.G. The Wings of Insects. Am. Nat. 1898, 32, 81–89. [Google Scholar] [CrossRef]
- Liu, C.; Du, R.; Li, F.; Sun, J. Bioinspiration of the vein structure of dragonfly wings on its flight characteristics. Microsc. Res. Tech. 2022, 85, 829–839. [Google Scholar] [CrossRef]
- Machida, K.; Oikawa, T.; Shimanuki, J. The effect of the costal vein configuration of the wings of a dragonfly. Key Eng. Mater. 2006, 326, 819–822. [Google Scholar] [CrossRef]
- Sudo, S.; Tsuyuki, K.; Ikohagi, T.; Ohta, F.; Shida, S.; Tani, J. A study on the wing structure and flapping behavior of a dragonfly. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 1999, 42, 721–729. [Google Scholar] [CrossRef]
- Combes, S.A.; Daniel, T.L. Flexural stiffness in insect wings I. Scaling and the influence of wing venation. J. Exp. Biol. 2003, 206, 2979–2987. [Google Scholar] [CrossRef]
- Combes, S.A.; Daniel, T.L. Into thin air: Contributions of aerodynamic and inertial-elastic forces to wing bending in the hawkmoth Manduca sexta. J. Exp. Biol. 2003, 206, 2999–3006. [Google Scholar] [CrossRef] [PubMed]
- Dudley, R. The Biomechanics of Insect Flight: Form, Function, Evolution; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Eshghi, S.; Nooraeefar, V.; Darvizeh, A.; Gorb, S.N.; Rajabi, H. WingMesh: A matlab-based application for finite element modeling of insect wings. Insects 2020, 11, 546. [Google Scholar] [CrossRef] [PubMed]
- Jin, T.; Goo, N.S.; Park, H.C. Finite element modeling of a beetle wing. J. Bionic Eng. 2010, 7, S145–S149. [Google Scholar] [CrossRef]
- Goel, A.K.; McAdams, D.A.; Stone, R.B. Biologically Inspired Design; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Eshghi, S.; Nabati, F.; Shafaghi, S.; Nooraeefar, V.; Darvizeh, A.; Gorb, S.N.; Rajabi, H. An image based application in Matlab for automated modelling and morphological analysis of insect wings. Sci. Rep. 2022, 12, 13917. [Google Scholar] [CrossRef]
- Eshghi, S. “WingGram”. Figshare, 4 August 2022. [Google Scholar] [CrossRef]
- Smith, C.; Herbert, R.; Wootton, R.; Evans, K. The hind wing of the desert locust (Schistocerca gregaria Forskål): II. Mechanical properties and functioning of the membrane. J. Exp. Biol. 2000, 203, 2933–2943. [Google Scholar] [CrossRef]
- Gorb, S.N. Serial elastic elements in the damselfly wing: Mobile vein joints contain resilin. Sci. Nat. 1999, 86, 552–555. [Google Scholar] [CrossRef]
- Haas, F.; Gorb, S.; Blickhan, R. The function of resilin in beetle wings. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2000, 267, 1375–1381. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Ling, M.; Pan, C.; Chen, D.; Tong, J.; Li, X. Biomimetic structure design of dragonfly wing venation using topology optimization method. J. Mech. Med. Biol. 2014, 14, 1450078. [Google Scholar] [CrossRef]
- Sun, J.; Pan, C.; Tong, J.; Zhang, J. Coupled model analysis of the structure and nano-mechanical properties of dragonfly wings. IET Nanobiotechnol. 2010, 4, 10–18. [Google Scholar] [CrossRef]
- Arjangpay, A.; Darvizeh, A.; Tooski, M.Y. Effects of structural characteristics of a bionic dragonfly wing on its low velocity impact resistance. J. Bionic Eng. 2018, 15, 859–871. [Google Scholar] [CrossRef]
- Ren, H.; Wang, X.; Li, X.; Chen, Y. Effects of dragonfly wing structure on the dynamic performances. J. Bionic Eng. 2013, 10, 28–38. [Google Scholar] [CrossRef]
- Li, Z.-X.; Shen, W.; Tong, G.-S.; Tian, J.-M.; Vu-Quoc, L. On the vein-stiffening membrane structure of a dragonfly hind wing. J. Zhejiang Univ. Sci. A 2009, 10, 72–81. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Ren, H.; Yin, H.; Jia, S. Hierarchical dragonfly wing: Microstructure-biomechanical behavior relations. J. Bionic Eng. 2012, 9, 185–191. [Google Scholar] [CrossRef]
- Cromroy, H.L.; Wainwright, S.A.; Biggs, W.D.; Currey, J.D.; Gosline, J.M. Mechanical Design in Organisms. Fla. Entomol. 1976, 59, 320. [Google Scholar] [CrossRef]
- Shi, X.; Yu, H. Finite element analysis of dragonfly wing structural stiffness. Trans. Chin. Soc. Agric. Mach. 2012, 43, 224. [Google Scholar]
- Vincent, J.F.; Wegst, U.G. Design and mechanical properties of insect cuticle. Arthropod Struct. Dev. 2004, 33, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, L.; Yu, Z.; Liu, J.; Li, X.; Liang, Y. In-situ mechanical test of dragonfly wing veins and their crack arrest behavior. Micron 2018, 110, 67–72. [Google Scholar] [CrossRef]
- Sun, J.; Du, R.; Liu, C.; Liu, X.; Zhang, Z. Effects of Dragonfly Wing Vein Structure on the Flight Charateristics. In Proceedings of the 2018 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Hangzhou, China, 13–17 August 2018; pp. 138–141. [Google Scholar]
- Combes, S.A.; Daniel, T. Flexural stiffness in insect wings II. Spatial distribution and dynamic wing bending. J. Exp. Biol. 2003, 206, 2989–2997. [Google Scholar]
- Wootton, R.J.; Newman, D.J. Evolution, diversification, and mechanics of dragonfly wings. Dragonflies & damselflies. Model Org. Ecol. Evol. Res. 2008, 261, 274. [Google Scholar]
- Appel, E.; Heepe, L.; Lin, C.P.; Gorb, S.N. Ultrastructure of dragonfly wing veins: Composite structure of fibrous material supplemented by resilin. J. Anat. 2015, 227, 561–582. [Google Scholar] [CrossRef] [PubMed]

| Objects | Young’s Modulus [46] | Specific Weight (kN/cm3) | Density (kg/m3) | Poisson’s Ratio | Reference |
|---|---|---|---|---|---|
| General main vein of dragonfly wing | 1200 | 1332 | 0.25 | [7,15,47,48] | |
| 6.1 | [44] | ||||
| 30 | 1200 | 0.3 | [13,49,50] | ||
| 2860 | [48] | ||||
| 3.8 | 0.25 | [51] | |||
| 6 | 1260 | 0.25 | [7] |
| Model Labels | Filled | Cross-Section | Diameter Variation | Thickness Variation |
|---|---|---|---|---|
| I | solid | circular | uniform | uniform |
| II | hollow | circular | uniform | uniform |
| III | hollow | ellipse | uniform | uniform |
| IV | hollow | changing cross-section | uniform | uniform |
| V | hollow | changing cross-section | variable | uniform |
| VI | hollow | changing cross-section | variable | taper |
| Objects | Diameter Max (μm) | Diameter Min (μm) | Thickness Max (μm) | Thickness Min (μm) | Reference |
|---|---|---|---|---|---|
| Costa | 175 | 60 | 42.41 | 6.21 | [30,48,53] |
| Subcosta | 96.84 | 58.68 | 15.8 | 8.68 | |
| Radius | 87.93 | 48.96 | 15.75 | 7.39 | |
| Other main vein (Media, Cubitus, Anal) | 45 | 5 | 40 | 2 | [13] |
| Cross-vein | 3 | 3 | [13] | ||
| Membrane | 25 | 3.6 | [47] |
| FE Simulation Result Under Uniform Vertical Loads | Modelling Data | ||||||
|---|---|---|---|---|---|---|---|
| Model Label | Total Material Mass (mg) | Max Displacement (μm) | Max Axial Stress (N) | Main Vein Diameter (μm) | Main Vein Thickness (μm) | Cross Vein Diameter (μm) | Cross Vein Thickness (μm) |
| I | 44.7 | 25.08 | −0.812 To 3.26 | 135 | 2.5 | 30 | 15 |
| II | 25.4 | 26.09 | −0.78 To 3.22 | ||||
| III | 23.2 | 25.09 | −0.895 To 3.88 | 135/80 | |||
| IV | 22.2 | 25.09 | −1.35 To 5.94 | ||||
| V | 7.2 | 29.51 | −0.557 To 2.89 | changing diameter | |||
| VI | 4.2 | 26.83 | −0.34 To 2.5 | changing diameter | changing thickness | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, G.; Teixeira, F.F.; Loh, P. Parametric FEM-Based Analysis on Adaptive Vein Morphology of Dragonfly Wings Toward Material Efficiency. Biomimetics 2025, 10, 799. https://doi.org/10.3390/biomimetics10120799
Zhu G, Teixeira FF, Loh P. Parametric FEM-Based Analysis on Adaptive Vein Morphology of Dragonfly Wings Toward Material Efficiency. Biomimetics. 2025; 10(12):799. https://doi.org/10.3390/biomimetics10120799
Chicago/Turabian StyleZhu, Guanqi, Fred Fialho Teixeira, and Paul Loh. 2025. "Parametric FEM-Based Analysis on Adaptive Vein Morphology of Dragonfly Wings Toward Material Efficiency" Biomimetics 10, no. 12: 799. https://doi.org/10.3390/biomimetics10120799
APA StyleZhu, G., Teixeira, F. F., & Loh, P. (2025). Parametric FEM-Based Analysis on Adaptive Vein Morphology of Dragonfly Wings Toward Material Efficiency. Biomimetics, 10(12), 799. https://doi.org/10.3390/biomimetics10120799







