FBCA: Flexible Besiege and Conquer Algorithm for Multi-Layer Perceptron Optimization Problems
Abstract
1. Introduction
1.1. Motivation
1.2. Contributions
- Sine-Guided Soft Asymmetric Gaussian Perturbation Mechanism: an optimization mechanism that integrates Gaussian flexible micro-perturbations under sine factor guidance, enhancing the ability to quickly detect high-precision solutions, reducing the risk of local stagnation.
- Exponentially Modulated Spiral Perturbation Mechanism: a position update mechanism that applies exponential modulation through an adaptive spiral factor to improve population diversity and ensure fast-adaptive global convergence.
- Nonlinear Cognitive Coefficient-Driven Velocity Update Mechanism: drawing on the PSO’s velocity-based update mechanism, the nonlinear cognitive coefficient dynamically regulates the soldier position update, thereby improving fast-convergent performance and achieving a balanced exploration–exploitation trade-off.
- Validation on IEEE CEC 2017 and Six MLP Problems: extensive experiments on the IEEE CEC 2017 benchmark set (30D, 50D, and 100D) demonstrate FBCA’s excellence in numerical accuracy, convergence behavior, stability, and the Wilcoxon rank sum test. Notably, FBCA shows outstanding performance in high-dimensional composite function optimization. Moreover, in six MLP optimization problems, FBCA achieves an order-of-magnitude lead in the mean results of MSE on XOR and Heart datasets, surpassing the original BCA and other state-of-the-art algorithms such as SMA in function approximation problems.
2. Related Work
2.1. BCA: Besiege and Conquer Algorithm
| Algorithm 1 The pseudocode of the BCA |
|
2.2. PSO: Particle Swarm Optimization
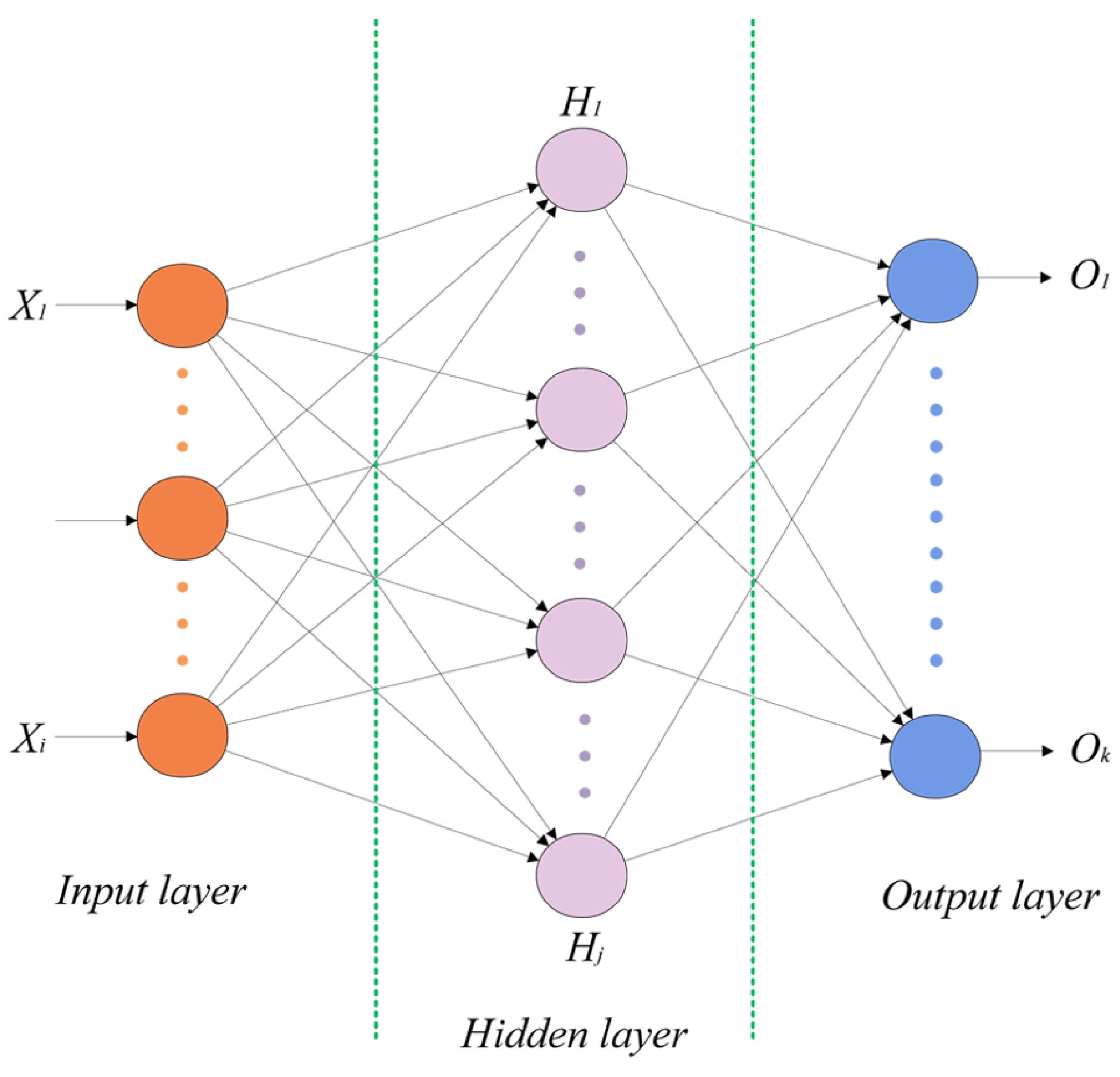
2.3. MLP: Multi-Layer Perceptron
3. Methods
3.1. Sine-Guided Soft Asymmetric Gaussian Perturbation Mechanism
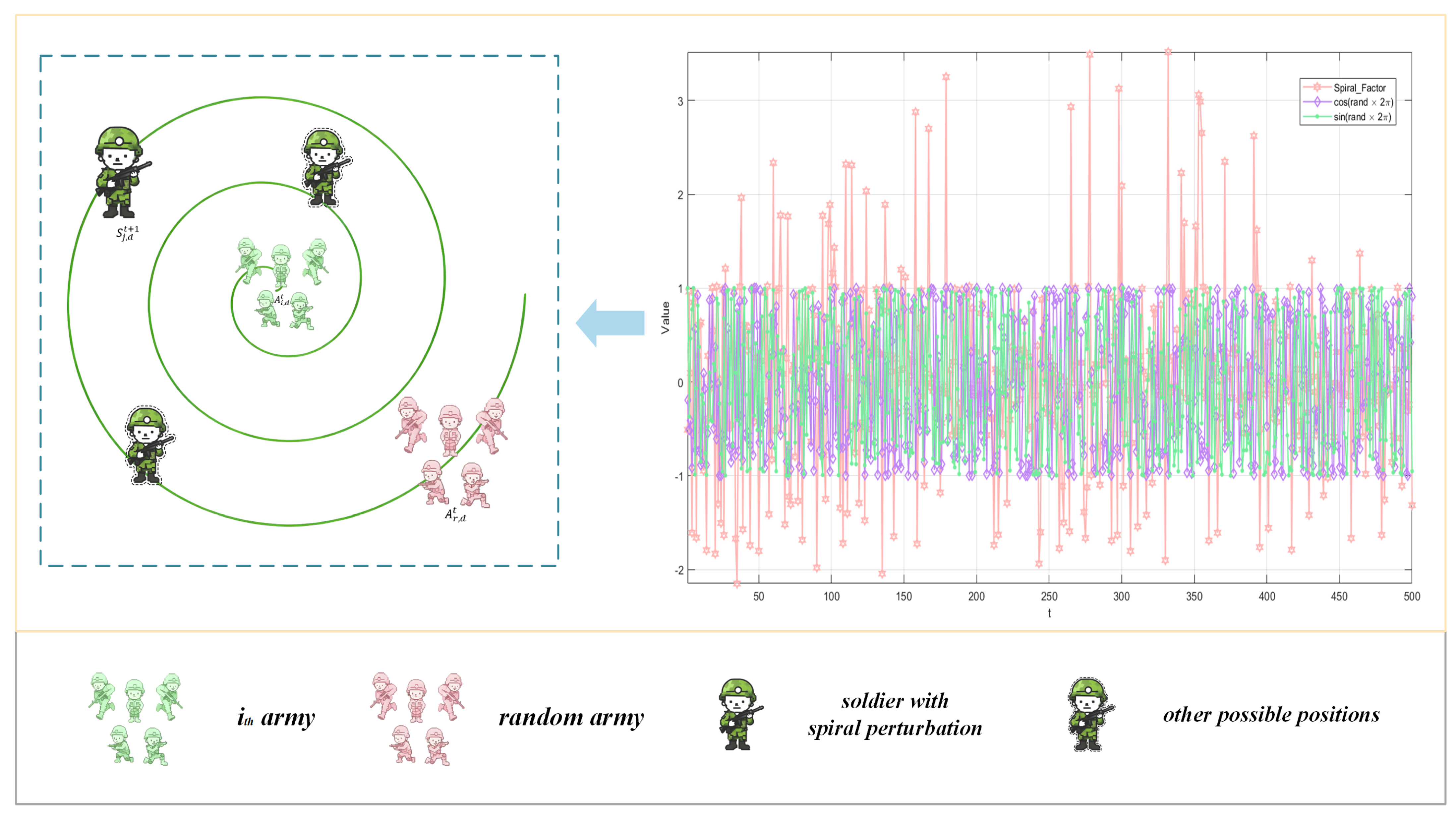
3.2. Exponentially Modulated Spiral Perturbation Mechanism
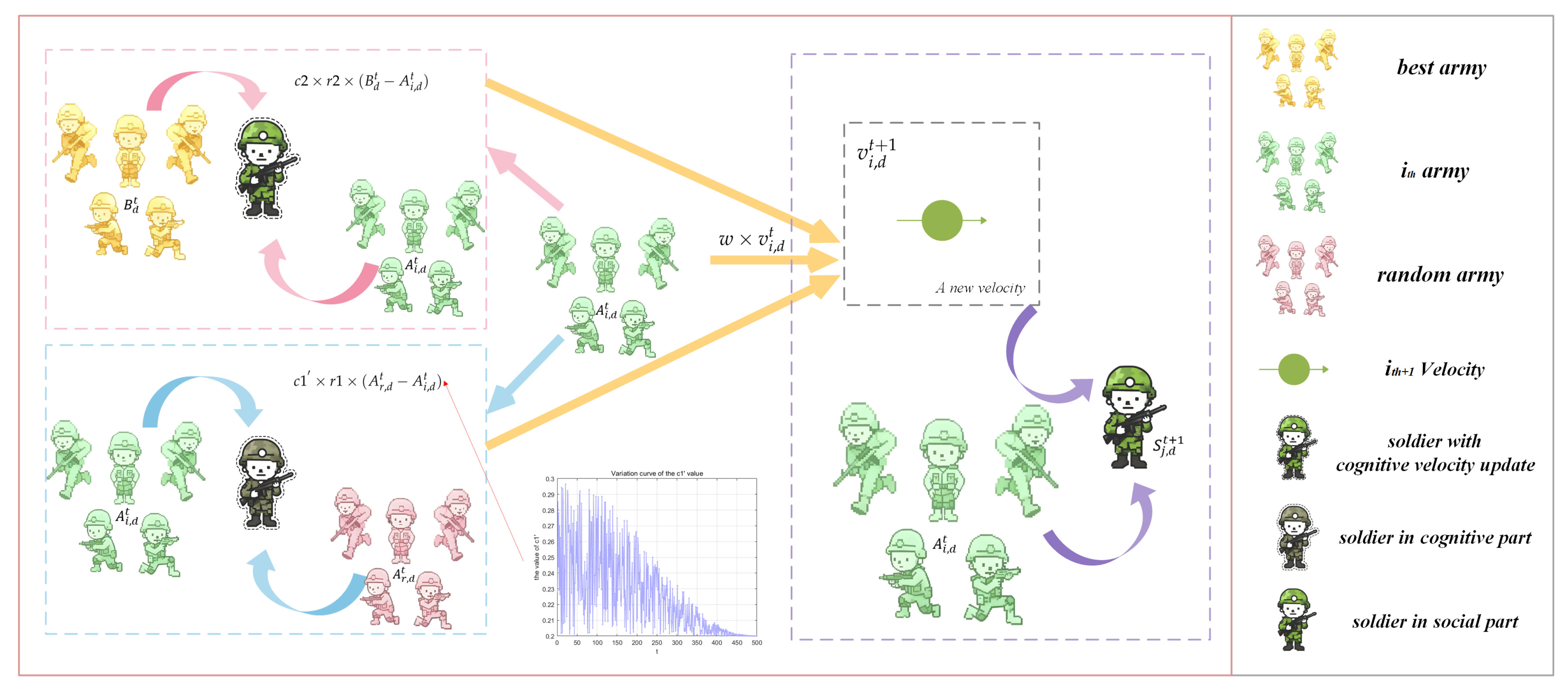
3.3. Nonlinear Cognitive Coefficient-Driven Velocity Update Mechanism
3.4. FBCA: Flexible Besiege and Conquer Algorithm
| Algorithm 2 The pseudocode of the FBCA |
|
3.5. Analyzing the Computational Complexity of FBCA
- Sine-Guided Soft Asymmetric Gaussian Perturbation Mechanism: Each dimension needs to perform a sine operation and Gaussian perturbation correction term once. The complexity of a single operation is O(1), so the complexity of a single soldier in a single dimension is O(1).
- Exponentially Modulated Spiral Perturbation Mechanism: including the calculation of exponential function (exp), cosine function (cos) and linear parameters b and l, the single-dimensional operation complexity is also O(1).
- Nonlinear Cognitive Coefficient-Driven Velocity Update Mechanism: It involves the calculation of the nonlinear cognitive coefficient () and the solution of speed update formula. The single-dimensional computational complexity is also O(1).
4. Experiments and Analysis
4.1. Experiment Settings
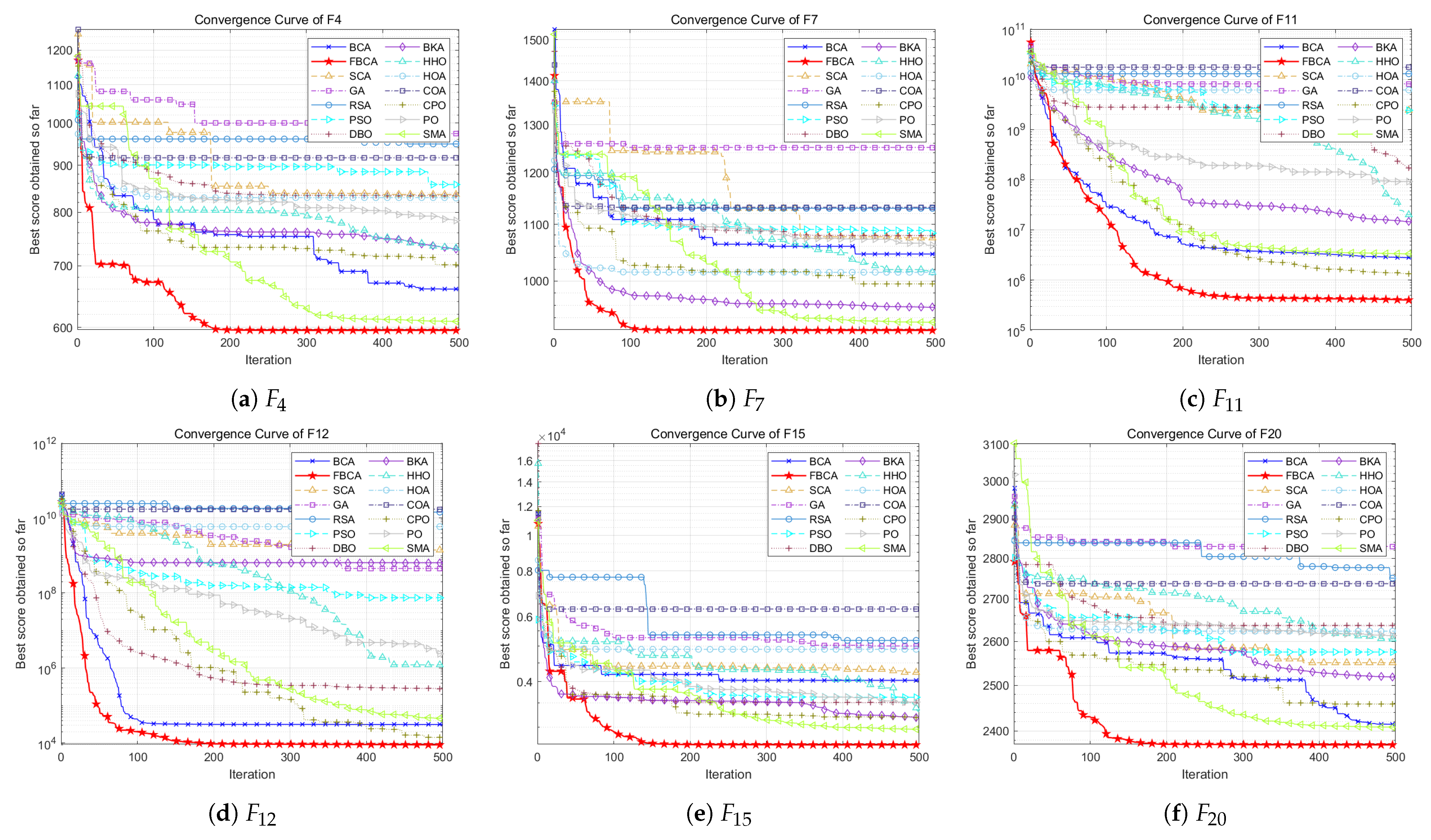
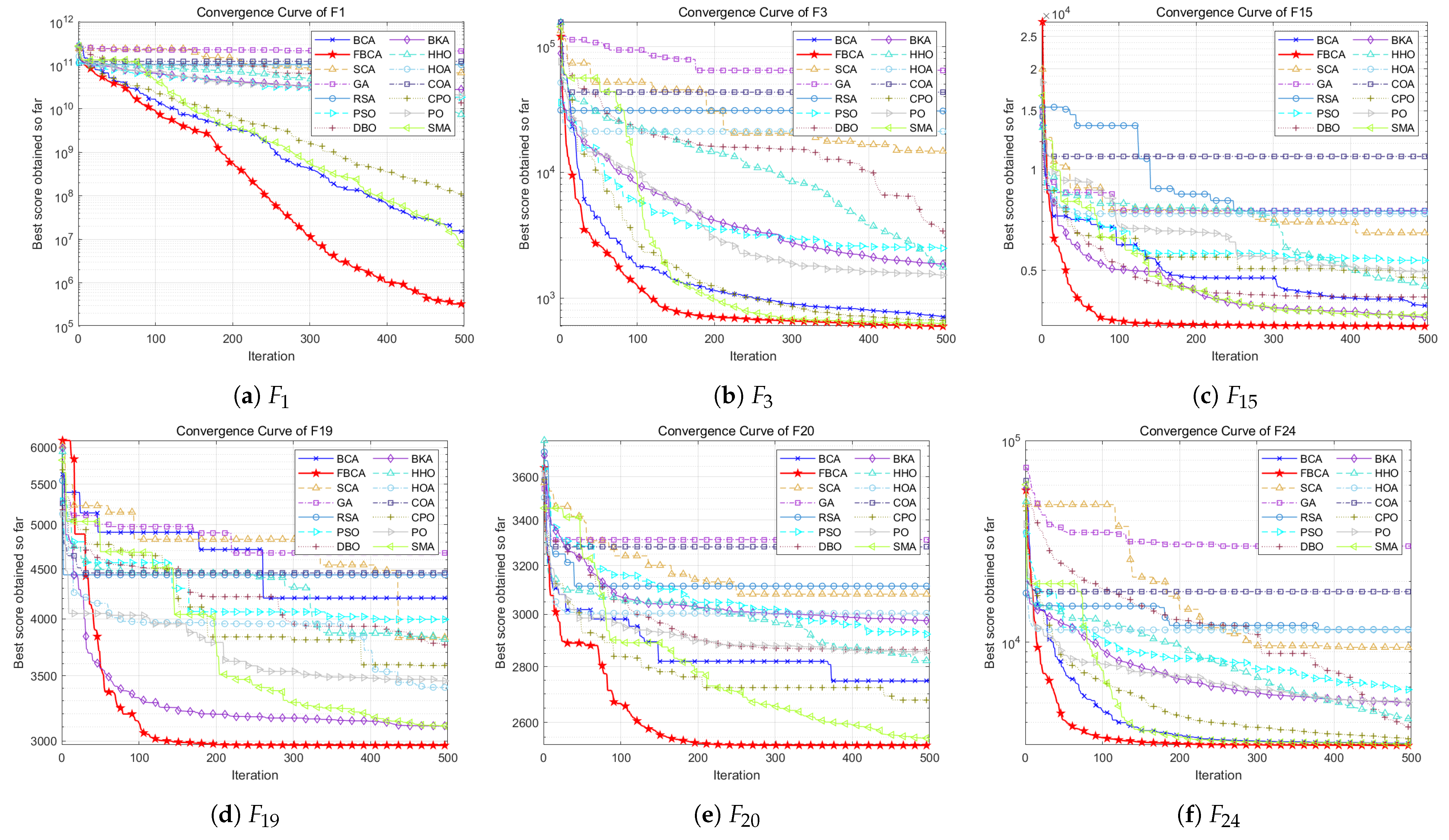
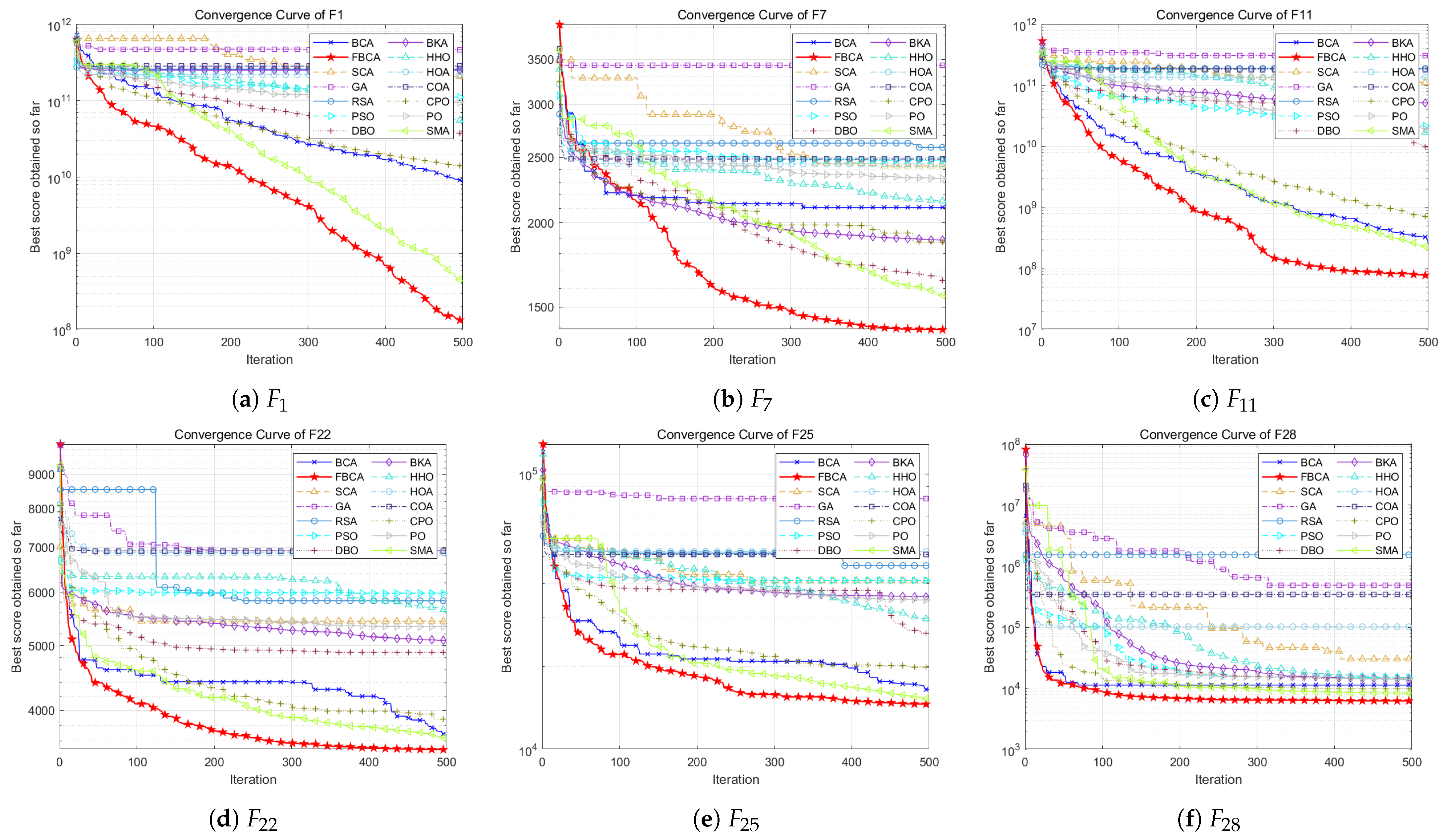
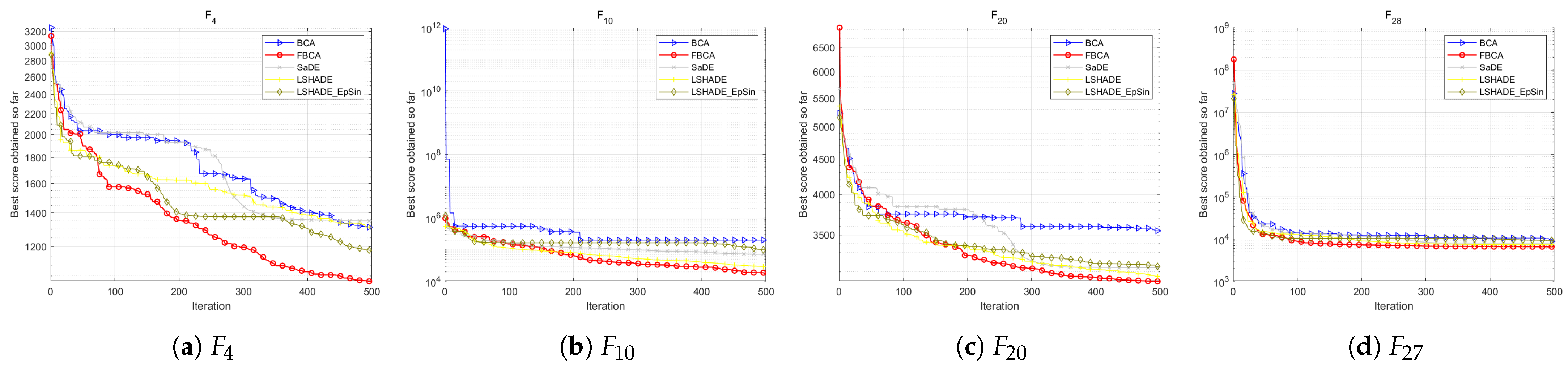
4.2. Qualitative Analysis
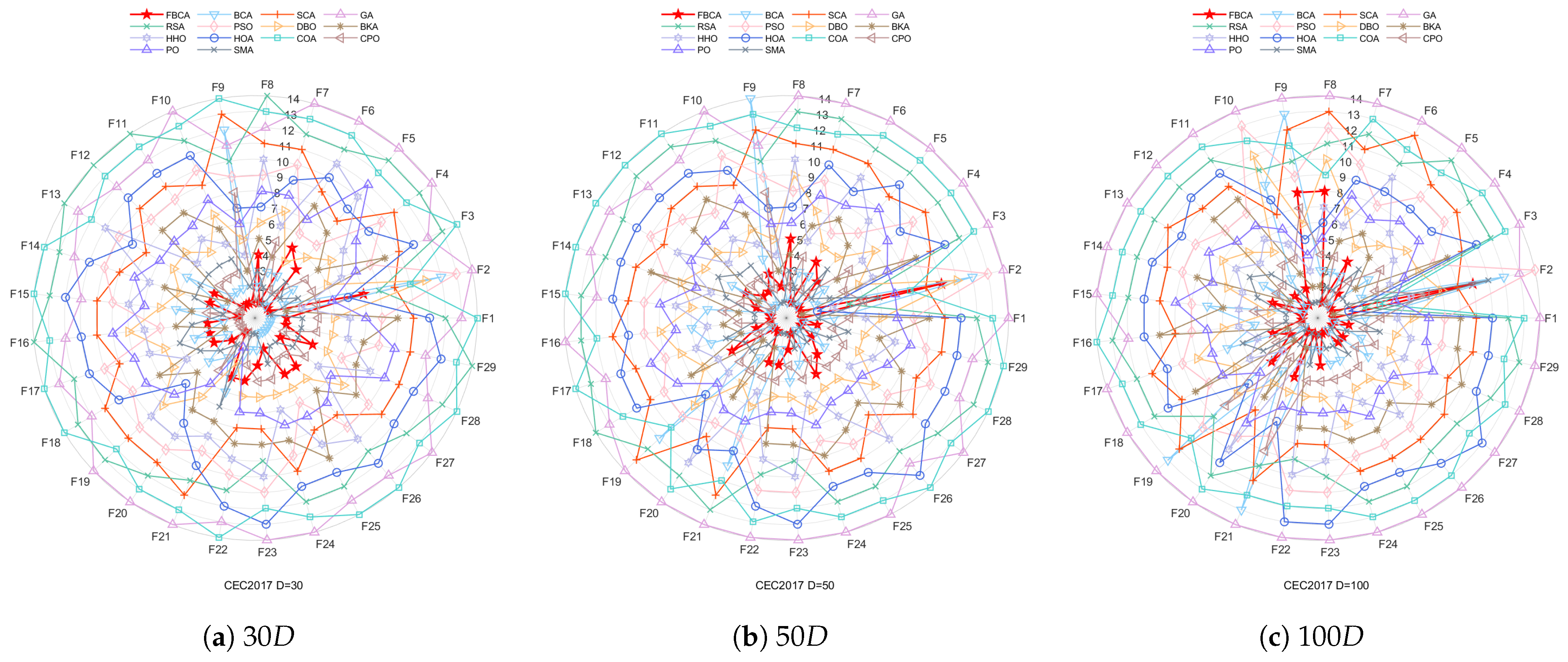
4.3. Quantitative Analysis
4.4. Statistical Testing
4.5. Stability Analysis
4.6. Parameter Sensitivity and Mechanism Validation
4.6.1. Influence of the Probability Parameter
4.6.2. Effect of Gaussian Perturbation Variance
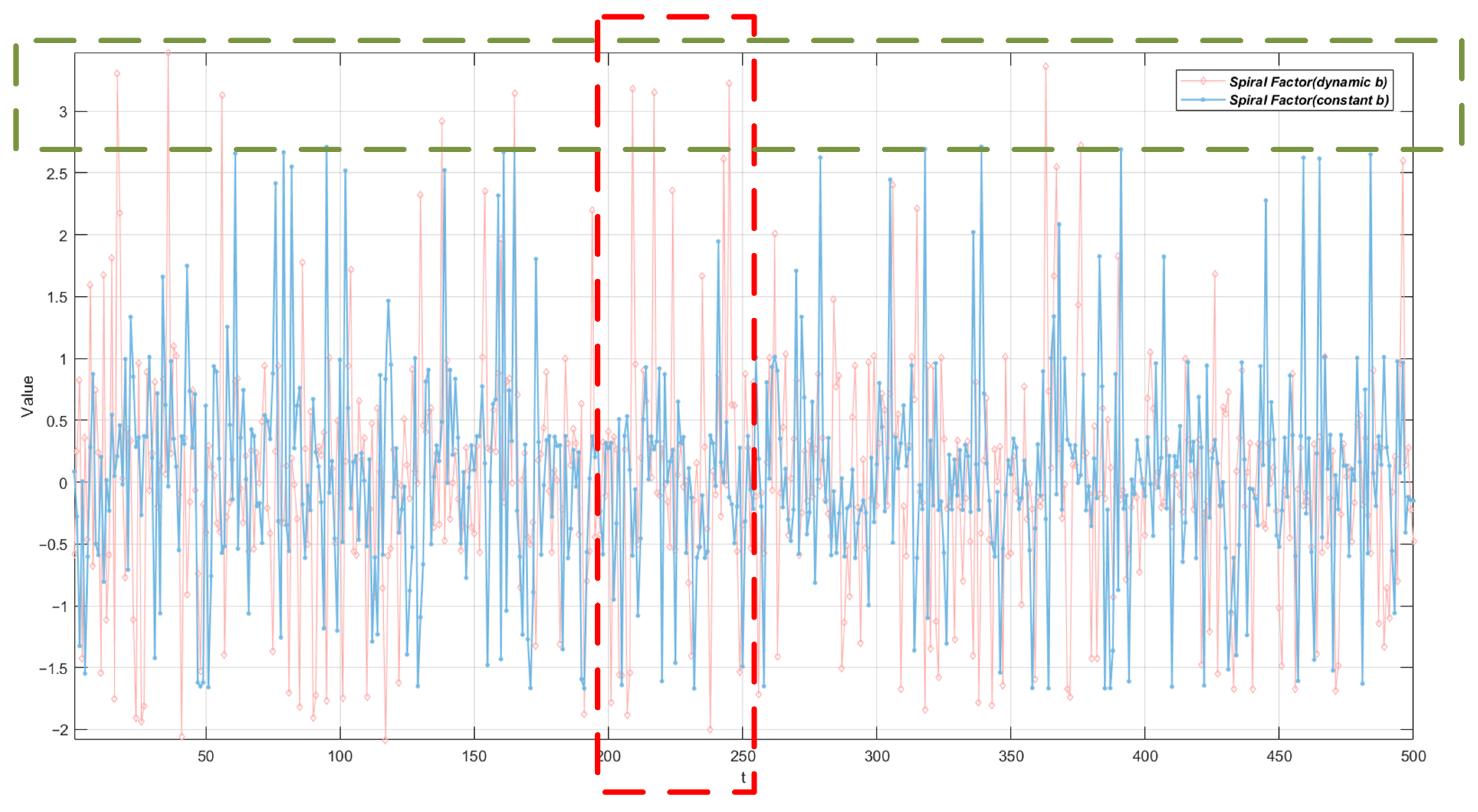
4.6.3. Comparison of Spiral Perturbation Mechanisms
4.6.4. Validation of the Velocity Update Mechanism
4.6.5. Comparison with SOTA Optimizers
5. MLP Optimization Problems
5.1. Training MLPs Using FBCA
5.2. MLP_XOR Problem
5.3. MLP_Iris Problem
5.4. MLP_Heart Problem
5.5. MLP_Sigmoid Problem
5.6. MLP_Cosine Problem
5.7. MLP_Sine Problem
5.8. Comparison with Gradient-Based Optimizers
5.9. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| F | Item | FBCA | BCA | SCA | GA | RSA | PSO | DBO | BKA | HHO | HOA | COA | CPO | PO | SMA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Std | 6.44 | 5.91 | 3.47 | 2.06 | 7.83 | 2.37 | 2.32 | 6.8 | 2.39 | 8.68 | 5.96 | 8.43 | 1.31 | 6.95 |
| Mean | 1.13 | 6.64 | 2.07 | 5.30 | 4.80 | 4.22 | 2.75 | 9.35 | 4.72 | 3.71 | 5.70 | 7.47 | 3.23 | 1.33 | |
| F2 | Std | 2.69 | 3.64 | 1.70 | 6.02 | 5.99 | 7.69 | 2.64 | 1.88 | 6.81 | 6.74 | 5.87 | 1.10 | 8.57 | 1.35 |
| Mean | 7.88 | 1.40 | 8.19 | 2.59 | 8.10 | 1.76 | 8.97 | 3.74 | 5.76 | 7.33 | 8.49 | 6.18 | 6.81 | 3.42 | |
| F3 | Std | 3.89 | 2.64 | 8.15 | 4.64 | 3.61 | 4.42 | 1.18 | 7.73 | 1.02 | 1.74 | 2.24 | 1.67 | 1.08 | 2.38 |
| Mean | 4.93 | 5.06 | 2.91 | 9.24 | 1.09 | 1.24 | 6.44 | 1.27 | 7.23 | 7.95 | 1.57 | 5.24 | 7.51 | 5.12 | |
| F4 | Std | 3.23 | 7.64 | 2.73 | 7.15 | 2.85 | 4.11 | 5.37 | 4.88 | 3.78 | 3.15 | 4.00 | 1.58 | 3.79 | 3.94 |
| Mean | 6.31 | 6.56 | 8.29 | 9.94 | 9.22 | 8.07 | 7.73 | 7.52 | 7.75 | 7.99 | 9.10 | 6.91 | 7.88 | 6.43 | |
| F5 | Std | 9.77 | 8.97 | 5.03 | 1.40 | 4.68 | 1.55 | 1.23 | 7.04 | 6.25 | 7.89 | 6.08 | 7.25 | 7.62 | 9.20 |
| Mean | 6.18 | 6.01 | 6.65 | 7.20 | 6.92 | 6.58 | 6.49 | 6.60 | 6.67 | 6.66 | 6.88 | 6.02 | 6.69 | 6.18 | |
| F6 | Std | 1.71 | 7.99 | 6.91 | 3.17 | 3.99 | 6.58 | 7.36 | 8.16 | 5.76 | 5.32 | 5.29 | 2.02 | 8.33 | 4.88 |
| Mean | 1.02 | 9.49 | 1.24 | 2.07 | 1.38 | 1.14 | 1.01 | 1.23 | 1.30 | 1.26 | 1.42 | 9.39 | 1.23 | 8.92 | |
| F7 | Std | 5.31 | 6.03 | 2.15 | 8.58 | 1.85 | 4.10 | 5.77 | 4.94 | 2.63 | 2.63 | 2.36 | 1.44 | 3.80 | 3.86 |
| Mean | 9.32 | 9.82 | 1.09 | 1.24 | 1.14 | 1.07 | 1.03 | 9.87 | 9.89 | 1.06 | 1.15 | 9.87 | 1.03 | 9.39 | |
| F8 | Std | 3.50 | 9.05 | 1.75 | 2.73 | 1.01 | 3.02 | 1.72 | 1.41 | 1.32 | 1.00 | 1.44 | 4.27 | 1.47 | 1.31 |
| Mean | 4.59 | 1.53 | 9.14 | 1.05 | 1.14 | 7.75 | 6.19 | 5.73 | 8.69 | 6.74 | 1.11 | 1.35 | 7.64 | 4.57 | |
| F9 | Std | 1.31 | 1.13 | 3.30 | 6.14 | 4.49 | 6.63 | 1.03 | 1.28 | 8.04 | 6.67 | 4.53 | 2.33 | 7.52 | 6.18 |
| Mean | 4.52 | 8.83 | 8.86 | 8.52 | 8.49 | 7.67 | 6.42 | 5.86 | 6.05 | 7.56 | 8.89 | 7.63 | 7.10 | 4.65 | |
| F10 | Std | 4.05 | 1.04 | 1.42 | 1.29 | 2.53 | 3.08 | 1.28 | 1.21 | 2.83 | 1.47 | 2.21 | 2.78 | 6.46 | 5.58 |
| Mean | 1.21 | 1.26 | 4.11 | 2.44 | 9.06 | 4.41 | 1.97 | 1.87 | 1.63 | 5.99 | 9.17 | 1.28 | 2.57 | 1.29 | |
| F11 | Std | 8.96 | 1.25 | 7.78 | 4.71 | 3.25 | 6.09 | 1.16 | 1.42 | 9.04 | 1.94 | 3.95 | 8.74 | 2.76 | 3.98 |
| Mean | 1.05 | 1.29 | 2.64 | 7.15 | 1.49 | 5.58 | 8.64 | 3.64 | 8.74 | 7.03 | 1.32 | 1.32 | 3.22 | 5.21 | |
| F12 | Std | 2.05 | 3.14 | 4.04 | 4.79 | 7.28 | 1.94 | 1.19 | 4.20 | 1.18 | 1.27 | 4.48 | 1.23 | 2.66 | 5.73 |
| Mean | 1.57 | 1.92 | 1.11 | 4.69 | 1.26 | 8.49 | 4.70 | 1.41 | 1.20 | 2.27 | 1.03 | 2.27 | 1.14 | 7.87 | |
| F13 | Std | 2.04 | 3.89 | 1.03 | 1.10 | 6.65 | 3.04 | 7.61 | 1.33 | 1.82 | 8.72 | 2.85 | 8.48 | 6.30 | 1.64 |
| Mean | 1.70 | 2.95 | 1.17 | 7.17 | 7.99 | 1.55 | 4.78 | 3.72 | 1.82 | 1.42 | 3.68 | 2.20 | 6.89 | 2.01 | |
| F14 | Std | 1.06 | 8.57 | 4.13 | 4.57 | 1.07 | 4.60 | 6.10 | 1.73 | 7.60 | 1.30 | 5.49 | 2.75 | 1.42 | 1.58 |
| Mean | 1.28 | 8.97 | 5.91 | 3.77 | 5.48 | 1.23 | 8.34 | 9.08 | 1.33 | 1.35 | 6.68 | 4.65 | 9.81 | 2.93 | |
| F15 | Std | 3.68 | 6.71 | 2.19 | 7.08 | 6.62 | 5.32 | 4.92 | 4.53 | 4.25 | 6.54 | 1.06 | 2.17 | 2.96 | 2.66 |
| Mean | 2.65 | 3.21 | 4.13 | 4.58 | 5.39 | 3.93 | 3.47 | 3.13 | 3.82 | 4.76 | 6.28 | 3.10 | 3.76 | 2.68 | |
| F16 | Std | 2.85 | 2.53 | 1.88 | 3.27 | 5.30 | 2.94 | 2.48 | 2.98 | 3.10 | 5.07 | 3.22 | 1.32 | 2.69 | 2.43 |
| Mean | 2.28 | 2.04 | 2.77 | 3.15 | 7.29 | 2.62 | 2.66 | 2.44 | 2.63 | 3.06 | 5.50 | 2.04 | 2.68 | 2.40 | |
| F17 | Std | 1.63 | 3.87 | 5.88 | 6.92 | 2.53 | 3.54 | 6.54 | 1.94 | 4.35 | 1.49 | 4.72 | 7.34 | 9.27 | 3.52 |
| Mean | 1.50 | 3.46 | 1.17 | 4.56 | 3.74 | 1.53 | 3.90 | 1.98 | 3.90 | 1.53 | 5.31 | 1.44 | 7.66 | 2.82 | |
| F18 | Std | 1.65 | 1.41 | 5.44 | 2.63 | 3.44 | 5.00 | 2.46 | 2.17 | 1.21 | 4.64 | 4.96 | 5.46 | 4.94 | 2.23 |
| Mean | 1.64 | 1.16 | 9.55 | 2.62 | 6.87 | 2.89 | 1.58 | 4.62 | 1.47 | 4.10 | 7.67 | 6.09 | 6.42 | 2.72 | |
| F19 | Std | 2.33 | 3.72 | 1.52 | 2.47 | 1.34 | 1.66 | 2.31 | 1.91 | 2.21 | 1.65 | 2.20 | 1.45 | 1.94 | 1.84 |
| Mean | 2.54 | 2.62 | 2.98 | 3.25 | 3.10 | 2.85 | 2.80 | 2.65 | 2.83 | 2.70 | 3.02 | 2.50 | 2.72 | 2.60 | |
| F20 | Std | 4.36 | 7.50 | 1.80 | 7.05 | 4.56 | 5.14 | 5.85 | 5.60 | 5.76 | 4.03 | 4.34 | 1.73 | 7.01 | 4.03 |
| Mean | 2.42 | 2.47 | 2.61 | 2.84 | 2.73 | 2.60 | 2.56 | 2.56 | 2.60 | 2.60 | 2.76 | 2.48 | 2.55 | 2.42 | |
| F21 | Std | 2.46 | 3.97 | 2.02 | 1.31 | 9.86 | 2.84 | 2.51 | 1.55 | 1.47 | 1.30 | 6.22 | 3.79 | 2.35 | 1.53 |
| Mean | 5.56 | 5.75 | 9.32 | 9.80 | 8.90 | 7.62 | 4.93 | 6.70 | 7.13 | 7.68 | 9.66 | 2.31 | 4.55 | 5.81 | |
| F22 | Std | 8.14 | 8.33 | 3.82 | 1.78 | 6.94 | 1.82 | 8.68 | 1.11 | 1.47 | 1.58 | 1.59 | 1.67 | 7.36 | 3.76 |
| Mean | 2.85 | 2.80 | 3.08 | 3.65 | 3.33 | 3.30 | 3.03 | 3.12 | 3.24 | 3.48 | 3.66 | 2.85 | 3.06 | 2.77 | |
| F23 | Std | 8.13 | 8.82 | 3.51 | 2.62 | 7.87 | 1.93 | 6.78 | 1.77 | 1.60 | 1.76 | 1.77 | 2.15 | 8.33 | 4.06 |
| Mean | 3.02 | 3.01 | 3.25 | 3.93 | 3.47 | 3.65 | 3.19 | 3.35 | 3.55 | 3.83 | 3.82 | 3.02 | 3.20 | 2.95 | |
| F24 | Std | 2.18 | 1.53 | 2.26 | 1.20 | 7.07 | 9.83 | 5.34 | 3.13 | 3.62 | 2.04 | 4.70 | 1.76 | 7.78 | 1.38 |
| Mean | 2.90 | 2.90 | 3.60 | 6.18 | 4.84 | 3.27 | 2.99 | 3.14 | 3.02 | 3.94 | 5.18 | 2.92 | 3.11 | 2.90 | |
| F25 | Std | 1.25 | 8.60 | 5.22 | 1.08 | 9.74 | 1.35 | 6.58 | 1.63 | 1.37 | 9.09 | 7.97 | 9.97 | 1.38 | 4.61 |
| Mean | 6.15 | 4.99 | 7.79 | 1.08 | 1.05 | 7.30 | 6.86 | 7.89 | 7.84 | 9.51 | 1.18 | 5.36 | 7.57 | 5.06 | |
| F26 | Std | 2.79 | 1.79 | 9.42 | 5.80 | 3.79 | 2.72 | 4.52 | 8.93 | 3.29 | 2.55 | 4.67 | 1.42 | 9.24 | 2.06 |
| Mean | 3.28 | 3.23 | 3.58 | 4.49 | 3.95 | 3.65 | 3.32 | 3.39 | 3.66 | 4.25 | 4.51 | 3.28 | 3.41 | 3.23 | |
| F27 | Std | 4.65 | 2.13 | 4.52 | 1.39 | 7.00 | 1.18 | 7.50 | 7.72 | 9.13 | 6.74 | 6.58 | 2.85 | 9.08 | 4.43 |
| Mean | 2.75 | 2.47 | 4.47 | 7.75 | 6.37 | 4.06 | 3.71 | 3.82 | 3.49 | 5.68 | 7.57 | 1.69 | 3.57 | 2.11 | |
| F28 | Std | 3.90 | 3.77 | 3.71 | 1.40 | 2.35 | 5.70 | 4.03 | 6.91 | 3.76 | 7.75 | 2.00 | 4.05 | 4.79 | 4.03 |
| Mean | 4.07 | 3.79 | 5.29 | 6.68 | 7.28 | 4.81 | 4.46 | 4.90 | 4.97 | 6.13 | 8.59 | 4.00 | 5.01 | 4.03 | |
| F29 | Std | 9.59 | 5.73 | 8.34 | 3.68 | 1.14 | 5.13 | 5.02 | 4.98 | 9.39 | 4.74 | 9.10 | 7.81 | 4.22 | 8.46 |
| Mean | 1.70 | 1.33 | 2.03 | 2.98 | 3.00 | 2.99 | 2.90 | 1.90 | 1.13 | 5.87 | 1.52 | 1.35 | 6.12 | 1.17 |
| F | Item | FBCA | BCA | SCA | GA | RSA | PSO | DBO | BKA | HHO | HOA | COA | CPO | PO | SMA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Std | 2.73 | 8.68 | 8.35 | 2.54 | 7.82 | 5.19 | 1.95 | 2.11 | 1.81 | 8.39 | 6.1 | 1.43 | 4.08 | 2.26 |
| Mean | 4.95 | 1.06 | 6.58 | 1.69 | 10.00 | 1.90 | 1.02 | 4.44 | 5.25 | 8.54 | 1.15 | 1.88 | 1.58 | 6.55 | |
| F2 | Std | 6.26 | 7.47 | 3.19 | 9.81 | 1.57 | 1.27 | 6.75 | 2.84 | 1.96 | 1.39 | 2.07 | 1.99 | 2.94 | 6.25 |
| Mean | 2.34 | 3.26 | 2.20 | 4.68 | 1.77 | 3.96 | 2.69 | 9.58 | 1.72 | 1.59 | 2.01 | 1.78 | 1.94 | 1.82 | |
| F3 | Std | 6.55 | 5.72 | 3.50 | 1.57 | 5.72 | 2.43 | 7.37 | 6.84 | 6.01 | 5.01 | 5.17 | 4.94 | 9.82 | 6.74 |
| Mean | 6.08 | 6.29 | 1.45 | 4.46 | 2.92 | 3.60 | 1.43 | 7.39 | 2.00 | 2.38 | 3.81 | 7.01 | 2.67 | 6.31 | |
| F4 | Std | 8.03 | 1.57 | 3.34 | 9.83 | 3.08 | 5.03 | 1.05 | 7.48 | 3.30 | 4.20 | 3.11 | 2.17 | 4.94 | 5.01 |
| Mean | 7.88 | 8.48 | 1.14 | 1.51 | 1.17 | 1.11 | 9.88 | 9.07 | 9.43 | 1.08 | 1.19 | 9.29 | 1.02 | 8.16 | |
| F5 | Std | 6.69 | 2.75 | 6.21 | 1.35 | 4.90 | 1.55 | 1.22 | 9.83 | 5.00 | 6.97 | 2.35 | 3.19 | 7.41 | 1.18 |
| Mean | 6.26 | 6.07 | 6.84 | 7.39 | 7.04 | 6.79 | 6.66 | 6.71 | 6.80 | 6.85 | 7.04 | 6.11 | 6.83 | 6.47 | |
| F6 | Std | 1.78 | 9.88 | 1.07 | 6.29 | 5.82 | 1.04 | 1.47 | 9.43 | 9.91 | 7.00 | 4.47 | 4.36 | 1.03 | 1.01 |
| Mean | 1.35 | 1.28 | 1.91 | 4.50 | 1.96 | 1.73 | 1.41 | 1.76 | 1.88 | 1.85 | 2.06 | 1.26 | 1.79 | 1.17 | |
| F7 | Std | 6.34 | 1.34 | 3.22 | 1.01 | 2.15 | 6.37 | 9.63 | 1.09 | 3.82 | 4.27 | 2.97 | 2.25 | 5.95 | 5.27 |
| Mean | 1.08 | 1.20 | 1.44 | 1.79 | 1.51 | 1.41 | 1.31 | 1.26 | 1.24 | 1.43 | 1.50 | 1.22 | 1.34 | 1.10 | |
| F8 | Std | 1.01 | 3.92 | 4.25 | 6.13 | 2.18 | 8.53 | 7.80 | 4.59 | 2.69 | 3.55 | 2.75 | 2.57 | 4.89 | 3.46 |
| Mean | 1.99 | 6.73 | 3.38 | 4.84 | 3.91 | 2.93 | 2.96 | 1.74 | 3.23 | 2.82 | 3.77 | 7.83 | 2.74 | 1.70 | |
| F9 | Std | 3.40 | 9.01 | 3.83 | 9.06 | 4.83 | 1.00 | 2.18 | 1.61 | 1.16 | 7.75 | 3.76 | 5.37 | 1.02 | 1.01 |
| Mean | 8.88 | 1.57 | 1.54 | 1.52 | 1.52 | 1.42 | 1.17 | 9.47 | 1.06 | 1.31 | 1.55 | 1.36 | 1.24 | 8.30 | |
| F10 | Std | 1.59 | 1.12 | 3.11 | 2.10 | 2.25 | 1.26 | 3.09 | 4.58 | 7.43 | 2.27 | 2.44 | 2.77 | 2.60 | 7.39 |
| Mean | 2.06 | 2.31 | 1.26 | 6.26 | 2.18 | 1.93 | 4.19 | 5.63 | 3.10 | 1.89 | 2.67 | 1.84 | 7.94 | 1.44 | |
| F11 | Std | 7.59 | 5.38 | 6.77 | 2.59 | 1.95 | 7.50 | 5.78 | 1.56 | 6.82 | 1.09 | 1.36 | 1.05 | 1.19 | 1.92 |
| Mean | 1.29 | 8.83 | 2.24 | 6.73 | 7.46 | 9.63 | 8.85 | 1.25 | 1.03 | 5.24 | 9.30 | 2.01 | 2.54 | 3.84 | |
| F12 | Std | 8.06 | 7.78 | 3.15 | 1.56 | 1.50 | 6.04 | 1.37 | 5.49 | 6.32 | 8.06 | 1.29 | 3.46 | 2.13 | 8.08 |
| Mean | 1.44 | 9.44 | 7.19 | 2.91 | 4.80 | 5.83 | 9.34 | 1.71 | 4.08 | 2.24 | 5.38 | 2.58 | 3.47 | 1.32 | |
| F13 | Std | 8.22 | 6.68 | 5.86 | 1.30 | 5.40 | 4.76 | 3.85 | 1.04 | 7.33 | 2.99 | 9.57 | 1.66 | 2.87 | 7.45 |
| Mean | 6.52 | 7.46 | 8.64 | 9.82 | 7.07 | 2.13 | 3.62 | 1.35 | 6.22 | 4.69 | 1.18 | 1.31 | 4.94 | 9.28 | |
| F14 | Std | 8.19 | 6.77 | 4.72 | 4.41 | 2.46 | 8.04 | 7.61 | 8.93 | 5.69 | 2.35 | 4.17 | 1.22 | 2.39 | 1.94 |
| Mean | 1.08 | 8.76 | 1.15 | 7.82 | 5.96 | 7.06 | 2.03 | 2.17 | 3.32 | 4.43 | 1.03 | 1.44 | 1.83 | 4.98 | |
| F15 | Std | 7.32 | 1.13 | 3.58 | 1.29 | 1.58 | 9.60 | 6.64 | 1.10 | 8.06 | 9.78 | 1.39 | 2.69 | 7.42 | 4.05 |
| Mean | 3.68 | 4.86 | 6.26 | 7.85 | 8.33 | 5.84 | 4.93 | 4.46 | 4.95 | 7.08 | 1.06 | 4.53 | 5.56 | 3.70 | |
| F16 | Std | 3.43 | 4.92 | 3.13 | 4.79 | 4.73 | 4.46 | 4.82 | 7.39 | 2.98 | 5.67 | 6.02 | 2.36 | 4.22 | 2.92 |
| Mean | 3.17 | 4.17 | 5.05 | 2.32 | 1.34 | 4.58 | 4.40 | 3.82 | 3.90 | 4.84 | 1.16 | 3.47 | 4.22 | 3.35 | |
| F17 | Std | 2.30 | 1.32 | 3.07 | 1.48 | 8.23 | 3.99 | 1.61 | 1.14 | 1.40 | 4.56 | 1.00 | 9.88 | 2.63 | 5.40 |
| Mean | 3.61 | 1.09 | 6.09 | 1.59 | 1.91 | 2.66 | 1.37 | 5.01 | 1.13 | 1.00 | 2.02 | 1.7 | 3.66 | 7.09 | |
| F18 | Std | 1.45 | 1.30 | 3.91 | 2.21 | 1.44 | 3.37 | 1.28 | 8.63 | 2.50 | 7.18 | 1.51 | 7.71 | 1.60 | 1.56 |
| Mean | 2.60 | 1.62 | 7.85 | 3.44 | 4.68 | 1.33 | 9.62 | 1.69 | 2.27 | 1.00 | 3.19 | 2.21 | 2.21 | 2.30 | |
| F19 | Std | 5.27 | 5.22 | 2.21 | 3.47 | 1.69 | 3.12 | 3.76 | 3.40 | 2.74 | 2.85 | 1.85 | 2.34 | 3.76 | 2.24 |
| Mean | 3.28 | 4.21 | 4.36 | 4.79 | 4.25 | 4.14 | 3.82 | 3.29 | 3.65 | 3.75 | 4.15 | 3.58 | 3.70 | 3.32 | |
| F20 | Std | 7.19 | 1.49 | 3.84 | 1.31 | 7.90 | 7.72 | 9.81 | 1.18 | 9.74 | 6.23 | 8.97 | 2.67 | 7.90 | 6.36 |
| Mean | 2.56 | 2.65 | 2.96 | 3.38 | 3.12 | 2.93 | 2.85 | 2.88 | 2.98 | 2.98 | 3.31 | 2.70 | 2.90 | 2.58 | |
| F21 | Std | 3.32 | 2.88 | 4.53 | 7.90 | 5.24 | 2.17 | 2.27 | 1.22 | 1.09 | 8.03 | 6.09 | 5.62 | 9.99 | 8.72 |
| Mean | 1.17 | 1.67 | 1.73 | 1.75 | 1.74 | 1.51 | 1.29 | 1.11 | 1.25 | 1.52 | 1.69 | 1.19 | 1.42 | 9.77 | |
| F22 | Std | 1.23 | 1.68 | 9.17 | 3.20 | 1.90 | 3.54 | 1.58 | 1.67 | 2.32 | 2.67 | 2.23 | 3.02 | 2.03 | 6.20 |
| Mean | 3.13 | 3.09 | 3.73 | 4.65 | 4.08 | 4.14 | 3.61 | 3.78 | 4.04 | 4.52 | 4.60 | 3.18 | 3.67 | 3.03 | |
| F23 | Std | 1.22 | 1.21 | 9.37 | 3.67 | 6.44 | 3.01 | 1.56 | 2.26 | 2.47 | 2.61 | 2.27 | 3.12 | 1.17 | 1.03 |
| Mean | 3.31 | 3.36 | 3.88 | 5.16 | 4.42 | 4.63 | 3.71 | 3.90 | 4.47 | 5.00 | 4.88 | 3.35 | 3.80 | 3.19 | |
| F24 | Std | 3.38 | 3.63 | 1.20 | 7.21 | 1.42 | 1.00 | 1.70 | 2.40 | 2.45 | 9.93 | 1.07 | 4.87 | 4.58 | 4.22 |
| Mean | 3.08 | 3.11 | 9.68 | 2.99 | 1.34 | 5.85 | 3.91 | 6.13 | 3.83 | 1.19 | 1.56 | 3.23 | 4.51 | 3.10 | |
| F25 | Std | 1.65 | 1.61 | 7.94 | 2.33 | 7.26 | 2.19 | 1.60 | 2.20 | 1.40 | 7.39 | 6.25 | 1.74 | 2.34 | 2.28 |
| Mean | 8.06 | 7.33 | 1.41 | 2.13 | 1.65 | 1.27 | 1.13 | 1.25 | 1.19 | 1.55 | 1.76 | 7.99 | 1.14 | 4.87 | |
| F26 | Std | 1.39 | 8.58 | 2.52 | 7.19 | 1.13 | 8.53 | 3.16 | 5.00 | 5.65 | 5.97 | 8.51 | 7.25 | 2.90 | 8.15 |
| Mean | 3.65 | 3.47 | 4.97 | 6.98 | 6.14 | 5.12 | 4.04 | 4.35 | 5.21 | 6.98 | 7.14 | 3.74 | 4.25 | 3.55 | |
| F27 | Std | 4.18 | 8.34 | 1.10 | 3.23 | 1.28 | 1.60 | 2.38 | 2.26 | 3.99 | 8.84 | 1.63 | 1.24 | 4.19 | 4.88 |
| Mean | 3.39 | 3.45 | 8.69 | 1.60 | 1.17 | 6.50 | 6.32 | 6.82 | 4.81 | 1.07 | 1.37 | 3.70 | 5.32 | 3.38 | |
| F28 | Std | 3.67 | 8.21 | 9.39 | 6.29 | 8.47 | 9.26 | 8.47 | 5.28 | 8.38 | 2.20 | 1.24 | 2.50 | 1.69 | 4.67 |
| Mean | 4.52 | 4.65 | 8.86 | 3.31 | 6.00 | 9.51 | 6.45 | 8.27 | 6.99 | 2.26 | 1.33 | 5.16 | 8.16 | 4.88 | |
| F29 | Std | 4.56 | 4.39 | 5.00 | 2.99 | 2.40 | 6.39 | 4.60 | 6.15 | 3.83 | 1.21 | 2.92 | 3.10 | 1.27 | 4.43 |
| Mean | 1.75 | 1.2 | 1.42 | 5.64 | 7.92 | 5.30 | 5.18 | 7.25 | 1.34 | 3.02 | 8.81 | 9.53 | 3.12 | 1.28 |
| F | Item | FBCA | BCA | SCA | GA | RSA | PSO | DBO | BKA | HHO | HOA | COA | CPO | PO | SMA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Std | 1.87 | 7.9 | 1.31 | 7.1 | 6.9 | 1.88 | 7.29 | 4.57 | 7.91 | 1.27 | 1.21 | 3.26 | 1.09 | 9.06 |
| Mean | 2.00 | 1.08 | 2.19 | 5.55 | 2.46 | 1.16 | 8.25 | 1.53 | 5.15 | 2.25 | 2.72 | 1.40 | 8.96 | 4.70 | |
| F2 | Std | 9.09 | 2.65 | 9.83 | 1.47 | 1.82 | 2.72 | 2.23 | 4.75 | 2.03 | 1.07 | 1.37 | 6.25 | 6.67 | 3.19 |
| Mean | 6.97 | 8.59 | 6.20 | 9.21 | 3.48 | 1.02 | 6.16 | 2.72 | 4.12 | 3.28 | 3.55 | 4.60 | 3.91 | 7.78 | |
| F3 | Std | 1.01 | 4.73 | 8.51 | 4.82 | 1.31 | 5.16 | 1.46 | 1.48 | 1.98 | 1.07 | 1.15 | 4.95 | 2.15 | 1.03 |
| Mean | 1.01 | 1.85 | 5.16 | 2.01 | 8.57 | 1.86 | 1.63 | 2.43 | 9.53 | 6.93 | 1.10 | 2.58 | 1.25 | 1.02 | |
| F4 | Std | 1.86 | 2.46 | 5.83 | 1.54 | 4.03 | 9.36 | 2.18 | 1.56 | 6.31 | 6.33 | 4.40 | 6.34 | 6.78 | 1.06 |
| Mean | 1.26 | 1.57 | 2.04 | 2.92 | 2.06 | 2.02 | 1.71 | 1.55 | 1.67 | 1.92 | 2.13 | 1.64 | 1.81 | 1.38 | |
| F5 | Std | 6.18 | 1.18 | 4.61 | 6.83 | 4.13 | 9.24 | 1.32 | 6.33 | 4.23 | 5.47 | 4.20 | 5.87 | 4.68 | 5.81 |
| Mean | 6.40 | 6.33 | 7.05 | 7.61 | 7.13 | 7.03 | 6.79 | 6.78 | 6.90 | 6.97 | 7.13 | 6.41 | 6.96 | 6.65 | |
| F6 | Std | 3.34 | 2.11 | 3.06 | 9.98 | 8.14 | 2.06 | 2.64 | 1.90 | 1.06 | 1.25 | 7.80 | 1.16 | 1.26 | 2.69 |
| Mean | 2.63 | 2.54 | 4.09 | 1.17 | 3.84 | 3.68 | 2.98 | 3.42 | 3.76 | 3.69 | 4.04 | 2.35 | 3.66 | 2.37 | |
| F7 | Std | 1.86 | 1.82 | 7.82 | 1.79 | 4.08 | 1.14 | 2.21 | 1.19 | 5.78 | 8.18 | 5.16 | 5.98 | 7.18 | 1.08 |
| Mean | 1.53 | 1.94 | 2.41 | 3.33 | 2.54 | 2.40 | 2.15 | 2.00 | 2.12 | 2.36 | 2.59 | 1.98 | 2.27 | 1.68 | |
| F8 | Std | 1.79 | 1.49 | 1.09 | 2.55 | 3.31 | 1.28 | 1.19 | 1.07 | 4.99 | 6.22 | 3.98 | 6.60 | 5.54 | 3.51 |
| Mean | 7.05 | 4.42 | 9.48 | 1.54 | 8.27 | 9.02 | 7.99 | 3.85 | 6.93 | 6.80 | 7.87 | 4.87 | 6.45 | 3.78 | |
| F9 | Std | 2.64 | 6.73 | 6.39 | 8.89 | 9.94 | 1.30 | 4.65 | 1.44 | 1.78 | 1.35 | 5.20 | 6.21 | 1.68 | 1.13 |
| Mean | 3.12 | 3.38 | 3.30 | 3.40 | 3.21 | 3.15 | 2.93 | 1.98 | 2.45 | 2.93 | 3.29 | 3.07 | 2.73 | 1.90 | |
| F10 | Std | 1.68 | 3.85 | 2.66 | 1.58 | 3.97 | 4.92 | 5.37 | 3.46 | 3.88 | 3.60 | 5.00 | 1.56 | 2.16 | 8.64 |
| Mean | 5.05 | 1.93 | 1.75 | 5.36 | 2.13 | 5.29 | 2.18 | 7.35 | 1.52 | 1.86 | 2.66 | 9.05 | 1.62 | 2.39 | |
| F11 | Std | 4.98 | 4.91 | 1.27 | 6.92 | 1.62 | 1.20 | 2.75 | 3.56 | 3.72 | 1.74 | 1.49 | 3.02 | 3.94 | 2.31 |
| Mean | 1.02 | 5.75 | 9.45 | 2.91 | 1.85 | 3.00 | 7.94 | 6.44 | 1.15 | 1.52 | 2.06 | 8.36 | 1.82 | 4.46 | |
| F12 | Std | 1.13 | 7.19 | 2.87 | 1.39 | 5.43 | 2.13 | 2.48 | 6.26 | 1.42 | 3.91 | 5.92 | 1.01 | 1.15 | 5.31 |
| Mean | 5.69 | 1.38 | 1.77 | 6.86 | 4.60 | 3.37 | 3.42 | 6.98 | 2.73 | 3.12 | 4.76 | 1.85 | 1.76 | 1.71 | |
| F13 | Std | 1.41 | 6.59 | 2.20 | 1.66 | 4.40 | 2.28 | 9.15 | 6.41 | 3.83 | 2.21 | 5.02 | 1.77 | 6.73 | 3.54 |
| Mean | 3.02 | 7.05 | 5.71 | 2.29 | 8.72 | 2.98 | 1.54 | 3.18 | 1.16 | 4.31 | 1.14 | 4.39 | 1.72 | 5.40 | |
| F14 | Std | 1.95 | 6.59 | 1.50 | 1.09 | 4.40 | 1.79 | 9.64 | 3.29 | 1.35 | 3.60 | 4.48 | 3.88 | 2.20 | 2.41 |
| Mean | 1.65 | 7.37 | 5.62 | 3.01 | 2.22 | 1.65 | 6.39 | 1.28 | 1.86 | 1.76 | 2.63 | 1.01 | 2.50 | 9.25 | |
| F15 | Std | 1.83 | 1.46 | 1.12 | 5.51 | 2.64 | 1.25 | 1.55 | 3.67 | 1.29 | 1.97 | 2.31 | 5.54 | 1.64 | 5.85 |
| Mean | 6.16 | 1.13 | 1.51 | 3.00 | 2.20 | 1.23 | 9.41 | 1.13 | 1.07 | 1.76 | 2.51 | 1.04 | 1.33 | 6.50 | |
| F16 | Std | 6.63 | 5.52 | 4.27 | 1.25 | 8.43 | 6.52 | 1.29 | 1.45 | 2.40 | 2.20 | 1.54 | 4.29 | 1.15 | 7.25 |
| Mean | 4.77 | 8.46 | 5.76 | 7.37 | 8.79 | 4.32 | 9.63 | 3.90 | 8.85 | 2.26 | 1.63 | 7.02 | 1.50 | 5.65 | |
| F17 | Std | 3.79 | 1.27 | 6.34 | 3.49 | 9.00 | 3.11 | 1.33 | 1.61 | 4.27 | 3.14 | 1.54 | 2.45 | 9.85 | 4.15 |
| Mean | 6.74 | 1.74 | 1.34 | 4.72 | 1.74 | 5.06 | 2.56 | 6.58 | 8.87 | 7.15 | 3.24 | 5.45 | 2.22 | 1.00 | |
| F18 | Std | 7.09 | 6.12 | 1.49 | 9.60 | 4.56 | 4.99 | 1.65 | 4.50 | 5.13 | 3.29 | 5.20 | 9.26 | 2.23 | 4.39 |
| Mean | 1.12 | 7.31 | 5.33 | 3.02 | 2.50 | 1.18 | 1.37 | 2.27 | 4.91 | 1.53 | 2.64 | 1.19 | 2.77 | 6.90 | |
| F19 | Std | 1.37 | 3.20 | 3.30 | 3.29 | 2.07 | 3.56 | 7.95 | 9.30 | 4.99 | 5.12 | 2.40 | 2.80 | 4.98 | 6.70 |
| Mean | 6.33 | 8.31 | 8.11 | 8.83 | 7.90 | 7.91 | 7.21 | 6.06 | 6.25 | 6.95 | 8.00 | 7.36 | 6.70 | 5.80 | |
| F20 | Std | 2.15 | 2.36 | 1.01 | 2.43 | 2.28 | 2.31 | 2.12 | 2.96 | 2.44 | 1.82 | 2.44 | 4.70 | 1.27 | 1.46 |
| Mean | 3.10 | 3.42 | 4.18 | 5.34 | 4.61 | 4.29 | 4.07 | 4.15 | 4.44 | 4.51 | 5.05 | 3.40 | 4.20 | 3.21 | |
| F21 | Std | 5.64 | 8.54 | 7.43 | 1.47 | 8.58 | 1.81 | 4.62 | 2.73 | 1.93 | 8.77 | 7.06 | 7.02 | 1.49 | 1.21 |
| Mean | 2.99 | 3.61 | 3.52 | 3.65 | 3.48 | 3.27 | 3.04 | 2.39 | 2.73 | 3.22 | 3.54 | 3.31 | 3.04 | 2.08 | |
| F22 | Std | 1.25 | 2.00 | 1.43 | 6.14 | 1.80 | 4.56 | 2.41 | 3.10 | 5.48 | 4.85 | 3.16 | 5.22 | 2.18 | 1.25 |
| Mean | 3.58 | 3.59 | 5.26 | 8.03 | 5.72 | 6.32 | 4.82 | 5.24 | 5.89 | 7.33 | 6.74 | 4.00 | 5.09 | 3.59 | |
| F23 | Std | 2.35 | 2.62 | 2.63 | 1.54 | 2.65 | 9.98 | 5.28 | 8.76 | 7.31 | 7.44 | 8.58 | 6.81 | 3.85 | 1.73 |
| Mean | 4.36 | 4.34 | 7.43 | 1.31 | 9.65 | 1.02 | 6.19 | 7.00 | 8.47 | 1.20 | 1.04 | 4.56 | 6.60 | 4.26 | |
| F24 | Std | 1.44 | 2.89 | 2.94 | 1.46 | 2.35 | 2.27 | 5.56 | 4.47 | 5.11 | 2.08 | 1.22 | 3.87 | 9.58 | 7.28 |
| Mean | 3.70 | 4.46 | 2.26 | 9.62 | 2.59 | 1.44 | 9.79 | 1.34 | 6.81 | 2.41 | 3.03 | 5.01 | 9.01 | 3.70 | |
| F25 | Std | 2.19 | 2.47 | 3.38 | 9.66 | 2.20 | 1.52 | 3.97 | 7.23 | 2.65 | 3.14 | 1.85 | 1.49 | 3.52 | 2.64 |
| Mean | 1.59 | 1.63 | 4.22 | 7.74 | 5.02 | 3.85 | 2.69 | 3.67 | 3.23 | 4.80 | 5.34 | 2.11 | 3.35 | 1.60 | |
| F26 | Std | 8.15 | 1.41 | 5.68 | 1.79 | 2.31 | 1.92 | 4.64 | 1.48 | 1.13 | 1.13 | 1.57 | 9.73 | 4.87 | 1.05 |
| Mean | 3.78 | 3.79 | 8.70 | 1.53 | 1.16 | 7.87 | 4.62 | 5.95 | 7.02 | 1.32 | 1.50 | 4.23 | 5.31 | 3.85 | |
| F27 | Std | 3.48 | 1.27 | 3.65 | 8.84 | 2.32 | 2.40 | 7.08 | 6.83 | 8.50 | 2.19 | 1.62 | 4.81 | 1.63 | 7.13 |
| Mean | 4.07 | 6.29 | 2.76 | 6.31 | 2.89 | 1.82 | 1.70 | 2.00 | 9.49 | 3.13 | 3.02 | 5.98 | 1.19 | 3.73 | |
| F28 | Std | 6.90 | 1.91 | 1.10 | 1.46 | 4.84 | 2.16 | 2.30 | 9.79 | 1.83 | 1.48 | 5.99 | 4.70 | 2.95 | 5.35 |
| Mean | 6.98 | 9.31 | 3.20 | 1.26 | 6.66 | 1.61 | 1.23 | 5.46 | 1.30 | 1.67 | 8.15 | 1.03 | 1.80 | 8.28 | |
| F29 | Std | 5.40 | 5.33 | 2.37 | 1.32 | 4.79 | 3.63 | 1.23 | 6.08 | 3.69 | 6.38 | 6.77 | 3.42 | 1.12 | 8.65 |
| Mean | 8.27 | 7.05 | 1.21 | 5.49 | 4.26 | 4.03 | 2.68 | 5.75 | 8.27 | 2.76 | 4.21 | 7.67 | 2.13 | 1.64 |
References
- Zhang, W.; Shen, X.; Zhang, H.; Yin, Z.; Sun, J.; Zhang, X.; Zou, L. Feature importance measure of a multilayer perceptron based on the presingle-connection layer. Knowl. Inf. Syst. 2024, 66, 511–533. [Google Scholar] [CrossRef]
- Chan, K.Y.; Abu-Salih, B.; Qaddoura, R.; Al-Zoubi, A.; Palade, V.; Pham, D.S.; Del Ser, J.; Muhammad, K. Deep neural networks in the cloud: Review, applications, challenges and research directions. Neurocomputing 2023, 545, 126327. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Zhang, Y.; Han, X.; Deveci, M.; Parmar, M. A review of convolutional neural networks in computer vision. Artif. Intell. Rev. 2024, 57, 99. [Google Scholar] [CrossRef]
- Sajun, A.R.; Zualkernan, I.; Sankalpa, D. A historical survey of advances in transformer architectures. Appl. Sci. 2024, 14, 4316. [Google Scholar] [CrossRef]
- Terven, J.; Córdova-Esparza, D.M.; Romero-González, J.A. A comprehensive review of yolo architectures in computer vision: From yolov1 to yolov8 and yolo-nas. Mach. Learn. Knowl. Extr. 2023, 5, 1680–1716. [Google Scholar] [CrossRef]
- Deng, Z.; Ma, W.; Han, Q.L.; Zhou, W.; Zhu, X.; Wen, S.; Xiang, Y. Exploring DeepSeek: A Survey on Advances, Applications, Challenges and Future Directions. IEEE/CAA J. Autom. Sin. 2025, 12, 872–893. [Google Scholar] [CrossRef]
- Jin, C.; Netrapalli, P.; Ge, R.; Kakade, S.M.; Jordan, M.I. On nonconvex optimization for machine learning: Gradients, stochasticity, and saddle points. J. ACM (JACM) 2021, 68, 1–29. [Google Scholar] [CrossRef]
- Swenson, B.; Murray, R.; Poor, H.V.; Kar, S. Distributed stochastic gradient descent: Nonconvexity, nonsmoothness, and convergence to local minima. J. Mach. Learn. Res. 2022, 23, 1–62. [Google Scholar]
- Van Thieu, N.; Mirjalili, S.; Garg, H.; Hoang, N.T. MetaPerceptron: A standardized framework for metaheuristic-driven multi-layer perceptron optimization. Comput. Stand. Interfaces 2025, 93, 103977. [Google Scholar] [CrossRef]
- Mirjalili, S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons. Appl. Intell. 2015, 43, 150–161. [Google Scholar] [CrossRef]
- Hai, T.; Li, H.; Band, S.S.; Shadkani, S.; Samadianfard, S.; Hashemi, S.; Chau, K.W.; Mousavi, A. Comparison of the efficacy of particle swarm optimization and stochastic gradient descent algorithms on multi-layer perceptron model to estimate longitudinal dispersion coefficients in natural streams. Eng. Appl. Comput. Fluid Mech. 2022, 16, 2207–2221. [Google Scholar] [CrossRef]
- Hameed, F.; Alkhzaimi, H. Hybrid genetic algorithm and deep learning techniques for advanced side-channel attacks. Sci. Rep. 2025, 15, 25728. [Google Scholar] [CrossRef]
- Gurgenc, E.; Altay, O.; Altay, E.V. AOSMA-MLP: A novel method for hybrid metaheuristics artificial neural networks and a new approach for prediction of geothermal reservoir temperature. Appl. Sci. 2024, 14, 3534. [Google Scholar] [CrossRef]
- Lu, Y.; Zhao, H. Research on Slope Stability Prediction Based on MC-BKA-MLP Mixed Model. Appl. Sci. 2025, 15, 3158. [Google Scholar] [CrossRef]
- Abu-Doush, I.; Ahmed, B.; Awadallah, M.A.; Al-Betar, M.A.; Rababaah, A.R. Enhancing multilayer perceptron neural network using archive-based harris hawks optimizer to predict gold prices. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101557. [Google Scholar] [CrossRef]
- Mohammadi, B.; Guan, Y.; Moazenzadeh, R.; Safari, M.J.S. Implementation of hybrid particle swarm optimization-differential evolution algorithms coupled with multi-layer perceptron for suspended sediment load estimation. Catena 2021, 198, 105024. [Google Scholar] [CrossRef]
- Ehteram, M.; Panahi, F.; Ahmed, A.N.; Huang, Y.F.; Kumar, P.; Elshafie, A. Predicting evaporation with optimized artificial neural network using multi-objective salp swarm algorithm. Environ. Sci. Pollut. Res. 2022, 29, 10675–10701. [Google Scholar] [CrossRef]
- Yang, Z.; Jiang, Y.; Yeh, W.C. Self-learning salp swarm algorithm for global optimization and its application in multi-layer perceptron model training. Sci. Rep. 2024, 14, 27401. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Cui, Z.; Wang, M.; Liu, B.; Tian, W. A machine learning proxy based multi-objective optimization method for low-carbon hydrogen production. J. Clean. Prod. 2024, 445, 141377. [Google Scholar] [CrossRef]
- Jiang, J.; Wu, J.; Luo, J.; Yang, X.; Huang, Z. MOBCA: Multi-Objective Besiege and Conquer Algorithm. Biomimetics 2024, 9, 316. [Google Scholar] [CrossRef]
- Jiang, J.; Meng, X.; Wu, J.; Tian, J.; Xu, G.; Li, W. BCA: Besiege and Conquer Algorithm. Symmetry 2025, 17, 217. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Qamar, R.; Zardari, B.A. Artificial Neural Networks: An Overview. Mesopotamian J. Comput. Sci. 2023, 2023, 124–133. [Google Scholar] [CrossRef] [PubMed]
- Xi, F. Stability for a random evolution equation with Gaussian perturbation. J. Math. Anal. Appl. 2002, 272, 458–472. [Google Scholar] [CrossRef]
- Omar, M.B.; Bingi, K.; Prusty, B.R.; Ibrahim, R. Recent advances and applications of spiral dynamics optimization algorithm: A review. Fractal Fract. 2022, 6, 27. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Yang, Q.; Hua, L.; Gao, X.; Xu, D.; Lu, Z.; Jeon, S.W.; Zhang, J. Stochastic cognitive dominance leading particle swarm optimization for multimodal problems. Mathematics 2022, 10, 761. [Google Scholar] [CrossRef]
- Yang, Q.; Jing, Y.; Gao, X.; Xu, D.; Lu, Z.; Jeon, S.W.; Zhang, J. Predominant cognitive learning particle swarm optimization for global numerical optimization. Mathematics 2022, 10, 1620. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.C.; Hu, X.X.; Qiu, L.; Zang, H.F. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl.-Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovskỳ, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G.; Ma, L.; Zhu, T.; Wu, X.; Heidari, A.A.; Chen, Y.; Chen, H. Parrot optimizer: Algorithm and applications to medical problems. Comput. Biol. Med. 2024, 172, 108064. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Zheng, B.; Chen, Y.; Wang, C.; Heidari, A.A.; Liu, L.; Chen, H. The moss growth optimization (MGO): Concepts and performance. J. Comput. Des. Eng. 2024, 11, 184–221. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, C. An Innovative Differentiated Creative Search Based on Collaborative Development and Population Evaluation. Biomimetics 2025, 10, 260. [Google Scholar] [CrossRef]
- Potter, K.; Hagen, H.; Kerren, A.; Dannenmann, P. Methods for presenting statistical information: The box plot. In Proceedings of the VLUDS, Seoul, Republic of Korea, 11 September 2006; pp. 97–106. Available online: https://api.semanticscholar.org/CorpusID:1344717 (accessed on 28 October 2025).
- Brest, J.; Zumer, V.; Maucec, M.S. Self-adaptive differential evolution algorithm in constrained real-parameter optimization. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; IEEE: New York, NY, USA, 2006; pp. 215–222. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; IEEE: New York, NY, USA, 2014; pp. 1658–1665. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017; IEEE: New York, NY, USA, 2017; pp. 372–379. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 2002, 1, 67–82. [Google Scholar] [CrossRef]
- Jia, H.; Lu, C. Guided learning strategy: A novel update mechanism for metaheuristic algorithms design and improvement. Knowl.-Based Syst. 2024, 286, 111402. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovskỳ, P. Osprey optimization algorithm: A new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front. Mech. Eng. 2023, 8, 1126450. [Google Scholar] [CrossRef]
- Meng, X.; Jiang, J.; Wang, H. AGWO: Advanced GWO in multi-layer perception optimization. Expert Syst. Appl. 2021, 173, 114676. [Google Scholar] [CrossRef]
- McGarry, K.J.; Wermter, S.; MacIntyre, J. Knowledge extraction from radial basis function networks and multilayer perceptrons. In Proceedings of the IJCNN’99. International Joint Conference on Neural Networks. Proceedings (Cat. No. 99CH36339), Washington, DC, USA, 10–16 July 1999; IEEE: New York, NY, USA, 1999; Volume 4, pp. 2494–2497. [Google Scholar] [CrossRef]
- Daniel, W.B.; Yeung, E. A constructive approach for one-shot training of neural networks using hypercube-based topological coverings. arXiv 2019, arXiv:1901.02878. [Google Scholar] [CrossRef]
- Fisher, R.A. Iris. UCI Machine Learning Repository. 1936. Available online: https://archive.ics.uci.edu/dataset/53/iris (accessed on 28 October 2025).
- Ay, Ş.; Ekinci, E.; Garip, Z. A comparative analysis of meta-heuristic optimization algorithms for feature selection on ML-based classification of heart-related diseases. J. Supercomput. 2023, 79, 11797. [Google Scholar] [CrossRef]
- Janosi, A.; Steinbrunn, W.; Pfisterer, M.; Detrano, R. Heart Disease. UCI Machine Learning Repository. 1989. Available online: https://archive.ics.uci.edu/dataset/45/heart+disease (accessed on 28 October 2025).
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. CoRR 2014, abs/1412.6980. Available online: https://api.semanticscholar.org/CorpusID:6628106 (accessed on 28 October 2025).
- Cao, J.; Qian, C.; Huang, Y.; Chen, D.; Gao, Y.; Dong, J.; Guo, D.; Qu, X. A Dynamics Theory of RMSProp-Based Implicit Regularization in Deep Low-Rank Matrix Factorization. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 18750–18764. [Google Scholar] [CrossRef] [PubMed]
- Ward, R.; Wu, X.; Bottou, L. Adagrad stepsizes: Sharp convergence over nonconvex landscapes. J. Mach. Learn. Res. 2020, 21, 1–30. [Google Scholar]
- Oyelade, O.N.; Aminu, E.F.; Wang, H.; Rafferty, K. An adaptation of hybrid binary optimization algorithms for medical image feature selection in neural network for classification of breast cancer. Neurocomputing 2025, 617, 129018. [Google Scholar] [CrossRef]
- Fu, Y. Research on Financial Time Series Prediction Model Based on Multifractal Trend Cross Correlation Removal and Deep Learning. Procedia Comput. Sci. 2025, 261, 217–226. [Google Scholar] [CrossRef]
- Wafa, A.A.; Eldefrawi, M.M.; Farhan, M.S. Advancing multimodal emotion recognition in big data through prompt engineering and deep adaptive learning. J. Big Data 2025, 12, 210. [Google Scholar] [CrossRef]




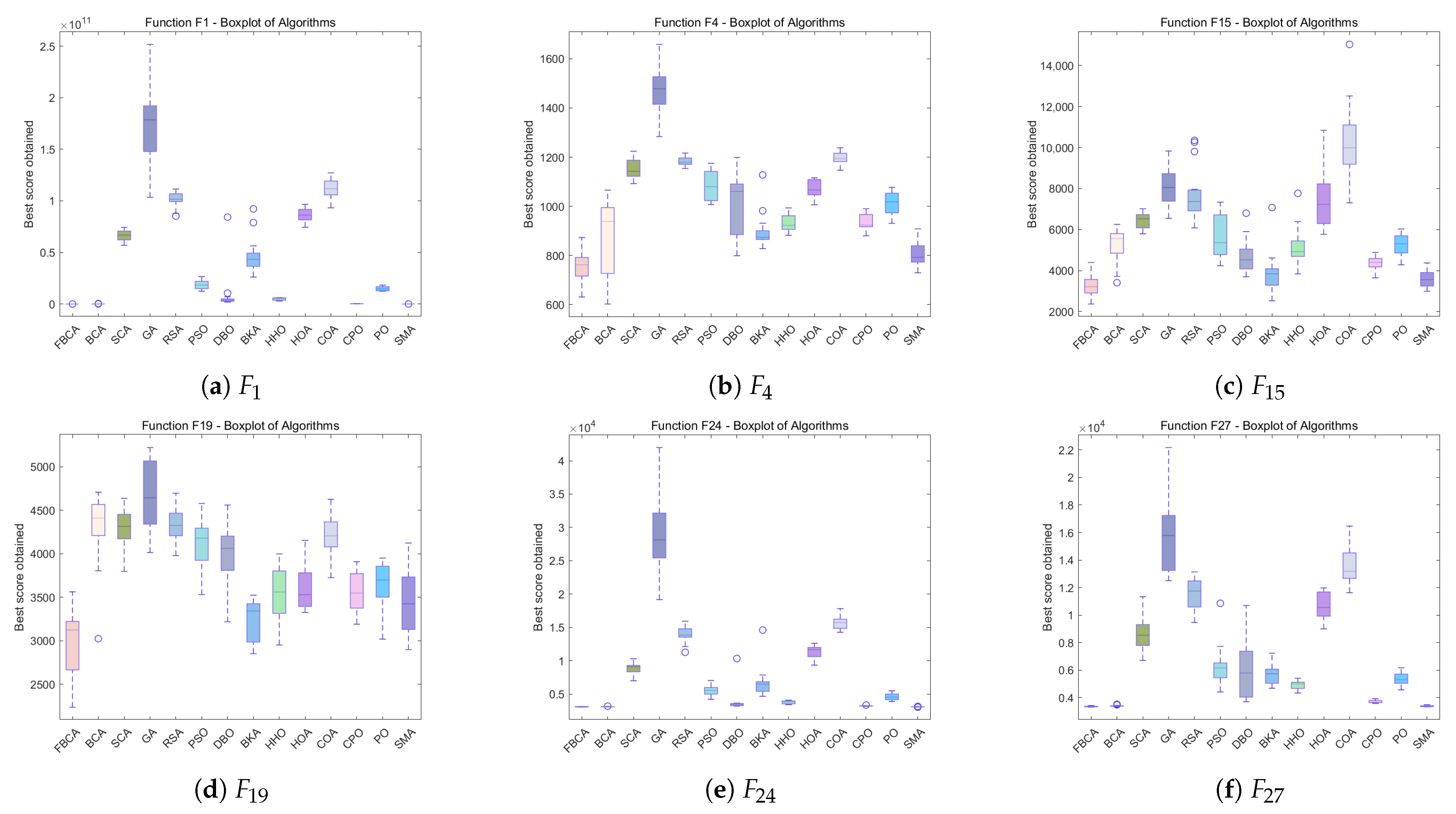


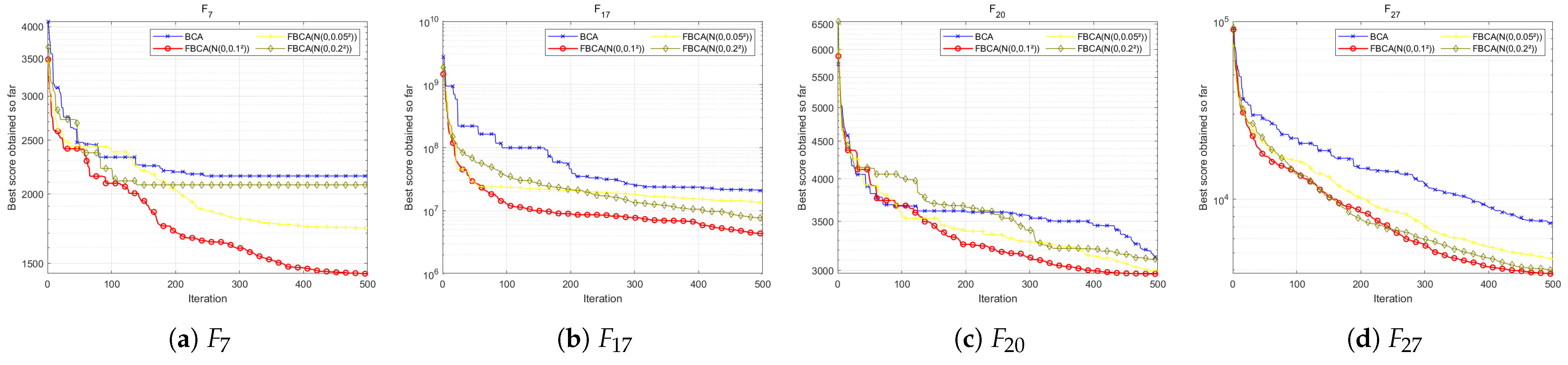
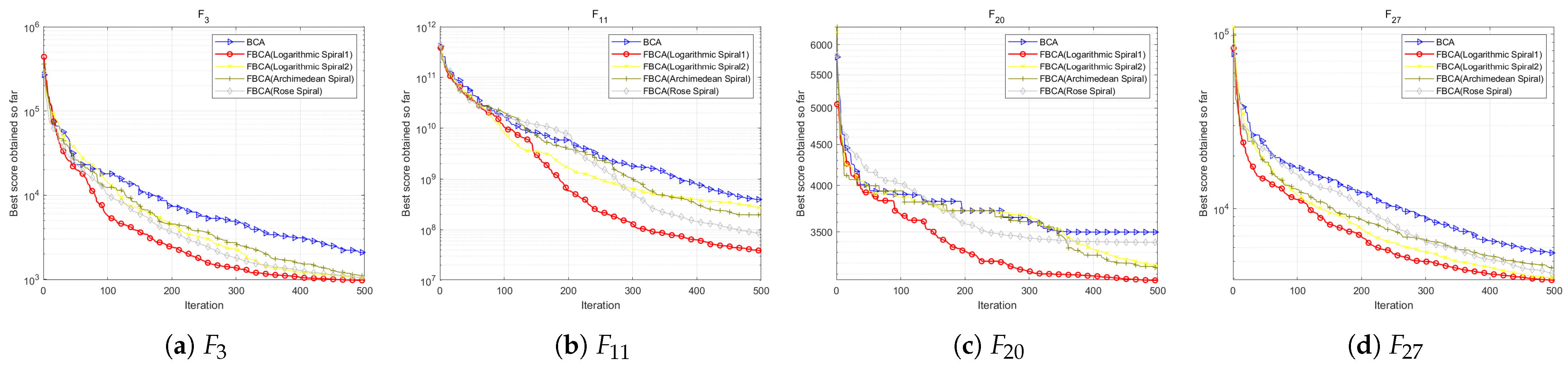
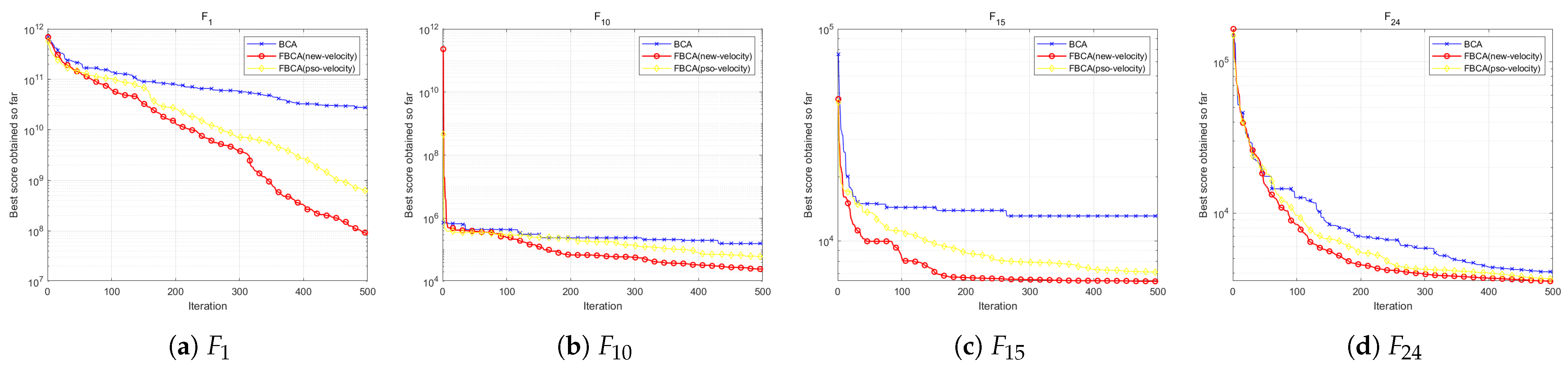

| Algorithms | Parameters | Values | Reference |
|---|---|---|---|
| SCA | a | 2 | [31] |
| r | Linearly decreased from a to 0 | ||
| GA | CrossPercent | 70% | [22] |
| MutatPercent | 20% | ||
| ElitPercent | 10% | ||
| RSA | Evolutionary sense | randomly decreasing values between 2 and −2 | [32] |
| Sensitive parameter | = 0.005 | ||
| Sensitive parameter | = 0.1 | ||
| PSO | Cognitive component | 2 | [24] |
| Social component | 2 | ||
| DBO | k and | 0.1 | [33] |
| b | 0.3 | ||
| S | 0.5 | ||
| BKA | p | 0.9 | [34] |
| r | range from [0, 1] | ||
| HHO | range from [−1, 1] | [35] | |
| 1.5 | |||
| HOA | Angle of inclination of the trail | range from [0, 50°] | [36] |
| Sweep Factor (SF) of the hiker | range from [1, 3] | ||
| COA | I | 1 or 2 | [37] |
| CPO | 0.1 | [38] | |
| 0.5 | |||
| T | 2 | ||
| PO | p | [0, 1] | [39] |
| SMA | Linearly decreased from 1 to 0 | [40] |
| Index | FBCA | BCA | SCA | GA | RSA | PSO | DBO | BKA | HHO | HOA | COA | CPO | PO | SMA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D = 30 | Average ranking | 2.72 | 3.10 | 9.72 | 12.93 | 12.28 | 8.90 | 5.79 | 6.24 | 7.34 | 10.10 | 13.10 | 2.79 | 7.14 | 2.83 |
| Total ranking | 1 | 4 | 10 | 13 | 12 | 9 | 5 | 6 | 8 | 11 | 14 | 2 | 8 | 3 | |
| D = 50 | Average ranking | 2.45 | 3.86 | 9.97 | 13.31 | 11.86 | 8.93 | 6.17 | 6 | 6.52 | 10.10 | 12.79 | 3.41 | 7.07 | 2.55 |
| Total ranking | 1 | 4 | 10 | 14 | 12 | 9 | 6 | 5 | 7 | 11 | 13 | 3 | 8 | 2 | |
| D = 100 | Average ranking | 2.52 | 4.55 | 10.10 | 13.90 | 11.17 | 9.24 | 6.24 | 6.03 | 5.93 | 9.79 | 12.17 | 4 | 6.69 | 2.66 |
| Total ranking | 1 | 4 | 11 | 14 | 12 | 9 | 7 | 6 | 5 | 10 | 13 | 3 | 8 | 2 |
| F | FBCA | BCA | SCA | GA | RSA | PSO | DBO | BKA | HHO | HOA | COA | CPO | PO | SMA | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | |
| F1 | 2 | 1 | 1 | 1 | 3 | 3 | 10 | 10 | 10 | 13 | 14 | 14 | 12 | 12 | 12 | 8 | 8 | 8 | 5 | 6 | 6 | 9 | 9 | 9 | 6 | 5 | 5 | 11 | 11 | 11 | 14 | 13 | 13 | 4 | 4 | 4 | 7 | 7 | 7 | 3 | 2 | 2 |
| F2 | 7 | 10 | 10 | 12 | 12 | 12 | 9 | 9 | 9 | 14 | 14 | 13 | 8 | 4 | 3 | 13 | 13 | 14 | 11 | 11 | 8 | 2 | 1 | 1 | 3 | 3 | 6 | 6 | 2 | 2 | 10 | 8 | 4 | 4 | 5 | 7 | 5 | 7 | 5 | 1 | 6 | 11 |
| F3 | 1 | 1 | 1 | 2 | 2 | 3 | 10 | 10 | 10 | 12 | 14 | 14 | 13 | 12 | 12 | 8 | 8 | 8 | 5 | 5 | 7 | 9 | 9 | 9 | 6 | 6 | 5 | 11 | 11 | 11 | 14 | 13 | 13 | 4 | 4 | 4 | 7 | 7 | 6 | 3 | 3 | 2 |
| F4 | 1 | 1 | 1 | 3 | 3 | 4 | 11 | 11 | 11 | 14 | 14 | 14 | 13 | 12 | 12 | 10 | 10 | 10 | 6 | 7 | 7 | 5 | 4 | 3 | 7 | 6 | 6 | 9 | 9 | 9 | 12 | 13 | 13 | 4 | 5 | 5 | 8 | 8 | 8 | 2 | 2 | 2 |
| F5 | 4 | 3 | 2 | 1 | 1 | 1 | 8 | 10 | 11 | 14 | 14 | 14 | 13 | 12 | 13 | 6 | 7 | 10 | 5 | 5 | 6 | 7 | 6 | 5 | 10 | 8 | 7 | 9 | 11 | 9 | 12 | 13 | 12 | 2 | 2 | 3 | 11 | 9 | 8 | 3 | 4 | 4 |
| F6 | 5 | 4 | 4 | 3 | 3 | 3 | 9 | 11 | 13 | 14 | 14 | 14 | 12 | 12 | 11 | 6 | 6 | 8 | 4 | 5 | 5 | 8 | 7 | 6 | 11 | 10 | 10 | 10 | 9 | 9 | 13 | 13 | 12 | 2 | 2 | 1 | 7 | 8 | 7 | 1 | 1 | 2 |
| F7 | 1 | 1 | 1 | 3 | 3 | 3 | 11 | 11 | 11 | 14 | 14 | 14 | 12 | 13 | 12 | 10 | 9 | 10 | 7 | 7 | 7 | 4 | 6 | 5 | 6 | 5 | 6 | 9 | 10 | 9 | 13 | 12 | 13 | 5 | 4 | 4 | 8 | 8 | 8 | 2 | 2 | 2 |
| F8 | 4 | 5 | 8 | 2 | 1 | 3 | 11 | 11 | 13 | 12 | 14 | 14 | 14 | 13 | 11 | 9 | 8 | 12 | 6 | 9 | 10 | 5 | 4 | 2 | 10 | 10 | 7 | 7 | 7 | 6 | 13 | 12 | 9 | 1 | 2 | 4 | 8 | 6 | 5 | 3 | 3 | 1 |
| F9 | 1 | 2 | 8 | 12 | 14 | 13 | 13 | 12 | 12 | 11 | 11 | 14 | 10 | 10 | 10 | 9 | 9 | 9 | 5 | 5 | 6 | 3 | 3 | 2 | 4 | 4 | 3 | 7 | 7 | 5 | 14 | 13 | 11 | 8 | 8 | 7 | 6 | 6 | 4 | 2 | 1 | 1 |
| F10 | 1 | 3 | 2 | 2 | 4 | 9 | 9 | 9 | 7 | 14 | 14 | 14 | 12 | 12 | 10 | 10 | 11 | 13 | 7 | 6 | 11 | 6 | 7 | 3 | 5 | 5 | 5 | 11 | 10 | 8 | 13 | 13 | 12 | 3 | 2 | 4 | 8 | 8 | 6 | 4 | 1 | 1 |
| F11 | 1 | 2 | 1 | 2 | 1 | 3 | 10 | 10 | 10 | 12 | 12 | 14 | 14 | 13 | 12 | 9 | 8 | 8 | 5 | 5 | 5 | 8 | 9 | 9 | 6 | 6 | 6 | 11 | 11 | 11 | 13 | 14 | 13 | 3 | 3 | 4 | 7 | 7 | 7 | 4 | 4 | 2 |
| F12 | 1 | 2 | 2 | 2 | 1 | 1 | 10 | 10 | 10 | 12 | 12 | 14 | 14 | 13 | 12 | 9 | 9 | 8 | 6 | 6 | 6 | 8 | 8 | 9 | 5 | 5 | 5 | 11 | 11 | 11 | 13 | 14 | 13 | 3 | 3 | 3 | 7 | 7 | 7 | 4 | 4 | 4 |
| F13 | 3 | 3 | 1 | 5 | 4 | 5 | 8 | 9 | 11 | 13 | 13 | 14 | 14 | 12 | 12 | 10 | 10 | 9 | 6 | 6 | 7 | 2 | 2 | 2 | 11 | 8 | 6 | 9 | 11 | 10 | 12 | 14 | 13 | 1 | 1 | 3 | 7 | 7 | 8 | 4 | 5 | 4 |
| F14 | 3 | 2 | 3 | 2 | 1 | 1 | 9 | 10 | 10 | 12 | 13 | 14 | 13 | 12 | 12 | 10 | 8 | 9 | 5 | 7 | 6 | 6 | 9 | 8 | 7 | 5 | 5 | 11 | 11 | 11 | 14 | 14 | 13 | 1 | 3 | 2 | 8 | 6 | 7 | 4 | 4 | 4 |
| F15 | 1 | 1 | 1 | 5 | 5 | 7 | 10 | 10 | 10 | 11 | 12 | 14 | 13 | 13 | 12 | 9 | 9 | 8 | 6 | 6 | 3 | 4 | 3 | 6 | 8 | 7 | 5 | 12 | 11 | 11 | 14 | 14 | 13 | 3 | 4 | 4 | 7 | 8 | 9 | 2 | 2 | 2 |
| F16 | 3 | 1 | 1 | 2 | 6 | 4 | 10 | 11 | 9 | 12 | 14 | 12 | 14 | 13 | 13 | 6 | 9 | 8 | 8 | 8 | 6 | 5 | 4 | 10 | 7 | 5 | 5 | 11 | 10 | 11 | 13 | 12 | 14 | 1 | 3 | 3 | 9 | 7 | 7 | 4 | 2 | 2 |
| F17 | 3 | 2 | 3 | 5 | 5 | 6 | 9 | 10 | 11 | 13 | 12 | 14 | 12 | 13 | 12 | 10 | 8 | 9 | 6 | 7 | 8 | 2 | 3 | 2 | 7 | 6 | 4 | 11 | 11 | 10 | 14 | 14 | 13 | 1 | 1 | 1 | 8 | 9 | 7 | 4 | 4 | 5 |
| F18 | 3 | 4 | 2 | 2 | 1 | 1 | 11 | 10 | 10 | 12 | 13 | 14 | 13 | 14 | 12 | 9 | 9 | 8 | 6 | 6 | 6 | 7 | 7 | 9 | 5 | 5 | 5 | 10 | 11 | 11 | 14 | 12 | 13 | 1 | 2 | 3 | 8 | 8 | 7 | 4 | 3 | 4 |
| F19 | 2 | 1 | 4 | 4 | 11 | 13 | 11 | 13 | 12 | 14 | 14 | 14 | 13 | 12 | 9 | 10 | 9 | 10 | 8 | 8 | 7 | 5 | 2 | 2 | 9 | 5 | 3 | 6 | 7 | 6 | 12 | 10 | 11 | 1 | 4 | 8 | 7 | 6 | 5 | 3 | 3 | 1 |
| F20 | 1 | 1 | 1 | 3 | 3 | 4 | 11 | 9 | 7 | 14 | 14 | 14 | 12 | 12 | 12 | 10 | 8 | 9 | 6 | 5 | 5 | 7 | 6 | 6 | 9 | 11 | 10 | 8 | 10 | 11 | 13 | 13 | 13 | 4 | 4 | 3 | 5 | 7 | 8 | 2 | 2 | 2 |
| F21 | 4 | 3 | 4 | 5 | 10 | 13 | 12 | 12 | 11 | 14 | 14 | 14 | 11 | 13 | 10 | 9 | 8 | 8 | 3 | 6 | 5 | 7 | 2 | 2 | 8 | 5 | 3 | 10 | 9 | 7 | 13 | 11 | 12 | 1 | 4 | 9 | 2 | 7 | 6 | 6 | 1 | 1 |
| F22 | 4 | 3 | 1 | 2 | 2 | 2 | 7 | 7 | 8 | 13 | 14 | 14 | 11 | 10 | 9 | 10 | 11 | 11 | 5 | 5 | 5 | 8 | 8 | 7 | 9 | 9 | 10 | 12 | 12 | 13 | 14 | 13 | 12 | 3 | 4 | 4 | 6 | 6 | 6 | 1 | 1 | 3 |
| F23 | 3 | 2 | 3 | 2 | 4 | 2 | 7 | 7 | 8 | 14 | 14 | 14 | 9 | 9 | 10 | 11 | 11 | 11 | 5 | 5 | 5 | 8 | 8 | 7 | 10 | 10 | 9 | 13 | 13 | 13 | 12 | 12 | 12 | 4 | 3 | 4 | 6 | 6 | 6 | 1 | 1 | 1 |
| F24 | 2 | 1 | 1 | 1 | 3 | 3 | 10 | 10 | 10 | 14 | 14 | 14 | 12 | 12 | 12 | 9 | 8 | 9 | 5 | 6 | 7 | 8 | 9 | 8 | 6 | 5 | 5 | 11 | 11 | 11 | 13 | 13 | 13 | 4 | 4 | 4 | 7 | 7 | 6 | 3 | 2 | 2 |
| F25 | 4 | 4 | 1 | 1 | 2 | 3 | 8 | 10 | 10 | 13 | 14 | 14 | 12 | 12 | 12 | 6 | 9 | 9 | 5 | 5 | 5 | 10 | 8 | 8 | 9 | 7 | 6 | 11 | 11 | 11 | 14 | 13 | 13 | 3 | 3 | 4 | 7 | 6 | 7 | 2 | 1 | 2 |
| F26 | 4 | 3 | 1 | 1 | 1 | 2 | 8 | 8 | 10 | 13 | 12 | 14 | 11 | 11 | 11 | 9 | 9 | 9 | 5 | 5 | 5 | 6 | 7 | 7 | 10 | 10 | 8 | 12 | 13 | 12 | 14 | 14 | 13 | 3 | 4 | 4 | 7 | 6 | 6 | 2 | 2 | 3 |
| F27 | 4 | 2 | 2 | 3 | 3 | 4 | 10 | 10 | 10 | 14 | 14 | 14 | 12 | 12 | 11 | 9 | 8 | 8 | 7 | 7 | 7 | 8 | 9 | 9 | 5 | 5 | 5 | 11 | 11 | 13 | 13 | 13 | 12 | 1 | 4 | 3 | 6 | 6 | 6 | 2 | 1 | 1 |
| F28 | 4 | 1 | 1 | 1 | 2 | 3 | 10 | 9 | 9 | 12 | 12 | 14 | 13 | 13 | 12 | 6 | 10 | 7 | 5 | 5 | 5 | 7 | 8 | 10 | 8 | 6 | 6 | 11 | 11 | 11 | 14 | 14 | 13 | 2 | 4 | 4 | 9 | 7 | 8 | 3 | 3 | 2 |
| F29 | 2 | 2 | 2 | 1 | 1 | 1 | 10 | 10 | 10 | 11 | 12 | 14 | 14 | 13 | 13 | 8 | 9 | 8 | 5 | 5 | 5 | 7 | 6 | 9 | 6 | 7 | 6 | 12 | 11 | 11 | 13 | 14 | 12 | 4 | 3 | 3 | 9 | 8 | 7 | 3 | 4 | 4 |
| Algorithms | D = 30 | D = 50 | D = 100 | Total |
|---|---|---|---|---|
| (+/=/−) | (+/=/−) | (+/=/−) | (+/=/−) | |
| FBCA vs. BCA | 7/16/6 | 13/8/8 | 18/6/5 | 38/30/19 |
| FBCA vs. SCA | 28/1/0 | 28/1/0 | 28/0/1 | 84/2/1 |
| FBCA vs. GA | 29/0/0 | 29/0/0 | 29/0/0 | 87/0/0 |
| FBCA vs. RSA | 28/1/0 | 28/0/1 | 27/1/1 | 83/2/2 |
| FBCA vs. PSO | 29/0/0 | 29/0/0 | 27/2/0 | 85/2/0 |
| FBCA vs. DBO | 25/3/1 | 27/2/0 | 26/2/1 | 78/7/2 |
| FBCA vs. BKA | 26/0/3 | 23/3/3 | 22/1/6 | 71/4/12 |
| FBCA vs. HHO | 28/0/1 | 28/0/1 | 24/2/3 | 80/2/5 |
| FBCA vs. HOA | 28/0/1 | 28/0/1 | 24/3/2 | 80/3/4 |
| FBCA vs. COA | 28/1/0 | 28/0/1 | 28/0/1 | 84/1/2 |
| FBCA vs. CPO | 12/6/11 | 17/6/6 | 20/5/4 | 49/17/21 |
| FBCA vs. PO | 27/1/1 | 28/0/1 | 24/3/2 | 79/4/4 |
| FBCA vs. SMA | 11/12/6 | 10/13/6 | 15/7/7 | 36/32/19 |
| F | BCA | FBCA () | FBCA () | FBCA () |
|---|---|---|---|---|
| F1 | 8.63 | 1.21 | 2.39 | |
| F2 | 8.22 | 6.76 | 7.20 | |
| F3 | 1.76 | 1.16 | 1.07 | |
| F4 | 1.63 | 1.30 | 1.32 | |
| F5 | 6.37 | 6.40 | 6.48 | |
| F6 | 2.67 | 2.75 | 3.31 | |
| F7 | 1.83 | 1.56 | 1.62 | |
| F8 | 6.88 | 7.71 | 8.82 | |
| F9 | 3.36 | 3.03 | 3.05 | |
| F10 | 1.94 | 6.24 | 5.70 | |
| F11 | 5.23 | 9.65 | 1.38 | |
| F12 | 3.18 | 5.12 | 1.89 | |
| F13 | 5.34 | 3.88 | 3.35 | |
| F14 | 1.80 | 2.25 | 2.66 | |
| F15 | 1.13 | 7.83 | 6.44 | |
| F16 | 8.20 | 6.15 | 5.12 | |
| F17 | 1.59 | 9.53 | 8.04 | |
| F18 | 1.16 | 1.21 | 4.32 | |
| F19 | 8.28 | 7.16 | 7.04 | |
| F20 | 3.43 | 3.12 | 3.17 | |
| F21 | 3.60 | 3.31 | 3.06 | |
| F22 | 3.64 | 3.55 | 3.78 | |
| F23 | 4.43 | 4.28 | 4.80 | |
| F24 | 4.74 | 3.85 | 3.79 | |
| F25 | 1.80 | 1.77 | 2.17 | |
| F26 | 3.78 | 3.84 | 4.06 | |
| F27 | 5.77 | 4.46 | 4.77 | |
| F28 | 1.02 | 6.87 | 7.46 | |
| F29 | 8.33 | 8.30 | 2.52 | |
| Average ranking | 3.21 | 2.10 | 1.97 | 2.72 |
| Total ranking | 4 | 2 | 1 | 3 |
| F | BCA | FBCA (()) | FBCA (()) | FBCA (()) |
|---|---|---|---|---|
| F1 | 9.34 | 4.95 | 3.25 | |
| F2 | 1.22 | 6.82 | 6.87 | |
| F3 | 1.72 | 1.06 | 1.03 | |
| F4 | 1.62 | 1.25 | 1.25 | |
| F5 | 6.39 | 6.40 | 6.42 | |
| F6 | 2.77 | 2.63 | 2.78 | |
| F7 | 1.84 | 1.61 | 1.57 | |
| F8 | 6.84 | 7.08 | 6.45 | |
| F9 | 3.37 | 2.93 | 2.84 | |
| F10 | 1.97 | 5.89 | 5.35 | |
| F11 | 5.26 | 1.18 | 1.27 | |
| F12 | 4.10 | 4.69 | 6.32 | |
| F13 | 5.30 | 3.71 | 2.85 | |
| F14 | 2.07 | 1.65 | 1.30 | |
| F15 | 1.16 | 7.53 | 6.57 | |
| F16 | 8.38 | 5.42 | 5.85 | |
| F17 | 2.33 | 8.70 | 7.92 | |
| F18 | 8.28 | 1.23 | 1.24 | |
| F19 | 8.27 | 6.81 | 7.15 | |
| F20 | 3.41 | 3.11 | 3.14 | |
| F21 | 3.61 | 3.16 | 3.11 | |
| F22 | 3.60 | 3.60 | 3.54 | |
| F23 | 4.45 | 4.38 | 4.34 | |
| F24 | 4.64 | 3.86 | 3.72 | |
| F25 | 1.74 | 1.72 | 1.74 | |
| F26 | 3.83 | 3.79 | 3.80 | |
| F27 | 5.98 | 4.35 | 4.03 | |
| F28 | 9.16 | 7.00 | 7.04 | |
| F29 | 8.00 | 9.02 | 1.26 | |
| Average ranking | 3.14 | 2.38 | 2.14 | 2.34 |
| Total ranking | 4 | 3 | 1 | 2 |
| F | BCA | FBCA () | FBCA () | FBCA () | FBCA () |
|---|---|---|---|---|---|
| F1 | 9.41 | 3.34 | 2.53 | ||
| F2 | 1.72 | 6.79 | 6.91 | 6.62 | |
| F3 | 1.74 | 1.02 | 1.43 | 1.11 | |
| F4 | 1.59 | 1.27 | 1.39 | 1.28 | |
| F5 | 6.39 | 6.41 | 6.38 | 6.41 | |
| F6 | 2.63 | 2.68 | 2.61 | 3.15 | |
| F7 | 1.80 | 1.59 | 1.69 | 1.57 | |
| F8 | 7.30 | 7.51 | 6.76 | 7.88 | |
| F9 | 3.37 | 3.00 | 2.92 | 3.08 | |
| F10 | 2.14 | 5.09 | 6.90 | 5.34 | |
| F11 | 4.22 | 1.11 | 2.11 | 2.00 | |
| F12 | 7.00 | 1.31 | 1.22 | 7.91 | |
| F13 | 4.32 | 2.93 | 3.90 | 3.74 | |
| F14 | 2.09 | 1.13 | 2.12 | 1.75 | |
| F15 | 1.13 | 6.01 | 7.56 | 6.87 | |
| F16 | 8.33 | 5.48 | 5.60 | 5.63 | |
| F17 | 2.38 | 6.50 | 7.75 | 6.48 | |
| F18 | 1.15 | 1.92 | 1.05 | 2.49 | |
| F19 | 8.27 | 6.80 | 6.43 | 6.99 | |
| F20 | 3.39 | 3.13 | 3.20 | 3.12 | |
| F21 | 3.62 | 2.99 | 3.14 | 3.32 | |
| F22 | 3.64 | 3.58 | 3.62 | 3.67 | |
| F23 | 4.40 | 4.32 | 4.49 | 4.63 | |
| F24 | 4.68 | 3.75 | 4.10 | 3.79 | |
| F25 | 1.67 | 1.69 | 1.77 | 2.08 | |
| F26 | 3.82 | 3.82 | 3.86 | 4.04 | |
| F27 | 5.86 | 4.31 | 4.68 | 4.68 | |
| F28 | 9.04 | 7.23 | 7.19 | 7.57 | |
| F29 | 9.12 | 7.95 | 8.41 | 2.11 | |
| Average ranking | 3.76 | 2.28 | 2.59 | 2.97 | 3.41 |
| Total ranking | 5 | 1 | 2 | 3 | 4 |
| F | BCA | FBCA () | FBCA () |
|---|---|---|---|
| F1 | 9.11 | 4.05 | |
| F2 | 9.05 | 6.76 | |
| F3 | 1.92 | 1.01 | |
| F4 | 1.62 | 1.23 | |
| F5 | 6.41 | 6.43 | |
| F6 | 2.78 | 2.71 | |
| F7 | 1.89 | 1.60 | |
| F8 | 7.03 | 7.28 | |
| F9 | 3.34 | 2.79 | |
| F10 | 1.95 | 5.86 | |
| F11 | 6.07 | 1.09 | |
| F12 | 2.82 | 5.38 | |
| F13 | 6.83 | 3.12 | |
| F14 | 1.50 | 1.17 | |
| F15 | 1.15 | 7.03 | |
| F16 | 8.24 | 5.67 | |
| F17 | 1.90 | 6.91 | |
| F18 | 1.35 | 1.17 | |
| F19 | 8.30 | 7.07 | |
| F20 | 3.42 | 3.17 | |
| F21 | 3.57 | 3.03 | |
| F22 | 3.65 | 3.59 | |
| F23 | 4.35 | 4.34 | |
| F24 | 4.76 | 3.74 | |
| F25 | 1.77 | 1.75 | |
| F26 | 3.80 | 3.81 | |
| F27 | 5.85 | 4.14 | |
| F28 | 9.33 | 7.28 | |
| F29 | 9.07 | 9.53 | |
| Average ranking | 2.48 | 1.66 | 1.86 |
| Total ranking | 3 | 1 | 2 |
| F | FBCA | BCA | SaDE | L-SHADE | L-SHADE_EpSin |
|---|---|---|---|---|---|
| F1 | 3.29 | 8.02 | 9.24 | 5.07 | |
| F2 | 6.90 | 1.21 | 5.85 | 3.85 | |
| F3 | 9.97 | 1.88 | 2.11 | 6.22 | |
| F4 | 1.55 | 1.37 | 1.51 | 1.23 | |
| F5 | 6.40 | 6.31 | 6.49 | 6.46 | |
| F6 | 2.66 | 2.47 | 2.53 | 2.56 | |
| F7 | 1.85 | 1.69 | 1.81 | 1.57 | |
| F8 | 7.07 | 4.35 | 5.61 | 2.69 | |
| F9 | 2.73 | 3.34 | 3.26 | 3.20 | |
| F10 | 2.15 | 6.63 | 1.20 | 7.87 | |
| F11 | 1.09 | 3.92 | 5.11 | 4.72 | |
| F12 | 4.09 | 9.59 | 1.46 | 8.09 | |
| F13 | 3.04 | 5.61 | 4.53 | 3.30 | |
| F14 | 1.24 | 7.58 | 2.14 | 3.60 | |
| F15 | 6.89 | 1.16 | 6.91 | 9.73 | |
| F16 | 5.21 | 8.13 | 6.70 | 7.18 | |
| F17 | 6.75 | 1.97 | 7.74 | 4.08 | |
| F18 | 1.25 | 1.10 | 4.10 | 7.06 | |
| F19 | 7.01 | 8.27 | 7.63 | 7.49 | |
| F20 | 3.47 | 3.30 | 3.36 | 3.15 | |
| F21 | 3.09 | 3.61 | 3.44 | 3.42 | |
| F22 | 3.61 | 3.69 | 3.83 | 3.99 | |
| F23 | 4.39 | 4.48 | 4.40 | 5.18 | |
| F24 | 3.68 | 4.54 | 4.82 | 7.38 | |
| F25 | 1.73 | 1.73 | 1.72 | 2.41 | |
| F26 | 3.83 | 3.81 | 3.87 | 4.82 | |
| F27 | 4.27 | 5.95 | 5.95 | 1.10 | |
| F28 | 9.42 | 8.30 | 9.42 | 9.72 | |
| F29 | 7.57 | 7.75 | 5.53 | 1.72 | |
| Average ranking | 2.24 | 3.51 | 3.34 | 2.41 | 3.48 |
| Total ranking | 1 | 5 | 3 | 2 | 4 |
| Datasets | Feature Numbers | Training Samples | Test Samples | Number of Classes | MLP Structure | Dimension |
|---|---|---|---|---|---|---|
| XOR | 3 | 8 | 8 | 2 | 3-7-1 | 36 |
| Iris | 4 | 150 | 150 | 3 | 4-9-3 | 75 |
| Heart | 22 | 80 | 80 | 2 | 22-45-1 | 1081 |
| Datasets | Training Samples | Test Samples | MLP Structure | Dimension |
|---|---|---|---|---|
| Sigmoid: | 61: x in [−3:0.1:3] | 121: x in [−3:0.05:3] | 1-15-1 | 46 |
| Cosine: | 31: x in [1.25:0.05:2.75] | 38: x in [1.25:0.04:2.75] | 1-15-1 | 46 |
| Sine: | 126: x in [−2:0.1:2] | 252: x in [−2:0.05:2] | 1-15-1 | 46 |
| FBCA | BCA | GA | SMA | HHO | OOA | COA | GLS | HOA | RSA | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 2.93 | 6.863 | 2.003 | 8.166 | 1.779 | 1.663 | 3.567 | 1.149 | 1.555 | |
| Std | 1.573 | 8.72 | 6.513 | 4.472 | 1.244 | 4.815 | 6.867 | 4.549 | 5.087 | 3.516 |
| Accuracy | 100% | 100% | 62.5% | 12.5% | 100% | 37.5% | 37.5% | 100% | 25% | 12.5% |
| FBCA | BCA | GA | SMA | HHO | OOA | COA | GLS | HOA | RSA | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 2.89 | 2.946 | 6.596 | 6.572 | 4.342 | 4.221 | 1.224 | 2.507 | 3.044 | |
| Std | 6.321 | 1.316 | 1.878 | 4.507 | 1.044 | 1.009 | 7.079 | 4.89 | 5.174 | 4.194 |
| Accuracy | 88.67% | 86% | 25.33% | 43.33% | 74% | 6.67% | 14% | 54% | 5.33% | 7.33% |
| FBCA | BCA | GA | SMA | HHO | OOA | COA | GLS | HOA | RSA | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 1.101 | 2.826 | 1.681 | 1.257 | 1.76 | 1.718 | 1.474 | 1.242 | 1.626 | |
| Std | 1.179 | 3.974 | 3.916 | 6.858 | 8.339 | 6.495 | 7.723 | 2.258 | 1.114 | 1.167 |
| Accuracy | 83.75% | 82.5% | 52.5% | 73.75% | 73.75% | 32.5% | 36.25% | 78.75% | 67.5% | 48.75% |
| FBCA | BCA | GA | SMA | HHO | OOA | COA | GLS | HOA | RSA | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 2.482 | 2.486 | 2.468 | 2.467 | 2.496 | 2.486 | 2.469 | 2.477 | 2.471 | |
| Std | 1.711 | 1.759 | 1.909 | 2.321 | 1.503 | 1.807 | 1.835 | 4.225 | 7.978 | 3.776 |
| Error | 17.5564 | 18.3290 | 19.4690 | 17.8225 | 17.5827 | 20.5183 | 17.7487 | 18.1118 | 17.8106 | 18.1837 |
| FBCA | BCA | GA | SMA | HHO | OOA | COA | GLS | HOA | RSA | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 1.826 | 1.98 | 1.816 | 1.774 | 2.756 | 2.244 | 1.79 | 1.85 | 2.001 | |
| Std | 4.262 | 4.262 | 4.262 | 4.262 | 4.262 | 4.262 | 4.262 | 4.262 | 4.262 | 4.262 |
| Error | 4.6792 | 5.2449 | 8.9720 | 4.7839 | 4.7741 | 6.0326 | 7.4608 | 5.0299 | 5.3183 | 6.0737 |
| FBCA | BCA | GA | SMA | HHO | OOA | COA | GLS | HOA | RSA | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 4.514 | 4.655 | 4.523 | 4.462 | 4.649 | 4.523 | 4.495 | 4.611 | 4.677 | |
| Std | 8.941 | 4.996 | 9.217 | 9.393 | 2.225 | 4.332 | 1.138 | 9.507 | 3.623 | 7.564 |
| Error | 146.5873 | 147.1405 | 157.9612 | 148.8101 | 147.4074 | 14.9740 | 146.9557 | 148.6581 | 151.0190 | 153.4001 |
| Datasets | Item | FBCA | BCA | SGD | Adam | RMSprop | Adagrad |
|---|---|---|---|---|---|---|---|
| Mean | 9.779 | 1.101 | 9.212 | 5.580 | 4.331 | 5.821 | |
| Accuracy | 83.75% | 82.5% | 31.25% | 71.25% | 72.5% | 76.25% | |
| Mean | 4.453 | 4.514 | 4.983 | 4.453 | 4.453 | 4.896 | |
| Error | 146.5873 | 147.1405 | 159.7947 | 148.4509 | 146.7834 | 157.5333 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Guo, C.; Jiang, J. FBCA: Flexible Besiege and Conquer Algorithm for Multi-Layer Perceptron Optimization Problems. Biomimetics 2025, 10, 787. https://doi.org/10.3390/biomimetics10110787
Guo S, Guo C, Jiang J. FBCA: Flexible Besiege and Conquer Algorithm for Multi-Layer Perceptron Optimization Problems. Biomimetics. 2025; 10(11):787. https://doi.org/10.3390/biomimetics10110787
Chicago/Turabian StyleGuo, Shuxin, Chenxu Guo, and Jianhua Jiang. 2025. "FBCA: Flexible Besiege and Conquer Algorithm for Multi-Layer Perceptron Optimization Problems" Biomimetics 10, no. 11: 787. https://doi.org/10.3390/biomimetics10110787
APA StyleGuo, S., Guo, C., & Jiang, J. (2025). FBCA: Flexible Besiege and Conquer Algorithm for Multi-Layer Perceptron Optimization Problems. Biomimetics, 10(11), 787. https://doi.org/10.3390/biomimetics10110787






