Multi-Strategy Improved POA for Global Optimization Problems and 3D UAV Path Planning
Abstract
1. Introduction
- 1.
- To enhance the quality of the initial population, a hybrid low-discrepancy and heuristic initialization method is proposed. This method ensures uniform coverage of the search space through low-difference sequences, while heuristics enhance the quality of some individuals and prevent futile searches.
- 2.
- We proposed a subgroup mean-guided update strategy to accelerate the algorithm’s convergence toward the global optimum.
- 3.
- We propose a random reinitialization boundary control to enhance the algorithm’s exploration capability, enabling it to effectively avoid local optima.
- 4.
- The proposed algorithm was evaluated on 30 benchmark functions from the CEC2017 test suite and compared against 11 state-of-the-art metaheuristic algorithms to demonstrate its competitiveness. Furthermore, a comprehensive statistical analysis was conducted to rigorously validate the superior performance of the MIPOA.
- 5.
- The MIPOA is applied to the 3D UAV path planning problem under four Scenario s in 3D environment and compared with other comparative algorithms.
2. Pelican Optimization Algorithm (POA)
2.1. Population Initialization
2.2. Moving Towards Prey (Exploration Phase)
2.3. Winging on the Water Surface (Exploitation Phase)
| Algorithm 1: the pseudo-code of the POA |
| 1: Begin 2: Initialize: the relevant parameters and algorithm initialization. 3: While do 4: Generate the position of the prey at random. 5: For 6: For 7: Moving towards prey (exploration phase): 8: Update the population by Equation (3) 9: End For 10: Update the member in the population by Equation (4) 11: End For 12: For 13: For 14: Winging on the water surface (exploitation phase): 15: Update the population by Equation (5) 16: End For 17: Update the member in the population by Equation (6) 18: End For 19: 20: Update best solution 21: End while 22: return best solution 23: end |
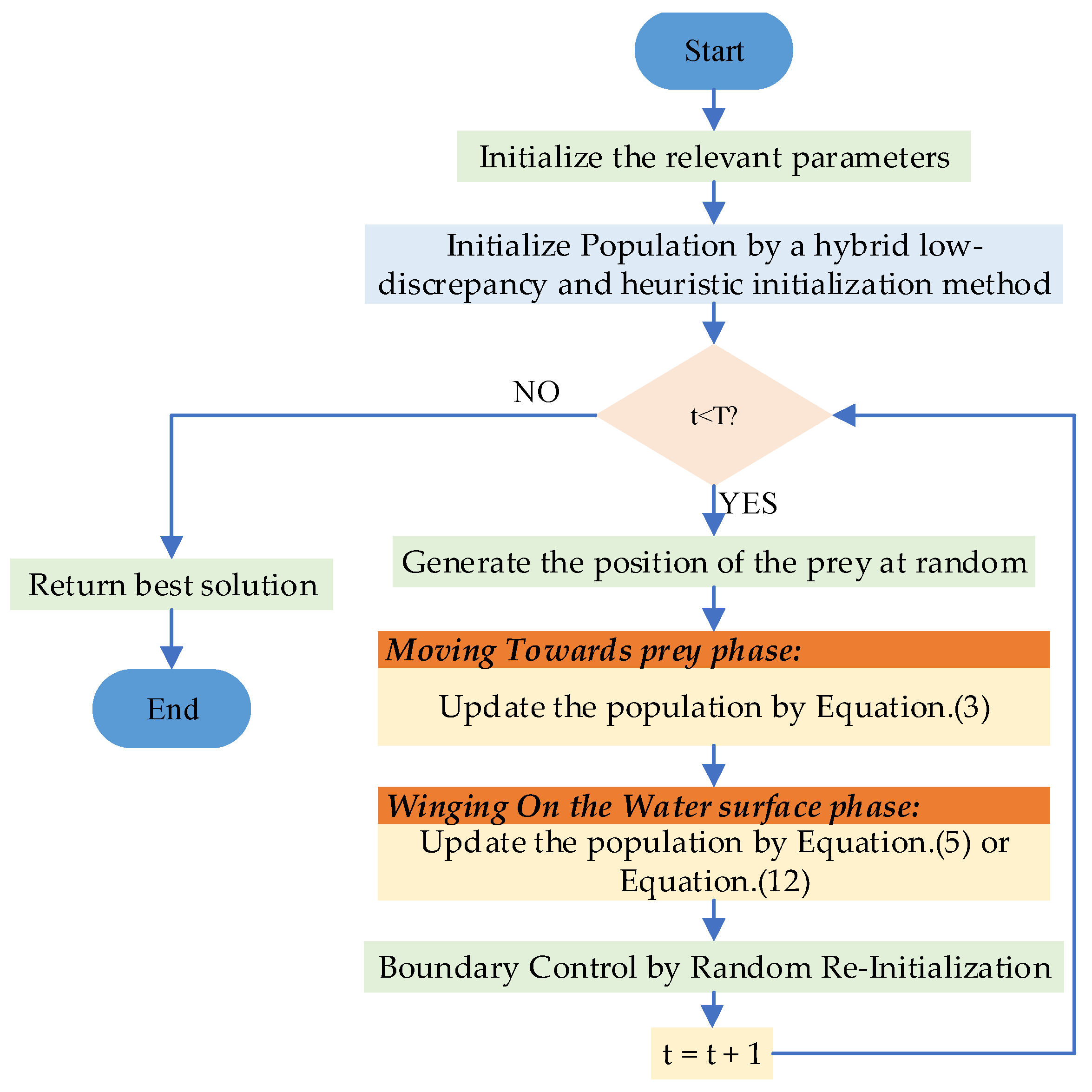
3. Proposed MIPOA
3.1. A Hybrid Low-Discrepancy and Heuristic Initialization Method
3.2. A Subgroup Mean-Guided Update Strategy
3.3. A Random Re-Initialization Boundary Control
| Algorithm 2: The pseudo-code of the MIPOA |
| 1: Begin 2: Initialize population by a hybrid low-discrepancy and heuristic initialization method. 3: While do 4: Generate the position of the prey at random. 5: For 6: For 7: Moving towards prey (exploration phase): 8: Update the population by Equation (3) 9: End For 10: Update the member in the population by Equation (4) 11: End For 12: For 13: For 14: Winging on the water surface (exploitation phase): 15: Update the population by Equation (12) 16: End For 17: Update the member in the population by Equation (6) 18: End For 19: Boundary Control by Random Re-Initialization 20: 21: Update best solution 22: End while 23: return best solution 24: end |
3.4. Time Complexity Analysis
4. Global Optimization Experimental and Detailed Analyses
4.1. Benchmark Test Functions
4.2. Competitor Algorithms and Parameters Setting
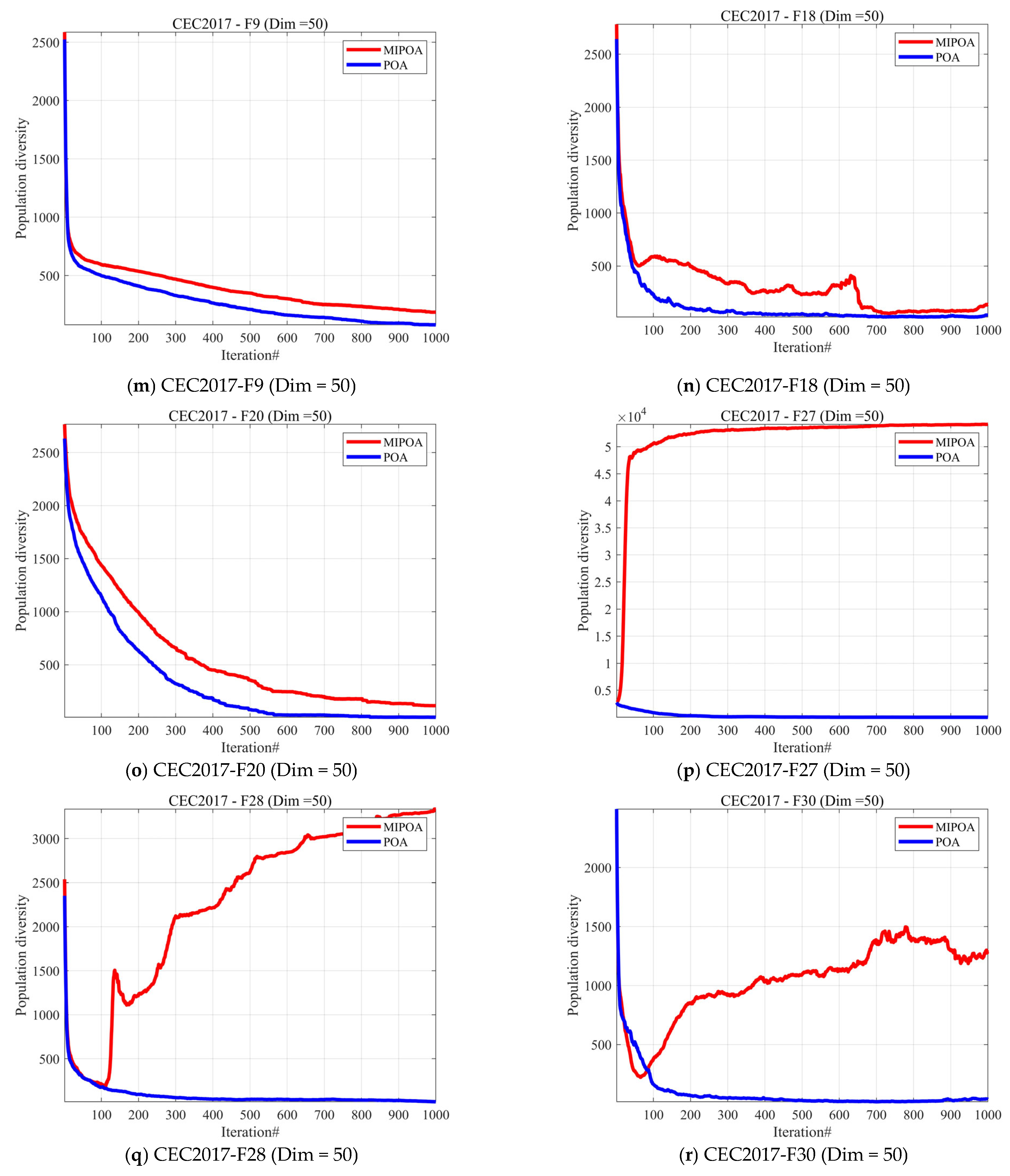
4.3. Analysis of the Population Diversity
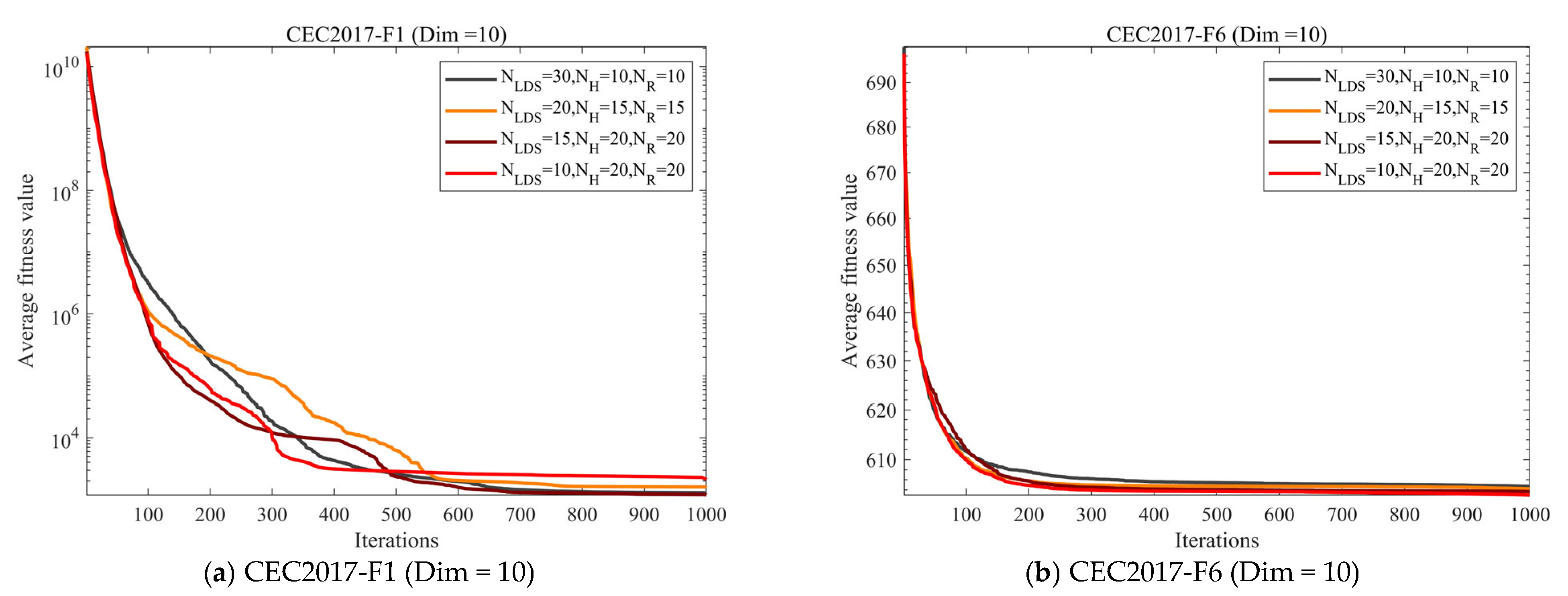
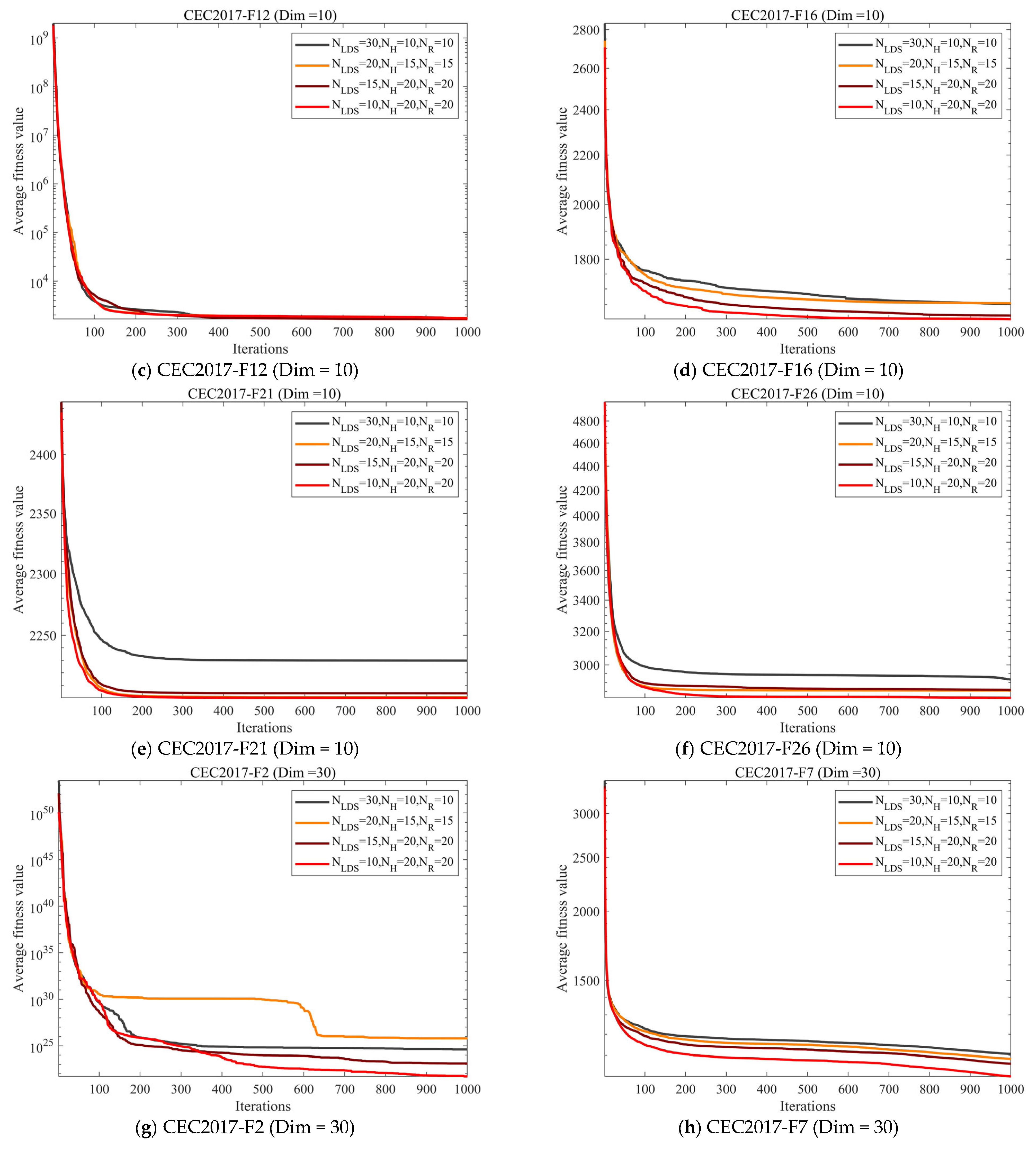
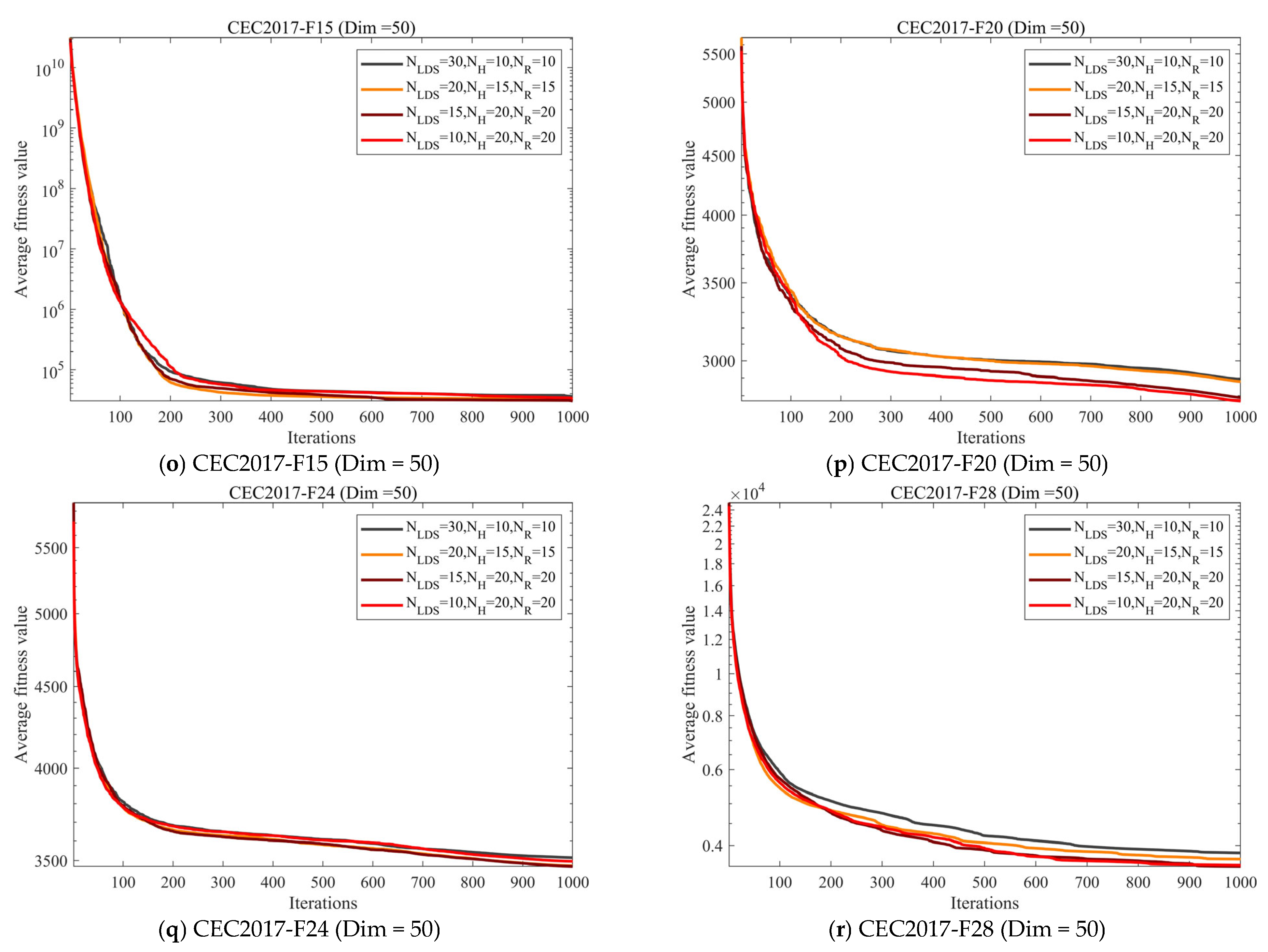
4.4. Parameter Sensitivity Analysis
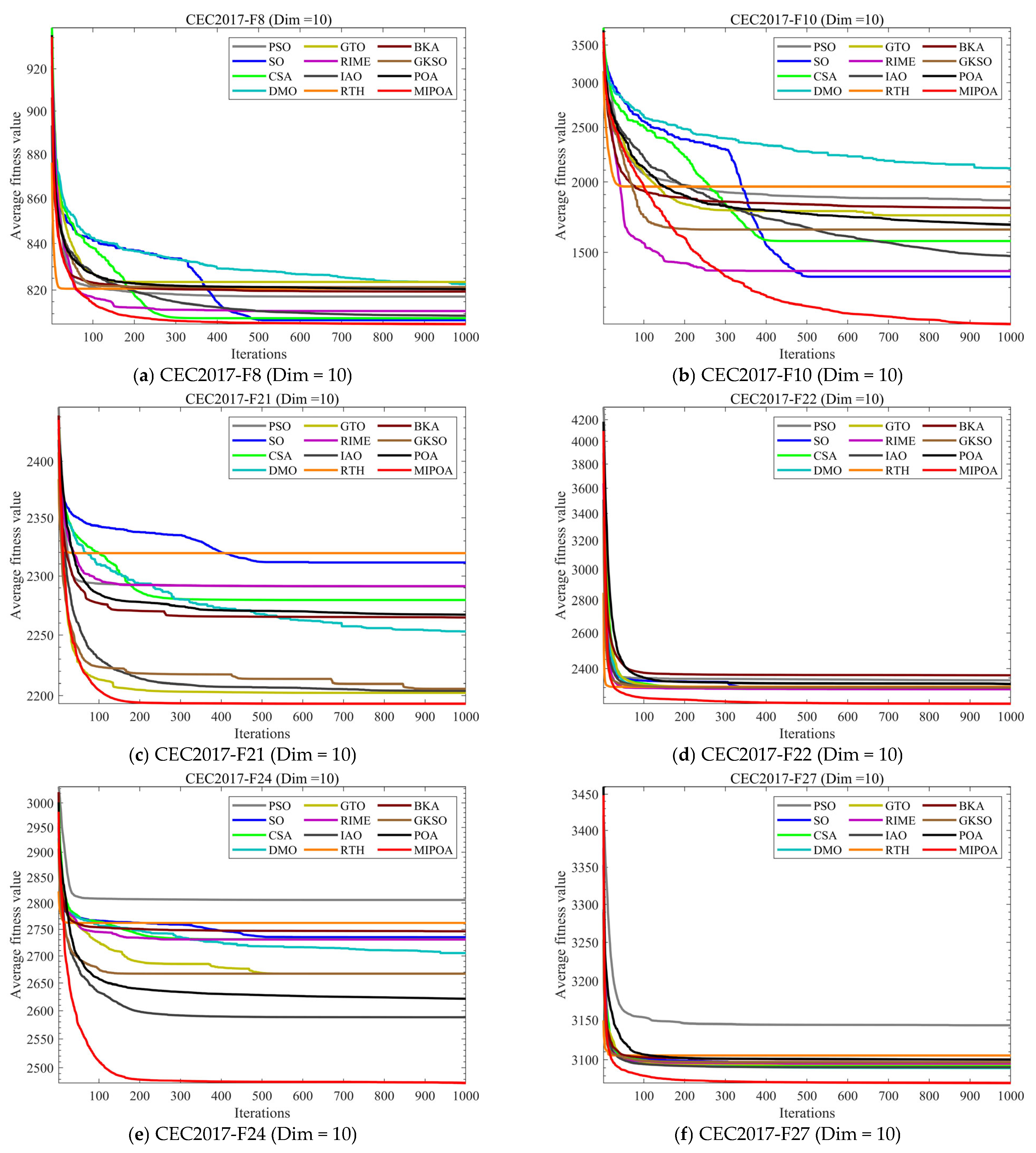
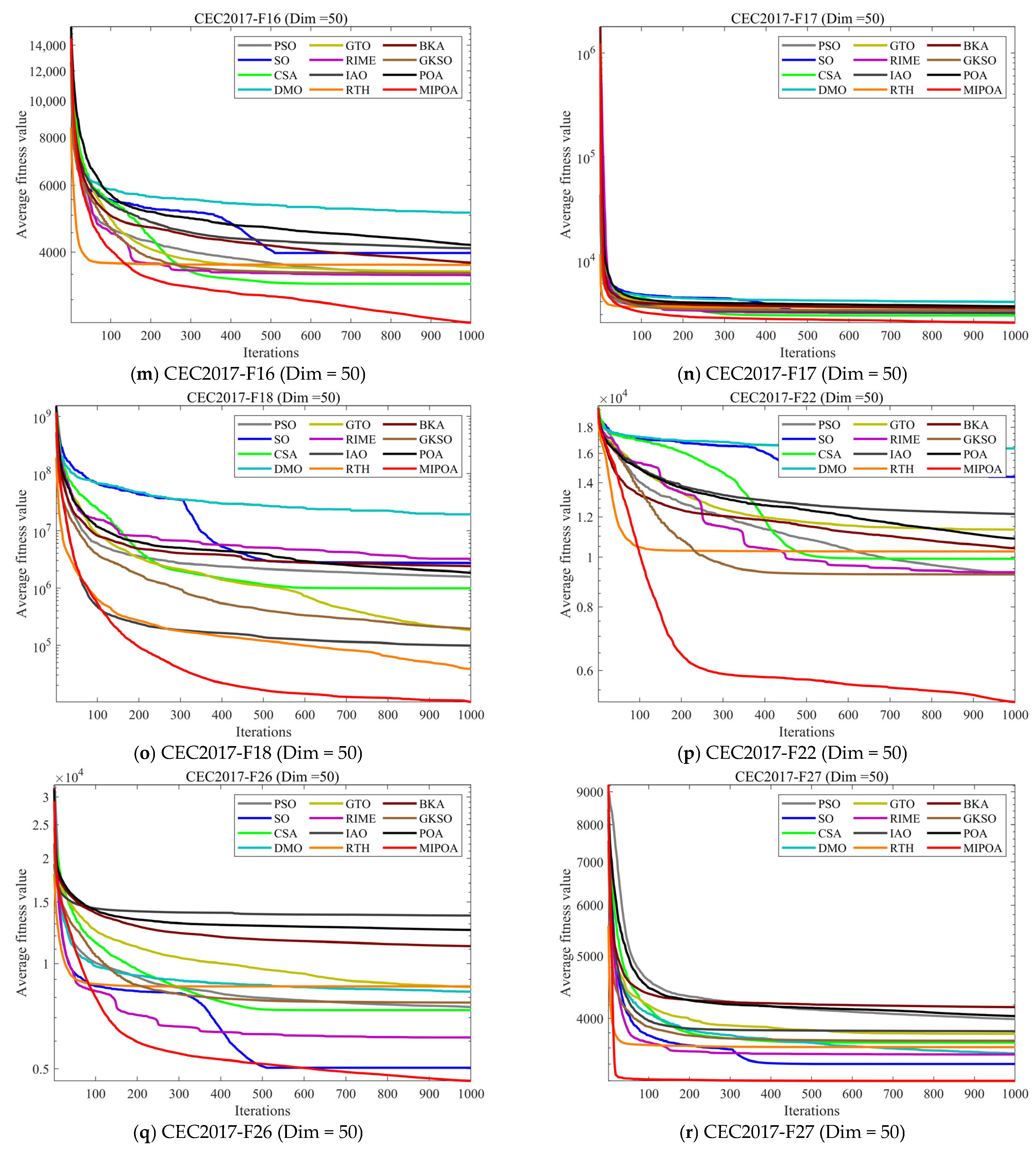
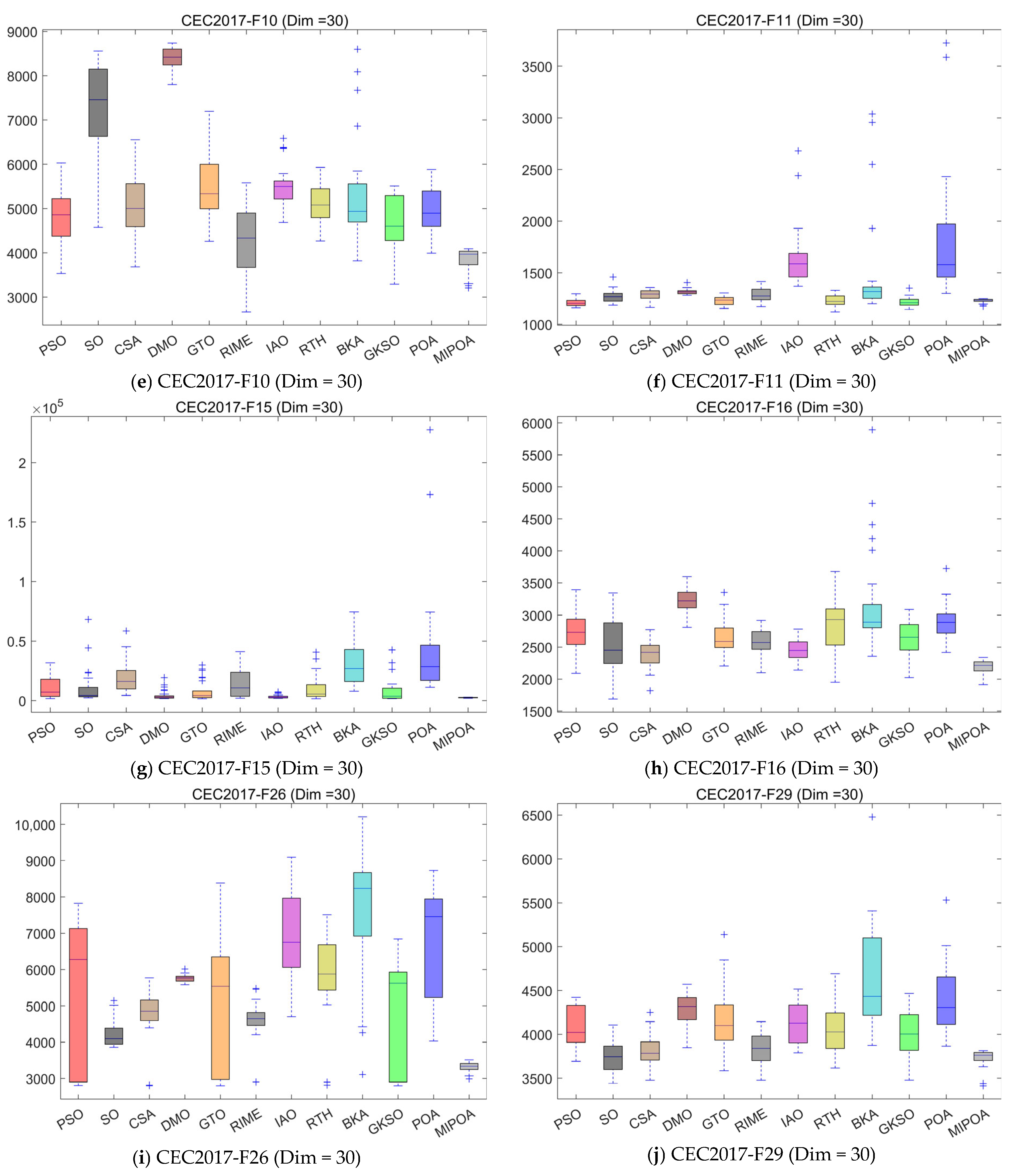
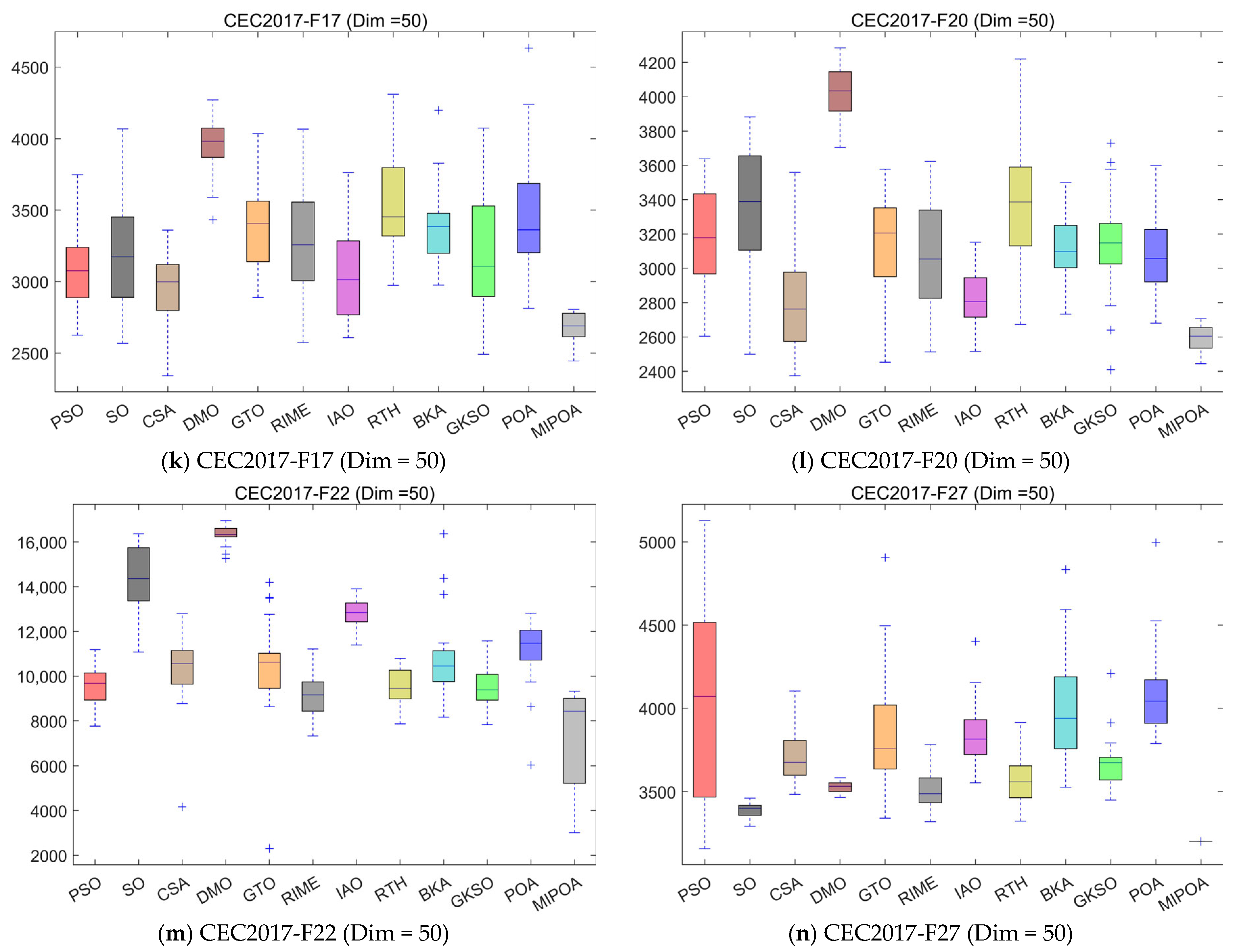
4.5. Compare Using CEC 2017 Test Functions
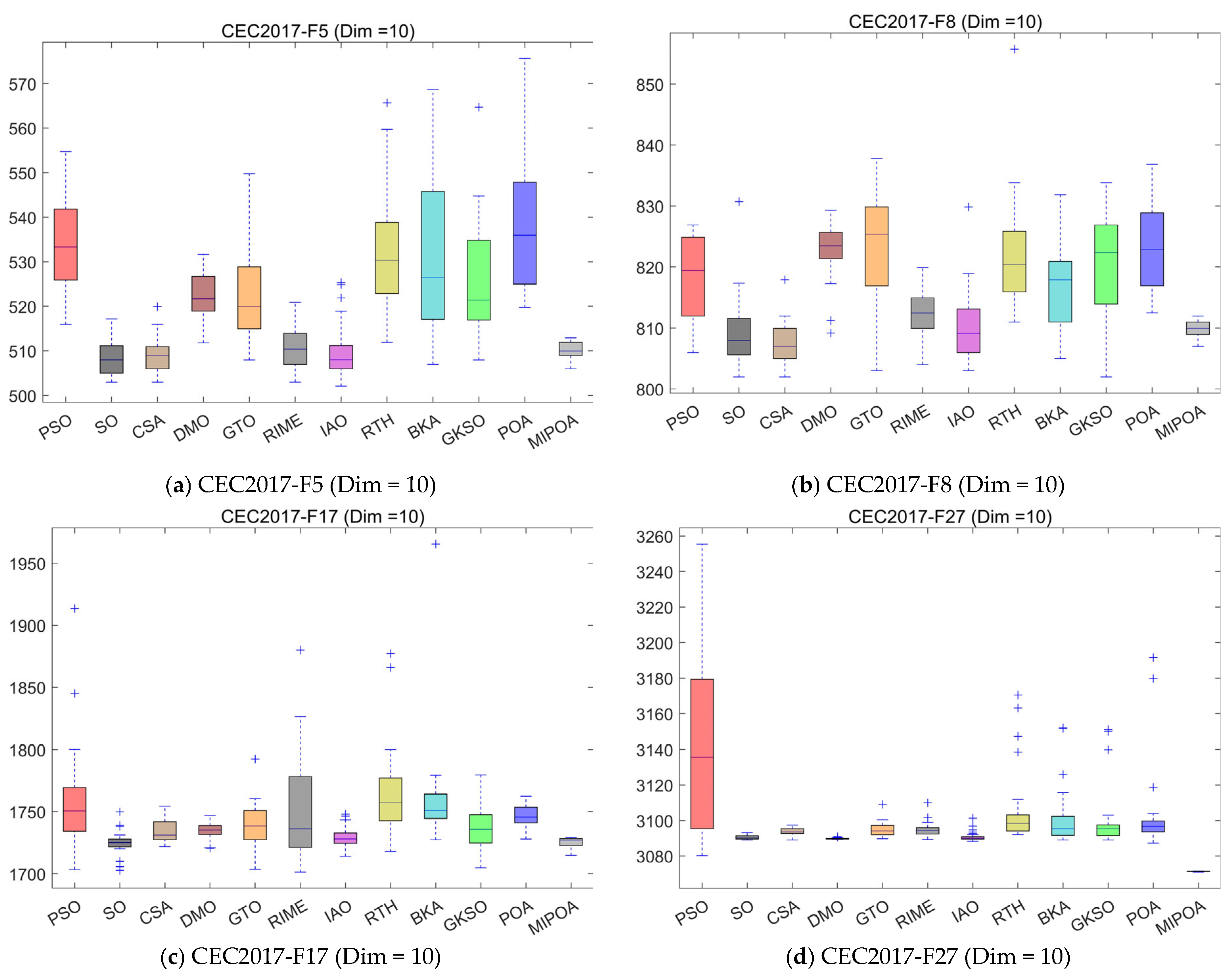
4.6. Statistical Analysis
4.6.1. Wilcoxon Rank Sum Test
4.6.2. Friedman Mean Rank Test
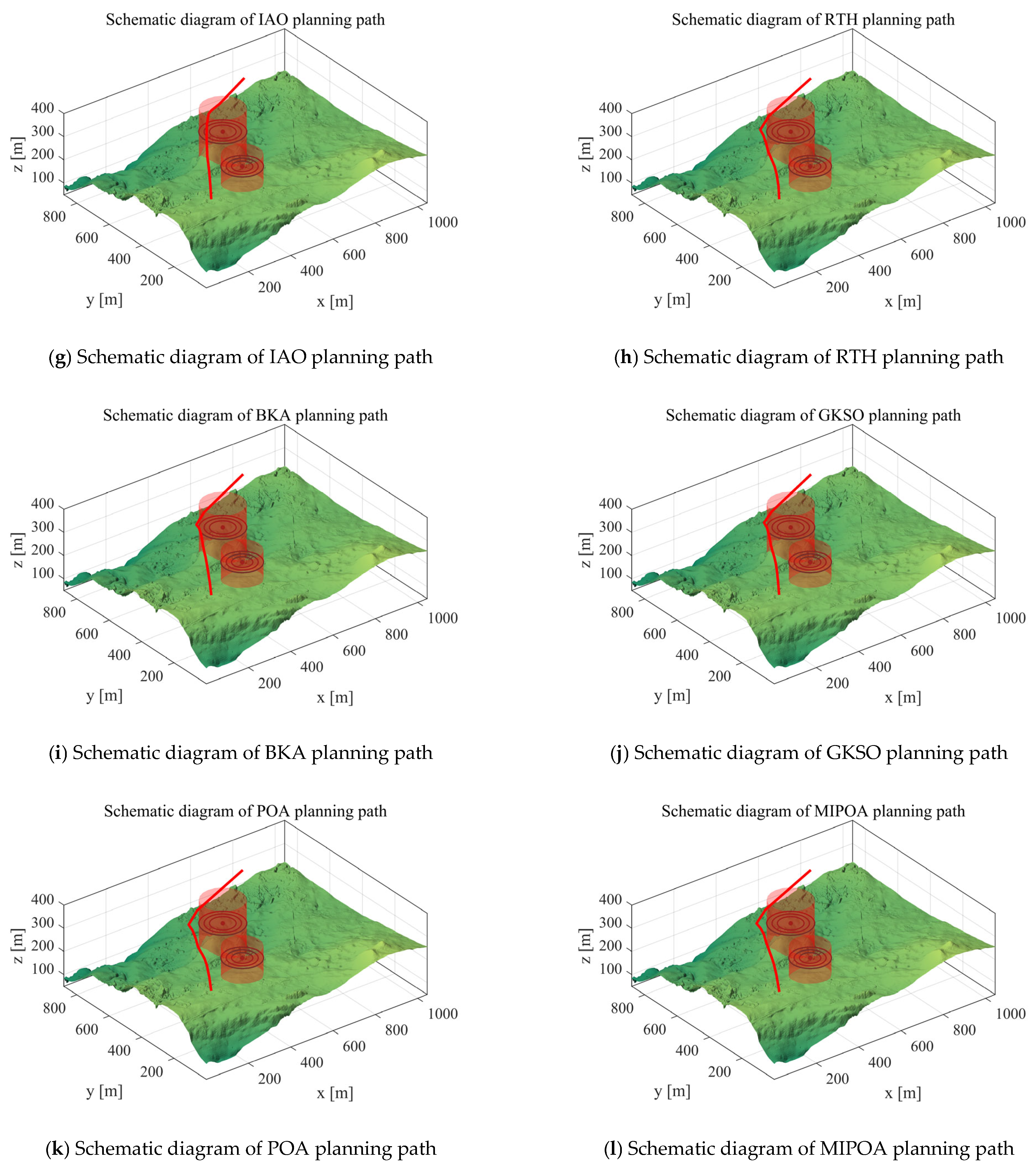
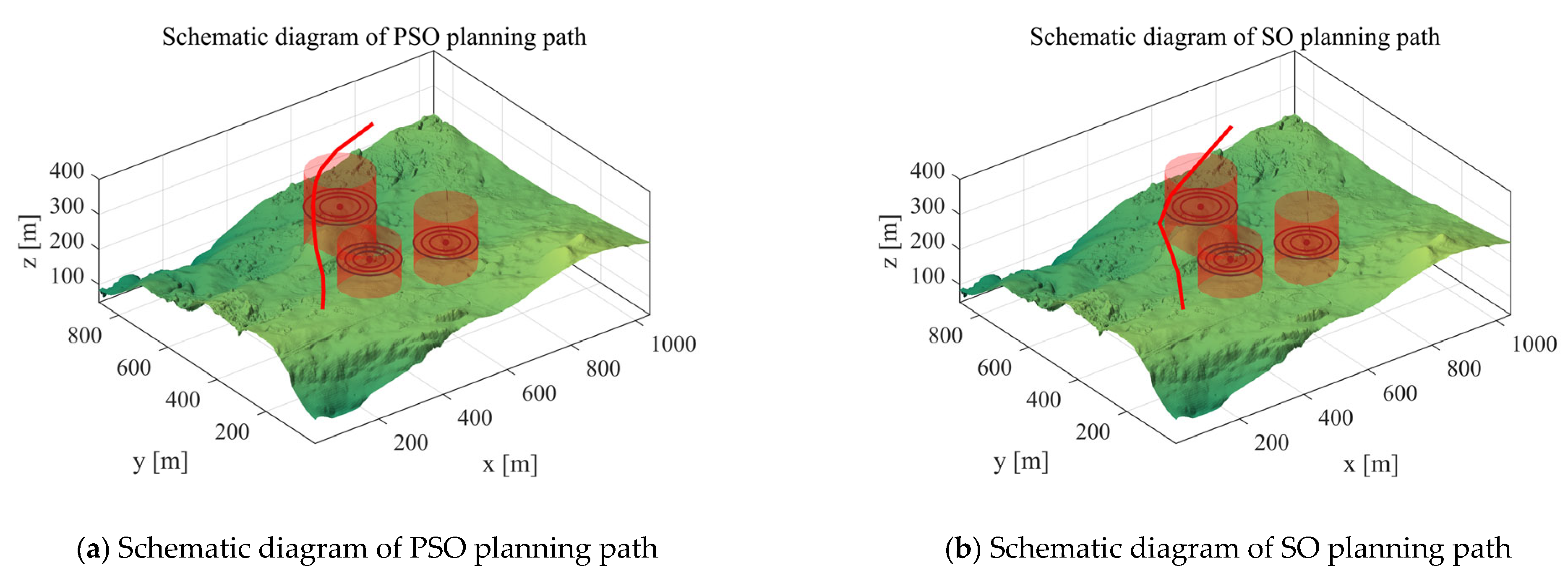
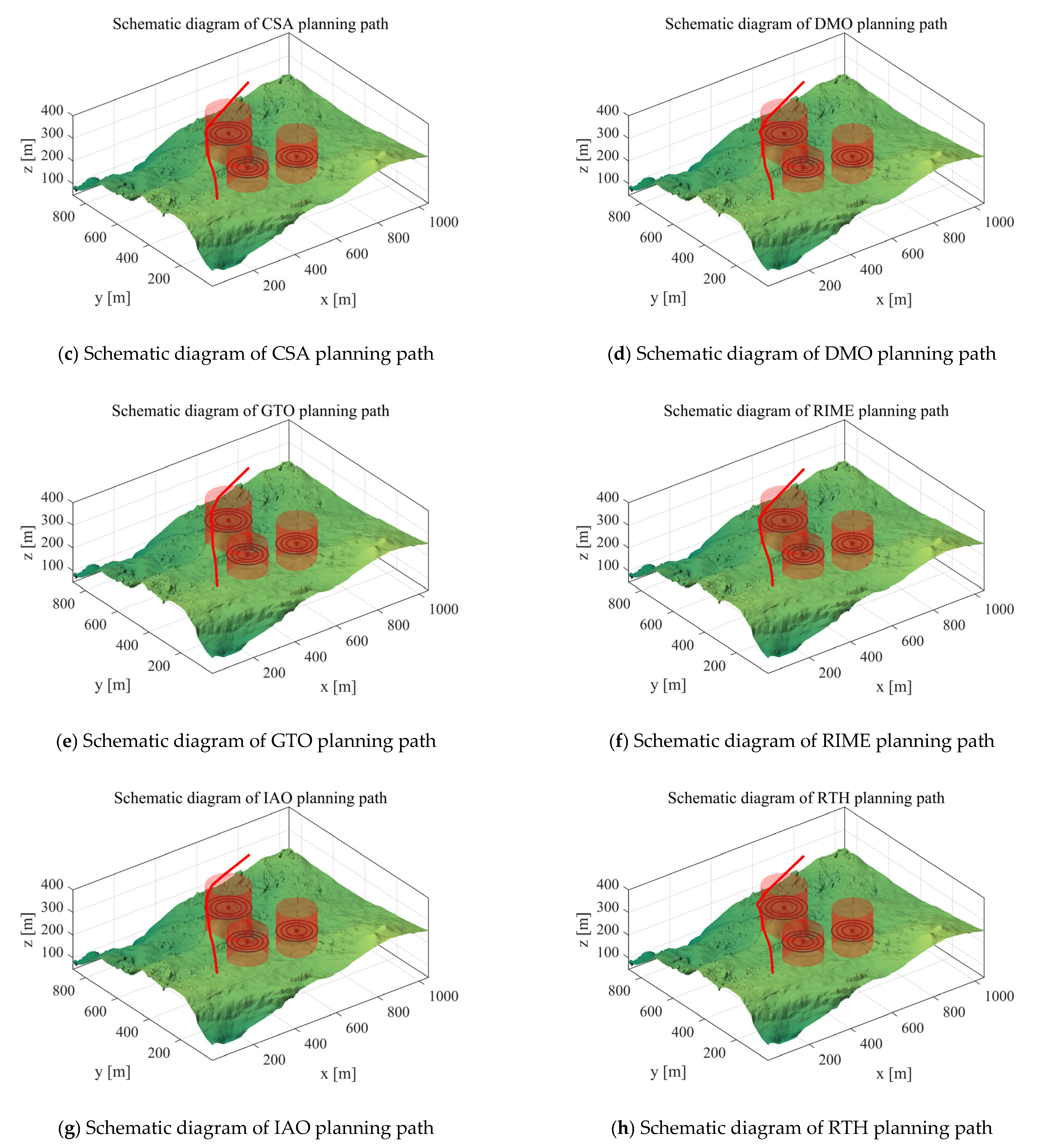
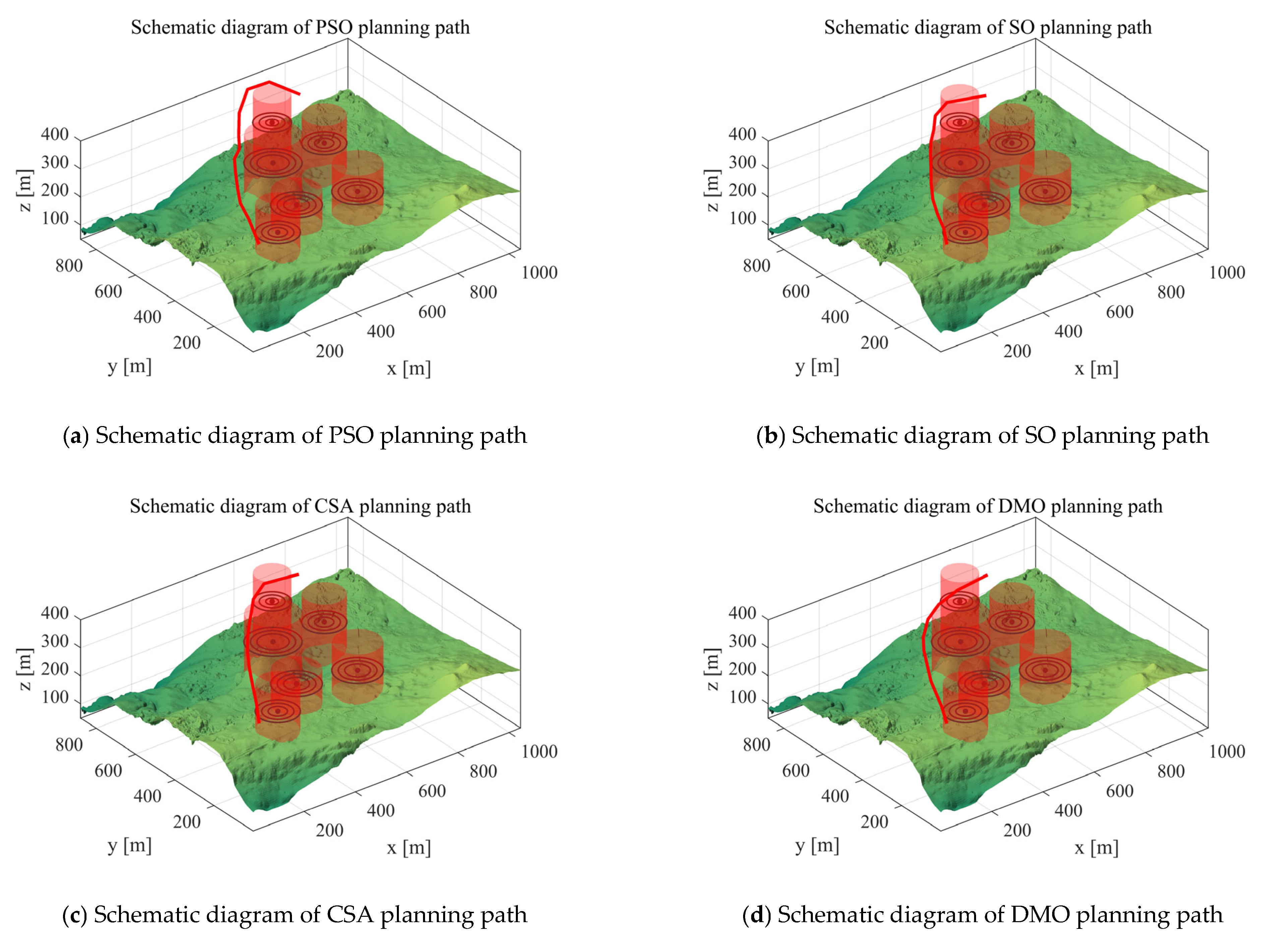
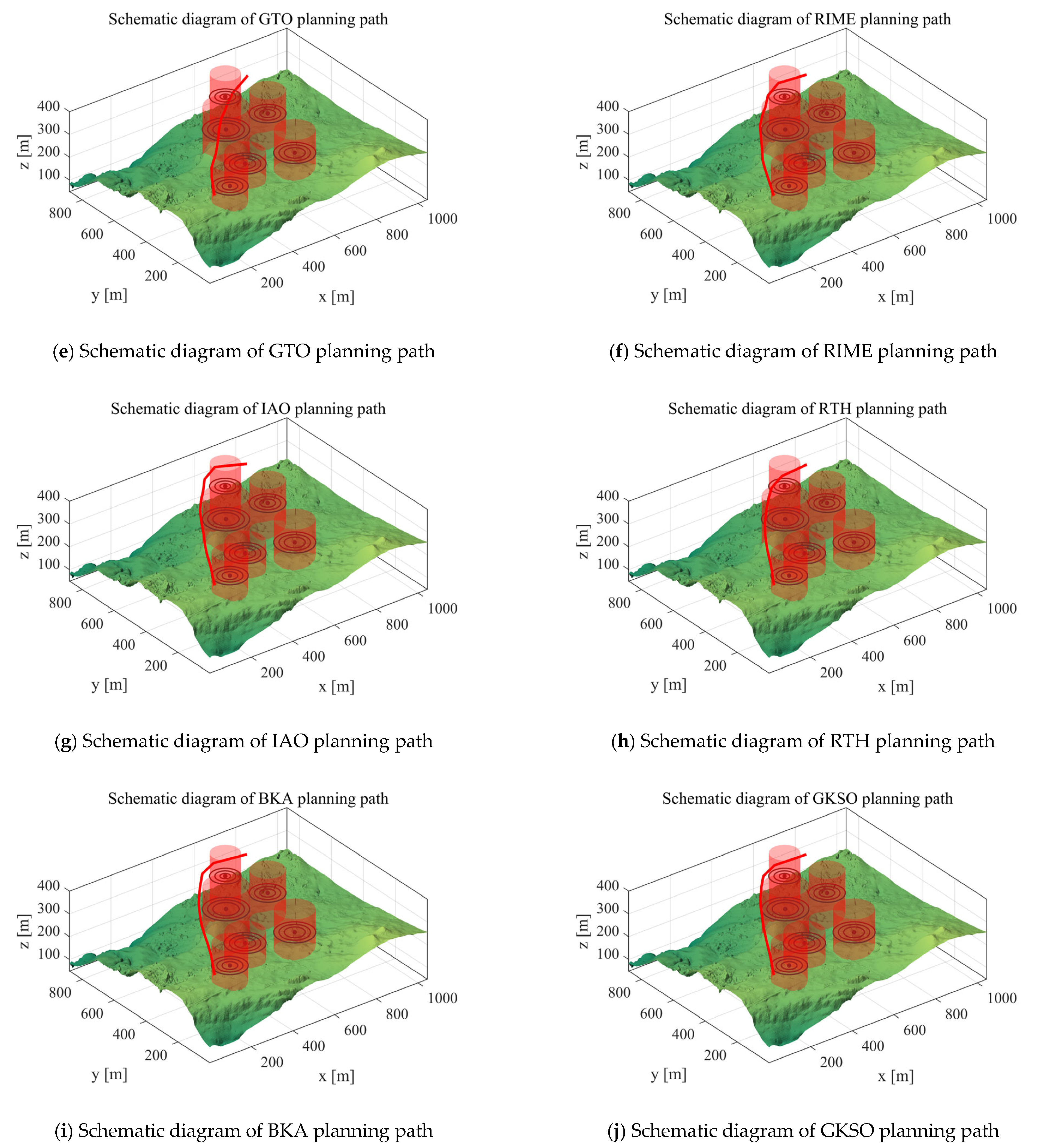
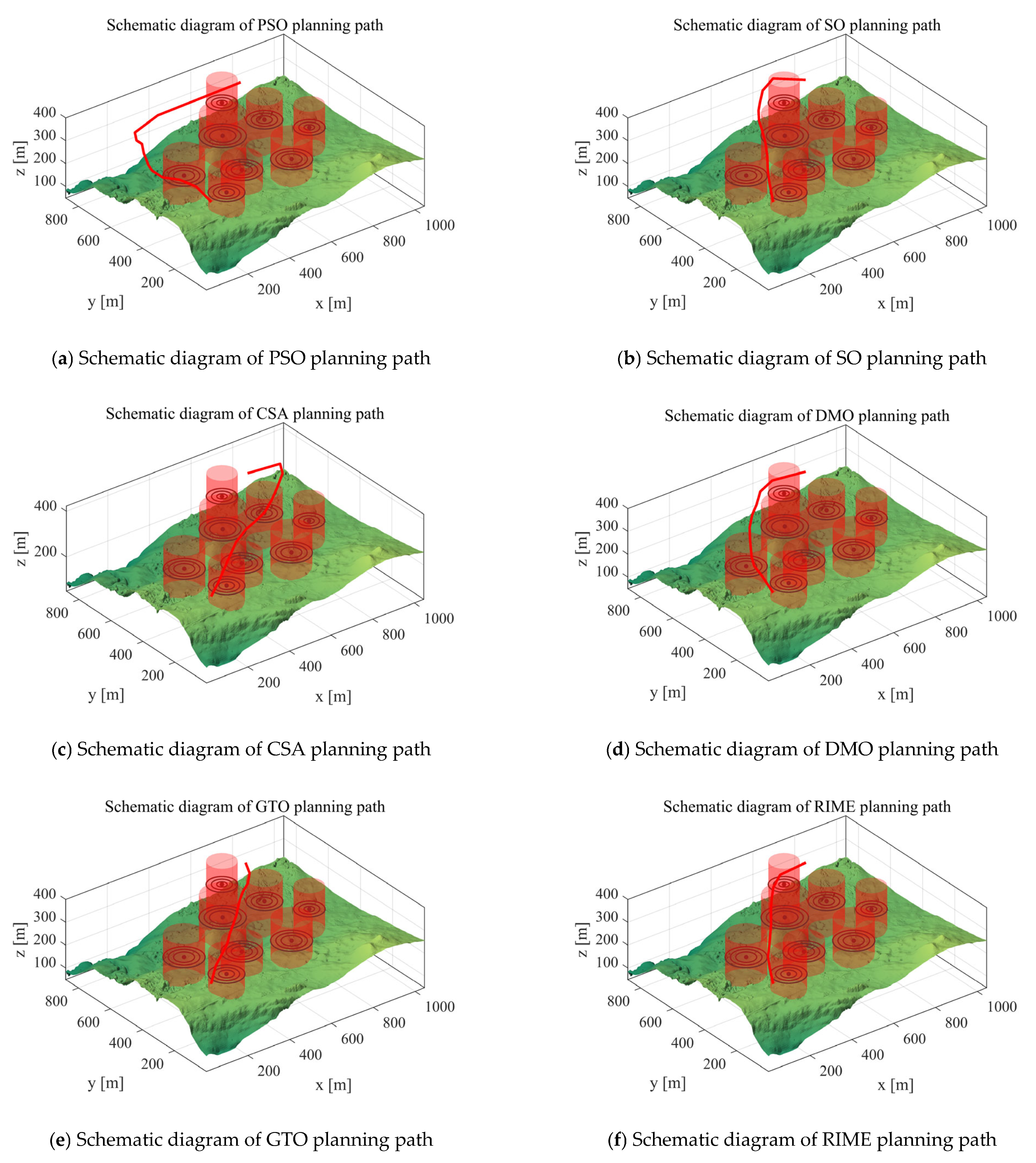
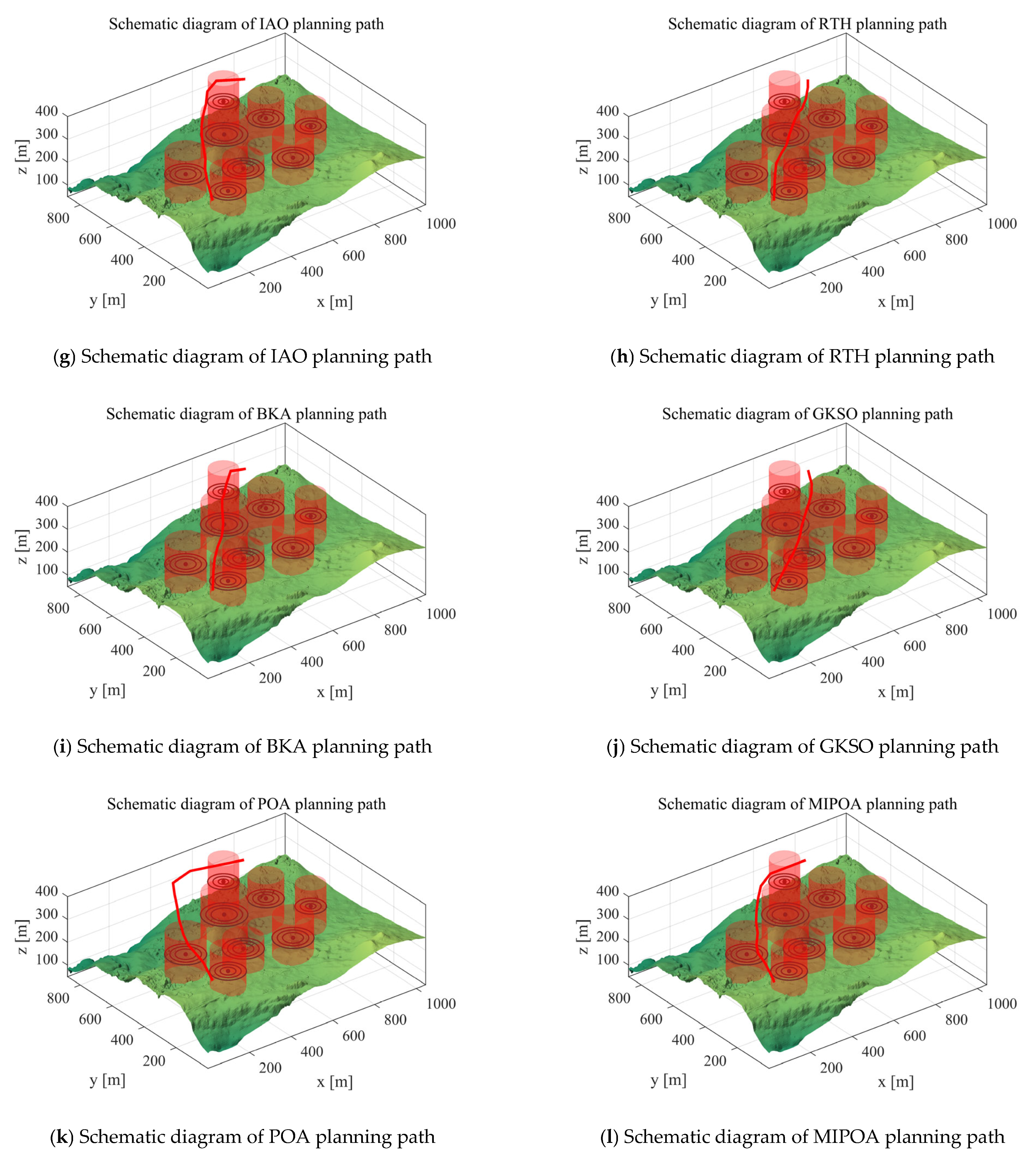
5. MIPOA for 3D UAV Path Planning
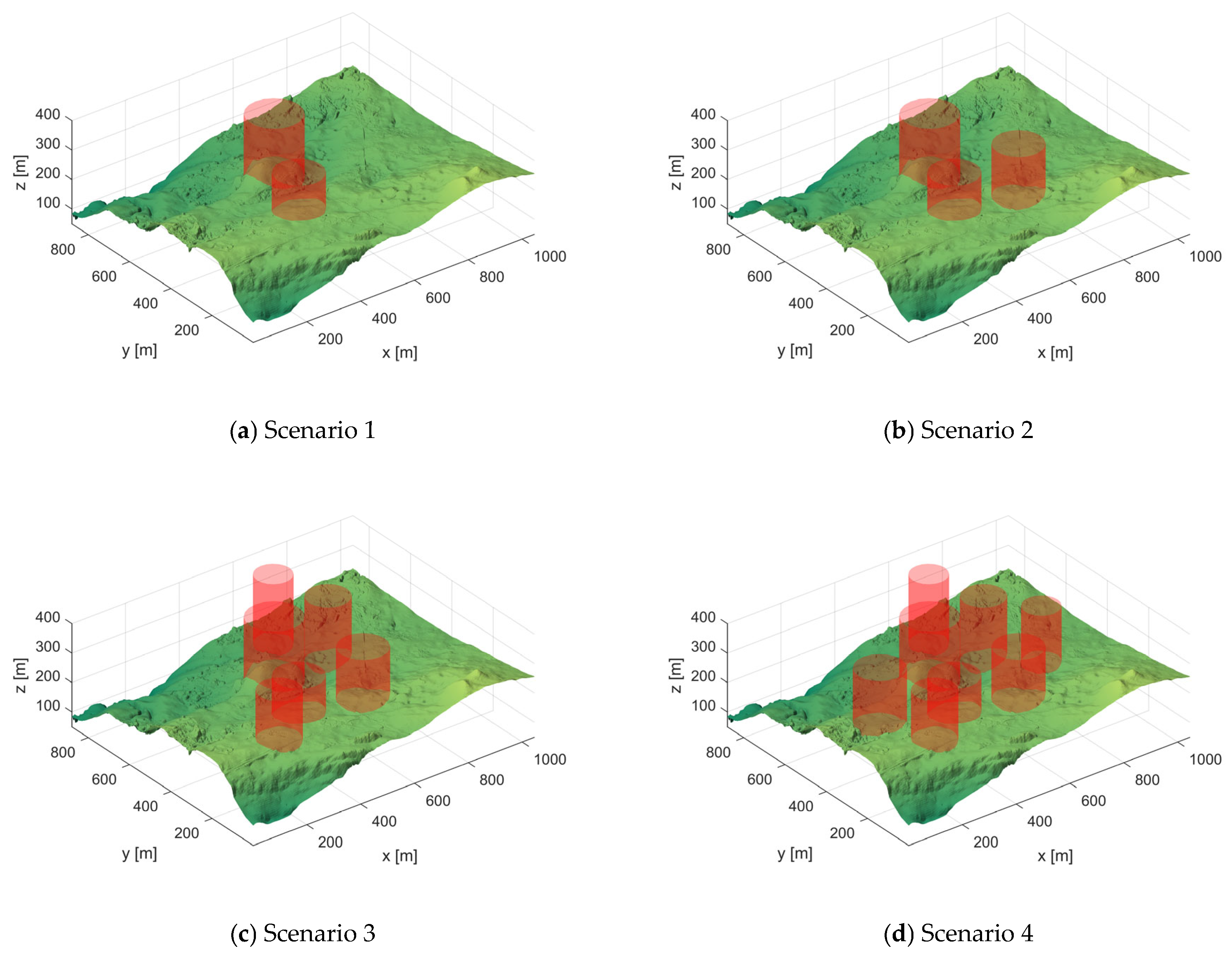
5.1. Scenarios and Objective Functions
5.1.1. Scenario Setting
5.1.2. Optimization Problem Definition
- 1.
- Path Length Costs
- 2.
- Threat Costs
- 3.
- High Costs
- 4.
- Smoothness Costs
- 5.
- Overall Objective Function (OEF)
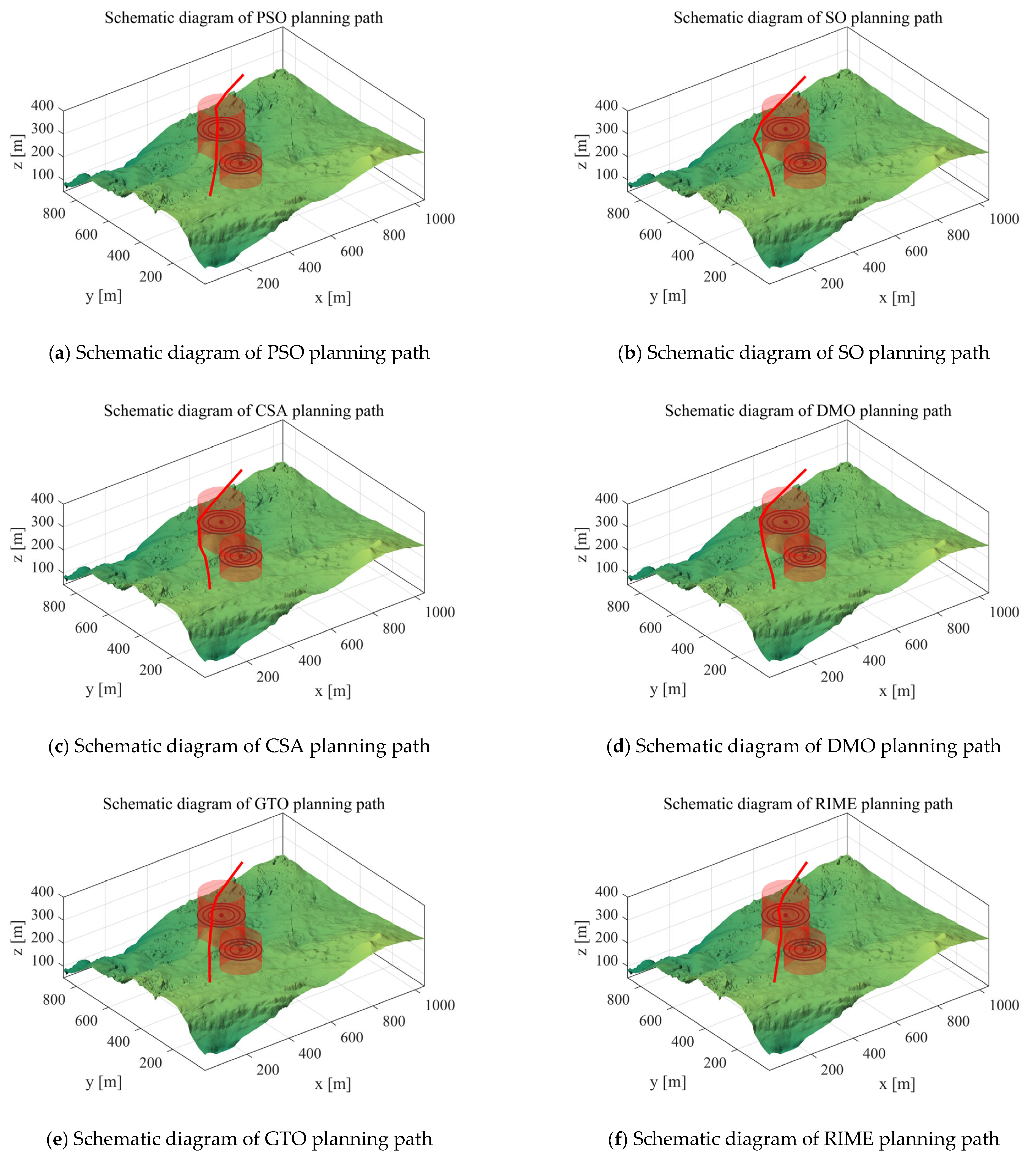
5.1.3. Analysis of Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| No. | Functions | Search Range | Dim | fmin |
|---|---|---|---|---|
| Unimodal functions | ||||
| F1 | Shifted and Rotated Bent Cigar Function | [−100, 100] | 30/50/100 | 100 |
| F3 | Shifted and Rotated Zakharov Function | [−100, 100] | 30/50/100 | 300 |
| Simple multimodal functions | ||||
| F4 | Shifted and Rotated Rosenbrock’s Function | [−100, 100] | 30/50/100 | 400 |
| F5 | Shifted and Rotated Rastrigin’s Function | [−100, 100] | 30/50/100 | 500 |
| F6 | Shifted and Rotated Expanded Scaffer’s F6 Function | [−100, 100] | 30/50/100 | 600 |
| F7 | Shifted and Rotated Lunacek Bi_Rastrigin’s Function | [−100, 100] | 30/50/100 | 700 |
| F8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | [−100, 100] | 30/50/100 | 800 |
| F9 | Shifted and Rotated Levy Function | [−100, 100] | 30/50/100 | 900 |
| F10 | Shifted and Rotated Schwefel’s Function | [−100, 100] | 30/50/100 | 1000 |
| Hybrid functions | ||||
| F11 | Hybrid Function 1 (N = 3) | [−100, 100] | 30/50/100 | 1100 |
| F12 | Hybrid Function 2 (N = 3) | [−100, 100] | 30/50/100 | 1200 |
| F13 | Hybrid Function 3 (N = 3) | [−100,100] | 30/50/100 | 1300 |
| F14 | Hybrid Function 4 (N = 4) | [−100, 100] | 30/50/100 | 1400 |
| F15 | Hybrid Function 5 (N = 4) | [−100, 100] | 30/50/100 | 1500 |
| F16 | Hybrid Function 6 (N = 4) | [−100, 100] | 30/50/100 | 1600 |
| F17 | Hybrid Function 6 (N = 5) | [−100, 100] | 30/50/100 | 1700 |
| F18 | Hybrid Function 6 (N = 5) | [−100, 100] | 30/50/100 | 1800 |
| F19 | Hybrid Function 6 (N = 5) | [−100, 100] | 30/50/100 | 1900 |
| F20 | Hybrid Function 6 (N = 6) | [−100, 100] | 30/50/100 | 2000 |
| Composition functions | ||||
| F21 | Composition Function 1 (N = 3) | [−100, 100] | 30/50/100 | 2100 |
| F22 | Composition Function 2 (N = 3) | [−100, 100] | 30/50/100 | 2200 |
| F23 | Composition Function 3 (N = 4) | [−100, 100] | 30/50/100 | 2300 |
| F24 | Composition Function 4 (N = 4) | [−100, 100] | 30/50/100 | 2400 |
| F25 | Composition Function 5 (N = 5) | [−100, 100] | 30/50/100 | 2500 |
| F26 | Composition Function 6 (N = 5) | [−100, 100] | 30/50/100 | 2600 |
| F27 | Composition Function 7 (N = 6) | [−100, 100] | 30/50/100 | 2700 |
| F28 | Composition Function 8 (N = 6) | [−100, 100] | 30/50/100 | 2800 |
| F29 | Composition Function 9 (N = 3) | [−100, 100] | 30/50/100 | 2900 |
| F30 | Composition Function 10 (N = 3) | [−100, 100] | 30/50/100 | 3000 |
| ID | Metric | PSO | SO | CSA | DMO | GTO | RIME | IAO | RTH | BKA | GKSO | POA | MIPOA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 2.3856 × 103 | 1.7081 × 103 | 2.0122 × 103 | 9.2414 × 102 | 1.2223 × 103 | 6.0571 × 103 | 1.0000 × 102 | 1.3941 × 102 | 2.7736 × 108 | 2.4571 × 103 | 7.6992 × 107 | 1.0171 × 102 |
| std | 2.9881 × 103 | 2.2529 × 103 | 1.8498 × 103 | 8.4574 × 102 | 1.1467 × 103 | 3.7123 × 103 | 1.6480 × 10−14 | 1.0087 × 102 | 9.0851 × 108 | 2.3363 × 103 | 2.9482 × 108 | 2.0654 | |
| F2 | mean | 2.0000 × 102 | 3.4207 × 103 | 1.9186 × 103 | 3.0307 × 102 | 5.4473 × 102 | 2.2760 × 102 | 2.0017 × 102 | 2.0853 × 102 | 1.3089 × 105 | 2.0003 × 102 | 1.9135 × 104 | 2.0000 × 102 |
| std | 0.0000 | 9.5181 × 103 | 2.9106 × 103 | 1.9163 × 102 | 1.7877 × 103 | 3.2860 × 101 | 3.7905 × 10−1 | 2.8470 × 101 | 4.6116 × 105 | 1.8257 × 10−1 | 7.8378 × 104 | 0.0000 | |
| F3 | mean | 3.0000 × 102 | 3.0000 × 102 | 3.0000 × 102 | 3.3189 × 102 | 3.0000 × 102 | 3.0005 × 102 | 3.0000 × 102 | 3.0000 × 102 | 3.0073 × 102 | 3.0000 × 102 | 4.9433 × 102 | 3.0000 × 102 |
| std | 1.6548 × 10−4 | 1.4877 × 10−3 | 9.1651 × 10−7 | 3.1247 × 101 | 4.7170 × 10−13 | 3.5916 × 10−2 | 1.8283 × 10−14 | 4.7206 × 10−14 | 1.7602 | 6.3448 × 10−13 | 4.7099 × 102 | 3.4059 × 10−6 | |
| F4 | mean | 4.0359 × 102 | 4.0432 × 102 | 4.0464 × 102 | 4.0483 × 102 | 4.0005 × 102 | 4.0515 × 102 | 4.0000 × 102 | 4.0000 × 102 | 4.1021 × 102 | 4.0000 × 102 | 4.1778 × 102 | 4.0001 × 102 |
| std | 1.3110 | 1.0064 | 2.3497 | 2.7069 × 10−1 | 1.4248 × 10−1 | 1.4139 | 6.2040 × 10−10 | 1.4749 × 10−12 | 2.8373 × 101 | 4.7864 × 10−3 | 2.3768 × 101 | 7.8635 × 10−3 | |
| F5 | mean | 5.3479 × 102 | 5.0860 × 102 | 5.0942 × 102 | 5.2225 × 102 | 5.2223 × 102 | 5.1093 × 102 | 5.0981 × 102 | 5.3177 × 102 | 5.3176 × 102 | 5.2564 × 102 | 5.3744 × 102 | 5.0993 × 102 |
| std | 1.0602 × 101 | 3.9774 | 4.1866 | 5.0772 | 1.0736 × 101 | 4.9328 | 5.8479 | 1.3190 × 101 | 1.7124 × 101 | 1.3279 × 101 | 1.4698 × 101 | 2.0623 | |
| F6 | mean | 6.0614 × 102 | 6.0006 × 102 | 6.0156 × 102 | 6.0000 × 102 | 6.0346 × 102 | 6.0008 × 102 | 6.0399 × 102 | 6.0745 × 102 | 6.2094 × 102 | 6.0229 × 102 | 6.1767 × 102 | 6.0054 × 102 |
| std | 5.4520 | 9.9274 × 10−2 | 9.2610 × 10−1 | 0.0000 | 2.9773 | 5.8481 × 10−2 | 5.8275 | 6.5398 | 1.1326 × 101 | 3.0874 | 9.4542 | 2.5883 × 10−1 | |
| F7 | mean | 7.2433 × 102 | 7.1977 × 102 | 7.2004 × 102 | 7.3488 × 102 | 7.4095 × 102 | 7.2099 × 102 | 7.2295 × 102 | 7.5242 × 102 | 7.5209 × 102 | 7.3464 × 102 | 7.6167 × 102 | 7.2076 × 102 |
| std | 5.5454 | 3.7734 | 3.5699 | 6.0218 | 1.4057 × 101 | 5.8978 | 7.0550 | 1.7280 × 101 | 1.5444 × 101 | 1.1282 × 101 | 1.5747 × 101 | 2.7182 | |
| F8 | mean | 8.1847 × 102 | 8.0907 × 102 | 8.0750 × 102 | 8.2290 × 102 | 8.2371 × 102 | 8.1224 × 102 | 8.1014 × 102 | 8.2186 × 102 | 8.1673 × 102 | 8.2083 × 102 | 8.2257 × 102 | 8.0982 × 102 |
| std | 6.7008 | 5.6088 | 3.6368 | 4.5489 | 8.5519 | 3.8679 | 5.7331 | 9.0077 | 6.5417 | 8.3118 | 6.7934 | 1.5402 | |
| F9 | mean | 9.2323 × 102 | 9.0022 × 102 | 9.0353 × 102 | 9.0000 × 102 | 9.3929 × 102 | 9.0001 × 102 | 9.1354 × 102 | 9.8679 × 102 | 1.0731 × 103 | 9.0148 × 102 | 1.0338 × 103 | 9.0008 × 102 |
| std | 8.1361 × 101 | 2.5522 × 10−1 | 2.7670 | 0.0000 | 3.8127 × 101 | 2.6785 × 10−2 | 3.8641 × 101 | 8.4907 × 101 | 8.4032 × 101 | 2.4557 | 9.6555 × 101 | 7.0933 × 10−2 | |
| F10 | mean | 1.9044 × 103 | 1.3797 × 103 | 1.5890 × 103 | 2.0561 × 103 | 1.8259 × 103 | 1.4082 × 103 | 1.4571 × 103 | 1.9452 × 103 | 1.8022 × 103 | 1.7535 × 103 | 1.6075 × 103 | 1.2400 × 103 |
| std | 2.7179 × 102 | 3.2223 × 102 | 2.4007 × 102 | 1.7430 × 102 | 2.4684 × 102 | 1.8170 × 102 | 1.4921 × 102 | 2.8712 × 102 | 2.9015 × 102 | 2.9005 × 102 | 2.4731 × 102 | 9.8284 × 101 | |
| F11 | mean | 1.1380 × 103 | 1.1068 × 103 | 1.1227 × 103 | 1.1041 × 103 | 1.1217 × 103 | 1.1103 × 103 | 1.1022 × 103 | 1.1411 × 103 | 1.1289 × 103 | 1.1170 × 103 | 1.1386 × 103 | 1.1046 × 103 |
| std | 2.0918 × 101 | 4.2264 | 1.4215 × 101 | 8.3713 × 10−1 | 1.4995 × 101 | 4.9238 | 2.5295 | 3.0737 × 101 | 2.3346 × 101 | 1.9158 × 101 | 2.6502 × 101 | 1.4261 | |
| F12 | mean | 1.2873 × 104 | 1.3038 × 104 | 8.9658 × 103 | 9.9579 × 104 | 9.0081 × 103 | 1.9553 × 104 | 1.4451 × 103 | 3.1185 × 103 | 1.8248 × 104 | 1.3108 × 104 | 5.3067 × 104 | 1.3427 × 103 |
| std | 7.9436 × 103 | 9.6121 × 103 | 8.2015 × 103 | 6.4623 × 104 | 9.4741 × 103 | 1.7285 × 104 | 1.8848 × 102 | 1.8207 × 103 | 1.2934 × 104 | 1.4147 × 104 | 1.0782 × 105 | 6.0159 × 101 | |
| F13 | mean | 8.1942 × 103 | 7.5436 × 103 | 1.8136 × 103 | 2.1975 × 103 | 1.5307 × 103 | 9.2592 × 103 | 1.3045 × 103 | 1.5467 × 103 | 1.8087 × 103 | 1.4932 × 103 | 2.0884 × 103 | 1.3082 × 103 |
| std | 6.1294 × 103 | 7.3509 × 103 | 3.5239 × 102 | 5.8766 × 102 | 2.2925 × 102 | 9.3058 × 103 | 3.8096 | 2.2020 × 102 | 2.9037 × 102 | 1.5354 × 102 | 5.3764 × 102 | 3.5778 | |
| F14 | mean | 1.6543 × 103 | 1.4767 × 103 | 1.4367 × 103 | 1.4787 × 103 | 1.4606 × 103 | 1.8200 × 103 | 1.4024 × 103 | 1.4880 × 103 | 1.4723 × 103 | 1.4331 × 103 | 1.4465 × 103 | 1.4056 × 103 |
| std | 4.5884 × 102 | 3.5938 × 101 | 1.2518 × 101 | 2.0636 × 101 | 3.1245 × 101 | 7.3630 × 102 | 3.9571 | 4.1668 × 101 | 2.7623 × 101 | 1.3177 × 101 | 1.7135 × 101 | 2.5043 | |
| F15 | mean | 1.9578 × 103 | 1.7259 × 103 | 1.5905 × 103 | 1.6893 × 103 | 1.5380 × 103 | 2.2626 × 103 | 1.5004 × 103 | 1.5828 × 103 | 1.6118 × 103 | 1.5202 × 103 | 1.5877 × 103 | 1.5025 × 103 |
| std | 8.0362 × 102 | 1.2566 × 102 | 6.5380 × 101 | 1.0283 × 102 | 3.4263 × 101 | 1.3272 × 103 | 3.2107 × 10−1 | 6.8018 × 101 | 2.3747 × 102 | 1.5937 × 101 | 5.9432 × 101 | 7.9964 × 10−1 | |
| F16 | mean | 1.8312 × 103 | 1.6028 × 103 | 1.6284 × 103 | 1.6062 × 103 | 1.6750 × 103 | 1.7116 × 103 | 1.6028 × 103 | 1.7831 × 103 | 1.7383 × 103 | 1.6561 × 103 | 1.7373 × 103 | 1.6016 × 103 |
| std | 1.3806 × 102 | 2.5135 | 3.6288 × 101 | 3.5341 | 8.4054 × 101 | 1.0041 × 102 | 1.8743 | 1.4627 × 102 | 9.2591 × 101 | 5.8843 × 101 | 8.4176 × 101 | 3.2442 × 10−1 | |
| F17 | mean | 1.7584 × 103 | 1.7240 × 103 | 1.7339 × 103 | 1.7343 × 103 | 1.7398 × 103 | 1.7522 × 103 | 1.7296 × 103 | 1.7671 × 103 | 1.7595 × 103 | 1.7354 × 103 | 1.7466 × 103 | 1.7255 × 103 |
| std | 3.9980 × 101 | 1.0670 × 101 | 8.9509 | 7.0625 | 1.7130 × 101 | 4.7848 × 101 | 7.7925 | 4.0761 × 101 | 4.1839 × 101 | 1.8294 × 101 | 1.0139 × 101 | 3.6943 | |
| F18 | mean | 9.4365 × 103 | 1.3079 × 104 | 2.0104 × 103 | 6.2453 × 103 | 1.9253 × 103 | 8.8219 × 103 | 1.8120 × 103 | 2.5851 × 103 | 1.9682 × 103 | 1.9692 × 103 | 2.4264 × 103 | 1.8167 × 103 |
| std | 7.0252 × 103 | 1.2328 × 104 | 1.9818 × 102 | 3.1808 × 103 | 8.7389 × 101 | 8.3142 × 103 | 9.6535 | 2.3981 × 103 | 1.2263 × 102 | 1.1552 × 102 | 1.8765 × 103 | 6.4960 | |
| F19 | mean | 3.0836 × 103 | 2.2656 × 103 | 1.9428 × 103 | 1.9940 × 103 | 1.9401 × 103 | 2.9815 × 103 | 1.9013 × 103 | 1.9662 × 103 | 1.9339 × 103 | 1.9099 × 103 | 1.9397 × 103 | 1.9025 × 103 |
| std | 1.7602 × 103 | 6.7206 × 102 | 6.0463 × 101 | 6.8486 × 101 | 3.1974 × 101 | 2.3355 × 103 | 7.8741 × 10−1 | 3.9985 × 101 | 2.9913 × 101 | 7.8082 | 3.5773 × 101 | 4.9913 × 10−1 | |
| F20 | mean | 2.1030 × 103 | 2.0178 × 103 | 2.0290 × 103 | 2.0006 × 103 | 2.0494 × 103 | 2.0148 × 103 | 2.0205 × 103 | 2.1460 × 103 | 2.0682 × 103 | 2.0306 × 103 | 2.0552 × 103 | 2.0215 × 103 |
| std | 6.7392 × 101 | 1.0731 × 101 | 9.1290 | 1.0886 | 3.1247 × 101 | 2.3151 × 101 | 7.0400 | 6.5394 × 101 | 3.7634 × 101 | 1.4306 × 101 | 2.6692 × 101 | 3.4791 | |
| F21 | mean | 2.3063 × 103 | 2.3109 × 103 | 2.2807 × 103 | 2.2679 × 103 | 2.2018 × 103 | 2.2874 × 103 | 2.2002 × 103 | 2.3304 × 103 | 2.2585 × 103 | 2.2049 × 103 | 2.2421 × 103 | 2.1967 × 103 |
| std | 5.5113 × 101 | 1.6946 × 101 | 4.8453 × 101 | 4.4057 × 101 | 1.5038 | 5.2954 × 101 | 7.5577 × 10−1 | 3.7695 × 101 | 6.2332 × 101 | 3.5387 × 101 | 5.8283 × 101 | 1.8257 × 101 | |
| F22 | mean | 2.3120 × 103 | 2.3021 × 103 | 2.2965 × 103 | 2.3002 × 103 | 2.3019 × 103 | 2.2936 × 103 | 2.3008 × 103 | 2.3022 × 103 | 2.3071 × 103 | 2.2986 × 103 | 2.3141 × 103 | 2.2768 × 103 |
| std | 5.5746 × 101 | 9.4581 × 10−1 | 1.9579 × 101 | 2.7318 | 1.5187 × 101 | 2.4258 × 101 | 5.7347 × 10−1 | 1.0909 × 101 | 6.5675 | 1.8050 × 101 | 3.3935 × 101 | 2.9977 × 101 | |
| F23 | mean | 2.6818 × 103 | 2.6099 × 103 | 2.6133 × 103 | 2.6175 × 103 | 2.6141 × 103 | 2.6159 × 103 | 2.6115 × 103 | 2.6289 × 103 | 2.6359 × 103 | 2.6293 × 103 | 2.6431 × 103 | 2.5799 × 103 |
| std | 3.3427 × 101 | 3.8647 | 5.4417 | 3.9944 | 6.0737 × 101 | 5.6617 | 6.0457 | 1.5901 × 101 | 1.9003 × 101 | 1.1956 × 101 | 1.6728 × 101 | 9.4920 × 101 | |
| F24 | mean | 2.7351 × 103 | 2.7396 × 103 | 2.7325 × 103 | 2.7043 × 103 | 2.7013 × 103 | 2.7315 × 103 | 2.5602 × 103 | 2.7503 × 103 | 2.7398 × 103 | 2.6891 × 103 | 2.6055 × 103 | 2.4924 × 103 |
| std | 1.2765 × 102 | 6.7077 | 4.4081 × 101 | 4.7028 × 101 | 1.0280 × 102 | 6.3243 × 101 | 1.0751 × 102 | 4.8868 × 101 | 6.6543 × 101 | 1.1667 × 102 | 1.2746 × 102 | 2.3448 × 101 | |
| F25 | mean | 2.9185 × 103 | 2.9232 × 103 | 2.9222 × 103 | 2.9222 × 103 | 2.9346 × 103 | 2.9243 × 103 | 2.9149 × 103 | 2.9173 × 103 | 2.9031 × 103 | 2.9300 × 103 | 2.9132 × 103 | 2.8879 × 103 |
| std | 6.5997 × 101 | 2.3744 × 101 | 2.3409 × 101 | 1.9438 × 101 | 2.2096 × 101 | 2.4286 × 101 | 2.2190 × 101 | 6.4741 × 101 | 8.8304 × 101 | 2.2608 × 101 | 2.3790 × 101 | 5.4167 × 101 | |
| F26 | mean | 3.1352 × 103 | 2.9334 × 103 | 2.9354 × 103 | 2.8739 × 103 | 2.9601 × 103 | 3.0111 × 103 | 2.8667 × 103 | 3.1586 × 103 | 3.0089 × 103 | 2.9109 × 103 | 3.0251 × 103 | 2.6404 × 103 |
| std | 3.5165 × 102 | 1.6621 × 102 | 5.1280 × 101 | 4.4012 × 101 | 7.5092 × 101 | 3.2461 × 102 | 9.2227 × 101 | 3.6605 × 102 | 2.5939 × 102 | 8.2133 × 101 | 3.0268 × 102 | 8.1179 × 101 | |
| F27 | mean | 3.1443 × 103 | 3.0905 × 103 | 3.0936 × 103 | 3.0898 × 103 | 3.0948 × 103 | 3.0947 × 103 | 3.0908 × 103 | 3.1055 × 103 | 3.1009 × 103 | 3.0996 × 103 | 3.1028 × 103 | 3.0714 × 103 |
| std | 5.1226 × 101 | 1.1505 | 2.1731 | 4.0542 × 10−1 | 3.9185 | 4.0787 | 2.7376 | 2.0760 × 101 | 1.6145 × 101 | 1.6508 × 101 | 2.3316 × 101 | 1.5662 × 10−1 | |
| F28 | mean | 3.1593 × 103 | 3.3700 × 103 | 3.3831 × 103 | 3.1948 × 103 | 3.2300 × 103 | 3.2441 × 103 | 3.1558 × 103 | 3.3667 × 103 | 3.2846 × 103 | 3.2949 × 103 | 3.2092 × 103 | 3.0816 × 103 |
| std | 3.9504 × 101 | 8.1749 × 101 | 1.3219 × 102 | 3.3446 × 101 | 1.4884 × 102 | 1.2724 × 102 | 1.0617 × 102 | 1.9725 × 102 | 1.3828 × 102 | 1.4833 × 102 | 9.7186 × 101 | 7.0302 × 101 | |
| F29 | mean | 3.2290 × 103 | 3.1639 × 103 | 3.1630 × 103 | 3.1908 × 103 | 3.1941 × 103 | 3.1768 × 103 | 3.1483 × 103 | 3.2723 × 103 | 3.2226 × 103 | 3.1888 × 103 | 3.2014 × 103 | 3.1439 × 103 |
| std | 4.6895 × 101 | 1.6912 × 101 | 2.8535 × 101 | 1.4277 × 101 | 5.0765 × 101 | 3.3359 × 101 | 1.2537 × 101 | 7.3769 × 101 | 4.7467 × 101 | 4.0145 × 101 | 3.5853 × 101 | 4.0749 | |
| F30 | mean | 1.7760 × 104 | 2.1272 × 105 | 1.4345 × 105 | 4.8851 × 104 | 8.9597 × 105 | 2.5868 × 105 | 4.8011 × 104 | 4.3742 × 105 | 2.6654 × 105 | 2.5003 × 105 | 1.2044 × 105 | 3.2026 × 103 |
| std | 1.3874 × 104 | 3.8309 × 105 | 2.3821 × 105 | 3.3600 × 104 | 1.1484 × 106 | 4.2288 × 105 | 1.7850 × 105 | 6.0427 × 105 | 6.2004 × 105 | 3.8000 × 105 | 3.4127 × 105 | 2.8759 × 10−1 |
| ID | Metric | PSO | SO | CSA | DMO | GTO | RIME | IAO | RTH | BKA | GKSO | POA | MIPOA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 2.3887 × 105 | 4.1212 × 106 | 5.3715 × 104 | 1.8116 × 106 | 5.5840 × 103 | 3.3394 × 105 | 2.2697 × 1010 | 2.4027 × 103 | 6.3356 × 109 | 3.0529 × 103 | 1.2952 × 1010 | 5.8125 × 107 |
| std | 2.0175 × 105 | 6.9561 × 106 | 1.4589 × 105 | 2.4935 × 106 | 6.2617 × 103 | 1.5203 × 105 | 7.8430 × 109 | 2.4311 × 103 | 9.6751 × 109 | 3.0859 × 103 | 5.2422 × 109 | 3.2562 × 107 | |
| F2 | mean | 8.8878 × 109 | 3.9737 × 1021 | 5.7904 × 1021 | 2.9900 × 1031 | 9.5564 × 1019 | 1.3117 × 1013 | 1.1162 × 1029 | 2.4334 × 1016 | 1.7475 × 1035 | 2.4919 × 1012 | 3.2294 × 1032 | 3.3591 × 1015 |
| std | 1.5201 × 1010 | 1.1207 × 1022 | 2.6129 × 1022 | 7.4630 × 1031 | 3.4676 × 1020 | 3.0103 × 1013 | 3.2659 × 1029 | 1.3319 × 1017 | 9.5713 × 1035 | 7.2226 × 1012 | 1.3240 × 1033 | 4.3542 × 1015 | |
| F3 | mean | 5.8438 × 103 | 5.8222 × 104 | 3.3874 × 104 | 1.2183 × 105 | 9.3618 × 102 | 6.2407 × 103 | 3.9258 × 104 | 3.0000 × 102 | 1.1287 × 104 | 3.0686 × 102 | 3.2265 × 104 | 1.3446 × 103 |
| std | 2.8840 × 103 | 1.1117 × 104 | 9.9291 × 103 | 1.6997 × 104 | 6.7845 × 102 | 3.1434 × 103 | 1.1985 × 104 | 3.2956 × 10−9 | 8.8805 × 103 | 8.7978 | 7.5831 × 103 | 4.1728 × 102 | |
| F4 | mean | 4.6617 × 102 | 5.0048 × 102 | 5.1651 × 102 | 5.1924 × 102 | 4.9865 × 102 | 5.0876 × 102 | 3.8591 × 103 | 4.1478 × 102 | 1.1379 × 103 | 5.0332 × 102 | 2.0709 × 103 | 4.9676 × 102 |
| std | 2.8965 × 101 | 7.4753 | 3.5997 × 101 | 1.4727 × 101 | 2.9284 × 101 | 1.7870 × 101 | 1.9037 × 103 | 2.3442 × 101 | 1.9227 × 103 | 2.0892 × 101 | 1.3256 × 103 | 1.2709 × 101 | |
| F5 | mean | 6.7086 × 102 | 5.6521 × 102 | 5.9546 × 102 | 7.1824 × 102 | 6.9096 × 102 | 5.8907 × 102 | 7.3458 × 102 | 6.8006 × 102 | 7.4552 × 102 | 6.7585 × 102 | 7.5945 × 102 | 6.5495 × 102 |
| std | 2.9210 × 101 | 2.3066 × 101 | 2.0244 × 101 | 1.2756 × 101 | 4.4679 × 101 | 1.9869 × 101 | 3.7477 × 101 | 4.6841 × 101 | 4.2469 × 101 | 4.7296 × 101 | 3.2677 × 101 | 1.1852 × 101 | |
| F6 | mean | 6.3913 × 102 | 6.0201 × 102 | 6.2206 × 102 | 6.0049 × 102 | 6.3917 × 102 | 6.0311 × 102 | 6.5288 × 102 | 6.3864 × 102 | 6.6084 × 102 | 6.3738 × 102 | 6.5892 × 102 | 6.3431 × 102 |
| std | 7.5776 | 6.2737 × 10−1 | 3.8666 | 1.0403 × 10−1 | 6.8787 | 2.4983 | 9.5613 | 8.7310 | 6.6730 | 8.3636 | 8.3218 | 3.9429 | |
| F7 | mean | 8.4865 × 102 | 7.8068 × 102 | 9.0196 × 102 | 9.6384 × 102 | 1.0353 × 103 | 8.2806 × 102 | 1.1142 × 103 | 1.0848 × 103 | 1.1631 × 103 | 9.4314 × 102 | 1.2456 × 103 | 9.4878 × 102 |
| std | 4.0650 × 101 | 1.3518 × 101 | 3.9050 × 101 | 1.2216 × 101 | 8.3044 × 101 | 2.8262 × 101 | 7.8197 × 101 | 1.0283 × 102 | 7.6104 × 101 | 7.8029 × 101 | 8.1429 × 101 | 3.5823 × 101 | |
| F8 | mean | 9.1568 × 102 | 8.8393 × 102 | 8.7566 × 102 | 1.0201 × 103 | 9.5238 × 102 | 8.8069 × 102 | 9.9803 × 102 | 9.3997 × 102 | 9.6763 × 102 | 9.3860 × 102 | 9.8721 × 102 | 9.1897 × 102 |
| std | 2.0356 × 101 | 4.0500 × 101 | 1.5559 × 101 | 1.6290 × 101 | 2.8459 × 101 | 1.7130 × 101 | 2.6693 × 101 | 2.5179 × 101 | 3.2740 × 101 | 2.6754 × 101 | 3.2120 × 101 | 1.0338 × 101 | |
| F9 | mean | 4.3171 × 103 | 9.4265 × 102 | 1.7217 × 103 | 1.0651 × 103 | 3.9133 × 103 | 1.7294 × 103 | 5.0062 × 103 | 4.2688 × 103 | 5.2233 × 103 | 3.0113 × 103 | 5.2922 × 103 | 2.7618 × 103 |
| std | 1.1451 × 103 | 1.8068 × 101 | 3.5158 × 102 | 4.6318 × 101 | 1.0492 × 103 | 9.8103 × 102 | 1.2513 × 103 | 8.4554 × 102 | 1.5914 × 103 | 7.3000 × 102 | 6.9489 × 102 | 3.4390 × 102 | |
| F10 | mean | 4.7853 × 103 | 7.2348 × 103 | 5.0804 × 103 | 8.3930 × 103 | 5.4580 × 103 | 4.2668 × 103 | 5.4988 × 103 | 5.0910 × 103 | 5.3249 × 103 | 4.6522 × 103 | 4.9332 × 103 | 3.8602 × 103 |
| std | 6.0241 × 102 | 1.1399 × 103 | 6.8059 × 102 | 2.4191 × 102 | 6.9727 × 102 | 8.1309 × 102 | 4.6110 × 102 | 4.7006 × 102 | 1.1317 × 103 | 6.4247 × 102 | 4.8405 × 102 | 2.5247 × 102 | |
| F11 | mean | 1.2108 × 103 | 1.2687 × 103 | 1.2831 × 103 | 1.3159 × 103 | 1.2277 × 103 | 1.2828 × 103 | 1.6494 × 103 | 1.2323 × 103 | 1.4747 × 103 | 1.2129 × 103 | 1.8163 × 103 | 1.2266 × 103 |
| std | 3.5856 × 101 | 5.9229 × 101 | 5.5672 × 101 | 2.4824 × 101 | 4.4392 × 101 | 6.1624 × 101 | 2.9170 × 102 | 5.6626 × 101 | 4.8748 × 102 | 4.4994 × 101 | 5.8934 × 102 | 2.0263 × 101 | |
| F12 | mean | 1.3674 × 106 | 4.6405 × 105 | 2.0060 × 107 | 1.1783 × 107 | 2.6780 × 105 | 6.4665 × 106 | 3.0142 × 108 | 2.3418 × 104 | 7.3454 × 108 | 1.4641 × 105 | 7.3355 × 108 | 4.1859 × 104 |
| std | 1.0342 × 106 | 6.7269 × 105 | 1.7733 × 107 | 4.9616 × 106 | 3.5112 × 105 | 4.6376 × 106 | 4.2146 × 108 | 9.9337 × 103 | 1.5460 × 109 | 1.4323 × 105 | 9.7443 × 108 | 2.0009 × 104 | |
| F13 | mean | 1.7251 × 104 | 3.3747 × 104 | 8.9635 × 104 | 1.2941 × 104 | 1.8523 × 104 | 7.5503 × 104 | 2.0894 × 104 | 2.0063 × 104 | 6.7048 × 107 | 1.2284 × 104 | 9.9304 × 106 | 1.6918 × 104 |
| std | 1.5792 × 104 | 3.1224 × 104 | 5.4861 × 104 | 6.6435 × 103 | 2.1306 × 104 | 8.2531 × 104 | 8.6800 × 103 | 2.1076 × 104 | 2.5169 × 108 | 1.1789 × 104 | 4.6597 × 107 | 5.7752 × 103 | |
| F14 | mean | 2.5616 × 104 | 2.7050 × 104 | 2.7686 × 103 | 6.2063 × 104 | 2.3805 × 103 | 3.4112 × 104 | 1.5248 × 103 | 1.8808 × 103 | 6.1431 × 103 | 2.4914 × 103 | 1.0540 × 104 | 1.5340 × 103 |
| std | 2.8730 × 104 | 3.7991 × 104 | 2.2196 × 103 | 3.6532 × 104 | 1.4626 × 103 | 2.9479 × 104 | 3.3099 × 101 | 4.5072 × 102 | 9.2527 × 103 | 1.1878 × 103 | 1.9051 × 104 | 1.4269 × 101 | |
| F15 | mean | 1.0135 × 104 | 1.0427 × 104 | 1.9123 × 104 | 4.4067 × 103 | 7.8583 × 103 | 1.4598 × 104 | 3.3242 × 103 | 1.0190 × 104 | 2.9930 × 104 | 8.6824 × 103 | 4.2329 × 104 | 2.5729 × 103 |
| std | 8.3846 × 103 | 1.4153 × 104 | 1.3021 × 104 | 4.0265 × 103 | 8.4136 × 103 | 1.2569 × 104 | 1.3391 × 103 | 1.0183 × 104 | 1.7070 × 104 | 1.1697 × 104 | 4.7107 × 104 | 2.7381 × 102 | |
| F16 | mean | 2.7400 × 103 | 2.5257 × 103 | 2.3963 × 103 | 3.2242 × 103 | 2.6644 × 103 | 2.5929 × 103 | 2.4643 × 103 | 2.8506 × 103 | 3.1579 × 103 | 2.6366 × 103 | 2.9138 × 103 | 2.2002 × 103 |
| std | 3.0491 × 102 | 4.4204 × 102 | 2.1649 × 102 | 1.8173 × 102 | 2.6823 × 102 | 2.0684 × 102 | 1.7104 × 102 | 3.6231 × 102 | 7.7074 × 102 | 2.6462 × 102 | 2.7651 × 102 | 1.0770 × 102 | |
| F17 | mean | 2.2757 × 103 | 1.9957 × 103 | 1.9544 × 103 | 2.3000 × 103 | 2.2977 × 103 | 2.0751 × 103 | 1.9801 × 103 | 2.4452 × 103 | 2.3502 × 103 | 2.1687 × 103 | 2.2254 × 103 | 1.8574 × 103 |
| std | 2.7626 × 102 | 1.6987 × 102 | 1.1393 × 102 | 1.2199 × 102 | 2.7606 × 102 | 2.0310 × 102 | 9.1128 × 101 | 2.4003 × 102 | 2.4509 × 102 | 2.2021 × 102 | 1.8528 × 102 | 2.9121 × 101 | |
| F18 | mean | 4.1652 × 105 | 6.4123 × 105 | 1.1114 × 105 | 4.0719 × 106 | 4.6263 × 104 | 6.7045 × 105 | 5.3089 × 103 | 1.6027 × 104 | 9.4520 × 104 | 6.2307 × 104 | 1.2719 × 105 | 2.7823 × 103 |
| std | 3.3795 × 105 | 5.7206 × 105 | 8.4463 × 104 | 1.5024 × 106 | 3.6244 × 104 | 4.6140 × 105 | 4.4383 × 103 | 1.6863 × 104 | 9.4900 × 104 | 3.7934 × 104 | 6.3967 × 104 | 3.2598 × 102 | |
| F19 | mean | 1.0421 × 104 | 1.3416 × 104 | 5.7798 × 104 | 4.1086 × 103 | 4.6849 × 103 | 1.2598 × 104 | 2.2757 × 103 | 7.6820 × 103 | 6.5206 × 105 | 9.8353 × 103 | 7.9636 × 105 | 2.1558 × 103 |
| std | 1.0218 × 104 | 1.7150 × 104 | 6.4123 × 104 | 2.6330 × 103 | 2.7085 × 103 | 1.4065 × 104 | 3.5961 × 102 | 8.3638 × 103 | 2.8344 × 106 | 9.4090 × 103 | 7.2657 × 105 | 7.1828 × 101 | |
| F20 | mean | 2.5924 × 103 | 2.3682 × 103 | 2.3296 × 103 | 2.6797 × 103 | 2.4606 × 103 | 2.4191 × 103 | 2.3063 × 103 | 2.6804 × 103 | 2.5009 × 103 | 2.4945 × 103 | 2.4323 × 103 | 2.2592 × 103 |
| std | 1.8659 × 102 | 1.6589 × 102 | 1.2553 × 102 | 1.4716 × 102 | 1.6846 × 102 | 1.8311 × 102 | 6.7487 × 101 | 1.8067 × 102 | 1.6437 × 102 | 1.8614 × 102 | 1.2110 × 102 | 3.5669 × 101 | |
| F21 | mean | 2.4777 × 103 | 2.3837 × 103 | 2.3806 × 103 | 2.5069 × 103 | 2.4340 × 103 | 2.3818 × 103 | 2.4849 × 103 | 2.4545 × 103 | 2.5256 × 103 | 2.4444 × 103 | 2.5237 × 103 | 2.3651 × 103 |
| std | 3.0931 × 101 | 3.8093 × 101 | 2.0688 × 101 | 1.4038 × 101 | 5.5433 × 101 | 2.2668 × 101 | 5.1195 × 101 | 3.7596 × 101 | 5.1834 × 101 | 3.1345 × 101 | 4.0025 × 101 | 7.7143 × 101 | |
| F22 | mean | 5.1053 × 103 | 4.4880 × 103 | 3.1461 × 103 | 4.0745 × 103 | 2.4836 × 103 | 4.2215 × 103 | 5.2023 × 103 | 4.4967 × 103 | 5.7815 × 103 | 2.9570 × 103 | 4.4516 × 103 | 2.3765 × 103 |
| std | 2.0751 × 103 | 2.6396 × 103 | 1.6627 × 103 | 1.9327 × 103 | 9.9718 × 102 | 1.9367 × 103 | 1.0728 × 103 | 2.2931 × 103 | 1.8194 × 103 | 1.5182 × 103 | 1.4247 × 103 | 2.4947 × 101 | |
| F23 | mean | 3.1018 × 103 | 2.7224 × 103 | 2.7458 × 103 | 2.8600 × 103 | 2.8650 × 103 | 2.7452 × 103 | 2.9335 × 103 | 2.8736 × 103 | 3.0395 × 103 | 2.8418 × 103 | 2.9698 × 103 | 2.8011 × 103 |
| std | 1.3152 × 102 | 2.8661 × 101 | 2.5012 × 101 | 8.2729 | 7.6955 × 101 | 2.7605 × 101 | 5.8486 × 101 | 5.3752 × 101 | 9.9087 × 101 | 5.4453 × 101 | 7.7357 × 101 | 2.2629 × 101 | |
| F24 | mean | 3.1921 × 103 | 2.9489 × 103 | 2.9055 × 103 | 3.0254 × 103 | 3.0159 × 103 | 2.9173 × 103 | 3.0897 × 103 | 3.0311 × 103 | 3.2070 × 103 | 3.0027 × 103 | 3.1525 × 103 | 2.9929 × 103 |
| std | 8.0100 × 101 | 3.6690 × 101 | 1.6597 × 101 | 9.3849 | 7.1895 × 101 | 2.2647 × 101 | 6.9183 × 101 | 7.0177 × 101 | 1.1067 × 102 | 7.1574 × 101 | 7.9576 × 101 | 2.3288 × 101 | |
| F25 | mean | 2.8862 × 103 | 2.8941 × 103 | 2.9443 × 103 | 2.8894 × 103 | 2.8982 × 103 | 2.8989 × 103 | 3.5185 × 103 | 2.8981 × 103 | 3.0669 × 103 | 2.8985 × 103 | 3.2020 × 103 | 2.9112 × 103 |
| std | 1.5937 × 101 | 7.3351 | 2.4522 × 101 | 1.2179 | 1.8471 × 101 | 1.7132 × 101 | 1.7983 × 102 | 1.8211 × 101 | 3.1970 × 102 | 1.5679 × 101 | 1.1255 × 102 | 7.4461 | |
| F26 | mean | 5.2287 × 103 | 4.1963 × 103 | 4.6871 × 103 | 5.7601 × 103 | 5.2996 × 103 | 4.6270 × 103 | 6.9391 × 103 | 5.7909 × 103 | 7.6339 × 103 | 4.9279 × 103 | 6.7626 × 103 | 3.3227 × 103 |
| std | 2.1491 × 103 | 3.2743 × 102 | 8.2109 × 102 | 9.9905 × 101 | 1.6888 × 103 | 4.5536 × 102 | 1.2496 × 103 | 1.1924 × 103 | 1.6083 × 103 | 1.4457 × 103 | 1.5083 × 103 | 1.2958 × 102 | |
| F27 | mean | 3.2838 × 103 | 3.2188 × 103 | 3.2598 × 103 | 3.2236 × 103 | 3.3012 × 103 | 3.2299 × 103 | 3.3003 × 103 | 3.2527 × 103 | 3.3877 × 103 | 3.2570 × 103 | 3.3383 × 103 | 3.2000 × 103 |
| std | 1.5555 × 102 | 7.2278 | 2.1788 × 101 | 5.1804 | 5.9822 × 101 | 1.4900 × 101 | 5.0375 × 101 | 3.1642 × 101 | 1.1881 × 102 | 2.6007 × 101 | 6.3667 × 101 | 4.2898 × 10−5 | |
| F28 | mean | 3.2236 × 103 | 3.2622 × 103 | 3.2915 × 103 | 3.2725 × 103 | 3.2191 × 103 | 3.2652 × 103 | 4.4828 × 103 | 3.1547 × 103 | 3.5331 × 103 | 3.2141 × 103 | 3.6918 × 103 | 3.2425 × 103 |
| std | 2.3672 × 101 | 2.0194 × 101 | 1.9313 × 101 | 1.6807 × 101 | 2.2995 × 101 | 2.4976 × 101 | 4.9612 × 102 | 6.0590 × 101 | 6.8972 × 102 | 1.6065 × 101 | 2.6725 × 102 | 1.6663 × 101 | |
| F29 | mean | 4.0703 × 103 | 3.7420 × 103 | 3.8102 × 103 | 4.2967 × 103 | 4.1527 × 103 | 3.8297 × 103 | 4.1396 × 103 | 4.0470 × 103 | 4.6176 × 103 | 4.0132 × 103 | 4.3910 × 103 | 3.7283 × 103 |
| std | 2.2803 × 102 | 1.6776 × 102 | 1.8370 × 102 | 1.6946 × 102 | 3.6060 × 102 | 1.8165 × 102 | 2.2584 × 102 | 2.5266 × 102 | 5.5424 × 102 | 2.6034 × 102 | 3.6668 × 102 | 9.7067 × 101 | |
| F30 | mean | 4.6868 × 104 | 2.8949 × 104 | 1.3896 × 106 | 1.6655 × 105 | 1.0816 × 104 | 1.8075 × 105 | 8.5158 × 104 | 9.1788 × 103 | 1.1683 × 106 | 1.7620 × 104 | 6.9311 × 106 | 3.2936 × 103 |
| std | 3.3144 × 104 | 2.7233 × 104 | 8.8381 × 105 | 1.6426 × 105 | 3.8082 × 103 | 1.7661 × 105 | 9.8783 × 104 | 2.6490 × 103 | 9.7566 × 105 | 8.4497 × 103 | 3.9271 × 106 | 2.5829 × 101 |
| ID | Metric | PSO | SO | CSA | DMO | GTO | RIME | IAO | RTH | BKA | GKSO | POA | MIPOA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 8.5322 × 106 | 1.3182 × 108 | 8.1797 × 107 | 7.1299 × 108 | 2.6675 × 104 | 4.5746 × 106 | 7.1322 × 1010 | 4.0937 × 103 | 3.0161 × 1010 | 5.2067 × 103 | 3.8340 × 1010 | 4.3821 × 109 |
| std | 3.6061 × 106 | 5.8847 × 107 | 3.4855 × 107 | 1.6615 × 108 | 7.0218 × 104 | 1.5657 × 106 | 1.2040 × 1010 | 5.4955 × 103 | 3.3311 × 1010 | 4.1093 × 103 | 1.0412 × 1010 | 1.3130 × 109 | |
| F2 | mean | 3.3451 × 1023 | 1.0677 × 1050 | 7.0058 × 1048 | 8.0154 × 1065 | 1.3052 × 1051 | 3.7055 × 1031 | 1.9450 × 1065 | 1.9841 × 1038 | 2.7610 × 1073 | 1.5453 × 1033 | 2.7359 × 1062 | 1.1111 × 1039 |
| std | 1.1709 × 1024 | 3.9862 × 1050 | 3.5959 × 1049 | 3.3513 × 1066 | 7.1481 × 1051 | 1.8617 × 1032 | 6.6565 × 1065 | 7.7519 × 1038 | 1.3339 × 1074 | 8.1890 × 1033 | 1.4980 × 1063 | 1.1899 × 1039 | |
| F3 | mean | 7.4690 × 104 | 1.3921 × 105 | 1.0563 × 105 | 2.8142 × 105 | 2.6173 × 104 | 8.0602 × 104 | 1.0691 × 105 | 5.8927 × 102 | 5.6031 × 104 | 1.1737 × 104 | 8.8027 × 104 | 2.1100 × 104 |
| std | 1.8443 × 104 | 1.7109 × 104 | 1.4670 × 104 | 3.0320 × 104 | 9.8587 × 103 | 2.0445 × 104 | 1.6013 × 104 | 3.3787 × 102 | 4.0457 × 104 | 3.7402 × 103 | 1.6103 × 104 | 1.9769 × 103 | |
| F4 | mean | 5.4667 × 102 | 6.3422 × 102 | 7.4275 × 102 | 8.7299 × 102 | 5.6879 × 102 | 6.3063 × 102 | 1.7383 × 104 | 4.6621 × 102 | 4.5076 × 103 | 5.8937 × 102 | 6.9702 × 103 | 8.2683 × 102 |
| std | 4.9719 × 101 | 1.2174 × 101 | 6.9804 × 101 | 5.8284 × 101 | 5.9510 × 101 | 4.6641 × 101 | 4.2194 × 103 | 4.4528 × 101 | 7.2882 × 103 | 6.2342 × 101 | 2.8651 × 103 | 6.8704 × 101 | |
| F5 | mean | 7.7232 × 102 | 6.4464 × 102 | 7.1702 × 102 | 9.6773 × 102 | 8.3540 × 102 | 6.8552 × 102 | 1.0094 × 103 | 8.2336 × 102 | 8.9177 × 102 | 8.2522 × 102 | 9.1650 × 102 | 8.1200 × 102 |
| std | 4.2135 × 101 | 4.9101 × 101 | 3.2432 × 101 | 1.7980 × 101 | 3.8732 × 101 | 3.9257 × 101 | 2.9639 × 101 | 3.7643 × 101 | 1.0364 × 102 | 3.7116 × 101 | 4.0602 × 101 | 2.2220 × 101 | |
| F6 | mean | 6.5314 × 102 | 6.0461 × 102 | 6.3610 × 102 | 6.1368 × 102 | 6.5278 × 102 | 6.1467 × 102 | 6.6799 × 102 | 6.4975 × 102 | 6.6623 × 102 | 6.5151 × 102 | 6.6895 × 102 | 6.5396 × 102 |
| std | 4.8792 | 9.9519 × 10−1 | 4.6832 | 1.4701 | 8.4103 | 4.6619 | 7.8117 | 6.2674 | 6.0349 | 5.8286 | 5.7334 | 3.2350 | |
| F7 | mean | 1.0872 × 103 | 8.8242 × 102 | 1.2364 × 103 | 1.2949 × 103 | 1.4708 × 103 | 9.8869 × 102 | 1.6877 × 103 | 1.4670 × 103 | 1.6924 × 103 | 1.2569 × 103 | 1.7833 × 103 | 1.3906 × 103 |
| std | 5.6970 × 101 | 2.6896 × 101 | 8.4577 × 101 | 2.7303 × 101 | 1.4863 × 102 | 3.8671 × 101 | 1.0677 × 102 | 1.2227 × 102 | 1.1478 × 102 | 1.0757 × 102 | 5.8390 × 101 | 6.8404 × 101 | |
| F8 | mean | 1.0936 × 103 | 9.6922 × 102 | 9.9360 × 102 | 1.2712 × 103 | 1.1297 × 103 | 1.0037 × 103 | 1.3071 × 103 | 1.1298 × 103 | 1.2083 × 103 | 1.1214 × 103 | 1.2415 × 103 | 1.1279 × 103 |
| std | 3.8918 × 101 | 7.3059 × 101 | 4.2196 × 101 | 2.1085 × 101 | 5.4943 × 101 | 5.6722 × 101 | 4.3024 × 101 | 4.4701 × 101 | 8.3692 × 101 | 3.6631 × 101 | 2.8555 × 101 | 1.9082 × 101 | |
| F9 | mean | 2.0387 × 104 | 1.1524 × 103 | 5.1556 × 103 | 6.3521 × 103 | 1.1516 × 104 | 5.4498 × 103 | 2.0472 × 104 | 1.1213 × 104 | 1.6058 × 104 | 9.3874 × 103 | 1.6463 × 104 | 1.0997 × 104 |
| std | 4.5273 × 103 | 1.0518 × 102 | 1.0245 × 103 | 1.1536 × 103 | 1.5536 × 103 | 3.1976 × 103 | 2.2451 × 103 | 1.2094 × 103 | 5.2639 × 103 | 2.0255 × 103 | 1.5556 × 103 | 9.1815 × 102 | |
| F10 | mean | 7.3083 × 103 | 1.3086 × 104 | 8.3853 × 103 | 1.4984 × 104 | 9.0466 × 103 | 7.0884 × 103 | 1.0457 × 104 | 7.8641 × 103 | 9.3145 × 103 | 8.0249 × 103 | 8.6790 × 103 | 6.8332 × 103 |
| std | 8.5951 × 102 | 1.4486 × 103 | 1.5879 × 103 | 3.2774 × 102 | 1.7814 × 103 | 7.8758 × 102 | 5.9894 × 102 | 8.6321 × 102 | 2.1231 × 103 | 8.2220 × 102 | 9.3685 × 102 | 4.0617 × 102 | |
| F11 | mean | 1.3210 × 103 | 1.6238 × 103 | 2.2796 × 103 | 3.2735 × 103 | 1.3240 × 103 | 1.5604 × 103 | 8.9185 × 103 | 1.3396 × 103 | 3.9391 × 103 | 1.3115 × 103 | 5.5198 × 103 | 1.4967 × 103 |
| std | 6.3277 × 101 | 1.1931 × 102 | 3.4834 × 102 | 4.8088 × 102 | 4.9314 × 101 | 1.1055 × 102 | 3.4274 × 103 | 7.2954 × 101 | 5.5897 × 103 | 3.5898 × 101 | 1.9716 × 103 | 4.4170 × 101 | |
| F12 | mean | 1.3110 × 107 | 1.5498 × 107 | 1.8457 × 108 | 3.5719 × 108 | 3.6492 × 106 | 8.3871 × 107 | 1.7431 × 1010 | 2.2180 × 105 | 3.9297 × 109 | 3.9625 × 106 | 9.3462 × 109 | 4.8477 × 107 |
| std | 7.0417 × 106 | 1.4563 × 107 | 9.9101 × 107 | 1.0246 × 108 | 2.0557 × 106 | 6.4504 × 107 | 8.5258 × 109 | 1.2964 × 105 | 1.1955 × 1010 | 3.5687 × 106 | 7.1303 × 109 | 1.7245 × 107 | |
| F13 | mean | 2.7805 × 104 | 5.9732 × 104 | 1.0392 × 105 | 5.5730 × 103 | 1.3001 × 104 | 1.9913 × 105 | 1.3113 × 109 | 9.2662 × 103 | 5.4103 × 108 | 1.4522 × 104 | 2.4145 × 109 | 1.5360 × 105 |
| std | 1.1439 × 104 | 5.4680 × 104 | 7.0988 × 104 | 1.9041 × 103 | 8.7837 × 103 | 9.6190 × 104 | 2.0765 × 109 | 8.6996 × 103 | 1.8483 × 109 | 8.8842 × 103 | 3.6263 × 109 | 4.7933 × 104 | |
| F14 | mean | 9.6615 × 104 | 1.4835 × 105 | 1.2913 × 105 | 1.4499 × 106 | 2.8051 × 104 | 2.4830 × 105 | 1.8883 × 103 | 4.5322 × 103 | 1.8367 × 105 | 2.6122 × 104 | 2.5267 × 105 | 1.8003 × 103 |
| std | 7.2069 × 104 | 9.6998 × 104 | 1.0661 × 105 | 5.1251 × 105 | 2.5840 × 104 | 1.3932 × 105 | 1.0230 × 102 | 1.8902 × 103 | 3.4754 × 105 | 2.1630 × 104 | 1.7517 × 105 | 4.2632 × 101 | |
| F15 | mean | 1.2254 × 104 | 2.7373 × 104 | 3.5084 × 104 | 1.1215 × 104 | 1.5084 × 104 | 5.7688 × 104 | 2.3708 × 104 | 9.5876 × 103 | 9.8547 × 107 | 8.6000 × 103 | 5.3648 × 107 | 1.3201 × 104 |
| std | 1.1324 × 104 | 2.8152 × 104 | 2.8007 × 104 | 4.7279 × 103 | 9.5968 × 103 | 2.3589 × 104 | 1.5003 × 104 | 8.0147 × 103 | 3.7479 × 108 | 6.8860 × 103 | 1.7192 × 108 | 3.2327 × 103 | |
| F16 | mean | 3.3719 × 103 | 3.8673 × 103 | 3.2003 × 103 | 5.0709 × 103 | 3.6610 × 103 | 3.5224 × 103 | 4.2102 × 103 | 3.6202 × 103 | 3.9494 × 103 | 3.5683 × 103 | 4.0847 × 103 | 2.8881 × 103 |
| std | 3.9454 × 102 | 6.1406 × 102 | 3.9749 × 102 | 2.0937 × 102 | 3.5012 × 102 | 3.6666 × 102 | 4.3956 × 102 | 3.7989 × 102 | 7.6131 × 102 | 3.8583 × 102 | 7.0843 × 102 | 1.4197 × 102 | |
| F17 | mean | 3.0972 × 103 | 3.2048 × 103 | 2.9675 × 103 | 3.9518 × 103 | 3.3964 × 103 | 3.2739 × 103 | 3.0417 × 103 | 3.5562 × 103 | 3.3776 × 103 | 3.2090 × 103 | 3.4619 × 103 | 2.6771 × 103 |
| std | 2.6084 × 102 | 4.4289 × 102 | 2.5697 × 102 | 1.8102 × 102 | 3.0592 × 102 | 3.9052 × 102 | 3.1113 × 102 | 3.7638 × 102 | 2.4464 × 102 | 4.1170 × 102 | 4.2054 × 102 | 1.0304 × 102 | |
| F18 | mean | 1.9105 × 106 | 3.3631 × 106 | 9.0861 × 105 | 2.0171 × 107 | 2.1176 × 105 | 3.8774 × 106 | 8.0538 × 104 | 4.6191 × 104 | 1.6569 × 106 | 1.9241 × 105 | 2.1752 × 106 | 1.4743 × 104 |
| std | 1.1776 × 106 | 2.8940 × 106 | 6.4474 × 105 | 7.3470 × 106 | 1.5122 × 105 | 2.7825 × 106 | 3.8083 × 104 | 2.8165 × 104 | 6.2137 × 106 | 1.1711 × 105 | 1.6950 × 106 | 4.3043 × 103 | |
| F19 | mean | 1.4261 × 104 | 2.0841 × 104 | 1.1195 × 106 | 1.5620 × 104 | 1.6993 × 104 | 7.0230 × 104 | 1.5301 × 105 | 1.7019 × 104 | 2.9209 × 107 | 1.9359 × 104 | 6.9796 × 106 | 4.0188 × 104 |
| std | 1.0451 × 104 | 1.2092 × 104 | 1.6224 × 106 | 5.8890 × 103 | 1.0320 × 104 | 4.2397 × 104 | 2.0527 × 105 | 1.2338 × 104 | 8.8353 × 107 | 1.2147 × 104 | 9.0392 × 106 | 1.7572 × 104 | |
| F20 | mean | 3.1793 × 103 | 3.3837 × 103 | 2.8044 × 103 | 4.0246 × 103 | 3.1375 × 103 | 3.0549 × 103 | 2.8223 × 103 | 3.3734 × 103 | 3.1326 × 103 | 3.1334 × 103 | 3.0664 × 103 | 2.5980 × 103 |
| std | 3.0554 × 102 | 3.6004 × 102 | 2.9719 × 102 | 1.6373 × 102 | 3.1284 × 102 | 3.1447 × 102 | 1.6460 × 102 | 3.4478 × 102 | 1.9898 × 102 | 2.8808 × 102 | 2.0241 × 102 | 7.4337 × 101 | |
| F21 | mean | 2.6740 × 103 | 2.4860 × 103 | 2.4984 × 103 | 2.7636 × 103 | 2.6113 × 103 | 2.4862 × 103 | 2.8268 × 103 | 2.6569 × 103 | 2.8345 × 103 | 2.6105 × 103 | 2.7526 × 103 | 2.5992 × 103 |
| std | 7.1743 × 101 | 6.7934 × 101 | 3.7843 × 101 | 1.7255 × 101 | 5.6371 × 101 | 4.5008 × 101 | 5.9263 × 101 | 8.5106 × 101 | 1.2556 × 102 | 7.0332 × 101 | 5.8617 × 101 | 1.9368 × 101 | |
| F22 | mean | 9.5696 × 103 | 1.4445 × 104 | 1.0385 × 104 | 1.6330 × 104 | 1.0240 × 104 | 9.0811 × 103 | 1.2799 × 104 | 9.4962 × 103 | 1.0677 × 104 | 9.5255 × 103 | 1.1190 × 104 | 7.4436 × 103 |
| std | 8.0283 × 102 | 1.5477 × 103 | 1.5686 × 103 | 3.9679 × 102 | 2.5635 × 103 | 8.7517 × 102 | 6.0063 × 102 | 8.3193 × 102 | 1.6694 × 103 | 9.7338 × 102 | 1.3694 × 103 | 2.0235 × 103 | |
| F23 | mean | 3.5653 × 103 | 2.8703 × 103 | 3.0335 × 103 | 3.1867 × 103 | 3.2445 × 103 | 2.9644 × 103 | 3.5057 × 103 | 3.2067 × 103 | 3.6776 × 103 | 3.1718 × 103 | 3.4901 × 103 | 3.1545 × 103 |
| std | 1.6994 × 102 | 3.3192 × 101 | 6.8988 × 101 | 1.7828 × 101 | 1.0191 × 102 | 4.6745 × 101 | 1.2350 × 102 | 1.2165 × 102 | 1.5194 × 102 | 8.3427 × 101 | 1.2886 × 102 | 3.4892 × 101 | |
| F24 | mean | 3.5423 × 103 | 3.2021 × 103 | 3.1310 × 103 | 3.3266 × 103 | 3.3340 × 103 | 3.1255 × 103 | 3.5924 × 103 | 3.3745 × 103 | 3.7701 × 103 | 3.3671 × 103 | 3.6480 × 103 | 3.3511 × 103 |
| std | 1.2730 × 102 | 7.4338 × 101 | 5.1960 × 101 | 1.4939 × 101 | 1.0669 × 102 | 6.6194 × 101 | 1.2112 × 102 | 1.1087 × 102 | 1.2268 × 102 | 1.1360 × 102 | 1.0341 × 102 | 4.9728 × 101 | |
| F25 | mean | 2.9978 × 103 | 3.0793 × 103 | 3.2971 × 103 | 3.3158 × 103 | 3.0976 × 103 | 3.0915 × 103 | 1.0230 × 104 | 3.0514 × 103 | 4.4812 × 103 | 3.0738 × 103 | 5.8084 × 103 | 3.3121 × 103 |
| std | 4.9334 × 101 | 1.5929 × 101 | 6.9890 × 101 | 5.3084 × 101 | 3.7034 × 101 | 3.7980 × 101 | 1.3500 × 103 | 3.4700 × 101 | 2.0357 × 103 | 2.7891 × 101 | 1.0673 × 103 | 5.7403 × 101 | |
| F26 | mean | 8.5450 × 103 | 5.0509 × 103 | 7.6002 × 103 | 8.3700 × 103 | 7.8072 × 103 | 6.0831 × 103 | 1.3754 × 104 | 9.0507 × 103 | 1.1233 × 104 | 7.3313 × 103 | 1.2268 × 104 | 5.5019 × 103 |
| std | 3.2402 × 103 | 3.3582 × 102 | 1.1500 × 103 | 1.6438 × 102 | 2.7339 × 103 | 6.1392 × 102 | 1.1604 × 103 | 2.4138 × 103 | 2.2651 × 103 | 3.6809 × 103 | 1.7113 × 103 | 6.1053 × 102 | |
| F27 | mean | 4.0427 × 103 | 3.3896 × 103 | 3.7181 × 103 | 3.5280 × 103 | 3.8386 × 103 | 3.5050 × 103 | 3.8432 × 103 | 3.5780 × 103 | 4.0038 × 103 | 3.6703 × 103 | 4.0771 × 103 | 3.2000 × 103 |
| std | 6.3349 × 102 | 4.3684 × 101 | 1.4754 × 102 | 3.0012 × 101 | 3.4820 × 102 | 1.0518 × 102 | 1.8209 × 102 | 1.4643 × 102 | 3.1717 × 102 | 1.4539 × 102 | 2.4562 × 102 | 5.5029 × 10−5 | |
| F28 | mean | 3.2966 × 103 | 3.3696 × 103 | 3.7508 × 103 | 3.8183 × 103 | 3.3694 × 103 | 3.3640 × 103 | 8.8216 × 103 | 3.3001 × 103 | 4.6452 × 103 | 3.3275 × 103 | 6.1658 × 103 | 3.3000 × 103 |
| std | 3.2128 × 101 | 2.5421 × 101 | 1.1214 × 102 | 1.2820 × 102 | 4.7126 × 101 | 2.9154 × 101 | 1.0316 × 103 | 3.6259 × 101 | 1.5556 × 103 | 2.6159 × 101 | 6.5590 × 102 | 1.2179 × 10−4 | |
| F29 | mean | 5.1317 × 103 | 4.2208 × 103 | 5.1651 × 103 | 5.6879 × 103 | 5.1170 × 103 | 4.7550 × 103 | 6.7152 × 103 | 4.8689 × 103 | 7.4650 × 103 | 5.1252 × 103 | 6.6963 × 103 | 4.7386 × 103 |
| std | 2.6153 × 102 | 3.7565 × 102 | 4.7302 × 102 | 2.3821 × 102 | 3.8304 × 102 | 4.2509 × 102 | 1.1421 × 103 | 5.2737 × 102 | 3.1215 × 103 | 3.4228 × 102 | 8.7449 × 102 | 3.2062 × 102 | |
| F30 | mean | 4.8818 × 106 | 2.0997 × 106 | 9.8432 × 107 | 1.7188 × 107 | 1.2291 × 106 | 2.2362 × 107 | 5.0711 × 107 | 8.4395 × 105 | 6.9653 × 107 | 5.5415 × 106 | 1.7851 × 108 | 4.5999 × 103 |
| std | 2.1182 × 106 | 7.3139 × 105 | 4.0720 × 107 | 8.5103 × 106 | 3.2638 × 105 | 7.7087 × 106 | 4.9564 × 107 | 1.6501 × 105 | 1.2096 × 108 | 2.3665 × 106 | 8.7983 × 107 | 7.2432 × 102 |
| Item | PSO | SO | CSA | DMO | GTO | RIME | IAO | RTH | BKA | GKSO | POA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.6897 × 10−11 | 1.2057 × 10−10 | 2.6099 × 10−10 | 3.0199 × 10−11 | 5.0723 × 10−10 | 3.0199 × 10−11 | 4.0988 × 10−12 | 3.5012 × 10−3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F2 | 3.0199 × 10−11 | 1.6810 × 10−8 | 1.6572 × 10−11 | 6.2258 × 10−10 | 5.0628 × 10−6 | 2.9329 × 10−5 | 2.1419 × 10−2 | 4.1926 × 10−2 | 1.9381 × 10−9 | 3.3371 × 10−1 | 5.7678 × 10−11 |
| F3 | 1.2057 × 10−10 | 8.1014 × 10−10 | 7.1021 × 10−10 | 3.0199 × 10−11 | 2.8422 × 10−11 | 3.0199 × 10−11 | 3.1507 × 10−12 | 1.1364 × 10−11 | 3.0199 × 10−11 | 3.2686 × 10−11 | 3.0199 × 10−11 |
| F4 | 2.6099 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.6427 × 10−1 | 3.0199 × 10−11 | 2.1822 × 10−11 | 2.7652 × 10−11 | 1.4643 × 10−10 | 3.8710 × 10−1 | 3.0199 × 10−11 |
| F5 | 3.0199 × 10−11 | 9.0490 × 10−2 | 7.4774 × 10−2 | 7.3891 × 10−11 | 2.5682 × 10−7 | 6.6273 × 10−1 | 6.3533 × 10−2 | 7.3846 × 10−11 | 5.4617 × 10−9 | 7.0430 × 10−7 | 3.0199 × 10−11 |
| F6 | 3.0811 × 10−8 | 3.4742 × 10−10 | 3.0103 × 10−7 | 1.2118 × 10−12 | 1.8567 × 10−9 | 9.9186 × 10−11 | 5.5699 × 10−3 | 6.7220 × 10−10 | 3.0199 × 10−11 | 1.2597 × 10−1 | 3.0199 × 10−11 |
| F7 | 3.6439 × 10−2 | 6.1452 × 10−2 | 5.0114 × 10−1 | 3.4742 × 10−10 | 2.3715 × 10−10 | 6.3088 × 10−1 | 9.0000 × 10−1 | 3.3384 × 10−11 | 3.0199 × 10−11 | 2.7829 × 10−7 | 3.0199 × 10−11 |
| F8 | 5.8587 × 10−6 | 7.2446 × 10−2 | 3.0001 × 10−4 | 3.1589 × 10−10 | 3.3520 × 10−8 | 2.3800 × 10−3 | 6.5204 × 10−1 | 7.3683 × 10−10 | 5.0912 × 10−6 | 1.8602 × 10−6 | 3.0199 × 10−11 |
| F9 | 1.0666 × 10−7 | 8.9999 × 10−1 | 3.1589 × 10−10 | 1.2118 × 10−12 | 1.0648 × 10−7 | 8.6844 × 10−3 | 4.6120 × 10−5 | 5.5727 × 10−10 | 3.0199 × 10−11 | 1.0892 × 10−5 | 3.0199 × 10−11 |
| F10 | 3.0199 × 10−11 | 6.7869 × 10−2 | 2.0275 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 6.3560 × 10−5 | 1.8731 × 10−7 | 9.9186 × 10−11 | 3.0199 × 10−11 | 2.4386 × 10−9 | 6.0104 × 10−8 |
| F11 | 3.0199 × 10−11 | 7.2446 × 10−2 | 1.1737 × 10−9 | 9.6263 × 10−2 | 7.5991 × 10−7 | 5.1857 × 10−7 | 1.1674 × 10−5 | 1.0702 × 10−9 | 1.6947 × 10−9 | 3.8307 × 10−5 | 4.9752 × 10−11 |
| F12 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.7142 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F13 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.9568 × 10−10 | 3.0199 × 10−11 | 1.4932 × 10−4 | 1.3289 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F14 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.9568 × 10−10 | 8.8910 × 10−10 | 6.5261 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.9673 × 10−9 | 3.0199 × 10−11 |
| F15 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.5726 × 10−9 | 3.0199 × 10−11 | 4.0772 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.4971 × 10−9 | 3.0199 × 10−11 |
| F16 | 3.1967 × 10−9 | 8.5000 × 10−2 | 5.9673 × 10−9 | 2.8716 × 10−10 | 3.4971 × 10−9 | 2.4913 × 10−6 | 2.9205 × 10−2 | 2.6695 × 10−9 | 4.1997 × 10−10 | 5.9706 × 10−5 | 3.0199 × 10−11 |
| F17 | 3.5201 × 10−7 | 4.4642 × 10−1 | 7.1988 × 10−5 | 3.5708 × 10−6 | 5.6073 × 10−5 | 2.2823 × 10−1 | 5.0120 × 10−2 | 1.6980 × 10−8 | 5.0723 × 10−10 | 2.4157 × 10−2 | 8.9934 × 10−11 |
| F18 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.3715 × 10−10 | 3.0199 × 10−11 | 4.0330 × 10−3 | 4.5043 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F19 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.4110 × 10−9 | 9.0632 × 10−8 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F20 | 2.6099 × 10−10 | 1.2235 × 10−1 | 5.2650 × 10−5 | 3.0199 × 10−11 | 1.1023 × 10−8 | 1.4932 × 10−4 | 7.2827 × 10−1 | 3.0199 × 10−11 | 1.0702 × 10−9 | 6.6689 × 10−3 | 2.2273 × 10−9 |
| F21 | 2.9590 × 10−5 | 3.0199 × 10−11 | 7.1152 × 10−9 | 3.0199 × 10−11 | 5.3672 × 10−2 | 3.0199 × 10−11 | 1.0276 × 10−7 | 5.0723 × 10−10 | 3.0199 × 10−11 | 1.2988 × 10−3 | 3.0199 × 10−11 |
| F22 | 1.4110 × 10−9 | 9.9186 × 10−11 | 8.8411 × 10−7 | 1.8577 × 10−1 | 7.3803 × 10−10 | 5.5999 × 10−7 | 2.4155 × 10−2 | 2.0338 × 10−9 | 3.0199 × 10−11 | 7.1186 × 10−9 | 3.8249 × 10−9 |
| F23 | 3.0199 × 10−11 | 2.0621 × 10−1 | 3.0317 × 10−2 | 1.6980 × 10−8 | 2.5721 × 10−7 | 7.1988 × 10−5 | 8.0727 × 10−1 | 6.1210 × 10−10 | 2.4386 × 10−9 | 5.4941 × 10−11 | 8.9934 × 10−11 |
| F24 | 2.1327 × 10−5 | 3.0199 × 10−11 | 4.1997 × 10−10 | 3.0199 × 10−11 | 2.1305 × 10−5 | 3.0199 × 10−11 | 3.3595 × 10−2 | 4.1997 × 10−10 | 3.0199 × 10−11 | 5.5591 × 10−4 | 3.0199 × 10−11 |
| F25 | 3.2555 × 10−7 | 5.5727 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.0723 × 10−10 | 3.0199 × 10−11 | 2.7500 × 10−3 | 5.5727 × 10−10 | 3.0103 × 10−7 | 2.8700 × 10−10 | 3.0199 × 10−11 |
| F26 | 1.6947 × 10−9 | 5.4941 × 10−11 | 2.4982 × 10−11 | 8.0555 × 10−11 | 2.9045 × 10−11 | 1.3289 × 10−10 | 1.2422 × 10−7 | 5.4773 × 10−11 | 5.4941 × 10−11 | 1.6755 × 10−9 | 9.9186 × 10−11 |
| F27 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0180 × 10−11 | 3.0199 × 10−11 | 3.0180 × 10−11 | 3.0199 × 10−11 | 2.9580 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F28 | 3.5012 × 10−3 | 4.4429 × 10−10 | 1.6168 × 10−11 | 3.0199 × 10−11 | 9.8230 × 10−1 | 3.0199 × 10−11 | 1.4319 × 10−2 | 1.6722 × 10−4 | 3.0199 × 10−11 | 1.2211 × 10−2 | 3.0199 × 10−11 |
| F29 | 3.0199 × 10−11 | 7.0430 × 10−7 | 1.0407 × 10−4 | 3.0199 × 10−11 | 1.1077 × 10−6 | 1.2541 × 10−7 | 7.2827 × 10−1 | 3.0199 × 10−11 | 2.1544 × 10−10 | 2.6695 × 10−9 | 5.4941 × 10−11 |
| F30 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0142 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0142 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| Item | PSO | SO | CSA | DMO | GTO | RIME | IAO | RTH | BKA | GKSO | POA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.0199 × 10−11 | 1.2057 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.6695 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F2 | 3.0199 × 10−11 | 6.1210 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.6243 × 10−3 | 1.1737 × 10−9 | 3.0199 × 10−11 | 1.6980 × 10−8 | 5.9673 × 10−9 | 1.2057 × 10−10 | 3.0199 × 10−11 |
| F3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.1738 × 10−3 | 6.0658 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F4 | 3.3520 × 10−8 | 6.2040 × 10−1 | 3.9167 × 10−2 | 1.2541 × 10−7 | 7.3940 × 10−1 | 2.8913 × 10−3 | 3.0199 × 10−11 | 5.4907 × 10−11 | 4.6856 × 10−8 | 9.0490 × 10−2 | 3.0199 × 10−11 |
| F5 | 2.3800 × 10−3 | 3.0199 × 10−11 | 3.3384 × 10−11 | 3.0199 × 10−11 | 3.5923 × 10−5 | 4.5043 × 10−11 | 6.7220 × 10−10 | 1.7649 × 10−2 | 1.7769 × 10−10 | 2.5188 × 10−1 | 3.0199 × 10−11 |
| F6 | 2.4994 × 10−3 | 3.0199 × 10−11 | 2.1544 × 10−10 | 3.0199 × 10−11 | 8.5641 × 10−4 | 3.0199 × 10−11 | 2.6099 × 10−10 | 6.3533 × 10−2 | 3.0199 × 10−11 | 3.5137 × 10−2 | 3.0199 × 10−11 |
| F7 | 8.1014 × 10−10 | 3.0199 × 10−11 | 2.7726 × 10−5 | 1.7145 × 10−1 | 7.2208 × 10−6 | 8.1527 × 10−11 | 1.0937 × 10−10 | 3.0103 × 10−7 | 3.0199 × 10−11 | 2.0621 × 10−1 | 3.0199 × 10−11 |
| F8 | 3.1830 × 10−1 | 4.2175 × 10−4 | 2.3715 × 10−10 | 3.0199 × 10−11 | 6.5261 × 10−7 | 4.6159 × 10−10 | 3.0199 × 10−11 | 1.8916 × 10−4 | 3.1967 × 10−9 | 1.1747 × 10−4 | 3.0199 × 10−11 |
| F9 | 4.3106 × 10−8 | 3.0199 × 10−11 | 3.8202 × 10−10 | 3.0199 × 10−11 | 2.7726 × 10−5 | 1.1937 × 10−6 | 1.6980 × 10−8 | 1.6947 × 10−9 | 3.0199 × 10−11 | 3.7904 × 10−1 | 3.0199 × 10−11 |
| F10 | 3.0103 × 10−7 | 3.0199 × 10−11 | 3.4742 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 7.4827 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.3715 × 10−10 | 1.2860 × 10−6 | 2.3715 × 10−10 |
| F11 | 1.6955 × 10−2 | 1.6798 × 10−3 | 2.9590 × 10−5 | 3.0199 × 10−11 | 6.6273 × 10−1 | 3.3681 × 10−5 | 3.0199 × 10−11 | 5.2978 × 10−1 | 7.5991 × 10−7 | 8.5000 × 10−2 | 3.0199 × 10−11 |
| F12 | 3.0199 × 10−11 | 3.1589 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 8.4848 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 9.0307 × 10−4 | 3.0199 × 10−11 | 1.6351 × 10−5 | 3.0199 × 10−11 |
| F13 | 2.1702 × 10−1 | 1.8368 × 10−2 | 3.1589 × 10−10 | 1.7649 × 10−2 | 3.5137 × 10−2 | 1.3594 × 10−7 | 1.0547 × 10−1 | 8.2357 × 10−2 | 9.9186 × 10−11 | 1.6798 × 10−3 | 3.0199 × 10−11 |
| F14 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.1947 × 10−8 | 3.0199 × 10−11 | 8.7710 × 10−2 | 4.1997 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F15 | 1.8682 × 10−5 | 2.9215 × 10−9 | 3.0199 × 10−11 | 1.9073 × 10−1 | 5.0842 × 10−3 | 2.1959 × 10−7 | 2.6077 × 10−2 | 1.2493 × 10−5 | 3.0199 × 10−11 | 2.1156 × 10−1 | 3.0199 × 10−11 |
| F16 | 4.1825 × 10−9 | 5.5611 × 10−4 | 1.1747 × 10−4 | 3.0199 × 10−11 | 3.1589 × 10−10 | 1.1737 × 10−9 | 9.8329 × 10−8 | 3.8249 × 10−9 | 3.0199 × 10−11 | 5.4617 × 10−9 | 3.0199 × 10−11 |
| F17 | 3.8202 × 10−10 | 4.6371 × 10−3 | 5.5611 × 10−4 | 3.0199 × 10−11 | 3.4971 × 10−9 | 3.9648 × 10−8 | 1.1077 × 10−6 | 3.0199 × 10−11 | 3.6897 × 10−11 | 4.9980 × 10−9 | 9.9186 × 10−11 |
| F18 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.3399 × 10−1 | 5.1857 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F19 | 4.6856 × 10−8 | 4.1825 × 10−9 | 3.0199 × 10−11 | 1.3111 × 10−8 | 1.2870 × 10−9 | 4.1997 × 10−10 | 9.1171 × 10−1 | 1.2870 × 10−9 | 3.0199 × 10−11 | 9.9186 × 10−11 | 3.0199 × 10−11 |
| F20 | 9.2603 × 10−9 | 2.8913 × 10−3 | 1.5178 × 10−3 | 3.0199 × 10−11 | 7.0430 × 10−7 | 1.1747 × 10−4 | 2.5306 × 10−4 | 3.0199 × 10−11 | 2.8716 × 10−10 | 5.5329 × 10−8 | 9.9186 × 10−11 |
| F21 | 6.6955 × 10−11 | 1.7613 × 10−1 | 2.5101 × 10−2 | 3.0199 × 10−11 | 1.5292 × 10−5 | 7.0127 × 10−2 | 6.7220 × 10−10 | 3.9648 × 10−8 | 3.0199 × 10−11 | 1.1567 × 10−7 | 3.0199 × 10−11 |
| F22 | 2.7086 × 10−2 | 6.7350 × 10−1 | 1.5014 × 10−2 | 3.6459 × 10−8 | 5.5727 × 10−10 | 6.6273 × 10−1 | 3.0199 × 10−11 | 1.0000 | 1.2057 × 10−10 | 9.5139 × 10−6 | 3.0199 × 10−11 |
| F23 | 3.0199 × 10−11 | 5.0723 × 10−10 | 2.4386 × 10−9 | 3.0199 × 10−11 | 1.8575 × 10−3 | 8.4848 × 10−9 | 4.5043 × 10−11 | 1.5964 × 10−7 | 3.0199 × 10−11 | 6.6689 × 10−3 | 3.0199 × 10−11 |
| F24 | 3.0199 × 10−11 | 1.1077 × 10−6 | 8.9934 × 10−11 | 2.6099 × 10−10 | 3.1830 × 10−1 | 3.4742 × 10−10 | 5.0723 × 10−10 | 1.0547 × 10−1 | 4.5043 × 10−11 | 8.1875 × 10−1 | 3.0199 × 10−11 |
| F25 | 2.1947 × 10−8 | 1.1023 × 10−8 | 2.8790 × 10−6 | 3.3384 × 10−11 | 5.2650 × 10−5 | 2.2539 × 10−4 | 3.0199 × 10−11 | 7.6588 × 10−5 | 7.3891 × 10−11 | 1.0407 × 10−4 | 3.0199 × 10−11 |
| F26 | 3.7904 × 10−1 | 3.0199 × 10−11 | 1.1077 × 10−6 | 3.0199 × 10−11 | 1.9527 × 10−3 | 5.5727 × 10−10 | 3.0199 × 10−11 | 1.0666 × 10−7 | 4.1997 × 10−10 | 7.9590 × 10−3 | 3.0199 × 10−11 |
| F27 | 1.0000 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.5727 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F28 | 1.0035 × 10−3 | 3.5638 × 10−4 | 1.9568 × 10−10 | 3.0811 × 10−8 | 1.0407 × 10−4 | 1.3250 × 10−4 | 3.0199 × 10−11 | 6.9935 × 10−9 | 2.3168 × 10−6 | 1.7294 × 10−7 | 3.0199 × 10−11 |
| F29 | 4.5726 × 10−9 | 6.6273 × 10−1 | 1.1536 × 10−1 | 3.0199 × 10−11 | 6.0459 × 10−7 | 4.0330 × 10−3 | 8.1527 × 10−11 | 8.3520 × 10−8 | 3.0199 × 10−11 | 9.5332 × 10−7 | 3.0199 × 10−11 |
| F30 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| Item | PSO | SO | CSA | DMO | GTO | RIME | IAO | RTH | BKA | GKSO | POA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 9.5332 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.1737 × 10−9 | 3.0199 × 10−11 | 2.7719 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.4617 × 10−9 | 3.0199 × 10−11 | 3.3384 × 10−11 | 3.0199 × 10−11 |
| F3 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.4157 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.1544 × 10−10 | 3.0199 × 10−11 |
| F4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 6.7650 × 10−5 | 1.6955 × 10−2 | 8.1527 × 10−11 | 4.5043 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.2023 × 10−8 | 7.3891 × 10−11 | 3.0199 × 10−11 |
| F5 | 7.2208 × 10−6 | 3.6897 × 10−11 | 8.9934 × 10−11 | 3.0199 × 10−11 | 2.1566 × 10−3 | 3.6897 × 10−11 | 3.0199 × 10−11 | 1.0233 × 10−1 | 4.4205 × 10−6 | 7.2446 × 10−2 | 2.1544 × 10−10 |
| F6 | 6.1001 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.1060 × 10−1 | 3.0199 × 10−11 | 6.5277 × 10−8 | 3.3386 × 10−3 | 6.0658 × 10−11 | 8.5000 × 10−2 | 2.1544 × 10−10 |
| F7 | 3.6897 × 10−11 | 3.0199 × 10−11 | 7.0881 × 10−8 | 4.1127 × 10−7 | 4.2067 × 10−2 | 3.0199 × 10−11 | 1.0937 × 10−10 | 2.8129 × 10−2 | 6.0658 × 10−11 | 6.2828 × 10−6 | 3.0199 × 10−11 |
| F8 | 9.2113 × 10−5 | 7.7725 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 8.7663 × 10−1 | 6.7220 × 10−10 | 3.0199 × 10−11 | 6.1001 × 10−1 | 2.3897 × 10−8 | 3.9527 × 10−1 | 3.0199 × 10−11 |
| F9 | 3.4742 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.4941 × 10−11 | 5.9428 × 10−2 | 6.5277 × 10−8 | 3.0199 × 10−11 | 4.0354 × 10−1 | 4.1825 × 10−9 | 3.3679 × 10−4 | 3.0199 × 10−11 |
| F10 | 6.6689 × 10−3 | 3.0199 × 10−11 | 4.1178 × 10−6 | 3.0199 × 10−11 | 1.2023 × 10−8 | 1.9579 × 10−1 | 3.0199 × 10−11 | 5.1857 × 10−7 | 5.4941 × 10−11 | 9.0632 × 10−8 | 8.1014 × 10−10 |
| F11 | 1.6132 × 10−10 | 3.3242 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.6897 × 10−11 | 2.2360 × 10−2 | 3.0199 × 10−11 | 1.2870 × 10−9 | 5.0723 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F12 | 1.7769 × 10−10 | 9.2603 × 10−9 | 6.1210 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.4412 × 10−2 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.4205 × 10−6 | 3.3384 × 10−11 | 3.0199 × 10−11 |
| F13 | 3.3384 × 10−11 | 9.8329 × 10−8 | 4.4592 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.4532 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F14 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.1058 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F15 | 5.9428 × 10−2 | 3.1466 × 10−2 | 1.0105 × 10−8 | 7.9782 × 10−2 | 3.5547 × 10−1 | 3.0199 × 10−11 | 3.5638 × 10−4 | 2.3800 × 10−3 | 3.0199 × 10−11 | 1.5846 × 10−4 | 3.0199 × 10−11 |
| F16 | 3.5708 × 10−6 | 1.0666 × 10−7 | 5.8737 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.4941 × 10−11 | 3.0199 × 10−11 | 1.0702 × 10−9 | 1.6132 × 10−10 | 9.7555 × 10−10 | 8.8910 × 10−10 |
| F17 | 2.4386 × 10−9 | 3.8053 × 10−7 | 3.0939 × 10−6 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.8500 × 10−8 | 6.5261 × 10−7 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0811 × 10−8 | 3.0199 × 10−11 |
| F18 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 4.6159 × 10−10 | 2.8314 × 10−8 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F19 | 5.0922 × 10−8 | 6.7650 × 10−5 | 6.1210 × 10−10 | 2.3897 × 10−8 | 8.8411 × 10−7 | 2.1566 × 10−3 | 7.9590 × 10−3 | 2.1540 × 10−6 | 7.3891 × 10−11 | 1.1674 × 10−5 | 3.0199 × 10−11 |
| F20 | 3.8202 × 10−10 | 4.6159 × 10−10 | 1.9527 × 10−3 | 3.0199 × 10−11 | 2.6015 × 10−8 | 1.3111 × 10−8 | 1.0666 × 10−7 | 5.4941 × 10−11 | 3.0199 × 10−11 | 1.6947 × 10−9 | 4.5043 × 10−11 |
| F21 | 5.0912 × 10−6 | 2.4386 × 10−9 | 6.6955 × 10−11 | 3.0199 × 10−11 | 4.5530 × 10−1 | 2.3715 × 10−10 | 3.0199 × 10−11 | 8.1200 × 10−4 | 3.0199 × 10−11 | 8.7663 × 10−1 | 3.0199 × 10−11 |
| F22 | 8.1975 × 10−7 | 3.0199 × 10−11 | 7.1186 × 10−9 | 3.0199 × 10−11 | 5.5329 × 10−8 | 4.7138 × 10−4 | 3.0199 × 10−11 | 2.1540 × 10−6 | 1.8567 × 10−9 | 9.5139 × 10−6 | 6.7220 × 10−10 |
| F23 | 2.8716 × 10−10 | 3.0199 × 10−11 | 7.1186 × 10−9 | 9.5139 × 10−6 | 2.5974 × 10−5 | 3.6897 × 10−11 | 4.9752 × 10−11 | 7.7272 × 10−2 | 3.0199 × 10−11 | 3.7904 × 10−1 | 1.2057 × 10−10 |
| F24 | 9.2603 × 10−9 | 8.1014 × 10−10 | 3.6897 × 10−11 | 7.2884 × 10−3 | 5.7929 × 10−1 | 1.3289 × 10−10 | 1.0937 × 10−10 | 4.8252 × 10−1 | 3.0199 × 10−11 | 9.4696 × 10−1 | 1.0937 × 10−10 |
| F25 | 3.0199 × 10−11 | 3.0199 × 10−11 | 2.8378 × 10−1 | 8.6499 × 10−1 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 5.5727 × 10−10 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F26 | 3.9881 × 10−4 | 5.5611 × 10−4 | 9.7555 × 10−10 | 3.0199 × 10−11 | 1.2362 × 10−3 | 1.3703 × 10−3 | 3.0199 × 10−11 | 1.0666 × 10−7 | 4.9752 × 10−11 | 7.7272 × 10−2 | 3.0199 × 10−11 |
| F27 | 6.7650 × 10−5 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
| F28 | 3.9881 × 10−4 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 8.4848 × 10−9 | 3.0199 × 10−11 | 3.0199 × 10−11 | 1.0000 | 3.0199 × 10−11 | 1.0666 × 10−7 | 3.0199 × 10−11 |
| F29 | 3.1573 × 10−5 | 4.7445 × 10−6 | 6.9125 × 10−4 | 3.0199 × 10−11 | 2.5306 × 10−4 | 6.7350 × 10−1 | 3.0199 × 10−11 | 1.6238 × 10−1 | 1.0937 × 10−10 | 2.6806 × 10−4 | 3.0199 × 10−11 |
| F30 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 | 3.0199 × 10−11 |
References
- Boursianis, A.; Papadopoulou, M.; Diamantoulakis, P.; Liopa-Tsakalidi, A.; Barouchas, P.; Salahas, G.; Karagiannidis, G.; Wan, S.; Goudos, S. Internet of Things (IoT) and Agricultural Unmanned Aerial Vehicles (UAVs) in Smart Farming: A Comprehensive Review. Internet Things 2022, 18, 100187. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, S.; Feng, O.; Tian, T.; Huang, Y.; Zhong, G. Research on Demand-Based Scheduling Scheme of Urban Low-Altitude Logistics UAVs. Appl. Sci. 2023, 13, 5370. [Google Scholar] [CrossRef]
- Tang, P.; Li, J.; Sun, H. A Review of Electric UAV Visual Detection and Navigation Technologies for Emergency Rescue Missions. Sustainability 2024, 16, 2105. [Google Scholar] [CrossRef]
- Ren, Z.; Zheng, H.; Chen, J.; Chen, T.; Xie, P.; Xu, Y.; Deng, J.; Wang, H.; Sun, M.; Jiao, W. Integrating UAV, UGV and UAV-UGV Collaboration in Future Industrialized Agriculture: Analysis, Opportunities and Challenges. Comput. Electron. Agric. 2024, 227, 109631. [Google Scholar] [CrossRef]
- Li, Y.; Liu, M.; Jiang, D. Application of Unmanned Aerial Vehicles in Logistics: A Literature Review. Sustainability 2022, 14, 14473. [Google Scholar] [CrossRef]
- Qadir, Z.; Ullah, F.; Munawar, H.; Al-Turjman, F. Addressing Disasters in Smart Cities through UAVs Path Planning and 5G Communications: A Systematic Review. Comput. Commun. 2021, 168, 114–135. [Google Scholar] [CrossRef]
- Tang, J.; Liang, Y.; Li, K. Dynamic Scene Path Planning of UAVs Based on Deep Reinforcement Learning. Drones 2024, 8, 60. [Google Scholar] [CrossRef]
- Zhao, J.; Gan, Z.; Liang, J.; Wang, C.; Yue, K.; Li, W.; Li, Y.; Li, R. Path Planning Research of a UAV Base Station Searching for Disaster Victims’ Location Information Based on Deep Reinforcement Learning. Entropy 2022, 24, 1767. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C. Towards Real-Time Path Planning through Deep Reinforcement Learning for a UAV in Dynamic Environments. J. Intell. Robot. Syst. 2020, 98, 297–309. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Alhijawi, B.; Awajan, A. Genetic Algorithms: Theory, Genetic Operators, Solutions, and Applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Hu, K.; Mo, Y. A Novel Unmanned Aerial Vehicle Path Planning Approach: Sand Cat Optimization Algorithm Incorporating Learned Behaviour. Meas. Sci. Technol. 2024, 35, 046203. [Google Scholar] [CrossRef]
- Lv, F.; Jian, Y.; Yuan, K.; Lu, Y. Unmanned Aerial Vehicle Path Planning Method Based on Improved Dung Beetle Optimization Algorithm. Symmetry 2025, 17, 367. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, L.; Li, S.; Wu, F.; Song, Q.; Zhang, X. Unmanned Aerial Vehicle 3D Path Planning Based on an Improved Artificial Fish Swarm Algorithm. Drones 2023, 7, 636. [Google Scholar] [CrossRef]
- Maiti, B.; Biswas, S.; Ezugwu, A.; Bera, U.; Alzahrani, A.; Alblehai, F.; Abualigah, L. Enhanced Crayfish Optimization Algorithm with Differential Evolution’s Mutation and Crossover Strategies for Global Optimization and Engineering Applications. Artif. Intell. Rev. 2025, 58, 69. [Google Scholar] [CrossRef]
- Xu, P.; Lan, D.; Yang, H.; Zhang, S.; Kim, H.; Shin, I. Ship Formation and Route Optimization Design Based on Improved PSO and D-P Algorithm. IEEE Access 2025, 13, 15529–15546. [Google Scholar] [CrossRef]
- Fu, S.; Ma, C.; Li, K.; Xie, C.; Fan, Q.; Huang, H.; Xie, J.; Zhang, G.; Yu, M. Modified LSHADE-SPACMA with New Mutation Strategy and External Archive Mechanism for Numerical Optimization and Point Cloud Registration. Artif. Intell. Rev. 2025, 58, 72. [Google Scholar] [CrossRef]
- Xiao, C.; Yang, H.; Zhang, B. Multi-Unmanned Aerial Vehicle Path Planning Based on Improved Nutcracker Optimization Algorithm. Drones 2025, 9, 116. [Google Scholar] [CrossRef]
- Liu, X.; Wang, F.; Liu, Y.; Li, L. A Multi-Objective Black-Winged Kite Algorithm for Multi-UAV Cooperative Path Planning. Drones 2025, 9, 118. [Google Scholar] [CrossRef]
- Tang, R.; Qi, L.; Ye, S.; Li, C.; Ni, T.; Guo, J.; Liu, H.; Li, Y.; Zuo, D.; Shi, J.; et al. Three-Dimensional Path Planning for AUVs Based on Interval Multi-Objective Secretary Bird Optimization Algorithm. Symmetry 2025, 17, 993. [Google Scholar] [CrossRef]
- Trojovsky, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Sang, B.; Zhang, Y. Application of an Improved Pelican Optimization Algorithm Based on Comprehensive Strategy in PV Parameter Identification. Sci. Rep. 2025, 15, 27931. [Google Scholar] [CrossRef]
- Naidu, Y. Multi-Objective Pelican Optimization Algorithm for Engineering Design Problems; Molla, A., Sharma, G., Kumar, P., Rawat, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; Volume 13776, pp. 362–368. [Google Scholar]
- Li, C.; Jiang, Z.; Huang, Y. Multi-Strategy Improved Pelican Optimization Algorithm for Mobile Robot Path Planning. Inf. Technol. Control. 2024, 53, 372–389. [Google Scholar] [CrossRef]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N.; Liang, J.J.; Qu, B.Y. Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Anantathanavit, M.; Munlin, M. IEEE Radius Particle Swarm Optimization; IEEE: Piscataway, NJ, USA, 2013; pp. 126–130. [Google Scholar]
- Hashim, F.; Hussien, A. Snake Optimizer: A Novel Meta-Heuristic Optimization Algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Braik, M.S. Chameleon Swarm Algorithm: A Bio-Inspired Optimizer for Solving Engineering Design Problems. Expert Syst. Appl. 2021, 174, 114685. [Google Scholar] [CrossRef]
- Agushaka, J.; Ezugwu, A.; Abualigah, L. Dwarf Mongoose Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.; Mirjalili, S. Artificial Gorilla Troops Optimizer: A New Nature-Inspired Metaheuristic Algorithm for Global Optimization Problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A Physics-Based Optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Wu, X.; Li, S.; Jiang, X.; Zhou, Y. Information Acquisition Optimizer: A New Efficient Algorithm for Solving Numerical and Constrained Engineering Optimization Problems. J. Supercomput. 2024, 80, 25736–25791. [Google Scholar] [CrossRef]
- Ferahtia, S.; Houari, A.; Rezk, H.; Djerioui, A.; Machmoum, M.; Motahhir, S.; Ait-Ahmed, M. Red-Tailed Hawk Algorithm for Numerical Optimization and Real-World Problems. Sci. Rep. 2023, 13, 12950. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H. Black-Winged Kite Algorithm: A Nature-Inspired Meta-Heuristic for Solving Benchmark Functions and Engineering Problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Hu, G.; Guo, Y.; Wei, G.; Abualigah, L. Genghis Khan Shark Optimizer: A Novel Nature-Inspired Algorithm for Engineering Optimization. Adv. Eng. Inform. 2023, 58, 102210. [Google Scholar] [CrossRef]
- Cheng, S.; Shi, Y. Normalized Population Diversity in Particle Swarm Optimization; Tan, Y., Shi, Y., Chai, Y., Wang, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6728, pp. 38–45. [Google Scholar]
- Dwivedi, A.; Mallawaarachchi, I.; Alvarado, L. Analysis of Small Sample Size Studies Using Nonparametric Bootstrap Test with Pooled Resampling Method. Stat. Med. 2017, 36, 2187–2205. [Google Scholar] [CrossRef]






| Algorithms | Parameter Name | Parameter Value | Population Size | Iter Counts | Reference |
|---|---|---|---|---|---|
| PSO | 6, 0.9, 0.6, 2, 2 | 50 | 1000 | [27] | |
| SO | 0.5, 0.5, 2 | 50 | 1000 | [28] | |
| CSA | 0.1, 1.0, 2.0, 4.0 | 50 | 1000 | [29] | |
| DMO | 2 | 50 | 1000 | [30] | |
| GTO | , , | 0.03, 3, 0.8 | 50 | 1000 | [31] |
| RIME | 5 | 50 | 1000 | [32] | |
| IAO | 0.5 | 50 | 1000 | [33] | |
| RTH | 15, 0.5, 1.5 | 50 | 1000 | [34] | |
| BKA | 0.9 | 50 | 1000 | [35] | |
| GKSO | 0.1 | 50 | 1000 | [36] | |
| POA | 2 | 50 | 1000 | [22] |
| Function | POA | MIPOA | Function | POA | MIPOA |
|---|---|---|---|---|---|
| F1 | 4433 | 4463 | F16 | 4678 | 5275 |
| F2 | 4483 | 4545 | F17 | 4555 | 4766 |
| F3 | 4434 | 4891 | F18 | 4434 | 4718 |
| F4 | 4662 | 5462 | F19 | 4433 | 4588 |
| F5 | 4497 | 4669 | F20 | 4535 | 4672 |
| F6 | 4500 | 5307 | F21 | 4476 | 5496 |
| F7 | 4442 | 4658 | F22 | 4433 | 4774 |
| F8 | 4433 | 4750 | F23 | 4817 | 4885 |
| F9 | 4433 | 4889 | F24 | 4431 | 4838 |
| F10 | 4435 | 4437 | F25 | 4451 | 4817 |
| F11 | 4750 | 5198 | F26 | 4452 | 4505 |
| F12 | 4433 | 4534 | F27 | 4433 | 5412 |
| F13 | 4433 | 4673 | F28 | 4440 | 4688 |
| F14 | 4596 | 4788 | F29 | 4513 | 5138 |
| F15 | 4433 | 4889 | F30 | 4532 | 4572 |
| Suites | CEC2017 | |||||
|---|---|---|---|---|---|---|
| Dimensions | 10 | 30 | 50 | |||
| Algorithms | M.R | T.R | M.R | T.R | M.R | T.R |
| PSO | 8.97 | 11 | 6.27 | 8 | 5.13 | 5 |
| SO | 6.07 | 5 | 5.10 | 3 | 5.27 | 6 |
| CSA | 5.83 | 3 | 5.57 | 7 | 5.73 | 7 |
| DMO | 6.90 | 8 | 8.07 | 9 | 8.37 | 9 |
| GTO | 6.87 | 6 | 5.53 | 6 | 5.73 | 8 |
| RIME | 6.87 | 7 | 5.30 | 4 | 4.87 | 4 |
| IAO | 2.53 | 2 | 8.40 | 10 | 9.87 | 11 |
| RTH | 8.30 | 9 | 5.37 | 5 | 4.63 | 3 |
| BKA | 8.53 | 10 | 10.10 | 11 | 9.17 | 10 |
| GKSO | 5.90 | 4 | 4.77 | 2 | 4.50 | 2 |
| POA | 8.97 | 12 | 10.23 | 12 | 10.40 | 12 |
| MIPOA | 2.27 | 1 | 3.30 | 1 | 4.33 | 1 |
| Algorithm | PSO | SO | CSA | DMO | GTO | RIME | IAO | RTH | BKA | GKSO | POA | MIPOA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | 455.47 | 416.46 | 418.66 | 426.14 | 417.06 | 418.67 | 422.64 | 422.47 | 418.89 | 417.70 | 419.11 | 416.01 |
| max | 501.23 | 418.27 | 429.04 | 430.93 | 421.85 | 424.53 | 427.74 | 458.59 | 424.55 | 420.83 | 424.53 | 416.34 |
| min | 426.22 | 414.70 | 415.11 | 420.52 | 414.49 | 415.57 | 414.74 | 415.87 | 415.87 | 415.82 | 416.63 | 414.90 |
| Algorithm | PSO | SO | CSA | DMO | GTO | RIME | SAO | ED | GKSO | IGWO | DOA | MIDOA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | 452.38 | 416.87 | 418.49 | 425.10 | 417.43 | 419.51 | 422.75 | 418.01 | 421.11 | 417.56 | 419.58 | 415.92 |
| max | 496.96 | 436.36 | 426.18 | 430.86 | 428.86 | 430.35 | 428.45 | 435.04 | 442.39 | 419.19 | 433.59 | 416.36 |
| min | 424.50 | 415.08 | 415.21 | 421.46 | 414.48 | 417.02 | 414.64 | 415.04 | 416.16 | 416.32 | 417.19 | 413.55 |
| Algorithm | PSO | SO | CSA | DMO | GTO | RIME | SAO | ED | GKSO | IGWO | DOA | MIDOA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | 529.43 | 455.54 | 451.09 | 459.28 | 442.88 | 453.12 | 448.24 | 439.91 | 450.59 | 436.22 | 446.35 | 433.61 |
| max | 745.03 | 495.73 | 493.30 | 469.72 | 460.18 | 478.94 | 471.14 | 474.17 | 593.09 | 467.04 | 524.56 | 434.58 |
| min | 487.58 | 434.39 | 436.75 | 447.71 | 433.33 | 434.32 | 437.42 | 433.44 | 435.91 | 417.19 | 437.49 | 423.28 |
| Algorithm | PSO | SO | CSA | DMO | GTO | RIME | SAO | ED | GKSO | IGWO | DOA | MIDOA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | 65535.00 | 481.01 | 521.68 | 498.37 | 472.38 | 469.24 | 464.25 | 496.19 | 508.45 | 442.62 | 488.93 | 433.14 |
| max | 65535.00 | 546.53 | 665.56 | 515.37 | 553.57 | 506.37 | 507.86 | 598.17 | 656.10 | 491.53 | 555.48 | 437.81 |
| min | 544.66 | 450.89 | 452.59 | 473.78 | 418.52 | 434.33 | 426.45 | 425.36 | 441.38 | 418.16 | 445.64 | 418.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Zhan, J.; Wang, J. Multi-Strategy Improved POA for Global Optimization Problems and 3D UAV Path Planning. Biomimetics 2025, 10, 760. https://doi.org/10.3390/biomimetics10110760
Zhang R, Zhan J, Wang J. Multi-Strategy Improved POA for Global Optimization Problems and 3D UAV Path Planning. Biomimetics. 2025; 10(11):760. https://doi.org/10.3390/biomimetics10110760
Chicago/Turabian StyleZhang, Rui, Jingbo Zhan, and Jianfeng Wang. 2025. "Multi-Strategy Improved POA for Global Optimization Problems and 3D UAV Path Planning" Biomimetics 10, no. 11: 760. https://doi.org/10.3390/biomimetics10110760
APA StyleZhang, R., Zhan, J., & Wang, J. (2025). Multi-Strategy Improved POA for Global Optimization Problems and 3D UAV Path Planning. Biomimetics, 10(11), 760. https://doi.org/10.3390/biomimetics10110760






