Three-Dimensional Printing Parameter Assessment of Elastomers for Tendon Graft Applications
Abstract
1. Introduction
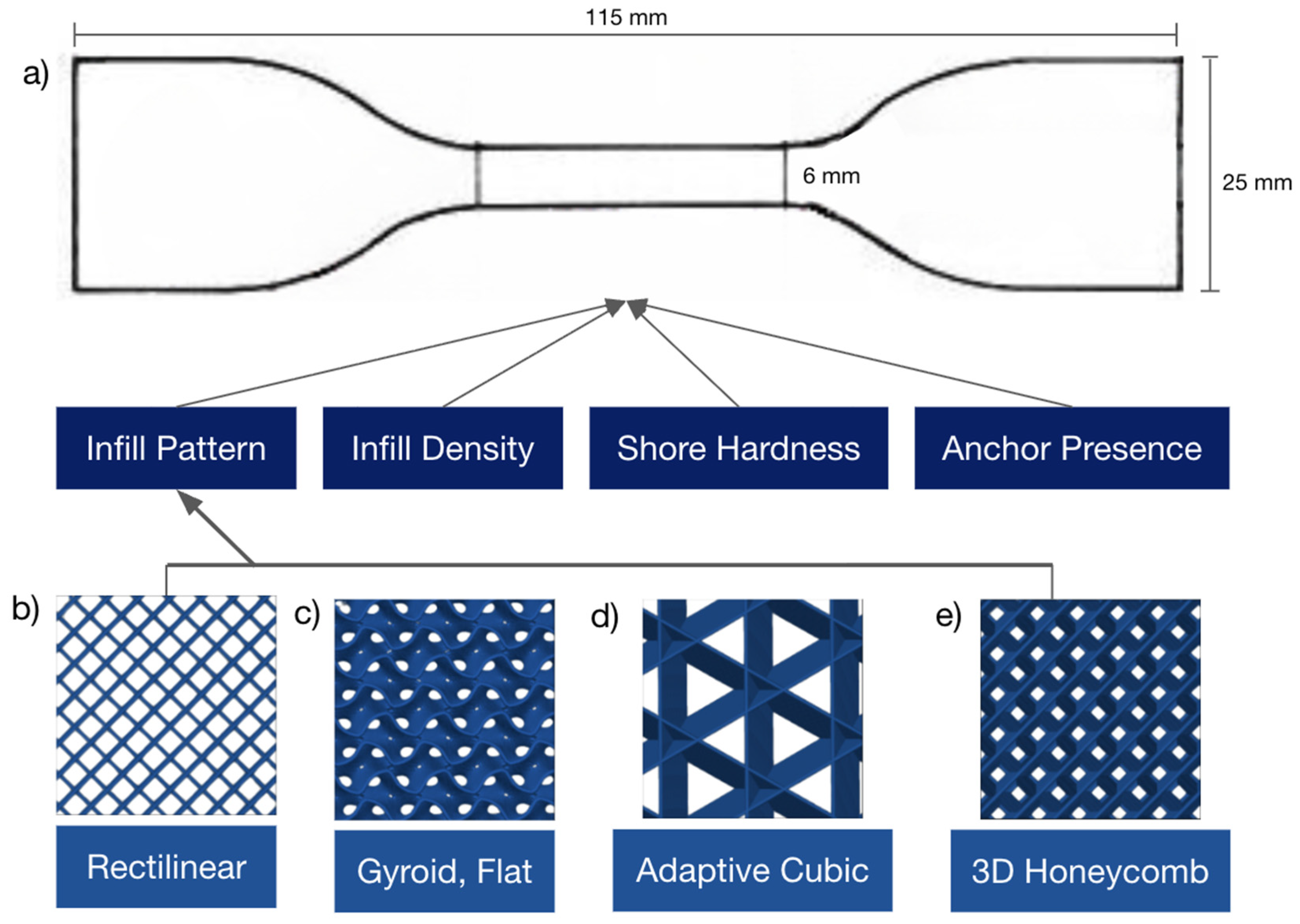
2. Materials and Methods
Statistical Analysis
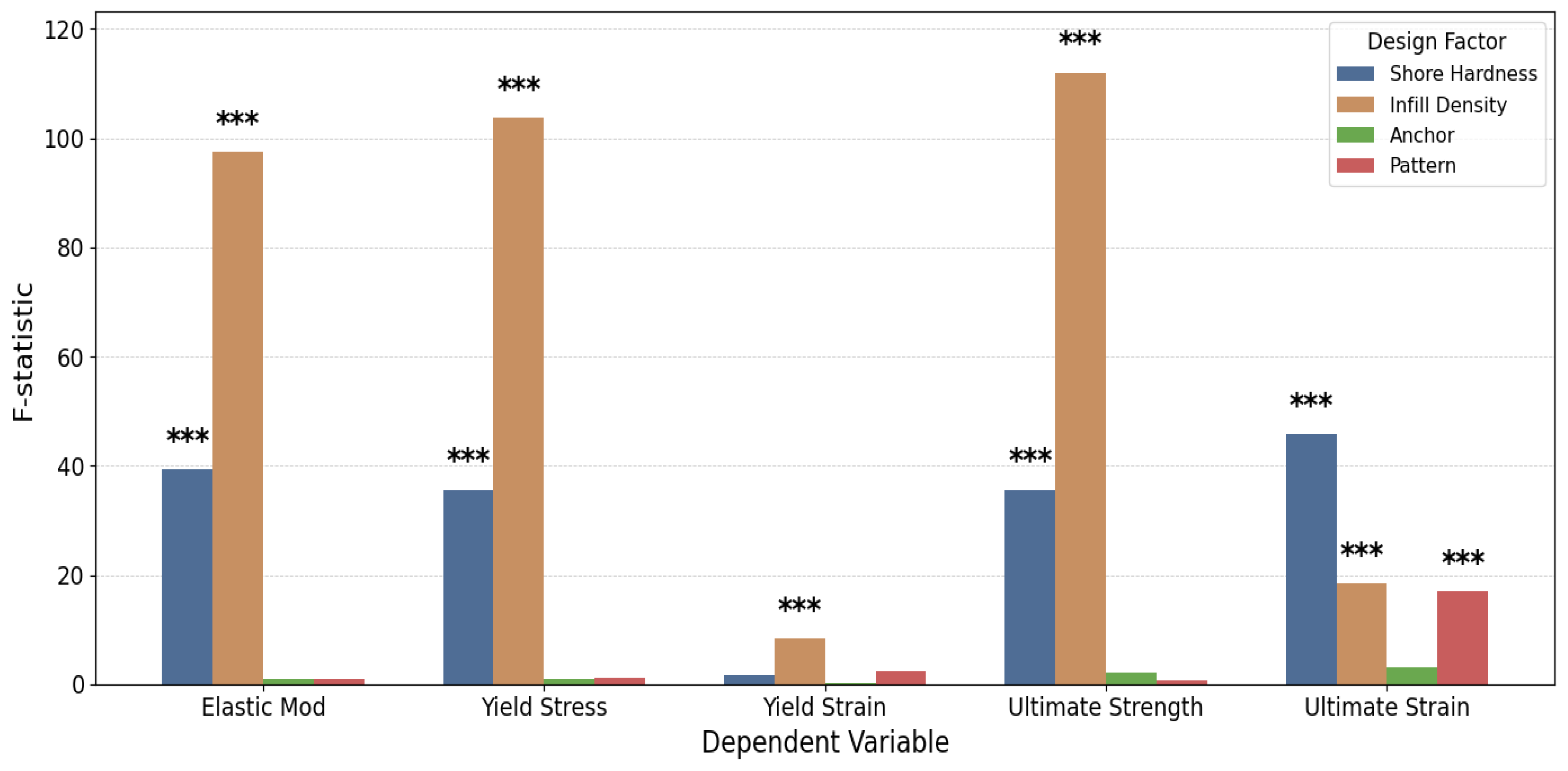
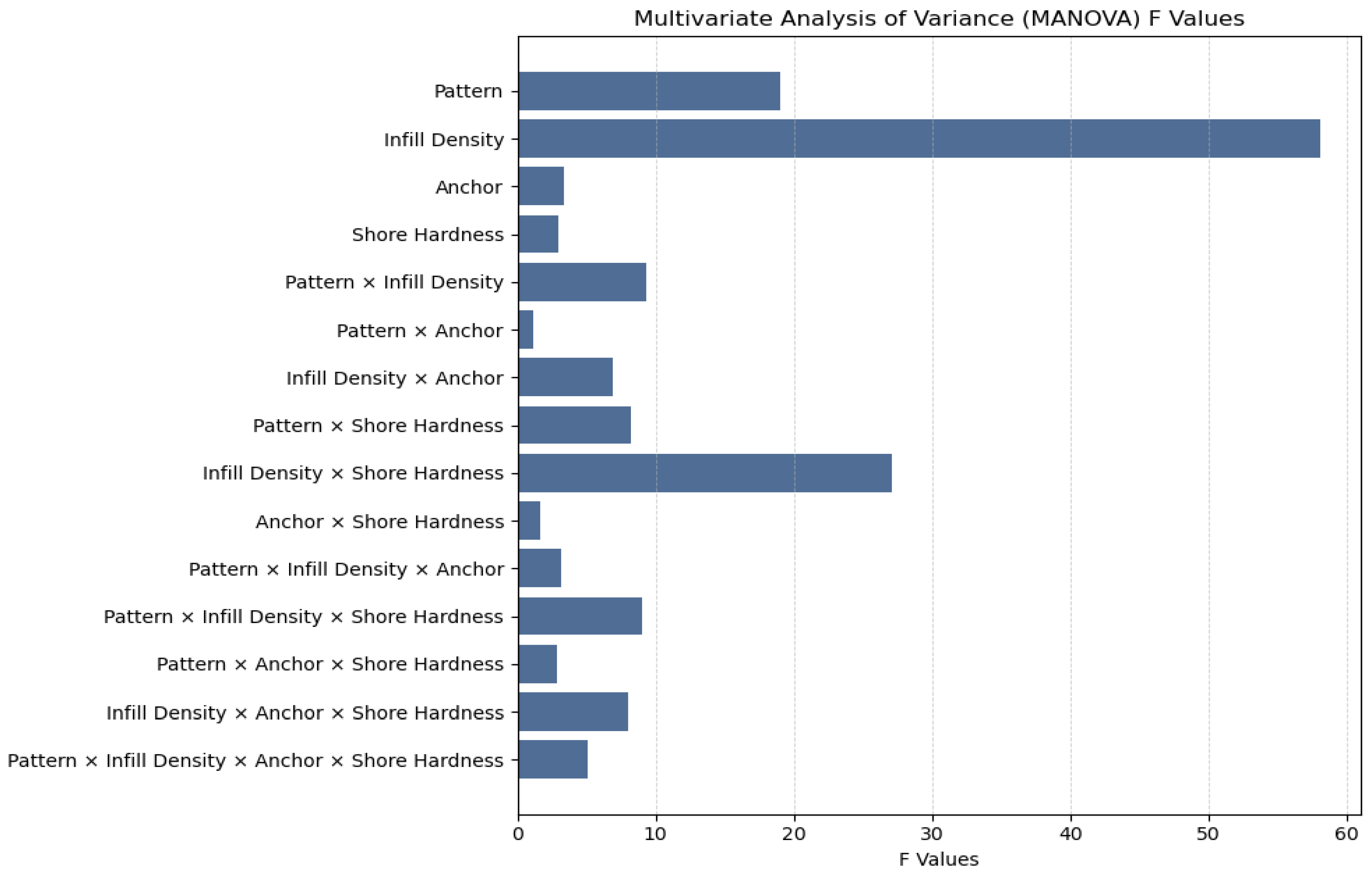
3. Results
Results Summary
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UTS | Ultimate tensile strength |
| ANOVA | Analysis of Variance |
| MANOVA | Multivariate Analysis of Variance |
| ANCOVA | Analysis of Covariance |
References
- Kennedy, S.M.; Amudhan, K.; Britto J, J.J.; Veeranan, E. Transformative applications of additive manufacturing in biomedical engineering: Bioprinting to surgical innovations. J. Med. Eng. Technol. 2024, 48, 151–168. [Google Scholar] [CrossRef]
- Fang, W.; Yang, M.; Liu, M.; Jin, Y.; Wang, Y.; Yang, R.; Wang, Y.; Zhang, K.; Fu, Q. Review on additives in hydrogels for 3D bioprinting of regenerative medicine: From mechanism to methodology. Pharmaceutics 2023, 15, 1700. [Google Scholar] [CrossRef]
- Mengsteab, P.Y.; Nair, L.S.; Laurencin, C.T. The past, present and future of ligament regenerative engineering. Regen. Med. 2016, 11, 871–881. [Google Scholar] [CrossRef] [PubMed]
- Kohn, D.; Sander-Beuermann, A. Donor-site morbidity after harvest of a bone-tendon-bone patellar tendon autograft. Knee Surg. Sports Traumatol. Arthrosc. 1994, 2, 219–223. [Google Scholar] [CrossRef]
- Civera, M.; Goggia, E.D.; De Ros, M.; Burgio, V.; Bergamin, F.; Reinoso, M.R.; Surace, C. Implantable medical devices for tendon and ligament repair: A review of patents and commercial products. Expert Rev. Med. Devices 2022, 19, 825–845. [Google Scholar] [CrossRef]
- Vieira, A.C.; Guedes, R.M.; Marques, A.T. Development of ligament tissue biodegradable devices: A review. J. Biomech. 2009, 42, 2421–2430. [Google Scholar] [CrossRef]
- Yamamoto, N.; Ohno, K.; Hayashi, K.; Kuriyama, H.; Yasuda, K.; Kaneda, K. Effects of stress shielding on the mechanical properties of rabbit patellar tendon. J. Biomech. Eng. 1993, 115, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.M.; Murawski, C.D.; Fu, F.H.; Kaufmann, R.A. Stress shielding of ligaments using nonabsorbable suture augmentation may influence the biology of ligament healing. J. Hand Surg. Am. 2022, 47, 275–278. [Google Scholar] [CrossRef]
- Xiao, J.; Gao, Y. The manufacture of 3D printing of medical grade TPU. Prog. Addit. Manuf. 2017, 2, 117–123. [Google Scholar] [CrossRef]
- Instron. The Definitive Guide to ASTM D412 Tensile Testing of Elastomers. Available online: https://www.instron.com/en/testing-solutions/astm-standards/astm-d412 (accessed on 19 June 2025).
- ISO. Part 10: Tests for skin sensitization. In Biological Evaluation of Medical Devices, 4th ed.; International Organization for Standardization, Ed.; International Organization for Standardization: Geneva, Switzerland, 2021; Volume 10, pp. 1–48. [Google Scholar]
- ISO. Part 5: Tests for in vitro cytotoxicity. In Biological Evaluation of Medical Devices, 3rd ed.; International Organization for Standardization, Ed.; International Organization for Standardization: Geneva, Switzerland, 2009; Volume 5, pp. 1–34. [Google Scholar]
- ISO. Part 23: Tests for irritation. In Biological Evaluation of Medical Devices, 1st ed.; International Organization for Standardization, Ed.; International Organization for Standardization: Geneva, Switzerland, 2021; Volume 23, pp. 1–60. [Google Scholar]
- Siraya Tech. Siraya Tech Flex TPU—85A Filament. Available online: https://siraya.tech/products/flex-tpu-85a-filament (accessed on 27 September 2025).
- Wevolver. TPU Glass Transition Temperature, Printing Temperature, and Other Thermal Considerations. Available online: https://www.wevolver.com/article/tpu-glass-transition-temperature-printing-temperature-and-other-thermal-considerations (accessed on 19 June 2025).
- Bruère, V.M.; Lion, A.; Holtmannspötter, J.; Johlitz, M. The influence of printing parameters on the mechanical properties of 3D printed TPU-based elastomers. Prog. Addit. Manuf. 2023, 8, 693–701. [Google Scholar] [CrossRef]
- Pan, B. Full-field strain measurement using a two-dimensional Savitzky–Golay digital differentiator in digital image correlation. Opt. Eng. 2007, 46, 033601. [Google Scholar] [CrossRef]
- Michigan Technological University. Tensile Test Experiment. Available online: https://www.mtu.edu/materials/k12/experiments/tensile/ (accessed on 1 September 2025).
- Pernet, B.; Nagel, J.K.; Zhang, H. Compressive strength assessment of 3D printing infill patterns. Procedia CIRP 2022, 105, 682–687. [Google Scholar] [CrossRef]
- Dudescu, M.C.; Racz, L.; Popa, F. Effect of infill pattern on fatigue characteristics of 3D printed polymers. Mater. Today Proc. 2023, 78, 263–269. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Aamir, M.; Tolouei-Rad, M. Effect of 3D printing parameters on the fatigue properties of parts manufactured by fused filament fabrication: A review. Appl. Sci. 2023, 13, 904. [Google Scholar] [CrossRef]
- Abar, B.; Alonso-Calleja, A.; Kelly, A.; Kelly, C.; Gall, K.; West, J.L. 3D printing of high-strength, porous, elastomeric structures to promote tissue integration of implants. J. Biomed. Mater. Res. A 2021, 109, 54–63. [Google Scholar] [CrossRef]
- Alasfar, R.H.; Ahzi, S.; Barth, N.; Kochkodan, V.; Khraisheh, M.; Koç, M. A review on the modeling of the elastic modulus and yield stress of polymers and polymer nanocomposites: Effect of temperature, loading rate and porosity. Polymers 2022, 14, 360. [Google Scholar] [CrossRef]
- Wang, S.-Q.; Fan, Z.; Gupta, C.; Siavoshani, A.; Smith, T. Fracture behavior of polymers in plastic and elastomeric states. Macromolecules 2024, 57, 3875–3900. [Google Scholar] [CrossRef]
- Sovol3D Blog. How Infill Percentage Affects Strength, Speed, and Filament Use. Available online: https://www.sovol3d.com/blogs/news/infill-percentage-3d-printing-strength-filament (accessed on 28 October 2025).
- ScienceDirect. Gibson–Ashby Model. Available online: https://www.sciencedirect.com/topics/engineering/gibson-ashby-model (accessed on 28 October 2025).
- Louis-Ugbo, J.; Leeson, B.; Hutton, W.C. Tensile properties of fresh human calcaneal (Achilles) tendons. Clin. Anat. 2004, 17, 30–35. [Google Scholar] [CrossRef]
- Wren, T.A.L.; Yerby, S.A.; Beaupré, G.S.; Carter, D.R. Mechanical properties of the human Achilles tendon. Clin. Biomech. 2001, 16, 245–251. [Google Scholar] [CrossRef]
- Maganaris, C.N.; Paul, J.P. In vivo human tendon mechanical properties. J. Physiol. 1999, 521, 307–313. [Google Scholar] [CrossRef]
- Nagelli, C.V.; Hooke, A.; Quirk, N.; De Padilla, C.; Hewett, T.; van Griensven, M.; Coenen, M.; Berglund, L.; Evans, C.; Müller, S. Mechanical and strain behaviour of human Achilles tendon during in vitro testing to failure. Eur. Cells Mater. 2022, 43, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Ng, B.H.; Chou, S.M.; Krishna, V. The influence of gripping techniques on the tensile properties of tendons. Proc. Inst. Mech. Eng. H 2005, 219, 349–354. [Google Scholar] [CrossRef]
- Aniţaş, R.; Lucaciu, D. A study of the Achilles tendon while running. Clujul Med. 2013, 86, 36–39. [Google Scholar] [PubMed]
- von Windheim, N.; Collinson, D.W.; Lau, T.; Brinson, L.C.; Gall, K. The influence of porosity, crystallinity and interlayer adhesion on the tensile strength of 3D printed polylactic acid (PLA). Rapid Prototyp. J. 2021, 27, 1327–1336. [Google Scholar] [CrossRef]



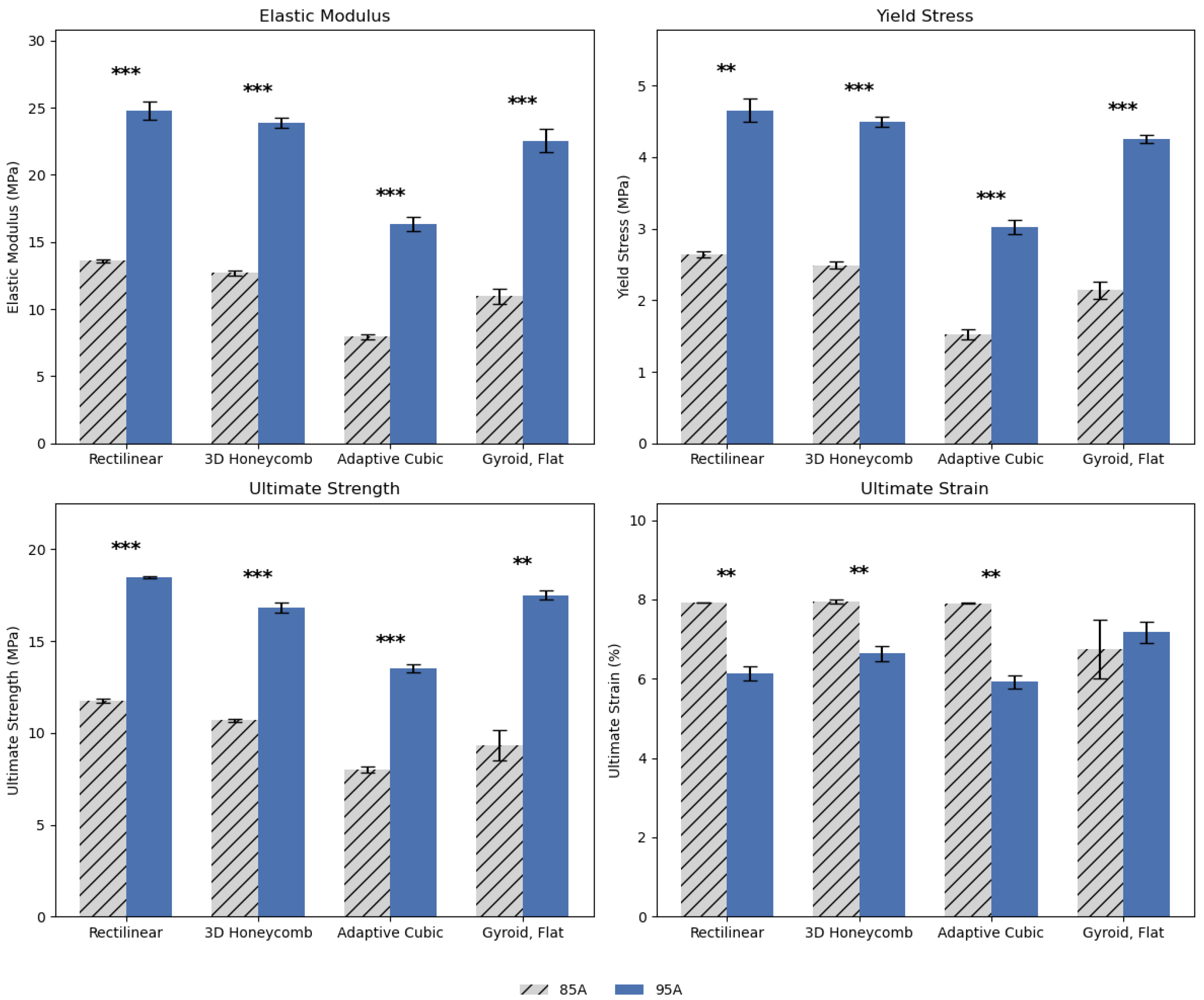

| Elastic Modulus—Anchor | Elastic Modulus—No Anchor | Yield Stress—Anchor | Yield Stress—No Anchor | Ultimate Strength—Anchor | Ultimate Strength—No Anchor | |
|---|---|---|---|---|---|---|
| Rectilinear | 24.78 ± 0.71 | 24.09 ± 0.17 | 4.66 ± 0.16 | 4.51 ± 0.08 | 18.50 ± 0.05 | 18.78 ± 0.33 |
| Three-dimensional Honeycomb | 23.89 ± 0.38 | 21.63 ± 0.38 | 4.49 ± 0.07 | 4.07 ± 0.07 | 16.83 ± 0.27 | 14.64 ± 0.10 |
| Adaptive Cubic | 16.33 ± 0.54 | 15.31 ± 0.27 | 3.03 ± 0.10 | 2.83 ± 0.09 | 13.51 ± 0.21 | 13.13 ± 0.25 |
| Gyroid, Flat | 22.66 ± 0.61 | 20.37 ± 0.40 | 4.21 ± 0.14 | 3.83 ± 0.08 | 17.51 ± 0.25 | 16.60 ± 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lau, T.; Talwar, A.; Abar, B.; Adams, S.B. Three-Dimensional Printing Parameter Assessment of Elastomers for Tendon Graft Applications. Biomimetics 2025, 10, 785. https://doi.org/10.3390/biomimetics10110785
Lau T, Talwar A, Abar B, Adams SB. Three-Dimensional Printing Parameter Assessment of Elastomers for Tendon Graft Applications. Biomimetics. 2025; 10(11):785. https://doi.org/10.3390/biomimetics10110785
Chicago/Turabian StyleLau, Trent, Ashley Talwar, Bijan Abar, and Samuel B. Adams. 2025. "Three-Dimensional Printing Parameter Assessment of Elastomers for Tendon Graft Applications" Biomimetics 10, no. 11: 785. https://doi.org/10.3390/biomimetics10110785
APA StyleLau, T., Talwar, A., Abar, B., & Adams, S. B. (2025). Three-Dimensional Printing Parameter Assessment of Elastomers for Tendon Graft Applications. Biomimetics, 10(11), 785. https://doi.org/10.3390/biomimetics10110785








