Author Contributions
Conceptualization, T.B. and P.P.; methodology, P.P.; software, P.P.; validation, S.C., T.B. and N.I.-O.; formal analysis, S.C.; investigation, P.P.; resources, T.B.; data curation T.B.; writing—original draft preparation, P.P.; writing—review and editing, P.P. and S.C.; visualization, P.P.; supervision, S.C., T.B. and N.I.-O.; project administration, S.C.; funding acquisition, T.B. and N.I.-O. All authors have read and agreed to the published version of the manuscript.
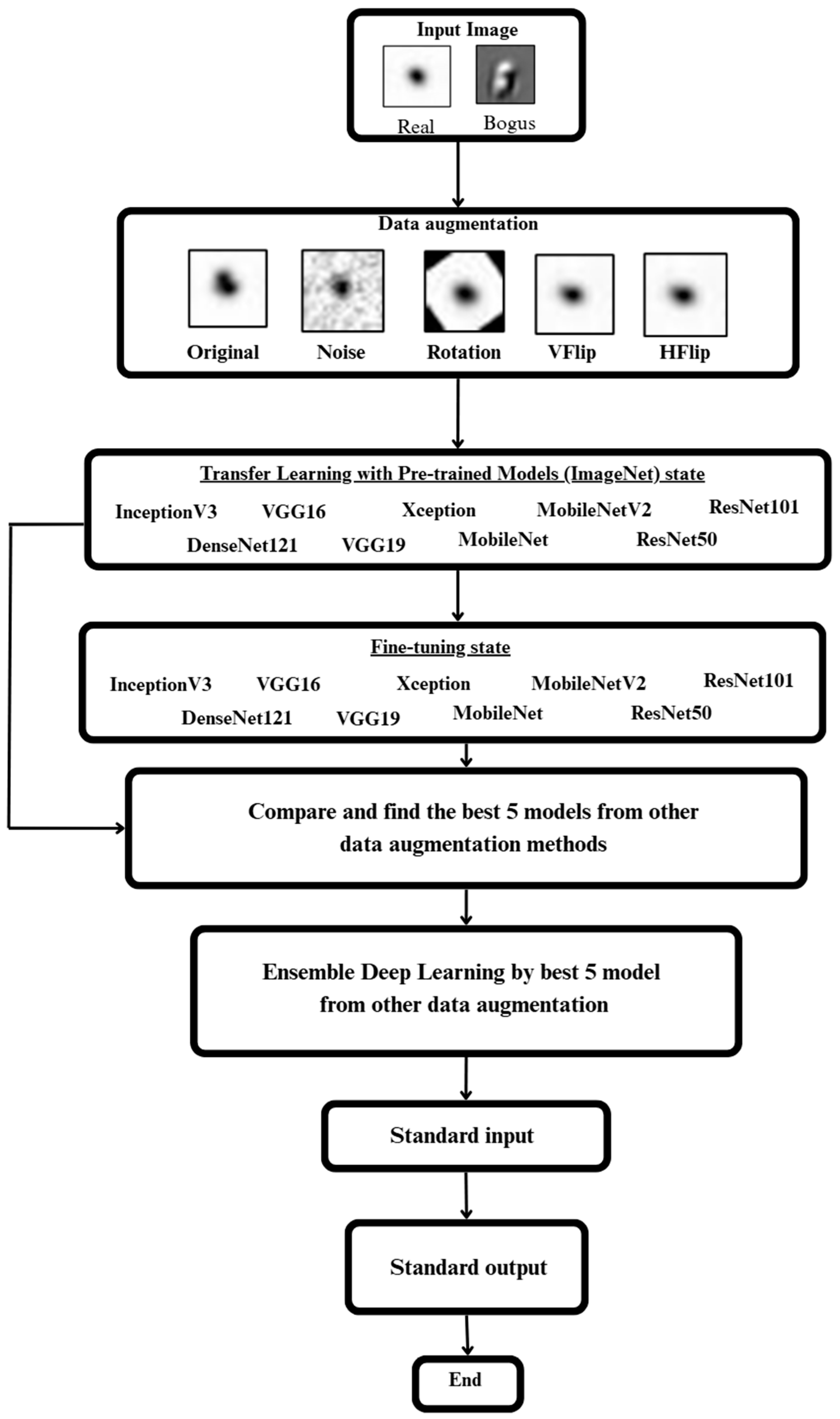
Figure 1.
Figure depicting the overall methods used.
Figure 1.
Figure depicting the overall methods used.
Figure 2.
Some examples of images in the dataset.
Figure 2.
Some examples of images in the dataset.
Figure 3.
An example of data augmentation.
Figure 3.
An example of data augmentation.
Figure 4.
The process of transferring learned features from a source domain (ImageNet) to a target domain (astronomical transient data) using the transfer learning approach.
Figure 4.
The process of transferring learned features from a source domain (ImageNet) to a target domain (astronomical transient data) using the transfer learning approach.
Figure 5.
Ensemble architecture combining multiple CNN models trained under different augmentation strategies and batch sizes.
Figure 5.
Ensemble architecture combining multiple CNN models trained under different augmentation strategies and batch sizes.
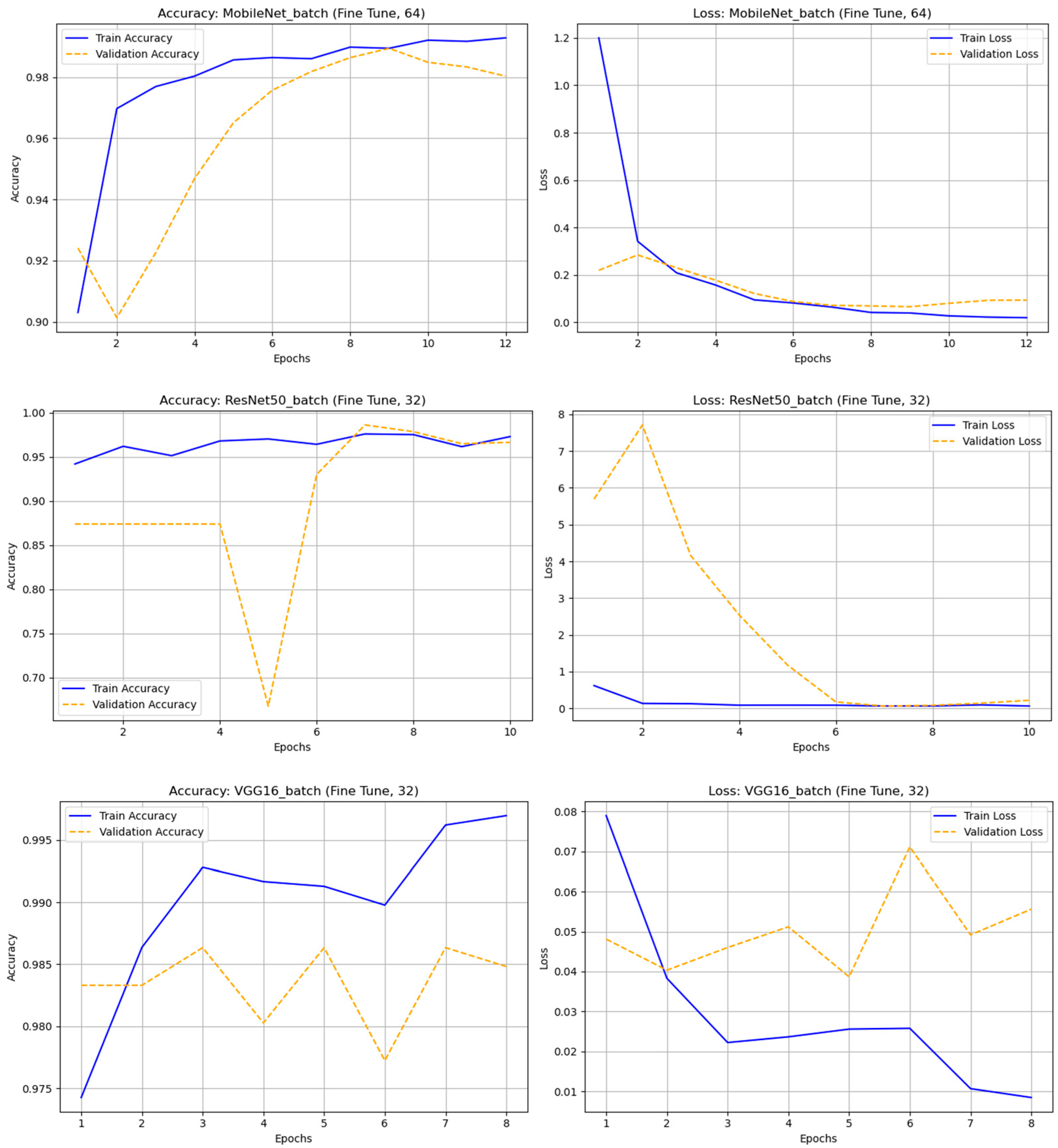
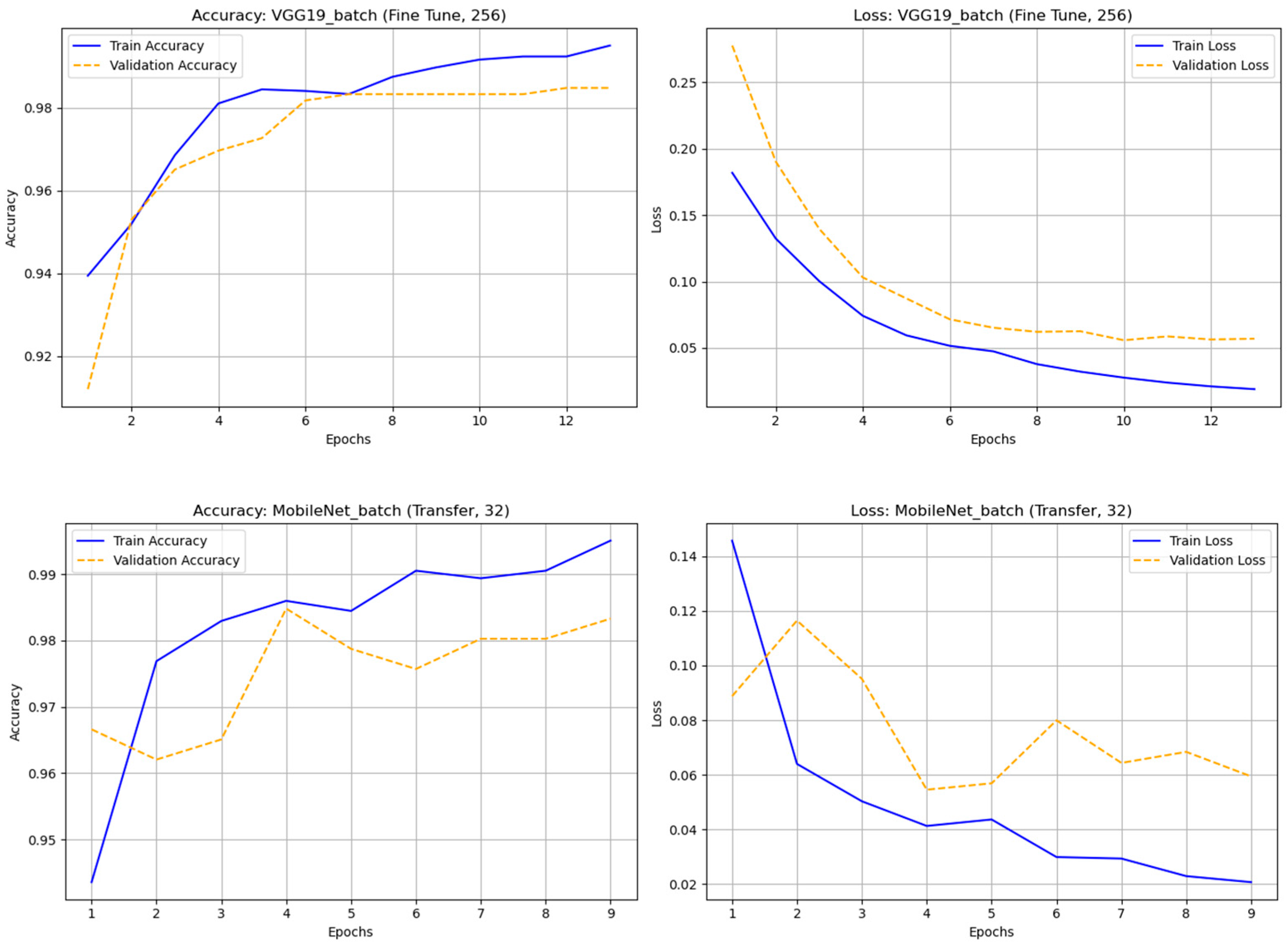
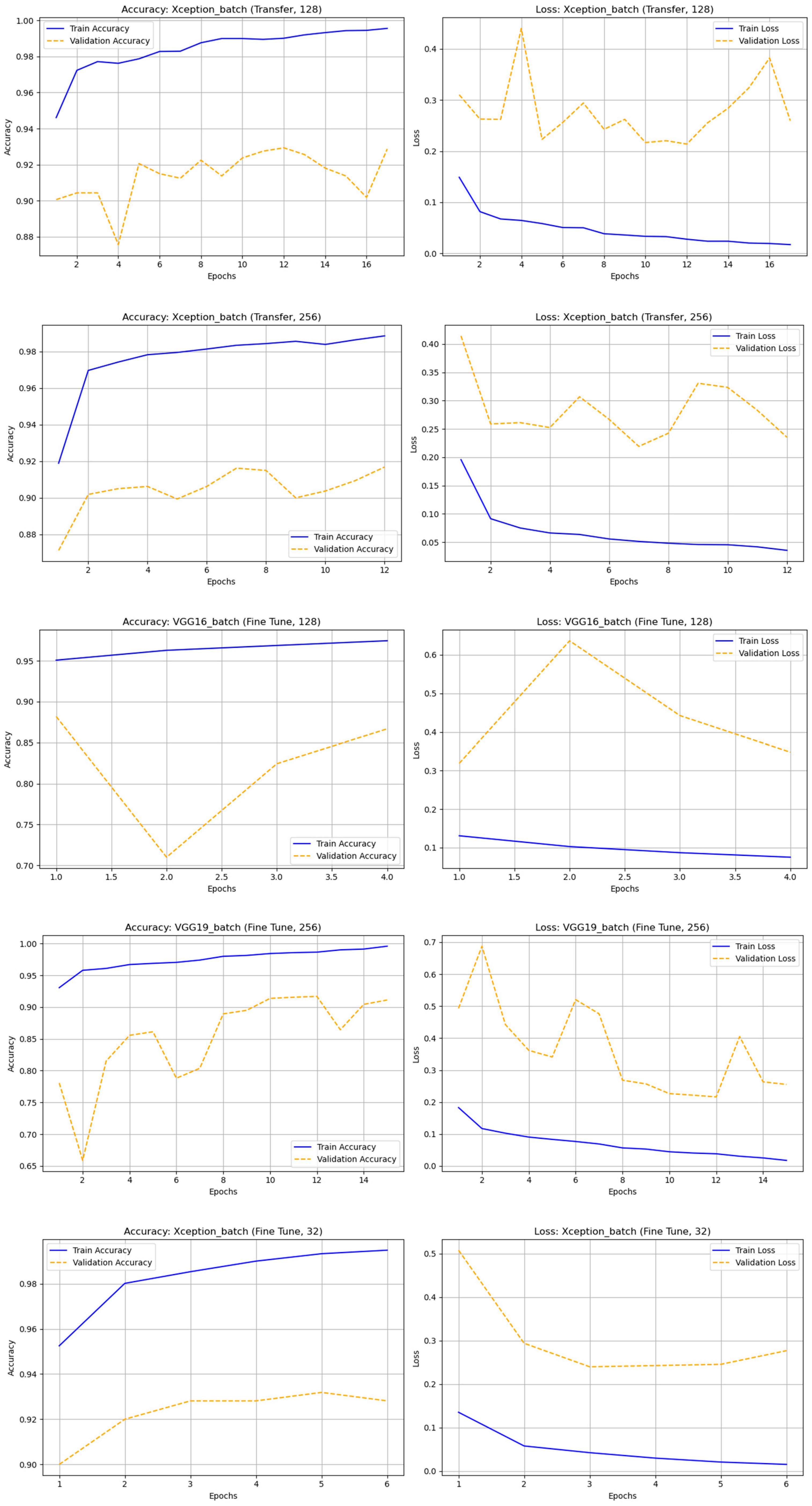
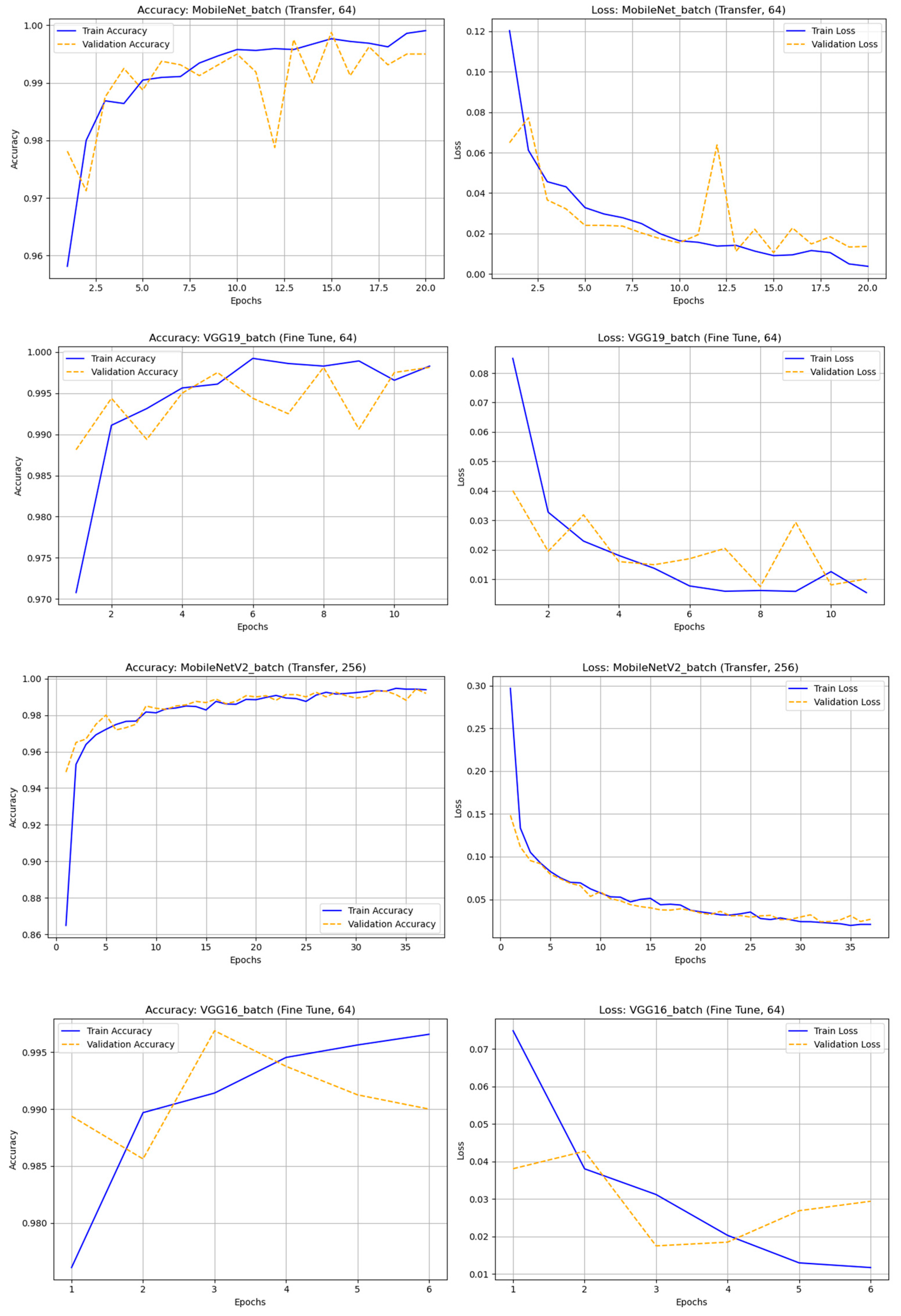
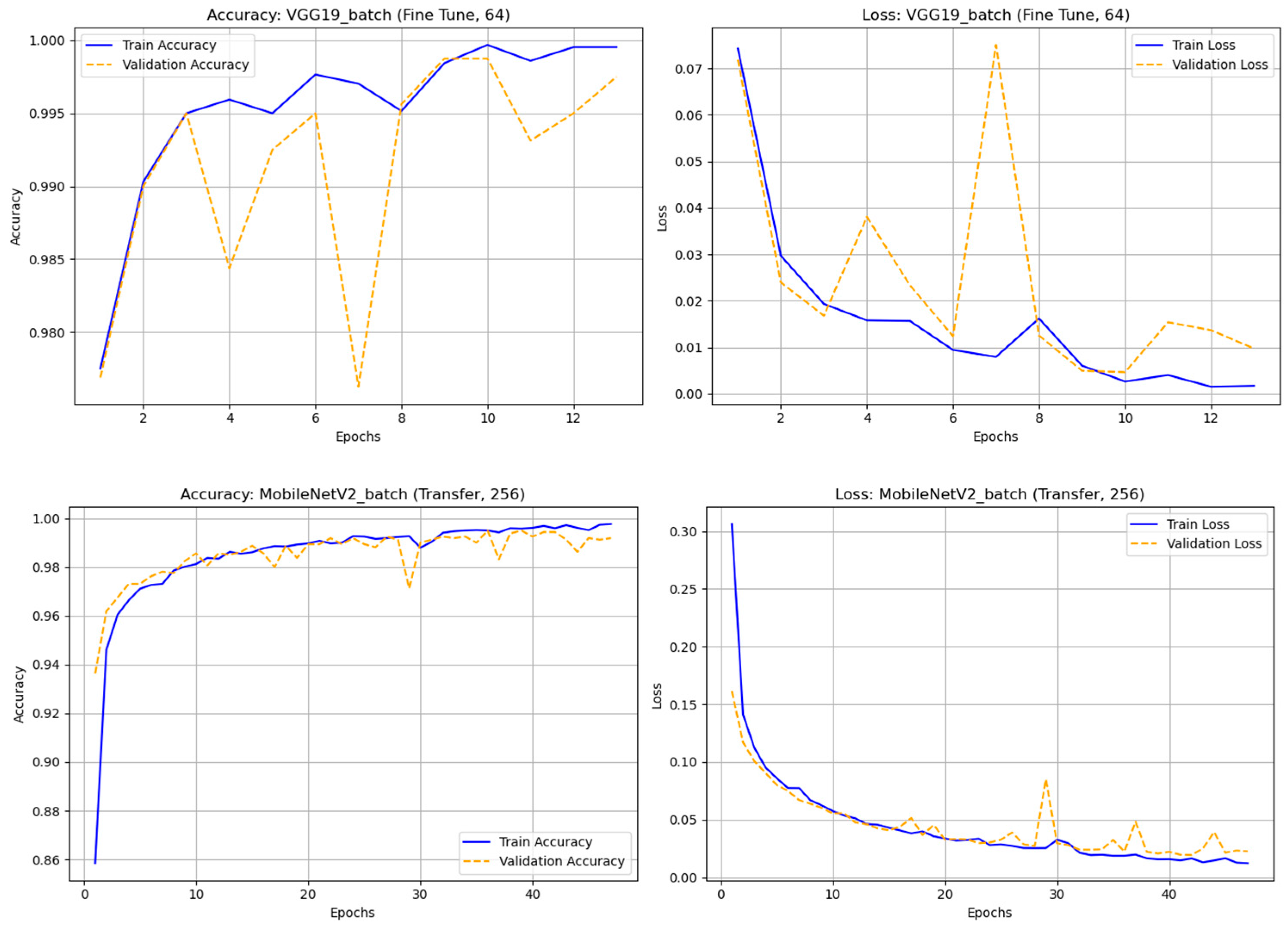
Figure 6.
The accuracy and loss graph of different deep learning techniques with original (nonaugmented) dataset.
Figure 6.
The accuracy and loss graph of different deep learning techniques with original (nonaugmented) dataset.
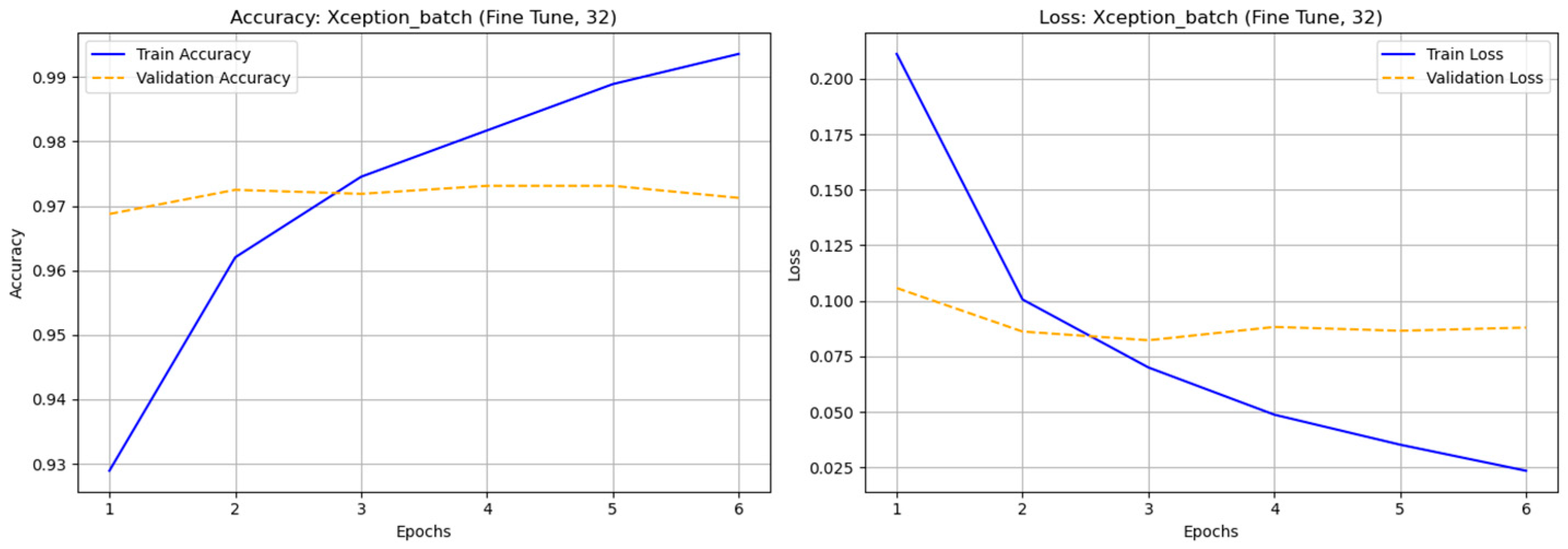
Figure 7.
The accuracy and loss graph of different deep learning techniques with rotation dataset.
Figure 7.
The accuracy and loss graph of different deep learning techniques with rotation dataset.
Figure 8.
The accuracy and loss graph of different deep learning techniques with noise dataset.
Figure 8.
The accuracy and loss graph of different deep learning techniques with noise dataset.
Figure 9.
The accuracy and loss graph of different deep learning techniques with hflip dataset.
Figure 9.
The accuracy and loss graph of different deep learning techniques with hflip dataset.
Figure 10.
The accuracy and loss graph of different deep learning techniques with vflip dataset.
Figure 10.
The accuracy and loss graph of different deep learning techniques with vflip dataset.
Table 1.
Training data before and after oversampling, applied to address the class imbalance problem.
Table 1.
Training data before and after oversampling, applied to address the class imbalance problem.
| Training Data | Bogus | Real |
|---|
| Before Oversampling | 2862 | 418 |
| After Oversampling | 4000 | 4000 |
Table 2.
Hyperparameter settings used for training and fine-tuning pretrained convolutional and deep learning architectures (e.g., VGG, ResNet, DenseNet, MobileNet, Xception, and InceptionV3) for astronomical transient image classification.
Table 2.
Hyperparameter settings used for training and fine-tuning pretrained convolutional and deep learning architectures (e.g., VGG, ResNet, DenseNet, MobileNet, Xception, and InceptionV3) for astronomical transient image classification.
| Parameter | Value |
|---|
| Batch Size | 3,264,128,256 |
| Epoch | 100, Early Stopping (Patience = 3) |
| Learning | 0.001 (TF), 0.00001 (FT) |
| Optimizer | Adam |
| Loss Function | Binary Cross-Entropy |
| Fine-Tuning Unlocks | Top 30% |
Table 3.
Performance indicators and formula.
Table 3.
Performance indicators and formula.
| Performance Indicators | Formula |
|---|
| Precision (P) | |
| Recall (R) | |
| F1-score | |
| Performance indicators | formula |
| Precision (P) | |
| Recall (R) | |
Table 4.
Comparison of classification results of different deep learning techniques with original dataset.
Table 4.
Comparison of classification results of different deep learning techniques with original dataset.
| Rank | Model | Method | Batch Size | Accuracy | F1-Score (Bogus) | F1-Score (Real) |
|---|
| 1 | MobileNet | fine-tuned | 64 | 0.98938 | 0.99393 | 0.95758 |
| 2 | ResNet50 | fine-tuned | 32 | 0.98634 | 0.99222 | 0.94410 |
| 3 | VGG16 | fine-tuned | 32 | 0.98634 | 0.99221 | 0.94479 |
| 4 | VGG19 | fine-tuned | 256 | 0.98331 | 0.99049 | 0.93168 |
| 5 | MobileNet | transfer | 32 | 0.98483 | 0.99130 | 0.94048 |
Table 5.
Comparison of classification results of different deep learning techniques with rotation dataset.
Table 5.
Comparison of classification results of different deep learning techniques with rotation dataset.
| Rank | Model | Method | Batch Size | Accuracy | F1-Score (Bogus) | F1-Score (Real) |
|---|
| 1 | Xception | transfer | 128 | 0.97750 | 0.97739 | 0.97761 |
| 2 | Xception | transfer | 256 | 0.97375 | 0.97352 | 0.97398 |
| 3 | VGG16 | fine-tuned | 128 | 0.97500 | 0.97497 | 0.97503 |
| 4 | VGG19 | fine-tuned | 256 | 0.97188 | 0.97168 | 0.97207 |
| 5 | Xception | fine-tuned | 32 | 0.97188 | 0.97146 | 0.97227 |
Table 6.
Comparison of classification results of different deep learning techniques with noise dataset.
Table 6.
Comparison of classification results of different deep learning techniques with noise dataset.
| Rank | Model | Method | Batch Size | Accuracy | F1-Score (Bogus) | F1-Score (Real) |
|---|
| 1 | ResNet50 | fine-tuned | 256 | 0.85000 | 0.86014 | 0.83827 |
| 2 | Xception | fine-tuned | 256 | 0.72625 | 0.76776 | 0.6667 |
| 3 | Xception | transfer | 256 | 0.64000 | 0.72932 | 0.46269 |
| 4 | Xception | fine-tuned | 32 | 0.65500 | 0.74085 | 0.48411 |
| 5 | InceptionV3 | transfer | 256 | 0.62125 | 0.72329 | 0.4000 |
Table 7.
Comparison of classification results of different deep learning techniques with HFlip dataset.
Table 7.
Comparison of classification results of different deep learning techniques with HFlip dataset.
| Rank | Model | Method | Batch Size | Accuracy | F1-Score (Bogus) | F1-Score (Real) |
|---|
| 1 | MobileNet | transfer | 64 | 0.99875 | 0.99875 | 0.99875 |
| 2 | Xception | transfer | 64 | 0.99875 | 0.99875 | 0.99875 |
| 3 | VGG19 | fine-tuned | 64 | 0.99875 | 0.99875 | 0.99875 |
| 4 | VGG16 | fine-tuned | 64 | 0.99687 | 0.99688 | 0.99688 |
| 5 | MobileNetV2 | transfer | 256 | 0.99375 | 0.99379 | 0.99379 |
Table 8.
Comparison of classification results of different deep learning techniques with VFlip dataset.
Table 8.
Comparison of classification results of different deep learning techniques with VFlip dataset.
| Rank | Model | Method | Batch Size | Accuracy | F1-Score (Bogus) | F1-Score (Real) |
|---|
| 1 | MobileNet | transfer | 32 | 0.99875 | 0.99875 | 0.99875 |
| 2 | VGG19 | fine-tuned | 32 | 0.99875 | 0.99875 | 0.99875 |
| 3 | InceptionV3 | transfer | 32 | 0.99750 | 0.99749 | 0.99751 |
| 4 | MobileNet | fine-tuned | 32 | 0.99750 | 0.99749 | 0.99751 |
| 5 | Xception | transfer | 32 | 0.99687 | 0.99687 | 0.99688 |
Table 9.
Selected models for ensemble learning based on best performance by augmentation type.
Table 9.
Selected models for ensemble learning based on best performance by augmentation type.
| Model | Method | Augmentation | Batch Size |
|---|
| MobileNet | Fine-Tuned | Original | 64 |
| Xception | Transfer | Rotation | 128 |
| Xception | Fine-Tuned | Noise | 256 |
| MobileNet | Transfer | HFlip | 64 |
| MobileNet | Transfer | VFlip | 32 |
Table 10.
Test with original data.
Table 10.
Test with original data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9937 | 0.9986 | 0.9930 | 0.9958 | 0.9541 | 0.9905 | 0.9720 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 711 | 5 |
| True: real | 1 | 104 |
Table 11.
Test with rotation data.
Table 11.
Test with rotation data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.7386 | 0.6584 | 0.992 | 0.7914 | 0.984 | 0.4852 | 0.6499 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3968 | 32 |
| True: real | 2059 | 1941 |
Table 12.
Test with noise data.
Table 12.
Test with noise data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.5006 | 0.5 | 1 | 0.6667 | 1 | 0.0012 | 0.0024 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 4000 | 0 |
| True: real | 3995 | 5 |
Table 13.
Test with HFlip data.
Table 13.
Test with HFlip data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9667 | 0.946 | 0.99 | 0.967 | 0.9895 | 0.9435 | 0.966 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3960 | 40 |
| True: real | 226 | 3774 |
Table 14.
Test with VFlip data.
Table 14.
Test with VFlip data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9889 | 0.9848 | 0.993 | 0.989 | 0.9929 | 0.9847 | 0.9888 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3972 | 28 |
| True: real | 61 | 3939 |
Table 15.
Parameters in first ensemble.
Table 15.
Parameters in first ensemble.
| Model | Method | Batch Size | Augmentation | Weight |
|---|
| MobileNet | fine_tuned | 64 | Original | 0.2 |
| Xception | transfer | 128 | Rotation | 0.2 |
| Xception | fine_tuned | 256 | Noise | 0.3 |
| MobileNet | transfer | 64 | HFlip | 0.15 |
| MobileNet | Transfer | 32 | VFlip | 0.15 |
Table 16.
Test with original data.
Table 16.
Test with original data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9926 | 1 | 0.9916 | 0.9958 | 0.9459 | 1 | 0.9722 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 710 | 6 |
| True: real | 0 | 105 |
Table 17.
Test with rotation data.
Table 17.
Test with rotation data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.7628 | 0.6805 | 0.9907 | 0.8068 | 0.983 | 0.535 | 0.6928 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3963 | 37 |
| True: real | 1560 | 2140 |
Table 18.
Test with noise data.
Table 18.
Test with noise data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.5013 | 0.5 | 1 | 0.6672 | 1 | 0.0027 | 0.0054 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 4000 | 0 |
| True: real | 3959 | 11 |
Table 19.
Test with HFlip data.
Table 19.
Test with HFlip data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9703 | 0.9556 | 0.9865 | 0.9708 | 0.986 | 0.9542 | 0.9698 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3946 | 54 |
| True: real | 183 | 3817 |
Table 20.
Test with VFlip data.
Table 20.
Test with VFlip data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.976 | 0.9625 | 0.9905 | 0.9763 | 0.9902 | 0.9615 | 0.9756 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3962 | 38 |
| True: real | 154 | 3846 |
Table 21.
Parameters in second ensemble.
Table 21.
Parameters in second ensemble.
| Model | Method | Batch Size | Augmentation | Weight |
|---|
| MobileNet | fine_tuned | 64 | Original | 0.2 |
| Xception | transfer | 128 | Rotation | 0.2 |
| Xception | fine_tuned | 256 | Noise | 0.50 |
| MobileNet | transfer | 64 | HFlip | 0.15 |
| MobileNet | transfer | 32 | VFlip | 0.15 |
Table 22.
Test with original data.
Table 22.
Test with original data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9902 | 1 | 0.9888 | 0.9943 | 0.9292 | 1 | 0.9633 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 708 | 8 |
| True: real | 0 | 105 |
Table 23.
Test with rotation data.
Table 23.
Test with rotation data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9203 | 0.8734 | 0.98325 | 0.9250 | 0.9808 | 0.8575 | 0.915 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3933 | 67 |
| True: real | 570 | 3430 |
Table 24.
Test with noise data.
Table 24.
Test with noise data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.6217 | 0.5706 | 0.9832 | 0.722 | 0.9395 | 0.2602 | 0.407 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3933 | 67 |
| True: real | 2959 | 1041 |
Table 25.
Test with HFlip data.
Table 25.
Test with HFlip data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.97125 | 0.9631 | 0.98 | 0.9714 | 0.9796 | 0.9625 | 0.970 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3920 | 80 |
| True: real | 150 | 3850 |
Table 26.
Test with VFlip data.
Table 26.
Test with VFlip data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.971 | 0.9584 | 0.9847 | 0.9714 | 0.9843 | 0.9572 | 0.9706 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3939 | 61 |
| True: real | 171 | 3829 |
Table 27.
Parameters in third ensemble.
Table 27.
Parameters in third ensemble.
| Model | Method | Batch Size | Augmentation | Weight |
|---|
| MobileNet | fine_tuned | 64 | Original | 0.20 |
| Xception | transfer | 128 | Rotation | 0.20 |
| Xception | fine_tuned | 256 | Noise | 0.80 |
| MobileNet | transfer | 64 | HFlip | 0.15 |
| MobileNet | transfer | 32 | VFlip | 0.15 |
Table 28.
Test with original data.
Table 28.
Test with original data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9842 | 0.9986 | 0.9832 | 0.991 | 0.8966 | 0.9904 | 0.9411 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 704 | 12 |
| True: real | 1 | 104 |
Table 29.
Test with rotation data.
Table 29.
Test with rotation data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9 | 0.872 | 0.9377 | 0.9 | 0.9327 | 0.863 | 0.8965 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3751 | 249 |
| True: real | 548 | 3452 |
Table 30.
Test with noise data.
Table 30.
Test with noise data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.885 | 0.9993 | 0.771 | 0.870 | 0.813 | 0.9995 | 0.897 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3084 | 916 |
| True: real | 2 | 3998 |
Table 31.
Test with HFlip data.
Table 31.
Test with HFlip data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9686 | 0.9694 | 0.9686 | 0.9678 | 0.9678 | 0.9695 | 0.9686 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3871 | 129 |
| True: real | 122 | 3878 |
Table 32.
Test with VFlip data.
Table 32.
Test with VFlip data.
| Model | Accuracy | Precision (Bogus) | Recall (Bogus) | F1-Score (Bogus) | Precision (Real) | Recall (Real) | F1-Score (Real) |
|---|
| Ensemble | 0.9617 | 0.9545 | 0.9692 | 0.962 | 0.968 | 0.9542 | 0.9614 |
| Confusion Matrix |
| | Pred: bogus | Pred: real |
| True: bogus | 3877 | 123 |
| True: real | 183 | 3817 |
Table 33.
Comparison with previous experimental results.
Table 33.
Comparison with previous experimental results.
| Ref./Year | Technique | Dataset | Accuracy/F1 (Class 1) |
|---|
| Tabacolde et al. [56] | ML with handcrafted
features (e.g., SVM,
Decision Tree) | GOTO | RF best precision, but
recall < 0.1 |
| Liu et al. [57] | CNN baseline (1 conv layer) with multiple optimizers and augmentation | GOTO | F1-class 1 = 0.917
(best at batch size 128) |
| Proposed | Ensemble of fine-tuned CNNs with
Weighted Voting with data augmentation | GOTO | F1-class 1 = 0.9717 |