The Impact of Collagen Fiber and Slit Orientations on Meshing Ratios in Skin Meshing Models
Abstract
1. Introduction
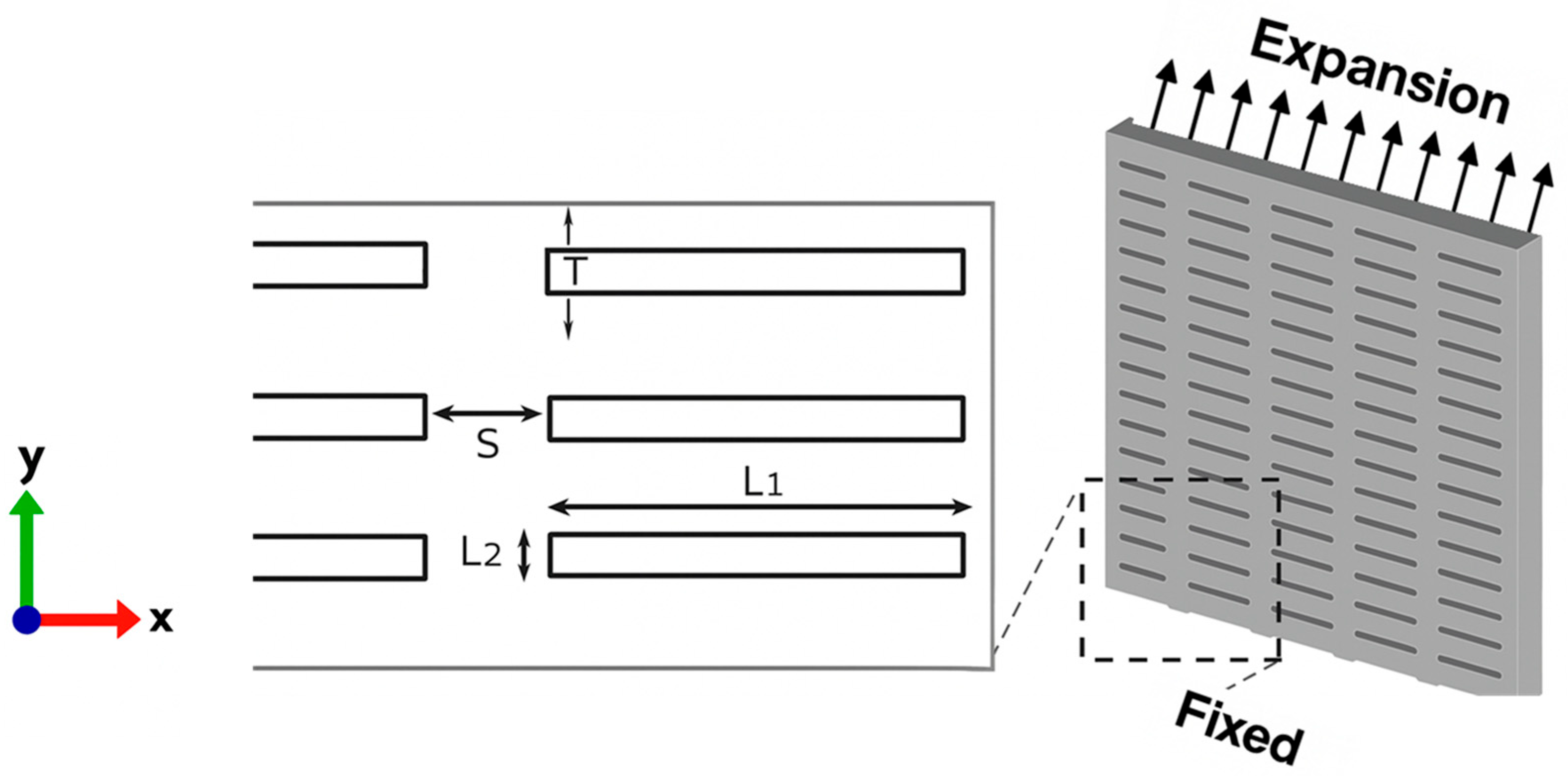
2. Materials and Methods
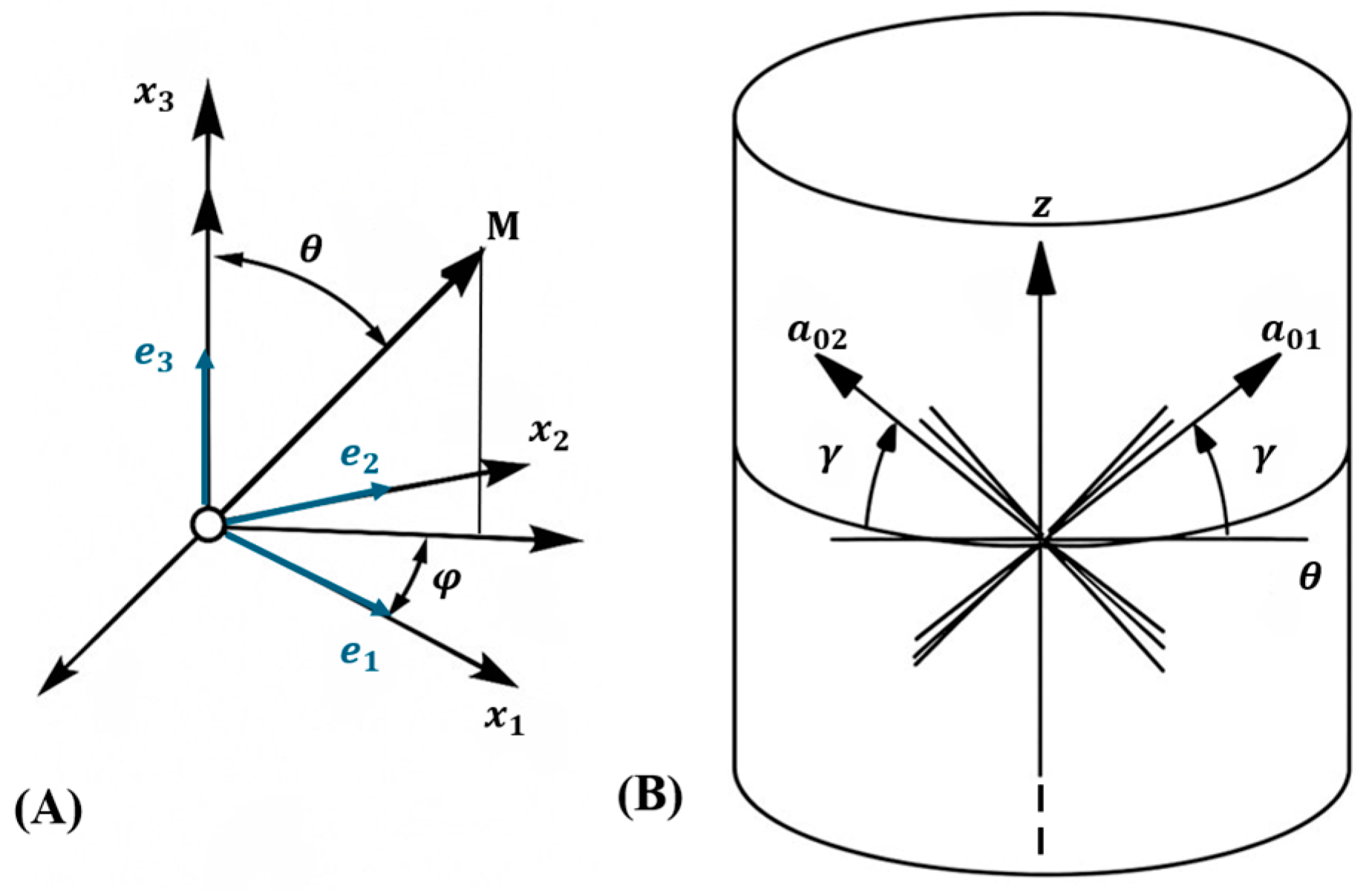
Gasser–Ogden–Holzapfel (GOH) Model
3. Results and Discussion
3.1. Inverse Analysis of Uncoupled GOH Model
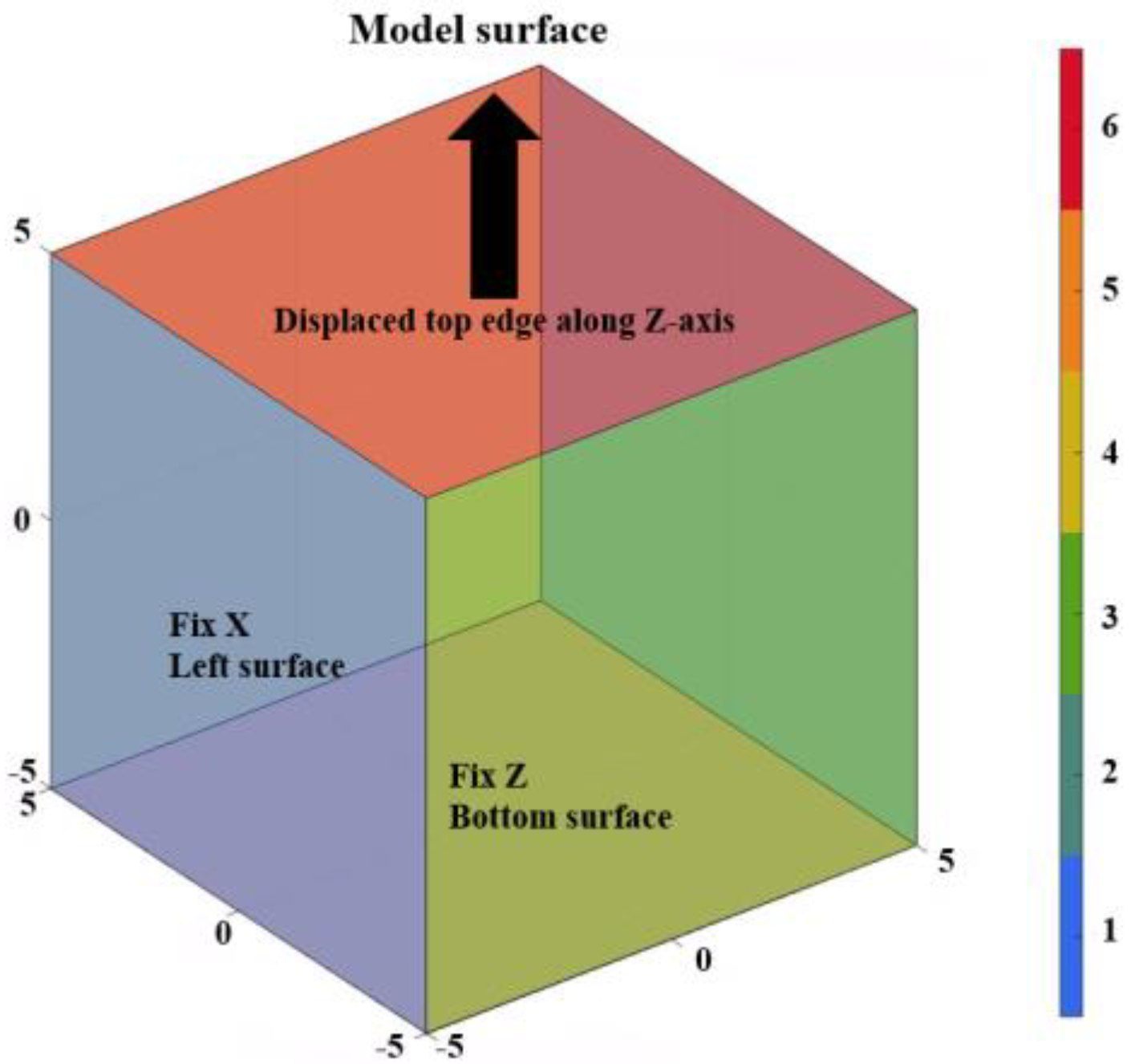
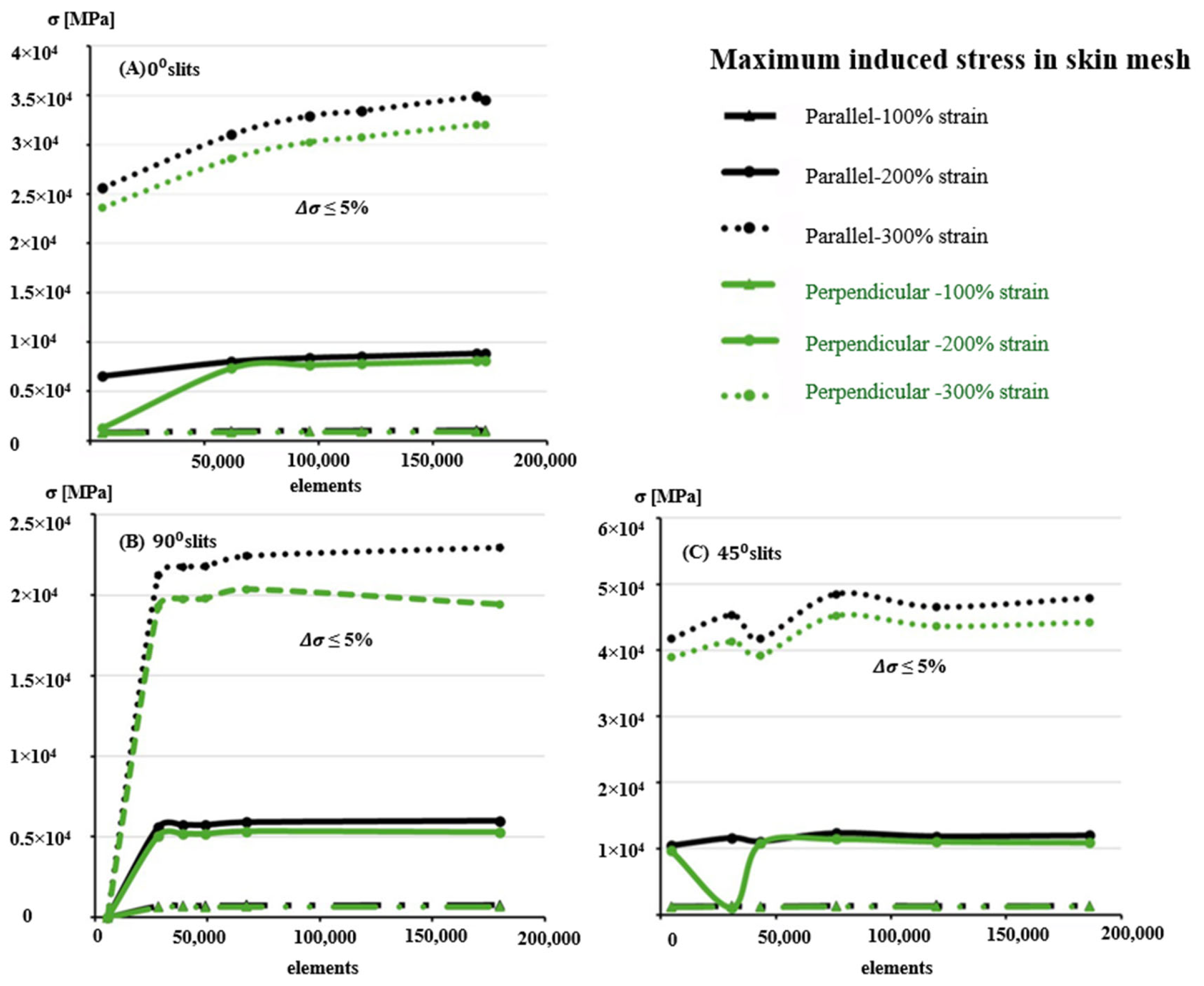
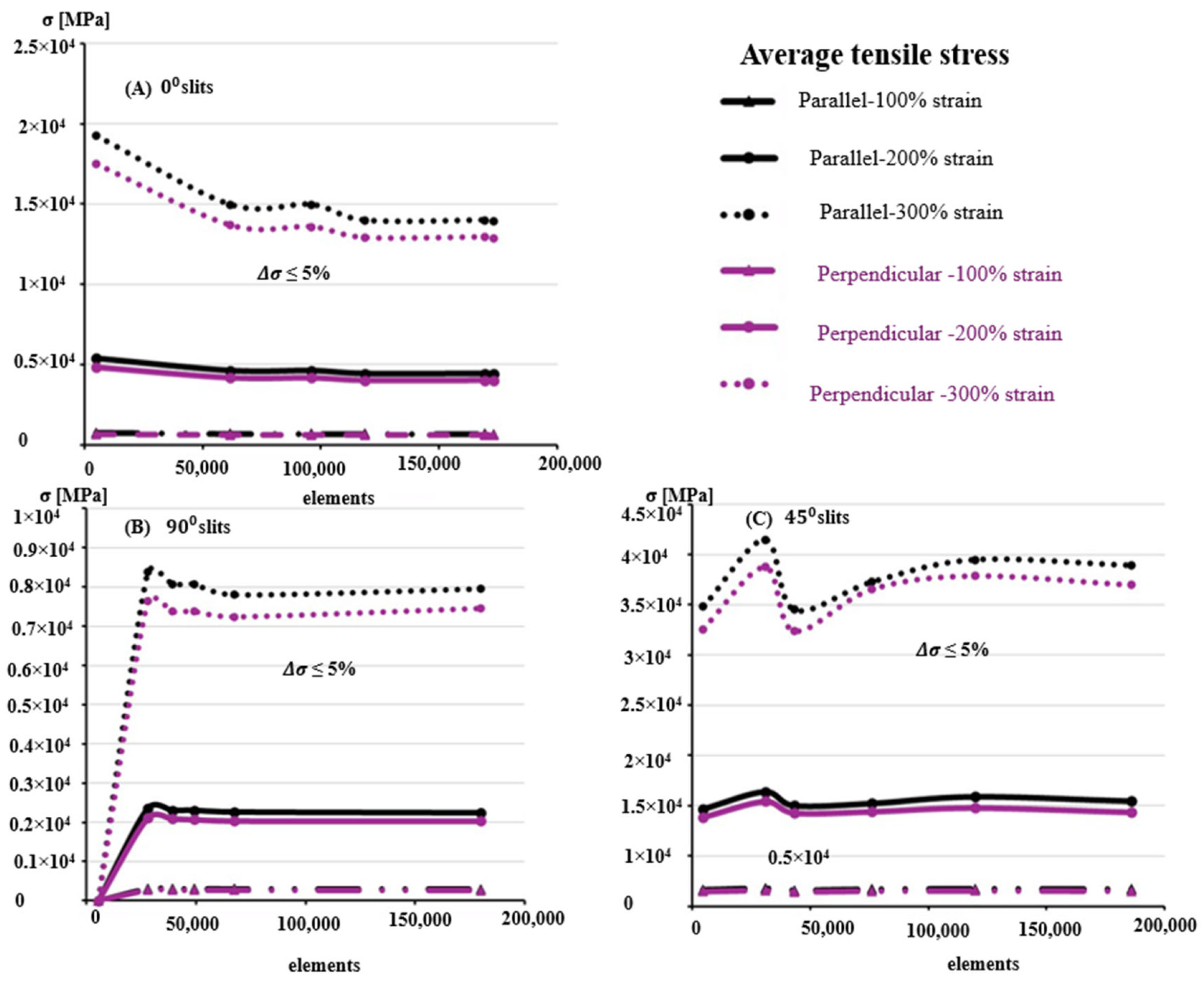
3.2. Finite Element Modeling and Convergence Analysis
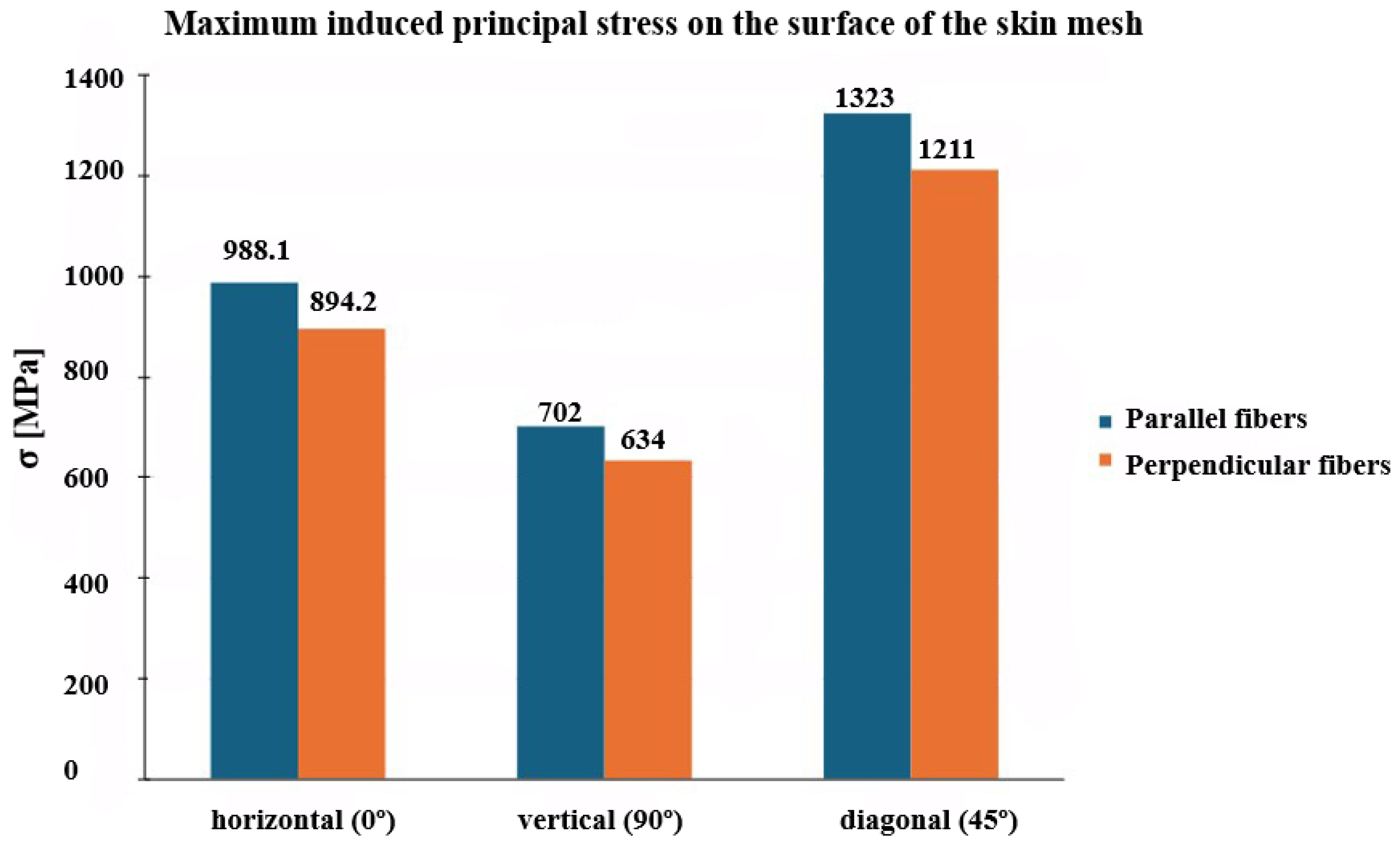
3.3. Influence of Anisotropy and Slit Orientation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Burns. Available online: https://www.who.int/news-room/fact-sheets/detail/burns (accessed on 21 December 2023).
- Peck, M.D. Epidemiology of Burns throughout the World. Part I: Distribution and Risk Factors. Burns 2011, 37, 1087–1100. [Google Scholar] [CrossRef] [PubMed]
- Radzikowska-Büchner, E.; Łopuszyńska, I.; Flieger, W.; Tobiasz, M.; Maciejewski, R.; Flieger, J. An Overview of Recent Developments in the Management of Burn Injuries. Int. J. Mol. Sci. 2023, 24, 16357. [Google Scholar] [CrossRef] [PubMed]
- Kohlhauser, M.; Luze, H.; Nischwitz, S.P.; Kamolz, L.P. Historical Evolution of Skin Grafting—A Journey through Time. Medicina (B Aires) 2021, 57, 348. [Google Scholar] [CrossRef]
- Vandeput, J.; Nelissen, M.; Tanner, J.C.; Boswick, J. A Review of Skin Meshers. Burns 1995, 21, 364–370. [Google Scholar] [CrossRef]
- Singh, M.; Nuutila, K.; Collins, K.C.; Huang, A. Evolution of Skin Grafting for Treatment of Burns: Reverdin Pinch Grafting to Tanner Mesh Grafting and Beyond. Burns 2017, 43, 1149–1154. [Google Scholar] [CrossRef]
- Noureldin, M.A.; Said, T.A.; Makeen, K.; Kadry, H.M. Comparative Study between Skin Micrografting (Meek Technique) and Meshed Skin Grafts in Paediatric Burns. Burns 2022, 48, 1632–1644. [Google Scholar] [CrossRef]
- Wainwright, D.J. Burn Reconstruction: The Problems, the Techniques, and the Applications. Clin. Plast. Surg. 2009, 36, 687–700. [Google Scholar] [CrossRef]
- Lyons, J.L.; Kagan, R.J. The True Meshing Ratio of Skin Graft Meshers. J. Burn. Care Res. 2014, 35, 257–260. [Google Scholar] [CrossRef]
- Gupta, V.; Singh, G.; Chanda, A. Development of Novel Hierarchical Designs for Skin Graft Simulants with High Expansion Potential. Biomed. Phys. Eng. Express 2023, 9, 035024. [Google Scholar] [CrossRef] [PubMed]
- Gupta, V.; Singh, G.; Chanda, A. Development and Testing of Skin Grafts Models with Varying Slit Orientations. Mater. Today: Proc. 2022, 62, 3462–3467. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, V.; Chanda, A. Biomechanical Modeling of Novel High Expansion Auxetic Skin Grafts. Int. J. Numer. Methods Biomed. Eng. 2022, 38, e3586. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Chanda, A. Mechanical Properties of Whole-Body Soft Human Tissues: A Review. Biomed. Mater. 2021, 16, 062004. [Google Scholar] [CrossRef]
- Hendriks, F.M.; Brokken, D.; Oomens, C.W.J.; Bader, D.L.; Baaijens, F.P.T. The Relative Contributions of Different Skin Layers to the Mechanical Behavior of Human Skin in Vivo Using Suction Experiments. Med. Eng. Phys. 2006, 28, 259–266. [Google Scholar] [CrossRef]
- Tortora, G.J.; Derrickson, B.H. Principles of Anatomy and Physiology, 15th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017; ISBN 9781119444459. [Google Scholar]
- Wilkes, G.L.; Brown, I.A.; Wildnauer, R.H. The Biomechanical Properties of Skin. CRC Crit. Rev. Bioeng. 1973, 1, 453–495. [Google Scholar]
- Flynn, C.O.; McCormack, B.A.O. A Three-Layer Model of Skin and Its Application in Simulating Wrinkling. Comput. Methods Biomech. Biomed. Eng. 2009, 12, 125–134. [Google Scholar] [CrossRef]
- Lanir, Y.; Fung, Y.C. Two-Dimensional Mechanical Properties of Rabbit Skin—II. Experimental Results. J. Biomech. 1974, 7, 171–182. [Google Scholar] [CrossRef]
- Brown, I.A. A Scanning Electron Microscope Study of the Effects of Uniaxial Tension on Human Skin. Br. J. Dermatol. 1973, 89, 383–393. [Google Scholar] [CrossRef]
- Gupta, V.; Chanda, A. Biomechanics of Skin Grafts: Effect of Pattern Size, Spacing and Orientation. Eng. Res. Express 2022, 4, 015006. [Google Scholar] [CrossRef]
- Chanda, A.; Gupta, V.; Gupta, S. Research on the Application of Auxetics in Skin Grafts; Springer: Singapore, 2024; pp. 37–59. [Google Scholar] [CrossRef]
- Gupta, V.; Gupta, S.; Chanda, A. Expansion Potential of Skin Grafts with Novel Rotating-Triangle-Shaped Auxetic Incisions. Emerg. Mater. Res. 2022, 11, 406–414. [Google Scholar] [CrossRef]
- Gupta, V.; Chanda, A. Expansion Potential of Skin Grafts with Alternating Slit Based Auxetic Incisions. Forces Mech. 2022, 7, 100092. [Google Scholar] [CrossRef]
- Gupta, V.; Chanda, A. Auxetic Incisions with Alternating Slit Shapes: A Promising Technique for Enhancing Synthetic Skin Grafts Expansion. Mater. Res. Express 2023, 10, 075802. [Google Scholar] [CrossRef]
- Gupta, V.; Singh, G.; Chanda, A. Modeling of Metamaterial Based Incision Patterns for Generating High Expansions in Skin Grafts. Clin. Biomech. 2023, 110, 106118. [Google Scholar] [CrossRef]
- Gupta, V.; Chanda, A. Expansion Potential of Skin Grafts with Novel I-Shaped Auxetic Incisions. Biomed. Phys. Eng. Express 2022, 8, 015016. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Gupta, V.; Chanda, A. Mechanical Characterization of Rotating Triangle Shaped Auxetic Skin Graft Simulants. Facta Univ. Ser. Mech. Eng. 2022, 23, 079–094. [Google Scholar] [CrossRef]
- Gupta, V.; Singh, G.; Chanda, A. High Expansion Auxetic Skin Graft Simulants for Severe Burn Injury Mitigation. Eur. Burn. J. 2023, 4, 108–120. [Google Scholar] [CrossRef] [PubMed]
- Gupta, V.; Singh, G.; Chanda, A. Development of Hierarchical Auxetic Skin Graft Simulants with High Expansion Potential. Biomed. Eng. Adv. 2023, 5, 100087. [Google Scholar] [CrossRef]
- Gupta, V.; Singla, R.; Chanda, A. Development and Characterization of Novel Anisotropic Skin Graft Simulants. Dermato 2023, 3, 114–130. [Google Scholar] [CrossRef]
- Gupta, V.; Chanda, A. Finite Element Analysis of Hierarchical Metamaterial-Based Patterns for Generating High Expansion in Skin Grafting. Math. Comput. Appl. 2023, 28, 89. [Google Scholar] [CrossRef]
- Capek, L.; Flynn, C.; Molitor, M.; Chong, S.; Henys, P. Graft Orientation Influences Meshing Ratio. Burns 2018, 44, 1439–1445. [Google Scholar] [CrossRef] [PubMed]
- Humbert, P.; Fanian, F.; Maibach, H.I.; Agache, P. Agache’s Measuring the Skin Non-Invasive Investigations, Physiology, Normal Constants, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Ní Annaidh, A.; Bruyère, K.; Destrade, M.; Gilchrist, M.D.; Maurini, C.; Otténio, M.; Saccomandi, G. Automated Estimation of Collagen Fibre Dispersion in the Dermis and Its Contribution to the Anisotropic Behaviour of Skin. Ann. Biomed. Eng. 2012, 40, 1666–1678. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic Modelling of Arterial Layers with Distributed Collagen Fibre Orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef]
- Bellini, C.; Glass, P.; Sitti, M.; Di Martino, E.S. Biaxial Mechanical Modeling of the Small Intestine. J. Mech. Behav. Biomed. Mater. 2011, 4, 1727–1740. [Google Scholar] [CrossRef]
- Shergold, O.A.; Fleck, N.A.; Radford, D. The Uniaxial Stress versus Strain Response of Pig Skin and Silicone Rubber at Low and High Strain Rates. Int. J. Impact Eng. 2006, 32, 1384–1402. [Google Scholar] [CrossRef]
- Aldieri, A.; Terzini, M.; Bignardi, C.; Zanetti, E.M.; Audenino, A.L. Implementation and Validation of Constitutive Relations for Human Dermis Mechanical Response. Med. Biol. Eng. Comput. 2018, 56, 2083–2093. [Google Scholar] [CrossRef] [PubMed]
- Moerman, K.M. GIBBON: The Geometry and Image-Based Bioengineering Add-On. J. Open Source Softw. 2018, 3, 506. [Google Scholar] [CrossRef]
- Nolan, D.R.; Gower, A.L.; Destrade, M.; Ogden, R.W.; McGarry, J.P. A Robust Anisotropic Hyperelastic Formulation for the Modelling of Soft Tissue. J. Mech. Behav. Biomed. Mater. 2014, 39, 48–60. [Google Scholar] [CrossRef]
- Gavin, H. The Levenberg-Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems. Dep. Civ. Environ. Eng. Duke Univ. August 2019, 3, 1–23. [Google Scholar]
- Taylor, B.C.; Triplet, J.J.; Wells, M. Split-Thickness Skin Grafting: A Primer for Orthopaedic Surgeons. J. Am. Acad. Orthop. Surg. 2021, 29, 855–861. [Google Scholar] [CrossRef]
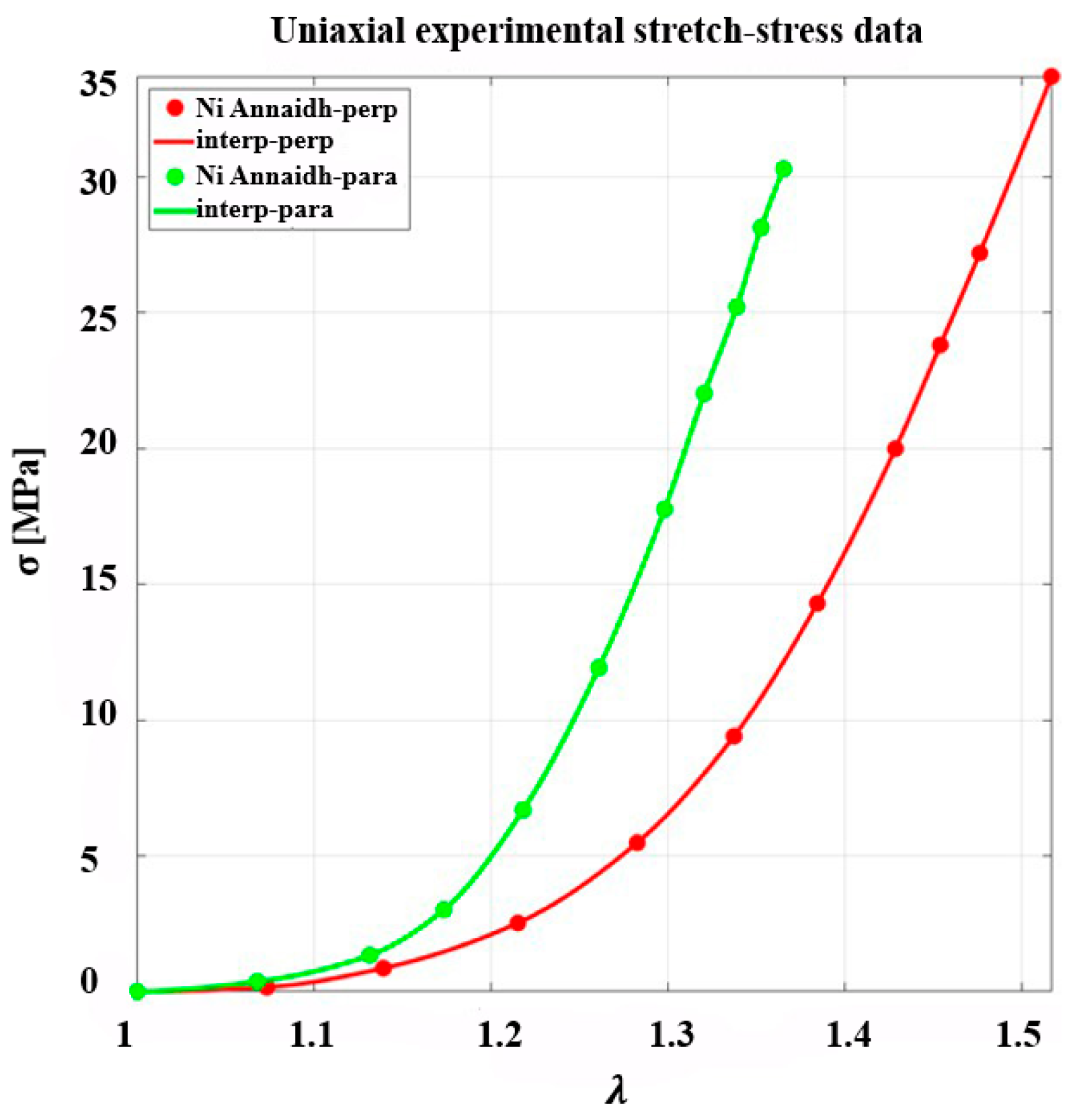



| Constitutive Model | ||||||
|---|---|---|---|---|---|---|
| Parallel and Perpendicular | 1.30259 | 124.351 | 0.00013 | 41° | 0.2985 | 1302.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razaghi Pey Ghaleh, M.; O’Mahoney, D. The Impact of Collagen Fiber and Slit Orientations on Meshing Ratios in Skin Meshing Models. Biomimetics 2025, 10, 771. https://doi.org/10.3390/biomimetics10110771
Razaghi Pey Ghaleh M, O’Mahoney D. The Impact of Collagen Fiber and Slit Orientations on Meshing Ratios in Skin Meshing Models. Biomimetics. 2025; 10(11):771. https://doi.org/10.3390/biomimetics10110771
Chicago/Turabian StyleRazaghi Pey Ghaleh, Masoumeh, and Denis O’Mahoney. 2025. "The Impact of Collagen Fiber and Slit Orientations on Meshing Ratios in Skin Meshing Models" Biomimetics 10, no. 11: 771. https://doi.org/10.3390/biomimetics10110771
APA StyleRazaghi Pey Ghaleh, M., & O’Mahoney, D. (2025). The Impact of Collagen Fiber and Slit Orientations on Meshing Ratios in Skin Meshing Models. Biomimetics, 10(11), 771. https://doi.org/10.3390/biomimetics10110771







