Compressive Behavior of 316L Stainless Steel Lattice Structures for Additive Manufacturing: Experimental Characterization and Numerical Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Design and Fabrication by Laser Powder Bed Fusion
2.2. Experimental Characterization of Mechanical Properties
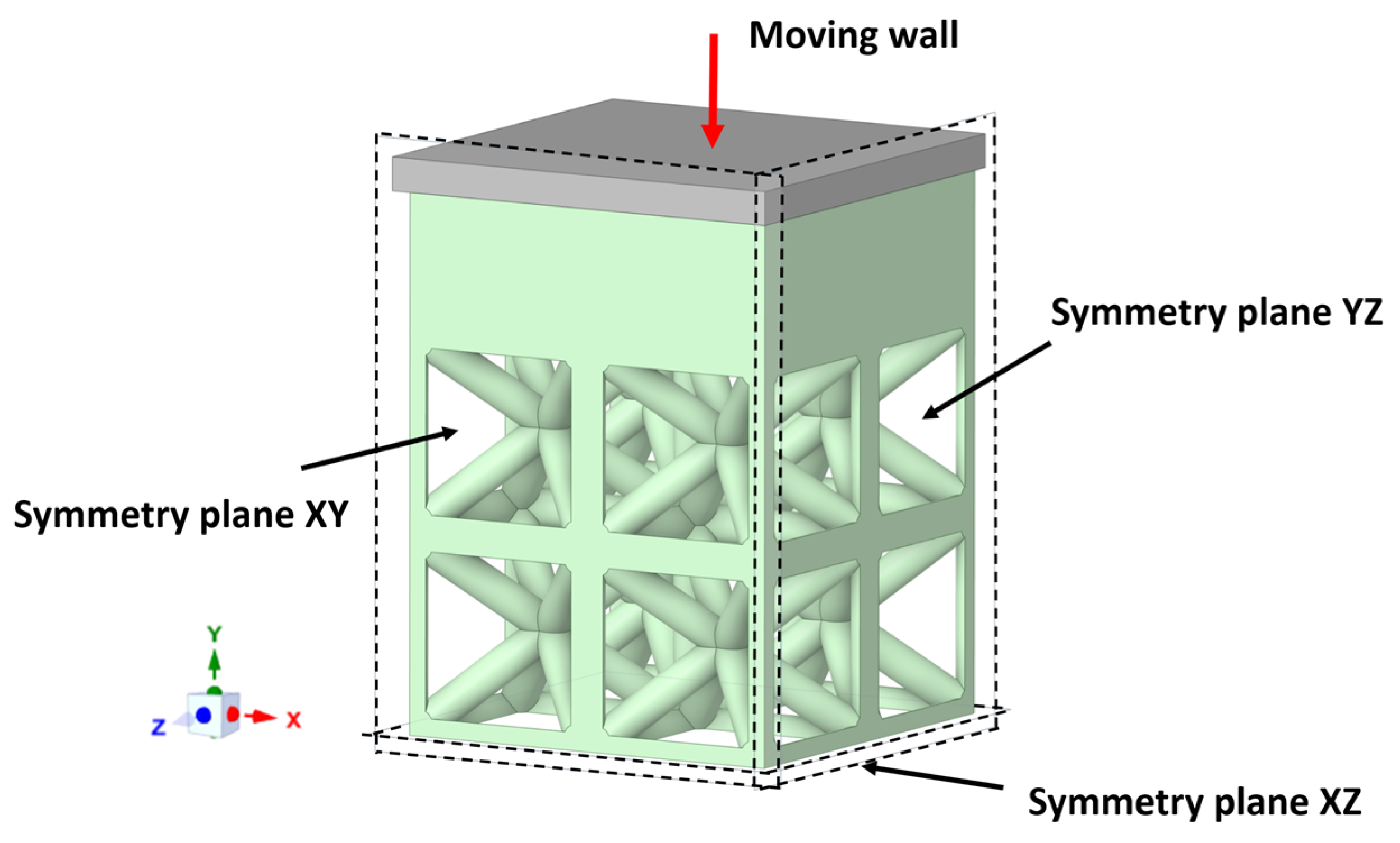
2.3. Finite Element Modeling
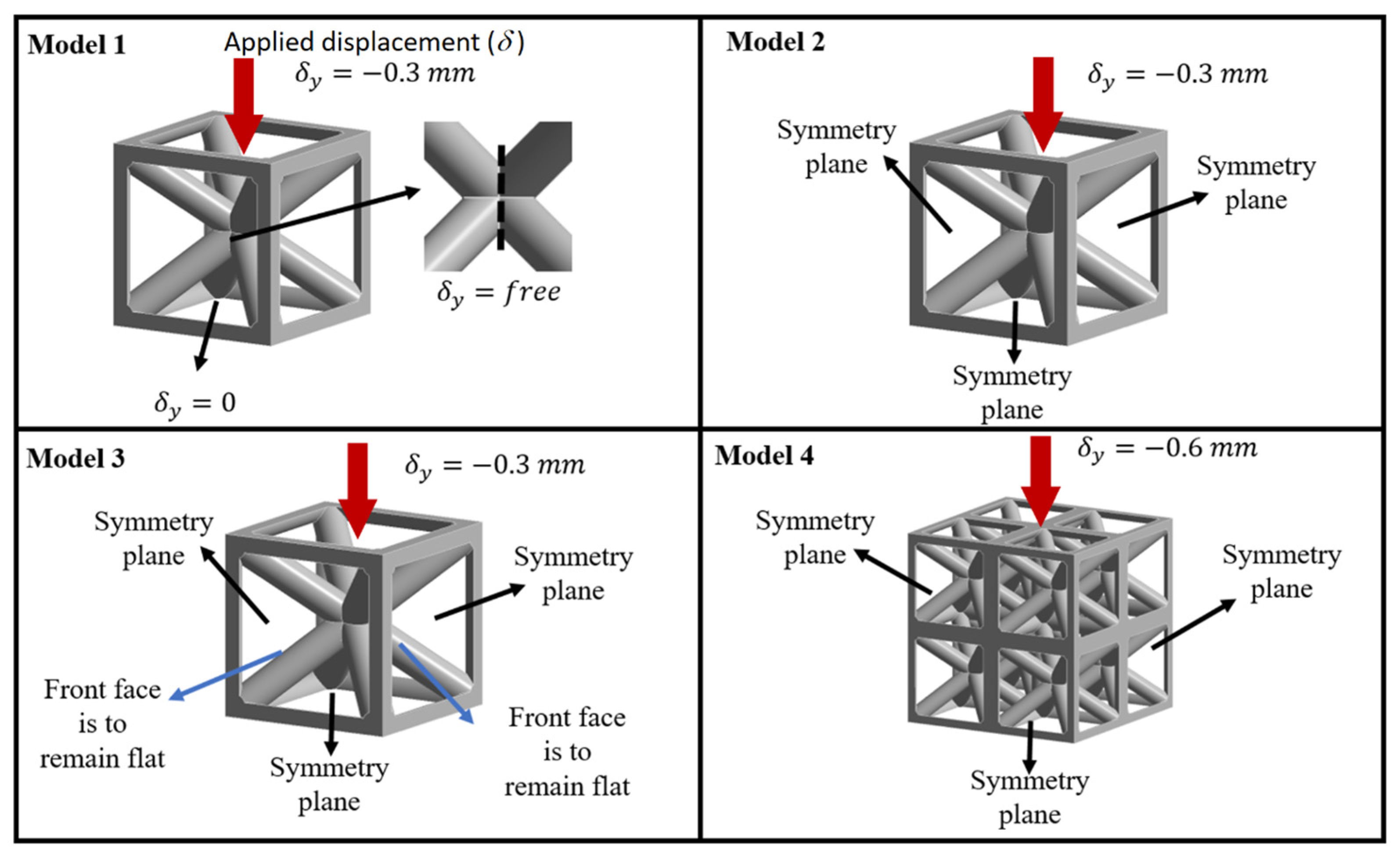
2.4. Modeling Boundary Conditions and Size Effect
- Model 1: Single cell with fixed base and free lateral faces.
- Model 2: Single cell with three symmetry planes (equivalent to eight cells).
- Model 3: Single cell with symmetry planes and coplanarity constraints (buckling suppressed).
- Model 4: 2 × 2 × 2 multi-cell model with symmetry planes (equivalent to 64 cells). All models were compressed to 10% strain under displacement control.
3. Results
3.1. Experimental Characterization and Analytical Modeling
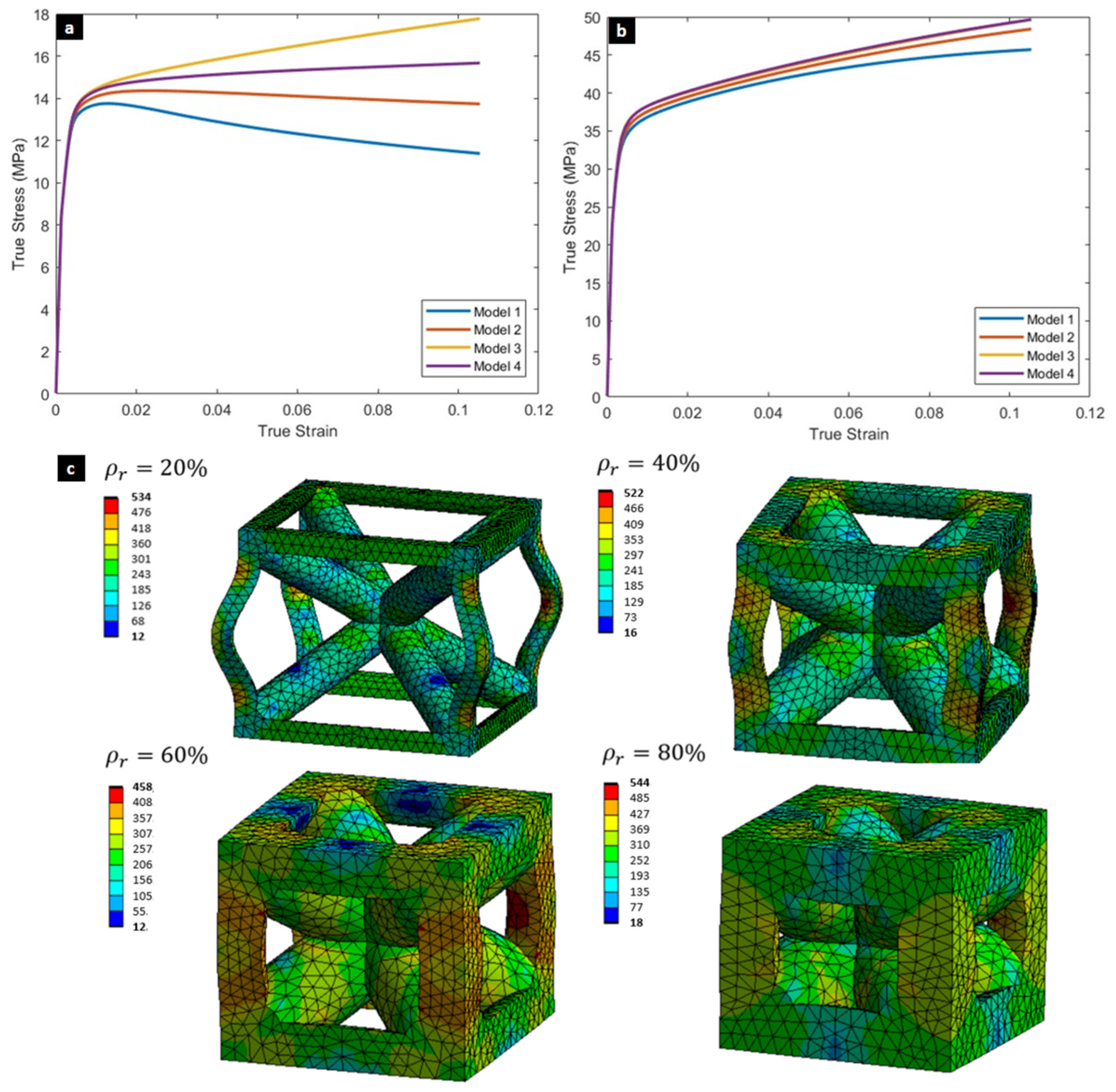
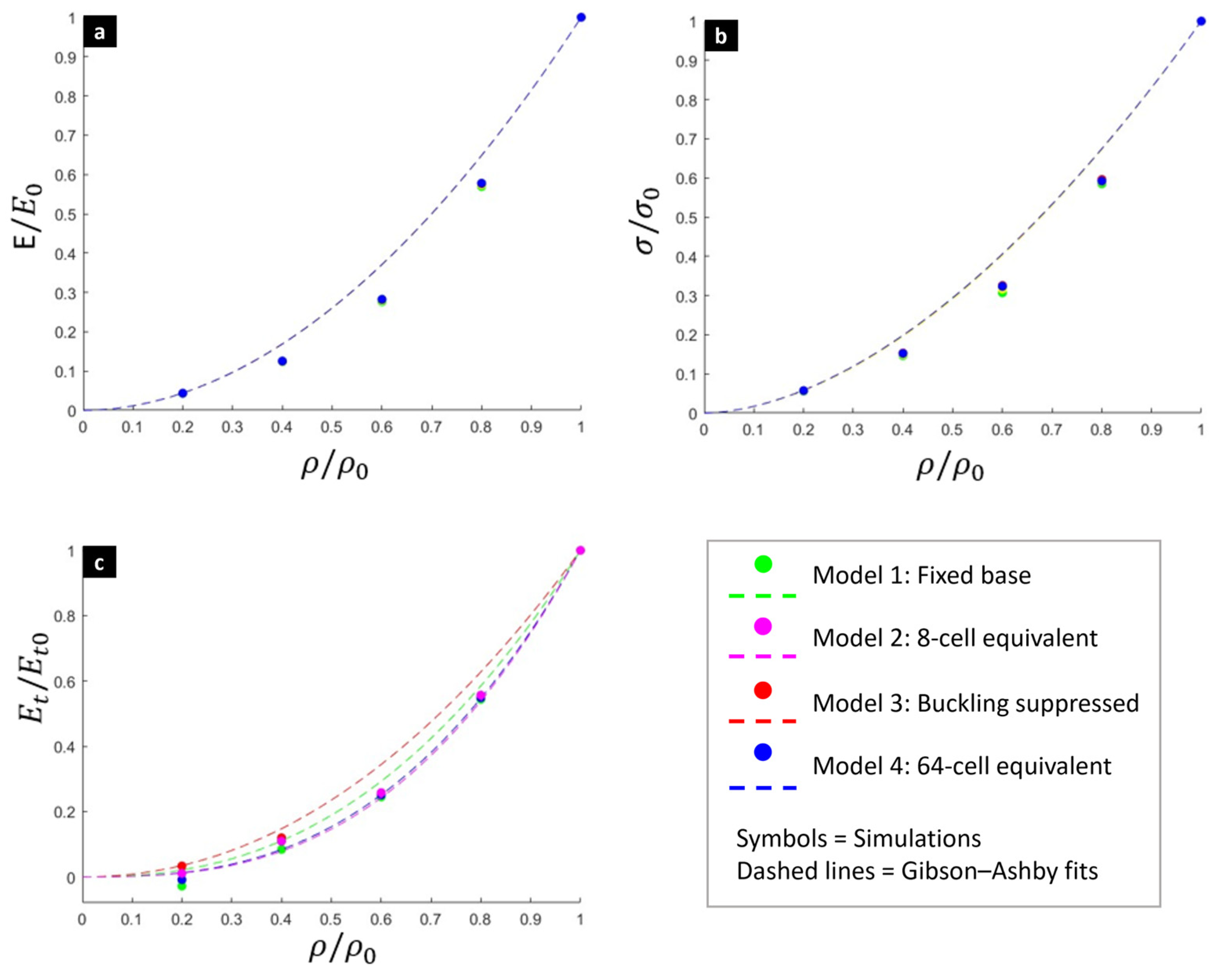
3.2. Numerical Simulation and Size Effect Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tuninetti, V.; Narayan, S.; Ríos, I.; Menacer, B.; Valle, R.; Al-lehaibi, M.; Kaisan, M.U.; Samuel, J.; Oñate, A.; Pincheira, G.; et al. Biomimetic Lattice Structures Design and Manufacturing for High Stress, Deformation, and Energy Absorption Performance. Biomimetics 2025, 10, 458. [Google Scholar] [CrossRef]
- Narayan, S.; Menacer, B.; Kaisan, M.U.; Samuel, J.; Al-Lehaibi, M.; Mahroogi, F.O.; Tuninetti, V. Global Research Trends in Biomimetic Lattice Structures for Energy Absorption and Deformation: A Bibliometric Analysis (2020–2025). Biomimetics 2025, 10, 477. [Google Scholar] [CrossRef]
- Castro, J.; Valle, R.; Leiva, J.; Oñate, A.; Saggionetto, E.; Mertens, A.; Tuninetti, V. Density-Based Topology-Optimized 3D-Printed Fixtures for Cyclic Mechanical Testing of Lattice Structures. Polymers 2025, 17, 2468. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V. Design of an auxetic cellular structure with different elastic properties in its three orthogonal directions. Proc. Inst. Mech. Eng. Part L 2021, 235, 1341–1350. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V.; Fernandez, E.; Uribe-Lam, E. Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response. Materials 2022, 15, 1841. [Google Scholar] [CrossRef]
- Olivas-Alanis, L.H.; Fraga-Martínez, A.A.; García-López, E.; Lopez-Botello, O.; Vazquez-Lepe, E.; Cuan-Urquizo, E.; Rodriguez, C.A. Mechanical Properties of AISI 316L Lattice Structures via Laser Powder Bed Fusion as a Function of Unit Cell Features. Materials 2023, 16, 1025. [Google Scholar] [CrossRef]
- Lin, Y.; Shi, W.; Sun, X.; Liu, S.; Li, J.; Zhou, Y.; Han, Y. Influence of Density Gradient on the Compression of Functionally Graded BCC Lattice Structure. Materials 2023, 16, 520. [Google Scholar] [CrossRef]
- Park, K.-M.; Roh, Y.-S. Design Optimization of Additive Manufactured Edgeless Simple Cubic Lattice Structures under Compression. Materials 2023, 16, 2870. [Google Scholar] [CrossRef]
- Gibson, L.J. Biomechanics of cellular solids. J. Biomech. 2005, 38, 377–399. [Google Scholar] [CrossRef]
- Ashby, M.F. The mechanical properties of cellular solids. Metall. Trans. A 1983, 14, 1755–1769. [Google Scholar] [CrossRef]
- Rahimi, S.; Asghari, M. Design and evaluation of two proposed hybrid FCC-BCC lattice structures for enhanced mechanical performance. Heliyon 2025, 11, e40911. [Google Scholar] [CrossRef]
- Guo, S.; Ma, Y.; Liu, P.; Chen, Y. Mechanical Properties of Lattice Structures with a Central Cube: Experiments and Simulations. Materials 2024, 17, 1329. [Google Scholar] [CrossRef]
- Cheng, H.; Zhu, X.; Cheng, X.; Cai, P.; Liu, J.; Yao, H.; Zhang, L.; Duan, J. Mechanical Metamaterials Made of Freestanding Quasi-BCC Nanolattices of Gold and Copper with Ultra-High Energy Absorption Capacity. Nat. Commun. 2023, 14, 1243. [Google Scholar] [CrossRef]
- Ali, H.M.A.; Abdi, M. Multi-Objective Parametric Shape Optimisation of Body-Centred Cubic Lattice Structures for Additive Manufacturing. J. Manuf. Mater. Process. 2023, 7, 156. [Google Scholar] [CrossRef]
- Lee, H.-S. Mechanical Properties of Bicrystal-Inspired Lattice Structures Fabricated by Additive Manufacturing. Crystals 2025, 15, 757. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef]
- D’Andrea, D. Additive Manufacturing of AISI 316L Stainless Steel: A Review. Metals 2023, 13, 1370. [Google Scholar] [CrossRef]
- Cheng, H.; Zhu, X.; Hao, L.; Hussein, A.; Raymont, D. Evaluations of Lattice Structures Manufactured Using Selective Laser Melting. Int. J. Mach. Tools Manuf. 2012, 62, 32–38. [Google Scholar] [CrossRef]
- Krakhmalev, P.; Yadroitsava, I.; Fredriksson, G.; Yadroitsev, I. In situ strength of 316L stainless steel micro-lattice structures manufactured by selective laser melting. Mater. Des. 2016, 106, 163–170. [Google Scholar] [CrossRef]
- Bakhtiarian, M.; Vafaei, M.; Mashhuriazar, A.; Omidvar, H. Impact of Build Direction on Microstructure and High-Temperature Mechanical Properties of SLM-Fabricated 316L Stainless Steel. Weld. World 2025, 69, 1501–1514. [Google Scholar] [CrossRef]
- Mines, R.A.W.; Tsopanos, S.; Shen, Y.; Cantwell, W.J.; Brooks, W.K.; Sutcliffe, C.J.; Smith, M. Drop weight impact behaviour of sandwich panels with metallic micro lattice cores. Int. J. Impact Eng. 2013, 60, 120–132. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.J.M. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Medina, F.; Lopez, H.; Martinez, E.; Machado, B.I.; Hernandez, D.H.; Martinez, J.L.; Lopez, M.I.; Wicker, R.B. Next-generation biomedical implants using additive manufacturing of complex cellular and functional mesh arrays. Philos. Trans. R. Soc. A 2010, 368, 1999–2032. [Google Scholar] [CrossRef]
- Ushijima, K.; Cantwell, W.J.; Mines, R.A.W.; Tsopanos, S.; Smith, M. An investigation into the compressive properties of stainless steel micro-lattice structures. J. Sandw. Struct. Mater. 2011, 13, 303–329. [Google Scholar] [CrossRef]
- Han, Q.; Gu, H.; Soe, S.; Setchi, R.; Lacan, F.; Hill, J. Manufacturability of AlSi10Mg Overhang Structures Fabricated by Laser Powder Bed Fusion. Mater. Des. 2018, 160, 1080–1095. [Google Scholar] [CrossRef]
- du Plessis, A.; Yadroitsava, I.; Yadroitsev, I. Effects of defects on mechanical properties in metal additive manufacturing: A review focusing on X-ray tomography insights. Mater. Des. 2020, 187, 108385. [Google Scholar] [CrossRef]
- Efremenko, B.; Chabak, Y.; Petryshynets, I.; Efremenko, V.; Wu, K.; Arshad, S.; Kromka, F. Microstructure Evolution, Tensile/Nanoindentation Response, and Work-Hardening Behaviour of Prestrained and Subsequently Annealed LPBF 316L Stainless Steel. Materials 2025, 18, 1102. [Google Scholar] [CrossRef]
- Lim, Y.; Jeon, C.; Lee, Y.-S.; Jo, I. Exploring the Microstructure Evolution, Mechanical and Wear Properties of LPBF-Processed 316L Stainless Steel. Metals 2025, 15, 971. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, P.; Yang, G.; Yan, Y. An Investigation of the Anisotropic Mechanical Properties of Additive-Manufactured 316L SS with SLM. Materials 2024, 17, 2017. [Google Scholar] [CrossRef]
- Barrionuevo, G.O.; Walczak, M.; Mendez, P.; La Fé-Perdomo, I.; Chiluisa-Palomo, E.; Navas-Pinto, W.; Cree, D.E. Effect of Porosity on Tribological Properties of Medical-Grade 316L Stainless Steel Manufactured by Laser-Based Powder Bed Fusion. Materials 2025, 18, 568. [Google Scholar] [CrossRef]
- Cegan, T.; Pagac, M.; Jurica, J.; Skotnicova, K.; Hajnys, J.; Horsak, L.; Soucek, K.; Krpec, P. Effect of Hot Isostatic Pressing on Porosity and Mechanical Properties of 316L Stainless Steel Prepared by the Selective Laser Melting Method. Materials 2020, 13, 4377. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, D.; Zhao, R.; Wang, X.; Wang, L.; Zhang, L.-C. High Mechanical Performance of Lattice Structures Fabricated by Additive Manufacturing. Metals 2024, 14, 1165. [Google Scholar] [CrossRef]
- Spierings, A.B.; Voegtlin, M.; Bauer, T.; Wegener, K. Powder flowability characterisation methodology for powder-bed-based metal additive manufacturing. Prog. Addit. Manuf. 2016, 1, 9–20. [Google Scholar] [CrossRef]
- Vilaro, T.; Colin, C.; Bartout, J.D. As-fabricated and heat-treated microstructures of the Ti–6Al–4V alloy processed by selective laser melting. Metall. Mater. Trans. A 2011, 42, 3190–3199. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Gusarov, A.; Yadroitsava, I.; Smurov, I. Single track formation in selective laser melting of metal powders. J. Mater. Process. Technol. 2010, 210, 1624–1631. [Google Scholar] [CrossRef]
- Cho, J.; Lee, E.S.; Kim, J.H.; Lee, C.-Y.; Cho, J.Y. Design of Lattice-Based Energy-Absorbing Structure for Enhancing the Crashworthiness of Advanced Air Mobility. Aerospace 2025, 12, 332. [Google Scholar] [CrossRef]
- Andrews, E.W.; Gioux, G.; Onck, P.; Gibson, L.J. Size effects in ductile cellular solids. Part II: Experimental results. Int. J. Mech. Sci. 2001, 43, 701–713. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X.; Shang, Y. Mechanical Properties and Energy Absorption Characteristics of a Combined Gradient BCC Lattice Structure: A Numerical Study. Materials 2025, 18, 3652. [Google Scholar] [CrossRef]
- Choy, S.Y.; Sun, C.-N.; Leong, K.F.; Wei, J. Compressive Properties of Functionally Graded Lattice Structures Manufactured by Selective Laser Melting. Mater. Des. 2017, 131, 112–120. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Carter, W.B. Architected cellular materials. Annu. Rev. Mater. Res. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Al-Rub, R.K.A. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet-based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, X.; Sun, L.; Hu, Q.; Li, N. Optimisation of Selective Laser Melted Ti6Al4V Functionally Graded Lattice Structures Accounting for Structural Safety. Materials 2022, 15, 9072. [Google Scholar] [CrossRef]
- Shahriyari, E.; Khiavi, S.G.; Divandari, M.; Boutorabi, S.M.A. Effect of Unit Cell Topologies on Mechanical Properties of Cylindrical Lattice Structures Fabricated by Indirect Additive Manufacturing. J. Mater. Res. Technol. 2025, 36, 2785–2798. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Bone tissue regeneration: The role of scaffold geometry. Biomater. Sci. 2015, 3, 231–245. [Google Scholar] [CrossRef] [PubMed]
- Zadpoor, A.A. Mechanical performance of additively manufactured meta-biomaterials. Acta Biomater. 2019, 85, 41–59. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, L.; Zhou, J.; Hodgson, P.; Wen, C. Porous titanium structures produced by additive manufacturing with osseointegration property: Experimental and simulation study. J. Mech. Behav. Biomed. Mater. 2014, 40, 1–9. [Google Scholar] [CrossRef]
- Arabnejad, S.; Johnston, R.B.; Tanzer, M.; Pasini, D. Fully porous 3D printed titanium femoral stem to reduce stress-shielding following total hip arthroplasty. J. Biomech. 2017, 60, 229–236. [Google Scholar] [CrossRef]
- Bobbert, F.S.L.; Lietaert, K.; Eftekhari, A.A.; Pouran, B.; Ahmadi, S.M.; Weinans, H.; Zadpoor, A.A. Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater. 2017, 53, 572–584. [Google Scholar] [CrossRef]
- He, S.; Zhu, J.; Jing, Y.; Long, S.; Tang, L.; Cheng, L.; Shi, Z. Effect of 3D-Printed Porous Titanium Alloy Pore Structure on Bone Regeneration: A Review. Coatings 2024, 14, 253. [Google Scholar] [CrossRef]
- Ryan, G.; Pandit, A.; Apatsidis, D.P. Fabrication methods of porous metals for use in orthopaedic applications. Biomaterials 2006, 27, 2651–2670. [Google Scholar] [CrossRef]
- Li, J.P.; de Wijn, J.R.; van Blitterswijk, C.A.; de Groot, K. Porous Ti6Al4V scaffold directly fabricated by selective laser melting: Preparation and experimental comparison with in vitro cell seeding. Biomaterials 2006, 27, 1223–1235. [Google Scholar] [CrossRef]
- Yan, L.; Wu, J.; Zhang, L.; Liu, X.; Zhou, K.; Su, B. Pore Structures and Mechanical Properties of Porous Titanium Scaffolds by Bidirectional Freeze Casting. Mater. Sci. Eng. C 2017, 75, 335–340. [Google Scholar] [CrossRef]
- Tuninetti, V.; Fuentes, G.; Oñate, A.; Narayan, S.; Celentano, D.; García-Herrera, C.; Menacer, B.; Pincheira, G.; Garrido, C.; Valle, R. Computational Shape Design Optimization of Femoral Implants: Towards Efficient Forging Manufacturing. Appl. Sci. 2024, 14, 8289. [Google Scholar] [CrossRef]
- Carraturo, M.; Alaimo, G.; Marconi, S.; Negrello, E.; Sgambitterra, E.; Maletta, C.; Reali, A.; Auricchio, F. Experimental and Numerical Evaluation of Mechanical Properties of 3D-Printed Stainless Steel 316L Lattice Structures. J. Mater. Eng. Perform. 2021, 30, 5247. [Google Scholar] [CrossRef]
- Nogueira, P.; Lopes, P.; Oliveira, L.; Alves, J.L.; Magrinho, J.P.G.; Deus, A.M.d.; Vaz, M.F.; Silva, M.B. Evaluation of Lattice Structures for Medical Implants: A Study on the Mechanical Properties of Various Unit Cell Types. Metals 2024, 14, 780. [Google Scholar] [CrossRef]
- Alomar, Z.; Concli, F. Numerical modeling of selective laser melting lattice structures: A review of approaches. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1038, 012002. [Google Scholar] [CrossRef]
- Benedetti, M.; du Plessis, A.; Raghavendra, R.; Dallago, M.; Razavi, S.M.J.; Berto, F. Architected cellular materials: A review on mechanical properties, applications and design methods. Adv. Eng. Mater. 2021, 23, 2001212. [Google Scholar]
- Iqbal, S.; Kamiński, M. Review Study on Mechanical Properties of Cellular Materials. Materials 2024, 17, 2682. [Google Scholar] [CrossRef]
- Maskery, I.; Sturm, L.; Aremu, A.O.; Panesar, A.; Williams, C.B.; Tuck, C.J.; Wildman, R.D.; Ashcroft, I.A.; Hague, R.J.M. Insights into the Mechanical Properties of Several Triply Periodic Minimal Surface Lattice Structures Made by Polymer Additive Manufacturing. Polymer 2018, 152, 62–71. [Google Scholar] [CrossRef]
- Isaenkova, M.G.; Yudin, A.V.; Rubanov, A.E.; Osintsev, A.V.; Degadnikova, L.A. Deformation behavior modelling of lattice structures manufactured by a selective laser melting of 316L steel powder. J. Mater. Res. Technol. 2020, 9, 15177–15184. [Google Scholar] [CrossRef]
- Aiza, I.; Baldi, C.; de la Vega, F.M.; Sebastiani, S.; Veronese, N.E.; Yousefi, M.; Mosallanejad, M.H.; Maleki, E.; Guagliano, M.; Iuliano, L.; et al. Effects of build orientation and inclined features on physical, microstructural and mechanical properties of powder bed fusion additively manufactured metallic parts. Prog. Mater. Sci. 2025, 147, 101357. [Google Scholar] [CrossRef]
- Papazoglou, D.P.; Neidhard-Doll, A.T.; Pinnell, M.F.; Erdahl, D.S.; Osborn, T.H. Compression and Tensile Testing of L-PBF Ti-6Al-4V Lattice Structures with Biomimetic Porosities and Strut Geometries for Orthopedic Implants. Metals 2024, 14, 232. [Google Scholar] [CrossRef]
- Tuninetti, V.; Flores, P.; Valenzuela, M.; Pincheira, G.; Medina, C.; Duchêne, L.; Habraken, A.-M. Experimental Characterization of the Compressive Mechanical Behaviour of Ti6Al4V Alloy at Constant Strain Rates over the Full Elastoplastic Range. Int. J. Mater. Form. 2020, 13, 709–724. [Google Scholar] [CrossRef]
- Tuninetti, V.; Gómez, Á.; Bustos, F.; Oñate, A.; Hinojosa, J.; Gallo, C.; Habraken, A.-M.; Duchêne, L. Computational Modeling of U-Shaped Seismic Dampers for Structural Damage Mitigation. Appl. Sci. 2024, 14, 10238. [Google Scholar] [CrossRef]
- Condruz, M.R.; Badea, T.A.; Paraschiv, A. Compressive Behavior of Inconel 625 and Ti-6Al-4V Strut Lattices Fabricated by LPBF. Appl. Sci. 2024, 14, 11909. [Google Scholar] [CrossRef]
- Aljaberi, M.H.K.; Aghdam, M.M.; Goudarzi, T.; Al-Waily, M. Compressive Behavior of Novel Additively Manufactured Ti-6Al-4V Lattice Structures: Experimental and Numerical Studies. Materials 2024, 17, 3691. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Yang, W.; Duan, S.; Yang, W.; Lin, Y. Theoretical investigation on crash performance of bamboo-inspired energy absorption systems based on systematic experimental and numerical analysis. Eng. Struct. 2025, 322 Pt B, 119154. [Google Scholar] [CrossRef]
- Yang, W.; Peng, B.; Yang, K. Multi-objective optimization of diaphragm reinforced bamboo-inspired energy absorption systems. Compos. Struct. 2025, 356, 118865. [Google Scholar] [CrossRef]
- Distefano, F.; Pasta, S.; Epasto, G. Titanium Lattice Structures Produced via Additive Manufacturing for a Bone Scaffold: A Review. J. Funct. Biomater. 2023, 14, 125. [Google Scholar] [CrossRef]
- Jardin, R.T.; Tuninetti, V.; Tchuindjang, J.T.; Mertens, A.; Habraken, A.M. Sensitivity Analysis in the Modeling of a High Speed Steel Thin Wall Produced by Directed Energy Deposition. Metals 2020, 10, 1554. [Google Scholar] [CrossRef]
- Jardin, R.T.; Tuninetti, V.; Tchuindjang, J.T.; Mertens, A.; Duchêne, L.; Habraken, A.M. Optimizing Laser Power of Directed Energy Deposition Process for Homogeneous AISI M4 Steel Microstructure. Opt. Laser Technol. 2023, 163, 109426. [Google Scholar] [CrossRef]


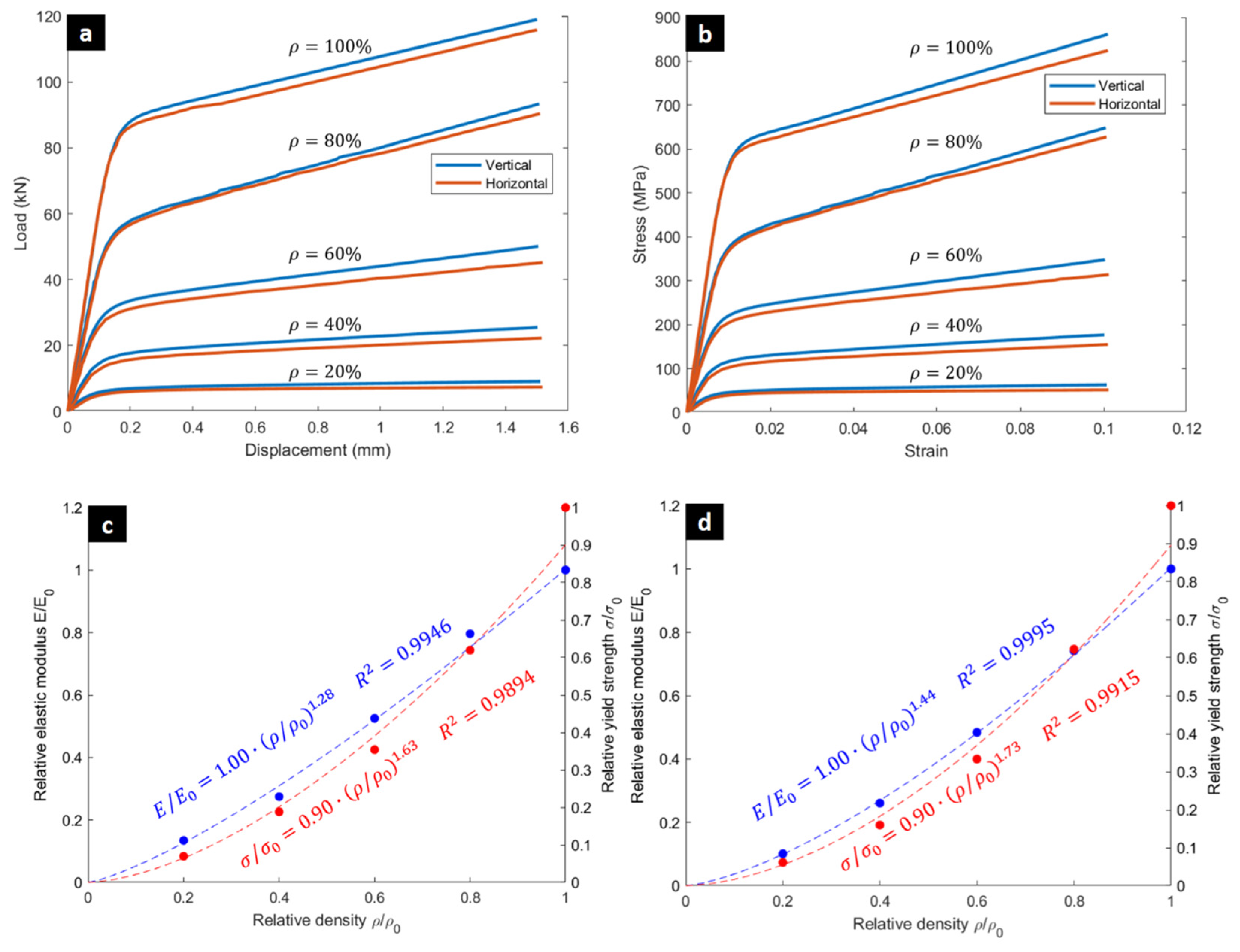
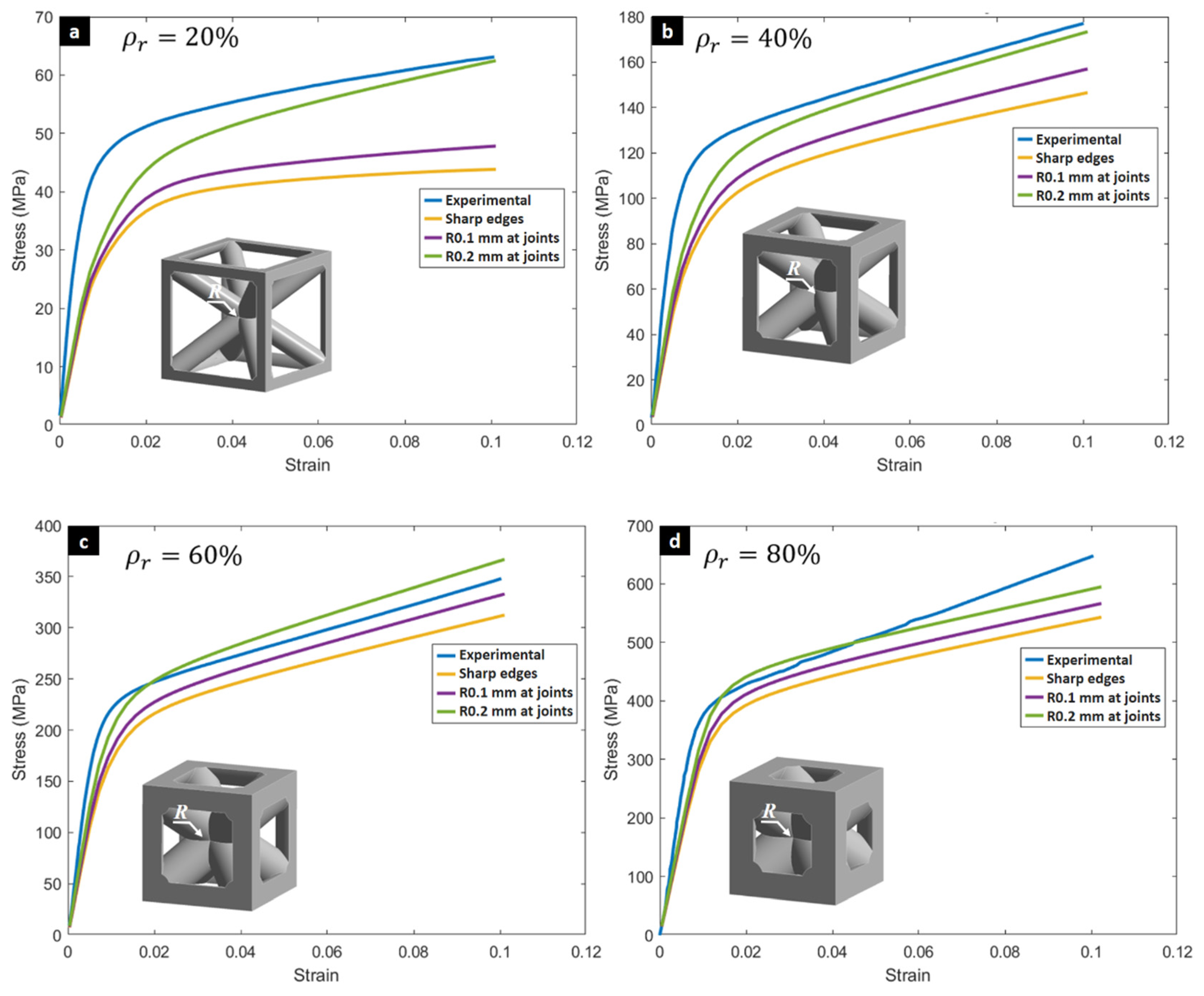

| Specimen | Elastic Modulus (GPa) | Yield Strength (MPa) | Tangent Modulus (GPa) | Total Energy Absorption, (J) | Specific Energy Absorption, (J/g) | Mean Force, (kN) |
|---|---|---|---|---|---|---|
| BCC-V-20 | 8.803 | 40.36 | 0.122 | 11.84 | 1.607 | 7.894 |
| BCC-V-40 | 17.96 | 109.1 | 0.545 | 31.13 | 3.103 | 20.75 |
| BCC-V-60 | 34.41 | 205.1 | 1.123 | 59.84 | 4.738 | 39.89 |
| BCC-V-80 | 52.12 | 358.8 | 2.711 | 107.2 | 6.701 | 71.47 |
| BCC-V-100 | 65.49 | 579.3 | 2.775 | 146.5 | 8.509 | 97.68 |
| BCC-H-20 | 6.44 | 35.7 | 0.059 | 10.02 | 1.209 | 6.68 |
| BCC-H-40 | 16.66 | 93.3 | 0.435 | 27.70 | 2.536 | 18.46 |
| BCC-H-60 | 30.95 | 194.7 | 0.941 | 55.48 | 4.125 | 37.00 |
| BCC-H-80 | 47.40 | 363.7 | 2.431 | 105.0 | 6.210 | 70.00 |
| BCC-H-100 | 63.94 | 584.5 | 2.488 | 142.7 | 7.842 | 95.16 |
| Relative Density | Boundary Condition | Elastic Modulus (GPa) | Yield Strength (MPa) |
|---|---|---|---|
| Model 1 | 6.433 | 12.6 | |
| 20% | Model 2 | 6.487 | 12.8 |
| Model 3 | 6.546 | 13 | |
| Model 4 | 6.526 | 13 | |
| Model 1 | 18.56 | 33.2 | |
| 40% | Model 2 | 18.68 | 33.9 |
| Model 3 | 18.79 | 34.7 | |
| Model 4 | 18.80 | 34.5 | |
| Model 1 | 41.71 | 69.6 | |
| 60% | Model 2 | 42.02 | 71.7 |
| Model 3 | 42.31 | 73.8 | |
| Model 4 | 42.36 | 73.3 | |
| Model 1 | 85.60 | 132.6 | |
| 80% | Model 2 | 86.06 | 133.9 |
| Model 3 | 86.55 | 135.1 | |
| Model 4 | 86.67 | 134.2 | |
| 100% | (Bulk material) | 14.94 | 226.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ríos, I.; Duchêne, L.; Habraken, A.M.; Oñate, A.; Valle, R.; Mertens, A.; Garrido, C.; Pincheira, G.; Tuninetti, V. Compressive Behavior of 316L Stainless Steel Lattice Structures for Additive Manufacturing: Experimental Characterization and Numerical Modeling. Biomimetics 2025, 10, 680. https://doi.org/10.3390/biomimetics10100680
Ríos I, Duchêne L, Habraken AM, Oñate A, Valle R, Mertens A, Garrido C, Pincheira G, Tuninetti V. Compressive Behavior of 316L Stainless Steel Lattice Structures for Additive Manufacturing: Experimental Characterization and Numerical Modeling. Biomimetics. 2025; 10(10):680. https://doi.org/10.3390/biomimetics10100680
Chicago/Turabian StyleRíos, Ignacio, Laurent Duchêne, Anne Marie Habraken, Angelo Oñate, Rodrigo Valle, Anne Mertens, César Garrido, Gonzalo Pincheira, and Víctor Tuninetti. 2025. "Compressive Behavior of 316L Stainless Steel Lattice Structures for Additive Manufacturing: Experimental Characterization and Numerical Modeling" Biomimetics 10, no. 10: 680. https://doi.org/10.3390/biomimetics10100680
APA StyleRíos, I., Duchêne, L., Habraken, A. M., Oñate, A., Valle, R., Mertens, A., Garrido, C., Pincheira, G., & Tuninetti, V. (2025). Compressive Behavior of 316L Stainless Steel Lattice Structures for Additive Manufacturing: Experimental Characterization and Numerical Modeling. Biomimetics, 10(10), 680. https://doi.org/10.3390/biomimetics10100680







