Safety Issues in the Seismic Design of Secondary Frameless Glass Structures
Abstract
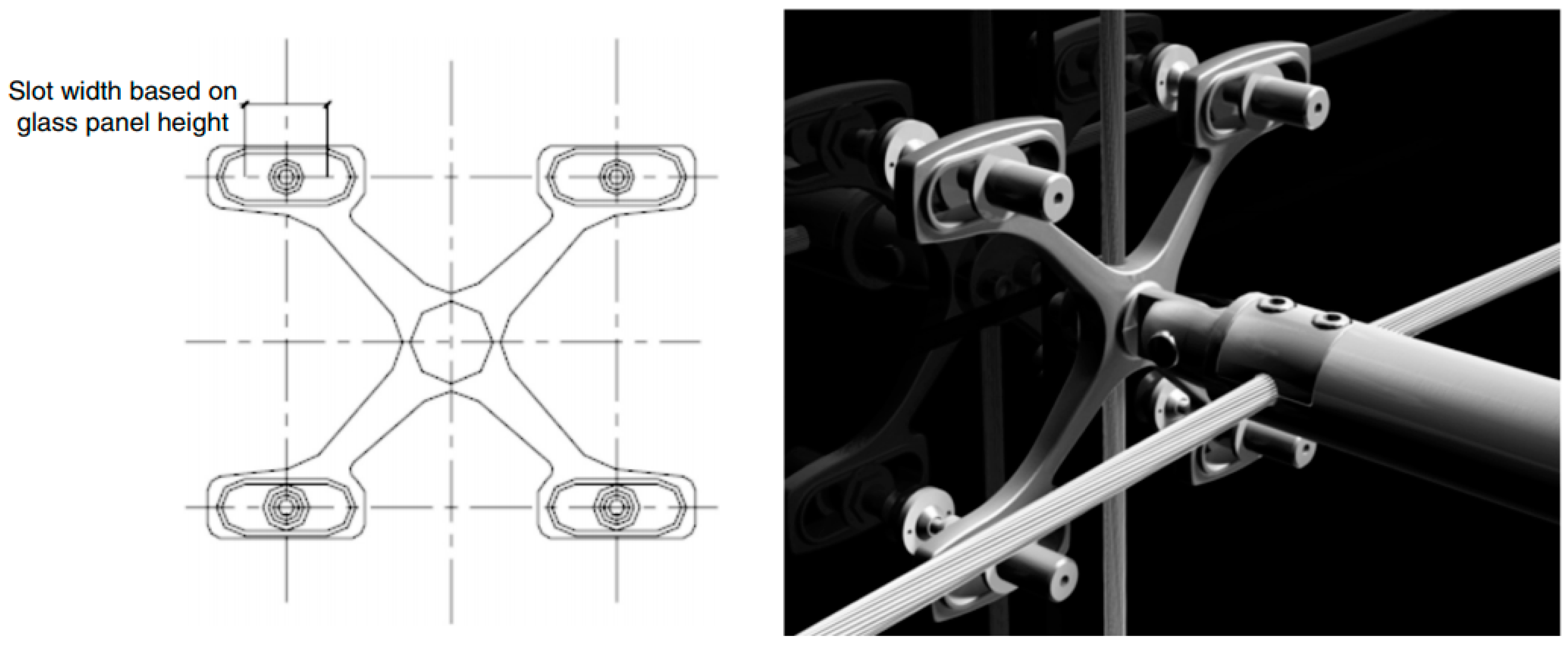
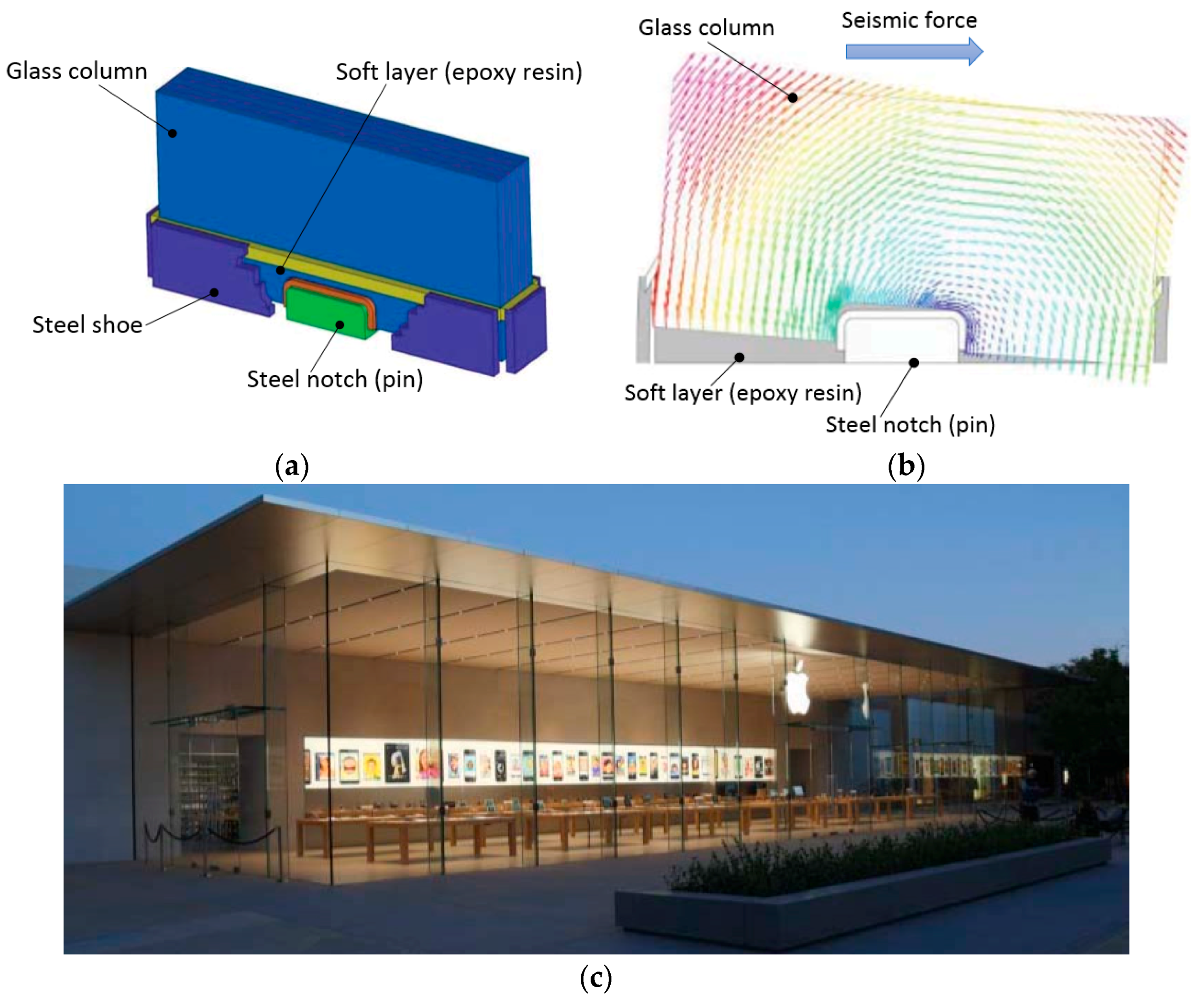
1. Introduction
2. Research in Support of Seismic Design
3. Seismic Design of Glass Systems Based on the CNR-DT 210 Guide
3.1. Basis of Design
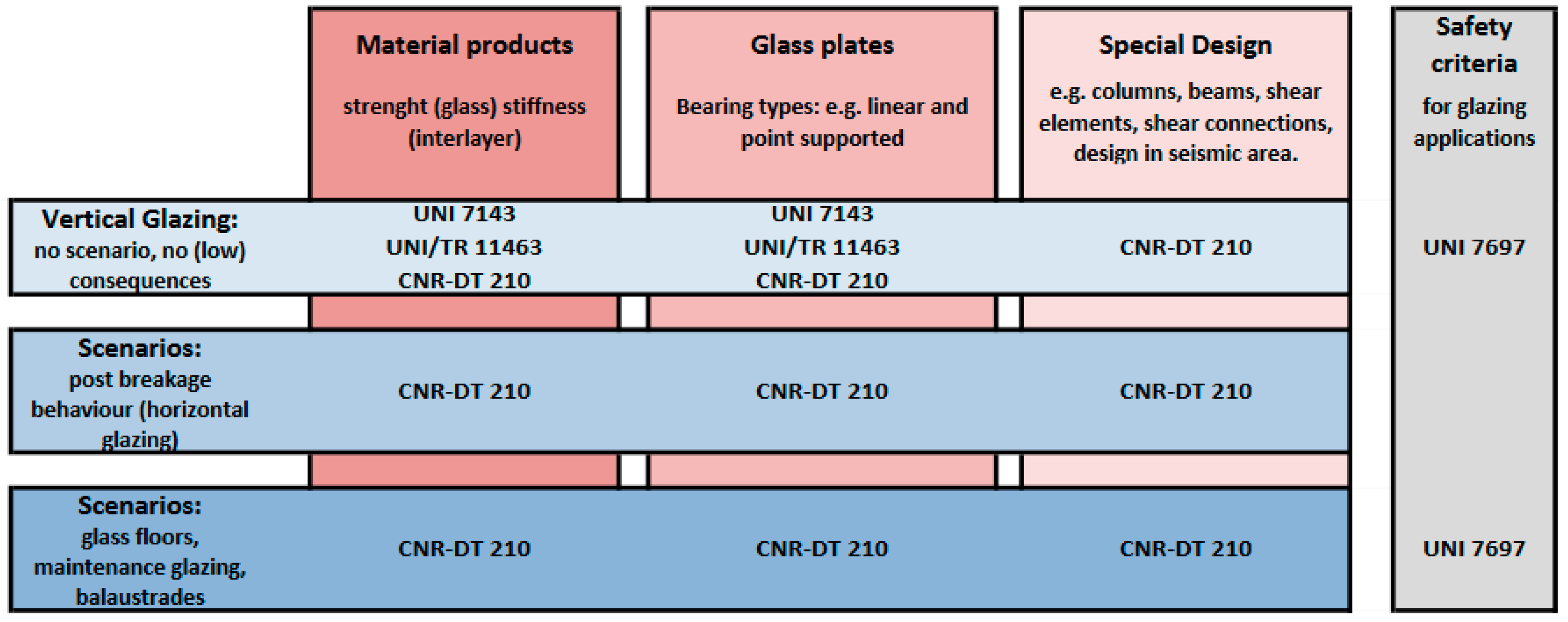
3.2. Consequences Classes and “Secondary” Structural Components
- CC1 = glass failure has limited consequences in terms of loss of human life and small or negligible consequences in economic, social or environmental terms. CC1 includes glass structures/elements in buildings characterized by occasional presence of people. The probability of failure is Pf,50 = 5.83 × 10−4 and Pf,1 = 1.335 × 10−5 (with 50 and 1 the period (in years) to which Pf refers);
- CC2 = failure has medium consequences for human life, but considerable consequences in economic, social and environmental terms. Typical examples are glass structures/elements for residential/office buildings. In this case, Pf,50 = 6.2353 × 10−5 and Pf,1 = 1.3 × 10−6;
- CC3 = failure has high consequences in terms of human life and very great consequences in economic, social terms. CC3 includes glass systems belonging to public buildings and places susceptible to overcrowding, but also stand-alone glass structures (Pf,50 = 8.54 × 10−6, Pf,1 = 9.96×108).
3.3. Nominal Design Life and Reference Life
3.4. Performance Levels
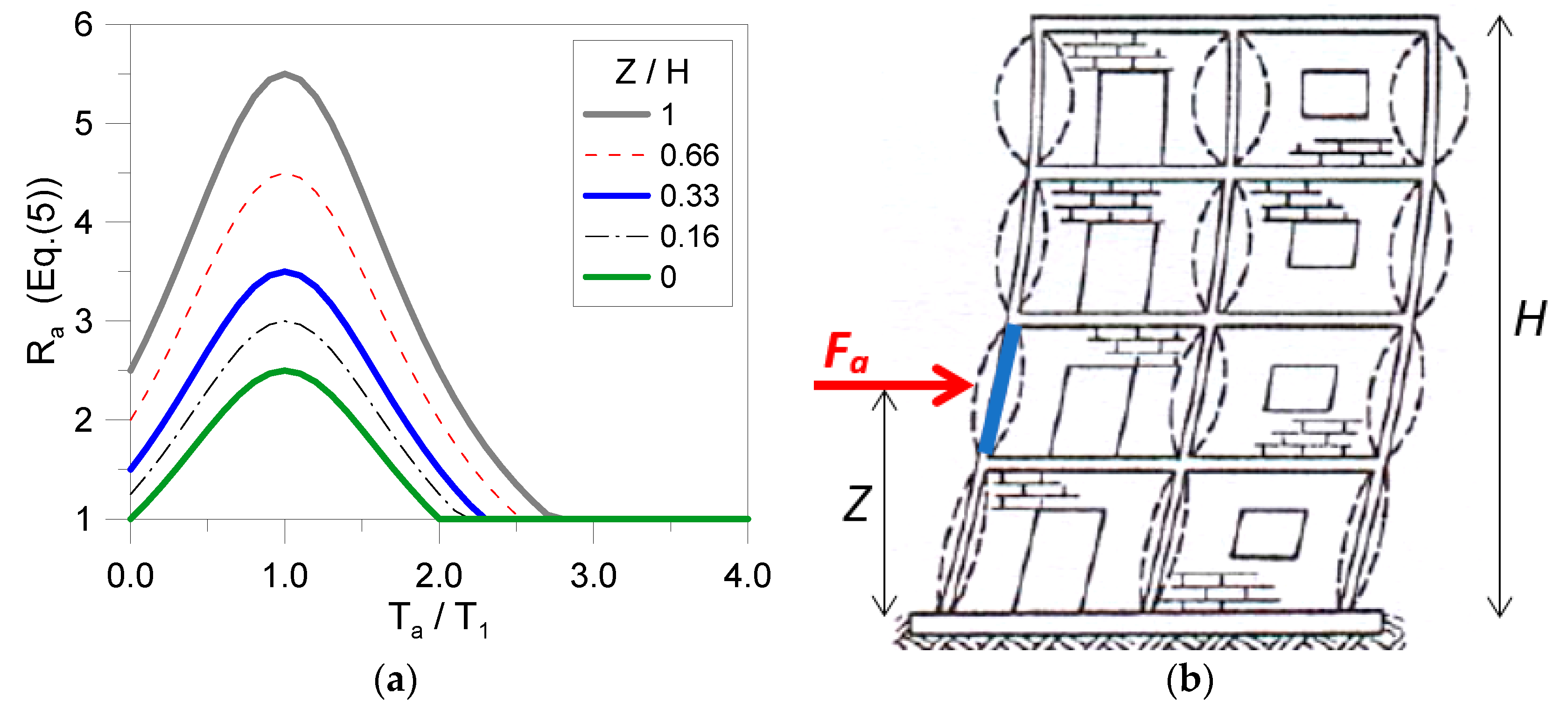
3.5. Design Seismic Force and Q-Behaviour Factor
- Wa is the weight of the element,
- qa is the behaviour factor of the glass element/system to verify, and
- Sa is the peak acceleration of interest, for the element/system to verify, normalized with respect to the acceleration of gravity g.
- ag the peak ground acceleration (rock soil) for the Limit State of interest; while
- S accounts for soil category and topographical conditions.
- Z represents the height of centre of gravity of the glass element to verify (from the foundation level);
- H is the height of the full assembly/building (from the foundation);
- Ta is the fundamental period of the glass element to verify;
- T1 is he fundamental period of the full assembly/building, in the direction of interest.
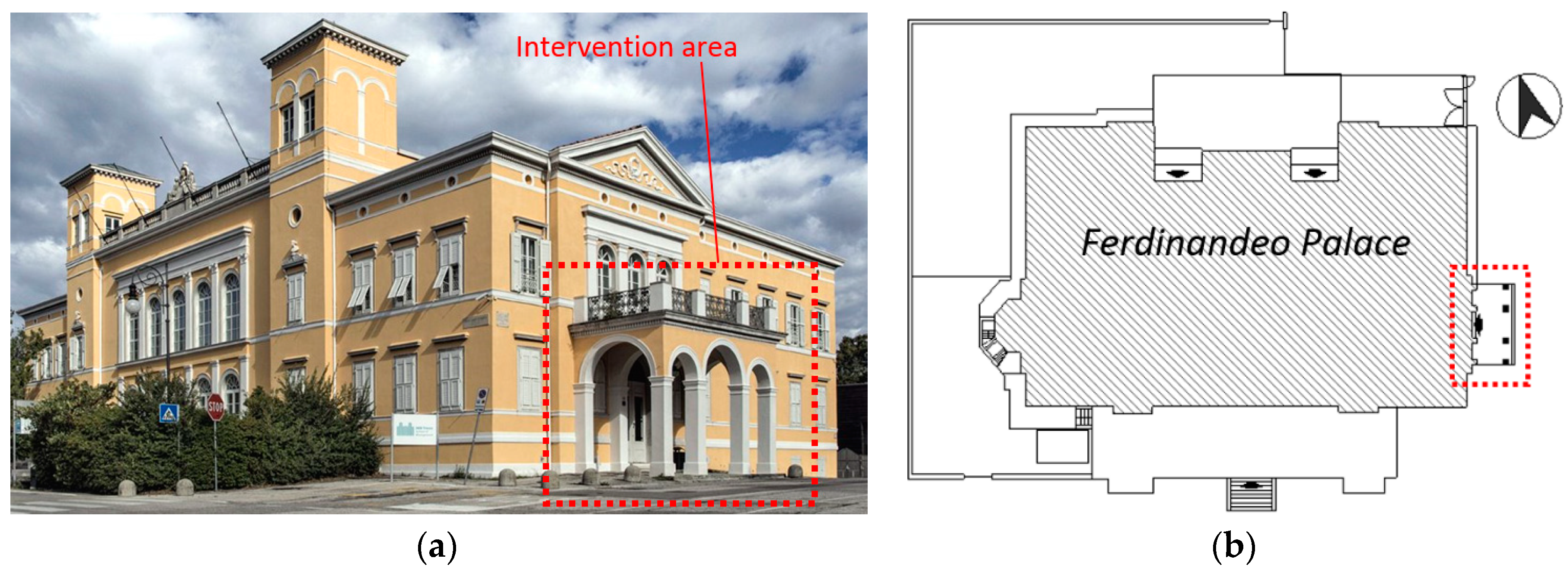
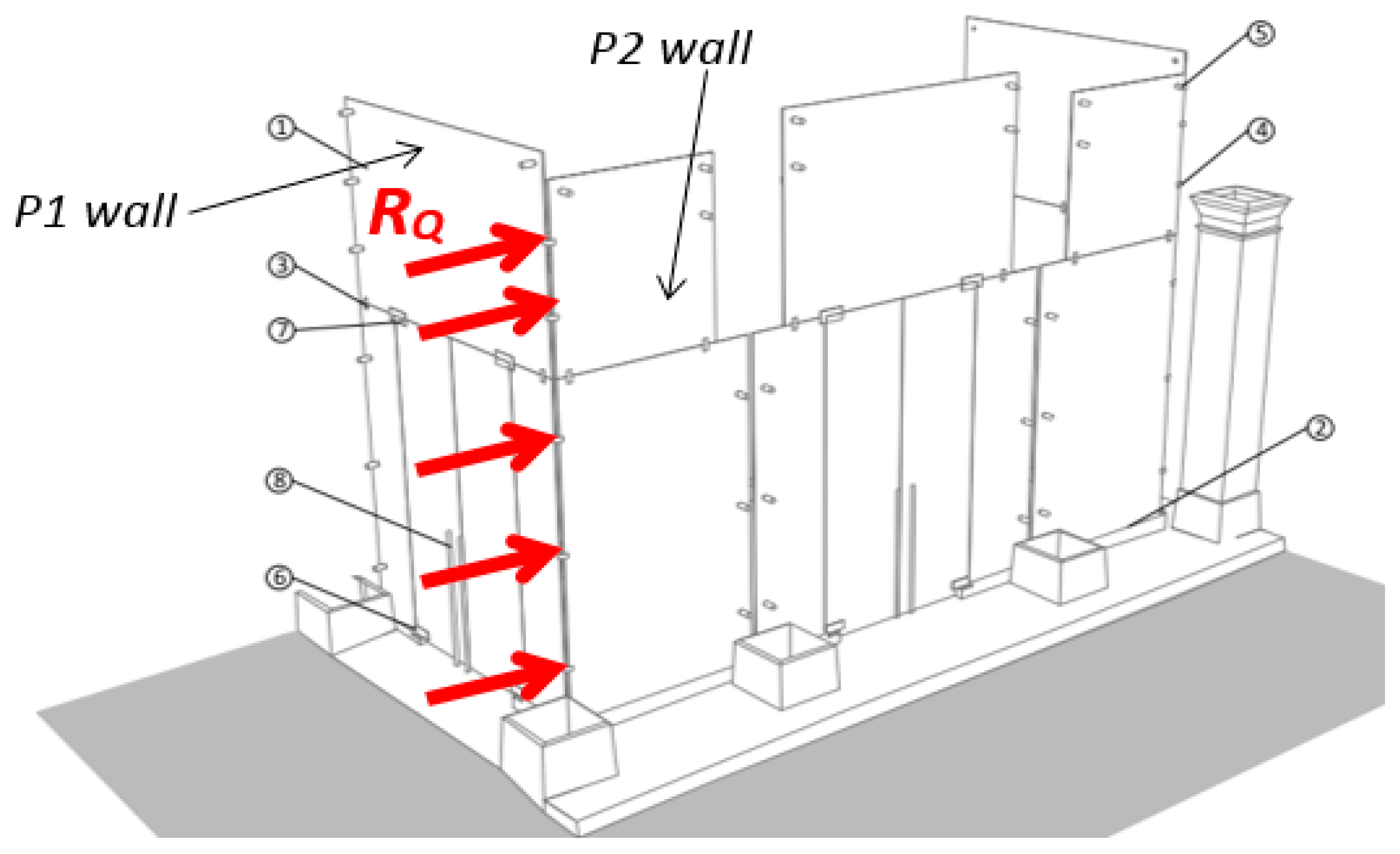
4. Case-Study Example: Glass Partition Assembly
4.1. Description of the System
4.2. Reference Design Parameters, Major Requirements and Loads
4.3. Design Strategy
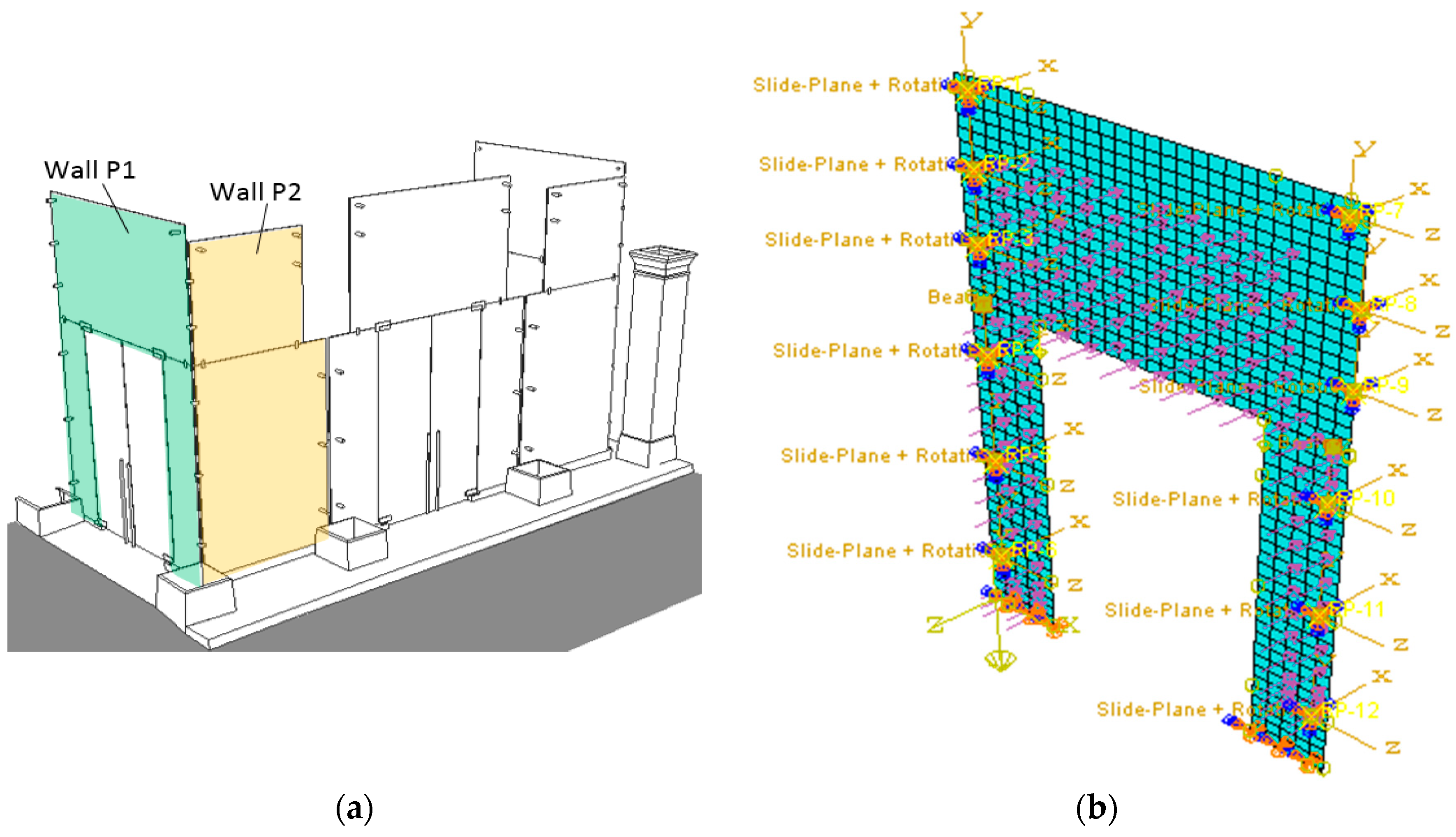
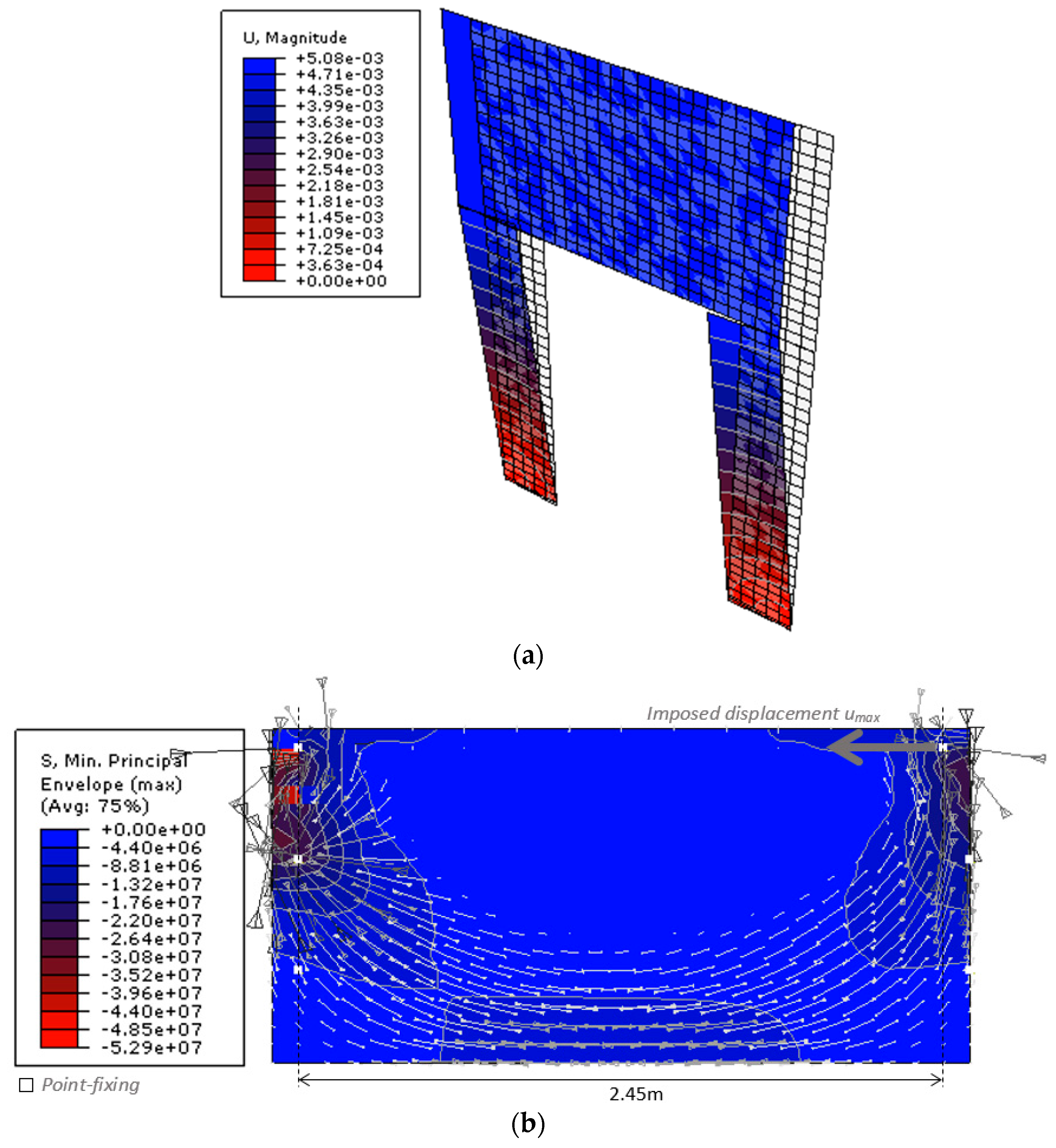
4.4. Seismic Analysis—Out-of-Plane Performance Assessment
4.5. Seismic Analysis—In-Plane Performance Assessment
- (1)
- the in-plane seismic force Fa that the independent glass panel must withstand, based on Equation (3), see Table 6, and
- (2)
- the additional series of in-plane seismic forces RQ deriving (when present) by orthogonal LG walls, being transferred by the frictional clamps.
4.6. Seismic Verification of the Glass Partition System
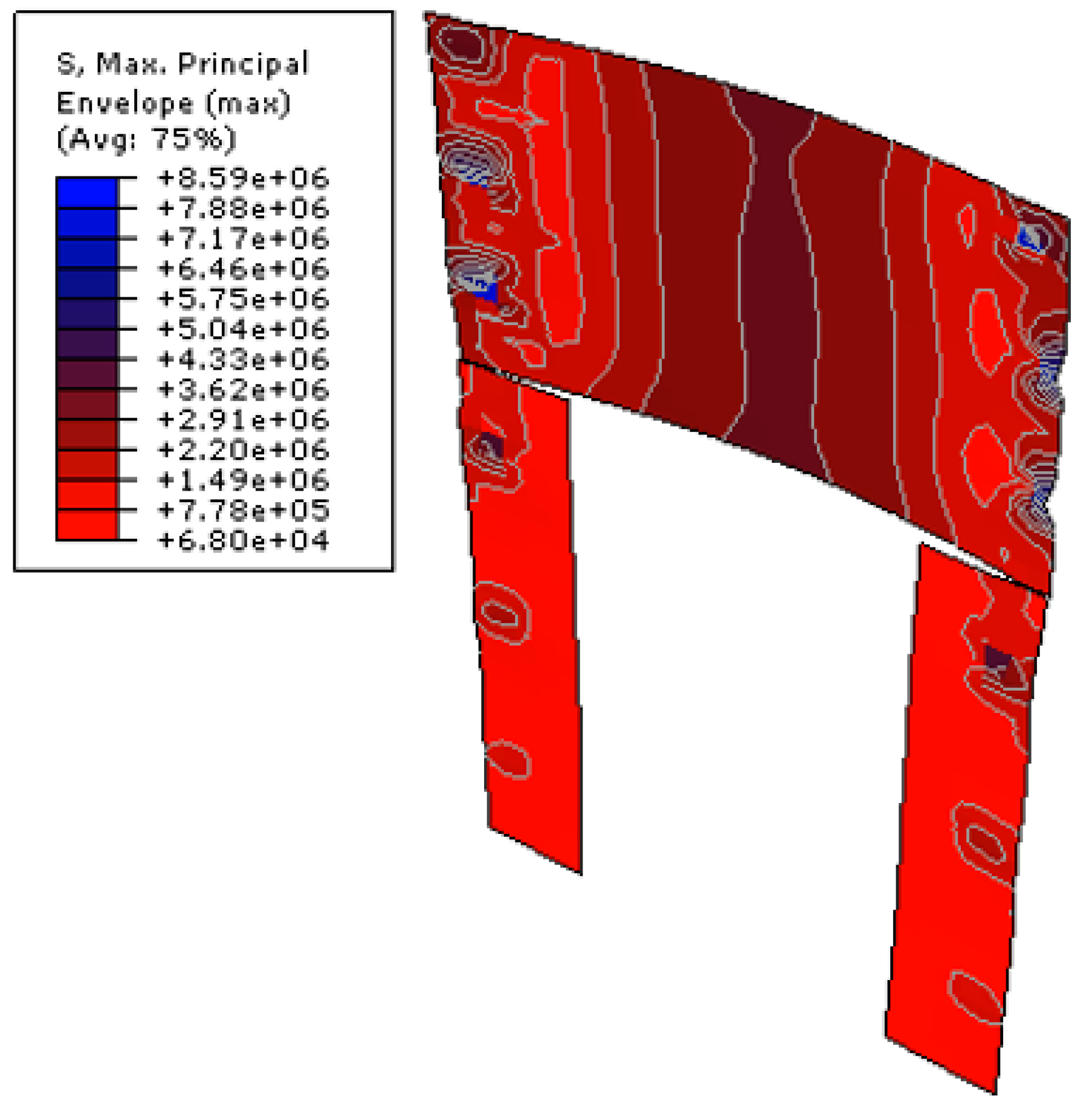
4.6.1. Resistance
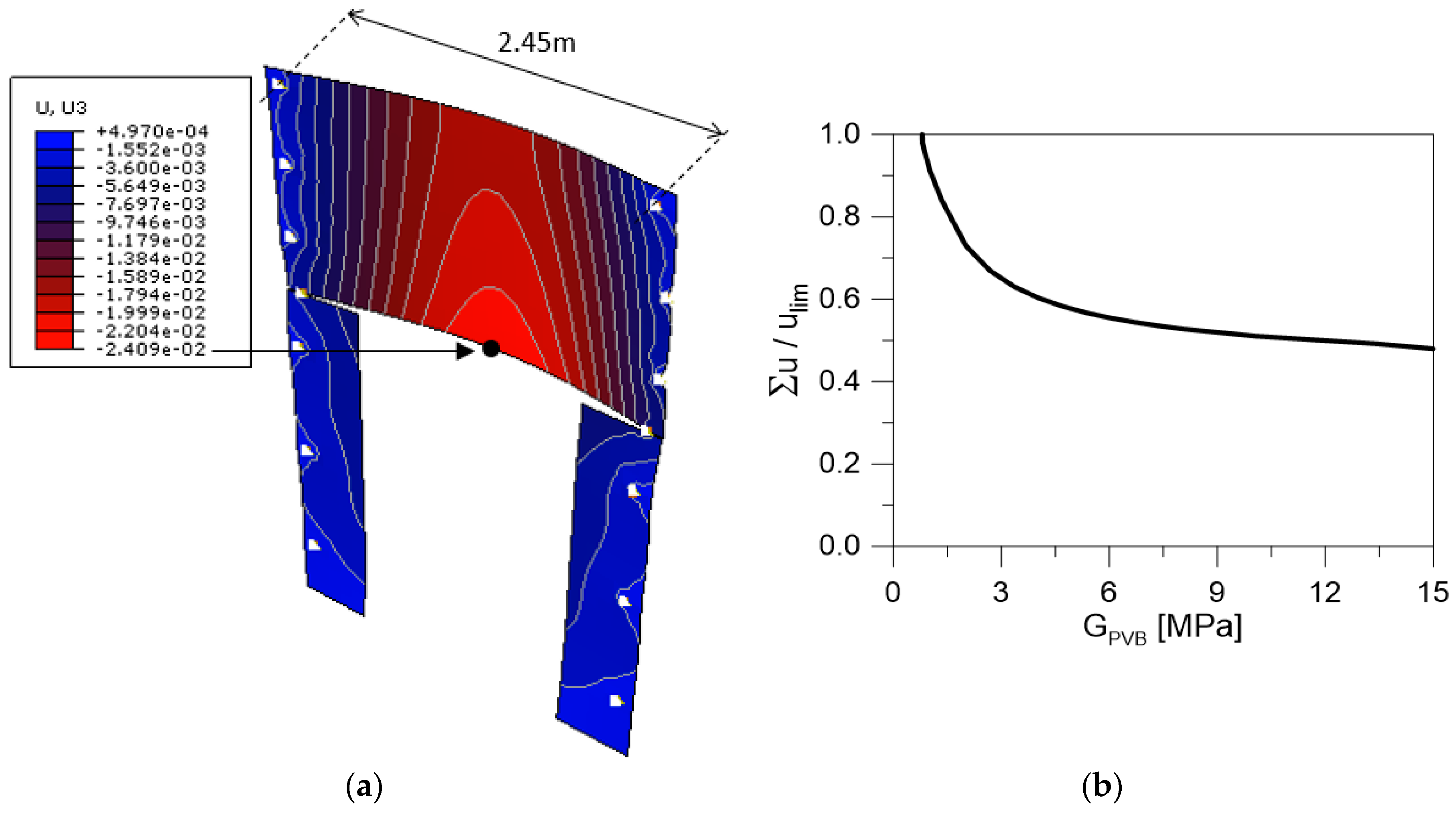
4.6.2. Displacements
- (a)
- ulim = Linf/100, with Linf the distance between two point supports (or ulim = Linf/50, in presence of spandrels), or
- (b)
- ulim = 50 mm.
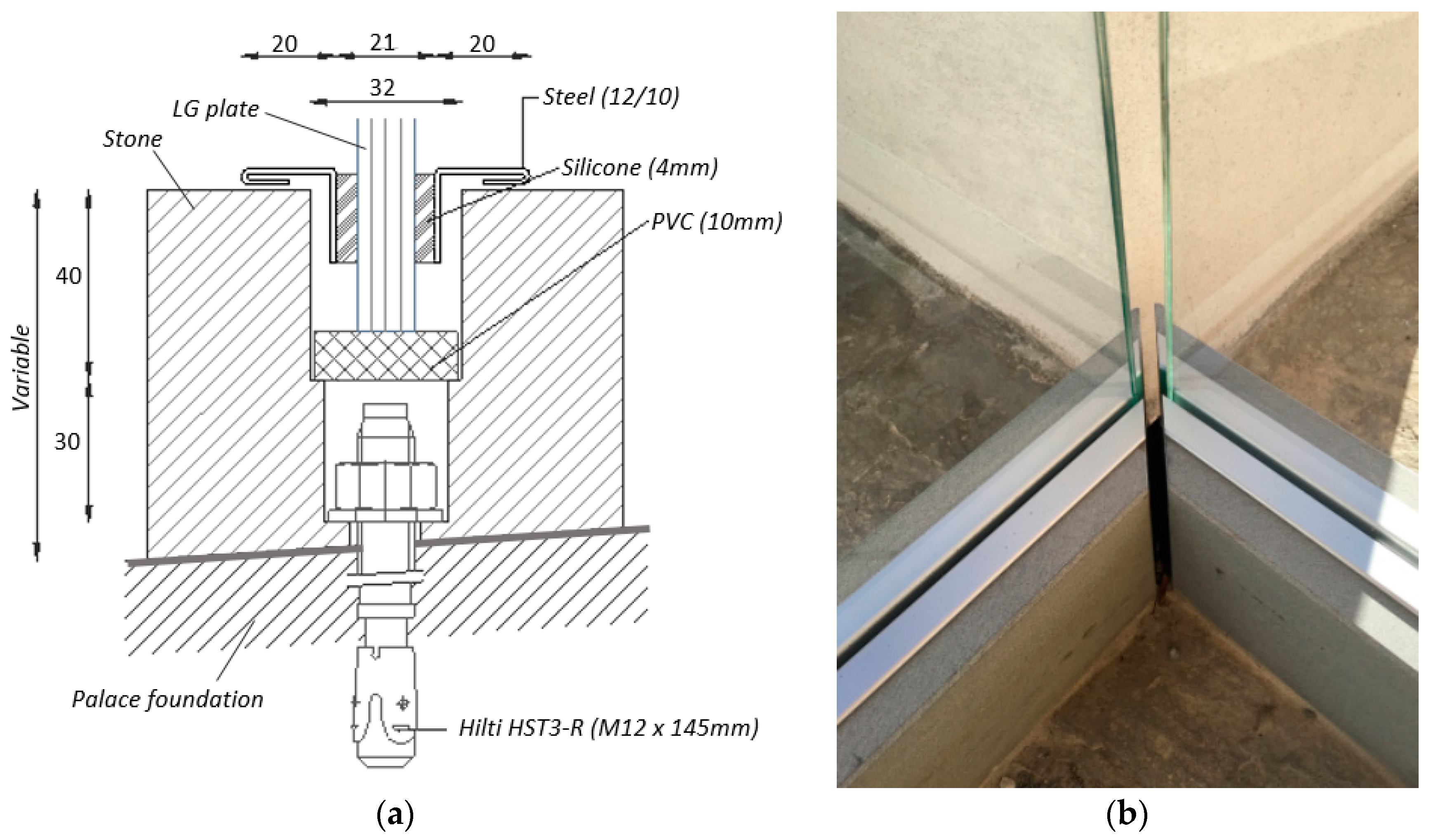
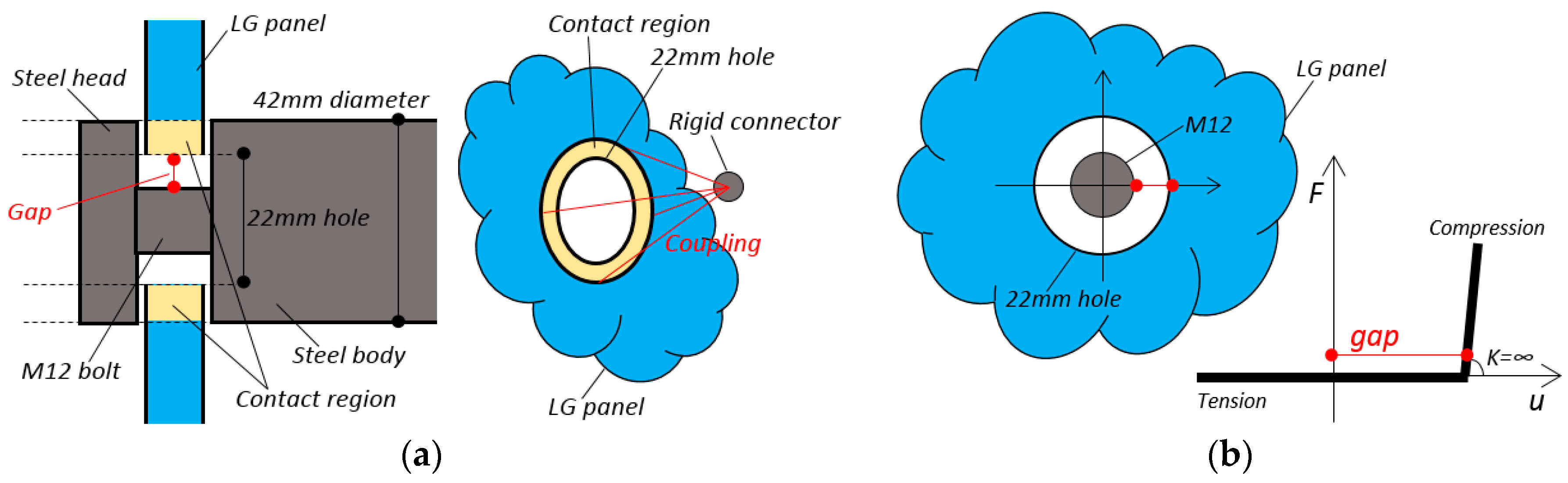
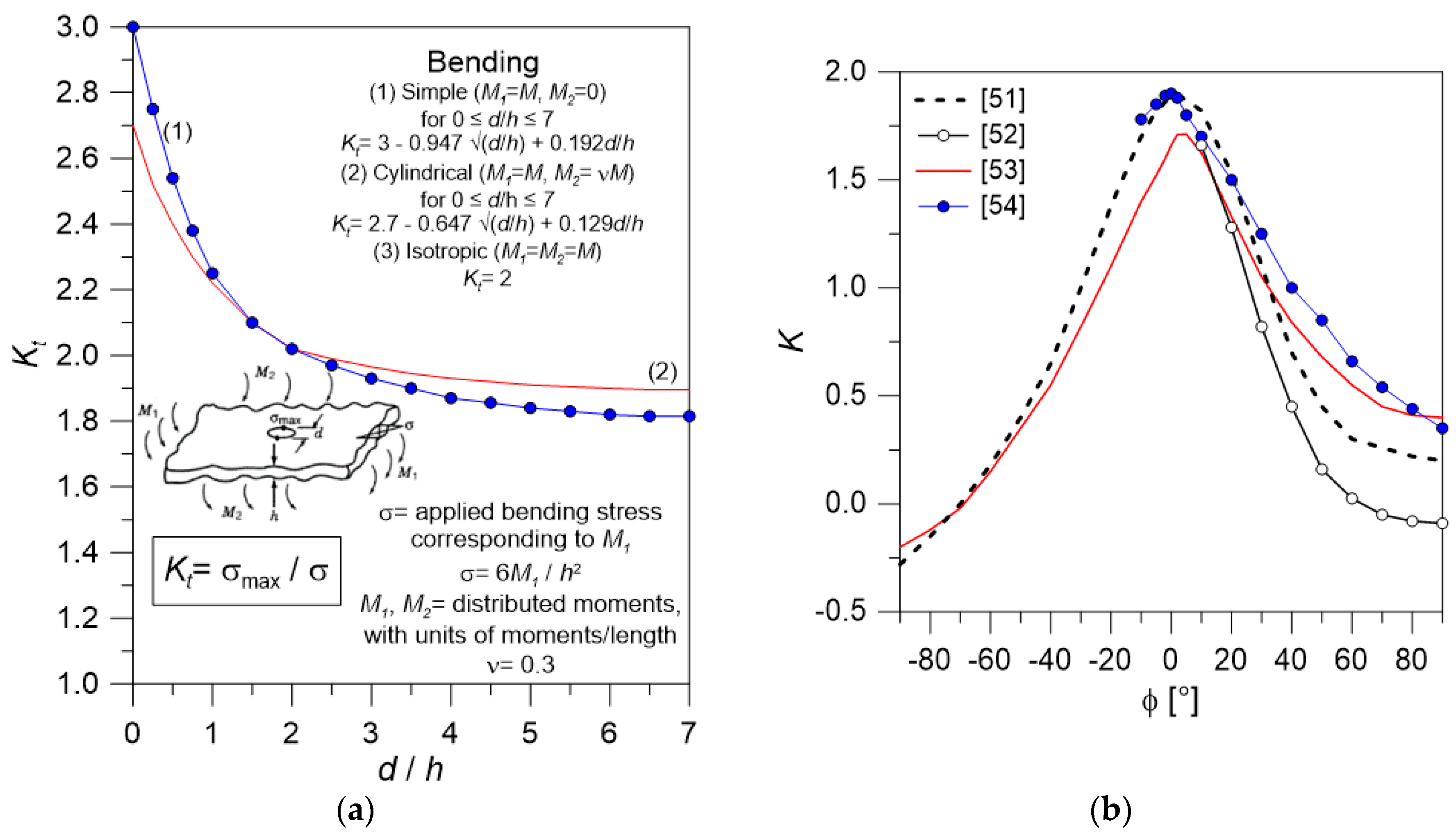
4.7. Verification of Restraints and Fasteners
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Santarsiero, M.; Bedon, C.; Moupagitsoglou, K. Energy-based considerations for the seismic design of ductile and dissipative glass frames. Soil Dyn. Earthq. Eng. 2019, 125, 105170. [Google Scholar] [CrossRef]
- Bedon, C.; Santarsiero, M. Transparency in structural glass systems via mechanical, adhesive, and laminated connections—Existing research and developments. Adv. Eng. Mater. 2018, 20, 1700815. [Google Scholar] [CrossRef]
- Haldimann, M.; Luible, A.; Overend, M. Structural Use of Glass; IABSE: Zurich, Switzerland, 2008; ISBN 978-3-85748-119-2. (CH). [Google Scholar]
- Feldmann, M.; Kasper, R.; Abeln, B.; Cruz, P.; Belis, J.; Beyer, J.; Colvin, J.; Ensslen, F.; Eliasova, M.; Galuppi, L.; et al. Guidance for European Structural Design of Glass Components—Support to the Implementation, Harmonization and Further Development of the Eurocodes; Dimova, S., Pinto, A.V., Feldmann, M., Denton, S., Eds.; Report EUR 26439–Joint Research Centre–Institute for the Protection and Security of the Citizen: Ispra, Italy, 2014. [Google Scholar] [CrossRef]
- Bedon, C.; Zhang, X.; Santos, F.; Honfi, D.; Kozlowski, M.; Arrigoni, M.; Figuli, L.; Lange, D. Performance of structural glass facades under extreme loads—Design methods, existing research, current issues and trends. Constr. Build. Mater. 2018, 163, 921–937. [Google Scholar] [CrossRef]
- Overend, M.; De Gaetano, S.; Haldimann, M. Diagnostic Interpretation of Glass Failure. Struct. Eng. Int. 2007, 17, 151–158. [Google Scholar] [CrossRef]
- Honfi, D.; Reith, A.; Vigh, L.G.; Stocker, G. Why Glass Structures Fail?—Learning from Failures of Glass Structures. In Proceedings of the Challenging Glass 4 & COST Action TU0905 Final Conference, Lausanne, Switzerland, 6–7 February 2014; pp. 791–800, ISBN 978-1-138-00164-0. [Google Scholar] [CrossRef]
- European Committee for Standardization. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; EN 1998-1:2004; CEN: Brussels, Belgium, 2014. [Google Scholar]
- CNR-DT 210/2013. Istruzioni per la Progettazione, L’esecuzione ed il Controllo di Costruzioni con Elementi Strutturali di vetro [Guide for the Design, Construction and Control of Buildings with Structural Glass Elements]; National Research Council of Italy (CNR): Roma, Italy, 2013; (Italian version); Available online: www.cnr.it/it/node/2630 (accessed on 1 November 2019).
- NTC2018. Norme Tecniche per le Costruzioni; Design Standard for Buildings; Ministero delle Infrastrutture e dei Trasporti: Roma, Italy, 17 Gennaio 2018. (In Italian)
- Overend, M. Recent developments in design methods for glass structures. Struct. Eng. 2010, 88, 18–26. [Google Scholar]
- Green, R. The Challenges of Writing a Structural Standard for Glass. In Proceedings of the Challenging Glass Conference, Ghent, Belgium, 16–17 June 2016; Volume 5, pp. 623–632. [Google Scholar] [CrossRef]
- Feldmann, M.; Di Biase, P. The CEN-TS “Structural Glass–Design and Construction Rules” as pre-standard for the Eurocode. In Proceedings of the Conference Engineered Transparency, Düsseldorf, Germany, 23–26 October 2018. [Google Scholar] [CrossRef]
- Sucuoglu, H.; Vallabhan, C.V.G. Behaviour of window glass panels during earthquakes. Eng. Struct. 1997, 19, 685–694. [Google Scholar] [CrossRef]
- Wensheng, L.; Baofeng, H. Discussion on Seismic Performance Indexes of Architectural Curtain Walls. In Proceedings of the 14th WCEE Conference—World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Sivanerupan, S.; Wilson, J.L.; Gad, E.F. Structural analysis and design of glazed curtain wall systems. Aust. J. Struct. Eng. 2011, 12, 57–67. [Google Scholar]
- Overend, M.; Nhamoinesu, S.; Watson, J. Structural Performance of Bolted Connections and Adhesively Bonded Joints in Glass Structures. J. Struct. Eng. 2013, 139, 04013015. [Google Scholar] [CrossRef]
- Bernard, F.; Daudeville, L. Point fixings in annealed and tempered glass structures: Modeling and optimization of bolted connections. Eng. Struct. 2009, 31, 946–955. [Google Scholar] [CrossRef]
- Nielsen, J.H.; Olesen, J.F.; Poulsen, P.N.; Stang, H. Simulation of residual stresses at holes in tempered glass: A parametric study. Mater. Struct. 2010, 43, 947–961. [Google Scholar] [CrossRef]
- Katsivalis, I.; Thomsen, O.T.; Feih, S.; Achintha, M. Strength evaluation and failure prediction of bolted and adhesive glass/steel joints. Glass Struct. Eng. 2018, 3, 183–196. [Google Scholar] [CrossRef]
- Amadio, C.; De Luca, O.; Fedrigo, C.; Fragiacomo, M.; Sandri, C. Experimental and numerical analysis of glass-to-steel joint. J. Struct. Eng. 2008, 134, 1389–1397. [Google Scholar] [CrossRef]
- Martins, L.; Delgado, R. Seismic Behavior of Point Supported Glass Panels. In Proceedings of the Challenging Glass 3—Conference on Architectural and Structural Applications of Glass, TU Delft, Delft, The Netherlands, 28–29 June 2012. [Google Scholar]
- Sivanerupan, S.; Wilson, J.L.; Gad, E.F.; Lam, N.T.K. Drift performance of point fixed glass façade systems. Adv. Struct. Eng. 2014, 17, 1481–1495. [Google Scholar] [CrossRef]
- Casagrande, L.; Bonati, A.; Occhiuzzi, A.; Caterino, N.; Auricchio, F. Numerical investigation on the seismic dissipation of glazed curtain wall equipped on high-rise buildings. Eng. Struct. 2019, 179, 225–245. [Google Scholar] [CrossRef]
- Aiello, C.; Caterino, N.; Maddaloni, G.; Bonati, A.; Franco, A.; Occhiuzzi, A. Experimental and numerical investigation of cyclic response of a glass curtain wall for seismic performance assessment. Constr. Build. Mater. 2018, 187, 596–609. [Google Scholar] [CrossRef]
- Krstevska, L.; Tashkov, L.; Rajcic, V.; Zarnic, R. Seismic behaviour of composite panel composed of laminated wood and bearing glass—Experimental investigation. Adv. Mater. Res. 2013, 778, 698–705. [Google Scholar] [CrossRef]
- Stepinac, M.; Rajcic, V.; Zarnic, R. Timber-structural glass composite systems in earthquake environment. Gradevinar 2016, 68, 211–219. [Google Scholar]
- Bedon, C.; Amadio, C. Numerical assessment of vibration control systems for multi-hazard design and mitigation of glass curtain walls. J. Build. Eng. 2018, 15, 1–13. [Google Scholar] [CrossRef]
- Bedon, C.; Amadio, C. Enhancement of the seismic performance of multi-storey buildings by means of dissipative glazing curtain walls. Eng. Struct. 2017, 152, 320–334. [Google Scholar] [CrossRef]
- Desai, P.; Golmohammadi, A.; Garlipp, R.; Gowda, B. New Point Supported Glass Seismic System. In Proceedings of the AESE 2005–First International Conference on Advances in Experimental Structural Engineering, Nagoya, Japan, 19–21 July 2005; p. 8. [Google Scholar]
- March, M. Structural glass columns in significant seismic zones. In Proceedings of the GlassCon Global 2014, Pennsylvania Convention Center, PA, USA, 7–10 July 2014; pp. 470–486. Available online: http://www.glassconglobal.com/pdfs/GlassCon-Global-2014-Proceedings-Book.pdf (accessed on 1 November 2019).
- European Committee for Standardization. Basis of Structural Design; EN 1990:2002; CEN: Brussels, Belgium, 2002. [Google Scholar]
- Bedon, C.; Fasan, M.; Amadio, C. Vibration analysis and dynamic characterization of structural glass elements with different restraints based on Operational Modal Analysis. Buildings 2019, 9, 13. [Google Scholar] [CrossRef]
- Lenci, S.; Consolini, L.; Clementi, F. On the experimental determination of dynamical properties of laminated glass. Ann. Solid Struct. Mech. 2015, 7, 27–43. [Google Scholar] [CrossRef]
- Zemanova, A.; Zeman, J.; Janda, T.; Schmidt, J.; Sejnoha, M. On modal analysis of laminated glass: Usability of simplified methods and Enhanced Effective Thickness. Compos. Part B Eng. 2018, 151, 92–105. [Google Scholar] [CrossRef]
- Bedon, C.; Amadio, C. Buckling of flat laminated glass panels under in-plane compression or shear. Eng. Struct. 2012, 36, 185–197. [Google Scholar] [CrossRef]
- Bedon, C.; Amadio, C. Shear glass panels with point-fixed mechanical connections: Finite-Element numerical investigation and buckling design recommendations. Eng. Struct. 2016, 112, 233–244. [Google Scholar] [CrossRef]
- Bedon, C.; Amadio, C. A unified approach for the shear buckling design of structural glass walls with non-ideal restraints. Am. J. Eng. Appl. Sci. 2016, 9, 64–78. [Google Scholar] [CrossRef]
- Mapei®. Technical Data Sheet and Catalogue for Silicone Sealants. Available online: www.mapei.com (accessed on 1 November 2019).
- Metalglas®. Technical Data Sheet for Mapesil GP Silicone. Available online: www.metalglas.it (accessed on 1 November 2019).
- Hilti®. Technical Data Sheet for HST3-R Expansion Anchor. Available online: www.hilti.it (accessed on 1 November 2019).
- European Committee for Standardization. Stainless Steels—Part 1: List of Stainless Steels; EN 10088-1: 2014; CEN: Brussels, Belgium, 2014. [Google Scholar]
- Simulia. ABAQUS Computer Software; Dassault Systemes Simulia Corporation: Johnston, RI, USA, 2019. [Google Scholar]
- Calderone, I.; Davies, P.S.; Bennison, S.J.; Huang, X.; Gang, L. Effective Laminate Thickness for the Design of Laminated Glass. In Proceedings of the Glass Performance Days, Tampere, Finland, 12–15 June 2009. [Google Scholar]
- Galuppi, L.; Royer-Carfagni, G.F. Effective thickness of laminated glass beams: New expression via a variational approach. Eng. Struct. 2012, 38, 53–67. [Google Scholar] [CrossRef]
- European Committee for Standardization. Glass in Buildings-Basic Soda Lime Silicate Glass Products; EN 572–2:2004; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Bommer, J.J.; Martinez-Pereira, A. The Prediction of Strong-Motion Duration for Engineering Design. In Proceedings of the 11th WCEE-Eleventh World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996; p. 84, ISBN 0080428223. [Google Scholar]
- Kempton, J.J.; Stewart, J.P. Prediction equations for significant duration of earthquake ground motions considering site and near-source effects. Earthq. Spectra 2006, 22, 985–1013. [Google Scholar] [CrossRef]
- Abdullah Sandikkaya, M.; Akkar, S. Cumulative absolute velocity, Arias intensity and significant duration predictive models from a pan-European strong-motion dataset. Bull. Earthq. Eng. 2017, 15, 1881–1898. [Google Scholar] [CrossRef]
- Pilkey, W.D. Peterson’s Stress Concentration Factors, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1997. [Google Scholar]
- Coker, E.G.; Filon, L.N.G. Photo-Elasticity; Cambridge University Press: London, UK, 1931. [Google Scholar]
- Frocht, M.M. Photoelasticity; Wiley: New York, NY, USA, 1949; Volume 1. [Google Scholar]
- Nisida, M.; Saito, H. Stress distributions in a semi-infinite plate due to a pin determined by interferometric method. Exp. Mech. 1966, 6, 273–279. [Google Scholar] [CrossRef]
- Hyer, M.W.; Liu, D. Stresses in pin-loaded orthotropic plates using photoelasticity. J. Compos. Mater. 1985, 19, 138–153. [Google Scholar] [CrossRef]
- Fink, A. Ein Beitrag zum Einsatz von Floatglass als Dauerhaft Tragender Konstruktionswerkstoff im Bauwesen. Ph.D. Thesis, Institut fur Statik, Technische Universitat Darmstadt, Darmstadt, Germany, June 2000. [Google Scholar]
- Oikonomopoulou, F.; van den Broek, E.A.M.; Bristogianni, T.; Veer, F.A.; Nijsse, R. Design and experimental testing of the bundled glass column. Glass Struct. Eng. 2017, 2, 183–200. [Google Scholar] [CrossRef]
- Peroni, M.; Solomos, G.; Pizzinato, V.; Larcher, M. Experimental investigation of high strain-rate behaviour of glass. Appl. Mech. Mater. 2011, 82, 38–63. [Google Scholar] [CrossRef]
- Haldimann, M. Fracture Strength of Structural Glass Elements—Analytical and Numerical Modelling, Testing and Design. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland, June 2006. [Google Scholar]
- Franco, A.; Royer-Carfagni, G. Verification formulae for structural glass under combined variable loads. Eng. Struct. 2015, 83, 233–242. [Google Scholar] [CrossRef]
- Bedon, C.; Amadio, C. Assessment of analytical formulations for the ULS resistance verification of structural glass elements accounting for the effects of different load durations. Structures 2017, 11, 218–228. [Google Scholar] [CrossRef]
- prEN 16612; CEN/TC 250. Glass in Building—Determination of the Load Resistance of Glass Panes by Calculation and Testing; European Committee for Standardization (CEN): Brussels, Belgium, 2013. [Google Scholar]
- Bedon, C. Diagnostic analysis and dynamic identification of a glass suspension footbridge via on-site vibration experiments and FE numerical modelling. Compos. Struct. 2019, 216, 336–378. [Google Scholar] [CrossRef]
- Ensslen, F. Influences of Laboratory and Natural Weathering on the Durability of Laminated Safety Glass. In Proceedings of the Glass Performance Days, GDP 2007, Tampere, Finland, 15–18 June 2007; p. 7. [Google Scholar]
- Hooper, P.A.; Blackman, B.R.K.; Dear, J.P. The mechanical behaviour of poly (vinyl butyral) at different strain magnitudes and strain rates. J. Mater. Sci. 2012, 47, 3564–3576. [Google Scholar] [CrossRef]
- Andreozzi, L.; Bati, S.B.; Fagone, M.; Ranocchiai, G.; Zulli, F. Dynamic torsion tests to characterize the thermo-viscoelastic properties of polymeric interlayers for laminated glass. Constr. Build. Mater. 2014, 65, 1–13. [Google Scholar] [CrossRef]
- Stevels, W.; D’Haene, P.; Zhang, P.; Haldeman, S. A Comparison of Different Methodologies for PVB Interlayer Modulus Characterization. In Proceedings of the Challenging Glass 5—Conference on Architectural and Structural Applications of Glass, Ghent, Belgium, 16–17 June 2016; ISBN 978-908-256-680-6. [Google Scholar]
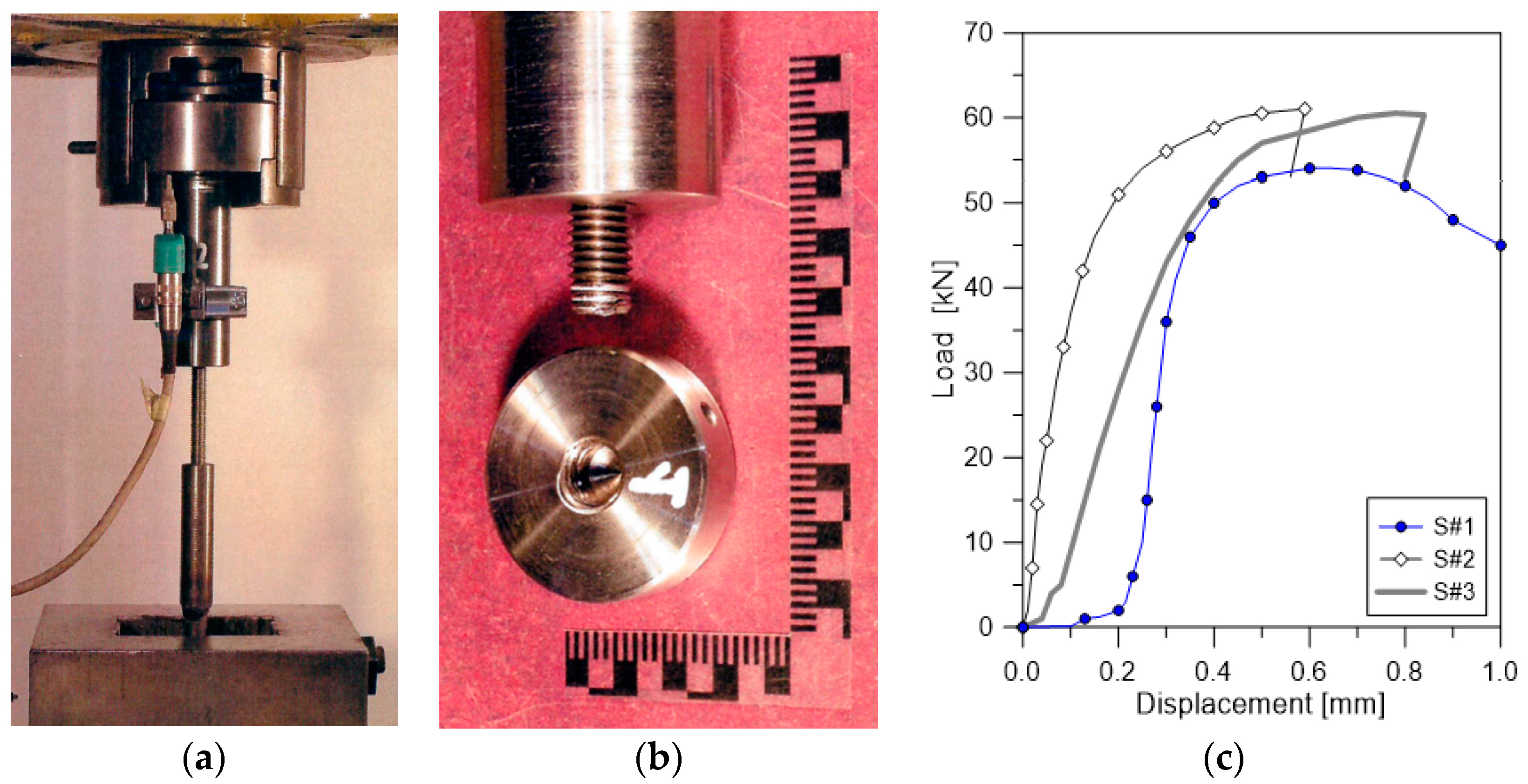
- Trevisan, F. Experimental Tests on Steel Fasteners for a Glass Partition System; Technical Report n. 19008; Department of Engineering and Architecture, University of Trieste: Trieste, Italy, 2019; p. 8, (For internal use only). [Google Scholar]






| Element | CC | |
|---|---|---|
| pre-F (SLS, ULS) | post-F (CLS) | |
| Vertical (with linear restraints) | 1 | 1/n.a. |
| Vertical (with point-fixings) | 2/1 | 1/n.a. |
| Roofs | 2 | 2/1 |
| Fins | 2 | 2/1 |
| Railings (fall danger) | 2 | 2/1 |
| Floors, beams | 2 | 2 |
| Pillars | 3 | 2 (with pre-F loads) |
| VN (in years) | Example | NTC2018 |
|---|---|---|
| 10 | Temporary structures 2 | Yes |
| 10–25 | Replaceable parts | No |
| 15–30 | Agricultural structures | No |
| 50 | Buildings, common structures | Yes |
| 100 | Monumental buildings, bridges, other | Yes |
| Importance Class | Description | CU |
|---|---|---|
| I | Occasional presence of people or agricultural buildings | 0.7 |
| II | Normal crowd levels or factories, without essential public/social functions | 1.0 |
| III | Significant crowd levels | 1.5 |
| IV | Important public, or construction with strategic functions | 2.0 |
| Performance Level | Description | |
|---|---|---|
| ND | No damage | No damage in glass; no replacement; watertightness preserved |
| SD | Slight damage | Partial loss of functionality; usable building; no risk for users |
| HD | Heavy damage | High degree (and cost) of functionality loss; still no risk for users |
| F | Failure | Severe damage; evidence of failure; risk for users |
| Importance class | ||||
|---|---|---|---|---|
| Limit State | I | II | III | IV |
| SLO | - | - | ND45 | ND60 |
| SLD | SD35 | SD50 | SD75 | SD100 |
| SLV | HD333 | HD475 | HD713 | HD950 |
| SLC | - | - | F1463 | F1950 |
| Ra = 1 (Equation (5)) | ||||
|---|---|---|---|---|
| Limit State | ag,max [g] | Sa [g] | Fa [kN] | Qa [kN/m2] |
| SLO | 0.128 | 0.154 | 0.385 | 0.049 |
| SLD | 0.167 | 0.201 | 0.503 | 0.064 |
| SLV | 0.442 | 0.531 | 1.328 | 0.170 |
| SLC | 0.546 | 0.655 | 1.638 | 0.210 |
| Design Load (Equation (6)) | tL (time) | TL [°C] | GPVB [MPa] |
|---|---|---|---|
| Dead | VN (50 years) | 50 | 0.052 |
| Seismic | 30 s * | 30 | 0.8 |
| Crowd | 30 s * | 30 | 0.8 |
| Near Holes | ||
|---|---|---|
| Method | (CLS comb. of Equation (6)) | Stress Verification |
| Equation (11) [9] | 0.99607 | Ok |
| Equation (12) [59] | 0.65315 | Ok |
| Equation (13) [61] | 0.99274 | Ok |
| Equation (14) [60] | 0.97373 | Ok |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedon, C.; Amadio, C.; Noè, S. Safety Issues in the Seismic Design of Secondary Frameless Glass Structures. Safety 2019, 5, 80. https://doi.org/10.3390/safety5040080
Bedon C, Amadio C, Noè S. Safety Issues in the Seismic Design of Secondary Frameless Glass Structures. Safety. 2019; 5(4):80. https://doi.org/10.3390/safety5040080
Chicago/Turabian StyleBedon, Chiara, Claudio Amadio, and Salvatore Noè. 2019. "Safety Issues in the Seismic Design of Secondary Frameless Glass Structures" Safety 5, no. 4: 80. https://doi.org/10.3390/safety5040080
APA StyleBedon, C., Amadio, C., & Noè, S. (2019). Safety Issues in the Seismic Design of Secondary Frameless Glass Structures. Safety, 5(4), 80. https://doi.org/10.3390/safety5040080






