Injury Threshold of Oral Contact with Hot Foods and Method for Its Sensory Evaluation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Simulation
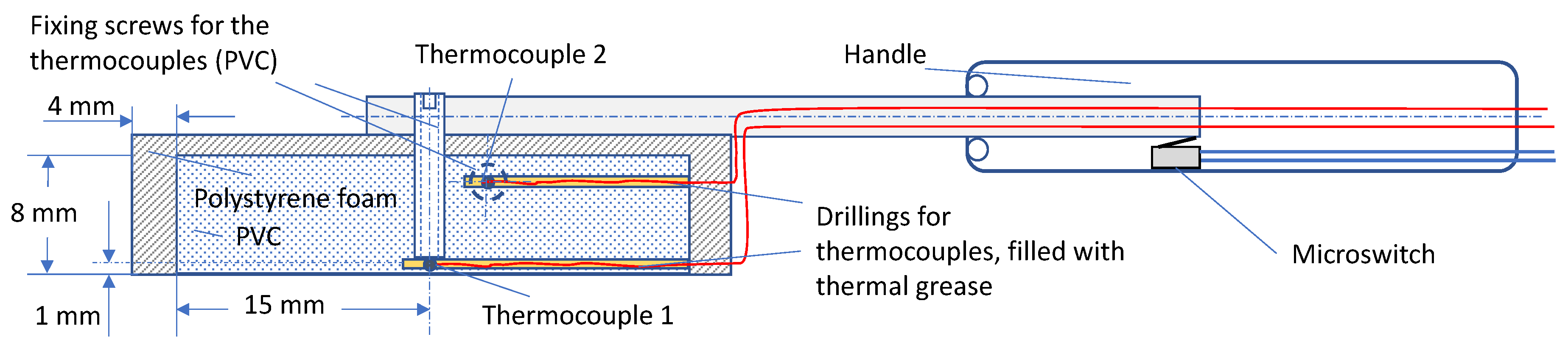
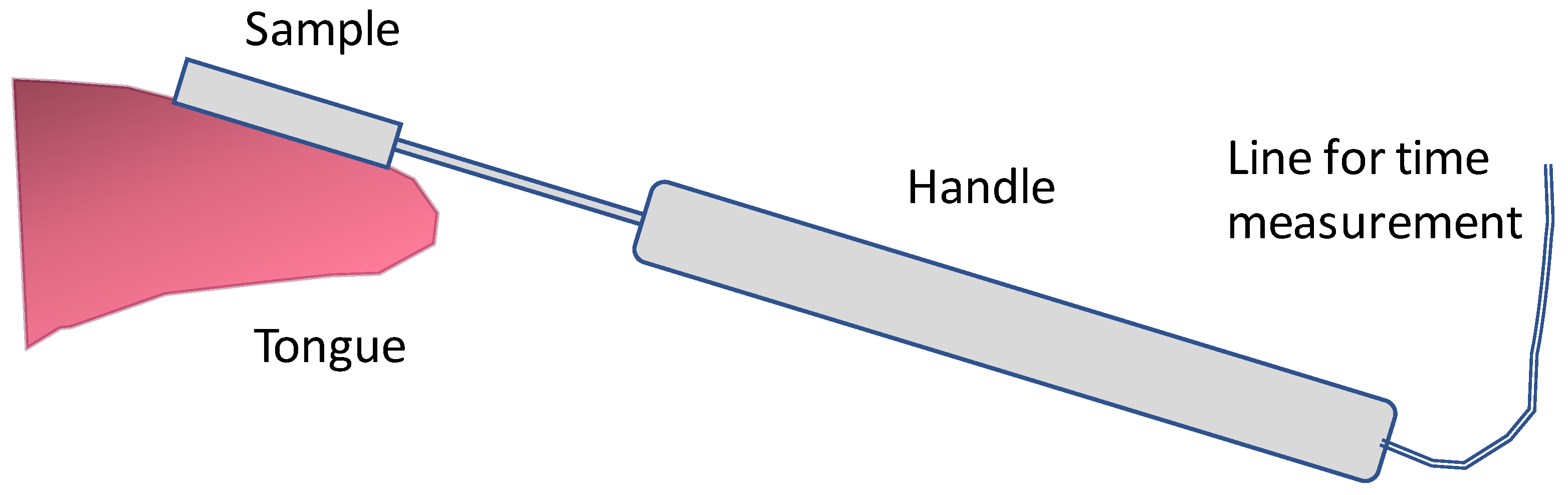
2.2. Sensory Analysis and Evaluation
- The temperature T0 perceived as pleasant/tolerable for any period of time t∞ > 10 s.
- The temperatures T(t), which are regarded as barely bearable for a limited time t of 3 to 10 s. The time until the contact is broken off is measured, which systematically decreases with increasing temperature.
3. Results
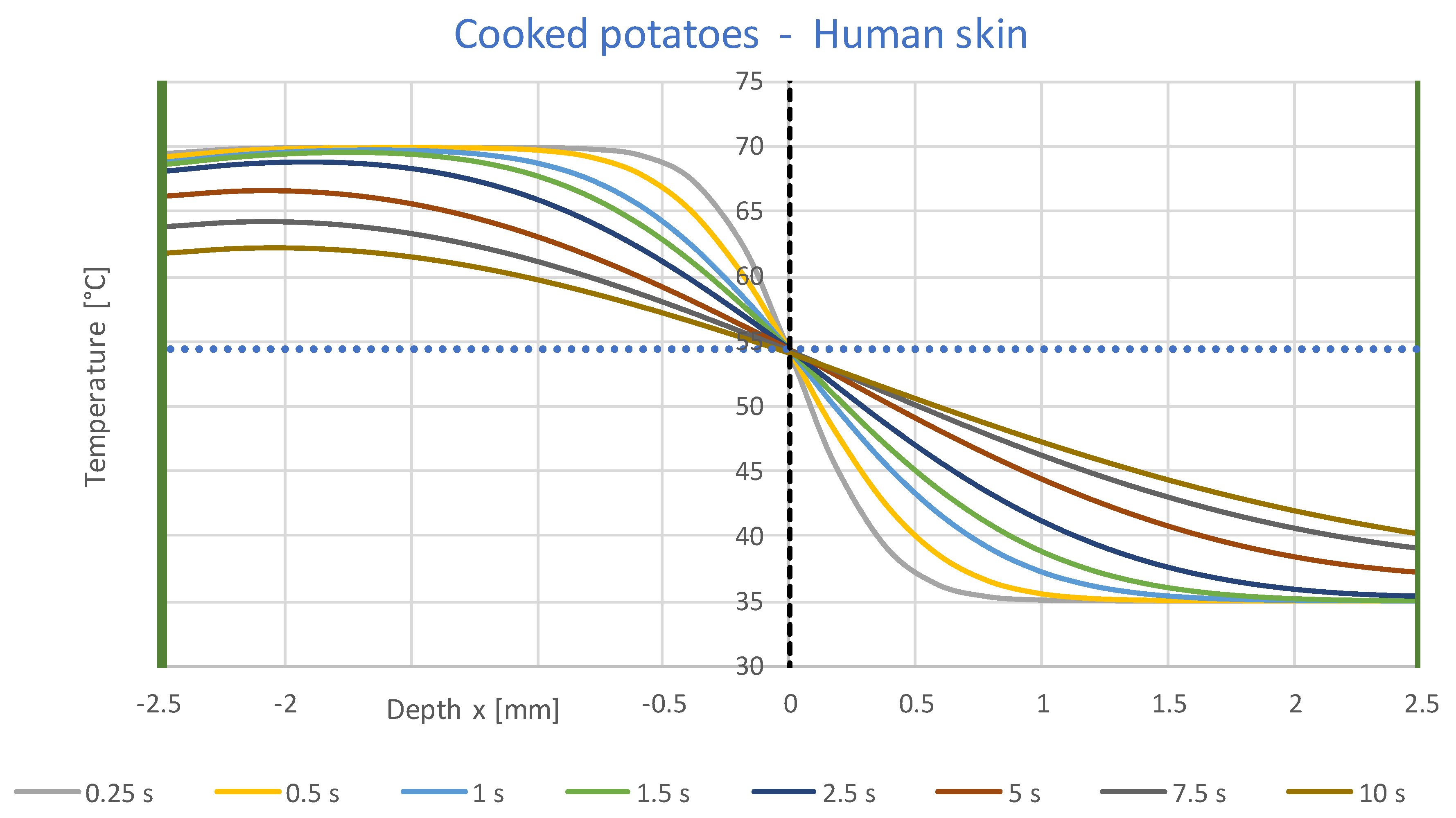
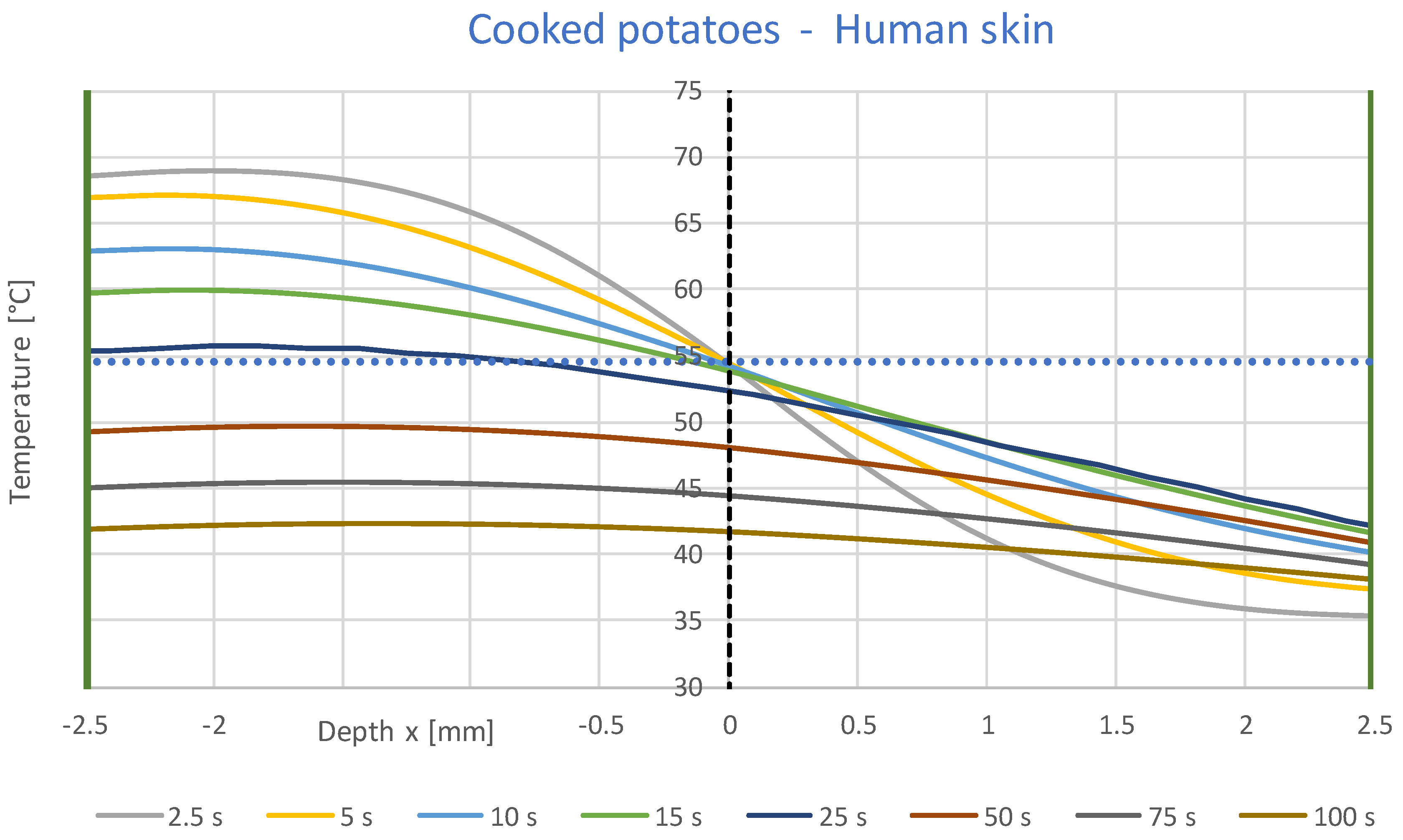
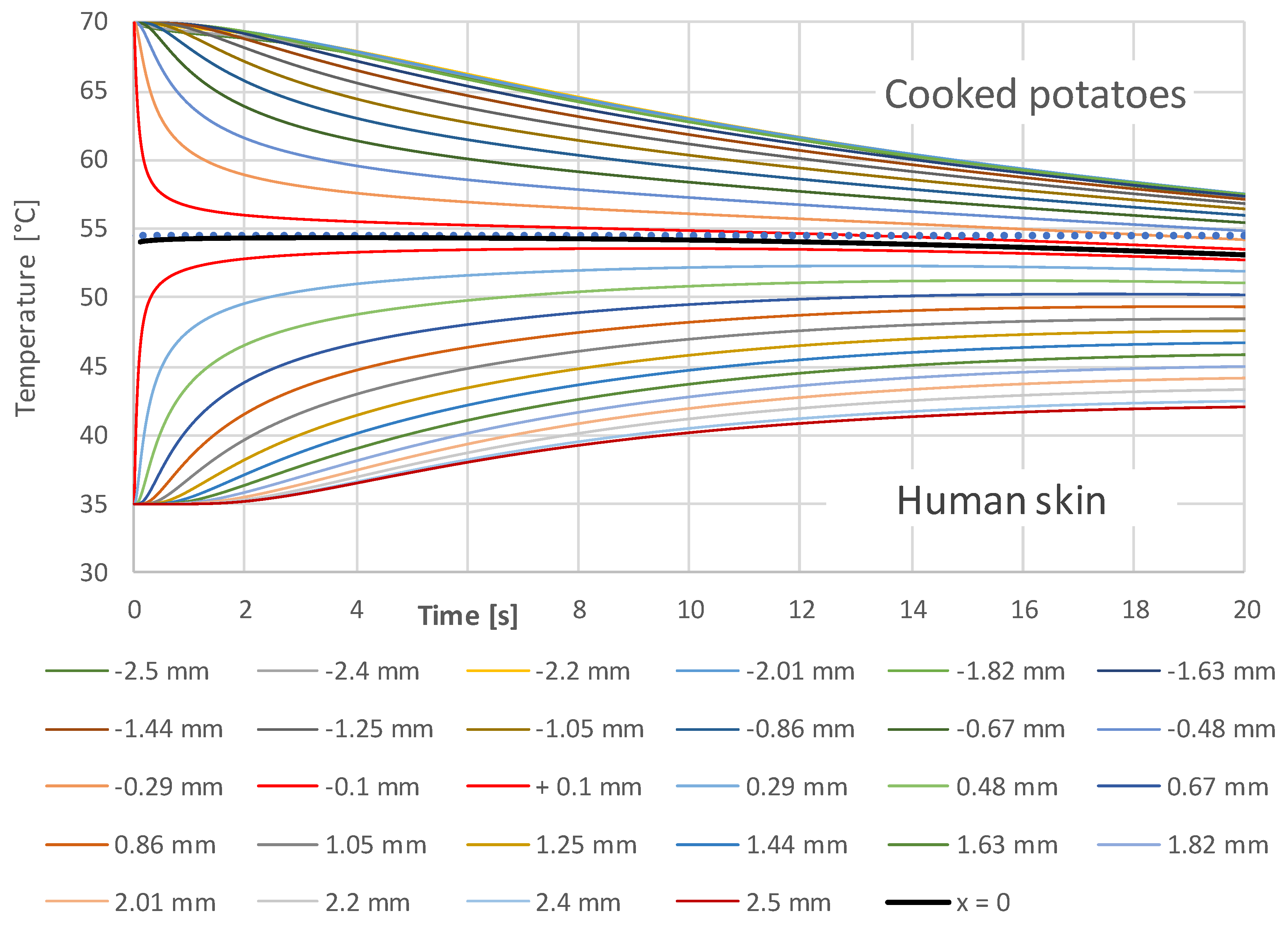
3.1. Simulation Results
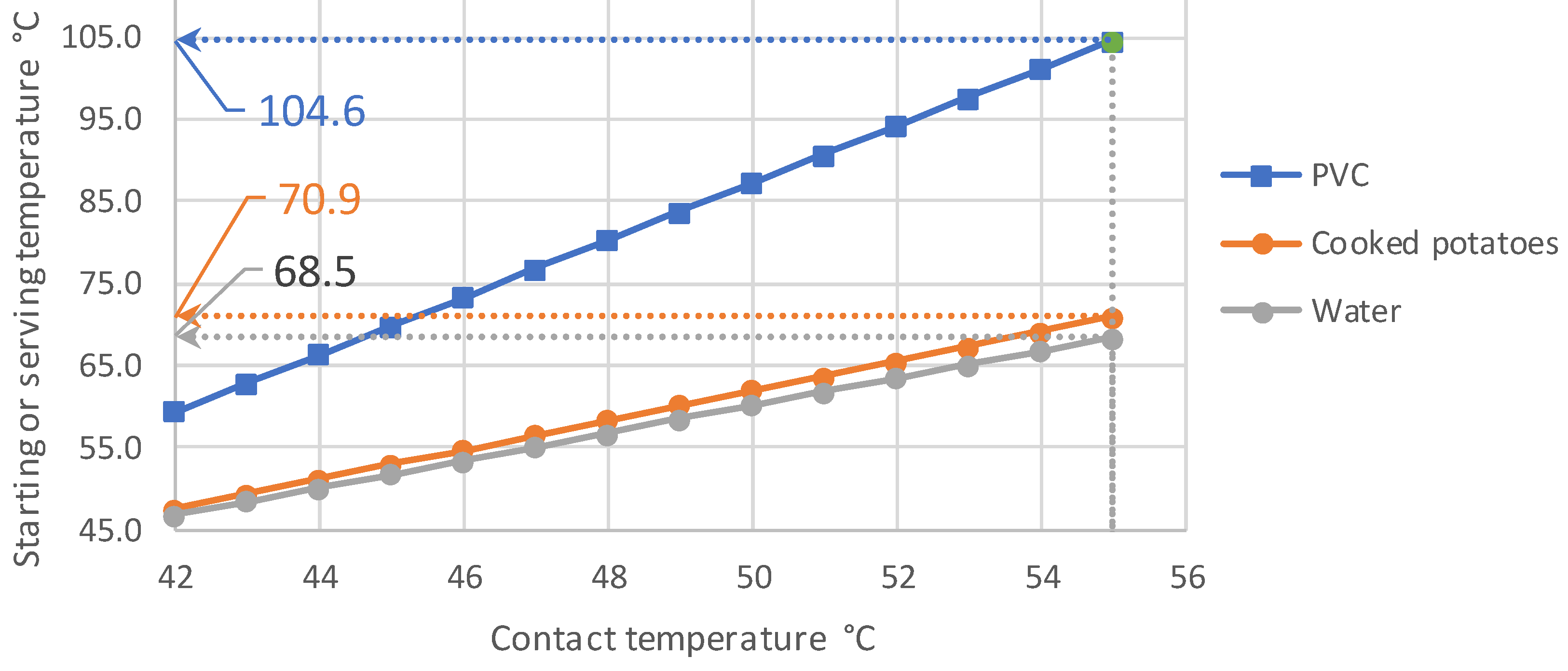
3.2. Initial Measurement Results
4. Discussion
- A constant contact temperature only occurs directly in the contact surface. Even at a distance of ±0.1 mm, deviations of about ±2 °C occur for times up to 2 s. Therefore, the contact temperature could only be measured with sensors much smaller than 0.1 mm, which are not commercially available.
- The contact temperature remains constant for about 10 s in the samples examined, which are only 2.5 mm thick, and only decreases continuously afterwards. Thus, the contact temperature represents the essential parameter for assessing the risk of injury.
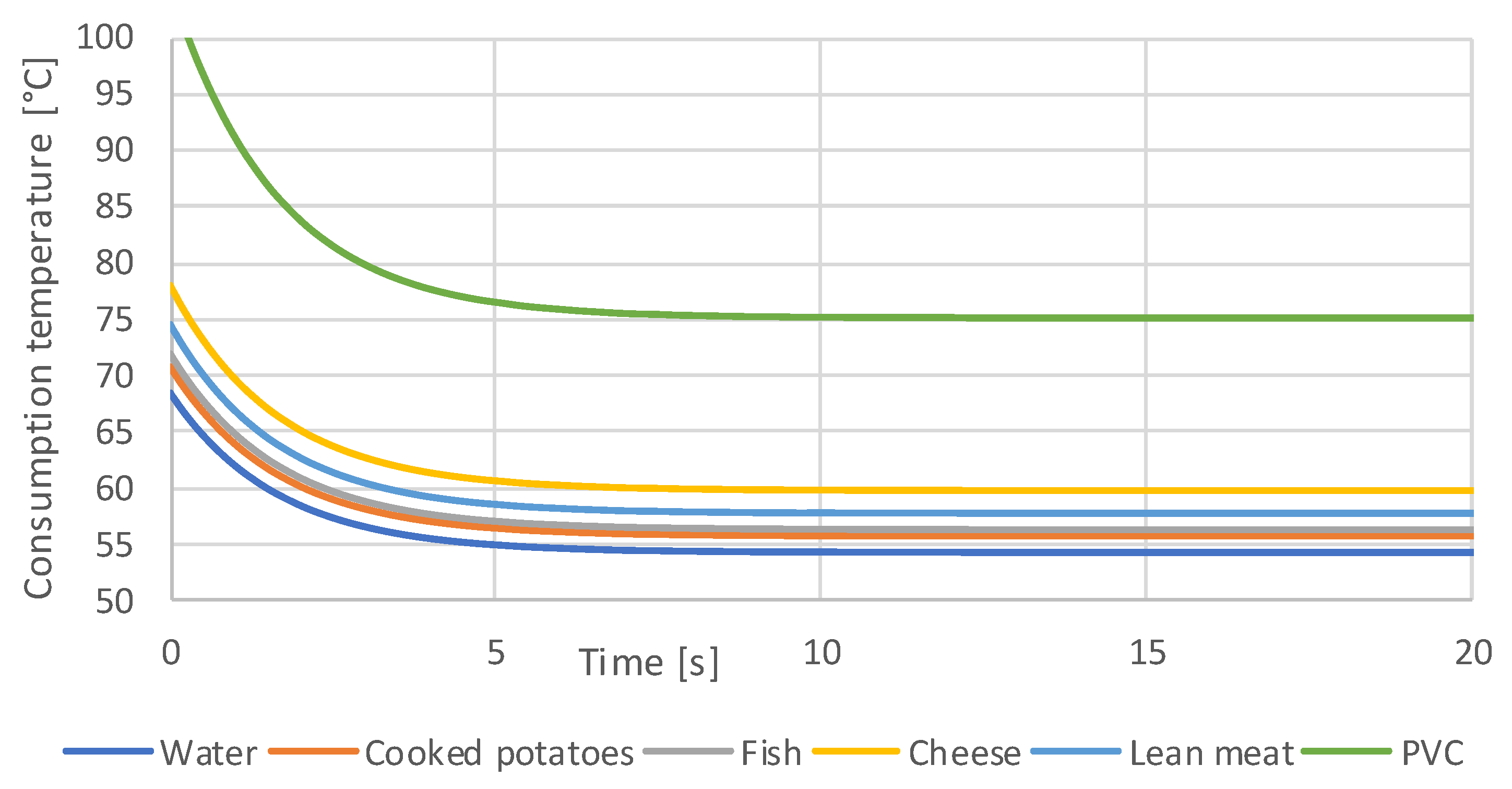
- Orienting experiments indicate that it is possible to define a generalizable threshold value for the contact temperature as a function of the contact time of hot foods, with which the consumption temperatures of any food can be calculated. A transfer to hot drinks is not easily possible and requires further investigation.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Marzetta, L.A. Engineering and constructional manual for an instrument to make burn hazard measurements in consumer products. Nat. Bur. Stand. (U.S.) Tech. Note 1974, 816, 1–48. [Google Scholar]
- Zhai, L.; Adlhart, C.; Spano, F.; Innocenti, M.R.; Piatek, A.K.; Li, J.; Rossi, R.M. Prediction of steam burns severity using Raman spectroscopy on ex vivo porcine skin. Sci. Rep. 2018, 8, 6946. [Google Scholar] [CrossRef] [PubMed]
- McMaster, P.D.; Hudack, S.S. The participation of skin lymphatics in repair of the lesions due to incisions and burns. J. Exp. Med. 1934, 60, 479–501. [Google Scholar] [CrossRef] [PubMed]
- Marzetta, L.A. A thermesthesiometer-An instrument for burn hazard measurement. IEEE Trans. Biomed. Eng. 1974, BME-21, 425–427. [Google Scholar] [CrossRef] [PubMed]
- Manzinger, H. Temperaturgrenzen für die Verbrennung der Haut: Ultraschall-B-Scan-Untersuchung. Dissertation; Ludwig Maximilians Universität: Munich, Germany, 1990. (In German) [Google Scholar]
- Cullen, R. The oral-burn syndrome and its effects on dental implants. J. Oral Implantol. 1998, 24, 219–221. [Google Scholar] [CrossRef]
- Siekmann, H. Recommended maximum temperatures for touchable surfaces. Appl. Ergon. 1990, 21, 69–73. [Google Scholar] [CrossRef]
- Siekmann, H. Determination of maximum temperatures that can be tolerated on contact with hot surfaces. Appl. Ergon. 1989, 20, 313–317. [Google Scholar] [CrossRef]
- Moritz, A.R.; Henriques, F.C. Studies of Thermal Injury: II. The Relative Importance of Time and Surface Temperature in the Causation of Cutaneous Burns. Am. J. Pathol. 1947, 23, 695–720. [Google Scholar] [PubMed]
- Madea, B. Basiswissen Rechtsmedizin; Springer: Berlin/Heidelberg, Germany, 2007. (In German) [Google Scholar]
- Parsons, K. Human Thermal Environments: The Effects of Hot, Moderate, and Cold Environments on Human Health, Comfort, and Performance; CRC press: Boca Raton, FL, USA, 2014. [Google Scholar]
- ISO. Ergonomics of the Thermal Environment—Methods for the Assessment of Human Responses to Contact with Surfaces—Part 1: Hot Surfaces; ISO 13732-1:2006; International Organization for Standardization: Geneva, Switzerland, 2006. [Google Scholar]
- Loomis, D.; Guyton, K.Z.; Grosse, Y.; Lauby-Secretan, B.; El, G.F.; Bouvard, V.; Benbrahim-Tallaa, L.; Guha, N.; Mattock, H.; Straif, K. Drinking Coffee, Mate, and Very Hot Beverages; IARC Publication: Lyon, France, 2018. [Google Scholar]
- Loomis, D.; Guyton, K.Z.; Grosse, Y.; Lauby-Secretan, B.; El, G.F.; Bouvard, V.; Benbrahim-Tallaa, L.; Guha, N.; Mattock, H.; Straif, K. IARC Working Group on the Evaluation of Carcinogenic Risks to Humans Carcinogenicity of drinking coffee, mate, and very hot beverages. Lancet Oncol. 2016, 17, 877–878. [Google Scholar] [CrossRef]
- Rapozo, D.C.; Blanco, T.C.; Reis, B.B.; Gonzaga, I.M.; Valverde, P.; Canetti, C.; Barja-Fidalgo, C.; Simao, T.A.; Albano, R.M.; Kruel, C.D.; et al. Recurrent acute thermal lesion induces esophageal hyperproliferative premalignant lesions in mice esophagus. Exp. Mol. Pathol. 2016, 100, 325–331. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.G.; Shimada, Y.; Sato, F.; Maeda, M.; Itami, A.; Kaganoi, J.; Komoto, I.; Kawabe, A.; Imamura, M. Promotion effects of hot water on N-nitrosomethylbenzylamine-induced esophageal tumorigenesis in F344 rats. Oncol. Rep. 2003, 10, 421–426. [Google Scholar] [CrossRef] [PubMed]
- Okaru, A.O.; Rullmann, A.; Farah, A.; Gonzalez de Mejia, E.; Stern, M.C.; Lachenmeier, D.W. Comparative oesophageal cancer risk assessment of hot beverage consumption (coffee, mate and tea): The margin of exposure of PAH vs very hot temperatures. BMC Cancer 2018, 18, 236. [Google Scholar] [CrossRef] [PubMed]
- Islami, F.; Boffetta, P.; Ren, J.S.; Pedoeim, L.; Khatib, D.; Kamangar, F. High-temperature beverages and foods and esophageal cancer risk—A systematic review. Int. J. Cancer 2009, 125, 491–524. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Zeng, R.; Cao, W.; Luo, R.; Chen, J.; Lin, Y. Hot beverage and food intake and esophageal cancer in southern China. Asian Pac. J. Cancer Prev. 2011, 12, 2189–2192. [Google Scholar] [PubMed]
- Andrici, J.; Eslick, G.D. Hot food and beverage consumption and the risk of esophageal cancer: A meta-analysis. Am. J. Prev. Med. 2015, 49, 952–960. [Google Scholar] [CrossRef] [PubMed]
- Dirler, J.; Winkler, G.; Lachenmeier, D.W. What temperature of coffee exceeds the pain threshold? Pilot study of a sensory analysis method as basis for cancer risk assessment. Foods 2018, 7, 83. [Google Scholar] [CrossRef] [PubMed]
- Baehr, H.D.; Stephan, K. Wärme- und Stoffübertragung; Springer: Berlin/Heidelberg, Germany, 2013. (In German) [Google Scholar]
- Jost, U. Kurzes Lehrbuch der Physikalischen Chemie; Dr. Dietrich Steinkopff Verlag: Darmstadt, Germany, 1966. [Google Scholar]
- Weigand, B.; Köhler, J.; von Wolfersdorf, J. Thermodynamik Kompakt; Springer: Berlin/Heidelberg, Germany, 2013; (In German). [Google Scholar] [CrossRef]
- Böckh, P.; Wetzel, T. Wärmeübertragung. Grundlagen und Praxis; Springer: Berlin/Heidelberg, Germany, 2017; (In German). [Google Scholar] [CrossRef]
- Green, B.G.; Gelhard, B. Perception of temperature on oral and facial skin. Somatosens. Res. 1987, 4, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Schlünder, E.-U. Einführung in die Wärme- und Stoffübertragung; Friedr. Vieweg + Sohn: Braunschweig, Germany, 1975; (In German). [Google Scholar] [CrossRef]
- Specht, E. Vorlesungsmanuskript: Grundlagen der Wärme- und Stoffübertragung. Wintersemester 2008/2009. Available online: http://www.uni-magdeburg.de/isut/TV/Download/Waerme-_und_Stoffuebertragung_Kapitel_1+2_WS0809.pdf (accessed on 6 August 2018). (In German).
- Log, T. Modeling skin injury from hot rice porridge spills. Int. J. Environ. Res. Public Health 2018, 15, 808. [Google Scholar] [CrossRef] [PubMed]
- Grimm, H. Eigenschaften von Wasser in Tabellen, 2006. Available online: http://www.wissenschaft-technik-ethik.de/wasser_eigenschaften.html (accessed on 3 August 2018). (In German).
- Kern. Polyvinyl Chloride (PVC-U). Technical Datasheet; Kern GmbH Kunststoffwerke: Großmaischeid, Germany, 2018. [Google Scholar]
- Spieß, W.E.L.; Walz, E.; Nesvadba, P.; Morley, M.; van Haneghem, I.A.; Salmon, D.R. Thermal conductivity of food materials at elevated temperatures. High Temp. High Press. 2001, 33, 693–697. [Google Scholar] [CrossRef]
- Kurzhals, H.-A. Kühlen und Gefrieren von Lebensmitteln; Behrs: Hamburg, Germany, 2007. (In German) [Google Scholar]
- Lee, H.S.; Carstens, E.; O’Mahony, M. Drinking hot coffee: Why doesn’t it burn the mouth? J. Sens. Stud. 2003, 18, 19–32. [Google Scholar] [CrossRef]
- Langer, T.; Winkler, G.; Lachenmeier, D.W. Untersuchungen zum Abkühlverhalten von Heißgetränken vor dem Hintergrund des temperaturbedingten Krebsrisikos. Deut. Lebensm. Rundsch. 2018, 114, 307–314. (In German) [Google Scholar] [CrossRef]
- DIN. Lebensmittelhygiene—Temperaturen für Lebensmittel; DIN 10508:2012-03; Beuth Verlag GmbH: Berlin, Germany, 2012. (In German) [Google Scholar]
- Riedl, R.; Lütgendorff-Gyllenstorm, H. Zu heißes Essen und Trinken—Die unbeachtete Gefahr. Deut. Lebensm. Rundsch. 2011, 107, 71–83. (In German) [Google Scholar]
- Lütgendorff-Gyllenstorm, H. Risikofaktor Nahrung Mit Mehr als 37 Grad Celsius. Wir essen und Trinken zu Heiß; Verlag Wilhelm Maudrich: Vienna, Austria, 1994. (In German) [Google Scholar]
- Verst, L.-M.; Winkler, G.; Lachenmeier, D.W. Dispensing and serving temperatures of coffee-based hot beverages. Exploratory survey as a basis for cancer risk assessment. Ernahrungs Umschau 2018, 65, 64–70. [Google Scholar] [CrossRef]


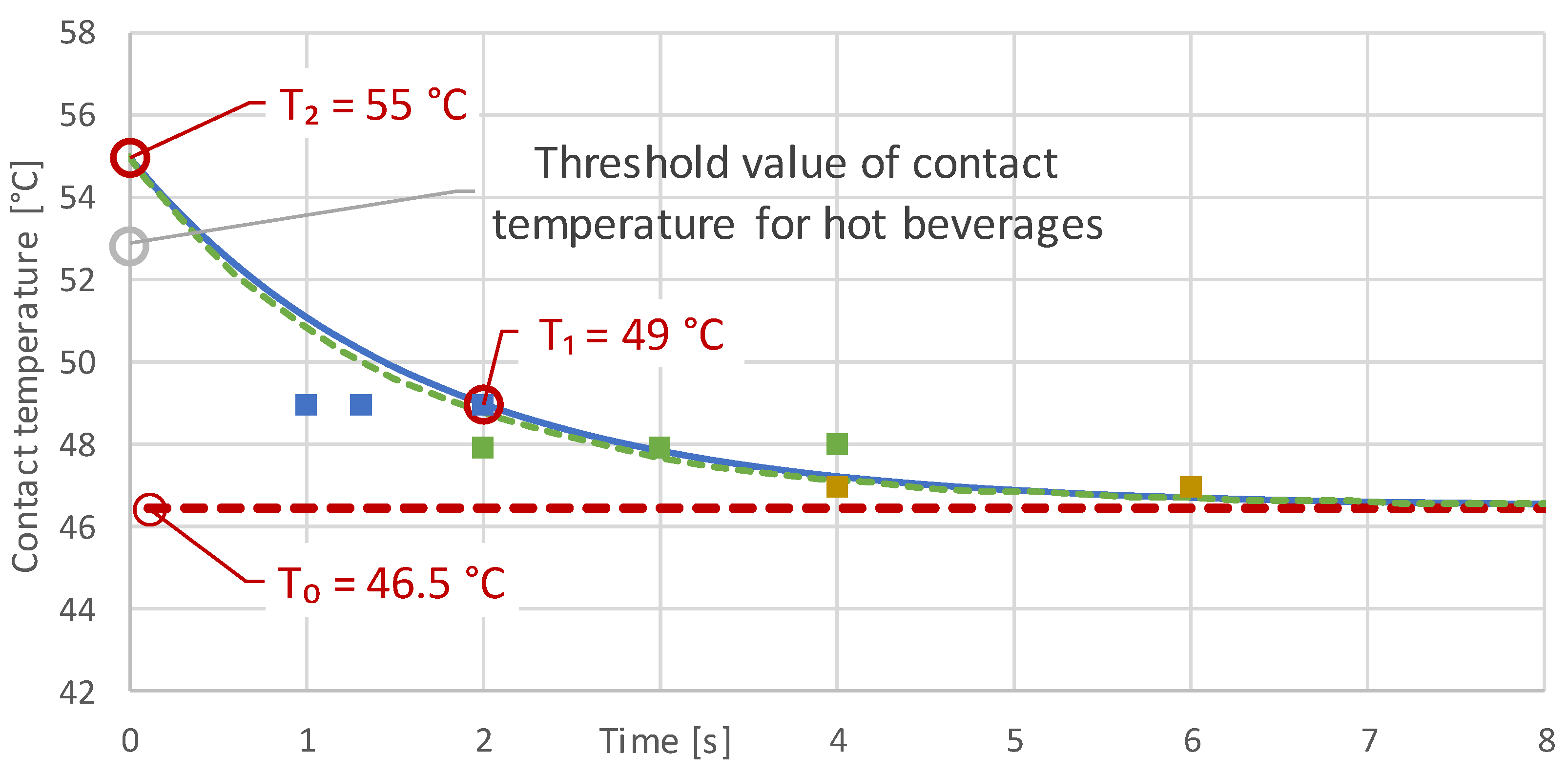
| Measurement | Starting Temperature T (°C) | Contact Temperature T0, T1 (°C) | Measuring Time t (s) |
|---|---|---|---|
| 1 | 75.0 | 46.5 | >10 |
| 2a | 76.8 | 47.0 | 4 |
| 2b | 76.8 | 47.0 | 6 |
| 3a | 80.3 | 48.0 | 3 |
| 3b | 80.3 | 48.0 | 2 |
| 3c | 80.3 | 48.0 | 4 |
| 4a | 83.7 | 49.0 | 1 |
| 4b | 83.7 | 49.0 | 2 |
| 4c | 83.7 | 49.0 | 1 |
| Material Properties | Human Skin | Water (60 °C) | PVC | Potatoes | Cheese | Fish | Meat (Lean) | Vegetables |
|---|---|---|---|---|---|---|---|---|
| Thermal conductivity λ [W/(m·K] | 0.50 | 0.65 | 0.15 | 0.55 | 0.35 | 0.50 | 0.40 | 0.50 |
| Density ρ [kg/m³] | 1020 | 983 | 1380 | 1050 | 1080 | 990 | 990 | 1050 |
| Specifiy heat c [J/(kg·K] | 2400 | 4184 | 960 | 3350 | 2430 | 3430 | 3200 | 3200 |
| Thermal effusivity b = (λ·ρ·c)0.5 | 1106.35 | 1640.23 | 445.78 | 1390.91 | 955.66 | 1303.02 | 1125.70 | 1296.15 |
| Literature | [25] | [30] | [31] | [32] | [33] | [32] | [32] | [32] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lachenmeier, D.W.; Lachenmeier, W. Injury Threshold of Oral Contact with Hot Foods and Method for Its Sensory Evaluation. Safety 2018, 4, 38. https://doi.org/10.3390/safety4030038
Lachenmeier DW, Lachenmeier W. Injury Threshold of Oral Contact with Hot Foods and Method for Its Sensory Evaluation. Safety. 2018; 4(3):38. https://doi.org/10.3390/safety4030038
Chicago/Turabian StyleLachenmeier, Dirk W., and Walter Lachenmeier. 2018. "Injury Threshold of Oral Contact with Hot Foods and Method for Its Sensory Evaluation" Safety 4, no. 3: 38. https://doi.org/10.3390/safety4030038
APA StyleLachenmeier, D. W., & Lachenmeier, W. (2018). Injury Threshold of Oral Contact with Hot Foods and Method for Its Sensory Evaluation. Safety, 4(3), 38. https://doi.org/10.3390/safety4030038






