LiDAR-Based Sensor Fusion SLAM and Localization for Autonomous Driving Vehicles in Complex Scenarios
Abstract
1. Introduction
- The NDT registration, scan context-based loop closure detection and RTK-GNSS are integrated into a LiDAR SLAM framework and innovative use of pose graph to combine multiple methods to optimize position and reduce map drift.
- LiDAR matching localization position and vehicle states are fused by ESKF, which takes full advantage of the vehicle velocity constraints of ground autonomous vehicles to optimize localization results and provide robust and accurate localization results.
- A general framework with mapping and localization is proposed, which is tested on the KITTI dataset [14] and real scenarios. Results demonstrate the effectiveness of the proposed framework.
2. Related Work
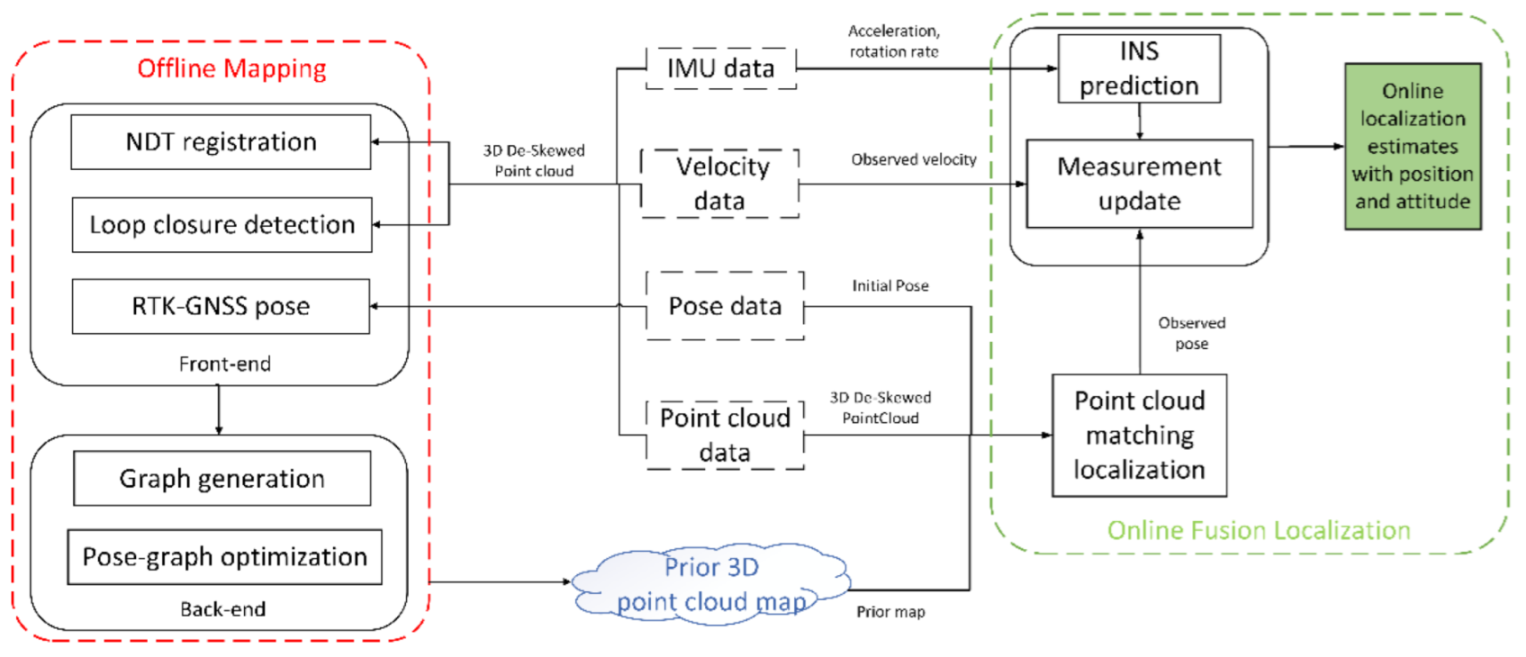
3. The Offline Mapping
3.1. LiDAR SLAM Front-End
3.1.1. NDT Based Registration
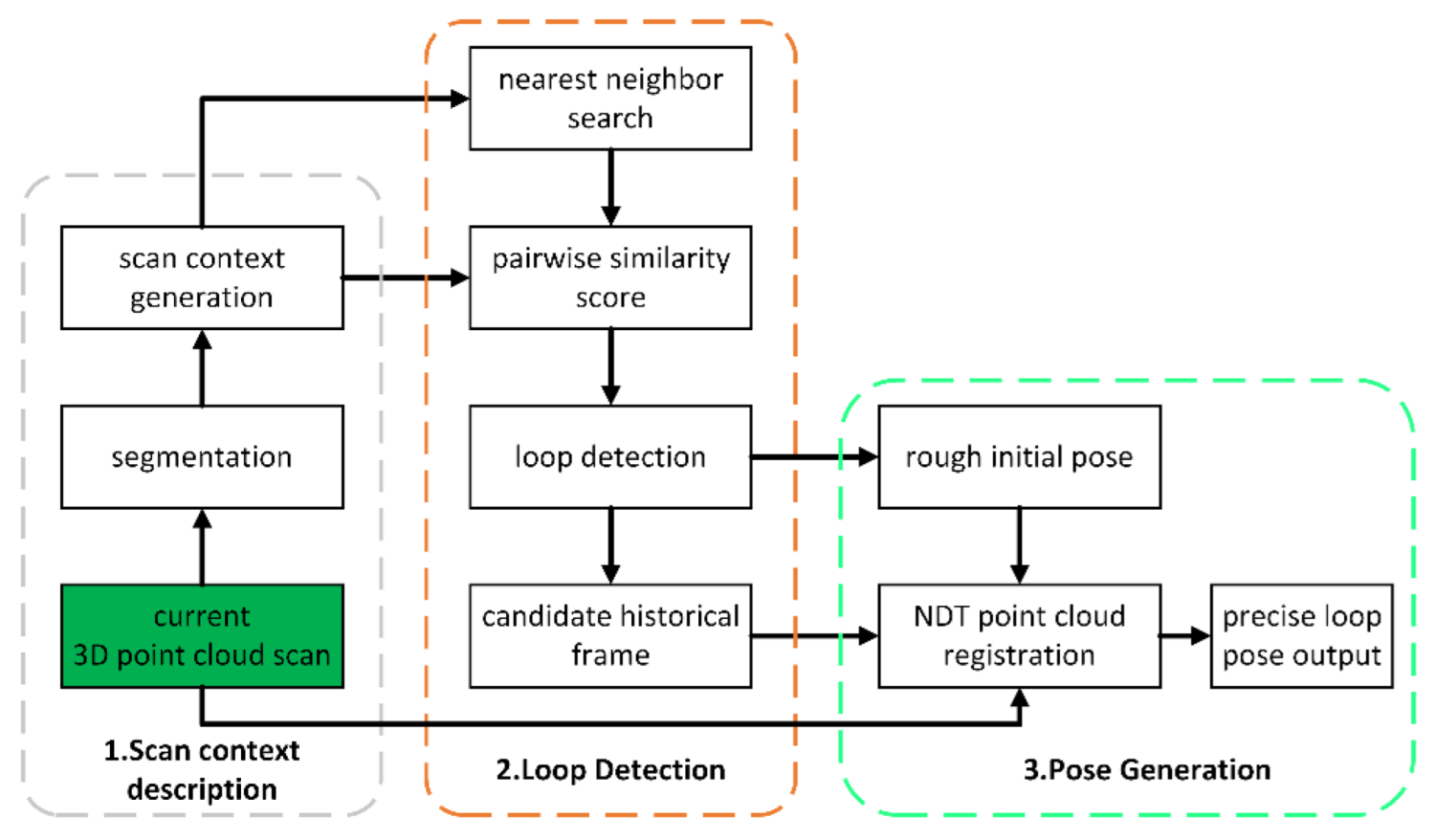
3.1.2. Scan Context Based Loop Closure Detection
3.1.3. RTK-GNSS Based Localization
3.2. Back-End Optimization
| Algorithm 1. The process of back-end optimization |
| Input: |
| LiDAR odometry position xi, xj |
| RTK-GNSS position zi |
| Loop closure position zi,j′ |
| Output: |
| Optimized vehicle position xopt |
| 1: Trajectory alignment for xi, zi and zi,j′ |
| 2: for each position xi do |
| 3: if meet optimization cycle times h then |
| 4: execute optimization process: |
| 5: xopt = arg min F(xi, xj, zi, zi,j′) |
| 6: else |
| 7: add RTK-GNSS position zi constraint |
| 8: if loop closure position detected then |
| 9: add loop closure position zi,j′ constraint |
| 10: end if |
| 11: end if |
| 12: end for |
| 13: return optimized vehicle position xopt |
3.2.1. Graph Generation
3.2.2. Graph Optimization
4. The Online Localization
4.1. LiDAR Localization Based on 3D Point Cloud Map
| Algorithm 2. LiDAR localization in prior 3D point cloud map |
| Input: |
| RTK-GNSS position zi |
| Point cloud pi |
| Prior 3D point cloud global map M |
| Output: |
| LiDAR localization position xlidar |
| 1: Load 3D point cloud map M |
| 2: if get the initial position zi then |
| 3: load local submap Msub from global map M |
| 4: if need update submap Msub then |
| 5: update submap Msub |
| 6: else |
| 7: calculate position between pi and Msub: |
| 8: NDT registration xlidar = pi ∝ Msub |
| 9: end if |
| 10: else |
| 11: wait for initial position zi |
| 12: end if |
| 13: return LiDAR localization position xlidar |
4.2. Filter State Equation
4.3. Filter Measurement Update Equation
5. Experimental Verification and Performance Analysis
5.1. The Experiment Based on KITTI Dataset
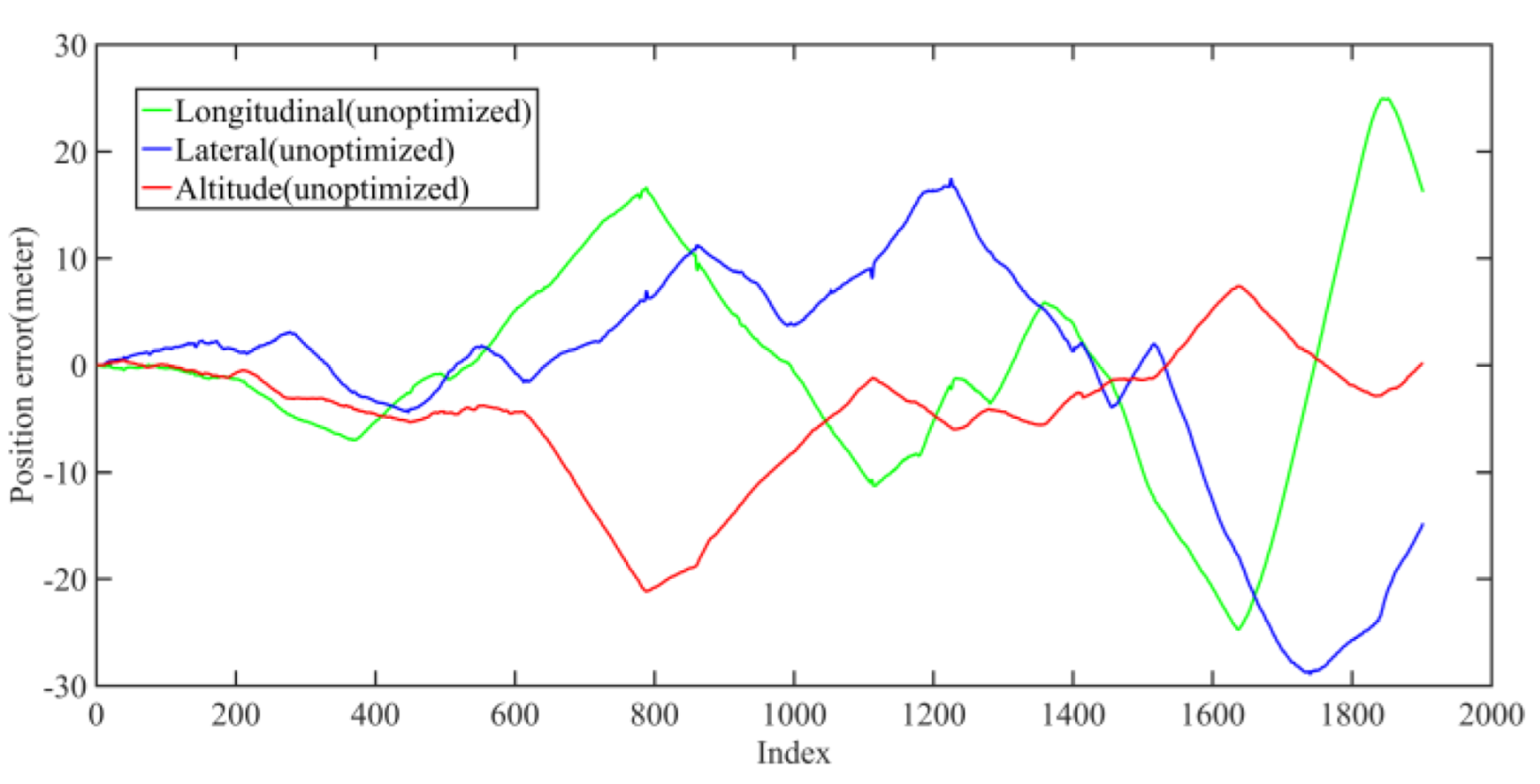
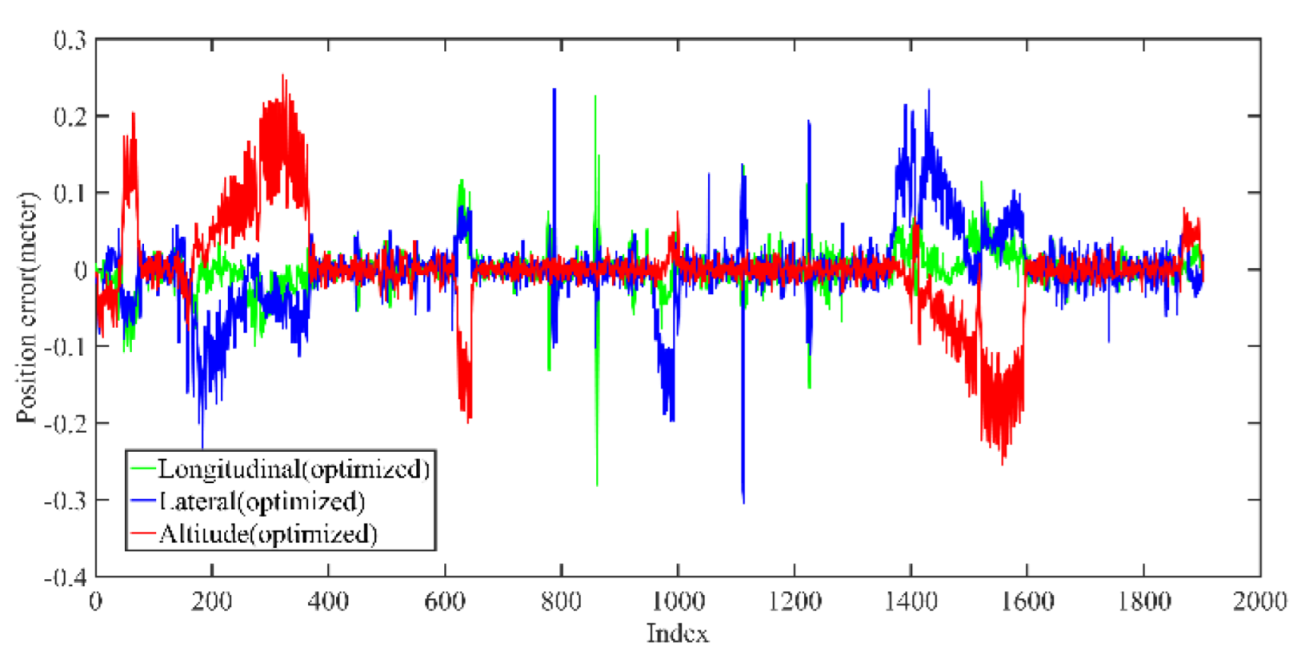
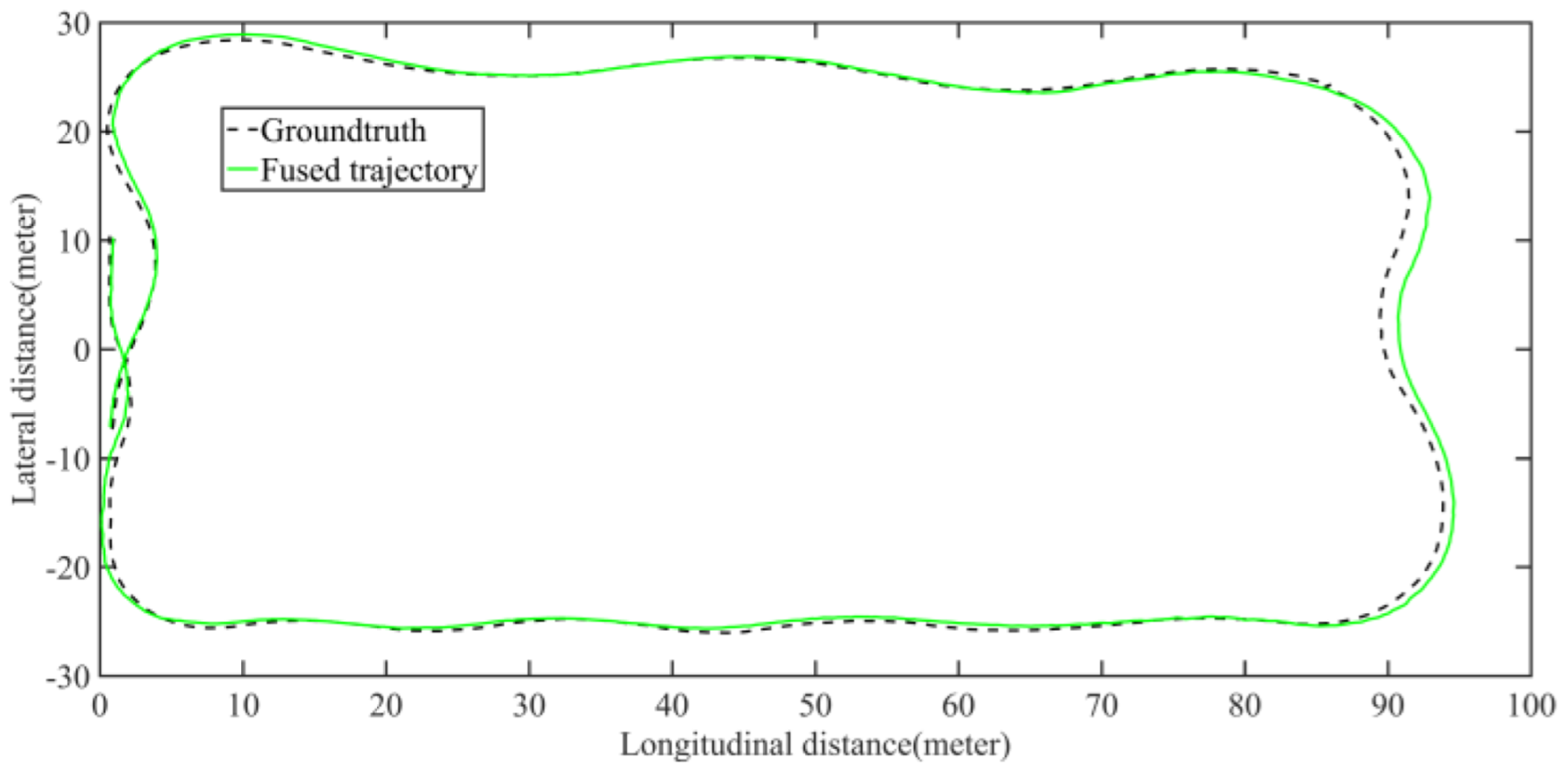
5.1.1. Mapping Performance Analysis Based on KITTI Dataset
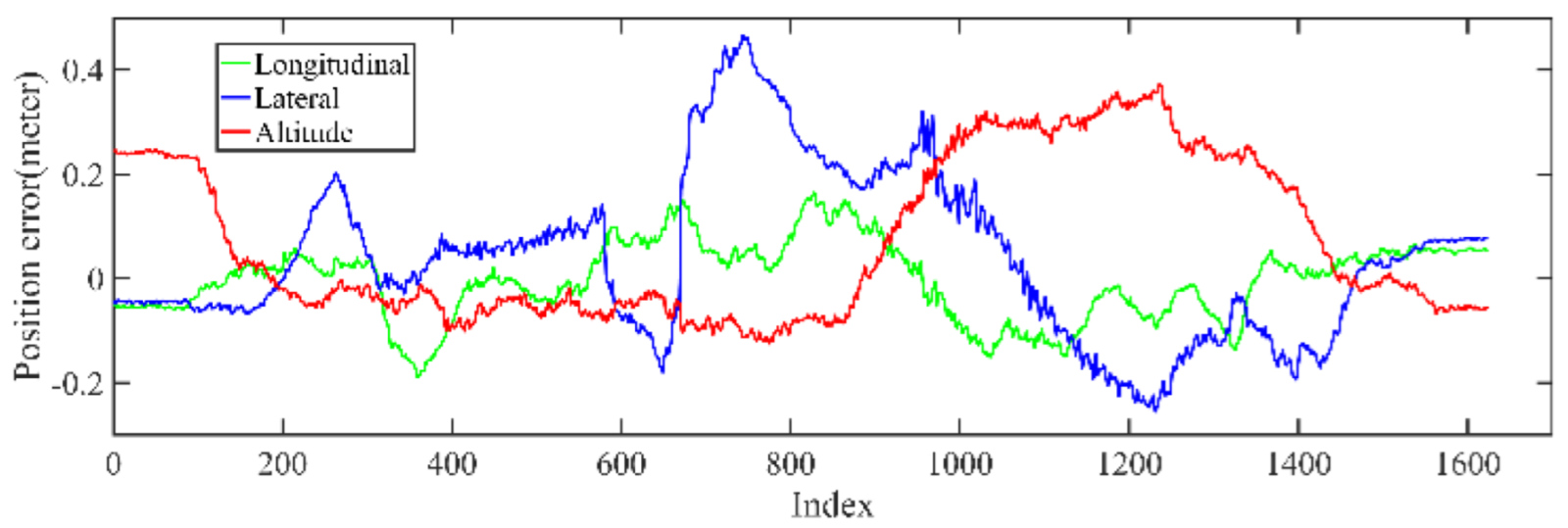
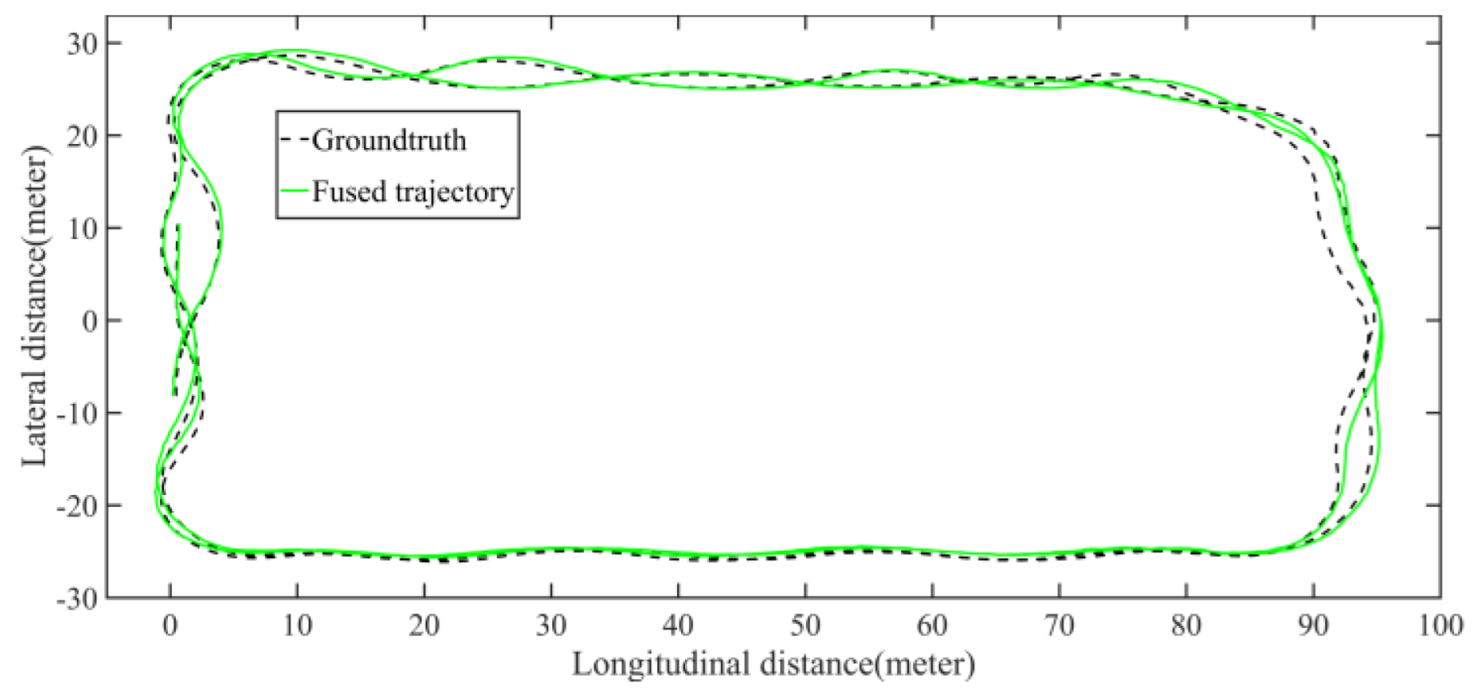
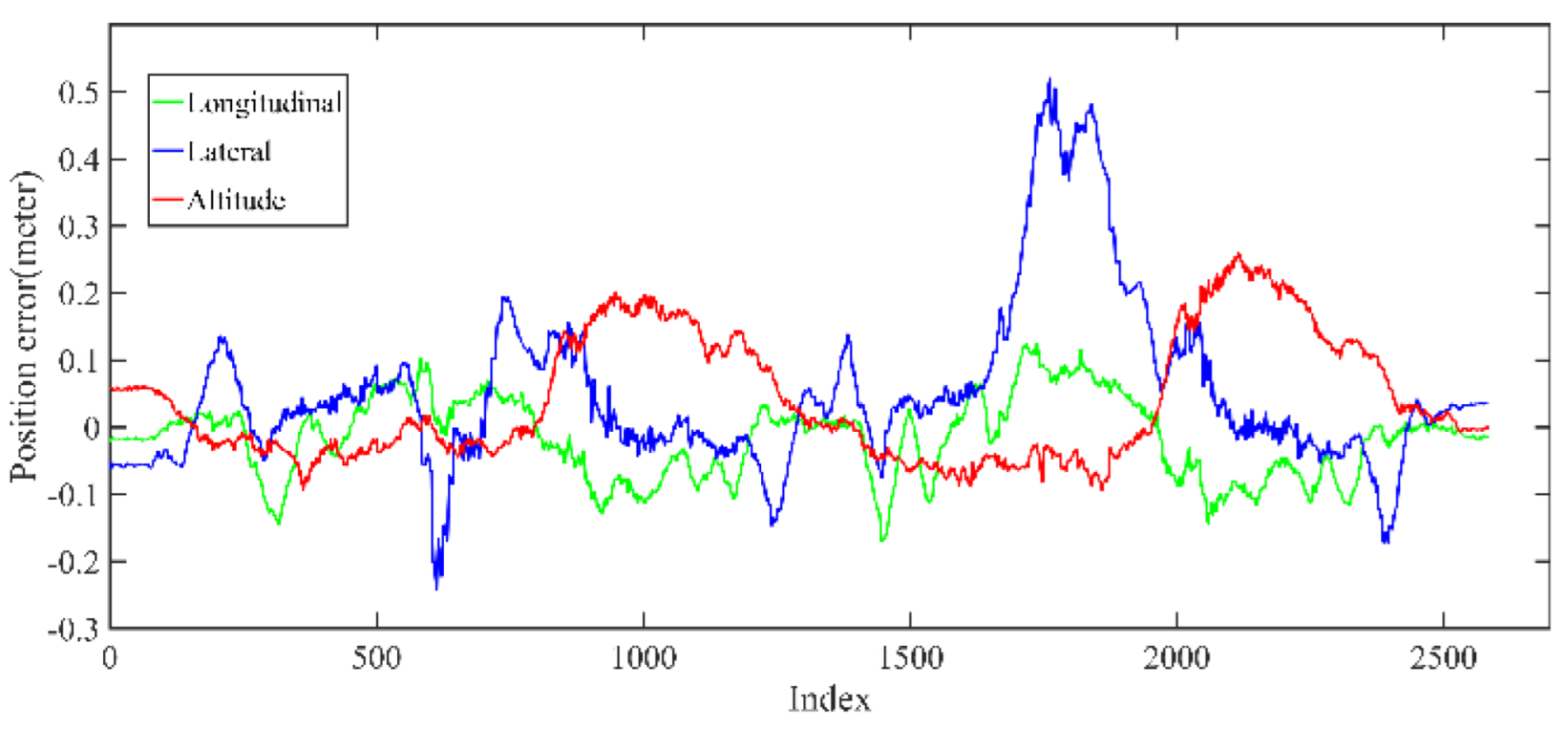
5.1.2. Localization Performance Analysis Based on KITTI Dataset
5.2. The Field Test Vehicle and Test Results
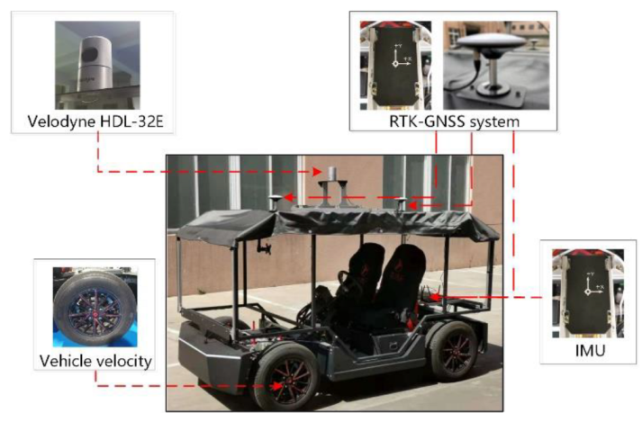
5.2.1. Test Vehicle and Sensor Configuration
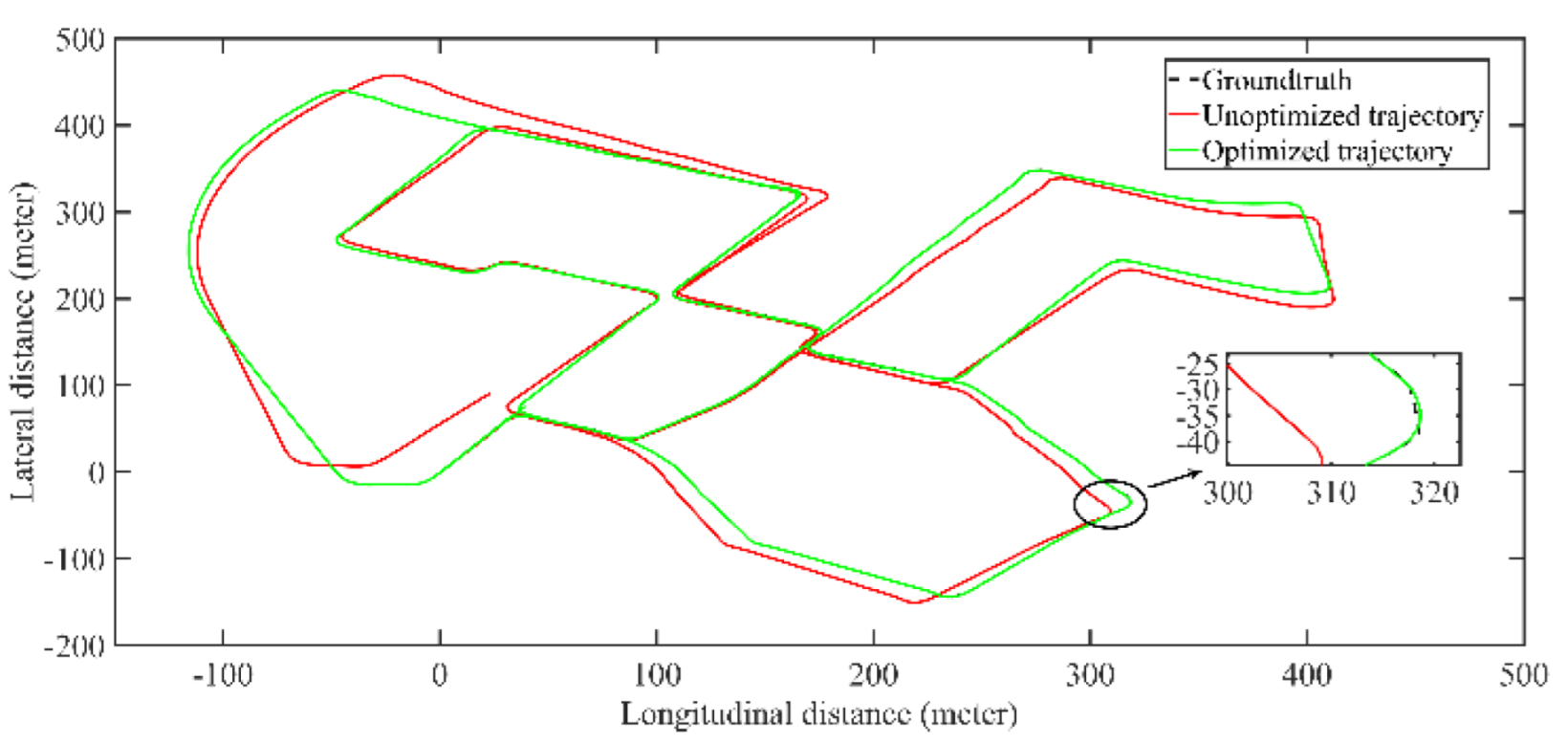
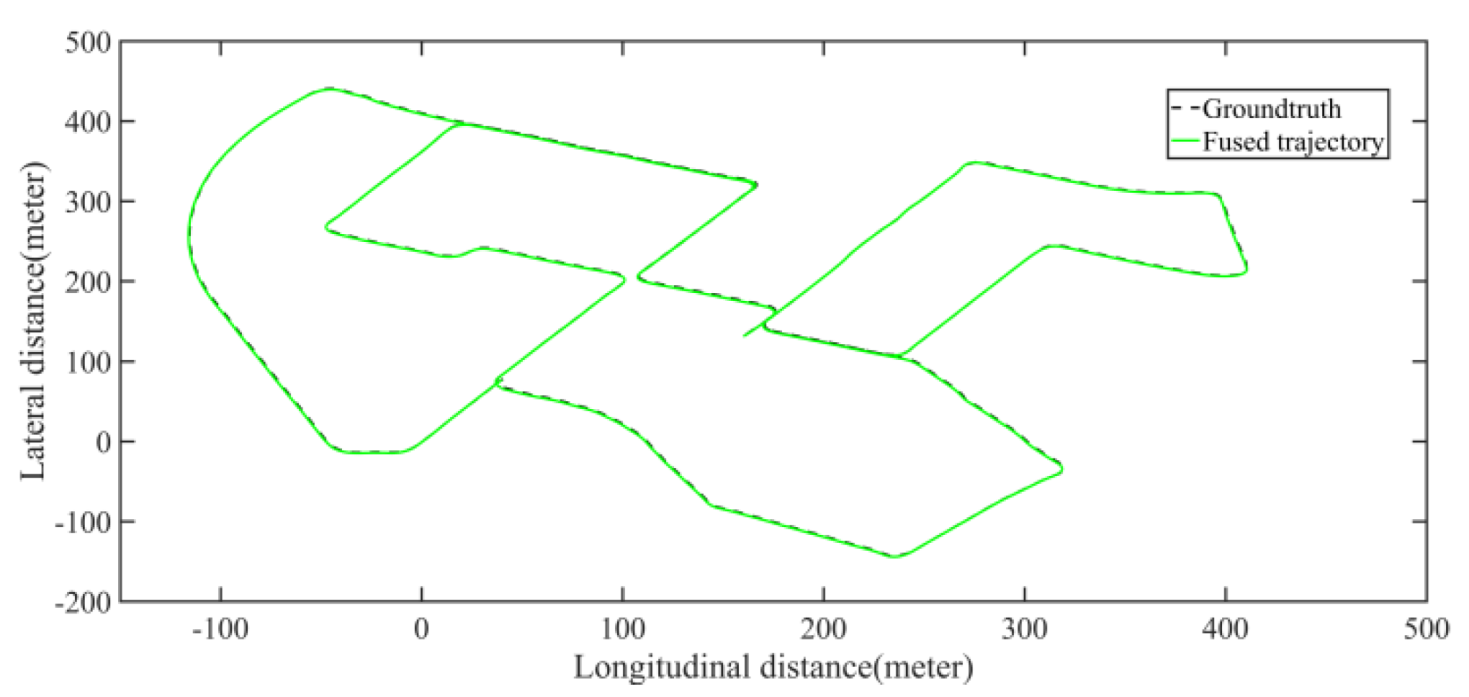
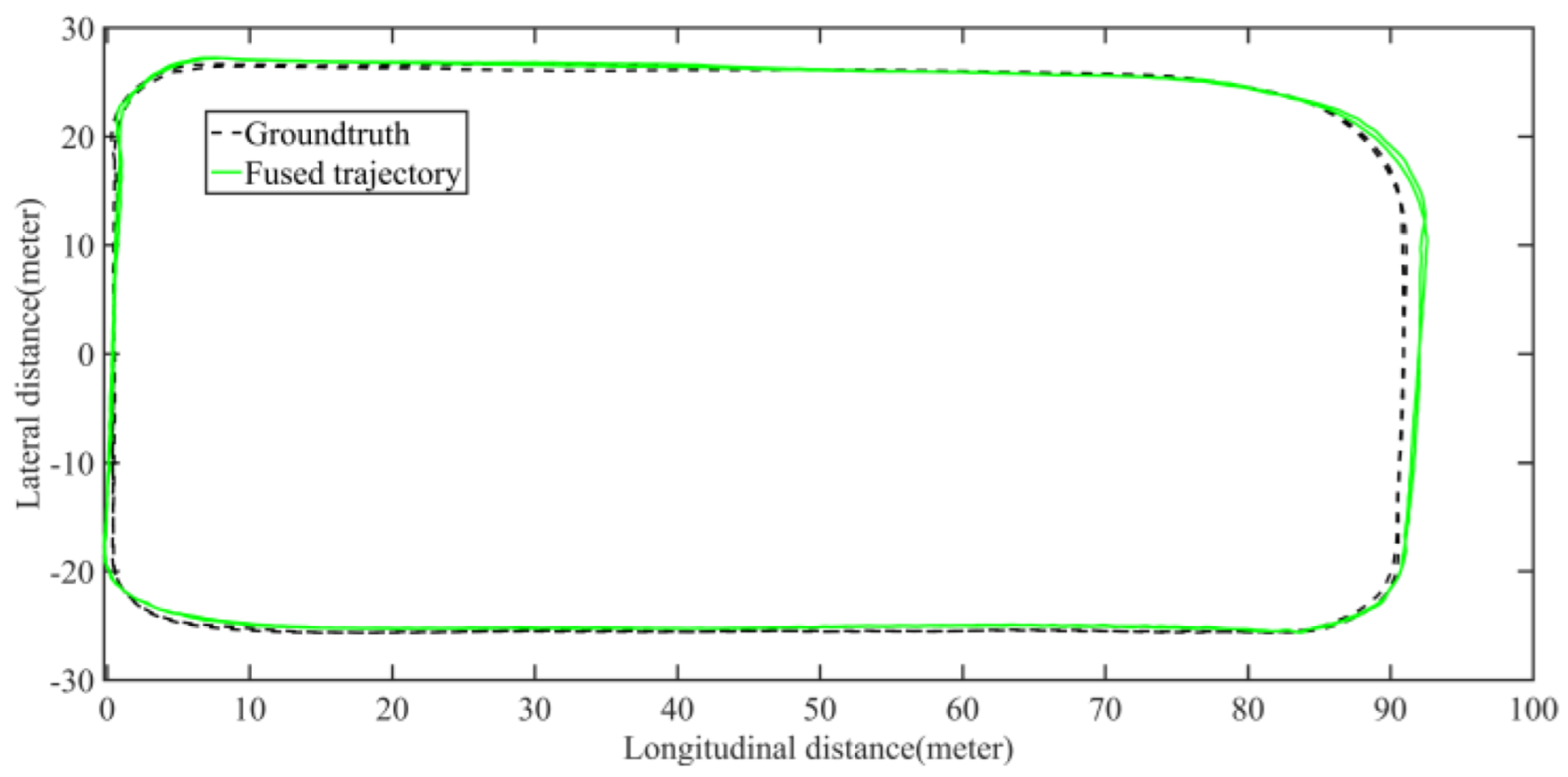
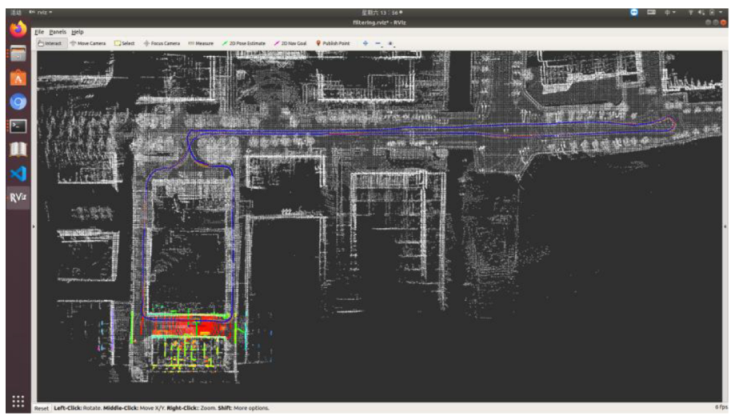
5.2.2. Field Test Mapping Performance Analysis
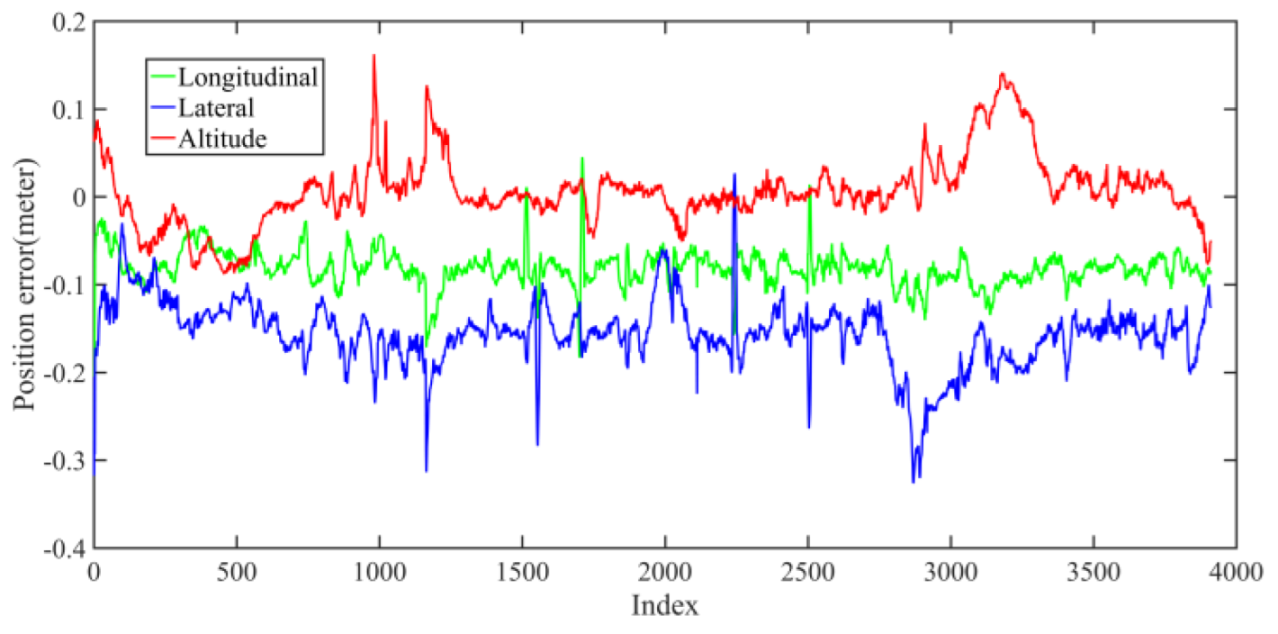
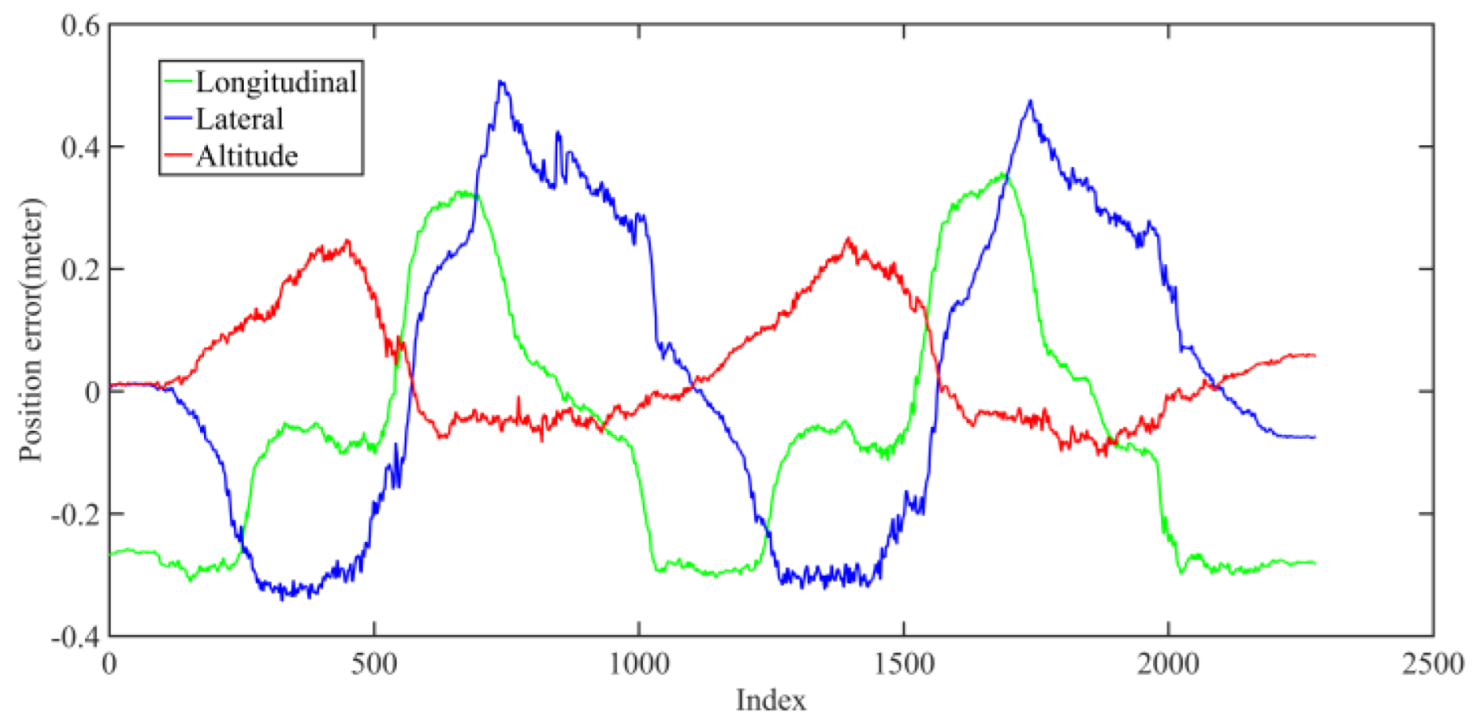
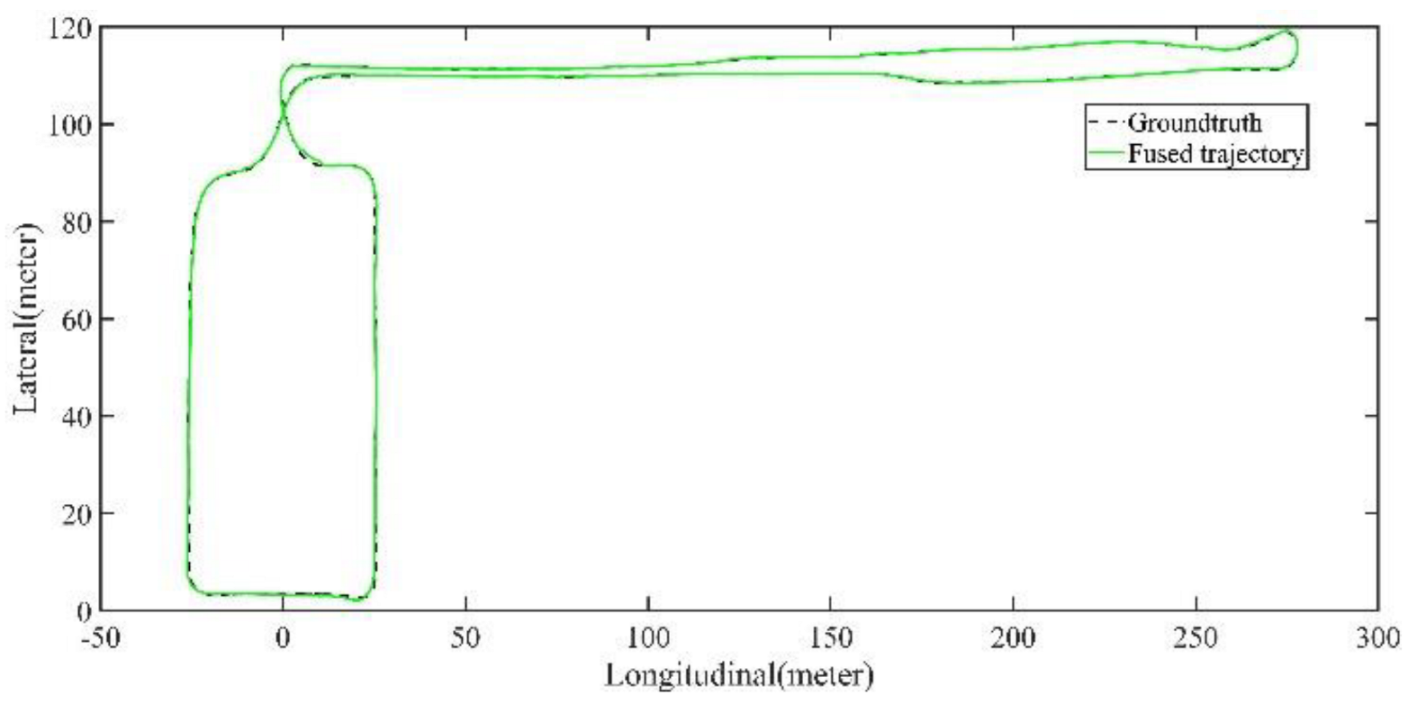
5.2.3. Field Test Localization Performance Analysis
6. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aslan, M.F.; Durdu, A.; Yusefi, A.; Sabanci, K.; Sungur, C. A tutorial: Mobile robotics, SLAM, bayesian filter, keyframe bundle adjustment and ROS applications. Robot Oper. Syst. (ROS) 2021, 6, 227–269. [Google Scholar]
- Suhr, J.K.; Jang, J.; Min, D.; Jung, H.G. Sensor fusion-based low-cost vehicle localization system for complex urban environments. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1078–1086. [Google Scholar] [CrossRef]
- Kuutti, S.; Fallah, S.; Katsaros, K.; Dianati, M.; Mccullough, F.; Mouzakitis, A. A survey of the state-of-the-art localization techniques and their potentials for autonomous vehicle applications. IEEE Internet Things J. 2018, 5, 829–846. [Google Scholar] [CrossRef]
- Kim, C.; Cho, S.; Sunwoo, M.; Resende, P.; Bradaï, B.; Jo, K. Updating Point Cloud Layer of High Definition (HD) Map Based on Crowd-Sourcing of Multiple Vehicles Installed LiDAR. IEEE Access 2021, 9, 8028–8046. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Pomerleau, F.; Colas, F.; Siegwart, R.; Magnenat, S. Comparing ICP variants on real-world data sets. Auton. Robot. 2013, 34, 133–148. [Google Scholar] [CrossRef]
- Einhorn, E.; Gross, H.-M. Generic NDT mapping in dynamic environments and its application for lifelong SLAM. Robot. Auton. Syst. 2015, 69, 28–39. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2007; Volume 2. [Google Scholar]
- Zhang, T.; Wu, K.; Song, J.; Huang, S.; Dissanayake, G. Convergence and consistency analysis for a 3-D invariant-EKF SLAM. IEEE Robot. Autom. Lett. 2017, 2, 733–740. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, L.; Bi, L. Robust GICP-based 3D LiDAR SLAM for underground mining environment. Sensors 2019, 19, 2915. [Google Scholar] [CrossRef]
- Fayyad, J.; Jaradat, M.A.; Gruyer, D.; Najjaran, H. Deep learning sensor fusion for autonomous vehicle perception and localization: A review. Sensors 2020, 20, 4220. [Google Scholar] [CrossRef]
- Ahmed, H.; Tahir, M. Accurate attitude estimation of a moving land vehicle using low-cost MEMS IMU sensors. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1723–1739. [Google Scholar] [CrossRef]
- Levinson, J.; Montemerlo, M.; Thrun, S. Map-based precision vehicle localization in urban environments. In Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2009; Volume 4. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Junior, E.M.O.; Santos, D.R.; Miola, G.A.R. A New Variant of the ICP Algorithm for Pairwise 3D Point Cloud Registration. Am. Acad. Sci. Res. J. Eng. Technol. Sci. 2022, 85, 71–88. [Google Scholar]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Robot. 2007, 24, 803–827. [Google Scholar] [CrossRef]
- Ren, R.; Fu, H.; Wu, M. Large-scale outdoor slam based on 2d lidar. Electronics 2019, 8, 613. [Google Scholar] [CrossRef]
- Li, G.; Liao, X.; Huang, H.; Song, S.; Zeng, Y. Robust Stereo Visual SLAM for Dynamic Environments with Moving Object. IEEE Access 2021, 9, 32310–32320. [Google Scholar] [CrossRef]
- Wen, W.; Hsu, L.-T.; Zhang, G. Performance analysis of NDT-based graph SLAM for autonomous vehicle in diverse typical driving scenarios of Hong Kong. Sensors 2018, 18, 3928. [Google Scholar] [CrossRef]
- Luo, L.; Cao, S.-Y.; Han, B.; Shen, H.-L.; Li, J. BVMatch: LiDAR-Based place recognition using bird’s-eye view images. IEEE Robot. Autom. Lett. 2021, 6, 6076–6083. [Google Scholar] [CrossRef]
- Kasaei, S.H.; Tomé, A.M.; Lopes, L.S.; Oliveira, M. GOOD: A global orthographic object descriptor for 3D object recognition and manipulation. Pattern Recognit. Lett. 2016, 83, 312–320. [Google Scholar] [CrossRef]
- Kim, G.; Park, B.; Kim, A. 1-day learning, 1-year localization: Long-term lidar localization using scan context image. IEEE Robot. Autom. Lett. 2019, 4, 1948–1955. [Google Scholar] [CrossRef]
- Xue, G.; Wei, J.; Li, R.; Cheng, J. LeGO-LOAM-SC: An Improved Simultaneous Localization and Mapping Method Fusing LeGO-LOAM and Scan Context for Underground Coalmine. Sensors 2022, 22, 520. [Google Scholar] [CrossRef]
- Arshad, S.; Kim, G.-W. Role of deep learning in loop closure detection for visual and lidar slam: A survey. Sensors 2021, 21, 1243. [Google Scholar] [CrossRef]
- Fan, T.; Wang, H.; Rubenstein, M.; Murphey, T. CPL-SLAM: Efficient and certifiably correct planar graph-based SLAM using the complex number representation. IEEE Trans. Robot. 2020, 36, 1719–1737. [Google Scholar] [CrossRef]
- Vallvé, J.; Solà, J.; Andrade-Cetto, J. Pose-graph SLAM sparsification using factor descent. Robot. Auton. Syst. 2019, 119, 108–118. [Google Scholar] [CrossRef]
- Macenski, S.; Jambrecic, I. SLAM Toolbox: SLAM for the dynamic world. J. Open Source Softw. 2021, 6, 2783. [Google Scholar] [CrossRef]
- Grisetti, G.; Kümmerle, R.; Stachniss, C.; Burgard, W. A tutorial on graph-based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Latif, Y.; Cadena, C.; Neira, J. Robust loop closing over time for pose graph SLAM. Int. J. Robot. Res. 2013, 32, 1611–1626. [Google Scholar] [CrossRef]
- Lin, R.; Xu, J.; Zhang, J. GLO-SLAM: A slam system optimally combining GPS and LiDAR odometry. Ind. Robot Int. J. Robot. Res. Appl. 2021; ahead-of-print. [Google Scholar] [CrossRef]
- Chang, L.; Niu, X.; Liu, T. GNSS/IMU/ODO/LiDAR-SLAM Integrated Navigation System Using IMU/ODO Pre-Integration. Sensors 2020, 20, 4702. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Wang, B.; Lu, C.X.; Trigoni, N.; Markham, A. A survey on deep learning for localization and mapping: Towards the age of spatial machine intelligence. arXiv 2020, arXiv:2006.12567. [Google Scholar]
- Wang, K.; Ma, S.; Chen, J.; Ren, F.; Lu, J. Approaches challenges and applications for deep visual odometry toward to complicated and emerging areas. IEEE Trans. Cogn. Dev. Syst. 2020, 14, 35–49. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, S.; Atia, M.M.; Noureldin, A. INS/GPS/LiDAR integrated navigation system for urban and indoor environments using hybrid scan matching algorithm. Sensors 2015, 15, 23286–23302. [Google Scholar] [CrossRef] [PubMed]
- Grupp, M. evo: Python Package for the Evaluation of Odometry and Slam. Available online: https://github.com/MichaelGrupp/evo (accessed on 16 November 2022).



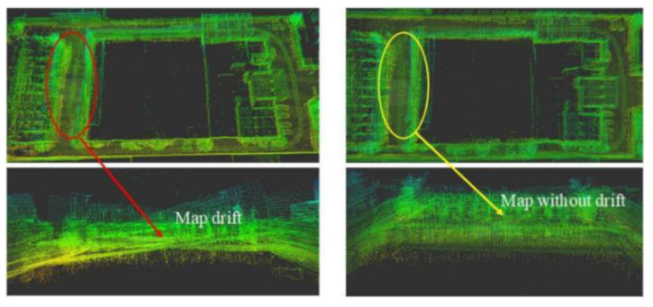

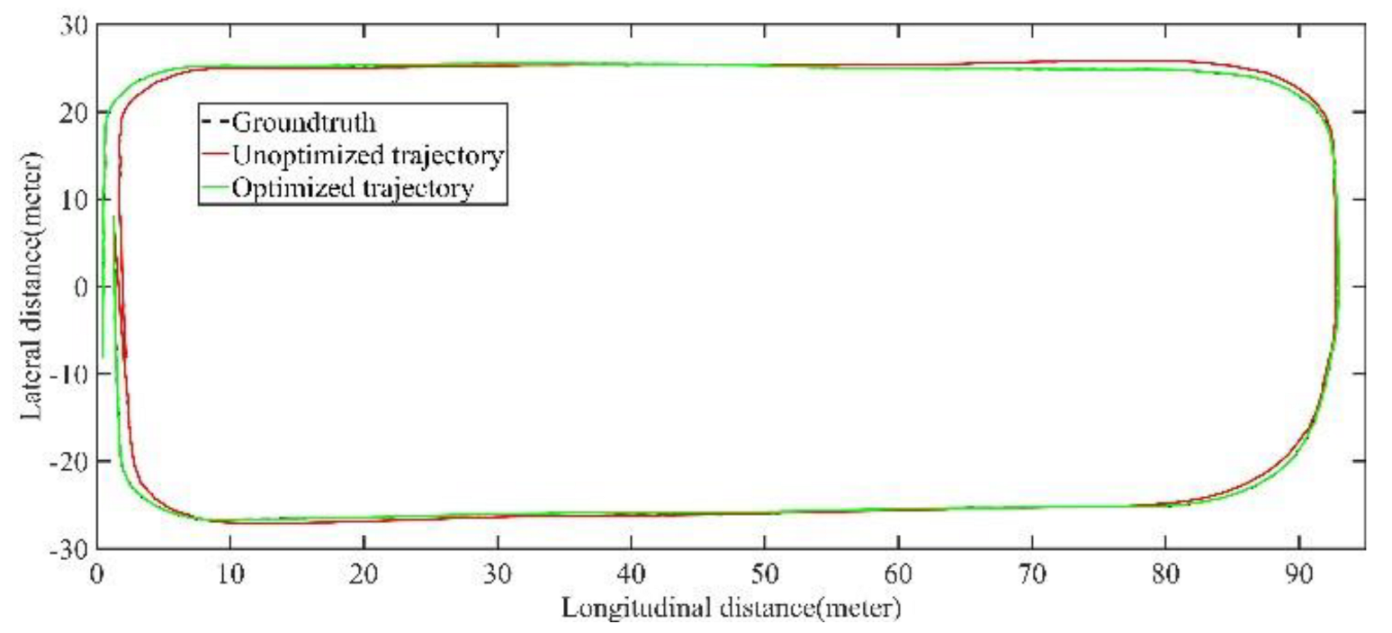
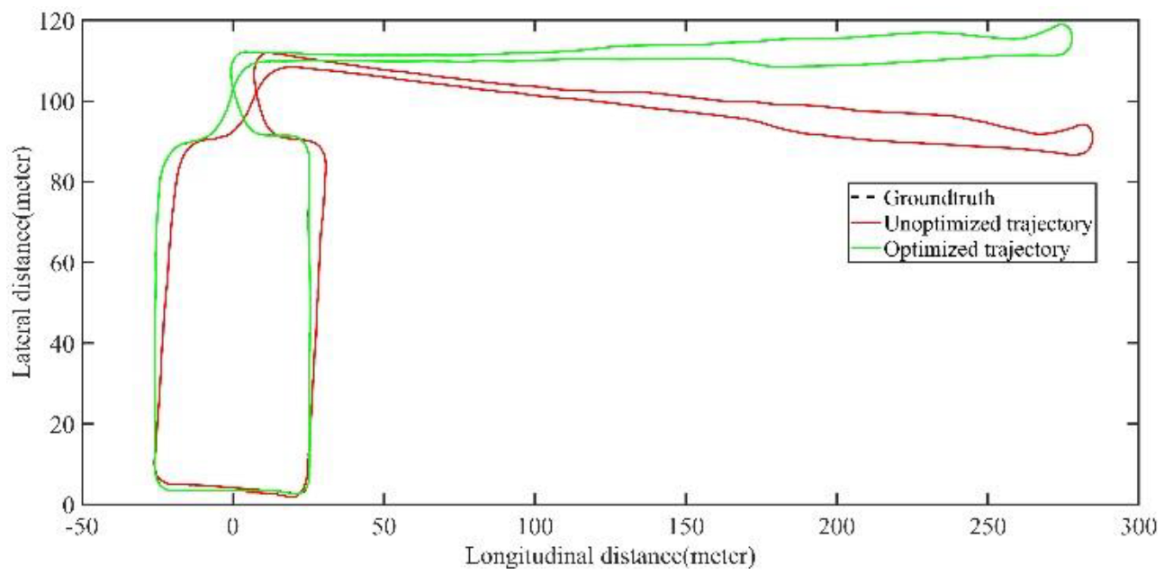

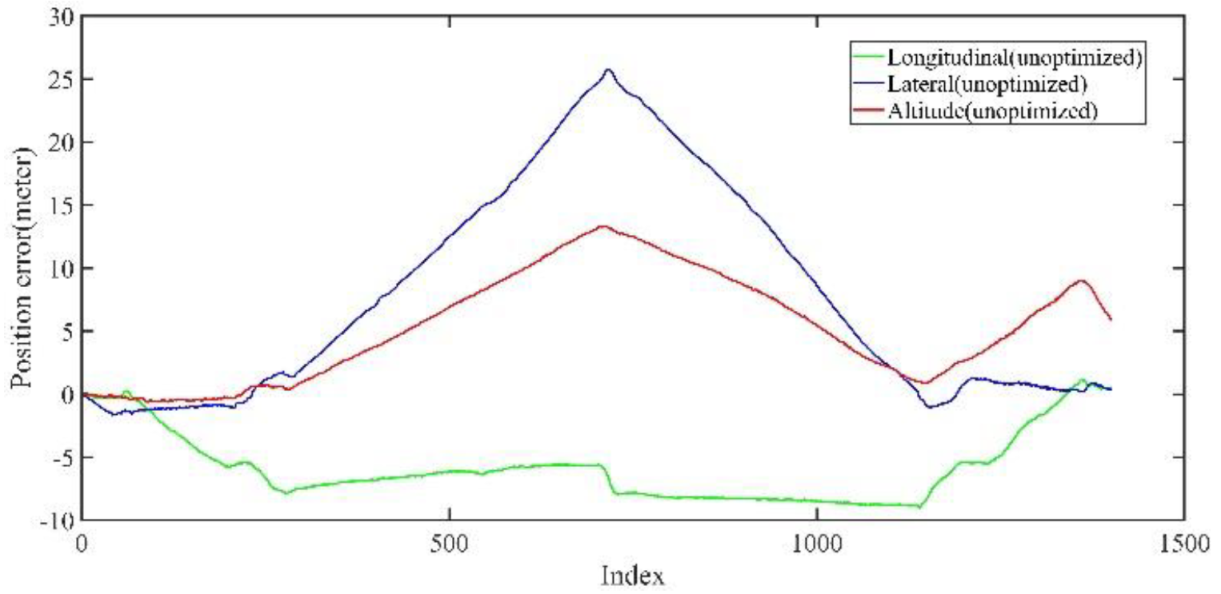
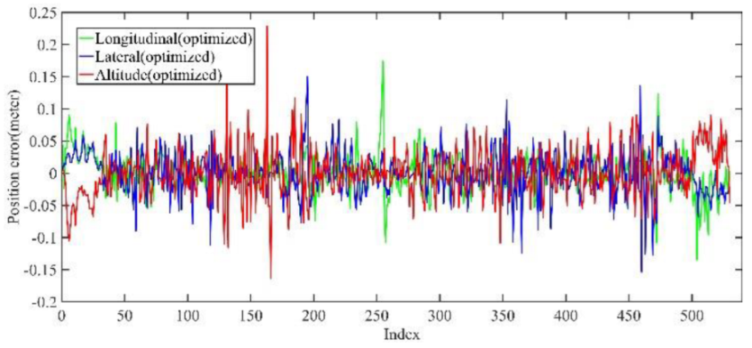
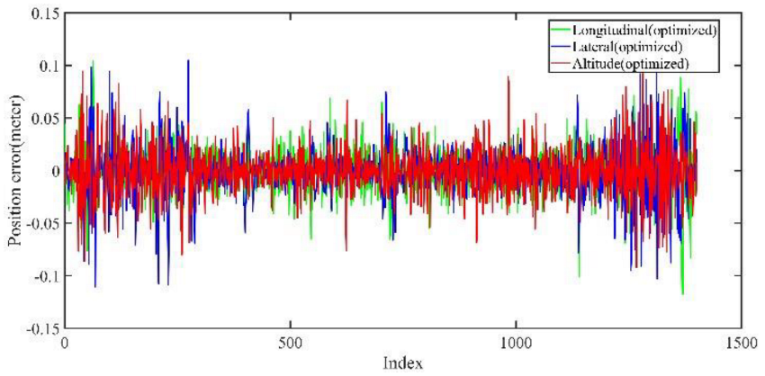

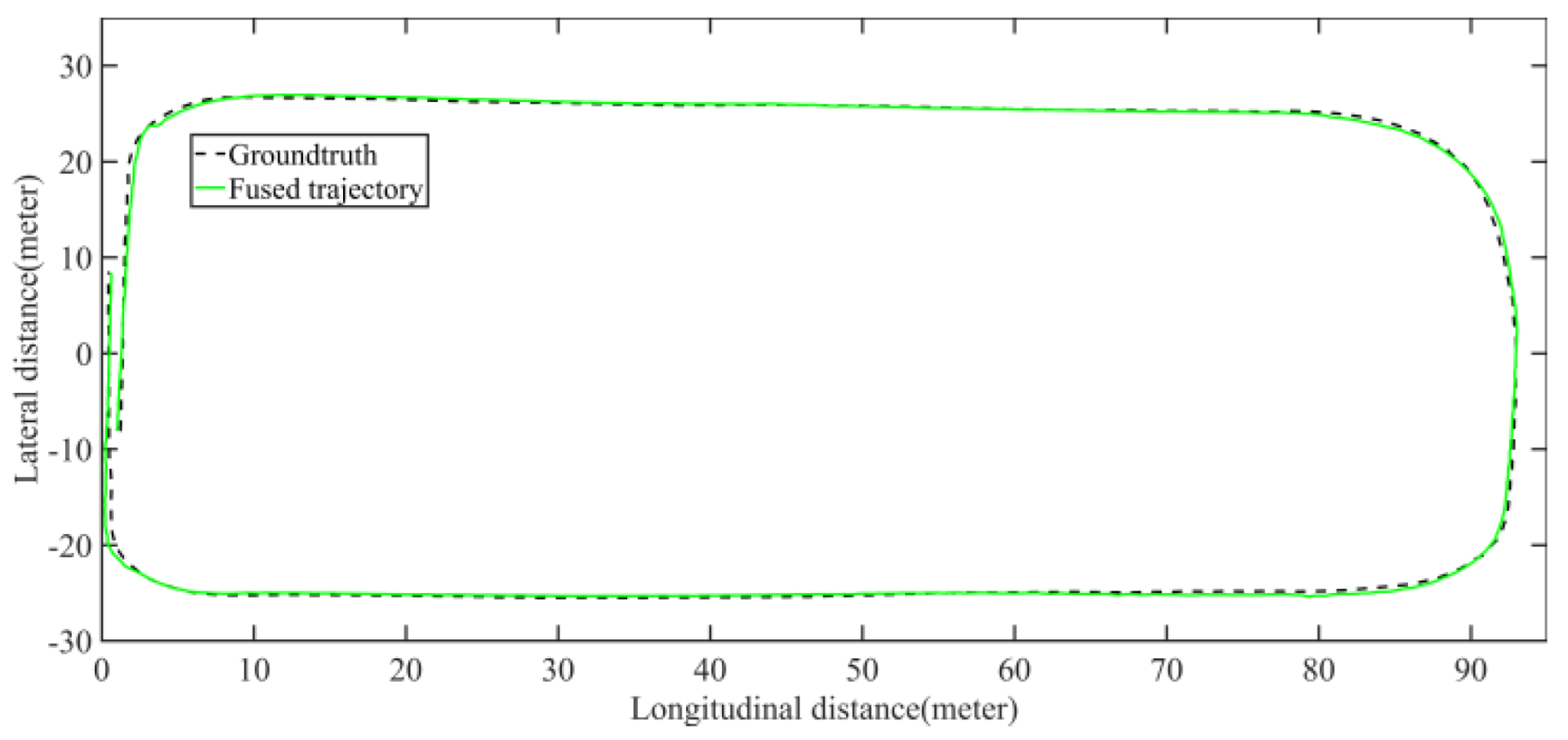
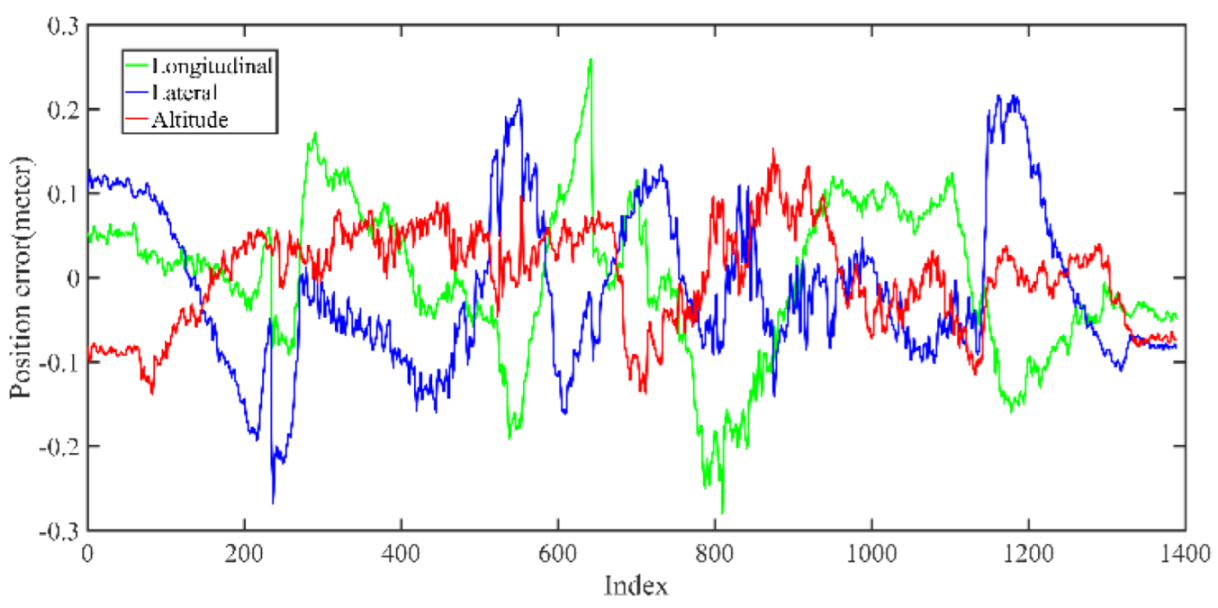



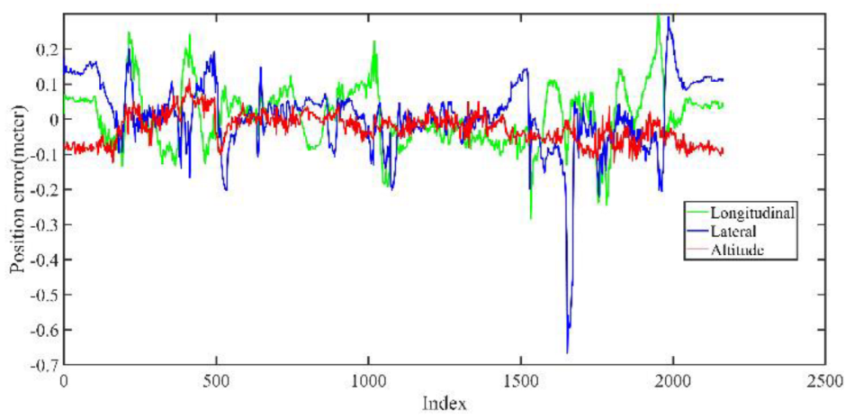
| Max | Min | Mean | RMSE | STD | |
|---|---|---|---|---|---|
| Before optimization | 34.31 | 0.02 | 13.61 | 16.61 | 9.53 |
| After optimization | 0.23 | 0.01 | 0.11 | 0.13 | 0.09 |
| Max | Min | Mean | RMSE | STD |
|---|---|---|---|---|
| 0.35 | 0.08 | 0.18 | 0.16 | 0.07 |
| Sensors | Specifications | No. | Frequency/Hz | Accuracy |
|---|---|---|---|---|
| 3D LiDAR | Velodyne, HDL-32E, 32 beams | 1 | 10 | 2 cm, 0.09 deg |
| RTK-GNSS system | StarNeto, Newton-M2, L1/L2 RTK | 1 | 50 | 2 cm, 0.1 deg |
| IMU | Newton-M2 | 1 | 100 | 5 deg/h, 0.5 mg |
| Vehicle velocity | On-board CAN bus | 1 | 100 | 0.1 m/s |
| Field Test Sequence | Test Scenario | Average Error | RMSE |
|---|---|---|---|
| 01 | Normal driving, 1 lap | 21.6 cm | 23.2 cm |
| 02 | Curve driving, 1 lap | 22.5 cm | 24.3 cm |
| 03 | Normal driving, 2 laps | 28.3 cm | 29.2 cm |
| 04 | Curve driving, 2 laps | 25.5 cm | 27.1 cm |
| 05 | Large scale, 1 laps | 29.2 cm | 29.6 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, K.; Sun, B.; Wu, G.; Zhao, S.; Ma, F.; Zhang, Y.; Wu, J. LiDAR-Based Sensor Fusion SLAM and Localization for Autonomous Driving Vehicles in Complex Scenarios. J. Imaging 2023, 9, 52. https://doi.org/10.3390/jimaging9020052
Dai K, Sun B, Wu G, Zhao S, Ma F, Zhang Y, Wu J. LiDAR-Based Sensor Fusion SLAM and Localization for Autonomous Driving Vehicles in Complex Scenarios. Journal of Imaging. 2023; 9(2):52. https://doi.org/10.3390/jimaging9020052
Chicago/Turabian StyleDai, Kai, Bohua Sun, Guanpu Wu, Shuai Zhao, Fangwu Ma, Yufei Zhang, and Jian Wu. 2023. "LiDAR-Based Sensor Fusion SLAM and Localization for Autonomous Driving Vehicles in Complex Scenarios" Journal of Imaging 9, no. 2: 52. https://doi.org/10.3390/jimaging9020052
APA StyleDai, K., Sun, B., Wu, G., Zhao, S., Ma, F., Zhang, Y., & Wu, J. (2023). LiDAR-Based Sensor Fusion SLAM and Localization for Autonomous Driving Vehicles in Complex Scenarios. Journal of Imaging, 9(2), 52. https://doi.org/10.3390/jimaging9020052






