Reconstructing Floorplans from Point Clouds Using GAN
Abstract
1. Introduction
- (1)
- The segmentation process by Mask-RCNN divides the overall density map into several room areas, and enlarges each room mask to the same size. It cuts each room into an individual area for further independent optimization and retains the semantic information well for each room. This method can amplify the room features, allowing the model to detect more subtle mask defects, especially in small rooms. At the same time, the zoning method can simplify the input features, prompting the generative model to focus its attention on a single room and improve the repair capability of the generative network.
- (2)
- The proposed method repairs the room mask using the generated network. By introducing a U-Net structure model into the generation network used in this paper, the room instances are regenerated piecewise-fully with a more regular geometric structure. The U-Net structure model can retain more details of the original mask and repair mask defects while preserving as much of the original geometric information as possible.
- (3)
- An edge optimization method is designed to remove those edge artifacts that Convolutional Neural Networks (CNN)-based algorithms cannot handle. It not only makes the mask edges as straight as possible, but also combines the mask instances into a compact and non-overlapping floorplan.
- (4)
- Compared with existing methods, the proposed method offers significant improvements in accuracy and efficiency.
2. Related Work
2.1. Floorplan Reconstruction
2.2. Image Generation
2.3. Instance Segmentation
3. Method
3.1. Region Segmentation
3.2. Room Mask Repair Process
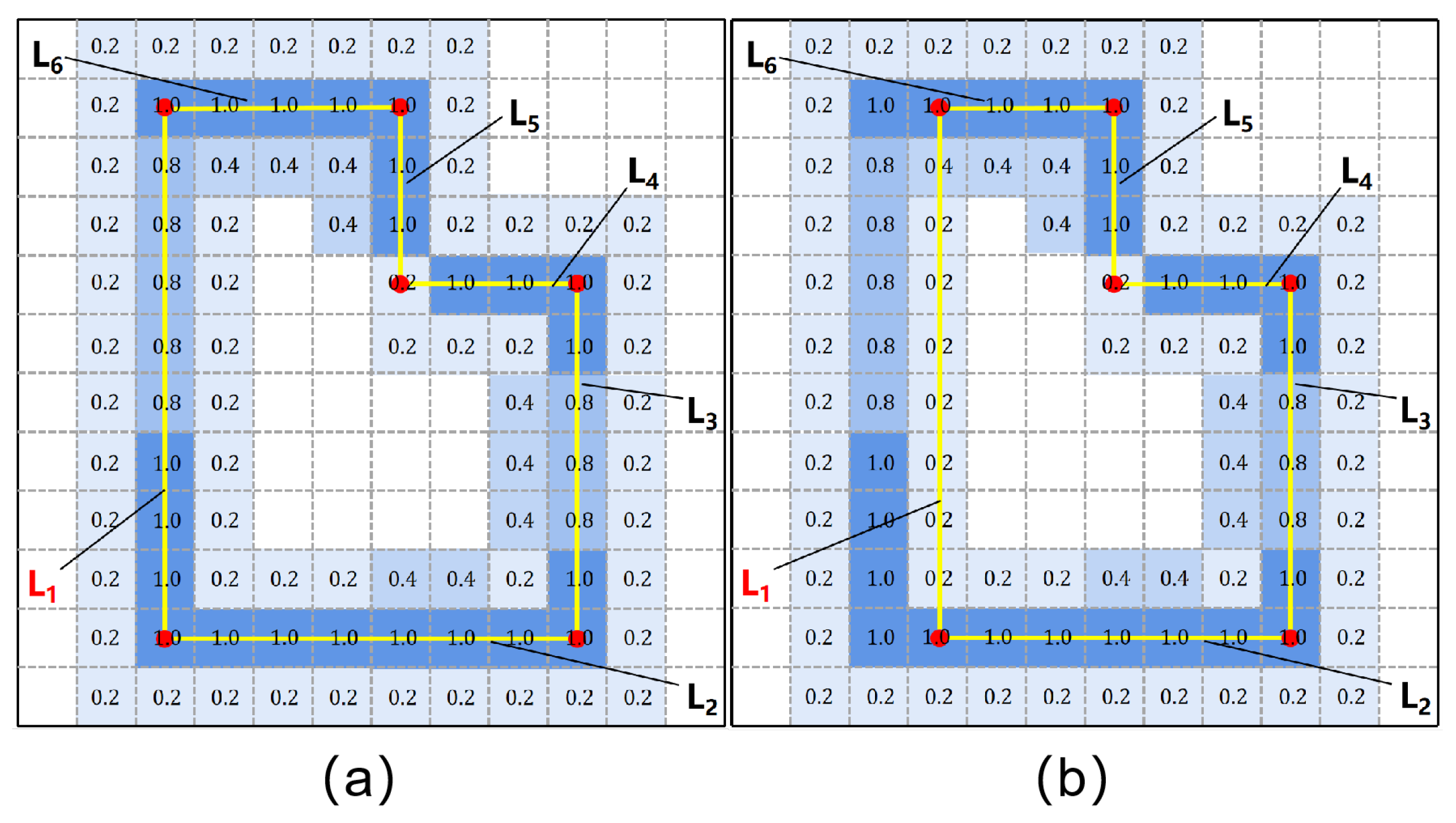
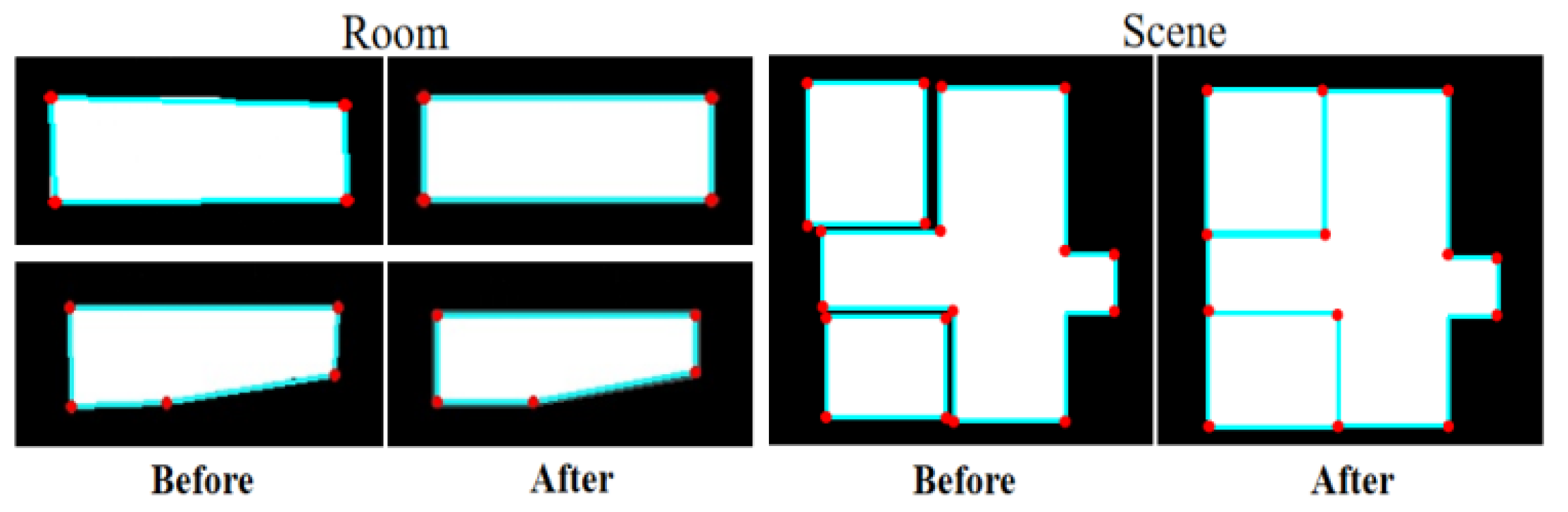
3.3. Edge Optimization
4. Experiment
4.1. Dataset and Setup
4.2. Qualitative Evaluation
4.3. Quantitative Evaluations
4.4. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ikehata, S.; Hang, Y.; Furukawa, Y. Structured Indoor Modeling. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 7–13 December 2015. [Google Scholar]
- Pintore, G.; Mura, C.; Ganovelli, F.; Fuentes-Perez, L.; Pajarola, R.; Gobbetti, E. State-of-the-art in Automatic 3D Reconstruction of Structured Indoor Environments. Comput. Graph. Forum 2020, 39, 667–699. [Google Scholar] [CrossRef]
- Chen, J.; Liu, C.; Wu, J.; Furukawa, Y. Floor-sp: Inverse cad for floorplans by sequential room-wise shortest path. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 2661–2670. [Google Scholar]
- Furukawa, Y.; Curless, B.; Seitz, S.; Szeliski, R. Manhattan-world stereo. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Liu, C.; Wu, J.; Furukawa, Y. Floornet: A unified framework for floorplan reconstruction from 3d scans. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 201–217. [Google Scholar]
- Monszpart, A.; Mellado, N.; Brostow, G.J.; Mitra, N.J. RAPter: Rebuilding man-made scenes with regular arrangements of planes. ACM Trans. Graph. 2015, 34, 103:1–103:12. [Google Scholar] [CrossRef]
- Xiao, J.; Furukawa, Y. Reconstructing the world’s museums. Int. J. Comput. Vis. 2014, 110, 243–258. [Google Scholar] [CrossRef]
- Rabbani, T.; Van Den Heuvel, F.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Rother, C.; Kolmogorov, V.; Blake, A. “GrabCut” interactive foreground extraction using iterated graph cuts. ACM Trans. Graph. 2004, 23, 309–314. [Google Scholar] [CrossRef]
- Xie, L.; Wang, R. Automatic indoor building reconstruction from mobile laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 417–422. [Google Scholar] [CrossRef]
- Stekovic, S.; Rad, M.; Fraundorfer, F.; Lepetit, V. Montefloor: Extending mcts for reconstructing accurate large-scale floor plans. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 16034–16043. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Processing Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein gans. Adv. Neural Inf. Process. Syst. 2017, 30, 5769–5779. [Google Scholar]
- Nauata, N.; Chang, K.H.; Cheng, C.Y.; Mori, G.; Furukawa, Y. House-gan: Relational generative adversarial networks for graph-constrained house layout generation. In Proceedings of the European Conference on Computer Vision, Online, 23–28 August 2020; pp. 162–177. [Google Scholar]
- Nauata, N.; Hosseini, S.; Chang, K.H.; Chu, H.; Cheng, C.Y.; Furukawa, Y. House-gan++: Generative adversarial layout refinement network towards intelligent computational agent for professional architects. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 13632–13641. [Google Scholar]
- Zhang, F.; Nauata, N.; Furukawa, Y. Conv-mpn: Convolutional message passing neural network for structured outdoor architecture reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2798–2807. [Google Scholar]
- Chen, K.; Pang, J.; Wang, J.; Xiong, Y.; Li, X.; Sun, S.; Lin, D. Hybrid task cascade for instance segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4974–4983. [Google Scholar]
- Chen, X.; Zhao, Y.; Qin, Y.; Jiang, F.; Tao, M.; Hua, X.; Lu, H. PANet: Perspective-Aware Network with Dynamic Receptive Fields and Self-Distilling Supervision for Crowd Counting. arXiv 2021, arXiv:2111.00406. [Google Scholar]
- Bolya, D.; Zhou, C.; Xiao, F.; Lee, Y.J. Yolact: Real-time instance segmentation. In Proceedings of the IEEE/CVF international Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 9157–9166. [Google Scholar]
- Wang, X.; Kong, T.; Shen, C.; Jiang, Y.; Li, L. Solo: Segmenting objects by locations. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 649–665. [Google Scholar]
- Xie, E.; Sun, P.; Song, X.; Wang, W.; Liu, X.; Liang, D.; Luo, P. Polarmask: Single shot instance segmentation with polar representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 12193–12202. [Google Scholar]
- Ling, H.; Gao, J.; Kar, A.; Chen, W.; Fidler, S. Fast interactive object annotation with curve-gcn. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5257–5266. [Google Scholar]
- Peng, S.; Jiang, W.; Pi, H.; Li, X.; Bao, H.; Zhou, X. Deep snake for real-time instance segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8533–8542. [Google Scholar]
- Zhang, T.; Wei, S.; Ji, S. E2EC: An End-to-End Contour-based Method for High-Quality High-Speed Instance Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 4443–4452. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Li, M.; Lafarge, F.; Marlet, R. Approximating shapes in images with low-complexity polygons. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8633–8641. [Google Scholar]
- Zhang, F.; Xu, X.; Nauata, N.; Furukawa, Y. Structured outdoor architecture reconstruction by exploration and classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 12427–12435. [Google Scholar]
- Zhang, G.; Lu, X.; Tan, J.; Li, J.; Zhang, Z.; Li, Q.; Hu, X. Refinemask: Towards high-quality instance segmentation with fine-grained features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6861–6869. [Google Scholar]






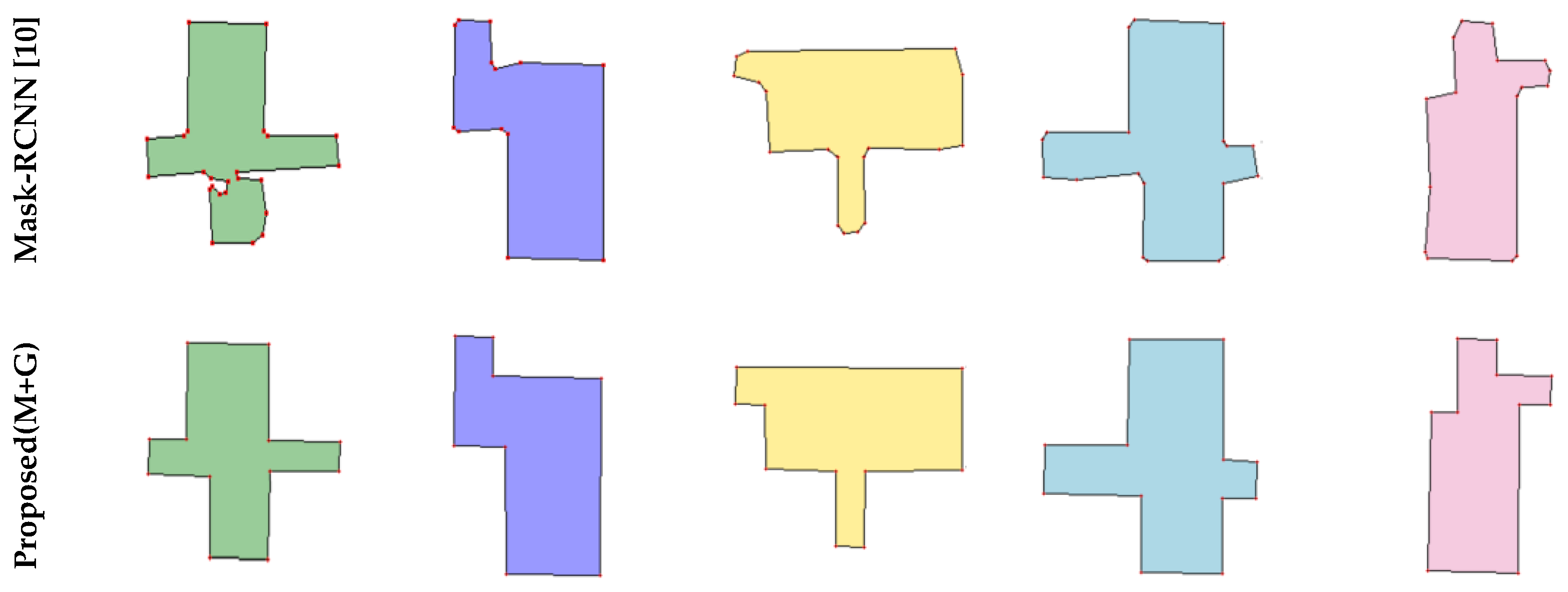


| E2EC [27] | Refine Mask [31] | Mask-RCNN [10] | Proposed (M + G) | ||
|---|---|---|---|---|---|
| Corner | Precision | 0.959 | 0.728 | 0.725 | 0.938 |
| Recall | 0.757 | 0.935 | 0.968 | 0.975 | |
| F1-score | 0.846 | 0.819 | 0.829 | 0.956 | |
| Method | Corner | Edge | Room | Efficiency | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pre. | Recall | F1-Score | Pre. | Recall | F1-Score | Pre. | Recall | F1-Score | Time (s) | |
| Floor-SP [3] | 0.93 | 0.97 | 0.95 | 0.93 | 0.95 | 0.94 | 0.93 | 0.94 | 0.93 | 32,667 |
| Zhang et al. [30] | 0.90 | 0.95 | 0.92 | 0.85 | 0.89 | 0.87 | 0.92 | 0.93 | 0.92 | 8452 |
| MonteFloor [13] | 0.94 | 0.96 | 0.95 | 0.93 | 0.95 | 0.94 | 0.94 | 0.95 | 0.94 | 6237 |
| ASIP [29] | 0.83 | 0.93 | 0.88 | 0.75 | 0.86 | 0.80 | 0.91 | 0.92 | 0.91 | 53 |
| Proposed | 0.96 | 0.97 | 0.96 | 0.94 | 0.96 | 0.95 | 0.94 | 0.96 | 0.95 | 222 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, T.; Zhuang, J.; Xiao, J.; Xu, N.; Qin, S. Reconstructing Floorplans from Point Clouds Using GAN. J. Imaging 2023, 9, 39. https://doi.org/10.3390/jimaging9020039
Jin T, Zhuang J, Xiao J, Xu N, Qin S. Reconstructing Floorplans from Point Clouds Using GAN. Journal of Imaging. 2023; 9(2):39. https://doi.org/10.3390/jimaging9020039
Chicago/Turabian StyleJin, Tianxing, Jiayan Zhuang, Jiangjian Xiao, Ningyuan Xu, and Shihao Qin. 2023. "Reconstructing Floorplans from Point Clouds Using GAN" Journal of Imaging 9, no. 2: 39. https://doi.org/10.3390/jimaging9020039
APA StyleJin, T., Zhuang, J., Xiao, J., Xu, N., & Qin, S. (2023). Reconstructing Floorplans from Point Clouds Using GAN. Journal of Imaging, 9(2), 39. https://doi.org/10.3390/jimaging9020039







