Automated Coronary Artery Tracking with a Voronoi-Based 3D Centerline Extraction Algorithm
Abstract
:1. Introduction
2. Materials and Methods
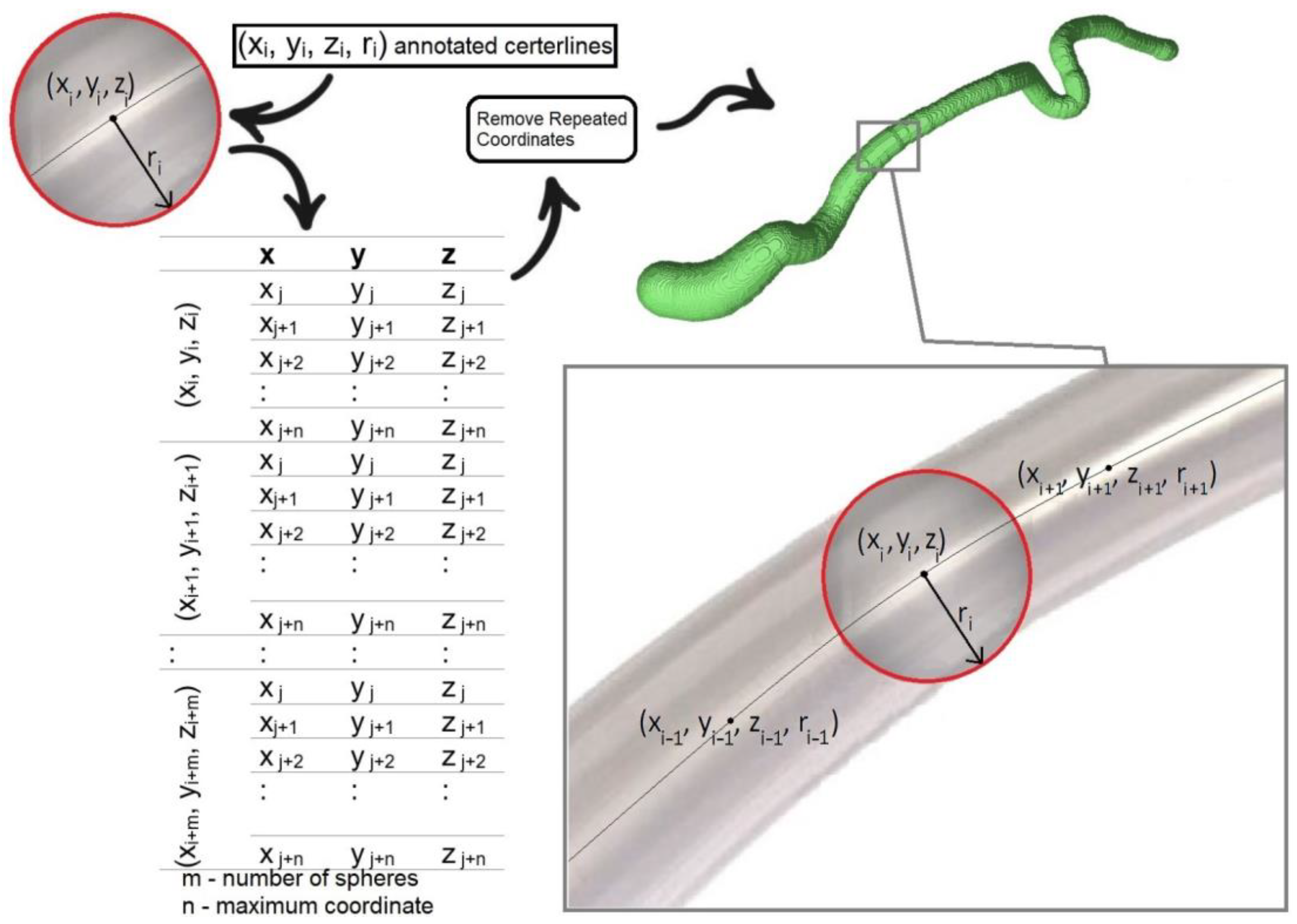
2.1. The 3D Centerline Extraction Methodology
2.2. Synthetic Dataset Generation
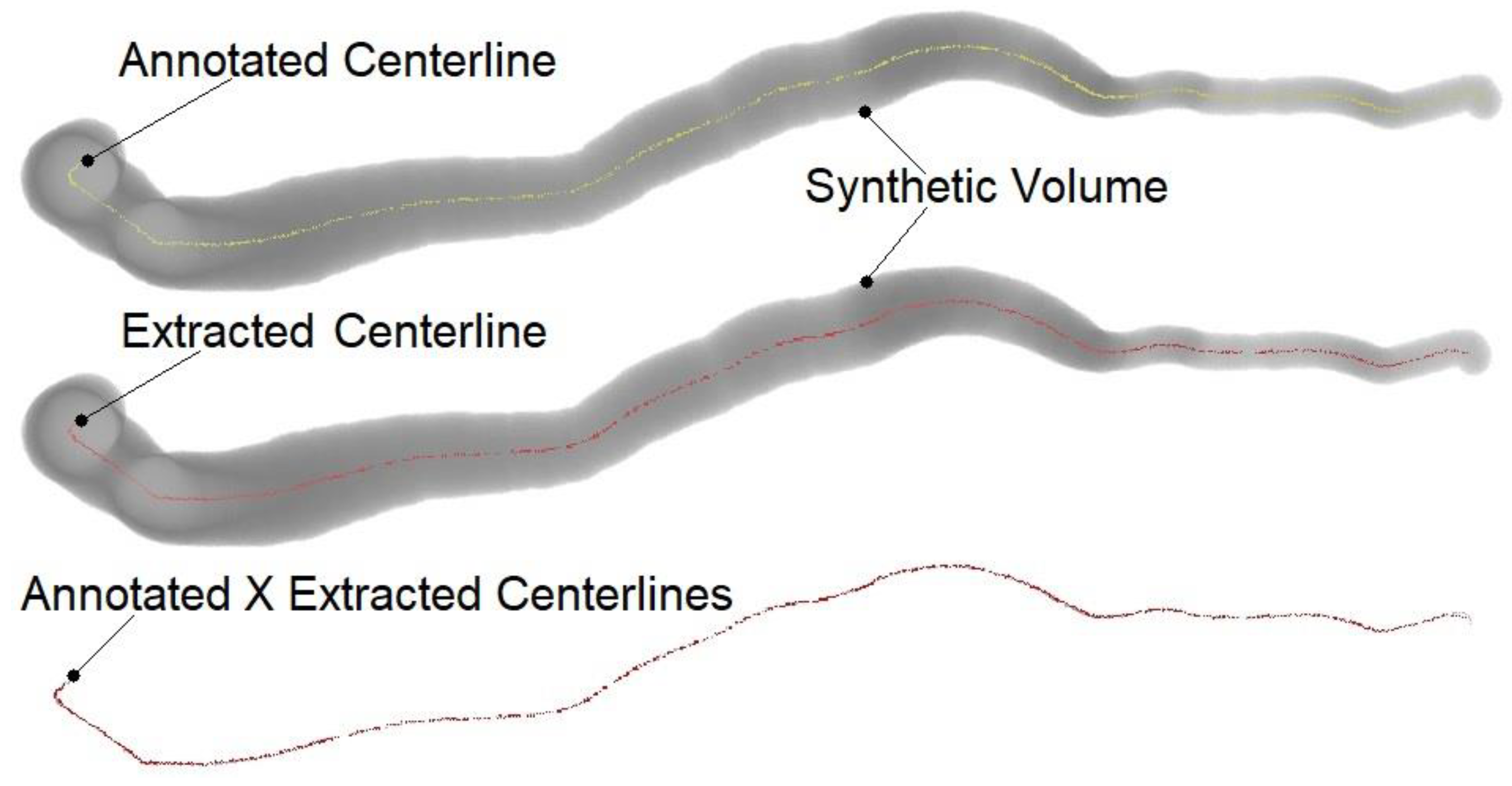
2.3. Model Performance Evaluation
3. Results
4. Discussion
| Centerline | Segmentation Method | Training Dataset Accuracy | Testing Dataset Accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | (Number of Training Set Vessels) | OV | OF | OT | AI | OV | OF | OT | AI |
| Voronoi method (XY) | Synthetic (32 vessels) | 99.98 | 100 | 99.99 | 0.17 | - | - | - | - |
| Voronoi method (YZ) | Synthetic (32 vessels) | 99.76 | 100 | 99.75 | 0.18 | - | - | - | - |
| Voronoi method (XZ) | Synthetic (32 vessels) | 99.79 | 99.97 | 99.87 | 0.19 | - | - | - | - |
| Voronoi method (XYZ) | Synthetic (32 vessels) | 99.97 | 100 | 99.98 | 0.13 | - | - | - | - |
| Jeon [32] (Deep-PF) | Real (32 vessels) | 92.00 | - | 93.00 | 0.36 | - | - | - | - |
| Zhang et al. [31] | Real (32 vessels) | 96.20 | 88.30 | 96.50 | 0.21 | - | - | - | - |
| Wolterink et al. [5] | Real (32 vessels) | 95.70 | 87.10 | 97.10 | 0.23 | 93.70 | - | - | - |
| Jia et al. [4] (MM-DFM) | Real (32 vessels) | 83.50 | 57.80 | 87.10 | 0.48 | 86.60 | - | - | - |
| Salehi et al. [30] (CCWT) | Real (32 vessels) | - | - | 99.01 | 0.27 | - | - | 98.39 | 0.26 |
| Cui et al. [29] (GVFFM) | Synthetic (17 vessels) | 98.20 | 91.70 | 98.30 | 0.25 | 95.20 | - | - | - |
| Cui et al. [27] (DTFM) | Synthetic (4 vessels) | 98.00 | 95.00 | 97.55 | - | - | - | - | - |
| Han et al. [28] (AS) | Real (32 vessels) | 81.40 | 77.30 | 87.80 | - | 84.30 | - | - | - |
4.1. Study Limitations
4.2. Future Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Salahuddin, Z.; Lenga, M.; Nickisch, H. Multi-Resolution 3d Convolutional Neural Networks for Automatic Coronary Centerline Extraction in Cardiac CT Angiography Scans. In Proceedings of the 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), Nice, France, 13–16 April 2021; pp. 91–95. [Google Scholar] [CrossRef]
- Malakar, A.; Choudhury, D.; Halder, B.; Paul, P.; Uddin, A.; Chakraborty, S. A Review on Coronary Artery Disease, Its Risk Factors, and Therapeutics. J. Cell. Physiol. 2019, 234, 16812–16823. [Google Scholar] [CrossRef]
- Brown, J.C.; Gerhardt, T.E.; Kwon, E. Risk Factors for Coronary Artery Disease. In StatPearls [Internet]; StatPearls Publishing: Treasure Island, FL, USA, 2023. [Google Scholar]
- Jia, D.; Zhuang, X. Directional Fast-Marching and Multi-Model Strategy to Extract Coronary Artery Centerlines. Comput. Biol. Med. 2019, 108, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Wolterink, J.M.; van Hamersvelt, R.W.; Viergever, M.A.; Leiner, T.; Išgum, I. Coronary Artery Centerline Extraction in Cardiac CT Angiography Using a CNN-Based Orientation Classifier. Med. Image Anal. 2019, 51, 46–60. [Google Scholar] [CrossRef]
- Schaap, M.; Metz, C.T.; van Walsum, T.; van der Giessen, A.G.; Weustink, A.C.; Mollet, N.R.; Bauer, C.; Bogunović, H.; Castro, C.; Deng, X.; et al. Standardized Evaluation Methodology and Reference Database for Evaluating Coronary Artery Centerline Extraction Algorithms. Med. Image Anal. 2009, 13, 701–714. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Yang, J.; Zhao, H. An Automatic Extraction Method of Coronary Arteries Centerline Based on Cellular Automata. In Proceedings of the 3rd International Conference on Computer Science and Software Engineering, Beijing China, 22–24 May 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 191–195. [Google Scholar] [CrossRef]
- Li, Z.; Xia, Q.; Hu, Z.; Wang, W.; Xu, L.; Zhang, S. A Deep Reinforced Tree-Traversal Agent for Coronary Artery Centerline Extraction. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2021; Lecture Notes in Computer Science; de Bruijne, M., Cattin, P.C., Cotin, S., Padoy, N., Speidel, S., Zheng, Y., Essert, C., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 418–428. [Google Scholar]
- Gao, R.; Hou, Z.; Li, J.; Han, H.; Lu, B.; Zhou, S.K. Joint Coronary Centerline Extraction and Lumen Segmentation from CCTA Using CNNTracker and Vascular Graph Convolutional Network. In Proceedings of the 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), Nice, France, 13–16 April 2021; pp. 1897–1901. [Google Scholar]
- Zhang, X.; Du, H.; Song, G.; Bao, F.; Zhang, Y.; Wu, W.; Liu, P. X-ray Coronary Centerline Extraction Based on C-UNet and a Multifactor Reconnection Algorithm. Comput. Methods Programs Biomed. 2022, 226, 107114. [Google Scholar] [CrossRef]
- Zhao, C.; Tang, H.; McGonigle, D.; He, Z.; Zhang, C.; Wang, Y.-P.; Deng, H.-W.; Bober, R.M.; Zhou, W. Development of an Approach to Extracting Coronary Arteries and Detecting Stenosis in Invasive Coronary Angiograms. J. Med. Imaging 2022, 9, 44002. [Google Scholar] [CrossRef] [PubMed]
- Kitamura, Y.; Li, Y.; Ito, W. Automatic Coronary Extraction by Supervised Detection and Shape Matching. In Proceedings of the 2012 9th IEEE International Symposium on Biomedical Imaging (ISBI), Barcelona, Spain, 2–5 May 2012; pp. 234–237. [Google Scholar]
- Zheng, Y.; Tek, H.; Funka-Lea, G. Robust and Accurate Coronary Artery Centerline Extraction in CTA by Combining Model-Driven and Data-Driven Approaches. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2013; Lecture Notes in Computer Science; Mori, K., Sakuma, I., Sato, Y., Barillot, C., Navab, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 74–81. [Google Scholar]
- Zhuang, X.; Bai, W.; Song, J.; Zhan, S.; Qian, X.; Shi, W.; Lian, Y.; Rueckert, D. Multiatlas Whole Heart Segmentation of CT Data Using Conditional Entropy for Atlas Ranking and Selection. Med. Phys. 2015, 42, 3822–3833. [Google Scholar] [CrossRef]
- Zhuang, X.; Shen, J. Multi-Scale Patch and Multi-Modality Atlases for Whole Heart Segmentation of MRI. Med. Image Anal. 2016, 31, 77–87. [Google Scholar] [CrossRef]
- Zhu, N.; Chung, A.C.S. Minimum Average-Cost Path for Real Time 3D Coronary Artery Segmentation of CT Images. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2011; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 436–444. [Google Scholar]
- Cetin, S.; Demir, A.; Yezzi, A.; Degertekin, M.; Unal, G. Vessel Tractography Using an Intensity Based Tensor Model with Branch Detection. IEEE Trans. Med. Imaging 2013, 32, 348–363. [Google Scholar] [CrossRef]
- Cetin, S.; Unal, G. A Higher-Order Tensor Vessel Tractography for Segmentation of Vascular Structures. IEEE Trans. Med. Imaging 2015, 34, 2172–2185. [Google Scholar] [CrossRef]
- Friman, O.; Hindennach, M.; Kühnel, C.; Peitgen, H.-O. Multiple Hypothesis Template Tracking of Small 3D Vessel Structures. Med. Image Anal. 2010, 14, 160–171. [Google Scholar] [CrossRef] [PubMed]
- Metz, C.T.; Schaap, M.; Weustink, A.C.; Mollet, N.R.; van Walsum, T.; Niessen, W.J. Coronary Centerline Extraction from CT Coronary Angiography Images Using a Minimum Cost Path Approach. Med. Phys. 2009, 36, 5568–5579. [Google Scholar] [CrossRef]
- Lesage, D.; Angelini, E.D.; Bloch, I.; Funka-Lea, G. Bayesian Maximal Paths for Coronary Artery Segmentation from 3D CT Angiograms. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2009; Lecture Notes in Computer Science; Yang, G.-Z., Hawkes, D., Rueckert, D., Noble, A., Taylor, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 222–229. [Google Scholar]
- Friman, O.; Kühnel, C.; Peitgen, H.-O. Coronary Centerline Extraction Using Multiple Hypothesis Tracking and Minimal Paths. Midas J. 2008, 42. [Google Scholar] [CrossRef]
- Zambal, S.; Hladuvka, J.; Kanitsar, A.; Bühler, K. Shape and Appearance Models for Automatic Coronary Artery Tracking. Midas J. 2008, 4. [Google Scholar] [CrossRef]
- Liu, L.; Xu, J.; Liu, Z. Automatic Extraction of Coronary Centerline Based on Model-Mapped and Inertia-Guided Minimum Path from CTA Images. Multimed. Tools Appl. 2019, 78, 8767–8782. [Google Scholar] [CrossRef]
- Lesage, D.; Angelini, E.D.; Funka-Lea, G.; Bloch, I. Adaptive Particle Filtering for Coronary Artery Segmentation from 3D CT Angiograms. Comput. Vis. Image Underst. 2016, 151, 29–46. [Google Scholar] [CrossRef]
- Younas, S.; Figley, C.R. Development, Implementation and Validation of an Automatic Centerline Extraction Algorithm for Complex 3D Objects. J. Med. Biol. Eng. 2019, 39, 184–204. [Google Scholar] [CrossRef]
- Cui, H.; Wang, D.; Wan, M.; Zhang, J.-M.; Zhao, X.; Tan, R.S.; Huang, W.; Xiong, W.; Duan, Y.; Zhou, J.; et al. Fast Marching and Runge-Kutta Based Method for Centreline Extraction of Right Coronary Artery in Human Patients. Cardiovasc. Eng. Technol. 2016, 7, 159–169. [Google Scholar] [CrossRef]
- Han, D.; Shim, H.; Jeon, B.; Jang, Y.; Hong, Y.; Jung, S.; Ha, S.; Chang, H.-J. Automatic Coronary Artery Segmentation Using Active Search for Branches and Seemingly Disconnected Vessel Segments from Coronary CT Angiography. PLoS ONE 2016, 11, e0156837. [Google Scholar] [CrossRef]
- Cui, H.; Xia, Y. Automatic Coronary Centerline Extraction Using Gradient Vector Flow Field and Fast Marching Method from CT Images. IEEE Access 2018, 6, 41816–41826. [Google Scholar] [CrossRef]
- Salehi, N.; Naghsh-Nilchi, A.R. Automatic 3-D Tubular Centerline Tracking of Coronary Arteries in Coronary Computed Tomographic Angiography. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 170–181. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, G.; Wang, W.; Wang, K. Branch-Aware Double DQN for Centerline Extraction in Coronary CT Angiography. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2020; Lecture Notes in Computer Science; Martel, A.L., Abolmaesumi, P., Stoyanov, D., Mateus, D., Zuluaga, M.A., Zhou, S.K., Racoceanu, D., Joskowicz, L., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 35–44. [Google Scholar]
- Jeon, B. Deep Recursive Bayesian Tracking for Fully Automatic Centerline Extraction of Coronary Arteries in CT Images. Sensors 2021, 21, 6087. [Google Scholar] [CrossRef] [PubMed]
- Aruoba, S.B.; Fernández-Villaverde, J. A Comparison of Programming Languages in Macroeconomics. J. Econ. Dyn. Control 2015, 58, 265–273. [Google Scholar] [CrossRef]
- Kirişli, H.A.; Schaap, M.; Metz, C.T.; Dharampal, A.S.; Meijboom, W.B.; Papadopoulou, S.L.; Dedic, A.; Nieman, K.; de Graaf, M.A.; Meijs, M.F.L.; et al. Standardized Evaluation Framework for Evaluating Coronary Artery Stenosis Detection, Stenosis Quantification and Lumen Segmentation Algorithms in Computed Tomography Angiography. Med. Image Anal. 2013, 17, 859–876. [Google Scholar] [CrossRef] [PubMed]

| Dataset | Image | Computational Time (Seconds) | |||
|---|---|---|---|---|---|
| (Vessel) | Size | XY | YZ | XZ | XYZ |
| 0(0) | 1056 × 650 × 609 | 218.48 | 148.09 | 143.75 | 254.95 |
| 0(1) | 475 × 685 × 179 | 15.81 | 17.32 | 15.45 | 24.26 |
| 0(2) | 842 × 402 × 332 | 25.96 | 21.23 | 25.03 | 36.10 |
| 0(3) | 619 × 258 × 139 | 9.14 | 8.89 | 11.00 | 14.51 |
| 1(0) | 915 × 830 × 675 | 212.24 | 136.12 | 152.67 | 250.46 |
| 1(1) | 441 × 877 × 935 | 133.83 | 120.82 | 53.11 | 153.87 |
| 1(2) | 721 × 185 × 577 | 19.97 | 12.48 | 21.43 | 26.93 |
| 1(3) | 691 × 489 × 469 | 30.33 | 27.64 | 29.18 | 43.57 |
| 2(0) | 531 × 687 × 582 | 54.95 | 42.43 | 41.53 | 69.44 |
| 2(1) | 422 × 587 × 843 | 51.87 | 46.65 | 34.79 | 66.65 |
| 2(2) | 426 × 494 × 436 | 25.36 | 22.50 | 20.92 | 34.38 |
| 2(3) | 529 × 288 × 317 | 12.35 | 10.91 | 13.27 | 18.26 |
| 3(0) | 863 × 767 × 678 | 153.67 | 98.73 | 112.10 | 182.23 |
| 3(1) | 742 × 901 × 739 | 190.47 | 136.74 | 97.51 | 212.35 |
| 3(2) | 807 × 353 × 630 | 41.98 | 23.50 | 36.88 | 51.17 |
| 3(3) | 770 × 355 × 279 | 14.95 | 12.49 | 17.57 | 22.50 |
| 4(0) | 872 × 606 × 763 | 135.94 | 70.00 | 105.20 | 155.56 |
| 4(1) | 588 × 643 × 902 | 100.41 | 71.77 | 56.31 | 114.24 |
| 4(2) | 447 × 500 × 753 | 29.69 | 23.12 | 19.84 | 36.31 |
| 4(3) | 736 × 265 × 409 | 13.63 | 9.53 | 15.03 | 19.09 |
| 5(0) | 438 × 599 × 579 | 31.26 | 26.29 | 22.48 | 40.01 |
| 5(1) | 630 × 747 × 861 | 134.86 | 102.24 | 74.33 | 155.70 |
| 5(2) | 516 × 324 × 335 | 12.82 | 10.72 | 13.40 | 18.46 |
| 5(3) | 662 × 341 × 192 | 10.25 | 12.72 | 16.16 | 19.56 |
| 6(0) | 801 × 683 × 718 | 124.02 | 76.51 | 88.85 | 144.69 |
| 6(1) | 709 × 809 × 727 | 134.48 | 97.65 | 77.94 | 155.02 |
| 6(2) | 509 × 327 × 546 | 18.05 | 13.27 | 15.73 | 23.52 |
| 6(3) | 724 × 610 × 381 | 29.07 | 25.52 | 26.85 | 40.71 |
| 7(0) | 816 × 369 × 803 | 75.40 | 40.13 | 61.44 | 88.48 |
| 7(1) | 639 × 666 × 943 | 138.07 | 93.55 | 78.38 | 154.98 |
| 7(2) | 304 × 311 × 330 | 7.66 | 5.85 | 7.00 | 10.25 |
| 7(3) | 506 × 126 × 283 | 6.28 | 5.01 | 7.14 | 9.21 |
| Average | 215,321,960 voxels (equivalent to 600 × 599 × 599) | 69.16 | 49.08 | 47.26 | 82.73 |
| Dataset | XY | YZ | XZ | XYZ | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Vessel) | OV | OF | OT | AI | OV | OF | OT | AI | OV | OF | OT | AI | OV | OF | OT | AI |
| 0(0) | 100 | 100 | 100 | 0.09 | 99.97 | 100 | 100 | 0.10 | 99.47 | 100 | 100 | 0.08 | 99.97 | 100 | 100 | 0.09 |
| 0(1) | 99.99 | 100 | 99.99 | 0.19 | 99.99 | 100 | 99.99 | 0.12 | 99.52 | 100 | 99.51 | 0.31 | 99.99 | 100 | 99.99 | 0.10 |
| 0(2) | 100 | 100 | 100 | 0.16 | 100 | 100 | 100 | 0.17 | 100 | 100 | 100 | 0.14 | 100 | 100 | 100 | 0.13 |
| 0(3) | 100 | 100 | 100 | 0.22 | 100 | 100 | 100 | 0.09 | 99.75 | 100 | 99.75 | 0.30 | 99.95 | 100 | 99.95 | 0.17 |
| 1(0) | 100 | 100 | 100 | 0.22 | 99.99 | 100 | 100 | 0.09 | 98.98 | 100 | 99.68 | 0.15 | 100 | 100 | 100 | 0.08 |
| 1(1) | 100 | 100 | 100 | 0.23 | 99.60 | 100 | 99.78 | 0.13 | 100 | 100 | 100 | 0.20 | 99.96 | 100 | 99.96 | 0.17 |
| 1(2) | 100 | 100 | 100 | 0.07 | 100 | 100 | 100 | 0.05 | 100 | 100 | 100 | 0.07 | 100 | 100 | 100 | 0.06 |
| 1(3) | 99.70 | 100 | 100 | 0.12 | 100 | 100 | 100 | 0.05 | 100 | 100 | 100 | 0.07 | 100 | 100 | 100 | 0.16 |
| 2(0) | 99.99 | 100 | 100 | 0.07 | 99.91 | 100 | 100 | 0.11 | 100 | 100 | 100 | 0.07 | 99.99 | 100 | 100 | 0.06 |
| 2(1) | 100 | 100 | 100 | 0.07 | 99.04 | 100 | 98.24 | 0.12 | 98.87 | 98.9 | 100 | 0.10 | 100 | 100 | 100 | 0.06 |
| 2(2) | 100 | 100 | 100 | 0.23 | 99.98 | 100 | 99.97 | 0.60 | 100 | 100 | 100 | 0.37 | 99.92 | 100 | 99.92 | 0.19 |
| 2(3) | 99.99 | 100 | 99.99 | 0.28 | 100 | 100 | 100 | 0.23 | 98.91 | 100 | 98.91 | 0.73 | 99.99 | 100 | 99.99 | 0.34 |
| 3(0) | 100 | 100 | 100 | 0.08 | 99.89 | 100 | 100 | 0.14 | 100 | 100 | 100 | 0.08 | 100 | 100 | 100 | 0.07 |
| 3(1) | 99.99 | 100 | 100 | 0.08 | 100 | 100 | 100 | 0.06 | 99.99 | 100 | 100 | 0.07 | 99.99 | 100 | 100 | 0.06 |
| 3(2) | 99.96 | 100 | 100 | 0.06 | 100 | 100 | 100 | 0.23 | 99.97 | 100 | 99.97 | 0.19 | 99.96 | 100 | 99.97 | 0.17 |
| 3(3) | 100 | 100 | 100 | 0.20 | 100 | 100 | 100 | 0.13 | 100 | 100 | 100 | 0.05 | 100 | 100 | 100 | 0.046 |
| 4(0) | 99.99 | 100 | 99.99 | 0.33 | 95.73 | 100 | 95.73 | 0.35 | 100 | 100 | 100 | 0.35 | 99.89 | 100 | 99.89 | 0.28 |
| 4(1) | 100 | 100 | 100 | 0.21 | 100 | 100 | 100 | 0.20 | 100 | 100 | 100 | 0.19 | 100 | 100 | 100 | 0.18 |
| 4(2) | 100 | 100 | 100 | 0.16 | 99.46 | 100 | 99.46 | 0.26 | 100 | 100 | 100 | 0.15 | 100 | 100 | 100 | 0.15 |
| 4(3) | 99.96 | 100 | 99.96 | 0.18 | 100 | 100 | 100 | 0.13 | 99.96 | 100 | 99.96 | 0.17 | 99.96 | 100 | 99.96 | 0.14 |
| 5(0) | 100 | 100 | 100 | 0.09 | 100 | 100 | 100 | 0.06 | 100 | 100 | 100 | 0.06 | 100 | 100 | 100 | 0.06 |
| 5(1) | 100 | 100 | 100 | 0.29 | 100 | 100 | 100 | 0.20 | 99.99 | 100 | 99.99 | 0.18 | 99.99 | 100 | 99.99 | 0.18 |
| 5(2) | 100 | 100 | 100 | 0.06 | 100 | 100 | 100 | 0.06 | 100 | 100 | 100 | 0.06 | 99.87 | 100 | 100 | 0.05 |
| 5(3) | 100 | 100 | 100 | 0.33 | 100 | 100 | 100 | 0.14 | 100 | 100 | 100 | 0.20 | 100 | 100 | 100 | 0.16 |
| 6(0) | 99.99 | 100 | 100 | 0.11 | 100 | 100 | 100 | 0.07 | 100 | 100 | 100 | 0.08 | 100 | 100 | 100 | 0.067 |
| 6(1) | 100 | 100 | 100 | 0.26 | 99.58 | 100 | 99.58 | 0.39 | 100 | 100 | 100 | 0.18 | 100 | 100 | 100 | 0.18 |
| 6(2) | 100 | 100 | 100 | 0.20 | 99.29 | 100 | 99.29 | 0.54 | 97.97 | 100 | 97.97 | 0.66 | 100 | 100 | 100 | 0.15 |
| 6(3) | 100 | 100 | 100 | 0.35 | 100 | 100 | 100 | 0.19 | 100 | 100 | 100 | 0.19 | 100 | 100 | 100 | 0.18 |
| 7(0) | 99.94 | 100 | 100 | 0.08 | 100 | 100 | 100 | 0.07 | 99.99 | 100 | 100 | 0.08 | 100 | 100 | 100 | 0.07 |
| 7(1) | 99.99 | 100 | 99.99 | 0.26 | 100 | 100 | 100 | 0.26 | 99.99 | 100 | 99.99 | 0.27 | 99.99 | 100 | 99.99 | 0.24 |
| 7(2) | 99.74 | 100 | 99.74 | 0.13 | 100 | 100 | 100 | 0.12 | 99.98 | 100 | 99.98 | 0.15 | 99.64 | 100 | 99.64 | 0.13 |
| 7(3) | 99.99 | 100 | 99.99 | 0.16 | 100 | 100 | 100 | 0.15 | 99.99 | 100 | 99.99 | 0.14 | 99.99 | 100 | 99.99 | 0.11 |
| Average | 99.98 | 100 | 99.99 | 0.17 | 99.76 | 100 | 99.75 | 0.18 | 99.79 | 99.97 | 99.87 | 0.19 | 99.97 | 100 | 99.98 | 0.13 |
| XY | YZ | XZ | XYZ | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OV | OF | OT | AI | OV | OF | OT | AI | OV | OF | OT | AI | OV | OF | OT | AI | |
| RCA | 99.99 | 100 | 100 | 0.13 | 99.44 | 100 | 99.47 | 0.12 | 99.81 | 100 | 99.96 | 0.12 | 99.98 | 100 | 99.99 | 0.10 |
| LAD | 100 | 100 | 100 | 0.20 | 99.77 | 100 | 99.70 | 0.18 | 99.80 | 99.86 | 99.94 | 0.19 | 99.99 | 100 | 99.99 | 0.15 |
| LCX | 99.96 | 100 | 99.97 | 0.13 | 99.84 | 100 | 99.84 | 0.26 | 99.74 | 100 | 99.74 | 0.22 | 99.93 | 100 | 99.94 | 0.13 |
| Large Branch | 99.96 | 100 | 99.99 | 0.23 | 100 | 100 | 100.00 | 0.14 | 99.83 | 100 | 99.83 | 0.23 | 99.99 | 100 | 99.99 | 0.16 |
| Average | 99.98 | 100 | 99.99 | 0.17 | 99.76 | 100 | 99.75 | 0.18 | 99.79 | 99.97 | 99.87 | 0.19 | 99.97 | 100 | 99.98 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dalvit Carvalho da Silva, R.; Soltanzadeh, R.; Figley, C.R. Automated Coronary Artery Tracking with a Voronoi-Based 3D Centerline Extraction Algorithm. J. Imaging 2023, 9, 268. https://doi.org/10.3390/jimaging9120268
Dalvit Carvalho da Silva R, Soltanzadeh R, Figley CR. Automated Coronary Artery Tracking with a Voronoi-Based 3D Centerline Extraction Algorithm. Journal of Imaging. 2023; 9(12):268. https://doi.org/10.3390/jimaging9120268
Chicago/Turabian StyleDalvit Carvalho da Silva, Rodrigo, Ramin Soltanzadeh, and Chase R. Figley. 2023. "Automated Coronary Artery Tracking with a Voronoi-Based 3D Centerline Extraction Algorithm" Journal of Imaging 9, no. 12: 268. https://doi.org/10.3390/jimaging9120268
APA StyleDalvit Carvalho da Silva, R., Soltanzadeh, R., & Figley, C. R. (2023). Automated Coronary Artery Tracking with a Voronoi-Based 3D Centerline Extraction Algorithm. Journal of Imaging, 9(12), 268. https://doi.org/10.3390/jimaging9120268






