Cardiac Disease Classification Using Two-Dimensional Thickness and Few-Shot Learning Based on Magnetic Resonance Imaging Image Segmentation
Abstract
:1. Introduction
- (1)
- Several lightweight encoders were ensembled using a block-inverted residual network in the UNet architecture for automatic cine MRI segmentation optimization.
- (2)
- We proposed a novel 2D thickness algorithm to decode the segmentation outputs to develop the 2D representation images of the ED and ES cardiac volumes as the input for of cardiac muscle heart disease patient groups classification without using clinical features.
- (3)
- A few-shot model with an adaptive subspace classifier was proposed, and various encoder few-shot models were investigated for deep-learning-based cardiac disease group classification. Unlike the general few-shot learning mechanism, the same classes and domain datasets are provided in the few-shot learning mechanisms in the training, validation, and testing phases.
- (4)
- The ensemble method was used to obtain an even distribution of the class representations from this few-shot mechanism [20]. The source code for the developed models is available at https:/github.com/bowoadi/cine_MRI_segmentation_classification (accessed on 6 July 2022).
2. Materials and Methods
2.1. Dataset
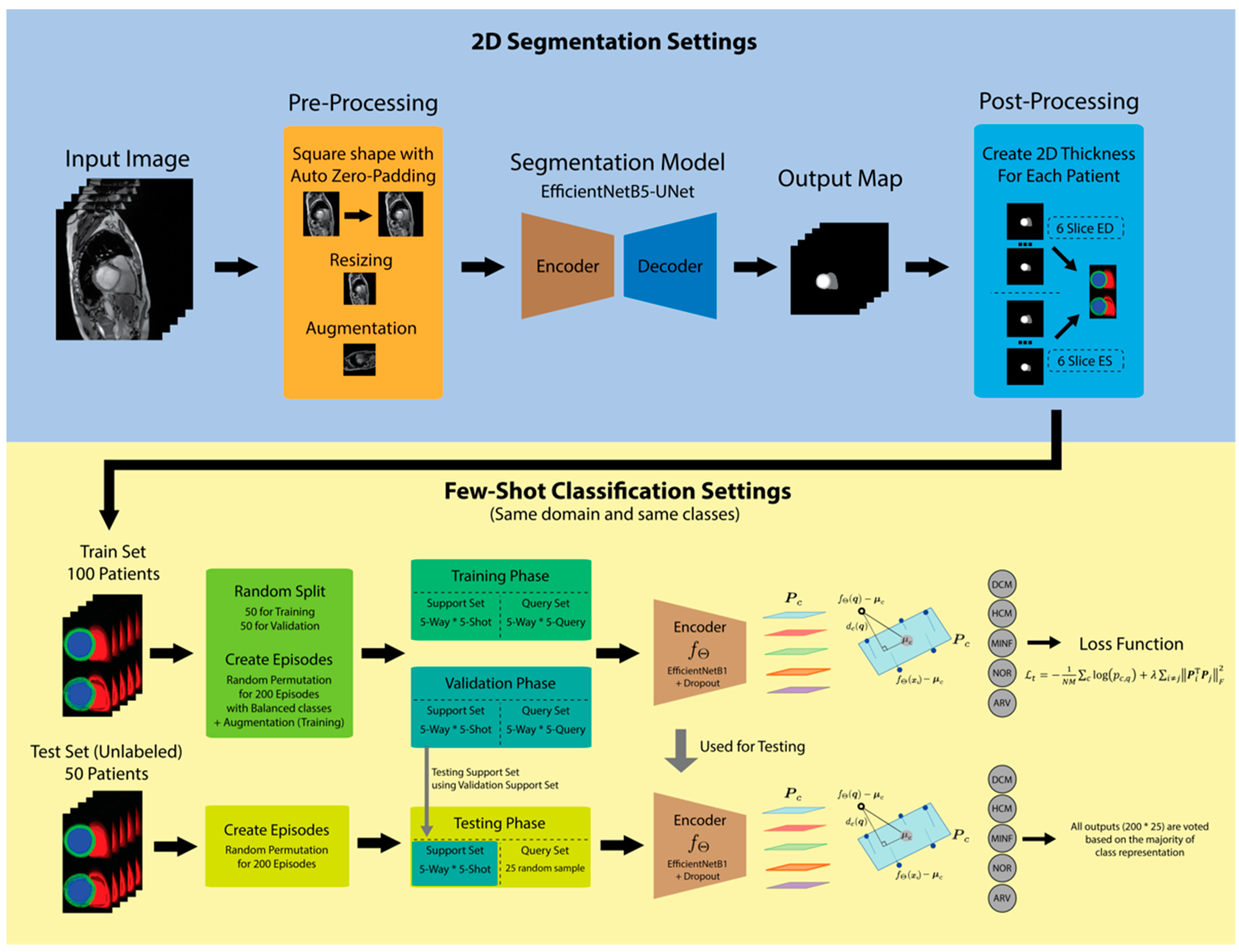
2.2. Proposed Method
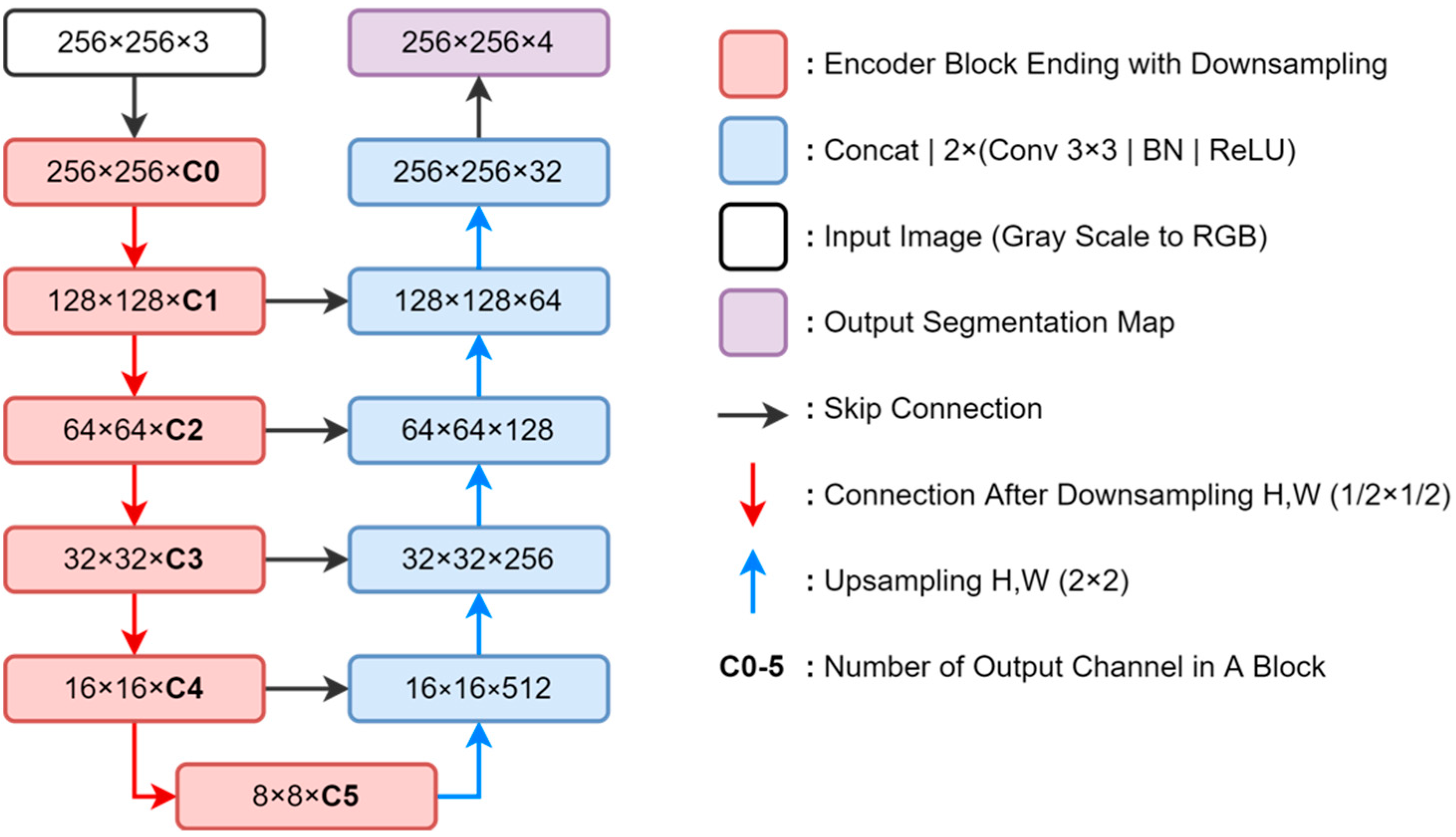
2.3. Segmentation Model and 2D Thickness Algorithm
| Algorithm 1 2D Thickness algorithm |
|
2.4. Few-Shot Learning Model
2.5. Segmentation Training and Testing Scenario
2.6. Few-Shot Classification Training and Testing Scenarios
3. Results
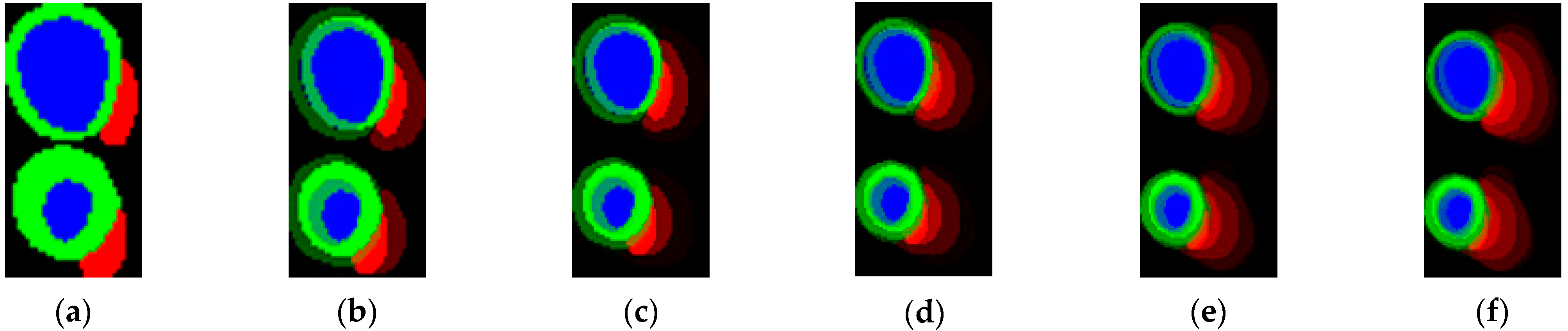
3.1. Segmentation Results
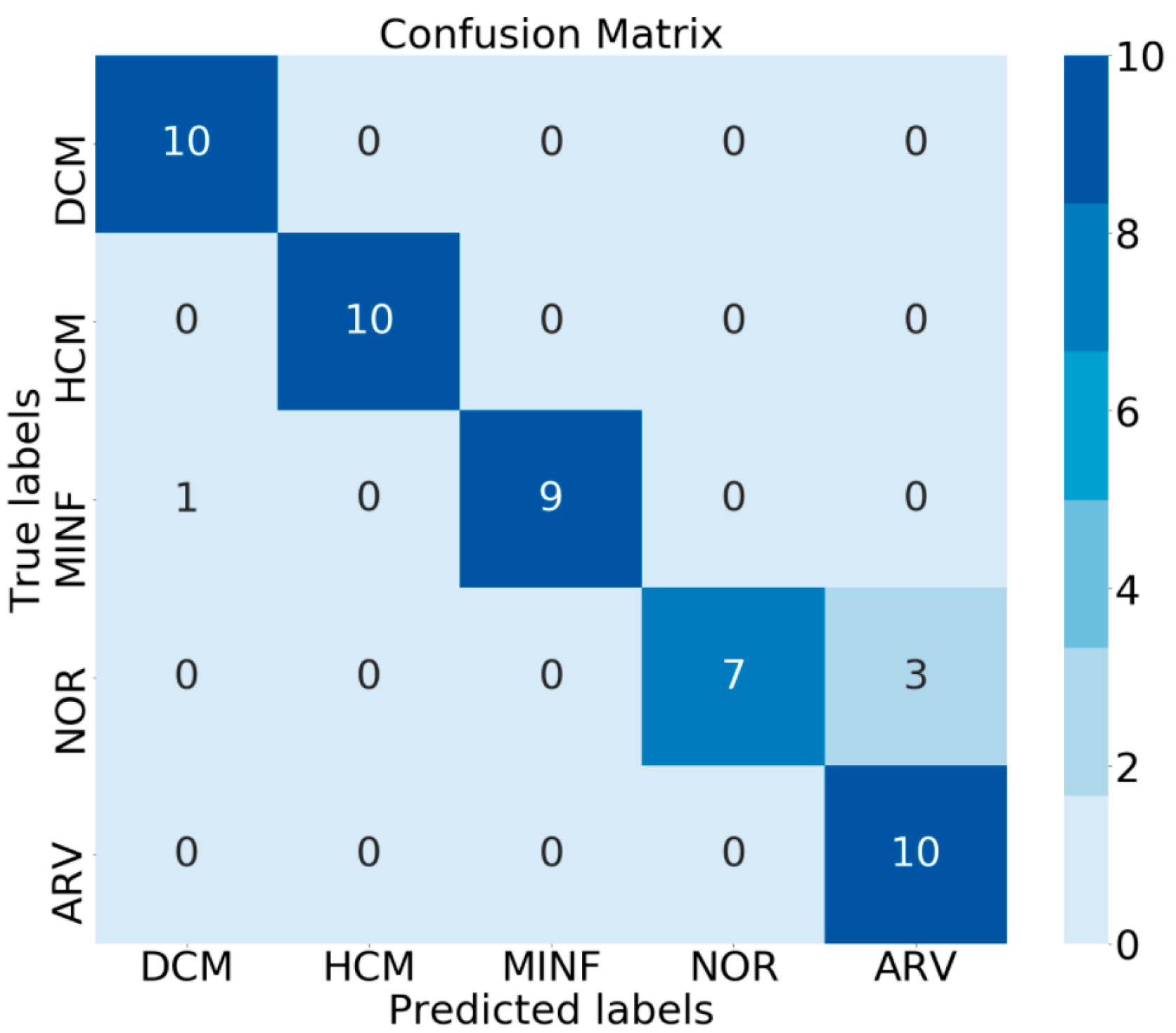
3.2. Classification Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kokubo, Y.; Matsumoto, C. Hypertension Is a Risk Factor for Several Types of Heart Disease: Review of Prospective Studies. Hypertens. Basic Res. Clin. Pract. Adv. Exp. Med. Biol. 2017, 956, 419–426. [Google Scholar] [CrossRef]
- Wexler, R.; Elton, T.; Pleister, A.; Feldman, D. Cardiomyopathy: An Overview. Am. Fam. Phys. 2009, 79, 778–784. [Google Scholar]
- Chugh, S.S. Early Identification of Risk Factors for Sudden Cardiac Death. Nat. Rev. Cardiol. 2010, 7, 318–326. [Google Scholar] [CrossRef] [PubMed]
- Clough, J.R.; Oksuz, I.; Puyol-Antón, E.; Ruijsink, B.; King, A.P.; Schnabel, J.A. Global and Local Interpretability for Cardiac MRI Classification. Lect. Notes Comput. Sci. (Incl. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform.) 2019, 11767 LNCS, 656–664. [Google Scholar] [CrossRef] [Green Version]
- Ammar, A.; Bouattane, O.; Youssfi, M. Automatic Cardiac Cine MRI Segmentation and Heart Disease Classification. Comput. Med. Imaging Graph. 2021, 88, 101864. [Google Scholar] [CrossRef]
- Tong, Q.; Li, C.; Si, W.; Liao, X.; Tong, Y.; Yuan, Z.; Heng, P.A. RIANet: Recurrent Interleaved Attention Network for Cardiac MRI Segmentation. Comput. Biol. Med. 2019, 109, 290–302. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, L.; Ma, Y.; Dong, M.; Du, S.; Sun, X. An SPCNN-GVF-Based Approach for the Automatic Segmentation of Left Ventricle in Cardiac Cine MR Images. Int. J. Comput. Assist. Radiol. Surg. 2016, 11, 242–255. [Google Scholar] [CrossRef]
- Isensee, F.; Jaeger, P.F.; Full, P.M.; Wolf, I.; Engelhardt, S.; Maier-Hein, K.H. Automatic Cardiac Disease Assessment on Cine-MRI via Time-Series Segmentation and Domain Specific Features. Lect. Notes Comput. Sci. (Incl. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform.) 2018, 10663 LNCS, 120–129. [Google Scholar] [CrossRef] [Green Version]
- Khened, M.; Kollerathu, V.A.; Krishnamurthi, G. Fully Convolutional Multi-scale Residual DenseNets for Cardiac Segmentation and Automated Cardiac Diagnosis Using Ensemble of Classifiers. Med. Image Anal. 2019, 51, 21–45. [Google Scholar] [CrossRef] [Green Version]
- Wolterink, J.M.; Leiner, T.; Viergever, M.A.; Išgum, I. Automatic Segmentation and Disease Classification Using Cardiac Cine MR Images. Lect. Notes Comput. Sci. (Incl. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform.) 2018, 10663 LNCS, 101–110. [Google Scholar] [CrossRef] [Green Version]
- Khened, M.; Alex, V.; Krishnamurthi, G. Densely Connected Fully Convolutional Network for Short-Axis Cardiac Cine MR Image Segmentation and Heart Diagnosis Using Random Forest. Lect. Notes Comput. Sci. (Incl. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform.) 2018, 10663 LNCS, 140–151. [Google Scholar] [CrossRef]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Kavukcuoglu, K.; Wierstra, D. Matching Networks for One Shot Learning. Adv. Neural Inf. Process. Syst. 2016, 3637–3645. [Google Scholar]
- Hu, J.; Lu, J.; Tan, Y.-P.; Zhou, J. Deep Transfer Metric Learning. IEEE Trans. Image Process. 2016, 25, 5576–5588. [Google Scholar] [CrossRef] [PubMed]
- Jake, S.; Kevin, S.; Richard, Z. Prototypical Networks for Few-Shot Learning. Adv. Neural Inf. Process. Syst. 2017, 30, 4077–4087. [Google Scholar]
- Simon, C.; Koniusz, P.; Nock, R.; Harandi, M. Adaptive Subspaces for Few-Shot Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 4135–4144. [Google Scholar]
- Wang, Y. Low-Shot Learning from Imaginary Data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7278–7286. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-learning for Fast Adaptation of Deep Networks. In Proceedings of the 34th International Conference Machinability Learned ICML, Sydney, Australia, 6–11 August 2017; Volume 3, pp. 1856–1868. [Google Scholar]
- Li, X.; Yang, X.; Ma, Z.; Xue, J.-H. Deep Metric Learning for Few-Shot Image Classification: A Selective Review. arXiv 2021, arXiv:2105.08149. [Google Scholar]
- Chen, W.; Wang, Y.F.; Liu, Y.; Kira, Z.; Tech, V. A Closer Look at Few-Shot Classification. international conference Learned Representacion. arXiv 2019, arXiv:1904.04232. [Google Scholar]
- Dvornik, N.; Mairal, J.; Schmid, C. Diversity with Cooperation: Ensemble Methods for Few-Shot Classification. Proc. IEEE Int. Conf. Comput. Vis. 2019, 2019, 3722–3730. [Google Scholar]
- Bernard, O.; Lalande, A.; Zotti, C.; Cervenansky, F.; Yang, X.; Heng, P.A.; Cetin, I.; Lekadir, K.; Camara, O.; Gonzalez Ballester, M.A.; et al. Deep Learning Techniques for Automatic MRI Cardiac Multi-structures Segmentation and Diagnosis: Is the Problem Solved? IEEE Trans. Med. Imaging 2018, 37, 2514–2525. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference Machinability Learned ICML, Long Beach, CA, USA, 9–15 June 2019; Volume 2019, pp. 10691–10700. [Google Scholar]
- Howard, A.; Wang, W.; Chu, G.; Chen, L.; Chen, B.; Tan, M. Searching for MobileNetV3. In Proceedings of the international conference Computability Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Wibowo, A.; Pratama, C.; Sahara, D.P.; Heliani, L.S.; Rasyid, S.; Akbar, Z.; Muttaqy, F.; Sudrajat, A. Earthquake Early Warning System Using Ncheck and Hard-Shared Orthogonal Multitarget Regression on Deep Learning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wibowo, A.; Purnama, S.R.; Wirawan, P.W.; Rasyidi, H. Lightweight Encoder-Decoder Model for Automatic Skin Lesion Segmentation. Inform. Med. Unlocked. 2021, 25, 100640. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Lect. Notes Comput. Sci. (Incl. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform.) 2015, 9351, 234–241. [Google Scholar] [CrossRef] [Green Version]
- Keskar, N.S.; Nocedal, J.; Tang, P.T.P.; Mudigere, D.; Smelyanskiy, M. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima. In Proceedings of the 5th International Conference Learned Representacion ICLR, Toulon, France, 24–26 April 2017; Volume 2017, pp. 1–16. [Google Scholar]
- Zhou, R.; Guo, F.; Azarpazhooh, M.R.; Hashemi, S.; Cheng, X.; Spence, J.D.; Ding, M.; Fenster, A. Deep Learning-Based Measurement of Total Plaque Area in B-Mode Ultrasound Images. IEEE J. Biomed. Heal. Inform. 2021, 25, 2194. [Google Scholar] [CrossRef] [PubMed]
- Simantiris, G.; Tziritas, G. Cardiac MRI Segmentation with a Dilated CNN Incorporating Domain-Specific Constraints. IEEE J. Sel. Top. Signal Process. 2020, 4553, 1–9. [Google Scholar] [CrossRef]
- Qin, J.; Huang, Y.; Wen, W. Multi-scale Feature Fusion Residual Network for Single Image Super-Resolution. Neurocomputing. 2020, 379, 334–342. [Google Scholar] [CrossRef]
- Cetin, I.; Sanroma, G.; Petersen, S.E.; Napel, S.; Camara, O.; Ballester, M.G.; Lekadir, K. A Radiomics Approach to Computer-Aided Diagnosis with Cardiac Cine-MRI. Lect. Notes Comput. Sci. (Incl. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform.) 2018, 10663 LNCS, 82–90. [Google Scholar] [CrossRef] [Green Version]
- Jefferies, J.L.; Towbin, J.A. Dilated Cardiomyopathy. Lancet. 2010, 375, 752–762. [Google Scholar] [CrossRef]
- Maron, B.J.; Maron, M.S. Hypertrophic Cardiomyopathy. Lancet 2013, 381, 242–255. [Google Scholar] [CrossRef]
- Thygesen, K.; Alpert, J.S.; Jaffe, A.S.; Chaitman, B.R.; Bax, J.J.; Morrow, D.A.; White, H.D.; Executive Group on behalf of the Joint European Society of Cardiology (ESC)/American College of Cardiology (ACC)/American Heart Association (AHA)/World Heart Federation (WHF) Task Force for the Universal Definition of Myocardial Infarction. Fourth Universal Definition of Myocardial Infarction (2018). J. Am. Coll. Cardiol. 2018, 72, 2231–2264. [Google Scholar] [CrossRef]
- de Groote, P.; Millaire, A.; Foucher-Hossein, C.; Nugue, O.; Marchandise, X.; Ducloux, G.; Lablanche, J.M. Right Ventricular Ejection Fraction Is an Independent Predictor of Survival in Patients with Moderate Heart Failure. J. Am. Coll. Cardiol. 1998, 32, 948–954. [Google Scholar] [CrossRef] [Green Version]



| Segmentation Model | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 | Average | Standard Deviation |
|---|---|---|---|---|---|---|---|
| MobileNetV3-UNet | 0.891 | 0.880 | 0.889 | 0.896 | 0.890 | 0.889 | 0.0052 |
| EfficientNetB0-UNet | 0.884 | 0.879 | 0.885 | 0.888 | 0.894 | 0.886 | 0.0049 |
| EfficientNetB1-UNet | 0.897 | 0.881 | 0.888 | 0.890 | 0.893 | 0.890 | 0.0053 |
| EfficientNetB2-UNet | 0.890 | 0.888 | 0.883 | 0.887 | 0.890 | 0.888 | 0.0026 |
| EfficientNetB3-UNet | 0.898 | 0.888 | 0.894 | 0.891 | 0.893 | 0.893 | 0.0033 |
| EfficientNetB4-UNet | 0.889 | 0.889 | 0.888 | 0.893 | 0.890 | 0.890 | 0.0015 |
| EfficientNetB5-UNet | 0.896 | 0.891 | 0.893 | 0.894 | 0.889 | 0.893 | 0.0024 |
| State-of-the-Art Methods | LV | RV | MYO | |||
|---|---|---|---|---|---|---|
| ED | ES | ED | ES | ED | ES | |
| Fabian Isensee [8] | 0.967 | 0.935 | 0.951 | 0.904 | 0.904 | 0.923 |
| Fumin Guo [29] | 0.968 | 0.935 | 0.955 | 0.894 | 0.906 | 0.923 |
| Georgios Simantris [30] | 0.967 | 0.928 | 0.936 | 0.889 | 0.891 | 0.904 |
| Mahendra Khened [11] | 0.964 | 0.917 | 0.935 | 0.879 | 0.889 | 0.898 |
| Ensemble B0-B5 (proposed) | 0.963 | 0.907 | 0.919 | 0.865 | 0.889 | 0.905 |
| Ensemble V3B5 (proposed) | 0.962 | 0.899 | 0.929 | 0.869 | 0.889 | 0.905 |
| EfficientNetB5-UNet (proposed) | 0.963 | 0.904 | 0.929 | 0.856 | 0.887 | 0.903 |
| MobileNetV3-UNet (proposed) | 0.960 | 0.887 | 0.885 | 0.858 | 0.885 | 0.898 |
| Encoder | Experiment 1 | Experiment 2 | Experiment 3 | Experiment 4 | Experiment 5 | Average | Standard Deviation |
|---|---|---|---|---|---|---|---|
| Conv4 | 0.6912 | 0.6692 | 0.6916 | 0.6568 | 0.6620 | 0.6742 | 0.0146 |
| MobileNetV3 without pre-trained | 0.4064 | 0.4092 | 0.4944 | 0.4988 | 0.5568 | 0.4731 | 0.0577 |
| MobileNetV3 pre-trained | 0.6304 | 0.5951 | 0.6140 | 0.6375 | 0.7156 | 0.6385 | 0.0412 |
| EfficientNetB1 without pre-trained | 0.5036 | 0.3620 | 0.5532 | 0.4474 | 0.6304 | 0.4993 | 0.0913 |
| EfficientNetB1 pre-trained | 0.6375 | 0.6916 | 0.6916 | 0.7220 | 0.7320 | 0.6949 | 0.0329 |
| Encoder (Pre-Trained) | Experiment 1 | Experiment 2 | Experiment 3 | Experiment 4 | Experiment 5 | Average | Standard Deviation |
|---|---|---|---|---|---|---|---|
| EfficientNetB1 | 0.6375 | 0.6916 | 0.6916 | 0.7220 | 0.7320 | 0.6949 | 0.0329 |
| EfficientNetB1—dropout | 0.5836 | 0.6952 | 0.6468 | 0.5848 | 0.6712 | 0.6363 | 0.0452 |
| EfficientNetB1—augment | 0.7368 | 0.7735 | 0.6808 | 0.7423 | 0.6948 | 0.7256 | 0.0363 |
| EfficientNetB1—dropout-augment | 0.8083 | 0.7622 | 0.7710 | 0.7900 | 0.7801 | 0.7823 | 0.0159 |
| Number of Shots | Experiment 1 | Experiment 2 | Experiment 3 | Experiment 4 | Experiment 5 | Average | Standard Deviation |
|---|---|---|---|---|---|---|---|
| 1-shot | 0.6360 | 0.5460 | 0.5620 | 0.5639 | 0.5460 | 0.5708 | 0.0348 |
| 2-shot | 0.7230 | 0.6780 | 0.7250 | 0.7200 | 0.6919 | 0.7076 | 0.0191 |
| 3-shot | 0.7007 | 0.7507 | 0.7120 | 0.7220 | 0.7080 | 0.7187 | 0.0174 |
| 4-shot | 0.7880 | 0.7150 | 0.7180 | 0.7410 | 0.7490 | 0.7422 | 0.0263 |
| 5-shot | 0.8083 | 0.7622 | 0.7710 | 0.7900 | 0.7801 | 0.7823 | 0.0159 |
| Number of Slice(s) | Accuracy Score |
|---|---|
| 1 | 0.6928 |
| 2 | 0.7184 |
| 3 | 0.7272 |
| 4 | 0.7548 |
| 5 | 0.7632 |
| 6 | 0.8083 |
| Method | Score on Leaderboard |
|---|---|
| Proposed Experiment 1 | 78 |
| Proposed Experiment 2 | 80 |
| Proposed Experiment 3 | 84 |
| Proposed Experiment 4 | 86 |
| Proposed Experiment 5 | 86 |
| Proposed Ensemble | 92 |
| [11] | 100 |
| [8] | 92 |
| [32] | 92 |
| [10] | 86 |
| Method | Stage | Strengths | Weaknesses |
|---|---|---|---|
| Proposed | Segmentation | Segmentation becomes lighter with UNet-EfficientNetB5 for data per slice. | The segmentation performance has not outperformed the previous method. |
| Classification | Only considers slices and does not depend on the parameter settings of the tool and the number of slices obtained. Can be compared between the number of slices. | This approach is only suitable for morphological problems. Uncertainty is high because depending on the training in each episode, this is handled by the ensemble. | |
| Mahendra Khened [9] | Segmentation | Segmentation using DenseNet which is suitable for limited data. | Segmentation using 2D UNet with dense block doesn’t outperform the ensemble of 2D and 3D DMR-UNet. |
| Classification | Classification becomes faster with Random Forest. | The classification most exclusively focus on end-diastole and end-systole features. | |
| Fabian Isensee [8] | Segmentation | Segmentation by combining 2D and 3D UNets slightly improved. | The 3D UNet has large slice gap on the input images, it causes pooling and upscaling operations are carried out only in the short-axis plane. Moreover, the 3D network involves a smaller number of feature maps. |
| Classification | Perform ensemble classification by combining MLP and Random Forest. | The ensemble method does not outperform single Random Forest. | |
| Irem Cetin [32] | Segmentation | The training data was manually segmented to produce accurate results. | They computed large number of computations manually. This method tends to overfitting. To prevent from overfitting, they selected the most discriminative features and used SVM for classification. |
| Classification | Classification using Support Vector Machines suitable for limited data. | The classification method does not outperform. | |
| Jelmer M Wolterink [10] | Segmentation | The network was designed to contain a number of convolutional layers with increasing levels of dilatation to produce high resolution feature maps. | Convolutional neural network does not exhibit an encoder–decoder architecture. |
| Classification | Classification becomes faster with Random Forest. | Classification methods most exclusively focus on end-diastole and end-systole features. It does not outperform other Random Forest. | |
| Fumin Guo [29] | Segmentation | Segmentation by combining UNet and Continuos Max-Flow. | Only for left ventricle. Other methods function for right ventricle and myocardium. |
| Classification | N/A | N/A | |
| Georgios Simantris [30] | Segmentation | Networks trains quickly and efficiently without overfitting. | Does not outperform to the state of art featured in the ACDC. |
| Classification | N/A | N/A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wibowo, A.; Triadyaksa, P.; Sugiharto, A.; Sarwoko, E.A.; Nugroho, F.A.; Arai, H.; Kawakubo, M. Cardiac Disease Classification Using Two-Dimensional Thickness and Few-Shot Learning Based on Magnetic Resonance Imaging Image Segmentation. J. Imaging 2022, 8, 194. https://doi.org/10.3390/jimaging8070194
Wibowo A, Triadyaksa P, Sugiharto A, Sarwoko EA, Nugroho FA, Arai H, Kawakubo M. Cardiac Disease Classification Using Two-Dimensional Thickness and Few-Shot Learning Based on Magnetic Resonance Imaging Image Segmentation. Journal of Imaging. 2022; 8(7):194. https://doi.org/10.3390/jimaging8070194
Chicago/Turabian StyleWibowo, Adi, Pandji Triadyaksa, Aris Sugiharto, Eko Adi Sarwoko, Fajar Agung Nugroho, Hideo Arai, and Masateru Kawakubo. 2022. "Cardiac Disease Classification Using Two-Dimensional Thickness and Few-Shot Learning Based on Magnetic Resonance Imaging Image Segmentation" Journal of Imaging 8, no. 7: 194. https://doi.org/10.3390/jimaging8070194
APA StyleWibowo, A., Triadyaksa, P., Sugiharto, A., Sarwoko, E. A., Nugroho, F. A., Arai, H., & Kawakubo, M. (2022). Cardiac Disease Classification Using Two-Dimensional Thickness and Few-Shot Learning Based on Magnetic Resonance Imaging Image Segmentation. Journal of Imaging, 8(7), 194. https://doi.org/10.3390/jimaging8070194






