Integration of Deep Learning and Active Shape Models for More Accurate Prostate Segmentation in 3D MR Images
Abstract
:1. Introduction
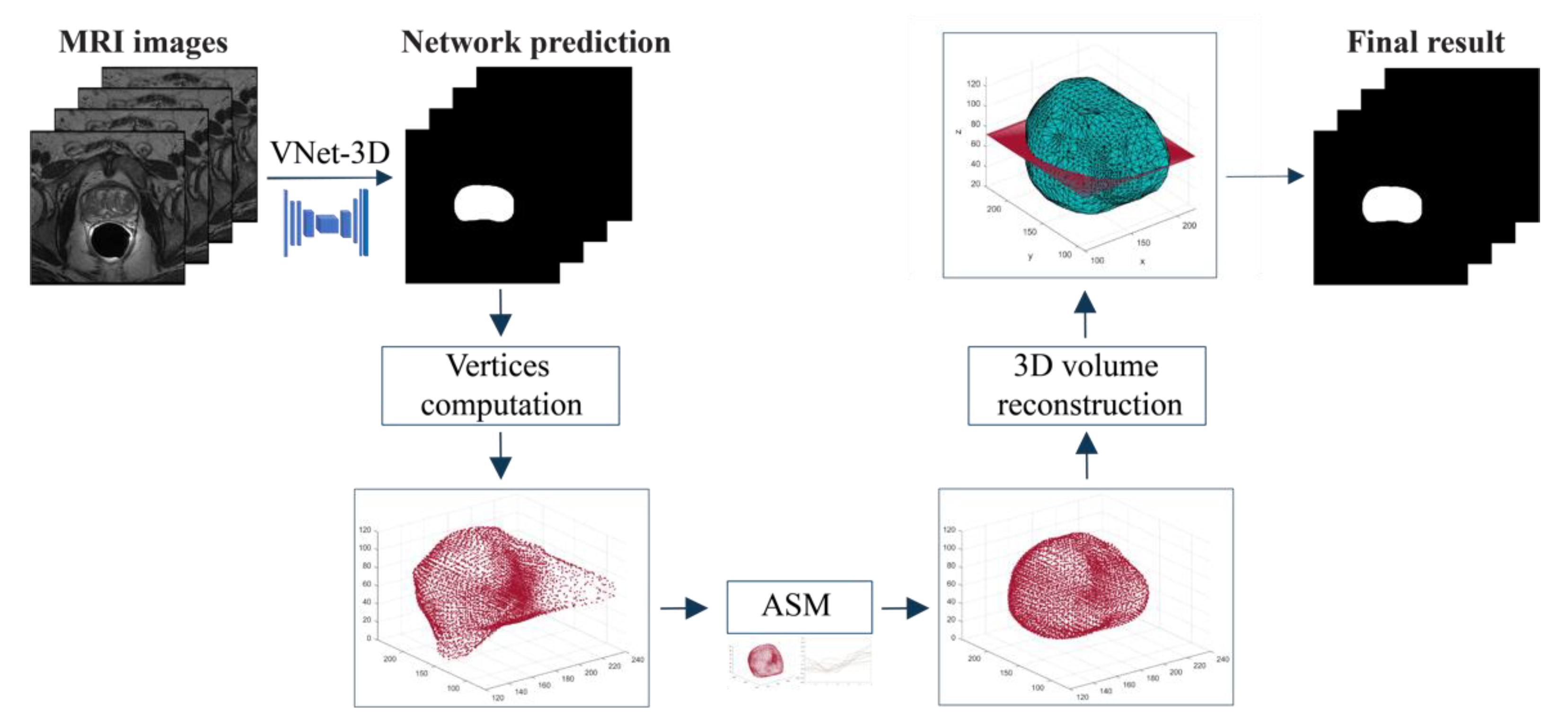
- We propose a fully automated hybrid approach for 3D MRI prostate segmentation using CNNs and ASMs. A custom 3D deep network is employed to provide a first segmentation of the prostate glands. Then, a statistical model is applied to refine the segmentation in correspondence of the prostate edges.
- We develop an effective approach based on the combination of semantic features extracted from the CNN and statistical features from the ASM. By using a CNN-based initialization, we can bypass the limitations of current ASMs.
- We improved the robustness of the ASM by removing noisy intensity profiles using the DB-SCAN clustering algorithm.
- We publicly release the code used in this work. An extended validation is also performed by comparing the proposed approach with two manual operators. Our algorithm obtains highly satisfactory results.
2. Materials and Methods
2.1. Patients and Dataset Composition
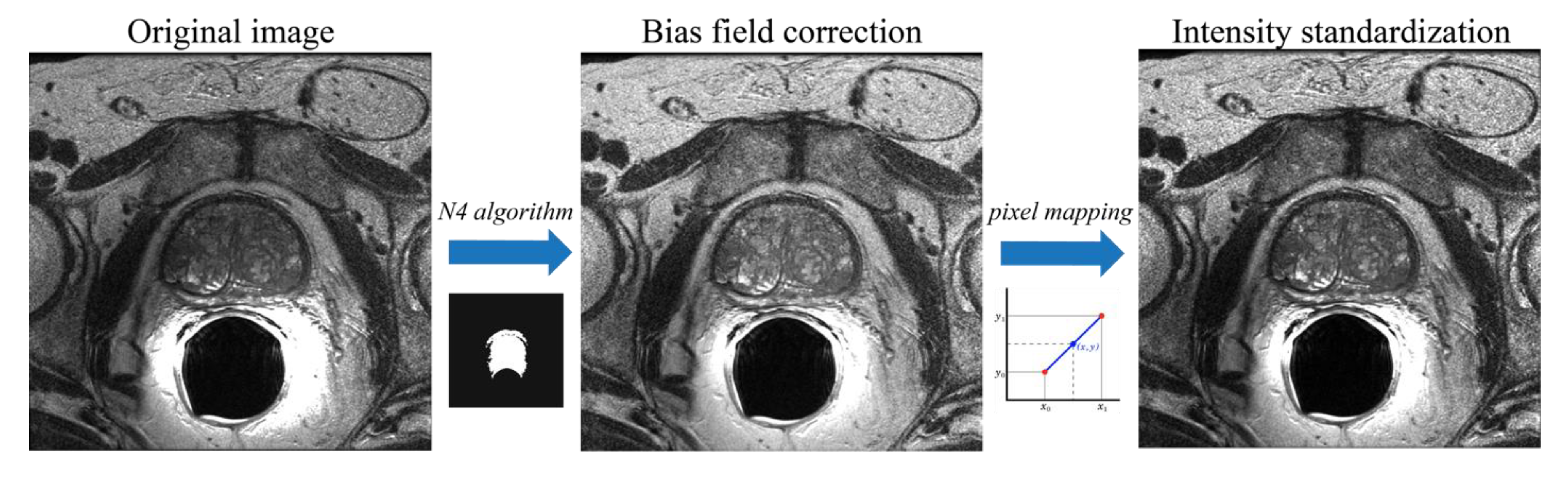
2.2. Bias Field Correction and Intensity Normalization
2.3. Deep Convolutional Networks
- A first convolutional layer (kernel size 3 × 3 × 3) followed by a layer of instance normalization;
- A second convolutional layer (kernel size 3 × 3 × 3) followed by a layer of instance normalization;
- A max-pooling layer in 3D with a pool size equal to (2, 2, 2).
- Class balancing: the network’s loss function is class-weighted by considering how frequently a class occurs in the training set. This means that the least represented class (prostate gland) will have a greater contribution than the more represented one (background) during the weight update. This is performed following the same approach of our previous work [35].
- Dice loss: the network loss function is calculated as 1-DSC, where DSC is the dice score computed between the manual annotation and the network prediction. The dice overlap is a widely used loss function for highly unbalanced segmentations [36].
2.4. Active Shape Models (ASM)
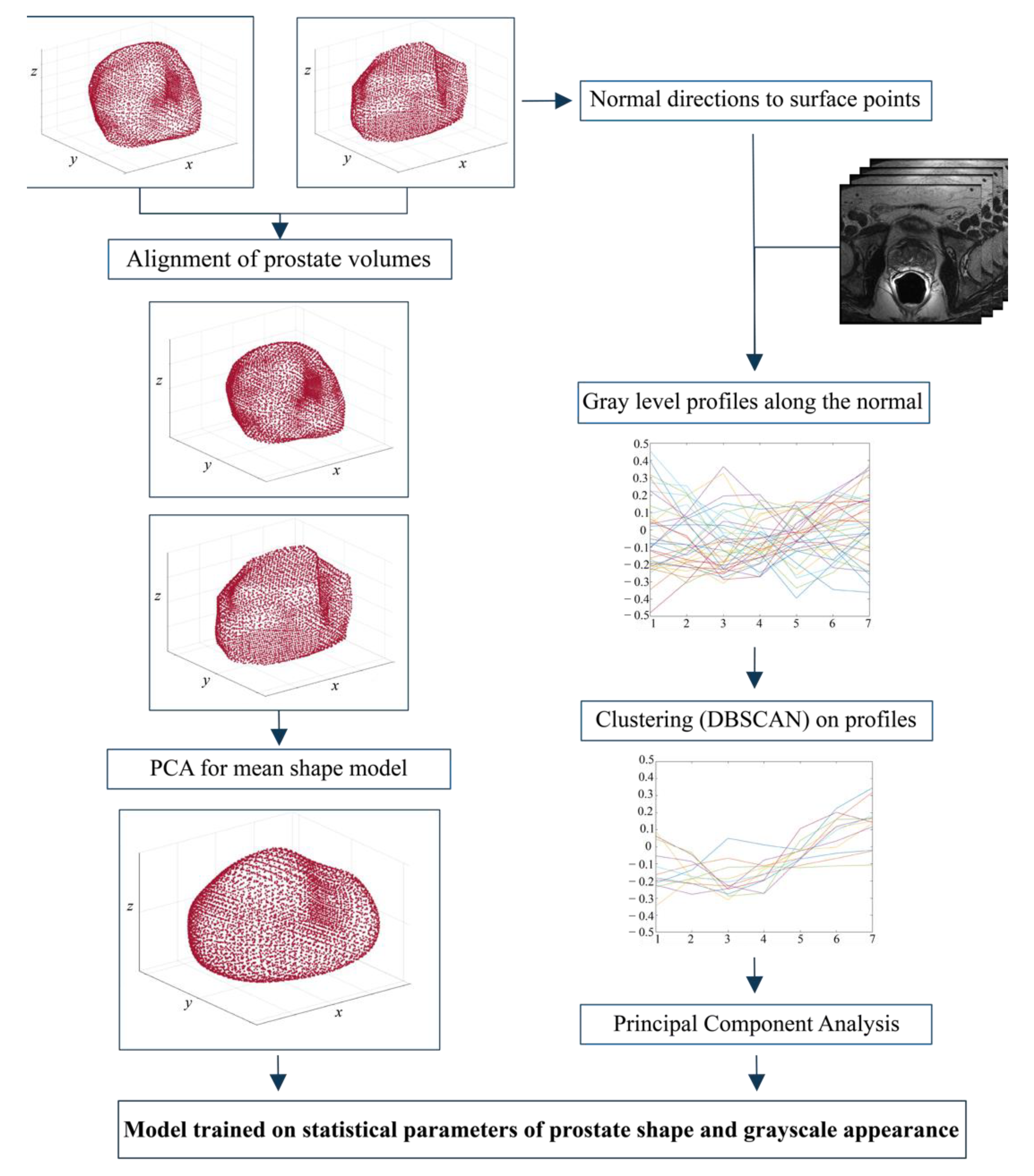
2.4.1. Mean Shape Model Determination and Appearance Data
- 1.
- 3D-surface fit: in this step, the external surface of each prostate is fitted with a three-dimensional ellipsoidal surface. Subsequently, key reference points are determined in both the x-y plane and the y-z planes as and , respectively, where and .
- 2.
- Triangulation: Starting from the 3D vertices obtained in step 1, the Alpha Shape Triangulation [38] is employed to divide the 3D surface into a variable number of triangles. This triangulation method requires an α parameter that defines the level of refinement of the structure. A value of α = 50 was used, as it was found to be appropriate for all prostate shapes included in the dataset.
- 3.
- Ray-Triangle intersection: This step is necessary to obtain corresponding key points in each prostate. To do so, the Moller-Trumbdor [38] algorithm is employed to compute the intersection between a set of rays originating in each of the key points found in step 1 (i.e., Fxy and Fxz) and each of the triangles that were obtained in step 2. A ray is defined as where O is the origin of the ray and D is a normalized direction. In this study, we chose 8 directions with a step angle (θ) of 360°/8. For a detailed description of how this algorithm works, please see the study by Moller et al. [38].
- 4.
- Vertices determination: For each direction D, the intersection points between the ray and the 3D model are determined and make up the final vertices.
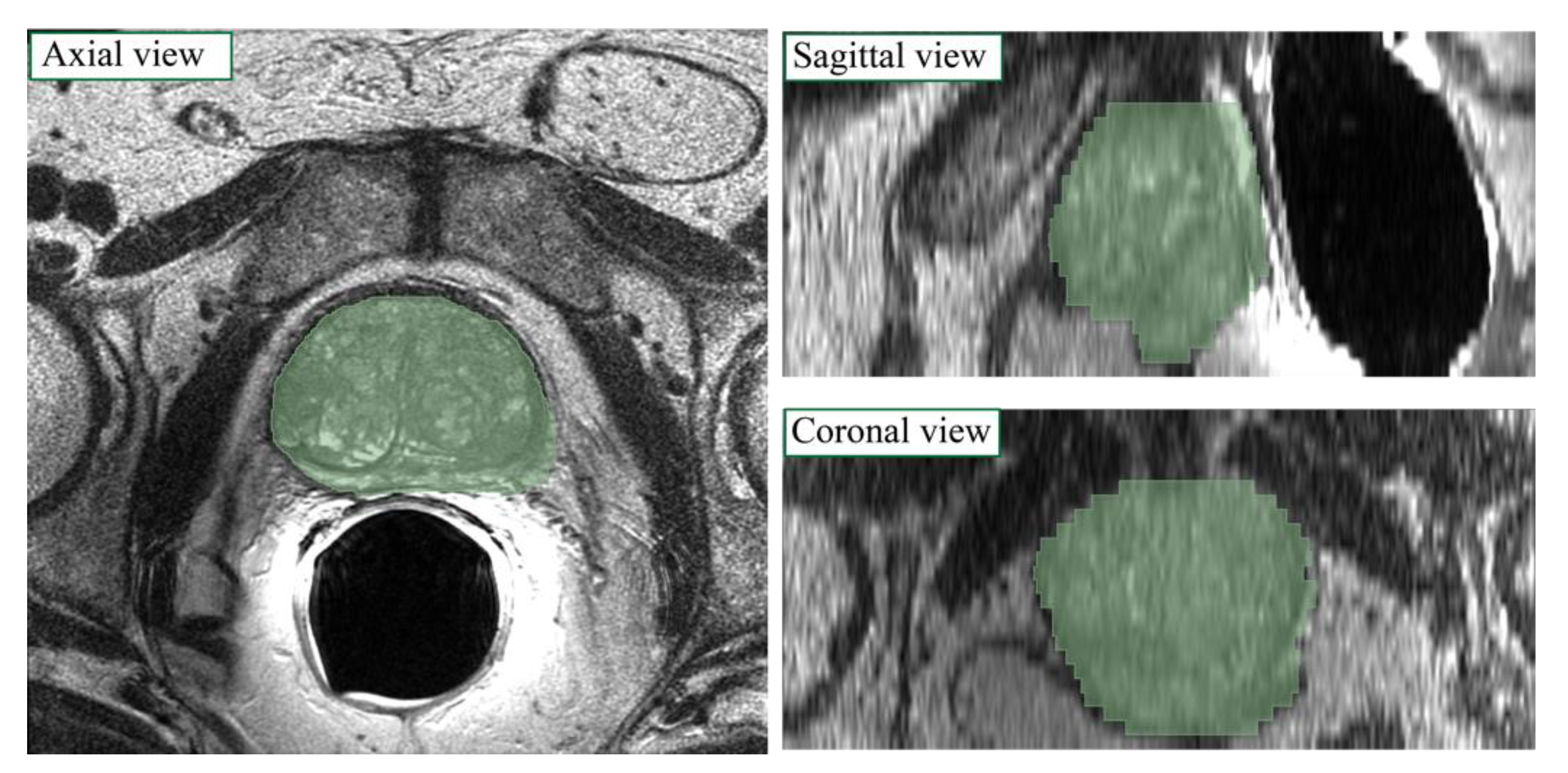
2.4.2. ASM Model Application on Network Output
2.4.3. Post-Processing
- Triangulation: the Alpha Shape Triangulation method is employed to divide the 3D surface into a variable number of triangles, with α = 30.
- 2D slices definition: to obtain the final 2D slices of the segmentation, the volume is divided into a number of planes whose z-coordinate corresponds to the number of slices. Then, similarly as to what was described previously, new vertices of the segmentation are found by computing the intersection between each ray and each triangle and taking the furthest point from the center, which is a first approximation of the points on the outermost surface.
- Final 3D volume reconstruction: the final 3D volume is obtained by stacking the 2D slices together, employing a hole-filling operation, and then a 3D morphological closing (spherical structural element, radius = 4). The post-processed binary volume is finally downsampled to the original resolution.
2.5. Performance Metrics
3. Results
3.1. Ablation Study
3.2. Inter-Observer Variability
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
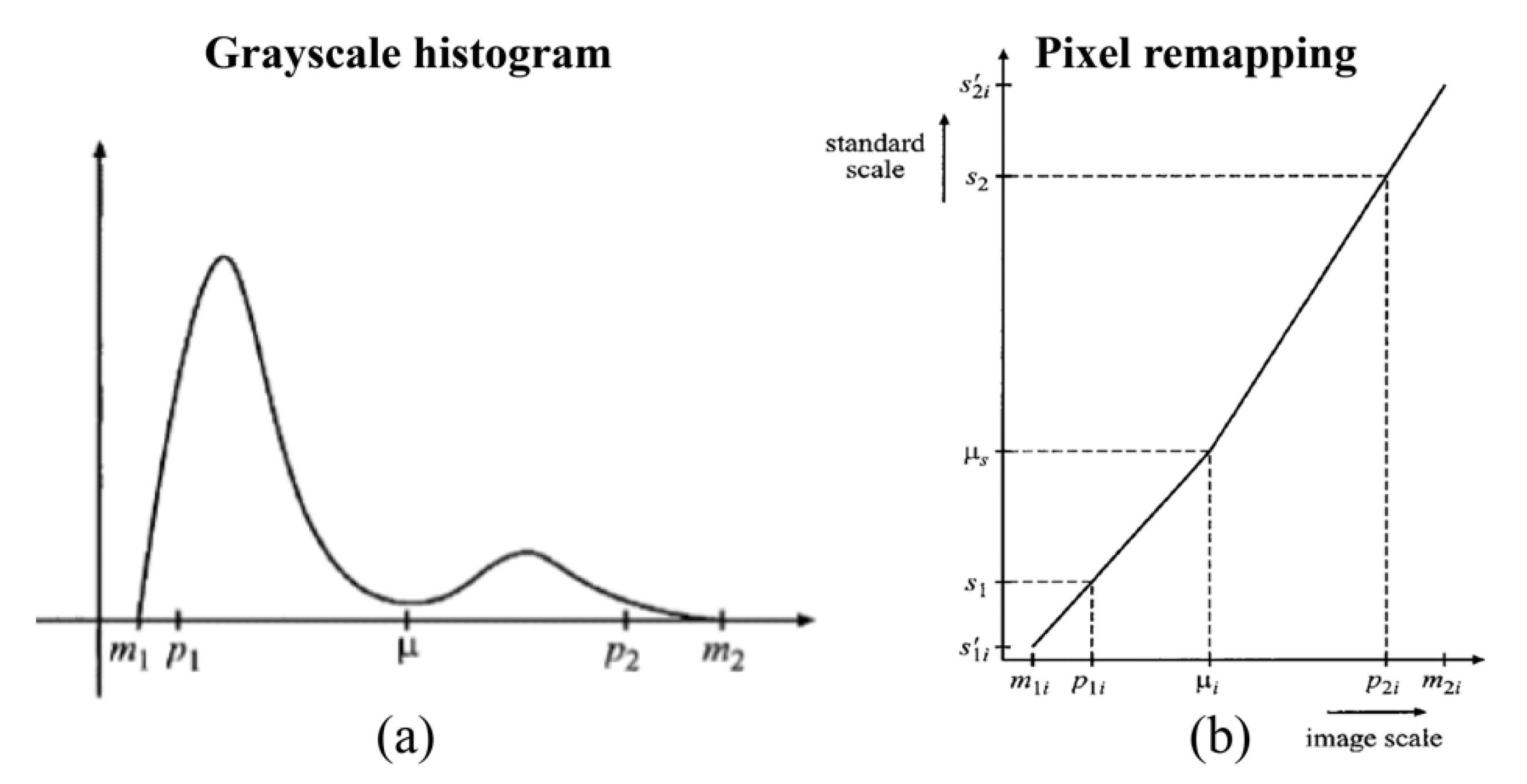
- [p1, p2]: min and max percentile ([2, 99.5])
- [m1, m2]: min and max intensity of the histogram
- [s1, s2]: min and max value of standardized range ([0, 255])
- μ: valley between the two modes of the histogram
Appendix B
References
- Rawla, P. Epidemiology of Prostate Cancer. World J. Oncol. 2019, 10, 63–89. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Litjens, G.; Toth, R.; van de Ven, W.; Hoeks, C.; Kerkstra, S.; van Ginneken, B.; Vincent, G.; Guillard, G.; Birbeck, N.; Zhang, J.; et al. Evaluation of Prostate Segmentation Algorithms for MRI: The PROMISE12 Challenge. Med. Image Anal. 2014, 18, 359–373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hricak, H.; Dooms, G.C.; McNeal, J.E.; Mark, A.S.; Marotti, M.; Avallone, A.; Pelzer, M.; Proctor, E.C.; Tanagho, E.A. MR Imaging of the Prostate Gland. PET Clin. 2009, 4, 139–154. [Google Scholar] [CrossRef]
- Cootes, T.F.; Taylor, C.J. Active Shape Models—‘Smart Snakes’. In BMVC92; Springer: London, UK, 1992; pp. 266–275. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Medioni, G. Object Modelling by Registration of Multiple Range Images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- He, B.; Xiao, D.; Hu, Q.; Jia, F. Automatic Magnetic Resonance Image Prostate Segmentation Based on Adaptive Feature Learning Probability Boosting Tree Initialization and CNN-ASM Refinement. IEEE Access 2017, 6, 2005–2015. [Google Scholar] [CrossRef]
- Salvi, M.; Molinaro, L.; Metovic, J.; Patrono, D.; Romagnoli, R.; Papotti, M.; Molinari, F. Fully Automated Quantitative Assessment of Hepatic Steatosis in Liver Transplants. Comput. Biol. Med. 2020, 123, 103836. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.W.M.; van Ginneken, B.; Sánchez, C.I. A Survey on Deep Learning in Medical Image Analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [Green Version]
- Chan, H.P.; Samala, R.K.; Hadjiiski, L.M.; Zhou, C. Deep Learning in Medical Image Analysis. Adv. Exp. Med. Biol. 2020, 1213, 3–21. [Google Scholar] [CrossRef]
- Liu, J.; Pan, Y.; Li, M.; Chen, Z.; Tang, L.; Lu, C.; Wang, J. Applications of Deep Learning to MRI Images: A Survey. Big Data Min. Anal. 2018, 1, 1–18. [Google Scholar] [CrossRef]
- Lundervold, A.S.; Lundervold, A. An Overview of Deep Learning in Medical Imaging Focusing on MRI. Z. Med. Phys. 2019, 29, 102–127. [Google Scholar] [CrossRef]
- Yu, L.; Yang, X.; Chen, H.; Qin, J.; Heng, P.A. Volumetric Convnets with Mixed Residual Connections for Automated Prostate Segmentation from 3d MR Images. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 66–72. [Google Scholar]
- Zhu, Q.; Du, B.; Yan, P. Boundary-Weighted Domain Adaptive Neural Network for Prostate MR Image Segmentation. IEEE Trans. Med. Imaging 2020, 39, 753–763. [Google Scholar] [CrossRef] [PubMed]
- Jia, H.; Xia, Y.; Song, Y.; Zhang, D.; Huang, H.; Zhang, Y.; Cai, W. 3D APA-Net: 3D Adversarial Pyramid Anisotropic Convolutional Network for Prostate Segmentation in MR Images. IEEE Trans. Med. Imaging 2020, 39, 447–457. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Roth, H.R.; Lu, L.; Wang, S.; Turkbey, B.; Gandler, W.; McCreedy, E.S.; Agarwal, H.K.; Choyke, P.; Summers, R.M.; et al. Active Appearance Model and Deep Learning for More Accurate Prostate Segmentation on MRI. Med. Imaging Image Process. 2016, 9784, 97842I. [Google Scholar] [CrossRef]
- Karimi, D.; Samei, G.; Kesch, C.; Nir, G.; Salcudean, S.E. Prostate Segmentation in MRI Using a Convolutional Neural Network Architecture and Training Strategy Based on Statistical Shape Models. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 1211–1219. [Google Scholar] [CrossRef] [PubMed]
- Ushinsky, A.; Bardis, M.; Glavis-Bloom, J.; Uchio, E.; Chantaduly, C.; Nguyentat, M.; Chow, D.; Chang, P.D.; Houshyar, R. A 3d-2d Hybrid u-Net Convolutional Neural Network Approach to Prostate Organ Segmentation of Multiparametric MRI. Am. J. Roentgenol. 2021, 216, 111–116. [Google Scholar] [CrossRef] [PubMed]
- Meyer, A.; Chlebus, G.; Rak, M.; Schindele, D.; Schostak, M.; van Ginneken, B.; Schenk, A.; Meine, H.; Hahn, H.K.; Schreiber, A.; et al. Anisotropic 3D Multi-Stream CNN for Accurate Prostate Segmentation from Multi-Planar MRI. Comput. Methods Programs Biomed. 2021, 200, 105821. [Google Scholar] [CrossRef]
- Pollastri, F.; Cipriano, M.; Bolelli, F.; Grana, C. Long-range 3d self-attention for mri prostate segmentation. In Proceedings of the 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI), Kolkata, India, 28–31 March 2022; pp. 1–5. [Google Scholar]
- Shahedi, M.; Cool, D.W.; Bauman, G.S.; Bastian-Jordan, M.; Fenster, A.; Ward, A.D. Accuracy Validation of an Automated Method for Prostate Segmentation in Magnetic Resonance Imaging. J. Digit. Imaging 2017, 30, 782–795. [Google Scholar] [CrossRef]
- Natarajan, S.; Priester, A.; Margolis, D.; Huang, J.; Marks, L. Prostate MRI and Ultrasound With Pathology and Coordinates of Tracked Biopsy (Prostate-MRI-US-Biopsy). Cancer Imaging Arch. 2020, 10, 7937. [Google Scholar]
- Sonn, G.A.; Natarajan, S.; Margolis, D.J.A.; MacAiran, M.; Lieu, P.; Huang, J.; Dorey, F.J.; Marks, L.S. Targeted Biopsy in the Detection of Prostate Cancer Using an Office Based Magnetic Resonance Ultrasound Fusion Device. J. Urol. 2013, 189, 86–92. [Google Scholar] [CrossRef] [Green Version]
- Clark, K.; Vendt, B.; Smith, K.; Freymann, J.; Kirby, J.; Koppel, P.; Moore, S.; Phillips, S.; Maffitt, D.; Pringle, M.; et al. The Cancer Imaging Archive (TCIA): Maintaining and Operating a Public Information Repository. J. Digit. Imaging 2013, 26, 1045–1057. [Google Scholar] [CrossRef] [Green Version]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision, Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar] [CrossRef] [Green Version]
- Mai, J.; Abubrig, M.; Lehmann, T.; Hilbert, T.; Weiland, E.; Grimm, M.O.; Teichgräber, U.; Franiel, T. T2 Mapping in Prostate Cancer. Investig. Radiol. 2019, 54, 146–152. [Google Scholar] [CrossRef] [PubMed]
- Pieper, S.; Halle, M.; Kikinis, R. 3D Slicer. In Proceedings of the 2004 2nd IEEE International Symposium on Biomedical Imaging--Macro to Nano, Arlington, VA, USA, 15–18 April 2004; Volume 1, pp. 632–635. [Google Scholar] [CrossRef]
- Tustison, N.J.; Avants, B.B.; Cook, P.A.; Zheng, Y.; Egan, A.; Yushkevich, P.A.; Gee, J.C. N4ITK: Improved N3 Bias Correction. IEEE Trans. Med. Imaging 2010, 29, 1310–1320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sled, J.G.; Zijdenbos, A.P.; Evans, A.C. A Nonparametric Method for Automatic Correction of Intensity Nonuniformity in Mri Data. IEEE Trans. Med. Imaging 1998, 17, 87–97. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Isaksson, L.J.; Raimondi, S.; Botta, F.; Pepa, M.; Gugliandolo, S.G.; De Angelis, S.P.; Marvaso, G.; Petralia, G.; De Cobelli, O.; Gandini, S.; et al. Effects of MRI Image Normalization Techniques in Prostate Cancer Radiomics. Phys. Med. 2020, 71, 7–13. [Google Scholar] [CrossRef]
- Shinohara, R.T.; Sweeney, E.M.; Goldsmith, J.; Shiee, N.; Mateen, F.J.; Calabresi, P.A.; Jarso, S.; Pham, D.L.; Reich, D.S.; Crainiceanu, C.M. Statistical Normalization Techniques for Magnetic Resonance Imaging. NeuroImage Clin. 2014, 6, 9–19. [Google Scholar] [CrossRef] [Green Version]
- Cutaia, G.; la Tona, G.; Comelli, A.; Vernuccio, F.; Agnello, F.; Gagliardo, C.; Salvaggio, L.; Quartuccio, N.; Sturiale, L.; Stefano, A.; et al. Radiomics and Prostate MRI: Current Role and Future Applications. J. Imaging 2021, 7, 34. [Google Scholar] [CrossRef]
- Nyúl, L.G.; Udupa, J.K. On Standardizing the MR Image Intensity Scale. Magn. Reson. Med. 1999, 42, 1072–1081. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Lect. Notes Comput. Sci. 2015, 9351, 234–241. [Google Scholar] [CrossRef] [Green Version]
- Keras: The Python Deep Learning Library—NASA/ADS. Available online: https://ui.adsabs.harvard.edu/abs/2018ascl.soft06022C/abstract (accessed on 29 March 2022).
- Salvi, M.; Bosco, M.; Molinaro, L.; Gambella, A.; Papotti, M.; Acharya, U.R.; Molinari, F. A Hybrid Deep Learning Approach for Gland Segmentation in Prostate Histopathological Images. Artif. Intell. Med. 2021, 115, 102076. [Google Scholar] [CrossRef]
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Jorge Cardoso, M. Generalised Dice Overlap as a Deep Learning Loss Function for Highly Unbalanced Segmentations. Lect. Notes Comput. Sci 2017, 10553, 240–248. [Google Scholar] [CrossRef] [Green Version]
- Cootes, T.; Hill, A.; Taylor, C.; Haslam, J. Use of Active Shape Models for Locating Structures in Medical Images. Image Vis. Comput. 1994, 12, 355–365. [Google Scholar] [CrossRef]
- Lee, D.T.; Schachter, B.J. Two Algorithms for Constructing a Delaunay Triangulation. Int. J. Comput. Inf. Sci. 1980, 9, 219–242. [Google Scholar] [CrossRef]
- Möller, T.; Trumbore, B. Fast, Minimum Storage Ray-Triangle Intersection. J. Graph. Tool 1998, 2, 21–28. [Google Scholar] [CrossRef]
- Salvi, M.; Molinari, F.; Dogliani, N.; Bosco, M. Automatic Discrimination of Neoplastic Epithelium and Stromal Response in Breast Carcinoma. Comput. Biol. Med. 2019, 110, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.; Liu, L.; Fei, B.; Sciences, I. Deep Convolutional Neural Network for Prostate MR Segmentation. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 1687–1696. [Google Scholar] [CrossRef]
- Qiu, W.; Yuan, J.; Ukwatta, E.; Sun, Y.; Rajchl, M.; Fenster, A. Efficient 3D Multi-Region Prostate MRI Segmentation Using Dual Optimization. Lect. Notes Comput. Sci. 2013, 7917, 304–315. [Google Scholar] [CrossRef]
- Shahedi, M.; Cool, D.W.; Romagnoli, C.; Bauman, G.S.; Bastian-Jordan, M.; Gibson, E.; Rodrigues, G.; Ahmad, B.; Lock, M.; Fenster, A.; et al. Spatially Varying Accuracy and Reproducibility of Prostate Segmentation in Magnetic Resonance Images Using Manual and Semiautomated Methods. Med. Phys. 2014, 41, 113503. [Google Scholar] [CrossRef]
- Marshall, B.; Eppstein, D. Mesh Generation and Optimal Triangulation. Comput. Euclidean Geom. 1992, 1, 23–90. [Google Scholar]



| Reference | Year | Dataset | Problem | Solution |
|---|---|---|---|---|
| Cheng et al. [15] | 2016 | 100 axial MR images | Image artifacts; Large inter-patient shape and texture variability; Unclear boundaries | Atlas-based model combined with a CNN to refine prostate boundaries |
| Yu et al. [12] | 2017 | 80 T2w images | Limited training data | Volumetric ConvNet with mixed residual connections |
| He et al. [6] | 2017 | 50 T2w axial MR images | Variability in prostate shape and appearance among different parts and subjects | Combine an adaptive feature learning probability boosting tree with CNN and ASM |
| Kamiri et al. [16] | 2018 | 49 T2w axial MR images | Variability of prostate shape and appearance; small amount of training data | Stage-wise training strategy with an ASM embedded into the last layer of a CNN to predict surface keypoints |
| Zhu et al. [13] | 2020 | 50 T2w images | Prostate variability; Weak contours; Limited training data | Boundary-weighted domain adaptive neural network |
| Jia et al. [14] | 2020 | 80 T2w images | Anisotropic spatial resolution | As-Conv block: two anisotropic convolutions for x-y features and z features independently |
| Ushinsky et al. [17] | 2021 | 299 T2w images | Variability in prostate appearance among different subjects | Customized hybrid 3D-2D U-Net CNN architecture |
| Meyer et al. [18] | 2021 | 89 T2w images | Anisotropic spatial resolution | Fusion of the information from anisotropic images to avoid resampling to isotropic voxels. |
| Pollastri et al. [19] | 2022 | Prostate-MRI-US-Biopsy dataset [21,22,23] | Variability of prostate shape and texture | Long-range 3D Self-Attention Block integrated within the CNN |
| Hyperparameter | Chosen Value |
|---|---|
| Network depth | 4 |
| Number of base filters | 8 |
| Number of trainable parameters | 1.192.593 |
| Learning rate | 10−4 |
| Loss function | Dice similarity loss |
| Metric | Dice score |
| Name | Number of Iterations (it) | Search Length (ns) | Shape Constraint (m) |
|---|---|---|---|
| ASM-1 | 1 | 8 | 3 |
| AMS-2 | 2 | 8 | 1 |
| ASM-3 | 2 | 8 | 2 |
| ASM-4 | 2 | 8 | 3 |
| Method | Subset | DSC | HD95 (mm) | RVD (%) |
|---|---|---|---|---|
| VNet-T2 | Train | 0.893 ± 0.020 | 7.94 ± 3.16 | 8.58 ± 5.52 |
| Val | 0.851 ± 0.027 | 6.98 ± 1.55 | 11.65 ± 7.01 | |
| Test | 0.840 ± 0.039 | 10.74 ± 5.21 | 11.22 ± 7.85 | |
| VNet-T2 + ASM-1 | Train | 0.880 ± 0.033 | 6.79 ± 3.06 | 11.92 ± 7.58 |
| Val | 0.858 ± 0.028 | 6.89 ± 1.89 | 9.78 ± 4.86 | |
| Test | 0.839 ± 0.055 | 8.87 ± 3.39 | 12.87 ± 4.53 | |
| VNet-T2 + ASM-2 | Train | 0.870 ± 0.039 | 6.05 ± 1.92 | 9.45 ± 8.53 |
| Val | 0.859 ± 0.042 | 6.44 ± 2.08 | 9.58 ± 9.92 | |
| Test | 0.851 ± 0.044 | 7.55 ± 2.76 | 9.60 ± 7.80 | |
| VNet-T2 + ASM-3 | Train | 0.878 ± 0.035 | 6.87 ± 3.47 | 9.38 ± 7.88 |
| Val | 0.853 ± 0.038 | 5.82 ± 1.05 | 8.09 ± 5.91 | |
| Test | 0.842 ± 0.049 | 7.26 ± 2.69 | 11.63 ± 9.31 | |
| VNet-T2 + ASM-4 | Train | 0.877 ± 0.036 | 6.73 ± 3.26 | 10.05 ± 7.92 |
| Val | 0.851 ± 0.038 | 6.48 ± 1.36 | 9.75 ± 5.87 | |
| Test | 0.839 ± 0.052 | 7.40 ± 2.79 | 12.72 ± 9.99 |
| Method | DSC | HD95 (mm) | RVD (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Average | Max | Min | Average | Max | Min | Average | Max | |
| Op1 vs. Op2 | 0.842 | 0.892 | 0.935 | 2.57 | 4.51 | 8.64 | 1.21 | 15.90 | 25.38 |
| VNet-T2 | 0.783 | 0.840 | 0.908 | 5.00 | 10.74 | 22.89 | 1.79 | 11.22 | 29.22 |
| VNet-T2 + ASM-2 | 0.761 | 0.851 | 0.917 | 3.80 | 7.55 | 12.78 | 0.33 | 9.60 | 27.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salvi, M.; De Santi, B.; Pop, B.; Bosco, M.; Giannini, V.; Regge, D.; Molinari, F.; Meiburger, K.M. Integration of Deep Learning and Active Shape Models for More Accurate Prostate Segmentation in 3D MR Images. J. Imaging 2022, 8, 133. https://doi.org/10.3390/jimaging8050133
Salvi M, De Santi B, Pop B, Bosco M, Giannini V, Regge D, Molinari F, Meiburger KM. Integration of Deep Learning and Active Shape Models for More Accurate Prostate Segmentation in 3D MR Images. Journal of Imaging. 2022; 8(5):133. https://doi.org/10.3390/jimaging8050133
Chicago/Turabian StyleSalvi, Massimo, Bruno De Santi, Bianca Pop, Martino Bosco, Valentina Giannini, Daniele Regge, Filippo Molinari, and Kristen M. Meiburger. 2022. "Integration of Deep Learning and Active Shape Models for More Accurate Prostate Segmentation in 3D MR Images" Journal of Imaging 8, no. 5: 133. https://doi.org/10.3390/jimaging8050133
APA StyleSalvi, M., De Santi, B., Pop, B., Bosco, M., Giannini, V., Regge, D., Molinari, F., & Meiburger, K. M. (2022). Integration of Deep Learning and Active Shape Models for More Accurate Prostate Segmentation in 3D MR Images. Journal of Imaging, 8(5), 133. https://doi.org/10.3390/jimaging8050133









