Fabrication of Black Body Grids by Thick Film Printing for Quantitative Neutron Imaging
Abstract
:1. Introduction
1.1. Quantitative Neutron Imaging with Black Body Grids
1.2. Candidate Materials for BB Grids
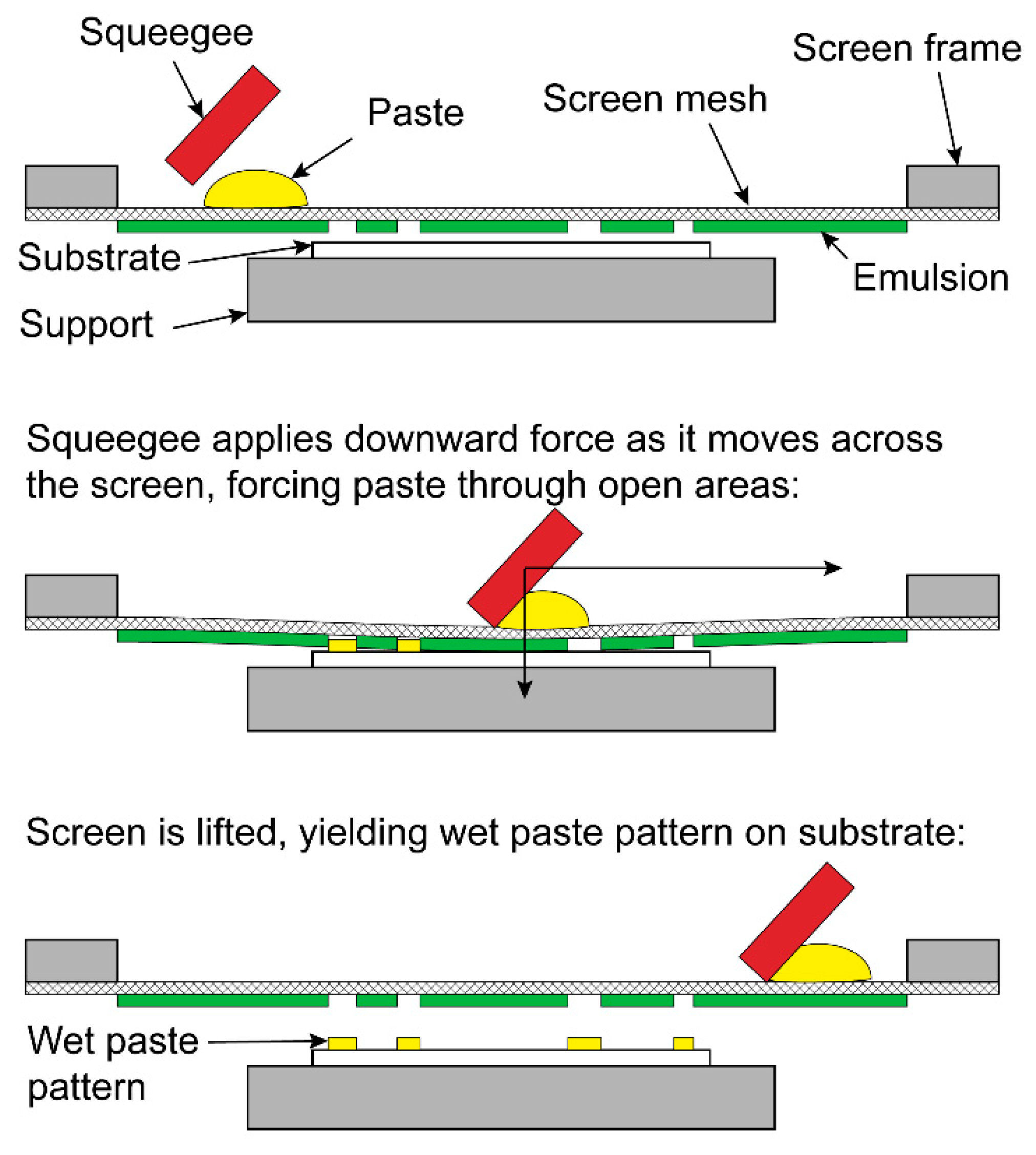
1.3. Thick Film Printing
2. Materials and Methods
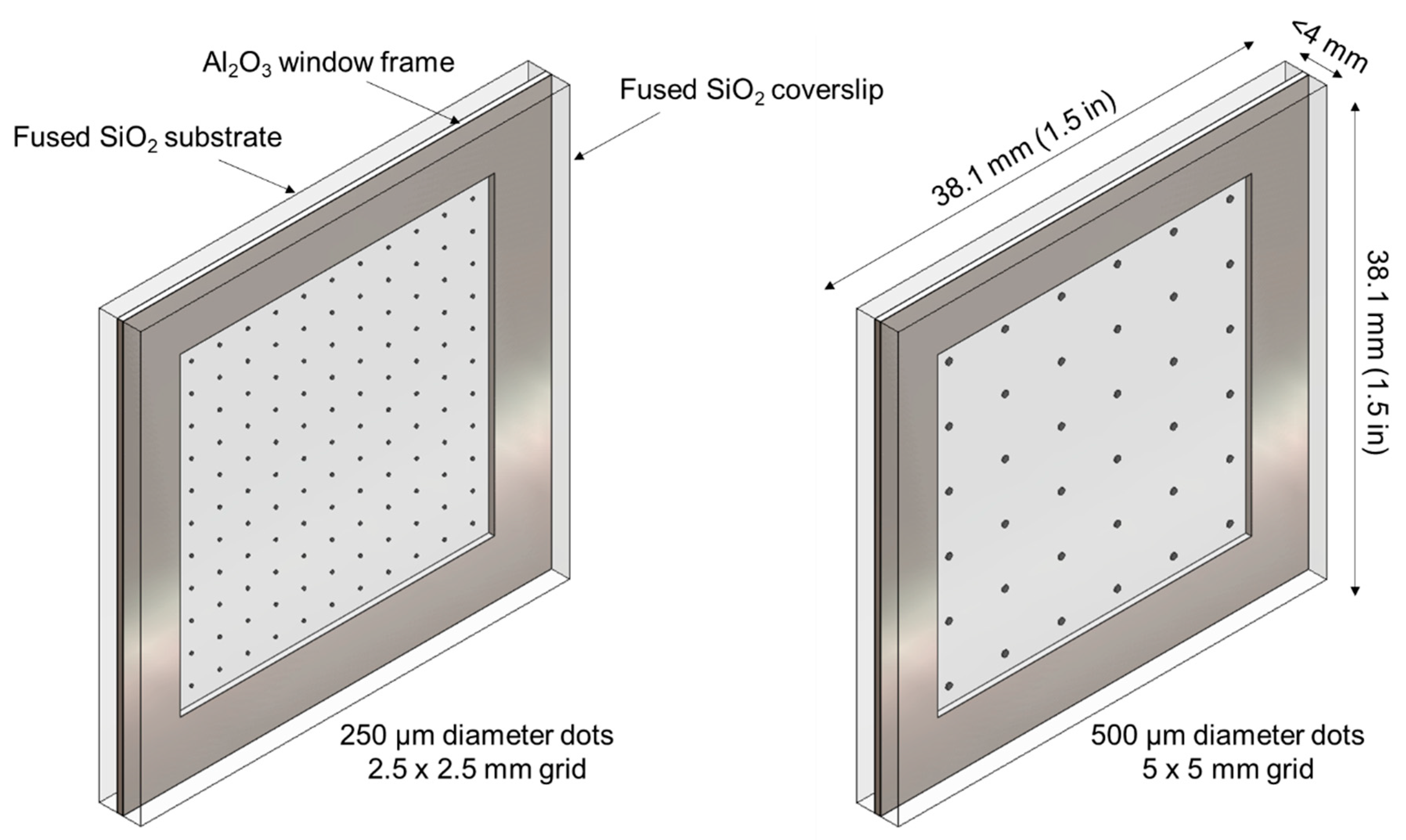
2.1. Fabrication of BB Grids
- Print Gd2O3 paste;
- Dry at 125 °C to 150 °C for 15 min;
- Increase snap-off distance as needed to accommodate increased print thickness;
- Repeat.
2.2. Neutron Imaging Configurations
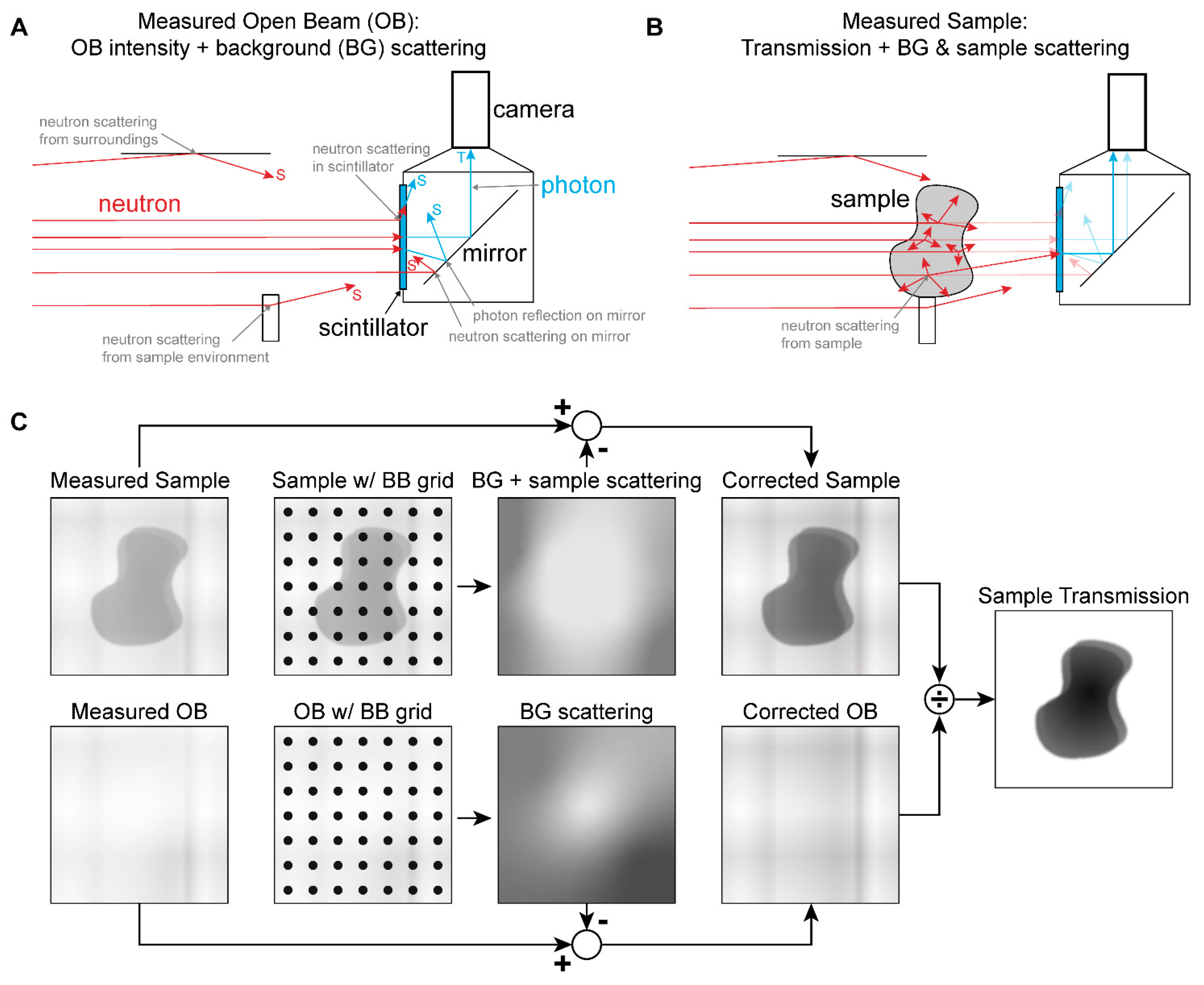
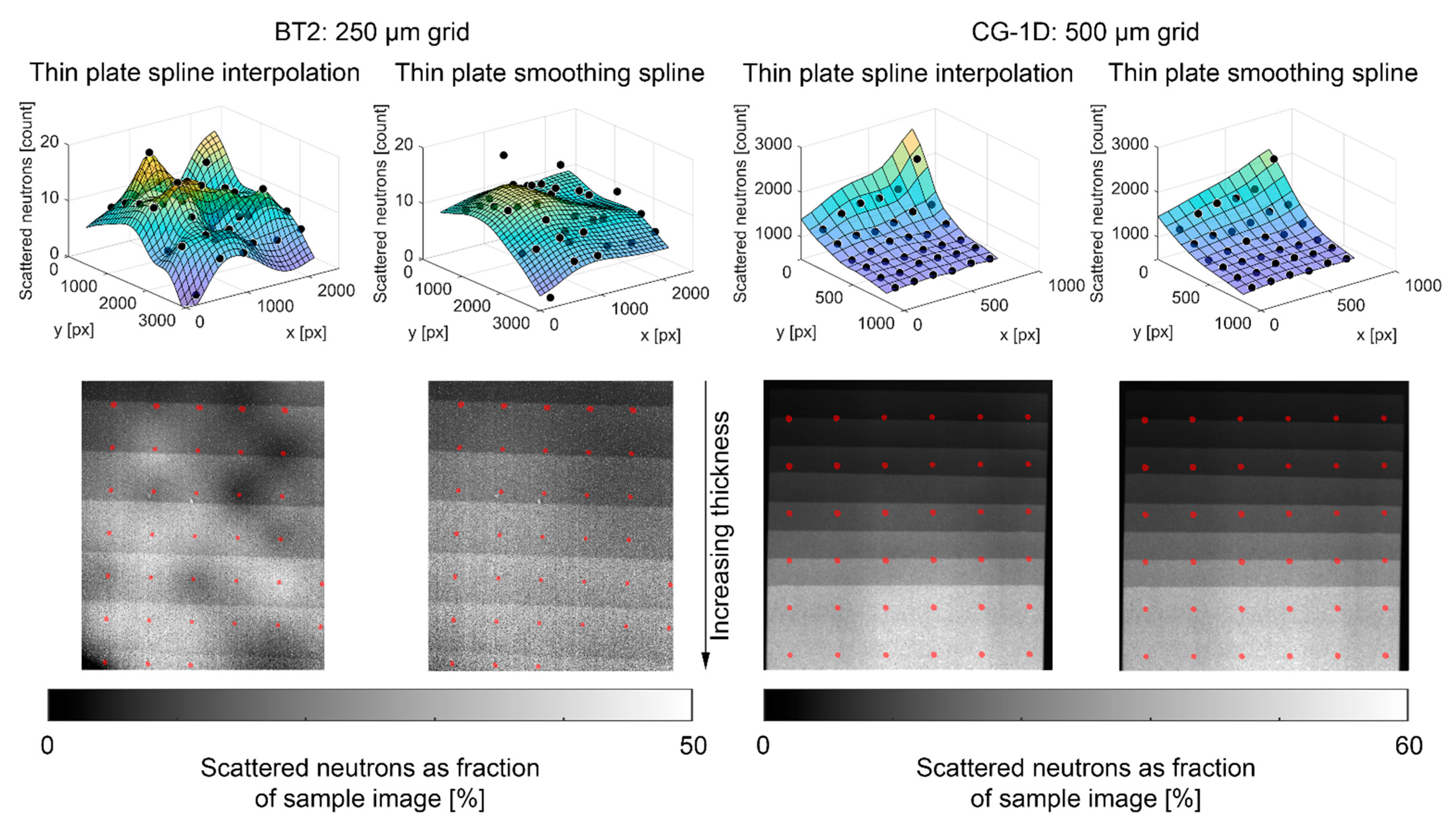
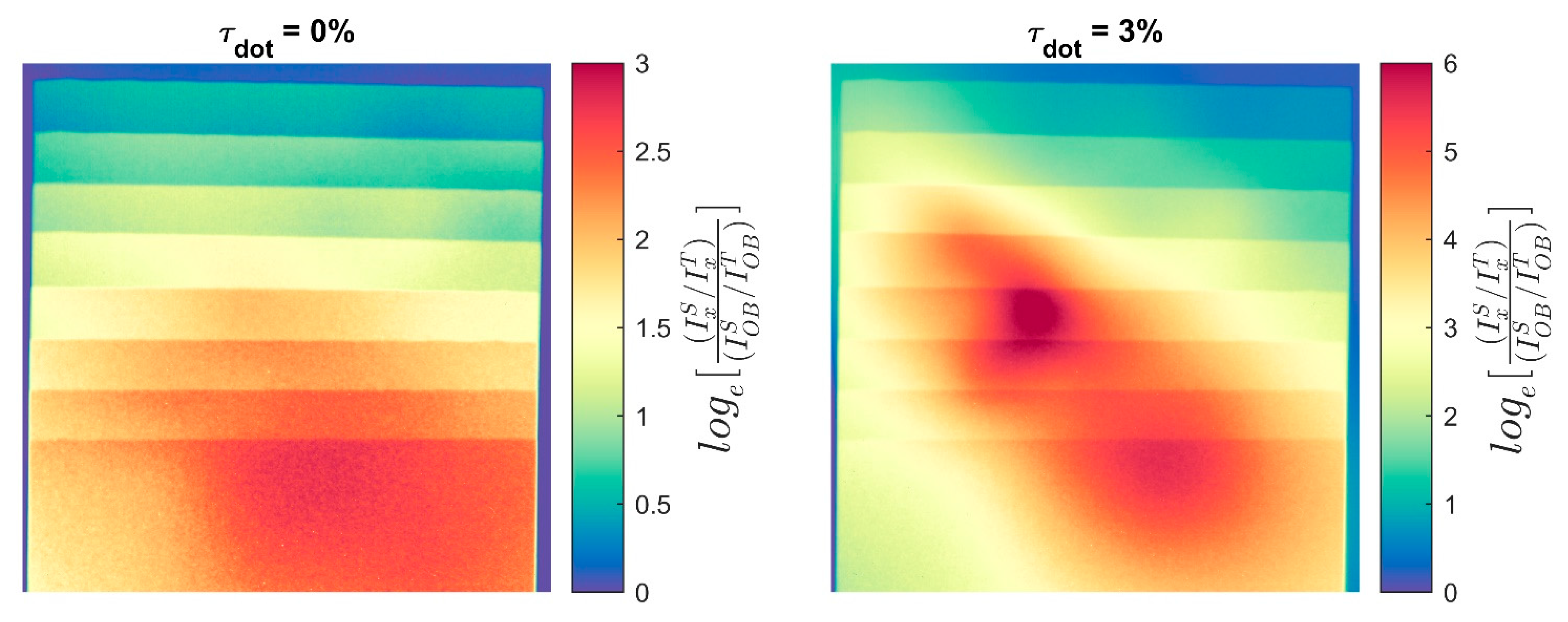
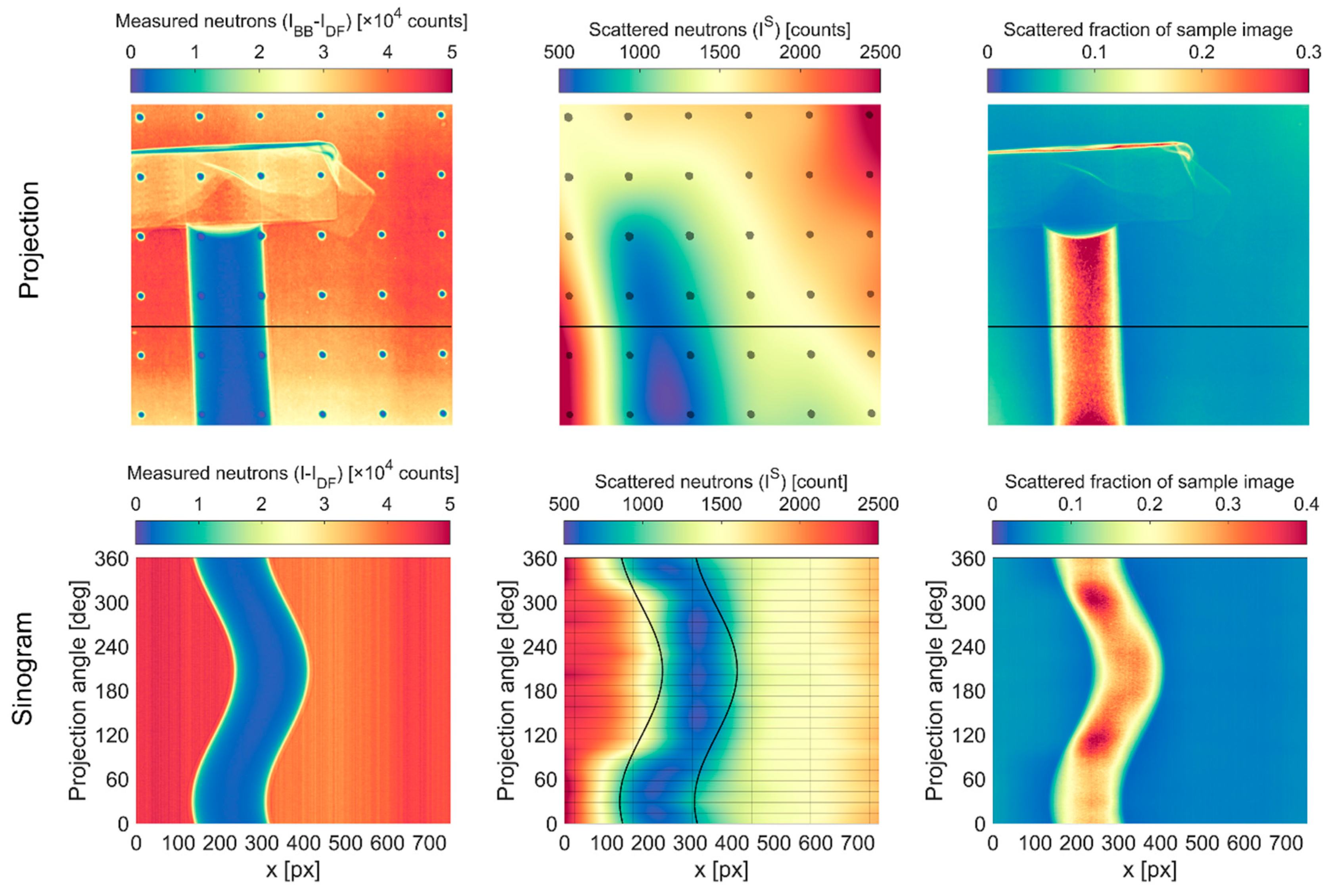
2.3. Image Normalization with Scattering Correction
- The “dark frame” image (), which measures the count rate of the detector system at a given exposure time (due to dark current, bias, and readout noise) with the neutron shutter closed.
- The measured sample image (), where denotes the sample (or for the ith projection in a tomographic scan), which is the sum of the true sample image () and the dark frame:
- The measured “open beam” image (), which accounts for the spatial inhomegeneity of the incident beam and the detector, and which is the sum of the true open beam image () and the dark frame: .
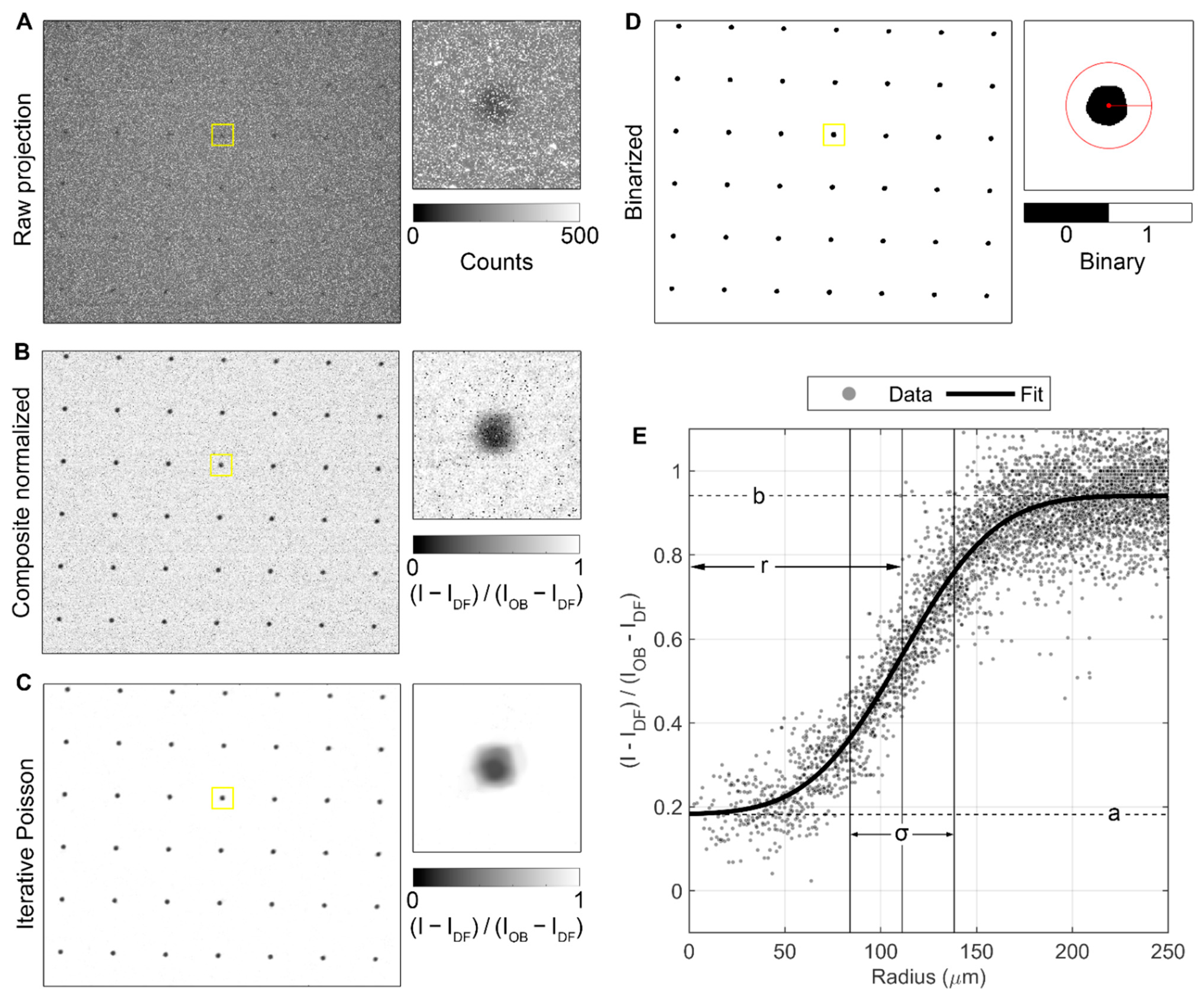
2.4. Image Processing
2.4.1. Statistical Analysis of BB Grids
2.4.2. PMMA Step Wedge
2.4.3. Water Column
3. Results
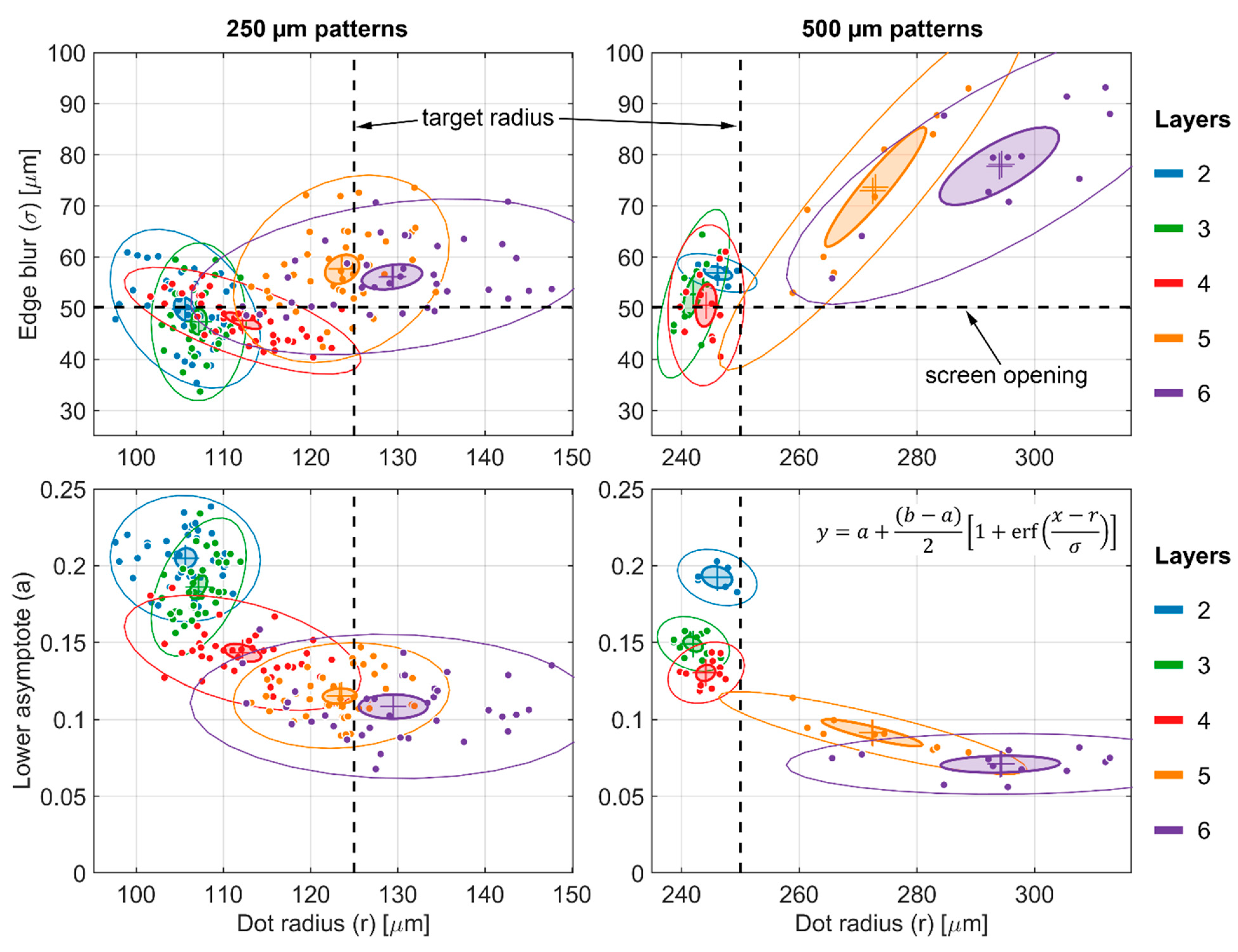
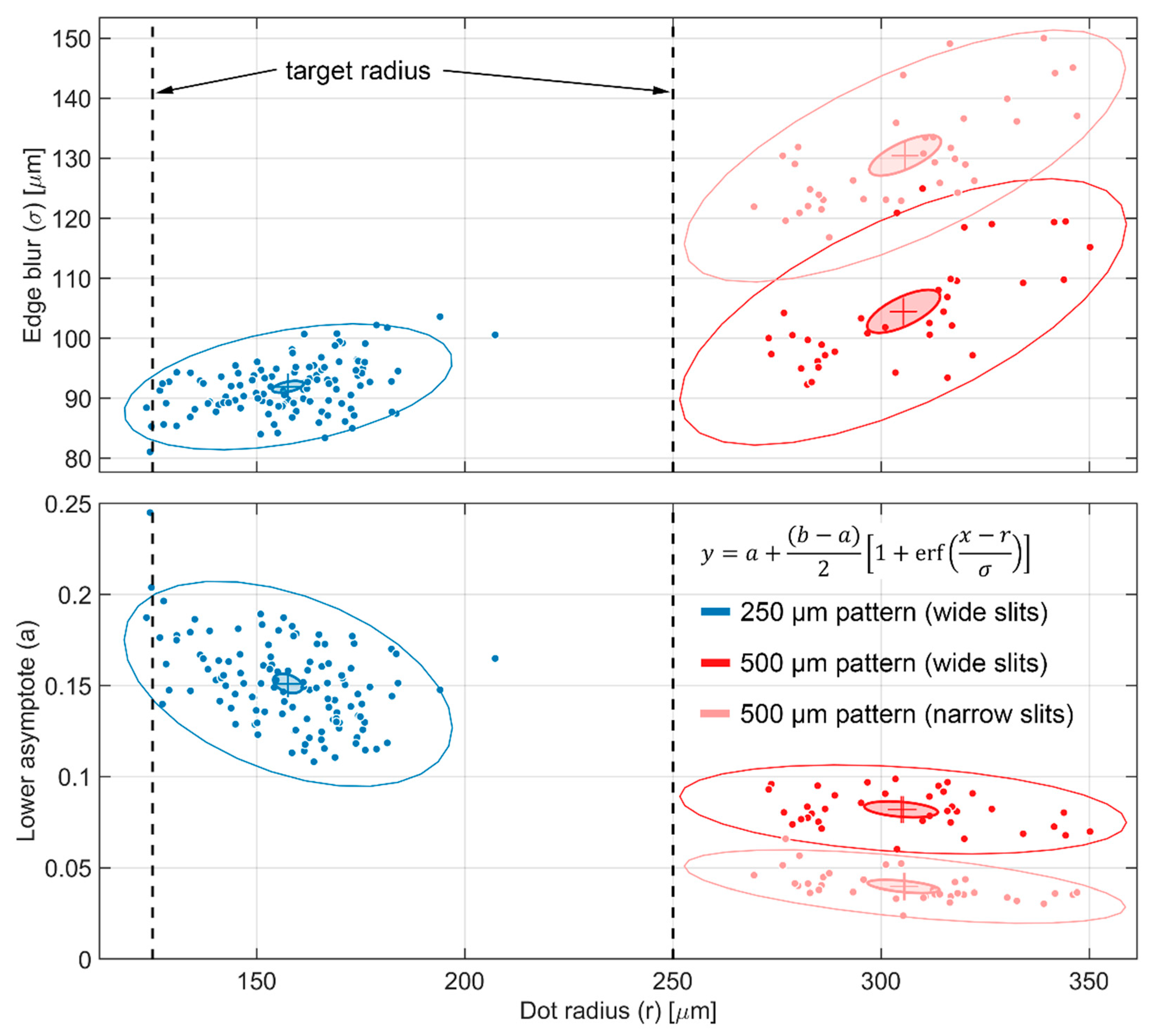
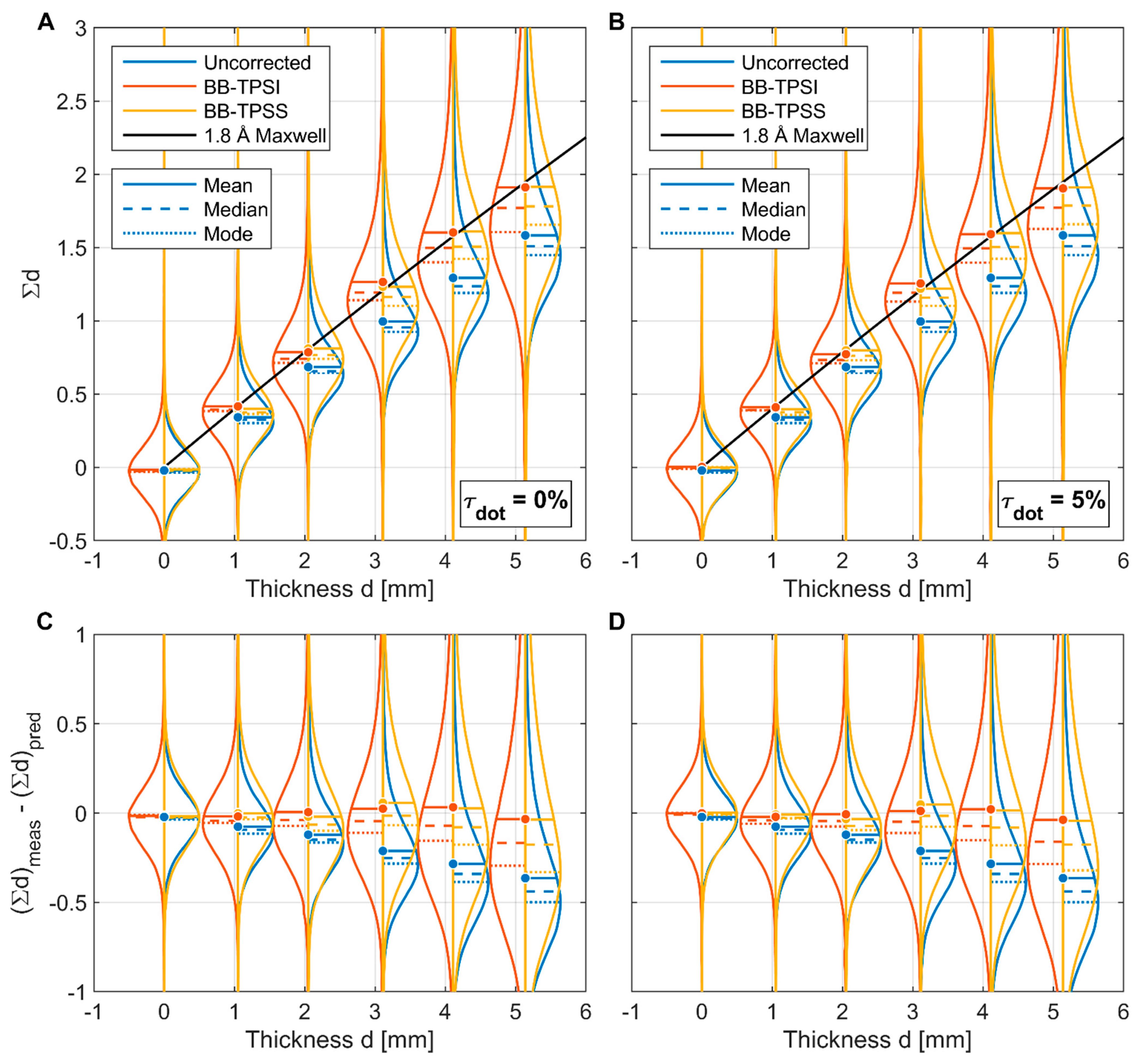
3.1. Statistical Analysis of BB Grids
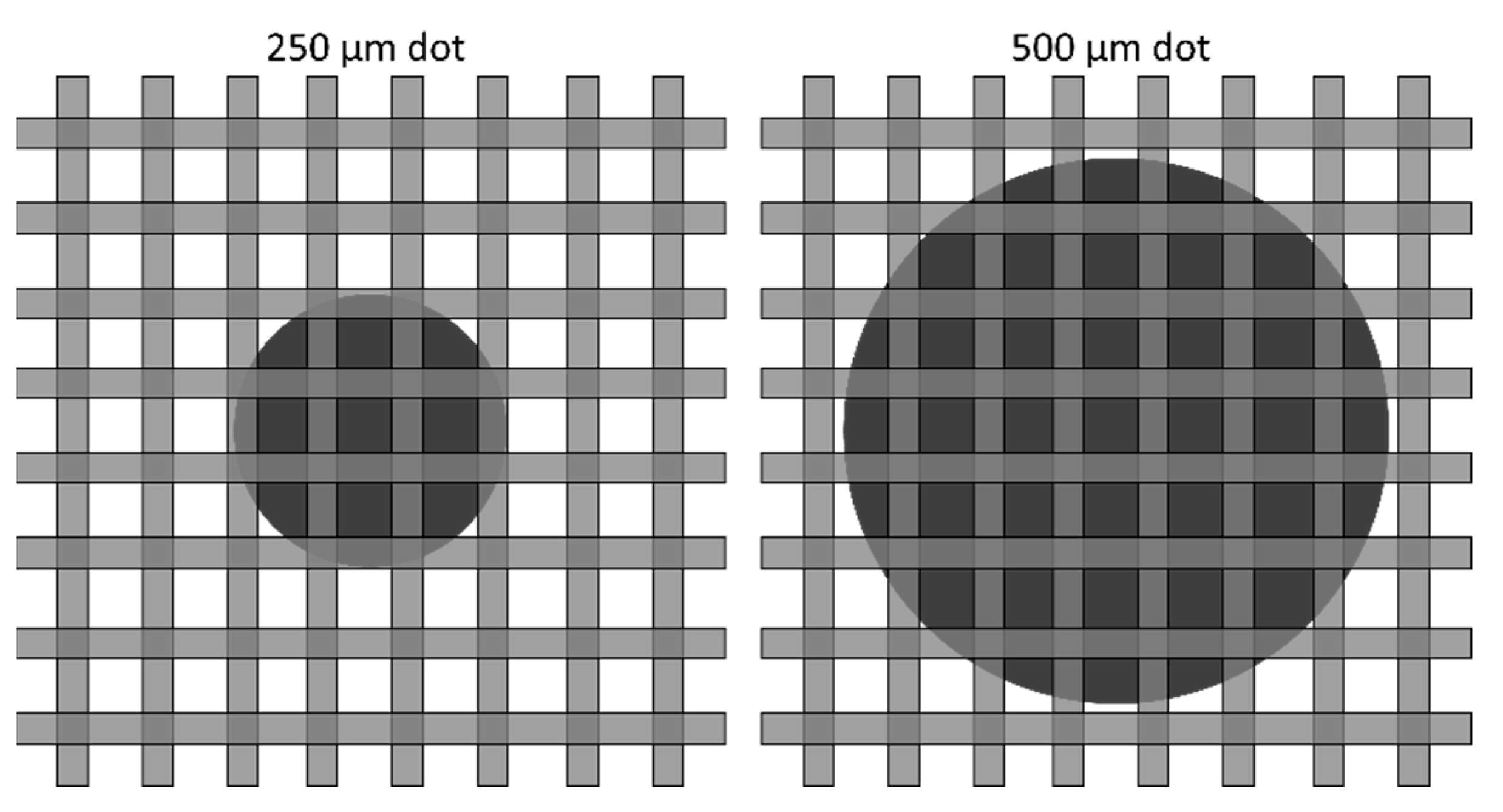
- Using the determination of for the imaging system at the position on the BB grid, select an acceptable transparency threshold and fabricate a grid with BBs of appropriate radius. Assuming an averaging region , a 1% transparency threshold would require , while a 0.1% threshold would require . This sets a lower bound on the BB radius, which may not be possible or desirable in all configurations. Generally, the BBs should cover as little area as possible to minimize their impact on the biases being measured. In kinetic studies where the BBs will be left in place continuously, there is also the concern of the BBs occluding interesting parts of the sample.
- Use the determination of the PSF for the imaging system at the position on the BB grid and perform deconvolution to recover the “true” signal at the BB centers. This approach has been demonstrated successfully with BBs [8] but has the added experimental complication of requiring detailed PSF measurements, which may not always be possible. Deconvolution may also introduce undesirable artifacts which can impact quantitative interpretation.
- Include the transparency of the BBs explicitly in the formulation of the scattering correction, as performed here in Equations (15)–(18) with the term . This approach has the advantage of allowing the imperfect opacity of the physical BB grid and the effects of the imaging system to be captured in a single term. We can bound with calibration samples of known composition and dimensions, or it may also be adjusted as a free parameter to establish an uncertainty range for the corrected data.
3.2. PMMA Step Wedge
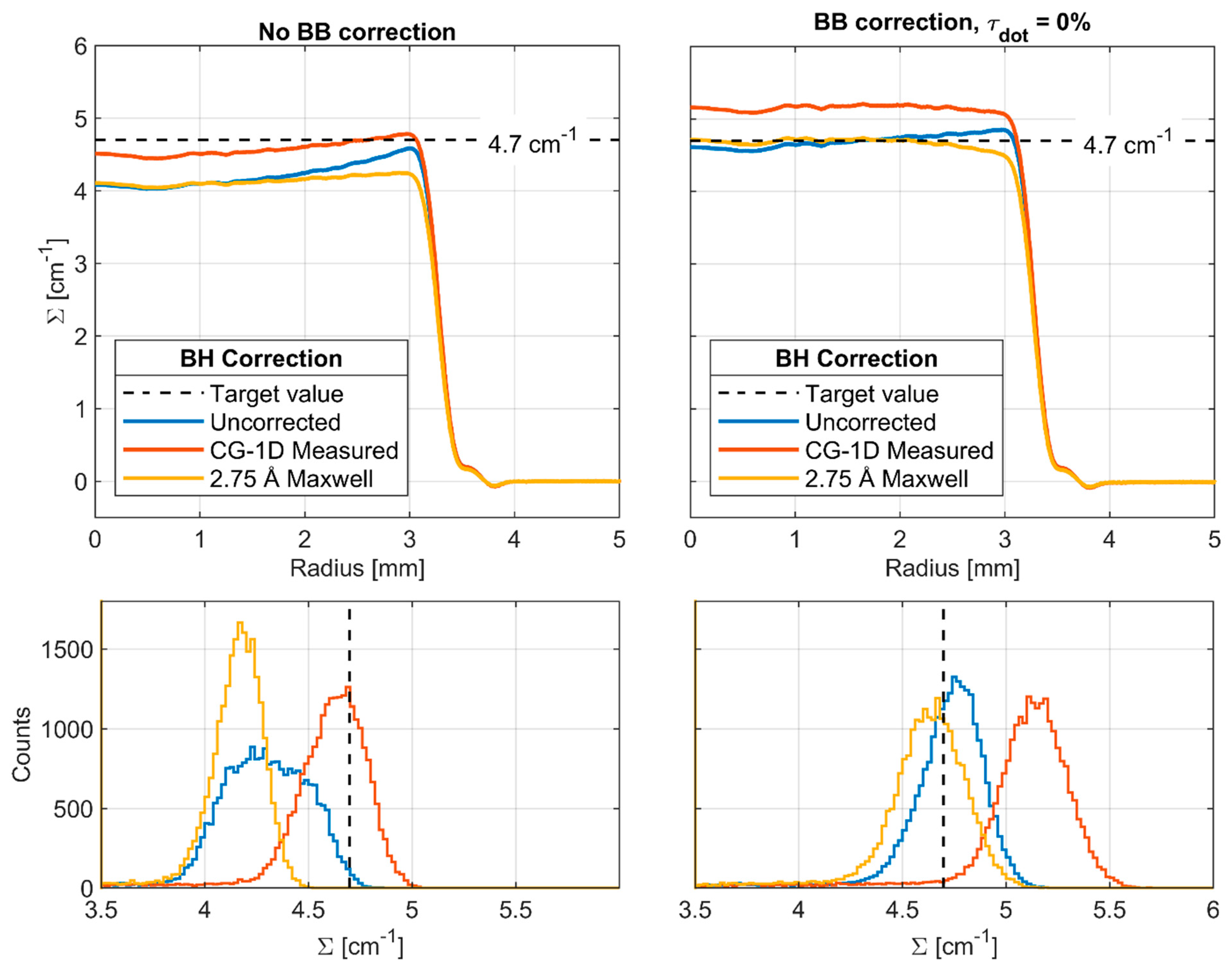
3.3. Water Column
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Copyright Notice
References
- Bilheux, H.Z.; McGreevy, R.; Anderson, I.S. Neutron Imaging and Applications: A Reference for the Imaging Community; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Kang, M.; Bilheux, H.Z.; Voisin, S.; Cheng, C.L.; Perfect, E.; Horita, J.; Warren, J.M. Water calibration measurements for neutron radiography: Application to water content quantification in porous media. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 708, 24–31. [Google Scholar] [CrossRef]
- Hassanein, R.; Lehmann, E.; Vontobel, P. Methods of scattering corrections for quantitative neutron radiography. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2005, 542, 353–360. [Google Scholar] [CrossRef]
- Hassanein, R.; de Beer, F.; Kardjilov, N.; Lehmann, E. Scattering correction algorithm for neutron radiography and tomography tested at facilities with different beam characteristics. Phys. B Condens. Matter 2006, 385–386, 1194–1196. [Google Scholar] [CrossRef]
- Kardjilov, N.; de Beer, F.; Hassanein, R.; Lehmann, E.; Vontobel, P. Scattering corrections in neutron radiography using point scattered functions. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2005, 542, 336–341. [Google Scholar] [CrossRef]
- Hassan, M.H. Point Scattered Function (PScF) for fast neutron radiography. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2009, 267, 2545–2549. [Google Scholar] [CrossRef]
- Liu, S.; Bücherl, T.; Zou, Y.; Wang, S.; Lu, Y.; Guo, Z. Study on scattering correction in fast neutron tomography at NECTAR facility. Sci. China Phys. Mech. Astron. 2014, 57, 244–250. [Google Scholar] [CrossRef]
- Boillat, P.; Carminati, C.; Schmid, F.; Grünzweig, C.; Hovind, J.; Kaestner, A.; Mannes, D.; Morgano, M.; Siegwart, M.; Trtik, P.; et al. Chasing quantitative biases in neutron imaging with scintillator-camera detectors: A practical method with black body grids. Opt. Express 2018, 26, 15769–15784. [Google Scholar] [CrossRef]
- Carminati, C.; Boillat, P.; Schmid, F.; Vontobel, P.; Hovind, J.; Morgano, M.; Raventos, M.; Siegwart, M.; Mannes, D.; Gruenzweig, C.; et al. Implementation and assessment of the black body bias correction in quantitative neutron imaging. PLoS ONE 2019, 14, e0210300. [Google Scholar] [CrossRef] [Green Version]
- Carminati, C.; Boillat, P.; Laemmlein, S.; Heckova, P.; Snehota, M.; Mannes, D.; Hovind, J.; Strobl, M.; Kaestner, A. Effect of Scattering Correction in Neutron Imaging of Hydrogenous Samples using the Black Body Approach. Mater. Res. Proc. 2020, 15, 174–179. [Google Scholar] [CrossRef] [Green Version]
- Grünzweig, C.; Frei, G.; Lehmann, E.; Kühne, G.; David, C. Highly absorbing gadolinium test device to characterize the performance of neutron imaging detector systems. Rev. Sci. Instrum. 2007, 78, 053708. [Google Scholar] [CrossRef]
- Bingham, P.; Santos-Villalobos, H.; Lavrik, N.; Gregor, J.; Bilheux, H. Magnified Neutron Radiography with Coded Sources. Phys. Procedia 2015, 69, 218–226. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Bilheux, J.-C.; Bilheux, H.Z.; Lin, J.Y.Y. An interactive web-based tool to guide the preparation of neutron imaging experiments at oak ridge national laboratory. J. Phys. Commun. 2019, 3, 103003. [Google Scholar] [CrossRef]
- Brown, D.A.; Chadwick, M.B.; Capote, R.; Kahler, A.C.; Trkov, A.; Herman, M.W.; Sonzogni, A.A.; Danon, Y.; Carlson, A.D.; Dunn, M.; et al. ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data. Nucl. Data Sheets 2018, 148, 1–142. [Google Scholar] [CrossRef]
- Crow, L.; Robertson, L.; Bilheux, H.; Fleenor, M.; Iverson, E.; Tong, X.; Stoica, D.; Lee, W.T. The CG1 instrument development test station at the high flux isotope reactor. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2011, 634, S71–S74. [Google Scholar] [CrossRef]
- Márquez Damián, J.I.; Granada, J.R.; Malaspina, D.C. CAB models for water: A new evaluation of the thermal neutron scattering laws for light and heavy water in ENDF-6 format. Ann. Nucl. Energy 2014, 65, 280–289. [Google Scholar] [CrossRef]
- Ramić, K.; Wendorff, C.; Cheng, Y.; Kolesnikov, A.I.; Abernathy, D.L.; Daemen, L.; Arbanas, G.; Leal, L.; Danon, Y.; Liu, L. Toward a better thermal scattering law of (C5O2H8)n: Inelastic neutron scattering and oClimax + NJOY2016. Ann. Nucl. Energy 2019, 133, 425–430. [Google Scholar] [CrossRef]
- White, N. Thick Films. In Springer Handbook of Electronic and Photonic Materials; Kasap, S., Capper, P., Eds.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- LaManna, J.M.; Hussey, D.S.; Baltic, E.; Jacobson, D.L. Neutron and X-ray Tomography (NeXT) system for simultaneous, dual modality tomography. Rev. Sci. Instrum. 2017, 88, 113702. [Google Scholar] [CrossRef] [PubMed]
- Santodonato, L.; Bilheux, H.; Bailey, B.; Bilheux, J.; Nguyen, P.; Tremsin, A.; Selby, D.; Walker, L. The CG-1D Neutron Imaging Beamline at the Oak Ridge National Laboratory High Flux Isotope Reactor. Phys. Procedia 2015, 69, 104–108. [Google Scholar] [CrossRef] [Green Version]
- MATLAB R2018b and Image Processing Toolbox; The MathWorks, Inc.: Natick, MA, USA, 2018.
- Azzari, L.; Foi, A. Variance Stabilization for Noisy + Estimate Combination in Iterative Poisson Denoising. IEEE Signal Processing Lett. 2016, 23, 1086–1090. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Bradley, D.; Roth, G. Adaptive Thresholding using the Integral Image. J. Graph. Tools 2007, 12, 13–21. [Google Scholar] [CrossRef]
- Kaestner, A.P. MuhRec—A new tomography reconstructor. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2011, 651, 156–160. [Google Scholar] [CrossRef]
- Kaestner, A.; Carminati, C. Improved User Experience and Speed-Up. Available online: https://zenodo.org/record/3661110#.YqA6hnZBxPY (accessed on 20 March 2022).
- Münch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and ring artifact removal with combined wavelet—Fourier filtering. Opt. Express 2009, 17, 8567–8591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hussey, D.S.; LaManna, J.M.; Baltic, E.; Jacobson, D.L. Neutron imaging detector with 2 μm spatial resolution based on event reconstruction of neutron capture in gadolinium oxysulfide scintillators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2017, 866, 9–12. [Google Scholar] [CrossRef] [PubMed]
- Song, B.; Dhiman, I.; Carothers, J.C.; Veith, G.M.; Liu, J.; Bilheux, H.Z.; Huq, A. Dynamic Lithium Distribution upon Dendrite Growth and Shorting Revealed by Operando Neutron Imaging. ACS Energy Lett. 2019, 4, 2402–2408. [Google Scholar] [CrossRef]
- Ibrahim, O.T.; Monroe, J.G.; Thompson, S.M.; Shamsaei, N.; Bilheux, H.; Elwany, A.; Bian, L. An investigation of a multi-layered oscillating heat pipe additively manufactured from Ti-6Al-4V powder. Int. J. Heat Mass Transf. 2017, 108, 1036–1047. [Google Scholar] [CrossRef] [Green Version]
- Siegmund, O.H.W.; Vallerga, J.V.; Martin, A.; Feller, B.; Arif, M.; Hussey, D.S.; Jacobson, D.L. A high spatial resolution event counting neutron detector using microchannel plates and cross delay line readout. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2007, 579, 188–191. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Evans, A.; Tahoori, M.B.; Seyyedi, R.; Costenaro, E.; Alexandrescu, D. Comprehensive analysis of alpha and neutron particle-induced soft errors in an embedded processor at nanoscales. In Proceedings of the 2014 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 24–28 March 2014; pp. 1–6. [Google Scholar] [CrossRef]
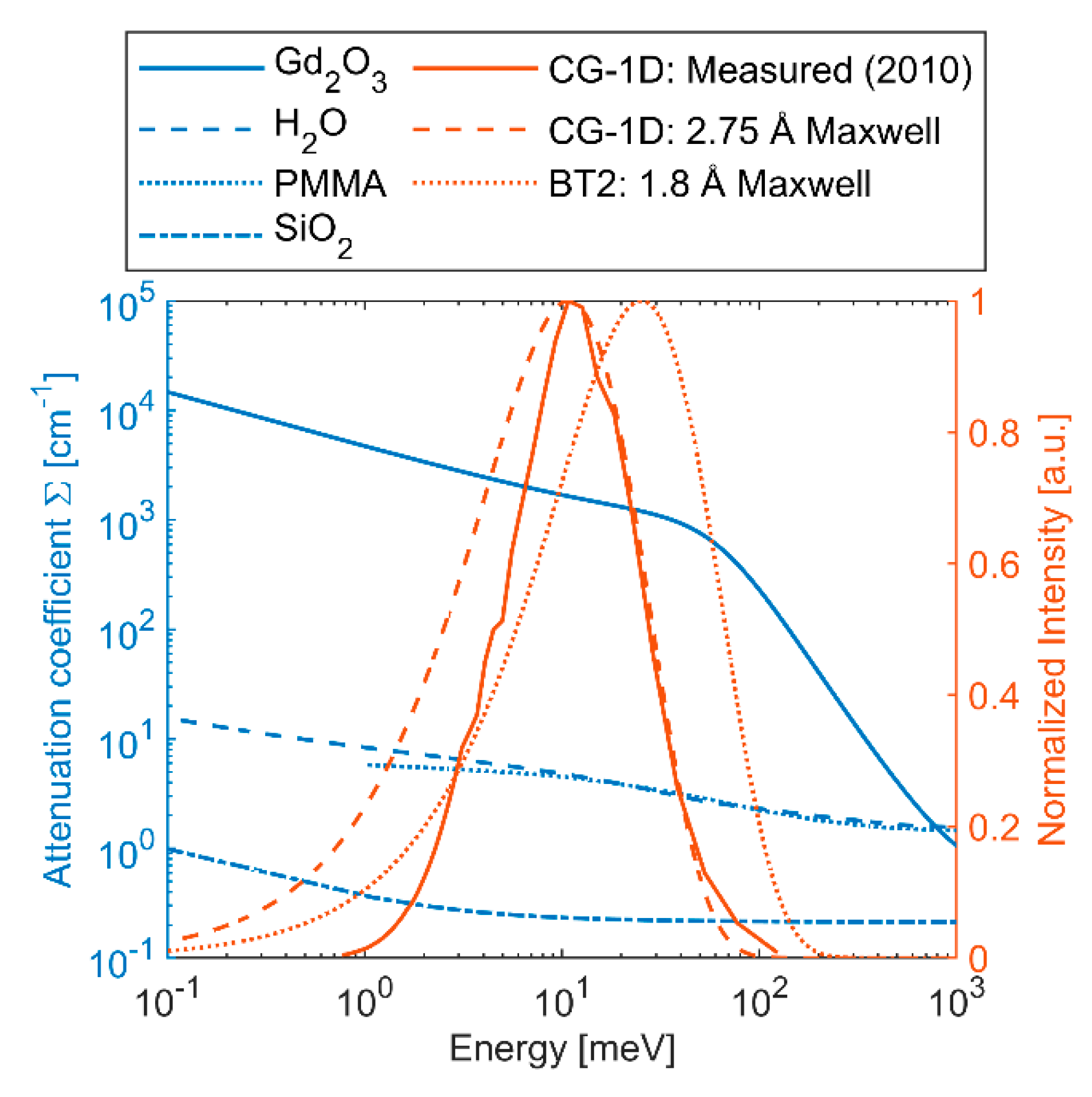







| Spectrum | HFIR CG-1D (2.75 Å) | NCNR BT2 (1.8 Å) | ||
|---|---|---|---|---|
| 99% | 99.9% | 99% | 99.9% | |
| Peak wavelength (mono) | 28 | 42 | 39 | 58 |
| Maxwell–Boltzmann (poly) | 31 | 54 | 79 | 259 |
| Measured (poly) | 37 | 81 | - | - |
| Number of Print Layers | 250 µm × 2.5 mm | 500 µm × 5 mm |
|---|---|---|
| 2 | 19.2 | 43.6 |
| 3 | 25.5 | 52.0 |
| 4 | 30.3 | 63.0 |
| 5 | 30.5 | 79.6 |
| 6 | 32.0 | 80.0 |
| Spectrum | ||||
|---|---|---|---|---|
| CG-1D: measured | 0 | 0.9942 | 0.0277 | 0.0006 |
| CG-1D: 2.75 Å Maxwell | 0 | 0.8501 | 0.0449 | −0.0009 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wissink, M.; Goldenberger, K.; Ferguson, L.; Zhang, Y.; Bilheux, H.; LaManna, J.; Jacobson, D.; Kass, M.; Finney, C.; Willocks, J. Fabrication of Black Body Grids by Thick Film Printing for Quantitative Neutron Imaging. J. Imaging 2022, 8, 164. https://doi.org/10.3390/jimaging8060164
Wissink M, Goldenberger K, Ferguson L, Zhang Y, Bilheux H, LaManna J, Jacobson D, Kass M, Finney C, Willocks J. Fabrication of Black Body Grids by Thick Film Printing for Quantitative Neutron Imaging. Journal of Imaging. 2022; 8(6):164. https://doi.org/10.3390/jimaging8060164
Chicago/Turabian StyleWissink, Martin, Kirk Goldenberger, Luke Ferguson, Yuxuan Zhang, Hassina Bilheux, Jacob LaManna, David Jacobson, Michael Kass, Charles Finney, and Jonathan Willocks. 2022. "Fabrication of Black Body Grids by Thick Film Printing for Quantitative Neutron Imaging" Journal of Imaging 8, no. 6: 164. https://doi.org/10.3390/jimaging8060164
APA StyleWissink, M., Goldenberger, K., Ferguson, L., Zhang, Y., Bilheux, H., LaManna, J., Jacobson, D., Kass, M., Finney, C., & Willocks, J. (2022). Fabrication of Black Body Grids by Thick Film Printing for Quantitative Neutron Imaging. Journal of Imaging, 8(6), 164. https://doi.org/10.3390/jimaging8060164






