Quantification of Sub-Pixel Dynamics in High-Speed Neutron Imaging †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Neutron Imaging Configurations
2.2. Injector and Operating Conditions
2.3. Neutron Attenuation Model
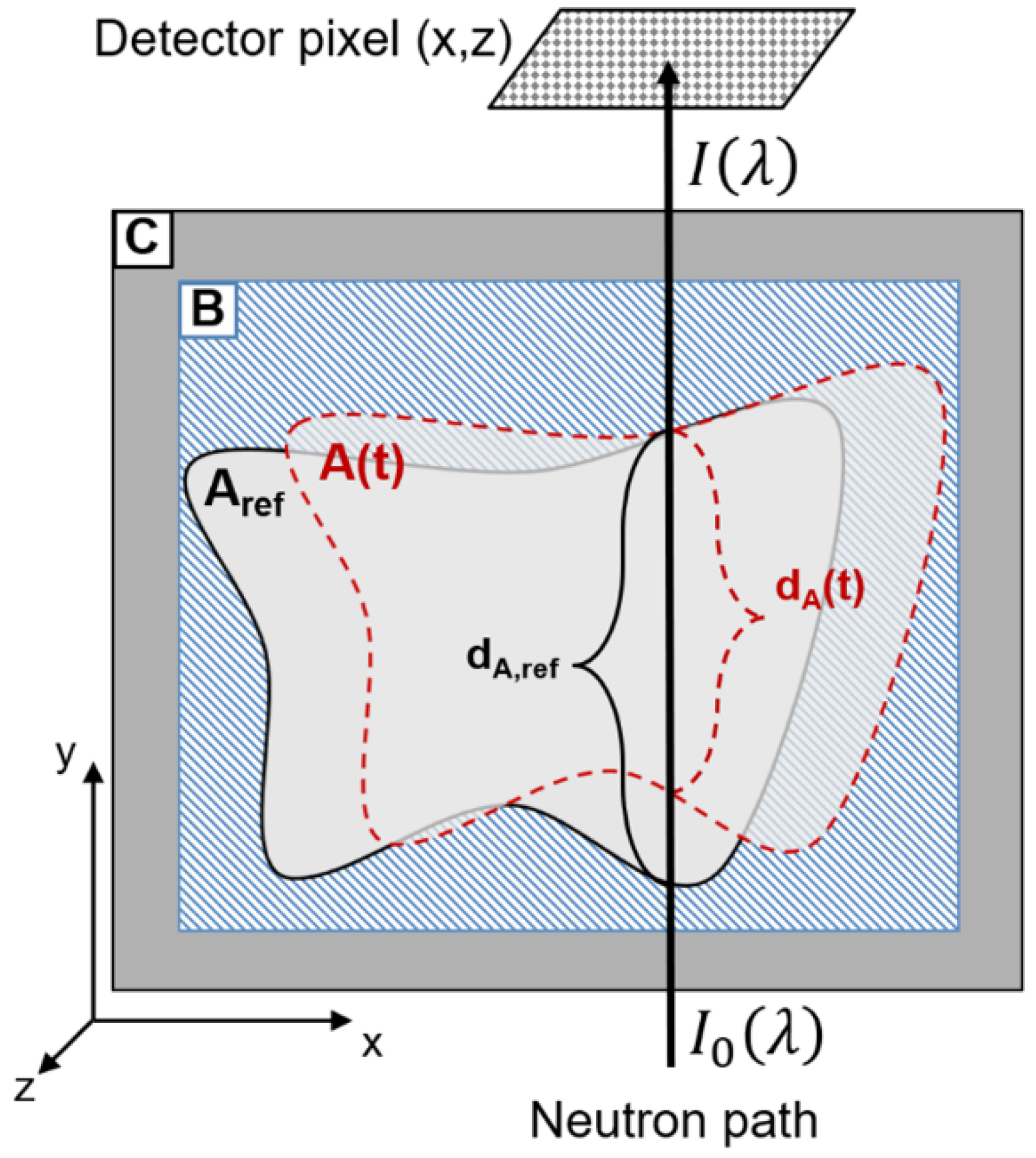
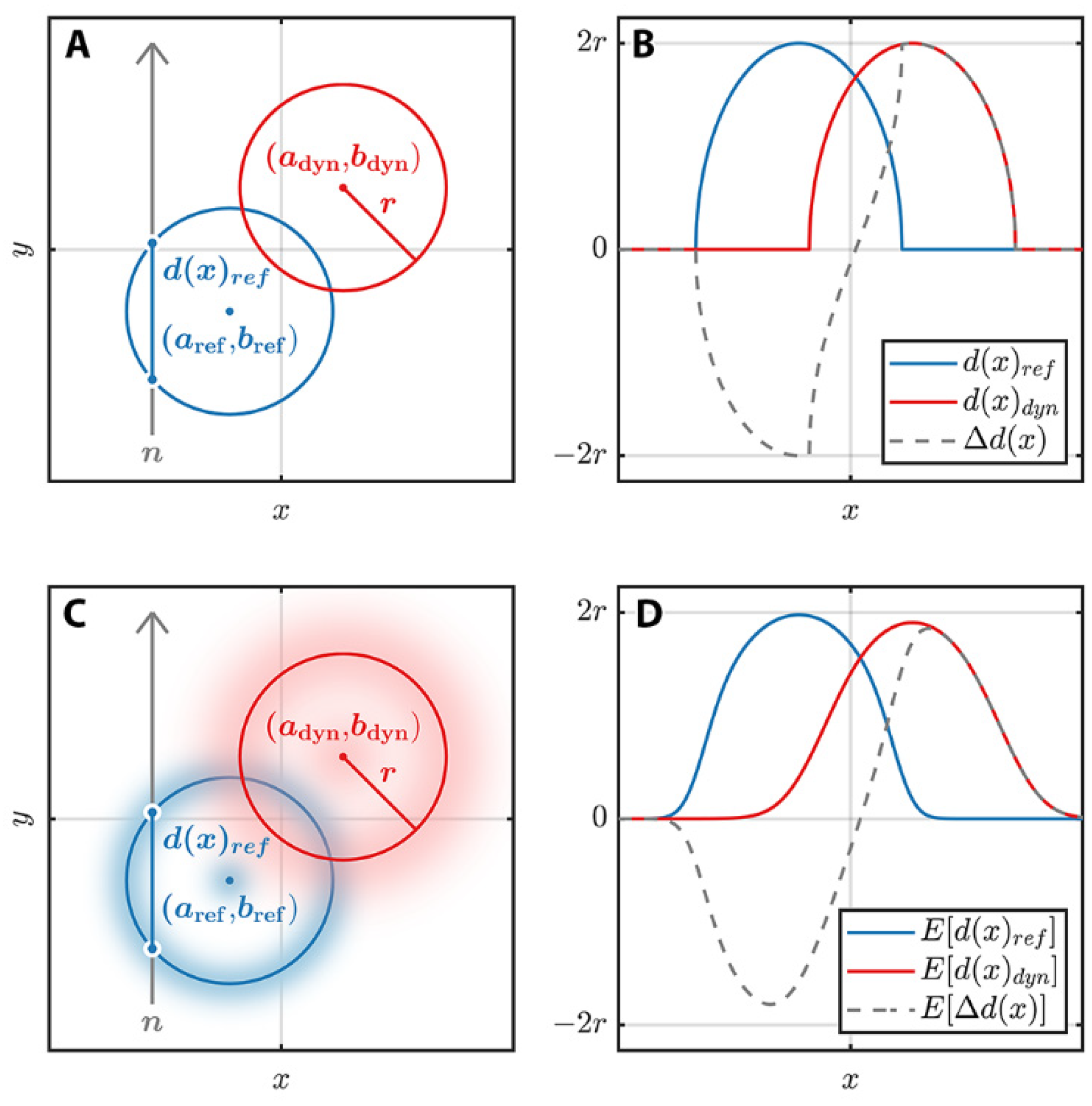
2.4. Path Length Model
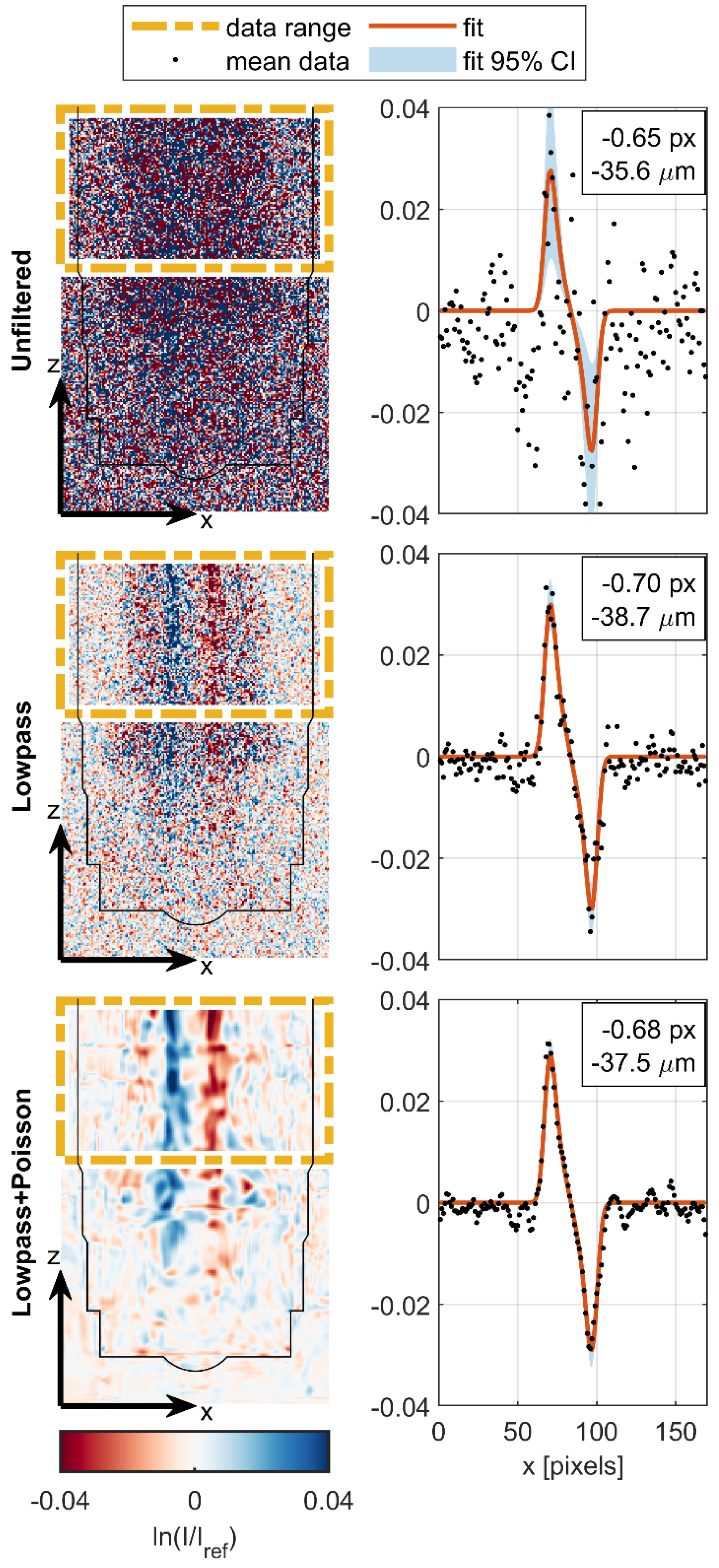
2.5. Image Processing
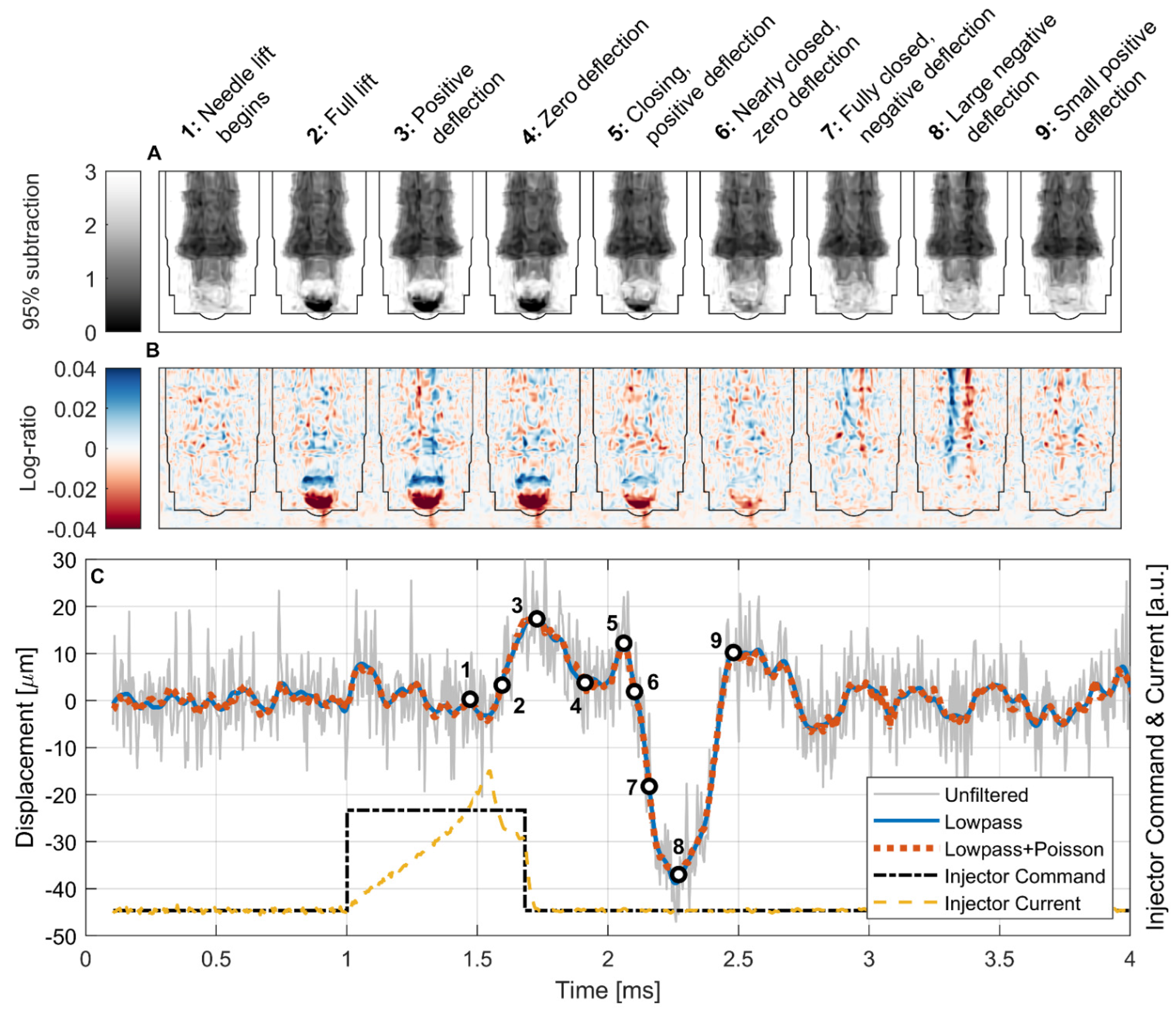
2.6. Extraction of Sample Parameters from Neutron Radiographs and CT
2.7. Model Fitting Procedure
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Experimental Conditions
| Parameter | Value |
|---|---|
| Fuel | iso-octane (C8H18, 2,2,4-trimethylpentane) |
| Fuel temperature (°C) | 90 |
| Injector temperature (°C) | 90 |
| Chamber temperature (°C) | 60 |
| Fuel pressure (MPa) | 20 |
| Chamber pressure (kPa) | 100 |
| Argon flow rate (slpm) | 41 |
| Injection rate (Hz) | 25 |
| Injections per cycle | 1 |
| Injection trigger delay (ms) | 1 |
| Injection command duration (µs) | 680 |
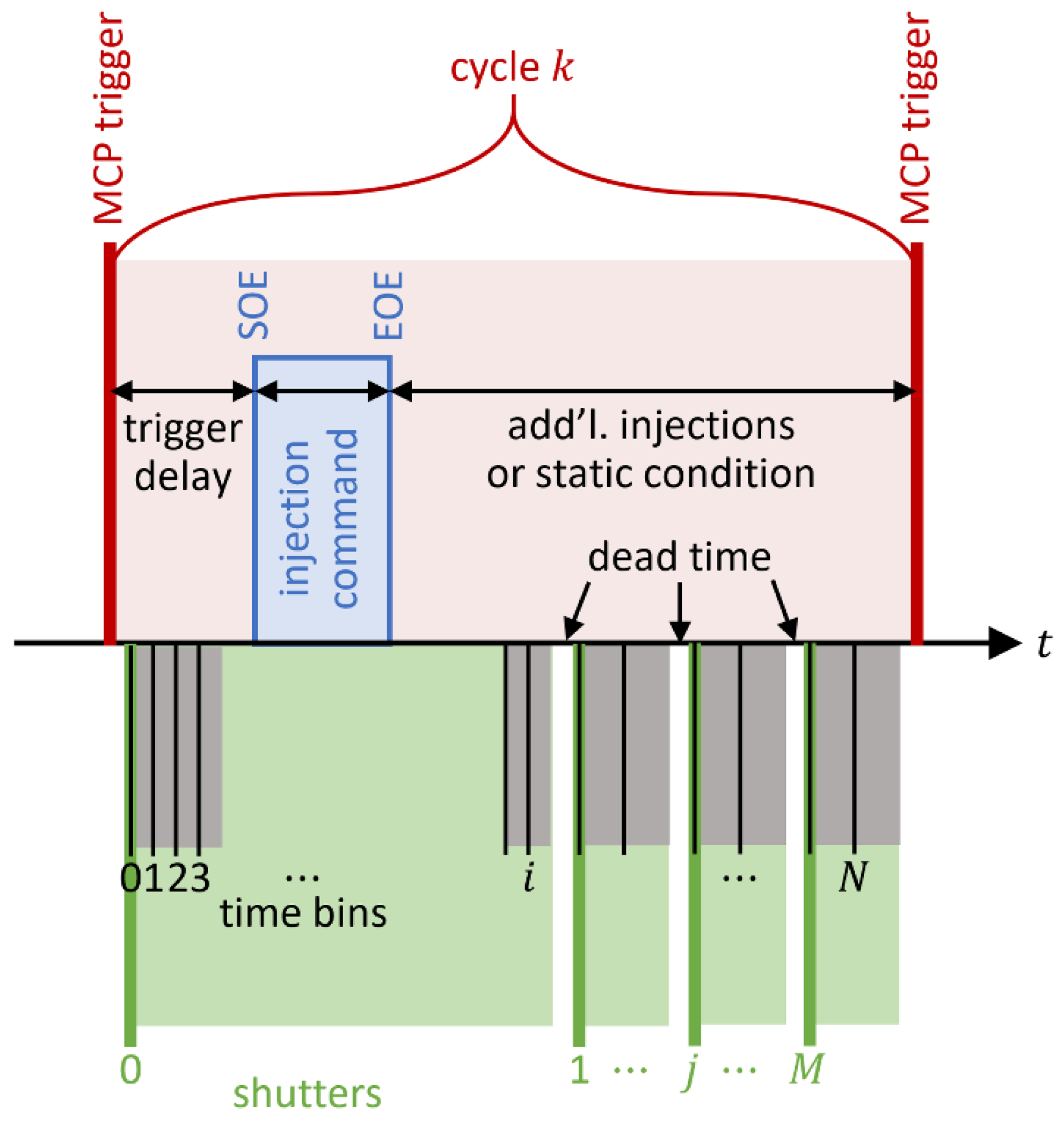
| Shutter | Dead Time (ms) | Start Time (ms) | End Time (ms) | Time Bins | Time Bin Length (μs) | Total Recorded |
|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.1 | 7.0 | 1348 | 5.12 | 1,339,654 |
| 1 | 0.4 | 7.4 | 9.0 | 78 | 20.48 | 1,291,400 |
| 2 | 0.4 | 9.4 | 15.0 | 273 | 20.48 | 1,292,873 |
| 3 | 0.4 | 15.4 | 25.0 | 449 | 20.48 | 1,309,046 |
| 4 | 0.4 | 25.0 | 28.0 | 146 | 20.48 | 1,288,513 |
| 5 | 0.4 | 28.4 | 35.0 | 322 | 20.48 | 1,307,914 |
Appendix B. Attenuation Coefficients and Beam Hardening


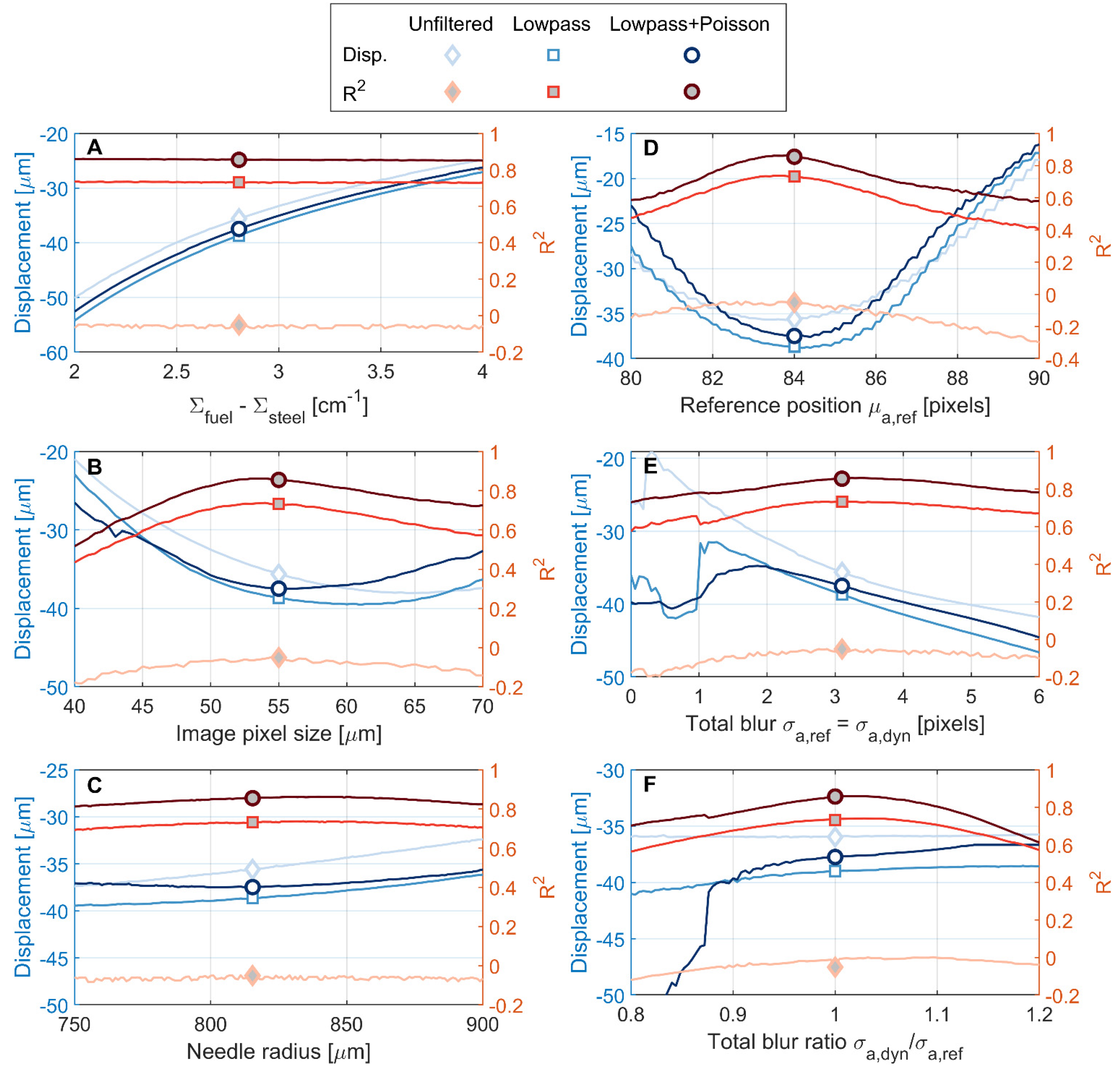
Appendix C. Parametric Investigation of Displacement Model
References
- Bilheux, H.Z.; McGreevy, R.; Anderson, I.S. Neutron Imaging and Applications: A Reference for the Imaging Community; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- The 2018 EPA Automotive Trends Report: Greenhouse Gas Emissions, Fuel Economy, and Technology since 1975. Available online: https://www.epa.gov/automotive-trends (accessed on 1 October 2020).
- Myung, C.L.; Park, S. Exhaust nanoparticle emissions from internal combustion engines: A review. Int. J. Automot. Technol. 2011, 13, 9. [Google Scholar] [CrossRef]
- Jatana, G.S.; Splitter, D.A.; Kaul, B.; Szybist, J.P. Fuel property effects on low-speed pre-ignition. Fuel 2018, 230, 474–482. [Google Scholar] [CrossRef]
- Strek, P.; Duke, D.; Swantek, A.; Kastengren, A.; Powell, C.F.; Schmidt, D.P. X-ray Radiography and CFD Studies of the Spray G Injector; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Neroorkar, K.; Schmidt, D. A Computational Investigation of Flash-Boiling Multi-Hole Injectors with Gasoline-Ethanol Blends; SAE International: Warrendale, PA, USA, 2011. [Google Scholar]
- Saha, K.; Som, S.; Battistoni, M.; Li, Y.; Pomraning, E.; Senecal, P. Numerical Investigation of Two-Phase Flow Evolution of In-and Near-Nozzle Regions of a Gasoline Direct Injection Engine During Needle Transients. SAE Int. J. Engines 2016, 9, 1230–1240. [Google Scholar] [CrossRef]
- Baldwin, E.T.; Grover, R.O.; Parrish, S.E.; Duke, D.J.; Matusik, K.E.; Powell, C.F.; Kastengren, A.L.; Schmidt, D.P. String flash-boiling in gasoline direct injection simulations with transient needle motion. Int. J. Multiph. Flow 2016, 87, 90–101. [Google Scholar] [CrossRef] [Green Version]
- Battistoni, M.; Xue, Q.; Som, S.; Pomraning, E. Effect of off-axis needle motion on internal nozzle and near exit flow in a multi-hole diesel injector. SAE Int. J. Fuels Lubr. 2014, 7, 167–182. [Google Scholar] [CrossRef]
- Powell, C.F.; Kastengren, A.L.; Liu, Z.; Fezzaa, K. The Effects of Diesel Injector Needle Motion on Spray Structure. J. Eng. Gas Turbines Power 2010, 133, 012802. [Google Scholar] [CrossRef]
- Kastengren, A.L.; Powell, C.F.; Liu, Z.; Fezzaa, K.; Wang, J. High-Speed X-ray Imaging of Diesel Injector Needle Motion. In Proceedings of the ASME 2009 Internal Combustion Engine Division Spring Technical Conference, Milwaukee, WI, USA, 3–6 May 2009. [Google Scholar]
- Kastengren, A.L.; Tilocco, F.Z.; Powell, C.F.; Manin, J.; Pickett, L.M.; Payri, R.; Bazyn, T. Engine Combustion Network (ECN): Measurements of nozzle geometry and hydraulic behavior. At. Sprays 2012, 22, 1011–1052. [Google Scholar] [CrossRef]
- Fansler, T.D.; Parrish, S.E. Spray measurement technology: A review. Meas. Sci. Technol. 2014, 26, 012002. [Google Scholar] [CrossRef]
- Kolakaluri, R.; Subramaniam, S.; Panchagnula, M.V. Trends in Multiphase Modeling and Simulation of Sprays. Int. J. Spray Combust. Dyn. 2014, 6, 317–356. [Google Scholar] [CrossRef]
- Tekawade, A.; Sforzo, B.A.; Matusik, K.E.; Fezzaa, K.; Kastengren, A.L.; Powell, C.F. Time-resolved 3D imaging of two-phase fluid flow inside a steel fuel injector using synchrotron X-ray tomography. Sci. Rep. 2020, 10, 8674. [Google Scholar] [CrossRef]
- Duke, D.J.; Finney, C.E.; Kastengren, A.; Matusik, K.; Sovis, N.; Santodonato, L.; Bilheux, H.; Schmidt, D.; Powell, C.; Toops, T. High-resolution x-ray and neutron computed tomography of an engine combustion network spray G gasoline injector. SAE Int. J. Fuels Lubr. 2017, 10, 328–343. [Google Scholar] [CrossRef]
- Santodonato, L.; Bilheux, H.; Bailey, B.; Bilheux, J.; Nguyen, P.; Tremsin, A.; Selby, D.; Walker, L. The CG-1D Neutron Imaging Beamline at the Oak Ridge National Laboratory High Flux Isotope Reactor. Phys. Procedia 2015, 69, 104–108. [Google Scholar] [CrossRef] [Green Version]
- Tremsin, A.S.; McPhate, J.B.; Vallerga, J.V.; Siegmund, O.H.W.; Hull, J.S.; Feller, W.B.; Lehmann, E. Detection efficiency, spatial and timing resolution of thermal and cold neutron counting MCP detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 604, 140–143. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Vallerga, J.V.; Siegmund, O.H.W. Overview of spatial and timing resolution of event counting detectors with Microchannel Plates. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 949, 162768. [Google Scholar] [CrossRef]
- Liu, D.; Hussey, D.; Gubarev, M.V.; Ramsey, B.D.; Jacobson, D.; Arif, M.; Moncton, D.E.; Khaykovich, B. Demonstration of achromatic cold-neutron microscope utilizing axisymmetric focusing mirrors. Appl. Phys. Lett. 2013, 102, 183508. [Google Scholar] [CrossRef]
- Trtik, P.; Hovind, J.; Grünzweig, C.; Bollhalder, A.; Thominet, V.; David, C.; Kaestner, A.; Lehmann, E.H. Improving the Spatial Resolution of Neutron Imaging at Paul Scherrer Institut—The Neutron Microscope Project. Phys. Procedia 2015, 69, 169–176. [Google Scholar] [CrossRef] [Green Version]
- Koerner, S.; Lehmann, E.; Vontobel, P. Design and optimization of a CCD-neutron radiography detector. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2000, 454, 158–164. [Google Scholar] [CrossRef]
- Tomviz 1.9.0. Available online: https://tomviz.org/ (accessed on 1 October 2020).
- Kang, M.; Bilheux, H.Z.; Voisin, S.; Cheng, C.L.; Perfect, E.; Horita, J.; Warren, J.M. Water calibration measurements for neutron radiography: Application to water content quantification in porous media. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 708, 24–31. [Google Scholar] [CrossRef]
- Boillat, P.; Carminati, C.; Schmid, F.; Grünzweig, C.; Hovind, J.; Kaestner, A.; Mannes, D.; Morgano, M.; Siegwart, M.; Trtik, P.; et al. Chasing quantitative biases in neutron imaging with scintillator-camera detectors: A practical method with black body grids. Opt. Express 2018, 26, 15769–15784. [Google Scholar] [CrossRef]
- Carminati, C.; Boillat, P.; Schmid, F.; Vontobel, P.; Hovind, J.; Morgano, M.; Raventos, M.; Siegwart, M.; Mannes, D.; Gruenzweig, C.; et al. Implementation and assessment of the black body bias correction in quantitative neutron imaging. PLoS ONE 2019, 14, e0210300. [Google Scholar] [CrossRef] [Green Version]
- MATLAB R2018b; The MathWorks, Inc.: Natick, MA, USA, 2018.
- Kaestner, A.P.; Kis, Z.; Radebe, M.J.; Mannes, D.; Hovind, J.; Grünzweig, C.; Kardjilov, N.; Lehmann, E.H. Samples to Determine the Resolution of Neutron Radiography and Tomography. Phys. Procedia 2017, 88, 258–265. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Vallerga, J.V.; McPhate, J.B.; Siegmund, O.H.W. Optimization of Timepix count rate capabilities for the applications with a periodic input signal. J. Instrum. 2014, 9, C05026. [Google Scholar] [CrossRef]
- Azzari, L.; Foi, A. Variance Stabilization for Noisy+Estimate Combination in Iterative Poisson Denoising. IEEE Signal Processing Lett. 2016, 23, 1086–1090. [Google Scholar] [CrossRef]
- Ballabriga, R.; Campbell, M.; Llopart, X. Asic developments for radiation imaging applications: The medipix and timepix family. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2018, 878, 10–23. [Google Scholar] [CrossRef] [Green Version]
- Llopart, X.; Alozy, J.; Ballabriga, R.; Campbell, M.; Egidos, N.; Fernandez, J.M.; Heijne, E.; Kremastiotis, I.; Santin, E.; Tlustos, L.; et al. Study of low power front-ends for hybrid pixel detectors with sub-ns time tagging. J. Instrum. 2019, 14, C01024. [Google Scholar] [CrossRef]
- Losko, A.S.; Han, Y.; Schillinger, B.; Tartaglione, A.; Morgano, M.; Strobl, M.; Long, J.; Tremsin, A.S.; Schulz, M. New perspectives for neutron imaging through advanced event-mode data acquisition. Sci. Rep. 2021, 11, 21360. [Google Scholar] [CrossRef]
- Zhang, Y.; Bilheux, J.C.; Bilheux, H.Z.; Lin, J.Y.Y. An interactive web-based tool to guide the preparation of neutron imaging experiments at oak ridge national laboratory. J. Phys. Commun. 2019, 3, 103003. [Google Scholar] [CrossRef]
- Zhang, Y.; Bilheux, J.C. ImagingReso: A tool for neutron resonance imaging. J. Open Source Softw. 2017, 2, 407. [Google Scholar] [CrossRef] [Green Version]
- Brown, D.A.; Chadwick, M.B.; Capote, R.; Kahler, A.C.; Trkov, A.; Herman, M.W.; Sonzogni, A.A.; Danon, Y.; Carlson, A.D.; Dunn, M.; et al. ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data. Nucl. Data Sheets 2018, 148, 1–142. [Google Scholar] [CrossRef]
- Melkonian, E. Slow Neutron Velocity Spectrometer Studies of O2, N2, A, H2, H2O, and Seven Hydrocarbons. Phys. Rev. 1949, 76, 1750–1759. [Google Scholar] [CrossRef]





| Parameter | Unit | Value |
|---|---|---|
| cm−1 | 2.82 | |
| Image pixel size | µm | 55 |
| Needle radius | µm | 815.4 |
| px | 84 | |
| px | 3.1 | |
| px | 3.1 | |
| Displacement range | px | ±5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wissink, M.L.; Toops, T.J.; Splitter, D.A.; Nafziger, E.J.; Finney, C.E.A.; Bilheux, H.Z.; Santodonato, L.J.; Zhang, Y. Quantification of Sub-Pixel Dynamics in High-Speed Neutron Imaging. J. Imaging 2022, 8, 201. https://doi.org/10.3390/jimaging8070201
Wissink ML, Toops TJ, Splitter DA, Nafziger EJ, Finney CEA, Bilheux HZ, Santodonato LJ, Zhang Y. Quantification of Sub-Pixel Dynamics in High-Speed Neutron Imaging. Journal of Imaging. 2022; 8(7):201. https://doi.org/10.3390/jimaging8070201
Chicago/Turabian StyleWissink, Martin L., Todd J. Toops, Derek A. Splitter, Eric J. Nafziger, Charles E. A. Finney, Hassina Z. Bilheux, Louis J. Santodonato, and Yuxuan Zhang. 2022. "Quantification of Sub-Pixel Dynamics in High-Speed Neutron Imaging" Journal of Imaging 8, no. 7: 201. https://doi.org/10.3390/jimaging8070201
APA StyleWissink, M. L., Toops, T. J., Splitter, D. A., Nafziger, E. J., Finney, C. E. A., Bilheux, H. Z., Santodonato, L. J., & Zhang, Y. (2022). Quantification of Sub-Pixel Dynamics in High-Speed Neutron Imaging. Journal of Imaging, 8(7), 201. https://doi.org/10.3390/jimaging8070201







