Unsupervised Approaches for the Segmentation of Dry ARMD Lesions in Eye Fundus cSLO Images
Abstract
:1. Introduction
- First, we propose a successful adaptation of the original developed by Xia et al. [2]. We modified the architecture to adapt it to our images and their specifics. In addition, furthermore, we fully trained our network and did not use any pre-trained model.
- Second, we propose the first realistic unsupervised approach to the very difficult problem of ARMD lesion segmentation. Indeed, this problem is already difficult for humans, and has very little labelled data (hence why we cannot use supervised neural networks), thus making it quite a challenging problem for unsupervised algorithms. In this regard, we achieve very decent performance considering the nature of the problem and the challenges it presents.
- Third, we propose a fair and extensive comparison with other unsupervised methods (neural networks and others) used in other fields that we have also adapted to tackle the same problem.
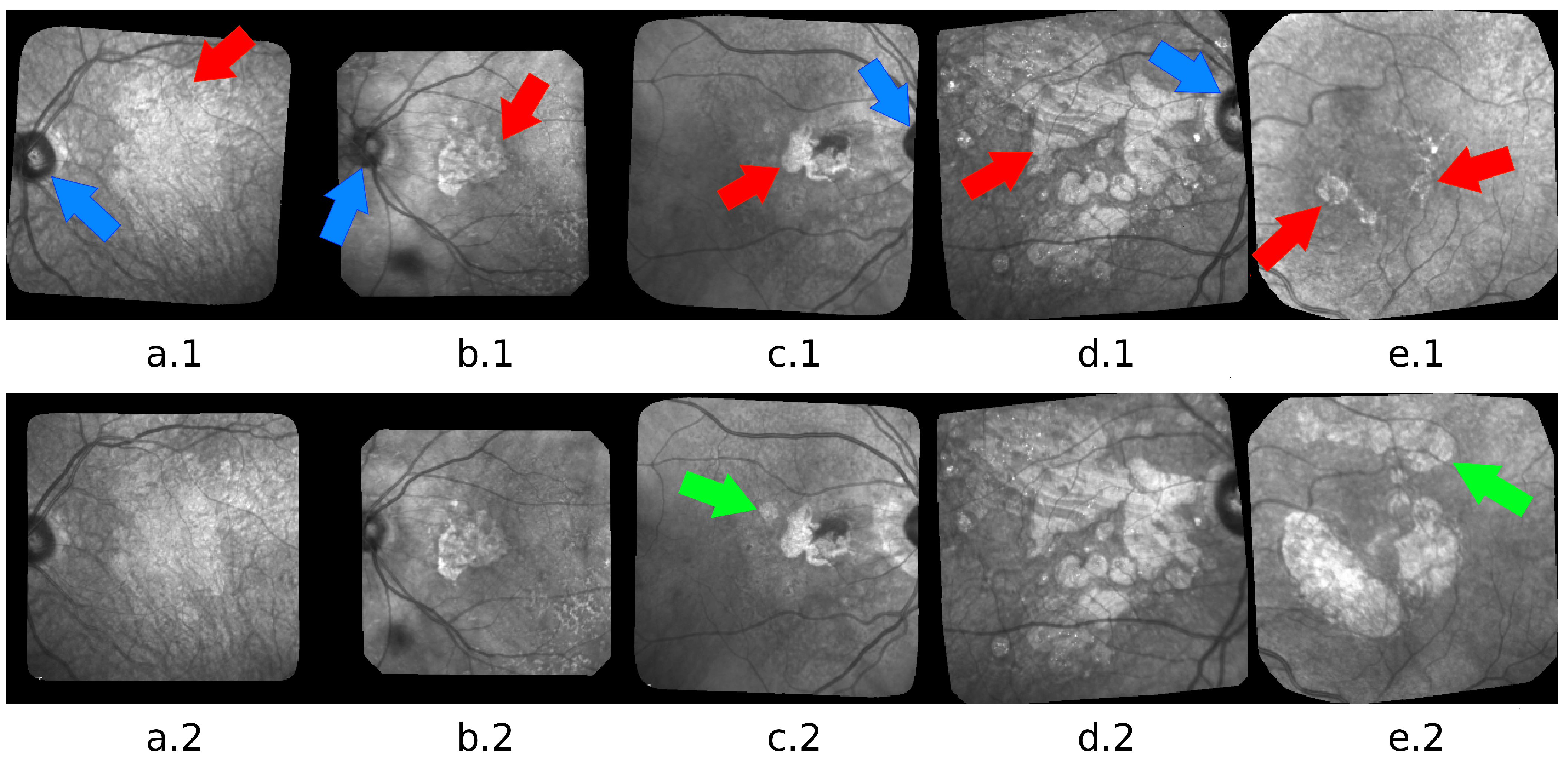
2. Materials
3. Related Work
4. Methods
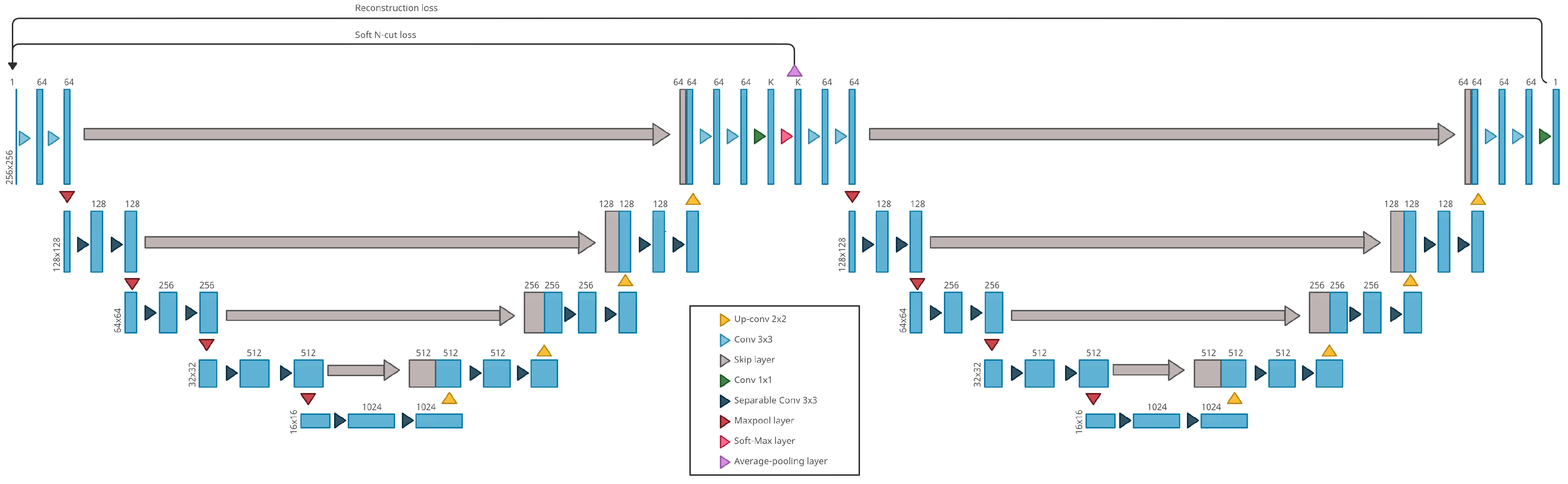
4.1. Our Method: W-Nets Adapted to ARMD Lesions Segmentation
4.2. Compared Methods
4.2.1. Gabor + KMeans
4.2.2. Active Contour Model without Edges
4.2.3. CNN + Superpixel Refinement
- “Pixels of similar features are desired to be assigned the same label”
- “Spatially continuous pixels are desired to be assigned the same label”
- “The number of unique cluster labels is desired to be large”
- forward process: prediction of clusters with the network and refined cluster with the superpixel refinement process
- backward process: backpropagation of the signal error (cross-entropy loss) between the network response and the refined cluster
5. Results
5.1. Experimental Setting
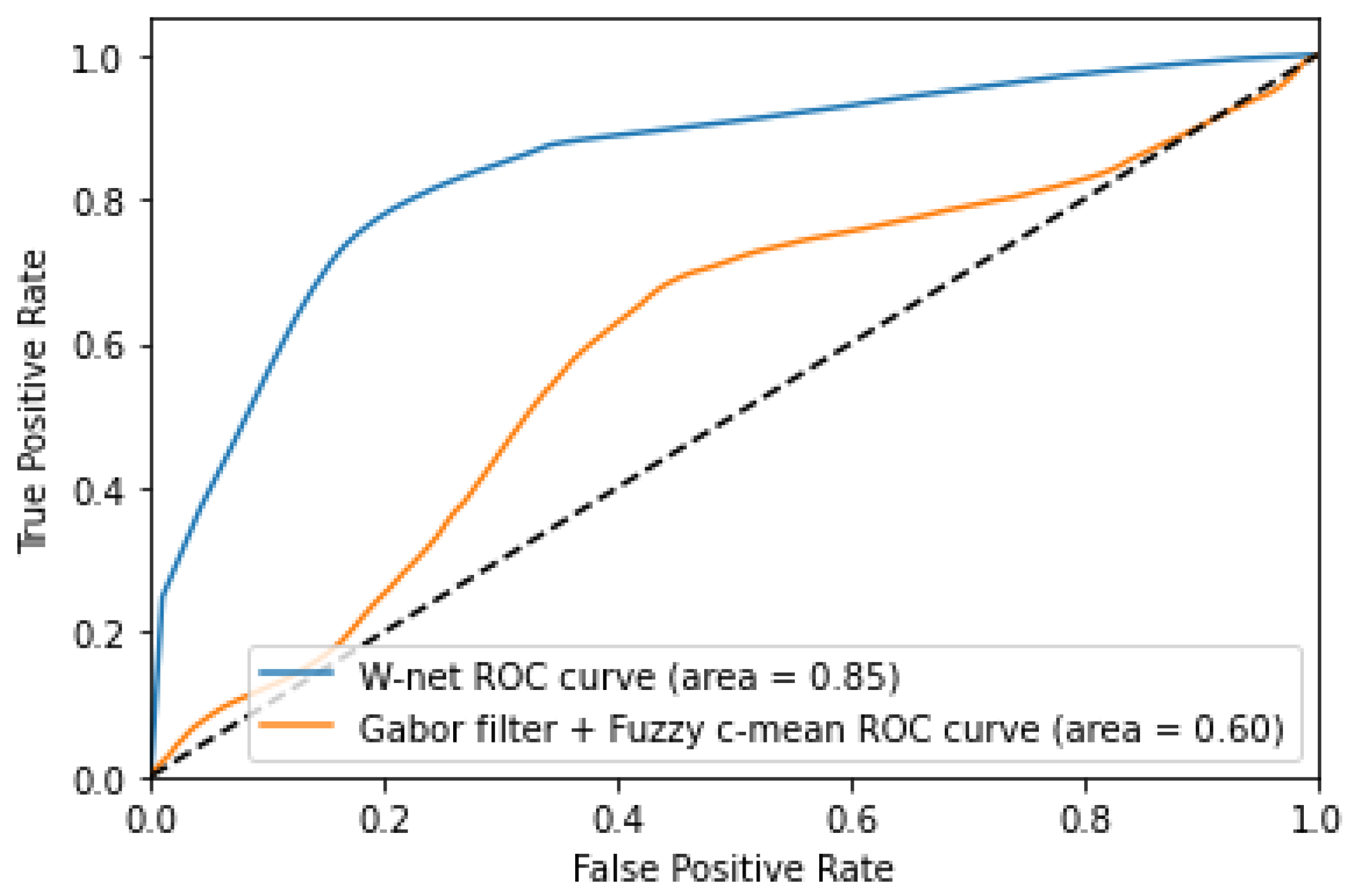
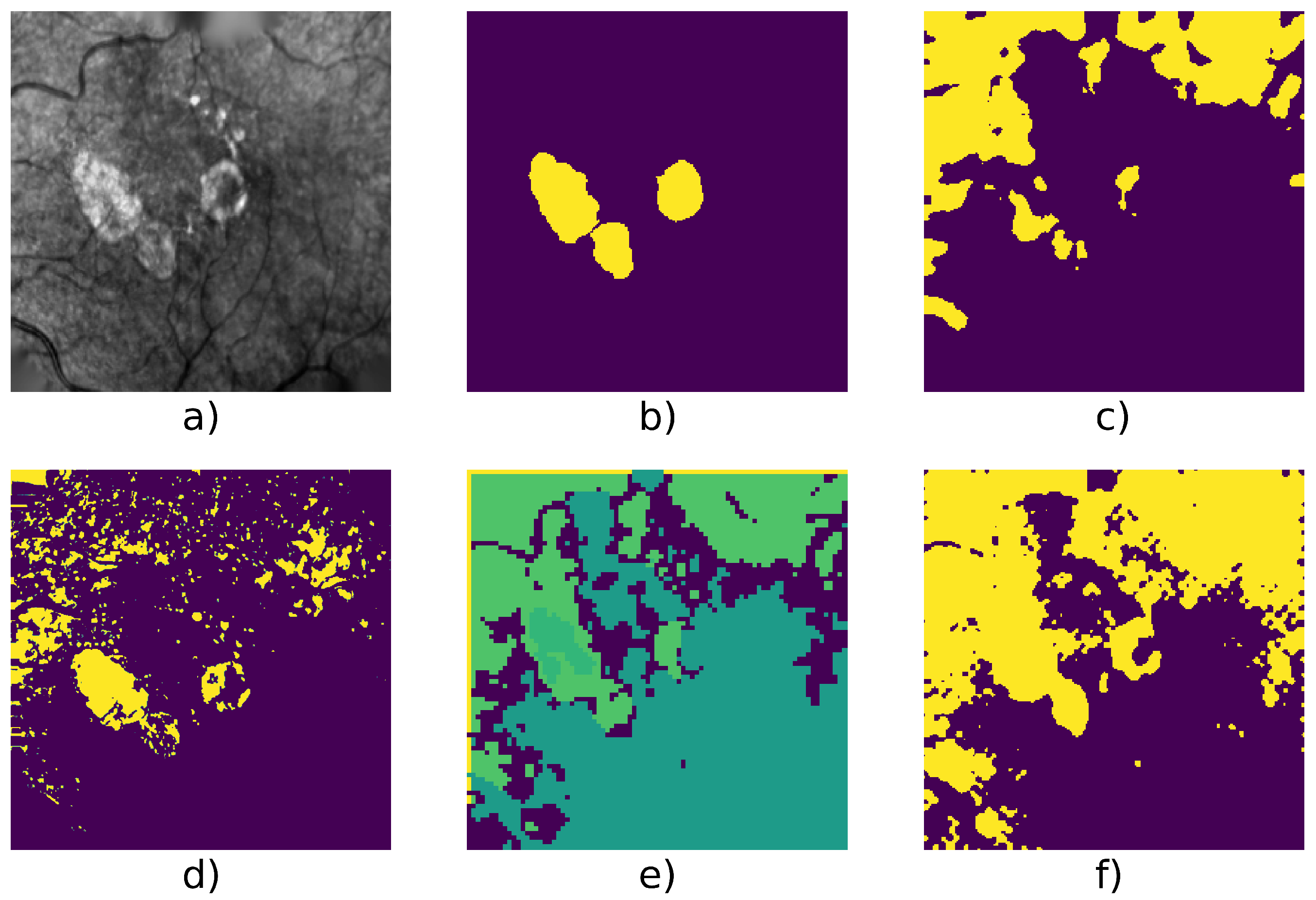
5.2. Experimental Results
6. Conclusions and Future Works
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AE | Autoencoder |
| APSP | Atrous Pyramid Spatial Pooling |
| ARMD or AMD | Age-Related Macular Degeneration |
| CNN | Convolutional Neural Networks |
| cSLO | confocal Scanning Laser Ophthalmoscopy |
| FAF | Fundus Autofluorescence |
| GA | Geographic Atrophy |
| IR | Infrared |
| OCT | Optical Coherence Tomography |
| PSP | Pyramid Spatial Pooling |
References
- Platanios, E.A.; Al-Shedivat, M.; Xing, E.; Mitchell, T. Learning from Imperfect Annotations: An End-to-End Approach. 2020. Available online: https://openreview.net/forum?id=rJlVdREKDS (accessed on 25 June 2021).
- Xia, X.; Kulis, B. W-Net: A Deep Model for Fully Unsupervised Image Segmentation. arXiv 2017, arXiv:1711.08506. [Google Scholar]
- Rossant, F.; Paques, M. Normalization of series of fundus images to monitor the geographic atrophy growth in dry age-related macular degeneration. Comput. Methods Programs Biomed. 2021, 208, 106234. [Google Scholar] [CrossRef] [PubMed]
- Köse, C.; Sevik, U.; Gençalioglu, O. Automatic segmentation of age-related macular degeneration in retinal fundus images. Comput. Biol. Med. 2008, 38, 611–619. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.; Vese, L. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdullah, A.S.; Rahebi, J.; Özok, Y.; Aljanabi, M. A new and effective method for human retina optic disc segmentation with fuzzy clustering method based on active contour model. Med. Biol. Eng. Comput. 2019, 58. [Google Scholar] [CrossRef]
- Hu, Z.; Medioni, G.; Hernandez, M.; Hariri, A.; Wu, X.; Sadda, S. Segmentation of the Geographic Atrophy in Spectral-Domain Optical Coherence Tomography and Fundus Autofluorescence Images. Investig. Ophthalmol. Vis. Sci. 2013, 54, 8375–8383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, N.; Laine, A.; Smith, R. A hybrid segmentation approach for geographic atrophy in fundus auto-fluorescence images for diagnosis of age-related macular degeneration. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007. [Google Scholar]
- Köse, C.; Sevik, U.; Gençalioğlu, O.; Ikibaş, C.; Kayikiçioğlu, T. A Statistical Segmentation Method for Measuring Age-Related Macular Degeneration in Retinal Fundus Images. J. Med. Syst. 2010, 34, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Cousty, J.; Bertrand, G.; Najman, L.; Couprie, M. Watershed Cuts: Thinnings, Shortest Path Forests, and Topological Watersheds. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 925–939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- G N, G.; Kothari, A.; Rajan, J. Marker Controlled Watershed Transform for Intra-Retinal Cysts Segmentation from Optical Coherence Tomography B-Scans. Pattern Recognit. Lett. 2017, 139, 86–94. [Google Scholar] [CrossRef]
- Köse, C.; İkibaş, C. Statistical Techniques for Detection of Optic Disc and Macula and Parameters Measurement in Retinal Fundus Images. J. Med. Biol. Eng. 2011, 31, 395–404. [Google Scholar] [CrossRef]
- Feeny, A.K.; Tadarati, M.; Freund, D.E.; Bressler, N.M.; Burlina, P. Automated segmentation of geographic atrophy of the retinal epithelium via random forests in AREDS color fundus images. Comput. Biol. Med. 2015, 65, 124–136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phan, T.V.; Seoud, L.; Chakor, H.; Cheriet, F. Automatic Screening and Grading of Age-Related Macular Degeneration from Texture Analysis of Fundus Images. J. Ophthalmol. 2016, 2016, 5893601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, Z.; Medioni, G.; Hernandez, M.; Sadda, S. Automated segmentation of geographic atrophy in fundus autofluorescence images using supervised pixel classification. J. Med. Imaging 2014, 2, 014501. [Google Scholar] [CrossRef] [PubMed]
- Lee, N.; Smith, R.T.; Laine, A.F. Interactive segmentation for geographic atrophy in retinal fundus images. Conf. Rec. Conf. Signals Syst. Comput. 2008, 2008, 655–658. [Google Scholar] [CrossRef] [Green Version]
- Deckert, A.; Schmitz-Valckenberg, S.; Jorzik, J.; Bindewald, A.; Holz, F.; Mansmann, U. Automated analysis of digital fundus autofluorescence images of geographic atrophy in advanced age-related macular degeneration using confocal scanning laser ophthalmoscopy (cSLO). BMC Ophthalmol. 2005, 5, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015—18th International Conference, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the Fourth International Conference on 3D Vision, 3DV 2016, Stanford, CA, USA, 25–28 October 2016; IEEE Computer Society: Washington, DC, USA, 2016; pp. 565–571. [Google Scholar] [CrossRef] [Green Version]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2016—19th International Conference, Athens, Greece, 17–21 October 2016; pp. 424–432. [Google Scholar]
- Hussain, M.A.; Govindaiah, A.; Souied, E.; Smith, R.T.; Bhuiyan, A. Automated tracking and change detection for Age-related Macular Degeneration Progression using retinal fundus imaging. In Proceedings of the 2018 Joint 7th International Conference on Informatics, Electronics & Vision (ICIEV) and 2018 2nd International Conference on Imaging, Vision & Pattern Recognition (icIVPR), Kitakyushu, Japan, 25–29 June 2018; pp. 394–398. [Google Scholar] [CrossRef]
- Burlina, P.; Freund, D.E.; Joshi, N.; Wolfson, Y.; Bressler, N.M. Detection of age-related macular degeneration via deep learning. In Proceedings of the 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 184–188. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Ramsey, D.J.; Sunness, J.S.; Malviya, P.; Applegate, C.; Hager, G.D.; Handa, J.T. Automated image alignment and segmentation to follow progression of geographic atrophy in age-related macular degeneration. Retina 2014, 34, 1296–1307. [Google Scholar] [CrossRef] [PubMed]
- Dupont, G.; Kalinicheva, E.; Sublime, J.; Rossant, F.; Pâques, M. Analyzing Age-Related Macular Degeneration Progression in Patients with Geographic Atrophy Using Joint Autoencoders for Unsupervised Change Detection. J. Imaging 2020, 6, 57. [Google Scholar] [CrossRef]
- Kalinicheva, E.; Sublime, J.; Trocan, M. Change Detection in Satellite Images using Reconstruction Errors of Joint Autoencoders. In Artificial Neural Networks and Machine Learning—ICANN 2019: Image Processing; Springer: Munich, Germany, 2019; pp. 637–648. [Google Scholar] [CrossRef]
- Kanezaki, A. Unsupervised Image Segmentation by Backpropagation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Tang, M.; Djelouah, A.; Perazzi, F.; Boykov, Y.; Schroers, C. Normalized Cut Loss for Weakly-Supervised CNN Segmentation. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.; Farrokhnia, F. Unsupervised Texture Segmentation Using Gabor Filters. Pattern Recognit. 1990, 24, 14–19. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]






| Method | Pros | Cons | |
|---|---|---|---|
| Region oriented [4,5] | High performance on ARMD, semi-supervised (seeds) | FAF/OCT images | Conventionnal methods |
| Active contour [5,6] | High performance on retinal cases | Segment optic discs | |
| Statistical [12] | High performance on retinal cases | Segment blood vessels and optic discs | |
| Random Forest [13] | High performance on ARMD | Color fundus images, supervised | |
| Random Forest + SVM [14] | High performance on ARMD | Screening and grading task, supervised | |
| Fuzzy C-means [25] | Unsupervised, high performance on ARMD | High contrast FAF images | |
| K-NN [15] | High performance on ARMD | FAF images, supervised | |
| Watershed [10,11] | Semi supervised (seeds) | OCT images | |
| U-net [18,21] | High performance on ARMD | Supervised, training on GPU | Deep learning methods |
| Transfert learning on ARMD [22] | High performance | Supervised, color fundus images | |
| Scene parsing [23,24] | High performance | Supervised, requires multiple objects in a scene, training on GPU | |
| Change detection [26] | Unsupervised, applied on the same dataset | Change detection task | |
| CNN + Superpixel refinement [28] | Unsupervised, no training | Produce a variable number of cluster in the segmentation | |
| W-net [2] | Unsupervised, robust | Training on GPU | |
| Our W-net | Unsupervised, fast inference use, robust, high performance on ARMD | Training on GPU | |
| Human interaction [16,17] | High performance on ARMD | Require human interaction | Other methods |
| Method | F1 | Precision | Recall |
|---|---|---|---|
| W-net | 0.83 ± 0.09 | 0.87 ± 0.08 | 0.81 ± 0.13 |
| W-net + | 0.82 ± 0.07 | 0.82 ± 0.10 | 0.82 ± 0.11 |
| Method | F1 | Precision | Recall |
|---|---|---|---|
| Active contour (Chan & Vese [5]) | 0.73 ± 0.07 | 0.64 ± 0.13 | 0.86 ± 0.05 |
| CNN + Superpixel Refinement (Kanezaki [28]) | 0.65 ± 0.07 | 0.54 ± 0.10 | 0.85 ± 0.06 |
| Gabor + KMeans [30] | 0.77 ± 0.08 | 0.80 ± 0.12 | 0.75 ± 0.08 |
| Our W-net | 0.87 ± 0.07 | 0.90 ± 0.07 | 0.85 ± 0.11 |
| W-net + | 0.85 ± 0.06 | 0.84 ± 0.07 | 0.87 ± 0.09 |
| Patient Id | Method | F1 | Precision | Recall | Nb. of Images | Fig. |
|---|---|---|---|---|---|---|
| 005 | Active Contour | 0.787 | 0.779 | 0.795 | 9 | Figure 6 |
| CNN + Superpixel refinement | 0.690 | 0.623 | 0.787 | |||
| Gabor + KMeans | 0.791 | 0.760 | 0.828 | |||
| Our W-net | 0.785 | 0.806 | 0.765 | |||
| W-net + | 0.799 | 0.805 | 0.792 | |||
| 010 | Active Contour | 0.644 | 0.504 | 0.892 | 6 | Figure 8 |
| CNN + Superpixel refinement | 0.589 | 0.440 | 0.909 | |||
| Gabor + KMeans | 0.809 | 0.907 | 0.731 | |||
| Our W-net | 0.922 | 0.921 | 0.922 | |||
| W-net + | 0.919 | 0.910 | 0.927 | |||
| 016 | Active Contour | 0.849 | 0.869 | 0.828 | 31 | Figure 7 |
| CNN + Superpixel refinement | 0.790 | 0.752 | 0.840 | |||
| Gabor + KMeans | 0.678 | 0.596 | 0.786 | |||
| Our W-net | 0.676 | 0.880 | 0.924 | |||
| W-net + | 0.706 | 0.817 | 0.622 | |||
| 020 | Active Contour | 0.654 | 0.516 | 0.901 | 50 | Figure 9 |
| CNN + Superpixel refinement | 0.622 | 0.489 | 0.898 | |||
| Gabor + KMeans | 0.744 | 0.903 | 0.640 | |||
| Our W-net | 0.946 | 0.977 | 0.920 | |||
| W-net + | 0.864 | 0.808 | 0.929 | |||
| 109 | Active Contour | 0.774 | 0.755 | 0.796 | 16 | Figure 10 |
| CNN + Superpixel refinement | 0.717 | 0.695 | 0.767 | |||
| Gabor + KMeans | 0.700 | 0.685 | 0.718 | |||
| Our W-net | 0.782 | 0.936 | 0.672 | |||
| W-net + | 0.799 | 0.903 | 0.717 | |||
| 117 | Active Contour | 0.658 | 0.512 | 0.920 | 6 | Figure 5 |
| CNN + Superpixel refinement | 0.609 | 0.469 | 0.892 | |||
| Gabor + KMeans | 0.933 | 0.966 | 0.902 | |||
| Our W-net | 0.987 | 0.995 | 0.979 | |||
| W-net + | 0.988 | 0.993 | 0.982 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Royer, C.; Sublime, J.; Rossant, F.; Paques, M. Unsupervised Approaches for the Segmentation of Dry ARMD Lesions in Eye Fundus cSLO Images. J. Imaging 2021, 7, 143. https://doi.org/10.3390/jimaging7080143
Royer C, Sublime J, Rossant F, Paques M. Unsupervised Approaches for the Segmentation of Dry ARMD Lesions in Eye Fundus cSLO Images. Journal of Imaging. 2021; 7(8):143. https://doi.org/10.3390/jimaging7080143
Chicago/Turabian StyleRoyer, Clément, Jérémie Sublime, Florence Rossant, and Michel Paques. 2021. "Unsupervised Approaches for the Segmentation of Dry ARMD Lesions in Eye Fundus cSLO Images" Journal of Imaging 7, no. 8: 143. https://doi.org/10.3390/jimaging7080143
APA StyleRoyer, C., Sublime, J., Rossant, F., & Paques, M. (2021). Unsupervised Approaches for the Segmentation of Dry ARMD Lesions in Eye Fundus cSLO Images. Journal of Imaging, 7(8), 143. https://doi.org/10.3390/jimaging7080143







