Direct and Indirect vSLAM Fusion for Augmented Reality
Abstract
:1. Introduction
2. State-of-the-Art
2.1. Indirect vSLAM
2.2. Direct vSLAM
2.3. Other Types of vSLAM
3. Materials and Methods
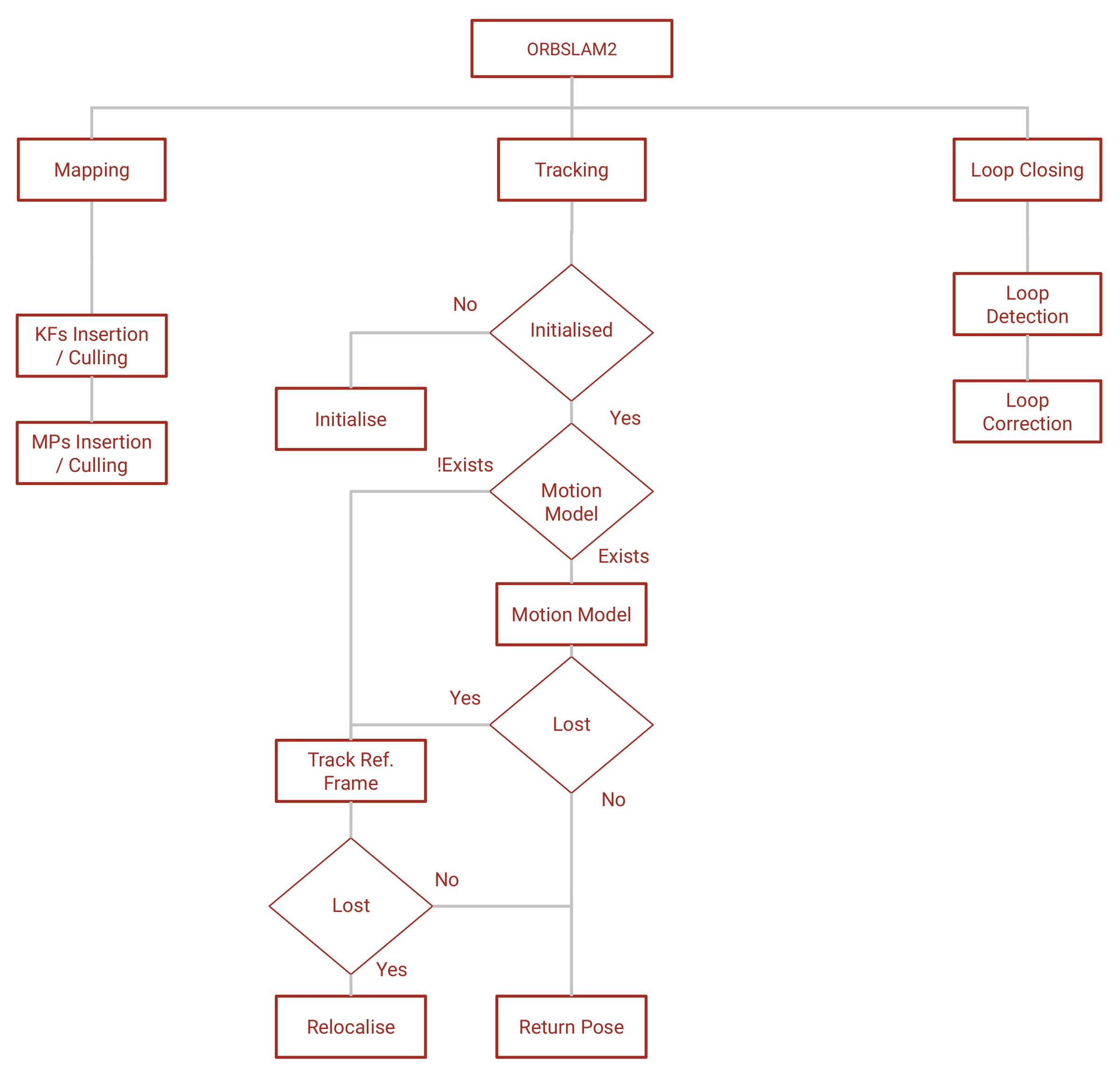
3.1. ORBSLAM2
3.1.1. Tracking
3.1.2. Mapping
3.1.3. Loop Closing
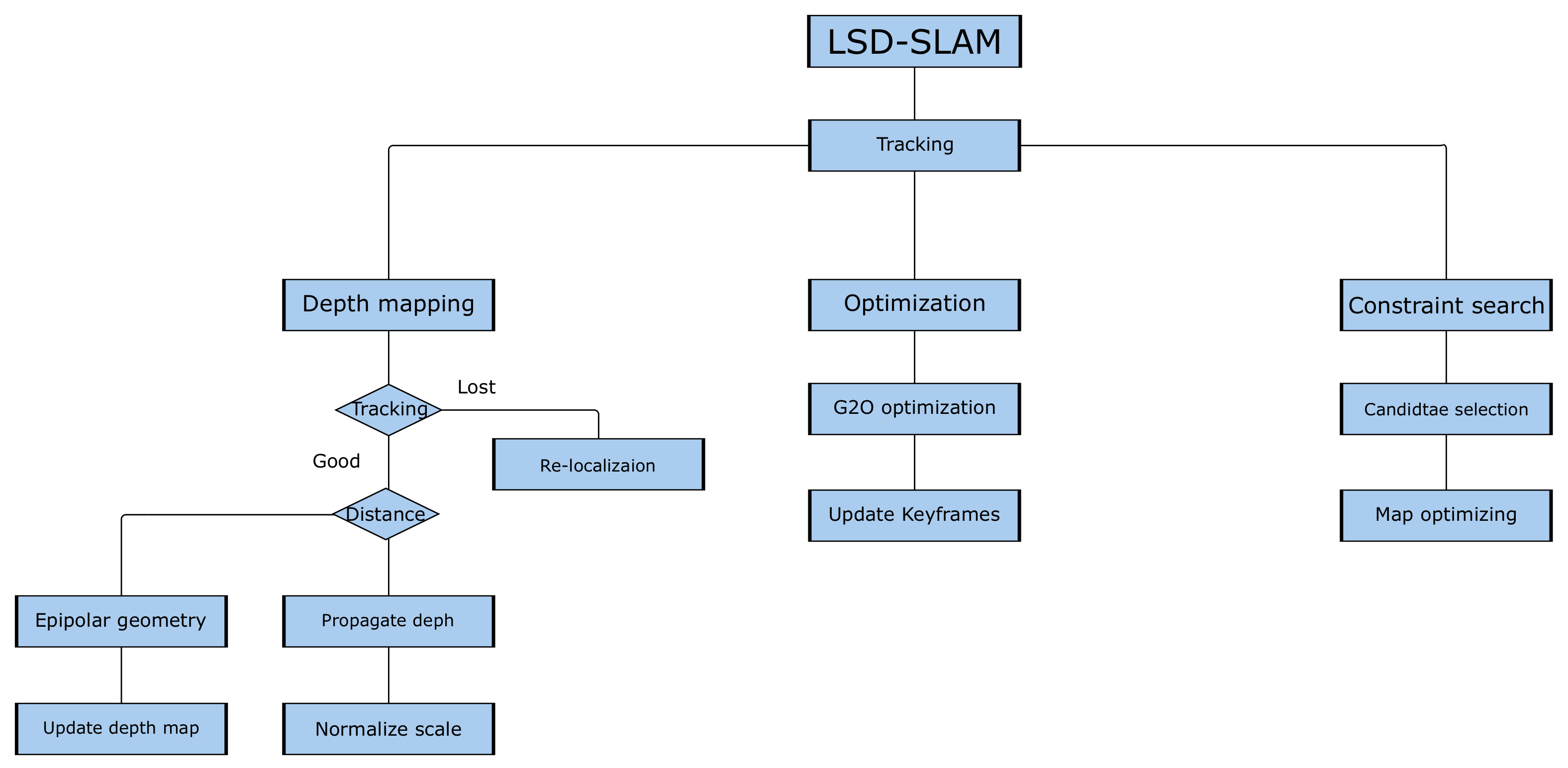
3.2. LSD-SLAM
3.2.1. Tracking
3.2.2. Depth Map Estimation
3.2.3. Pose Graph Optimization
3.2.4. Constraint Search
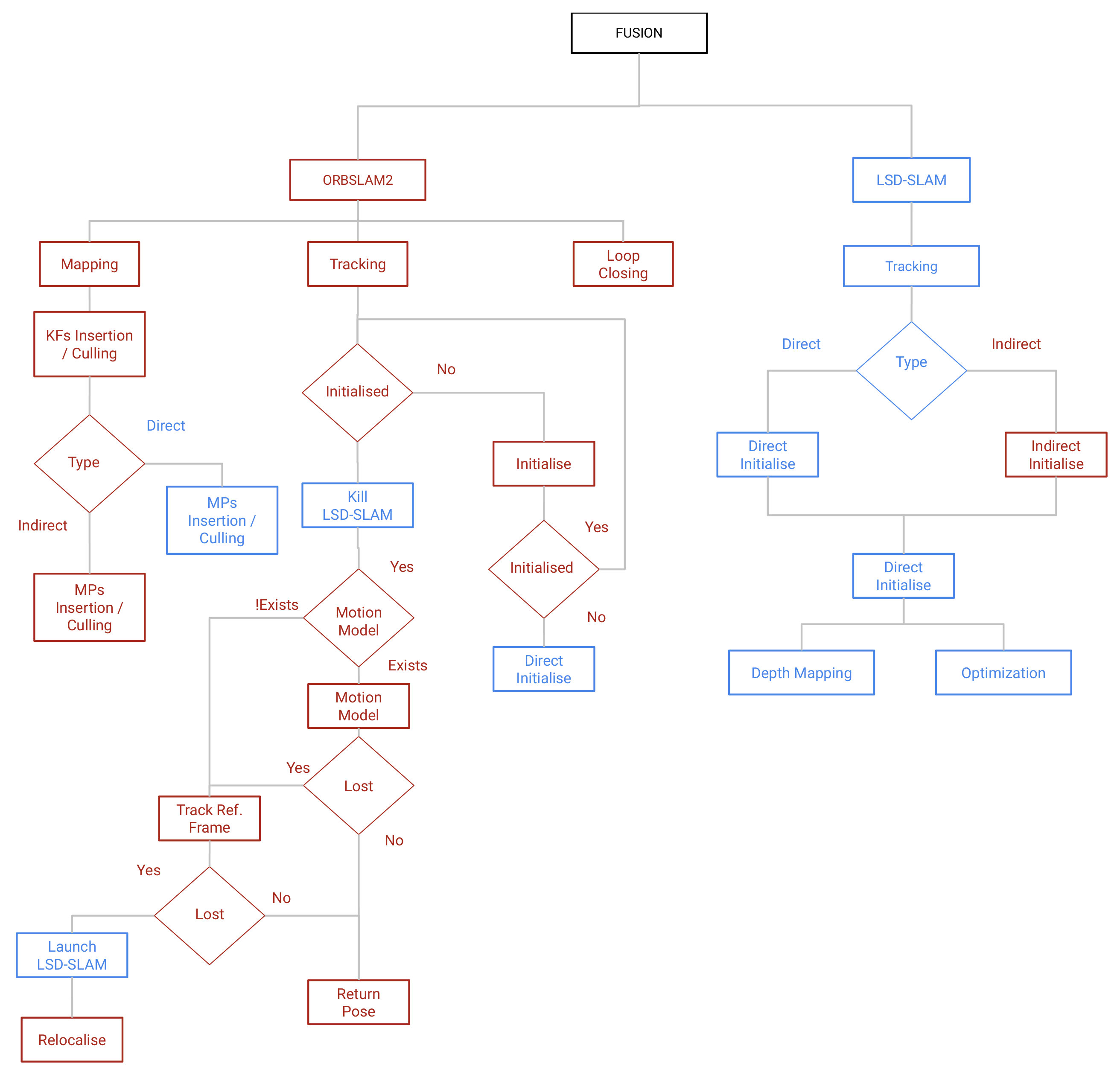
3.3. The Proposed Fusion System
4. Results
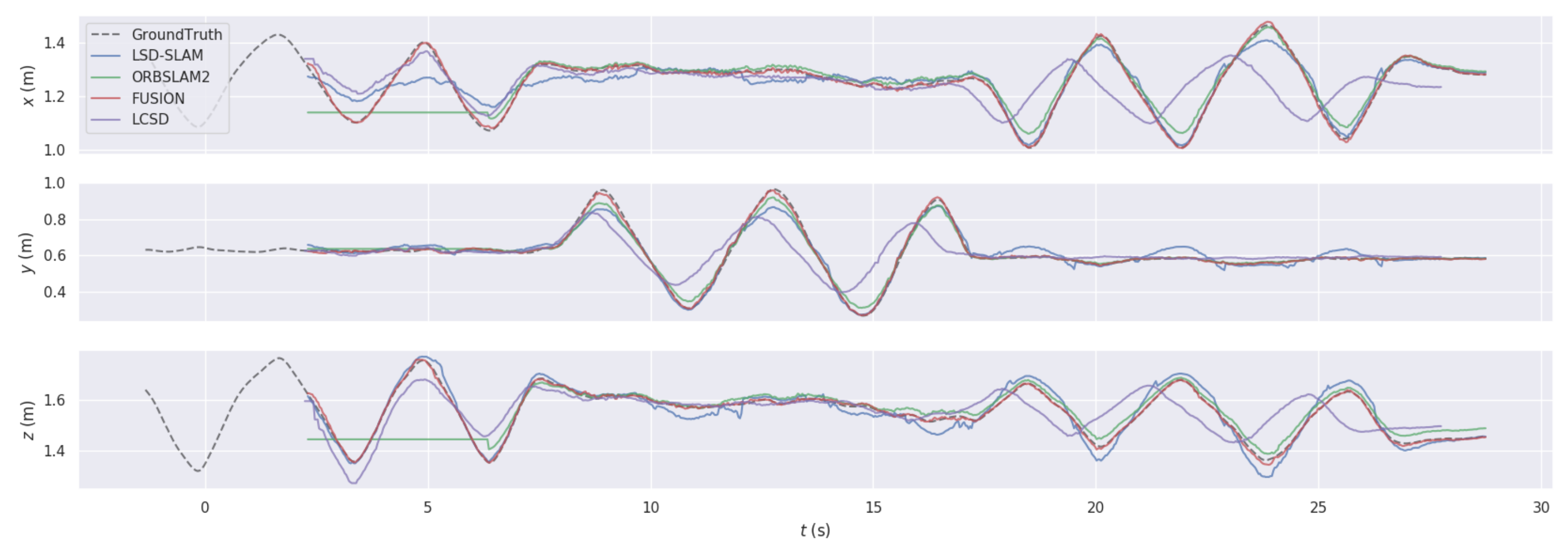
4.1. Trajectory Comparison
4.2. Execution Time
4.3. Augmentations
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Newcombe, R.A.; Lovegrove, S.J.; Davison, A.J. DTAM: Dense tracking and mapping in real-time. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2320–2327. [Google Scholar]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [Green Version]
- Jinyu, L.; Bangbang, Y.; Danpeng, C.; Nan, W.; Guofeng, Z.; Hujun, B. Survey and evaluation of monocular visual-inertial SLAM algorithms for augmented reality. Virtual Real. Intell. Hardw. 2019, 1, 386–410. [Google Scholar] [CrossRef]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. arXiv 2016, arXiv:1607.02565. [Google Scholar] [CrossRef] [PubMed]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo and RGB-D Cameras. arXiv 2016, arXiv:1610.06475. [Google Scholar] [CrossRef] [Green Version]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Ramezani, M.; Tinchev, G.; Iuganov, E.; Fallon, M. Online LiDAR-SLAM for Legged Robots with Robust Registration and Deep-Learned Loop Closure. arXiv 2020, arXiv:cs.RO/2001.10249. [Google Scholar]
- Aghili, F. 3D SLAM using IMU and its observability analysis. In Proceedings of the 2010 IEEE International Conference on Mechatronics and Automation, Xi’an, China, 4–7 August 2010; pp. 377–383. [Google Scholar] [CrossRef]
- Pire, T.; Fischer, T.; Castro, G.; De Cristóforis, P.; Civera, J.; Jacobo Berlles, J. S-PTAM: Stereo Parallel Tracking and Mapping. Robot. Auton. Syst. 2017, 93, 27–42. [Google Scholar] [CrossRef] [Green Version]
- Kerl, C.; Sturm, J.; Cremers, D. Dense Visual SLAM for RGB-D Cameras. In Proceedings of the International Conference on Intelligent Robot Systems (IROS), Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Liu, Y.; Chen, Z.; Zheng, W.; Wang, H.; Liu, J. Monocular Visual-Inertial SLAM: Continuous Preintegration and Reliable Initialization. Sensors 2017, 17, 2613. [Google Scholar] [CrossRef] [Green Version]
- Casarrubias-Vargas, H.; Petrilli-Barceló, A.; Bayro-Corrochano, E. EKF-SLAM and Machine Learning Techniques for Visual Robot Navigation. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 396–399. [Google Scholar]
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. FastSLAM: A Factored Solution to the Simultaneous Localization and Mapping Problem. In Proceedings of the AAAI National Conference on Artificial Intelligence, Edmonton, AB, Canada, 30 July–1 August 2002; pp. 593–598. [Google Scholar]
- Van Goor, P.; Mahony, R.; Hamel, T.; Trumpf, J. An Observer Design for Visual Simultaneous Localisation and Mapping with Output Equivariance. arXiv 2020, arXiv:cs.RO/2005.14347. [Google Scholar]
- De Croce, M.; Pire, T.; Bergero, F. DS-PTAM: Distributed Stereo Parallel Tracking and Mapping SLAM System. J. Intell. Robot. Syst. 2018. [Google Scholar] [CrossRef]
- Sumikura, S.; Shibuya, M.; Sakurada, K. OpenVSLAM: A Versatile Visual SLAM Framework. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019. [Google Scholar]
- Cummins, M.; Newman, P. FAB-MAP: Probabilistic Localization and Mapping in the Space of Appearance. Int. J. Robot. Res. 2008, 27, 647–665. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, R.; Zhou, Z.H. Understanding bag-of-words model: A statistical framework. Int. J. Mach. Learn. Cybern. 2010, 1, 43–52. [Google Scholar] [CrossRef]
- Kaess, M.; Ranganathan, A.; Dellaert, F. iSAM: Incremental Smoothing and Mapping. IEEE Trans. Robot. 2008, 24, 1365–1378. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Zhang, G.; Bao, H. Robust Keyframe-Based Monocular SLAM for Augmented Reality. In Proceedings of the 2016 IEEE International Symposium on Mixed and Augmented Reality (ISMAR-Adjunct), Merida, Mexico, 19–23 September 2016; pp. 340–341. [Google Scholar]
- Audi, A.; Pierrot-Deseilligny, M.; Meynard, C.; Thom, C. Implementation of an IMU Aided Image Stacking Algorithm in a Digital Camera for Unmanned Aerial Vehicles. Sensors 2017, 17, 1646. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engel, J.; Sturm, J.; Cremers, D. Semi-Dense Visual Odometry for a Monocular Camera. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Sattler, T.; Zhou, Q.; Pollefeys, M.; Leal-Taixé, L. Understanding the Limitations of CNN-based Absolute Camera Pose Regression. arXiv 2019, arXiv:1903.07504. [Google Scholar]
- Brachmann, E.; Michel, F.; Krull, A.; Yang, M.Y.; Gumhold, S.; Rother, C. Uncertainty-Driven 6D Pose Estimation of Objects and Scenes from a Single RGB Image. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3364–3372. [Google Scholar]
- Nain, N.; Laxmi, V.; Bhadviya, B.; Deepak, B.M.; Ahmed, M. Fast Feature Point Detector. In Proceedings of the 2008 IEEE International Conference on Signal Image Technology and Internet Based Systems (SITIS ’08), Bali, Indonesia, 30 November–3 December 2008; IEEE Computer Society: New York, NY, USA, 2008; pp. 301–306. [Google Scholar] [CrossRef]
- Sultana, F.; Sufian, A.; Dutta, P. Evolution of Image Segmentation using Deep Convolutional Neural Network: A Survey. Knowl. Based Syst. 2020, 201–202, 106062. [Google Scholar] [CrossRef]
- Zhao, Z.; Zheng, P.; Xu, S.; Wu, X. Object Detection with Deep Learning: A Review. arXiv 2018, arXiv:1807.05511. [Google Scholar] [CrossRef] [Green Version]
- Shima, R.; Yunan, H.; Fukuda, O.; Okumura, H.; Arai, K.; Bu, N. Object classification with deep convolutional neural network using spatial information. In Proceedings of the 2017 International Conference on Intelligent Informatics and Biomedical Sciences (ICIIBMS), Okinawa, Japan, 24–26 November 2017; pp. 135–139. [Google Scholar]
- Duong, N.; Kacete, A.; Soladie, C.; Richard, P.; Royan, J. Accurate Sparse Feature Regression Forest Learning for Real-Time Camera Relocalization. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 643–652. [Google Scholar] [CrossRef]
- Rambach, J.R.; Tewari, A.; Pagani, A.; Stricker, D. Learning to Fuse: A Deep Learning Approach to Visual-Inertial Camera Pose Estimation. In Proceedings of the 2016 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Merida, Mexico, 19–23 September 2016; pp. 71–76. [Google Scholar] [CrossRef]
- Lee, S.H.; Civera, J. Loosely-Coupled Semi-Direct Monocular SLAM. IEEE Robot. Autom. Lett. 2018, 4, 399–406. [Google Scholar] [CrossRef] [Green Version]
- Taketomi, T.; Uchiyama, H.; Ikeda, S. Visual SLAM algorithms: A survey from 2010 to 2016. IPSJ Trans. Comput. Vis. Appl. 2017, 9. [Google Scholar] [CrossRef]
- Kahlefendt, C. List of SLAM and Visual Odometry Algorithms. 2017. Available online: https://github.com/kafendt/List-of-SLAM-VO-algorithms/ (accessed on 24 May 2021).
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G2o: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3607–3613. [Google Scholar] [CrossRef]
- Civera, J.; Davison, A.J.; Montiel, J.M.M. Inverse Depth Parametrization for Monocular SLAM. IEEE Trans. Robot. 2008, 24, 932–945. [Google Scholar] [CrossRef] [Green Version]
- Glover, A.; Maddern, W.; Warren, M.; Reid, S.; Milford, M.; Wyeth, G. OpenFABMAP: An open source toolbox for appearance-based loop closure detection. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MI, USA, 14–18 May 2012; pp. 4730–4735. [Google Scholar] [CrossRef] [Green Version]
- Benhimane, S.; Malis, E. Real-time image-based tracking of planes using efficient second-order minimization. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 1, pp. 943–948. [Google Scholar] [CrossRef] [Green Version]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual-Inertial and Multi-Map SLAM. arXiv 2020, arXiv:2007.11898. [Google Scholar]
- Grupp, M. evo: Python Package for the Evaluation of Odometry and SLAM. 2017. Available online: https://github.com/MichaelGrupp/evo (accessed on 24 May 2021).
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A Benchmark for the Evaluation of RGB-D SLAM Systems. In Proceedings of the International Conference on Intelligent Robot Systems (IROS), Vilamoura, Algarve, Portugal, 7–12 October 2012. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for Autonomous Driving? The KITTI Vision Benchmark Suite. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Burri, M.; Nikolic, J.; Gohl, P.; Schneider, T.; Rehder, J.; Omari, S.; Achtelik, M.W.; Siegwart, R. The EuRoC micro aerial vehicle datasets. Int. J. Robot. Res. 2016, 35, 1157–1163. Available online: http://xxx.lanl.gov/abs/http://ijr.sagepub.com/content/early/2016/01/21/0278364915620033.full.pdf+html (accessed on 24 May 2021).
- Qian, Z.; Patath, K.; Fu, J.; Xiao, J. Semantic SLAM with Autonomous Object-Level Data Association. arXiv 2020, arXiv:2011.10625. [Google Scholar]

| Sequence System | ORBSLAM2 | LSD-SLAM | Fusion | LCSD |
|---|---|---|---|---|
| fr1/xyz | 0.12390 | 0.05949 | 0.01452 | 0.07423 |
| fr2/xyz | 0.09311 | 0.03560 | 0.063873 | 0.0111458 |
| 2_360_kidnap | 1.6157 | 1.66422 | 1.4376 | 1.58857 |
| 1_360 | 0.2089 | 0.20669 | 0.2028 | N/A |
| 1_desk | 0.047611 | 0.629381 | 0.04365 | 0.304522 |
| 1_desk2 | 0.7025 | 0.9130 | 0.89436 | 0.8298 |
| fr3_str_tex_far | 0.46528 | 0.46511 | 0.580506 | 0.488473 |
| fr3_str_tex_near | 0.01555 | 0.72177 | 0.16201 | 0.19618 |
| floor | 0.5121 | 0.7008 | 0.4334 | 1.0191 |
| Sequence System | ORBSLAM2 | LSD-SLAM | Fusion | LCSD |
|---|---|---|---|---|
| seq_00 | 37.8645 | 76.587 | 31.007 | 54.479 |
| seq_01 | 408.565 | 379.22 | 279.259 | 99.4138 |
| seq_02 | 305.26 | 305.425 | 303.352 | 284.359 |
| seq_03 | 152.68 | 169.73 | 152.68 | N/A |
| seq_04 | 112.781 | 112.973 | 109.136 | N/A |
| seq_05 | 27.6416 | 160.466 | 29.1424 | N/A |
| seq_06 | 35.42 | 137.64 | 35.42 | N/A |
| Sequence System | ORBSLAM2 | LSD-SLAM | Fusion | LCSD |
|---|---|---|---|---|
| mav1 | 0.053 | 4.162 | 0.071 | 4.157 |
| mav2 | 0.0325 | 4.232 | 0.4522 | 4.010 |
| mav3 | 0.0757 | 3.565 | 0.0469 | 3.496 |
| mav4 | 0.0661 | 6.781 | 0.1999 | 6.714 |
| mav5 | 0.0452 | 6.707 | 0.280 | 6.678 |
| mav6 | 0.08 | 1.699 | 0.08 | 1.76 |
| Max | Mean | Median | Min | RMSE | SSE | std | |
|---|---|---|---|---|---|---|---|
| FUSION | 0.0451 | 0.0101 | 0.0083 | 0.00048 | 0.0122 | 0.1194 | 0.0068 |
| LCSD | 0.2988 | 0.1222 | 0.1130 | 0.00243 | 0.1416 | 15.943 | 0.0715 |
| LSD-SLAM | 0.13568 | 0.0495 | 0.0462 | 0.00413 | 0.0562 | 2.5085 | 0.0266 |
| ORBSLAM2 | 0.40340 | 0.0552 | 0.0349 | 0.00685 | 0.0873 | 6.0390 | 0.0675 |
| System | Mean | std | 99% Upper Limit |
|---|---|---|---|
| Fusion | 0.0101 | 0.0068 | 0.0305 |
| LCSD | 0.1222 | 0.0715 | 0.3367 |
| LSD-SLAM | 0.0495 | 0.0266 | 0.1293 |
| ORBSLAM2 | 0.0552 | 0.0675 | 0.2577 |
| Scene | Fus. Median | Fus. Mean | Median | Mean | Adj. Median | Adj. Mean |
|---|---|---|---|---|---|---|
| fr1/xyzt | 0.0282 | 0.0290 | 0.0204 | 0.0227 | 0.0197 | 0.0299 |
| fr1/xyzf | 35.39 | 34.41 | 49.01 | 43.86 | 50.69 | 33.37 |
| seq_06t | 0.0277 | 0.0330 | 0.0274 | 0.0320 | 0.0274 | 0.0321 |
| seq_06f | 36.08 | 30.28 | 36.39 | 31.15 | 36.39 | 31.13 |
| mav1t | 0.0306 | 0.0336 | 0.0288 | 0.0309 | 0.02874 | 0.0311 |
| mav1f | 32.62 | 29.74 | 34.71 | 32.34 | 34.78 | 32.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Outahar, M.; Moreau, G.; Normand, J.-M. Direct and Indirect vSLAM Fusion for Augmented Reality. J. Imaging 2021, 7, 141. https://doi.org/10.3390/jimaging7080141
Outahar M, Moreau G, Normand J-M. Direct and Indirect vSLAM Fusion for Augmented Reality. Journal of Imaging. 2021; 7(8):141. https://doi.org/10.3390/jimaging7080141
Chicago/Turabian StyleOutahar, Mohamed, Guillaume Moreau, and Jean-Marie Normand. 2021. "Direct and Indirect vSLAM Fusion for Augmented Reality" Journal of Imaging 7, no. 8: 141. https://doi.org/10.3390/jimaging7080141
APA StyleOutahar, M., Moreau, G., & Normand, J.-M. (2021). Direct and Indirect vSLAM Fusion for Augmented Reality. Journal of Imaging, 7(8), 141. https://doi.org/10.3390/jimaging7080141