Performance Evaluation of Source Camera Attribution by Using Likelihood Ratio Methods
Abstract
:1. Introduction
2. Prnu-Based Source Camera Attribution
2.1. Peak-to-Correlation Energy
2.2. Extension to Videos
2.3. Reference PRNU Creation
- Using flat-field video recording to extract key-frame sensor noise and compute PRNU camera digital fingerprint according to (2). Still videos are used to limit the effect of motion stabilization. For the sake of simplicity, we name it RT1.
- Employing both flat-field images and flat-field videos [34] in order to lessen the impact of motion stabilization as well as the impact of video compression, which is typically stronger for video frames compared to images. We name this second type RT2.
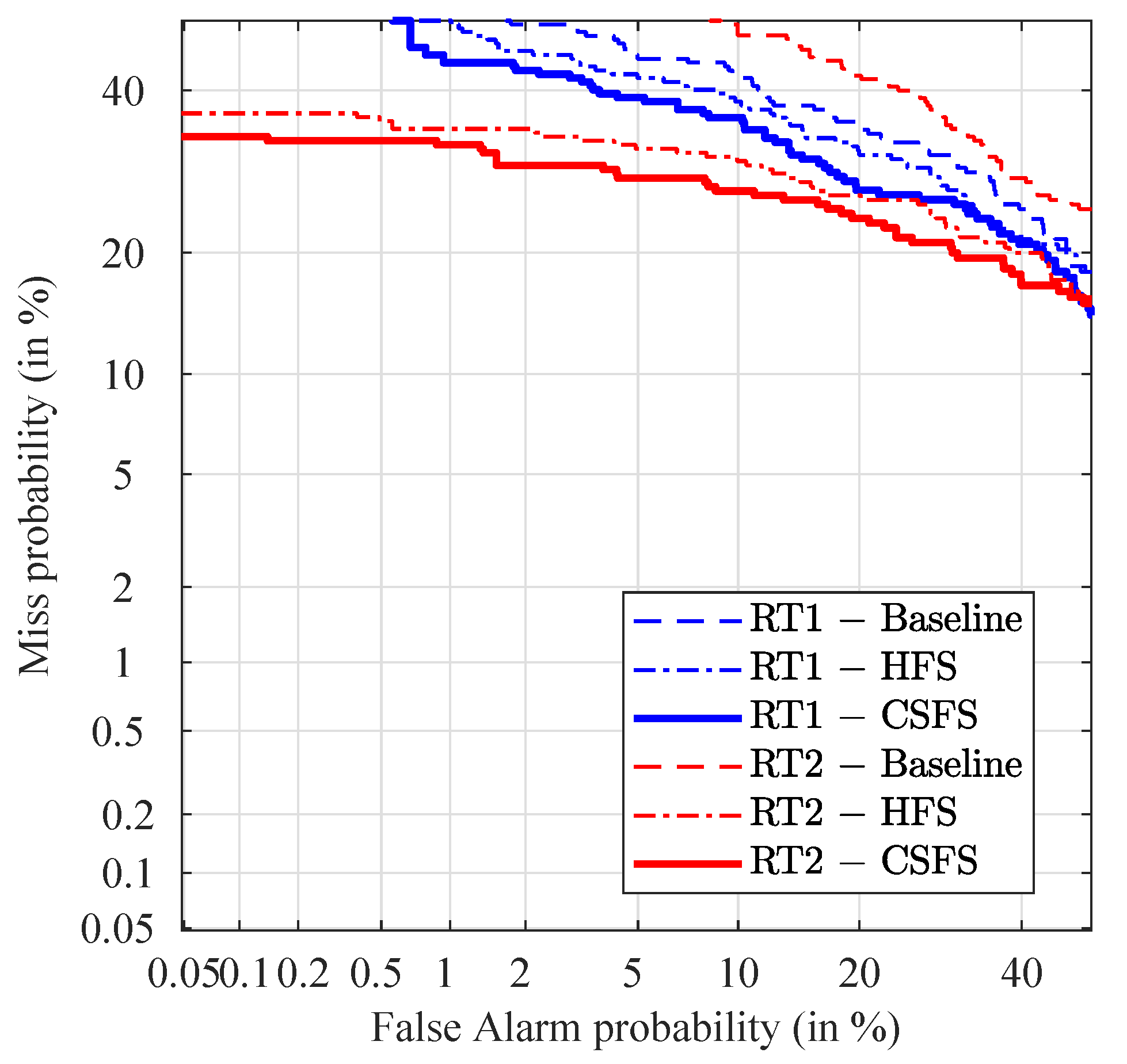
2.4. Similarity Scores
- (a)
- Baseline: PRNU is obtained by cumulating the noise patterns extracted frame-by-frame according to (2), and the PCE is computed.
- (b)
- Highest Frame Score (HFS): PRNU is extracted and compared frame-by-frame against the reference PRNU, and the maximum PCE is taken [30].
- (c)
- Cumulated Sorted Frames Score (CSFS): PRNUs, extracted from each frame and compared with the reference signal, are first sorted in a descending order according to their individual PCE values; then, they are progressively cumulated, according to (2); finally, the maximum of PCE values obtained at each cumulation step is taken [31].
3. Performance Evaluation
- (Prosecution): the Questioned Data (QD) comes from the camera C (mated trial).
- (Defense): the QD does not come from the camera C (non-mated trial).
3.1. Bayesian Interpretation Framework
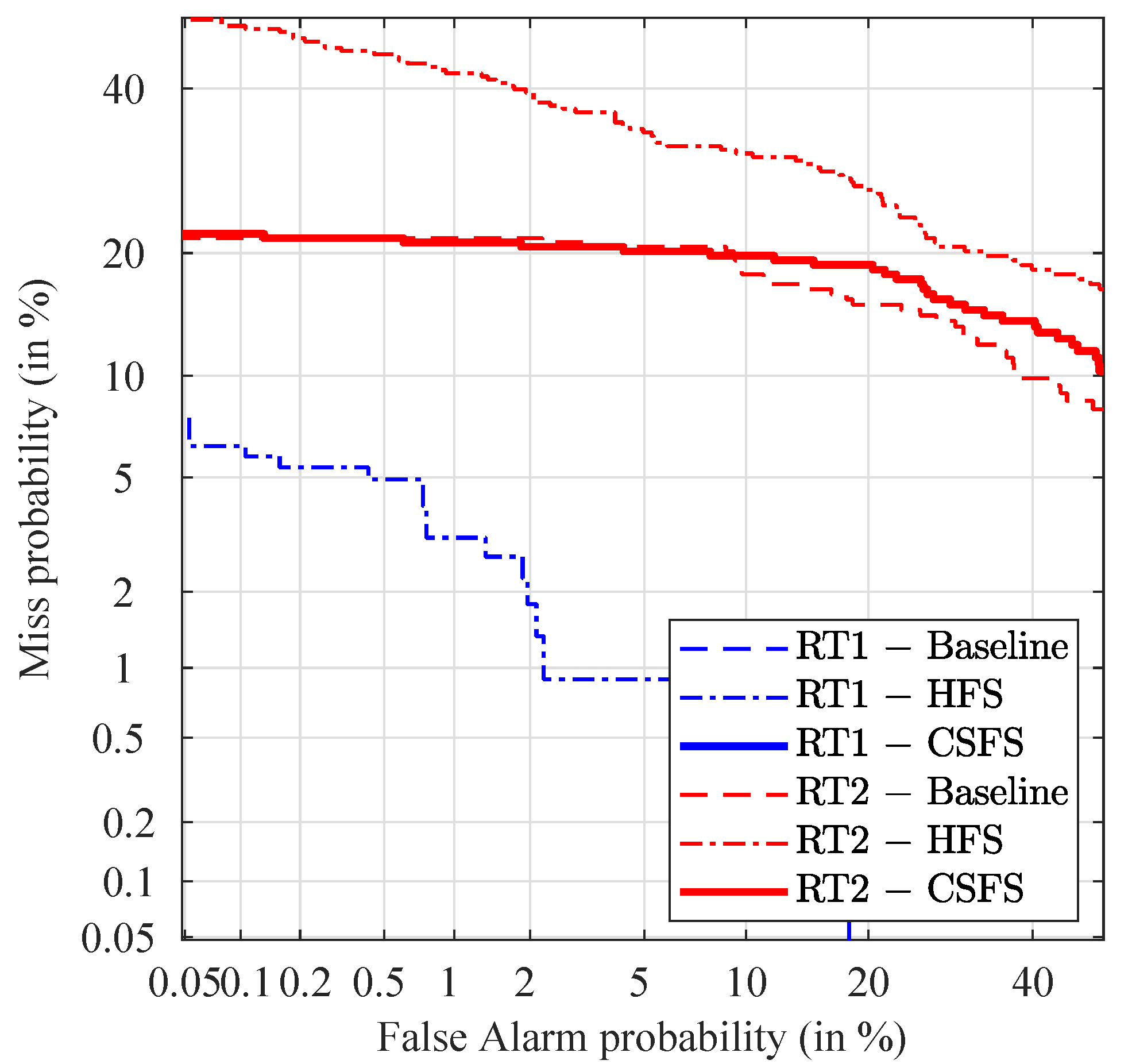
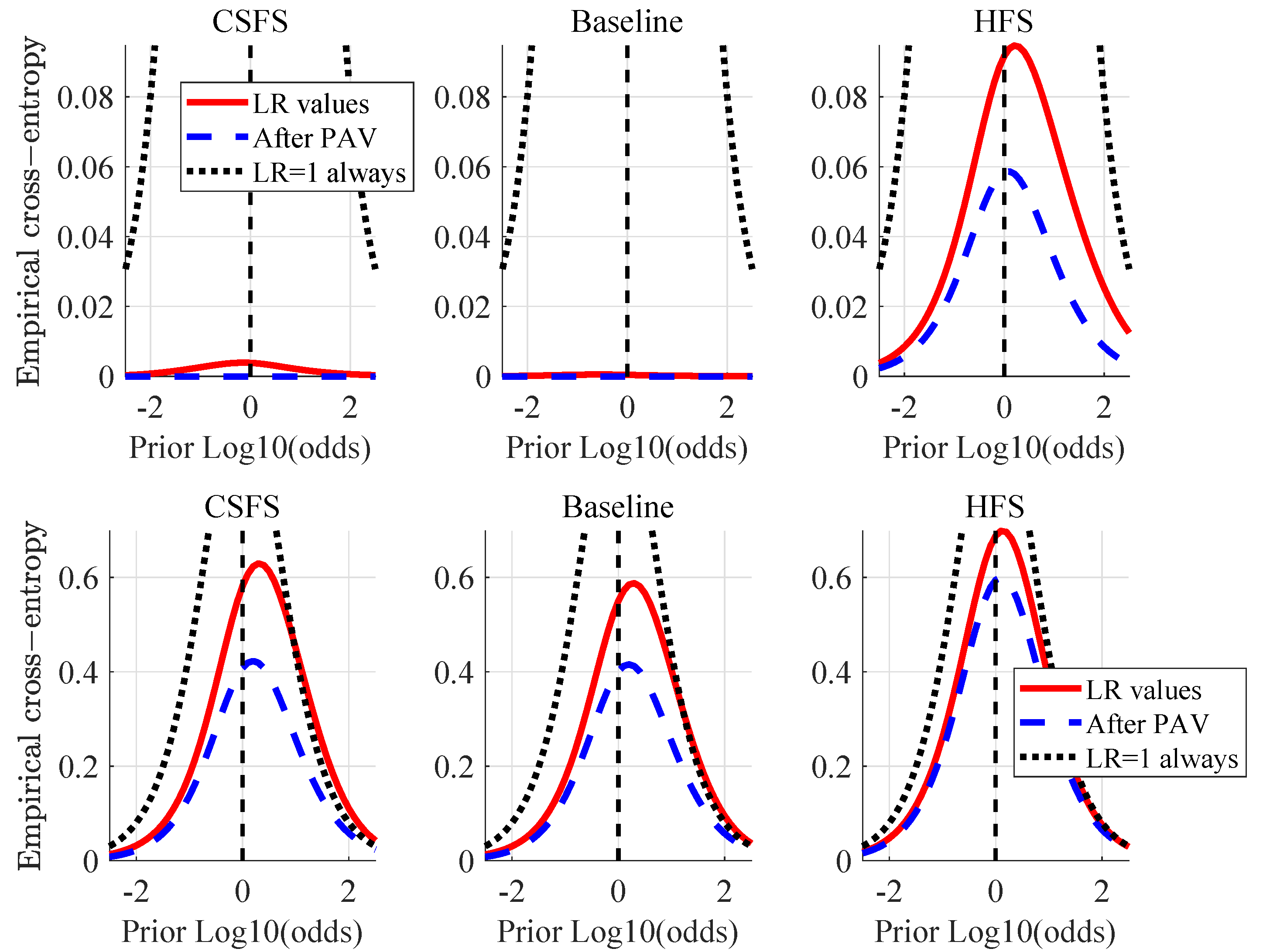
3.2. Performance Evaluation Tools
- accuracy, as sum of discriminating power and calibration, represented by the Empirical Cross Entropy (ECE) plot and measured by the log LR cost (CLLR) [37];
- discriminating power represented by the DET and plots and measured by the Equal Error Rate (EER) and [38];
- calibration represented by the Tippet and the ECE plots and measured by [37].
4. Experimental Protocol
4.1. Data Corpus
- A set of 30 randomly selected flat-field images, from which we extracted the image PRNU .
- A set of flat-field static (labelled as still) and moving (labeled as panrot and move) videos. These videos are used to create reference PRNU per device.
- A set of images with natural content that we used as query data. The set is composed of at least 200 pictures per devices.
- A set of non-flat query videos including still, pan-rotating and moving videos.
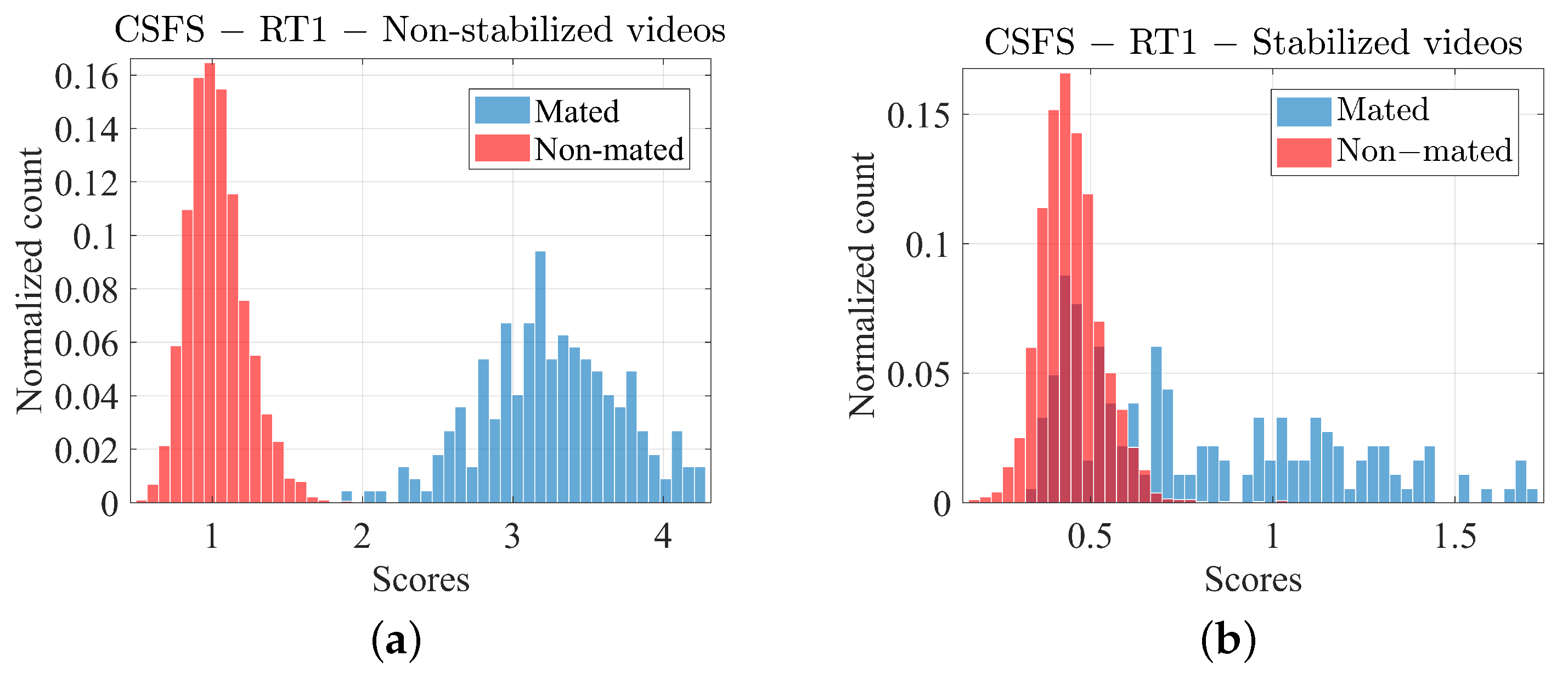
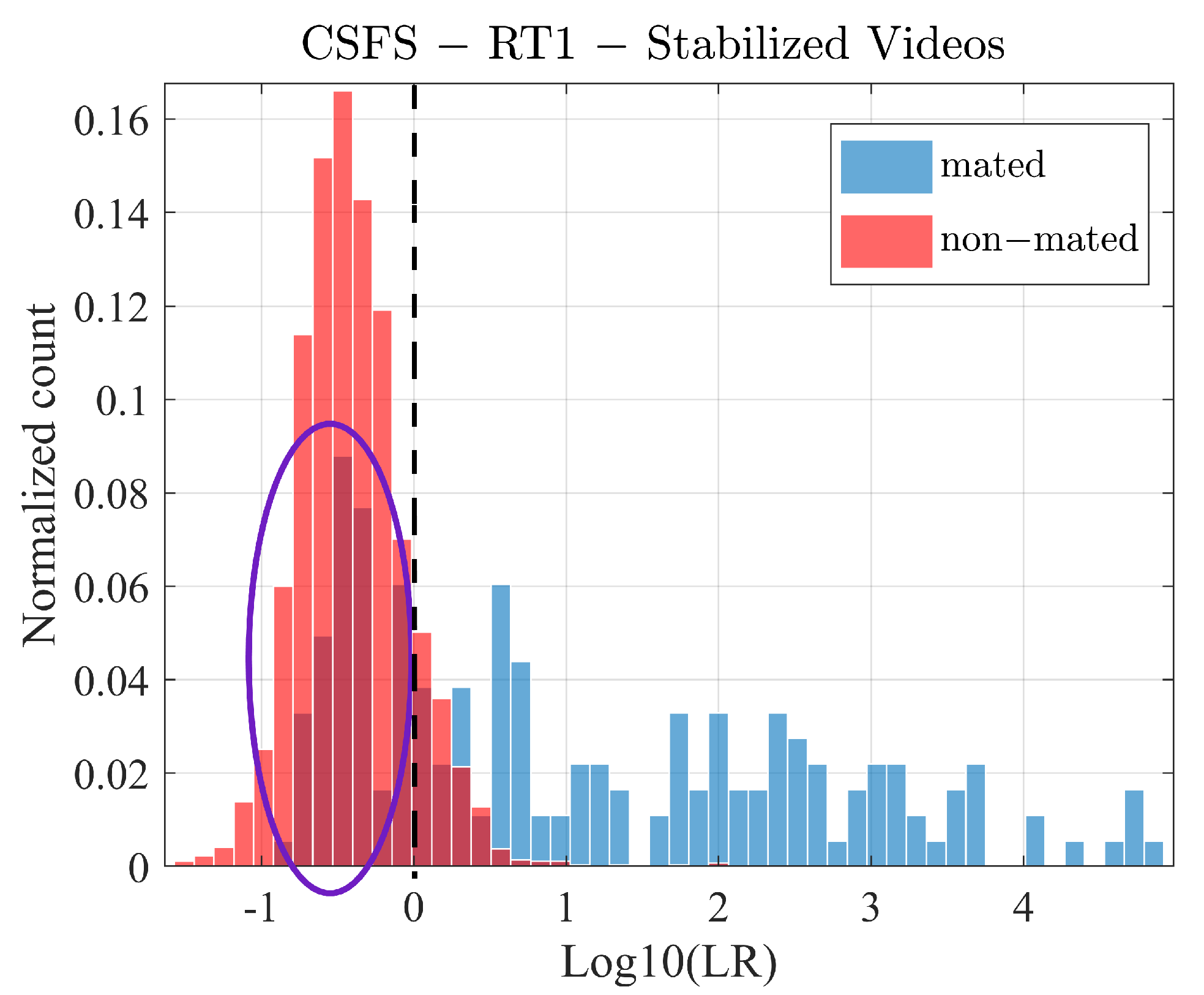
4.2. Preliminary Analysis of the Similarity Scores
4.3. Score to LR Calibration Transformation
4.3.1. Images
- Iterative use of leave-one-out cross validation for both mated and non-mated scores, where each of the left-out scores “plays” the role of the evidence;
- One-to-one mapping from probability to log-odds domain is performed using a logit function [37];
- Calibrated LRs are calculated iteratively for each evidence score.
4.3.2. Video Recordings
- Iterative use of leave-one-out cross-validation for mated and non-mated scores, where each of the left-out scores “plays” the role of the evidence;
- A normal distribution is fitted to the rest of the mated and non-mated scores;
- Calculation of the numerator and denominator of the LR for each left-out score;
- Calibrated LRs are calculated according to (6).
5. Performance Evaluation Results
5.1. Images
5.2. Non-Stabilized Video Recordings
5.3. Stabilized Videos
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PRNU | Photo Response Non-Uniformity |
| DMS | Digital Motion Stabilization |
| LR | Likelihood Ratio |
| ENFSI | European Network of Forensic Science Institutes |
| SPN | Sensor Pattern Noise |
| PCE | Peak-to-Correlation Energy |
| RT1 | Reference Type 1 |
| RT2 | Reference Type 2 |
| HFS | Highest Frame Score |
| CSFS | Cumulated Sorted Frame Score |
| QD | Questioned Data |
| ROC | Receiver Operating Characteristic |
| DET | Detection Error Trade-off |
| ECE | Empirical Cross Entropy |
| CLLR | Curves and Log LR (cost) |
| EER | Equal Error Rate |
References
- Casey, E. Standardization of forming and expressing preliminary evaluative opinions on digital evidence. Forensic Sci. Int. Digit. Investig. 2020, 32, 200888. [Google Scholar] [CrossRef]
- European Network of Forensic Science Institutes. Best Practice Manuals. Available online: http://enfsi.eu/documents/best-practice-manuals/ (accessed on 15 February 2021).
- European Network of Forensic Science Institutes—Forensic Information Technology Working Group. Best Practice Manual for the Forensic Examination of Digital Technology. Available online: https://enfsi.eu/wp-content/uploads/2016/09/1._forensic_examination_of_digital_technology_0.pdf (accessed on 15 February 2021).
- Lukas, J.; Fridrich, J.; Goljan, M. Digital camera identification from sensor pattern noise. IEEE Trans. Inf. Forensics Secur. 2006, 1, 205–214. [Google Scholar] [CrossRef]
- Li, C.T. Source camera identification using enhanced sensor pattern noise. IEEE Trans. Inf. Forensics Secur. 2010, 5, 280–287. [Google Scholar]
- Goljan, M.; Fridrich, J. Camera identification from cropped and scaled images. In Security, Forensics, Steganography, and Watermarking of Multimedia Contents X; SPIE: San Jose, CA, USA, 2008; Volume 6819, p. 68190E. [Google Scholar]
- Gonzalez-Rodriguez, J.; Fierrez-Aguilar, J.; Ramos-Castro, D.; Ortega-Garcia, J. Bayesian analysis of fingerprint, face and signature evidences with automatic biometric systems. Forensic Sci. Int. 2005, 155, 126–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Egli, N.; Champod, C.; Margot, P. Evidence evaluation in fingerprint comparison and automated fingerprint identification systems–modelling within finger variability. Forensic Sci. Int. 2007, 167, 189–195. [Google Scholar] [CrossRef]
- Hepler, A.B.; Saunders, C.P.; Davis, L.J.; Buscaglia, J. Score-based likelihood ratios for handwriting evidence. Forensic Sci. Int. 2012, 219, 129–140. [Google Scholar] [CrossRef]
- Champod, C.; Evett, I.; Kuchler, B. Earmarks as evidence: A critical review. J. Forensic Sci. 2001, 46, 1275–1284. [Google Scholar] [CrossRef]
- Meuwly, D. Forensic individualization from biometric data. Sci. Justice 2006, 46, 205–213. [Google Scholar] [CrossRef]
- Zadora, G.; Martyna, A.; Ramos, D.; Aitken, C. Statistical Analysis in Forensic Science: Evidential Values of Multivariate Physicochemical Data; John Wiley and Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Perlin, M.; Legler, M.; Spencer, C.; Smith, J.; Allan, W.; Belrose, J.; Duceman, B. Validating true allele DNA mixture interpretation. J. Forensic Sci. 2011, 56, 1430–1447. [Google Scholar] [CrossRef]
- Hoffman, K. Statistical evaluation of the evidential value of human hairs possibly coming from multiple sources. J. Forensic Sci. 1991, 36, 1053–1058. [Google Scholar] [CrossRef]
- Champod, C.; Baldwin, D.; Taroni, F.; Buckleton, S.J. Firearms and tool marks identification: The Bayesian approach. AFTE J. 2003, 35, 307–316. [Google Scholar]
- van Houten, W.; Alberink, I.; Geradts, Z. Implementation of the likelihood ratio framework for camera identification based on sensor noise patterns. Law Probab. Risk 2011, 10, 149–159. [Google Scholar] [CrossRef]
- Ramos, D. Forensic Evaluation of the Evidence Using Automatic Speaker Recognition Systems. Ph.D. Thesis, Escuela Politecnica Superior, Universidad Autonoma de Madrid, Madrid, Spain, 2007. [Google Scholar]
- Champod, C.; Taroni, F. Interpretation of Evidence: The Bayesian Approach; Taylor and Francis: London, UK, 1999; pp. 379–398. [Google Scholar]
- Haraksim, R. Validation of Likelihood Ratio Methods Used for Forensic Evidence Evaluation: Application in Forensic Fingerprints. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2014. [Google Scholar]
- Haraksim, R.; Ramos, D.; Meuwly, D. Validation of likelihood ratio methods for forensic evidence evaluation handling multimodal score distributions. IET Biom. 2016, 6, 61–69. [Google Scholar] [CrossRef] [Green Version]
- Meuwly, D.; Ramos, D.; Haraksim, R. A guideline for the validation of likelihood ratio methods used for forensic evidence evaluation. Forensic Sci. Int. 2017, 276, 142–153. [Google Scholar] [CrossRef]
- Ramos, D.; Haraksim, R.; Meuwly, D. Likelihood ratio data to report the validation of a forensic fingerprint evaluation method. Data Brief 2017, 10, 75–92. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramos, D.; Meuwly, D.; Haraksim, R.; Berger, C. Validation of Forensic Automatic Likelihood Ratio Methods. Chapman & Hall/CRC Handbooks of Modern Statistical Methods; In Handbook of Forensic Statistics; Banks, D., Kafadar, K., Kaye, D., Eds.; Chapman & Hall/CRC: Boca Raton, FL, USA, in press.
- European Commission. EU Security Union Strategy: Connecting the Dots in a New Security Ecosystem. Available online: https://ec.europa.eu/commission/presscorner/detail/en/ip_20_1379 (accessed on 15 September 2020).
- Chen, M.; Fridrich, J.; Goljan, M.; Lukáš, J. Source digital camcorder identification using sensor photo response non-uniformity. In Proceedings of the SPIE 6505, Security, Steganography, and Watermarking of Multimedia Contents IX, San Jose, CA, USA, 29 January–1 February 2007. [Google Scholar]
- van Houten, W.; Geradts, Z. Using sensor noise to identify low resolution compressed videos from YouTube. In Computational Forensics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 104–115. [Google Scholar]
- Chen, M.; Fridrich, J.; Goljan, M.; Lukáš, J. Determining image origin and integrity using sensor noise. IEEE Trans. Inf. Forensics Secur. 2008, 3, 74–90. [Google Scholar] [CrossRef] [Green Version]
- Goljan, M.; Fridrich, J.; Filler, T. Large scale test of sensor fingerprint camera identification. In Media Forensics and Security; SPIE: San Jose, CA, USA, 2009; Volume 7254, p. 72540I. [Google Scholar]
- Taspinar, S.; Mohanty, M.; Memon, N. Source camera attribution using stabilized video. In Proceedings of the IEEE International Workshop on Information Forensics and Security, Abu Dhabi, United Arab Emirates, 4–7 December 2016; pp. 1–6. [Google Scholar]
- Mandelli, S.; Bestagini, P.; Verdoliva, L.; Tubaro, S. Facing device attribution problem for stabilized video sequences. IEEE Trans. Inf. Forensics Secur. 2020, 15, 14–27. [Google Scholar] [CrossRef] [Green Version]
- Ferrara, P.; Beslay, L. Robust video source recognition in presence of motion stabilization. In Proceedings of the 8th IEEE International Workshop on Biometrics and Forensics, Porto, Portugal, 29–30 April 2020; pp. 1–6. [Google Scholar]
- Mandelli, S.; Argenti, F.; Bestagini, P.; Iuliani, M.; Piva, A.; Tubaro, S. A Modified Fourier-Mellin Approach For Source Device Identification On Stabilized Videos. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 1266–1270. [Google Scholar]
- Altinisik, E.; Sencar, H.T. Source Camera Verification for Strongly Stabilized Videos. IEEE Trans. Inf. Forensics Secur. 2021, 16, 643–657. [Google Scholar] [CrossRef]
- Iuliani, M.; Fontani, M.; Shullani, D.; Piva, A. Hybrid reference-based Video Source Identification. Sensors 2019, 19, 649. [Google Scholar] [CrossRef] [Green Version]
- Bellavia, F.; Iuliani, M.; Fanfani, M.; Colombo, C.; Piva, A. PRNU pattern alignment for images and videos based on scene content. In Proceedings of the IEEE International Conference on Image Processing, Taipei, Taiwan, 22–25 September 2019; pp. 91–95. [Google Scholar]
- Ommen, D.M.; Saunders, C.P. Building a unified statistical framework for the forensic identification of source problems. Law Probab. Risk 2018, 17, 179–197. [Google Scholar] [CrossRef] [Green Version]
- Brümmer, N.; du Preez, J. Application-independent evaluation of speaker detection. Comput. Speech Lang. 2006, 20, 230–275. [Google Scholar] [CrossRef]
- Meuwly, D. Reconnaissance de Locuteurs en Sciences Forensiques: L’apport d’une Approche Automatique. Ph.D. Thesis, Université de Lausanne, Lausanne, Switzerland, 2000. [Google Scholar]
- Shullani, D.; Fontani, M.; Iuliani, M.; Shaya, O.A.; Piva, A. VISION: A video and image dataset for source identification. EURASIP J. Inf. Secur. 2017, 2017, 15. [Google Scholar] [CrossRef]
- Morrison, G.; Poh, N. Avoiding overstating the strength of forensic evidence: Shrunk likelihood ratios/Bayes factors. Sci. Justice J. Forensic Sci. Soc. 2018, 58, 200–218. [Google Scholar] [CrossRef]
- Leadbetter, M.R.; Lindgren, G.; Rootzen, H. Extremes and Related Properties of Random Sequences and Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ramos, D.; Gonzalez-Rodriguez, J. Reliable support: Measuring calibration of likelihood ratios. Forensic Sci. Int. 2013, 230, 156–169. [Google Scholar] [CrossRef] [PubMed] [Green Version]









| # Mated Scores | # Non-Mated Scores | |
|---|---|---|
| Images | 7393 | 243,969 |
| Non-stabilized videos | 223 | 3791 |
| Stabilized videos | 190 | 2850 |
| Image Resolution | |||
|---|---|---|---|
| (%) EER | 5.984 | 11.83 | 12.83 |
| CLLR | 0.2798 | 0.3802 | 0.4428 |
| 0.1836 | 0.3127 | 0.3377 | |
| 0.09614 | 0.06744 | 0.1051 | |
| 7.074 | 14.12 | 14.27 | |
| 0.2049 | 1.347 | 5.24 | |
| RT1 | RT2 | |||||
|---|---|---|---|---|---|---|
| CSFS | Baseline | HFS | CSFS | Baseline | HFS | |
| (%) EER | 0.08 | 0.08 | 1.98 | 17.43 | 16.48 | 23.85 |
| CLLR | 0.004 | 0.003 | 0.092 | 0.58 | 0.55 | 0.69 |
| 0.003 | 0.003 | 0.062 | 0.41 | 0.4 | 0.59 | |
| 0.001 | 0 | 0.03 | 0.17 | 0.15 | 0.1 | |
| 0 | 0 | 1.34 | 21.07 | 21.5 | 36.77 | |
| 0.13 | 0 | 2.24 | 1.5 | 1.66 | 3.66 | |
| RT1 | RT2 | |||||
|---|---|---|---|---|---|---|
| CSFS | Baseline | HFS | CSFS | Baseline | HFS | |
| (%) EER | 26.46 | 30.85 | 28.64 | 22.7 | 33.5 | 25.86 |
| CLLR | 0.66 | 0.73 | 0.69 | 0.55 | 0.77 | 0.58 |
| 0.62 | 0.69 | 0.66 | 0.52 | 0.74 | 0.56 | |
| 0.04 | 0.04 | 0.03 | 0.03 | 0.03 | 0.04 | |
| 33.52 | 37.91 | 37.36 | 31.58 | 47.89 | 33.68 | |
| 12.37 | 15.07 | 10.9 | 1.47 | 12.35 | 2.49 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrara, P.; Haraksim, R.; Beslay, L. Performance Evaluation of Source Camera Attribution by Using Likelihood Ratio Methods. J. Imaging 2021, 7, 116. https://doi.org/10.3390/jimaging7070116
Ferrara P, Haraksim R, Beslay L. Performance Evaluation of Source Camera Attribution by Using Likelihood Ratio Methods. Journal of Imaging. 2021; 7(7):116. https://doi.org/10.3390/jimaging7070116
Chicago/Turabian StyleFerrara, Pasquale, Rudolf Haraksim, and Laurent Beslay. 2021. "Performance Evaluation of Source Camera Attribution by Using Likelihood Ratio Methods" Journal of Imaging 7, no. 7: 116. https://doi.org/10.3390/jimaging7070116
APA StyleFerrara, P., Haraksim, R., & Beslay, L. (2021). Performance Evaluation of Source Camera Attribution by Using Likelihood Ratio Methods. Journal of Imaging, 7(7), 116. https://doi.org/10.3390/jimaging7070116






