Restoration and Enhancement of Historical Stereo Photos †
Abstract
:1. Introduction
- With respect to SMR, the novel SMR+ is redesigned so as to better preserve finer details while at the same time improving further the restoration quality. This is accomplished by employing supersampling [25] at the image fusion step in conjunction with a weighting scheme guided by the original restoration approach.
- The recent state-of-the-art deep network BOPBtL [26], specifically designed for old photo restoration, is now included in the comparison, both as standalone and to serve as post-processing of SMR+.
- The collection of historical stereo photos employed as a dataset is roughly doubled to provide a more comprehensive evaluation.
- The use of renowned image quality assessment metrics is investigated and discussed for these kinds of applications.
Note: To ease the inspection and the comparison of the different images presented, an interactive PDF document is provided in the additional material (https://drive.google.com/drive/folders/1Fmsm50bMMDSd0z4JXOhCZ3hPDIXdwMUL) to allow readers to view each image at its full dimensions and quickly switch to the other images to be compared.
2. Proposed Method
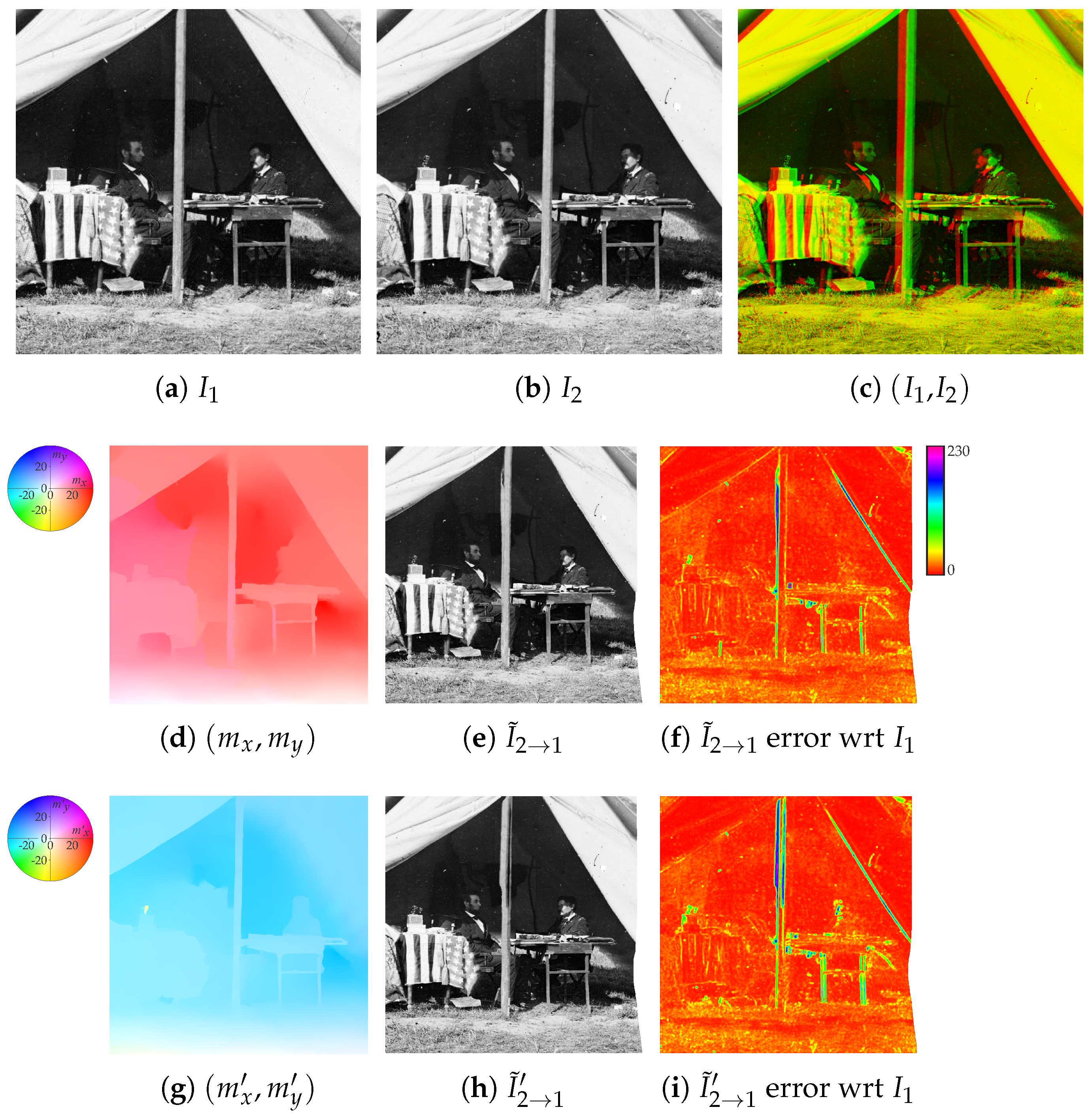
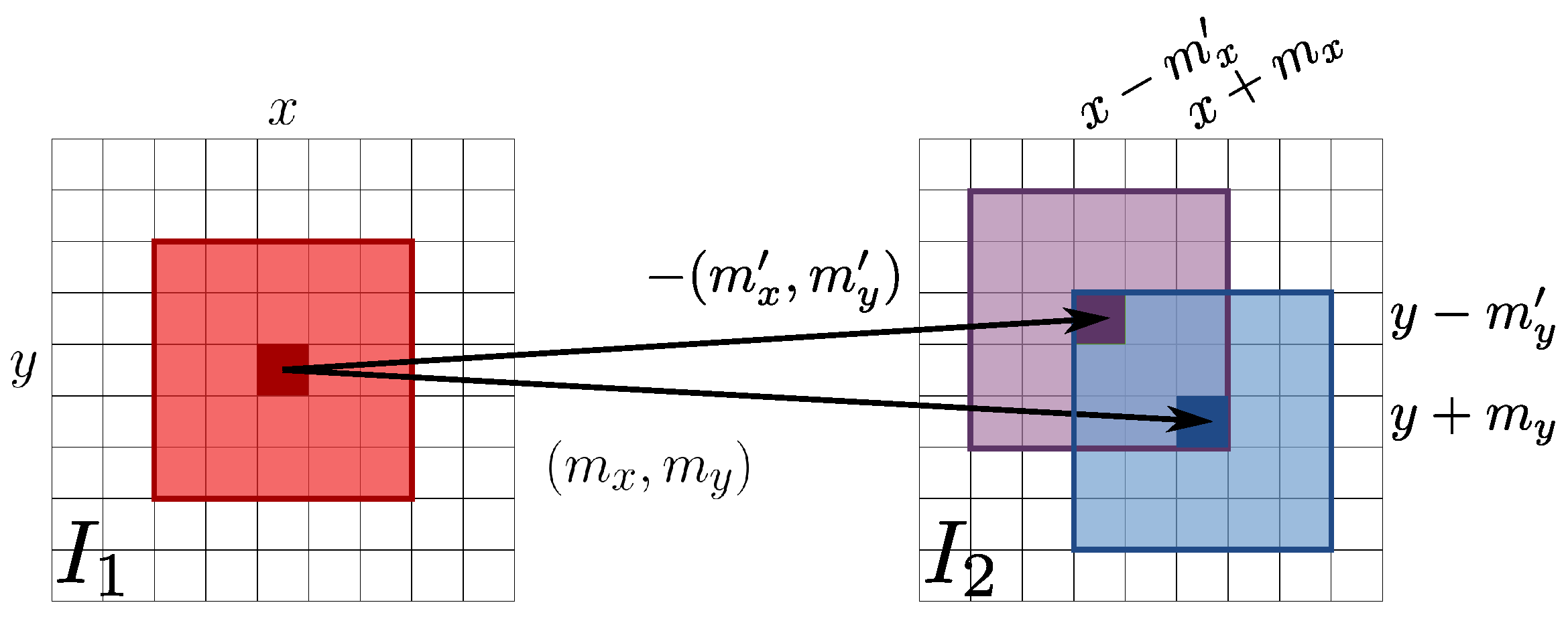
2.1. Auxiliary Image Pointwise Transfer
2.2. Color Correction
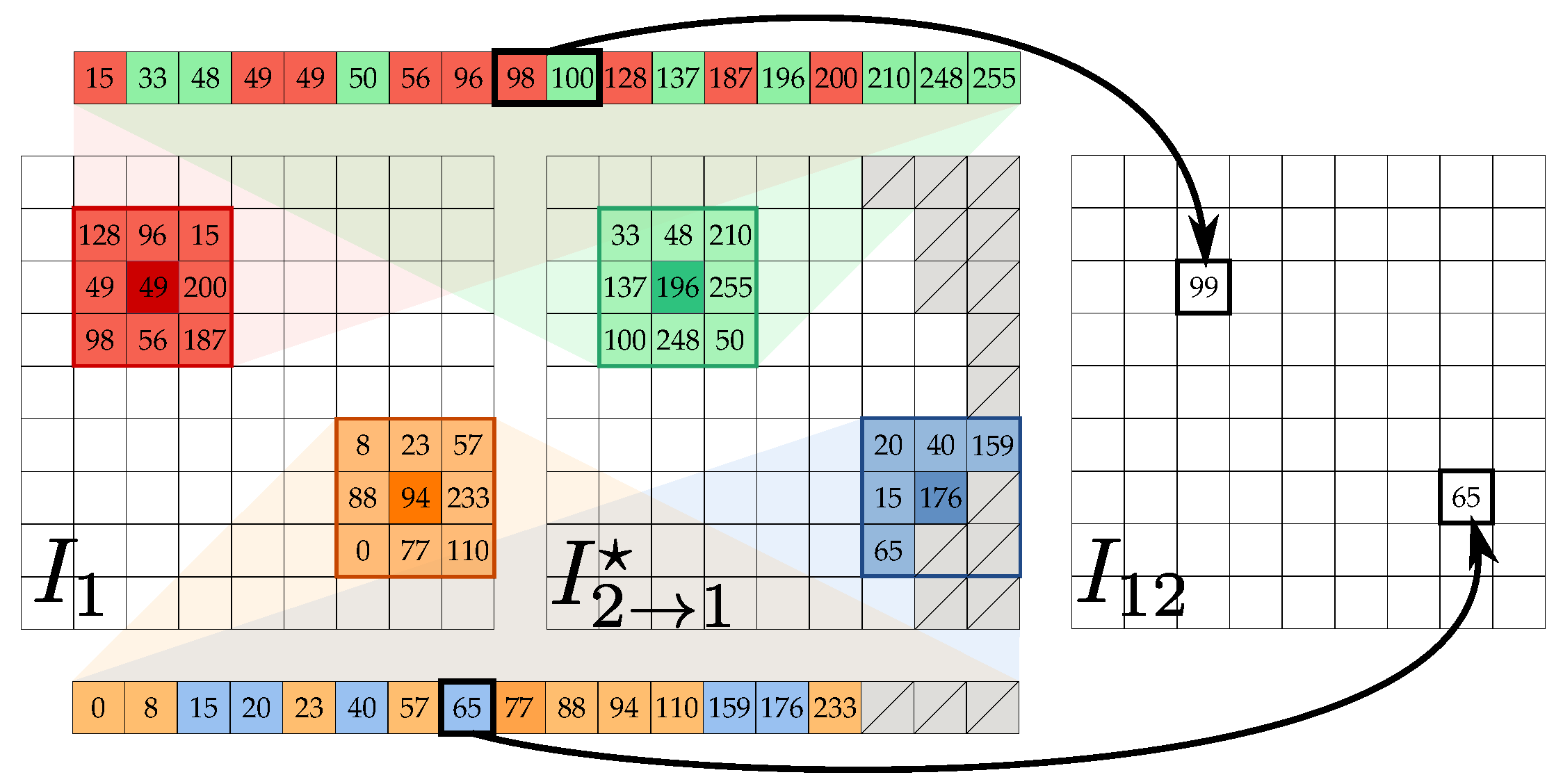
2.3. Data Fusion
2.4. Refinement
- Detection. A binary correction mask is computed by considering the error image the local window centered at each . Given as the subset of pixels with intensity values lower than the 66% percentile on , the pixel is marked as requiring adjustment if the square root of the average intensity value on is higher than (chosen experimentally). This results in a binary correction mask B that is smoothed with a Gaussian kernel and then binarized again by a threshold value of 0.5. As clear from Figure 6a, using the percentile-based subset is more robust than working with the whole window .
- Adjustment. Data fusion is repeated again after updating pixels on that need to be adjusted with the corresponding ones of . Since is a sort of average between and , the operation just described pushes marked pixels towards . At the end of this step, the gradient enhanced image is also updated accordingly and, in case of no further iterations, it constitutes the final output.
2.5. Guided Supersampling
3. Evaluation
3.1. Dataset
3.2. Compared Methods
3.3. Results
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ardizzone, E.; De Polo, A.; Dindo, H.; Mazzola, G.; Nanni, C. A Dual Taxonomy for Defects in Digitized Historical Photos. In Proceedings of the 10th International Conference on Document Analysis and Recognition, Barcelona, Spain, 26–29 July 2009; pp. 1166–1170. [Google Scholar]
- Kokaram, A.C. Motion Picture Restoration: Digital Algorithms for Artefact Suppression in Degraded Motion Picture Film and Video; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Tegolo, D.; Isgrò, F. A genetic algorithm for scratch removal in static images. In Proceedings of the International Conference on Image Analysis and Processing (ICIAP2001), Palermo, Italy, 26–28 September 2001; pp. 507–511. [Google Scholar]
- Stanco, F.; Tenze, L.; Ramponi, G. Virtual restoration of vintage photographic prints affected by foxing and water blotches. J. Electron. Imaging 2005, 14, 043008. [Google Scholar] [CrossRef]
- Besserer, B.; Thiré, C. Detection and Tracking Scheme for Line Scratch Removal in an Image Sequence. In Proceedings of the European Conference on Computer Vision (ECCV2004), Prague, Czech Republic, 11–14 May 2004; pp. 264–275. [Google Scholar]
- Criminisi, A.; Perez, P.; Toyama, K. Object removal by exemplar-based inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR2003), Madison, WI, USA, 16–22 June 2003; Volume 2. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Zhang, L.; Yu, H. External Patch Prior Guided Internal Clustering for Image Denoising. In Proceedings of the IEEE International Conference on Computer Vision (ICCV2015), Santiago, Chile, 7–13 December 2015; pp. 603–611. [Google Scholar]
- Buades, A.; Lisani, J.; Miladinović, M. Patch-Based Video Denoising With Optical Flow Estimation. IEEE Trans. Image Process. 2016, 25, 2573–2586. [Google Scholar] [CrossRef]
- Nasrollahi, K.; Moeslund, T.B. Super-resolution: A comprehensive survey. Mach. Vis. Appl. 2014, 25, 1423–1468. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Castellano, G.; Vessio, G. Deep learning approaches to pattern extraction and recognition in paintings and drawings: An overview. Neural Comput. Appl. 2021. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep Image Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR2018), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Wang, Z.; Chen, J.; Hoi, S.C.H. Deep Learning for Image Super-resolution: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 2480–2495. [Google Scholar] [CrossRef] [Green Version]
- Teed, Z.; Deng, J. RAFT: Recurrent All-Pairs Field Transforms for Optical Flow. In Proceedings of the European Conference on Computer Vision (ECCV2020, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Jeon, D.S.; Baek, S.; Choi, I.; Kim, M.H. Enhancing the Spatial Resolution of Stereo Images Using a Parallax Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR2018), Salt Lake City, UT, USA, 18–23 June 2018; pp. 1721–1730. [Google Scholar]
- Zhou, S.; Zhang, J.; Zuo, W.; Xie, H.; Pan, J.; Ren, J.S. DAVANet: Stereo Deblurring With View Aggregation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR2019), Long Beach, CA, USA, 16–20 June 2019; pp. 10988–10997. [Google Scholar]
- Yan, B.; Ma, C.; Bare, B.; Tan, W.; Hoi, S. Disparity-Aware Domain Adaptation in Stereo Image Restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR2020), Seattle, WA, USA, 14–18 June 2020; pp. 13176–13184. [Google Scholar]
- Schindler, G.; Dellaert, F. 4D Cities: Analyzing, Visualizing, and Interacting with Historical Urban Photo Collections. J. Multimed. 2012, 7, 124–131. [Google Scholar] [CrossRef] [Green Version]
- Fanfani, M.; Bellavia, F.; Bassetti, G.; Argenti, F.; Colombo, C. 3D Map Computation from Historical Stereo Photographs of Florence. IOP Conf. Ser. Mater. Sci. Eng. 2018, 364, 012044. [Google Scholar] [CrossRef]
- Luo, X.; Kong, Y.; Lawrence, J.; Martin-Brualla, R.; Seitz, S. KeystoneDepth: Visualizing History in 3D. arXiv 2019, arXiv:1908.07732. [Google Scholar]
- Fanfani, M.; Colombo, C.; Bellavia, F. Restoration and Enhancement of Historical Stereo Photos through Optical Flow. In Proceedings of the ICPR Workshop on Fine Art Pattern Extraction and Recognition (FAPER), Milan, Italy, 18 September 2021. [Google Scholar]
- McCann, J.J.; Rizzi, A. The Art and Science of HDR Imaging; John Wiley & Sons Inc.: Chichester, UK, 2011. [Google Scholar]
- Sherrod, A. Game Graphic Programming; Course Technology: Boston, MA, USA, 2008. [Google Scholar]
- Wan, Z.; Zhang, B.; Chen, D.; Zhang, P.; Chen, D.; Liao, J.; Wen, F. Bringing Old Photos Back to Life. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–18 June 2020. [Google Scholar]
- Chambon, S.; Crouzil, A. Similarity measures for image matching despite occlusions in stereo vision. Pattern Recognit. 2011, 44, 2063–2075. [Google Scholar] [CrossRef]
- Bellavia, F.; Colombo, C. Dissecting and Reassembling Color Correction Algorithms for Image Stitching. IEEE Trans. Image Process. 2018, 27, 735–748. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-Reference Image Quality Assessment in the Spatial Domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef] [PubMed]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “Completely Blind” Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Venkatanath, N.; Praneeth, D.; Chandrasekhar, B.; Channappayya, S.; Medasani, S. Blind image quality evaluation using perception based features. In Proceedings of the 21st National Conference on Communications (NCC), Mumbai, India, 27 February–1 March 2015; pp. 1–6. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]










| 0.00 | 0.05 | 0.11 | 0.16 | 0.21 | 0.26 | 0.32 | 0.37 | 0.42 | 0.47 | 0.53 | 0.58 | 0.63 | 0.68 | 0.74 | 0.79 | 0.84 | 0.89 | 0.95 | |
| 0.05 | 0.11 | 0.16 | 0.21 | 0.26 | 0.32 | 0.37 | 0.42 | 0.47 | 0.53 | 0.58 | 0.63 | 0.68 | 0.74 | 0.79 | 0.84 | 0.89 | 0.95 | 1.00 | |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| BM3D | DIP | SMR | SMR+ | BOPBtL | SMR+ BOPBtL | |||
|---|---|---|---|---|---|---|---|---|
| Figure 1 and Figure 9 | BRISQUE | 41.89 | 54.34 | 51.47 | 53.11 | 43.46 | 24.15 | 24.20 |
| NIQE | 4.23 | 5.31 | 5.31 | 5.09 | 3.98 | 4.09 | 4.24 | |
| PIQE | 45.97 | 78.93 | 85.33 | 50.60 | 46.35 | 22.55 | 25.90 | |
| Figure 10a | BRISQUE | 10.74 | 46.03 | 31.11 | 42.18 | 33.06 | 25.41 | 31.37 |
| NIQE | 2.79 | 3.83 | 3.94 | 3.28 | 3.76 | 4.05 | 4.08 | |
| PIQE | 25.02 | 79.24 | 81.50 | 43.32 | 28.09 | 38.50 | 35.35 | |
| Figure 10b | BRISQUE | 9.84 | 48.68 | 35.95 | 41.57 | 29.69 | 14.17 | 34.69 |
| NIQE | 3.16 | 4.07 | 3.92 | 2.92 | 3.34 | 3.65 | 4.01 | |
| PIQE | 29.73 | 78.53 | 78.16 | 37.26 | 23.61 | 29.98 | 34.31 | |
| Figure 10c | BRISQUE | 9.26 | 44.97 | 31.28 | 38.29 | 33.94 | 12.13 | 19.06 |
| NIQE | 2.79 | 4.22 | 4.11 | 3.47 | 4.04 | 5.43 | 5.31 | |
| PIQE | 15.80 | 60.33 | 53.28 | 42.81 | 23.02 | 20.30 | 20.00 | |
| Figure 10d | BRISQUE | 14.57 | 31.93 | 22.82 | 36.91 | 25.66 | 15.89 | 10.96 |
| NIQE | 2.61 | 3.11 | 3.72 | 3.49 | 3.65 | 3.97 | 3.62 | |
| PIQE | 9.31 | 43.23 | 52.66 | 38.28 | 24.24 | 10.48 | 11.76 | |
| Figure 10e | BRISQUE | 12.85 | 30.58 | 28.31 | 31.95 | 22.40 | 29.13 | 28.87 |
| NIQE | 2.17 | 2.26 | 3.30 | 3.13 | 2.92 | 4.05 | 3.97 | |
| PIQE | 27.52 | 42.54 | 45.40 | 40.00 | 24.43 | 14.67 | 16.92 | |
| Figure 11a | BRISQUE | 42.58 | 48.03 | 40.26 | 51.88 | 41.23 | 38.48 | 39.21 |
| NIQE | 3.80 | 4.77 | 4.97 | 4.66 | 3.93 | 4.57 | 4.75 | |
| PIQE | 26.39 | 74.37 | 79.44 | 45.89 | 36.91 | 13.28 | 14.60 | |
| Figure 11b | BRISQE | 39.15 | 49.22 | 53.80 | 45.41 | 40.85 | 14.75 | 17.74 |
| NIQE | 4.33 | 5.43 | 5.78 | 4.93 | 4.15 | 4.32 | 4.56 | |
| PIQE | 28.96 | 82.41 | 84.95 | 46.49 | 38.68 | 15.54 | 17.70 | |
| Figure 11c | BRISQE | 30.43 | 52.90 | 55.07 | 52.86 | 39.59 | 25.54 | 20.06 |
| NIQE | 3.13 | 5.22 | 5.53 | 4.25 | 3.20 | 4.59 | 4.36 | |
| PIQE | 17.20 | 85.95 | 88.53 | 43.98 | 30.33 | 25.39 | 27.83 | |
| Figure 11d | BRISQUE | 28.40 | 45.63 | 47.19 | 41.24 | 31.51 | 22.09 | 23.47 |
| NIQE | 2.11 | 4.17 | 6.28 | 3.89 | 2.85 | 3.49 | 3.85 | |
| PIQE | 31.65 | 72.88 | 94.84 | 48.02 | 36.64 | 20.68 | 22.81 | |
| Figure 11e | BRISQUE | 40.12 | 38.54 | 37.95 | 20.01 | 22.15 | 38.12 | 22.07 |
| NIQE | 6.27 | 3.49 | 4.08 | 2.84 | 3.06 | 4.60 | 4.42 | |
| PIQE | 58.45 | 51.79 | 48.00 | 19.77 | 13.28 | 13.35 | 11.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fanfani, M.; Colombo, C.; Bellavia, F. Restoration and Enhancement of Historical Stereo Photos. J. Imaging 2021, 7, 103. https://doi.org/10.3390/jimaging7070103
Fanfani M, Colombo C, Bellavia F. Restoration and Enhancement of Historical Stereo Photos. Journal of Imaging. 2021; 7(7):103. https://doi.org/10.3390/jimaging7070103
Chicago/Turabian StyleFanfani, Marco, Carlo Colombo, and Fabio Bellavia. 2021. "Restoration and Enhancement of Historical Stereo Photos" Journal of Imaging 7, no. 7: 103. https://doi.org/10.3390/jimaging7070103
APA StyleFanfani, M., Colombo, C., & Bellavia, F. (2021). Restoration and Enhancement of Historical Stereo Photos. Journal of Imaging, 7(7), 103. https://doi.org/10.3390/jimaging7070103







