Volumetric Semantic Instance Segmentation of the Plasma Membrane of HeLa Cells
Abstract
1. Introduction
2. Materials and Methods
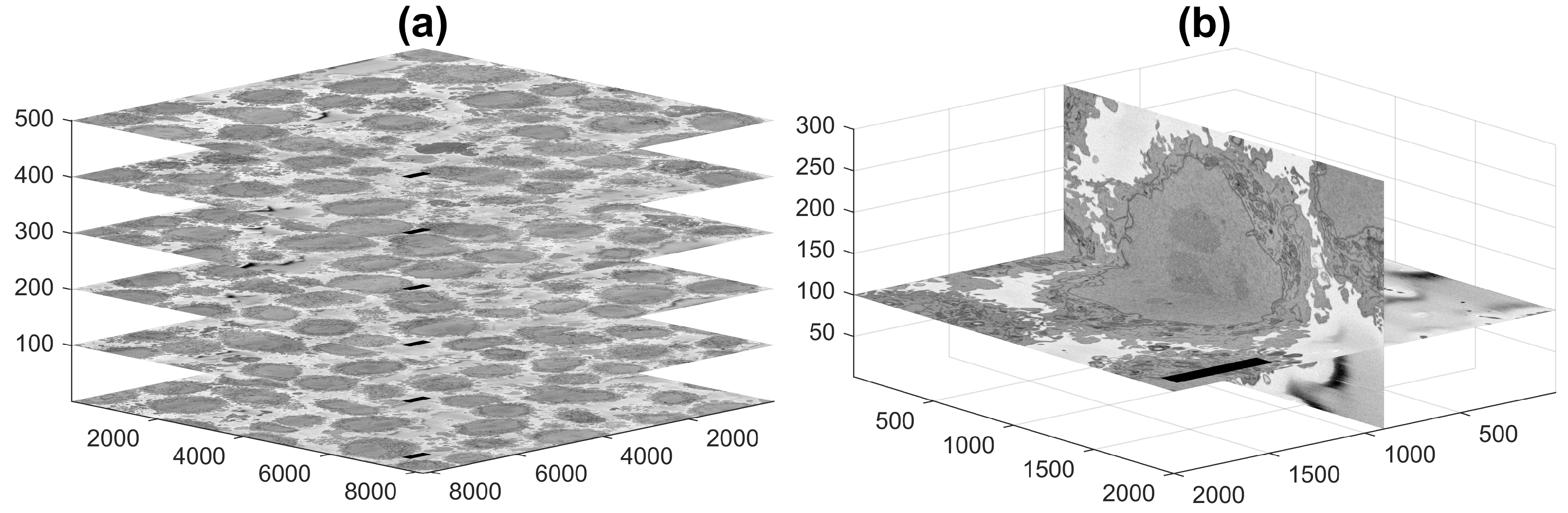
2.1. Cell Preparation and Acquisition
2.2. Segmentation of Background and Identification of Cells
2.3. Semantic Segmentation of the Nuclear Envelope
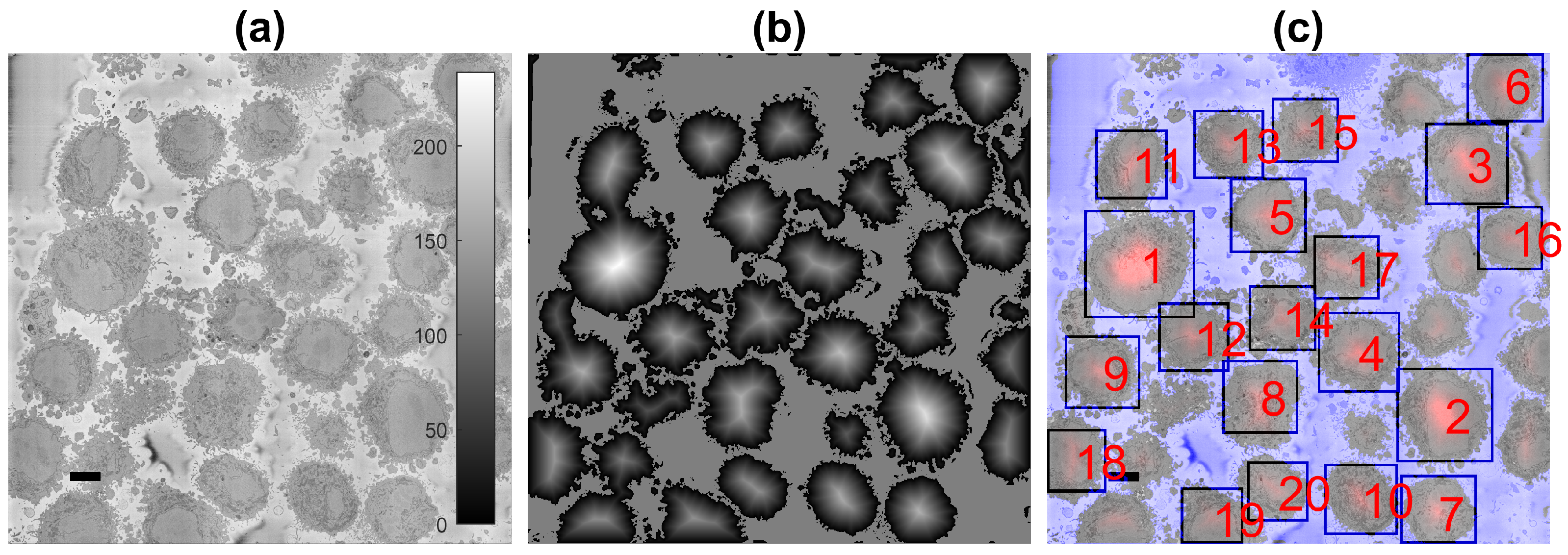
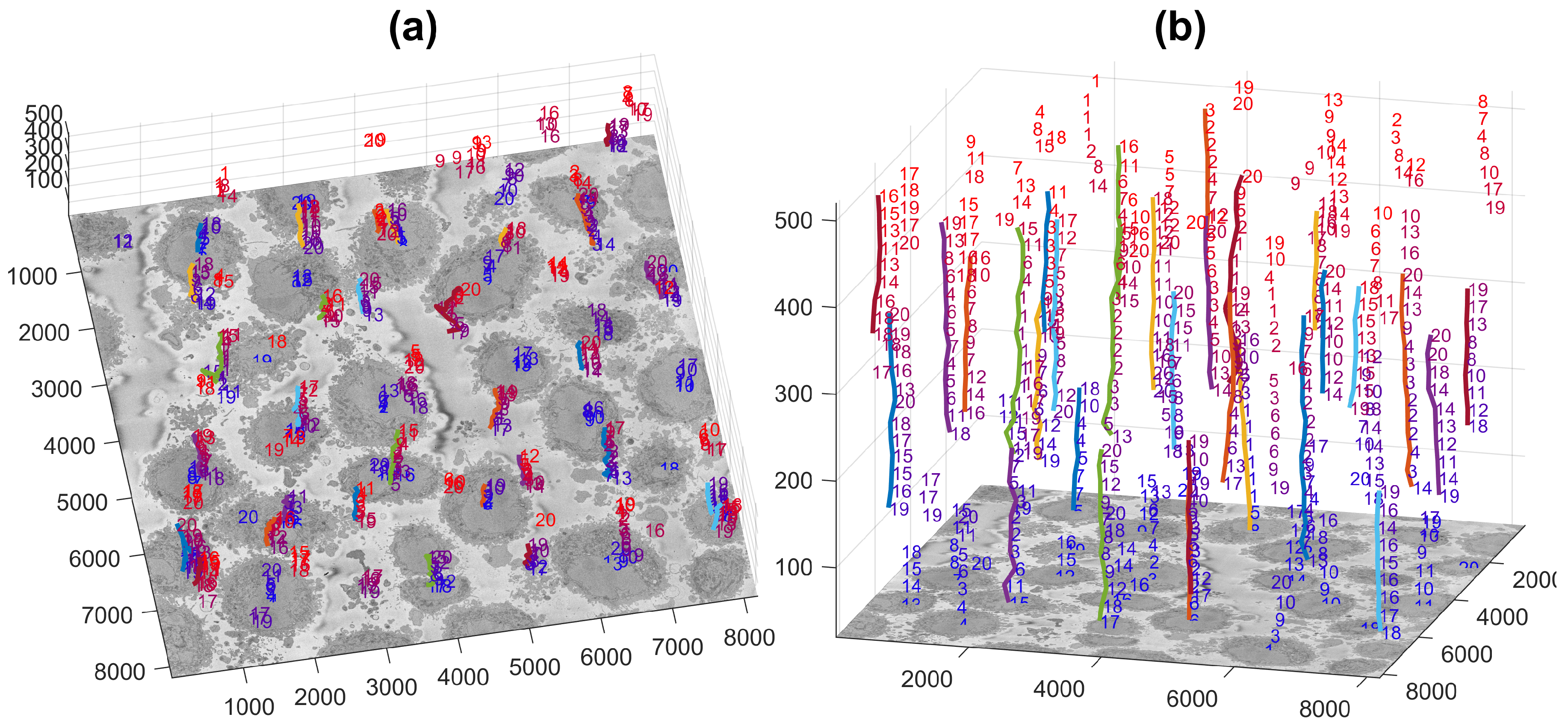
2.4. Semantic Segmentation of the Plasma Membrane of a Cell
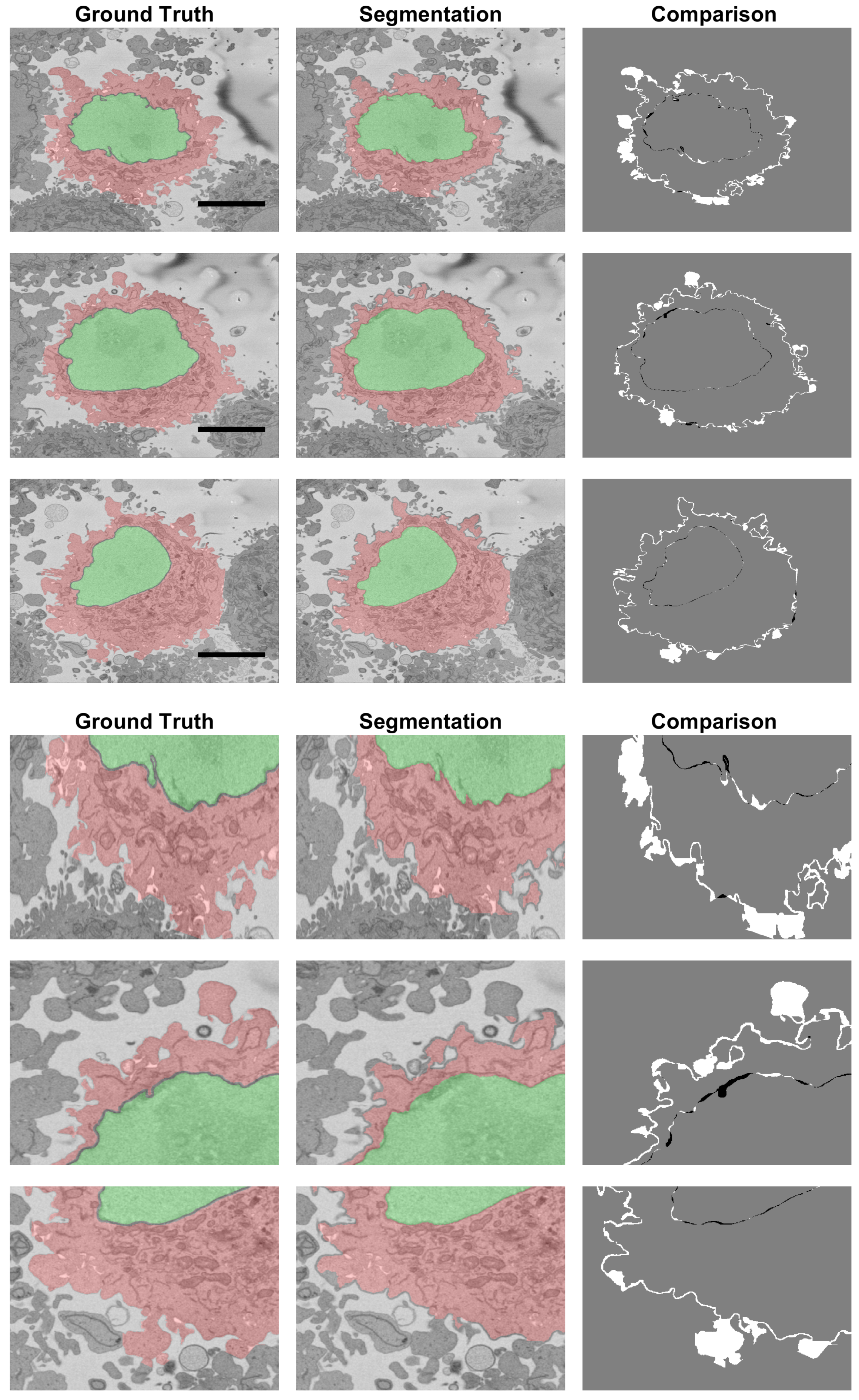
2.5. Quantitative Comparison
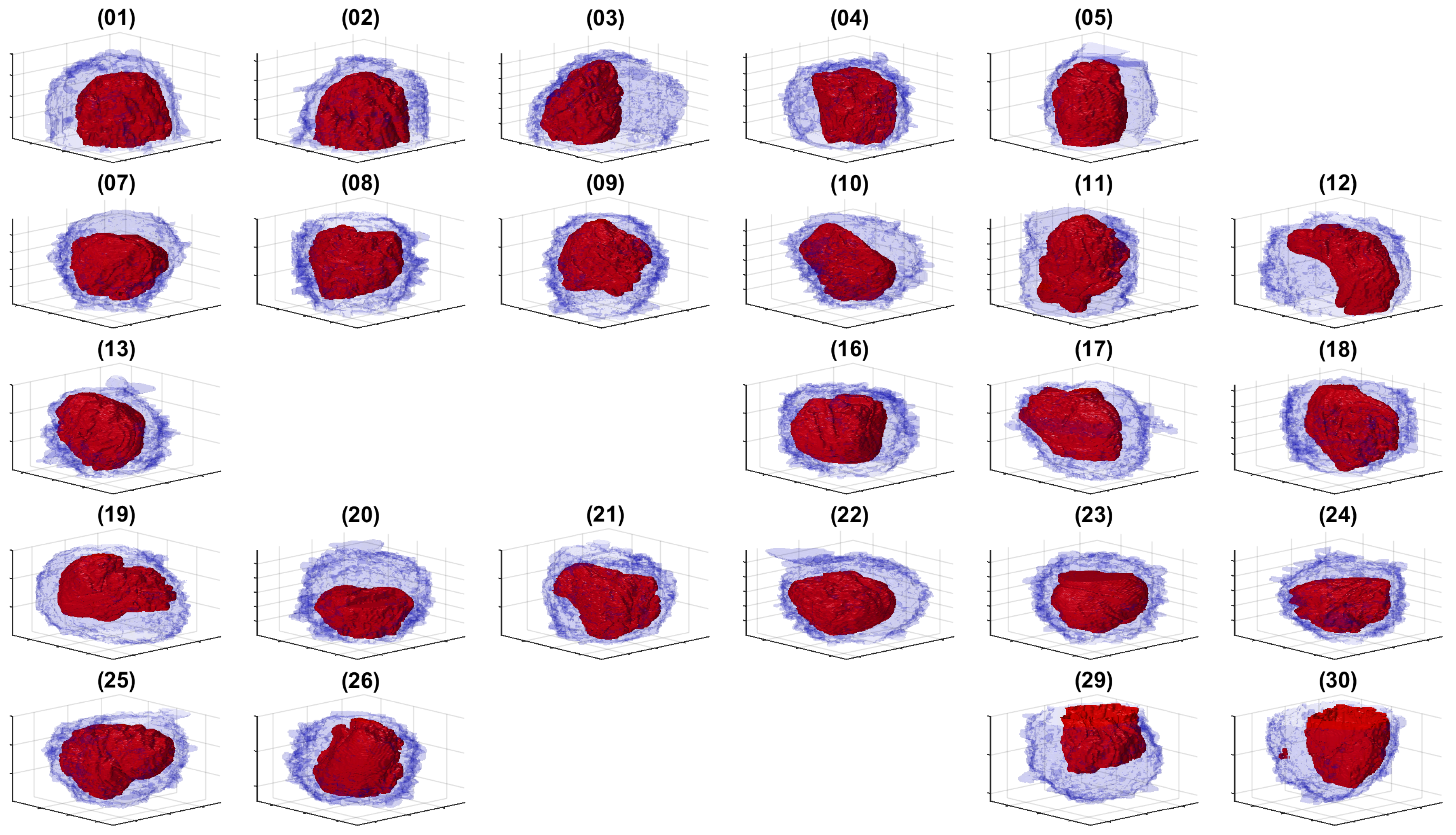
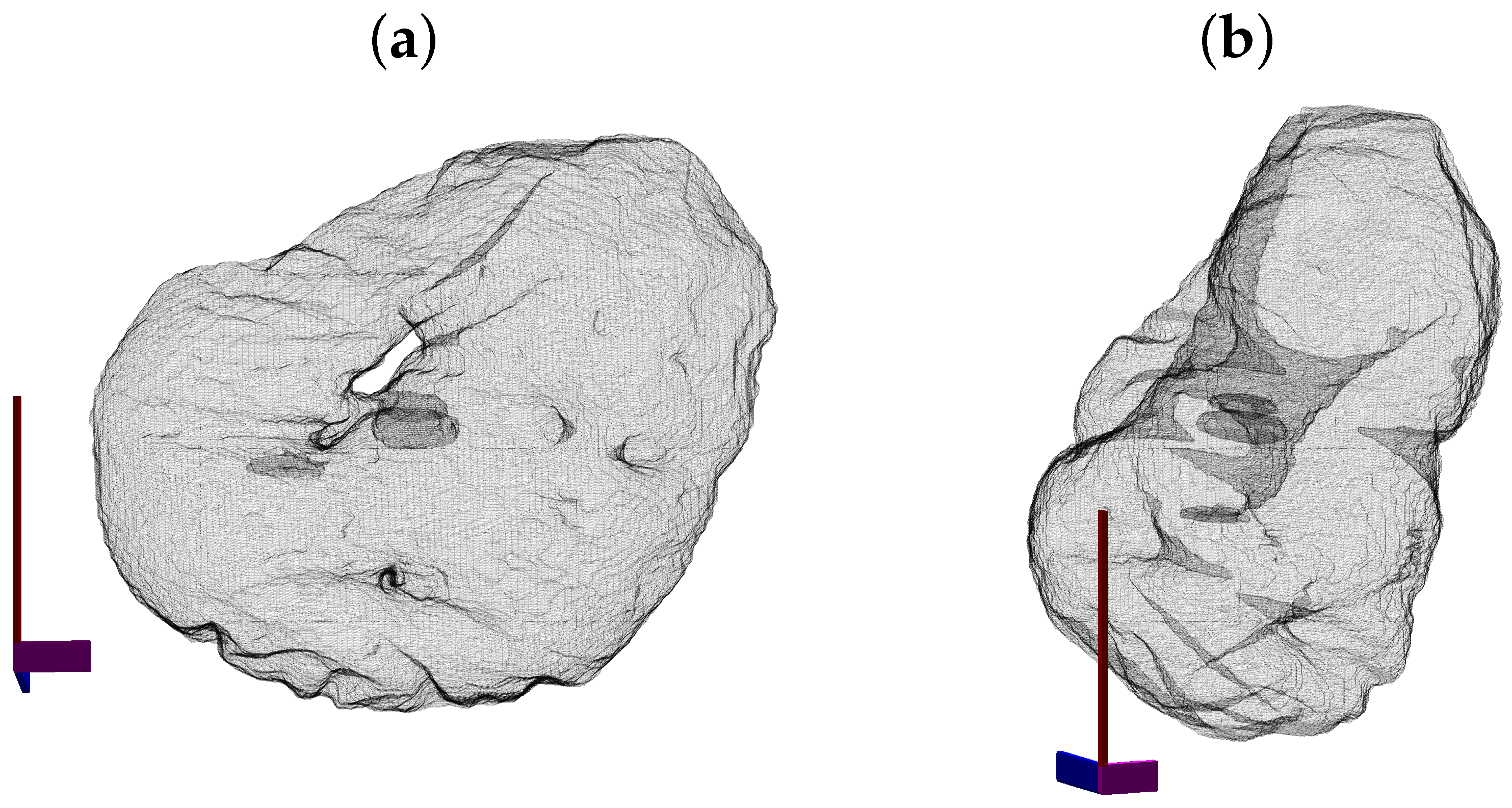
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Abbreviations
Abbreviations
Abbreviations
| EM | Electron Microscopy |
| ER | Endoplasmic Reticulum |
| TP | True Positive |
| TN | True Negative |
| FP | False Positive |
| FN | False Negative |
| GT | Ground Truth |
| AC | Accuracy |
| JI | Jaccard Index |
| NCMIR | National Centre for Microscopy and Imaging Research |
| CIL | Cell Image Library |
| NE | Nuclear Envelope |
| ROI | Region Of Interest |
| SBF SEM | Scanning Block Face Electron Microscopy |
| TIFF | Tagged Image File Format |
References
- Masters, J.R. HeLa cells 50 years on: The good, the bad and the ugly. Nat. Rev. Cancer 2002, 2, 315–319. [Google Scholar] [CrossRef]
- Chesebro, B.; Wehrly, K.; Metcalf, J.; Griffin, D.E. Use of a new CD4-positive HeLa cell clone for direct quantitation of infectious human immunodeficiency virus from blood cells of AIDS patients. J. Infect. Dis. 1991, 163, 64–70. [Google Scholar] [CrossRef]
- Bich-Loan, N.T.; Kien, K.T.; Thanh, N.L.; Kim-Thanh, N.T.; Huy, N.Q.; The-Hai, P.; Muller, M.; Nachtergael, A.; Duez, P.; Thang, N.D. Toxicity and Anti-Proliferative Properties of Anisomeles indica Ethanol Extract on Cervical Cancer HeLa Cells and Zebrafish Embryos. Life 2021, 11, 257. [Google Scholar] [CrossRef]
- Li, L.; Collins, N.D.; Widen, S.G.; Davis, E.H.; Kaiser, J.A.; White, M.M.; Greenberg, M.B.; Barrett, A.D.T.; Bourne, N.; Sarathy, V.V. Attenuation of Zika Virus by Passage in Human HeLa Cells. Vaccines 2019, 7, 93. [Google Scholar] [CrossRef]
- Kemet, S. Insight Medicine Lacks—The Continuing Relevance of Henrietta Lacks. N. Engl. J. Med. 2019, 381, 800–801. [Google Scholar] [CrossRef]
- Witze, A. Wealthy funder pays reparations for use of HeLa cells. Nature 2020, 587, 20–21. [Google Scholar] [CrossRef] [PubMed]
- Wolinetz, C.D.; Collins, F.S. Recognition of Research Participants’ Need for Autonomy: Remembering the Legacy of Henrietta Lacks. JAMA 2020, 324, 1027–1028. [Google Scholar] [CrossRef]
- Beskow, L.M. Lessons from HeLa Cells: The Ethics and Policy of Biospecimens. Annu. Rev. Genom. Hum. Genet. 2016, 17, 395–417. [Google Scholar] [CrossRef]
- Ribatti, D. An historical note on the cell theory. Exp. Cell Res. 2018, 364, 1–4. [Google Scholar] [CrossRef]
- Peddie, C.; Collinson, L. Exploring the third dimension: Volume electron microscopy comes of age. Micron 2014, 61, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Denk, W.; Horstmann, H. Serial block-face scanning electron microscopy to reconstruct three-dimensional tissue nanostructure. PLoS Biol. 2004, 2, e329. [Google Scholar] [CrossRef] [PubMed]
- Nagle, J.F.; Tristram-Nagle, S. Structure of lipid bilayers. Biochim. Biophys. Acta 2000, 1469, 159–195. [Google Scholar] [CrossRef]
- De Magistris, P.; Antonin, W. The Dynamic Nature of the Nuclear Envelope. Curr. Biol. CB 2018, 28, R487–R497. [Google Scholar] [CrossRef] [PubMed]
- Kwok, R. Cell biology: The new cell anatomy. Nat. News 2011, 480, 26. [Google Scholar] [CrossRef][Green Version]
- Amadoruge, P.C.; Barnham, K.J. Alzheimer’s disease and metals: A review of the involvement of cellular membrane receptors in metallosignalling. Int. J. Alzheimer’s Dis. 2011, 2011, 542043. [Google Scholar] [CrossRef]
- Stiller, C.; Viktorsson, K.; Paz Gomero, E.; Haag, P.; Arapi, V.; Kaminskyy, V.O.; Kamali, C.; De Petris, L.; Ekman, S.; Lewensohn, R.; et al. Detection of Tumor-Associated Membrane Receptors on Extracellular Vesicles from Non-Small Cell Lung Cancer Patients via Immuno-PCR. Cancers 2021, 13, 922. [Google Scholar] [CrossRef]
- Cabrera-Andrade, A.; López-Cortés, A.; Muñoz, M.J.; Jaramillo-Koupermann, G.; Rodriguez, O.; Leone, P.E.; Paz-y Miño, C. Association of genetic variants of membrane receptors related to recognition and induction of immune response with Helicobacter pylori infection in Ecuadorian individuals. Int. J. Immunogenet. 2014, 41, 281–288. [Google Scholar] [CrossRef]
- Fairbanks, G.; Patel, V.P.; Dino, J.E. Biochemistry of ATP-dependent red cell membrane shape change. Scand. J. Clin. Lab. Investig. Suppl. 1981, 156, 139–144. [Google Scholar] [CrossRef]
- Alhanaty, E.; Sheetz, M.P. Cell membrane shape control–effects of chloromethyl ketone peptides. Blood 1984, 63, 1203–1208. [Google Scholar] [CrossRef]
- Alimohamadi, H.; Smith, A.S.; Nowak, R.B.; Fowler, V.M.; Rangamani, P. Non-uniform distribution of myosin-mediated forces governs red blood cell membrane curvature through tension modulation. PLoS Comput. Biol. 2020, 16, e1007890. [Google Scholar] [CrossRef]
- Sakamoto, K.; Morishita, T.; Aburai, K.; Ito, D.; Imura, T.; Sakai, K.; Abe, M.; Nakase, I.; Futaki, S.; Sakai, H. Direct entry of cell-penetrating peptide can be controlled by maneuvering the membrane curvature. Sci. Rep. 2021, 11, 31. [Google Scholar] [CrossRef] [PubMed]
- Weber, G.; Bianciardi, G.; Toti, P. Circulating platelets plasma-membrane of normocholesterolemic and hypercholesterolemic rabbits tested with aspirin: A freeze etching study of the platelet plasma-membrane “protuberances”. Pharmacol. Res. Commun. 1980, 12, 49–55. [Google Scholar] [CrossRef]
- Hennig, T.; O’Hare, P. Viruses and the nuclear envelope. Curr. Opin. Cell Biol. 2015, 34, 113–121. [Google Scholar] [CrossRef] [PubMed]
- Chow, K.H.; Factor, R.E.; Ullman, K.S. The nuclear envelope environment and its cancer connections. Nat. Rev. Cancer 2012, 12, 196. [Google Scholar] [CrossRef]
- Bkaily, G.; Avedanian, L.; Al-Khoury, J.; Provost, C.; Nader, M.; D’Orléans-Juste, P.; Jacques, D. Nuclear membrane receptors for ET-1 in cardiovascular function. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2011, 300, R251–R263. [Google Scholar] [CrossRef] [PubMed]
- Hogeboom, G.H.; Schneider, W.C. On the Nuclear Envelope. Science 1953, 118, 419. [Google Scholar] [CrossRef]
- Gall, J.G. Observations on the nuclear membrane with the electron microscope. Exp. Cell Res. 1954, 7, 197–200. [Google Scholar] [CrossRef]
- Candia, J.; Maunu, R.; Driscoll, M.; Biancotto, A.; Dagur, P.; McCoy, J.P.; Sen, H.N.; Wei, L.; Maritan, A.; Cao, K.; et al. From Cellular Characteristics to Disease Diagnosis: Uncovering Phenotypes with Supercells. PLoS Comput. Biol. 2013, 9, e1003215. [Google Scholar] [CrossRef]
- Candia, J.; Banavar, J.R.; Losert, W. Understanding health and disease with multidimensional single-cell methods. J. Phys. Condens. Matter Inst. Phys. J. 2014, 26, 073102. [Google Scholar] [CrossRef]
- Zhao, J. Cell individuality: A basic multicellular phenomenon and its role in the pathogenesis of disease. Med. Hypotheses 1995, 44, 400–402. [Google Scholar] [CrossRef]
- Zhao, J. A liability theory of disease: The foundation of cell population pathology. Med. Hypotheses 1997, 48, 341–346. [Google Scholar] [CrossRef]
- Orrenius, S. Apoptosis: Molecular mechanisms and implications for human disease. J. Intern. Med. 1995, 237, 529–536. [Google Scholar] [CrossRef]
- Prame Kumar, K.; Nicholls, A.J.; Wong, C.H.Y. Partners in crime: Neutrophils and monocytes/macrophages in inflammation and disease. Cell Tissue Res. 2018, 371, 551–565. [Google Scholar] [CrossRef]
- Lombard, J. Once upon a time the cell membranes: 175 years of cell boundary research. Biol. Direct 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Haralick, R.M.; Shapiro, L.G. Computer and Robot Vision, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1992. [Google Scholar]
- Taghanaki, S.A.; Abhishek, K.; Cohen, J.P.; Cohen-Adad, J.; Hamarneh, G. Deep semantic segmentation of natural and medical images: A review. Artif. Intell. Rev. 2021, 54, 137–178. [Google Scholar] [CrossRef]
- Romera-Paredes, B.; Torr, P.H.S. Recurrent Instance Segmentation; European Conference on Computer Vision; Springer: Berlin, Germany, 2016; pp. 312–329. [Google Scholar]
- Vincent, L.; Soille, P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 583–598. [Google Scholar] [CrossRef]
- Cousty, J.; Bertrand, G.; Najman, L.; Couprie, M. Watershed cuts: Thinnings, shortest path forests, and topological watersheds. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 925–939. [Google Scholar] [CrossRef]
- Gamarra, M.; Zurek, E.; Escalante, H.J.; Hurtado, L.; San-Juan-Vergara, H. Split and merge watershed: A two-step method for cell segmentation in fluorescence microscopy images. Biomed. Signal Process. Control 2019, 53, 101575. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Lindeberg, T. Edge Detection and Ridge Detection with Automatic Scale Selection. Int. J. Comput. Vis. 1998, 30, 117–156. [Google Scholar] [CrossRef]
- Ren, X.; Malik, J. Proceeings of the Learning a classification model for segmentation. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 1, pp. 10–17. [Google Scholar] [CrossRef]
- Stutz, D.; Hermans, A.; Leibe, B. Superpixels: An evaluation of the state-of-the-art. Comput. Vis. Image Underst. 2018, 166, 1–27. [Google Scholar] [CrossRef]
- Albayrak, A.; Bilgin, G. Automatic cell segmentation in histopathological images via two-staged superpixel-based algorithms. Med. Biol. Eng. Comput. 2019, 57, 653–665. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Ciecholewski, M.; Spodnik, J.H. Semi–Automatic Corpus Callosum Segmentation and 3D Visualization Using Active Contour Methods. Symmetry 2018, 10, 589. [Google Scholar] [CrossRef]
- Song, T.H.; Sanchez, V.; EIDaly, H.; Rajpoot, N.M. Dual-Channel Active Contour Model for Megakaryocytic Cell Segmentation in Bone Marrow Trephine Histology Images. IEEE Trans. Biomed. Eng. 2017, 64, 2913–2923. [Google Scholar] [CrossRef]
- Pal, N.R.; Pal, S.K. A review on image segmentation techniques. Pattern Recognit. 1993, 26, 1277–1294. [Google Scholar] [CrossRef]
- Pham, D.L.; Xu, C.; Prince, J.L. Current methods in medical image segmentation. Annu. Rev. Biomed. Eng. 2000, 2, 315–337. [Google Scholar] [CrossRef]
- Meijering, E. Cell Segmentation: 50 Years Down the Road [Life Sciences]. IEEE Signal Process. Mag. 2012, 29, 140–145. [Google Scholar] [CrossRef]
- Perez, A.; Seyedhosseini, M.; Deerinck, T.; Bushong, E.; Panda, S.; Tasdizen, T.; Ellisman, M. A workflow for the automatic segmentation of organelles in electron microscopy image stacks. Front. Neuroanat. 2014, 8, 126. [Google Scholar] [CrossRef] [PubMed]
- Wilke, S.; Antonios, J.; Bushong, E.; Badkoobehi, A.; Malek, E.; Hwang, M. Deconstructing complexity: Serial block-face electron microscopic analysis of the hippocampal mossy fiber synapse. J. Neurosci. 2013, 33, 507–522. [Google Scholar] [CrossRef] [PubMed]
- Bohorquez, D.; Samsa, L.; Roholt, A.; Medicetty, S.; Chandra, R.; Liddle, R. An enteroendocrine cell-enteric glia connection revealed by 3D electron microscopy. PLoS ONE 2014, 9, e89881. [Google Scholar] [CrossRef]
- Ørting, S.N.; Doyle, A.; Hilten, A.V.; Hirth, M.; Inel, O.; Madan, C.R.; Mavridis, P.; Spiers, H.; Cheplygina, V. A Survey of Crowdsourcing in Medical Image Analysis. Hum. Comput. 2020, 7, 1–26. [Google Scholar] [CrossRef]
- Schnoor, J. Citizen science. Environ. Sci. Technol. 2007, 41, 5923. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Spiers, H.; Songhurst, H.; Nightingale, L.; de Folter, J.; Community, Z.V.; Hutchings, R.; Peddie, C.J.; Weston, A.; Strange, A.; Hindmarsh, S.; et al. Deep learning for automatic segmentation of the nuclear envelope in electron microscopy data, trained with volunteer segmentations. Traffic 2021. [Google Scholar] [CrossRef]
- Cireşan, D.C.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J. Mitosis detection in breast cancer histology images with deep neural networks. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI); Springer: Berlin, Germany, 2013; pp. 411–418. [Google Scholar]
- Urakubo, H.; Bullmann, T.; Kubota, Y.; Oba, S.; Ishii, S. UNI-EM: An Environment for Deep Neural Network-Based Automated Segmentation of Neuronal Electron Microscopic Images. bioRxiv 2019, 607366. Available online: https://www.nature.com/articles/s41598-019-55431-0 (accessed on 30 May 2021). [CrossRef] [PubMed]
- Liu, J.; Li, W.; Xiao, C.; Hong, B.; Xie, Q.; Han, H. Automatic Detection and Segmentation of Mitochondria from SEM Images using Deep Neural Network. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 628–631. [Google Scholar]
- Dorkenwald, S.; Schubert, P.J.; Killinger, M.F.; Urban, G.; Mikula, S.; Svara, F.; Kornfeld, J. Automated synaptic connectivity inference for volume electron microscopy. Nat. Methods 2017, 14, 435. [Google Scholar] [CrossRef]
- Konishi, K.; Mimura, M.; Nonaka, T.; Sase, I.; Nishioka, H.; Suga, M. Practical method of cell segmentation in electron microscope image stack using deep convolutional neural network. Microscopy 2019, 68, 338–341. [Google Scholar] [CrossRef]
- Domart, M.C.; Hobday, T.M.C.; Peddie, C.J.; Chung, G.H.C.; Wang, A.; Yeh, K.; Jethwa, N.; Zhang, Q.; Wakelam, M.J.O.; Woscholski, R.; et al. Acute Manipulation of Diacylglycerol Reveals Roles in Nuclear Envelope Assembly & Endoplasmic Reticulum Morphology. PLoS ONE 2012, 7, e51150. [Google Scholar] [CrossRef]
- Grove, J.; Metcalf, D.J.; Knight, A.E.; Wavre-Shapton, S.T.; Sun, T.; Protonotarios, E.D.; Griffin, L.D.; Lippincott-Schwartz, J.; Marsh, M. Flat clathrin lattices: Stable features of the plasma membrane. Mol. Biol. Cell 2014, 25, 3581–3594. [Google Scholar] [CrossRef]
- Mageswaran, S.K.; Yang, W.Y.; Chakrabarty, Y.; Oikonomou, C.M.; Jensen, G.J. A cryo–electron tomography workflow reveals protrusion-mediated shedding on injured plasma membrane. Sci. Adv. 2021, 7, eabc6345. [Google Scholar] [CrossRef]
- Fernández de Castro, I.; Tenorio, R.; Ortega-González, P.; Knowlton, J.J.; Zamora, P.F.; Lee, C.H.; Fernández, J.J.; Dermody, T.S.; Risco, C. A modified lysosomal organelle mediates nonlytic egress of reovirus. J. Cell Biol. 2020, 219. [Google Scholar] [CrossRef]
- Mbogba, M.K.; Haider, Z.; Hossain, S.M.C.; Huang, D.; Memon, K.; Panhwar, F.; Lei, Z.; Zhao, G. The application of convolution neural network based cell segmentation during cryopreservation. Cryobiology 2018, 85, 95–104. [Google Scholar] [CrossRef] [PubMed]
- Machado, S.; Mercier, V.; Chiaruttini, N. LimeSeg: A coarse-grained lipid membrane simulation for 3D image segmentation. BMC Bioinform. 2019, 20, 2. [Google Scholar] [CrossRef] [PubMed]
- Karabağ, C.; Jones, M.L.; Peddie, C.J.; Weston, A.E.; Collinson, L.M.; Reyes-Aldasoro, C.C. Segmentation and Modelling of the Nuclear Envelope of HeLa Cells Imaged with Serial Block Face Scanning Electron Microscopy. J. Imaging 2019, 5, 75. [Google Scholar] [CrossRef]
- Caicedo, J.C.; Roth, J.; Goodman, A.; Becker, T.; Karhohs, K.W.; McQuin, C.; Singh, S.; Carpenter, A.E. Evaulation of Deep Learning Strategies for Nucleus Segmentation in Fluorescence Images. IEEE Rev. Biomed. Eng. 2018, 2, 147–171. [Google Scholar]
- Quan, T.M.; Hildebrand, D.G.C.; Jeong, W. FusionNet: A deep fully residual convolutional neural network for image segmentation in connectomics. CoRR 2016. abs/1612.05360. Available online: http://xxx.lanl.gov/abs/1612.05360 (accessed on 30 May 2021).
- Dinggang Shen, G.W.; Suk, H.I. Deep Learning in Medical Image Analysis. Annu. Rev. Biomed. Eng. 2017, 19, 221–248. [Google Scholar] [CrossRef] [PubMed]
- Antropova, N.; Huynh, B.Q.; Giger, M.L. A deep feature fusion methodology for breast cancer diagnosis demonstrated on three imaging modality datasets. Med. Phys. 2017, 44, 5162–5171. [Google Scholar] [CrossRef]
- Gulshan, V.; Peng, L.; Coram, M.; Stumpe, M.C.; Wu, D.; Narayanaswamy, A.; Venugopalan, S.; Widner, K.; Madams, T.; Cuadros, J.; et al. Development and Validation of a Deep Learning Algorithm for Detection of Diabetic Retinopathy in Retinal Fundus Photographs. JAMA 2016, 316, 2402–2410. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Wu, Y.; Lin, T.; Li, S.; Chen, B. Quantification of full left ventricular metrics via deep regression learning with contour-guidance. IEEE Access 2019, 7, 47918–47928. [Google Scholar] [CrossRef]
- Bosch, C.; Ackels, T.; Pacureanu, A.; Zhang, Y.; Peddie, C.J.; Berning, M.; Rzepka, N.; Zdora, M.C.; Whiteley, I.; Storm, M.; et al. Functional and multiscale 3D structural investigation of brain tissue through correlative in vivo physiology, synchrotron micro-tomography and volume electron microscopy. bioRxiv 2021. [Google Scholar] [CrossRef]
- Heinrich, L.; Bennett, D.; Ackerman, D.; Park, W.; Bogovic, J.; Eckstein, N.; Petruncio, A.; Clements, J.; Xu, C.S.; Funke, J.; et al. Automatic whole cell organelle segmentation in volumetric electron microscopy. bioRxiv 2020. [Google Scholar] [CrossRef]
- Conrad, R.; Narayan, K. CEM500K, a large-scale heterogeneous unlabeled cellular electron microscopy image dataset for deep learning. Elife 2021, 10, e65894. [Google Scholar] [CrossRef] [PubMed]
- Karabağ, C.; Jones, M.L.; Peddie, C.J.; Weston, A.E.; Collinson, L.M.; Reyes-Aldasoro, C.C. Semantic segmentation of HeLa cells: An objective comparison between one traditional algorithm and four deep-learning architectures. PLoS ONE 2020, 15, e0230605. [Google Scholar] [CrossRef]
- Deerinck, T.J.; Bushong, E.; Thor, A.; Ellisman, M.H. NCMIR-National Center for Microscopy and Imaging Research. NCMIR Methods for 3D EM: A New Protocol for Preparation of Biological Specimens for Serial Block-Face SEM Microscopy. 2010. Available online: https://ncmir.ucsd.edu/sbem-protocol (accessed on 30 May 2021).
- Iudin, A.; Korir, P.K.; Salavert-Torres, J.; Kleywegt, G.J.; Patwardhan, A. EMPIAR: A public archive for raw electron microscopy image data. Nat. Methods 2016, 13, 387–388. [Google Scholar] [CrossRef] [PubMed]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Jaccard, P. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Soc. Vaudoise Sci. 1901, 37, 547–579. [Google Scholar]
- Lee, J.K.; Enciso, G.A.; Boassa, D.; Chander, C.N.; Lou, T.H.; Pairawan, S.S.; Guo, M.C.; Wan, F.Y.; Ellisman, M.H.; Sütterlin, C.; et al. Replication-dependent size reduction precedes differentiation in Chlamydia trachomatis. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karabağ, C.; Jones, M.L.; Reyes-Aldasoro, C.C. Volumetric Semantic Instance Segmentation of the Plasma Membrane of HeLa Cells. J. Imaging 2021, 7, 93. https://doi.org/10.3390/jimaging7060093
Karabağ C, Jones ML, Reyes-Aldasoro CC. Volumetric Semantic Instance Segmentation of the Plasma Membrane of HeLa Cells. Journal of Imaging. 2021; 7(6):93. https://doi.org/10.3390/jimaging7060093
Chicago/Turabian StyleKarabağ, Cefa, Martin L. Jones, and Constantino Carlos Reyes-Aldasoro. 2021. "Volumetric Semantic Instance Segmentation of the Plasma Membrane of HeLa Cells" Journal of Imaging 7, no. 6: 93. https://doi.org/10.3390/jimaging7060093
APA StyleKarabağ, C., Jones, M. L., & Reyes-Aldasoro, C. C. (2021). Volumetric Semantic Instance Segmentation of the Plasma Membrane of HeLa Cells. Journal of Imaging, 7(6), 93. https://doi.org/10.3390/jimaging7060093






