Calibration-Less Multi-Coil Compressed Sensing Magnetic Resonance Image Reconstruction Based on OSCAR Regularization
Abstract
1. Introduction
1.1. Related Works
1.2. Our Contributions
1.3. Outline of the Paper
2. Problem Statement
2.1. Notation and Definitions
2.2. General Problem Formulation
2.3. Primal-Dual Optimization Algorithm
| Algorithm 1: Condat-Vú algorithm |
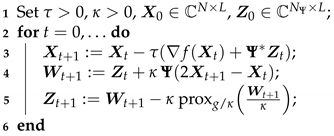 |
3. Octagonal Shrinkage and Clustering Algorithm for Regression
3.1. OSCAR Regularizer
3.1.1. Definition
3.1.2. Proximity Operator
| Algorithm 2: Proximity operator of the OWL norm. |
| 1 Input: , ; |
| 2 ; |
| 3 Let s.t. ; |
| 4 Return ; |
3.2. OSCAR-Based Image Reconstruction
3.2.1. Global OSCAR Regularization
3.2.2. Scalewise OSCAR Regularization
3.2.3. Subbandwise OSCAR Regularization
3.2.4. Coefficientwise OSCAR Regularization
4. Materials and Methods
4.1. Reconstruction Parameters and Computational Complexity
4.2. Retrospective Study
4.3. Prospective Study
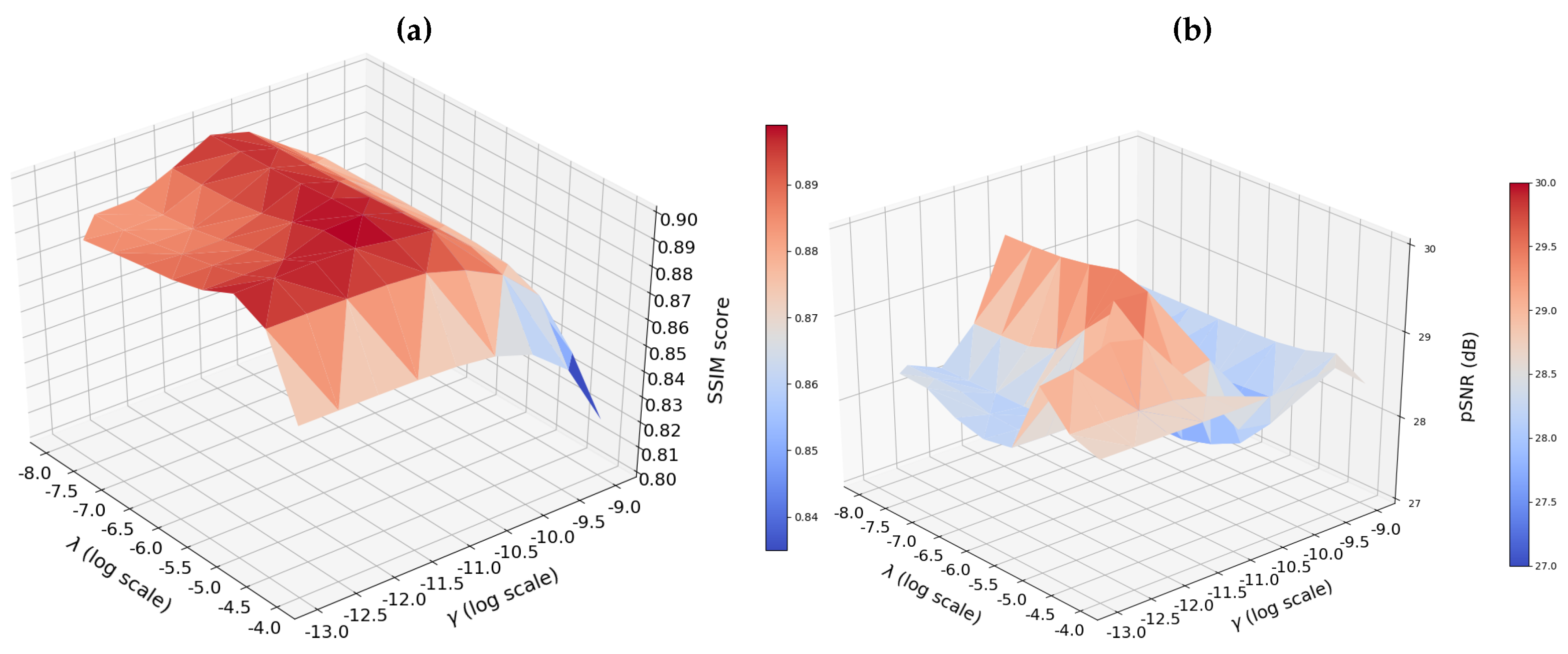
4.4. Hyper-Parameters Search and Sensitivity
4.5. Phase Processing
5. Results
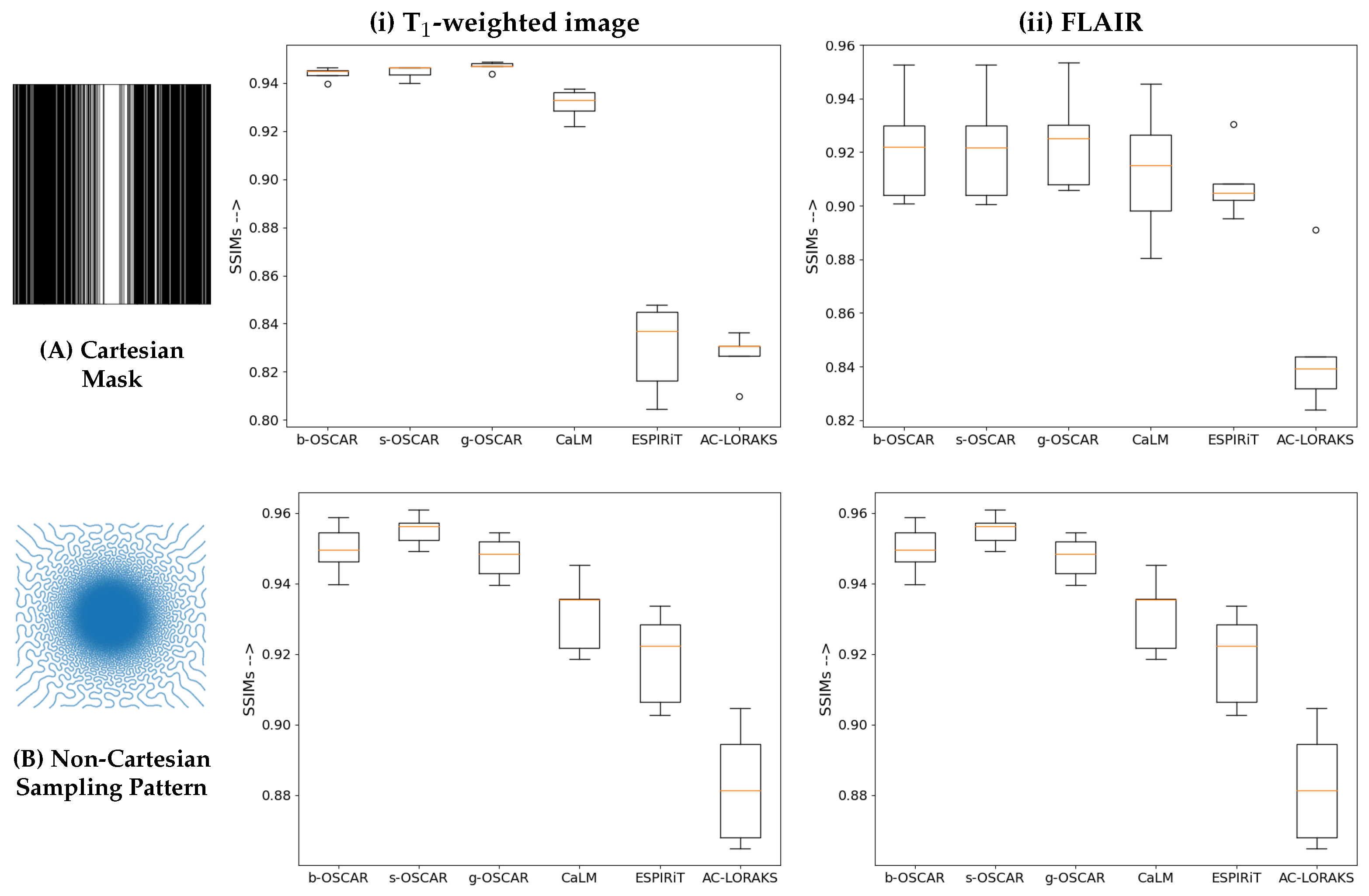
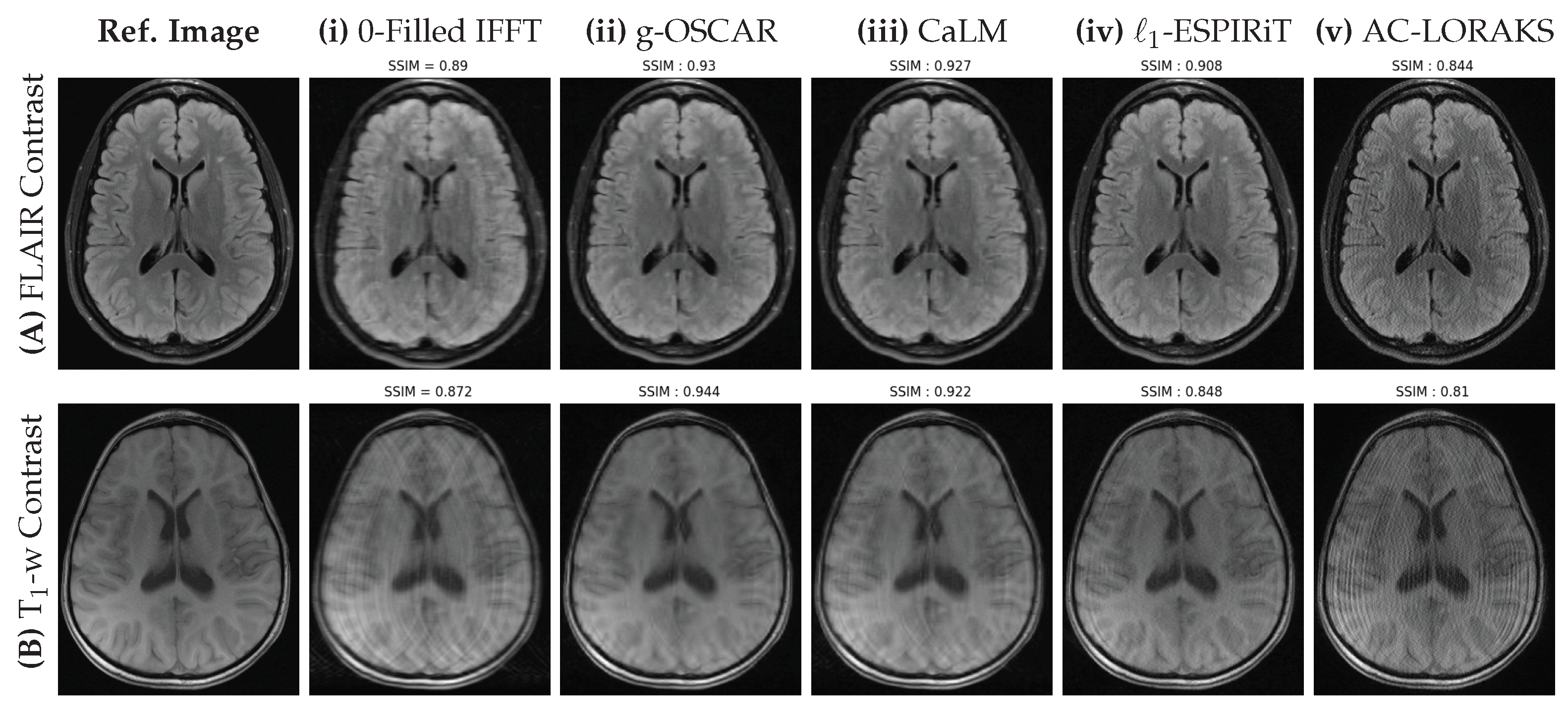
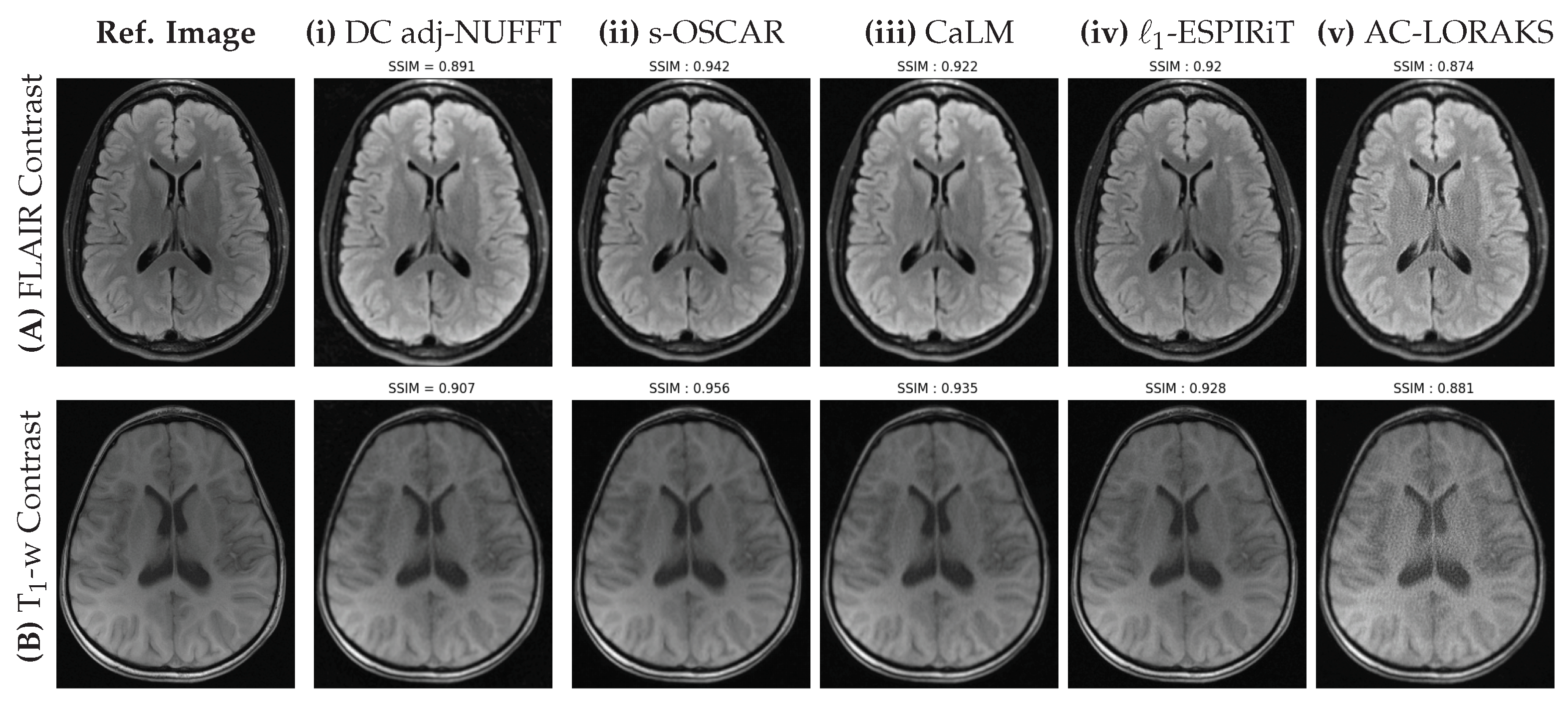
5.1. Retrospective Studies
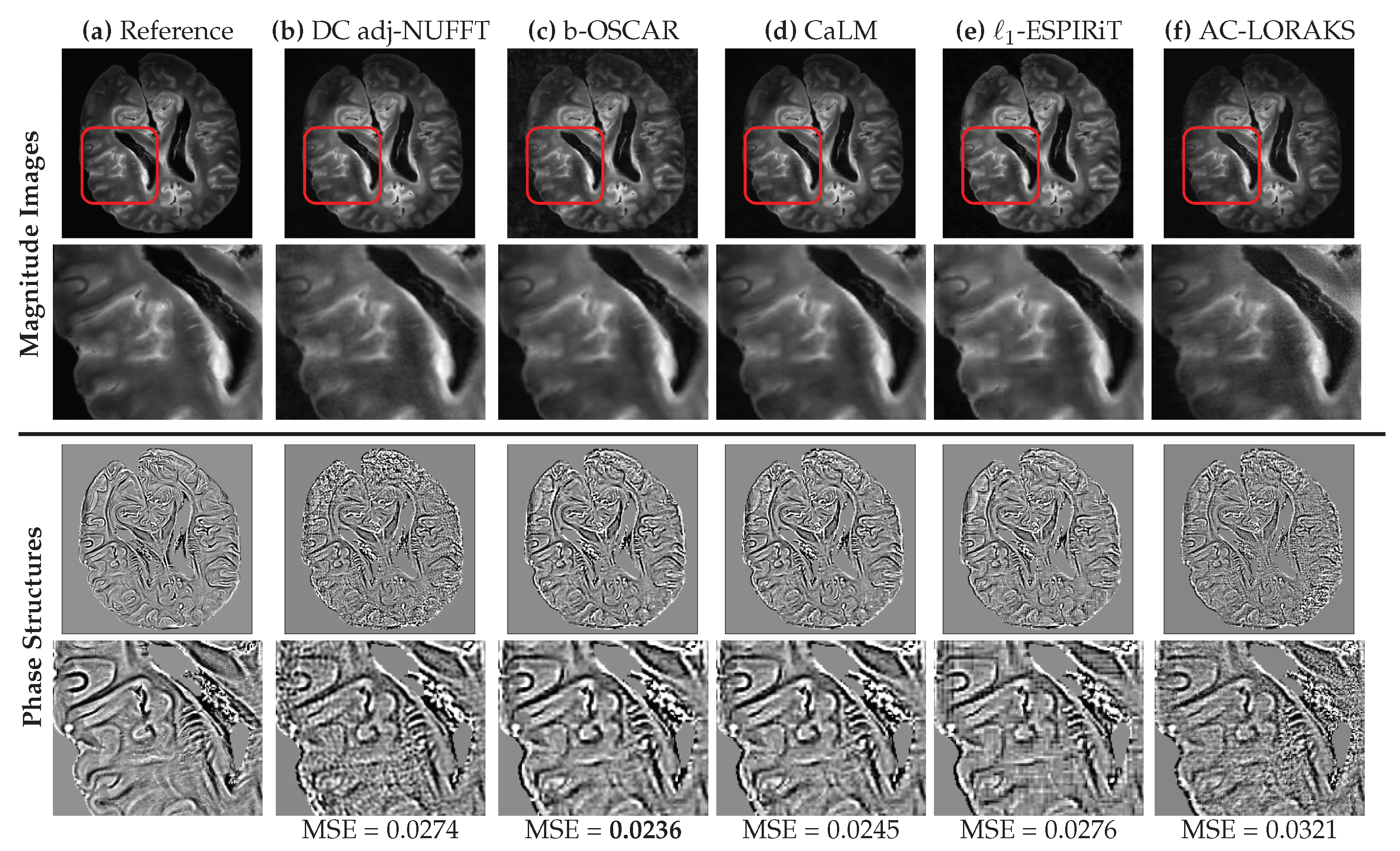
5.2. Prospective Studies
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Donoho, D. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.; Pauly, J. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed Sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- FDA Clears Compressed Sensing MRI Acceleration Technology from Siemens Healthineers. Available online: https://www.siemens-healthineers.com/en-us/news/fda-clears-mri-technology-02-21-2017.html (accessed on 15 April 2019).
- Pipe, J.G. Motion correction with PROPELLER MRI: Application to head motion and free-breathing cardiac imaging. Magn. Reson. Med. 1999, 42, 963–969. [Google Scholar] [CrossRef]
- Lee, J.H.; Hargreaves, B.A.; Hu, B.S.; Nishimura, D.G. Fast 3D imaging using variable-density spiral trajectories with applications to limb perfusion. Magn. Reson. Med. 2003, 50, 1276–1285. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Axel, L.; Chandarana, H.; Block, K.T.; Sodickson, D.K.; Otazo, R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn. Reson. Med. 2016, 75, 775–788. [Google Scholar] [CrossRef] [PubMed]
- Boyer, C.; Chauffert, N.; Ciuciu, P.; Kahn, J.; Weiss, P. On the generation of sampling schemes for magnetic resonance imaging. SIAM J. Imaging Sci. 2016, 9, 2039–2072. [Google Scholar] [CrossRef]
- Kasper, L.; Engel, M.; Barmet, C.; Haeberlin, M.; Wilm, B.; Dietrich, B.; Schmid, T.; Gross, S.; Brunner, D.; Stephan, K.; et al. Rapid anatomical brain imaging using spiral acquisition and an expanded signal model. Neuroimage 2018, 168, 88–100. [Google Scholar] [CrossRef]
- Lazarus, C.; Weiss, P.; Chauffert, N.; Mauconduit, F.; Gueddari, L.E.; Destrieux, C.; Zemmoura, I.; Vignaud, A.; Ciuciu, P. SPARKLING: Variable-density k-space filling curves for accelerated T2*-weighted MRI. Magn. Reson. Med. 2019, 81, 3643–3661. [Google Scholar] [CrossRef] [PubMed]
- Chaithya, G.R.; Weiss, P.; Massire, A.; Vignaud, A.; Ciuciu, P. Globally optimized 3D SPARKLING trajectories for high-resolution T2*-weighted Magnetic Resonance imaging. IEEE Trans. Med. Imaging 2020. under review. [Google Scholar]
- Roemer, P.; Edelstein, W.; Hayes, C.; Souza, S.; Mueller, O. The NMR phased array. Magn. Reson. Med. 1990, 16, 192–225. [Google Scholar] [CrossRef] [PubMed]
- Shin, P.J.; Larson, P.E.; Ohliger, M.A.; Elad, M.; Pauly, J.M.; Vigneron, D.B.; Lustig, M. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn. Reson. Med. 2014, 72, 959–970. [Google Scholar] [CrossRef] [PubMed]
- Haldar, J.P.; Zhuo, J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn. Reson. Med. 2016, 75, 1499–1514. [Google Scholar] [CrossRef] [PubMed]
- Guerquin-Kern, M.; Haberlin, M.; Pruessmann, K.P.; Unser, M. A fast wavelet-based reconstruction method for magnetic resonance imaging. IEEE Trans. Med. Imaging 2011, 30, 1649–1660. [Google Scholar] [CrossRef]
- Chaâri, L.; Pesquet, J.C.; Benazza-Benyahia, A.; Ciuciu, P. A wavelet-based regularized reconstruction algorithm for SENSE parallel MRI with applications to neuroimaging. Med. Image Anal. 2011, 15, 185–201. [Google Scholar] [CrossRef]
- Chauffert, N.; Ciuciu, P.; Weiss, P. Variable density compressed sensing in MRI. Theoretical vs heuristic sampling strategies. In Proceedings of the 10th IEEE International Symposium on Biomedical Imaging (ISBI 2013), San Francisco, CA, USA, 7–11 April 2013; pp. 298–301. [Google Scholar]
- Chauffert, N.; Ciuciu, P.; Kahn, J.; Weiss, P. Variable density sampling with continuous trajectories. Application to MRI. SIAM J. Imaging Sci. 2014, 7, 1962–1992. [Google Scholar] [CrossRef]
- McKenzie, C.A.; Yeh, E.N.; Ohliger, M.A.; Price, M.D.; Sodickson, D.K. Self-calibrating parallel imaging with automatic coil sensitivity extraction. Magn. Reson. Med. 2002, 47, 529–538. [Google Scholar] [CrossRef] [PubMed]
- Uecker, M.; Lai, P.; Murphy, M.; Virtue, P.; Elad, M.; Pauly, J.; Vasanawala, S.; Lustig, M. ESPIRiT—An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014, 71, 990–1001. [Google Scholar] [CrossRef]
- Gueddari, L.; Lazarus, C.; Carrié, H.; Vignaud, A.; Ciuciu, P. Self-calibrating nonlinear reconstruction algorithms for variable density sampling and parallel reception MRI. In Proceedings of the IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM 2018), Sheffield, UK, 8–11 July 2018; pp. 415–419. [Google Scholar]
- Ying, L.; Sheng, J. Joint image reconstruction and sensitivity estimation in SENSE (JSENSE). Magn. Reson. Med. 2007, 57, 1196–1202. [Google Scholar] [CrossRef]
- Uecker, M.; Hohage, T.; Block, K.; Frahm, J. Image reconstruction by regularized nonlinear inversion—Joint estimation of coil sensitivities and image content. Magn. Reson. Med. 2008, 60, 674–682. [Google Scholar] [CrossRef]
- Majumdar, A.; Ward, R.K. Iterative estimation of MRI sensitivity maps and image based on sense reconstruction method (isense). Concepts Magn. Reson. Part A 2012, 40, 269–280. [Google Scholar] [CrossRef]
- Dwork, N.; Johnson, E.M.; O’Connor, D.; Gordon, J.W.; Kerr, A.B.; Baron, C.A.; Pauly, J.M.; Larson, P.E. Calibrationless Multi-coil Magnetic Resonance Imaging with Compressed Sensing. arXiv 2020, arXiv:2007.00165. [Google Scholar]
- Majumdar, A.; Ward, R.K. Calibration-less multi-coil MR image reconstruction. Magn. Reson. Imaging 2012, 30, 1032–1045. [Google Scholar] [CrossRef]
- Chun, I.; Adcock, B.; Talavage, T. Efficient compressed sensing SENSE pMRI reconstruction with joint sparsity promotion. IEEE Trans. Med Imaging 2016, 35, 354–368. [Google Scholar] [CrossRef]
- Trzasko, J.; Manduca, A. Calibrationless parallel MRI using CLEAR. In Proceedings of the 45th Asilomar Conference on Signals, Systems and Computers (ASILOMAR 2011), Pacific Grove, CA, USA, 6–9 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 75–79. [Google Scholar]
- Bondell, H.; Reich, B. Simultaneous regression shrinkage, variable selection, and supervised clustering of predictors with OSCAR. Biometrics 2008, 64, 115–123. [Google Scholar] [CrossRef]
- Bogdan, M.; Van Den Berg, E.; Sabatti, C.; Su, W.; Candès, E.J. SLOPE-adaptive variable selection via convex optimization. Ann. Appl. Stat. 2015, 9, 1103. [Google Scholar] [CrossRef] [PubMed]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Moreau, J.J. Proximité et dualité dans un espace hilbertien. Bull. De La Société Mathématique De Fr. 1965, 93, 273–299. [Google Scholar] [CrossRef]
- Man, L.C.; Pauly, J.M.; Macovski, A. Multifrequency interpolation for fast off-resonance correction. Magn. Reson. Med. 1997, 37, 785–792. [Google Scholar] [CrossRef]
- Keiner, J.; Kunis, S.; Potts, D. Using NFFT 3—a software library for various nonequispaced fast Fourier transforms. ACM Trans. Math. Softw. (TOMS) 2009, 36, 19. [Google Scholar] [CrossRef]
- Fessler, J.; Sutton, B. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans. Signal Process. 2003, 51, 560–574. [Google Scholar] [CrossRef]
- Elad, M.; Milanfar, P.; Rubinstein, R. Analysis versus synthesis in signal priors. Inverse Probl. 2007, 23, 947. [Google Scholar] [CrossRef]
- Florescu, A.; Chouzenoux, E.; Pesquet, J.C.; Ciuciu, P.; Ciochina, S. A majorize-minimize memory gradient method for complex-valued inverse problems. Signal Process. 2014, 103, 285–295. [Google Scholar] [CrossRef]
- Parker, D.L.; Payne, A.; Todd, N.; Hadley, J.R. Phase reconstruction from multiple coil data using a virtual reference coil. Magn. Reson. Med. 2014, 72, 563–569. [Google Scholar] [CrossRef]
- Komodakis, N.; Pesquet, J. Playing with Duality: An overview of recent primal-dual approaches for solving large-scale optimization problems. IEEE Signal Process. Mag. 2015, 32, 31–54. [Google Scholar] [CrossRef]
- Combettes, P.; Pesquet, J. Fixed Point Strategies in Data Science. arXiv 2021, arXiv:2008.02260. [Google Scholar]
- Condat, L. A Primal–Dual Splitting Method for Convex Optimization Involving Lipschitzian, Proximable and Linear Composite Terms. J. Optim. Theory Appl. 2013, 158, 460–479. [Google Scholar] [CrossRef]
- Vũ, B. A splitting algorithm for dual monotone inclusions involving cocoercive operators. Adv. Comput. Math. 2013, 38, 667–681. [Google Scholar] [CrossRef]
- Combettes, P.L.; Pesquet, J.C. Proximal splitting methods in signal processing. In Fixed-Point Algorithms for Inverse Problems in Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2011; pp. 185–212. [Google Scholar]
- Zeng, X.; Figueiredo, M.A. The Ordered Weighted l1 Norm: Atomic Formulation, Projections, and Algorithms. arXiv 2014, arXiv:1409.4271. [Google Scholar]
- Mair, P.; Hornik, K.; de Leeuw, J. Isotone optimization in R: Pool-adjacent-violators algorithm (PAVA) and active set methods. J. Stat. Softw. 2009, 32, 1–24. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Argyriou, A.; Foygel, R.; Srebro, N. Sparse Prediction with the k-Support Norm. arXiv 2012, arXiv:1204.5043. [Google Scholar]
- Haldar, J.P. Autocalibrated LORAKS for fast constrained MRI reconstruction. In Proceedings of the IEEE 12th International Symposium on Biomedical Imaging (ISBI 2015), Brooklyn, NY, USA, 16–19 April 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 910–913. [Google Scholar]
- Cherkaoui, H.; Gueddari, L.; Lazarus, C.; Grigis, A.; Poupon, F.; Vignaud, A.; Farrens, S.; Starck, J.; Ciuciu, P. Analysis vs Synthesis-based Regularization for combined Compressed Sensing and Parallel MRI Reconstruction at 7 Tesla. In Proceedings of the 26th European Signal Processing Conference (EUSIPCO 2018), Rome, Italy, 3–7 September 2018. [Google Scholar]
- Gueddari, L.E.; Chaithya, G.R.; Ramzi, Z.; Farrens, S.; Starck, S.; Grigis, A.; Starck, J.L.; Ciuciu, P. PySAP-MRI: A Python Package for MR Image Reconstruction. In Proceedings of the ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona, AZ, USA, 26–29 January 2020. [Google Scholar]
- Farrens, S.; Grigis, A.; El Gueddari, L.; Ramzi, Z.; Chaithya, G.R.; Starck, S.; Sarthou, B.; Cherkaoui, H.; Ciuciu, P.; Starck, J.L. PySAP: Python Sparse Data Analysis Package for multidisciplinary image processing. Astron. Comput. 2020, 32, 100402. [Google Scholar] [CrossRef]
- Knoll, F.; Schwarzl, A.; Diwoky, C.; Sodickson, D. gpuNUFFT—An Open Source GPU Library for 3D Regridding with Direct Matlab Interface. In Proceedings of the 22nd Annual Meeting of ISMRM, Milan, Italy, 10–16 May 2014. [Google Scholar]
- Zbontar, J.; Knoll, F.; Sriram, A.; Muckley, M.J.; Bruno, M.; Defazio, A.; Parente, M.; Geras, K.J.; Katsnelson, J.; Chandarana, H.; et al. fastMRI: An Open Dataset and Benchmarks for Accelerated MRI. arXiv 2018, arXiv:1811.08839. [Google Scholar]
- Knoll, F.; Zbontar, J.; Sriram, A.; Muckley, M.J.; Bruno, M.; Defazio, A.; Parente, M.; Geras, K.J.; Katsnelson, J.; Chandarana, H.; et al. fastMRI: A publicly available raw k-space and DICOM dataset of knee images for accelerated MR image reconstruction using machine learning. Radiol. Artif. Intell. 2020, 2, e190007. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Haacke, E.M.; Xu, Y.; Cheng, Y.C.N.; Reichenbach, J.R. Susceptibility weighted imaging (SWI). Magn. Reson. Med. 2004, 52, 612–618. [Google Scholar] [CrossRef] [PubMed]
- Ramani, S.; Fessler, J.A. Parallel MR image reconstruction using augmented Lagrangian methods. IEEE Trans. Med Imaging 2010, 30, 694–706. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Liu, J.Z.; Cauley, S.F.; Rosen, B.R.; Rosen, M.S. Image reconstruction by domain-transform manifold learning. Nature 2018, 555, 487. [Google Scholar] [CrossRef]
- Mardani, M.; Gong, E.; Cheng, J.Y.; Vasanawala, S.S.; Zaharchuk, G.; Xing, L.; Pauly, J.M. Deep generative adversarial neural networks for compressive sensing MRI. IEEE Trans. Med. Imaging 2018, 38, 167–179. [Google Scholar] [CrossRef]
- Ramzi, Z.; Ciuciu, P.; Starck, J.L. Benchmarking MRI reconstruction neural networks on large public datasets. Appl. Sci. 2020, 10, 1816. [Google Scholar] [CrossRef]
- Antun, V.; Renna, F.; Poon, C.; Adcock, B.; Hansen, A.C. On instabilities of deep learning in image reconstruction-Does AI come at a cost? arXiv 2019, arXiv:1902.05300. [Google Scholar]
- Ramani, S.; Liu, Z.; Rosen, J.; Nielsen, J.F.; Fessler, J.A. Regularization parameter selection for nonlinear iterative image restoration and MRI reconstruction using GCV and SURE-based methods. IEEE Trans. Image Process. 2012, 21, 3659–3672. [Google Scholar] [CrossRef] [PubMed]
- Ma, J. Generalized sampling reconstruction from Fourier measurements using compactly supported shearlets. Appl. Comput. Harmon. Anal. 2017, 42, 294–318. [Google Scholar] [CrossRef][Green Version]
- El Gueddari, L.; Chouzenoux, E.; Vignaud, A.; Pesquet, J.C.; Ciuciu, P. Online MR image reconstruction for compressed sensing acquisition in T2* imaging. In Proceedings of the Wavelets and Sparsity XVIII. International Society for Optics and Photonics, San Diego, CA, USA, 13–15 August 2019; Volume 11138, p. 1113819. [Google Scholar]

| Proximity Numerical Complexity | Computation Time Per Prox. (S) | Parallelization | Computation Time Per Iter. (S) | |
|---|---|---|---|---|
| g-OSCAR | 0.334 | N.A. | 2.894 | |
| s-OSCAR | 1.005 | C | 6.711 | |
| b-OSCAR | 3.094 | 4.418 | ||
| c-OSCAR | 159.75 | 161.13 | ||
| CaLM | 1.944 | |||
| -ESPIRiT | 4.360 | |||
| AC-LORAKS | 2.516 |
| AF | g-OSCAR | s-OSCAR | b-OSCAR | CaLM | -ESPIRiT | AC-LORAKS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSIM | pSNR | SSIM | pSNR | SSIM | pSNR | SSIM | pSNR | SSIM | pSNR | SSIM | pSNR | |
| 8 | 0.923 | 30.52 | 0.925 | 31.66 | 0.926 | 31.68 | 0.921 | 30.51 | 0.911 | 27.82 | 0.894 | 26.09 |
| 10 | 0.920 | 29.21 | 0.921 | 29.62 | 0.922 | 30.28 | 0.921 | 29.54 | 0.906 | 26.58 | 0.897 | 26.23 |
| 12 | 0.916 | 28.81 | 0.918 | 28.40 | 0.918 | 29.78 | 0.917 | 29.05 | 0.904 | 27.17 | 0.893 | 26.25 |
| 15 | 0.912 | 29.28 | 0.912 | 29.05 | 0.913 | 29.52 | 0.912 | 28.87 | 0.900 | 26.29 | 0.884 | 25.94 |
| 20 | 0.899 | 29.12 | 0.896 | 28.35 | 0.899 | 29.52 | 0.897 | 28.59 | 0.885 | 26.48 | 0.753 | 25.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Gueddari, L.; Giliyar Radhakrishna, C.; Chouzenoux, E.; Ciuciu, P. Calibration-Less Multi-Coil Compressed Sensing Magnetic Resonance Image Reconstruction Based on OSCAR Regularization. J. Imaging 2021, 7, 58. https://doi.org/10.3390/jimaging7030058
El Gueddari L, Giliyar Radhakrishna C, Chouzenoux E, Ciuciu P. Calibration-Less Multi-Coil Compressed Sensing Magnetic Resonance Image Reconstruction Based on OSCAR Regularization. Journal of Imaging. 2021; 7(3):58. https://doi.org/10.3390/jimaging7030058
Chicago/Turabian StyleEl Gueddari, Loubna, Chaithya Giliyar Radhakrishna, Emilie Chouzenoux, and Philippe Ciuciu. 2021. "Calibration-Less Multi-Coil Compressed Sensing Magnetic Resonance Image Reconstruction Based on OSCAR Regularization" Journal of Imaging 7, no. 3: 58. https://doi.org/10.3390/jimaging7030058
APA StyleEl Gueddari, L., Giliyar Radhakrishna, C., Chouzenoux, E., & Ciuciu, P. (2021). Calibration-Less Multi-Coil Compressed Sensing Magnetic Resonance Image Reconstruction Based on OSCAR Regularization. Journal of Imaging, 7(3), 58. https://doi.org/10.3390/jimaging7030058






