Detecting and Locating Passive Video Forgery Based on Low Computational Complexity Third-Order Tensor Representation
Abstract
1. Introduction
- The method is based on comparing a limited number of orthogonal-features extracted from third-order tensor video decomposition;
- First, the whole video sequence is geometrically constructed into sub-groups, and each sub-group is mathematically decomposed into a group of third-order tensors. Then, instead of comparing all the frame/feature correlations, a group of arbitrarily chosen core sub-groups is orthogonally transformed to obtain essential features to trace along the tube fibers. Moreover, if a forgery is detected, these features can be used to localize the forged frames with high accuracy;
- The novelty of this paper is the great accuracy in detecting inter-frame forgeries. Hence, the geometric construction of successive video frames into third-order tensor tube fiber mode offers a great reduction in the number of pixels needed to trace forgeries;
- Checking one or two core sub-groups/third-order tensors of a limited number of pixels in the orthogonal domain is enough to detect frame discontinuities, compared with classic passive methods that examine the entire frame sequences. Additionally, this construction encapsulates the spatial and temporal features of successive frames into 2D matrices which can be manipulated and tested easily with high accuracy and less computational complexity.
2. Related Work
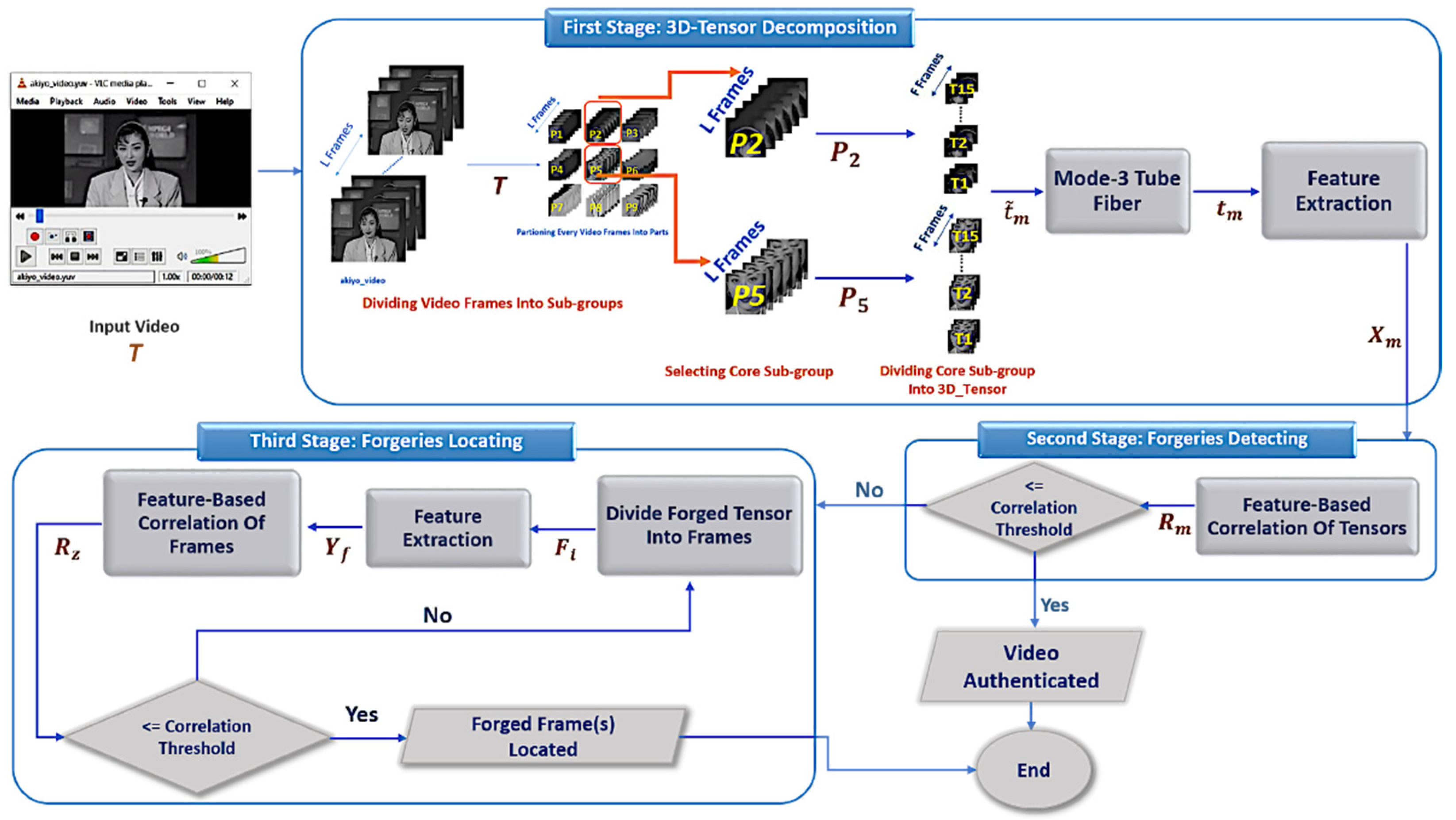
3. Proposed Method
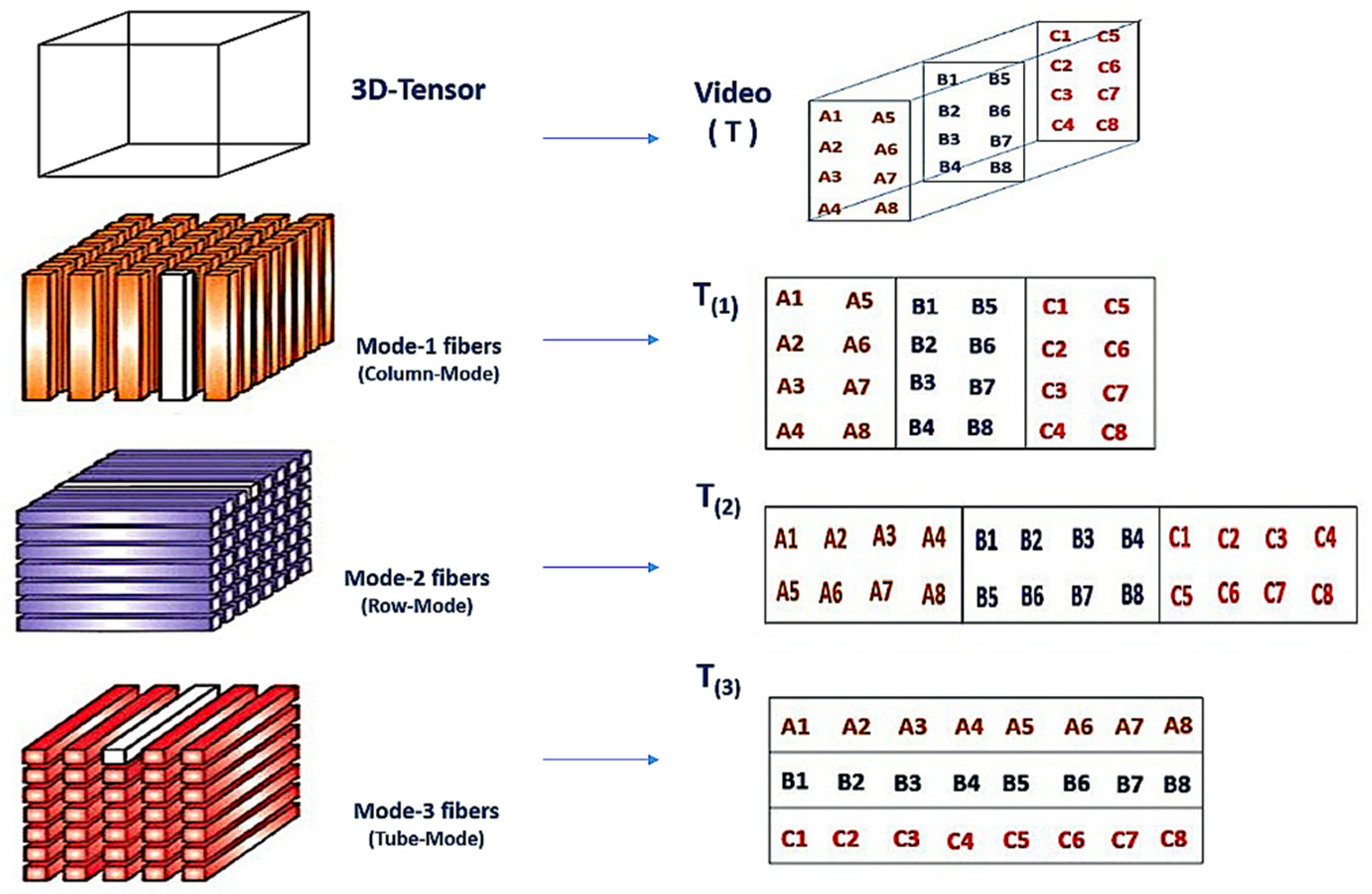
3.1. First Phase: 3D-Tensor Decomposition
3.1.1. Tube Fibers Representation
3.1.2. Feature Extraction
Harris Feature Extraction
GLCM Feature Extraction
SVD Feature Extraction
3.2. Second Phase: Forgery Detecting
3.2.1. Features-Based Correlation of Tensors
| Algorithm 1 Forgery Type Determination. |
| Input: Correlation values Rm where m = 1: M and Threshold. (14)–(15) |
| Output: Forgery type. |
| 1. Begin |
| 2. for where m = 1: M do |
| 3. if & <= Threshold then |
| 4. Forgery type is insertion |
| 5. else if <= Threshold then |
| 6. Divide tensors with suspected values into Sub-Frames. |
| 7. if two suspected points are found then |
| 8. Forgery type is insertion |
| 9. else |
| 10. Forgery type is deletion |
| 11. end |
| 12. else |
| 13. No forgery (video is original) |
| 14. end |
| 15. end |
| 16. end |
3.2.2. Insertion Forgery Detecting
3.2.3. Deletion Forgery Detecting
3.3. Third Phase: Forgery Locating
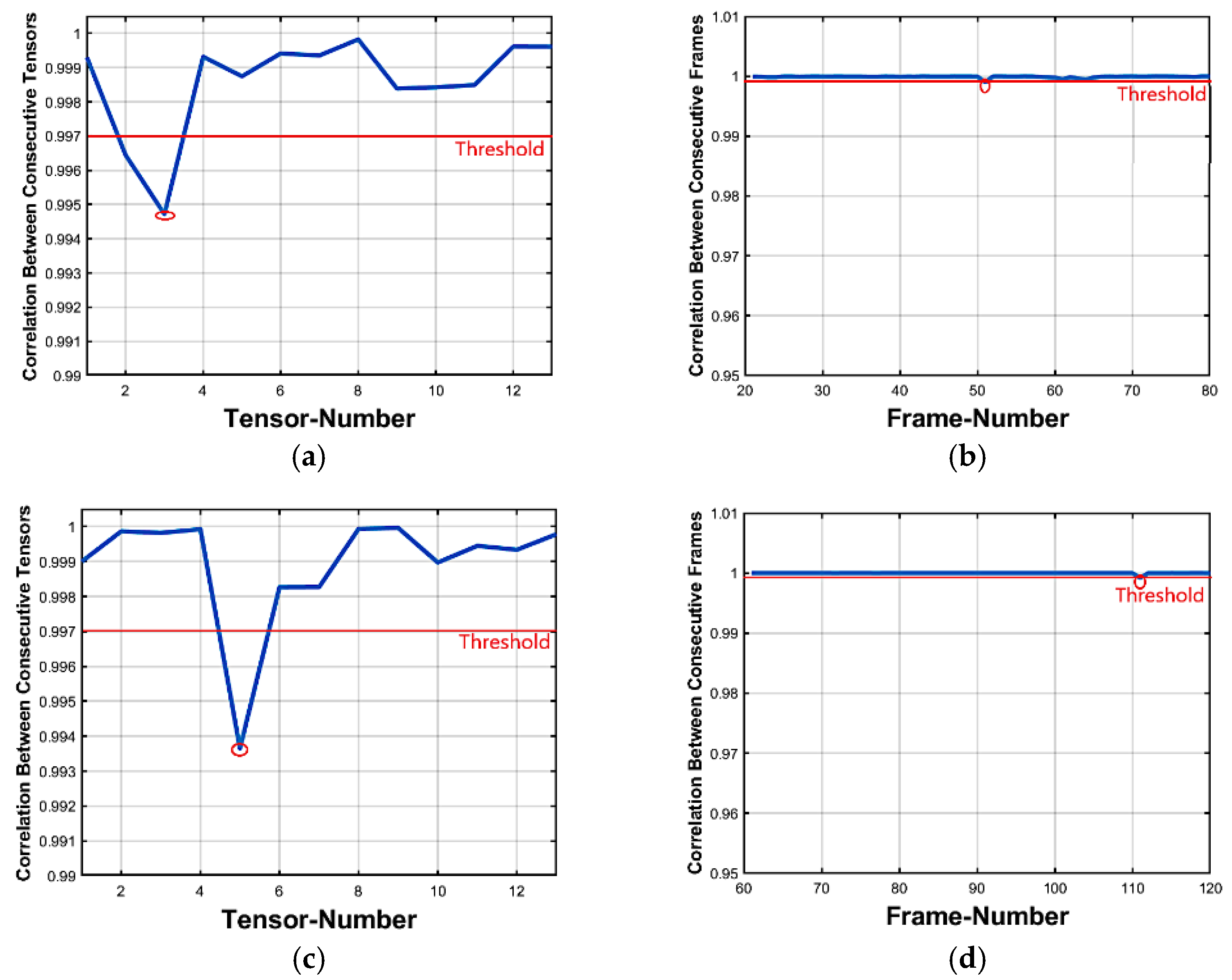
3.3.1. Tensors Analysis
3.3.2. Features-Based Correlation of Frames
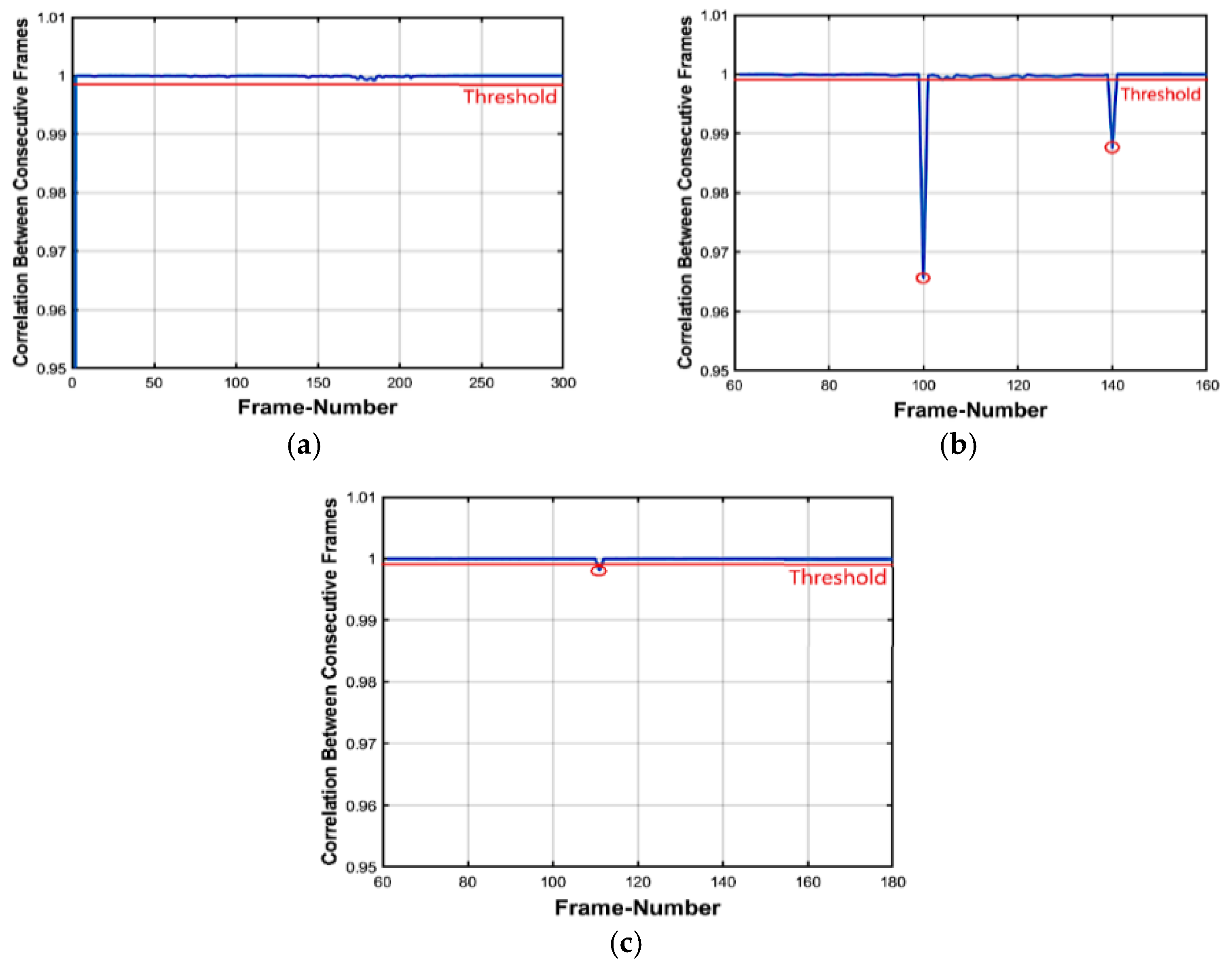
3.3.3. Locating Forgeries
Insertion Forgeries
Deletion Forgeries
| Algorithm 2 Forgery Location Determination. |
| Input: Correlation values Rm where m = 1: M, Threshold, t which is tensor number. |
| Output: Number of inserted or deleted Forged frames. |
| 1. begin |
| 2. for where m = 1:M do |
| 3. if Forgery is detected at & then |
| 4. Forgery type is insertion. |
| 5. Divide tensors whose numbers are t − 1, t, t + 1, t + 2 into frames (from s to n). |
| 6. Compute correlation between every two consecutive frames in . |
| 7. for where z = 1:n-1 do |
| 8. if Two suspected values are found then |
| 9. Forgery location determined |
| 10. end |
| 11. else if forgery is detected at then |
| 12. Repeat steps 5, 6. |
| 13. if two suspected values are found then |
| 14. Forgery type is insertion and forgery determined |
| 15. else if one suspected value is found then |
| 16. Forgery type is deletion and forgery determined |
| 17. end |
| 18. else |
| 19. No forgery |
| 20. end |
| 21. end |
| 22. end |
4. Experimental Results and Discussion
4.1. Tested Dataset Description
4.2. Evaluation Standards
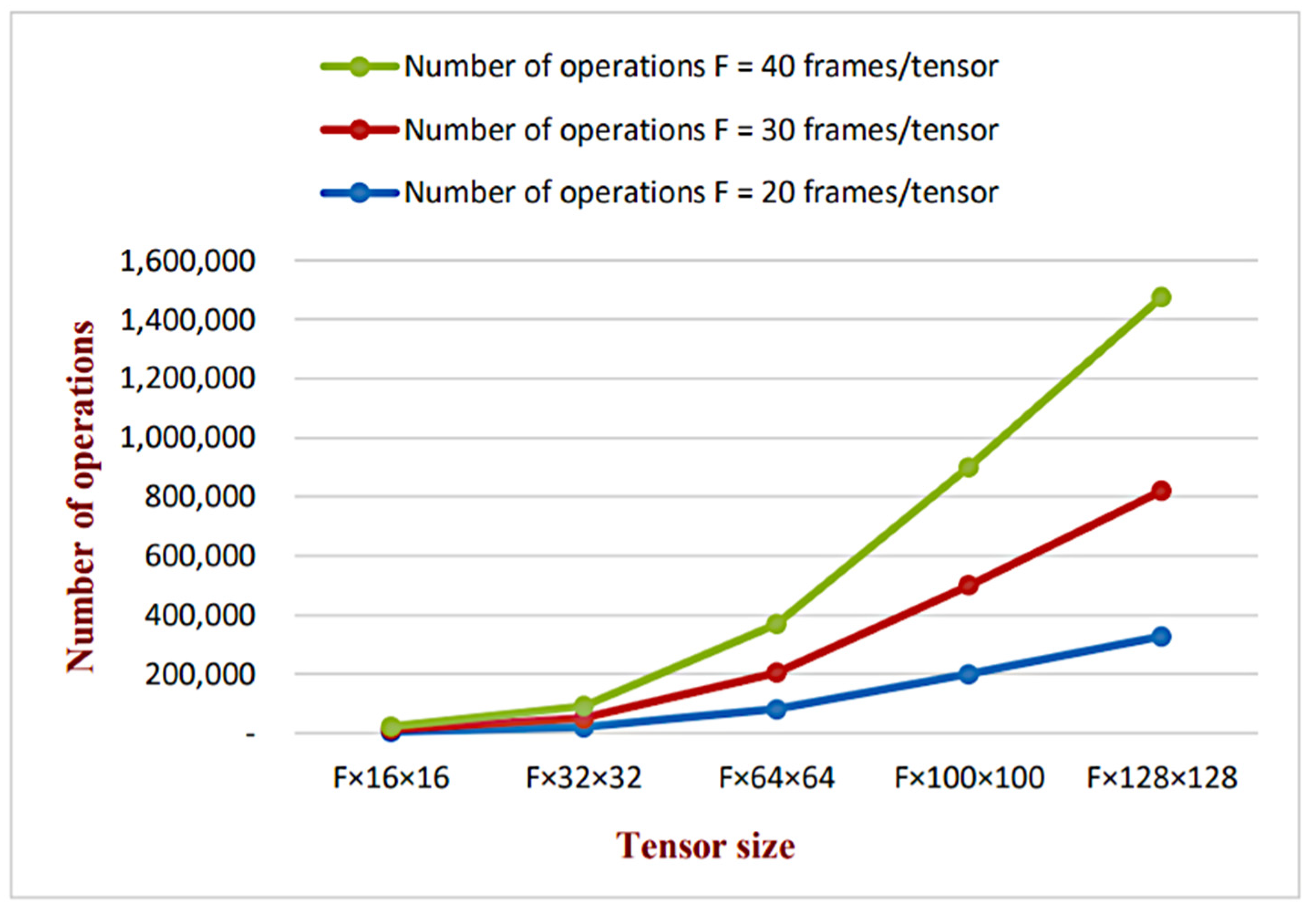
4.3. Computational Complexity Analysis
5. Comparisons and Discussion
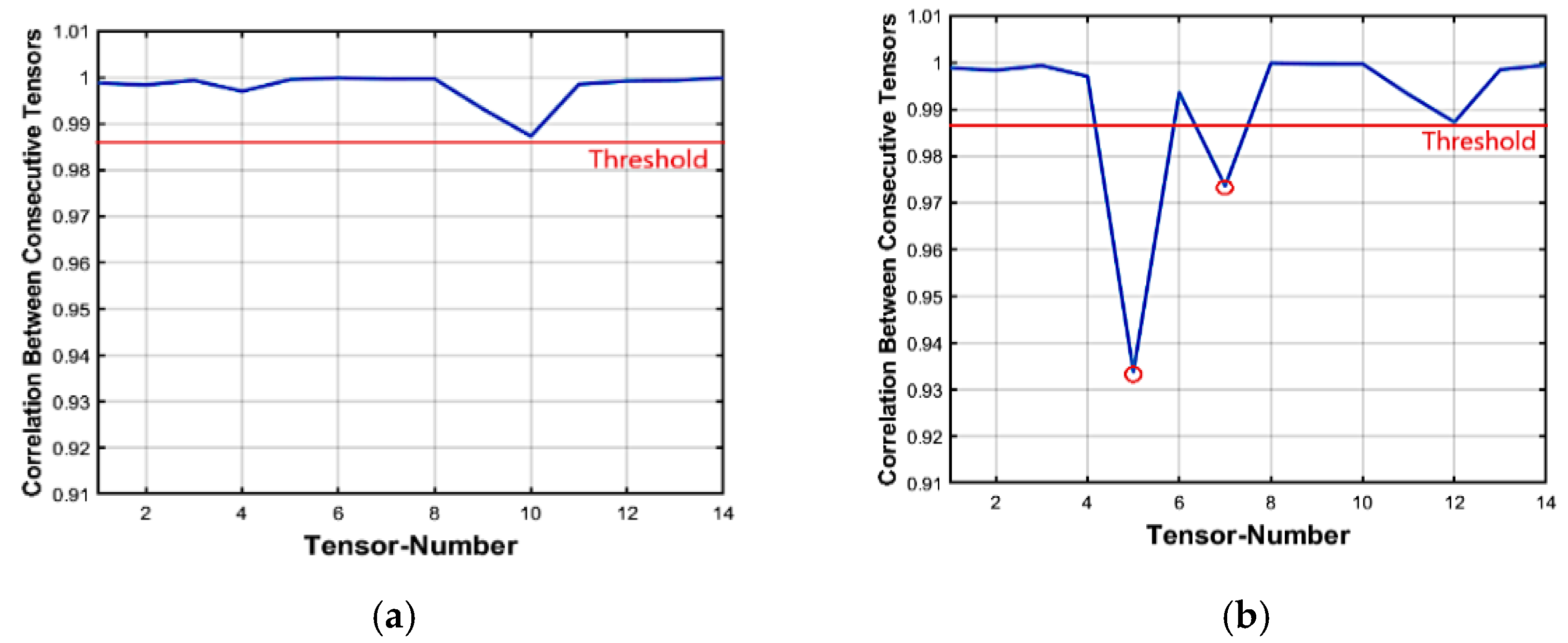
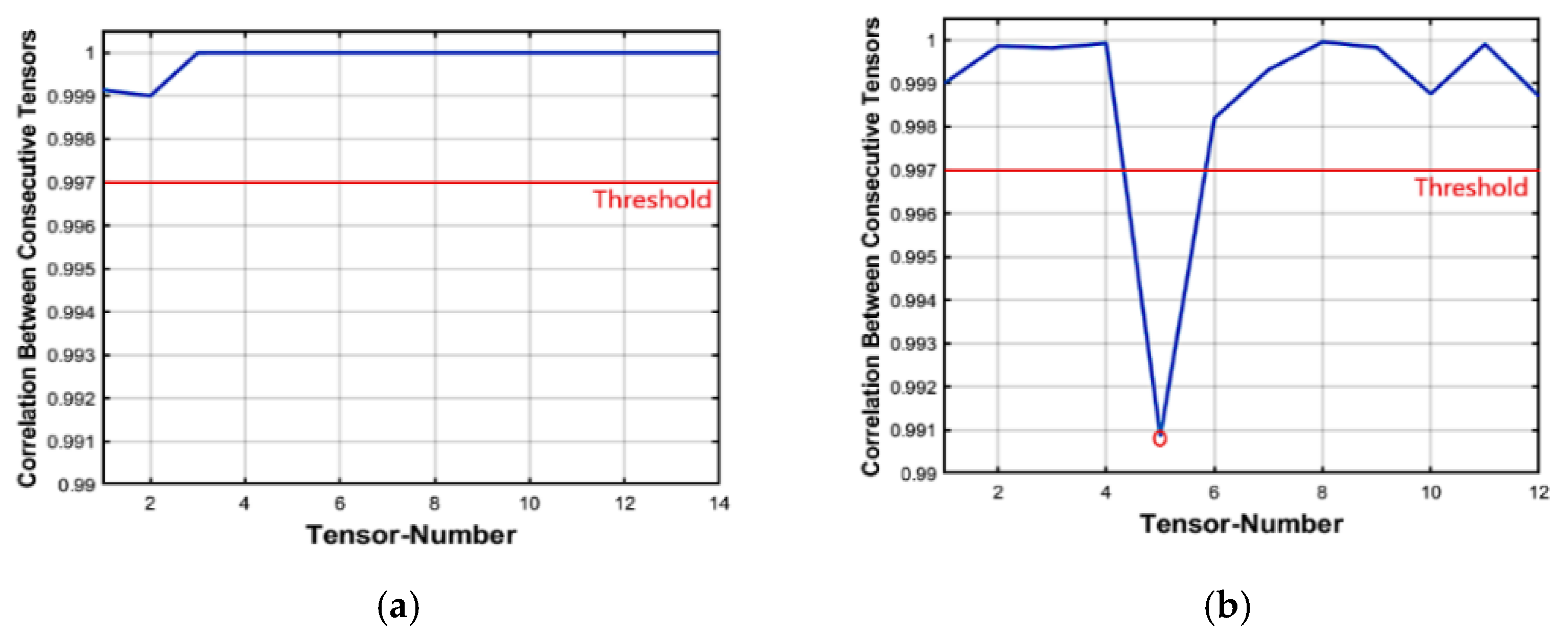
5.1. Insertion Forgery
5.2. Deletion Forgery
5.3. Comparison with State-of-the-Art
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Zhang, Z.; Guo, S.; Wang, J. Video inter-frame forgery identification based on the consistency of quotient of MSSIM. Secur. Commun. Netw. 2016, 9, 4548–4556. [Google Scholar] [CrossRef]
- Sencar, H.T.; Memon, N. Overview of state-of-the-art in digital image forensics. In Algorithms, Architectures and Information Systems Security; World Scientific: Singapore, 2009; pp. 325–347. [Google Scholar]
- Abdulhussain, S.H.; Al-Haddad, S.A.R.; Saripan, M.I.; Mahmmod, B.M.; Hussien, A.J.I.A. Fast Temporal Video Segmentation Based on Krawtchouk-Tchebichef Moments. IEEE Access 2020, 8, 72347–72359. [Google Scholar] [CrossRef]
- Mehta, V.; Jaiswal, A.K.; Srivastava, R. Copy-Move Image Forgery Detection Using DCT and ORB Feature Set. In Proceedings of the International Conference on Futuristic Trends in Networks and Computing Technologies, Chandigarh, India, 22–23 November 2013; Springer: Singapore, 2019; pp. 532–544. [Google Scholar]
- Kobayashi, M.; Okabe, T.; Sato, Y. Detecting forgery from static-scene video based on inconsistency in noise level functions. IEEE Trans. Inf. Forensics Secur. 2010, 5, 883–892. [Google Scholar] [CrossRef]
- Bakas, J.; Naskar, R.; Dixit, R. Detection and localization of inter-frame video forgeries based on inconsistency in correlation distribution between Haralick coded frames. Multimed. Tools Appl. 2019, 78, 4905–4935. [Google Scholar] [CrossRef]
- Sitara, K.; Mehtre, B.M. Digital video tampering detection: An overview of passive techniques. Digit. Investig. 2016, 18, 8–22. [Google Scholar] [CrossRef]
- Cheng, Y.H.; Huang, T.M.; Huang, S.Y. Tensor decomposition for dimension reduction. Comput. Stat. 2020, 12, e1482. [Google Scholar] [CrossRef]
- Nanni, L.; Ghidoni, S.; Brahnam, S. Handcrafted vs. non-handcrafted features for computer vision classification. Pattern Recognit. 2017, 71, 158–172. [Google Scholar] [CrossRef]
- Yang, J.; Huang, T.; Su, L. Using similarity analysis to detect frame duplication forgery in videos. Multimed. Tools Appl. 2016, 75, 1793–1811. [Google Scholar] [CrossRef]
- Singh, V.K.; Pant, P.; Tripathi, R.C. Detection of frame duplication type of forgery in digital video using sub-block based features. In Proceedings of the International Conference on Digital Forensics and Cyber Crime, Seoul, Korea, 6–8 October 2015; Springer: Cham, Switzerland, 2015; pp. 29–38. [Google Scholar]
- Liu, H.; Li, S.; Bian, S. Detecting frame deletion in H. 264 video. In Proceedings of the International Conference on Information Security Practice and Experience, Fuzhou, China, 5–8 May 2014; Springer: Cham, Switzerland, 2014; pp. 262–270. [Google Scholar]
- Yu, L.; Wang, H.; Han, Q.; Niu, X.; Yiu, S.-M.; Fang, J.; Wang, Z. Exposing frame deletion by detecting abrupt changes in video streams. Neurocomputing 2016, 205, 84–91. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Zhang, Z.; Ma, Q.J. Video inter-frame forgery identification based on consistency of correlation coefficients of gray values. J. Comput. Commun. 2014, 2, 51. [Google Scholar] [CrossRef]
- Zhang, Z.; Hou, J.; Ma, Q.; Li, Z. Efficient video frame insertion and deletion detection based on inconsistency of correlations between local binary pattern coded frames. Secur. Commun. Netw. 2015, 8, 311–320. [Google Scholar] [CrossRef]
- Aghamaleki, J.A.; Behrad, A. Inter-frame video forgery detection and localization using intrinsic effects of double compression on quantization errors of video coding. Signal Process. Image Commun. 2016, 47, 289–302. [Google Scholar] [CrossRef]
- Zhao, D.-N.; Wang, R.-K.; Lu, Z.-M. Inter-frame passive-blind forgery detection for video shot based on similarity analysis. Multimed. Tools Appl. 2018, 77, 25389–25408. [Google Scholar] [CrossRef]
- Fadl, S.; Han, Q.; Qiong, L. Exposing video inter-frame forgery via histogram of oriented gradients and motion energy image. Multidimens. Syst. Signal Process. 2020, 31, 1365–1384. [Google Scholar] [CrossRef]
- Long, C.; Basharat, A.; Hoogs, A. A Coarse-to-fine Deep Convolutional Neural Network Framework for Frame Duplication Detection and Localization in Video Forgery. CVPR Workshops 2019. pp. 1–10. Available online: http://www.chengjianglong.com/publications/CopyPaste.pdf (accessed on 10 February 2021).
- Bakas, J.; Naskar, R. A Digital Forensic Technique for Inter–Frame Video Forgery Detection Based on 3D CNN. In Proceedings of the International Conference on Information Systems Security, Bangalore, India, 17–19 December 2014; Springer: Cham, Switzerland, 2018; pp. 304–317. [Google Scholar]
- Li, Q.; Wang, R.; Xu, D. An Inter-Frame Forgery Detection Algorithm for Surveillance Video. Information 2018, 9, 301. [Google Scholar] [CrossRef]
- Subramanyam, A.V.; Emmanuel, S. Pixel estimation based video forgery detection. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3038–3042. [Google Scholar]
- Huang, Z.; Huang, F.; Huang, J. Detection of double compression with the same bit rate in MPEG-2 videos. In Proceedings of the 2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014; pp. 306–309. [Google Scholar]
- Chen, S.; Tan, S.; Li, B.; Huang, J. Automatic detection of object-based forgery in advanced video. IEEE Trans. Circuits Syst. Video Technol. 2015, 26, 2138–2151. [Google Scholar] [CrossRef]
- D’Amiano, L.; Cozzolino, D.; Poggi, G.; Verdoliva, L. Video forgery detection and localization based on 3D patchmatch. In Proceedings of the 2015 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Torino, Italy, 29 June–3 July 2015; pp. 1–6. [Google Scholar]
- Bidokhti, A.; Ghaemmaghami, S. Detection of regional copy/move forgery in MPEG videos using optical flow. In Proceedings of the 2015 The International Symposium on Artificial Intelligence and Signal Processing (AISP), Mashhad, Iran, 3–5 March 2015; pp. 13–17. [Google Scholar]
- Kountchev, R.; Anwar, S.; Kountcheva, R.; Milanova, M. Face Recognition in Home Security System Using Tensor Decomposition Based on Radix-(2 × 2) Hierarchical SVD. In Multimodal Pattern Recognition of Social Signals in Human-Computer-Interaction; Schwenker, F., Scherer, S., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 48–59. [Google Scholar]
- Kountchev, R.K.; Iantovics, B.L.; Kountcheva, R.A. Hierarchical third-order tensor decomposition through inverse difference pyramid based on the three-dimensional Walsh–Hadamard transform with app.lications in data mining. Data Min. Knowl. Discov. 2020, 10, e1314. [Google Scholar]
- Kountchev, R.K.; Mironov, R.P.; Kountcheva, R.A. Hierarchical Cubical Tensor Decomposition through Low Complexity Orthogonal Transforms. Symmetry 2020, 12, 864. [Google Scholar] [CrossRef]
- Kountchev, R.; Kountcheva, R. Low Computational Complexity Third-Order Tensor Representation Through Inverse Spectrum Pyramid. In Advances in 3D Image and Graphics Representation, Analysis, Computing and Information Technology; Springer: Singapore, 2020; pp. 61–76. [Google Scholar]
- Abdulhussain, S.H.; Mahmmod, B.M.; Saripan, M.I.; Al-Haddad, S.; Jassim, W.A.J. A new hybrid form of krawtchouk and tchebichef polynomials: Design and application. J. Math. Imaging Vis. 2019, 61, 555–570. [Google Scholar] [CrossRef]
- Mahmmod, B.M.; Abdul-Hadi, A.M.; Abdulhussain, S.H.; Hussien, A.J. On computational aspects of Krawtchouk polynomials for high orders. J. Imaging 2020, 6, 81. [Google Scholar] [CrossRef]
- Shivakumar, B.; Baboo, S.S. Automated forensic method for copy-move forgery detection based on Harris interest points and SIFT descriptors. Int. J. Comput. Appl. 2011, 27, 9–17. [Google Scholar]
- Chen, L.; Lu, W.; Ni, J.; Sun, W.; Huang, J. Region duplication detection based on Harris corner points and step sector statistics. J. Vis. Commun. Image Represent. 2013, 24, 244–254. [Google Scholar] [CrossRef]
- Van Loan, C.F. Generalizing the singular value decomposition. J. Numer. Anal. 1976, 13, 76–83. [Google Scholar] [CrossRef]
- Sedgwick, P.J.B. Pearson’s correlation coefficient. BMJ 2012, 345, e4483. [Google Scholar] [CrossRef]
- Amidan, B.G.; Ferryman, T.A.; Cooley, S.K. Data outlier detection using the Chebyshev theorem. In Proceedings of the 2005 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2005; IEEE: Big Sky, MT, USA, 2005; pp. 3814–3819. [Google Scholar]
- Pulipaka, A.; Seeling, P.; Reisslein, M.; Karam, L.J. Traffic and statistical multiplexing characterization of 3-D video representation formats. IEEE Trans. Broadcasting 2013, 59, 382–389. [Google Scholar] [CrossRef]
- Su, Y.; Nie, W.; Zhang, C. A frame tampering detection algorithm for MPEG videos. In Proceedings of the 2011 6th IEEE Joint International Information Technology and Artificial Intelligence Conference, Chongqing, China, 20–22 August 2015; IEEE: Chongqing, China, 2011; pp. 461–464. [Google Scholar]
- Mizher, M.A.; Ang, M.C.; Mazhar, A.A.; Mizher, M.A. A review of video falsifying techniques and video forgery detection techniques. Int. J. Electron. Secur. Digit. Forensics 2017, 9, 191–208. [Google Scholar] [CrossRef]
- Shanableh, T. Detection of frame deletion for digital video forensics. Digit. Investig. 2013, 10, 350–360. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, T. Exposing video inter-frame forgery by Zernike opponent chromaticity moments and coarseness analysis. Multimed. Syst. 2017, 23, 223–238. [Google Scholar] [CrossRef]





| References | Forgery Type | Feature Method Used | Strengths | Limitations |
|---|---|---|---|---|
| [10] | Frame duplication | Similarity between SVD features vector of each frame. | High accuracy in detecting forgery | Failed in detecting other types of forgery such as insertion or reshuffling. |
| [11] | Frame duplication | Correlation between the successive frames. | Detected and localized frame duplication in higher accuracy. | Failed when frame duplication was performed in a different order. |
| [12] | Frame deletion | Sequence of average residual of P-frames (SARP) and its time- and frequency-domain features. | Was very effective with the detecting. | Worked with fixed GOP only. |
| [13] | Frame deletion | Magnitude variation in prediction residual and intra macro blocks number. | Worked stably under various configurations. | Failed if the number of deleted frames was very small. |
| [14] | Frame insertion and deletion. | Correlation coefficients of gray values. | Efficient in classifying original videos and forgeries. | Worked with still background datasets. |
| [15] | Frame insertion and deletion. | Quotients of correlation coefficients between (LBPs) coded frames. | High detecting accuracy and low computational complexity. | Detected only if forgeries exist but cannot distinguish frame insertion and deletion. |
| [16] | Frame insertion and deletion. | Quantization error in residual errors of P-MB in P frames. | Effective detecting. | Not suitable for videos with a low compression ratio. |
| [6] | Frame insertion, deletion and duplication. | Correlation between the Haralick coded frame. | Worked efficiently for static as well as dynamic videos. | Not able to detect other types of forgery such as frame reshuffling and replacement. |
| [17] | Frame insertion, deletion and duplication. | HSV color histogram comparison and SURF. | Was efficient and accurate in terms of forgery identification and locating. | Failed to detect inter-frame video with many shots. |
| [18] | Frame insertion, deletion and duplication. | HOG and MOI. | Was efficient in insertion and duplication. | Failed to detect frame deletion in silent scenes. |
| [19] | Frame duplication. | An I3D network and a Siamese network were used. | Detected frame duplication in an effective method. | Compression might decrease the accuracy and failed to detect frame deletion forgery. |
| [20] | Frame insertion, deletion and duplication. | (3D-CNN) is used for detecting the inter-frame video forgery. | Detected inter-frame video forgeries for static as well as dynamic single-shot videos. | Failed in localization of forgeries and detecting of multiple video shot forgeries. |
| [21] | Frame insertion, deletion and duplication. | Correlation between 2-D phase congruency of successive frames. | Localized the tampered positions efficiently. | Failed in distinguishing whether the inserted frames are copied from the same video or not. |
| [22] | Multiple/double compression | Pixel estimation and double compression statistics. | High detection accuracies. | Failed in localization forged frames. |
| [23] | Multiple/double compression | Number of different coefficients between I frames of the singly and doubly compressed MPEG-2 videos. | Effective in double compression detection with same bit rate. | Performance depends on proper selection of recompression bitrate. |
| [24] | Region tampering | Motion residuals. | High accuracy. | Failed in forgery localization. |
| [25] | Region tampering | Zernike moments and 3D patch match. | Effective in forgery detecting and locating regions. | Accuracy was very low. |
| [26] | Region tampering | Optical flow coefficient is computed for each part. | Detected copy/move forgery effectively. | Detection failed in videos with a high amount of motion. |
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| T | The input video. | U and VT | Unitary matrix. |
| L | Total number of all video frames. | Xm | SVD feature matrix of every 3D-tensor of the selected Pn. |
| H × W | Total number of rows and columns. | Q | Total number of 3D-tensor feature vectors of selected Pn. |
| Pn | nth sub-group of a total number of N sub-groups consisting the whole T. | Rm | Correlation between the successive 3D-tensors of the selected Pn. |
| mth 3D-tensors of a total number of M tensors consisting P. | Sf | SVD matrix of each frame in 3D-tensor of the selected Pn. | |
| I | Frame matrix of each Pn. | Yf | SVD feature matrix of every frame of the 3D-tensor. |
| tx, ty | Partial derivatives of the pixel intensity with coordinates (x,y) in horizontal and vertical direction. | B | Total number of each frame feature vectors of the selected Pn. |
| Corn | Harris corner response. | Rz | Correlation values between successive frames of 3D-tensors. |
| {(xc, yc)} | All Harris corner points. | F | Number of frames of forged 3d-tensors. |
| NO. | Dataset Name | Length | Frame Rate | Format | Resolution |
|---|---|---|---|---|---|
| 1 | Akyio | 300 | 30 fps | YUV | 176 × 144 |
| 2 | Hall Monitor | 300 | 30 fps | YUV | 176 × 144 |
| 3 | Paris | 1065 | 30 fps | YUV | 352 × 288 |
| 4 | Suzie | 150 | 30 fps | YUV | 176 × 144 |
| 5 | Flower | 250 | 30 fps | YUV | 352 × 288 |
| 6 | Miss America | 150 | 30 fps | YUV | 352 × 288 |
| 7 | Waterfall | 260 | 30 fps | YUV | 352 × 288 |
| 8 | Container | 300 | 30 fps | YUV | 352 × 288 |
| 9 | Salesman | 449 | 30 fps | YUV | 176 × 144 |
| 10 | Claire | 494 | 30 fps | YUV | 176 × 144 |
| 11 | Bus | 150 | 30 fps | YUV | 352 × 288 |
| 12 | Foreman | 300 | 30 fps | YUV | 176 × 144 |
| 13 | Tempete | 260 | 30 fps | YUV | 352 × 288 |
| 14 | Coastguard | 300 | 30 fps | YUV | 176 × 144 |
| 15 | Carphone | 382 | 30 fps | YUV | 176 × 144 |
| 16 | Mobile | 300 | 30 fps | YUV | 176 × 144 |
| 17 | Mother and Daughter | 300 | 30 fps | YUV | 176 × 144 |
| 18 | News | 300 | 30 fps | YUV | 176 × 144 |
| Number of Operations | |||
|---|---|---|---|
| Tensor Size | F = 20 frames/tensor | F = 30 frames/tensor | F = 40 frames/tensor |
| F × 16 × 16 | 5136 | 7696 | 10,256 |
| F × 32 × 32 | 20,512 | 30,752 | 40,992 |
| F × 64 × 64 | 81,984 | 122,944 | 163,904 |
| F ×100 × 100 | 200,100 | 300,100 | 400,100 |
| F × 128 × 128 | 327,808 | 491,648 | 655,488 |
| Detecting Stage | Locating Stage | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HARRIS | GLCM | SVD | HARRIS | GLCM | SVD | |||||||||||||
| No | Precision (%) | Recall (%) | F1 Score (%) | Precision (%) | Recall (%) | F1 Score (%) | Precision (%) | Recall (%) | F1 Score (%) | Precision (%) | Recall (%) | F1 Score (%) | Precision (%) | Recall (%) | F1 Score (%) | Precision (%) | Recall (%) | F1 Score (%) |
| 10 | 77 | 54 | 63 | 84 | 56 | 67 | 96 | 94 | 95 | 90 | 81 | 85 | 96 | 82 | 88 | 98 | 98 | 98 |
| 20 | 77 | 54 | 63 | 84 | 56 | 67 | 96 | 94 | 95 | 93 | 84 | 88 | 96 | 87 | 91 | 98 | 100 | 99 |
| 30 | 77 | 54 | 63 | 84 | 56 | 67 | 96 | 94 | 95 | 96 | 87 | 91 | 96 | 87 | 91 | 100 | 100 | 100 |
| 40 | 77 | 54 | 63 | 84 | 56 | 67 | 96 | 94 | 95 | 96 | 87 | 91 | 96 | 87 | 91 | 100 | 100 | 100 |
| 50 | 77 | 54 | 63 | 84 | 56 | 67 | 96 | 94 | 95 | 96 | 87 | 91 | 96 | 87 | 91 | 100 | 100 | 100 |
| Avg. | 77 | 54 | 63 | 84 | 56 | 67 | 96 | 94 | 95 | 94 | 85 | 89 | 96 | 86 | 90 | 99.2 | 99.6 | 99.4 |
| Detecting | Locating | |||||
|---|---|---|---|---|---|---|
| No. of Forged Frames | Precision (%) | Recall (%) | F1 Score (%) | Precision (%) | Recall (%) | F1 Score (%) |
| <10 | None | None | None | None | None | none |
| 10 | 92 | 90 | 91 | 98 | 96 | 97 |
| 20 | 92 | 90 | 91 | 98 | 98 | 98 |
| 30 | 92 | 90 | 91 | 98 | 98 | 98 |
| 40 | 92 | 90 | 91 | 98 | 98 | 98 |
| 50 | 92 | 90 | 91 | 100 | 100 | 100 |
| Avg. | 92 | 90 | 91 | 98.4 | 98 | 98.2 |
| Methods | Attacks Types | Precision (%) | Recall (%) | F1 Score (%) |
|---|---|---|---|---|
| Ref. [16] | Insertion, Deletion | 89 | 86 | 87 |
| Ref. [15] | Insertion, Deletion | 95 | 92 | 93 |
| Ref. [13] | Deletion | 72 | 66 | 69 |
| Ref. [6] | Insertion, Deletion | 85 | 89 | 87 |
| Ref. [18] | Insertion, Deletion and Duplication | 98 | 99 | 98 |
| Proposed | Insertion, Deletion | 99 | 99 | 99 |
| Video | Original Length | Forgery Operation | Tampered Length | Total Time (Seconds) |
|---|---|---|---|---|
| 1 | 300 | 10 frames inserted in 101:110 | 310 | 39.42 |
| 2 | 300 | 20 frames inserted in 50:70 | 320 | 39.49 |
| 3 | 250 | 30 frames inserted in 101:130 | 280 | 38.24 |
| 4 | 300 | 40 frames inserted in 100:140 | 340 | 39.89 |
| 5 | 382 | 50 frames inserted in 221:270 | 432 | 40.97 |
| 6 | 449 | 20 frames inserted in 201:220 | 469 | 41.40 |
| 7 | 300 | 50 frames inserted in 101:150 | 350 | 40.01 |
| 8 | 1065 | 30 frames inserted in 50:80 | 1086 | 46.24 |
| 9 | 300 | 40 frames inserted in 170:210 | 340 | 39.75 |
| 10 | 300 | 10 frames deleted in 50:59 | 290 | 27.46 |
| 11 | 300 | 20 frames deleted in 50:69 | 280 | 26.45 |
| 12 | 260 | 30 frames deleted in 160:190 | 230 | 23.89 |
| 13 | 449 | 40 frames deleted in 360:400 | 409 | 29.02 |
| 14 | 300 | 40 frames deleted in 200:240 | 260 | 25.22 |
| 15 | 150 | 10 frames deleted in 60:79 | 140 | 22.02 |
| 16 | 300 | 20 frames deleted in 100:119 | 280 | 26.44 |
| 17 | 250 | 30 frames deleted in 160:190 | 220 | 23.42 |
| 18 | 300 | 40 frames deleted in 170:210 | 260 | 25.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsakar, Y.M.; Mekky, N.E.; Hikal, N.A. Detecting and Locating Passive Video Forgery Based on Low Computational Complexity Third-Order Tensor Representation. J. Imaging 2021, 7, 47. https://doi.org/10.3390/jimaging7030047
Alsakar YM, Mekky NE, Hikal NA. Detecting and Locating Passive Video Forgery Based on Low Computational Complexity Third-Order Tensor Representation. Journal of Imaging. 2021; 7(3):47. https://doi.org/10.3390/jimaging7030047
Chicago/Turabian StyleAlsakar, Yasmin M., Nagham E. Mekky, and Noha A. Hikal. 2021. "Detecting and Locating Passive Video Forgery Based on Low Computational Complexity Third-Order Tensor Representation" Journal of Imaging 7, no. 3: 47. https://doi.org/10.3390/jimaging7030047
APA StyleAlsakar, Y. M., Mekky, N. E., & Hikal, N. A. (2021). Detecting and Locating Passive Video Forgery Based on Low Computational Complexity Third-Order Tensor Representation. Journal of Imaging, 7(3), 47. https://doi.org/10.3390/jimaging7030047








