Comparison of Different Image Data Augmentation Approaches
Abstract
:1. Introduction
- An evaluation across four benchmarks of some of the best augmentation methods based on image manipulations;
- The introduction of two new augmentation methods utilizing the DWT and CQT transforms (DWT achieves a top performance of 98.41% accuracy on the GRAV data set);
- An experimentally derived ensemble that achieves state-of-the-art performance on the VIR (90.00%), BARK (91.27%), POR (89.21%), and GRAV (98.33%) benchmarks. This result shows that varying data augmentation is a feasible way for building an ensemble of classifiers for image classification.
- Access to all the MATLAB source code for the experiments reported in this work (available at https://github.com/LorisNanni, accessed on 24 November 2021).
2. Related Works
3. Materials and Methods
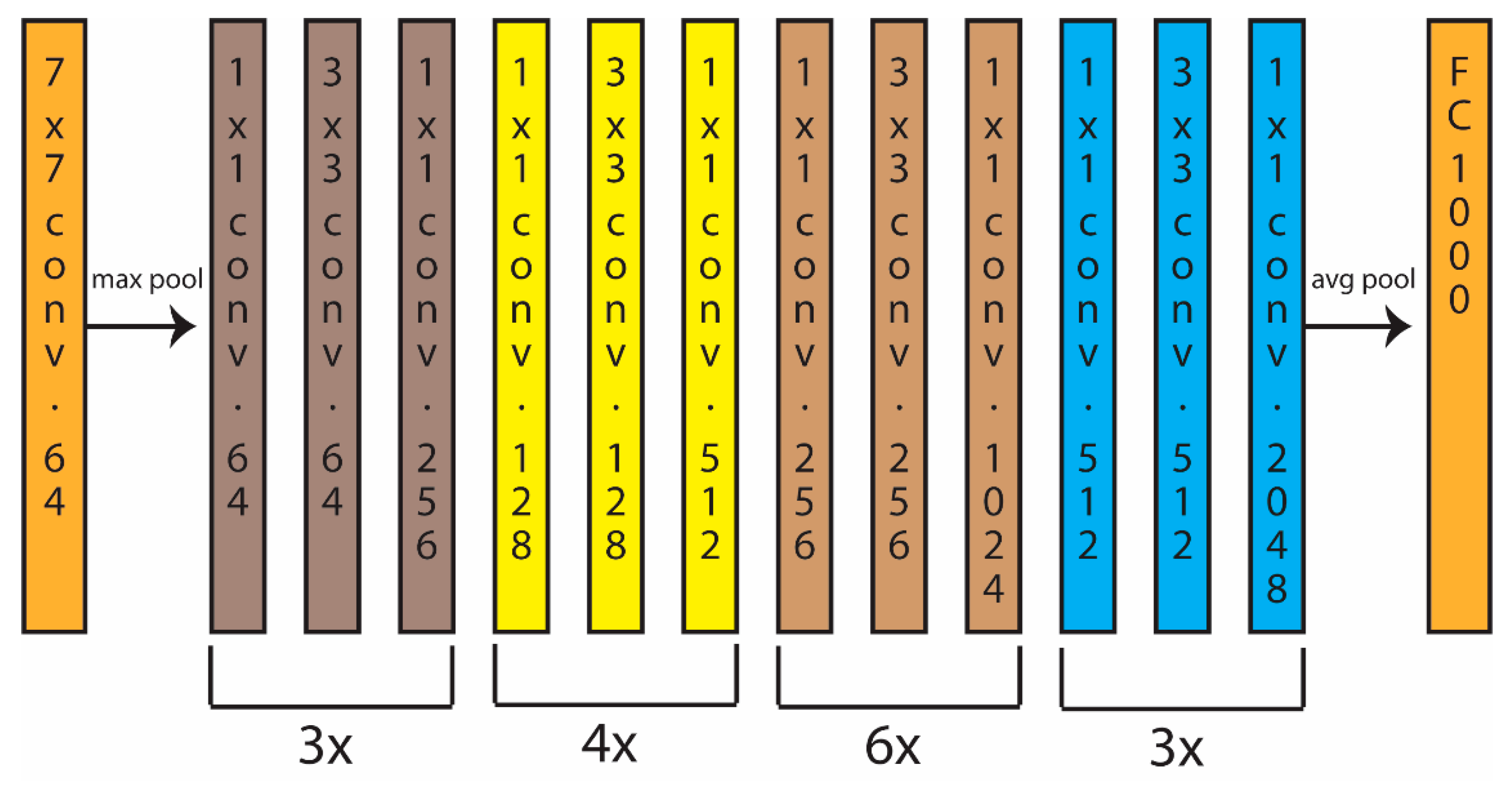
3.1. Proposed Approach
3.2. Data Augmentation Methods
3.3. Data Sets
4. Experimental Results
- EnsDA_all: this is the fusion by sum rule among all the ResNet50 trained using all eleven data augmentation approaches; a separate ResNet50 is trained for each of the data augmentation approaches. The virus data set has gray level images; for this reason, the three data augmentation methods based on color (App6–8) perform poorly on VIR, so these methods are not used for VIR.
- EnsDA_5: this is a fusion where only five ResNet50 networks are trained, a separate one on the first five data augmentation approaches (App1–5).
- EnsBase: this is a baseline approach intended to validate the performance of EnsDA_all; EnsBase is an ensemble (combined by sum rule) of eleven ResNet50 networks each trained only on App3, selected because it obtains the highest average performance among all the data augmentation approaches.
- EnsBase_5: this is another baseline approach intended to validate the performance of EnsDA_5; it is an ensemble of five ResNet50 with each coupled with App3.
- Data augmentation approaches strongly boost performance, as evident by comparing the ensembles using augmentation to the low performance of NoDA (well known in the literature).
- There is no clear winner among the data augmentation approaches; in each data set, the best method is different.
- The best performance is obtained by EnsDA_all; this ensemble obtains the best performance, even when compared with the state of the art, on all the data sets. This result shows that varying data augmentation is a feasible way for building an ensemble of classifiers for image classification.
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Landau, Y.E.; Kiryati, N. Dataset Growth in Medical Image Analysis Research. J. Imaging 2021, 7, 8. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Shirke, V.; Walika, R.; Tambade, L. Drop: A Simple Way to Prevent Neural Network by Overfitting. Int. J. Res. Eng. Sci. Manag. 2018, 1, 2581–5782. [Google Scholar]
- Palatucci, M.; Pomerleau, D.A.; Hinton, G.E.; Mitchell, T.M. Zero-shot Learning with Semantic Output Codes. In Proceedings of the Advances in Neural Information Processing Systems 22: 23rd Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009. [Google Scholar]
- Xian, Y.; Lampert, C.H.; Schiele, B.; Akata, Z. Zero-Shot Learning-A Comprehensive Evaluation of the Good, the Bad and the Ugly. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2251–2265. [Google Scholar] [CrossRef] [Green Version]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Naveed, H. Survey: Image Mixing and Deleting for Data Augmentation. arXiv 2021, arXiv:2106.07085. [Google Scholar]
- Khosla, C.; Saini, B.S. Enhancing Performance of Deep Learning Models with different Data Augmentation Techniques: A Survey. In Proceedings of the International Conference on Intelligent Engineering and Management (ICIEM), London, UK, 17–19 June 2020; pp. 79–85. [Google Scholar] [CrossRef]
- Chlap, P.; Min, H.; Vandenberg, N.; Dowling, J.; Holloway, L.; Haworth, A. A review of medical image data augmentation techniques for deep learning applications. J. Med Imaging Radiat. Oncol. 2021, 65, 545–563. [Google Scholar] [CrossRef]
- Lindner, L.; Narnhofer, D.; Weber, M.; Gsaxner, C.; Kolodziej, M.; Egger, J. Using Synthetic Training Data for Deep Learning-Based GBM Segmentation. In Proceedings of the 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 6724–6729. [Google Scholar] [CrossRef]
- Lu, C.-Y.; Rustia, D.J.A.; Lin, T.-T. Generative Adversarial Network Based Image Augmentation for Insect Pest Classification Enhancement. IFAC-PapersOnLine 2019, 52, 1–5. [Google Scholar] [CrossRef]
- Shin, Y.; Qadir, H.A.; Balasingham, I. Abnormal Colon Polyp Image Synthesis Using Conditional Adversarial Networks for Improved Detection Performance. IEEE Access 2018, 6, 56007–56017. [Google Scholar] [CrossRef]
- Velasco, G.A.; Holighaus, N.; Dörfler, M.; Grill, T. Constructing an invertible constant-q transform with nonstationary gabor frames. In Proceedings of the 14th International Conference on Digital Audio Effects (DAFx 11), Paris, France, 19–23 September 2011. [Google Scholar]
- Kylberg, G.; Uppström, M.; Sintorn, I.-M. Virus texture analysis using local binary patterns and radial density profiles. In Proceedings of the 18th Iberoamerican Congress on Pattern Recognition (CIARP), Pucón, Chile, 15–18 November 2011. [Google Scholar]
- Liu, S.; Yang, J.; Agaian, S.S.; Yuan, C. Novel features for art movement classification of portrait paintings. Image Vis. Comput. 2021, 108, 104121. [Google Scholar] [CrossRef]
- Carpentier, M.; Giguère, P.; Gaudreault, J. Tree Species Identification from Bark Images Using Convolutional Neural Networks. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1075–1081. [Google Scholar]
- Bahaadini, S.; Noroozi, V.; Rohani, N.; Coughlin, S.; Zevin, M.; Smith, J.R.; Kalogera, V.; Katsaggelos, A. Machine learning for Gravity Spy: Glitch classification and dataset. Inf. Sci. 2018, 444, 172–186. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. COPY ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1106–1114. [Google Scholar] [CrossRef]
- Shijie, J.; Ping, W.; Peiyi, J.; Siping, H. Research on data augmentation for image classification based on convolution neural networks. In Proceedings of the Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the MICCAI: International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015. [Google Scholar]
- Mikołajczyk, A.; Grochowski, M. Data augmentation for improving deep learning in image classification problem. In Proceedings of the International Interdisciplinary PhD Workshop (IIPhDW), Swinoujscie, Poland, 9–12 May 2018; pp. 117–122. [Google Scholar] [CrossRef]
- Moreno-Barea, F.J.; Strazzera, F.; Jerez, J.M.; Urda, D.; Franco, L. Forward Noise Adjustment Scheme for Data Augmentation. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bengaluru, India, 18–21 November 2018; pp. 728–734. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images. University of Toronto. 2009. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 24 November 2021).
- Ojala, T.; Mäenpää, T.; Pietikäinen, M.; Viertola, J.; Kyllönen, J.; Huovinen, S. Outex: New framework for empirical evaluation of texture analysis algorithms. In Proceedings of the ICPR’02: Proceedings of the 16th International Conference on Pattern Recognition, Quebec City, QC, Canada, 11–15 August 2002; IEEE Computer Society: Washington, DC, USA, 2002; Volume 1. [Google Scholar]
- Picard, R.; Graczyk, C.; Mann, S.; Wachman, J.; Picard, L.; Campbell, L. Vision Texture Database. Available online: http://vismod.media.mit.edu/pub/VisTex/VisTex.tar.gz (accessed on 24 November 2021).
- Backes, A.R.; Casanova, D.; Bruno, O.M. Color texture analysis based on fractal descriptors. Pattern Recognit. 2012, 45, 1984–1992. [Google Scholar] [CrossRef]
- Kwitt, R.; Meerwald, P. Salzburg Texture Image Database (STex). Available online: https://wavelab.at/sources/STex/ (accessed on 24 November 2021).
- Porebski, A.; Vandenbroucke, N.; Macaire, L.; Hamad, D. A new benchmark image test suite for evaluating colour texture classification schemes. Multimed. Tools Appl. 2013, 70, 543–556. [Google Scholar] [CrossRef]
- Caputo, B.; Hayman, E.; Mallikarjuna, P.B. Class-Specific Material Categorisation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Beijing, China, 17–20 October 2005; pp. 1597–1604. [Google Scholar]
- Bianconi, F.; Fernández, A.; González, E.; Saetta, S.A. Performance analysis of colour descriptors for parquet sorting. Expert Syst. Appl. 2013, 40, 1636–1644. [Google Scholar] [CrossRef]
- Cusano, C.; Napoletano, P.; Schettini, R. T1K+: A Database for Benchmarking Color Texture Classification and Retrieval Methods. Sensors 2021, 21, 1010. [Google Scholar] [CrossRef]
- Chatfield, K.; Simonyan, K.; Vedaldi, A.; Zisserman, A. Return of the Devil in the Details: Delving Deep into Convolutional Nets. arXiv 2014, arXiv:1405.3531. [Google Scholar]
- Taylor, L.; Nitschke, G. Improving Deep Learning with Generic Data Augmentation. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI), Bengaluru, India, 18–21 November 2018; pp. 1542–1547. [Google Scholar]
- Kang, G.; Dong, X.; Zheng, L.; Yang, Y. PatchShuffle Regularization. arXiv 2017, arXiv:1707.07103. [Google Scholar]
- Inoue, H. Data Augmentation by Pairing Samples for Images Classification. arXiv 2018, arXiv:1801.02929. [Google Scholar]
- Hendrycks, D.; Mu, N.; Cubuk, E.D.; Zoph, B.; Gilmer, J.; Lakshminarayanan, B. AugMix: A Simple Data Processing Method to Improve Robustness and Uncertainty. arXiv 2020, arXiv:1912.02781. [Google Scholar]
- Summers, C.; Dinneen, M.J. Improved Mixed-Example Data Augmentation. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; pp. 1262–1270. [Google Scholar]
- Liang, D.; Yang, F.; Zhang, T.; Yang, P. Understanding Mixup Training Methods. IEEE Access 2018, 6, 58774–58783. [Google Scholar] [CrossRef]
- Zhong, Z.; Zheng, L.; Kang, G.; Li, S.; Yang, Y. Random Erasing Data Augmentation. arXiv 2020, arXiv:1708.04896. [Google Scholar] [CrossRef]
- Devries, T.; Taylor, G.W. Improved Regularization of Convolutional Neural Networks with Cutout. arXiv 2017, arXiv:1708.04552. [Google Scholar]
- Nanni, L.; Brahnam, S.; Ghidoni, S.; Maguolo, G. General Purpose (GenP) Bioimage Ensemble of Handcrafted and Learned Features with Data Augmentation. arXiv 2019, arXiv:1904.08084. [Google Scholar]
- Nalepa, J.; Myller, M.; Kawulok, M. Training- and Test-Time Data Augmentation for Hyperspectral Image Segmentation. IEEE Geosci. Remote. Sens. Lett. 2020, 17, 292–296. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Khan, A.M.; Rajpoot, N.; Treanor, D.; Magee, D. A Nonlinear Mapping Approach to Stain Normalization in Digital Histopathology Images Using Image-Specific Color Deconvolution. IEEE Trans. Biomed. Eng. 2014, 61, 1729–1738. [Google Scholar] [CrossRef]
- Gupta, D.; Choubey, S. Discrete Wavelet Transform for Image Processing. Int. J. Emerg. Technol. Adv. Eng. 2014, 4, 598–602. [Google Scholar]
- Nanni, L.; Ghidoni, S.; Brahnam, S. Deep features for training support vector machines. J. Imaging 2021, 7, 177. [Google Scholar] [CrossRef]
- Remes, V.; Haindl, M. Rotationally Invariant Bark Recognition. In Proceedings of the IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR S+SSPR), Beijing, China, 17–19 August 2018. [Google Scholar]
- Forcen, J.I.; Pagola, M.; Barrenechea, E.; Bustince, H. Co-occurrence of deep convolutional features for image search. Image Vis. Comput. 2020, 97, 103909. [Google Scholar] [CrossRef] [Green Version]
- Feig, E.; Winograd, S. Fast algorithms for the discrete cosine transform. IEEE Trans. Signal Process. 1992, 49, 2174–2193. [Google Scholar] [CrossRef]
- Xie, Y.; Lin, B.; Qu, Y.; Li, C.; Zhang, W.; Ma, L.; Wen, Y.; Tao, D. Joint Deep Multi-View Learning for Image Clustering. IEEE Trans. Knowl. Data Eng. 2021, 33, 3594–3606. [Google Scholar] [CrossRef]
- Nanni, L.; Luca, E.D.; Facin, M.L. Deep learning and hand-crafted features for virus image classification. J. Imaging 2020, 6, 143. [Google Scholar] [CrossRef] [PubMed]
- Geus, A.R.; Backes, A.R.; Souza, J.R. Variability Evaluation of CNNs using Cross-validation on Viruses Images. In Proceedings of the VISIGRAPP 2020: 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Valletta, Malta, 27–29 February 2020. [Google Scholar]
- Wen, Z.-J.; Liu, Z.; Zong, Y.; Li, B. Latent Local Feature Extraction for Low-Resolution Virus Image Classification. J. Oper. Res. Soc. China 2020, 8, 117–132. [Google Scholar] [CrossRef]
- ABackes, R.; Junior, J.J. Virus Classification by Using a Fusion of Texture Analysis Methods. In Proceedings of the International Conference on Systems, Signals and Image Processing (IWSSIP), Niteroi, Rio de Janeiro, Brazil, 1–3 July 2020; pp. 290–295. [Google Scholar]
- De Santosa, F.L.C.; Paci, M.; Nanni, L.; Brahnam, S.; Hyttinen, J. Computer vision for virus image classification. Biosyst. Eng. 2015, 138, 11–22. [Google Scholar] [CrossRef]
- Boudra, S.; Yahiaoui, I.; Behloul, A. A set of statistical radial binary patterns for tree species identification based on bark images. Multimed. Tools Appl. 2021, 80, 22373–22404. [Google Scholar] [CrossRef]
- Remeš, V.; Haindl, M. Bark recognition using novel rotationally invariant multispectral textural features. Pattern Recognit Lett. 2019, 125, 612–617. [Google Scholar] [CrossRef]



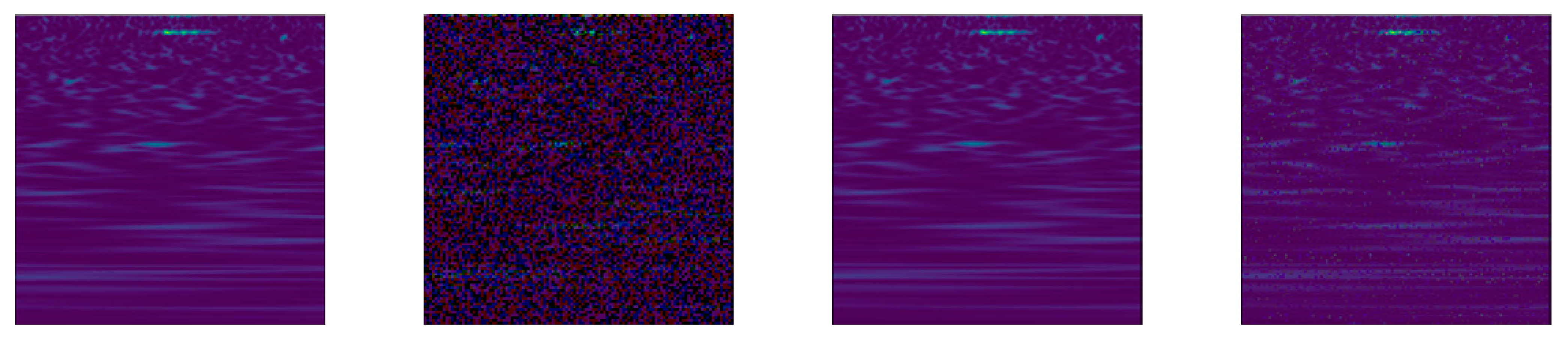
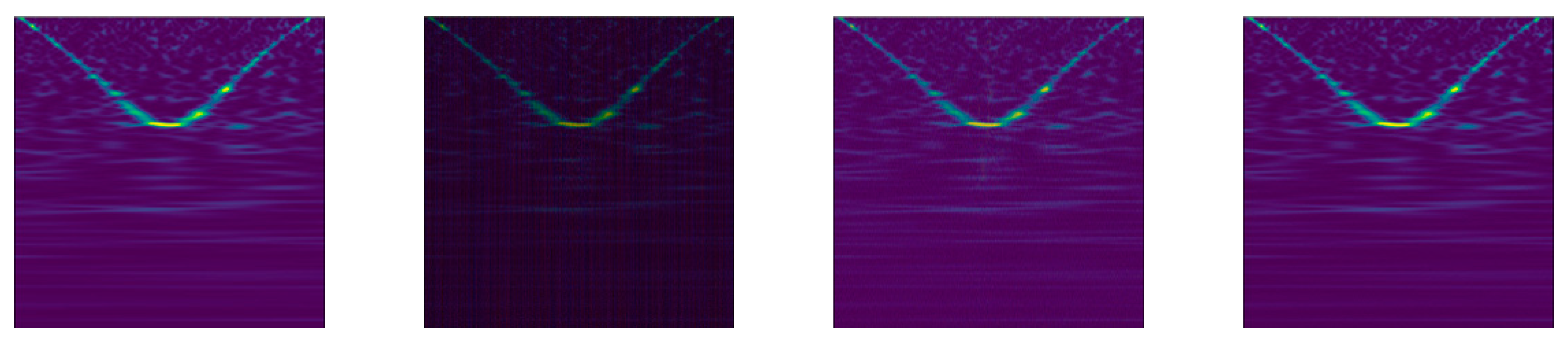
| Data Augmentation Method | Number of Generated Images |
|---|---|
| App1 | 3 |
| App2 | 6 |
| App3 | 4 |
| App4 | 3 |
| App5 | 3 |
| App6 | 3 |
| App7 | 7 |
| App8 | 2 |
| App9 | 6 |
| App10 | 3 |
| App11 | 3 |
| DataAUG | VIR | BARK | GRAV | POR |
|---|---|---|---|---|
| NoDA | 85.53 | 87.48 | 97.66 | 86.29 |
| App1 | 87.00 | 89.60 | 97.83 | 87.05 |
| App2 | 86.87 | 90.17 | 98.08 | 85.97 |
| App3 | 87.80 | 89.45 | 97.99 | 87.05 |
| App4 | 86.33 | 87.91 | 97.74 | 84.90 |
| App5 | 86.00 | 87.61 | 97.83 | 86.41 |
| App6 | -- | 88.63 | 98.08 | 87.37 |
| App7 | -- | 89.28 | 97.99 | 88.13 |
| App8 | -- | 87.29 | 97.74 | 86.06 |
| App9 | 85.67 | 88.86 | 98.24 | 86.19 |
| App10 | 84.20 | 86.39 | 98.41 | 85.10 |
| App11 | 85.47 | 89.20 | 97.91 | 86.71 |
| [29] | 82.93 | -- | -- | -- |
| [33] | 83.07 | -- | -- | -- |
| EnsDA_all | 90.00 | 91.27 | 98.33 | 89.21 |
| EnsDA_5 | 89.60 | 91.01 | 98.08 | 88.56 |
| EnsBase | 89.73 | 90.67 | 98.16 | 87.58 |
| EnsBase_5 | 89.60 | 90.66 | 97.99 | 87.48 |
| State of the art | 89.60 | 90.40 | 98.21 | 80.09/90.08 * |
| EnsDA_all | [46] | [51] | [52] | [53] | [54] | [14] | [53] | [55] |
|---|---|---|---|---|---|---|---|---|
| 90.00 | 89.60 | 89.47 | 89.00 | 88.00 | 87.27 | 87.00 * | 86.20 | 85.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nanni, L.; Paci, M.; Brahnam, S.; Lumini, A. Comparison of Different Image Data Augmentation Approaches. J. Imaging 2021, 7, 254. https://doi.org/10.3390/jimaging7120254
Nanni L, Paci M, Brahnam S, Lumini A. Comparison of Different Image Data Augmentation Approaches. Journal of Imaging. 2021; 7(12):254. https://doi.org/10.3390/jimaging7120254
Chicago/Turabian StyleNanni, Loris, Michelangelo Paci, Sheryl Brahnam, and Alessandra Lumini. 2021. "Comparison of Different Image Data Augmentation Approaches" Journal of Imaging 7, no. 12: 254. https://doi.org/10.3390/jimaging7120254
APA StyleNanni, L., Paci, M., Brahnam, S., & Lumini, A. (2021). Comparison of Different Image Data Augmentation Approaches. Journal of Imaging, 7(12), 254. https://doi.org/10.3390/jimaging7120254








