Improved Coefficient Recovery and Its Application for Rewritable Data Embedding
Abstract
1. Introduction
2. Related Work
3. Proposed method
3.1. Improved Coefficient Recovery
3.2. Rewritable Data Embedding
3.3. Data Extraction and Image Recovery
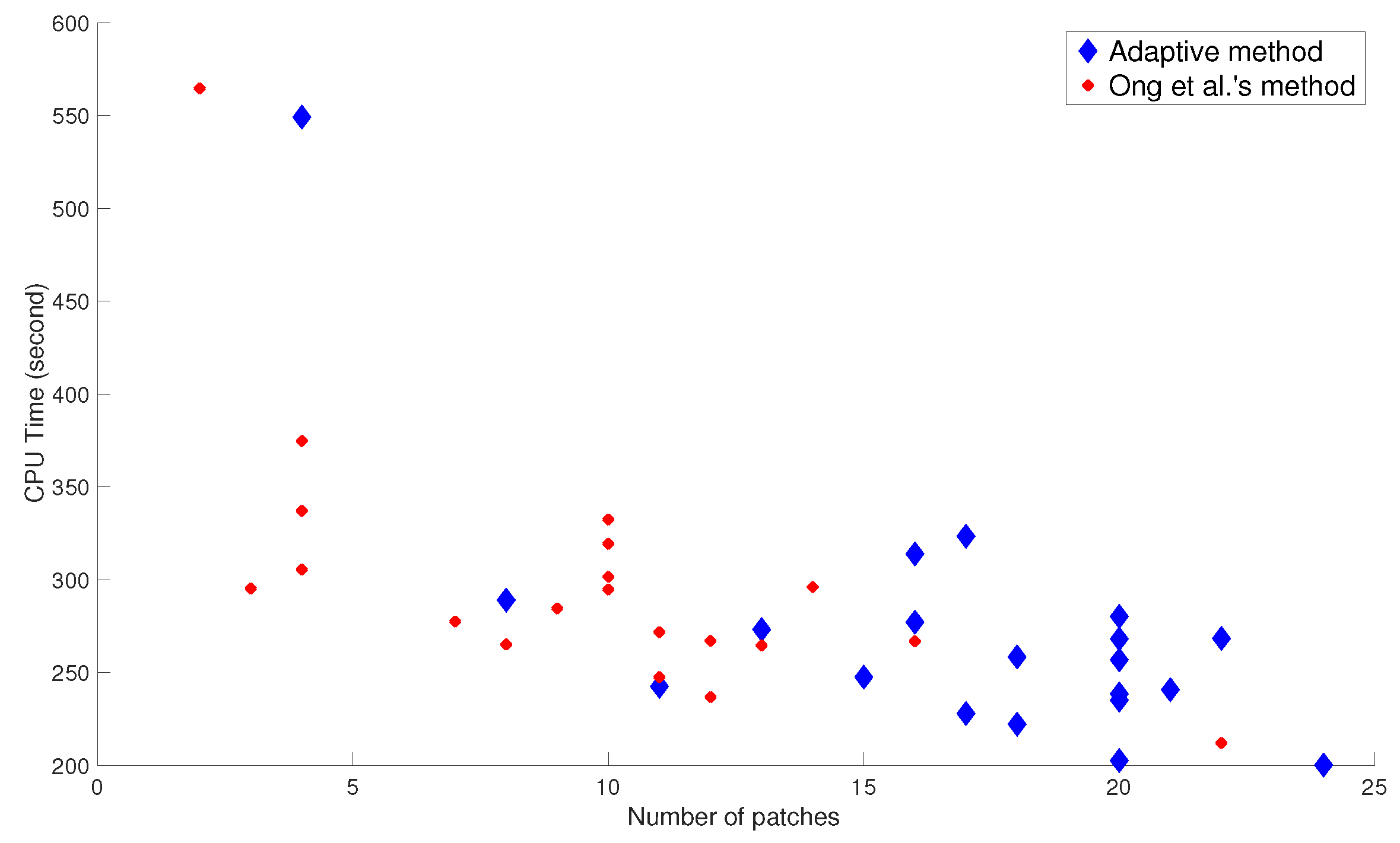
4. Experiment
4.1. Coefficient Recovery
4.2. Rewritable Data Embedding
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Wallace, G. The JPEG Still Picture Compression Standard. IEEE Trans. Consum. Electron. 1992, 38, 18–34. [Google Scholar] [CrossRef]
- Grangetto, M.; Magli, E.; Olmo, G. Ensuring quality of service for image transmission: Hybrid loss protection. IEEE Trans. Image Process. 2004, 13, 751–757. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Huang, S.; Liang, S.; Fu, S.; Shi, W.; Tiwari, D.; Chen, H.b. Characterizing Disk Health Degradation and Proactively Protecting Against Disk Failures for Reliable Storage Systems. In Proceedings of the 2019 IEEE International Conference on Autonomic Computing (ICAC), Umeå, Sweden, 16–20 June 2019; pp. 157–166. [Google Scholar] [CrossRef]
- Uehara, T.; Safavi-Naini, R.; Ogunbona, P. Recovering DC Coefficients in Block-Based DCT. IEEE Trans. Image Process. 2006, 15, 3592–3596. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, S.; Ahmad, J.J.; Saupe, D.; Kuo, C.C.J. An improved DC recovery method from AC coefficients of DCT-transformed images. In Proceedings of the 2010 IEEE International Conference on Image Processing, IEEE, Athens, Greece, 7–10 October 2010. [Google Scholar] [CrossRef]
- Li, S.; Karrenbauer, A.; Saupe, D.; Kuo, C.C.J. Recovering missing coefficients in DCT-transformed images. In Proceedings of the 2011 18th IEEE International Conference on Image Processing, IEEE, Brussels, Belgium, 11–14 September 2011. [Google Scholar] [CrossRef]
- Ong, S.; Li, S.; Wong, K.; Tan, K. Fast recovery of unknown coefficients in DCT-transformed images. Signal Process. Image Commun. 2017, 58, 1–13. [Google Scholar] [CrossRef]
- Minemura, K.; Wong, K.; Phan, R.C.W.; Tanaka, K. A Novel Sketch Attack for H.264/AVC Format-Compliant Encrypted Video. IEEE Trans. Circuits Syst. Video Technol. 2017, 27, 2309–2321. [Google Scholar] [CrossRef]
- Kitanovski, V.; Pedersen, M. Detection of Orientation-Modulation Embedded Data in Color Printed Natural Images. J. Imaging 2018, 4, 56. [Google Scholar] [CrossRef]
- Tan, K.; Wong, K.; Ong, S.; Tanaka, K. Rewritable data insertion in encrypted JPEG using coefficient prediction method. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), IEEE, Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 214–219. [Google Scholar] [CrossRef]
- Dragoi, I.C.; Coltuc, D. Reversible Data Hiding in Encrypted Images Based on Reserving Room After Encryption and Multiple Predictors. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2102–2105. [Google Scholar] [CrossRef]
- Gardella, M.; Musé, P.; Morel, J.M.; Colom, M. Forgery Detection in Digital Images by Multi-Scale Noise Estimation. J. Imaging 2021, 7, 119. [Google Scholar] [CrossRef]
- Bas, P.; Filler, T.; Pevný, T. “Break Our Steganographic System”: The Ins and Outs of Organizing BOSS. In Information Hiding; Filler, T., Pevný, T., Craver, S., Ker, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 59–70. [Google Scholar]
- Bradley, D.; Roth, G. Adaptive Thresholding using the Integral Image. J. Graph. Tools 2007, 12, 13–21. [Google Scholar] [CrossRef]
- Sii, A. MDPI Test Images, School of Information Technology. Test Images. 2021. Available online: https://bit.ly/3lTSUNu (accessed on 24 September 2021).
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Guo, J.M.; Chang, C.H. Prediction-based watermarking schemes using ahead/post AC prediction. Signal Process. 2010, 90, 2552–2566. [Google Scholar] [CrossRef]





| Image | Adaptive Method | Ong et al.’s Method | CPU Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | No. of | CPU | PSNR | SSIM | No. of | CPU | Improvement | |
| (dB) | Patches | Time (s) | (dB) | Patches | Time (s) | (%) | |||
| N1 | 25.59 | 0.9433 | 4 | 549.13 | 25.49 | 0.9366 | 2 | 564.66 | 2.75 |
| N2 | 31.88 | 0.9497 | 16 | 277.17 | 31.00 | 0.9410 | 10 | 301.63 | 8.11 |
| N3 | 31.66 | 0.9445 | 18 | 258.42 | 31.64 | 0.9442 | 13 | 264.72 | 2.38 |
| N4 | 16.50 | 0.8881 | 18 | 222.23 | 16.41 | 0.8873 | 12 | 236.81 | 6.16 |
| N5 | 30.29 | 0.9277 | 17 | 323.44 | 30.00 | 0.9273 | 10 | 332.45 | 2.71 |
| N6 | 37.06 | 0.9602 | 21 | 240.80 | 37.12 | 0.9604 | 4 | 305.56 | 21.19 |
| N7 | 33.50 | 0.9230 | 20 | 238.56 | 33.11 | 0.9372 | 9 | 284.53 | 16.16 |
| N8 | 26.50 | 0.9624 | 24 | 200.23 | 25.96 | 0.9601 | 7 | 277.55 | 27.86 |
| N9 | 33.33 | 0.9658 | 8 | 289.05 | 33.14 | 0.9514 | 4 | 374.75 | 22.87 |
| N10 | 35.24 | 0.9600 | 17 | 227.97 | 35.03 | 0.9592 | 11 | 247.58 | 7.92 |
| N11 | 31.87 | 0.9419 | 20 | 235.14 | 25.81 | 0.9101 | 16 | 266.94 | 11.91 |
| N12 | 12.00 | 0.6400 | 11 | 242.56 | 11.79 | 0.6511 | 8 | 265.23 | 8.55 |
| N13 | 33.50 | 0.9312 | 20 | 202.63 | 33.11 | 0.9300 | 22 | 212.13 | 4.48 |
| N14 | 27.08 | 0.9288 | 22 | 268.38 | 26.88 | 0.9278 | 4 | 337.06 | 20.38 |
| N15 | 32.98 | 0.9351 | 20 | 256.88 | 32.54 | 0.9344 | 10 | 294.77 | 12.85 |
| N16 | 36.23 | 0.9508 | 20 | 268.14 | 25.81 | 0.9382 | 11 | 271.80 | 1.35 |
| N17 | 29.58 | 0.9422 | 20 | 280.23 | 30.02 | 0.9501 | 14 | 296.08 | 5.35 |
| N18 | 36.01 | 0.9692 | 16 | 313.91 | 35.17 | 0.9639 | 10 | 319.34 | 1.70 |
| N19 | 30.47 | 0.9097 | 13 | 273.19 | 28.81 | 0.8921 | 3 | 295.27 | 7.48 |
| N20 | 31.80 | 0.9214 | 15 | 247.58 | 30.94 | 0.9122 | 12 | 267.06 | 7.29 |
| Average | 30.15 | 0.9248 | 17.0 | 270.78 | 28.99 | 0.9207 | 9.6 | 286.01 | 10.02 |
| Image | Capacity | Qualified Blocks | Qualified Patches | ||
|---|---|---|---|---|---|
| N1 | 26.06/0.8673 | 25.51/0.9431 | 18,036 | 2004 | 4 |
| N2 | 24.10/0.8381 | 31.85/0.9494 | 21,708 | 2412 | 16 |
| N3 | 26.13/0.8293 | 31.61/0.9350 | 26,325 | 2925 | 18 |
| N4 | 28.95/0.8504 | 16.38/0.8571 | 18,063 | 2007 | 18 |
| N5 | 24.32/0.7709 | 30.27/0.9275 | 24,516 | 2724 | 17 |
| N6 | 28.58/0.8787 | 37.05/0.9600 | 31,779 | 3531 | 20 |
| N7 | 28.48/0.7967 | 33.49/0.9226 | 21,519 | 2391 | 20 |
| N8 | 33.60/0.9196 | 26.49/0.9619 | 23,355 | 2595 | 20 |
| N9 | 22.61/0.8059 | 33.28/0.9650 | 12,636 | 1404 | 8 |
| N10 | 27.47/0.8470 | 35.24/0.9597 | 15,255 | 1695 | 17 |
| N11 | 23.54/0.7833 | 31.84/0.9410 | 16,173 | 1797 | 20 |
| N12 | 36.04/0.9344 | 11.60/0.6340 | 17,118 | 1902 | 11 |
| N13 | 29.91/0.7995 | 33.15/0.9304 | 15,336 | 1704 | 20 |
| N14 | 24.77/0.8248 | 27.06/0.9281 | 22,977 | 2553 | 20 |
| N15 | 25.96/0.8097 | 32.93/0.9346 | 22,491 | 2499 | 20 |
| N16 | 28.61/0.8314 | 36.20/0.9501 | 23,328 | 2592 | 20 |
| N17 | 23.30/0.8165 | 29.55/0.9420 | 20,871 | 2319 | 20 |
| N18 | 23.30/0.8043 | 35.30/0.9644 | 17,145 | 1905 | 16 |
| N19 | 24.67/0.7776 | 30.39/0.9093 | 16,254 | 1806 | 13 |
| N20 | 25.66/0.7602 | 31.04/0.9171 | 18,036 | 2004 | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sii, A.; Ong, S.; Wong, K. Improved Coefficient Recovery and Its Application for Rewritable Data Embedding. J. Imaging 2021, 7, 244. https://doi.org/10.3390/jimaging7110244
Sii A, Ong S, Wong K. Improved Coefficient Recovery and Its Application for Rewritable Data Embedding. Journal of Imaging. 2021; 7(11):244. https://doi.org/10.3390/jimaging7110244
Chicago/Turabian StyleSii, Alan, Simying Ong, and KokSheik Wong. 2021. "Improved Coefficient Recovery and Its Application for Rewritable Data Embedding" Journal of Imaging 7, no. 11: 244. https://doi.org/10.3390/jimaging7110244
APA StyleSii, A., Ong, S., & Wong, K. (2021). Improved Coefficient Recovery and Its Application for Rewritable Data Embedding. Journal of Imaging, 7(11), 244. https://doi.org/10.3390/jimaging7110244







