5.2. Experiment Settings
All the experiments were implemented on a Windows workstation with an Intel Core i9 CPU at 3.3GHz and an Nvidia GTX-1080Ti GPU with 11 GB of graphics card memory via TensorFlow [
64]. The parameters in the proposed network were initialized by using Xavier initialization [
65]. We trained the meta-learning network with four tasks synergistically associated with four different CS ratios—10%, 20%, 30%, and 40%—and tested the well-trained model on the testing dataset with the same masks of these four ratios. We used 300 training data for each CS ratio, amounting to a total of 1200 images in the training dataset. The results for T1 and T2 MR reconstructions are shown in
Table 1 and
Table 2, respectively. The associated reconstructed images are displayed in
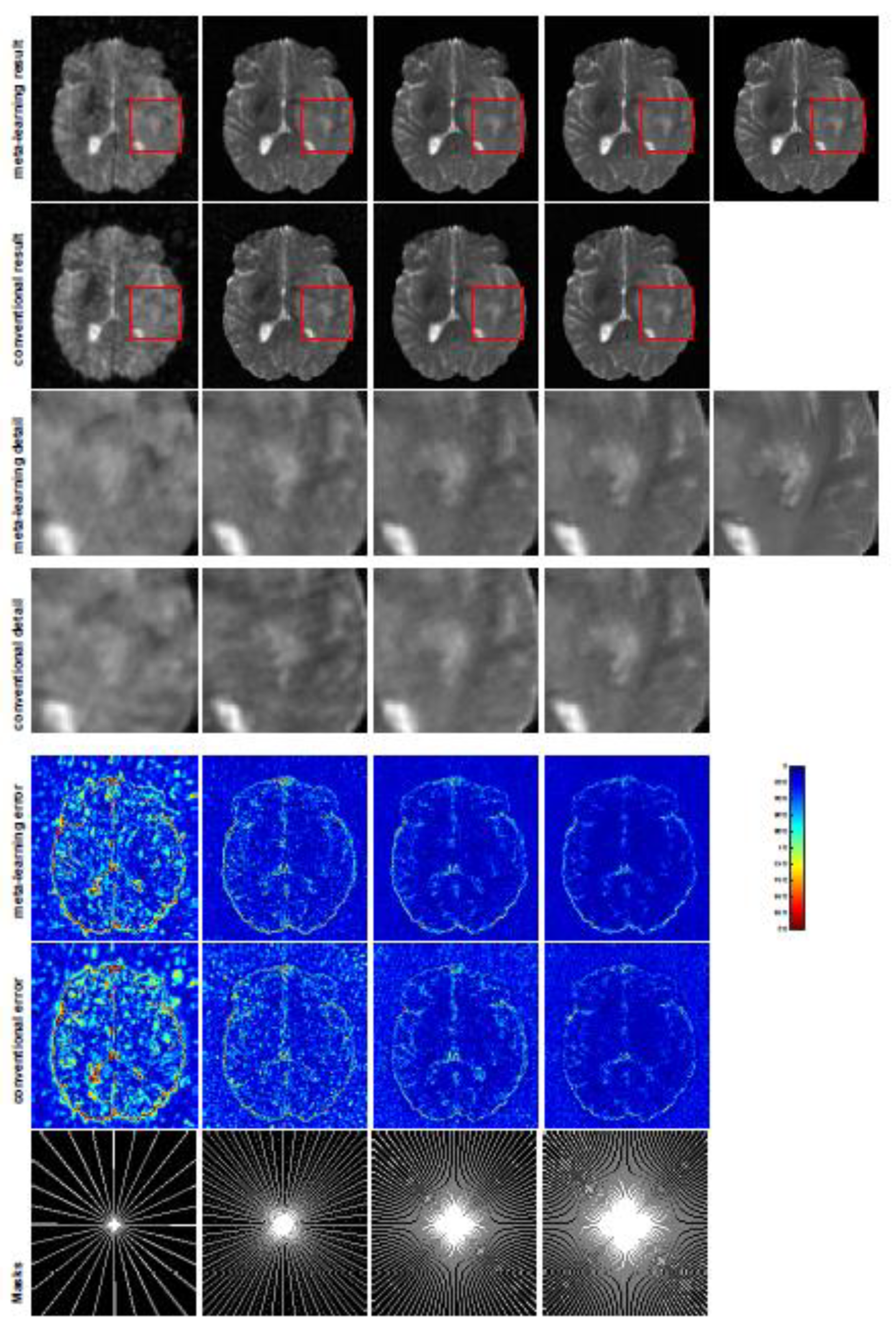
Figure 1 and
Figure 2. We also tested the well-trained meta-learning model on unseen tasks with radial masks for unseen ratios of 15%, 25%, and 35% and random Cartesian masks with ratios of 10%, 20%, 30%, and 40%. The task-specific parameters for the unseen tasks were retrained for different masks with different sampling ratios individually with fixed task-invariant parameters
. In this experiments, we only needed to learn
for three unseen CS ratios with radial mask and four regular CS ratios with Cartesian masks. The experimental training proceeded with fewer data and iterations, where we used 100 MR images with 50 epochs. For example, to reconstruct MR images with a CS ratio of 15% from the radial mask, we fixed the parameter
and retrained the task-specific parameter
on 100 raw data points with 50 epochs, then tested with renewed
on our testing data set with raw measurements sampled from the radial mask with a CS radial of 15%. The results associated with radial masks are shown in
Table 3 and
Table 4,
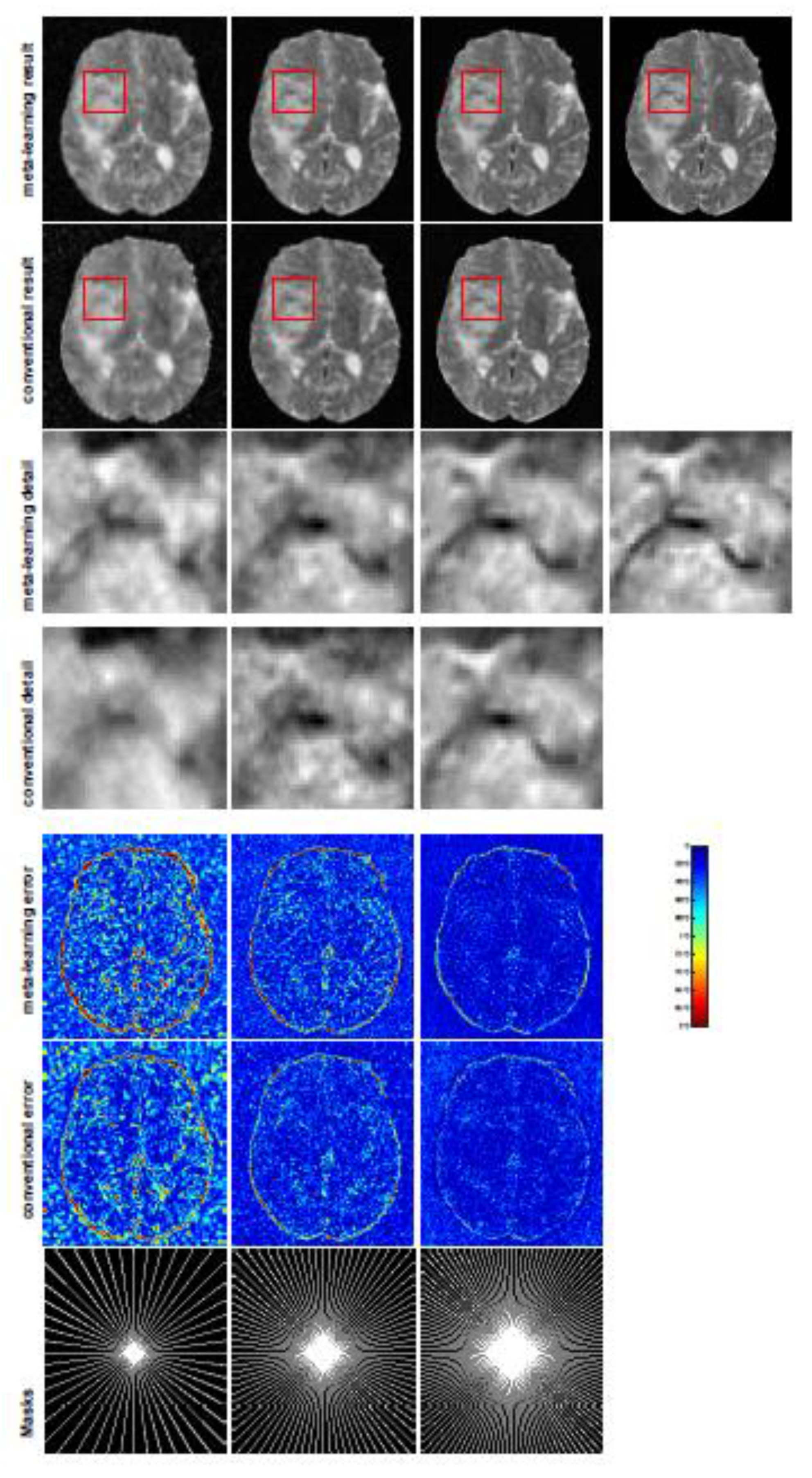
Figure 3 and
Figure 4 for T1 and T2 images, respectively. The results associated with Cartesian masks are listed in
Table 5 and reconstructed images are displayed in
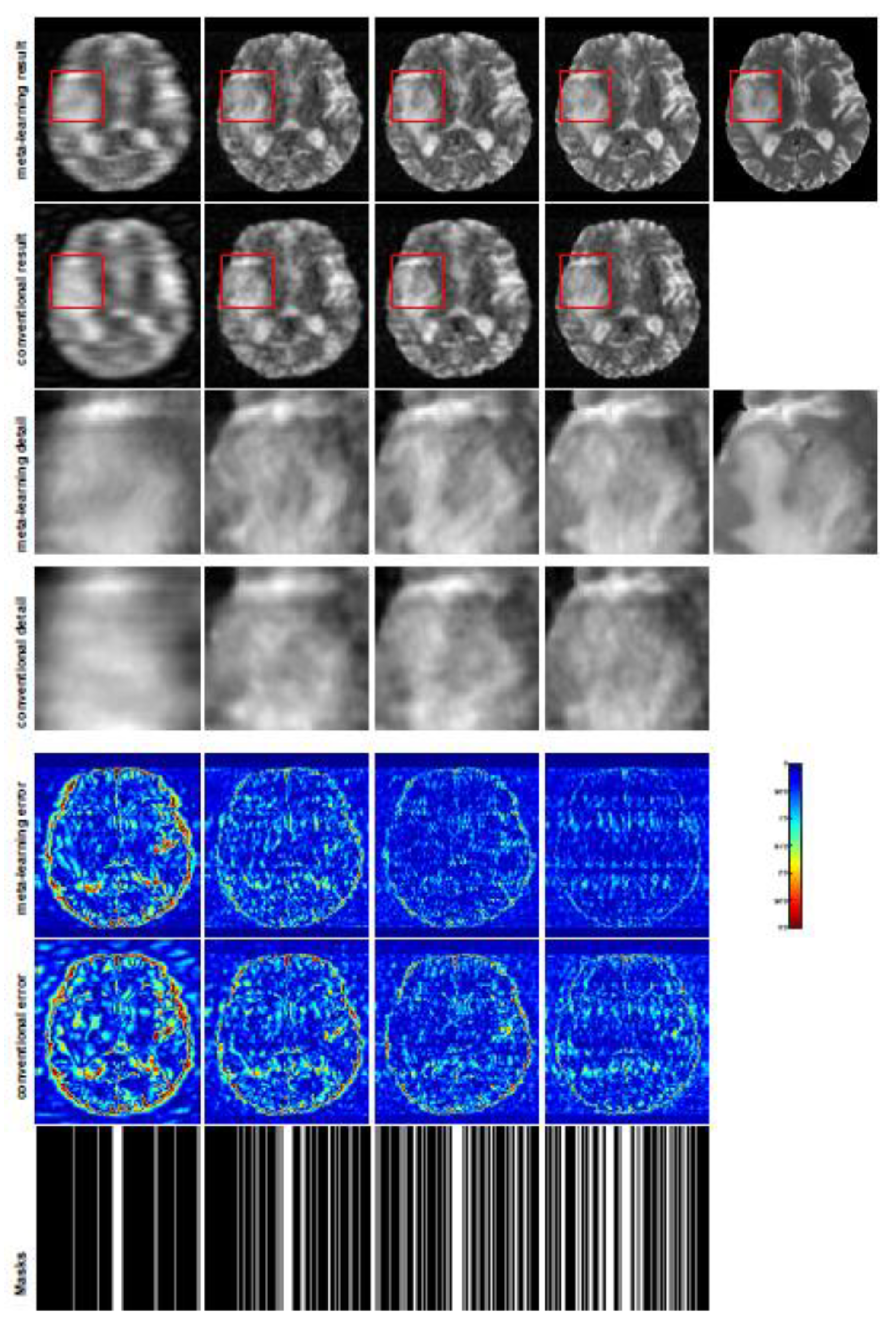
Figure 5.
We compared our proposed meta-learning method with conventional supervised learning, which was trained with one task at each time and only learned the task-invariant parameter without the task-specific parameter . The forward network of conventional learning unrolled Algorithm 1 with 11 phases, which was the same as meta-learning. We merged the training set and validation set, resulting in 450 images for the training of the conventional supervised learning. The training batch size was set as 25 and we applied a total of 2000 epochs, while in meta-learning, we applied 100 epochs with a batch size of 8. The same testing set was used in both meta-learning and conventional learning to evaluate the performance of these two methods.
We made comparisons between meta-learning and the conventional network on the seven different CS ratios (10%, 20%, 30%, 40%, 15%, 25%, and 35%) in terms of two types of random under-sampling patterns: radial sampling mask and Cartesian sampling mask. The parameters for both meta-learning and conventional learning networks were trained via the Adam optimizer [
59], and they both learned the forward unrolled task-invariant parameter
. The network training of the conventional method used the same network configuration as the meta-learning network in terms of the number of convolutions, depth and size of CNN kernels, phase numbers and parameter initializer, etc. The major difference in the training process between these two methods is that meta-learning is performed for multi-tasks by leveraging the task-specific parameter
learned from Algorithm 2, and the common features among tasks are learned from the feed-forward network that unrolls Algorithm 1, while conventional learning solves the task-specific problem by simply unrolling the forward network via Algorithm 1, where both training and testing are implemented on the same task. To investigate the generalizability of meta-learning, we tested the well-trained meta-learning model on MR images in different distributions in terms of two types of sampling masks with various trajectories. The training and testing of conventional learning were applied with the same CS ratios; that is, if the conventional method was trained with a CS ratio 10%, then it was also tested on a dataset with a CS ratio of 10%, etc.
Because MR images are represented as complex values, we applied complex convolutions [
66] for each CNN; that is, every kernel consisted of a real part and imaginary part. Three convolutions were used in
, where each convolution contained four filters with a spatial kernel size of
. In Algorithm 1, a total of 11 phases can be achieved if we set the termination condition
, and the parameters of each phase are shared except for the step sizes. For the hyperparameters in Algorithm 1, we chose an initial learnable step size
, and we set prefixed values of
, and
. The principle behind the choices of those parameters is based on the convergence of the algorithm and effectiveness of the computation. The parameter
is the reduction rate of the step size during the line search used to guarantee the convergence. The parameter
at step 15 is the reduction rate for
. In Algorithm 1, from step 2 to step 14, the smoothing level
is fixed. When the gradient of the smoothed function is small enough, we reduce
by a fraction factor
to find an approximate accumulation point of the original nonsmooth nonconvex problem. We chose a larger
a in order to have more iterations
k for which
satisfies the conditions in step 5, so that there would be fewer iterations requiring the computation of
. Moreover, the scheme for computing
is in accordance with the residual learning architecture that has been proven effective for reducing training error.
In Algorithm 2, we set and the parameter was initialized as and stopped at value , and a total of 100 epochs were performed. To train the conventional method, we set 2000 epochs with the same number of phases, convolutions, and kernel sizes as used to train the meta-learning approach. The initial was set as and .
We evaluated our reconstruction results on the testing data sets using three metrics: peak signal-to-noise ratio (PSNR) [
67], structural similarity (SSIM) [
68], and normalized mean squared error (NMSE) [
69]. The following formulations compute the PSNR, SSIM, and NMSE between the reconstructed image
and ground truth
. PSNR can be induced by the mean square error (MSE) where
where
N is the total number of pixels of the ground truth and MSE is defined by
.
where
represent local means,
denote standard deviations,
represents the covariance between
and
,
are two constants which avoid the zero denominator, and
.
L is the largest pixel value of MR image.
where NMSE is used to measure the mean relative error. For detailed information of these three metrics mentioned above, please refer to [
67,
68,
69].
5.3. Experimental Results with Different CS Ratios in Radial Mask
In this section, we evaluate the performance of well-trained meta-learning and conventional learning approaches.
Table 1,
Table 2 and
Table 5 report the quantitative results of averaged numerical performance with standard deviations and associated descaled task-specific meta-knowledge
. From the experiments implemented with radial masks, we observe that the average PSNR value of meta-learning improved by 1.54 dB in the T1 brain image for all four CS ratios compared with the conventional method, and for the T2 brain image, the average PSNR of meta-learning improved by 1.46 dB. Since the general setting of meta-learning aims to take advantage of the information provided from each individual task, with each task associated with an individual sampling mask that may have complemented sampled points, the performance of the reconstruction from each task benefits from other tasks. Smaller CS ratios will inhibit the reconstruction accuracy, due to the sparse undersampled trajectory in raw measurement, while meta-learning exhibits a favorable potential ability to solve this issue even in the situation of insufficient amounts of training data.
In general supervised learning, training data need to be in the same or a similar distribution; heterogeneous data exhibit different structural variations of features, which hinder CNNs from extracting features efficiently. In our experiments, raw measurements sampled from different ratios of compressed sensing display different levels of incompleteness; these undersampled measurements do not fall in the same distribution but they are related. Different sampling masks are shown at the bottom of
Figure 1 and
Figure 3, and these may have complemented sampled points, in the sense that some of the points which a
sampling ratio mask did not sample were captured by other masks. In our experiment, different sampling masks provided their own information from their sampled points, meaning that four reconstruction tasks helped each other to achieve an efficient performance. Therefore, this explains why meta-learning is still superior to conventional learning when the sampling ratio is large.
Meta-learning expands a new paradigm for supervised learning—the purpose is to quickly learn multiple tasks. Meta-learning only learns task-invariant parameters once for a common feature that can be shared with four different tasks, and each
provides task-specific weighting parameters according to the principle of “learning to learn”. In conventional learning, the network parameter needs to be trained four times with four different masks since the task-invariant parameter cannot be generalized to other tasks, which is time-intensive. From
Table 1 and
Table 2, we observe that a small CS ratio needs a higher value of
. In fact, in our model (11), the task-specific parameters behave as weighted constraints for task-specific regularizers, and the tables indicate that lower CS ratios require larger weights to be applied for the regularization.
A qualitative comparison between conventional and meta-learning methods is shown in
Figure 1 and
Figure 2, displaying the reconstructed MR images of the same slice for T1 and T2, respectively. We label the zoomed-in details of HGG in the red boxes. We observe evidence that conventional learning is more blurry and loses sharp edges, especially with lower CS ratios. From the point-wise error map, we find that meta-learning has the ability to reduce noises, especially in some detailed and complicated regions, compared to conventional learning.
We also tested the performance of meta-learning with two-thirds of the training and validation data for the T1-weighted image used in the previous experiment, denoted as “meta-learning”. For conventional learning, the network was also trained by using two-thirds of the training samples in the previous experiment. The testing dataset remained the same as before. These results are displayed in
Table 1, where we denote the reduced data experiments as “meta-learning
” and “conventional
”. These experiments reveal that the accuracy of test data decreases when we reduce the training data size, but it is not a surprise that meta-learnining
still outperforms conventional learning
, and even conventional learning.
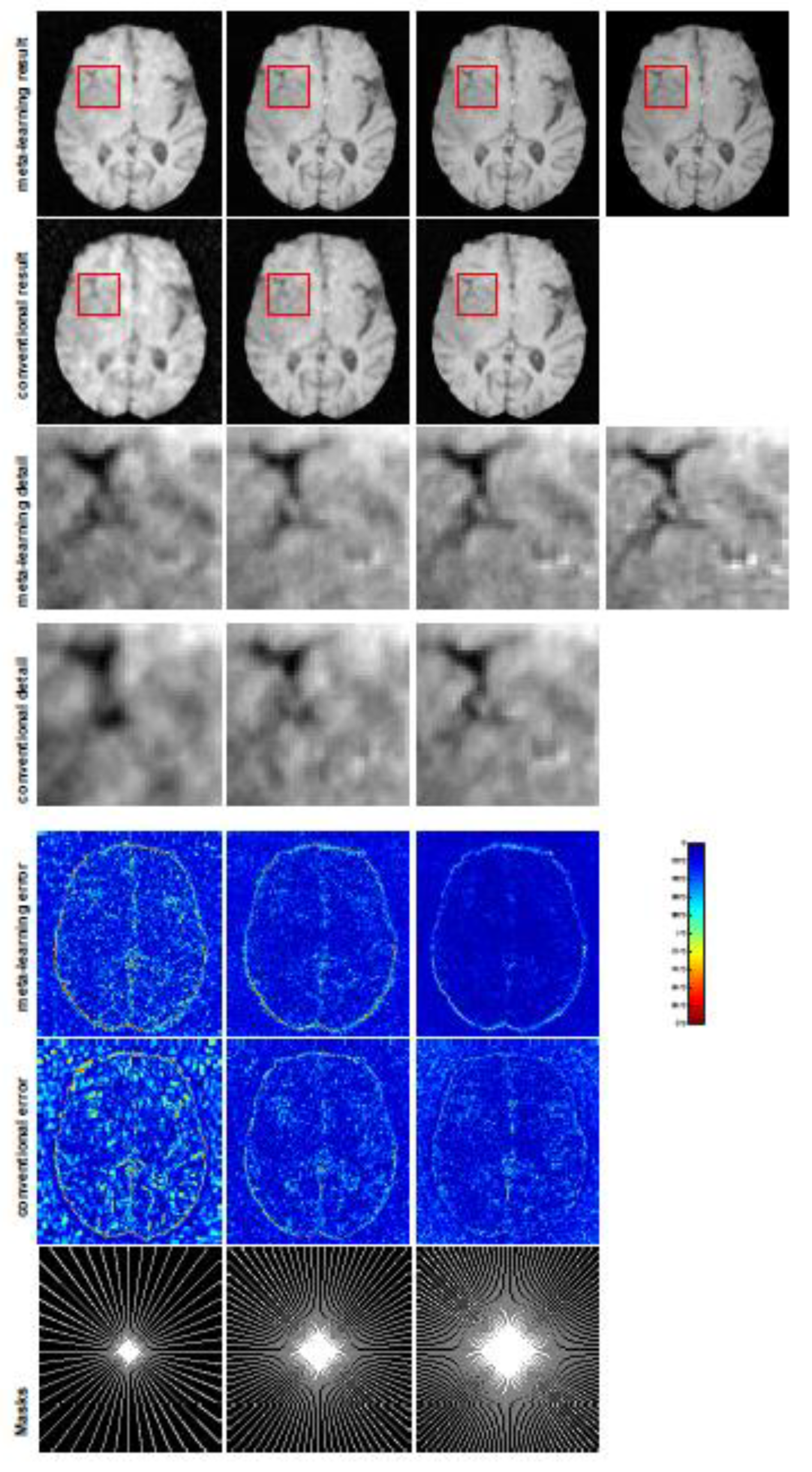
To verify the reconstruction performance of the proposed LOA 1, we compared the proposed conventional learning with ISTA-Net
[
54], which is a state-of-the-art deep unfolded network for MRI reconstruction. We retrained ISTA-Net
with the same training dataset and testing dataset as conventional learning on the T1-weighted image. For a fair comparison, we used the same number of convolution kernels, the same dimension of kernels for each convolution during training, and the same phase numbers as conventional learning. The testing numerical results are listed in
Table 1 and the MRI reconstructions are displayed in
Figure 1. We can observe that the conventional learning which unrolls Algorithm 1 outperforms ISTA-Net
in any of the CS ratios. From the corresponding point-wise absolute error, the conventional learning attains a much lower error and much better reconstruction quality.
5.4. Experimental Results with Different Unseen CS Ratios in Different Sampling Patterns
In this section, we test the generalizability of the proposed model for unseen tasks. We fixed the well-trained task-invariant parameter
and only trained
for sampling ratios of 15%, 25%, and 35% with radial masks and sampling ratios of 10%, 20%, 30%, and 40% with Cartesian masks. In this experiment, we only used 100 training data points for each CS ratio and applied a total of 50 epochs. The averaged evaluation values and standard deviations are listed in
Table 3 and
Table 4 for reconstructed T1 and T2 brain images, respectively, with radial masks, and
Table 5 shows the qualitative performance for the reconstructed T2 brain image with random Cartesian sampling masks applied. In the T1 image reconstruction results, meta-learning showed an improvement of 1.6921 dB in PSNR for the 15% CS ratio, 1.6608 dB for the 25% CS ratio, and 0.5764 dB for the 35% ratio compared to the conventional method, showing the tendency that the level of reconstruction quality for lower CS ratios improved more than higher CS ratios. A similar trend was found for T2 reconstruction results with different sampling masks. The qualitative comparisons are illustrated in
Figure 3,
Figure 4 and
Figure 5 for T1 and T2 images tested with unseen CS ratios in radial masks and T2 images tested with Cartesian masks with regular CS ratios, respectively. In the experiments conducted with radial masks, meta-learning was superior to conventional learning, especially at a CS ratio of 15%—one can observe that the detailed regions in red boxes maintained their edges and were closer to the true image, while the conventional method reconstructions are hazier and lost details in some complicated tissues. The point-wise error map also indicates that meta-learning has the ability to suppress noises.
Training with Cartesian masks is more difficult than radial masks, especially for conventional learning, where the network is not very deep since the network only applies three convolutions each with four kernels.
Table 5 indicates that the average performance of Meta-learning improved about 1.87 dB compared to conventional methods with T2 brain images. These results further demonstrate that meta-learning has the benefit of parameter efficiency, and the performance is much better than conventional learning even if we apply a shallow network with a small amount of training data.
The numerical experimental results discussed above show that meta-learning is capable of fast adaption to new tasks and has more robust generalizability for a broad range of tasks with heterogeneous, diverse data. Meta-learning can be considered as an efficient technique for solving difficult tasks by leveraging the features extracted from easier tasks.
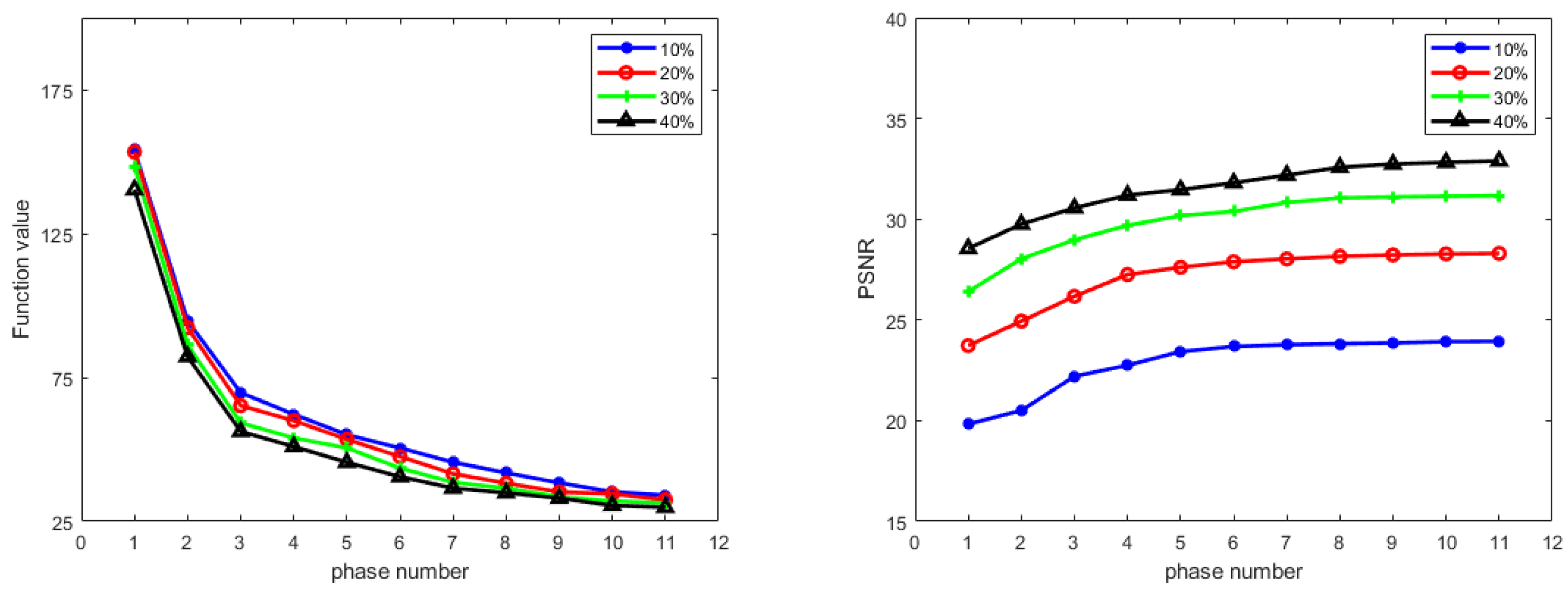
Next, we empirically demonstrate the convergence of Algorithm 1 in
Figure 6. This shows that the objective function value
decreases and the PSNR value for testing data increases steadily as the number of phases increases, which indicates that the learned algorithm is indeed minimizing the learned function as we desired.