Classification of Microcalcification Clusters in Digital Mammograms Using a Stack Generalization Based Classifier †
Abstract
1. Introduction
2. Materials and Methods
2.1. Image Databases
2.2. Preprocessing and Segmentation
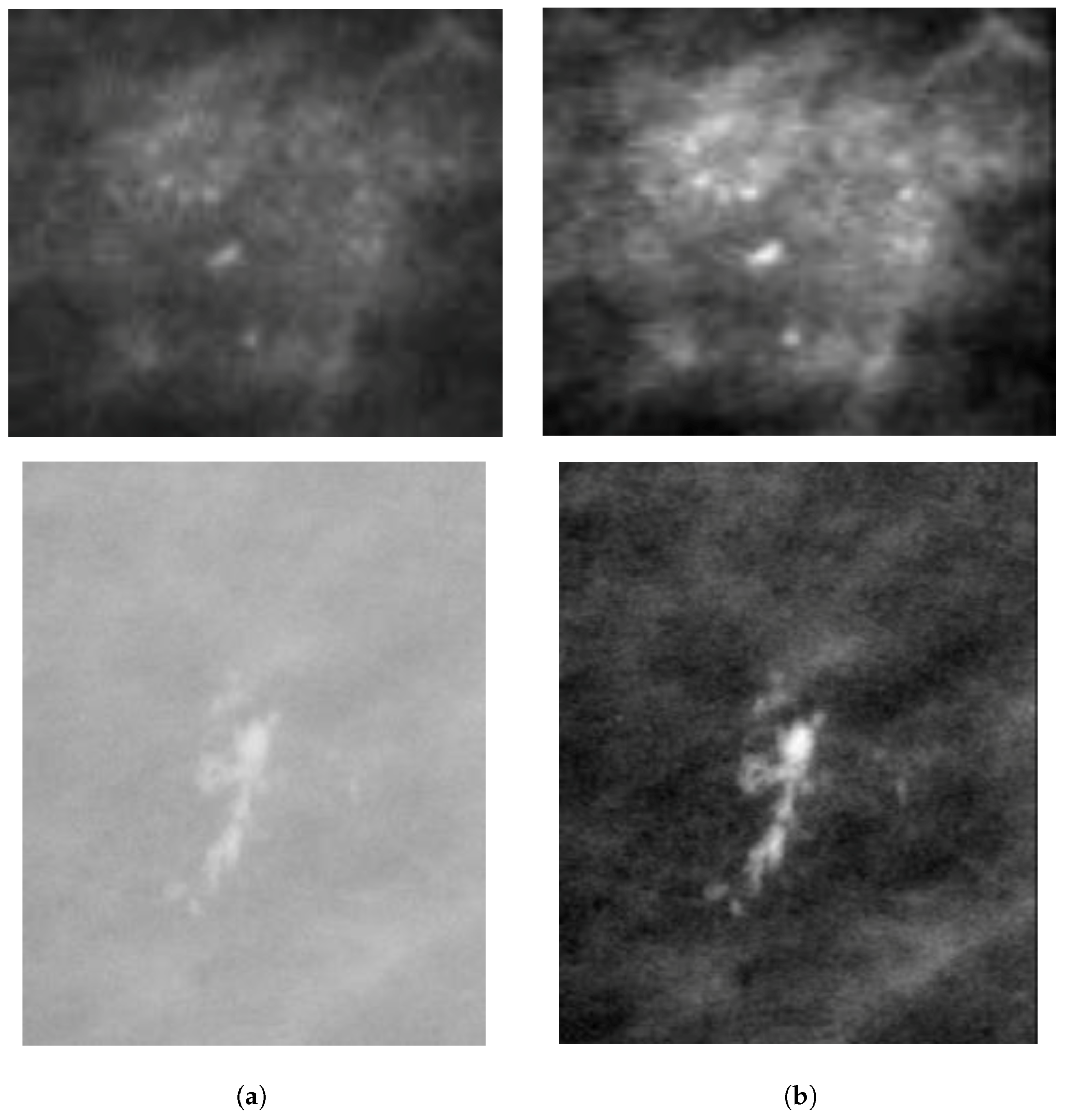
2.2.1. Mammogram Enhancement and Patch Extraction
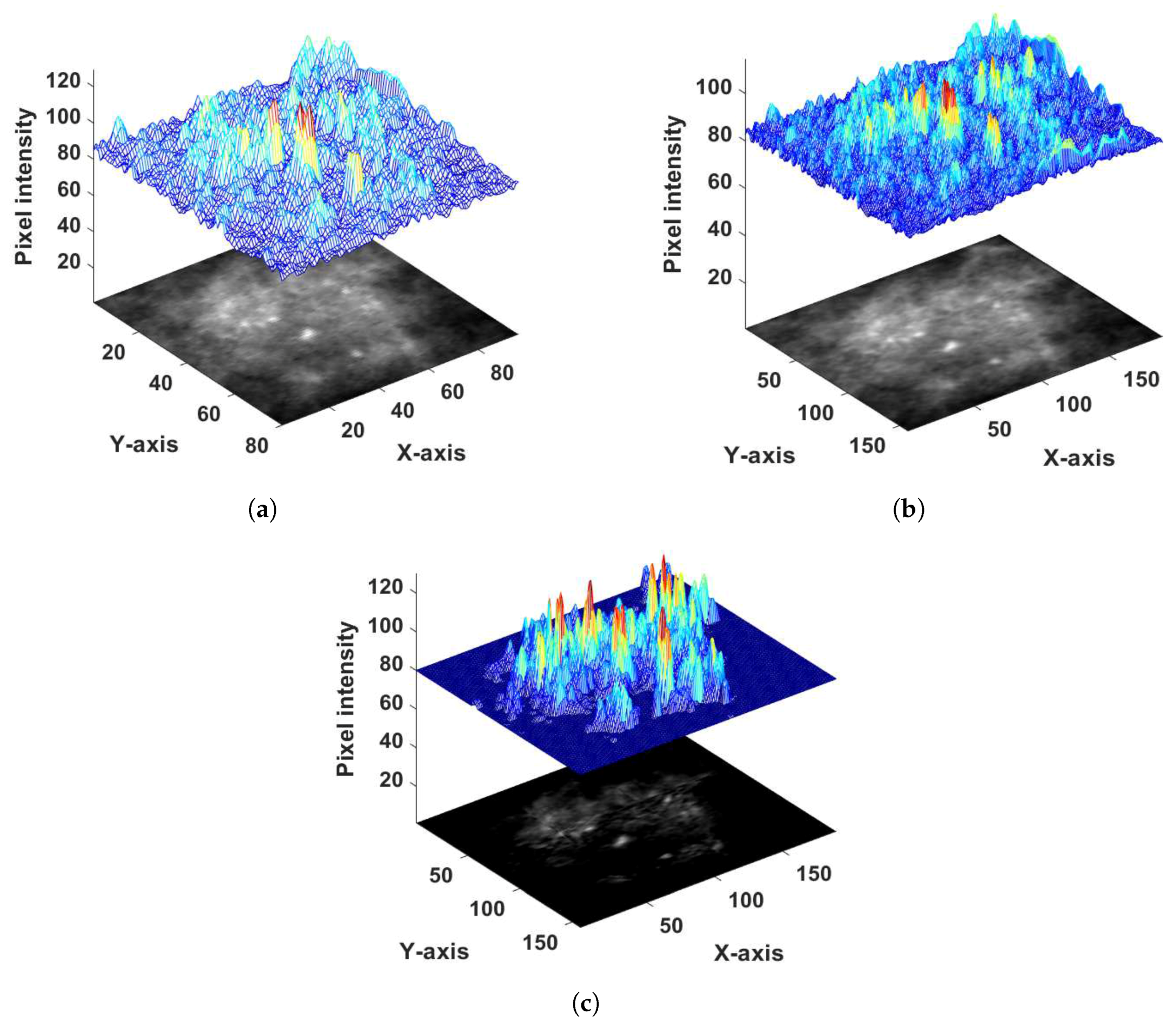
2.2.2. Probability Image Generation for MC Cluster
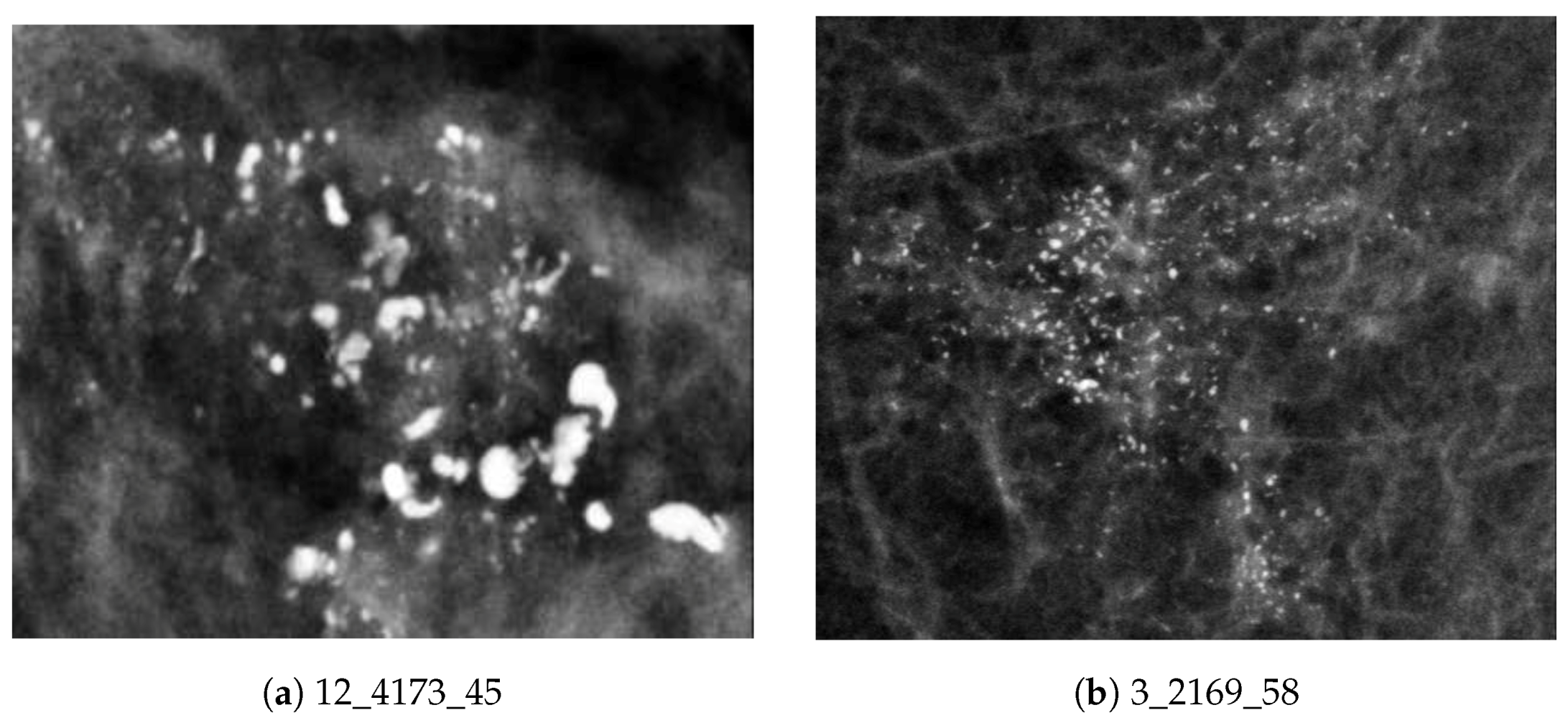
2.2.3. Specifying MC Cluster
3. Segmentation Evaluation
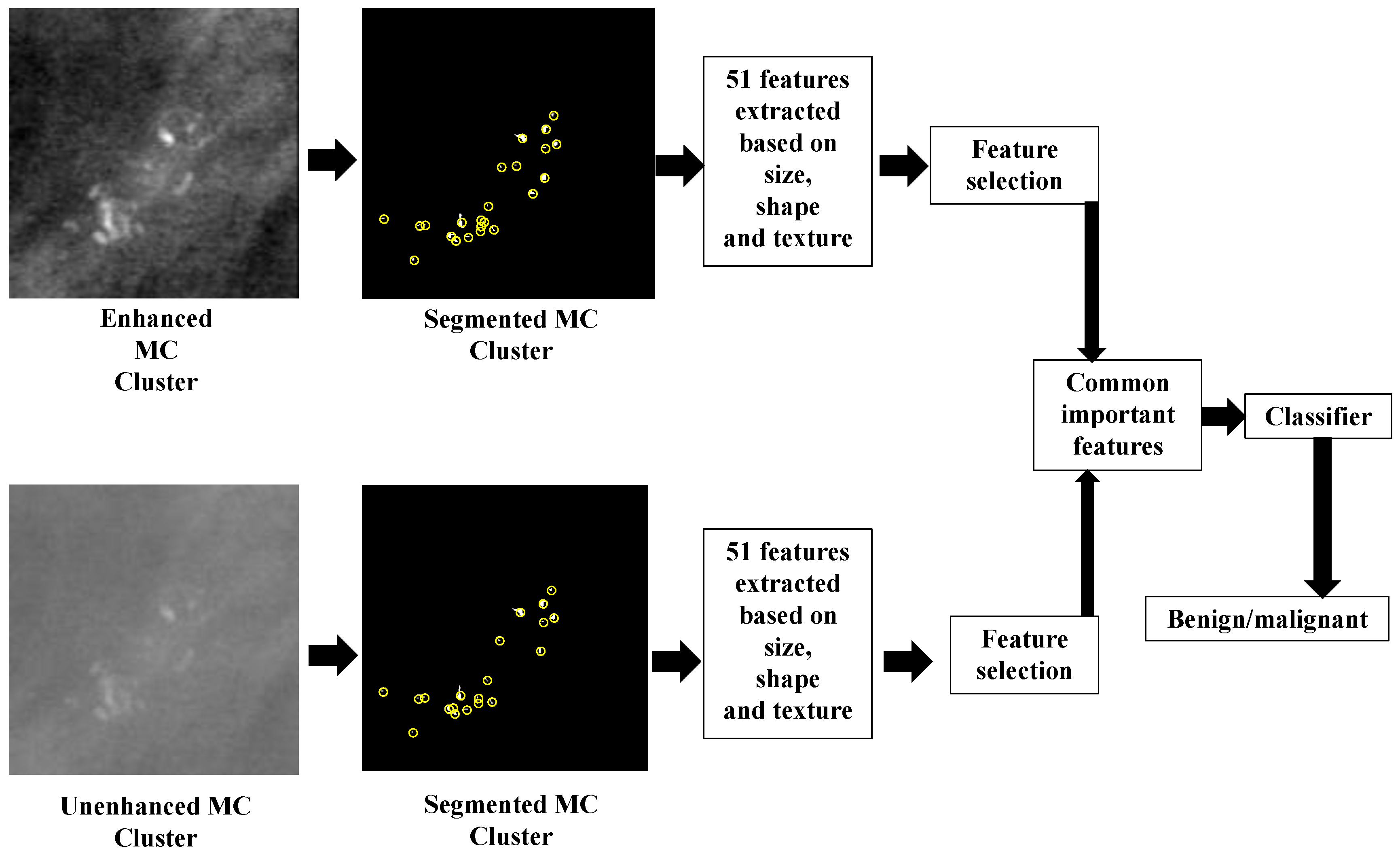
4. Classification Module Construction
5. Feature Extraction and Feature Selection
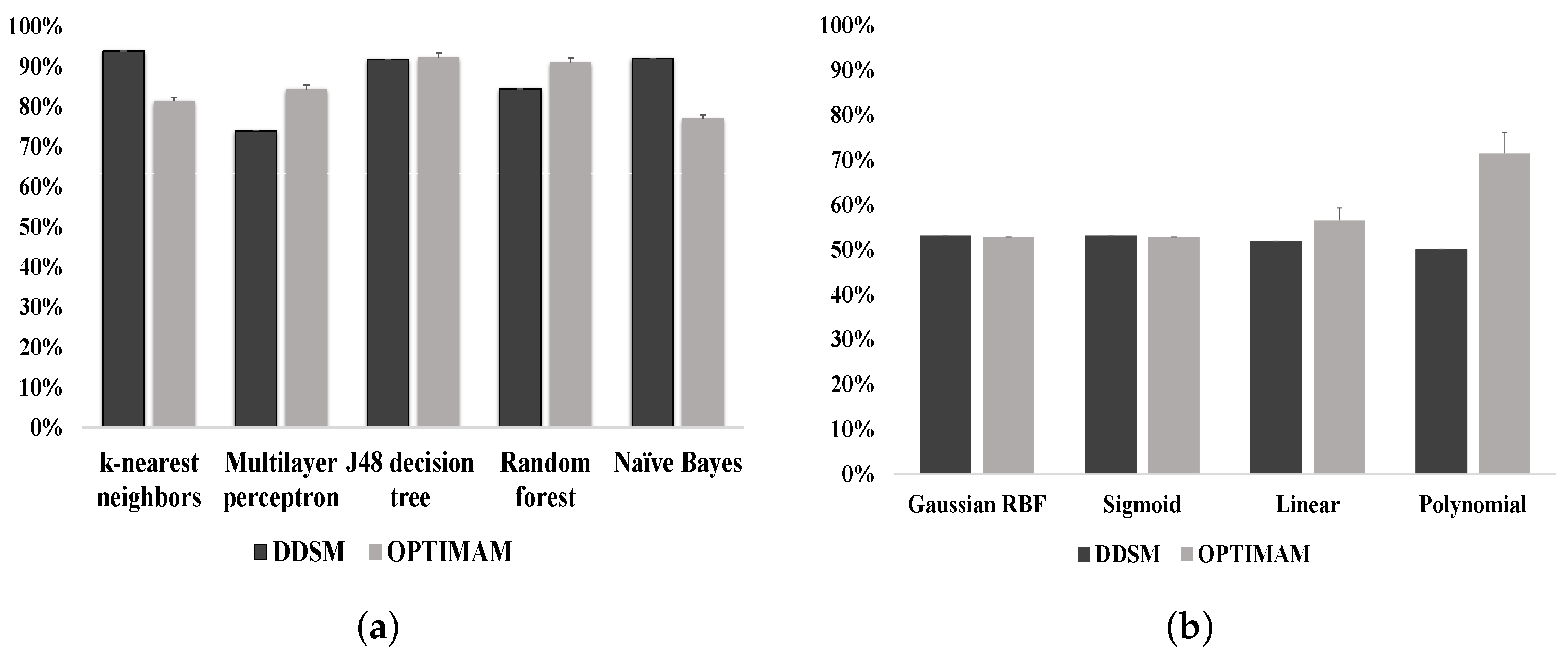
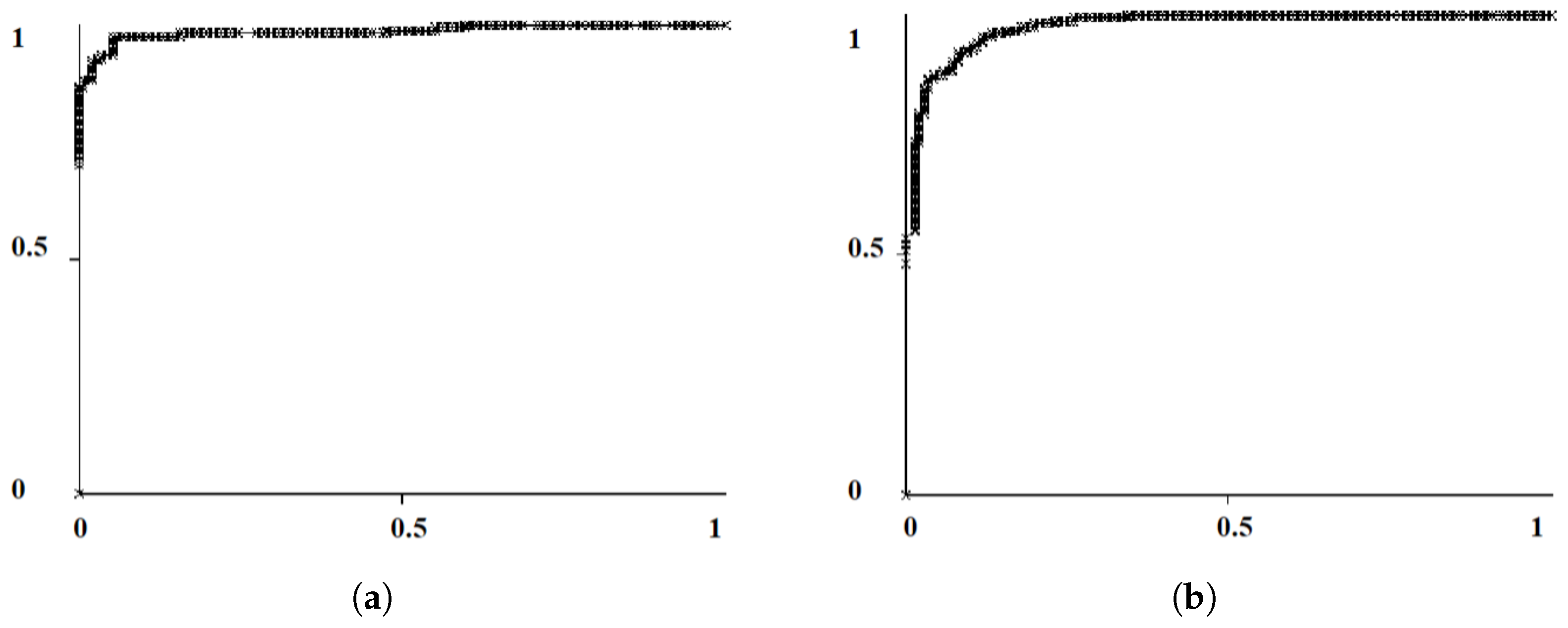
6. Result Analysis
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018. [Google Scholar] [CrossRef] [PubMed]
- DeSantis, C.E.; Bray, F.; Ferlay, J.; Lortet-Tieulent, J.; Anderson, B.O.; Jemal, A. International variation in female breast cancer incidence and mortality rates. Cancer Epidemiol. Prev. Biomark. 2015, 24, 1495–1506. [Google Scholar] [CrossRef] [PubMed]
- Jalalian, A.; Mashohor, S.; Mahmud, R.; Karasfi, B.; Saripan, M.I.B.; Ramli, A.R.B. Foundation and methodologies in computer-aided diagnosis systems for breast cancer detection. EXCLI J. 2017, 16, 113–137. [Google Scholar] [PubMed]
- Baker, R.; Rogers, K.D.; Shepherd, N.; Stone, N. New relationships between breast microcalcifications and cancer. Br. J. Cancer 2010, 103, 1034–1039. [Google Scholar] [CrossRef] [PubMed]
- Tabar, L.; Tot, T.; Dean, P.B. Breast Cancer: Early Detection with Mammography. Perception, Interpretation, Histopathologic Correlation; Georg Thieme Verlag: Stuttgart, Germany, 2005. [Google Scholar]
- Gubern-Mérida, A.; Bria, A.; Tortorella, F.; Mann, R.M.; Broeders, M.J.M.; den Heeten, G.J.; Karssemeijer, N. The importance of early detection of calcifications associated with breast cancer in screening. Breast Cancer Res. Treat. 2018, 167, 451–458. [Google Scholar]
- Henriksen, E.L.; Carlsen, J.F.; Vejborg, I.M.; Nielsen, M.B.; Lauridsen, C.A. The efficacy of using computer-aided detection (CAD) for detection of breast cancer in mammography screening: A systematic review. Acta Radiol. 2018, 167. [Google Scholar] [CrossRef] [PubMed]
- Scimeca, M.; Giannini, E.; Antonacci, C.; Pistolese, C.A.; Spagnoli, L.G.; Bonanno, E. Microcalcifications in breast cancer: An active phenomenon mediated by epithelial cells with mesenchymal characteristics. BMC Cancer 2014, 14, 286–296. [Google Scholar] [CrossRef]
- Von Euler-Chelpin, M.; Lillholm, M.; Napolitano, G.; Vejborg, I.; Nielsen, M.; Lynge, E. Screening mammography: Benefit of double reading by breast density. Breast Cancer Res. Treatment. 2018, 171, 767–776. [Google Scholar] [CrossRef]
- Hawley, J.R.; Taylor, C.R.; Cubbison, A.M.; Erdal, B.S.; Yildiz, V.O.; Carkaci, S. Influences of radiology trainees on screening mammography interpretation. J. Am. Coll. Radiol. 2016, 13, 554–561. [Google Scholar] [CrossRef]
- Alam, N.; Oliver, A.; Denton, E.R.E.; Zwiggelaar, R. Automatic Segmentation of Microcalcification Clusters. In Proceedings of the Annual Conference on Medical Image Understanding and Analysis, Southampton, UK, 9–11 July 2018; pp. 251–261. [Google Scholar]
- Suhail, Z.; Denton, E.R.; Zwiggelaar, R. Tree-based modelling for the classification of mammographic benign and malignant micro-calcification clusters. Multimed. Tools Appl. 2018, 77, 6135–6148. [Google Scholar] [CrossRef]
- Singh, B.; Kaur, M. An approach for classification of malignant and benign microcalcification clusters. Sādhanā 2018, 43, 39–57. [Google Scholar] [CrossRef]
- Suhail, Z.; Denton, E.R.; Zwiggelaar, R. Classification of micro-calcification in mammograms using scalable linear Fisher discriminant analysis. Med. Biol. Eng. Comput. 2018, 56, 1475–1485. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Strange, H.; Oliver, A.; Denton, E.R.; Boggis, C.; Zwiggelaar, R. Topological modeling and classification of mammographic microcalcification clusters. IEEE Trans. Biomed. Eng. 2015, 62, 1203–1214. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Strange, H.; Oliver, A.; Denton, E.R.; Boggis, C.; Zwiggelaar, R. Classification of mammographic microcalcification clusters with machine learning confidence levels. In Proceedings of the 14th International Workshop on Breast Imaging, Atlanta, GA, USA, 8–11 July 2018; Volume 10718. [Google Scholar]
- Bekker, A.J.; Shalhon, M.; Greenspan, H.; Goldberger, J. Multi-view probabilistic classification of breast microcalcifications. IEEE Trans. Med. Imaging 2016, 35, 645–653. [Google Scholar] [CrossRef] [PubMed]
- Shachor, Y.; Greenspan, H.; Goldberger, J. A mixture of views network with applications to the classification of breast microcalcifications. arXiv 2018, arXiv:1803.06898. [Google Scholar]
- Hu, K.; Yang, W.; Gao, X. Microcalcification diagnosis in digital mammography using extreme learning machine based on hidden Markov tree model of dual-tree complex wavelet transform. Expert Syst. Appl. 2017, 86, 135–144. [Google Scholar] [CrossRef]
- Diamant, I.; Shalhon, M.; Goldberger, J.; Greenspan, H. Mutual information criterion for feature selection with application to classification of breast microcalcifications. Med. Imaging 2016 Image Proc. 2016, 9784, 97841S. [Google Scholar]
- Wang, J.; Yang, X.; Cai, H.; Tan, W.; Jin, C.; Li, L. Discrimination of breast cancer with microcalcifications on mammography by deep learning. Sci. Rep. 2016, 6, 27327. [Google Scholar] [CrossRef] [PubMed]
- Sert, E.; Ertekin, S.; Halici, U. Ensemble of convolutional neural networks for classification of breast microcalcification from mammograms. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Korea, 11–15 July 2017; pp. 689–692. [Google Scholar]
- Nguyen, B.P.; Heemskerk, H.; So, P.T.; Tucker-Kellogg, L. Superpixel-based segmentation of muscle fibers in multi-channel microscopy. BMC Syst. Biol. 2016, 10, 39–50. [Google Scholar] [CrossRef]
- Halling-Brown, M.D.; Looney, P.T.; Patel, M.N.; Warren, L.M.; Mackenzie, A.; Young, K.C. The oncology medical image database (OMI-DB). Med. Imaging 2014 PACS Imaging Inform. Next Gener. Innov. 2014, 9039, 903906. [Google Scholar] [CrossRef]
- Selenia Dimensions with AWS 8000. Available online: https://www.partnershipsbc.ca/files-4/project-prhpct-schedules/Appendix_2E_Attachment_2/3021_Mammography_Hologic_Dimensions_8000.pdf (accessed on 8 February 2019).
- Suckling, J.; Parker, J.; Dance, D.; Astley, S.; Hutt, I.; Boggis, C.; Ricketts, I.; Stamatakis, E.; Cerneaz, N.; Kok, S.; et al. Mammographic Image Analysis Society (MIAS) database v1. 21. Med. Imaging 2014 PACS Imaging Inform. Next Gener. Innov. 2015, 2015, 9039. Available online: https://www.repository.cam.ac.uk/handle/1810/250394/ (accessed on 25 November 2018).
- Heath, M.; Bowyer, K.; Kopans, D.; Moore, R.; Kegelmeyer, W.P. The digital database for screening mammography. In Proceedings of the 5th International Workshop on Digital Mammography, Toronto, ON, Canada, 11–14 June 2000; pp. 212–218. [Google Scholar]
- American College of Radiology. BI-RADS Committee, Breast Imaging Reporting and Data System; American College of Radiology: Reston, VA, USA, 1998. [Google Scholar]
- Mishra, S.; Patra, R.; Pattanayak, A.; Pradhan, S. Block based enhancement of satellite images using sharpness indexed filtering. IOSR J. Electron. Commun. Eng. 2013, 8, 20–24. [Google Scholar] [CrossRef]
- Agaian, S.S.; Panetta, K.; Grigoryan, A.M. Transform-based Image Enhancement Algorithms With Performance Measure. IEEE Trans. Image Process. 2001, 10, 367–382. [Google Scholar] [CrossRef]
- Starck, J.L.; Fadili, J.; Murtagh, F. The undecimated wavelet decomposition and its reconstruction. IEEE Trans. Image Process. 2007, 16, 297–309. [Google Scholar] [CrossRef] [PubMed]
- Ferzli, R.; Karam, L.J.; Caviedes, J. A robust image sharpness metric based on kurtosis measurement of wavelet coefficients. In Proceedings of the International Workshop on Video Processing and Quality Metrics for Consumer Electronics, Scottsdale, Arizona, 11–14 January 2005; pp. 38–46. [Google Scholar]
- Papadopoulos, A.; Fotiadis, D.I.; Likas, A. An automatic microcalcification detection system based on a hybrid neural network classifier. Artif. Intell. Med. 2002, 25, 149–167. [Google Scholar] [CrossRef]
- Kopans, D.B. Mammography, Breast Imaging; JB Lippincott Company: Philadelphia, PA, USA, 1989; Volume 30, pp. 34–59. [Google Scholar]
- Chan, H.P.; Lo, S.C.B.; Sahiner, B.; Lam, K.L.; Helvie, M.A. Computer-aided detection of mammographic microcalcifications: Pattern recognition with an artificial neural network. Med. Phys. 1995, 2, 1555–1567. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, T.J. A method of establishing groups of equal amplitude in plant sociology based on similarity of species and its application to analyses of the vegetation on Danish commons. Biol. Skr. 1948, 5, 1–34. [Google Scholar]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Oliver, A.; Albert, T.; Xavier, L.; Meritxell, T.; Lidia, T.; Melcior, S.; Jordi, F.; Zwiggelaar, R. Automatic microcalcification and cluster detection for digital and digitised mammograms. Knowl.-Based Syst. 2012, 28, 68–75. [Google Scholar] [CrossRef]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef]
- Delashmit, W.H.; Manry, M.T. Recent developments in multilayer perceptron neural networks. In Proceedings of the Seventh Annual Memphis Area Engineering and Science Conference (MAESC 2005), Memphis, TN, USA, 11–13 May 2005; pp. 1–15. [Google Scholar]
- Quinlan, J.R. C4. 5: Programs For Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- John, G.H.; Langley, P. Estimating continuous distributions in Bayesian classifiers. In Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–20 August 1995; pp. 338–345. [Google Scholar]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Chan, P.K.; Stolfo, S.J. A comparative evaluation of voting and meta-learning on partitioned data. Mach. Learn. 1995, 90–98. [Google Scholar] [CrossRef]
- Tahmassebi, A.; Gandomi, A.; Amir, H.; McCannand, I.; Goudriaan, M.H.; Meyer-Baese, A. Deep Learning in Medical Imaging: fMRI Big Data Analysis via Convolutional Neural Networks. In Proceedings of the PEARC, Pittsburgh, PA, USA, 22–26 July 2018; Volume 85. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Alam, N.; Zwiggelaar, R. Automatic classification of clustered microcalcifications in digitized mammogram using ensemble learning. In Proceedings of the 14th International Workshop on Breast Imaging (IWBI 2018), Atlanta, GA, USA, 8–11 July 2018; Volume 10718, p. 1071816. [Google Scholar]
- Peng, Y.; Kou, G.; Ergu, D.; Wu, W.; Shi, Y. An integrated feature selection and classification scheme. Stud. Inform. Control. 2012, 1220–1766. [Google Scholar] [CrossRef][Green Version]
- Weik, M.H. Best-first search. In Computer Science and Communications Dictionary; Springer: New York, NY, USA, 2000; p. 115. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- About Default Parameter Values of Weka. Available online: http://weka.8497.n7.nabble.com/About-default-parameter-values-of-weka-td29652.html (accessed on 8 February 2019).
- Brownlee, D.J. Gentle Introduction to the Bias-Variance Trade-Off in Machine Learning. Artif. Intell. 2016. Available online: https://machinelearningmastery.com/gentle-introduction-to-the-biasvariance-trade-off-in-machine-learning/ (accessed on 8 February 2019).
- Beck, J.R.; Shultz, E.K. The use of relative operating characteristic (ROC) curves in test performance evaluation. Arch. Pathol. Lab. Med. 1986, 110, 13–20. [Google Scholar] [PubMed]
- Huang, J.; Ling, C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005, 17, 299–310. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: an update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Strange, H.; Chen, Z.; Denton, E.R.; Zwiggelaar, R. Modelling mammographic microcalcification clusters using persistent mereotopology. Pattern Recognit. Lett. 2014, 47, 157–163. [Google Scholar] [CrossRef]
- Nees, A.V. Digital mammography: Are there advantages in screening for breast cancer? Acad. Radiol. 2008, 15, 401–407. [Google Scholar] [CrossRef] [PubMed]
- Ting, K.M.; Witten, I.H. Issues in stacked generalization. J. Artif. Intell. Res. 1999, 10, 271–289. [Google Scholar] [CrossRef]
- Iman, R.L. Use of a t-statistic as an approximation to the exact distribution of the wildcoxon signed ranks test statistic. Commun. Stat.-Theory Methods 1974, 3, 795–806. [Google Scholar] [CrossRef]
- Mason, S.J.; Graham, N.E. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q. J. R. Meteorol. Soc. 2002, 128, 2145–2166. [Google Scholar] [CrossRef]
- John, G.; Trigg, L.E. K*: An Instance-based Learner Using an Entropic Distance Measure. In Proceedings of the 12th International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 108–114. [Google Scholar]
- Sumner, M.; Frank, E.; Hall, M. Speeding up Logistic Model Tree Induction. In Proceedings of the 9th European Conference on Principles and Practice of Knowledge Discovery in Databases, Porto, Portugal, 3–7 October 2005; pp. 675–683. [Google Scholar]
- Kohavi, R. The Power of Decision Tables. In Proceedings of the 8th European Conference on Machine Learning, Heraclion, Greece, 25–17 April 1995; pp. 174–189. [Google Scholar]
- Yoav, F.; Robert, S.; Naoki, A. A short introduction to boosting. J.-Jpn. Soc. Artif. Intell. 1999, 14, 771–780. [Google Scholar]
- Lior, R. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar]





| MC Cluster Classification Features | Radiologists Characterization Features |
|---|---|
| Summation of the mean of individual MC intensity | Density of MC cluster |
| Variance of the standard deviation of the distances from cluster centroids | MC distribution |
| MC cluster convex hull area | Cluster size |
| Mean of MC perimeter | Individual MC size |
| MC Cluster Classification Features | Radiologists Characterization Features |
|---|---|
| MC cluster area | Cluster size |
| Size of individual MC | Individual MC size |
| Feature Selection | Feature Category | No. of Feature | Total Feature No. | A (AUC) | ||
|---|---|---|---|---|---|---|
| OMI-DB | DDSM | MIAS | ||||
| Size | 17 | |||||
| No | Shape | 17 | 51 | |||
| Texture | 17 | |||||
| Size | 7 | |||||
| Yes | Shape | 4 | 12 | |||
| Texture | 5 | |||||
| Database Name | Feature Number | LOOCV | 10-FCV | ||
|---|---|---|---|---|---|
| CA | A (AUC) | CA | A (AUC) | ||
| OMI-DB | 51 | 86.49% | 0.85 | % | |
| (286) | 4 | 85.71% | 0.84 | % | |
| 2 | 91.12% | 0.91 | % | ||
| DDSM | 51 | 73.98% | 0.73 | % | |
| (280) | 4 | 80.66% | 0.80 | % | |
| 2 | 88.48% | 0.88 | % | ||
| MIAS | 51 | 82.35% | 0.79 | % | |
| (24) | 4 | 100.00% | 1.00 | % | |
| 2 | 100.00% | 1.00 | % | ||
| Database Name | Feature Number | LOOCV | 10-FCV | ||
|---|---|---|---|---|---|
| CA | A (AUC) | CA | A (AUC) | ||
| OMI-DB | 51 | 91.89% | 0.97 | % | |
| (286) | 4 | 92.66% | 0.98 | % | |
| 2 | 95.75% | 0.97 | % | ||
| DDSM | 51 | 89.96% | 0.95 | % | |
| (280) | 4 | 92.19% | 0.96 | % | |
| 2 | 95.17% | 0.98 | % | ||
| MIAS | 51 | 100% | 1.00 | % | |
| (24) | 4 | 100% | 1.00 | % | |
| 2 | 100% | 1.00 | % | ||
| Database Name | Feature Number | LOOCV | 10-FCV | ||
|---|---|---|---|---|---|
| CA | A (AUC) | CA | A (AUC) | ||
| OMI-DB | 51 | 93.66% | 0.97 | % | |
| (286) | 4 | 95.77% | 0.98 | % | |
| DDSM | 51 | 90.68% | 0.96 | % | |
| (280) | 4 | 93.91% | 0.97 | % | |
| MIAS | 51 | 100% | 1.00 | % | |
| (24) | 4 | 100% | 1.00 | % | |
| Method | Databases | Cases | Features | Classifier | Results |
|---|---|---|---|---|---|
| Akram et al. [12] | DDSM | 288 | Tree-based modeling | tree-structure height | CA = 91% |
| Akram et al. [14] | DDSM | 288 | Scalable−LDA | SVM | CA = 96% |
| Strange et al. [58] | DDSM | 150 | Cluster | barcodes | CA = 95%, A = 0.82 |
| Strange et al. [58] | MIAS | 20 | Cluster | barcodes | CA = 80%, A = 0.80 |
| Chen et al. [15] | MIAS I (Manual Annotation) | 20 | Topology | kNN/FNN/ FRNN/VQNN | CA = 95%, A = 0.96 |
| Chen et al. [15] | Digital | 25 | Topology | kNN/FNN | CA = 96%, A = 0.96 |
| Chen et al. [15] | DDSM (LOOCV) | 300 | Topology | kNN | CA = 86.0%, A = 0.90 |
| Chen et al. [15] | DDSM (10-fold CV) | 300 | Topology | kNN | CA = %, A = |
| Alam et al. [11] | MIAS (LOOCV) | 24 | Morphology, Texture & Cluster | Ensemble classifier | CA = 100%, A = 1 |
| Alam et al. [11] | MIAS (10-fold CV) | 24 | Morphology, Texture & Cluster | Ensemble classifier | CA = %, A = |
| Alam et al. [11] | DDSM (LOOCV) | 280 | Morphology, Texture & Cluster | Ensemble classifier | CA = , A = |
| Alam et al. [11] | DDSM (10-fold CV) | 280 | Morphology, Texture & Cluster | Ensemble classifier | CA = %, A = |
| Ours | OMI-DB (10-fold CV) | 286 | Morphology, Texture & Cluster | Ensemble classifier (Extended) | CA = %, A = |
| Ours | OMI-DB (10-fold CV) | 286 | Morphology, Texture & Cluster | Stack generalization (meta-classifier: Naive Bayes) | CA = %, A = |
| Ours | OMI-DB (10-fold CV) | 286 | Morphology, Texture & Cluster (selected features) | Stack generalization (meta-classifier: Naive Bayes) | CA = %, A = |
| Ours | OMI-DB (10-fold CV) | 286 | Morphology, Texture & Cluster (selected features) | Stack generalization (meta-classifier: Adapting Boosting) | CA = %, A = |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, N.; R. E. Denton, E.; Zwiggelaar, R. Classification of Microcalcification Clusters in Digital Mammograms Using a Stack Generalization Based Classifier. J. Imaging 2019, 5, 76. https://doi.org/10.3390/jimaging5090076
Alam N, R. E. Denton E, Zwiggelaar R. Classification of Microcalcification Clusters in Digital Mammograms Using a Stack Generalization Based Classifier. Journal of Imaging. 2019; 5(9):76. https://doi.org/10.3390/jimaging5090076
Chicago/Turabian StyleAlam, Nashid, Erika R. E. Denton, and Reyer Zwiggelaar. 2019. "Classification of Microcalcification Clusters in Digital Mammograms Using a Stack Generalization Based Classifier" Journal of Imaging 5, no. 9: 76. https://doi.org/10.3390/jimaging5090076
APA StyleAlam, N., R. E. Denton, E., & Zwiggelaar, R. (2019). Classification of Microcalcification Clusters in Digital Mammograms Using a Stack Generalization Based Classifier. Journal of Imaging, 5(9), 76. https://doi.org/10.3390/jimaging5090076






