Comparative Study on Local Binary Patterns for Mammographic Density and Risk Scoring †
Abstract
1. Introduction
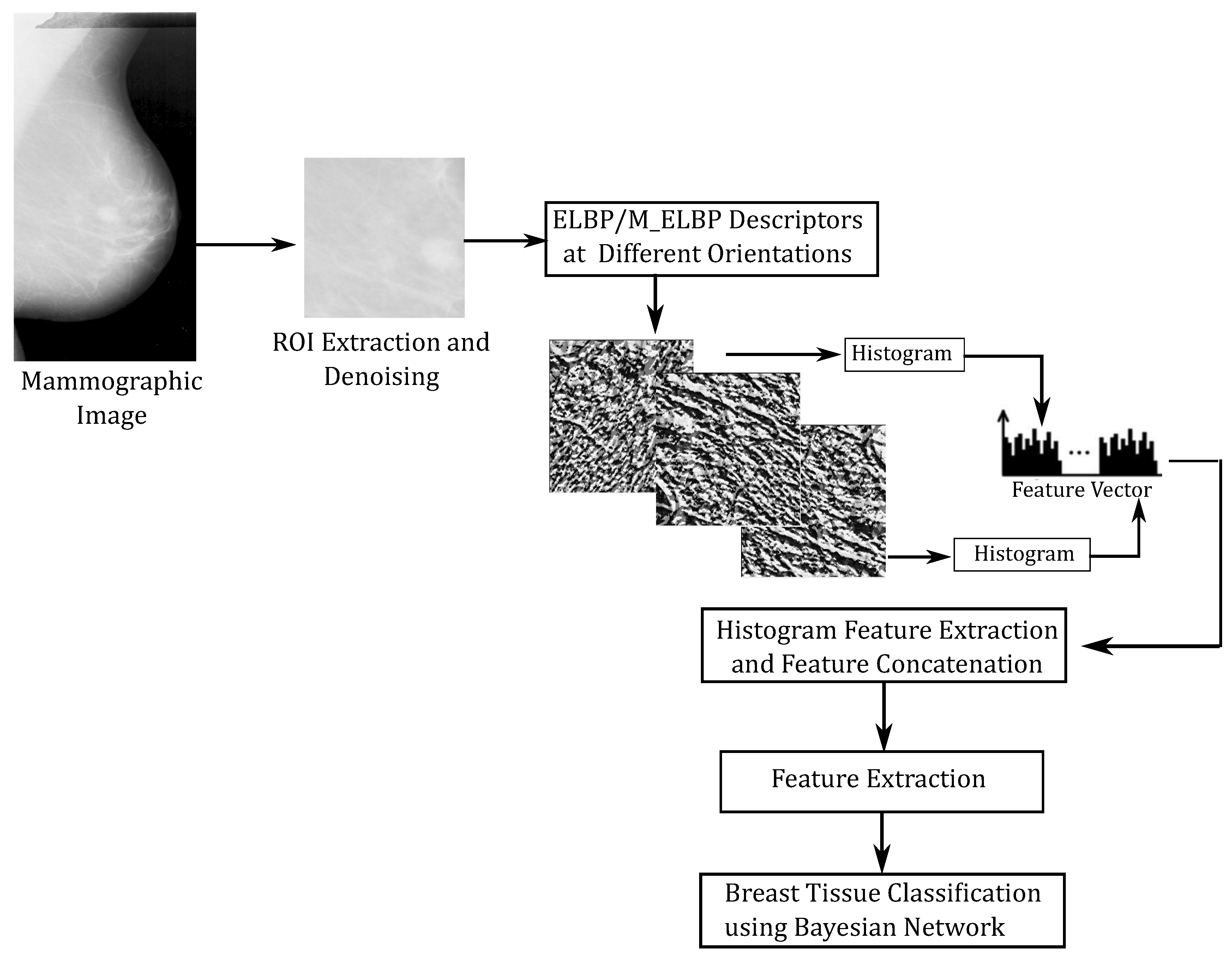
2. Methodology
2.1. Pre-Processing
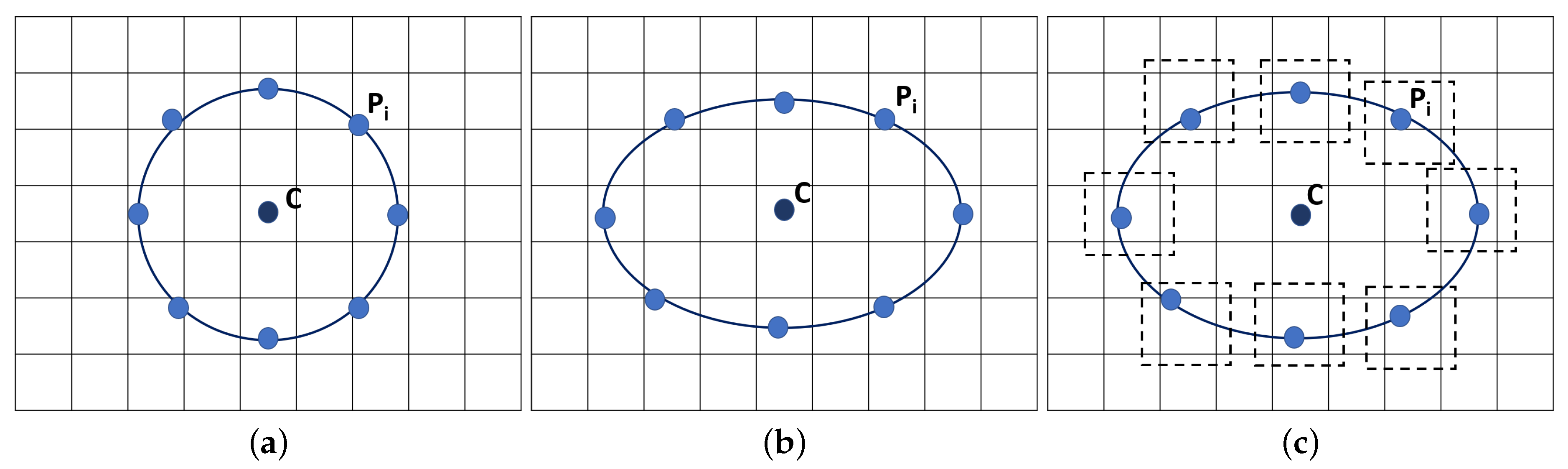
2.2. Feature Extraction and Feature Selection
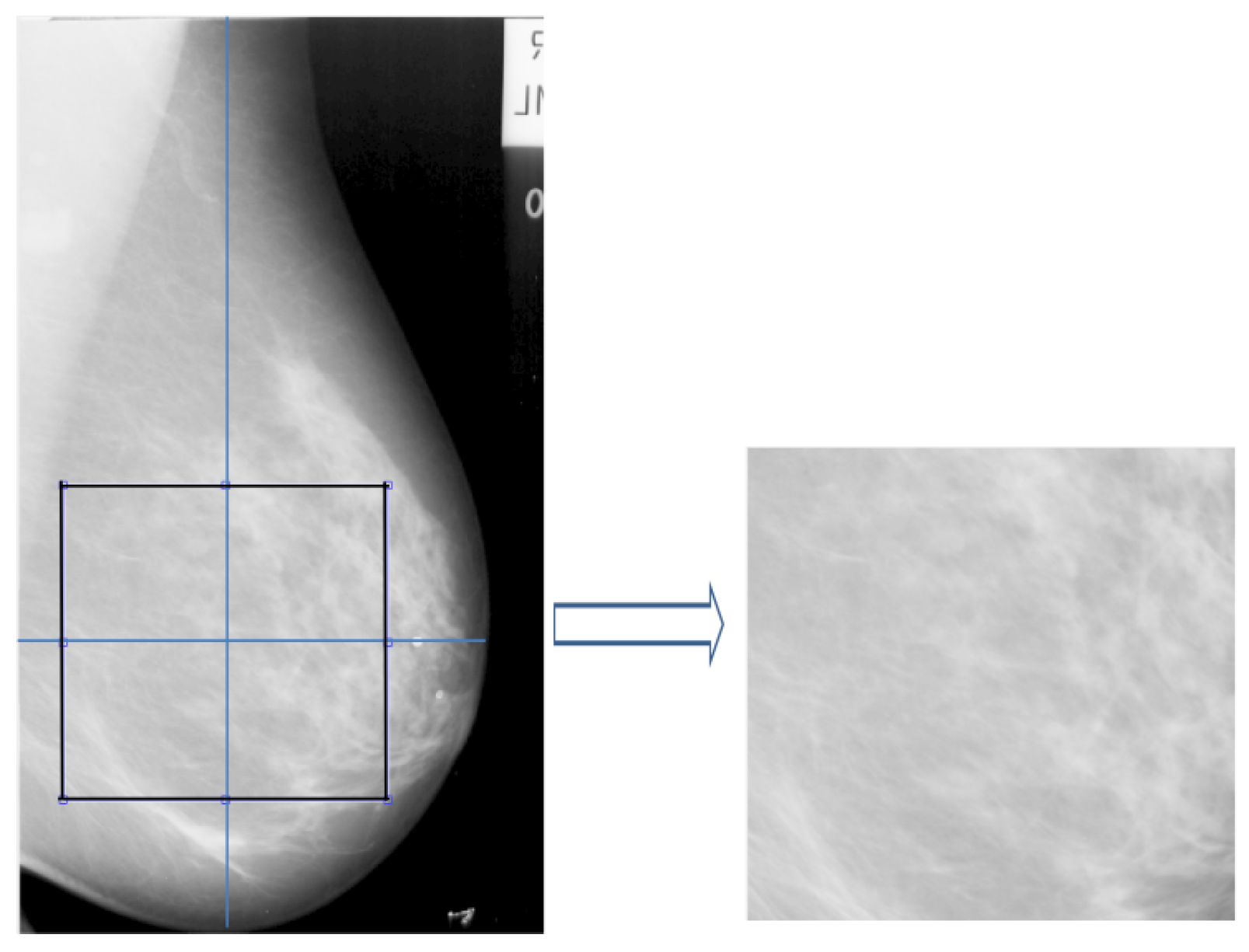
2.3. Extraction of ROIs
3. Experimental Results
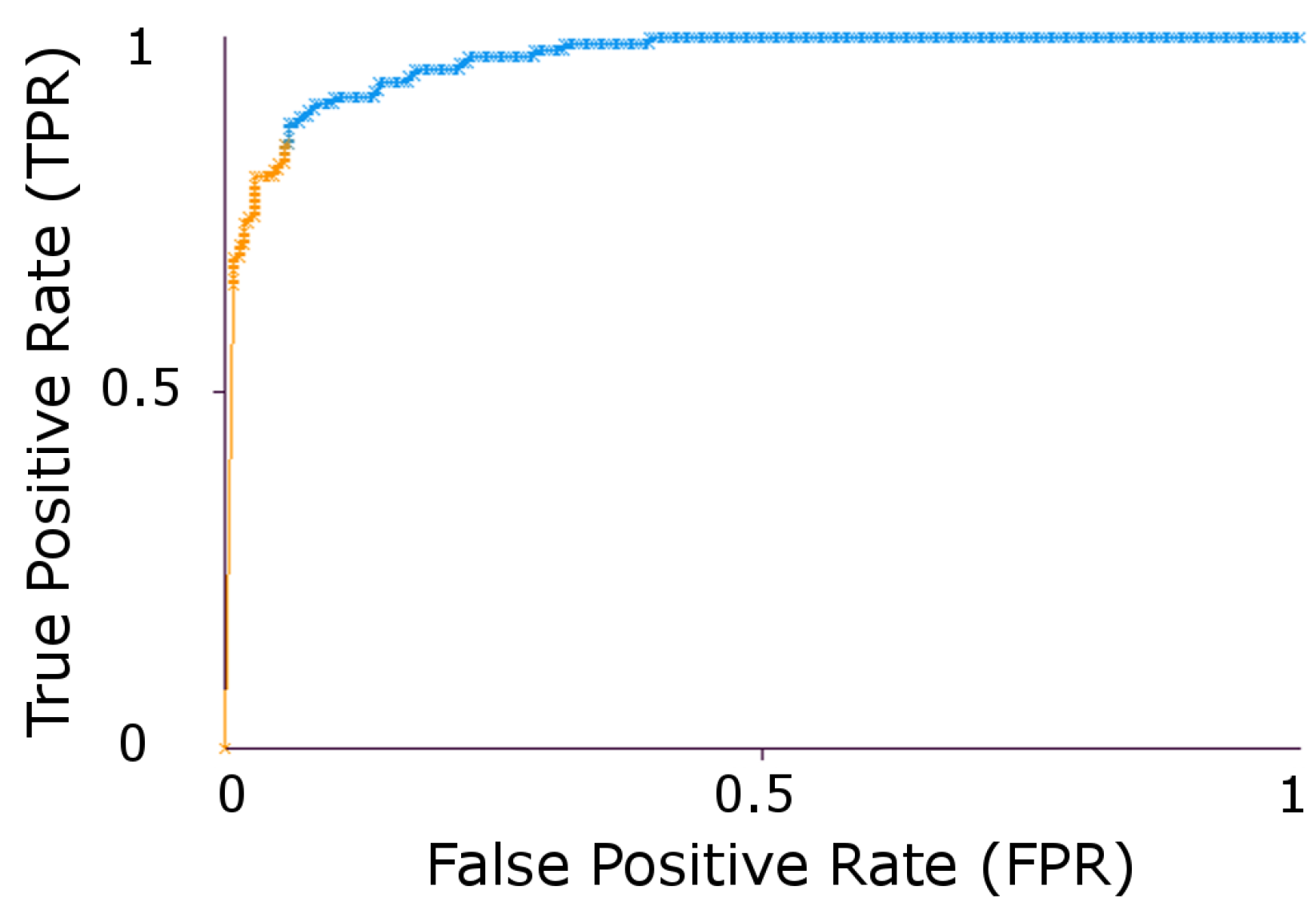
3.1. Comparison between LBP Variants
3.2. Study on Classifier Effect on Classifications
3.3. Study on Descriptor Size
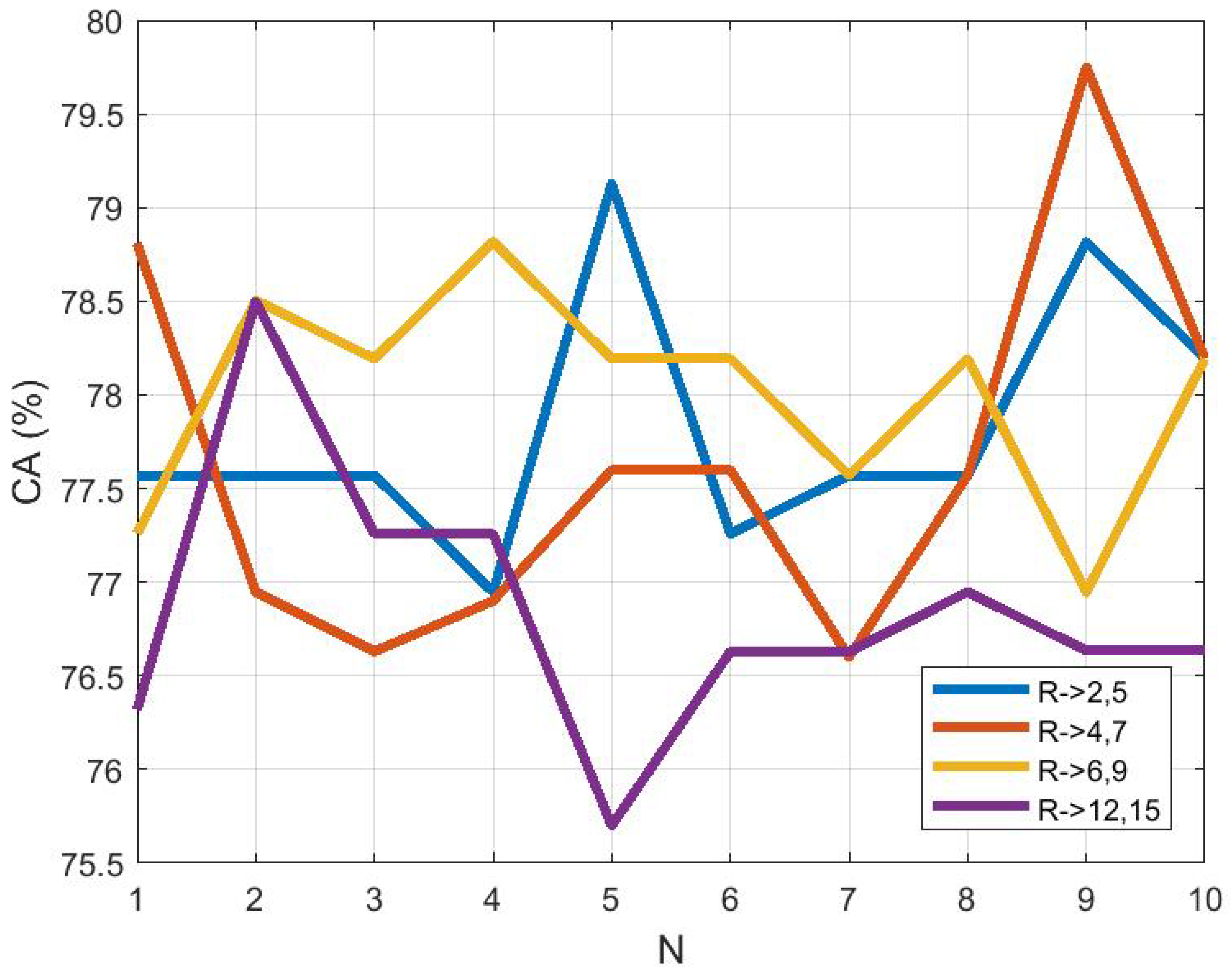
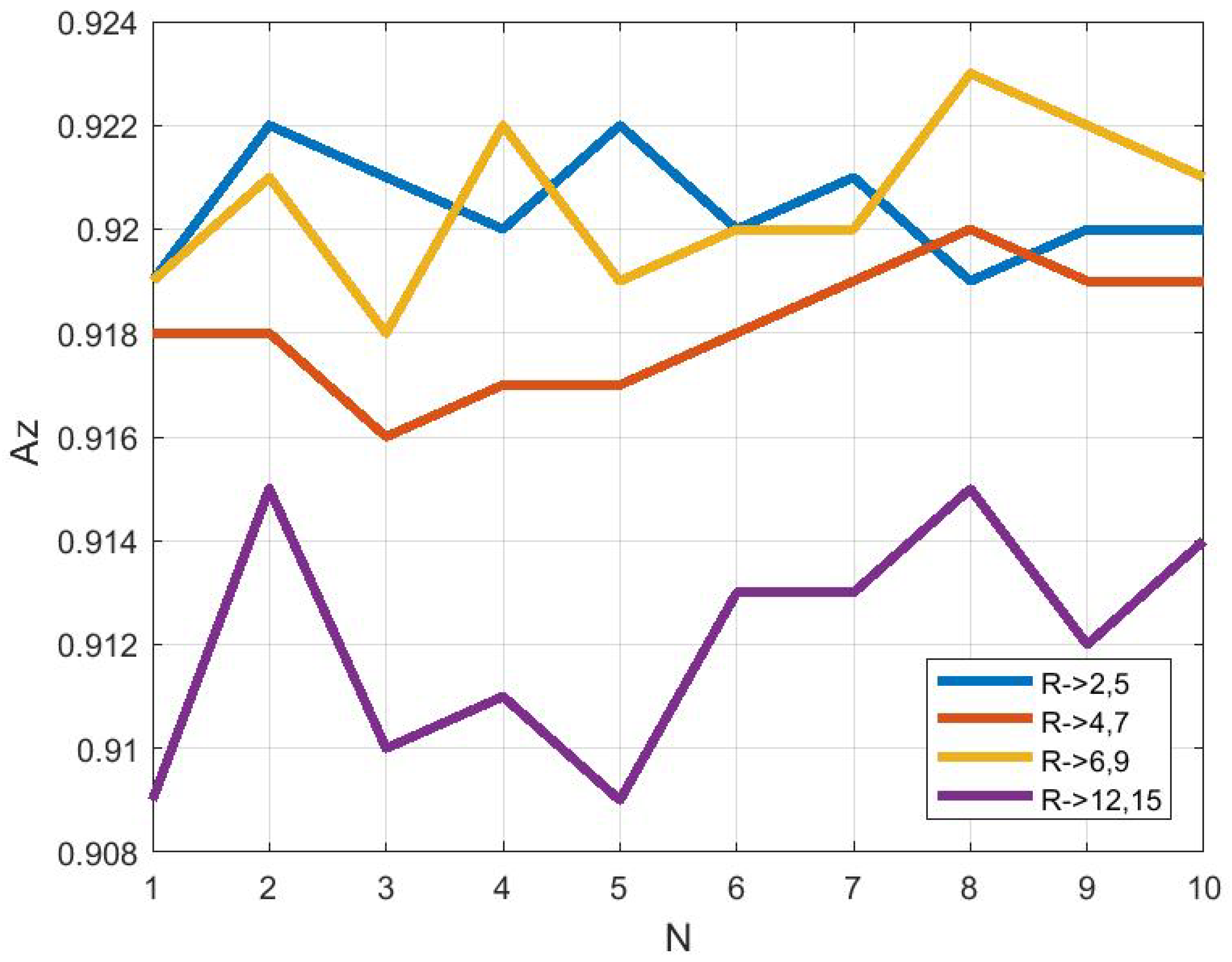
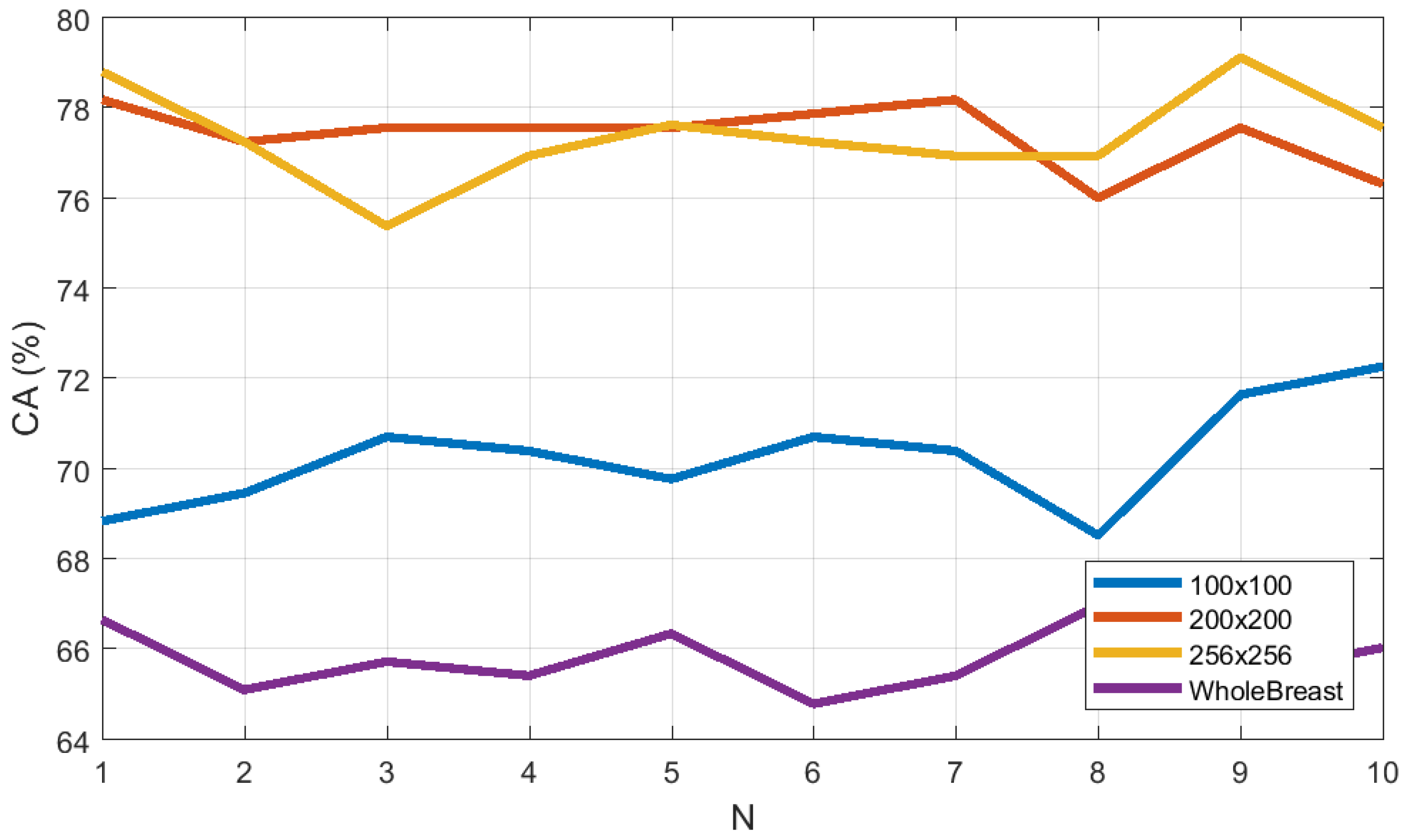
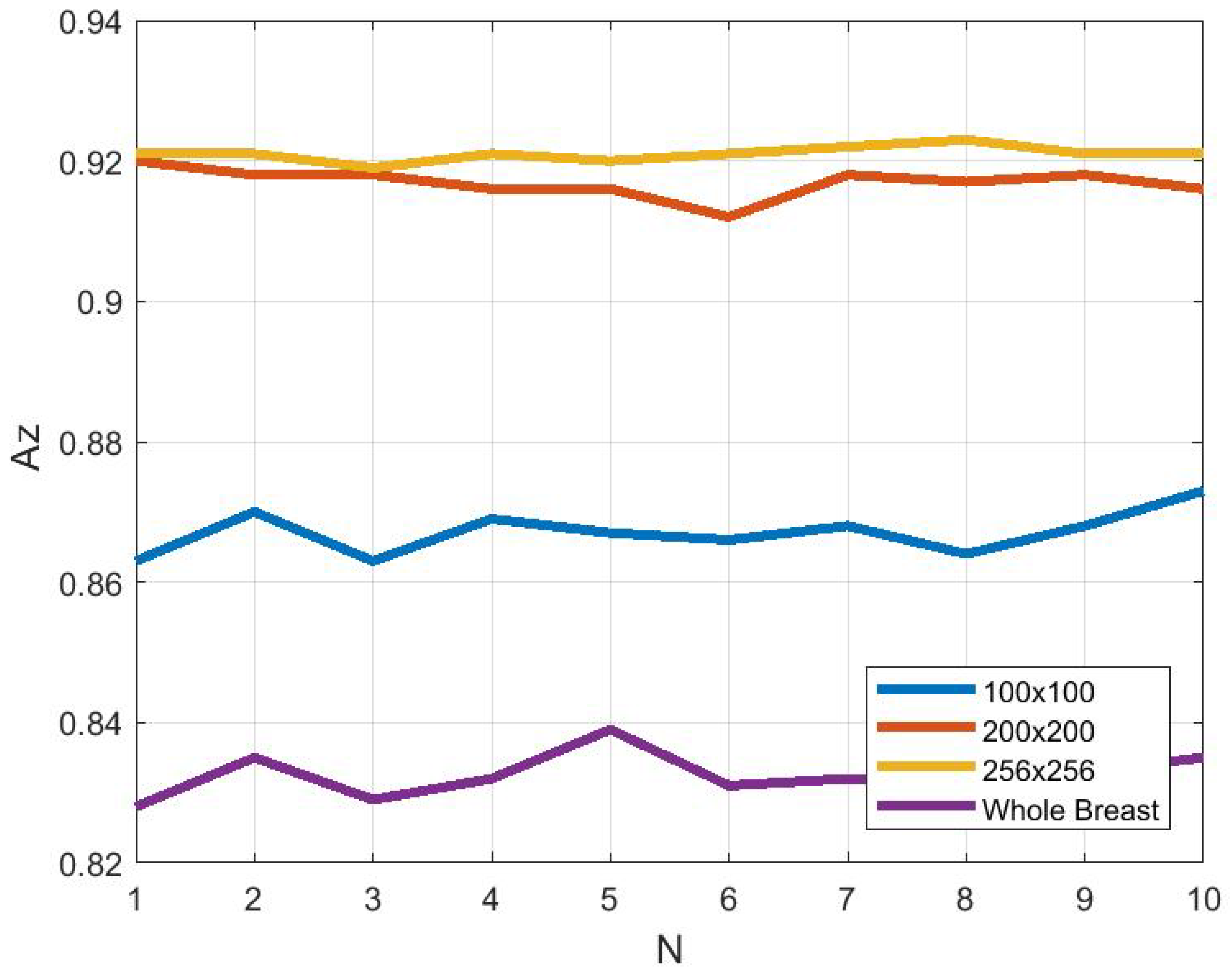
3.4. Effect of ROI Size and Location in Classification
4. Discussions and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ferlay, J.; Soerjomataram, I.; Dikshit, R.; Eser, S.; Mathers, C.; Rebelo, M.; Parkin, D.M.; Forman, D.; Bray, F. Cancer incidence and mortality worldwide: Sources, methods and major patterns in GLOBOCAN 2012. Int. J. Cancer 2015, 136, E359–E386. [Google Scholar] [CrossRef] [PubMed]
- Carioli, G.; Malvezzi, M.; Rodriguez, T.; Bertuccio, P.; Negri, E.; La Vecchia, C. Trends and predictions to 2020 in breast cancer mortality in Europe. Breast 2017, 36, 89–95. [Google Scholar] [CrossRef] [PubMed]
- Day, N.; Williams, D.; Khaw, K. Breast cancer screening programmes: The development of a monitoring and evaluation system. Br. J. Cancer 1989, 59, 954. [Google Scholar] [CrossRef] [PubMed]
- Autier, P.; Héry, C.; Haukka, J.; Boniol, M.; Byrnes, G. Advanced breast cancer and breast cancer mortality in randomized controlled trials on mammography screening. J. Clin. Oncol. 2009, 27, 5919–5923. [Google Scholar] [CrossRef] [PubMed]
- Kuhl, C.; Kuhn, W.; Schild, H. Management of women at high risk for breast cancer: New imaging beyond mammography. Breast 2005, 14, 480–486. [Google Scholar] [CrossRef] [PubMed]
- Oliver, A.; Freixenet, J.; Marti, R.; Pont, J.; Pérez, E.; Denton, E.R.; Zwiggelaar, R. A novel breast tissue density classification methodology. IEEE Trans. Inf. Technol. Biomed. 2008, 12, 55–65. [Google Scholar] [CrossRef] [PubMed]
- McCormack, V.A.; dos Santos Silva, I. Breast density and parenchymal patterns as markers of breast cancer risk: A meta-analysis. Cancer Epidemiol. Prev. Biomark. 2006, 15, 1159–1169. [Google Scholar] [CrossRef]
- George, M.; Rampun, A.; Denton, E.; Zwiggelaar, R. Mammographic ellipse modelling towards birads density classification. In Proceedings of the International Workshop on Digital Mammography, Malmo, Sweden, 19–22 June 2016; pp. 423–430. [Google Scholar]
- Kallenberg, M.; Petersen, K.; Nielsen, M.; Ng, A.Y.; Diao, P.; Igel, C.; Vachon, C.M.; Holland, K.; Winkel, R.R.; Karssemeijer, N.; et al. Unsupervised deep learning applied to breast density segmentation and mammographic risk scoring. IEEE Trans. Med Imaging 2016, 35, 1322–1331. [Google Scholar] [CrossRef]
- Boyd, N.F.; Martin, L.J.; Bronskill, M.; Yaffe, M.J.; Duric, N.; Minkin, S. Breast tissue composition and susceptibility to breast cancer. J. Natl. Cancer Inst. 2010, 102, 1224–1237. [Google Scholar] [CrossRef]
- Byng, J.W.; Boyd, N.; Fishell, E.; Jong, R.; Yaffe, M.J. The quantitative analysis of mammographic densities. Phys. Med. Biol. 1994, 39, 1629. [Google Scholar] [CrossRef]
- Petroudi, S.; Brady, M. Breast density segmentation using texture. In Proceedings of the International Workshop on Digital Mammography, Malmo, Sweden, 19–22 June 2016; pp. 609–615. [Google Scholar]
- Ho, W.; Lam, P. Clinical performance of computer-assisted detection (CAD) system in detecting carcinoma in breasts of different densities. Clin. Radiol. 2003, 58, 133–136. [Google Scholar] [CrossRef] [PubMed]
- Obenauer, S.; Sohns, C.; Werner, C.; Grabbe, E. Impact of breast density on computer-aided detection in full-field digital mammography. J. Digit. Imaging 2006, 19, 258. [Google Scholar] [CrossRef] [PubMed]
- Wolfe, J.N. Risk for breast cancer development determined by mammographic parenchymal pattern. Cancer 1976, 37, 2486–2492. [Google Scholar] [CrossRef]
- Boyd, N.; Byng, J.; Jong, R.; Fishell, E.; Little, L.; Miller, A.; Lockwood, G.; Tritchler, D.; Yaffe, M.J. Quantitative classification of mammographic densities and breast cancer risk: Results from the Canadian National Breast Screening Study. J. Natl. Cancer Inst. 1995, 87, 670–675. [Google Scholar] [CrossRef] [PubMed]
- Tabár, L.; Dean, P.B. Mammographic parenchymal patterns: Risk indicator for breast cancer? JAMA 1982, 247, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Warfield, S.K.; Zou, K.H.; Wells, W.M. Validation of image segmentation by estimating rater bias and variance. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2006; pp. 839–847. [Google Scholar]
- Kauppi, T.; Kamarainen, J.K.; Lensu, L.; Kalesnykiene, V.; Sorri, I.; Kälviäinen, H.; Uusitalo, H.; Pietilä, J. Fusion of multiple expert annotations and overall score selection for medical image diagnosis. In Proceedings of the Scandinavian Conference on Image Analysis, Oslo, Norway; 2009; pp. 760–769. [Google Scholar]
- American College of Radiology, B.R.C. Breast Imaging Reporting and Data System; American College of Radiology: Reston, VA, USA, 1998. [Google Scholar]
- Muhimmah, I.; Oliver, A.; Denton, E.R.; Pont, J.; Pérez, E.; Zwiggelaar, R. Comparison between Wolfe, Boyd, BI-RADS and Tabár based mammographic risk assessment. In Proceedings of the International Workshop on Digital Mammography, Malmo, Sweden, 19–22 June 2006; pp. 407–415. [Google Scholar]
- Sickles, E.A. Wolfe mammographic parenchymal patterns and breast cancer risk. Am. J. Roentgenol. 2007, 188, 301–303. [Google Scholar] [CrossRef] [PubMed]
- Muhimmah, I.; Zwiggelaar, R. Mammographic density classification using multiresolution histogram information. In Proceedings of the International Special Topic Conference on Information Technology in Biomedicine, Epirus, Greece, 26–28 October 2006; pp. 26–28. [Google Scholar]
- Zwiggelaar, R.; Muhimmah, I.; Denton, E. Mammographic density classification based on statistical gray-level histogram modelling. In Proceedings of the Medical Image Understanding and Analysis Conference, Bristol, UK; 2005; pp. 183–186. [Google Scholar]
- Hadjidemetriou, E.; Grossberg, M.D.; Nayar, S.K. Multiresolution histograms and their use for recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 831–847. [Google Scholar] [CrossRef]
- Kallenberg, M.G.; Lokate, M.; Van Gils, C.H.; Karssemeijer, N. Automatic breast density segmentation: An integration of different approaches. Phys. Med. Biol. 2011, 56, 2715. [Google Scholar] [CrossRef]
- Zhou, C.; Chan, H.P.; Petrick, N.; Helvie, M.A.; Goodsitt, M.M.; Sahiner, B.; Hadjiiski, L.M. Computerized image analysis: Estimation of breast density on mammograms. Med. Phys. 2001, 28, 1056–1069. [Google Scholar] [CrossRef]
- He, W.; Denton, E.R.; Zwiggelaar, R. Mammographic segmentation and risk classification using a novel binary model based bayes classifier. In Proceedings of the International Workshop on Digital Mammography, Philadelphia, PA, USA, 8–11 July 2012; pp. 40–47. [Google Scholar]
- Oliver, A.; Freixenet, J.; Zwiggelaar, R. Automatic classification of breast density. In Proceedings of the IEEE International Conference on Image Processing 2005, Genova, Italy, 14 September 2005; Volume 2. [Google Scholar]
- Muštra, M.; Grgić, M.; Delač, K. Breast density classification using multiple feature selection. Automatika 2012, 53, 362–372. [Google Scholar] [CrossRef]
- Vállez, N.; Bueno, G.; Déniz, O.; Dorado, J.; Seoane, J.A.; Pazos, A.; Pastor, C. Breast density classification to reduce false positives in CADe systems. Comput. Methods Programs Biomed. 2014, 113, 569–584. [Google Scholar] [CrossRef] [PubMed]
- Bovis, K.; Singh, S. Classification of mammographic breast density using a combined classifier paradigm. In Proceedings of the 4th International Workshop on Digital Mammography, Bremen, Germany, 22–25 June 2002; pp. 177–180. [Google Scholar]
- He, W.; Juette, A.; Denton, E.R.; Oliver, A.; Martí, R.; Zwiggelaar, R. A review on automatic mammographic density and parenchymal segmentation. Int. J. Breast Cancer 2015, 2015. [Google Scholar] [CrossRef] [PubMed]
- Tahmassebi, A.; Gandomi, A.; McCann, I.; Schulte, M.; Goudriaan, A.; Meyer-Baese, A. Deep learning in medical imaging: fMRI big data analysis via convolutional neural networks. Proc. Pract. Exp. Adv. Res. Comput. ACM 2018. [Google Scholar] [CrossRef]
- Hamidinekoo, A.; Suhail, Z.; Qaiser, T.; Zwiggelaar, R. Investigating the effect of various augmentations on the input data fed to a convolutional neural network for the task of mammographic mass classification. In Proceedings of the Annual Conference on Medical Image Understanding and Analysis, Edinburgh, UK, 11–13 July 2017; pp. 398–409. [Google Scholar]
- Wu, N.; Geras, K.J.; Shen, Y.; Su, J.; Kim, S.G.; Kim, E.; Wolfson, S.; Moy, L.; Cho, K. Breast density classification with deep convolutional neural networks. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 6682–6686. [Google Scholar]
- Wainer, J. Breast Density Classification with Convolutional Neural Networks. In Proceedings of the Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications: 21st Iberoamerican Congress, Lima, Peru, 8–11 November 2016; Volume 10125, p. 101. [Google Scholar]
- Ciritsis, A.; Rossi, C.; Vittoria De Martini, I.; Eberhard, M.; Marcon, M.; Becker, A.S.; Berger, N.; Boss, A. Determination of mammographic breast density using a deep convolutional neural network. Br. J. Radiol. 2018, 91. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, A.A.; Berg, W.A.; Peng, H.; Luo, Y.; Jankowitz, R.C.; Wu, S. A deep learning method for classifying mammographic breast density categories. Med. Phys. 2018, 45, 314–321. [Google Scholar] [CrossRef] [PubMed]
- Karssemeijer, N. Automated classification of parenchymal patterns in mammograms. Phys. Med. Biol. 1998, 43, 365. [Google Scholar] [CrossRef] [PubMed]
- Blot, L.; Zwiggelaar, R. Background texture extraction for the classification of mammographic parenchymal patterns. In Proceedings of the 15th Medical Image Understanding and Analysis Meeting, Birmingham, UK, 2001; pp. 145–148. [Google Scholar]
- Petroudi, S.; Kadir, T.; Brady, M. Automatic classification of mammographic parenchymal patterns: A statistical approach. In Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Cancun, Mexico, 17–21 September 2003; Volume 1, pp. 798–801. [Google Scholar]
- Subashini, T.; Ramalingam, V.; Palanivel, S. Automated assessment of breast tissue density in digital mammograms. Comput. Vis. Image Underst. 2010, 114, 33–43. [Google Scholar] [CrossRef]
- Oliver, A.; Lladó, X.; Pérez, E.; Pont, J.; Denton, E.R.; Freixenet, J.; Martí, J. A statistical approach for breast density segmentation. J. Digit. Imaging 2010, 23, 527–537. [Google Scholar] [CrossRef]
- Zwiggelaar, R. Local greylevel appearance histogram based texture segmentation. In Proceedings of the International Workshop on Digital Mammography, Girona, Spain, 16–18 June 2010; pp. 175–182. [Google Scholar]
- Liu, Q.; Liu, L.; Tan, Y.; Wang, J.; Ma, X.; Ni, H. Mammogram density estimation using sub-region classification. In Proceedings of the 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; Volume 1, pp. 356–359. [Google Scholar]
- Tzikopoulos, S.D.; Mavroforakis, M.E.; Georgiou, H.V.; Dimitropoulos, N.; Theodoridis, S. A fully automated scheme for mammographic segmentation and classification based on breast density and asymmetry. Comput. Methods Programs Biomed. 2011, 102, 47–63. [Google Scholar] [CrossRef]
- Chen, Z.; Denton, E.; Zwiggelaar, R. Local feature based mammographic tissue pattern modelling and breast density classification. In Proceedings of the 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; Volume 1, pp. 351–355. [Google Scholar]
- Qu, Y.; Shang, C.; Wu, W.; Shen, Q. Evolutionary Fuzzy Extreme Learning Machine for Mammographic Risk Analysis. Int. J. Fuzzy Syst. 2011, 13, 4. [Google Scholar]
- Rampun, A.; Morrow, P.; Scotney, B.; Winder, J. Breast Density Classification Using Local Ternary Patterns in Mammograms. In Proceedings of the International Conference Image Analysis and Recognition, Montreal, QC, Canada, 5–7 July 2017; pp. 463–470. [Google Scholar]
- George, M.; Denton, E.; Zwiggelaar, R. Mammogram breast density classification using mean-elliptical local binary patterns. In Proceedings of the 14th International Workshop on Breast Imaging (IWBI 2018), Atlanta, GA, USA, 8–11 July 2018; p. 107180. [Google Scholar]
- Ojala, T.; Pietikäinen, M.; Mäenpää, T. Gray scale and rotation invariant texture classification with local binary patterns. In Proceedings of the European Conference on Computer Vision, Dublin, Ireland, 26 June–1 July 2000; pp. 404–420. [Google Scholar]
- Nanni, L.; Lumini, A.; Brahnam, S. Local binary patterns variants as texture descriptors for medical image analysis. Artif. Intell. Med. 2010, 49, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Jabid, T.; Kabir, M.H.; Chae, O. Local directional pattern (LDP) for face recognition. In Proceedings of the International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 9–13 January 2010; pp. 329–330. [Google Scholar]
- George, M.; Zwiggelaar, R. Breast tissue classification using Local Binary Pattern variants: A comparative study. In Proceedings of the Annual Conference on Medical Image Understanding and Analysis, Southampton, UK, 9–11 July 2018; pp. 143–152. [Google Scholar]
- De Oliveira, J.E.; Machado, A.M.; Chavez, G.C.; Lopes, A.P.B.; Deserno, T.M.; Araújo, A.d.A. MammoSys: A content-based image retrieval system using breast density patterns. Comput. Methods Programs Biomed. 2010, 99, 289–297. [Google Scholar] [CrossRef] [PubMed]
- Epischina, J.; De Albuquerque, A.; Deserno, T. Content-based image retrieval applied to BI-RADS tissue classification in screening mammography. World J. Radiol. 2011, 28, 24–31. [Google Scholar]
- Li, H.; Giger, M.L.; Huo, Z.; Olopade, O.I.; Lan, L.; Weber, B.L.; Bonta, I. Computerized analysis of mammographic parenchymal patterns for assessing breast cancer risk: Effect of ROI size and location. Med. Phys. 2004, 31, 549–555. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V. Comparative analysis of region of interest of different sizes for breast density classification. Int. J. Med. Res. Health Sci. 2017, 6, 76–84. [Google Scholar]
- Chen, Z.; Zwiggelaar, R. Segmentation of the breast region with pectoral muscle removal in mammograms. Med. Image Underst. Anal. 2010, 71–76. [Google Scholar]
- Suckling, J.; Parker, J.; Dance, D.; Astley, S.; Hutt, I.; Boggis, C.; Ricketts, I.; Stamatakis, E.; Cerneaz, N.; Kok, S.; et al. The Mammographic Image Analysis Society Digital Mammogram Database; International Congress Series; Exerpta Medica: Bridgewater, NJ, USA, 1994; Volume 1069, pp. 375–378. [Google Scholar]
- Liu, L.; Fieguth, P.; Guo, Y.; Wang, X.; Pietikäinen, M. Local binary features for texture classification: Taxonomy and experimental study. Pattern Recognit. 2017, 62, 135–160. [Google Scholar] [CrossRef]
- Rampun, A.; Scotney, B.W.; Morrow, P.J.; Wang, H.; Winder, J. Breast Density Classification Using Local Quinary Patterns with Various Neighbourhood Topologies. J. Imaging 2018, 4, 14. [Google Scholar] [CrossRef]
- Barkan, O.; Weill, J.; Wolf, L.; Aronowitz, H. Fast high dimensional vector multiplication face recognition. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Austrailia, 1–8 December 2013; pp. 1960–1967. [Google Scholar]
- Hall, M.A. Correlation-Based Feature Selection for Machine Learning. Ph.D. Thesis, University of Waikato, Hillcrest, New Zealand, 1999. [Google Scholar]
- Jabid, T.; Kabir, M.H.; Chae, O. Gender classification using local directional pattern (LDP). In Proceedings of the 2010 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; pp. 2162–2165. [Google Scholar]
- Tahmassebi, A.; Pinker-Domenig, K.; Wengert, G.; Helbich, T.; Bago-Horvath, Z.; Meyer-Baese, A. Determining the importance of parameters extracted from multi-parametric mri in the early prediction of the response to neo-adjuvant chemotherapy in breast cancer. Med. Imaging 2018. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Caplier, A. Elliptical local binary patterns for face recognition. In Proceedings of the Asian Conference on Computer Vision, Daejeon, Korea, 5–6 November 2012; pp. 85–96. [Google Scholar]
- Stąpor, K. Evaluating and Comparing Classifiers: Review, Some Recommendations and Limitations. In Proceedings of the International Conference on Computer Recognition Systems, Polanica Zdroj, Poland, 22–24 May 2017; pp. 12–21. [Google Scholar]
- Tahmassebi, A.; Wengert, G.J.; Helbich, T.H.; Bago-Horvath, Z.; Alaei, S.; Bartsch, R.; Dubsky, P.; Baltzer, P.; Clauser, P.; Kapetas, P.; et al. Impact of machine learning with multiparametric magnetic resonance imaging of the breast for early prediction of response to neoadjuvant chemotherapy and survival outcomes in breast cancer patients. Investig. Radiol. 2019, 54, 110–117. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Pattern Classification and Scene Analysis; A Wiley-Interscience Publication; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference On Knowledge Discovery and Data Mining, San Francisco, CA, USA, 24–27 August 2016; pp. 785–794. [Google Scholar]


| Author | Features | Classifiers | Dataset | Number of Images | Result | Density Class | Year |
|---|---|---|---|---|---|---|---|
| Karssemeijer [40] | Grey level histograms | KNN | Nijmegen | 615 | 65.0% | BIRADS I-IV | 1998 |
| Blot and Zwiggelaar [41] | Texture GLCM | KNN | MIAS | 265 | 65.00% | Fatty, Glandular and Dense | 2001 |
| Bovis and Singh [32] | SGLD | ANN | DDSM | 377 | 71.40% | BIRADS I-IV | 2002 |
| Petroudi et al. [42] | Textons based on MR8 filters | KNN | Oxford | 132 | 75.75% | 2 Class-Fatty and Dense | 2003 |
| Zwiggelaar et al. [24] | Gray level histogram | PCA +KNN | MIAS | 312 | 71.5% | Fatty, Glandular and Dense | 2005 |
| Oliver et al. [29] | Morphological Features | KNN Decision Tree | MIAS DDSM | 270 300 R-MLO | 67.0% 73.0% 47.0% | BIRADS I-IV | 2005 |
| Muhimmah and Zwiggelaar [23] | Multiresolution histogram Features | DAG-SVM | MIAS | 321 | 77.57% | Fatty, Glandular and Dense | 2006 |
| Oliver et al. [6] | Texture | KNN+SFS (sequential forward selection (SFS)) | MIAS DDSM | 322 831 | 86.0% 77.0% | BIRADS I-IV | 2008 |
| Subashini et al. [43] | Statistical features | SVM | MIAS | 43 | 95.55% | Fatty, Glandular and Dense | 2010 |
| Oliver et al. [44] | Connected density clusters taking the spatial information | LDA-PCA | DDSM | 831 | 79.0% | Fatty and dense | 2010 |
| Zwiggelaar [45] | LGA | KNN | MIAS | 322 | 64.0% | BIRADS I-IV | 2010 |
| Liu et al. [46] | Statistical | SVM | Tianjin Tumor Hospital | 88 | 86.40% | BIRADS I-IV | 2011 |
| Tzikopoulos et al. [47] | Intensity based | SVM | MIAS | 322 | 85.70% | Fatty, Glandular and Dense | 2011 |
| Chen et al. [48] | LBP LGA BIF Textons Topographic | KNN, Bayesian | MIAS | 322 | 59.0% 72.0% 70.0% 75.0% 76.0% | BIRADS I-IV | 2011 |
| Qu et al. [49] | Unknown | E-FELM (Evolutionary Fuzzy Extreme Learning Machine) | MIAS | 322 | 72.6% | BIRADS I-IV | 2011 |
| Muštra et al. [30] | GLCM | KNN+Naïve Bayesian | KBD-FER, University Hospital Dubrava, Zagreb | 144 | 79.30% | 2 Class-Fatty and Dense | 2012 |
| Muštra et al. [30] | GLCM | KNN+Naive Bayesian | MIAS | 144 | 82.0% | 2 class-Fatty, Dense | 2012 |
| He et al. [28] | Texture | Binary model based Bayes Classifier | MIAS | 322 | 78.0% | BIRADS I-IV | 2012 |
| Rampun et al. [50] | LTP | SVM | MIAS | 322 | 82.3% | BIRADS I-IV | 2017 |
| George et al. [51] | M-ELBP LBP | Bayesian | MIAS | 321 | 74.0% 66.5% | BIRADS I-IV | 2018 |
| Automatic Classification | |||
|---|---|---|---|
| Truth Data | Fatty | Glandular | Dense |
| Fatty | 86 | 19 | 1 |
| Glandular | 16 | 73 | 15 |
| Dense | 7 | 38 | 66 |
| Automatic Classification | |||
|---|---|---|---|
| Truth Data | Fatty | Glandular | Dense |
| Fatty | 86 | 20 | 0 |
| Glandular | 11 | 68 | 25 |
| Dense | 3 | 22 | 86 |
| Automatic Classification | |||
|---|---|---|---|
| Truth Data | Fatty | Glandular | Dense |
| Fatty | 86 | 19 | 1 |
| Glandular | 11 | 69 | 24 |
| Dense | 2 | 27 | 82 |
| Automatic Classification | |||
|---|---|---|---|
| Truth Data | Fatty | Glandular | Dense |
| Fatty | 92 | 14 | 0 |
| Glandular | 13 | 76 | 15 |
| Dense | 0 | 23 | 88 |
| Automatic Classification | |||
|---|---|---|---|
| Truth Data | Fatty | Glandular | Dense |
| Fatty | 92 | 13 | 1 |
| Glandular | 10 | 74 | 20 |
| Dense | 3 | 32 | 76 |
| Classifier | LBP | ELBP | Uniform ELBP | M-ELBP | LDP |
|---|---|---|---|---|---|
| Bayesian Network | |||||
| KNN | |||||
| SVM | |||||
| Random Forest |
| Classifier | LBP | ELBP | Uniform ELBP | M-ELBP | LDP |
|---|---|---|---|---|---|
| Bayesian Network | |||||
| KNN | |||||
| SVM | |||||
| Random Forest |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
George, M.; Zwiggelaar, R. Comparative Study on Local Binary Patterns for Mammographic Density and Risk Scoring. J. Imaging 2019, 5, 24. https://doi.org/10.3390/jimaging5020024
George M, Zwiggelaar R. Comparative Study on Local Binary Patterns for Mammographic Density and Risk Scoring. Journal of Imaging. 2019; 5(2):24. https://doi.org/10.3390/jimaging5020024
Chicago/Turabian StyleGeorge, Minu, and Reyer Zwiggelaar. 2019. "Comparative Study on Local Binary Patterns for Mammographic Density and Risk Scoring" Journal of Imaging 5, no. 2: 24. https://doi.org/10.3390/jimaging5020024
APA StyleGeorge, M., & Zwiggelaar, R. (2019). Comparative Study on Local Binary Patterns for Mammographic Density and Risk Scoring. Journal of Imaging, 5(2), 24. https://doi.org/10.3390/jimaging5020024






