What’s in a Smile? Initial Analyses of Dynamic Changes in Facial Shape and Appearance †
Abstract
1. Introduction
2. Materials and Methods
2.1. Image Capture, Preprocessing, and Subject Characteristics
2.2. Multilevel Principal Components Analysis (mPCA)
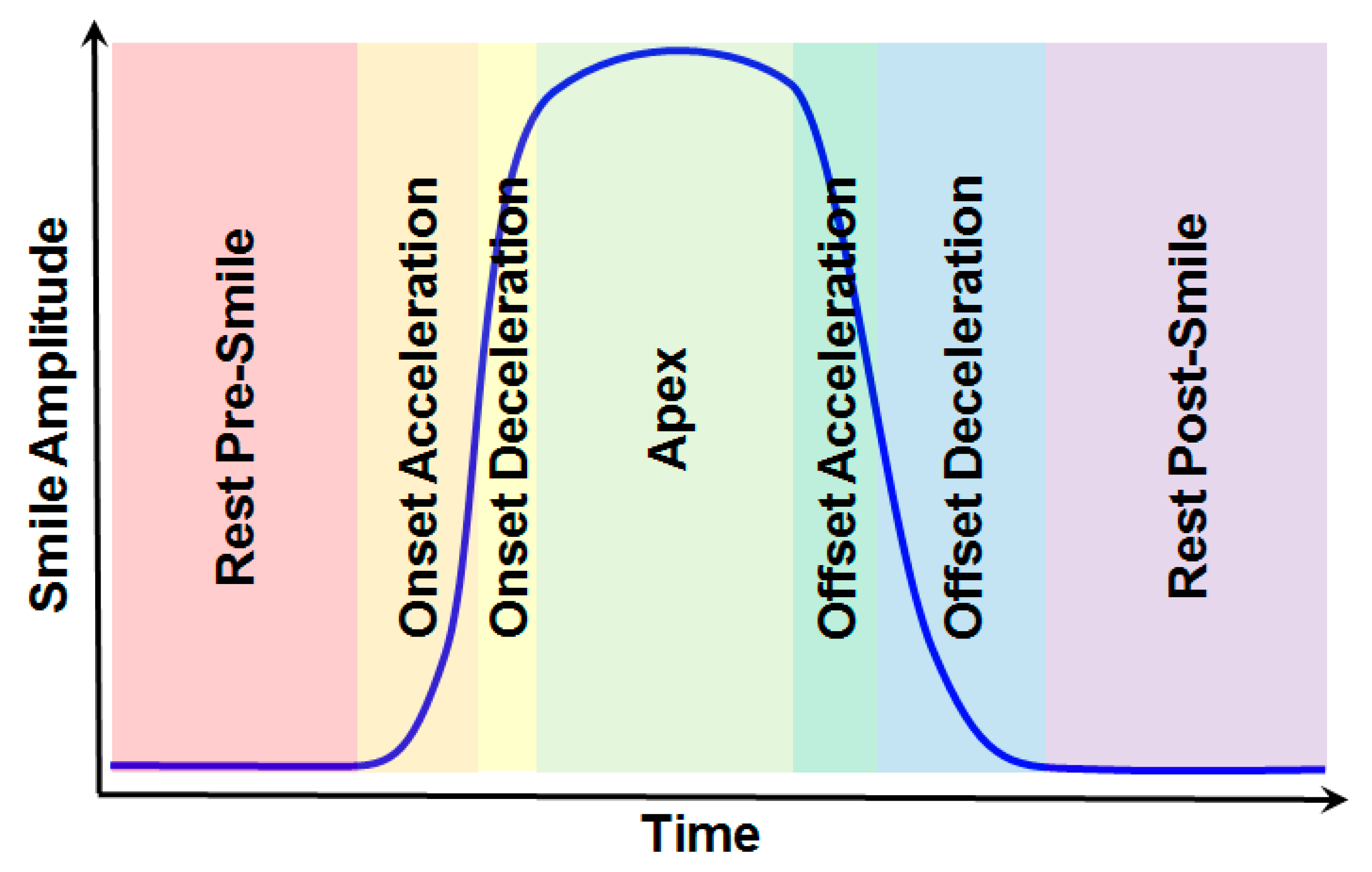
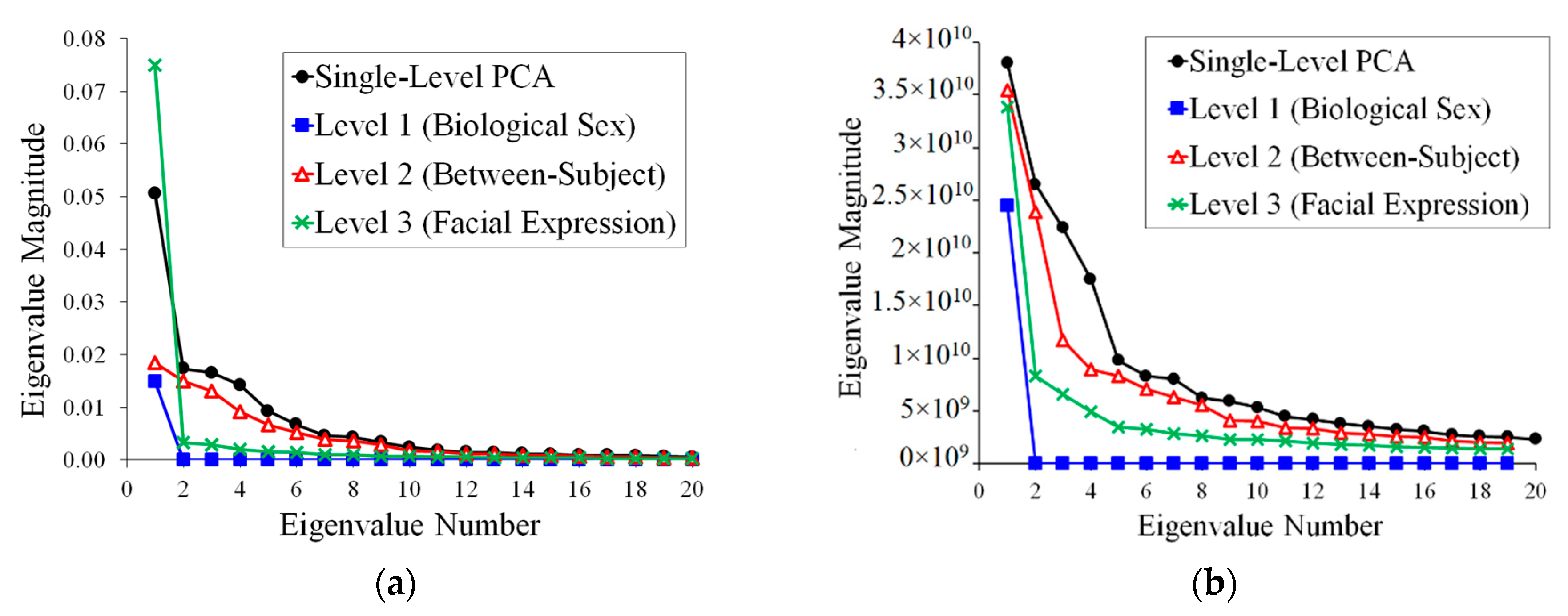
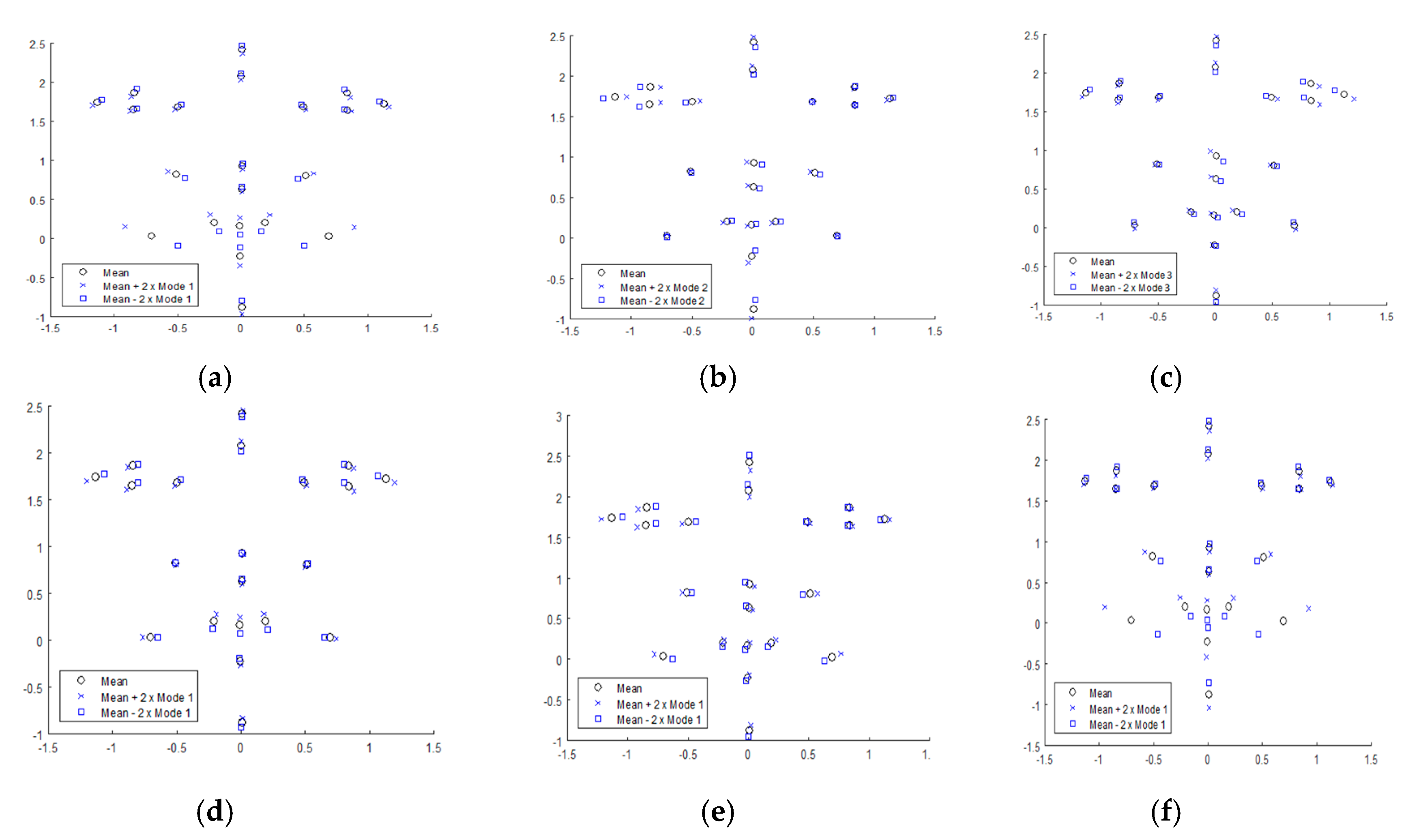
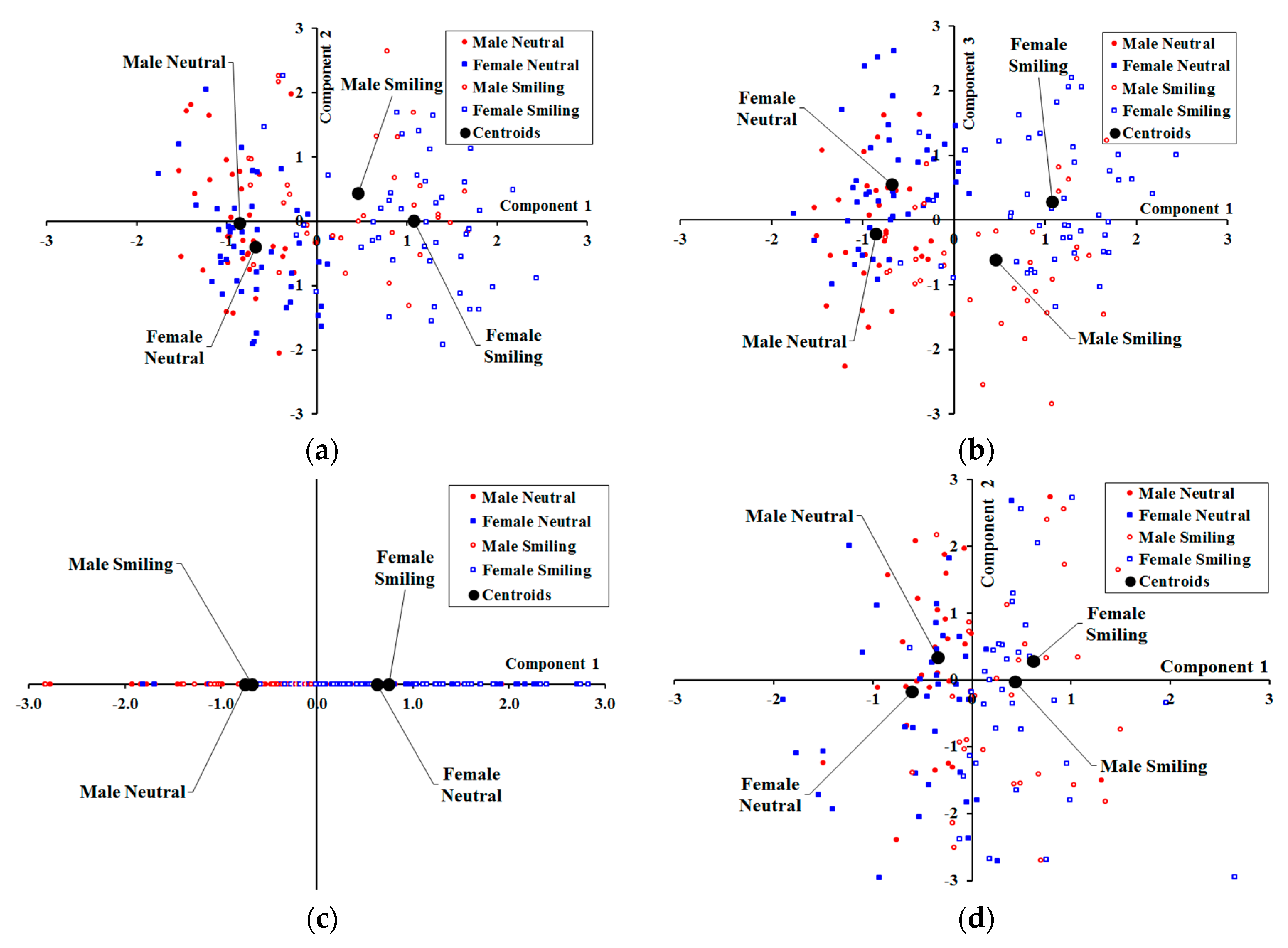
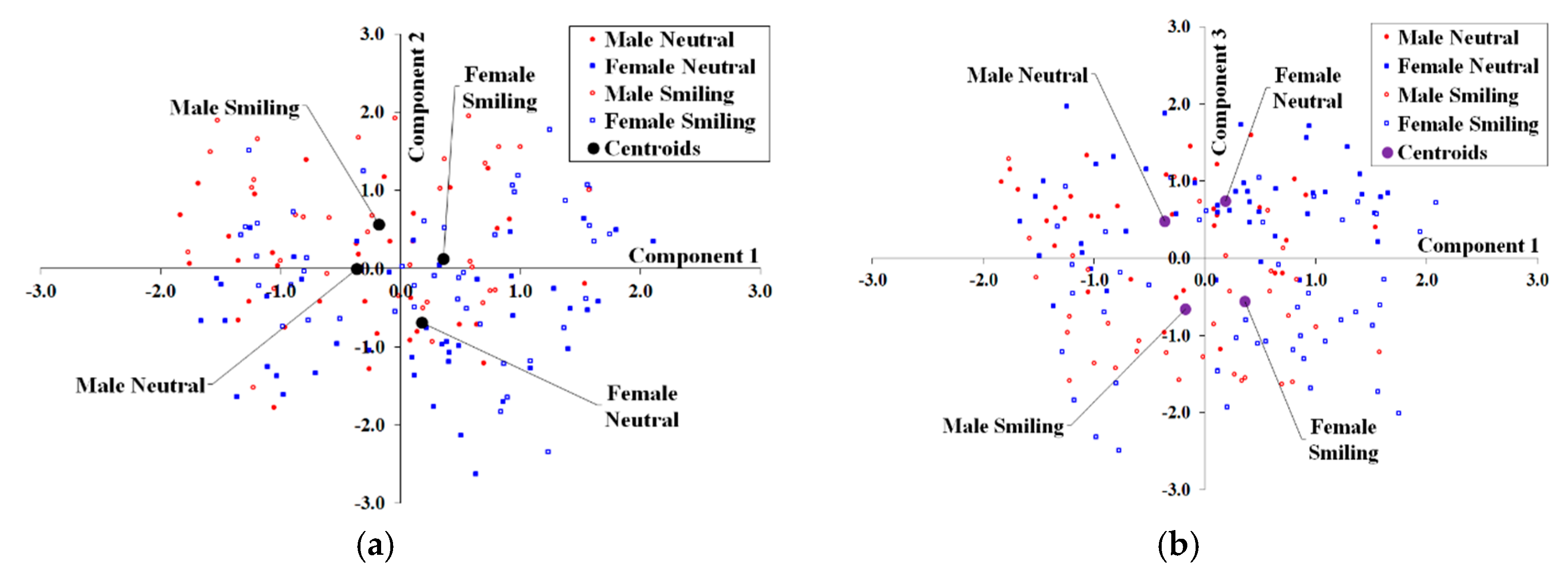
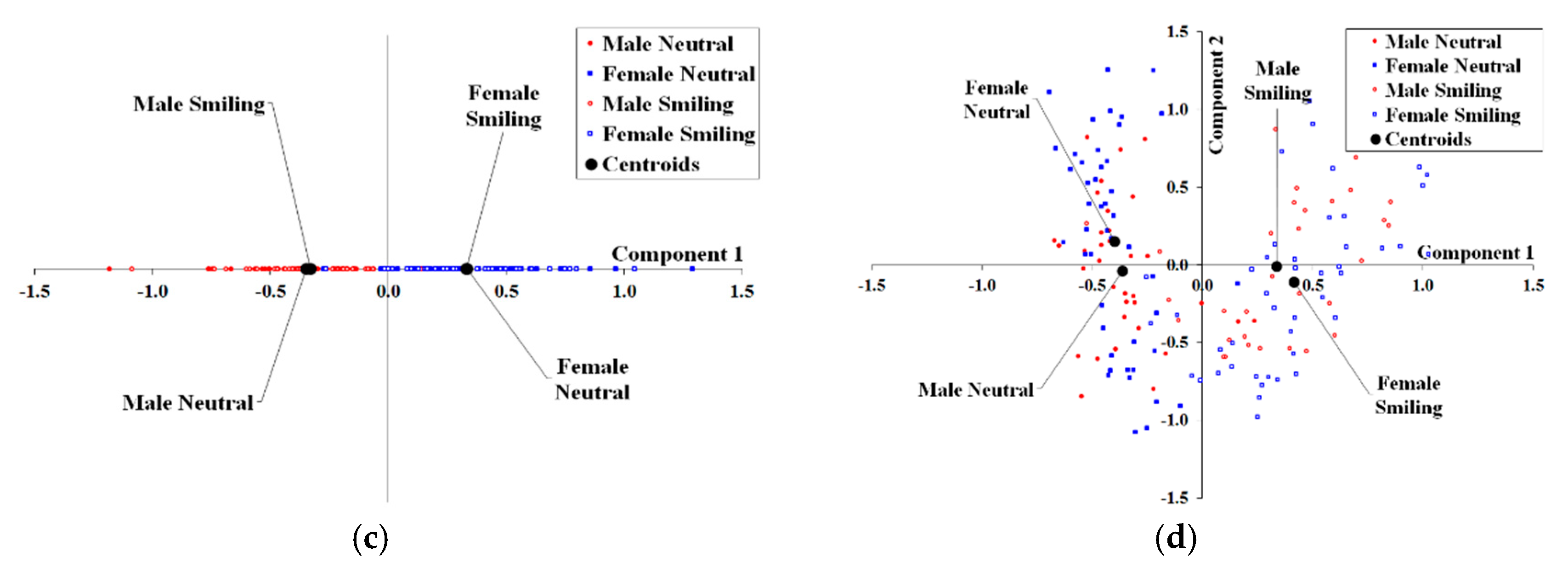
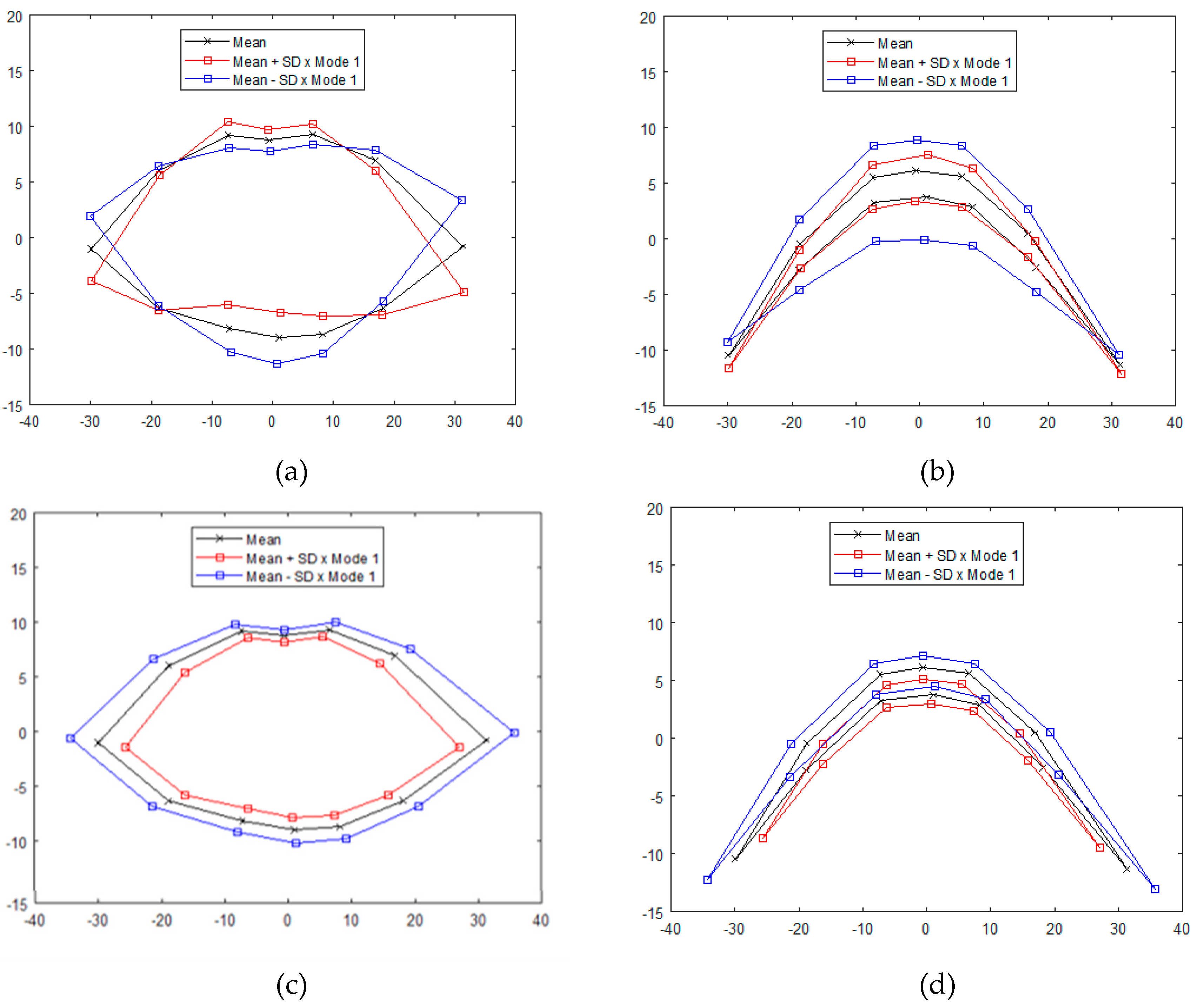
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sarver, D.M.; Ackerman, M.B. Dynamic smile visualization and quantification: Part 1. Evolution of the concept and dynamic records for smile capture. Am. J. Orthod. Dentofac. Orthop. 2003, 124, 4–12. [Google Scholar] [CrossRef]
- Sarver, D.M.; Ackerman, M.B. Dynamic smile visualization and quantification: Part 2. Smile analysis and treatment strategies. Am. J. Orthod. Dentofac. Orthop. 2003, 124, 116–127. [Google Scholar] [CrossRef]
- Dong, J.K.; Jin, T.H.; Cho, H.W.; Oh, S.C. The esthetics of the smile: A review of some recent studies. Int. J. Prosthodont. 1999, 12, 9–19. [Google Scholar]
- Otta, E. Sex differences over age groups in self-posed smiling in photographs. Psychol. Rep. 1998, 83, 907–913. [Google Scholar] [CrossRef]
- Drummond, S.; Capelli, J., Jr. Incisor display during speech and smile: Age and gender correlations. Angle Orthod. 2015, 86, 631–637. [Google Scholar] [CrossRef] [PubMed]
- Chetan, P.; Tandon, P.; Singh, G.K.; Nagar, A.; Prasad, V.; Chugh, V.K. Dynamics of a smile in different age groups. Angle Orthod. 2012, 83, 90–96. [Google Scholar] [CrossRef] [PubMed]
- Dibeklioğlu, H.; Gevers, T.; Salah, A.A.; Valenti, R. A smile can reveal your age: Enabling facial dynamics in age estimation. In Proceedings of the 20th ACM International Conference on Multimedia, Nara, Japan, 29 October–2 November 2012; pp. 209–218. [Google Scholar] [CrossRef]
- Dibeklioğlu, H.; Alnajar, F.; Salah, A.A.; Gevers, T. Combining facial dynamics with appearance for age estimation. IEEE Trans. Image Process. 2015, 24, 1928–1943. [Google Scholar] [CrossRef] [PubMed]
- Kau, C.H.; Cronin, A.; Durning, P.; Zhurov, A.I.; Sandham, A.; Richmond, S. A new method for the 3D measurement of postoperative swelling following orthognathic surgery. Orthod. Craniofac. Res. 2006, 9, 31–37. [Google Scholar] [CrossRef] [PubMed]
- Krneta, B.; Primožič, J.; Zhurov, A.; Richmond, S.; Ovsenik, M. Three-dimensional evaluation of facial morphology in children aged 5–6 years with a Class III malocclusion. Eur. J. Orthod. 2012, 36, 133–139. [Google Scholar] [CrossRef]
- Djordjevic, J.; Lawlor, D.A.; Zhurov, A.I.; Toma, A.M.; Playle, R.; Richmond, S. A population-based cross-sectional study of the association between facial morphology and cardiometabolic risk factors in adolescence. BMJ Open 2013, 3, e002910. [Google Scholar] [CrossRef]
- Popat, H.; Zhurov, A.I.; Toma, A.M.; Richmond, S.; Marshall, D.; Rosin, P.L. Statistical modeling of lip movement in the clinical context. Orthod. Craniofac. Res. 2012, 15, 92–102. [Google Scholar] [CrossRef] [PubMed]
- Alqattan, M.; Djordjevic, J.; Zhurov, A.I.; Richmond, S. Comparison between landmark and surface-based three-dimensional analyses of facial asymmetry in adults. Eur. J. Orthod. 2013, 37, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Al Ali, A.; Richmond, S.; Popat, H.; Playle, R.; Pickles, T.; Zhurov, A.I.; Marshall, D.; Rosin, P.L.; Henderson, J.; Bonuck, K. The influence of snoring, mouth breathing and apnoea on facial morphology in late childhood: A three-dimensional study. BMJ Open 2015, 5, e009027. [Google Scholar] [CrossRef] [PubMed]
- Vandeventer, J. 4D (3D Dynamic) Statistical Models of Conversational Expressions and the Synthesis of Highly-Realistic 4D Facial Expression Sequences. Ph.D. Thesis, Cardiff University, Cardiff, UK, 2015. [Google Scholar]
- Vandeventer, J.; Graser, L.; Rychlowska, M.; Rosin, P.L.; Marshall, D. Towards 4D coupled models of conversational facial expression interactions. In Proceedings of the British Machine Vision Conference; BMVA Press: Durham, UK, 2015; p. 142-1. [Google Scholar] [CrossRef]
- Al-Meyah, K.; Marshall, D.; Rosin, P. 4D Analysis of Facial Ageing Using Dynamic Features. Procedia Comput. Sci. 2017, 112, 790–799. [Google Scholar] [CrossRef]
- Paternoster, L.; Zhurov, A.I.; Toma, A.M.; Kemp, J.P.; St. Pourcain, B.; Timpson, N.J.; McMahon, G.; McArdle, W.; Ring, S.M.; Davey Smith, G.; et al. Genome-wide Association Study of Three–Dimensional Facial Morphology Identifies a Variant in PAX3 Associated with Nasion Position. Am. J. Hum. Genet. 2012, 90, 478–485. [Google Scholar] [CrossRef] [PubMed]
- Fatemifar, G.; Hoggart, C.J.; Paternoster, L.; Kemp, J.P.; Prokopenko, I.; Horikoshi, M.; Wright, V.J.; Tobias, J.H.; Richmond, S.; Zhurov, A.I.; et al. Genome-wide association study of primary tooth eruption identifies pleiotropic loci associated with height and craniofacial distances. Hum. Mol. Gen. 2013, 22, 3807–3817. [Google Scholar] [CrossRef] [PubMed]
- Claes, P.; Hill, H.; Shriver, M.D. Toward DNA-based facial composites: Preliminary results and validation. Forensic. Sci. Int. Genet. 2014, 13, 208–216. [Google Scholar] [CrossRef]
- Djordjevic, J.; Zhurov, A.I.; Richmond, S.; Visigen Consortium. Genetic and Environmental Contributions to Facial Morphological Variation: A 3D Population-Based Twin Study. PLoS ONE 2016, 11, e0162250. [Google Scholar] [CrossRef]
- Lecron, F.; Boisvert, J.; Benjelloun, M.; Labelle, H.; Mahmoudi, S. Multilevel statistical shape models: A new framework for modeling hierarchical structures. In Proceedings of the 2012 9th IEEE International Symposium on Biomedical Imaging (ISBI), Barcelona, Spain, 2–5 May 2012; pp. 1284–1287. [Google Scholar] [CrossRef]
- Farnell, D.J.J.; Popat, H.; Richmond, S. Multilevel principal component analysis (mPCA) in shape analysis: A feasibility study in medical and dental imaging. Comput. Methods Programs Biomed. 2016, 129, 149–159. [Google Scholar] [CrossRef]
- Farnell, D.J.J.; Galloway, J.; Zhurov, A.; Richmond, S.; Perttiniemi, P.; Katic, V. Initial results of multilevel principal components analysis of facial shape. In Annual Conference on Medical Image Understanding and Analysis; Springer: Cham, Switzerland, 2017; pp. 674–685. [Google Scholar]
- Farnell, D.J.J.; Galloway, J.; Zhurov, A.; Richmond, S.; Perttiniemi, P.; Katic, V. An Initial Exploration of Ethnicity, Sex, and Subject Variation on Facial Shape. in preparation.
- Farnell, D.J.J.; Galloway, J.; Zhurov, A.; Richmond, S.; Pirttiniemi, P.; Lähdesmäki, R. What’s in a Smile? Initial Results of Multilevel Principal Components Analysis of Facial Shape and Image Texture. In Annual Conference on Medical Image Understanding and Analysis; Springer: Cham, Switzerland, 2018; Volume 894, pp. 177–188. [Google Scholar]
- Cootes, T.F.; Hill, A.; Taylor, C.J.; Haslam, J. Use of Active Shape Models for Locating Structure in Medical Images. Image Vis. Comput. 1994, 12, 355–365. [Google Scholar] [CrossRef]
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. Active Shape Models—Their Training and Application. Comput. Vis. Image Underst. 1995, 61, 38–59. [Google Scholar] [CrossRef]
- Hill, A.; Cootes, T.F.; Taylor, C.J. Active shape models and the shape approximation problem. Image Vis. Comput. 1996, 12, 601–607. [Google Scholar] [CrossRef]
- Cootes, T.F.; Taylor, C.J. A mixture model for representing shape variation. Image Vis. Comput. 1999, 17, 567–573. [Google Scholar] [CrossRef]
- Allen, P.D.; Graham, J.; Farnell, D.J.J.; Harrison, E.J.; Jacobs, R.; Nicopolou-Karayianni, K.; Lindh, C.; van der Stelt, P.F.; Horner, K.; Devlin, H. Detecting reduced bone mineral density from dental radiographs using statistical shape models. IEEE Trans. Inf. Technol. Biomed. 2007, 11, 601–610. [Google Scholar] [CrossRef] [PubMed]
- Edwards, G.J.; Lanitis, A.; Taylor, C.J.; Cootes, T. Statistical Models of Face Images: Improving Specificity. In Proceedings of the British Machine Vision Conference, Edinburgh, UK, 9–12 September 1996. [Google Scholar] [CrossRef]
- Taylor, C.J.; Cootes, T.F.; Lanitis, A.; Edwards, G.; Smyth, P.; Kotcheff, A.C. Model-based interpretation of complex and variable images. Philos. Trans. R. Soc. Lond. Biol. 1997, 352, 1267–1274. [Google Scholar] [CrossRef] [PubMed]
- Edwards, G.J.; Cootes, T.F.; Taylor, C.J. Face recognition using active appearance models. In Computer Vision; Burkhardt, H., Neumann, B., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1407, pp. 581–595. [Google Scholar]
- Cootes, T.F.; Edwards, G.J.; Taylor, C.J. Active appearance models. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 681–685. [Google Scholar] [CrossRef]
- Cootes, T.F.; Taylor, C.J. Anatomical statistical models and their role in feature extraction. Br. J. Radiol. 2004, 77, S133–S139. [Google Scholar] [CrossRef]
- Matthews, I.; Baker, S. Active Appearance Models Revisited. Int. J. Comput. Vis. 2004, 60, 135–164. [Google Scholar] [CrossRef]
- Candemir, S.; Borovikov, E.; Santosh, K.C.; Antani, S.K.; Thoma, G.R. RSILC: Rotation- and Scale-Invariant, Line-based Color-aware descriptor. Image Vision Comput. 2005, 42, 1–12. [Google Scholar] [CrossRef]
- Doersch, C. Tutorial on variational autoencoders. arXiv, 2016; arXiv:1606.05908. [Google Scholar]
- Pu, Y.; Gan, Z.; Henao, R.; Yuan, X.; Li, C.; Stevens, A.; Carin, L. Variational autoencoder for deep learning of images, labels and captions. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2016; pp. 2352–2360. [Google Scholar]
- Wetzel, S.J. Unsupervised learning of phase transitions: From principal component analysis to variational autoencoders. Phys. Rev. E. 2017, 96, 022140. [Google Scholar] [CrossRef] [PubMed]
- Etemad, K.; Chellappa, R. Discriminant analysis for recognition of human face images. J. Opt. Soc. Am. A 1997, 14, 1724–1733. [Google Scholar] [CrossRef]
- Kim, T.-K.; Kittler, J. Locally Linear Discriminant Analysis for Multimodally Distributed Classes for Face Recognition with a Single Model Image. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 318–327. [Google Scholar] [CrossRef] [PubMed]
- Dibeklioglu, H.; Valenti, R.; Salah, A.A.; Gevers, T. Eyes do not lie: Spontaneous versus posed smiles. In Proceedings of the 18th ACM International Conference on Multimedia, Firenze, Italy, 25–29 October 2010; pp. 703–706. [Google Scholar] [CrossRef]
- Velemínská, J.; Bigoni, L.; Krajíček, V.; Borský, J.; Šmahelová, D.; Cagáňová, V.; Peterka, M. Surface facial modeling and allometry in relation to sexual dimorphism. HOMO 2012, 63, 81–93. [Google Scholar] [CrossRef] [PubMed]
- Toma, A.M.; Zhurov, A.; Playle, R.; Richmond, S. A three-dimensional look for facial differences between males and females in a British-Caucasian sample aged 15 ½ years old. Orthol. Craniofac. Res. 2008, 11, 180–185. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J.; Driessen, K.V. A fast algorithm for the minimum covariance determinant estimator. Technometrics 1999, 41, 212–223. [Google Scholar] [CrossRef]
- Maronna, R.; Zamar, R.H. Robust estimates of location and dispersion for high dimensional datasets. Technometrics 2002, 50, 307–317. [Google Scholar] [CrossRef]
- Olive, D.J. A resistant estimator of multivariate location and dispersion. Comput. Stat. Data Anal. 2004, 46, 93–102. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? JACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S.; Peng, Y.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2009; pp. 2080–2088. [Google Scholar]
- Hubert, M.; Engelen, S. Robust PCA and classification in biosciences. Bioinformatics 2004, 20, 1728–1736. [Google Scholar] [CrossRef]
- Andersen, R. Modern Methods for Robust Regression; Quantitative Applications in the Social Sciences. 152; Sage Publications: Los Angeles, CA, USA, 2008; ISBN 978-1-4129-4072-6. [Google Scholar]
- Godambe, V.P. Estimating Functions; Oxford Statistical Science Series. 7; Clarendon Press: New York, NY, USA, 1991; ISBN 978-0-19-852228-7. [Google Scholar]
- Ulukaya, S.; Erdem, C.E. Gaussian mixture model based estimation of the neutral face shape for emotion recognition. Digit. Signal Process. 2014, 32, 11–23. [Google Scholar] [CrossRef]
- Patenaude, B.; Smith, S.M.; Kennedy, D.N.; Jenkinson, M. A Bayesian model of shape and appearance for subcortical brain segmentation. Neuroimage 2011, 56, 907–922. [Google Scholar] [CrossRef]
- Li, F.; Fergus, R.; Perona, P. Learning generative visual models from few training examples: An incremental bayesian approach tested on 101 object categories. Comput. Vis. Image Underst. 2007, 106, 59–70. [Google Scholar] [CrossRef]
- Bouguelia, M.-R.; Nowaczyk, S.; Santosh, K.C.; Verikas, A. Agreeing to disagree: Active learning with noisy labels without crowdsourcing. Int. J. Mach. Learn. Cybern. 2018, 9, 1307–1319. [Google Scholar] [CrossRef]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farnell, D.J.J.; Galloway, J.; Zhurov, A.I.; Richmond, S.; Marshall, D.; Rosin, P.L.; Al-Meyah, K.; Pirttiniemi, P.; Lähdesmäki, R. What’s in a Smile? Initial Analyses of Dynamic Changes in Facial Shape and Appearance. J. Imaging 2019, 5, 2. https://doi.org/10.3390/jimaging5010002
Farnell DJJ, Galloway J, Zhurov AI, Richmond S, Marshall D, Rosin PL, Al-Meyah K, Pirttiniemi P, Lähdesmäki R. What’s in a Smile? Initial Analyses of Dynamic Changes in Facial Shape and Appearance. Journal of Imaging. 2019; 5(1):2. https://doi.org/10.3390/jimaging5010002
Chicago/Turabian StyleFarnell, Damian J. J., Jennifer Galloway, Alexei I. Zhurov, Stephen Richmond, David Marshall, Paul L. Rosin, Khtam Al-Meyah, Pertti Pirttiniemi, and Raija Lähdesmäki. 2019. "What’s in a Smile? Initial Analyses of Dynamic Changes in Facial Shape and Appearance" Journal of Imaging 5, no. 1: 2. https://doi.org/10.3390/jimaging5010002
APA StyleFarnell, D. J. J., Galloway, J., Zhurov, A. I., Richmond, S., Marshall, D., Rosin, P. L., Al-Meyah, K., Pirttiniemi, P., & Lähdesmäki, R. (2019). What’s in a Smile? Initial Analyses of Dynamic Changes in Facial Shape and Appearance. Journal of Imaging, 5(1), 2. https://doi.org/10.3390/jimaging5010002





