An Ensemble SSL Algorithm for Efficient Chest X-Ray Image Classification
Abstract
1. Introduction
- classifying and/or detecting the presence of an abnormality (image classification);
- segmenting images into normal and abnormal (medical image segmentation).
2. A Review of Semi-Supervised Self-Labeled Learning
2.1. Self-training
| Algorithm 1: Self-training |
| Input: L − Set of labeled instances. U − Set of unlabeled instances. Parameters: ConLev − Confidence level. C − Base learner. Output: Trained classifier. 1: repeat 2: Train C on L. 3: Apply C on U. 4: Select instances with a predicted probability more than ConLev per iteration (). 5: Remove from U, and add to L. 6: until some stopping criterion is met or U is empty. |
2.2. Co-training
| Algorithm 2: Co-training |
| Input: L − Set of labeled instances. U − Set of unlabeled instances. − Base learner (). Output: Trained classifier. 1: Create a pool of u examples by randomly choosing from U. 2: repeat 3: Train on . 4: Train on . 5: for each classifier do () 6: chooses p samples (P) that it most confidently labels as positive and n sentences (N) that it most confidently labels as negative from U. 7: Remove P and N from . 8: Add P and N to L. 9: end for 10: Refill with examples from U to keep at a constant size of u examples. 11: until some stopping criterion is met or U is empty. |
2.3. Tri-training
- (1)
- Excessively-confined restrictions introduce further classification noise.
- (2)
- Estimation of the classification error is unsuitable.
- (3)
- Differentiation between the initial labeled example and the label of a previously unlabeled example is deficient.
| Algorithm 3: Tri-training |
| Input: L-Set of labeled instances. U-Set of unlabeled instances. Parameters: -Base learner (). Output: Trained classifier. 1: for do 2: . 3: Train on . 4: end for 5: repeat 6: for do 7: . 8: for do 9: if then () 10: . 11: end if 12: end for 13: end for 14: for do 15: Train on . 16: end for 17: until some stopping criterion is met or U is empty. |
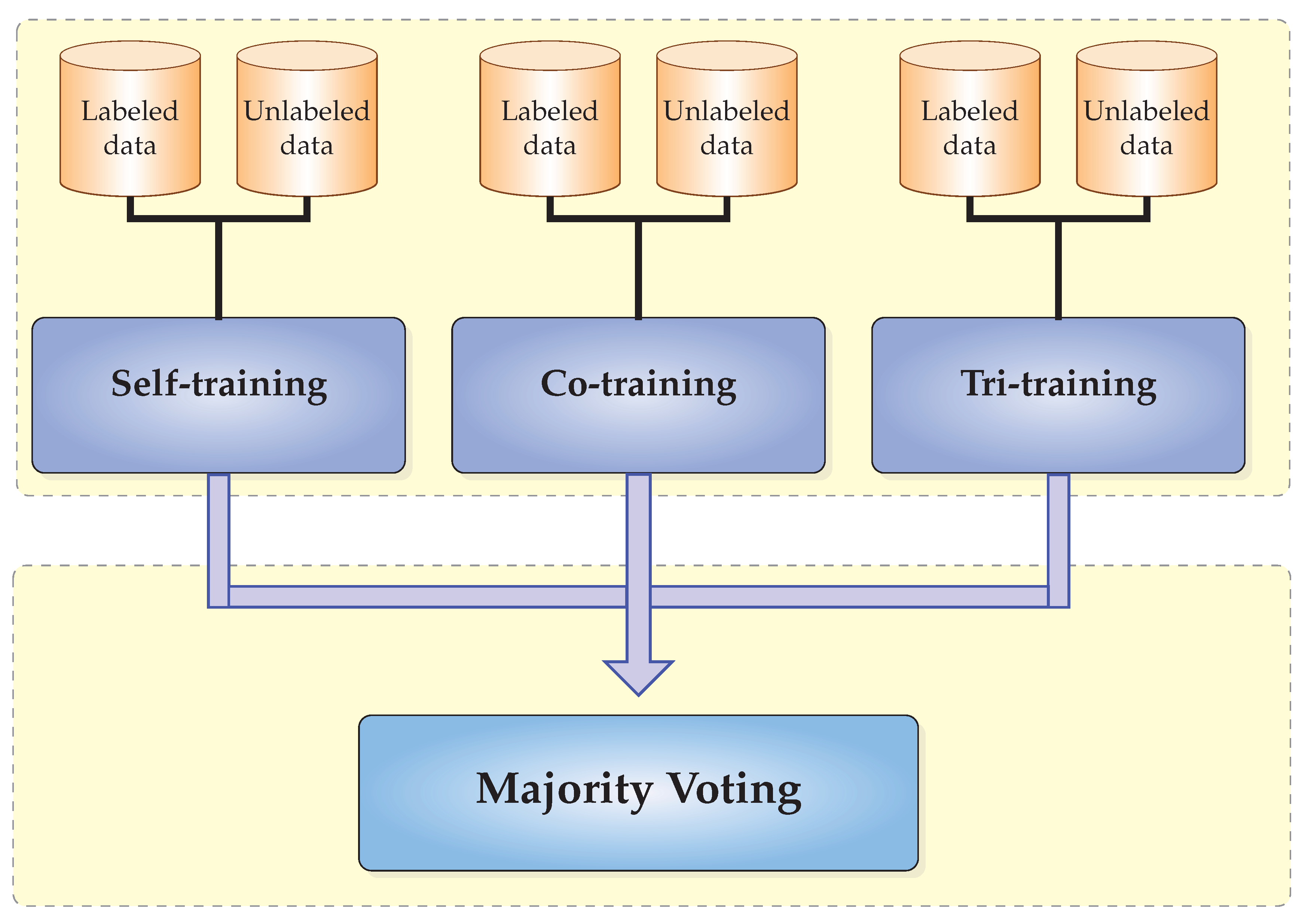
2.4. CST-Voting Algorithm
| Algorithm 4: CST-Voting |
| Input: L-Set of labeled instances. U-Set of unlabeled instances. C-Base learner. Output: The labels of instances in the testing set. /* Training phase */ 1: Self-training 2: Co-training 3: Tri-training /* Voting phase */ 4: for each do 5: Apply self-training, co-training and tri-training on x. 6: Use majority vote to predict the label of x. 7: end for |
3. Experimental Results
3.1. Dataset Description
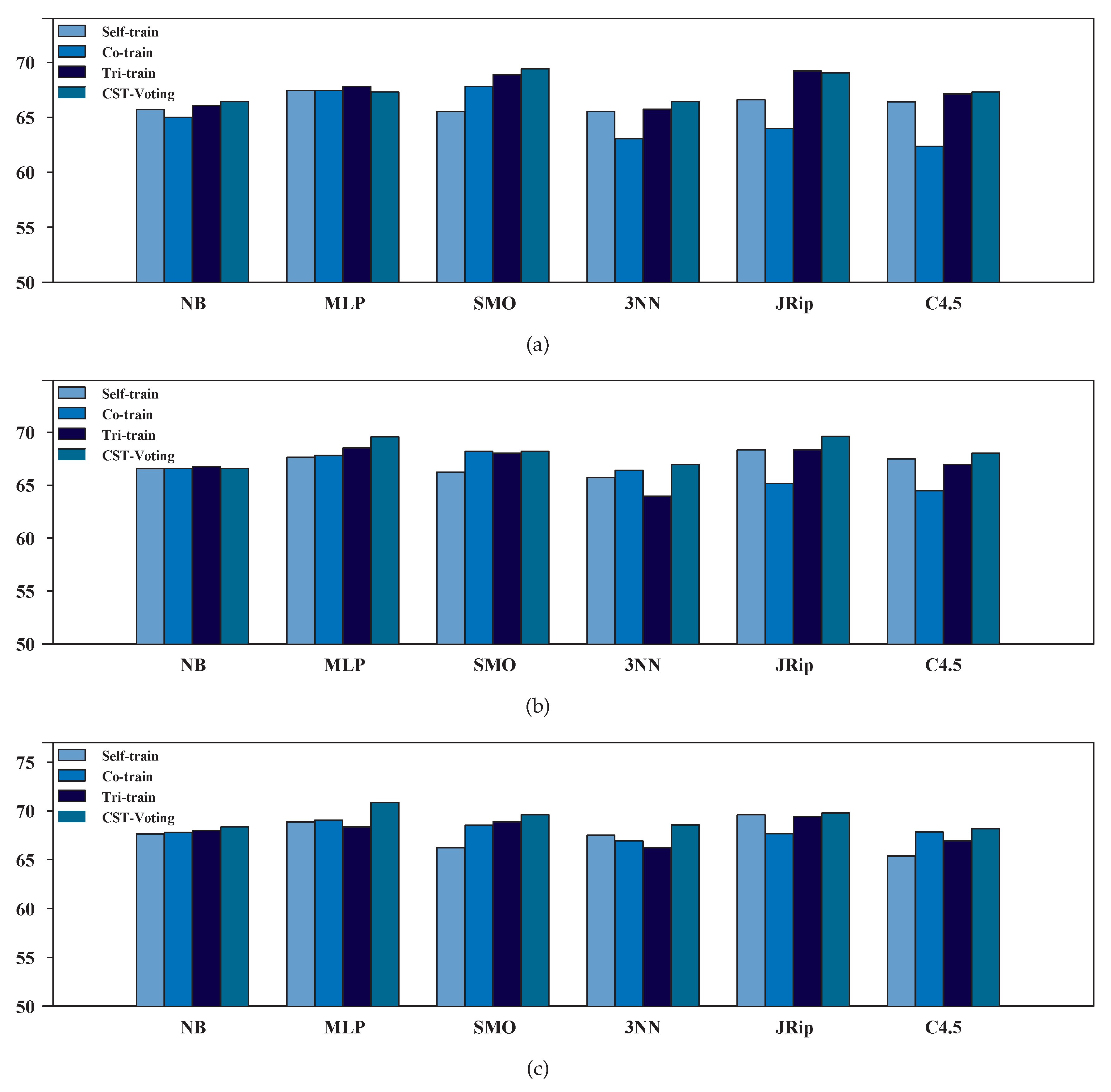
3.2. Performance Evaluation of SSL Algorithms
3.3. Statistical and Post-Hoc Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Livieris, I.E.; Apostolopoulou, M.S.; Sotiropoulos, D.G.; Sioutas, S.A.; Pintelas, P. Classification of large biomedical data using ANNs based on BFGS method. In Proceedings of the 13th Panhellenic Conference on Informatics (PCI’19), Corfu, Greece, 10–12 September 2009; pp. 87–91. [Google Scholar]
- Melendez, J.; van Ginneken, B.; Maduskar, P.; Philipsen, R.; Reither, K.; Breuninger, M.; Adetifa, I.; Maane, R.; Ayles, H.; Sánchez, C. A novel multiple-instance learning-based approach to computer-aided detection of tuberculosis on chest X-rays. IEEE Trans. Med. Imaging 2015, 34, 179–192. [Google Scholar] [CrossRef] [PubMed]
- Doi, K. Computer-aided diagnosis in medical imaging: historical review, current status and future potential. Comput. Med. Imaging Graph. 2007, 31, 198–211. [Google Scholar] [CrossRef] [PubMed]
- Rangayyan, R.; Suri, J. Recent Advances in Breast Imaging, Mammography, and Computer-Aided Diagnosis of Breast Cancer; SPIE Publications: Bellingham, WA, USA, 2006. [Google Scholar]
- Hogeweg, L.; Mol, C.; de Jong, P.; Ayles, R.; van Ginneken, B. Fusion of local and global detection systems to detect tuberculosis in chest radiographs. Med. Image Comput. Comput.-Assist. Interv. 2010, 13, 650–657. [Google Scholar] [PubMed]
- Hogeweg, L.; Sánchez, C.; de Jong, P.; Maduskar, P.; van Ginneken, B. Clavicle segmentation in chest radiographs. Med. Image Anal. 2012, 16, 1490–1502. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, S.; Karargyris, A.; Candemir, S.; Folio, L.; Siegelman, J.; Callaghan, F.; Xue, Z.; Palaniappan, K.; Singh, R.; Antani, S.; et al. Automatic tuberculosis screening using chest radiographs. IEEE Trans. Med. Imaging 2014, 33, 233–245. [Google Scholar] [CrossRef] [PubMed]
- Candemir, S.; Jaeger, S.; Musco, K.P.J.; Singh, R.; Xue, Z.; Karargyris, A.; Antani, S.; Thoma, G.; McDonald, C. Lung segmentation in chest radiographs using anatomical atlases with nonrigid registration. IEEE Trans. Med. Imaging 2014, 33, 577–590. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Goldberg, A. Introduction to semi-supervised learning. Synth. Lect. Artif. Intell. Mach. Learn. 2009, 3, 1–130. [Google Scholar] [CrossRef]
- Blum, A.; Chawla, S. Learning from labeled and unlabeled data using graph mincuts. In Proceedings of the 8th International Conference on Machine Learning (ICML), Williamstown, MA, USA, 28 June–1 July 2001; pp. 19–26. [Google Scholar]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the 11th Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; pp. 92–100. [Google Scholar]
- Triguero, I.; García, S.; Herrera, F. Self-labeled techniques for semi-supervised learning: Taxonomy, software and empirical study. Knowl. Inform. Syst. 2015, 42, 245–284. [Google Scholar] [CrossRef]
- Nigam, K.; Ghani, R. Analyzing the effectiveness and applicability of co-training. In Proceedings of the ACM International Conference on Information and Knowledge Management, McLean, VA, USA, 6–11 November 2000; pp. 86–93. [Google Scholar]
- Guo, T.; Li, G. Improved tri-training with unlabeled data. In Software Engineering and Knowledge Engineering: Theory and Practice; Springer: Berlin, Heidelberg/ Germany, 2012; pp. 139–147. [Google Scholar]
- Liu, C.; Yuen, P. A boosted co-training algorithm for human action recognition. IEEE Trans. Circuits Syst. Video Technol. 2011, 21, 1203–1213. [Google Scholar] [CrossRef]
- Livieris, I.; Drakopoulou, K.; Tampakas, V.; Mikropoulos, T.; Pintelas, P. Predicting secondary school students’ performance utilizing a semi-supervised learning approach. J. Educ. Comput. Res. 2018. [Google Scholar] [CrossRef]
- Livieris, I.; Drakopoulou, K.; Tampakas, V.; Mikropoulos, T.; Pintelas, P. An ensemble-based semi-supervised approach for predicting students’ performance. In Research on e-Learning and ICT in Education; Elsevier: New York, NY, USA, 2018. [Google Scholar]
- Zhou, Z.; Li, M. Tri-training: Exploiting unlabeled data using three classifiers. IEEE Trans. Knowl. Data Eng. 2005, 17, 1529–1541. [Google Scholar] [CrossRef]
- Zhu, X. Semi-supervised learning. In Encyclopedia of Machine Learning; Springer: New York, NY, USA, 2011; pp. 892–897. [Google Scholar]
- Sigdel, M.; Dinç, I.; Dinç, S.; Sigdel, M.; Pusey, M.; Aygün, R. Evaluation of semi-supervised learning for classification of protein crystallization imagery. In Proceedings of the IEEE Southeastcon 2014, Lexington, KY, USA, 13–16 March 2014; pp. 1–6. [Google Scholar]
- Triguero, I.; Sáez, J.; Luengo, J.; García, S.; Herrera, F. On the characterization of noise filters for self-training semi-supervised in nearest neighbor classification. Neurocomputing 2014, 132, 30–41. [Google Scholar] [CrossRef]
- Ng, V.; Cardie, C. Weakly supervised natural language learning without redundant views. In Proceedings of the 2003 conference of the North American Chapter of the Association for Computational Linguistics on Human Language Technology, Edmonton, AB, Canada, 27 May–1 June 2003; Volume 1, pp. 94–101. [Google Scholar]
- Roli, F.; Marcialis, G. Semi-supervised PCA-based face recognition using self-training. Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR); Springer: Berlin/Heidelberg, Germany, 2006; pp. 560–568. [Google Scholar]
- Sun, S.; Jin, F. Robust co-training. Int. J. Pattern Recognit. Artif. Intell. 2011, 25, 1113–1126. [Google Scholar] [CrossRef]
- Du, J.; Ling, C.; Zhou, Z. When does co-training work in real data? IEEE Trans. Knowl. Data Eng. 2011, 23, 788–799. [Google Scholar] [CrossRef]
- Kostopoulos, G.; Livieris, I.E.; Kotsiantis, S.; Tampakas, V. CST-Voting-A semi-supervised ensemble method for classification problems. J. Intell. Fuzzy Syst. 2018, 1–11. [Google Scholar] [CrossRef]
- Stirenko, S.; Kochura, Y.; Alienin, O.; Rokovyi, O.; Gang, P.; Zeng, W.; Gordienko, Y. Chest X-ray analysis of tuberculosis by deep learning with segmentation and augmentation. arXiv, 2018; arXiv:1803.01199. [Google Scholar]
- Domingos, P.; Pazzani, M. On the optimality of the simple Bayesian classifier under zero-one loss. Mach. Learn. 1997, 29, 103–130. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning internal representations by error propagation. In Parallel Distributed Processing: Explorations in The Microstructure of Cognition; Rumelhart, D., McClelland, J., Eds.; MIT Press: Cambridge, MA, USA, 1986; pp. 318–362. [Google Scholar]
- Platt, J. Using sparseness and analytic QP to speed training of support vector machines. In Advances in Neural Information Processing Systems; Kearns, M., Solla, S., Cohn, D., Eds.; MIT Press: Cambridge, MA, USA, 1999; pp. 557–563. [Google Scholar]
- Aha, D. Lazy Learning; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Cohen, W. Fast effective rule induction. In Proceedings of the International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 115–123. [Google Scholar]
- Quinlan, J. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Wu, X.; Kumar, V.; Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.; Ng, A.; Liu, B.; Yu, P.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I. The WEKA data mining software: An update. SIGKDD Explor. Newslett. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Tanha, J.; van Someren, M.; Afsarmanesh, H. Semi-supervised self-training for decision tree classifiers. Int. J. Mach. Learn. Cybern. 2015, 8, 355–370. [Google Scholar] [CrossRef]
- Weka 3: Data Mining Software in Java. Available online: https://www.cs.waikato.ac.nz/ml/weka/ (accessed on 15 July 2018).
- Van Rijsbergen, C. Information Retrieval, 2nd ed.; Butterworths: London, UK, 1979. [Google Scholar]
- Hodges, J.; Lehmann, E. Rank methods for combination of independent experiments in analysis of variance. Ann. Math. Stat. 1962, 33, 482–497. [Google Scholar] [CrossRef]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Finner, H. On a monotonicity problem in step-down multiple test procedures. J. Am. Stat. Assoc. 1993, 88, 920–923. [Google Scholar] [CrossRef]
- Holm, S. A simple sequentially rejective multiple test procedure. Scandi. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Hochberg, Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika 1988, 75, 800–802. [Google Scholar] [CrossRef]
| SSL Algorithm | Parameters |
|---|---|
| Self-training | . |
| . | |
| Co-training | . |
| . | |
| Tri-training | No parameters specified. |
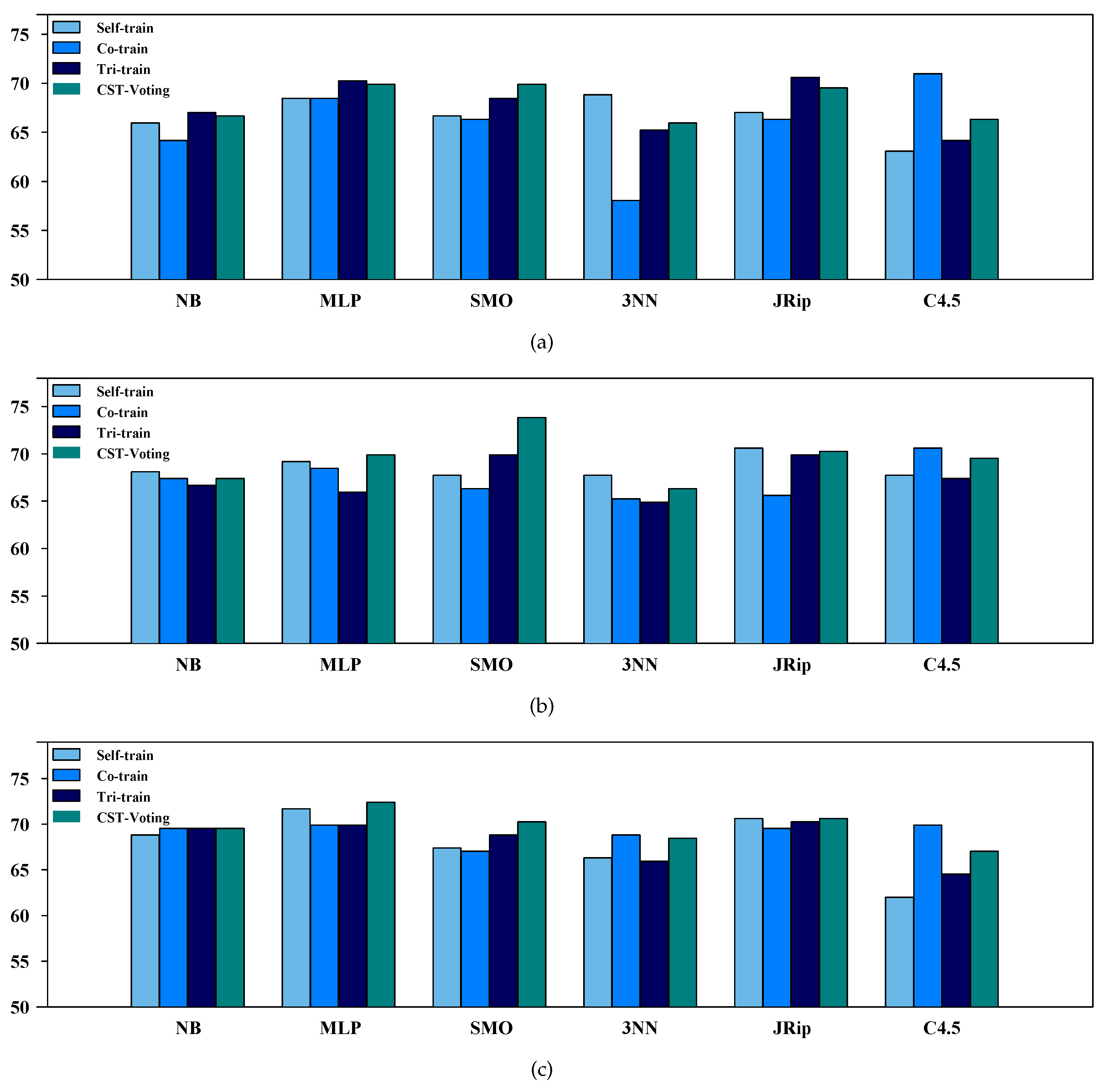
| Self | Co | Tri | CST | Self | Co | Tri | CST | Self | Co | Tri | CST | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NB | 65.9% | 64.2% | 67.0% | 66.7% | 68.1% | 67.4% | 66.7% | 67.4% | 68.8% | 69.5% | 69.5% | 69.5% | ||||||
| MLP | 68.5% | 68.5% | 70.3% | 69.9% | 69.2% | 68.5% | 65.9% | 69.9% | 71.7% | 69.9% | 69.9% | 72.4% | ||||||
| SMO | 66.7% | 66.3% | 68.5% | 69.9% | 67.7% | 66.3% | 69.9% | 73.8% | 67.4% | 67.0% | 68.8% | 70.3% | ||||||
| 3NN | 68.8% | 58.1% | 65.2% | 65.9% | 67.7% | 65.2% | 64.9% | 66.3% | 66.3% | 68.8% | 65.9% | 68.5% | ||||||
| JRip | 67.0% | 66.3% | 70.6% | 69.5% | 70.6% | 65.6% | 69.9% | 70.3% | 70.6% | 69.5% | 70.3% | 70.6% | ||||||
| C4.5 | 63.1% | 71.0% | 64.2% | 66.3% | 67.7% | 70.6% | 67.4% | 69.5% | 62.0% | 69.9% | 64.5% | 67.0% | ||||||
| Self | Co | Tri | CST | Self | Co | Tri | CST | Self | Co | Tri | CST | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NB | 65.5% | 65.9% | 65.2% | 66.2% | 65.2% | 65.9% | 66.9% | 65.9% | 66.6% | 65.9% | 66.6% | 67.2% | ||||||
| MLP | 66.6% | 67.2% | 65.5% | 64.8% | 66.2% | 66.6% | 71.1% | 69.3% | 66.2% | 68.3% | 66.9% | 69.3% | ||||||
| SMO | 64.5% | 69.3% | 69.3% | 69.0% | 64.8% | 70.0% | 62.4% | 66.6% | 65.2% | 70.0% | 69.0% | 69.0% | ||||||
| 3NN | 62.4% | 67.9% | 66.2% | 66.9% | 63.8% | 67.6% | 63.1% | 67.6% | 68.6% | 65.2% | 66.6% | 68.6% | ||||||
| JRip | 66.2% | 61.7% | 67.9% | 68.6% | 66.2% | 64.8% | 66.9% | 69.0% | 68.6% | 65.9% | 68.6% | 69.0% | ||||||
| C4.5 | 69.7% | 54.0% | 70.0% | 68.3% | 67.2% | 58.5% | 66.6% | 66.6% | 68.6% | 65.9% | 69.3% | 69.3% | ||||||
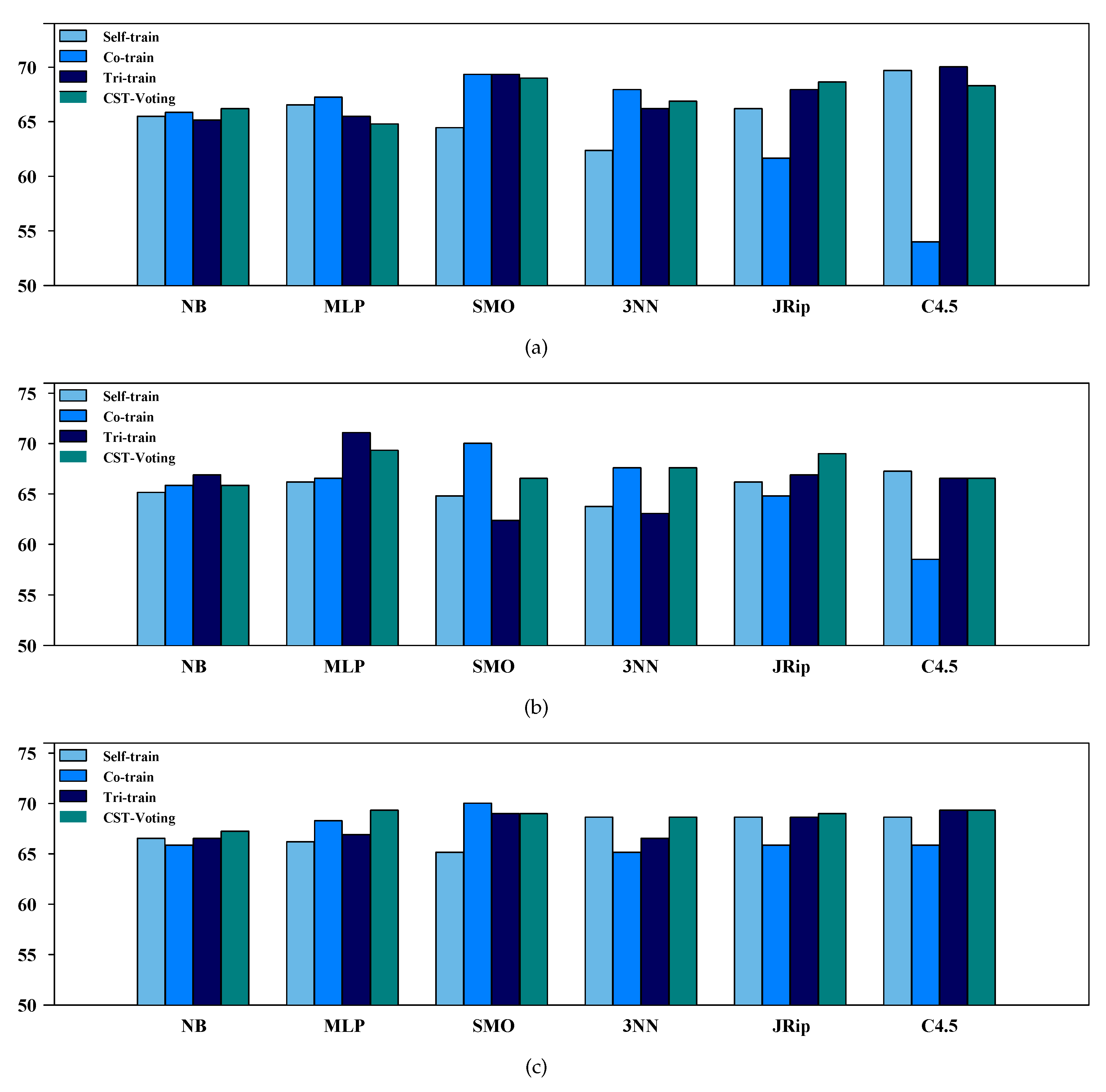
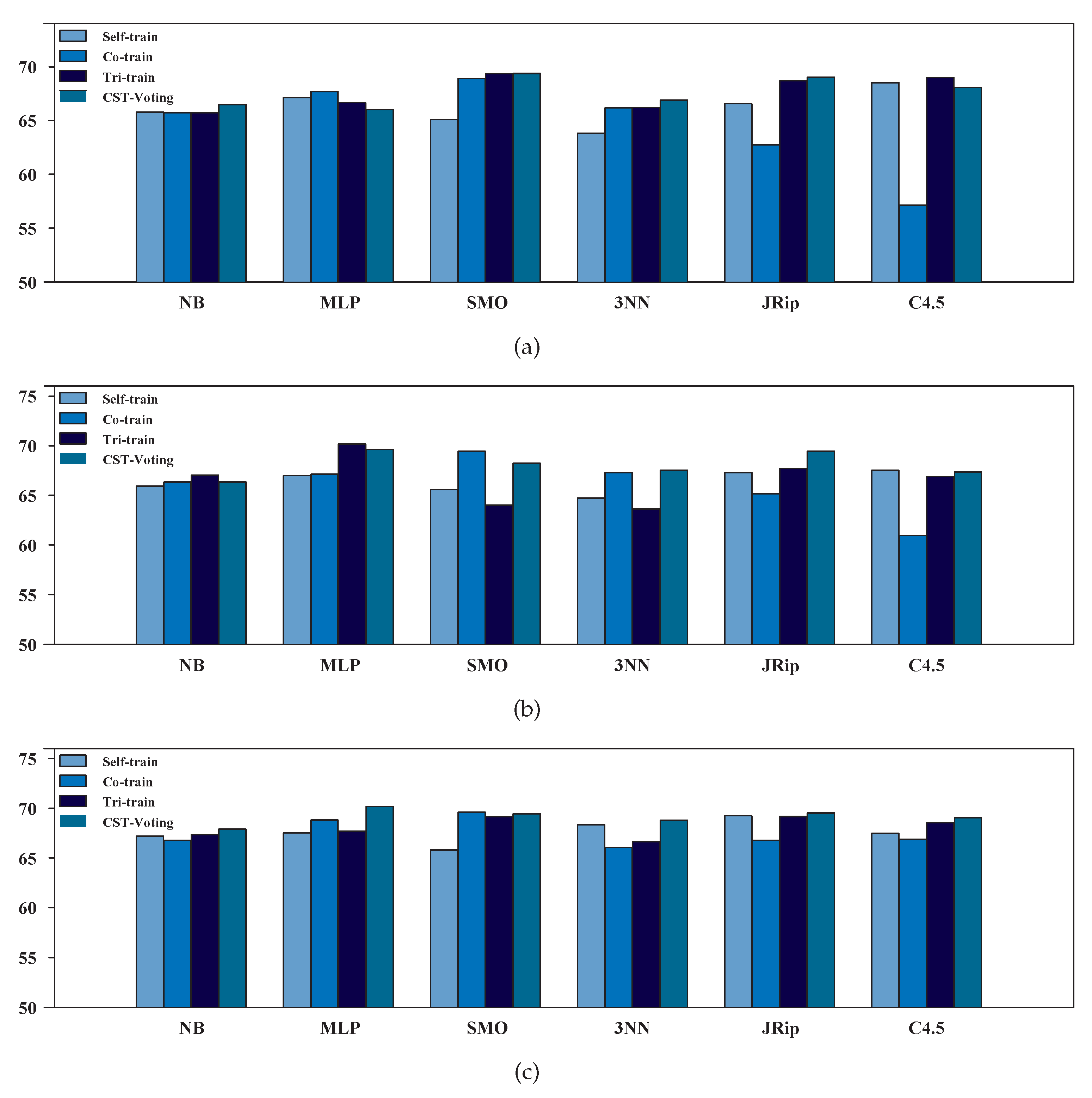
| Self | Co | Tri | CST | Self | Co | Tri | CST | Self | Co | Tri | CST | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NB | 65.8% | 65.7% | 65.7% | 66.5% | 65.9% | 66.4% | 67.0% | 66.4% | 67.2% | 66.8% | 67.3% | 67.9% | ||||||
| MLP | 67.1% | 67.7% | 66.6% | 66.0% | 67.0% | 67.1% | 70.2% | 69.6% | 67.5% | 68.8% | 67.7% | 70.2% | ||||||
| SMO | 65.1% | 68.9% | 69.3% | 69.4% | 65.6% | 69.4% | 64.0% | 68.2% | 65.8% | 69.6% | 69.1% | 69.4% | ||||||
| 3NN | 63.8% | 66.2% | 66.2% | 66.9% | 64.7% | 67.3% | 63.6% | 67.5% | 68.3% | 66.1% | 66.6% | 68.8% | ||||||
| JRip | 66.6% | 62.7% | 68.7% | 69.0% | 67.3% | 65.2% | 67.7% | 69.4% | 69.2% | 66.8% | 69.2% | 69.5% | ||||||
| C4.5 | 68.5% | 57.1% | 69.0% | 68.1% | 67.5% | 61.0% | 66.9% | 67.3% | 67.5% | 66.9% | 68.5% | 69.0% | ||||||
| Self | Co | Tri | CST | Self | Co | Tri | CST | Self | Co | Tri | CST | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NB | 65.7% | 65.0% | 66.1% | 66.4% | 66.6% | 66.6% | 66.8% | 66.6% | 67.6% | 67.8% | 68.0% | 68.4% | ||||||
| MLP | 67.5% | 67.5% | 67.8% | 67.3% | 67.6% | 67.8% | 68.5% | 69.6% | 68.9% | 69.1% | 68.4% | 70.8% | ||||||
| SMO | 65.5% | 67.8% | 68.9% | 69.4% | 66.2% | 68.2% | 68.0% | 68.2% | 66.2% | 68.6% | 68.9% | 69.6% | ||||||
| 3NN | 65.6% | 63.1% | 65.7% | 66.5% | 65.7% | 66.4% | 64.0% | 67.0% | 67.5% | 66.9% | 66.3% | 68.6% | ||||||
| JRip | 66.6% | 64.0% | 69.2% | 69.1% | 68.4% | 65.2% | 68.4% | 69.6% | 69.6% | 67.7% | 69.4% | 69.8% | ||||||
| C4.5 | 66.4% | 62.4% | 67.1% | 67.3% | 67.5% | 64.5% | 67.0% | 68.0% | 65.4% | 67.8% | 67.0% | 68.2% | ||||||
| SSL Algorithm | Friedman Aligned | Finner Post-Hoc Test | |
|---|---|---|---|
| Ranking | -value | Null Hypothesis | |
| CST-Voting | 6.8333 | - | - |
| Tri-training | 8.0000 | 0.775051 | accepted |
| Self-training | 15.3333 | 0.037336 | rejected |
| Co-training | 19.8333 | 0.001451 | rejected |
| SSL Algorithm | Friedman Aligned | Finner Post-Hoc Test | |
|---|---|---|---|
| Ranking | -value | Null Hypothesis | |
| CST-Voting | 5.75 | - | - |
| Tri-training | 13.50 | 0.047649 | rejected |
| Self-training | 15.00 | 0.023465 | rejected |
| Co-training | 15.75 | 0.014306 | rejected |
| SSL Algorithm | Friedman Aligned | Finner Post-Hoc Test | |
|---|---|---|---|
| Ranking | -value | Null Hypothesis | |
| CST-Voting | 4.1667 | - | - |
| Tri-training | 14.1667 | 0.014306 | rejected |
| Co-training | 14.5000 | 0.011369 | rejected |
| Self-training | 17.1667 | 0.001451 | rejected |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Livieris, I.E.; Kanavos, A.; Tampakas, V.; Pintelas, P. An Ensemble SSL Algorithm for Efficient Chest X-Ray Image Classification. J. Imaging 2018, 4, 95. https://doi.org/10.3390/jimaging4070095
Livieris IE, Kanavos A, Tampakas V, Pintelas P. An Ensemble SSL Algorithm for Efficient Chest X-Ray Image Classification. Journal of Imaging. 2018; 4(7):95. https://doi.org/10.3390/jimaging4070095
Chicago/Turabian StyleLivieris, Ioannis E., Andreas Kanavos, Vassilis Tampakas, and Panagiotis Pintelas. 2018. "An Ensemble SSL Algorithm for Efficient Chest X-Ray Image Classification" Journal of Imaging 4, no. 7: 95. https://doi.org/10.3390/jimaging4070095
APA StyleLivieris, I. E., Kanavos, A., Tampakas, V., & Pintelas, P. (2018). An Ensemble SSL Algorithm for Efficient Chest X-Ray Image Classification. Journal of Imaging, 4(7), 95. https://doi.org/10.3390/jimaging4070095







