Compressive Online Video Background–Foreground Separation Using Multiple Prior Information and Optical Flow
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
2. Compressive Online Robust PCA Using Multiple Prior Information and Optical Flow
2.1. Compressive Online Robust PCA (CORPCA) for Video Separation
2.2. Video Foreground and Background Separation Using CORPCA-OF
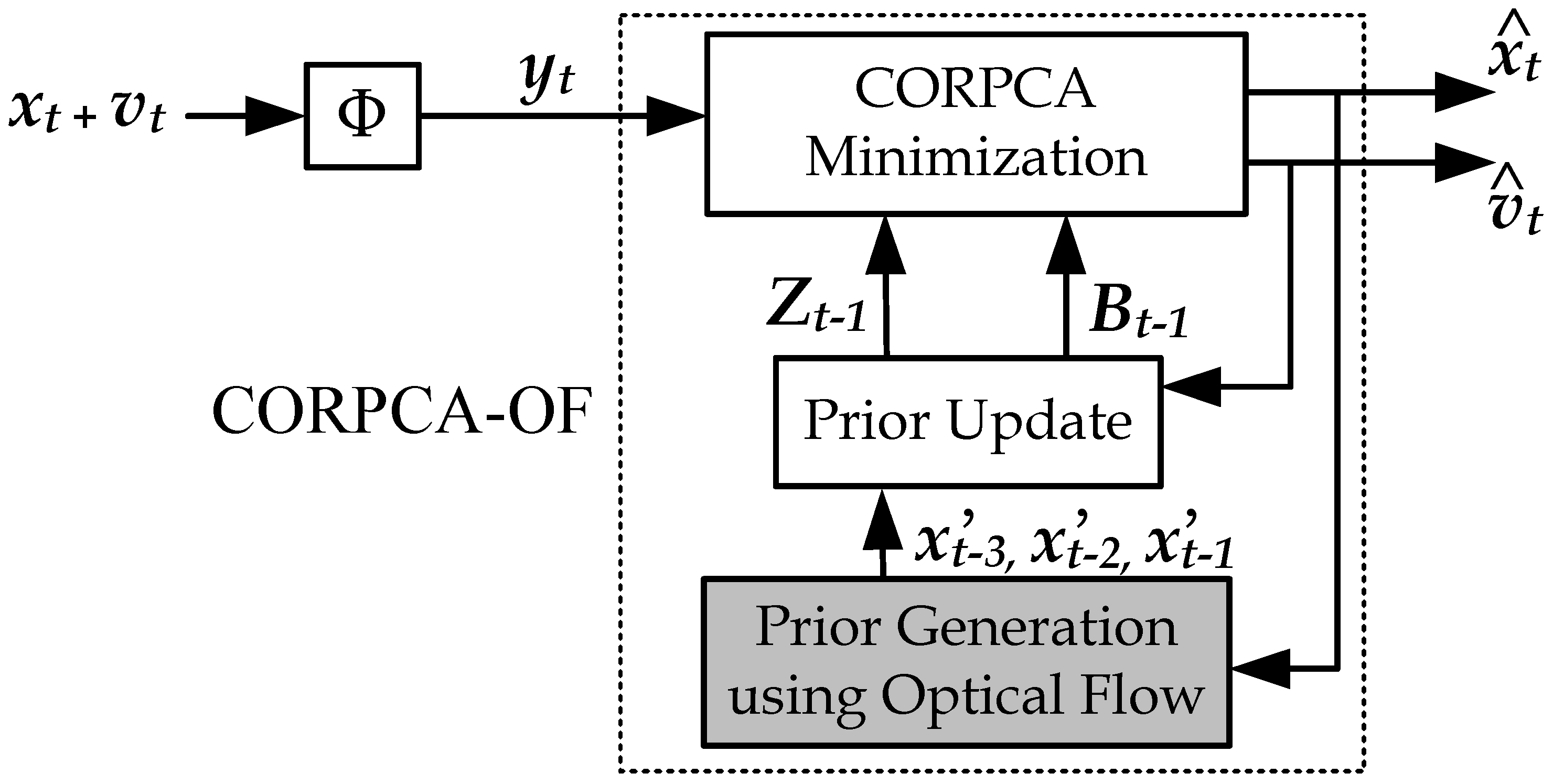
2.2.1. Compressive Separation Model with CORPCA-OF
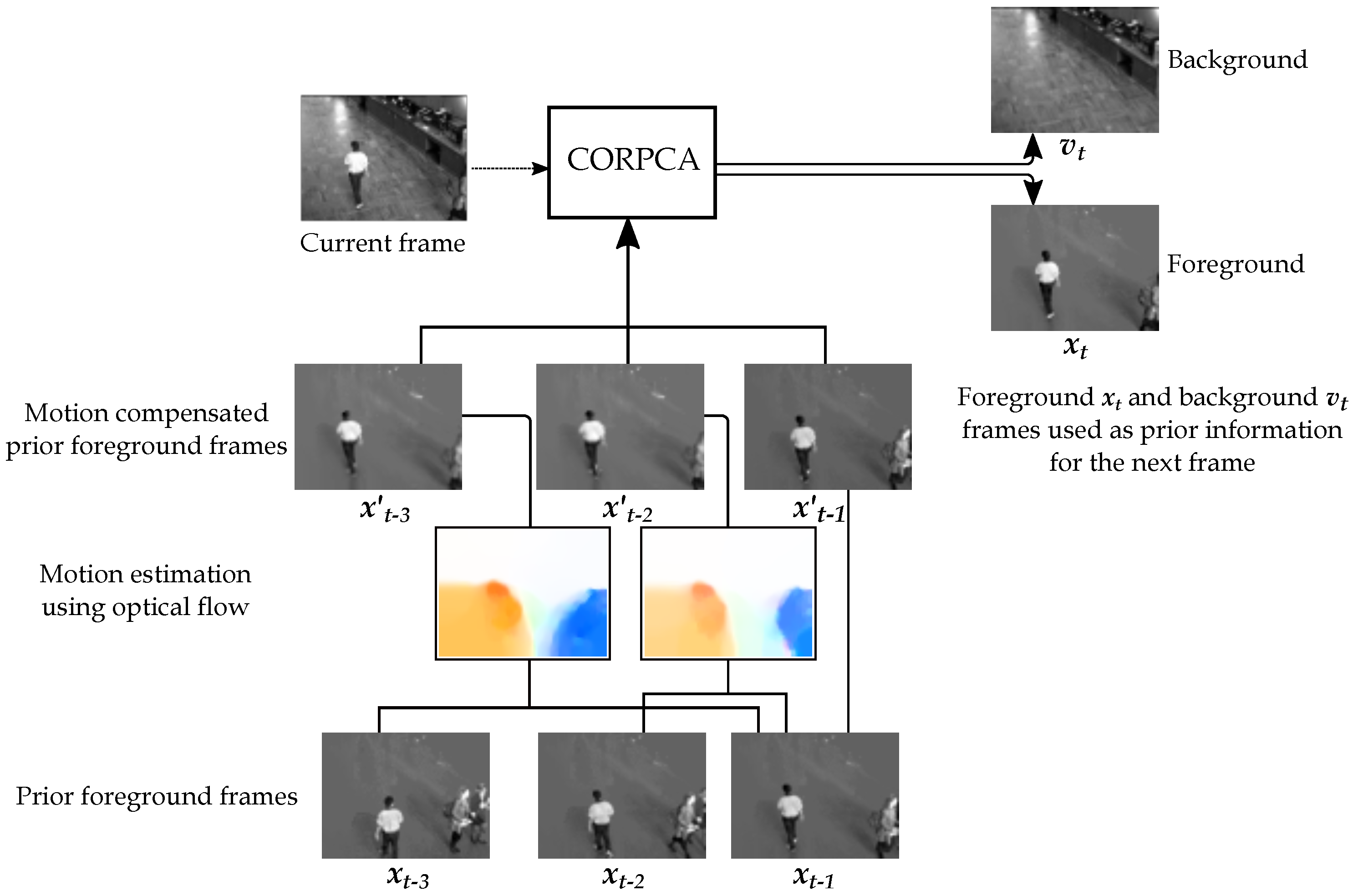
2.2.2. Prior Generation using Optical Flow
| Algorithm 1: The proposed CORPCA-OF algorithm. |
 |
2.2.3. Prior Update
3. Experimental Results
3.1. Prior Information Evaluation
3.2. Compressive Video Foreground and Background Separation
3.2.1. Visual Evaluation
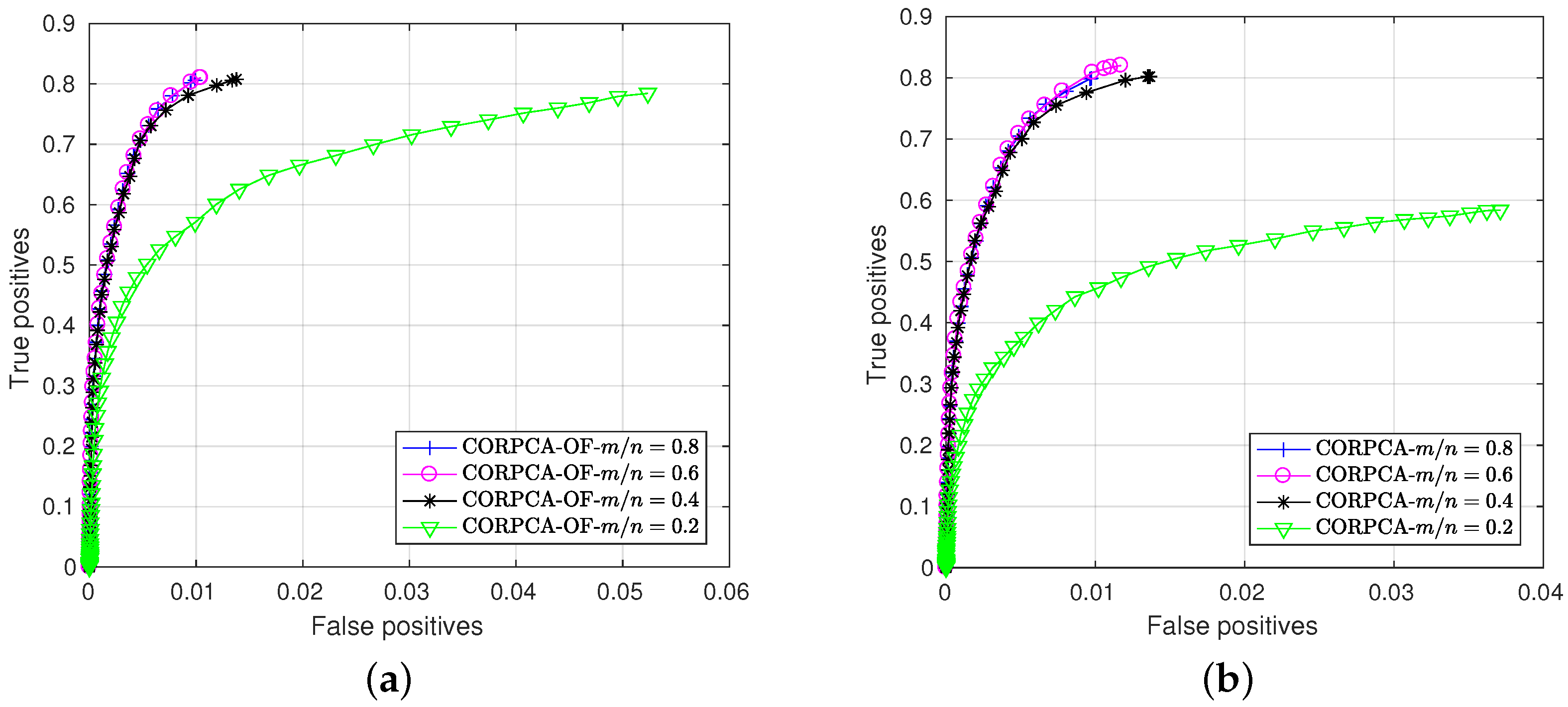
3.2.2. Quantitative Results
3.3. Additional Results
3.3.1. Escalator and Fountain sequences
3.3.2. Visual Comparison of CORPCA-OF and CORPCA for Full Resolution
3.3.3. Separation Results with Various Datasets
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CDnet | ChangeDetection.NET |
| CORPCA | Compressive Online Robust Principal Component Analysis |
| CORPCA-OF | Compressive Online Robust Principal Component Analysis with Optical Flow |
| GPU | Graphics Processing Unit |
| GRASTA | Grassmannian Robust Adaptive Subspace Tracking Algorithm |
| OF | Optical Flow |
| PCA | Principal Component Analysis |
| PCP | Principal Component Pursuit |
| RAMSIA | Reconstruction Algorithm with Multiple Side Information using Adaptive weights |
| ReProCS | Recursive Projected Compressive Sensing |
| ROC | Receiver Operating Curve |
| RPCA | Robust Principal Component Analysis |
| SBMnet | SceneBackgroundModeling.NET |
| SVD | Singular Value Decomposition |
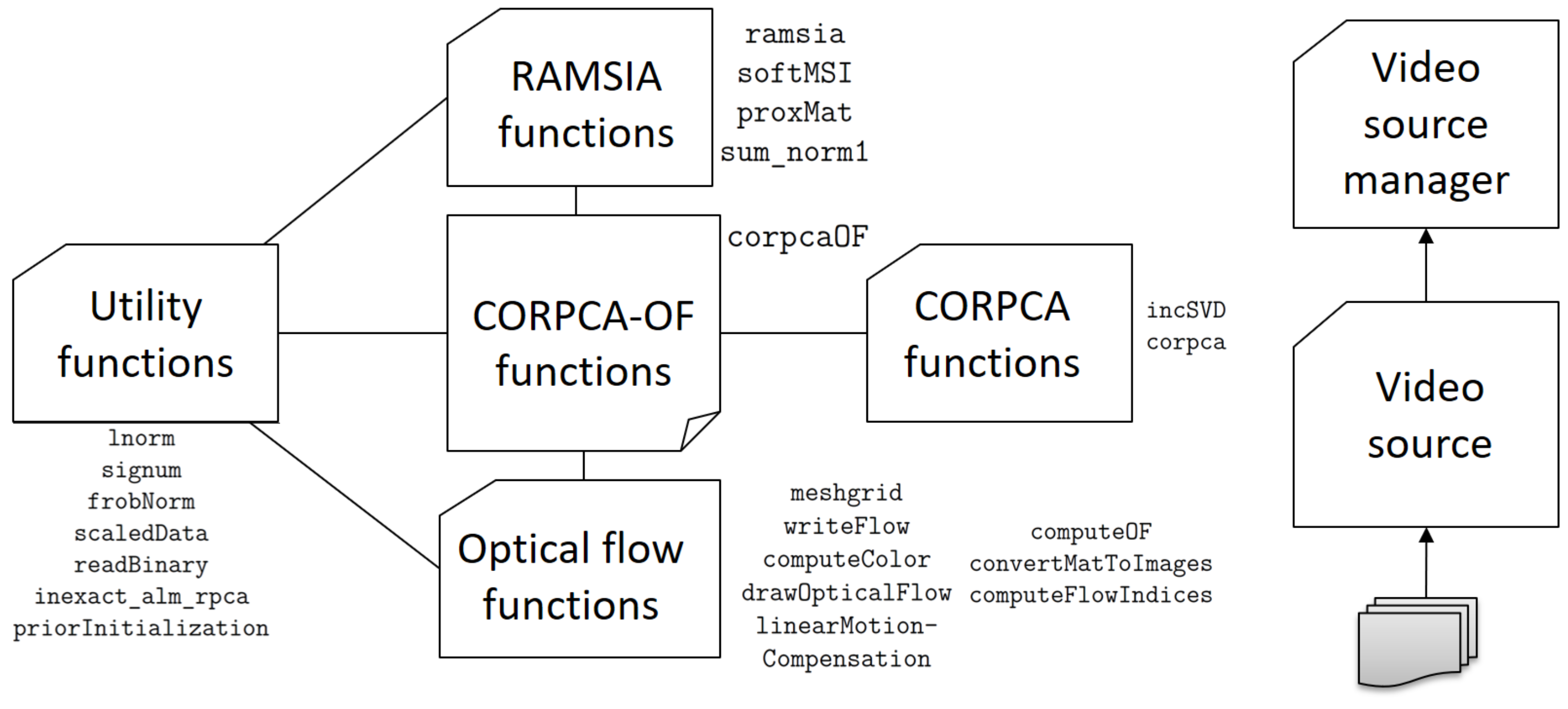
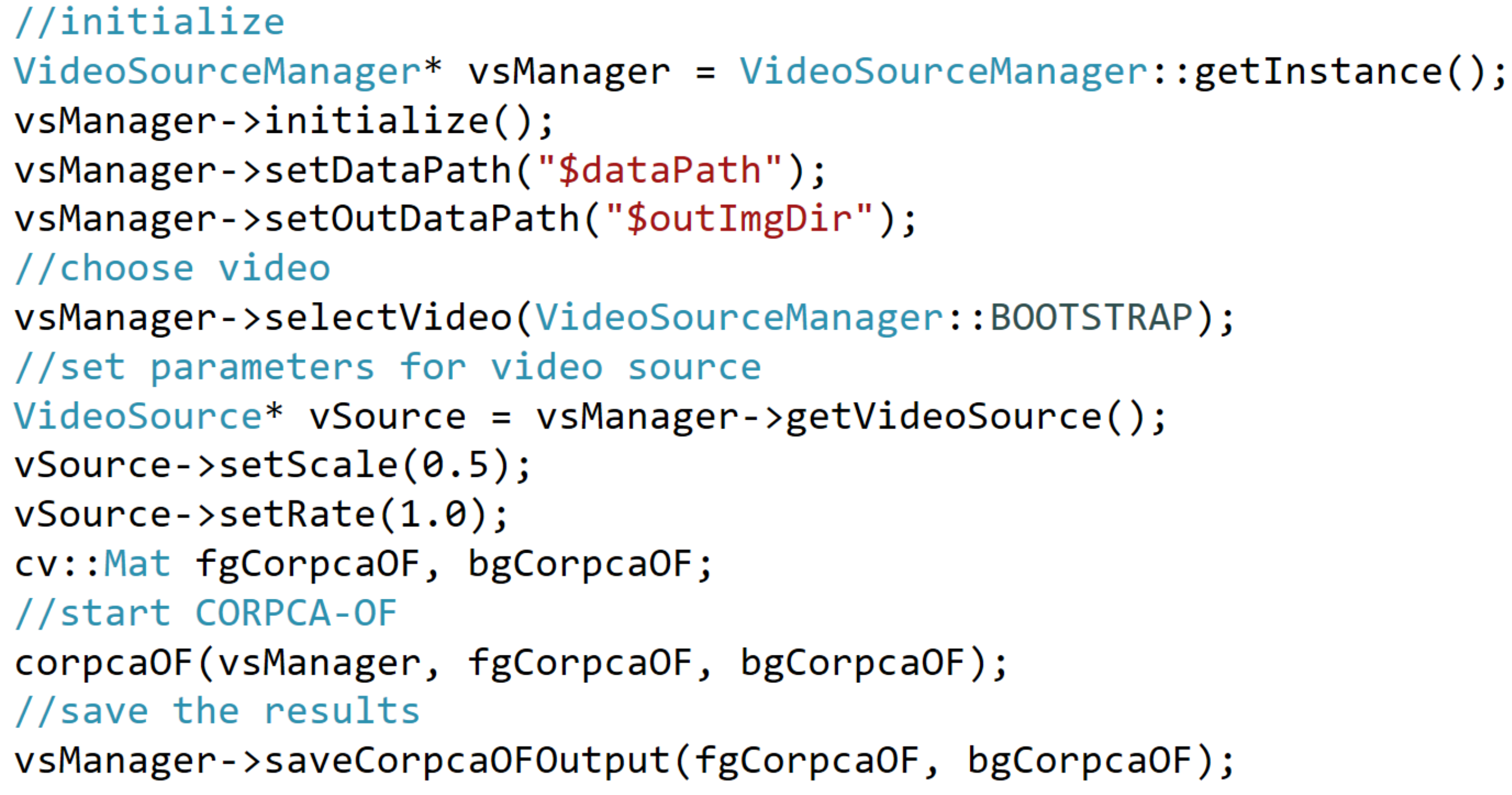
Appendix A. Overview of CORPCA-OF Implementaion in C++
References
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? JACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S.; Peng, Y.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. Adv. Neural Inf. Process. Syst. 2009, 2080–2088. [Google Scholar]
- Horn, B.K.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef] [Green Version]
- Bruhn, A.; Weickert, J.; Schnörr, C. Lucas/Kanade meets Horn/Schunck: Combining local and global optic flow methods. Int. J. Comput. Vis. 2005, 61, 211–231. [Google Scholar] [CrossRef]
- Baker, S.; Scharstein, D.; Lewis, J.; Roth, S.; Black, M.J.; Szeliski, R. A database and evaluation methodology for optical flow. Int. J. Comput. Vis. 2011, 92, 1–31. [Google Scholar] [CrossRef]
- Brox, T.; Malik, J. Large displacement optical flow: Descriptor matching in variational motion estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 500–513. [Google Scholar] [CrossRef] [PubMed]
- Luong, H.V.; Deligiannis, N.; Seiler, J.; Forchhammer, S.; Kaup, A. Compressive online robust principal component analysis with multiple prior information. In Proceedings of the IEEE Global Conference on Signal and Information Processing, Montreal, QC, Canada, 14–16 November 2017. [Google Scholar]
- Rodriguez, P.; Wohlberg, B. Incremental principal component pursuit for video background modeling. J. Math. Imaging Vis. 2016, 55, 1–18. [Google Scholar] [CrossRef]
- Hong, B.; Wei, L.; Hu, Y.; Cai, D.; He, X. Online robust principal component analysis via truncated nuclear norm regularization. Neurocomputing 2016, 175, 216–222. [Google Scholar] [CrossRef]
- Xiao, W.; Huang, X.; Silva, J.; Emrani, S.; Chaudhuri, A. Online Robust Principal Component Analysis with Change Point Detection. arXiv, 2017; arXiv:1702.05698. [Google Scholar]
- He, J.; Balzano, L.; Szlam, A. Incremental gradient on the grassmannian for online foreground and background separation in subsampled video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 1568–1575. [Google Scholar]
- Xu, J.; Ithapu, V.K.; Mukherjee, L.; Rehg, J.M.; Singh, V. Gosus: Grassmannian online subspace updates with structured-sparsity. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 3376–3383. [Google Scholar]
- Feng, J.; Xu, H.; Yan, S. Online robust pca via stochastic optimization. Adv. Neural Inf. Process. Syst. 2013, 26, 404–412. [Google Scholar]
- Mansour, H.; Jiang, X. A robust online subspace estimation and tracking algorithm. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 4065–4069. [Google Scholar]
- Wright, J.; Ganesh, A.; Min, K.; Ma, Y. Compressive principal component pursuit. Inf. Inference J. IMA 2013, 2, 32–68. [Google Scholar] [CrossRef] [Green Version]
- Pan, P.; Feng, J.; Chen, L.; Yang, Y. Online compressed robust PCA. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1041–1048. [Google Scholar]
- Guo, H.; Qiu, C.; Vaswani, N. An online algorithm for separating sparse and low-dimensional signal sequences from their sum. IEEE Trans. Signal Process. 2014, 62, 4284–4297. [Google Scholar] [CrossRef]
- Mota, J.F.; Deligiannis, N.; Sankaranarayanan, A.C.; Cevher, V.; Rodrigues, M.R. Adaptive-rate reconstruction of time-varying signals with application in compressive foreground extraction. IEEE Trans. Signal Process. 2016, 64, 3651–3666. [Google Scholar] [CrossRef]
- Warnell, G.; Bhattacharya, S.; Chellappa, R.; Basar, T. Adaptive-Rate Compressive Sensing Using Side Information. IEEE Trans. Image Process. 2015, 24, 3846–3857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiu, C.; Vaswani, N.; Lois, B.; Hogben, L. Recursive Robust PCA or Recursive Sparse Recovery in Large but Structured Noise. IEEE Trans. Inf. Theory 2014, 60, 5007–5039. [Google Scholar] [CrossRef] [Green Version]
- Zhan, J.; Vaswani, N. Robust PCA with partial subspace knowledge. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014. [Google Scholar] [CrossRef]
- Vaswani, N.; Zhan, J. Recursive Recovery of Sparse Signal Sequences From Compressive Measurements: A Review. IEEE Trans. Signal Process. 2016, 64, 3523–3549. [Google Scholar] [CrossRef]
- Bouwmans, T.; Sobral, A.; Javed, S.; Jung, S.K.; Zahzah, E.H. Decomposition into Low-rank Plus Additive Matrices for Background/Foreground Separation. Comput. Sci. Rev. 2017, 23, 1–71. [Google Scholar] [CrossRef]
- Vaswani, N.; Lu, W. Modified-CS: Modifying compressive sensing for problems with partially known support. IEEE Trans. Signal Process. 2010, 58, 4595–4607. [Google Scholar] [CrossRef]
- Gonzalez, C.G.; Absil, O.; Absil, P.A.; Van Droogenbroeck, M.; Mawet, D.; Surdej, J. Low-rank plus sparse decomposition for exoplanet detection in direct-imaging ADI sequences-The LLSG algorithm. Astron. Astrophys. 2016, 589, A54. [Google Scholar] [CrossRef]
- Sobral, A.; Bouwmans, T.; ZahZah, E.H. Double-constrained RPCA based on saliency maps for foreground detection in automated maritime surveillance. In Proceedings of the 12th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Karlsruhe, Germany, 25–28 August 2015; pp. 1–6. [Google Scholar]
- Javed, S.; Mahmood, A.; Bouwmans, T.; Jung, S.K. Background–Foreground Modeling Based on Spatiotemporal Sparse Subspace Clustering. IEEE Trans. Image Process. 2017, 26, 5840–5854. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Javed, S.; Mahmood, A.; Bouwmans, T.; Jung, S.K. Spatiotemporal low-rank modeling for complex scene background initialization. IEEE Trans. Circuits Syst. Video Technol. 2016, 28, 1315–1329. [Google Scholar] [CrossRef]
- Berjón, D.; Cuevas, C.; Morán, F.; García, N. Real-time nonparametric background subtraction with tracking-based foreground update. Pattern Recognit. 2018, 74, 156–170. [Google Scholar] [CrossRef]
- Benezeth, Y.; Jodoin, P.M.; Emile, B.; Laurent, H.; Rosenberger, C. Comparative study of background subtraction algorithms. J. Electron. Imaging 2010, 19, 033003. [Google Scholar] [Green Version]
- Bouwmans, T. Traditional and recent approaches in background modeling for foreground detection: An overview. Comput. Sci. Rev. 2014, 11, 31–66. [Google Scholar] [CrossRef]
- Cuevas, C.; Martínez, R.; García, N. Detection of stationary foreground objects: A survey. Comput. Vis. Image Underst. 2016, 152, 41–57. [Google Scholar] [CrossRef]
- Vacavant, A.; Chateau, T.; Wilhelm, A.; Lequièvre, L. A benchmark dataset for outdoor foreground/ background extraction. Asian Conf. Comput. Vis. 2012, 7728, 291–300. [Google Scholar]
- Sobral, A.; Vacavant, A. A comprehensive review of background subtraction algorithms evaluated with synthetic and real videos. Comput. Vis. Image Underst. 2014, 122, 4–21. [Google Scholar] [CrossRef]
- Bianco, S.; Ciocca, G.; Schettini, R. Combination of video change detection algorithms by genetic programming. IEEE Trans. Evol. Comput. 2017, 21, 914–928. [Google Scholar] [CrossRef]
- Braham, M.; Piérard, S.; Van Droogenbroeck, M. Semantic background subtraction. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 4552–4556. [Google Scholar]
- Lee, S.H.; Kwon, S.C.; Shim, J.W.; Lim, J.E.; Yoo, J. WisenetMD: Motion Detection Using Dynamic Background Region Analysis. arXiv, 2018; arXiv:1805.09277. [Google Scholar]
- St-Charles, P.L.; Bilodeau, G.A.; Bergevin, R. Universal background subtraction using word consensus models. IEEE Trans. Image Process. 2016, 25, 4768–4781. [Google Scholar] [CrossRef]
- Wang, Y.; Jodoin, P.M.; Porikli, F.; Konrad, J.; Benezeth, Y.; Ishwar, P. CDnet 2014: An expanded change detection benchmark dataset. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Columbus, OH, USA, 23–28 June 2014; pp. 393–400. [Google Scholar]
- Bouwmans, T.; Maddalena, L.; Petrosino, A. Scene background initialization: A taxonomy. Pattern Recognit. Lett. 2017, 96, 3–11. [Google Scholar] [CrossRef]
- Jodoin, P.M.; Maddalena, L.; Petrosino, A.; Wang, Y. Extensive benchmark and survey of modeling methods for scene background initialization. IEEE Trans. Image Process. 2017, 26, 5244–5256. [Google Scholar] [CrossRef] [PubMed]
- Maddalena, L.; Bouwmans, T. Scene Background Modeling and Initialization (SBMI) Workshop. Genova, Italy, 2015. Available online: http://sbmi2015.na.icar.cnr.it (accessed on 1 July 2018).
- Laugraud, B.; Piérard, S.; Van Droogenbroeck, M. LaBGen: A method based on motion detection for generating the background of a scene. Pattern Recognit. Lett. 2017, 96, 12–21. [Google Scholar] [CrossRef] [Green Version]
- Laugraud, B.; Van Droogenbroeck, M. Is a Memoryless Motion Detection Truly Relevant for Background Generation with LaBGen? In Proceedings of the International Conference on Advanced Concepts for Intelligent Vision Systems, Antwerp, Belgium, 18–21 September 2017; pp. 443–454. [Google Scholar]
- De Gregorio, M.; Giordano, M. Background estimation by weightless neural networks. Pattern Recognit. Lett. 2017, 96, 55–65. [Google Scholar] [CrossRef]
- Prativadibhayankaram, S.; Luong, H.V.; Le, T.H.; Kaup, A. Compressive Online Robust Principal Component Analysis with Optical Flow for Video Foreground-Background Separation. In Proceedings of the Eighth International Symposium on Information and Communication Technology, Nha Trang, Vietnam, 7–8 December 2017; pp. 385–392. [Google Scholar]
- Brand, M. Incremental Singular Value Decomposition of Uncertain Data with Missing Values. In Proceedings of the European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002. [Google Scholar]
- Luong, H.V.; Seiler, J.; Kaup, A.; Forchhammer, S. Sparse Signal Reconstruction with Multiple Side Information using Adaptive Weights for Multiview Sources. In Proceedings of the IEEE International Conference on Image Processing, Phoenix, AZ, USA, 25–28 September 2016. [Google Scholar]
- Luong, H.V. Available online: https://github.com/huynhlvd/corpca (accessed on 1 July 2018).
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.F.; Candès, E.J.; Shen, Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef] [Green Version]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Li, L.; Huang, W.; Gu, I.Y.H.; Tian, Q. Statistical modeling of complex backgrounds for foreground object detection. IEEE Trans. Image Process. 2004, 13, 1459–1472. [Google Scholar] [CrossRef] [PubMed]
- Dikmen, M.; Tsai, S.F.; Huang, T.S. Base selection in estimating sparse foreground in video. In Proceedings of the 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 3217–3220. [Google Scholar]
- Cucchiara, R.; Grana, C.; Piccardi, M.; Prati, A. Detecting moving objects, ghosts, and shadows in video streams. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1337–1342. [Google Scholar] [CrossRef] [Green Version]
- Luong, H.V.; Prativadibhayankaram, S. Available online: https://github.com/huynhlvd/corpca-of (accessed on 1 July 2018).














© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prativadibhayankaram, S.; Luong, H.V.; Le, T.H.; Kaup, A. Compressive Online Video Background–Foreground Separation Using Multiple Prior Information and Optical Flow. J. Imaging 2018, 4, 90. https://doi.org/10.3390/jimaging4070090
Prativadibhayankaram S, Luong HV, Le TH, Kaup A. Compressive Online Video Background–Foreground Separation Using Multiple Prior Information and Optical Flow. Journal of Imaging. 2018; 4(7):90. https://doi.org/10.3390/jimaging4070090
Chicago/Turabian StylePrativadibhayankaram, Srivatsa, Huynh Van Luong, Thanh Ha Le, and André Kaup. 2018. "Compressive Online Video Background–Foreground Separation Using Multiple Prior Information and Optical Flow" Journal of Imaging 4, no. 7: 90. https://doi.org/10.3390/jimaging4070090
APA StylePrativadibhayankaram, S., Luong, H. V., Le, T. H., & Kaup, A. (2018). Compressive Online Video Background–Foreground Separation Using Multiple Prior Information and Optical Flow. Journal of Imaging, 4(7), 90. https://doi.org/10.3390/jimaging4070090




