LaBGen-P-Semantic: A First Step for Leveraging Semantic Segmentation in Background Generation
Abstract
1. Introduction
2. The LaBGen-P Stationary Background Generation Method
2.1. Step 1: Motion Detection Step
2.2. Step 2: Estimation Step
2.3. Step 3: Selection Step
2.4. Step 4: Generation Step
- Online mode: A background image is generated after the processing of each frame , starting from the second one. Consequently, the channel-wise median filter is applied on each intermediate subset of intensities . Thus, the background intensity corresponding to pixel position after the processing of frame is generated as follows:
- Offline mode: A unique background image is generated after processing the final frame . The background intensity corresponding to pixel position is generated as follows:Even though only the subset of intensities is used in this mode, building all intermediate subsets , with , in the estimation step is necessary to build iteratively. Note that using the offline mode offers a better computational performance as the generation step is applied only after a unique frame. In return, one has to wait for the end of the processing of the whole input video sequence to get a background estimate.
3. LaBGen-P-Semantic: The First Background Generation Method Leveraging Semantics
- Two new intra-frame methods, based on different hypotheses, to get a motion score from a vector of scores . The first, referred to as the complete vector (CV) method, estimates the probability that belongs to the foreground, given the complete vector of scores , using a Bayesian framework. The second, referred to as the most probable (MP) method, estimates the same probability, given the most probable object class (i.e., the object class with the largest score in ).
- Along with our two methods, we provide a solution to estimate the probability to observe foreground, given an object class, from a dataset of video sequences provided with a motion ground-truth (i.e., a set of annotations indicating for each pixel whether it belongs to the foreground or background).
3.1. Motion Score Estimation from the Complete Vector of Scores
- The appearance depends on the type of car (shape, color), on the relative orientation of the car with respect to the camera, on the lighting conditions, and so on. Because the type of car could influence , the random vector and variable G may be dependent, even when the real object class o is known: a very old car is more likely to be in a museum and, therefore, motionless. However, we believe that such particular cases are rare, so that neglecting this kind of relationship between and G is reasonable. Moreover, this difficulty is related to a particular semantic segmentation algorithm as it originates from the fact that all types of cars are within the same object class.
- Concerning the surrounding objects, it is clear that the probability for an object to be a car is higher when the object is on a road than on a boat, and the probability for a car to move when it is on a road is higher than when it is on a boat. However, there is no evidence that the surrounding elements highly influence the contents of for the considered object.
3.2. Motion Score Estimation from the Most Probable Object Class
4. Experiments
4.1. Experimental Setup
- SceneBackgroundModeling.NET (SBMnet; http://scenebackgroundmodeling.net) [3]: This gathers 79 video sequences composed of 6–9370 frames and whose dimensions vary from –. They are scattered though 8 categories, a category being associated with a specific challenge: “Basic”, “Intermittent Motion”, “Clutter”, “Jitter”, “Illumination Changes”, “Background Motion”, “Very Long” and “Very Short”. The ground-truth is provided for only 13 sequences distributed among the categories. For an evaluation using the complete dataset, one has to send its results on a web platform, which, in addition to computing the evaluation metrics, aims at maintaining a public ranking of background generation methods.
- Scene Background Initialization (SBI; http://sbmi2015.na.icar.cnr.it/SBIdataset.html) [19]: This gathers 14 video sequences made up of 6–740 frames and whose dimensions vary from –. Unlike SBMnet, the sequences of SBI are all provided with a ground-truth background image. Note that 7 video sequences are common to SBI and SBMnet: “Board”, “Candela_m1.10”, “CaVignal”, “Foliage”, “HumanBody2”, “People&Foliage” and “Toscana”.
- SBI+SBMnet-GT: In order to get the largest dataset of video sequences provided with a ground-truth background image, we simultaneously consider the video sequences of SBMnet provided with the ground-truth and the ones of SBI (excluding “Board”, whose ground-truth is available in both datasets). This special set of 26 video sequences (13 from SBMnet and 13 from SBI, with 6 that are also in SBMnet) will be referred to as the SBI+SBMnet-GT dataset.
- Universal training dataset: To apply our universal estimators, we need a motion ground-truth indicating which pixels belong to the foreground. Even though motion ground-truths are not provided with datasets related to the background generation field, we managed to find motion annotations for some of the SBMnet and SBI video sequences.Several video sequences of SBMnet are available in other datasets, which are mostly associated with background subtraction challenges. Thus, we managed to gather motion ground-truths from the original datasets for 53 of 79 video sequences. Some of these motion ground-truths have been processed since frame reduction and/or cropping operations were applied on the SBMnet version of their corresponding video sequence. Note that a large majority of motion ground-truths is formatted according to the ChangeDetection.NET (CDnet) format [21,22]. Specifically, in addition to being labeled as belonging either to the foreground or background, a pixel can be labeled as a shadow, impossible to classify or outside the region of interest.Concerning the SBI dataset, Wang et al. provided for all video sequences a motion ground-truth produced with a CNN-based semi-interactive method [20]. In addition to the 53 SBMnet video sequences for which we managed to find motion ground-truths, we consider only the 7 SBI video sequences that are not shared with SBMnet. This set of 60 (53 + 7) video sequences, along with their corresponding motion ground-truth will be referred to as the universal training dataset.
- Average gray-level error (AGE, ↓, ): average of the absolute difference between the luminance values of an input and a ground-truth background image.
- Percentage of error pixels (pEPs, ↓, in %): percentage of pixels whose absolute difference of luminance values between an input and a ground-truth background image is larger than 20.
- Percentage of clustered error pixels (pCEPs, ↓, in %): percentage of error pixels whose 4-connected neighbors are also error pixels according to pEPs.
- Multi-scale structural similarity index (MS-SSIM, ↑, ) [23]: pyramidal version of the structural similarity index (SSIM), which measures the change of structural information for approximating the perceived distortion between an input and a ground-truth background image. The SSIM measure is based on the assumption that the human visual system is adapted to extract structural information from the viewing field [24].
- Peak signal to noise ratio (PSNR, ↑, in dB): it is defined by the following equation, with being the mean squared error:
- Color image quality measure (CQM, ↑, in dB) [25]: combination of per-channel PSNRs computed on an approximated reversible RGB to YUV transformation.
4.2. Application of the Estimators
- A training video sequence provided with a motion ground-truth for the scene-specific estimators.
- A dataset of such video sequences, as large and representative of the real-world as possible, for the universal estimators.
- The vector of scores returned by PSPNet for each pixel in the video sequences of the training dataset. The knowledge of the most probable object classes is sufficient for the MP estimators.
4.3. Comparison of the CV and MP Methods with Universal and Scene-Specific Estimators
4.4. Performance Evaluation
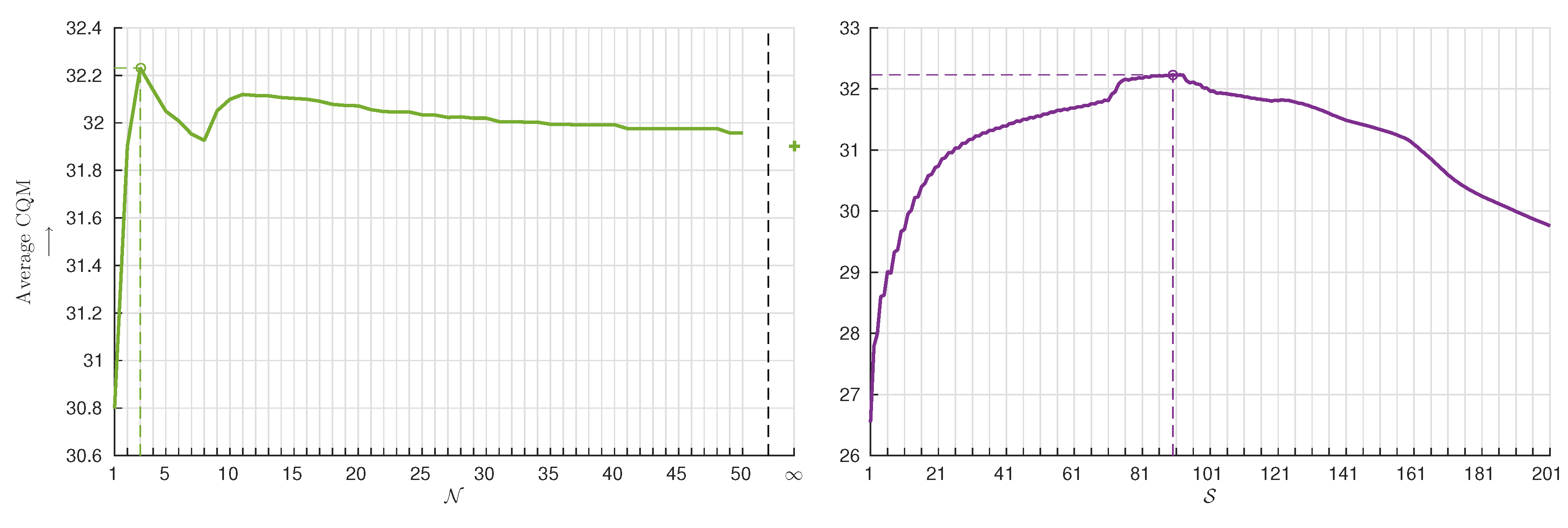
4.5. Performance Stability
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Maddalena, L.; Petrosino, A. Background Model Initialization for Static Cameras. In Background Modeling and Foreground Detection for Video Surveillance; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014; Chapter 3; pp. 114–129. [Google Scholar]
- Bouwmans, T.; Maddalena, L.; Petrosino, A. Scene Background Initialization: A Taxonomy. Pattern Recognit. Lett. 2017, 96, 3–11. [Google Scholar] [CrossRef]
- Jodoin, P.M.; Maddalena, L.; Petrosino, A.; Wang, Y. Extensive Benchmark and Survey of Modeling Methods for Scene Background Initialization. IEEE Trans. Image Process. 2017, 26, 5244–5256. [Google Scholar] [CrossRef] [PubMed]
- Laugraud, B.; Piérard, S.; Braham, M.; Van Droogenbroeck, M. Simple median-based method for stationary background generation using background subtraction algorithms. In Proceedings of the International Conference on Image Analysis and Processing (ICIAP), Workshop on Scene Background Modeling and Initialization (SBMI), Genoa, Italy, 7–11 September 2015; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2015; Volume 9281, pp. 477–484. [Google Scholar]
- Laugraud, B.; Piérard, S.; Van Droogenbroeck, M. LaBGen: A method based on motion detection for generating the background of a scene. Pattern Recognit. Lett. 2017, 96, 12–21. [Google Scholar] [CrossRef]
- Laugraud, B.; Piérard, S.; Van Droogenbroeck, M. LaBGen-P: A Pixel-Level Stationary Background Generation Method Based on LaBGen. In Proceedings of the 23rd International Conference on IEEE International Conference on Pattern Recognition (ICPR), Cancún, Mexico, 4–8 December 2016; pp. 107–113. [Google Scholar]
- Laugraud, B.; Van Droogenbroeck, M. Is a Memoryless Motion Detection Truly Relevant for Background Generation with LaBGen? In Proceedings of the International Conference on Advanced Concepts for Intelligent Vision Systems (ACIVS), Antwerp, Belgium, 18–21 September 2017; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2017; Volume 10617, pp. 443–454. [Google Scholar]
- Braham, M.; Piérard, S.; Van Droogenbroeck, M. Semantic Background Subtraction. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 4552–4556. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar]
- Bouwmans, T. Recent Advanced Statistical Background Modeling for Foreground Detection—A Systematic Survey. Recent Pat. Comput. Sci. 2011, 4, 147–176. [Google Scholar]
- Bouwmans, T. Subspace Learning for Background Modeling: A Survey. Recent Pat. Comput. Sci. 2009, 2, 223–234. [Google Scholar] [CrossRef]
- Bouwmans, T.; Sobral, A.; Javed, S.; Jung, S.K.; Zahzah, E.H. Decomposition into low-rank plus additive matrices for background/foreground separation: A review for a comparative evaluation with a large-scale dataset. Comput. Sci. Rev. 2017, 23, 1–71. [Google Scholar] [CrossRef]
- Sobral, A.; Javed, S.; Jung, S.K.; Bouwmans, T.; Zahzah, E.H. Online Stochastic Tensor Decomposition for Background Subtraction in Multispectral Video Sequences. In Proceedings of the International Conference on Computer Vision Workshops (ICCV Workshops), Santiago, Chile, 11–18 December 2015; pp. 946–953. [Google Scholar]
- Bouwmans, T. Background Subtraction for Visual Surveillance: A Fuzzy Approach. In Handbook on Soft Computing for Video Surveillance; Pal, S.K., Petrosino, A., Maddalena, L., Eds.; Taylor and Francis Group: Abingdon, UK, 2012; Chapter 5; pp. 103–138. [Google Scholar]
- Bouwmans, T. Traditional and recent approaches in background modeling for foreground detection: An overview. Comput. Sci. Rev. 2014, 11–12, 31–66. [Google Scholar] [CrossRef]
- Crow, F. Summed-area tables for texture mapping. In Proceedings of the 11th Annual Conference on Computer Graphics and Interactive Techniques SIGGRAPH, Minneapolis, MN, USA, 23–27 July 1984; Computer Graphics. ACM: New York, NY, USA, 1984; Volume 18, pp. 207–212. [Google Scholar]
- Zhou, B.; Zhao, H.; Puig, X.; Fidler, S.; Barriuso, A.; Torralba, A. Semantic understanding of scenes through the ADE20K dataset. arXiv 2016, arXiv:arXiv:1608.05442. [Google Scholar]
- Zhou, B.; Zhao, H.; Puig, X.; Fidler, S.; Barriuso, A.; Torralba, A. Scene Parsing through ADE20K Dataset. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5122–5130. [Google Scholar]
- Maddalena, L.; Petrosino, A. Towards Benchmarking Scene Background Initialization. In Proceedings of the International Conference on Image Analysis and Processing Workshops (ICIAP Workshops), Genova, Italy, 7–11 September 2015; Volume 9281, pp. 469–476. [Google Scholar]
- Wang, Y.; Luo, Z.; Jodoin, P.M. Interactive Deep Learning Method for Segmenting Moving Objects. Pattern Recognit. Lett. 2017, 96, 66–75. [Google Scholar] [CrossRef]
- Goyette, N.; Jodoin, P.M.; Porikli, F.; Konrad, J.; Ishwar, P. changedetection.net: A New Change Detection Benchmark Dataset. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Wang, Y.; Jodoin, P.M.; Porikli, F.; Konrad, J.; Benezeth, Y.; Ishwar, P. CDnet 2014: An Expanded Change Detection Benchmark Dataset. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Columbus, OH, USA, 23–28 June 2014; pp. 393–400. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Yalman, Y.; Ertürk, I. A new color image quality measure based on YUV transformation and PSNR for human vision system. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 603–613. [Google Scholar]
- Javed, S.; Mahmood, A.; Bouwmans, T.; Jung, S.K. Background-Foreground Modeling Based on Spatiotemporal Sparse Subspace Clustering. IEEE Trans. Image Process. 2017, 26, 5840–5854. [Google Scholar] [CrossRef] [PubMed]
- De Gregorio, M.; Giordano, M. Background estimation by weightless neural networks. Pattern Recognit. Lett. 2017, 96, 55–65. [Google Scholar] [CrossRef]
- Maddalena, L.; Petrosino, A. Extracting a Background Image by a Multi-modal Scene Background Model. In Proceedings of the 23rd International Conference on IEEE International Conference on Pattern Recognition (ICPR), Cancún, Mexico, 4–8 December 2016; pp. 143–148. [Google Scholar]
- Javed, S.; Mahmmod, A.; Bouwmans, T.; Jung, S.K. Motion-Aware Graph Regularized RPCA for Background Modeling of Complex Scene. In Proceedings of the IEEE International Conference on Pattern Recognition (ICPR), Cancún, Mexico, 4–8 December 2016; pp. 120–125. [Google Scholar]
- Liu, W.; Cai, Y.; Zhang, M.; Li, H.; Gu, H. Scene Background Estimation Based on Temporal Median Filter with Gaussian Filtering. In Proceedings of the IEEE International Conference on Pattern Recognition (ICPR), Cancún, Mexico, 4–8 December 2016; pp. 132–136. [Google Scholar]
- Agarwala, A.; Dontcheva, M.; Agrawala, M.; Drucker, S.; Colburn, A.; Curless, B.; Salesin, D.; Cohen, M. Interactive Digital Photomontage. ACM Trans. Graph. 2004, 23, 294–302. [Google Scholar] [CrossRef]
- Ortego, D.; SanMiguel, J.M.; Martínez, J.M. Rejection based multipath reconstruction for background estimation in video sequences with stationary objects. Comput. Vis. Image Underst. 2016, 147, 23–37. [Google Scholar] [CrossRef]
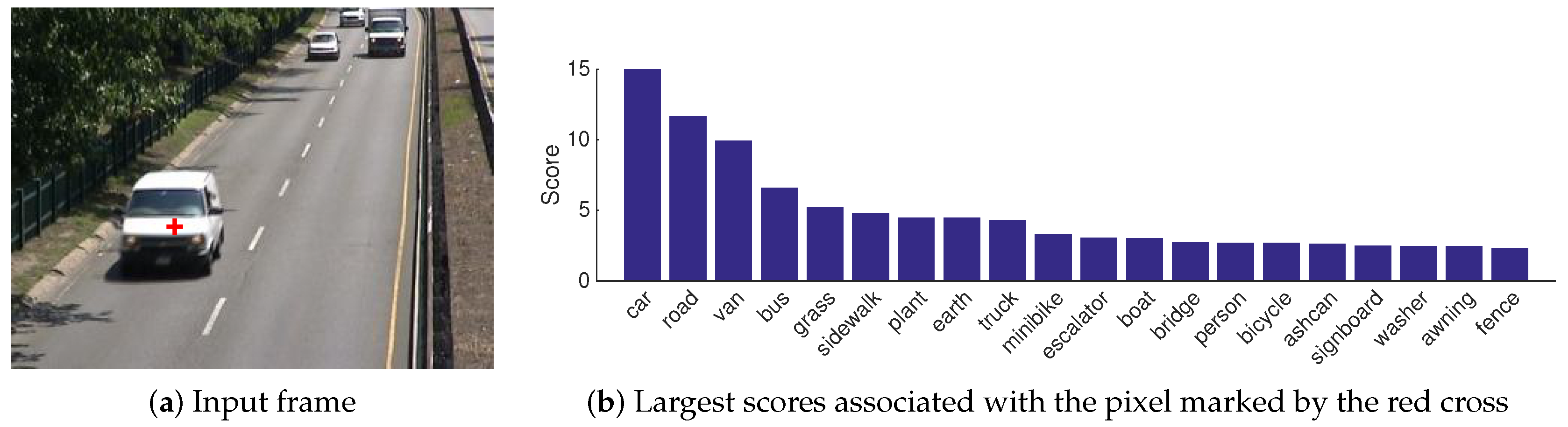
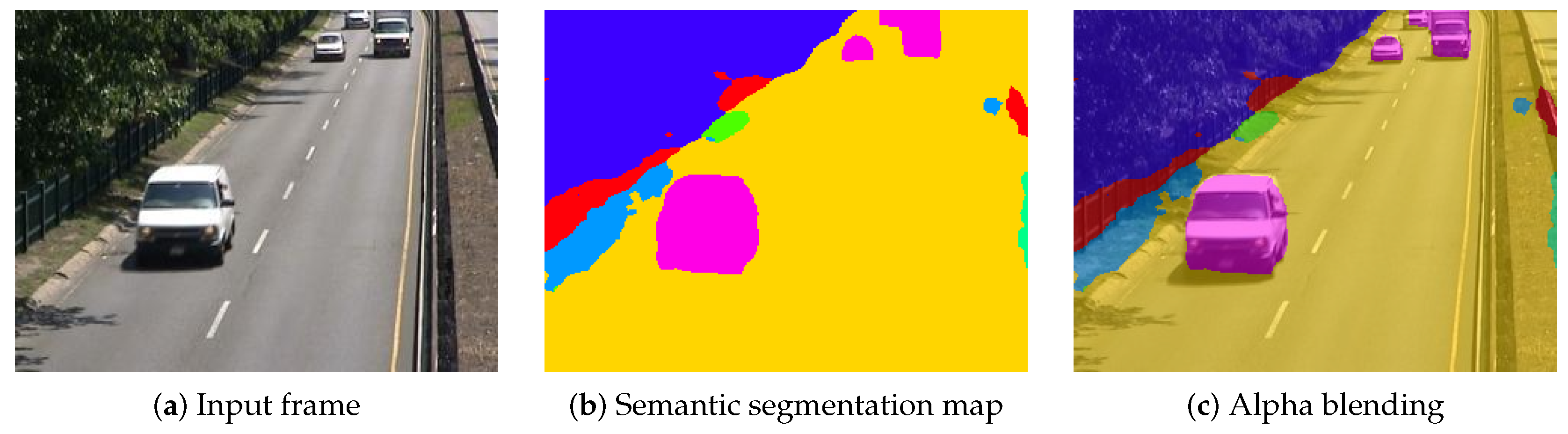





| Dataset | Sequences | Categories | Background GT | Motion GT |
|---|---|---|---|---|
| SBMnet [3] | 79 | 8 | ✔ | ✔ |
| (for 13 sequences) | (can be found for 53) | |||
| SBI [19] | 14 | ✘ | ✔ | ✔ |
| (made in [20]) | ||||
| SBI+SBMnet-GT | 26 | - | ✔ | - |
| 13 (SBMnet) + 13 (SBI) | ||||
| Universal training dataset | 60 | - | - | ✔ |
| 53 (SBMnet) + 7 (SBI) | ||||
| SBMnet ∩ SBI | 7 | - | ✔ | ✔ |
| (6 from SBI) | ||||
| SBMnet ∩ SBI+SBMnet-GT | 19 | - | ✔ | - |
| (6 from SBI) |
| Object | P | Object | P | Object | P | |||
|---|---|---|---|---|---|---|---|---|
| barrel | 229 | vase | 64,945 | floor | 692,516,995 | |||
| toilet | 1216 | curtain | 576,979 | monitor | 121,745 | |||
| blanket | 3268 | bicycle | 121,066 | bed | 47,475 | |||
| ottoman | 7704 | painting | 5,221,976 | field | 556,031 | |||
| plaything | 141,170 | sink | 150,386 | pole | 1,938,557 | |||
| fan | 347 | river | 264,941 | step | 6070 | |||
| tower | 2608 | mirror | 17,050,284 | cabinet | 6,919,138 | |||
| pillow | 16 | case | 1,178,259 | road | 303,326,231 | |||
| truck | 467,985 | counter | 268,319 | windowpane | 13,890,350 | |||
| bag | 1,135,277 | seat | 4,098,086 | grandstand | 2,354,843 | |||
| sconce | 27,871 | lamp | 362,771 | grass | 22,630,677 | |||
| bus | 311,982 | washer | 21,636 | blind | 85,026 | |||
| ball | 70,287 | runway | 77,137 | water | 24,823,194 | |||
| person | 134,152,198 | plate | 4862 | booth | 373,955 | |||
| traffic light | 6403 | escalator | 1,744,085 | hill | 122,589 | |||
| boat | 1,114,323 | base | 7,840,733 | table | 5,375,958 | |||
| sculpture | 376,879 | fence | 10,031,657 | refrigerator | 65,061 | |||
| microwave | 1793 | ashcan | 2,036,851 | bulletin board | 2,031,323 | |||
| ship | 24,139 | box | 55,702,183 | desk | 21,227,639 | |||
| airplane | 43,314 | food | 11,594 | railing | 15,610,594 | |||
| tray | 32,230 | basket | 31,777 | path | 293,258 | |||
| flag | 39,355 | conveyer belt | 628,771 | pot | 355,237 | |||
| van | 1,342,081 | building | 167,956,405 | stairway | 994,290 | |||
| minibike | 18,806 | computer | 6,958,428 | sand | 796,415 | |||
| cushion | 1,568,774 | wall | 1,109,638,501 | television | 1,939,717 | |||
| car | 24,511,746 | lake | 10,272 | chest of drawers | 7,586,777 | |||
| flower | 919,044 | swivel chair | 564,579 | shelf | 26,638,839 | |||
| chandelier | 6265 | tree | 144,037,610 | bannister | 778,884 | |||
| animal | 426,393 | sea | 345,077 | pier | 8814 | |||
| signboard | 11,488,355 | clock | 23,843 | hood | 113 | |||
| tank | 8492 | streetlight | 35,315 | oven | 49,380 | |||
| tent | 194,742 | palm | 1,831,650 | swimming pool | 1,767,585 | |||
| armchair | 387,787 | bridge | 646,579 | canopy | 750 | |||
| towel | 145,877 | sidewalk | 30,737,151 | stage | 9537 | |||
| trade name | 284,467 | sky | 14,141,894 | land | 22 | |||
| screen | 3189 | stool | 7502 | arcade machine | 52 | |||
| plant | 71,642,620 | stairs | 72,947 | countertop | 2619 | |||
| glass | 91,069 | ceiling | 59,792,355 | coffee table | 29,170 | |||
| awning | 26,312 | sofa | 29,893,141 | bookcase | 268 | |||
| house | 5636 | light | 838,444 | pool table | 4266 | |||
| bathtub | 33,153 | bench | 329,276 | rug | 10,300 | |||
| bar | 893,190 | mountain | 48,916,336 | radiator | - | 0 | ||
| bottle | 118,313 | fountain | 2,554,931 | shower | - | 0 | ||
| column | 31,374 | wardrobe | 74,702 | dishwasher | - | 0 | ||
| apparel | 511,132 | book | 4,312,650 | cradle | - | 0 | ||
| rock | 583,174 | stove | 271,253 | buffet | - | 0 | ||
| skyscraper | 13,417 | chair | 7,061,521 | dirt track | - | 0 | ||
| waterfall | 2,015,304 | door | 36,383,787 | hovel | - | 0 | ||
| poster | 1,648,714 | earth | 53,211,792 | kitchen island | - | 0 | ||
| vase | 64,945 | CRT screen | 412,979 | screen door | - | 0 |
| Best Parameter Sets | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Average CQM ↑ | CV+U | CV+S | MP+U | MP+S | |||||
| Method | CV+U | ||||||||
| CV+S | |||||||||
| MP+U | |||||||||
| MP+S | |||||||||
| Method | A. R. Across | Average | Average | Average | Average | Average | Average | Average |
|---|---|---|---|---|---|---|---|---|
| Categories ↓ | Ranking ↓ | AGE ↓ | pEPs ↓ | pCEPs ↓ | MS-SSIM ↑ | PSNR ↑ | CQM ↑ | |
| LaBGen-OF [7] | ||||||||
| MSCL [26] | ||||||||
| BEWiS [27] | ||||||||
| LaBGen [5] | ||||||||
| LaBGen-P-Semantic (CV+U) | ||||||||
| LaBGen-P [6] | ||||||||
| Temporal median | ||||||||
| SC-SOBS-C4 [28] | ||||||||
| MAGRPCA [29] | ||||||||
| TMFG [30] | ||||||||
| Photomontage [31] |
| Method | A. R. Across | Average | Average | Average | Average | Average | Average | Average |
|---|---|---|---|---|---|---|---|---|
| Categories ↓ | Ranking ↓ | AGE ↓ | pEPs ↓ | pCEPs ↓ | MS-SSIM ↑ | PSNR ↑ | CQM ↑ | |
| LaBGen-OF [7] | ||||||||
| MSCL [26] | ||||||||
| BEWiS [27] | ||||||||
| LaBGen [5] | ||||||||
| LaBGen-P-Semantic (MP+U) | ||||||||
| LaBGen-P [6] | ||||||||
| Temporal median | ||||||||
| MAGRPCA [29] | ||||||||
| SC-SOBS-C4 [28] | ||||||||
| TMFG [30] | ||||||||
| Photomontage [31] |
| Average Ranking ↓ | Average CQM ↑ | |||||||
|---|---|---|---|---|---|---|---|---|
| Category | 1st | CV+U | LaBGen-P | MP+U | LaBGen-P | CV+U | MP+U | LaBGen-P |
| Basic | ||||||||
| Intermittent Motion | ✔ | |||||||
| Clutter | ||||||||
| Jitter | ||||||||
| Illumination Changes | ||||||||
| Background Motion | ✔ | |||||||
| Very Long | ||||||||
| Very Short | ✔ | |||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laugraud, B.; Piérard, S.; Van Droogenbroeck, M. LaBGen-P-Semantic: A First Step for Leveraging Semantic Segmentation in Background Generation. J. Imaging 2018, 4, 86. https://doi.org/10.3390/jimaging4070086
Laugraud B, Piérard S, Van Droogenbroeck M. LaBGen-P-Semantic: A First Step for Leveraging Semantic Segmentation in Background Generation. Journal of Imaging. 2018; 4(7):86. https://doi.org/10.3390/jimaging4070086
Chicago/Turabian StyleLaugraud, Benjamin, Sébastien Piérard, and Marc Van Droogenbroeck. 2018. "LaBGen-P-Semantic: A First Step for Leveraging Semantic Segmentation in Background Generation" Journal of Imaging 4, no. 7: 86. https://doi.org/10.3390/jimaging4070086
APA StyleLaugraud, B., Piérard, S., & Van Droogenbroeck, M. (2018). LaBGen-P-Semantic: A First Step for Leveraging Semantic Segmentation in Background Generation. Journal of Imaging, 4(7), 86. https://doi.org/10.3390/jimaging4070086





