Abstract
Pixelated images are used to transmit data between computing devices that have cameras and screens. Significant compression of pixelated images has been achieved by an “edge-based transformation and entropy coding” (ETEC) algorithm recently proposed by the authors of this paper. The study of ETEC is extended in this paper with a comprehensive performance evaluation. Furthermore, a novel algorithm termed “prediction-based transformation and entropy coding” (PTEC) is proposed in this paper for pixelated images. In the first stage of the PTEC method, the image is divided hierarchically to predict the current pixel using neighboring pixels. In the second stage, the prediction errors are used to form two matrices, where one matrix contains the absolute error value and the other contains the polarity of the prediction error. Finally, entropy coding is applied to the generated matrices. This paper also compares the novel ETEC and PTEC schemes with the existing lossless compression techniques: “joint photographic experts group lossless” (JPEG-LS), “set partitioning in hierarchical trees” (SPIHT) and “differential pulse code modulation” (DPCM). Our results show that, for pixelated images, the new ETEC and PTEC algorithms provide better compression than other schemes. Results also show that PTEC has a lower compression ratio but better computation time than ETEC. Furthermore, when both compression ratio and computation time are taken into consideration, PTEC is more suitable than ETEC for compressing pixelated as well as non-pixelated images.
1. Introduction
In today’s information age, the world is overwhelmed with a huge amount of data. With the increasing use of computers, laptops, smartphones, and other computing devices, the amount of multimedia data in the form of text, audio, video, image, etc. are growing at an enormous speed. Storage of large volumes of data has already become an important concern for social media, email providers, medical institutes, universities, banks, and many other offices. In digital media such as in digital cameras, digital cinemas, and films, high resolution images are needed. In addition to the storage, data are often required to be transmitted over the Internet at the highest possible speed. Due to the constraint in storage facility and limitation in transmission bandwidth, compression of data is vital [1,2,3,4,5,6,7,8].
The basic idea of compressing images lies in the fact that several image pixels are correlated, and this correlation can be exploited to remove the redundant information [9]. The removal of redundancy and irrelevancy leads to a reduction in image size. There are two major types of image compression—lossy and lossless [10,11,12]. In the case of lossless compression, the reconstruction process can recover the original image from the compressed images. On the other hand, images that go through the lossy compression process cannot be precisely recovered to its actual form. Examples of lossy compression are some of the wavelet-based compressions such as embedded zerotrees of wavelet transforms (EZW), joint photographic experts group (JPEG) and the moving picture experts group (MPEG) compression.
A large number of research papers report image compression algorithms. For example, one study [13] is about discrete cosine transform (DCT)-based lossless image compression where the higher energy coefficients in each block are quantized. Next, an inverse DCT is performed only on the quantized coefficients. The resultant pixel values are in the 2-D spatial domain. The pixel values of two neighboring regions are then subtracted to obtain residual error sequence. The error sequence is encoded by an entropy coder such as Arithmetic or Huffman coding [13]. Image compression in the frequency domain using wavelets is reported in several studies [12,14,15,16,17]. In the method described in [14] lifting-based bi-orthogonal wavelet transform is used which produces coefficients that can be rounded without any loss of data. In the work of [18] wavelet transform limits the image energy within fewer coefficients which are encoded by “set partitioning in hierarchical trees” (SPIHT) algorithm.
In [19] JPEG lossless (JPEG-LS), a prediction-based lossless scheme, is proposed for continuous tone images. In [14] embedded zero tree coding (EZW) method is proposed based on the zero tree hypothesis. The study in [12] proposes a compression algorithm based on combination of discrete wavelet transform (DWT) and intensity-based adaptive quantization coding (AQC). In this AQC method, the image is divided into sub-blocks. Next, the quantizer step in each sub-block is computed by subtracting the maximum and the minimum values of the block and then dividing the result by the quantization level. In the case of intensity-based adaptive quantizer coding (IBAQC) reported in [12] the image sub-block is classified into low and high intensity blocks based on the intensity variation of each block. To encode high intensity block, it is required to have large quantization level depending on the desired peak signal to noise ratio (PSNR). On the other hand, if the pixel value in the low intensity block is less than the threshold, it is required to encode this value without quantization; otherwise, it is required to quantize the bit value with less quantization level. In case of the composite DWT-IBAQC method, IBAQC is applied to the DWT coefficients of the image. Since the whole energy of the image is carried by only a few wavelet (DWT) coefficients, the IBQAC is used to encode only the coarse (low pass) wavelet coefficients [12].
Some researchers describe prediction-based lossless compression [1,3,19,20,21,22,23,24]. Moreover, the combination of wavelet transform and the concept of prediction are presented in some studies [25,26]. In [25], the image is pre-processed by DPCM and then the wavelet transform is applied to the output of the DPCM. In [26], the image pixels are predicted by a hierarchical prediction scheme and then the wavelet transform is applied to the prediction error. Some work [5,9,11,27,28,29,30] applies various types of image transformation or pixel difference or simple entropy coding. An image transformation scheme known as “J bit encoding” (JBE) has been proposed in [11]. It can be noted that image transformation means rearranging the positions of the image components or pixels to make the image suitable for huge compression. In this [11] work, the original data are divided into two matrices where one matrix is for original nonzero data bytes, while the other matrix is for defining the positions of the zero/nonzero bytes.
A number of research papers use the high efficiency video coding (HEVC) standard for image compression [31,32,33,34]. The work in [31] describes a lossless scheme that carries out sample-based prediction in the spatial domain. The work in [33] provides an overview of the intra coding techniques in the HEVC. The authors of [32] present a collection of DPCM-based intra-prediction method which is effective to predict strong edges and discontinuities. The work in [34] proposes piecewise mapping functions on residual blocks computed after DPCM-based prediction for lossless coding. Besides, the compression using HEVC, JPEG2000 [35,36] and graph-based transforms [37] are also reported. Moreover, the work in [5] presents a combination of fixed-size codebook and row-column reduction coding for lossless compression of discrete-color images. Table 1 provides a comparative study of different image compression algorithms reported in the literature.

Table 1.
Technical scenarios of few existing lossless and near lossless image compression algorithms.
One special type of image is the pixelated images that are used to carry data between optical modulators and optical detectors. This is known as pixelated optical wireless communication system in the literature. Figure 1 illustrates one example of a pixelated system [38]. In such systems, a sequence of image frames is transmitted by liquid crystal display (LCD) or light emitting diodes (LED) arrays. A smart-phone with camera or an array of photodiode with imaging lens can be used as optical receivers [6,7,8]. Such systems have the potential to have huge data rates as there are millions of pixels on the transmitter screens. The images created on the optical transmitter are required to be within the field of view (FOV) of the receiver imaging lens. Pixelated links can be used for secure data communication in banking and military applications. For instance, pixelated systems can be useful at gatherings such as shopping malls, retail store, trade shows, galleries, conferences, etc. where business cards, product videos, brochures, and photos can be exchanged without the help of the Internet (www) connection. The storage of pixelated images may be vital for offline processing. Since data are embedded within image pixels, the pixelated images must be processed by lossless compression methods. Any amount of loss in image entropy may lead to loss in the embedded data. A very important feature of pixelated images is that a single intensity value made of pixel blocks contains a single data, and this value of intensity changes abruptly at the transition of pixel blocks. This feature is not particularly exploited in the existing image compression techniques. Hence, none of the above-mentioned research reports are optimum for pixelated images as the special features of these images are yet to be exploited for compression. In fact, a new compression algorithm for pixelated images has been proposed by the authors of this paper in a very recent study [39]. This new algorithm is termed as edge-based transformation and entropy coding (ETEC) having high compression ratio at moderate computation time. In this previous study [39], the ETEC method is evaluated for only four pixelated images. This paper extends the study of ETEC method for fifty (50) different pixelated images. Moreover, a new algorithm termed as prediction-based transformation and entropy coding (PTEC) is proposed to overcome the limitations of computation time of ETEC. The main contributions of this paper can be summarized as follows:
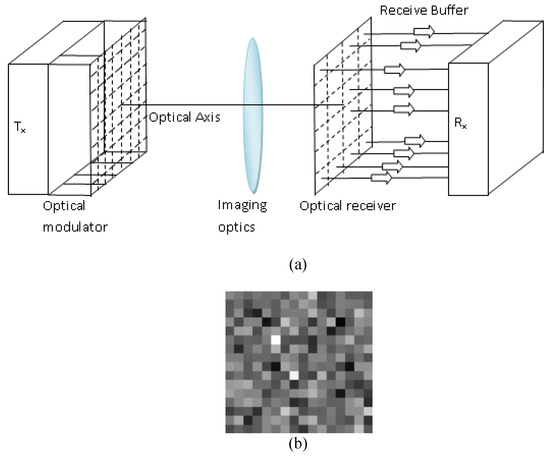
Figure 1.
Illustration of (a) a pixelated optical wireless communication system [38] (b) a transmitted pixelated image.
- (1)
- Providing a framework for ETEC method as a combination of JBE and entropy coding, and then evaluating its effectiveness for compressing a wide range of pixelated images.
- (2)
- Developing a new algorithm termed as PTEC by combining the aspects of hierarchical prediction approach, JBE method, and entropy coding.
- (3)
- Comparing the proposed ETEC and PTEC schemes with the existing compression techniques for a number of pixelated and non-pixelated standard images.
The rest of the paper is summarized as follows. Section 2 describes JPEG-LS, SPIHT, Huffman coding, Arithmetic coding and other existing methods. Section 3 describes the new ETEC and PTEC methods. The results on different image compression methods are reported in Section 4. Finally, Section 5 presents the concluding remarks.
2. Existing Image Compression Techniques
The JPEG-LS compression algorithm is suited for continuous tone images. The compression algorithm consists of four main parts, which are fixed predictor, bias canceller or adaptive corrector, context modeler and entropy coder [19]. In JPEG-LS, the edge detection is performed by “median edge detection” (MED) process [19]. JPEG-LS uses context modeling to measure the quantized gradient of surrounding image pixels. This context modeling of the predication error gives good results for images with texture pattern. Next correction values are added to the prediction error, and the remaining or residual error is encoded by Golomb coding [40] scheme. SPIHT [18,41] is an advanced encoding technique based on progressive image coding. SPIHT uses a threshold and encodes the most significant bit of the transformed image, followed by the application of increasing refinement. This paper considers SPIHT algorithm with lifting-based wavelet transform for 5/3 Le Gall wavelet filter.
Differential pulse code modulation (DPCM) [42] predictor can predict the current pixel based on its neighboring pixels as mentioned in the JPEG-LS predictor. The subtraction of the current pixel intensity and the predictor output gives predictor error e. The quantizer quantizes the error value using suitable quantization level. In case of lossless compression, the quantized level is unity. Next, an entropy coding is performed to get the final bit streams. The predictor operator can be expressed by the following equation
where is predictor output, the terms a, b, c and d are constant, I is the intensity value and (x,y) represent the spatial indices of the pixels.
Arithmetic coding is an entropy coding used for lossless compression [43]. In this method, the infrequently occurring symbols/characters are encoded with greater number of bits than frequent occurring symbols/characters. An important feature of Arithmetic coding is that it encodes the full information into a single long number and represents current information as a range. Huffman coding [44] is basically a prefix coding method which assigns variable length codes to input characters/symbols. In this scheme, the least frequently occurring character is assigned with the smallest of the codes within a code table.
3. Proposed Algorithms
This section describes the recently proposed ETEC method and then proposes the PTEC method.
3.1. ETEC
The study of ETEC is extended in this paper with a detailed analysis of the ETEC algorithm. It has already been mentioned in Section I that each pixel block of a pixelated image carries a single intensity value or a single piece of data. The pixel blocks have abrupt transition and thus have many directional edges. The ETEC method can be described by three steps. In the first step, the special feature of pixelated images is used to calculate a residual error € by using the following intensity gradient
where is the derivative with respect to the x direction, is the derivative with respect to the y direction, I is the intensity value and (x,y) represent the spatial indices of the pixels. The maximum change of gradient between two co-ordinates represents the presence of edge either in the vertical or the horizontal direction.
The edge pixels are responsible for the increase in the level of the residual error €. It can be noted that for the presence of vertical edges, the value of € can be reduced to obtain the vertical intensity gradient. Similarly, for the presence of horizontal edges, the value of € can be reduced to obtain the horizontal intensity gradient. In order to detect a strong edge, a threshold Th is applied to the residual error in between the previous neighbors. If the previous residual error is greater than the threshold Th, then the present pixel I(x,y) is considered to be on the edge. So, the direction of gradient is changed. This can be mathematically described as:
As long as the previous residual error is less than the threshold, i.e., , the scanning direction remains the same. After the whole scanning, the term € contains lower entropy compared to the original image.
In the second step of ETEC method, two matrices A and B are generated to encode €. The dimensions of the matrix A is X × Y. The possible values of matrix A are 0 or 1 or 2 depending on the value of €. The matrix A is assigned a value of 0 where has a value of 0. Moreover, the matrix A is assigned values of 1 and 2 where has a value greater than and less than 0, respectively. On the other hand, the matrix B is assigned with the absolute value of , except for . After assigning the values for the two matrices, run-length coding [45] is applied to A. This coding is applied to the values whose corresponding run is greater than other values. This method manipulates bits of data to reduce the size and optimize input of the other algorithm. Figure 2 shows the block diagram of step 2 of ETEC method.
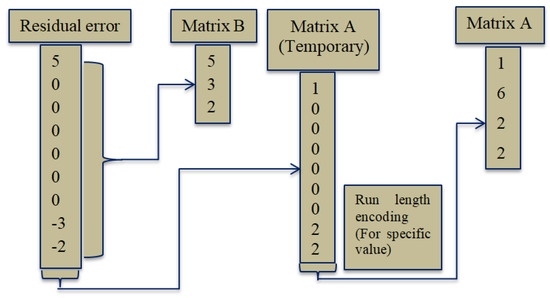
Figure 2.
Modified J-bit encoding process.
In the third step of ETEC, Huffman or Arithmetic coding is applied to matrices A and B. Like other image compression methods, in ETEC, the general process of image decompression is just the opposite of compression. Figure 3 shows the flowchart of proposed ETEC algorithm.
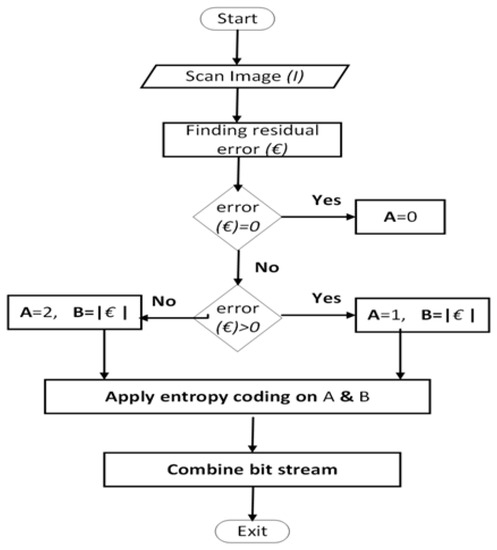
Figure 3.
Flowchart of the “edge-based transformation and entropy coding” (ETEC) algorithm.
3.2. PTEC
The main purpose of the proposed PTEC algorithm is to optimize the compression ratio and computational time for pixelated images as well as for other continuous tone images. In the case of a gray scale image, the signal variation is generally much smaller than that of a color image, but the intensity variation is still large near the edges of a gray scale image. For more accurate prediction of these signals and for accurate modeling of the prediction error, the hierarchical prediction scheme is used in PTEC. This method is described for the case where any image is divided into four subimages. At first, the gray scale image is decomposed into two subimages, i.e., a set of even numbered rows and a set of odd numbered rows, respectively. Figure 4 and Figure 5 show the hierarchical decomposition of the input image . The input image is separated into two subimages: an even subimage and an odd subimage . Here the even subimage is formed by gathering all even rows of the input image, and the odd subimage is formed of the collection of all odd rows of the input image. Each subimage is further divided into two subimages based on the even columns and the odd columns. Then is encoded and is used to predict the pixels in . In addition, is also used to estimate the statistics of prediction errors of . After encoding and , these are used to predict the pixels in . Furthermore, three subimages , , are used to predict a given subimage . With the increase in the number of subimages used to predict a given subimage, the probability of the prediction error may be decreased. To predict the pixels of the last subimage , maximum of eight (8) adjacent neighbors are used. This is evident from Figure 5. It can be noted that if the original image is divided into eight or more subimages instead of only four, the complexity and computation time will increase.
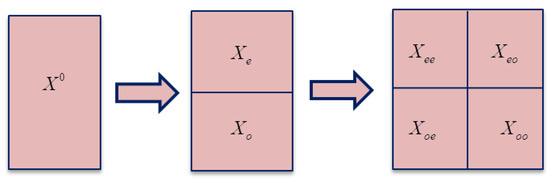
Figure 4.
Illustration of hierarchical decompression.
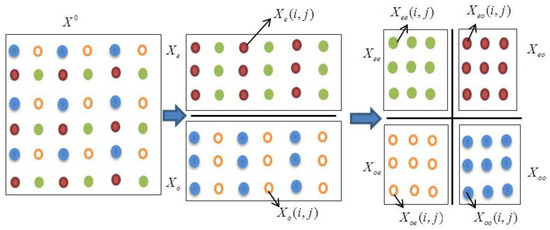
Figure 5.
Input image and its decomposition image.
Suppose the image is scanned in a raster-scanning order; then the predictor is always based on its past casual neighbors (“context”). Figure 6 shows the order of the casual neighbors. The current pixels of the subimage are predicted based on the casual neighbors. A reasonable assumption made with this subimage source is the order Markovian property. This means in order to predict a pixel, N nearest casual neighbors are required. Then the prediction of current pixel is predicted as follows:
where is the prediction coefficient, and is the neighbors of . For the prediction of pixels using , directional prediction is attached to avoid large prediction errors near the edge. For each pixel in , the horizontal predictor and vertical predictor are defined as shown in the following. Both and are determined by calculating the average of two different predictions. First, consider the case for . The prediction value, , is expressed as
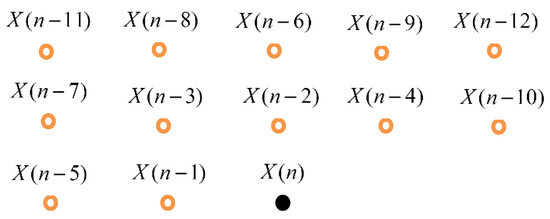
Figure 6.
Ordering of the casual neighbors.
The second prediction value, , is expressed as
Now, the term is determined using the average of and as follows:
Similarly, the term can be expressed as follows:
Among these, one is selected as a predictor for from Equations (10) and (11). With these possible two predictors, the most common approach to encoding is mode selection; where better predictor for each pixel is selected and the mode selection is dependent on the vertical and horizontal edges. If is smaller than , the horizontal edge is stronger than the vertical edge. Otherwise, the vertical edge is stronger than horizontal edge. For the prediction of using and , the vertical and horizontal edges as well as diagonal edges can be suitably predicted. For each pixel in , the horizontal predictor , vertical predictor , and diagonal predictor (left), (right) are defined in the following. Again, , , and are determined by taking the average of two different predictions. The term is determined as follows
Now, consider the case for . The first prediction value, , is expressed as
The second prediction value, , is expressed as
The term is determined using the average of and as follows:
Now, consider the case for . The first prediction value, , is expressed as
The second prediction value, , is expressed as
The term is determined using the average of and as follows:
Now, consider the case for . The first prediction value, , is expressed as
The second prediction value, , is expressed as
The term is determined using the average of and as follows:
Moreover, the selection of predictor is dependent on the presence of the directivity of the strong edges. By using Equations (12) and (21), it is possible to find an edge with a specified direction. Next, the residual error is encoded using modified J bit encoding. At the final stage, entropy coding is applied to the J bit encoded data.
4. Results and Discussion
This section evaluates the performance of ETEC and PTEC schemes for various types of images. The evaluation is done with the help of MATLAB tool and computer having specifications of Intel core i3 (Intel, Shanghai, China), 3110M 2.4GHz processor, RAM 4GB (Kingston, Shanghai, China), 1 GB VGA graphics card (Intel, Shanghai, China) and Windows 7 (32 bits) operating system (Microsoft, Shanghai, China). The intensity levels of the images are from 0 to 255 and the threshold term Th is assumed to have a value of 20. It can be noted that this value of Th has been selected as a near optimal value. Since a high value of Th may not recognize some edges in the images, whereas low values of Th may unnecessary consider any small transition as an edge
Figure 7 shows 50 different types of pixelated images used for evaluating the compression algorithms. Some of these images are created using MATLAB tool, and the remaining ones are available in [46,47,48,49]. Both Figure 7a,b have 25 images each. These images are made of different pixel blocks and each block is of different pixel sizes. Each pixel block has uniform intensity level. In some cases, a pixelated image may have very small pixel block or no block (each pixel block made of one pixel only). A number of metrics such as compression ratio, bits per pixel, saving percentage [28], and computation time are considered for comparing the algorithms. It can be noted that in this study the compression ratio is defined as the ratio of the size of the original image to the compressed image. Moreover, the saving percentage parameter is the difference between the original image and the compressed image as a percentage of the original image. Mathematically, the compression ratio is , and the saving percentage is where and are the size of the original image and the compressed image, respectively. The bit per pixel parameter is obtained by dividing the image size (in bytes) by the number of pixels in the compressed image. The computation time is the total amount of time required to perform the image compression using MATLAB tool with the given computer specified earlier in this section.


Figure 7.
Tested pixelated images [46,47,48,49].
First, consider the compression ratio (denoted as CR) and bits/pixel parameters. In Table 2, compression ratio and bits/pixel metrics are compared for the proposed ETEC and PTEC techniques with the existing JPEG-LS, SPIHT, and DPCM methods. The comparison is done for the 50 pixelated images illustrated in Figure 7. The bits per pixel parameter of the first 15 images are plotted in Figure 8 for the proposed and existing compression algorithms. Now consider the saving percentage and computation time. Table 3 represents the percentage saving and computation time for the case of those 50 images. The computation time in seconds is also plotted for the first 15 images in Figure 9. It can be seen from Table 2 that for the pixelated images, the average bits per pixel for ETEC (0.299) and PTEC (0.592) are lower (better) than the existing JPEG-LS (0.836), SPIHT (2.105) and DPCM (2.17). Table 2 shows that the average compression ratio of ETEC (29.39) and PTEC (10.28) are better than SPIHT (3.178) and JPEG-LS (9.264) and DPCM (3.09). Table 2 also shows that the compression ratio of PTEC is not always better than JPEG-LS for all the 50 pixelated images. In particular, PTEC has better compression than JPEG-LS for pixelated images having large pixel blocks. For small pixel blocks, the compression performance of PTEC is worse than JPEG-LS. This is because of the hierarchical prediction of PTEC. In case of small pixel block images, the prediction error for the first subimage is very high due to the high randomness of pixel intensity. For large pixel block images, this problem is significantly reduced. Table 3 indicates that the computational time of ETEC (62.58 s) is worse than SPIHT (13.9 s), but better than JPEG-LS (526 s) and DPCM (17.48 s). Furthermore, PTEC method has a computation time of 18.406 s which is much better than ETEC (62.58 s) and comparable to SPIHT (13.9 s). So, for pixelated images and for the case where both compression and computation time are important, PTEC may be more suitable than ETEC, SPIHT, JPEG-LS and DPCM.

Table 2.
Comparison of bits per pixel and compression ratio for pixelated images.
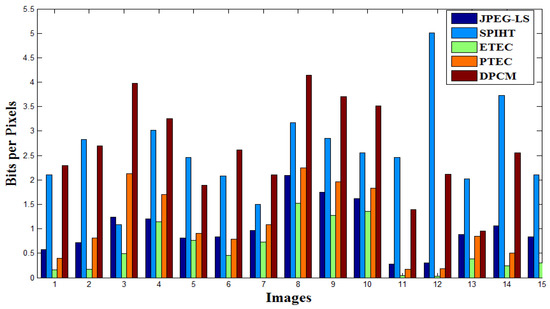
Figure 8.
Comparison of bits per pixels for pixelated images.

Table 3.
Comparison of percentage saving and computation time for pixelated images.
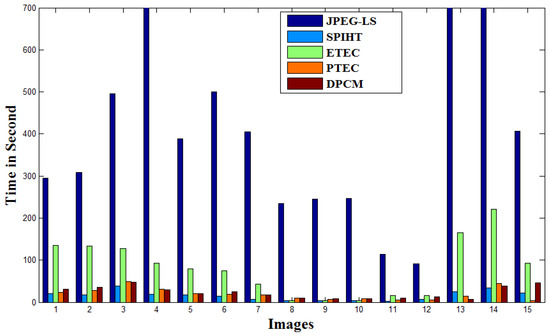
Figure 9.
Comparison of computation time for pixelated images.
In the following, different compression algorithms are shown for standard images particularly, non-pixelated images. Figure 10 illustrates eight standard test images available in [50,51,52,53,54]. These images have a resolution of 512 × 512 pixels. All these eight images are used to test compression ratio of different algorithms. For example, the Lena image is of 2,097,152 bits, but this image results in 1,063,464, 1,399,968, 1,170,220, 1,145,985 and 1,263,345 bits by using compression schemes of JPEG-LS, SPIHT, ETEC, PTEC and DPCM, respectively. Therefore, for the use of JPEG-LS on Lena image, the compression ratio is 1.972 (2,097,152/1,063,464) and bits/pixel is 4.0567 (1,063,464/512 × 512). Similarly, the compression ratio and bits/pixel values for different algorithms on different images can be easily obtained. These values are summarized in Table 4. Table 4 shows the comparison of compression ratio and bits per pixel representation of the ETEC and PTEC techniques with the existing JPEG-LS, SPIHT and DPCM for non-pixelated images. Figure 11 and Figure 12 are the corresponding visual representation of Table 4 for the case of bits per pixel and compression ratio, respectively. When the average compression ratio is considered, PTEC (2.06) is better than SPIHT (1.76), ETEC (1.93) and DPCM (1.72), but worse than JPEG-LS (2.16). Similarly, PTEC is better than SPIHT, ETEC and DPCM but worse than JPEG-LS in terms of average bits/pixel metric. Table 5 represents the percentage of saving area and computation time for the compression algorithms. It can be seen from Table 5 that the PTEC is better than SPIHT, ETEC and DPCM but worse than JPEG-LS in terms of percentage saving metric. Table 5 also shows that for the non-pixelated images, the average computation time of PTEC (74.50 s) is comparable to SPIHT (43.45 s) and DPCM (43.48 s), but better than ETEC (347.44 s) and JPEG-LS (2279.36 s). Note that PTEC has much better computation time than ETEC. This is because the use of hierarchical approach in PTEC. In the hierarchical approach, the computational data matrix is reduced to ¼ of the original data matrix. To handle a smaller matrix requires less time than handling a large one.
Figure 10.
Standard test images: (a) lena [51] (b) peppers [51] (c) ankle [52] (d) brain [53] (e) Mri_top [54](f) boat [51] (g) barbara [50] (h) house [51].

Table 4.
Comparison of bits per pixel and compression ratio for non-pixelated images.
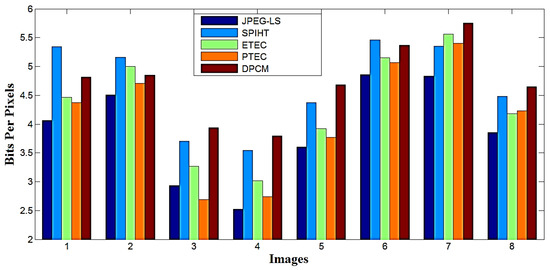
Figure 11.
Comparison of bits per pixels for non-pixelated images.
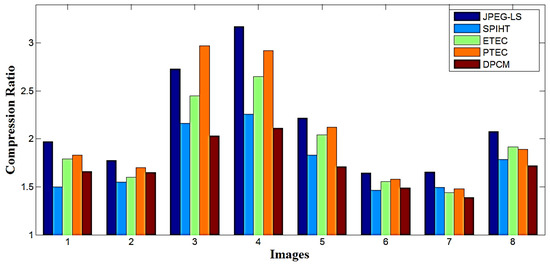
Figure 12.
Comparison of compression ratio for non-pixelated images.

Table 5.
Comparison of percentage saving and computation time for non-pixelated images.
So, for non-pixelated images and for the case where both compression and computation time are important, PTEC, SPIHT and DPCM may be more suitable than ETEC and JPEG-LS.
5. Conclusions
This work describes two algorithms for compression of images, particularly pixelated images. One algorithm is termed as ETEC, which has recently been conceptualized by the authors of this paper. The other one is a prediction-based new algorithm termed as PTEC. The ETEC and PTEC techniques are compared with the existing JPEG-LS, SPIHT, and DPCM methods in terms of compression ratio and computation time. For the case of pixelated images, the compression ratio for PTEC is around 10.28, which is worse than ETEC (29.39) but better than JPEG-LS (9.264), SPIHT (3.178), and DPCM (3.09). In particular, for images having large pixel-blocks, the PTEC method provides a much greater compression ratio than JPEG-LS. In terms of average computational time, the PTEC (18.406 s) is comparable with SPIHT (13.90 s) and DPCM (17.42 s) for pixelated images, and better than JPEG-LS (526 s) and ETEC (62.58 s). The compression ratio of PTEC (2.06) for non-pixelated images is comparable with JPEG-LS (2.16), but better than SPIHT (1.76), ETEC (1.93), and DPCM (1.72). Therefore, for the cases where compression ratios, as well as computational time, are required and for the case of pixelated images, PTEC is a better choice than ETEC, JPEG-LS, SPIHT, and DPCM. Moreover, for the case of non-pixelated images, PTEC, along with DPCM and SPIHT, are better choices than ETEC and JPEG-LS when both compression ratio and computational time are important. Therefore, PTEC is an attractive candidate for lossless compression of standard images including pixelated and non-pixelated images. The proposed PTEC method may be modified in future by applying an error correction algorithm to the prediction error caused by hierarchical prediction. The resultant values will be encoded by JBE and entropy coder as usual.
Author Contributions
M.A.K. performed the study under the guidance of M.R.H.M. Both M.A.K. and M.R.H.M. wrote the paper.
Funding
This research received no external funding.
Acknowledgments
This work is a part of Master’s thesis of the author M.A.K. under the supervision of the author M.R.H.M. submitted to the Institute of Information and Communication Technology (IICT) of Bangladesh University of Engineering and Technology (BUET). Therefore, the authors would like to thank IICT, BUET for providing research facilities.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Koc, B.; Arnavut, Z.; Kocak, H. Lossless compression of dithered images. IEEE Photonics J. 2013, 5, 6800508. [Google Scholar] [CrossRef]
- Jain, A.K. Image data compression: A review. Proc. IEEE 1981, 69, 349–389. [Google Scholar] [CrossRef]
- Kim, S.; Cho, N.I. Hierarchical prediction and context adaptive coding for lossless color image compression. IEEE Trans. Image Process. 2014, 23, 445–449. [Google Scholar] [CrossRef] [PubMed]
- Kabir, M.A.; Khan, M.A.M.; Islam, M.T.; Hossain, M.L.; Mitul, A.F. Image compression using lifting based wavelet transform coupled with SPIHT algorithm. In Proceedings of the 2nd International Conference on Informatics, Electronics & Vision, Dhaka, Bangladesh, 17–18 May 2013. [Google Scholar]
- Alzahir, S.; Borici, A. An innovative lossless compression method for discrete-color images. IEEE Trans. Image Process. 2015, 24, 44–56. [Google Scholar] [CrossRef] [PubMed]
- Mondal, M.R.H.; Armstrong, J. Analysis of the effect of vignetting on MIMO optical wireless systems using spatial OFDM. J. Lightwave Technol. 2014, 32, 922–929. [Google Scholar] [CrossRef]
- Mondal, M.R.H.; Panta, K. Performance analysis of spatial OFDM for pixelated optical wireless systems. Trans. Emerg. Telecommun. Technol. 2017, 28, e2948. [Google Scholar] [CrossRef]
- Perli, S.D.; Ahmed, N.; Katabi, D. PixNet: Interference-free wireless links using LCD-camera pairs. In Proceedings of the 16th Annual International Conference on Mobile Computing and Networking (MOBICOM), Chicago, IL, USA, 20–24 September 2010. [Google Scholar]
- Shantagiri, P.V.; Saravanan, K.N. Pixel size reduction loss-less image compression algorithm. Int. J. Comput. Sci. Inf. Technol. 2013, 5, 87. [Google Scholar] [CrossRef]
- Ambadekar, S.; Gandhi, K.; Nagaria, J.; Shah, R. Advanced data compression using J-bit Algorithm. Int. J. Sci. Res. 2015, 4, 1366–1368. [Google Scholar]
- Suarjaya, A.D. A new algorithm for data compression optimization. Int. J. Adv. Comput. Sci. Appl. 2012, 3, 14–17. [Google Scholar]
- Al-Azawi, S.; Boussakta, S.; Yakovlev, A. Image compression algorithms using intensity based adaptive quantization coding. Am. J. Eng. Appl. Sci. 2011, 4, 504–512. [Google Scholar]
- Mandyam, G.; Ahmed, N.; Magotra, N. Lossless Image Compression Using the Discrete Cosine Transform. J. Vis. Commun. Image Represent. 1997, 8, 21–26. [Google Scholar] [CrossRef]
- Munteanu, A.; Cornelis, J.; Cristea, P. Wavelet-Based Lossless Compression of Coronary Angiographic Images. IEEE Trans. Med. Imaging 1999, 18, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Taujuddin, N.S.A.M.; Ibrahim, R.; Sari, S. Progressive pixel to pixel evaluation to obtain hard and smooth region for image compression. In Proceedings of the 6th International Conference on Intelligent Systems, Modeling and Simulation, Kuala Lumpur, Malaysia, 9–12 February 2015. [Google Scholar]
- Oh, H.; Bilgin, A.; Marcellin, M.W. Visually Lossless Encoding for JPEG2000. IEEE Trans. Image Process. 2013, 22, 189–201. [Google Scholar] [PubMed]
- Yea, S.; Pearlman, W.A. A Wavelet-Based Two-Stage Near-Lossless Coder. IEEE Trans. Image Process. 2006, 15, 3488–3500. [Google Scholar] [CrossRef] [PubMed]
- Usevitch, B.E. A Tutorial on Modern Lossy Wavelet Image Compression: Foundations of JPEG 2000. IEEE Signal Process. Mag. 2001, 18, 22–35. [Google Scholar] [CrossRef]
- Weinberger, M.J.; Seroussi, G.; Sapiro, G. The LOCO-I Lossless Image Compression Algorithm: Principles and Standardization into JPEG-LS. IEEE Trans. Image Process. 2000, 9, 1309–1324. [Google Scholar] [CrossRef] [PubMed]
- Santos, L.; Lopez, S.; Callico, G.M.; Lopez, J.F.; Sarmiento, R. Performance Evaluation of the H.264/AVC Video Coding Standard for Lossy Hyperspectral Image Compression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 451–461. [Google Scholar] [CrossRef]
- Al-Khafaji, G.; Rajab, M.A. Lossless and Lossy Polynomial Image Compression. OSR J. Comput. Eng. 2016, 18, 56–62. [Google Scholar] [CrossRef]
- Wu, X. Lossless Compression of Continuous-Tone Images via Context Selection, Quantization, and Modeling. IEEE Trans. Image Process. 1997, 6, 656–664. [Google Scholar] [PubMed]
- Said, A.; Pearlman, W.A. An Image Multiresolution Representation for Lossless and Lossy Compression. IEEE Trans. Image Process. 1996, 5, 1303–1310. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Orchard, M.T. Edge-Directed Prediction for Lossless Compression of Natural Images. IEEE Trans. Image Process. 2001, 10, 813–817. [Google Scholar]
- Abo-Zahhad, M.; Gharieb, R.R.; Ahmed, S.M.; Abd-Ellah, M.K. Huffman Image Compression Incorporating DPCM and DWT. J. Signal Inf. Process. 2015, 6, 123–135. [Google Scholar] [CrossRef][Green Version]
- Lohitha, P.; Ramashri, T. Color Image Compression Using Hierarchical Prediction of Pixels. Int. J. Adv. Comput. Electron. Technol. 2015, 2, 99–102. [Google Scholar]
- Wu, H.; Sun, X.; Yang, J.; Zeng, W.; Wu, F. Lossless Compression of JPEG Coded Photo Collections. IEEE Trans. Image Process. 2016, 25, 2684–2696. [Google Scholar] [CrossRef] [PubMed]
- Kaur, M.; Garg, E.U. Lossless Text Data Compression Algorithm Using Modified Huffman Algorithm. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2015, 5, 1273–1276. [Google Scholar]
- Rao, D.; Kamath, G.; Arpitha, K.J. Difference based Non-linear Fractal Image Compression. Int. J. Comput. Appl. 2011, 30, 41–44. [Google Scholar]
- Oshri, E.; Shelly, N.; Mitchell, H.B. Interpolative three-level block truncation coding algorithm. Electron. Lett. 1993, 29, 1267–1268. [Google Scholar] [CrossRef]
- Tan, Y.H.; Yeo, C.; Li, Z. Residual DPCM for lossless coding in HEVC. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 2021–2025. [Google Scholar]
- Sanchez, V.; Aulí-Llinàs, F.; Serra-Sagristà, J. DPCM-Based Edge Prediction for Lossless Screen Content Coding in HEVC. IEEE J. Emerg. Sel. Top. Circuits Syst. 2016, 6, 497–507. [Google Scholar] [CrossRef]
- Lainema, J.; Bossen, F.; Han, W.J.; Min, J.; Ugur, K. Intra Coding of the HEVC Standard. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1792–1801. [Google Scholar] [CrossRef]
- Sanchez, V.; Aulí-Llinàs, F.; Serra-Sagristà, J. Piecewise Mapping in HEVC Lossless Intra-Prediction Coding. IEEE Trans. Image Process. 2016, 25, 4004–4017. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Cabronero, M.; Marcellin, M.W.; Blanes, I.; Serra-Sagristà, J. Lossless Compression of Color Filter Array Mosaic Images with Visualization via JPEG 2000. IEEE Trans. Multimedia 2018, 20, 257–270. [Google Scholar] [CrossRef]
- Taubman, D.S.; Marcellin, M.W. JPEG2000: Standard for interactive imaging. Proc. IEEE 2002, 90, 1336–1357. [Google Scholar] [CrossRef]
- Egilmez, H.E.; Said, A.; Chao, Y.H.; Ortega, A. Graph-based transforms for inter predicted video coding. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 3992–3996. [Google Scholar]
- Hranilovic, S.; Kschischang, F.R. A pixelated MIMO wireless optical communication system. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 859–874. [Google Scholar] [CrossRef]
- Kabir, M.A.; Mondal, M.R.H. Edge-based Transformation and Entropy Coding for Lossless Image Compression. In Proceedings of the International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 16–18 February 2017; pp. 717–722. [Google Scholar]
- Huffman, D. A method for the construction of minimum redundancy codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Miaou, S.-G.; Chen, S.-T.; Chao, S.-N. Wavelet-based Lossy-to-lossless Medical Image Compression using Dynamic VQ and SPIHT Coding. Biomed. Eng. Appl. Basis Commun. 2003, 15, 235–242. [Google Scholar] [CrossRef]
- Tomar, R.R.S.; Jain, K. Lossless Image Compression Using Differential Pulse Code Modulation and Its Application. Int. J. Signal Process. Image Process. Pattern Recognit. 2016, 9, 197–202. [Google Scholar] [CrossRef]
- Chen, Y.-Y.; Tai, S.-C. Embedded Medical Image Compression using DCT based Subband Decomposition and Modified SPIHT Data Organization. In Proceedings of the IEEE Symposium on Bioinformatics and Bioengineering, Taichung, Taiwan, 21–21 May 2004; pp. 167–175. [Google Scholar]
- Sharma, M. Compression using Huffman Coding. Int. J. Comput. Sci. Netw. Secur. 2010, 10, 133–141. [Google Scholar]
- Salomon, D. A Concise Introduction to Data Compression; Springer: London, UK, 2008. [Google Scholar]
- Wallpaperswide. Available online: http://wallpaperswide.com/pixelate-wallpapers.html (accessed on 23 April 2018).
- Freepik. Available online: https://www.freepik.com/free-photo/pixelated-image_946034.htm (accessed on 23 April 2018).
- Famed Pixelated Paintings. Available online: https://www.trendhunter.com/trends/digitzed-classic-paintings (accessed on 23 April 2018).
- Pixabay. Available online: https://pixabay.com/en/pattern-super-mario-pixel-art-block-1929506/ (accessed on 23 April 2018).
- Image Processing Place. Available online: http://www.imageprocessingplace.com/root_files_V3/image_databases.htm (accessed on 23 April 2018).
- Computational Imaging and Visual Image Processing. Available online: https://www.io.csic.es/PagsPers/JPortilla/image-processing/bls-gsm/63-test-images (accessed on 23 April 2018).
- Wikimedia Commons: Sprgelenkli. Available online: https://commons.wikimedia.org/wiki/File:Sprgelenkli131107.jpg#filelinks (accessed on 23 April 2018).
- Wikimedia Commons: Putamen. Available online: https://commons.wikimedia.org/wiki/File:Putamen.jpg (accessed on 23 April 2018).
- Wikimedia Commons: MRI Glioma 28 Yr Old Male. Available online: https://commons.wikimedia.org/wiki/File:MRI_glioma_28_yr_old_male.JPG (accessed on 23 April 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).