Abstract
This paper provides a comprehensive analysis of the performance of hyperspectral imaging for detecting adulteration in red-meat products. A dataset of line-scanning images of lamb, beef, or pork muscles was collected taking into account the state of the meat (fresh, frozen, thawed, and packing and unpacking the sample with a transparent bag). For simulating the adulteration problem, meat muscles were defined as either a class of lamb or a class of beef or pork. We investigated handcrafted spectral and spatial features by using the support vector machines (SVM) model and self-extraction spectral and spatial features by using a deep convolution neural networks (CNN) model. Results showed that the CNN model achieves the best performance with a 94.4% overall classification accuracy independent of the state of the products. The CNN model provides a high and balanced F-score for all classes at all stages. The resulting CNN model is considered as being simple and fairly invariant to the condition of the meat. This paper shows that hyperspectral imaging systems can be used as powerful tools for rapid, reliable, and non-destructive detection of adulteration in red-meat products. Also, this study confirms that deep-learning approaches such as CNN networks provide robust features for classifying the hyperspectral data of meat products; this opens the door for more research in the area of practical applications (i.e., in meat processing).
1. Introduction
Recently, hyperspectral imaging (HSI) systems have gained attention in a plethora of research areas such as medical applications, remote sensing imagery [1,2,3], food and meat processing [4,5,6,7,8,9], etc. The key advantage of HSI systems is that they provide a combination of spectroscopy technologies [10] (i.e., availability of spectral information) and conventional imaging systems (i.e., availability of spatial information). Thus, this combination covers information about the objects shown in an image across the electromagnetic spectrum; this means it provides a unique signature for each visualized material. Figure 1c shows examples of the spectral signatures of four types of materials: lamb, beef, pork, and fat.
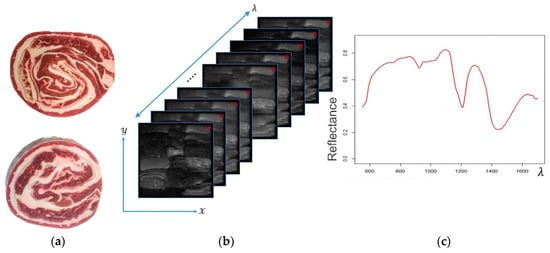
Figure 1.
(a) Example of rolled meat products; (b) A representation of an HSI hyper-cube, where red points represent a pixel in the hyper-cube; (c) Example of a spectral signature extracted from the HSI hyper-cube (a pixel across the spectral dimension ).
HSI systems facilitate the visualization of materials inside the image and the distribution of their chemical components. Thus, an HSI image is structured as a 3D cube (called a hyper-cube) with the following coordinates: the spectral coordinates (wavelength) provide the intensity of the reflected light on the material surface over a range of contiguous wavelengths; and the spatial pixel locations represent the shape of the objects in the image. Thus, tells us the type of material, and conveys where these materials are located inside the field of view of a hyperspectral camera. Both of these format the hyper-cube in space. Figure 1b shows an example of a hyper-cube (HSI image of red-meat species).
Meat processing is generally evaluated in terms of quality and safety attributes. HSI systems are used to assess both attributes and lead to good results in terms of accuracy and applicability, compared with traditional methods (i.e., lab-based and spectroscopy methods) [11]. A meat-quality evaluation approach provides a scaling factor indicating the quality of meat at the time of taking the HSI image (i.e., quantitative indicator). A safety-evaluation approach aims at detecting unusual artifacts that may be added or accrued in the meat sample. One of the critical safety-based evaluation methods of meat products is the detection of adulteration of meat products, for example, the addition of another type of meat which may have a lower price compared to the original material. From an industry point-of-view, this type of adulteration requires greater attention, e.g., detecting any adulteration in pre-packed rolled meat products (Figure 1a shows an example of these products). HSI offers the possibility of detecting the unique characteristics of meat both spectrally or structurally (i.e., based on texture) but there are still no approaches that are able to extract these two types of characteristics within a single modeling framework. Thus, the aim of this study is to develop a novel approach that combines both spectral and textural information into a single model.
The rest of this paper is organized as follows. Section 2 reviews the state-of-the-art techniques in HSI classification and analysis. Section 3 describes the used dataset, HSI imaging system, and the developed models and methods. Section 4 provides the experiments setup and experimental results of the proposed frameworks for classifying red-meat species. Result analysis and discussions are given in Section 5. Section 6 concludes this article.
2. Literature Review
Traditionally, quality and safety attributes of food are evaluated either by spectroscopic tools [10,12] or traditional color images. The studies described in [13,14,15] show applications of color images for the assessment of food quality. Recently, HSI systems have been considered as robust tools for processing and evaluating food products, for example, classifying or predicting attributes related to meat quality and safety. In [4], a principal component analysis (PCA) model was used to select the wavelengths of an HSI system, that play the most important role in discriminating between three types of lamb muscles: semitendinosus (ST), longissimus dorsi (LD), and psoas major (PM). Then, the selected wavelengths were used as input for linear discrimination analysis (LDA) for classifying lamb muscles as one of the three predefined classes of muscles; in both the PCA and LDA models, the average spectra of the samples were used for constructing the models. In addition, the HSI system was compared with two other optical systems: traditional RGB images and Minolta measurements. The results showed that the HSI system outperforms the other optical systems with 100% overall accuracy.
In [5], LD muscles of lamb, beef, and pork were used to evaluate the robustness of an HSI system for discriminating between red-meat species. The extracted spectrum of each sample was pretreated with spectral second derivatives; this was used to independently obtain optimal wavelengths of additive or multiplicative noise. Then, partial least-square discriminant analysis (PLS-DA) was employed for the optimal wavelengths for conducting the classification. The resulting model showed good results in the case of sample-based evaluation; but it misclassified the pixels in the case of pixel-based evaluation. Thus, the authors utilized a majority-voting technique to obtain final classification maps. In [6], two algorithms, PLS-DA and soft independent modelling of class analogy (SIMCA), were tested for discriminating the lamb muscle from other red meat (i.e., beef or pork). The results show that the PLS model outperforms the SIMCA model, but the performance of the PLS model was unstable and it is dependent on the way samples were presented (i.e., vacuum packed or without packaging).
Also, the results in [7,8,9] showed that an HSI system is able to provide significant information for performing classification in a plurality of applications for meat, such as detection of adulteration of minced meat [7], detection of chicken adulteration in minced beef [8], and lamb muscle discrimination [9]. In all of these studies, the models produced misclassification of pixels in pixel-based prediction, although they performed well in the case of sample-based prediction. Reasons for the misclassified pixels include the construction of models by using the average spectrum over the whole sample and ignorance of the spatial variation in the pixel space. In fact, the source light strongly affects the pixels in the acquired HSI image (light scattering or illumination effects).
In the case of heterogeneous samples, classifying HSI data is a real challenge; that is, covering the variation of spectral and spatial information in the sample and pixel space, respectively. As an example, the detection of any adulteration is seen in the case of pre-packed rolled meat products (an example is shown in Figure 1a). In this case, it is more practical and reliable to perform a pixel-wise classification (i.e., local) than a sample-wise classification [16]. For dealing with spectral variations, several methods were established and used such as spectral derivatives [5], unit-vector normalization [16], standard normal variates (SNV) [8], and multiplicative scatter correction (MSC) [8]. In [16], SNV and unit-vector normalization were evaluated with regard to the problem of classifying red-meat; SNV performed better than unit-vector normalization in this classification.
The basic strategy for classifying hyperspectral data is to treat the contribution of each pixel (i.e., the spectrum signature) as a sample. This strategy is usually applied to HSI for remote sensing applications [1] due to the limitation in images. Thus, it provides a powerful model which takes the local variation in the image into account. In HSI for meat processing [4,5,6,7,8,9], the used strategy is averaging all pixels in the region of interest (ROI) as a spectral signature of the ROI. In this case, the resulting models consider only the spectral features to be used, while the spatial features were ignored. So, the results were useful but not fully satisfactory, especially in the case of heterogeneous samples. As a solution, converting the image data into an object-oriented structure (i.e., image segmentation) enhances the performance of any HSI classification model with the advantages of the joint features (i.e., spectral and spatial) [16].
In [2], a method for joint feature extraction was proposed by using superpixel segmentation. Simple linear iterative clustering (SLIC) was employed to produce superpixels of HSI images. Then, the mean of each super-pixel was calculated and used as input for an SVM model. Then, the resulting SVM decision values were post-processed by using a linear conditional random-field model to give a class label for each superpixel. In general, the use of superpixels in HSI classification tasks adds the following advantages: (1) stability of the extracted signatures by averaging the superpixel at each wavelength [2]; and (2) the possibility of exploring the neighbourhood relationship between highly correlated pixels [3].
In [3], three types of features were evaluated through a multi-kernel composition of an SVM-RBF: raw spectrum, the average of each superpixel, and the weighted average of neighbours for each superpixel. In both [2,3], the results show that superpixels enhance the fitted models. However, this consideration may badly affect the fitted model if the extracted superpixels are inaccurate. So, the application of ensemble-based classification methods is recommended [3].
Recently, deep learning-based approaches have successfully provided highly accurate models in many research areas. Convolutional neural networks (CNN) are commonly successful in the case of vision-based tasks: image classification [17,18], object detection [19], semantic segmentation [19], and face recognition [20]. Moreover, CNNs achieve good performance in the field of signal analysis and speech recognition [21,22]. For HSI applications, numerous deep learning models have been proposed as classification and self-feature extraction models for analyzing HSI data, such as CNN [23,24,25,26,27], stacked autoencoder (SAE) [28,29,30], or recurrent neural network (RNN) [31,32].
In [23], a CNN model was introduced for the first time for HSI remote sensing data. Five layers of deep learning architecture were proposed and structured as follows: spectrum signature (i.e., pixel vector) as an input layer, two 1D CNN layers with a max pooling operation, and one fully connected layer followed by an output layer. The model has parameters (to be optimized), such as the number and length of hidden layers, the size of filters of the convolution operations. However, the results show that the 1D CNN model is able to understand and extract a nonlinear relationship of the samples of each class and outperforms the traditional models for classifying HSI data such as SVM or multilayer perceptron (MLP) networks. For the achieved results, the model was only considered for the spectral features; the spatial features have been ignored.
Practically, standard 2D CNNs, such as in [17], are not applicable for HSI due to their nature (i.e., high-dimensionality problems) [24]. In [24], deeper and more complex CNN models were evaluated on HSI for remote sensing. Besides a 1D CNN model, a 2D CNN was proposed and extended to be applicable for HSI application. The PCA was applied to reduce the dimensionality of the input (i.e., the depth of the hyper-cube) for three channels (i.e., the highest three components); a window around each pixel was used as input to the model. Then, the input was passed through two convolution layers, a pooling layer, and a fully connected layer. Also, the 2D CNN model was extended into a 3D CNN model. In the case of the 3D CNN, 3D convolution filters were used to extract features across the whole dimensions of the input; which means that there is no need for the PCA to preprocess the input. The evaluation results show that the 3D CNN achieved optimal performance, but has more parameters (like the size of the 3D window around the target pixel) to be optimized; more samples are required to train the model, where the window size was the most effective parameter.
Models as proposed in [24] considered a large window (like 27 × 27) as input. In fact, the use of a large window affects the performance of CNN models, especially in the case of heterogeneous images; the window borders contribute badly to pixel-based classification [25]. In [25], a 3D-CNN model was proposed considering the input as a small window (like 5 × 5) size around the target pixel. Also, small kernels were used to perform the convolution operation. Extracted features are inspired by 3D texture measures in the spectral and spatial domain. Moreover, the features are invariant to the effects of local edges in the case of pixel-based classification [25]. The comparison between [24,25] shows that the architecture in [25] performed better with the following advantages: it is a light-weight model (there is no need for a huge number of samples), it is not affected by local edges, and it is suitable for pixel-wise classification.
In general, this research work investigates the robustness of line-scanning hyper-spectral imaging systems to discriminate between the types of red-meat muscles. The main objectives of this paper are as follows:
- Investigate the influence of practical conditions on the spectral response of red meat. Considered conditions are (1) packing meat into a transparent bag; (2) freezing meat for 3 days; and (3) thawing meat after being frozen.
- Develop a classification model to discriminate one type of meat muscle from the others (e.g., in the case of adulteration), for example, identify lamb meat that is different to beef or pork with the conditions mentioned above.
- Develop a methodology to extract joint features (i.e., spectral and textural features) for HSI images applied to this type of application.
- Investigate the applicability of deep learning approaches and their robustness on this type of application (i.e., meat-processing applications).
- Develop and evaluate a deep-learning model for self-feature extraction of HSI images of red-meat products (i.e., by handling the raw input instead of handcrafted feature extraction).
3. Materials and Methods
3.1. Hyperspectral Imaging Systems
HSI images were acquired in reflectance mode using a pushbroom hyperspectral imaging system as shown in Figure 2. The used HSI system consists of a line-scanning hyperspectral camera (Xenics XEVA 1.7-320: Xenics nv, Leuven, Belgium), an illumination unit of two halogen lambs (150 W), a controlled movable stage, and a computer running an image acquisition software (Hyperspec III software: Headwall Photonics, Inc., Fitchburg, MA, USA).
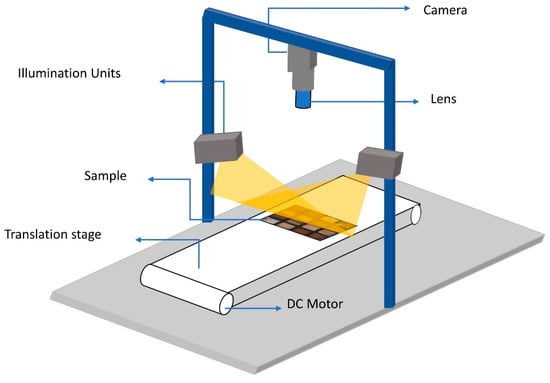
Figure 2.
Schematic demonstration of the main components of the used hyperspectral imaging system.
The camera detector has 320 × 235 (spatial × spectral) pixels with a spectral resolution of 5 nm. The speed of the movable stage was set to a constant speed of 11.1 and synchronized with the camera to obtain HSI images with spatial resolution of 0.44 0.44 . The used camera covers a spectral range of 548–1701 (this range covers the visible light and NIR reigns in the electromagnetic spectrum) with 235 spectral bands. By adjusting the lighting conditions and the integration time of the camera, the speed of scanning can be increased for faster data collection, if required.
Practically, the HSI system was set up and configured as in [5]. Thus, the reflectance is computed as follows:
where is the reflectance value, is the raw value in irradiance, and are the dark and white reference images. After this calibration process, the first and the last five bands were removed due to a low SNR ratio.
3.2. Dataset and Sample Preparation
Meat and fat samples were procured from three local butcher shops and two different local supermarkets. A total number of 75 samples, including lamb (18), beef (13), pork (13), and fat (31), were prepared (i.e., cutting and then drying with normal tissue). Then, the samples were labeled and kept at 2 °C for 16 h. The next day, the samples were taken from the fridge and put into well-designed containers (frames shaped as a matrix of meat and fat species; Figure 3a shows examples of these frames).

Figure 3.
(a) The calibration samples in frames: Ground-truth and false-color images for frames 1–4 (top to bottom), where FSUP is short for fresh red-meat unpacked, FSP for fresh packed, FRUP for frozen unpacked, FRP for frozen packed, and THUP for frozen-thawed unpacked. In the cells of ground truth, F is for fat, L for lamb, B for beef, and P for pork; (b) Evaluation-sample frame in case of FSUP.
Then, each frame was scanned with the HSI camera (meat and fat were in a fresh). Then, all frames were vacuum packed into a transparent bag, and re-scanned with the HSI system (in a fresh state with packing). After that, all frames were frozen (−4 °C for 3 days).
After 3 days, the same frames were re-scanned by using the hyperspectral camera (frozen state with packing). Then, the packing was removed and HSI images were collected for the frames (frozen state without packing). Finally, the frames were left at room temperature for 3 h for thawing; then, the frames were re-scanned in the HSI system.
As shown in Figure 3, the total number of prepared frames is 6 frames: 4 frames [including 57 samples of lamb (12), beef (9), pork (9), and fat (27)] were used for training purposes and one special frame for testing purposes (18 samples of lamb (6), beef (4), pork (4), and fat (4)). In the frames, the meat and fat samples preserved their original meat textural characteristics, similar to retail-ready products commonly found at supermarkets.
3.3. Spectral Data Analysis and Visualization
The adulteration in red-meat products is simulated by defining the following classes of labels: lamb meat is labelled as one class (called LAMB), another class for both beef and pork (called OTHER), and a class FAT for visualization purposes. By defining this structure, the model predicts the probability of lamb meat against the others. This situation is more practical and reliable from an industry point-of-view. Moreover, we evaluate the power of HSI images to discriminate one material from any other predefined material.
When dealing with HSI data, multivariate analysis methods are needed in high-dimensional space. This high dimensionality prevents the visualization and pattern investigation steps during the analysis of the data. However, PCA is considered as an appropriate model for HSI image data in terms of data distribution visualization and reducing the dimensions of the data (i.e., extracting the most important information) [5,9,15].
In this work, the dataset that is described in Section 3.2 was used for estimating a PCA model. The calibration set of images was manually segmented (according to the ground truth) into small regions (like 100 pixels); then, the mean spectrum of each segment was extracted. A PCA model was fitted for these spectra. In fact, we used the estimated PCA model for the following purposes: (1) for visualizing the patterns between the pre-defined classes (LAMB and OTHER); and (2) as a preprocessing step for extracting the spatial features. Figure 4a shows the mean spectrum of the extracted spectra for each class; it clearly shows that there are significant differences in the mean spectrum for each class. Figure 4b visualizes the class separation in the PCA space; the class distribution shows that the classes are separated into regions with minor over-lapping regions (this overlapping is due to the frozen status of the meat).
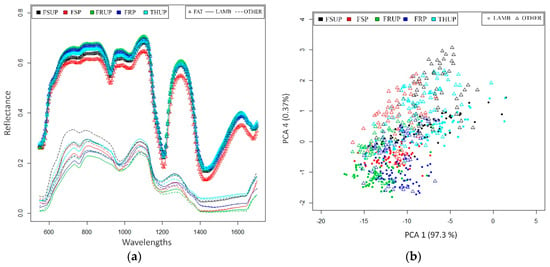
Figure 4.
PCA analysis. (a) Mean spectrum of each of the three classes for each of the five statuses; (b) Scatter plot for the LAMB and OTHER classes, showing 97.67% of the total variances of the original data.
3.4. Model-Based Classification Framework
In general, the selection of each pixel in an image as a sample is impractical in terms of computation resources and time due to the large number of those pixels. Also, hand-segmentation for sampling each class is inefficient because the local features of the segments are not accurate in this case. For these reasons, we proposed superpixel segmentation as a sampling method to collect representative samples for each class from the dataset. In fact, the pixels in each superpixel share the same local spectral and spatial features that reflect on the performance and stability of any fitting model.
In this study, the SLIC superpixel algorithm [33] is adapted to generate the superpixels of HSI images. SLIC was originally proposed for three-channel images (RGB or LAB space). However, in this study, we used SLIC in the PCA space to adapt the algorithms with HSI images; the Euclidian distance in the PCA space is used as the similarity measure. The estimated PCA, described in Section 3.3, is used to extract five-score images; these score images are obtained by projecting the loading PCA model on the HSI image, where these scores have the highest information from the original HSI image. Then, the scores of images were used as input to SLIC algorithm; Figure 5b shows an example of these images, Figure 5c shows the resultant superpixels of an HSI image by using the proposed method.
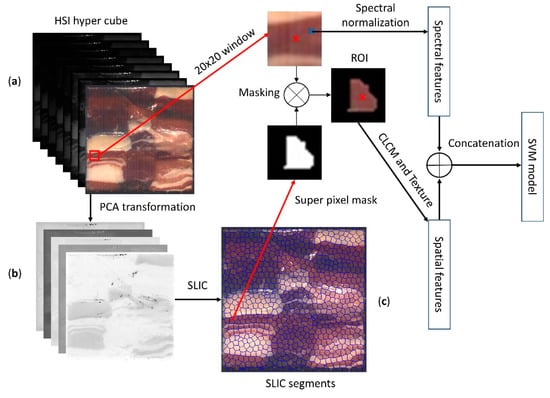
Figure 5.
A representation of ROI extraction from an HSI image for extracting the texture features. (a) A heterogeneous hyperspectral image of meat muscles; (b) the first five score images of the HSI image; (c) Superpixel segments of the HSI image.
3.4.1. Extraction of Spectral Features
The resultant SLIC-segmented labels are utilized to extract the spectra of each class. In fact, due to the computation costs and class balancing, representative pixels from each superpixel need to be extracted. So, we use the Kennard-Stone (KS) algorithm [34] to sample each superpixel into a subset of representative pixels (raw spectral features) as final samples for modelling. After extracting the raw features, we proposed two types of spectral normalizations: L2 norm and standard normal variation (SNV-norm). Let be a pixel in an HSI image at location . The L2 norm and SNV norm are computed by using Equations (2) and (3), respectively.
where , and are the mean and standard deviation of the target pixel, respectively.
Practically, we found that these normalization techniques are very sensitive to spike points, usually accrued in HSI systems due to the effects of lighting. Thus, we used Savitzky-Golay (SG) algorithm [35] as a preprocessing step for de-spiking the raw spectral and spectral domain smoothing by estimating the shape of a group of contiguous bands.
3.4.2. Extraction of Spatial Features
In fact, hyperspectral cameras are established for a wide range of applications, such as fruit sorting, medical applications, and meat processing. They provide an enormous amount of spectral information, represented as a group of grey-level images for each HSI image. So, the extraction of the spatial features of an object inside an HSI image is a real challenge; especially the decision of which grey-level image (or images) is more useful in order to extract the spatial features. For dealing with this challenge, we adapt recursive feature elimination (RFE) [36,37] and random forest (RF) [37,38] algorithms to select the most significant wavelengths for discriminating between the red-meat muscles. Recursively, RFE chooses a set of features and eliminates the remainders. Then, the RF algorithm is used to rank the selected features according to the performance of the fitted RF classifier. Finally, the recursive processes provide a rank value for each feature; this value represents the importance of a feature in fulfilling a particular classification task.
From our PCA analysis, we observed that the spectral response of each class is strongly influenced by the status of the meat (i.e., the overlapping regions between the classes as shown in (Figure 4b). For this reason, we propose a meat status-based methodology to select a set of bands to be used as a reference image for the spatial features process. Five models were estimated (one for each status) by using RFE with RF. From the results of the RFE procedure, we chose six features (i.e., wavelengths), which have the highest rank at each status. These wavelengths (all in nm) are listed as 636, 646, 656, 932, 1134, and 1154.
Texture-based models are generally used in computer vision as the spatial features. The grey-level co-occurrence matrix (GLCM) is one of the standard ways for extracting the textural properties of a set of neighbouring pixels, defined by a window around the target pixel. GLCM is computed by calculating how often a pair of pixels with the same intensity values occur in an image. In addition, the moving distance and angle between the target pixel and the others need to be defined [39]. A set of statistical features were proposed by Haralick [40] so as to define the spatial relationships between the neighbouring pixels (textural properties). These features are computed from the CLCM matrix. Thus, we propose the following textural features for defining the texture of red-meat muscles: homogeneity, contrast, inverse difference moment (IDM), entropy, energy, and correlation.
In the case of HSI images, the texture features are not directly extractable due to the nature of the HSI image (hyper-cube). However, the optimized gray-level bands (i.e., the resulting six wavelengths) were used to compute the GLCM matrix and then extract the mentioned textural features. As our application is a heterogeneous sample, we utilized the superpixel method to extract the masked textural features. The developed feature extraction (masked features) method includes the following steps as shown in Figure 5:
- Project the PCA model based on an HIS image to produce the score images.
- Compute the superpixel by using the first five score images as an input for the SLIC algorithm.
- Normalize the selected optimal bands into a range of 1~255.
- Compute the centroid of each superpixel (we defined it as the first moment), then take a 20 × 20 window around the center.
- For each pixel, mask the selected window by using its superpixel mask to obtain the ROI.
- Compute the CLCM matrix with a distance of 1 and direction of 0.
- Eliminate the first raw and column of the resulting CLCM matrix.
- Compute the proposed textural features from the final CLCM matrix.
In fact, the masked textural features allow the model to be robust with regard to the heterogeneous sample (it avoids the overlapping between muscles) and provide more accurate texture representation (considering large window size while computing the texture).
In this section, spectral-based features of meat and the joint features of meat texture, as well as its spectral features are proposed to be extracted. To evaluate the proposed features, we used support vector machines with radial biases functions (SVM-RBF) as a classifier; the final classification maps were obtained by SVM-RBF.
3.5. Deep Learning-Based Classification Framework
In this section, we introduce a novel deep learning approach for detecting the adulteration in red-meat products. Based on our knowledge, this is the first time that deep learning methods are applied to HSI imaging for meat processing, the novelty of this proposed model will be compared with several models with handcrafted features. The proposed deep learning model includes a combination of two types of convolution operation: 1D and 3D convolution. In fact, this combination aims at crossing both the spectral and spatial domains for extracting self-features of an HSI image. Hereinafter, we explain the basics of 1D CNN, 3D CNN, and our proposed combination of them.
CNN models are mostly utilized as a 2D CNN in computer vision like image classification and recognition. However, CNNs are successfully used as 1D CNN in signal processing such as speech recognition and noise filtering. In these cases, the input of 1D CNN is illustrated as a vector (or array). Thus, the dimensionality of this spectral signature of HSI data is applied to CNN classification models [23]. Also, 3D CNN models are proposed for handling the temporal features of video sequences in time series, for example, in action recognition tasks. The HSI hyper-cube can be illustrated as a sequence of spectral 2D bands. So, the 3D coevolution operations are able to extract joint features across the spatial and spectral domains of an HSI image data [24,25,26].
3.5.1. Architecture of the Proposed CNN Model
Multi-input deep learning models provide robustness in terms of considering the different shape and nature of the samples, while different types of features are shared in one deep model. This inspired us to propose a CNN model which can handle two inputs of data (input layers): spectral features (mean spectrum of the neighbours of the target pixel) and spatial features (the region around the target pixel). Each of these input layers is a sub-CNN model, which extracts local features from its input. Then, the extracted local features from each sub-model are combined and connected with a fully connected layer as a global set of features crossing the two input domains (i.e., spectral and spatial domains). The proposed CNN model consists of a hierarchical structure of layers: two input layers, convolution layers, down sampling layer (pooling layer), concatenation layer, fully connected layer, and one output layer (classification layer). Figure 6 shows the structure and the combination of these layers.
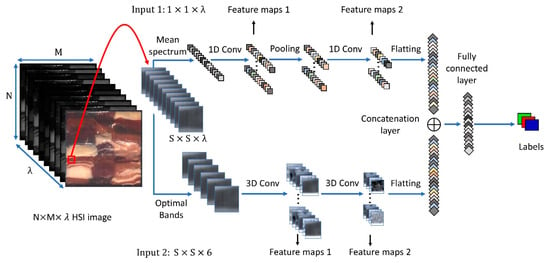
Figure 6.
An illustration of the proposed CNN model. Input 1 represents the mean spectrum as the vector. Input 2 shows the spatial window at the selected optimal bands as a 3D cube. The labels represent the predefined classes (i.e., Lamb, Other, Fat).
The extracted mean spectrum, represented in Figure 6 as input 1, has a size of and feeds forward to the first convolution operation with kernel size and feature maps with a shape of where . The max pooling layer has a kernel size of and has nodes, where . The next convolution layer has kernel size and produces features maps with nodes, where . Then, these nodes are flattened into one vector as the first local feature with dimensions of .
The second input is defined as a 3D fixed window around the target pixel, then masked with only the selected optimal wavelengths (in Section 3.4.2). This input layer is shaped as, where 6 is the number of optimal bands, which will be passed into two convolution layers. In this case, the convolution operations are carried out by using a 3D kernel. So, the first convolution layer has kernels of size. Then, the resultant maps are passed to the next convolution layer in the same way and generate another set of kernels and maps. In these 3D coevolution operations, we pad the input with the same value, so the output of these convolution layers will be the same as the input layer. Similar to the first input, the final features are flattened as a vector having dimensions of .
The local features from these two inputs are then connected with a fully connected layer. This layer extracts a high level of features from spectral and spatial inputs (global features), then, the classification layer makes the final prediction based on these global features.
3.5.2. Training Strategy of the Proposed CNN Model
Training the model aims at adjusting the model weights based on an error loss between the actual output and the model prediction (model output). Thus, the training procedure consists of two main processes: forward propagation and backpropagation. The forward process takes each input layer and passes it through the convolution layers. The input of i-th or output of -th convolution layer is computed as follow:
where , and and are the weight matrix and the bias vector of the previous layer. For nonlinear transformation, is utilized as an activation function for these convolution layers. Then, the features are concatenated and passed to the next layer with the same process. The output layer of the model is defined as the Softmax layer; the Softmax activation function produces an output with a probability distribution over the predefined classes.
In the backpropagation process, the weights of this model are updated by using the standard mini-batch stochastic gradient descent (SGD). SGD adjusts the model weights by minimizing a loss function between the actual output and the model output. In the proposed model, we used the categorical cross entropy function as the loss function of this model and it is computed as follows:
where is the batch size, is the ground-truth vector (encoded as one hot vector style), and is the model prediction vector.
The SGD algorithm iteratively adjusts the weights of the model over many iterations (i.e., epochs), which means the model sees the same samples many times. In fact, this process could produce an overfitting problem in the model. In this case, the model performs well on the training samples but poorly on the test samples. To avoid the overfitting problem, several regularization techniques are proposed in the literature, such as the dropout L1 and L2 regularization. In the proposed CNN model, we adapt the L2 regularization as a generalization method. L2 regularization encourages the model weights to be small by adding penalization terms to loss function in Equation (5). The loss function is defined as:
where m is the number of weights w and is the tunable parameter.
4. Experiments and Results
We used the dataset described in Section 3.2 for obtaining the results of the proposed methods. The proposed features of model-based methods were evaluated by using the SVM-RBF classifier. For model assessment, we used a 10-fold cross-validation with grid search [41] for hyper-parameter selection. SVM and RFE methods were implemented based on caret package [42], an R-analysis tool for classification and regression models. Also, the results of the proposed deep learning model were obtained based on KERAS API [43], a python library for high-level deep learning.
For evaluating the proposed methods, we used the F1 score and the overall accuracy as measures to evaluate the performance of each method. The F1 score shows the accuracy of each class by combining both precision and the recall which provides a harmonic mean of both. F1 and overall accuracy are computed as follows:
4.1. Model-Based Classification Framework
The estimated PCA model in Section 3.3 was used to transform the original HSI image into its PCA space (i.e., score images). Then, the first five scores are selected and used for generating the superpixels. The region size of each pixel was set to 100 pixels (i.e., ). The pixels in each superpixel were resampled into a limited number of pixels as follows: 11 for lamb and 9 for the other classes. The KS algorithm was used for resampling the superpixels into a group of represented pixels.
The selected pixels of each class were smoothed across the spectral domain by using the SGD method. Empirically, we choose 9 and 2 for the window size and the order of the polynomial function of the SGD algorithm, respectively. Then, the following feature vectors were obtained (the length of these vectors is 225), the by using Equation (2), and by Equation (3). Also, the raw spectral was considered for comparing the results. Table 1 shows the results of the SVM-RBF classifier of the proposed spectral features; the results of each meat status are also shown in Table 1.

Table 1.
Performance evaluations (F1-score of each class and overall accuracy) of the proposed spectral feature vectors over each meat status.
As described in Section 3.4.2, the textural features were extracted and then concatenated with the spectral vector of the target pixel. By using the SVM-RBF model, we investigated the effect of adding the textural features into different types of spectral features (i.e., the joint features of spatial and spectral features). Thus, the investigated feature vectors are as follows: raw spectral with textures (raw texture), L2 normalized spectral with texture (L2-norm-texture), and SNV normalized spectral with texture (SNV-norm-texture). Table 2 shows the influence on the performance of adding these textural properties into the spectral response of the muscle types.

Table 2.
Performance evaluations of the proposed combination of spectral feature vectors and textural features over each meat status.
4.2. Deep Learning-Based Classification Framework
Pertaining to the evaluation of the proposed CNN model, we used the dataset in Section 3.2. The training set of images were sampled into a set of samples by using the superpixel labelled images; after computing the superpixel, the corresponding centroid of each superpixel is obtained. We extracted a as in Section 3.5.1) 3D window around the centroid of each superpixel in the training images. The first and last five bands were removed as described in Section 3.1 after reflectance calibration (the input range is between 0 and 1). In fact, the superpixels are only used to prepare the training samples; in testing, the same window size is selected around each pixel to predict the class of this pixel, which means that no preprocessing needs to be applied in the test phase.
In Section 3.5.1, the proposed CNN model has two inputs. For the first, we computed the mean spectrum of the selected windows and then reshaped it into. The second input is prepared as by masking the whole 3D window using the selected optimal bands. Table 3 summarizes the specifications of the proposed CNN model, which shows the species of each hidden layer including the kernel size in the convolution and pooling operations, padding and striding for down-up sampling, and the number of the extracted features from each convolution layer.

Table 3.
The specs of the architecture of the proposed CNN model for detection of the adulteration in red-meat products.
The proposed CNN model is a light-weight model where the total number of trainable parameters is 145,322. Thus, the network is easy to train and converge; this increases the probability of generalization on unseen samples.
At each hidden convolution layer, we applied rectified linear unit function (ReLU) to nonlinearity transformation for accelerating the training processes. In the classification layer (i.e., the output layer), the Softmax activation is used to produce the probabilities over the predefined 3 classes.
For training the model, we used mini-batch SGD with the backpropagation algorithm for minimizing the loss function in Equation (6) and updating the weights of each layer. The learning rate of SGD is set as 0.003. As we used a small learning rate and the training processes are repeated for 500 iterations (i.e., 500 epochs), we decided to add a momentum term into the weights updating criteria for accelerating the training processes, where the momentum value was set to 0.90. Figure 7 shows the loss of training and validation samples during the training iterations. The learning curve shows that the validation error converged after 300 iterations, while the training is still decreased, which means that the model learns generalized features and no overfitting accrues. Both of the losses are converged after 450 iterations; thus, the means of these final weights (i.e., the weights of last 50 iterations) were used as the final.
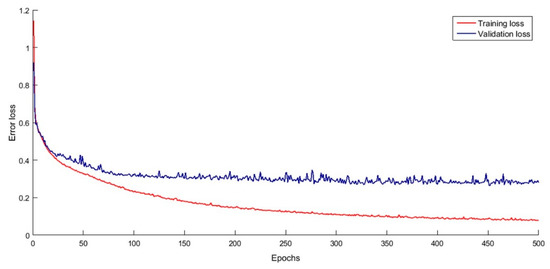
Figure 7.
The learning curve of the proposed CNN model.
The performance of the proposed CNN model was evaluated by using the test images. We used the F1 and overall accuracy to obtain the prediction stability of each class for overall classification. Table 3 shows the results of the proposed CNN model. The model achieves good accuracy independently of the state of the meat (i.e., fresh, frozen, thawed, and packed).
The proposed CNN model extracts a set of features crossing the spectral and spatial domains. In our experiments, we investigated the influence of the spatial window size (i.e., input 2 in our architecture in Table 3). We completed many experiments to optimize the best spatial size. The results show that the best spatial size is 3 × 3 in applying the model to our application (meat processing). Figure 8 shows the influence of the spatial size on the overall accuracy.
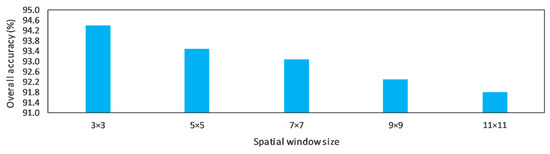
Figure 8.
The effect of spatial size on the accuracy of the proposed CNN.
5. Analysis and Discussion
In this paper, we investigated several methods for detecting adulteration in red-meat products. Two types of handcraft features were tested and evaluated by using the SVM model: spectral-based features and joint spectral and spatial features (textural properties of the meat surface). The results from the only spectral response (as shown in Table 1) show that normalizing the raw spectral by SNV transformation performed better than L2 normalization and raw spectral in all meat states. However, it achieved poor results in the case of frozen-packed and thawed meat (84.1 and 90.7%, respectively) compared with the other meat states. These unbiased results suggest the model is invariant to the state of the tested red-meat.
Adding the textural features into the spectral features slightly improved the accuracy of the SVM model. Table 2 shows the performance of this model by adding the texture features into three types of spectral features, individually. The combination of SNV and texture outperformed the other combination (i.e., L2 norm and raw spectral). Combining the SNV normalization with the texture significantly enhances the accuracy for FSP and THUP meat statuses although there was no improvement in the accuracy of the other statuses; for example, in the case of THUP, only spectral with SNV normalization achieved 90.7% overall accuracy while both spectral and texture achieved 95.5%. Also, the results of taking the texture properties into consideration show more reliability in terms of averaging the accuracy over all meat statuses compared with the model with only the spectral features.
The proposed deep CNN model achieved excellent results on the test samples. Table 4 shows the achieved results at each meat status. The best achieved accuracy is 96.1% when the meat was thawed. The accuracy of the CNN model provides better overall accuracy compared to the other investigated SVM models. Moreover, it provided more stability in the prediction of each class, where the F score increased for all classes. Also, the F1 score of the OTHER class significantly increased overall; which means that the CNN model is more suitable for detecting the undesired meat (i.e., beef or pork), where this is the main objective of this article.

Table 4.
The performance of the proposed CNN at each meat status on the test set of images.
Table 5 provides a comprehensive comparison between the investigated models. In Table 5 the averaging overall accuracies of all meat statuses are provided. Clearly, the results show that the CNN model outperforms the other models, at each meat status, in terms of overall accuracy and the F score for all classes. For example, SNV-norm-texture has the best results (92.8% overall accuracy), compared with the other feature vectors, when it is used as a features vector for the SVM model. The proposed CNN model significantly increases the overall accuracy to 94.4%.

Table 5.
Performance evaluation of all proposed models on average of all meat statuses (i.e., summarizing FSUP, FSP, FRUP, FRP, and THUP).
Selecting the best of the proposed model depends on the robustness of the model to be invariant related to the meat status, the ability to detect the undesired meat (i.e., the adulteration situation), and the simplicity of the model. The results show that the proposed CNN model satisfies these conditions where it performed better in the average overall accuracy. In addition, we analyzed the variation in the accuracies over all statuses; Figure 9 shows the standard deviation of the accuracies for all meat states. The CNN model had the lowest standard deviation compared with the other models; for example, SVM with SNV-texture has 2.31 standard deviation. This result means that the performance of the CNN model is more stable compared with the others.
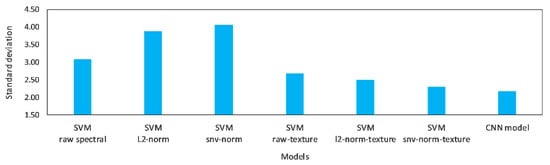
Figure 9.
The standard deviation (STD) of overall accuracies of each model over all investigated meat conditions (i.e., FSUP, FSP, FRUP, FRP, and THUP).
The visual results in Figure 10 show the robustness of the proposed CNN model. In Figure 10, we see that the detection of the undesired muscles is significantly improved; the visual comparison between SVM and CNN shows that the detection of OTHER class is more accurate and the edges between the meats types are well maintained.

Figure 10.
Visualization results (classification maps) of the SVM and CNN models provide a visual comparison between the models that have the highest accuracy (i.e., SVM with combining the texture and SNV norm, and the deep learning model with combining 1D and 3D CNN networks). The colours Red, Green, and Blue represent classes LAMB, OTHER (beef or pork), and FAT, respectively.
In addition to the robust performance of the CNN model, the model is simple and it is able to extract intelligent features from the raw input image. The SVM model used a handcraft feature; that is, a strong preprocessing (i.e., normalization) and manual feature extraction (i.e., superpixel and texture). Also, the CNN model does not need any preprocessing and pre-segmentation, because the superpixels were used only in the training stage. Thus, due to its simplicity, the CNN model is more suitable for any real-time applications, and the fitted model can be applied instantly to collect new hyperspectral images.
6. Conclusions
Adulteration of red-meat products is an increasing concern to the industry. In this work, we investigated the robustness of hyperspectral imaging systems for detecting adulteration independently of the state of the products (fresh, packed, frozen, or thawed). Different types of spectral and spatial features were investigated by using SVM model-based and deep learning-based approaches. The deep learning approach included a combination of several layers of 1D and 3D convolution operations. The quantitative analysis shows that the proposed CNN model outperformed the state-of-the-art models by achieving an average overall accuracy of 94.4%. Also, the results show that the CNN model is stable and fairly invariant to the meat status. Moreover, the CNN is simpler than the SVM in terms of extracting features and testing time. The CNN model is able to handle raw input images without any preprocessing or pre-segmentation methods.
Author Contributions
All the authors made significant contributions to this work. Mahmoud Al-Sarayreh contributed in devising the approach, analyzing the data, and writing the manuscript. Marlon M. Reis contributed in the design and development of the experiments, supervision of data analysis and manuscript preparation. Wei Qi Yan and Reinhard Klette contributed by initialization and supervision of the academic work of the first author, also to the manuscript preparation, and in multiple iterations to manuscript writing and reviewing.
Acknowledgments
This work was supported by Auckland University of Technology and by the AgResearch Strategic Science Investment Fund.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ghamisi, P.; Couceiro, M.; Benediktsson, J. Integration of segmentation techniques for classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2014, 11, 342–346. [Google Scholar] [CrossRef]
- Hu, Y.; Monteiro, S.; Saber, E. Super pixel based classification using conditional random fields for hyperspectral images. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016. [Google Scholar]
- Fang, L.; Li, S.; Duan, W. Classification of hyperspectral images by exploiting spectral-spatial information of superpixel via multiple kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Elmasry, G.; Sun, D.W.; Allen, P. Application of NIR hyperspectral imaging for discrimination of lamb muscles. J. Food Eng. 2012, 104, 332–340. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Barbin, D.; Elmasry, G.; Sun, D.; Allen, P. Potential of hyper spectral imaging and pattern recognition for categorization and authentication of red meat. Innov. Food Sci. Emerg. Technol. 2012, 104, 332–340. [Google Scholar]
- Karrer, A.; Stuart, A.; Craigie, C.; Taukiri, K.; Reis, M.M. Detection of adulteration in meat product using of hyperspectral imaging. In Proceedings of the Chemometrics Analytical Chemistry, Barcelona, Spain, 6–11 June 2016; p. 177. [Google Scholar]
- Ropodi, A.; Pavlidis, D.; Moharebb, F.; Panagou, E.; Nychas, G. Multispectral image analysis approach to detect adulteration of beef and pork in raw meats. Food Res. Int. 2015, 67, 12–18. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Makino, Y.; Oshita, S. Rapid and Non-destructive detection of chicken adulteration in minced beef using visible near-infrared hyperspectral imaging and machine learning. J. Food Eng. 2016, 170, 8–15. [Google Scholar] [CrossRef]
- Sanz, J.; Fernandes, A.; Barrenechea, E.; Silva, S.; Santos, V.; Goncalves, N.; Pater-nain, D.; Jurio, A.; Melo-Pinto, P. Lamb muscle discrimination using hyperspectral imaging comparison of various machine learning algorithms. J. Food Eng. 2016, 174, 92–100. [Google Scholar] [CrossRef]
- Cen, H.; He, Y. Theory and application of near-infrared reflectance spectroscopy in determination of food quality. Trends Food Sci. Technol. 2007, 18, 72–83. [Google Scholar] [CrossRef]
- Elmasry, G.; Kamruzzaman, M.; Sun, D.W.; Allen, P. Principles and applications of hyperspectral imaging in quality evaluation of agro-food products: A review. Crit. Rev. Food Sci. Nutr. 2012, 52, 999–1023. [Google Scholar] [CrossRef] [PubMed]
- Bock, J.; Connelly, R. Innovative uses of near-infrared spectroscopy in food processing. J. Food Sci. 2008, 73, 91–98. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Sun, D. Comparison of three methods for classification of pizza topping using different colour space transformations. J. Food Eng. 2005, 68, 277–287. [Google Scholar] [CrossRef]
- Zheng, C.; Sun, D.; Zheng, L. Recent developments and applications of image features for food quality evaluation and inspection: A review. Trends Food Sci. Technol. 2006, 17, 642–655. [Google Scholar] [CrossRef]
- Wu, D.; Sun, D. Colour measurements by computer vision for food quality control: A review. Trends Food Sci. Technol. 2013, 29, 5–20. [Google Scholar] [CrossRef]
- Al-Sarayreh, M.; Reis, M.; Yan, W.Y.; Klette, R. Detection of Adulteration in Red Meat Species Using Hyperspectral Imaging. In Proceedings of thePacific-Rim Symposium on Image and Video Technology (PSIVT), Wuhan, China, 20–24 November 2017. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NA, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Ciregan, D.; Meier, U.; Schmidhuber, J. Multi-column deep neural networks for image classification. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 3642–3649. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the Conference Computer Vision and Pattern Recognition, Washington, DC, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Taigman, T.; Yang, M.; Ranzato, M.; Wolf, L. DeepFace: Closing the gap to human-level performance in face verification. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1701–1708. [Google Scholar]
- Sainath, T.N.; Mohamed, A.R.; Kingsbury, B.; Ramachandran, B. Deep convolutional neural networks for LVCSR. In Proceedings of the 38th IEEE International Conference on Acoustics, Speech, and Signal Processing, Vancouver, BC, Canada, 26 May 2013; pp. 8614–8618. [Google Scholar]
- Abdel-Hamid, O.; Mohamed, A.R.; Jiang, H.; Penn, G. Applying convolutional neural networks concepts to hybrid NN-HMM model for speech recognition. In Proceedings of the IEEE International Conference Acoustics, Speech, and Signal Processing, Berkeley, CA, USA, 25–30 March 2012; pp. 4277–4280. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 12. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, C.; Xu, A.; Shi, Y.; Duan, Y. 3D Convolutional Neural Networks for Crop Classification with Multi-Temporal Remote Sensing Images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef]
- Yue, Q.; Ma, C. Deep Learning for Hyperspectral Data Classification through Exponential Momentum Deep Convolution Neural Networks. J. Sens. 2016, 2015, 8. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Wan, X.; Zhao, C.; Wang, Y.; Liu, W. Stacked sparse autoencoder in hyperspectral data classification using spectral-spatial, higher order statistics and multifractal spectrum features. Infrared Phys. Technol. 2017, 86, 77–89. [Google Scholar] [CrossRef]
- Xing, C.; Ma, L.; Yang, X. Stacked denoise autoencoder based feature extraction and classification for hyperspectral images. J. Sens. 2016, 2016, 10. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, F.; Hang, R.; Yuan, X. Bidirectional-Convolutional LSTM Based Spectral-Spatial Feature Learning for Hyperspectral Image Classification. Remote Sens. 2017, 9, 1330. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Susstrunk, S. SLIC superpixiels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Kennard, R.; Stone, L. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Ambroise, C.; McLachlan, G. Selection bias in gene extraction on the basis of microarray gene-expression data. Proc. Natl. Acad. Sci. USA 2002, 99, 6562–6566. [Google Scholar] [CrossRef] [PubMed]
- Granitto, P.M.; Furlanello, C.; Biasioli, F.; Gasperi, F. Recursive feature elimination with random forest for PTR-MS analysis of agroindustrial products. Chemom. Intell. Lab. Syst. 2006, 83, 83–90. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Wang, T. Application of Breiman's random forest to modeling structure activity relationships of pharmaceutical molecules. In Proceedings of the International Workshop Multiple Classifer Systems, Cagliari, Italy, 9–11 June 2004; pp. 334–343. [Google Scholar]
- Klette, R. Concise Computer Vision; Springer: London, UK, 2014. [Google Scholar]
- Haralick, R. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification; Technical Report; National Taiwan University: Taipei, Taiwan, 2003; Last Update 2016. [Google Scholar]
- Kuhn, M. Caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar]
- Chollet, F. Keras. GitHub 2015. Available online: https://github.com/keras-team/keras (accessed on 15 January 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).