State of the Art of X-ray Speckle-Based Phase-Contrast and Dark-Field Imaging
Abstract
1. Introduction
2. Basic Principles of X-ray Speckle-Based Multimodal Imaging
2.1. X-ray Speckle as a Wavefront Marker
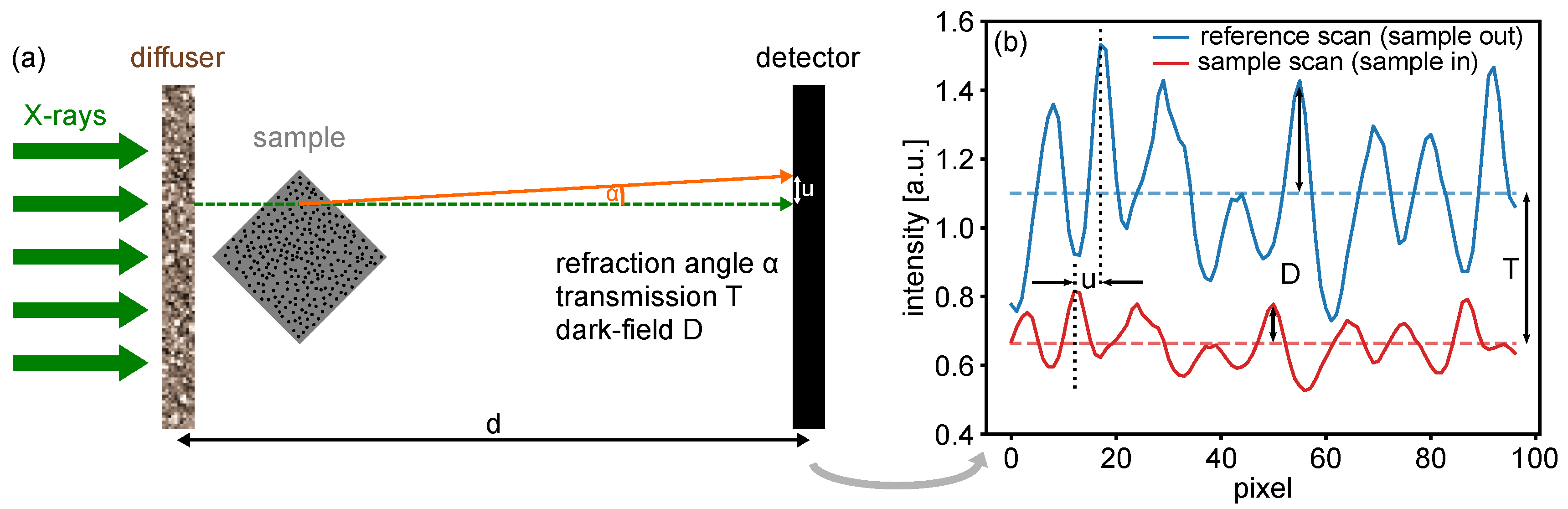
2.2. Differential Phase, Transmission and Dark-Field Signals
2.3. Practical Experimental Considerations
2.4. Related Techniques
3. Experimental Implementations
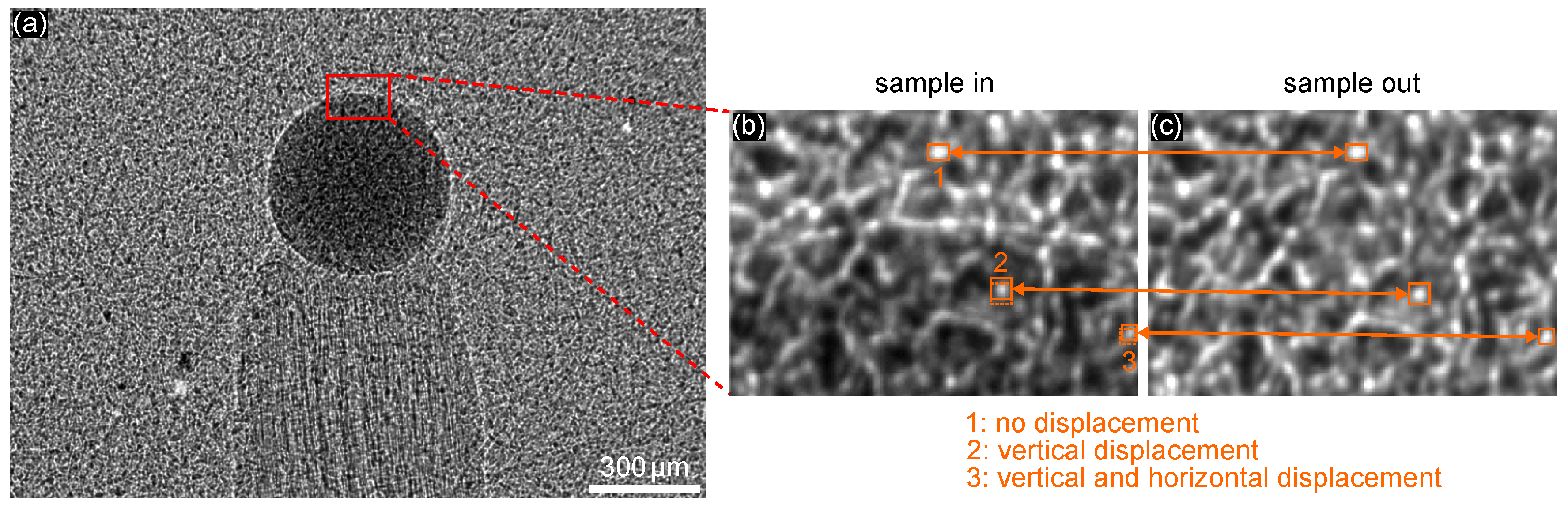
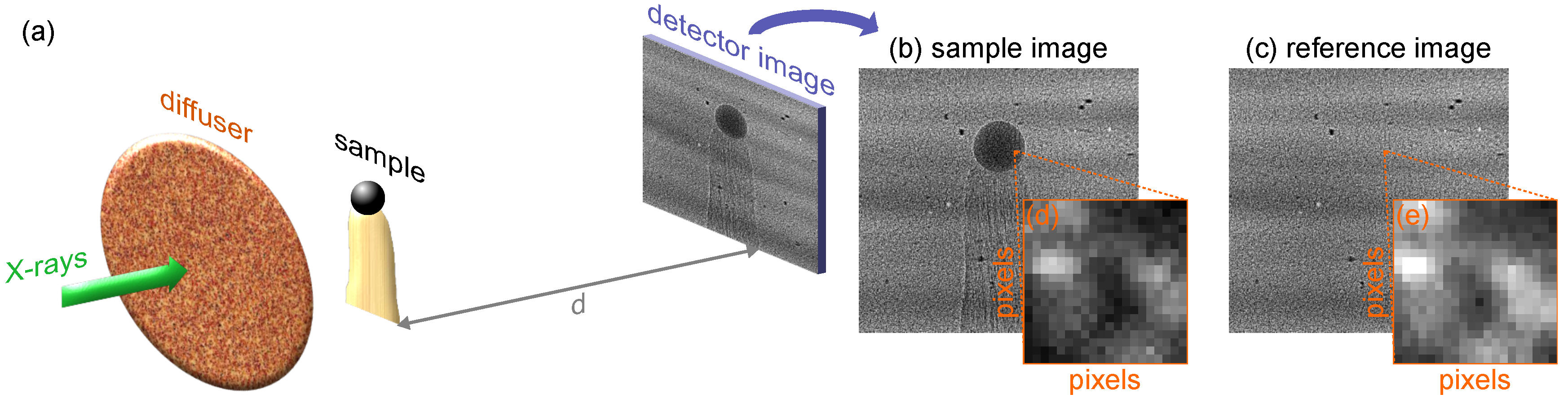
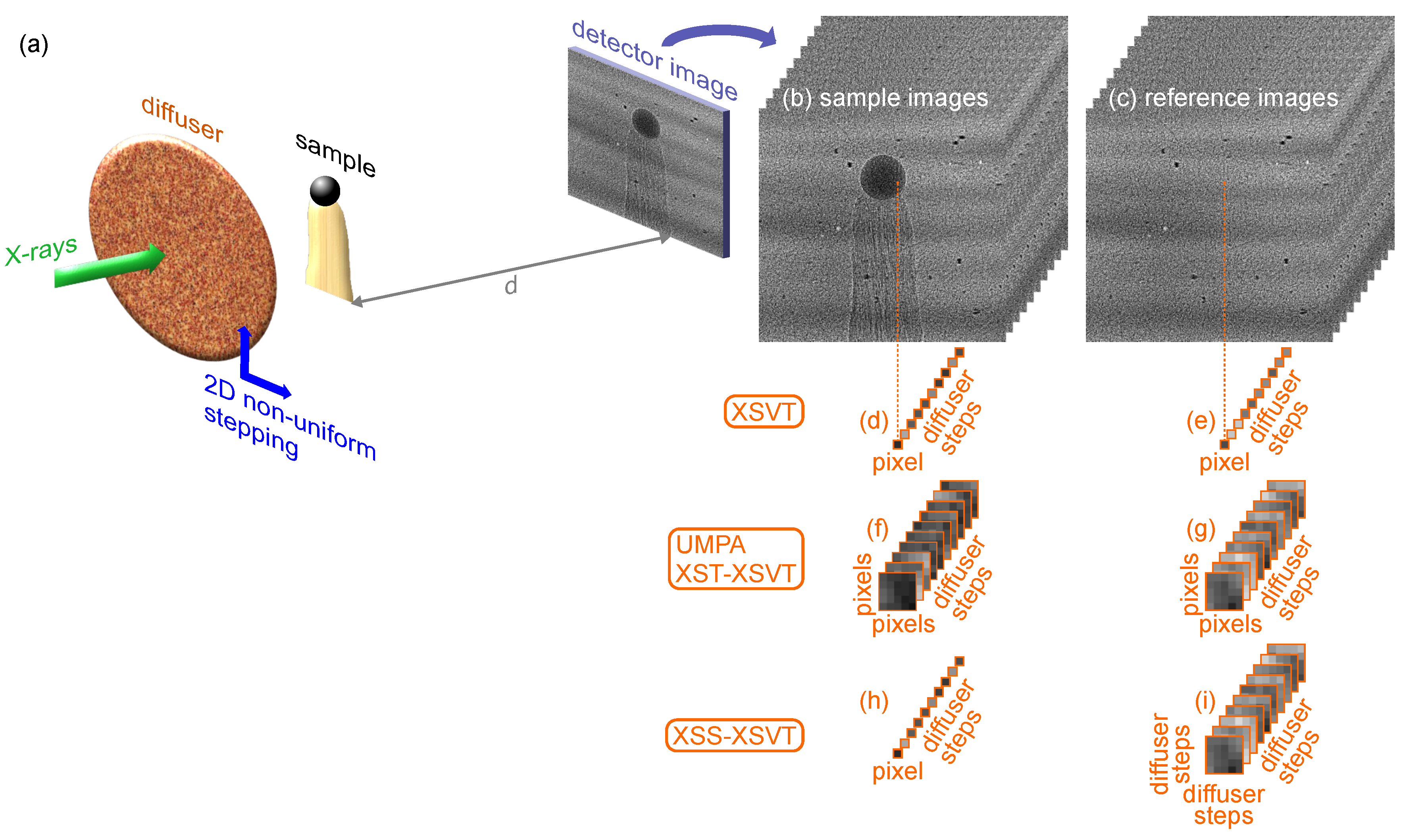
3.1. Single-Shot X-ray Speckle-Tracking Mode (XST)
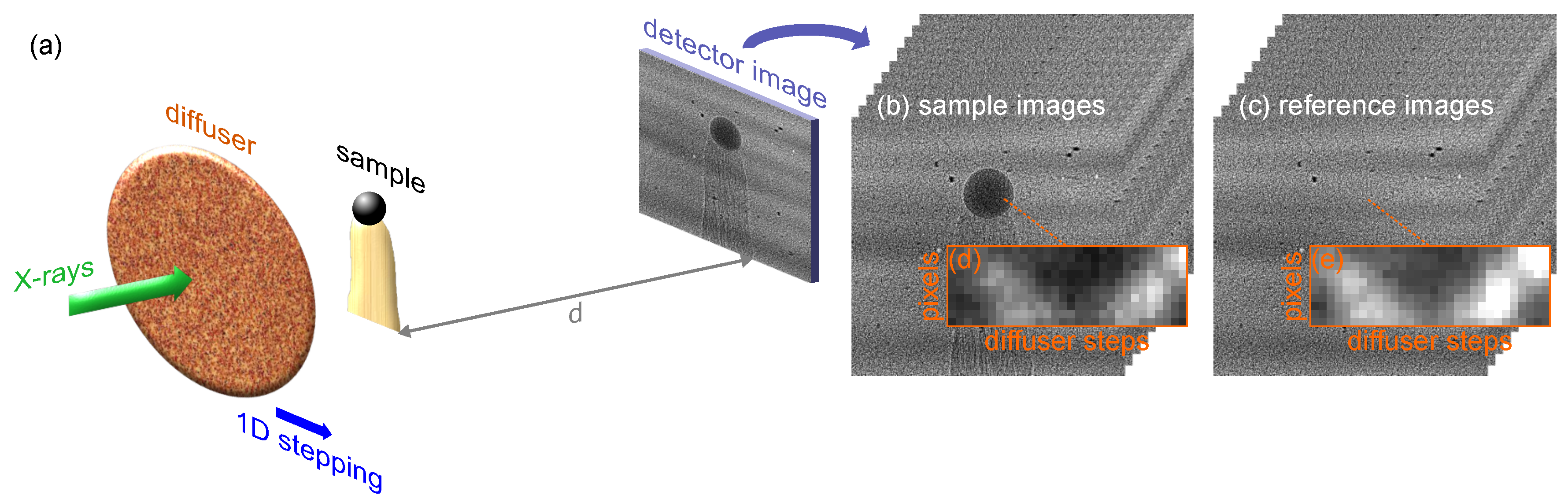
3.2. X-ray Speckle-Scanning Modes (XSS)
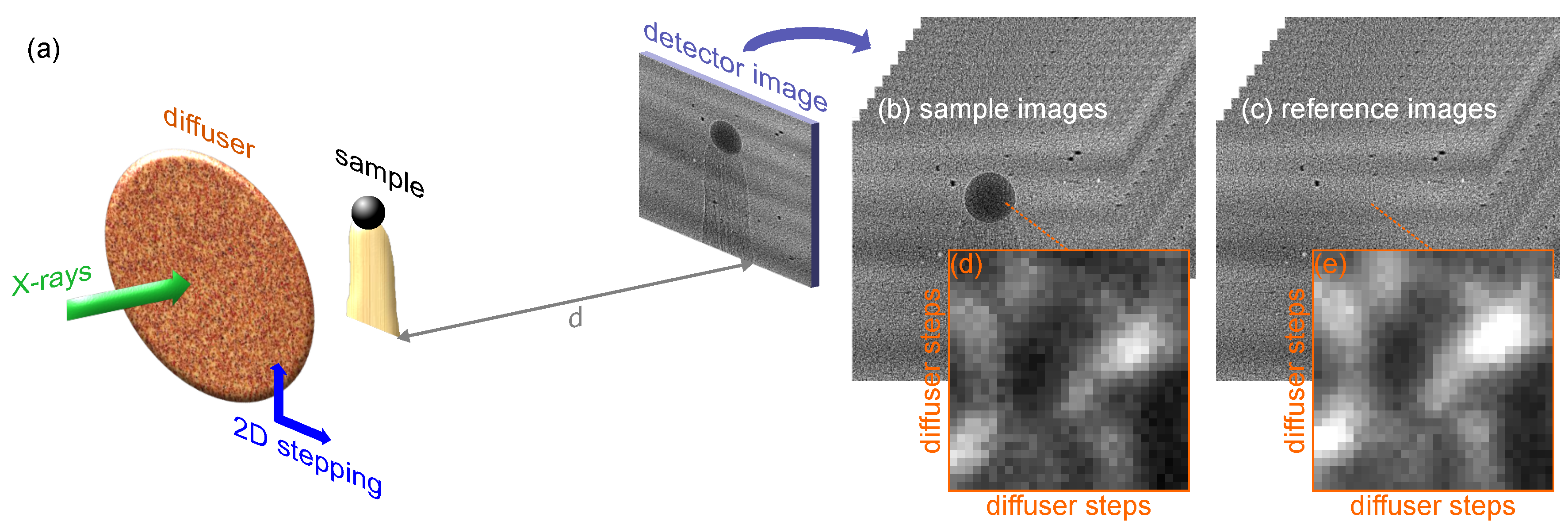
3.2.1. 2D Scanning (2D XSS)
3.2.2. 1D Scanning (1D XSS)
3.2.3. Scanning with Self-Correlation Analysis
3.2.4. 2D Scanning with Sparse Sampling
3.2.5. Analysis of the Scattering Distribution
3.3. Acquisition with Random Diffuser Positions
3.3.1. X-ray Speckle-Vector Tracking (XSVT) and Mixed XSVT Approaches
3.3.2. Unified Modulated Pattern Analysis (UMPA)
3.4. Angular Sensitivity and Spatial Resolution
4. Speckle-Based X-ray Dark-Field Imaging Approaches
5. Translation to Laboratory Sources and High X-ray Energies
6. Speckle-Based X-ray Phase-Contrast and Dark-Field Tomography
7. Applications of the X-ray Speckle-Based Technique
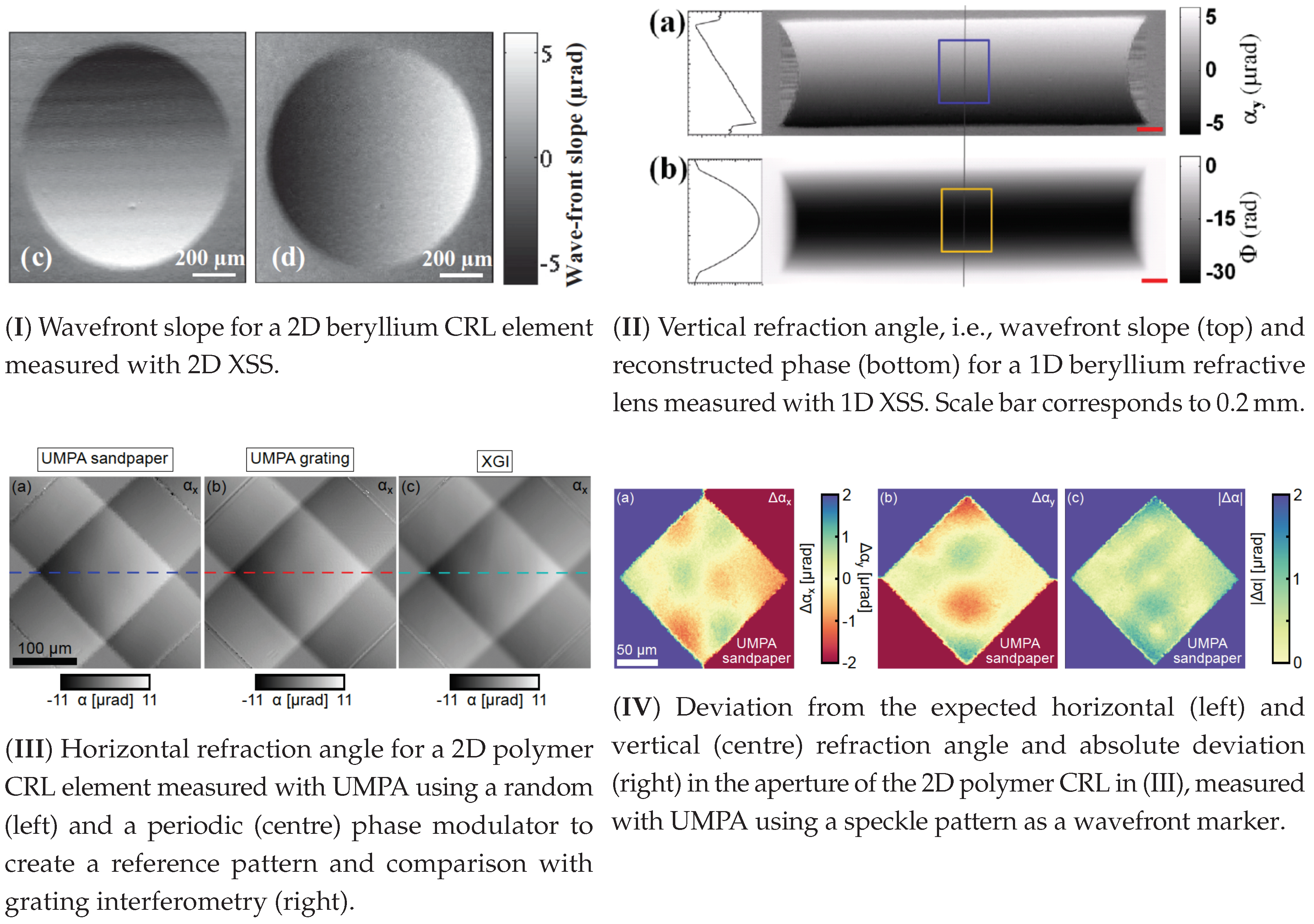
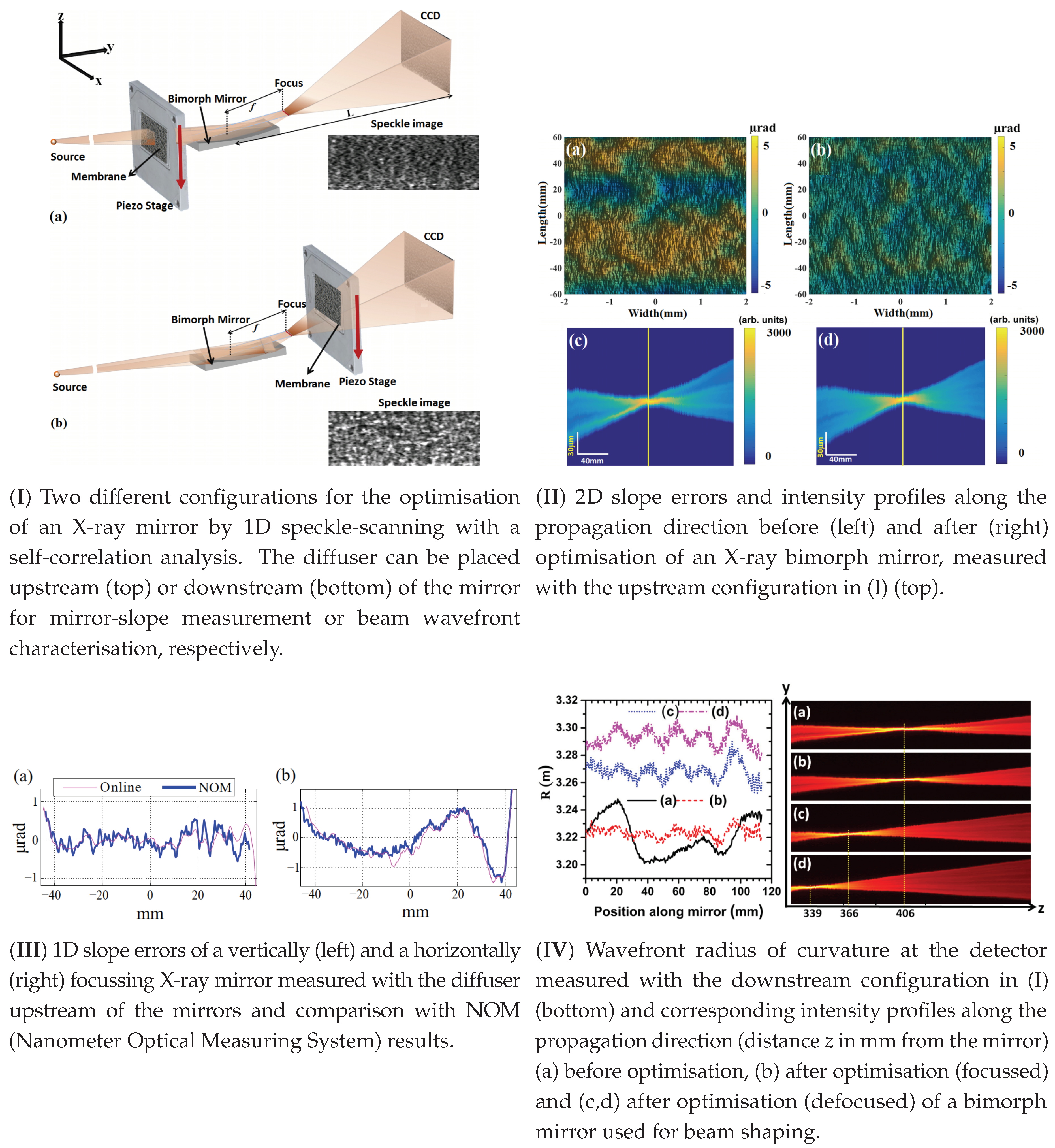
7.1. Metrology and Wavefront Sensing
7.2. Imaging for Biomedical and Materials Science Applications
7.3. Other Applications
8. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
Abbreviations
| 1D | one-dimensional |
| 2D | two-dimensional |
| 3D | three-dimensional |
| FWHM | full width at half maximum |
| XST | X-ray speckle tracking |
| XSS | X-ray speckle scanning |
| XSVT | X-ray speckle-vector tracking |
| UMPA | unified modulated pattern analysis |
| CRL | compound refractive lens |
References
- Röntgen, W.C. Über eine neue Art von Strahlen (Vorläufige Mittheilung). Sitzungsber. Der Würzburger Physik.-Medic. Gesellsch. 1895, 9, 132–141. [Google Scholar]
- Röntgen, W.C. Über eine neue Art von Strahlen (Erste Mittheilung). Ann. Phys. (Berl.) 1898, 300, 1–11. [Google Scholar] [CrossRef]
- Codman, E.A. Radiograph of fetal arm. Boston Med. Surg. J. 1896, 134, 327. [Google Scholar]
- Editorial. Rare anomalies of the phalanges shown by the Röntgen process. Boston Med. Surg. J. 1896, 134, 198–199. [Google Scholar]
- Editorial. On the application of the Röntgen rays to the diagnosis of arterio-sclerosis. Boston Med. Surg. J. 1896, 134, 550–551. [Google Scholar]
- Spiegel, P.K. The first clinical X-ray made in America—100 years. AJR Am. J. Roentgenol. 1995, 164, 241–243. [Google Scholar] [CrossRef] [PubMed]
- Hounsfield, G.N. Computerized transverse axial scanning (tomography): Part 1. Description of system. Br. J. Radiol. 1973, 46, 1016–1022. [Google Scholar] [CrossRef] [PubMed]
- Ambrose, J. Computerized transverse axial scanning (tomography): Part 2. Clinical application. Br. J. Radiol. 1973, 46, 1023–1047. [Google Scholar] [CrossRef] [PubMed]
- Beckmann, E.C. CT scanning the early days. Br. J. Radiol. 2006, 79, 5–8. [Google Scholar] [CrossRef] [PubMed]
- Pollock, H.C. The discovery of synchrotron radiation. Am. J. Phys. 1983, 51, 278–280. [Google Scholar] [CrossRef]
- Bilderback, D.H.; Elleaume, P.; Weckert, E. Review of third and next generation synchrotron light sources. J. Phys. B 2005, 38, S773–S797. [Google Scholar] [CrossRef]
- Kunz, C. Synchrotron radiation: Third generation sources. J. Phys. Condens. Matter 2001, 13, 7499–7510. [Google Scholar] [CrossRef]
- Zernike, F. Phase contrast, a new method for the microscopic observation of transparent objects. Physica 1942, 9, 686–698. [Google Scholar] [CrossRef]
- Bonse, U.; Hart, M. An X-ray interferometer. Appl. Phys. Lett. 1965, 6, 155–156. [Google Scholar] [CrossRef]
- Fitzgerald, R. Phase-Sensitive X-ray Imaging. Phys. Today 2000, 53, 23. [Google Scholar] [CrossRef]
- Lewis, R.A. Medical phase contrast X-ray imaging: Current status and future prospects. Phys. Med. Biol. 2004, 49, 3573. [Google Scholar] [CrossRef] [PubMed]
- Momose, A. Recent Advances in X-ray Phase Imaging. Jpn. J. Appl. Phys. 2005, 44, 6355. [Google Scholar] [CrossRef]
- Betz, O.; Wegst, U.; Weide, D.; Heethoff, M.; Helfen, L.; Lee, W.-K.; Cloetens, P. Imaging applications of synchrotron X-ray phase-contrast microtomography in biological morphology and biomaterials science. I. General aspects of the technique and its advantages in the analysis of millimetre-sized arthropod structure. J. Microsc. 2007, 227, 51–71. [Google Scholar] [CrossRef] [PubMed]
- Williams, I.; Siu, K.; Runxuan, G.; He, X.; Hart, S.; Styles, C.; Lewis, R. Towards the clinical application of X-ray phase contrast imaging. Eur. J. Radiol. 2008, 68, S73–S77. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.-A.; Brahme, A. Development of phase-contrast X-ray imaging techniques and potential medical applications. Phys. Med. 2008, 24, 129–148. [Google Scholar] [CrossRef] [PubMed]
- Bravin, A.; Coan, P.; Suortti, P. X-ray phase-contrast imaging: From pre-clinical applications towards clinics. Phys. Med. Biol. 2013, 58, R1. [Google Scholar] [CrossRef] [PubMed]
- Coan, P.; Bravin, A.; Tromba, G. Phase-contrast X-ray imaging of the breast: Recent developments towards clinics. J. Phys. D 2013, 46, 494007. [Google Scholar] [CrossRef]
- Koehler, T.; Daerr, H.; Martens, G.; Kuhn, N.; Löscher, S.; van Stevendaal, U.; Roessl, E. Slit-scanning differential X-ray phase-contrast mammography: Proof-of-concept experimental studies. Med. Phys. 2015, 42, 1959–1965. [Google Scholar] [CrossRef] [PubMed]
- Horn, F.; Hauke, C.; Lachner, S.; Ludwig, V.; Pelzer, G.; Rieger, J.; Schuster, M.; Seifert, M.; Wandner, J.; Wolf, A.; et al. High-energy X-ray grating-based phase-contrast radiography of human anatomy. Proc. SPIE 2016, 9783. [Google Scholar]
- Momose, A.; Yashiro, W.; Kido, K.; Kiyohara, J.; Makifuchi, C.; Ito, T.; Nagatsuka, S.; Honda, C.; Noda, D.; Hattori, T.; et al. X-ray phase imaging: From synchrotron to hospital. Philos. Trans. Royal Soc. A 2014, 372, 20130023. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cloetens, P.; Pateyron-Salomé, M.; Buffière, J.Y.; Peix, G.; Baruchel, J.; Peyrin, F.; Schlenker, M. Observation of microstructure and damage in materials by phase sensitive radiography and tomography. J. Appl. Phys. 1997, 81, 5878–5886. [Google Scholar] [CrossRef]
- Stevenson, A.W.; Gureyev, T.E.; Paganin, D.; Wilkins, S.W.; Weitkamp, T.; Snigirev, A.; Rau, C.; Snigireva, I.; Youn, H.S.; Dolbnya, I.P.; et al. Phase-contrast X-ray imaging with synchrotron radiation for materials science applications. Nucl. Instr. Meth. Phys. Res. B 2003, 199, 427–435. [Google Scholar] [CrossRef]
- Zoofan, B.; Kim, J.-Y.; Rokhlin, S.I.; Frankel, G.S. Phase-contrast X-ray imaging for nondestructive evaluation of materials. J. Appl. Phys. 2006, 100, 014502. [Google Scholar] [CrossRef]
- Mayo, S.C.; Stevenson, A.W.; Wilkins, S.W. In-Line Phase-Contrast X-ray Imaging and Tomography for Materials Science. Materials 2012, 5, 937–965. [Google Scholar] [CrossRef] [PubMed]
- Weitkamp, T.; Nöhammer, B.; Diaz, A.; David, C.; Ziegler, E. X-ray wavefront analysis and optics characterization with a grating interferometer. Appl. Phys. Lett. 2005, 86, 054101. [Google Scholar] [CrossRef]
- Engelhardt, M.; Baumann, J.; Schuster, M.; Kottler, C.; Pfeiffer, F.; Bunk, O.; David, C. Inspection of refractive X-ray lenses using high-resolution differential phase contrast imaging with a microfocus X-ray source. Rev. Sci. Instrum. 2007, 78, 093707. [Google Scholar] [CrossRef] [PubMed]
- Diaz, A.; Mocuta, C.; Stangl, J.; Keplinger, M.; Weitkamp, T.; Pfeiffer, F.; David, C.; Metzger, T.H.; Bauer, G. Coherence and wavefront characterization of Si-111 monochromators using double-grating interferometry. J. Synchrotron Radiat. 2010, 17, 299–307. [Google Scholar] [CrossRef] [PubMed]
- Rutishauser, S.; Zanette, I.; Weitkamp, T.; Donath, T.; David, C. At-wavelength characterization of refractive X-ray lenses using a two-dimensional grating interferometer. Appl. Phys. Lett. 2011, 99, 221104. [Google Scholar] [CrossRef]
- Wang, H.; Sawhney, K.; Berujon, S.; Ziegler, E.; Rutishauser, S.; David, C. X-ray wavefront characterization using a rotating shearing interferometer technique. Opt. Express 2011, 19, 16550–16559. [Google Scholar] [CrossRef] [PubMed]
- Berujon, S.; Ziegler, E. Grating-based at-wavelength metrology of hard X-ray reflective optics. Opt. Lett. 2012, 37, 4464–4466. [Google Scholar] [CrossRef] [PubMed]
- Kayser, Y.; David, C.; Flechsig, U.; Krempasky, J.; Schlott, V.; Abela, R. X-ray grating interferometer for in situ and at-wavelength wavefront metrology. J. Synchrotron Radiat. 2017, 24, 150–162. [Google Scholar] [CrossRef] [PubMed]
- Kewish, C.M.; Guizar-Sicairos, M.; Liu, C.; Qian, J.; Shi, B.; Benson, C.; Khounsary, A.M.; Vila-Comamala, J.; Bunk, O.; Fienup, J.R.; et al. Reconstruction of an astigmatic hard X-ray beam and alignment of K-B mirrors from ptychographic coherent diffraction data. Opt. Express 2010, 18, 23420–23427. [Google Scholar] [CrossRef] [PubMed]
- Kewish, C.M.; Thibault, P.; Dierolf, M.; Bunk, O.; Menzel, A.; Vila-Comamala, J.; Jefimovs, K.; Pfeiffer, F. Ptychographic characterization of the wavefield in the focus of reflective hard X-ray optics. Ultramicroscopy 2010, 110, 325–329. [Google Scholar] [CrossRef] [PubMed]
- Vila-Comamala, J.; Diaz, A.; Guizar-Sicairos, M.; Mantion, A.; Kewish, C.M.; Menzel, A.; Bunk, O.; David, C. Characterization of high-resolution diffractive X-ray optics by ptychographic coherent diffractive imaging. Opt. Express 2011, 19, 21333–21344. [Google Scholar] [CrossRef] [PubMed]
- Schropp, A.; Hoppe, R.; Meier, V.; Patommel, J.; Seiboth, F.; Lee, H.J.; Nagler, B.; Galtier, E.C.; Arnold, B.; Zastrau, U.; et al. Full spatial characterization of a nanofocused X-ray free-electron laser beam by ptychographic imaging. Sci. Rep. 2013, 3, 1633. [Google Scholar] [CrossRef] [PubMed]
- Momose, A.; Takeda, T.; Itai, Y.; Hirano, K. Phase-contrast X-ray computed tomography for observing biological soft tissues. Nat. Med. 1996, 2, 473–475. [Google Scholar] [CrossRef] [PubMed]
- Förster, E.; Goetz, K.; Zaumseil, P. Double crystal diffractometry for the characterization of targets for laser fusion experiments. Krist. Tech. 1980, 15, 937–945. [Google Scholar] [CrossRef]
- Davis, T.J.; Gao, D.; Gureyev, T.E.; Stevenson, A.W.; Wilkins, S.W. Phase-contrast imaging of weakly absorbing materials using hard X-rays. Nature 1995, 373, 595–598. [Google Scholar] [CrossRef]
- Chapman, D.; Thomlinson, W.; Johnston, R.E.; Washburn, D.; Pisano, E.; Gmür, N.; Zhong, Z.; Menk, R.; Arfelli, F.; Sayers, D. Diffraction enhanced X-ray imaging. Phys. Med. Biol. 1997, 42, 2015. [Google Scholar] [CrossRef] [PubMed]
- Pagot, E.; Cloetens, P.; Fiedler, S.; Bravin, A.; Coan, P.; Baruchel, J.; Härtwig, J.; Thomlinson, W. A method to extract quantitative information in analyzer-based X-ray phase contrast imaging. Appl. Phys. Lett. 2003, 82, 3421–3423. [Google Scholar] [CrossRef]
- Bravin, A. Exploiting the X-ray refraction contrast with an analyser: The state of the art. J. Phys. D 2003, 36, A24. [Google Scholar] [CrossRef]
- Snigirev, A.; Snigireva, I.; Kohn, V.; Kuznetsov, S.; Schelokov, I. On the possibilities of X-ray phase contrast microimaging by coherent high-energy synchrotron radiation. Rev. Sci. Instrum. 1995, 66, 5486–5492. [Google Scholar] [CrossRef]
- Wilkins, S.W.; Gureyev, T.E.; Gao, D.; Pogany, A.; Stevenson, A.W. Phase-contrast imaging using polychromatic hard X-rays. Nature 1996, 384, 335–338. [Google Scholar] [CrossRef]
- Cloetens, P.; Barrett, R.; Baruchel, J.; Guigay, J.-P.; Schlenker, M. Phase objects in synchrotron radiation hard X-ray imaging. J. Phys. D 1996, 29, 133–146. [Google Scholar] [CrossRef]
- Nugent, K.A.; Gureyev, T.E.; Cookson, D.F.; Paganin, D.; Barnea, Z. Quantitative Phase Imaging Using Hard X-rays. Phys. Rev. Lett. 1996, 77, 2961–2964. [Google Scholar] [CrossRef] [PubMed]
- Cloetens, P.; Ludwig, W.; Baruchel, J.; Dyck, D.V.; Landuyt, J.V.; Guigay, J.-P.; Schlenker, M. Holotomography: Quantitative phase tomography with micrometer resolution using hard synchrotron radiation X-rays. Appl. Phys. Lett. 1999, 75, 2912–2914. [Google Scholar] [CrossRef]
- Paganin, D.; Mayo, S.C.; Gureyev, T.E.; Miller, P.R.; Wilkins, S.W. Simultaneous phase and amplitude extraction from a single defocused image of a homogeneous object. J. Microsc. 2002, 206, 33–40. [Google Scholar] [CrossRef] [PubMed]
- David, C.; Nöhammer, B.; Solak, H.H.; Ziegler, E. Differential X-ray phase contrast imaging using a shearing interferometer. Appl. Phys. Lett. 2002, 81, 3287–3289. [Google Scholar] [CrossRef]
- Momose, A.; Kawamoto, S.; Koyama, I.; Hamaishi, Y.; Takai, K.; Suzuki, Y. Demonstration of X-ray Talbot Interferometry. Jpn. J. Appl. Phys. 2003, 42, L866–L868. [Google Scholar] [CrossRef]
- Weitkamp, T.; Diaz, A.; David, C.; Pfeiffer, F.; Stampanoni, M.; Cloetens, P.; Ziegler, E. X-ray phase imaging with a grating interferometer. Opt. Express 2005, 13, 6296–6304. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, F.; Weitkamp, T.; Bunk, O.; David, C. Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources. Nat. Phys. 2006, 2, 258–261. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Maikusa, H.; Takeda, Y. High-speed X-ray phase imaging and X-ray phase tomography with Talbot interferometer and white synchrotron radiation. Opt. Express 2009, 17, 12540–12545. [Google Scholar] [CrossRef] [PubMed]
- Olivo, A.; Arfelli, F.; Cantatore, G.; Longo, R.; Menk, R.H.; Pani, S.; Prest, M.; Poropat, P.; Rigon, L.; Tromba, G.; et al. An innovative digital imaging set-up allowing a low-dose approach to phase contrast applications in the medical field. Med. Phys. 2001, 28, 1610–1619. [Google Scholar] [CrossRef] [PubMed]
- Olivo, A.; Speller, R. A coded-aperture technique allowing X-ray phase contrast imaging with conventional sources. Appl. Phys. Lett. 2007, 91, 074106. [Google Scholar] [CrossRef]
- Olivo, A.; Speller, R. Modelling of a novel X-ray phase contrast imaging technique based on coded apertures. Phys. Med. Biol. 2007, 52, 6555. [Google Scholar] [CrossRef] [PubMed]
- Olivo, A.; Speller, R. Image formation principles in coded-aperture based X-ray phase contrast imaging. Phys. Med. Biol. 2008, 53, 6461. [Google Scholar] [CrossRef] [PubMed]
- Olivo, A.; Ignatyev, K.; Munro, P.R.T.; Speller, R.D. Noninterferometric phase-contrast images obtained with incoherent X-ray sources. Appl. Opt. 2011, 50, 1765–1769. [Google Scholar] [CrossRef] [PubMed]
- Bérujon, S.; Ziegler, E.; Cerbino, R.; Peverini, L. Two-Dimensional X-ray Beam Phase Sensing. Phys. Rev. Lett. 2012, 108, 158102. [Google Scholar] [CrossRef] [PubMed]
- Morgan, K.S.; Paganin, D.M.; Siu, K.K.W. X-ray phase imaging with a paper analyzer. Appl. Phys. Lett. 2012, 100, 124102. [Google Scholar] [CrossRef]
- Berujon, S.; Wang, H.; Sawhney, K. X-ray multimodal imaging using a random-phase object. Phys. Rev. A 2012, 86, 063813. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Bech, M.; Bunk, O.; Kraft, P.; Eikenberry, E.F.; Brönnimann, C.; Grünzweig, C.; David, C. Hard-X-ray dark-field imaging using a grating interferometer. Nat. Mater. 2008, 7, 134–137. [Google Scholar] [CrossRef] [PubMed]
- Nesterets, Y.I. On the origins of decoherence and extinction contrast in phase-contrast imaging. Opt. Commun. 2008, 281, 533–542. [Google Scholar] [CrossRef]
- Yashiro, W.; Terui, Y.; Kawabata, K.; Momose, A. On the origin of visibility contrast in X-ray Talbot interferometry. Opt. Express 2010, 18, 16890–16901. [Google Scholar] [CrossRef] [PubMed]
- Baum, T.; Eggl, E.; Malecki, A.; Schaff, F.; Potdevin, G.; Gordijenko, O.; Garcia, E.G.; Burgkart, R.; Rummeny, E.J.; Noël, P.B.; et al. X-ray Dark-Field Vector Radiography—A Novel Technique for Osteoporosis Imaging. J. Comput. Assist. Tomogr. 2015, 39, 286–289. [Google Scholar] [CrossRef] [PubMed]
- Ando, M.; Sunaguchi, N.; Shimao, D.; Pan, A.; Yuasa, T.; Mori, K.; Suzuki, Y.; Jin, G.; Kim, J.-K.; Lim, J.-H.; et al. Dark-Field Imaging: Recent developments and potential clinical applications. Phys. Med. 2016, 32, 1801–1812. [Google Scholar] [CrossRef] [PubMed]
- Schleede, S.; Meinel, F.G.; Bech, M.; Herzen, J.; Achterhold, K.; Potdevin, G.; Malecki, A.; Adam-Neumair, S.; Thieme, S.F.; Bamberg, F.; et al. Emphysema diagnosis using X-ray dark-field imaging at a laser-driven compact synchrotron light source. Proc. Natl. Acad. Sci. USA 2012, 109, 17880–17885. [Google Scholar] [CrossRef] [PubMed]
- Meinel, F.G.; Yaroshenko, A.; Hellbach, K.; Bech, M.; Müller, M.; Velroyen, A.; Bamberg, F.; Eickelberg, O.; Nikolaou, K.; Reiser, M.F.; et al. Improved Diagnosis of Pulmonary Emphysema Using In Vivo Dark-Field Radiography. Investig. Radiol. 2014, 51, 653–658. [Google Scholar] [CrossRef] [PubMed]
- Yaroshenko, A.; Hellbach, K.; Yildirim, A.Ö.; Conlon, T.M.; Fernandez, I.E.; Bech, M.; Velroyen, A.; Meinel, F.G.; Auweter, S.; Reiser, M.; et al. Improved In vivo Assessment of Pulmonary Fibrosis in Mice using X-ray Dark-Field Radiography. Sci. Rep. 2015, 5, 17492. [Google Scholar] [CrossRef] [PubMed]
- Yaroshenko, A.; Pritzke, T.; Koschlig, M.; Kamgari, N.; Willer, K.; Gromann, L.; Auweter, S.; Hellbach, K.; Reiser, M.; Eickelberg, O.; et al. Visualization of neonatal lung injury associated with mechanical ventilation using X-ray dark-field radiography. Sci. Rep. 2016, 6, 24269. [Google Scholar] [CrossRef] [PubMed]
- Hellbach, K.; Yaroshenko, A.; Willer, K.; Pritzke, T.; Baumann, A.; Hesse, N.; Auweter, S.; Reiser, M.F.; Eickelberg, O.; Pfeiffer, F.; et al. Facilitated Diagnosis of Pneumothoraces in Newborn Mice Using X-ray Dark-Field Radiography. Invest. Radiol. 2016, 49, 597–601. [Google Scholar] [CrossRef] [PubMed]
- Noël, P.B.; Willer, K.; Fingerle, A.A.; Gromann, L.B.; Marco, F.D.; Scherer, K.H.; Herzen, J.; Achterhold, K.; Gleich, B.; Münzel, D.; et al. First experience with X-ray dark-field radiography for human chest imaging (Conference Presentation). Proc. SPIE 2017, 10132, 10132. [Google Scholar]
- Gromann, L.B.; De Marco, F.; Willer, K.; Noël, P.B.; Scherer, K.; Renger, B.; Gleich, B.; Achterhold, K.; Fingerle, A.A.; Münzel, D.; et al. In-vivo X-ray Dark-Field Chest Radiography of a Pig. Sci. Rep. 2017, 7, 4807. [Google Scholar] [CrossRef] [PubMed]
- Revol, V.; Jerjen, I.; Kottler, C.; Schütz, P.; Kaufmann, R.; Lüthi, T.; Sennhauser, U.; Straumann, U.; Urban, C. Sub-pixel porosity revealed by X-ray scatter dark field imaging. J. Appl. Phys. 2011, 110, 044912. [Google Scholar] [CrossRef]
- Revol, V.; Plank, B.; Kaufmann, R.; Kastner, J.; Kottler, C.; Neels, A. Laminate fibre structure characterisation of carbon fibre-reinforced polymers by X-ray scatter dark field imaging with a grating interferometer. NDT E Int. 2013, 58, 64–71. [Google Scholar] [CrossRef]
- Lauridsen, T.; Willner, M.; Bech, M.; Pfeiffer, F.; Feidenhans’l, R. Detection of sub-pixel fractures in X-ray dark-field tomography. Appl. Phys. A 2015, 121, 1243–1250. [Google Scholar] [CrossRef]
- Yang, F.; Prade, F.; Griffa, M.; Jerjen, I.; Bella, C.D.; Herzen, J.; Sarapata, A.; Pfeiffer, F.; Lura, P. Dark-field X-ray imaging of unsaturated water transport in porous materials. Appl. Phys. Lett. 2014, 105, 154105. [Google Scholar] [CrossRef]
- Prade, F.; Chabior, M.; Malm, F.; Grosse, C.U.; Pfeiffer, F. Observing the setting and hardening of cementitious materials by X-ray dark-field radiography. Cem. Concr. Res. 2015, 74, 19–25. [Google Scholar] [CrossRef]
- Prade, F.; Fischer, K.; Heinz, D.; Meyer, P.; Mohr, J.; Pfeiffer, F. Time resolved X-ray Dark-Field Tomography Revealing Water Transport in a Fresh Cement Sample. Sci. Rep. 2016, 6, 29108. [Google Scholar] [CrossRef] [PubMed]
- Schaff, F.; Bachmann, A.; Zens, A.; Zäh, M.F.; Pfeiffer, F.; Herzen, J. Grating-based X-ray dark-field computed tomography for the characterization of friction stir welds: A feasibility study. Mater. Charact. 2017, 129, 143–148. [Google Scholar] [CrossRef]
- Zanette, I.; Zhou, T.; Burvall, A.; Lundström, U.; Larsson, D.H.; Zdora, M.-C.; Thibault, P.; Pfeiffer, F.; Hertz, H.M. Speckle-Based X-ray Phase-Contrast and Dark-Field Imaging with a Laboratory Source. Phys. Rev. Lett. 2014, 112, 253903. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Zanette, I.; Zdora, M.-C.; Lundström, U.; Larsson, D.H.; Hertz, H.M.; Pfeiffer, F.; Burvall, A. Speckle-based X-ray phase-contrast imaging with a laboratory source and the scanning technique. Opt. Lett. 2015, 40, 2822–2825. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Kashyap, Y.; Sawhney, K. From synchrotron radiation to lab source: Advanced speckle-based X-ray imaging using abrasive paper. Sci. Rep. 2016, 6, 20476. [Google Scholar] [CrossRef] [PubMed]
- Zanette, I.; Zdora, M.-C.; Zhou, T.; Burvall, A.; Larsson, D.H.; Thibault, P.; Hertz, H.M.; Pfeiffer, F. X-ray microtomography using correlation of near-field speckles for material characterization. Proc. Natl. Acad. Sci. USA 2015, 112, 12569–12573. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Berujon, S.; Herzen, J.; Atwood, R.; Laundy, D.; Hipp, A.; Sawhney, K. X-ray phase contrast tomography by tracking near-field speckle. Sci. Rep. 2015, 5, 8762. [Google Scholar] [CrossRef] [PubMed]
- Berujon, S.; Wang, H.; Alcock, S.; Sawhney, K. At-wavelength metrology of hard X-ray mirror using near-field speckle. Opt. Express 2014, 22, 6438–6446. [Google Scholar] [CrossRef] [PubMed]
- Berujon, S.; Ziegler, E.; Cloetens, P. X-ray pulse wavefront metrology using speckle tracking. J. Synchrotron Radiat. 2015, 22, 886–894. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, Y.; Wang, H.; Sawhney, K. Two-dimensional transverse coherence measurement of hard-X-ray beams using near-field speckle. Phys. Rev. A 2015, 92, 033842. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, T.; Kashyap, Y.; Sawhney, K. Speckle-based at-wavelength metrology of X-ray optics at Diamond Light Source. Proc. SPIE 2017, 10388, 103880I. [Google Scholar]
- Dainty, J.C. (Ed.) Laser Speckle and Related Phenomena; Topics in Applied Physics; Springer: Englewood, CO, USA, 1975; Volume 9. [Google Scholar]
- Goodman, J.W. Speckle Phenomena in Optics. Theory and Application; Roberts and Company: Greenwood Village, CO, USA, 2007. [Google Scholar]
- Chellappan, K.V.; Erden, E.; Urey, H. Laser-based displays: A review. Appl. Opt. 2010, 49, F79–F98. [Google Scholar] [CrossRef] [PubMed]
- Kuratomi, Y.; Sekiya, K.; Satoh, H.; Tomiyama, T.; Kawakami, T.; Katagiri, B.; Suzuki, Y.; Uchida, T. Speckle reduction mechanism in laser rear projection displays using a small moving diffuser. J. Opt. Soc. Am. A 2010, 27, 1812–1817. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.-W.; Shih, C.-H. Speckle reduction and maintaining contrast in a LASER pico-projector using a vibrating symmetric diffuser. Opt. Express 2014, 22, 6464–6477. [Google Scholar] [CrossRef] [PubMed]
- Liba, O.; Lew, M.D.; SoRelle, E.D.; Dutta, R.; Sen, D.; Moshfeghi, D.M.; Chu, S.; de la Zerda, A. Speckle-modulating optical coherence tomography in living mice and humans. Nat. Commun. 2017, 8, 15845. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, J.M.; Xiang, S.H.; Yung, K.M. Speckle in optical coherence tomography. J. Biomed. Opt. 1999, 4, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Bates, R.H.T. Astronomical speckle imaging. Phys. Rep. 1982, 90, 203–297. [Google Scholar] [CrossRef]
- Horch, E. Speckle imaging in astronomy. Int. J. Imaging Syst. Technol. 1995, 6, 401–417. [Google Scholar] [CrossRef]
- Dainty, J.C. Stellar Speckle Interferometry. In Laser Speckle and Related Phenomena; Topics in Applied Physics; Dainty, J.C., Ed.; Springer: Englewood, CO, USA, 1975; Volume 9, Chapter 7. [Google Scholar]
- Jones, R.; Wykes, C. Holographic and Speckle Interferometry; Cambridge Studies in Modern Optics; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Høgmoen, K.; Pedersen, H.M. Measurement of small vibrations using electronic speckle pattern interferometry: Theory. J. Opt. Soc. Am. 1977, 67, 1578–1583. [Google Scholar] [CrossRef]
- Ennos, A.E. Speckle interferometry. In Laser Speckle and Related Phenomena; Topics in Applied Physics; Dainty, J.C., Ed.; Springer: Englewood, CO, USA, 1975; Volume 9, Chapter 6. [Google Scholar]
- Sharp, B. Electronic speckle pattern interferometry (ESPI). Opt. Laser Eng. 1989, 11, 241–255. [Google Scholar] [CrossRef]
- Yang, L.; Xie, X.; Zhu, L.; Wu, S.; Wang, Y. Review of electronic speckle pattern interferometry (ESPI) for three dimensional displacement measurement. Chin. J. Mech. Eng. En. 2014, 27, 1–13. [Google Scholar] [CrossRef]
- Aizu, Y.; Asakura, T. Bio-speckles. In Trends in Optics; Consortini, A., Ed.; Lasers and Optical Engineering, Academic Press: San Diego, CA, USA, 1996; Chapter 2; pp. 27–49. [Google Scholar]
- Aizu, Y.; Asakura, T. Bio-speckle phenomena and their application to the evaluation of blood flow. Opt. Laser Technol. 1991, 23, 205–219. [Google Scholar] [CrossRef]
- Fujii, H.; Asakura, T.; Nohira, K.; Shintomi, Y.; Ohura, T. Blood flow observed by time-varying laser speckle. Opt. Lett. 1985, 10, 104–106. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Pleass, C.M.; Ih, C.S. Feature information extraction from dynamic biospeckle. Appl. Opt. 1994, 33, 231–237. [Google Scholar] [CrossRef] [PubMed]
- Rabal, H.; Braga, R. (Eds.) Dynamic Laser Speckle and Applications; Optical Science and Engineering, CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Boas, D.A.; Dunn, A.K. Laser speckle contrast imaging in biomedical optics. J. Biomed. Opt. 2010, 15, 011109. [Google Scholar] [CrossRef] [PubMed]
- Mohon, N.; Rodemann, A. Laser Speckle for Determining Ametropia and Accommodation Response of the Eye. Appl. Opt. 1973, 12, 783–787. [Google Scholar] [CrossRef] [PubMed]
- Giglio, M.; Carpineti, M.; Vailati, A. Space Intensity Correlations in the Near Field of the Scattered Light: A Direct Measurement of the Density Correlation Function g(r). Phys. Rev. Lett. 2000, 85, 1416–1419. [Google Scholar] [CrossRef] [PubMed]
- Giglio, M.; Carpineti, M.; Vailati, A.; Brogioli, D. Near-field intensity correlations of scattered light. Appl. Opt. 2001, 40, 4036–4040. [Google Scholar] [CrossRef] [PubMed]
- Brogioli, D.; Vailati, A.; Giglio, M. Heterodyne near-field scattering. Appl. Phys. Lett. 2002, 81, 4109–4111. [Google Scholar] [CrossRef]
- Giglio, M.; Brogiol, D.; Potenza, M.A.C.; Vailati, A. Near field scattering. Phys. Chem. Chem. Phys. 2004, 6, 1547–1550. [Google Scholar] [CrossRef]
- Cerbino, R. Correlations of light in the deep Fresnel region: An extended Van Cittert and Zernike theorem. Phys. Rev. A 2007, 75, 053815. [Google Scholar] [CrossRef]
- Gatti, A.; Magatti, D.; Ferri, F. Three-dimensional coherence of light speckles: Theory. Phys. Rev. A 2008, 78, 063806. [Google Scholar] [CrossRef]
- Magatti, D.; Gatti, A.; Ferri, F. Three-dimensional coherence of light speckles: Experiment. Phys. Rev. A 2009, 79, 053831. [Google Scholar] [CrossRef]
- Cerbino, R.; Peverini, L.; Potenza, M.A.C.; Robert, A.; Bösecke, P.; Giglio, M. X-ray-scattering information obtained from near-field speckle. Nat. Phys. 2008, 4, 238–243. [Google Scholar] [CrossRef]
- Suzuki, Y.; Yagi, N.; Uesugi, K. X-ray refraction-enhanced imaging and a method for phase retrieval for a simple object. J. Synchrotron Radiat. 2002, 9, 160–165. [Google Scholar] [CrossRef] [PubMed]
- Kitchen, M.J.; Paganin, D.; Lewis, R.A.; Yagi, N.; Uesugi, K.; Mudie, S.T. On the origin of speckle in X-ray phase contrast images of lung tissue. Phys. Med. Biol. 2004, 49, 4335. [Google Scholar] [CrossRef] [PubMed]
- Kim, G.B.; Lee, S.J. X-ray PIV measurements of blood flows without tracer particles. Exp. Fluids 2006, 41, 195–200. [Google Scholar] [CrossRef]
- Federation of European Producers of Abrasives. FEPA P-Grit Sizes Coated Abrasives. Available online: http://www.fepa-abrasives.org/Abrasiveproducts/Grains/Pgritsizescoated.aspx (accessed on 16 February 2018).
- Aloisio, I.A.; Paganin, D.M.; Wright, C.A.; Morgan, K.S. Exploring experimental parameter choice for rapid speckle-tracking phase-contrast X-ray imaging with a paper analyzer. J. Synchrotron Radiat. 2015, 22, 1279–1288. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Kashyap, Y.; Sawhney, K. Quantitative X-ray dark-field and phase tomography using single directional speckle scanning technique. Appl. Phys. Lett. 2016, 108. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical properties of laser speckle patterns. In Laser Speckle and Related Phenomena; Topics in Applied Physics; Dainty, J.C., Ed.; Springer: Englewood, CO, USA, 1984; Volume 9, Chapter 2. [Google Scholar]
- Alexander, T.L.; Harvey, J.E.; Weeks, A.R. Average speckle size as a function of intensity threshold level: Comparison of experimental measurements with theory. Appl. Opt. 1994, 33, 8240–8250. [Google Scholar] [CrossRef] [PubMed]
- Hamed, A. Recognition of direction of new apertures from the elongated speckle images: Simulation. Opt. Photonics J. 2013, 3, 250–258. [Google Scholar] [CrossRef]
- Zdora, M.-C.; Thibault, P.; Pfeiffer, F.; Zanette, I. Simulations of X-ray speckle-based dark-field and phase-contrast imaging with a polychromatic beam. J. Appl. Phys. 2015, 118, 113105. [Google Scholar] [CrossRef]
- Zdora, M.-C.; Thibault, P.; Zhou, T.; Koch, F.J.; Romell, J.; Sala, S.; Last, A.; Rau, C.; Zanette, I. X-ray Phase-Contrast Imaging and Metrology through Unified Modulated Pattern Analysis. Phys. Rev. Lett. 2017, 118, 203903. [Google Scholar] [CrossRef] [PubMed]
- Berujon, S.; Ziegler, E. X-ray Multimodal Tomography Using Speckle-Vector Tracking. Phys. Rev. Appl. 2016, 5, 044014. [Google Scholar] [CrossRef]
- Wang, H.; Kashyap, Y.; Cai, B.; Sawhney, K. High energy X-ray phase and dark-field imaging using a random absorption mask. Sci. Rep. 2016, 6, 30581. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Kashyap, Y.; Sawhney, K. Hard-X-ray Directional Dark-Field Imaging Using the Speckle Scanning Technique. Phys. Rev. Lett. 2015, 114, 103901. [Google Scholar] [CrossRef] [PubMed]
- Zdora, M.-C.; Thibault, P.; Rau, C.; Zanette, I. Characterisation of speckle-based X-ray phase-contrast imaging. J. Phys. Conf. Ser. 2017, 849, 012024. [Google Scholar] [CrossRef]
- Berujon, S.; Wang, H.; Pape, I.; Sawhney, K. X-ray phase microscopy using the speckle tracking technique. Appl. Phys. Lett. 2013, 102, 154105. [Google Scholar] [CrossRef]
- Kottler, C.; David, C.; Pfeiffer, F.; Bunk, O. A two-directional approach for grating based differential phase contrast imaging using hard X-rays. Opt. Express 2007, 15, 1175–1181. [Google Scholar] [CrossRef] [PubMed]
- Frankot, R.T.; Chellappa, R. A method for enforcing integrability in shape from shading algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 439–451. [Google Scholar] [CrossRef]
- Harker, M.; O’Leary, P. Least squares surface reconstruction from measured gradient fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–7. [Google Scholar]
- Jiang, M.; Wyatt, C.L.; Wang, G. X-ray Phase-Contrast Imaging with Three 2D Gratings. Int. J. Biomed. Imaging 2008, 2008. [Google Scholar] [CrossRef] [PubMed]
- Zanette, I.; Weitkamp, T.; Donath, T.; Rutishauser, S.; David, C. Two-Dimensional X-ray Grating Interferometer. Phys. Rev. Lett. 2010, 105, 248102. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, Y.; Wang, H.; Sawhney, K. Experimental comparison between speckle and grating-based imaging technique using synchrotron radiation X-rays. Opt. Express 2016, 24, 18664–18673. [Google Scholar] [CrossRef] [PubMed]
- Bennett, E.E.; Kopace, R.; Stein, A.F.; Wen, H. A grating-based single-shot X-ray phase contrast and diffraction method for in vivo imaging. Med. Phys. 2010, 37, 6047–6054. [Google Scholar] [CrossRef] [PubMed]
- Wen, H.H.; Bennett, E.E.; Kopace, R.; Stein, A.F.; Pai, V. Single-shot X-ray differential phase-contrast and diffraction imaging using two-dimensional transmission gratings. Opt. Lett. 2010, 35, 1932–1934. [Google Scholar] [CrossRef] [PubMed]
- Morgan, K.S.; Paganin, D.M.; Siu, K.K.W. Quantitative X-ray phase-contrast imaging using a single grating of comparable pitch to sample feature size. Opt. Lett. 2011, 36, 55–57. [Google Scholar] [CrossRef] [PubMed]
- Morgan, K.S.; Paganin, D.M.; Siu, K.K.W. Quantitative single-exposure X-ray phase contrast imaging using a single attenuation grid. Opt. Express 2011, 19, 19781–19789. [Google Scholar] [CrossRef] [PubMed]
- Morgan, K.S.; Modregger, P.; Irvine, S.C.; Rutishauser, S.; Guzenko, V.A.; Stampanoni, M.; David, C. A sensitive X-ray phase contrast technique for rapid imaging using a single phase grid analyzer. Opt. Lett. 2013, 38, 4605–4608. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Wang, Y.; Wei, G.; Du, G.; Xue, Y.; Hu, T.; Li, K.; Deng, B.; Xie, H.; Xiao, T. Speckle-tracking X-ray phase-contrast imaging for samples with obvious edge-enhancement effect. Appl. Phys. Lett. 2017, 111, 174101. [Google Scholar] [CrossRef]
- Cloetens, P.; Guigay, J.P.; Martino, C.D.; Baruchel, J.; Schlenker, M. Fractional Talbot imaging of phase gratings with hard x rays. Opt. Lett. 1997, 22, 1059–1061. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Wang, H.; Kashyap, Y.; Laundy, D.; Sawhney, K. Two-dimensional in situ metrology of X-ray mirrors using the speckle scanning technique. J. Synchrotron Radiat. 2015, 22, 925–929. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, Y.; Wang, H.; Sawhney, K. Speckle-based at-wavelength metrology of X-ray mirrors with super accuracy. Rev. Sci. Instrum. 2016, 87, 052001. [Google Scholar] [CrossRef] [PubMed]
- Berujon, S.; Ziegler, E. Near-field speckle-scanning-based X-ray tomography. Phys. Rev. A 2017, 95, 063822. [Google Scholar] [CrossRef]
- Berujon, S.; Ziegler, E. Near-field speckle-scanning-based X-ray imaging. Phys. Rev. A 2015, 92, 013837. [Google Scholar] [CrossRef]
- Modregger, P.; Scattarella, F.; Pinzer, B.R.; David, C.; Bellotti, R.; Stampanoni, M. Imaging the Ultrasmall-Angle X-ray Scattering Distribution with Grating Interferometry. Phys. Rev. Lett. 2012, 108, 048101. [Google Scholar] [CrossRef] [PubMed]
- Modregger, P.; Rutishauser, S.; Meiser, J.; David, C.; Stampanoni, M. Two-dimensional ultra-small angle X-ray scattering with grating interferometry. Appl. Phys. Lett. 2014, 105, 024102. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745. [Google Scholar] [CrossRef]
- Richardson, W.H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Zhou, T.; Zdora, M.-C.; Zanette, I.; Romell, J.; Hertz, H.M.; Burvall, A. Noise analysis of speckle-based X-ray phase-contrast imaging. Opt. Lett. 2016, 41, 5490–5493. [Google Scholar] [CrossRef] [PubMed]
- Berujon, S. Comment on “Hard-X-ray Directional Dark-Field Imaging Using the Speckle Scanning Technique” 2015. Available online: https://doi.org/10.13140/rg.2.1.3975.9608 (accessed on 20 February 2018).
- Hemberg, O.; Otendal, M.; Hertz, H.M. Liquid-metal-jet anode electron-impact X-ray source. Appl. Phys. Lett. 2003, 83, 1483–1485. [Google Scholar] [CrossRef]
- Vittoria, F.A.; Endrizzi, M.; Olivo, A. Retrieving the Ultrasmall-Angle X-ray Scattering Signal with Polychromatic Radiation in Speckle-Tracking and Beam-Tracking Phase-Contrast Imaging. Phys. Rev. Appl. 2017, 7, 034024. [Google Scholar] [CrossRef]
- Kak, A.C.; Slaney, M. Principles of Computerized Tomographic Imaging; IEEE Press: New York, USA, 1988. [Google Scholar]
- Zanette, I.; Bech, M.; Pfeiffer, F.; Weitkamp, T. Interlaced phase stepping in phase-contrast X-ray tomography. Appl. Phys. Lett. 2011, 98, 094101. [Google Scholar] [CrossRef]
- Berujon, S.; Wang, H.; Sawhney, K.J.S. At-wavelength metrology using the X-ray speckle tracking technique: Case study of a X-ray compound refractive lens. J. Phys. Conf. Ser. 2013, 425, 052020. [Google Scholar] [CrossRef]
- Wang, H.; Berujon, S.; Sutter, J.; Alcock, S.G.; Sawhney, K. At-wavelength metrology of X-ray optics at Diamond Light Source. Proc. SPIE 2014, 9206, 9206. [Google Scholar]
- Wang, H.; Kashyap, Y.; Sawhney, K. Speckle based X-ray wavefront sensing with nanoradian angular sensitivity. Opt. Express 2015, 23, 23310–23317. [Google Scholar] [CrossRef] [PubMed]
- Zdora, M.-C.; Zanette, I.; Zhou, T.; Koch, F.J.; Romell, J.; Sala, S.; Last, A.; Ohishi, Y.; Hirao, N.; Rau, C.; et al. At-wavelength optics characterisation via X-ray speckle- and grating-based unified modulated pattern analysis. Opt. Express 2018, 26, 4989–5004. [Google Scholar] [CrossRef] [PubMed]
- Sawhney, K.; Alcock, S.; Sutter, J.; Berujon, S.; Wang, H.; Signorato, R. Characterisation of a novel super-polished bimorph mirror. J. Phys. Conf. Ser. 2013, 425, 052026. [Google Scholar] [CrossRef]
- Wang, H.; Sutter, J.; Sawhney, K. Advanced in situ metrology for X-ray beam shaping with super precision. Opt. Express 2015, 23, 1605–1614. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, Y.; Wang, H.; Sawhney, K. Development of a speckle-based portable device for in situ metrology of synchrotron X-ray mirrors. J. Synchrotron Radiat. 2016, 23, 1131–1136. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Kashyap, Y.; Zhou, T.; Sawhney, K. Speckle-based portable device for in-situ metrology of X-ray mirrors at Diamond Light Source. Proc. SPIE 2017, 10385, 1038504. [Google Scholar]
- Alaimo, M.D.; Potenza, M.A.C.; Manfredda, M.; Geloni, G.; Sztucki, M.; Narayanan, T.; Giglio, M. Probing the Transverse Coherence of an Undulator X-ray Beam Using Brownian Particles. Phys. Rev. Lett. 2009, 103, 194805. [Google Scholar] [CrossRef] [PubMed]
- Nazmov, V.; Reznikova, E.; Mohr, J.; Snigirev, A.; Snigireva, I.; Achenbach, S.; Saile, V. Fabrication and preliminary testing of X-ray lenses in thick SU-8 resist layers. Microsys. Technol. 2004, 10, 716–721. [Google Scholar] [CrossRef]
- Kim, G.B.; Lee, S.J. Contrast enhancement of speckle patterns from blood in synchrotron X-ray imaging. J. Biomech. 2009, 42, 449–454. [Google Scholar] [CrossRef] [PubMed]
- Irvine, S.C.; Paganin, D.M.; Dubsky, S.; Lewis, R.A.; Fouras, A. Phase retrieval for improved three-dimensional velocimetry of dynamic X-ray blood speckle. Appl. Phys. Lett. 2008, 93, 153901. [Google Scholar] [CrossRef]
- Park, H.; Yeom, E.; Lee, S.J. X-ray PIV measurement of blood flow in deep vessels of a rat: An in vivo feasibility study. Sci. Rep. 2016, 6, 19194. [Google Scholar] [CrossRef] [PubMed]
- Izadifar, M.; Kelly, M.E.; Peeling, L. Synchrotron speckle-based X-ray phase-contrast imaging for mapping intra-aneurysmal blood flow without contrast agent. Biomed. Phys. Eng. Express 2018, 4, 015011. [Google Scholar] [CrossRef]
- Murrie, R.P.; Morgan, K.S.; Maksimenko, A.; Fouras, A.; Paganin, D.M.; Hall, C.; Siu, K.K.W.; Parsons, D.W.; Donnelley, M. Live small-animal X-ray lung velocimetry and lung micro-tomography at the Australian Synchrotron Imaging and Medical Beamline. J. Synchrotron Radiat. 2015, 22, 1049–1055. [Google Scholar] [CrossRef] [PubMed]
- Murrie, R.P.; Paganin, D.M.; Fouras, A.; Morgan, K.S. Phase contrast X-ray velocimetry of small animal lungs: Optimising imaging rates. Biomed. Opt. Express 2016, 7, 79–92. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zdora, M.-C. State of the Art of X-ray Speckle-Based Phase-Contrast and Dark-Field Imaging. J. Imaging 2018, 4, 60. https://doi.org/10.3390/jimaging4050060
Zdora M-C. State of the Art of X-ray Speckle-Based Phase-Contrast and Dark-Field Imaging. Journal of Imaging. 2018; 4(5):60. https://doi.org/10.3390/jimaging4050060
Chicago/Turabian StyleZdora, Marie-Christine. 2018. "State of the Art of X-ray Speckle-Based Phase-Contrast and Dark-Field Imaging" Journal of Imaging 4, no. 5: 60. https://doi.org/10.3390/jimaging4050060
APA StyleZdora, M.-C. (2018). State of the Art of X-ray Speckle-Based Phase-Contrast and Dark-Field Imaging. Journal of Imaging, 4(5), 60. https://doi.org/10.3390/jimaging4050060




